Abstract
Understanding bacterial population genetics is vital for interpreting the response of bacterial populations to selection pressures such as antibiotic treatment or vaccines targeted at only a subset of strains. The evolution of transmissible bacteria occurs by mutation and localized recombination and is influenced by epidemiological as well as molecular processes. We demonstrate that the observed population genetic structure of three important human pathogens, Streptococcus pneumoniae, Neisseria meningitidis, and Staphylococcus aureus, can be explained by using a simple evolutionary model that is based on neutral mutational drift, modulated by recombination, and which incorporates the impact of epidemic transmission in local populations. The predictions of this neutral “microepidemic” model are found to closely fit observed genetic relatedness distributions of bacteria sampled from their natural population, and it provides estimates of the relative rate of recombination that agree well with empirical estimates. The analysis suggests the emergence of neutral bacterial population structure from overlapping microepidemics within clustered host populations and provides insight into the nature and size distribution of these clusters. These findings challenge the assumption that strains of bacterial pathogens differ markedly in relative fitness.
Keywords: infinite-alleles model, multilocus sequence typing, recombination
It is now accepted that bacteria do not conform to the clonal model of evolution (1). The importance of recombination has become increasingly clear in recent years, both as a fundamental process in strain diversification (2) and as a mechanism by which strains acquire virulence factors or resistance determinants (3). Homologous recombination in bacteria involves the replacement of a small segment of the bacterial chromosome (a few kilobases) with the corresponding region from another isolate (2). The frequency of these localized recombinational events may be extremely rare, resulting in species that are highly clonal [e.g., Mycobacterium species (4, 5)], or extremely frequent, resulting in species that are almost completely nonclonal [e.g., Helicobacter pylori (6)]. Consequently, theoretical approaches developed for exclusively sexual or asexual organisms are inappropriate, and, at present, there is no general theory reconciling these variable properties of bacteria. The problem is further complicated by serious sampling biases arising as a result of overrepresentation of disease isolates or antibiotic-resistant isolates in clinical strain collections (1). This problem is especially acute for some species, including Streptococcus pneumoniae, Staphylococcus aureus, and Neisseria meningitidis, which we focus on here and which are “accidental” pathogens in that healthy carriage is common, with disease a rare outcome. Finally, the host population structure will influence transmission and needs to be accounted for when considering bacterial population structure: Spread of directly transmitted bacteria within a social group is much more likely than between randomly chosen hosts from the population as a whole (7, 8).
Methods
We develop a multilocus model of bacterial evolution that incorporates varying levels of recombination (Fig. 1). To fit the predictions of the model to empirical data requires representative samples of the natural population. Here we use four samples from cross-sectional studies of carriage within a local area (9–12) in which isolates were characterized by using multilocus sequence typing (MLST), a technique in which DNA sequences are obtained for seven housekeeping loci and the different sequences at each locus are assigned as different alleles (13). The samples are described in more detail in Table 3, which is published as supporting information on the PNAS web site.
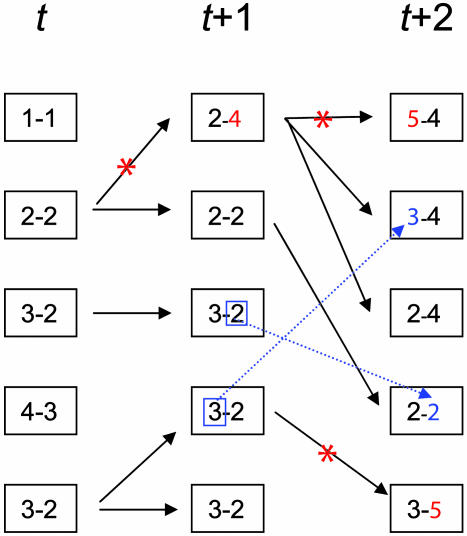
Fig. 1.
A neutral multilocus infinite alleles model of bacterial evolution. Schematic illustrating the model for a population of five individuals. The bacterial strain infecting each individual is characterized by two integers that identify the alleles at two loci. At time t, for example, there are two cases of colonization by bacteria of genotype 3-2. At each generation, each individual can infect any other (represented by black arrows). Mutations occur during the transmission step with rate m and are indicated by red asterisks: Each mutation always generates a new allele. Recombination events, occurring with rate r and illustrated by blue dotted arrows, result in an allele being inherited from a random donor. Mutations and recombination events can affect more than one allele in a single step (not shown) and are not exclusive. More generally, the model is defined for i loci in a population of size N. The model is simulated by starting from a single genotype until equilibrium levels of diversity are reached.
Results
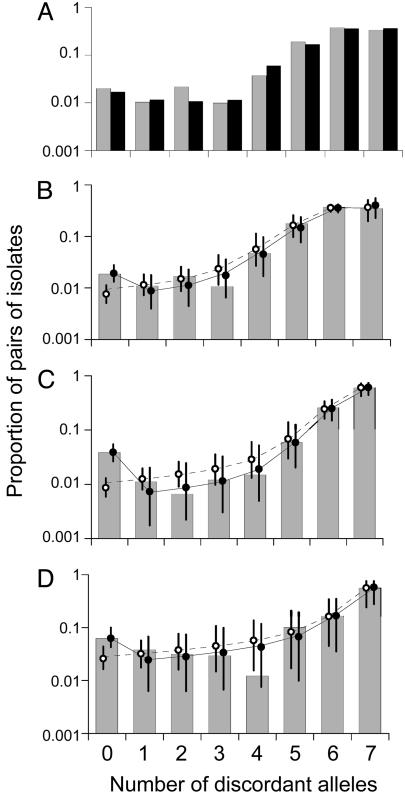
A null model for evolutionary change is the neutral infinitealleles model (IAM) (14), in which mutation and drift are the primary determinants of gene frequencies. We extend the IAM model to include variation at multiple loci and varying levels of localized recombination (Fig. 1). To compare the predictions of our evolutionary model with observed population genetic structure, we initially use the distribution of pairwise allelic mismatches: i.e., the proportion of pairs of isolates that differ at zero, one, two, or more of the seven sequenced loci (Fig. 2, filled bars). This distribution has been used previously to detect linkage between loci and to infer the degree of clonality within different species (1, 15), because the expected allelic mismatch distribution can easily be computed in the limit of complete linkage equilibrium (16). Interestingly, this distribution is remarkably similar for the two samples of S. pneumoniae from infants at different locations (Fig. 2 A), despite marked differences in the strains composing each sample [only 17% are present in both samples, and those that are have markedly different frequencies in each (Fig. 3A)]. We derive an analytical expression for this distribution in our model (see Appendix); the best fit is shown in Fig. 2 as a dotted line.
Fig. 2.
Model fit to data. The allelic mismatch distributions 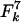 are shown as filled bars for S. pneumoniae (A and B), N. meningitidis (C), and Staphylococcus aureus (D). (A) In the case of S. pneumoniae, two samples were included (Oxford, gray bars; Tampere, Finland, black bars). (B) Weighted mean of the two samples in A. The predictions of the purely neutral model and the neutral microepidemic model are shown fitted to samples as dashed and solid lines, respectively. Maximum likelihood parameter estimates are shown in Table 1. Parameter estimates obtained by fitting to the two pneumococcal studies independently were virtually identical to the joint estimate, reflecting the strong similarity in population structure seen in A. Simulation results are also shown (open circles for the neutral IAM and solid circles for the neutral microepidemic model), along with 95% prediction intervals.
are shown as filled bars for S. pneumoniae (A and B), N. meningitidis (C), and Staphylococcus aureus (D). (A) In the case of S. pneumoniae, two samples were included (Oxford, gray bars; Tampere, Finland, black bars). (B) Weighted mean of the two samples in A. The predictions of the purely neutral model and the neutral microepidemic model are shown fitted to samples as dashed and solid lines, respectively. Maximum likelihood parameter estimates are shown in Table 1. Parameter estimates obtained by fitting to the two pneumococcal studies independently were virtually identical to the joint estimate, reflecting the strong similarity in population structure seen in A. Simulation results are also shown (open circles for the neutral IAM and solid circles for the neutral microepidemic model), along with 95% prediction intervals.
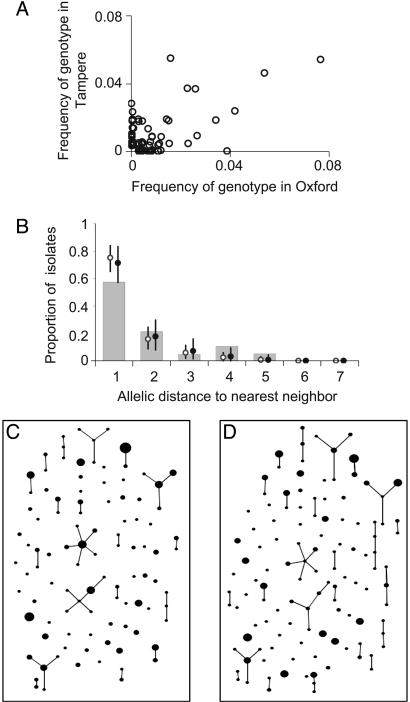
Fig. 3.
Additional tests of the model. (A) To display differences in content between the two S. pneumoniae samples, we plotted the frequency of each genotype (strain) in each sample. (B) The agreement between simulation and data from the S. pneumoniae sample in Oxford was then examined by using the nearest neighbor distribution, defined as the proportion of isolates whose distance to the most similar nonidentical isolate is k = 1... 7, shown plotted as a function of k. Results from the purely neutral model are shown as open circles, and the neutral microepidemic model results are shown as solid circles. The same distribution was plotted for the three other samples in Fig. 6. Differences in fit between the models are slight, reflecting the fact that the greatest difference is an excess of homozygosity, to which the nearest neighbor analysis is relatively insensitive. We also performed eburst analysis of the Oxford data set (C) and a single realization of the neutral microepidemic model (D) simulated by using parameters from Table 1. Each different strain is represented by a point, the size of which is the frequency of the strain. Strains differing at a single locus, which are inferred to be linked by descent, are joined by lines. A summary of the clustering inferred by eburst is shown in Table 2.
This model, which has only two parameters, namely, the rate at which new alleles enter the population θ and the rate at which they are shuffled by recombination ρ, superficially fits this distribution quite well for all three species. Simulations show, however, that the model consistently differs significantly at the leftmost bar (Fig. 2, open circles), corresponding to an underestimate of the frequency of pairs of isolates that are identical at all loci. The model also is inconsistent with other features of the data. Specifically, it overestimates the number of different strains in the sample (Table 2), does not reproduce the “nearest neighbor” distribution (Fig. 3B and Fig. 5, which is published as supporting information on the PNAS web site) and does not match the genotypic clustering as assessed by eburst (17) (Table 2 and Table 4, which is published as supporting information on the PNAS web site). The purely neutral model can therefore be rejected. The deviation from the basic model is largely due to an excess of identical pairs of isolates in the natural populations. We initially account for this excess by introducing an empirical parameter, he, equivalent to the magnitude of this deviation (see Appendix for formulas). In all four carriage samples, he is positive (Table 2) and significantly improved the fit to the data (solid lines in Fig. 2). We then explored possible mechanisms by which the excess of identical strains measured by he could be generated. The most obvious source is sampling bias (e.g., overrepresentation of isolates associated with disease or antibiotic resistance), which is unlikely because the populations studied in this work were specifically designed to minimize this type of bias by cross-sectional sampling of the natural carried population.
Table 2. Summary of eburst analysis.
| NStrains | Neburst groups | NSingletons | |
|---|---|---|---|
| S. pneumoniae (Oxford study) | 100 | 19 | 46 |
| Neutral (95% PI) | 145 (138.0-152.6) | 30.1 (22.5-37.7) | 40.3 (23.5-57.1) |
| Neutral microepidemic (95% PI) | 97 (81.4-112.6) | 18.5 (12.8-24.2) | 45.2 (34.1-56.3) |
Simulations were conducted by using the pure neutral and neutral micro-epidemic models to generate populations that were then analyzed by using eburst. The numbers of strains, clusters of related genotypes (eburst groups or clonal complexes), and genotypes that were distantly related to all others (singletons) are shown, as well as 95% prediction intervals (PI). Default settings for eburst were used (17).
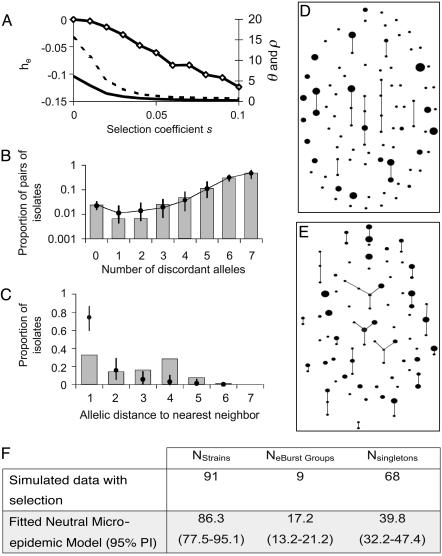
Another potential source of this excess is an inflation of the frequencies of certain strains through selective advantage. However, simulations of populations under selection result in negative estimates of the parameter he (Fig. 4A). This counterintuitive result does not indicate that selection reduces the proportion of identical pairs of isolates. Rather, selection alters the whole allelic mismatch distribution. Instead of only changing the leftmost bar, the proportions of strains that differ at multiple loci are also altered. If we naively fit a neutral (i.e., mis-specified) model to data generated with selection, these differences across the mismatch distribution lead to the best fit being a negative value of he.
Fig. 4.
Analysis of a model with hitch-hiking selection. Selection acts upon a single unobserved locus that entirely determines the fitness of a strain. Variation occurs at the same population diversification rates, θ and ρ, as the MLST-defining loci. Mutation causes the fitness of an allele to be multiplied by a log-normal random deviate of mean 1 and standard deviation s, the selection coefficient. We also tested a normal random deviate, and truncated distributions including only beneficial or harmful mutations. Results were similar in each case. (A) The allelic mismatch distribution obtained for the neutral microepidemic model is refitted to simulated populations with no clustering, produced with θ = 5.7, ρ = 17.1, and varying values of the selection coefficient. The fit remains good, but selection results in reduced estimates of θ (solid line) and ρ (dashed line) and negative values of he (diamonds). (B–F) A single sample is drawn from a simulated population with both selection and clustering, with θ = ρ = 64, N = 2,000, and s = 0.1. The sample of size n = 250 includes nc = 25 epidemic clusters of mean size 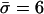 , and we attempt to refit the neutral microepidemic model to this sample produced with selection. (B) The allelic mismatch distribution fits acceptably, resulting in estimates θ = 6.4, ρ = 9.6, and he = 0.015. However, the resulting nearest neighbor distribution (C) and the eburst analyses (D, sample simulated with selection and clustering; E, sample from best-fit neutral microepidemic model; F, summary statistics) fit poorly.
, and we attempt to refit the neutral microepidemic model to this sample produced with selection. (B) The allelic mismatch distribution fits acceptably, resulting in estimates θ = 6.4, ρ = 9.6, and he = 0.015. However, the resulting nearest neighbor distribution (C) and the eburst analyses (D, sample simulated with selection and clustering; E, sample from best-fit neutral microepidemic model; F, summary statistics) fit poorly.
A further potential source of deviation from the purely neutral model is infectious transmission: Two or more isolates may be identical because they form part of the same short transmission chain, which is likely in samples taken from a local population. Such “microepidemics” have been directly observed in families, daycare centers, and villages (7, 8). We therefore simulated neutral microepidemic evolution by using maximum likelihood estimated parameters (Table 1) and incorporating a final step to simulate epidemic linkage as measured by he (see Appendix). The consistency of the simulated populations with both the results of the analytical solution and real data are remarkable (results shown as filled circles in Figs. 2 and 3). The simulated populations were also analyzed by using eburst (17), and the results are shown compared with real data in Fig. 3 C and D; summary statistics of eburst output were found to be strikingly similar to observed patterns for all three species (Tables 2 and 4).
Table 1. Parameter estimates.
| Neutral model
|
Neutral microepidemic model
|
Epidemic clusters
|
Relative recombination rate
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Species | θ | ρ | θ | ρ | he | nc | 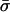 |
nrec:nmos:nmut | (r/m)pred | (r/m)obs |
| S. pneumoniae | 5.0 | 12.4 | 5.3 | 17.3 | 0.011 | 22/24 | 5.0/5.8 | 44:6:15 | 2.7 | 2.1 |
| N. meningitidis | 8.2 | 5.7 | 10.2 | 13.6 | 0.033 | 9 | 13.1 | 13:7:5 | 1.2 | 1.1 |
| Staphylococcus aureus | 4.6 | 0.37 | 5.6 | 0.98 | 0.026 | 7 | 13.6 | 2:0:19 | 0.13 | 0.11 |
θ and ρ are, respectively, the maximum likelihood population mutation and recombination rates obtained for the neutral multilocus model. The model fit is improved significantly by the introduction of the parameter he, which allows for an excess of identical pairs of isolates. nc and 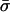 are the number and mean size of the clusters inferred from the samples (the two values for S. pneumoniae are for the Tampere, Finland, and Oxford studies, respectively). nrec, nmos and nmut are the number of pairs of isolates differing at a single locus that are classified as being the result of whole-locus recombination, mosaic recombination (i.e., recombination between a donor and recipient that occurs within the allele and produces a new mosaic allele), and point mutation by adapting the empirical method of Feil et al. (21). Patterns of descent among closely related genotypes were determined by using eburst (17) to identify ancestral and descendant alleles among strains differing at a single locus. Recombination was identified if the descendant allele was found in other lineages (eburst groups) within the sample (22). Variants differing at a single base pair were assigned as mutations; the remainder were identified as mosaic recombination. (r/m)obs is the resulting empirical estimate of the relative recombination rate, i.e., (r/m)obs = nrec/(nmos + nmut); (r/m)pred is the value predicted by our model adjusted for homozygous recombination, i.e., (r/m)pred = F′11ρ/θ.
are the number and mean size of the clusters inferred from the samples (the two values for S. pneumoniae are for the Tampere, Finland, and Oxford studies, respectively). nrec, nmos and nmut are the number of pairs of isolates differing at a single locus that are classified as being the result of whole-locus recombination, mosaic recombination (i.e., recombination between a donor and recipient that occurs within the allele and produces a new mosaic allele), and point mutation by adapting the empirical method of Feil et al. (21). Patterns of descent among closely related genotypes were determined by using eburst (17) to identify ancestral and descendant alleles among strains differing at a single locus. Recombination was identified if the descendant allele was found in other lineages (eburst groups) within the sample (22). Variants differing at a single base pair were assigned as mutations; the remainder were identified as mosaic recombination. (r/m)obs is the resulting empirical estimate of the relative recombination rate, i.e., (r/m)obs = nrec/(nmos + nmut); (r/m)pred is the value predicted by our model adjusted for homozygous recombination, i.e., (r/m)pred = F′11ρ/θ.
The final sampling step in the model effectively reconstructs a local population, consisting of a limited number of sociospatial clusters, skewed in size, taken from a purely neutral global population. This relation between local and global populations arises dynamically, provided microepidemics are indeed restricted in size (Fig. 6, which is published as supporting information on the PNAS web site). We thus predict that for an unbiased global sample, very little epidemic linkage should be observed (i.e., he ≈ 0); in the absence of such an unbiased sample, we examined the largest available sample of S. pneumoniae, the MLST database of isolates submitted from global sources (n = 1,856 at the time of study). Although these are not systematically sampled and, therefore, the results should be treated with caution, the estimate of he is very close to zero (0.002). We also predict from this model that if we were to combine different local samples from a global population, only the estimate of he would change. Analysis of the combined pneumococcal data sets supports this view, because neither θ nor ρ changes; as expected, the estimate of he is reduced (0.0087). This value is not as low as predicted by complete independence of the samples (0.0059), but we believe the question of whether this difference is caused by some epidemiological linkage between the populations, chance, or other factors can only be resolved by gathering further samples.
The principal effect of microepidemic population structure at larger scales is to reduce the effective population size to a fraction of the number of infected hosts (Fig. 6). More realistic nonlinear scaling of mean cluster size with census size would reduce the effective population size still further. The suggestion that the basic unit of transmission is in some sense larger than the individual infected host is in accordance with recent developments in theoretical epidemiology, which have redefined key parameters such as the basic reproduction number, R0, for macroepidemics in terms of transmission between closely linked clusters of individuals rather than between individuals themselves (18).
Although methods are available that estimate the bacterial recombination rate from sequence data, this remains a major computational challenge (19, 20). Our model can estimate this quantity with ease from multilocus allelic data (e.g., MLST data). To test the validity of the estimates, we calculate the ratio (ρ/θ = r/m) and compare it with empirical estimates obtained by a modification of the method of Feil et al. (21) (Table 1); these two estimates are essentially independent, because the approach of Feil et al. examines only the most recent evolutionary changes (those generating strains with differences at single loci; second bar from left in Fig. 2), whereas our estimate uses the entire mismatch distribution but gains most of its information from distantly related pairs of strains because these are far more frequent. This concordance offers further support for our underlying model, and we note that this estimate of r/m is robust to variation in he [unlike previous methods based on the index of association (1)]. The neutral microepidemic model also estimates the extent of epidemiological clustering in real data (he), which allows estimation of two new parameters: the number of clusters, nc, and their mean size, 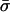 . We found quite different values for these parameters for the three species (Table 1), suggesting differences in transmission patterns. Interestingly, S. pneumoniae, which is not typically associated with outbreaks, had the lowest mean cluster size (
. We found quite different values for these parameters for the three species (Table 1), suggesting differences in transmission patterns. Interestingly, S. pneumoniae, which is not typically associated with outbreaks, had the lowest mean cluster size (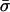 ). In contrast, N. meningitidis, which is more associated with community outbreaks, had a larger mean cluster size.
). In contrast, N. meningitidis, which is more associated with community outbreaks, had a larger mean cluster size.
It is often assumed that strains of bacterial pathogens differ markedly in fitness, and it is surprising that, after accounting for microepidemics, the observed population structures fit a neutral model. We therefore attempted to fit the neutral microepidemic model to samples generated from a simulation incorporating selection. Although the fit to the allelic mismatch distribution was acceptable (Fig. 4B), the model comprehensively failed to capture other features of these populations (Fig. 4 C–F). Thus, if selection had played a major role in structuring the bacterial populations we examined, we would have expected a poor fit to these metrics. Preliminary analyses of a diverse range of scenarios, including direct selection, balancing selection, population subdivision, hypermutation, and hyperrecombination, all failed to generate results consistent with the data. We cannot, however, exclude the possibility that much more complex models could fit the data as well as, or better than, that which we propose here. Nonetheless, we are struck by the success of this simple model, although we recognize the need to further test it against such alternative hypotheses.
Discussion
We have developed a model of bacterial evolution and tested it with samples from three different species. This model is defined by only three parameters: the population mutation and recombination rates and the degree of epidemic linkage in the sample. The model successfully captures the observed structure, measured by using multiple metrics, of the four samples studied (Figs. 2, 3, and 6 and Tables 2 and 4). The flexibility of our model and the ease of computing the key parameters should make it ideal for further exploring the effect of different epidemic scenarios on the population genetics of a species and for realistic parameterized simulations of evolutionary scenarios. We have also shown that differences in transmission patterns may be detected by using this approach.
A key finding is that given the well known phenomenon of microepidemics within host clusters, the population structure of the three pathogens studied is consistent with neutral drift. The poor fit of samples generated under selection to the model support our view that the imprint of selection is not present in our four population samples, although it would be interesting to explore our ability to detect selection by using samples where selection should be present, such as those exposed to a new vaccine or antibiotic. These findings challenge us to either identify the signature of selection by other means or to accept that the common assumption that directly transmitted pathogens must be subject to strong selection is not supported by the data. This latter conclusion has implications for modeling and public health.
Supplementary Material
Acknowledgments
We dedicate this work to the memory of John Maynard Smith. We thank Ed Feil and Roy Anderson for useful comments. This work was funded in part by The Medical Research Council (C.F.), The Wellcome Trust (W.P.H. and B.G.S.), and the Royal Society (C.F.).
Appendix
Analytic Expression for the Allelic Mismatch Distribution. Consider the neutral multilocus IAM with recombination, described in Fig. 1, and define the allelic mismatch distribution 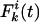 as the probability that any two isolates differ at k of i studied loci at time t. The aim is to obtain equilibrium expressions by considering first the changes that occur during a single generation. For a single locus, the distribution is unaffected by recombination, and thus the classic result of Kimura (14),
as the probability that any two isolates differ at k of i studied loci at time t. The aim is to obtain equilibrium expressions by considering first the changes that occur during a single generation. For a single locus, the distribution is unaffected by recombination, and thus the classic result of Kimura (14), 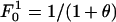 , holds, where m is the per locus mutation rate, N is the population size, and θ = 2mN. For more loci, consider first the probability
, holds, where m is the per locus mutation rate, N is the population size, and θ = 2mN. For more loci, consider first the probability 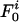 that a pair of isolates is identical at all loci. We study the model in the limit where it is vanishingly unlikely that two or more events could occur simultaneously, although, in fact, the result can be shown numerically to be valid even away from this limit. In a generation, there are three events that could affect this: the isolates could be from an identical progenitor (with probability 1/N), in which case they are always identical; one of the isolates could mutate (with total probability 2im), in which case they will fail to be identical; or they could recombine (with total probability 2ir), where r is the per locus recombination rate. The effect of recombination is to separate the inheritance at the recombinant locus from the others, thus reducing the pair comparison to that between the recombinant locus and the i – 1 others. In summary, the change is
that a pair of isolates is identical at all loci. We study the model in the limit where it is vanishingly unlikely that two or more events could occur simultaneously, although, in fact, the result can be shown numerically to be valid even away from this limit. In a generation, there are three events that could affect this: the isolates could be from an identical progenitor (with probability 1/N), in which case they are always identical; one of the isolates could mutate (with total probability 2im), in which case they will fail to be identical; or they could recombine (with total probability 2ir), where r is the per locus recombination rate. The effect of recombination is to separate the inheritance at the recombinant locus from the others, thus reducing the pair comparison to that between the recombinant locus and the i – 1 others. In summary, the change is
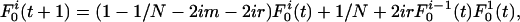 |
[1] |
which results in the equilibrium expression
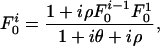 |
[2] |
where we have defined the population recombination rate ρ = 2rN by analogy with θ. For the more general expression 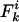 , where k > 0, note that the mismatch will increase to
, where k > 0, note that the mismatch will increase to 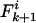 if a mutation occurs at any of the i – k identical loci, but it can be reached from
if a mutation occurs at any of the i – k identical loci, but it can be reached from 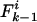 if mutation occurs at any of the i – k + 1 identical loci. In the case of recombination, the possibility that the recombinant locus may be either concordant or discordant must be accounted for. The change in a single generation is thus
if mutation occurs at any of the i – k + 1 identical loci. In the case of recombination, the possibility that the recombinant locus may be either concordant or discordant must be accounted for. The change in a single generation is thus
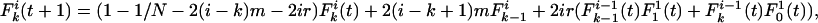 |
[3] |
which results in the equilibrium expression
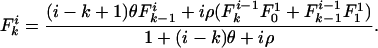 |
[4] |
Fitting the Model. The model was fitted by maximizing the multinomial log-likelihood with respect to the parameters θ and ρ, which is given by
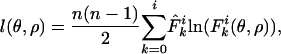 |
[5] |
where n is the sample size, 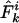 is the observed allelic mismatch distribution, and additive constants have been ignored.
is the observed allelic mismatch distribution, and additive constants have been ignored.
Modified Allelic Mismatch Distribution. A modified allelic mismatch distribution 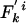 is introduced to allow for an excess of identical pairs of isolates by introducing the empirical h e parameter as follows:
is introduced to allow for an excess of identical pairs of isolates by introducing the empirical h e parameter as follows: 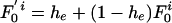 and
and 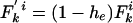 for k > 0. The pure IAM model is recovered by setting he = 0. The likelihood remains as defined above but is now maximized with respect to the three parameters θ, ρ, and he. Improvement in fit was assessed by the likelihood ratio test, allowing for the extra parameter. Because the multinomial likelihood (Eq. 5) overestimates the degrees of freedom in the data, we used the conservative replacement of n(n – 1)/2 by n in Eq. 5. P values for the improved fit were 0.03 for Fig. 2B, <0.001 for Fig. 2C, and <0.01 for Fig. 2D.
for k > 0. The pure IAM model is recovered by setting he = 0. The likelihood remains as defined above but is now maximized with respect to the three parameters θ, ρ, and he. Improvement in fit was assessed by the likelihood ratio test, allowing for the extra parameter. Because the multinomial likelihood (Eq. 5) overestimates the degrees of freedom in the data, we used the conservative replacement of n(n – 1)/2 by n in Eq. 5. P values for the improved fit were 0.03 for Fig. 2B, <0.001 for Fig. 2C, and <0.01 for Fig. 2D.
Simulation of Epidemic Linkage in a Local Sample. Initially, we construct a truly neutral global sample. To constitute a locally clustered sample of size n, we took nc samples from the global population in which a single isolate was included σ times (drawn from a Poisson distribution with mean 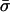 ), and we completed the sample by taking randomly drawn isolates, included once. This skewed sampling process creates an excess of identical pairs relative to the underlying neutral population. The best fit values of the parameters nc and
), and we completed the sample by taking randomly drawn isolates, included once. This skewed sampling process creates an excess of identical pairs relative to the underlying neutral population. The best fit values of the parameters nc and 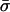 are determined by matching to the number of distinct strains recorded in the sample, subject to the constraint that
are determined by matching to the number of distinct strains recorded in the sample, subject to the constraint that 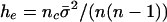 , where the metaparameter he is determined by fitting the analytical formula to the allelic mismatch distribution. The formula he can be derived as follows. First, consider a cluster of size σ. This results in an extra σ(σ – 1)/2 identical pairs of isolates. The expected increase in identical pairs of isolates per cluster is
, where the metaparameter he is determined by fitting the analytical formula to the allelic mismatch distribution. The formula he can be derived as follows. First, consider a cluster of size σ. This results in an extra σ(σ – 1)/2 identical pairs of isolates. The expected increase in identical pairs of isolates per cluster is 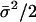 , and there are nc such clusters. Thus, the proportionate increase in the number of identical pairs of the total
, and there are nc such clusters. Thus, the proportionate increase in the number of identical pairs of the total 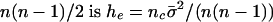 .
.
Author contributions: C.F., W.P.H., and B.G.S. designed research; C.F. and W.P.H. performed research; C.F. and W.P.H. analyzed data; and C.F., W.P.H., and B.G.S. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: IAM, infinite-alleles model; MLST, multilocus sequence typing.
References
- 1.Maynard Smith, J., Smith, N. H., O'Rourke, M. & Spratt, B. G. (1993) Proc. Natl. Acad. Sci. USA 90, 4384–4388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Spratt, B. G., Hanage, W. P. & Feil, E. J. (2001) Curr. Opin. Microbiol. 4, 602–606. [DOI] [PubMed] [Google Scholar]
- 3.Ochman, H., Lawrence, J. G. & Groisman, E. A. (2000) Nature 405, 299–304. [DOI] [PubMed] [Google Scholar]
- 4.Supply, P., Warren, R. M., Banuls, A. L., Lesjean, S., Van Der Spuy, G. D., Lewis, L. A., Tibayrenc, M., Van Helden, P. D. & Locht, C. (2003) Mol. Microbiol. 47, 529–538. [DOI] [PubMed] [Google Scholar]
- 5.Smith, N. H., Dale, J., Inwald, J., Palmer, S., Gordon, S. V., Hewinson, R. G. & Smith, J. M. (2003) Proc. Natl. Acad. Sci. USA 100, 15271–15275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Falush, D., Kraft, C., Taylor, N. S., Correa, P., Fox, J. G., Achtman, M. & Suerbaum, S. (2001) Proc. Natl. Acad. Sci. USA 98, 15056–15061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Leino, T., Auranen, K., Jokinen, J., Leinonen, M., Tervonen, P. & Takala, A. K. (2001) Pediatr. Infect. Dis. J. 20, 1022–1027. [DOI] [PubMed] [Google Scholar]
- 8.Hope Simpson, R. E. (1952) Lancet, 260, 549–554. [DOI] [PubMed] [Google Scholar]
- 9.Jolley, K. A., Kalmusova, J., Feil, E. J., Gupta, S., Musilek, M., Kriz, P. & Maiden, M. C. (2000) J. Clin. Microbiol. 38, 4492–4498, and correction (2002) 40 3549–3550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hanage, W. P., Auranen, K., Syrjanen, R., Herva, E., Makela, P. H., Kilpi, T. & Spratt, B. G. (2004) Infect. Immun. 72, 76–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Day, N. P., Moore, C. E., Enright, M. C., Berendt, A. R., Smith, J. M., Murphy, M. F., Peacock, S. J., Spratt, B. G. & Feil, E. J. (2001) Science 292, 114–116, and retraction (2002) 295, 971. [DOI] [PubMed] [Google Scholar]
- 12.Meats, E., Brueggemann, A. B., Enright, M. C., Sleeman, K., Griffiths, D. T., Crook, D. W. & Spratt, B. G. (2003) J. Clin. Microbiol. 41, 386–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Maiden, M. C., Bygraves, J. A., Feil, E., Morelli, G., Russell, J. E., Urwin, R., Zhang, Q., Zhou, J., Zurth, K., Caugant, D. A., et al. (1998) Proc. Natl. Acad. Sci. USA 95, 3140–3145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kimura, M. (1968) Nature 217, 624–626. [DOI] [PubMed] [Google Scholar]
- 15.Whittam, T. S., Ochman, H. & Selander, R. K. (1983) Proc. Natl. Acad. Sci. USA, 80, 1751–1755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brown, A. H. D., Feldman, M. W. & Nevo, E. (1980) Genetics, 96, 523–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Feil, E. J., Li, B. C., Aanensen, D. M., Hanage, W. P. & Spratt, B. G. (2004) J. Bacteriol. 186, 1518–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ball, F. & Neal, P. (2002) Math. Biosci. 180, 73–102. [DOI] [PubMed] [Google Scholar]
- 19.Stumpf, M. P. & McVean, G. A. (2003) Nat. Rev. Genet. 4, 959–968. [DOI] [PubMed] [Google Scholar]
- 20.McVean, G., Awadalla, P. & Fearnhead, P. (2002) Genetics 160, 1231–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Feil, E. J., Maiden, M. C., Achtman, M. & Spratt, B. G. (1999) Mol. Biol. Evol. 16, 1496–1502. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.