Demographic dynamics and kinship in anthropological populations

Abstract

Changes in fertility and mortality affect the size of surviving sibling sets and thus numbers of surviving kin. Because the genealogical generations specifying kinship relations are not temporal cohorts and most plausible demographic changes in anthropological populations are period shocks, the effect of such shocks on kin counts are complex. Shocks increasing fertility or decreasing mortality produce larger numbers of kin per ego and decrease the inequality of the distribution of kin and vice versa. Effects are more diffuse at more distant collateral ranges. Effects are stronger the more intense the shock and the longer its duration. Kinship distributions return to their initial state after the shock and as the original age structure of the population is ergodically reattained. Alternating shocks produce more complex patterns. Implications of these outcomes are that opportunities for political networking and consolidation by means of kinship are altered by demographic instabilities, as are the dynamics of kin selection. This analysis is limited for simplicity to unilineal agnatic reckoning of kin.

Most work on the demography of kinship has concentrated on the nuclear family, lineal consanguineals, and household structure and has been informed by stable population theory. This article focuses on demographic instability, collateral kin, inferences for political life, and kin selection and implicitly on “anthropological societies.” Anthropological societies are small and structured by “status” rather than “contract” (1). Kinship is the most important component of organization in such societies, within which most of the history of the genus Homo has been played out. Kinship is also an important component of political and economic activity in other societies, especially among elites or ethnic subgroups (see, for example, ref. 2; see also refs. 3–12). The moral imperatives governing relations between kin of different categories and the role of kinship as the foundation of social structure are explicated especially in the work of Radcliffe-Brown and Forde (13), Evans-Pritchard (14), Fortes (15, 16), E. N. Goody (5), and J. Goody (6, 7). Because males are usually the publicly predominant political actors in anthropological societies, this analysis focuses on the male siblings and agnatic cousins of adult males. (Agnatic kinship is kinship through males only. Analysis of kinship networks of and through females would mirror those presented here. Modeling using both sexes as links would differ in level, because the joint probability of having neither a male nor a female link would be less than that of not having only one of these. However, overall patterns should remain similar.)

Some of the implications of the present research may also be applicable to the social organization of other animals insofar as kinship is a component of hierarchy or coalition formation.

Relative advantage in numbers of kin between political actors is conjectured here to have an important influence on coalition formation and relative political power, all else being equal. Additionally, power tends to accrete, and political actors profit from it in two ways. It enhances their survivability, i.e., inclusive fitness and ability to perpetuate themselves as either genetic bundles or social actors. It permits human actors to manipulate cultural institutions to maintain or increase their own relative power. The numbers of kin per ego and the relative inequality of the kin distribution are responsive to demographic fluctuations. Kin increase and inequality is decreased with population growth and vice versa. Such fluctuations, which must have been the rule in small groups over most of human and precursor history, provided a varied and shifting environment within which behavioral and institutional selection from diversity might have occurred and under which there would have been incentives to the innovation of new forms that might benefit their inventors.

The ethnographic literature is replete with examples of kinship as social foundation. The historical or ethnohistorical literature also provides examples of kinship innovation and manipulation for political purposes [see, for example, Hammel (17) on ritual sponsorship as an alternative social structure complementing consanguinity and affinity, Parkes (8–10) on contractual extensions of kinship through fosterage and surrogate nursing used for political effect in Europe and the Near East, Mintz and Wolf (18) on church control of ritual sponsorship to improve the probability of donations, and Goody (19) on how restrictions on cousin marriage and other aspects of domestic life were imposed with the same intent]. The church and the nobility are good examples of powerful political actors struggling against each other by the manipulation of kinship and inheritance norms.

There is substantial literature on the relationships between population processes and the social units in which individuals are located (20–28). However, there has been little attention to siblings or wider collaterals. In the historical demographic literature, most analyses have focused on nuclear and stem families, with emphasis on lineal descendants and heirship (29–37), with broader coverage in some instances (e.g., ref. 38). The supply of kin has been related to the rate of population growth (39–43). The effects of major changes in stable regimes have been explored, usually by using historical rates, through microsimulation (38, 44–46), with some cross-validation between kinship microsimulation results and census data (47). Such work has concentrated on kin within the nuclear family and sometimes grandparents and grandchildren.

Different demographic regimes produce different numbers of individuals at genealogical loci, and insofar as kinship systems rely on genealogical networks, the density and functioning of kinship networks will be affected accordingly. These effects may be most important in anthropological populations because of their small size, the fact that their simpler technological levels afford less buffering from exogenous influences, because of the predominance of status-based (rather than contractual) social relations, or all of the above. Because the span of living kin for living social actors is usually wider than it is deep, this analysis concentrates on collaterals.

Methods

Six demographic scenarios are explored as prototypical examples (Table 1). The socsim microsimulation program (32, 33) was run 100 times for each of the scenarios. Each run began with the same starting population of 5,000 persons but a different starting random number. Each run lasted 1,000 years in addition to the 100 years of experience embedded in the starting population. A population and kinship census was taken every 25 years in each run, starting at year 500. Fertility was heterogeneous, in addition to purely random differences, but not heritable. Frailty was not heterogeneous or heritable. Marriage between agnates was prohibited. There were no feedbacks from kinship density to demographic processes. Table 2 shows approximate demographic parameters from the simulation outputs and illuminates the specifications in the following paragraphs.

Table 1. Nature of the experiments.

	Years
Scenario	0-499	500-524	525-549	550-574	575-599	600-624	625-649	651-1000
Stationarity	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat
Increased fertility	w7.stat	w7.++	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat
Decreased fertility	w7.stat	w7.--	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat
Alternating fertility	w7.stat	w7.++	w7.--	w7.++	w7.--	w7.++	w7.--	repeat...
Increased mortality	w7.stat	w1.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat
Decreased mortality	w7.stat	w19.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat	w7.stat

See Methods for definitions.

Table 2. Approximate demographic parameters.

Mortality	Fertility	eof	TFR	NRR	r
w7	w7.stat	37	3.94	1.06	0.00186
w7	w7.++	37	7.87	2.11	0.02572
w7	w7.--	37	1.96	0.49	-0.02447
w1	w7.stat	20	3.94	0.57	-0.01945
w19	w7.stat	65	3.94	1.92	0.01824

Definitions: the mortality schedule is Coale-Demeny Model West at the indicated level, fertility is that of the scenario indicated in Table 1, e_of is the expectation of life at birth for females, TFR is the total fertility rate or the number of children a woman would expect to have if she lived to age 50 years, NRR is the net reproduction ratio or the number of daughters a woman would expect to have surviving to reproduce, hence the ratio between generations, and r is the annual rate of population growth assuming a mean age of child bearing of 29 years, hence the length of a generation. The fertility and growth calculations are only approximate because they do not reflect the birth-spacing and marital-status specifications in the simulations.

Monthly mortality rates were calculated from the Coale–Demeny model life tables (48). Model west level 7 (w7) was used as the base (Table 1). Fertility was first tuned by using socsim to achieve approximate stationarity at w7 mortality with the shape of age-specific fertility modeled on Hutterite rates. (Reproduction begins early and ends late, with no parity-specific diminution.) The resulting population was used as the starting population in all experiments. In Table 1, “w7.stat” means that in the period indicated, mortality was w7, with stationary fertility rates. Scenario “Stationarity” maintains that combination over the entire 1,000 years; it serves as a baseline.

Scenario “Increased fertility” starts in the same way but at year 500 shifts to a fertility schedule double that of w7.stat (w7.+ +) for 25 years. Scenario “Decreased fertility” does the opposite, shifting to a schedule that is approximately half that of w7.stat (w7.- -). (Milder scenarios were tested also, e.g., w7.+ and w7.-; they have detectable but milder results and are not shown. Similarly, scenarios were tested with briefer shock periods, e.g., 5 or 10 instead of 25 years. They also show detectable but milder results and are not shown.)

Scenario “Alternating fertility” combines these two approaches, with nine paired alternations of w7.+ + and w7.- -, with a final positive shock at year 950, then returning to stationarity. These shocks subject the simulated populations to alternations in period fertility.

Scenario “Increased mortality” begins in the same way but at year 500 shifts for 25 years to level 1 mortality (w1), maintaining the same fertility rates. Scenario “Decreased mortality” does the opposite, shifting to level 19 mortality (w19) while maintaining the same fertility rates.

After the shocks, mortality and fertility rates returned to those of the first 500 years.

In the censuses of qualifying egos and their kin, only males aged 15–60 years, thus presumably significant political actors, were counted. Brothers, patrilateral first cousins, and patrilateral second cousins were the kin counted. In traditional notation (B = brother, F = father, and S = son), these kin are B, FBS, and FFBSS. (In the computer code, these kin are traced purely agnatically as FS, FFSS, and FFFSSS.)

Results

1. Under stationary conditions, as expected, there are no significant changes in kinship patterns. This is the baseline.

2. If a single shock is applied, there is a single response in kinship patterns and then a return to the pattern of stationarity. The amplitude and duration of the response depend on the intensity and duration of the shock. Shocks that increase the growth rate result in increased numbers of kin and decreased inequality and vice versa. Effects are stronger with longer and stronger shocks and vice versa.

3. If alternating fertility shocks are applied, the initial response is similar to that to a single shock, but over time this response is modified by the subsequent alternating shocks. Eventually the kinship patterns and the inequality of distribution achieve a resonance between the fertility shocks and the periodicity of changes in age structure and settle into a pattern of alternation.

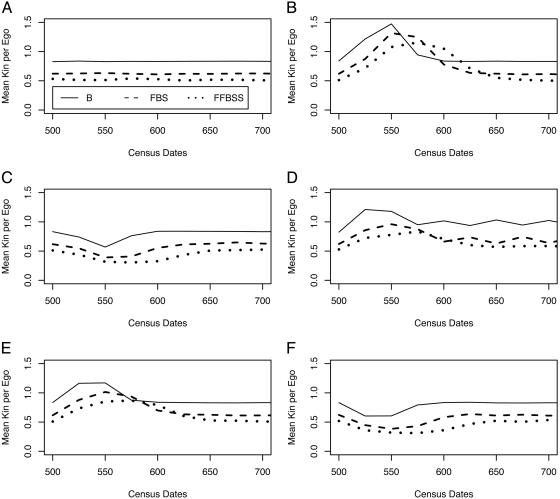
Fig. 1 shows the effects on mean kin per ego. The abscissa is truncated at year 725 for graphical convenience; the patterns in force at that point simply continue. The means are steady under stationarity (with some random variation). They increase with fertility increase or mortality decrease, peaking ≈25 years after termination of the 25-year shock, then fall back ≈75 years after termination of the shock. The reverse holds for mortality increase and fertility decrease. Under alternation, there is an initial surge (because the first shock is positive); then a fluctuating pattern sets in. The magnitude of effects weakens as collaterality increases, and the peak and duration of effect are delayed also. These differences appear because the probability of not having an intervening kin node increases with collaterality and the probability of not having kin within the census age range also increases with collaterality as the age range of living kin becomes more diffuse.

Fig. 1.

Mean kin under each scenario by scenario. Shown are mean kin per ego under stationarity (A), with fertility increase (B), with fertility decrease (C), with fertility alternation (D), with mortality decrease (E), and with mortality increase (F).

Inequality between individuals (aggregated across all runs) is affected also. (The variances in this exercise have two components: that between runs and that between individuals within a run. The former is ignored in this exercise and treated as noise. The differences between individuals would appear more sharply if interrun variation were controlled; thus, the conclusions of the analysis are conservative.) Lorentz curves for each of the three kin types under each scenario at each census show the following patterns: Under stationarity, there are, as expected, only minor, random shifts between each census for a particular kin type. The degree of inequality in the distribution of kin increases with collaterality and is driven largely by the proportion of egos who have no kin. Approximately half have no B, two-thirds have no FBS, and three-fourths have no FFBSS. Under conditions that increase population growth, inequality decreases, driven largely by a reduction in the proportion of egos who have no kin of each type. Inequality increases with collaterality. Under conditions that decrease population growth, inequality is increased, driven by an increasing proportion of egos with no kin. Inequality again increases with collaterality. Under the alternation scenario, these characteristics oscillate with the alternating shocks. Table 3 summarizes a key feature of the Lorentz curves by showing the proportion of the population with zero kin at the maximum divergence in each scenario from the stationary baseline and the census in which that point is reached. The mean abscissal value at which the ordinal value is first greater than zero is given for the stationarity scenario. This is the baseline point from which other scenarios are evaluated. Under fertility increase and mortality decrease, this point shifts left, resulting in less inequality (the maximum shift is shown as “Left point”). Under fertility decrease and mortality increase, this point shifts right, resulting in more inequality (“Right point”). Under the alternation scenario, the point shifts back and forth, and both limits are shown in Table 3.

Table 3. Nonzero abscissal limits for Lorentz curves.

Scenario	Kin type	Census	Left point	Right point
	B	Mean	0.48	0.48
Stationary	FBS	Mean	0.67	0.67
	FFBSS	Mean	0.76	0.76
	B	3	0.33
Fertility increase	FBS	4	0.53
	FFBSS	5	0.63
	B	3		0.60
Fertility decrease	FBS	4		0.77
	FFBSS	4		0.84
	B	21,1	0.36	0.49
Fertility alternation	FBS	3,11	0.59	0.68
	FFBSS	4,19	0.68	0.76
	B	2	0.37
Mortality decrease	FBS	3	0.58
	FFBSS	4	0.67
	B	3		0.58
Mortality increase	FBS	3		0.76
	FFBSS	4		0.84

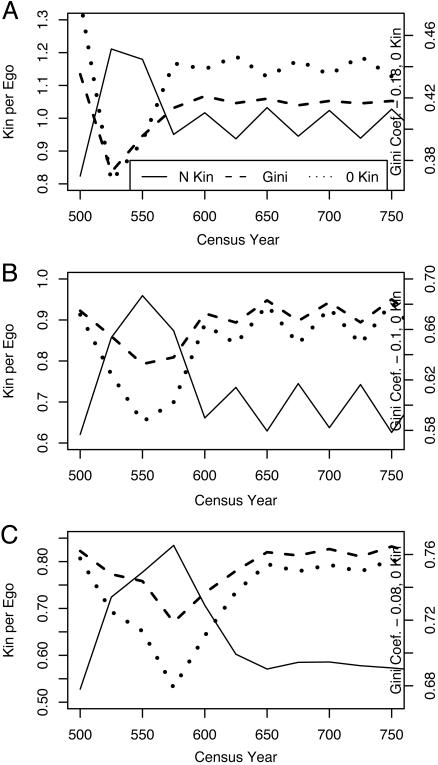
Fig. 2 summarizes these results by giving the alternation results for the three kin types and showing the proportion of egos with no kin and the Gini coefficient of the kin distribution per ego. (The abscissa is again truncated. The Gini coefficients and the proportion with no kin are rescaled in some plots for graphical convenience; see the legend for the right ordinate. Note that, to maximize resolution, the right ordinates are not uniform across the subplots.) The results for all other scenarios can be deduced from these figures for alternation. Under stationarity, mean numbers of kin per ego, the proportion with no kin, and the Gini coefficients change only randomly over time. For all three kin types, the initial positive shock of the alternation scenario raises the mean number of kin, depresses the proportion with no kin, and depresses inequality. These same effects hold for the scenarios of fertility increase and mortality decrease. Those effects are inverted for the scenarios of fertility decrease and mortality increase. In all nonalternating scenarios, responses return to the pattern of stationarity around year 600. It can be shown that the Gini coefficient is driven largely by the change in the proportion of egos with no kin.

Fig. 2.

Inequality with alternation. Shown are kin per ego (Gini coefficients) for brothers with fertility alternation (A), FBS with fertility alternation (B), and FFBSS with fertility alternation (C).

Under alternation, the results are complex because of the interaction of the fertility alternations with the waves set up in the age structure. The first positive increase in fertility sets up a wave of increased population 25 years long. The following negative fertility change applies to the enlarged population, producing a population reduction that is less than would have occurred with the same negative shock to the stationary population. These countervailing forces damp the oscillation. The results for kinship counts become more diffuse with increasing collaterality, and the countervailing influences are sometimes in phase and sometimes not.

For brothers (Fig. 2 A), the peak of mean kin per ego is found in year 525, after 25 years of the shock. Under the influence of the reverse shock, the mean descends slightly at year 550 and then more steeply at year 575 because of the interaction of the fertility changes with the age structure. The proportion with zero kin alternates out of phase with the mean of kin. The Gini coefficient does not reach its extreme until year 600. Beginning at year 575 for the mean and proportion with zero kin and year 600 for the Gini coefficient, regular alternation sets in, but the peaks of the latter are now in phase with the mean of kin because of the lag in the response of the Gini coefficient that appeared after year 550.

The pattern is different for FBS (Fig. 2B), and the extreme values of the mean of kin, proportion with zero kin, and the Gini coefficient are not reached until year 550 rather than 525, as for brothers. After year 600, the patterns for all three conform to the expectations generated by the single-shock scenarios. The mean level of kin and the Gini coefficient are out of phase.

Fig. 2C shows that the peak of the mean number of FFBSS does not occur until year 575 and that the low point for the Gini coefficient is reached at the same time. By year 650, the mean level of kin has descended to a plateau that shows irregular and miniscule alternation, invisible at the scale of this graph; the Gini coefficient and proportion with zero kin show visible alternation, in phase with each other but not regularly related to the mean of kin, beginning approximately at year 650.

Discussion

Many of the outcomes shown are entirely expectable. If the population is driven upward, the number of kin increases and vice versa. Changes in the number of kin per ego lag the shock with increasing collaterality and are also more diffuse. The number of kin per ego under a given scenario is less with increasing collaterality. The lags, diffuseness, and diminution with increasing collaterality may be attributed to the fact that generations are not cohorts, and the period shocks affect individuals in different generations for differing periods of time. For example, if the span of child bearing for women is 30 years, uterine siblings can differ in age by 30 years, first cousins in the female line by 60 years, and second cousins by 90 years. If reckoned agnatically for a child-fathering span of 50 years (15–65), these differences are 50, 100, and 150 years. This is especially true for fertility shocks, because the reproductive span is briefer than the lifespan. The diminution effect with increasing collaterality is the result of the increased probability of failure to complete a genealogical path when several generations are crossed. When the scenario is one of fertility alternation, the picture is more complex and especially interesting, because the alternations for numbers of brothers and first cousins (FBS) are inversely correlated. A surfeit of one occurs with a deficit of the other. As Figs. 1 and 2 show, the timing of the effects differs for the three kin types. The degree to which these phenomena occur is surely affected by the duration of the fertility shock and resonances with waves in the age structure. In the world of real populations, alternations might have been partly cyclical but are often quite irregular. The initial effects would have been similar to those of single shocks.

The most intriguing results have to do less with mean numbers of kin than with inequalities in their distribution. If kin simply increase, we may conclude that a rising tide lifts all boats. If there is a shift in inequality, we must consider the mechanics and implications of those shifts for social and political life, the development of institutions, and the inclusive fitness of sets of kin. The data show that when shocks are simple, the primary effect is to alter the number of persons who have no kin at all of a particular type. A positive shock to the population creates more kin on average but does so principally by reducing the number of persons with no kin. Thus, a rising tide lifts some boats more than others and decreases the intrinsic inequality seen at the stationary baseline. Conversely, a negative shock has its primary effect in increasing the number of egos with no kin at all, lowering some boats more than others, and increasing the intrinsic inequality.

Despite the apparent simplicity of this outcome, there is a complication in the scenario of fertility alternation. When the collateral span is narrow and only two generations are in the genealogical path (i.e., FS = B), the effect of alternation in the cross section is to coordinate the peaks of mean numbers of kin per ego with the peaks of inequality rather than to coordinate the peak of one with the trough of the other. This effect is not because the underlying relationship has changed but because population momentum has shifted the distribution in time. This shifting would change if the duration of the shock were altered and were not so close to the mean duration of child bearing. Other experiments testing for this kind of resonance would have to be carried out to describe the processes more exactly, especially if shocks were of random occurrence and duration.

Although these experiments were designed to examine unstable regimes, we may surmise that stable regimes with high growth rates would manifest higher numbers of kin per ego and lower levels of interego inequality (because there would be proportionally fewer egos with no kin at all) and vice versa. This surmise could be verified by using known analytic procedures (39, 40). Similarly, it would be possible to interpolate between and extend beyond the target points of the current exercise by using analytic techniques. Other extensions of the work could involve feedbacks, in which, for example, numbers of kin per ego affected demographic outcomes by the use of ego-specific multipliers that would modify the base rates of fertility, mortality, and chances on the marriage market.

Conclusions

The breeding populations of Homo sapiens over most of their history have been small and relatively unbuffered from exogenous shocks with demographic outcomes. In that respect they are similar to many other animal populations. Even as larger aggregates of human beings developed after 10,000 years ago, the effective size of breeding populations was probably not large. Within these breeding populations, from the earliest times to the present, kinship connections remained important in social, economic, and political life.

These kinship connections are affected by current and past demographic conditions. Especially in the prototypical hunter-gatherer populations and their animal analogs, demographic instability would have been the rule, centered in the long run slightly on the positive side of stationarity for surviving populations. Short-term departures from the long run, either through changes in fertility or mortality or both, affected population size and the density of kin networks. Demographic shocks would alter the social landscape, changing the distribution of social assets. Under negative shocks or stably low growth rates, some egos would be relatively much better off than the rest, whereas under positive shocks, such inequality would be less. In times of demographic stress (or stably low growth rates), those with more assets may consolidate their power more easily and achieve dominance that may improve their well-being and survival. They may acquire the power to develop or alter social institutions that would consolidate and perpetuate that power. Conversely, in times of demographic abundance, those with more assets, although still dominant, would be relatively less dominant. Under a scenario of alternation, which we surmise must have been, on average, the situation for much of human history, opportunities for dominance generated by kin assets and their fluctuating inequality would have waxed and waned. If political behavior and the development of institutions were contingent on the presence of social assets, the nature of these phenomena, and indeed their elaboration over time, would be constrained or impelled by the underlying demographic shocks.

This article calls attention to a previously unrecognized and consequential variability in the environment of human groups. The claim is made that when demography alters the kinship distributions, social cooperation and competition take place under different circumstances. When those distributions are altered, some egos behaviorally inclined or institutionally equipped in a cultural context to form coalitions may enjoy positive selection, natural or cultural. Those institutions that are kinship-elastic, such as classificatory systems that permit broader kin definitions under one rubric (e.g., FBS = B), buffer these changes and may have developed in response to demographic shocks and so also would alternatives to reliance on strict consanguinity or affinity, such as fosterage, adoption, and ritual kinship, and ultimately contractual relations that are not kinship analogs. Demographic instability may have been a factor in the evolution of kinship institutions.