Shape Based Segmentation of Anatomical Structures in Magnetic Resonance Images

Abstract

Standard image based segmentation approaches perform poorly when there is little or no contrast along boundaries of different regions. In such cases, segmentation is largely performed manually using prior knowledge of the shape and relative location of the underlying structures combined with partially discernible boundaries. We present an automated approach guided by covariant shape deformations of neighboring structures, which is an additional source of prior information. Captured by a shape atlas, these deformations are transformed into a statistical model using the logistic function. Structure boundaries, anatomical labels, and image inhomogeneities are estimated simultaneously within an Expectation-Maximization formulation of the maximum a posteriori probability estimation problem. We demonstrate the approach on 20 brain magnetic resonance images showing superior performance, particularly in cases where purely image based methods fail.

1 Introduction

To better understand brain diseases, many neuroscientists analyze medical images for cortical and subcortical structures that seem to be influenced by the disease [1]. The analysis is based on segmentations of the structures of interests, often performed by human experts. However, this manual process is not only expensive, but in addition, it increases risks related to inter- and intra-observer reliability [2]. In this paper, we describe an automatic method, which accurately segments these structures by considering anatomical shape constraints and image artifacts of Magnetic Resonance (MR) images.

The detection of substructures is difficult as many of them are defined by partially discernible boundaries, such as in the case of the boundary between thalamus and white matter [3]. However, the ventricles, the structure above the thalamus, is more easily identified. In order for the ventricles to guide the boundary detection between the thalamus and the white matter, automatic segmentation algorithms use spatial priors [4–6]. These spatial priors capture the spatial relationship between structures such as the fact that the ventricles are above the thalamus. This is one example in which neighboring structures are of great utility for segmentation purposes.

These types of priors are often characterized by soft boundaries representing the large spatial variability of a structure within a population. Deformable models offer an alternative as they capture the shape and permissible modes of variation within a population. In contrast to spatial priors on tissue labels, segmentation methods based on deformable models are guided by structure specific boundary conditions such as the length of the boundary in relation to others.

The work of this paper is motived by the class of deformable model-based approaches called active contour methods [7–9], in which the shape of an anatomical structure is represented as a level set function in a higher dimensional space. Similarly, our method defines anatomical shape constraints using signed distance maps in combination with the modes of variations of a Principle Component Analysis (PCA) [13]. While active contour methods were originally motivated by physical models [10], many methods are based on a Bayesian framework [11, 14, 12], which we chose for our algorithm. A Bayesian framework allows us to explicitly model the image inhomogeneities of MR images in order to segment large data sets without manual intervention.

The optimal solution within our framework is defined by a Maximum A posteriori Probability (MAP) estimation problem with incomplete data. From the MAP estimation problem we derive an instance of the Expectation Maximization algorithm (EM). The main contribution of the current work is that while we represent the shape variations through an implicit low-dimensional PCA, we additionally derive from this an explicit space-conditioned probability model by way of the logistic function. When combined with image-coupling and other terms in our Bayesian framework, the mechanism is able to identify shapes that are not restricted to the low-dimensional PCA space.

In contrast to other EM implementations [11, 14, 15], our method explicitly models the boundary via the shape model. Consequently, we achieve smooth segmentations without underestimating fine structures; a common problem in EM implementations [15]. To demonstrate the capabilities of our approach, we outline 20 sets of MR images into the major tissue classes as well as subcortical structures. The reliability of our approach is determined by the correspondence of the automatic segmentations to expert manual ones.

2 Deriving a Unified Framework for Image Inhomogeneity Correction, Shape Modeling, and Segmentation

The accuracy of outlining structures with indistinct boundaries in MR images significantly depends on properly modeling the boundary of the structure as well as estimating the inhomogeneities in the image. In this section, we develop a unified framework that performs segmentation, shape detection, and inhomogeneity correction simultaneously.

Without additional assumptions, it is difficult to extract the inhomogeneities ℬ and the shape parameters $\mathcal{S}$ from the MR images I due to their complex dependencies. However, this problem is greatly simplified when formulated as an incomplete data problem via EM. Within this framework, we define the following MAP estimation problem:

$$\left(\widehat{\mathcal{B}},\widehat{\mathcal{S}}\right)=\arg {max}_{\mathcal{B},\mathcal{S}}\log P\left(\mathcal{B},\mathcal{S}|I\right).$$ (1)

In general, this results in a system of equations for which there is no analytical solution. We introduce the labelmap $\mathcal{T}$, which assigns each voxel in the image to an anatomical structure. If $\mathcal{T}$ is known it eases the estimation of ℬ and $\mathcal{S}$ based on I. In our problem, the labelmap $\mathcal{T}$ is unknown so that the instance of the EM algorithm iteratively determines the solution of [16]. At each iteration, the method improves the estimates $\left({\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }\right)$ of $\left(\widehat{\mathcal{B}},\widehat{\mathcal{S}}\right)$ through

$$\left({\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }\right)\leftarrow \arg {max}_{\mathcal{B},\mathcal{S}}{E}_{\mathcal{T}|I,{\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }}\left(\log P\left(\mathcal{B},\mathcal{S},\mathcal{T}|I\right)\right).$$ (2)

The expected value is defined as $E_{A|B}\left(f\left(C\right)\right)\triangleq {\displaystyle {\sum }_{A}P\left(A|B\right)f\left(C\right)}$.

In our case, Equation (2) is a less complicated MAP problem than Equation (1). However, we would like to further simplify this update rule as it depends on both shape $\mathcal{S}$ and inhomogeneities ℬ. To split Equation (2) into two separate MAP problems, we first rephrase Equation (2) by simply applying Bayes’ rule and dropping terms that do not depend on $\left(\mathcal{B},\mathcal{S}\right)$:

$$\begin{array}{l}\left({\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }\right)\leftarrow \arg {max}_{\mathcal{B},\mathcal{S}}{E}_{\mathcal{T}|I,{\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }}\left(\log P\left(\mathcal{B},\mathcal{S}|\mathcal{T},I\right)+\log P\left(\mathcal{T},I\right)\right)\\ =\arg {max}_{\mathcal{B},\mathcal{S}}{E}_{\mathcal{T}|I,{\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }}\left(\log P\left(I|\mathcal{T},\mathcal{B},\mathcal{S}\right)+\log P\left(\mathcal{B},\mathcal{S}|\mathcal{T}\right)-\log P\left(I|\mathcal{T}\right)\right)\\ =\arg {max}_{\mathcal{B},\mathcal{S}}{E}_{\mathcal{T}|I,{\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }}\left(\log P\left(I|\mathcal{T},\mathcal{B},\mathcal{S}\right)+\log P\left(\mathcal{S}|\mathcal{T},\mathcal{B}\right)+\log P\left(\mathcal{B}|\mathcal{T}\right)\right)\end{array}$$ (3)

The optimization procedure decomposes nicely as a consequence of the following independence assumptions: First, we assume independence of I with respect to $\mathcal{S}$ conditioned on $\mathcal{T}$ and ℬ because our model characterizes each anatomical structure by a stationary intensity distribution [11, 14]. Next, we assume independence of $\mathcal{S}$ with respect to ℬ conditioned on $\mathcal{T}$, as the image inhomogeneities do not influence the shape of a structure. Finally, we assume independence of ℬ with respect to $\mathcal{T}$ and that the two conditional probabilities $P\left(I|\mathcal{T},\mathcal{B}\right)$ and $P\left(\mathcal{S}|\mathcal{T}\right)$ are defined by the product of the corresponding conditional probabilities over all the voxels in the image space. Thus, Equation (3) simplifies to

$$\begin{array}{l}\left({\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }\right)\leftarrow \arg {max}_{\mathcal{B},\mathcal{S}}{E}_{\mathcal{T}|I,{\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }}\left(\log P\left(I|\mathcal{T},\mathcal{B}\right)+\log P\left(\mathcal{S}|\mathcal{T}\right)+\log P\left(\mathcal{B}\right)\right)\\ =\arg {max}_{\mathcal{B},\mathcal{S}}{\displaystyle {\sum }_x{E}_{{\mathcal{T}}_x|I,{\mathcal{B}}^{\prime },{\mathcal{S}}^{\prime }}}\left[\log P\left(I|{\mathcal{T}}_{x,}\mathcal{B}\right)+\log P\left(\mathcal{S}{|\mathcal{T}}_x\right)\right]+\log P\left(\mathcal{B}\right)\end{array}$$ (4)

The labelmap $\mathcal{T}=\left({\mathcal{T}}_1,\dots ,{\mathcal{T}}_M\right)$ is composed of the indicator random vector ${\mathcal{T}}_x\in \left\{e_1,\dots ,e_N\right\}$, where x represents a voxel on the image grid. The vector e_a is zero at every position but a, where its value is one. For example, if ${\mathcal{T}}_x=e_a$ then voxel x is assigned to the structure a. We now define the E-Step of our EM implementation as

$${\mathcal{W}}_x\left(a\right)\triangleq E_{{\mathcal{T}}_x|I,{{\mathcal{B}}^{\prime }}_x,{\mathcal{S}}^{\prime }}\left({\mathcal{T}}_x\left(a\right)\right)=1\cdot P\left({\mathcal{T}}_x=e_a|I_x,{{\mathcal{B}}^{\prime }}_x,{\mathcal{S}}^{\prime }\right)+0\cdot P\left({\mathcal{T}}_x\left(a\right)\ne e_a|I_x,{{\mathcal{B}}^{\prime }}_x,{\mathcal{S}}^{\prime }\right).$$

If we assume that $\mathcal{S}$ is independent of ℬ then

$${\mathcal{W}}_x\left(a\right)=\frac{P\left(I_x|{\mathcal{T}}_x\left(a\right)=e_a,{\mathcal{B}}_X^{\prime },{\mathcal{S}}^{\prime }\right)·P({\mathcal{I}}_x(a)=e_a|{\mathcal{B}}_X^{\prime },{\mathcal{S}}^{\prime })}{P\left(I_x|{\mathcal{B}}_X^{\prime },{\mathcal{S}}^{\prime }\right)}=\frac{P\left(I_x|{\mathcal{T}}_x\left(a\right)=1,{\mathcal{B}}_X^{\prime }\right)\cdot P\left({\mathcal{T}}_x\left(a\right)=1|{\mathcal{S}}^{\prime }\right)}{P\left(I_x|{\mathcal{B}}_X^{\prime },{\mathcal{S}}^{\prime }\right)}$$ (5)

and Equation (4) reduces to

$$\left({ℬ}^{\prime },{\mathcal{S}}^{\prime }\right)\leftarrow \arg {\max }_{ℬ,\mathcal{S}}{\displaystyle {\sum }_x{\displaystyle {\sum }_a{\mathcal{W}}_x\left(a\right)\left[\log P\left(I|{\mathcal{T}}_x=e_a,ℬ\right)+\log P\left(\mathcal{S}|{\mathcal{T}}_x=e_a\right)\right]+\log P\left(ℬ\right).}}$$

Now, the M-Step solves the following two separate MAP problems

$${\mathcal{S}}^{\prime }\leftarrow \arg {max}_{\mathcal{S}}{\displaystyle {\sum }_x{\displaystyle {\sum }_a{\mathcal{W}}_x\left(a\right)\log P\left({\mathcal{T}}_x=e_a|\mathcal{S}\right)}}+\log P\left(\mathcal{S}\right)$$ (6)

$${\mathcal{B}}^{\prime }\leftarrow \arg {max}_{\mathcal{B}}{\displaystyle {\sum }_x{\displaystyle {\sum }_a{\mathcal{W}}_x\left(a\right)\cdot \log P\left(I|{\mathcal{T}}_x=e_a,\mathcal{B}\right)}}+\log P\left(\mathcal{B}\right)$$ (7)

A variety of closed-form solutions for Equation (7) have been proposed in the literature such as by [14] and [11]. The remainder of this paper therefore focuses on Equation (6).

In summary, we find a local maxima to the difficult MAP estimation problem of Equation (1) by solving the simpler Equation (2), derived from an EM formulation. Based on independence assumptions, our instance of the EM algorithm iterates between the E-Step, which calculates $\mathcal{W}$ via Equation (5), and the M-Step, which solves the MAP problems of Equation (6) and Equation (7).

3 Logistic Maps for Shape Probabilities

The solution of Equation (6) greatly depends on the shape representation that defines the space of $\mathcal{S}$ and the probabilities that define the relationship of the attributes within our model. This section gives an example for a derivation of this equation. Before we do so, we briefly review the shape representation defined by the signed distance map.

Note, while we adopt a PCA representation of shape information, the final estimate is not restricted to the PCA parameterization of shape. This is facilitated by the use of the logistic function as described in Section 3.2. Consequently, our model captures a broader class of shapes than those methods that are restricted to the PCA model.

3.1 Shape Representation

As mentioned, the results of level set methods [7, 8, 17] using a PCA model on signed distance maps inspired us to introduce shape constraints in an EM framework. We follow the suggestion by Tsai [7], who applies PCA to all structures simultaneously to capture the covariation between structures. We initially model the shapes of all structures of interest by the distance map $\mathcal{D}$. $\mathcal{D}$ (x) is a vector of dimension equal to the number of structures of interests. It defines the distance of voxel x to the boundary of each structure. Positive values are assigned to voxels within the boundary of the object, while negative values indicate voxels outside the object.

We first turn a set of manual segmentations into signed distance maps and then apply PCA to the maps in order to determine the modes of variations of each structure. The resulting shape model is represented by the eigenvector or modes of variation matrix U, eigenvalue matrix Λ, and $\overline{\mathcal{D}}:={({\overline{\mathcal{D}}}_1^T,\dots ,{\overline{\mathcal{D}}}_N^T)}^T$, where ${\overline{\mathcal{D}}}_a$ is the mean distance map of the anatomical structure a. To reduce the computational complexity for the EM implementation, U and Λ are only defined by the first K eigenvectors. In our case K represents 99 % of the eigenvalues’ energy, which corresponds to the first five eigenvectors.

The shapes in a specific image are described by the expansion coefficients of the eigenvector representation, which are the shape parameters $\mathcal{S}=\left({\mathcal{S}}_1,\dots ,{\mathcal{S}}_K\right)$. $\mathcal{S}$ relates to the distance maps by ${\mathcal{D}}_{\mathcal{S}}=\overline{\mathcal{D}}+U\cdot \mathcal{S}$, where ${\mathcal{D}}_{\mathcal{S}}$ captures the distance maps of all structures of interest. We refer to the distance map of a specific structure a defined by shape $\mathcal{S}$ as ${\mathcal{D}}_{\mathcal{S},a}={\overline{\mathcal{D}}}_a+U_a·\mathcal{S}$, where U_a are the entries in U corresponding to structure a. This type of shape representation is only appropriate for defining local shape deformations as the space defined by signed distance maps is not a linear vector space. Thus, ${\mathcal{D}}_{\mathcal{S},a}$ is a local approximation to the manifold of distance maps.

We end this brief description of the shape model by defining the prior over the shape parameters as

$$p\left(\mathcal{S}\right)=\frac{1}{\sqrt{{\left(2\mathrm{\pi }\right)}^K\left|\mathrm{\Lambda }\right|}}\exp \left(-\frac{1}{2}{\mathcal{S}}^T{\mathrm{\Lambda }}^{-1}\mathcal{S}\right),$$ (8)

which is based on the hidden Gaussian assumption in PCA.

3.2 Estimating the Shape

In this section, we define the relationship of the unknown labelmap $\mathcal{T}$ and the shape parameter $\mathcal{S}$ captured by the conditional probability $P\left({\mathcal{T}}_x=e_a|\mathcal{S}\right)$ of Equation (6). The task is not straight-forward because unlike active contour methods, we also model the unknown labelmap $\mathcal{T}$ and the image inhomogeneities ℬ explicitly. The shape $\mathcal{S}$ captures global characteristics of structures, while $\mathcal{T}$ and ℬ characterize local properties. Motivated by the need to combine global and local information, we describe the use of the logistic function of the distance transform. The logistic function provides an implicit representation of the shape and an explicit space-conditioned probability model.

As mentioned previously, our model captures the relationship between the shape parameters $\mathcal{S}$ (which corresponds to a signed distance map) and the labelmap $\mathcal{T}$ through the conditional probability $P\left({\mathcal{T}}_x=e_a|\mathcal{S}\right)$ Since the random variable ${\mathcal{T}}_x$ is discrete, we define the conditional probability in terms of a generic shape function $\mathcal{A}$(·,·) as

$$P\left({\mathcal{T}}_x=e_a|\mathcal{S}\right)\equiv \frac{\mathcal{A}\left(a,{\mathcal{D}}_{\mathcal{S},a}\left(x\right)\right)}{{\displaystyle {\sum }_{a^{\prime }}\mathcal{A}\left(a,{\mathcal{D}}_{{\mathcal{S}}^{\prime },a}\left(x\right)\right)}}.$$

Given the motivation above, a natural choice for this formulation is the logistic function

$$\mathcal{A}\left(a,v\right)\equiv \frac{1}{1+e^{-c_{a}v}},$$

which maps the distance map to the range [0,1]. For example, if ${\mathcal{D}}_{\mathcal{S},a}\left(x\right)$ is positive, then the voxel is inside the object and $\mathcal{A}\left(a,{\mathcal{D}}_{\mathcal{S},a}\left(x\right)\right)\in \left(0.5,1\right]$. The variations within $\mathcal{A}\left(a,{\mathcal{D}}_{\mathcal{S},a}(\cdot )\right)$ depend on c_a, which captures the certainty of the method with respect to the shape model. Uncertainty about the shape model is represented by relative small c_a. This results in a wide slope of the spatial distribution (see Figure 1), which allows greater mobility of the boundary. Large c_a define spatial priors with steep slopes, which tend to position the boundary of a structure.

Fig. 1.

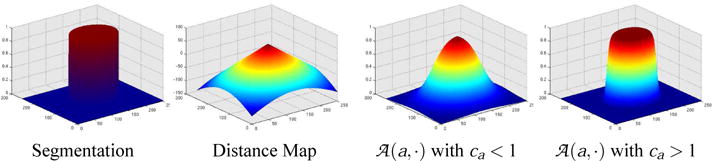
The image to the left is a labelmap of a circle whose corresponding distance map is shown to its right. Based on the distance map, two different logistic functions are plotted. The first logistic function is defined by a large slope (c_a < 1) and the second plot represents a logistic function with a steep slope (c_a > 1).

The probability of the segmentation conditioned on the shape is now defined as

$$P\left({\mathcal{T}}_x=e_a|\mathcal{S}\right)={\left(\left(1+e^{-c_a{\mathcal{D}}_{\mathcal{S},a}\left(x\right)}\right)\cdot \left({\displaystyle {\sum }_{a^{\prime }}\frac{1}{1+e^{-c_{a^{\prime }}{\mathcal{D}}_{\mathcal{S},a^{\prime }}\left(x\right)}}}\right)\right)}^{-1},$$ (9)

so that the MAP estimation problem of Equation (6) transforms to

$$\begin{array}{c}{\mathcal{S}}^{\prime }\leftarrow \arg {\max }_{\mathcal{S}}-{\displaystyle {\sum }_x{\displaystyle {\sum }_a{\mathcal{W}}_x}\left(a\right)}\left(\log \left(1+e^{-c_a{\mathcal{D}}_{\mathcal{S},a}\left(X\right)}\right)+\log \left({\displaystyle {\sum }_{a^{\prime }}\frac{1}{1+e^{-c_{a^{\prime }}{\mathcal{D}}_{\mathcal{S},a^{\prime }}\left(X\right)}}}\right)\right)+\log P\left(\mathcal{S}\right)\\ =\arg {\max }_{\mathcal{S}}-{\displaystyle {\sum }_x\left[{\displaystyle {\sum }_a{\mathcal{W}}_x}\left(a\right)\log \left(1+e^{-c_{a^{\prime }}{\mathcal{D}}_{\mathcal{S},a^{\prime }}\left(X\right)}\right)+\log \left({\displaystyle {\sum }_{a^{\prime }}\frac{1}{1+e^{-c_{a^{\prime }}{\mathcal{D}}_{\mathcal{S},a^{\prime }}\left(X\right)}}}\right)\right]+\frac{1}{2}}{\mathcal{S}}^t\mathrm{\Lambda }\mathcal{S}\end{array}$$ (10)

Determining a closed form solution to this estimation problem is generally very difficult so that we approximate its solution using Powell’s method [18].

In summary, the parameters $\mathcal{S}$ are seen within the context of a shape atlas created by PCA on signed distance maps. We relate the shape model to the EM algorithm of the previous section by defining $P\left({\mathcal{T}}_x=e_a|\mathcal{S}\right)$ of Equation (6) as a composition of logistic functions on distance maps. The E-Step of the EM algorithm calculates the $\mathcal{W}$ based on the shape parameters ${\mathcal{S}}^{\prime }$, intensity I, image inhomogeneities ${\mathcal{B}}^{\prime }$, and voxel x

$${\mathcal{W}}_x\left(a\right)={\left({\displaystyle {\sum }_{a^{\prime }}\frac{P\left(I_x|{\mathcal{T}}_x=e_{a^{\prime }},{\mathcal{B}}_X^{\prime }\right)}{1+e^{-c_{a^{\prime }}{{\mathcal{D}}_{{\mathcal{S}}^{\prime }}}_{,a^{\prime }}\left(X\right)}}}\right)}^{-1}\cdot \frac{P\left(I_x|{\mathcal{T}}_x=e_a,{\mathcal{B}}_X^{\prime }\right)}{1+e^{-c_a{{\mathcal{D}}_{{\mathcal{S}}^{\prime }}}_{,a}\left(X\right)}}$$

The distribution of $P\left(I_x|{\mathcal{T}}_x=e_a,{\mathcal{B}}_X^{\prime }\right)$ depends on the underlying image inhomogeneity model, which is an ongoing discussion [11, 14]. We choose the model by Wells et al. [11] that defines $P\left(I_x|{\mathcal{T}}_x=e_a,{\mathcal{B}}_X^{\prime }\right)$ by the Gaussian distribution $\mathcal{N}\left({\mathcal{B}}_X^{\prime }+{\mu }_a,{\mathrm{\gamma }}_a\right)$. $\left({\mu }_a,{\mathrm{\gamma }}_a\right)$ capture the mean and variance of the intensity distribution of the structure a.

The M-Step updates the estimates of the inhomogeneities ${\mathcal{B}}^{\prime }$ and shape ${\mathcal{S}}^{\prime }$ based on the weights ${\mathcal{W}}_x$. The update rule of ${\mathcal{B}}^{\prime }$ (Equation (7)) reduces to a system of linear equations and is solved in closed form [11]. The shape ${\mathcal{S}}^{\prime }$ is updated according to Equation (10) for which a solution is found via Powell’s method [18].

4 Validation

This section compares the accuracy of our new method with (EM-Shape) and without shape modeling (EM-NoShape). Both methods segment 22 test cases into the three brain tissue classes - white matter, grey matter and corticospinal fluid. As in Figure 2, the right (pink) and left ventricle (turquoise) are extracted from the corticospinal fluid, and the grey matter is further parcellated into right (red) and left (purple) thalamus, and right (green) and left caudate (blue). We determine the accuracy of the approaches by comparing the automatic segmentations of the thalamus and the caudate to manual ones, which we view as ground-truth.

Fig. 2.

A 3D model generated by EM-Shape of the right (red) and left thalamus (purple), right (green) and left caudate (blue), and the right (pink) and left ventricle (turquoise). The graph to the right summarizes the validation results. For both structures EM-Shape clearly performs better than EM-NoShape.

With respect to EM-Shape, the atlas of Section 3.1 represents the shape of the thalamus, caudate, and the ventricles. The three brain tissue classes are excluded from the dynamic shape model as their spatial distributions are defined by the spatial atlas of [15] and not Equation (9). The model of EM-NoShape represents all anatomical structures by the spatial atlas.

We focus on the thalamus and caudate as they are challenging structures to segment. Purely intensity based segmentation methods, such as EM without spatial priors, cannot outline these structures because part of the boundary is invisible on MR images. Consequently, EM relies heavily on the prior information. In addition, the two structures are characterized by very different shapes (see Figure 2). While the right and left thalamus are shaped like an oval with a hook attached to it, the caudate is defined by long, thin horns wrapped around the ventricles. The segmentation methods also segment the ventricles because they are clearly visible on MR images. This structure further constrains the space of possible solutions for EM-Shape as all structures of interest have to be in proper proportion to each other.

To measure the quality of the automatic generated results, we compare them to the manual segmentations using the volume overlap measure DICE [19]. The graph in Figure 2 shows the average DICE measures and standard error for the two methods with respect to the thalamus and caudate. For the thalamus, EM-Shape achieves a higher average score (88.4 ±1.0%; mean DICE score ± standard error) than EM-NoShape (87.3 ±1.2%). The impact of the shape model on the segmentation results is even more apparent in the case of the caudate, where EM-Shape (84.9 ± 0.8%) is significantly better than EM-NoShape (82.7 ±1.2%). The greater accuracy of EM-Shape is attributed to the shape atlas, which better captures the subject specific bending of the horn shaped caudate than the spatial atlas.

The initial DICE score of EM-Shape is generally lower than that of EM-NoShape because the shape model misrepresents the patient specific structures. For example, Figure 3 shows the outcome of EM-Shape after every fifth iteration. Initially, the segmentation is noisy, which indicates discrepancy between the initial shape model defined by the mean shape and the patient specific shape. With each iteration, the arch of the caudate widens and the segmentations get smoother. After 20 iterations the method converges to a solution that generally outperforms EM-NoShape.

Fig. 3.

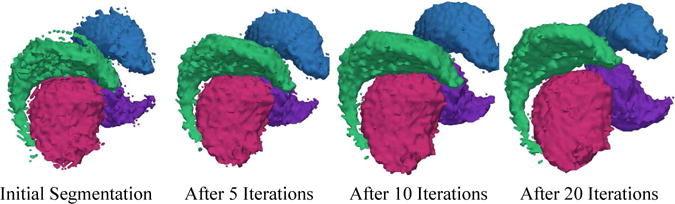
The 3D models are based on the segmentations generated by our new method through 20 iterations. The method is initialized with the mean shape of each structure. The very noisy initial segmentation is an indication of the disagreement between the mean and the patient specific shape. As the algorithm proceeds the shape of the caudate and thalamus adjusts to the patient specific situation. After about 20 iterations the algorithm converges to a smoother segmentation.

As mentioned, it is difficult to determine the exact shape of a structure with weakly visible boundaries. From the MR images, the size of the oval and the position of the hook of the thalamus are often not clearly defined. The top-left image of Figure 4 shows an example of such a scenario. The segmentations are the results of the two automatic segmentation methods where black indicates the outline of the human expert. In this example, EM-NoShape underestimates the hook of the thalamus, which we found to be true throughout this experiment. EM-Shape can better cope with this problem as the shape model adds global constraints to the local analysis of the intensities. An example of a global constraint is the explicit definition of shape dependencies across anatomical structures. This causes the shape of the thalamus to be proportional to one of the easily segmentable ventricles. This impacts the accuracy of EM-Shape as it further constrains the space of possible segmentations.

Fig. 4.

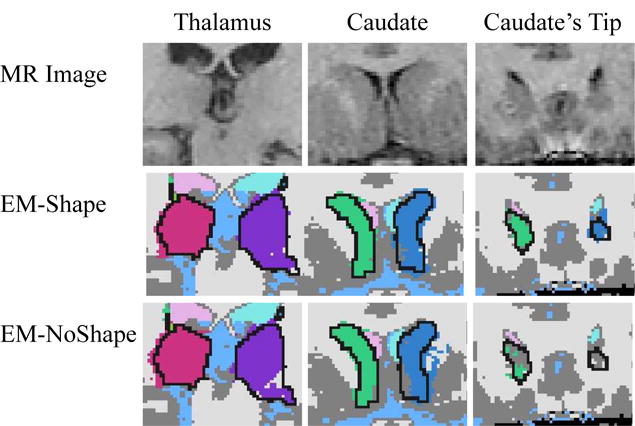
The figure is a collection of different subcortical regions. The black lines in the automatic segmentations are the thalamus or caudate outlined by the human expert. The left column shows a MR image with corresponding segmentations of the oval shaped body of the thalamus with attached hook. The middle column shows part of the caudate which is adjacent to the putamen, another subcortical structure with identical intensity distribution. The right column shows the top of the caudate which is generally is underestimated by EM-NoShape. In all three examples, EM-NoShape performs worse than EM-Shape because the discriminatory power of spatial prior and intensity pattern is too low to determine the boundary of the structure.

The other structure of interest in this experiment is the caudate. The structure is adjacent to the putamen, another subcortical structure with an identical intensity distribution. In the MR image of the middle column of Figure 4, the putamen is located on the outside of image. Neither the intensity pattern nor the spatial prior can properly separate these two structures, as indicated by the noisy segmentations of EM-NoShape. The outliers visible in EM-NoShape violate the shape constraints of EM-Shape as the boundary has to satisfy the conditions set by the ventricles and the thalamus.

For both structures, EM-NoShape did not adequately segment the ends of the structure. In the right column of Figure 4, EM-NoShape underestimates the tip of the caudate. The opposite is true for the thalamus where EM-NoShape overestimates the ends. Again, spatial and intensity distributions do not allow discrimination between anatomical structures in this area. In summary, on the 20 test cases our shape based method EM-Shape was performing much better than EM-NoShape, which uses a spatial atlas instead of a shape atlas.

5 Summary and Conclusions

We presented a statistical framework for the segmentation of anatomical structures in MR images. The framework is guided but not restricted to the low-dimensional PCA shape model as the shape representation is turned into space-conditioned probability model using the logistic function. The approach is especially well suited for structures with weakly visible boundaries as it simultaneously estimates the image inhomogeneities, explicitly models the boundaries through a deformable shape model, and segments the MR images into anatomical structures. Our approach was validated by automatically segmenting 20 test cases and comparing the results to a similar EM implementation without shape priors. In general, our new method performs much better. The improvement is primarily due to explicit modelling of the shape constraints along the boundary of anatomical structures.