Hierarchical disruption in the Bayesian brain: Focal epilepsy and brain networks

Abstract

In this opinion paper, we describe a combined view of functional and effective brain connectivity along with the free-energy principle for investigating persistent disruptions in brain networks of patients with focal epilepsy. These changes are likely reflected in effective connectivity along the cortical hierarchy and construct the basis of increased local functional connectivity in focal epilepsy. We propose a testable framework based on dynamic causal modelling and functional connectivity analysis with the capacity of explaining commonly observed connectivity changes during interictal periods. We then hypothesise their possible relation with disrupted free-energy minimisation in the Bayesian brain. This may offer a new approach for neuroimaging to specifically develop and address hypotheses regarding the network pathomechanisms underlying epileptic phenotypes.

Highlights

• •A combined view of functional brain connectivity and dynamic causal modeling of persistent networks changes in focal epilepsy.
• •Increased functional connectivity in focal epilepsy is likely reflected in effective connectivity of cortical hierarchy.
• •A testable framework based on dynamic causal modeling and functional connectivity analysis during interictal periods.

1. Background

Focal epilepsy is a dynamic disorder of the brain that is characterized by both paroxysmal abnormal states (e.g. epileptic seizures), and persistent abnormalities across the functional brain networks (Powell et al., 2007). Advances in understanding the relationship between these observable phenomena and underlying pathophysiology have improved current treatment approaches, such as epilepsy surgery, and can potentially improve patient outcomes (Goodfellow et al., 2016). However, the neuronal mechanisms underlying the complex symptomatology observed in patients are still not fully understood. Here we describe a novel conceptual and analysis framework that allows for the integration of observations at various scales into a fully specified dynamic network model of brain function that can be used to test specific hypotheses regarding the network pathophysiological mechanisms underlying common symptoms in focal epilepsy. This framework rests on the free-energy principle in the brain's structure-function relationships and will be illustrated using focal epilepsy as a possible use-case.

Neuronal architectures in the brain are inherently hierarchical and modular. Dynamic processes within this ‘global integrating system of local integrators’ can be investigated from two distinct, but closely related perspectives; namely, functional and effective connectivity. Functional connectivity analysis provides no directionality between brain regions and is usually assessed at the macroscopic scale, i.e., within or between brain areas. On the other hand, effective connectivity considers directed inter-cortical (intrinsic) and intra-cortical (extrinsic) coupling at the mesoscopic (neuronal assemblies) and macroscopic scales. Several attempts have been made to understand functional integration mediated by effective connectivity under an overarching framework. Among them, the formulation of the brain as a predictive organ that minimises the free-energy of its internal states has attracted attention (Friston, 2010). Per the free-energy principle, the brain acts as a Bayesian inference machine that adaptively changes its internal states or actively re-samples the sensorium to minimize prediction-errors. In other words, the brain attempts to minimise surprise or the difference between prior expectations/beliefs and sensory evidence.

A widely accepted mathematical model of free-energy minimisation in the brain is known as predictive coding (Friston, 2010, Rao and Ballard, 1999). In this approach, cortical pyramidal cells are divided into prediction and prediction-error neurons that form a hierarchy of cortical regions. This hierarchy integrates prior knowledge with incoming sensory evidence to update beliefs about the causes of sensory inputs. This type of inference can be formulated in terms of Bayesian statistics, reducing the problem to a simple set of neurobiologically plausible computations (Bastos et al., 2012). These computations produce expectations about the causes of a sensory input that can be equated with conscious or unconscious percepts and ensuing action. Because predictive coding can be cast as a simple set of mathematical operations, it provides a computational framework for understanding how abnormal neuronal message passing leads to aberrant behaviors and psychopathology.

Focal epilepsy is defined as consistent seizure onset from a particular cortical or sub-cortical source with consequent network-wide changes. Common regions involved in functional network changes in focal epilepsy include “default mode” cortical areas, piriform cortex, insula, cingulate cortex, cerebellum, and thalamus (Fahoum et al., 2012, Fahoum et al., 2013, Flanagan et al., 2014, Laufs et al., 2011, Laufs et al., 2007, Pedersen et al., 2016). The complex neurobiological underpinnings of these persistent features are not yet clearly understood. Effective tools to link empirical observations at the network scale to the underlying pathophysiology are currently missing.

In this opinion paper, we consider a framework for studying interictal disruptions of brain networks in patients with focal epilepsy, based on predictive coding and the concept of a hierarchically organized Bayesian brain. We will suggest that specific, identifiable changes in effective connectivity along the cortical hierarchy can be the basis of increased connectivity in focal epilepsy. First, we outline the free-energy principle and Bayesian inference and their relationship to brain dynamics. Second, we explain the link between free-energy and functional/effective connectivity. Third, we describe connectivity changes during interictal periods in focal epilepsy and hypothesise their possible relation with disrupted free-energy minimisation in the brain. Finally, we propose an analytical test for our hypothesis and possible treatment avenues, in intractable focal epilepsy.

2. The free-energy principle and brain dynamics

2.1. Bayesian inference

We start with explanation of a few basic concepts about Bayesian inference, necessary for clarifying the rest of our discussion. A conditional probability P(ϑ|y) quantifies the probability of an event ϑ given the occurrence of another event y:

$$P\left(\vartheta |y\right)=\frac{P\left(\vartheta ,y\right)}{P\left(y\right)}$$ (1)

where P(y) is the evidence or marginal probability of y and P(ϑ,y) is the probability of ϑ and y occurring together. The general form of Bayes' rule is then given by:

$$P\left(\vartheta |y\right)=\frac{P\left(y|\vartheta \right)P\left(\vartheta \right)}{P\left(y\right)}.$$ (2)

In this formulation, P(ϑ|y) is the posterior density (distribution of our belief ϑ given observations y), P(y|ϑ) is the likelihood of observations given the belief and P(ϑ) is the prior density of the belief. Based on Eqs. (1) and (2), one can rewrite P(y) as:

$$P\left(y\right)=P\left(y|\vartheta \right)P\left(\vartheta \right)+P\left(y|~\vartheta \right)P\left(~\vartheta \right)$$ (3)

where ~ϑ is the complement of the event ϑ. This leads to a more explicit form of Bayes' theorem for estimating the posterior density with respect to an uncertain event:

$$P\left(\vartheta |y\right)=\frac{P\left(y|\vartheta \right)P\left(\vartheta \right)}{P\left(y|\vartheta \right)P\left(\vartheta \right)+P\left(y|~\vartheta \right)P\left(~\vartheta \right)}.$$ (4)

Intuitively, Bayes' rule tells us how to ‘learn’ from sampled data using our beliefs about the causes of observations, shaped by some priors. This perspective contrasts with frequentist inference, where conclusions are drawn based on the frequencies of events happening, with no prior beliefs about the causes of observations. The Bayesian formulation provides the background for characterizing the brain as a Helmholtz machine “whose function is to infer the probable causes of the sensory input” (Dayan et al., 1995). The learning process is then associated with Bayesian belief-updating in which prior beliefs are converted into posterior beliefs (the distribution of our beliefs given our observations) through simulating observations or sensory information. This ‘belief-updating’ can be performed in many ways. At present, predictive coding is a very popular process theory for Bayesian belief-updating in the brain. Effectively, this process can be expressed as a recursive updating of the expected causes of sensation through a minimization of precision-weighted prediction errors (Hohwy, 2013, Mathys et al., 2011):

$$\mathit{New}\mathit{prediction}=\mathit{Old}\mathit{prediction}+\mathit{precision}\times \mathit{prediction\; error}.$$ (5)

In the next section, we explain the free-energy principle and its relationship to the Bayesian brain.

2.2. The Bayesian brain

The free-energy principle is a global theoretic framework about how brain function supports action, perception and learning. This principle describes biological systems that resist a tendency to disorder by adapting internal dynamical states through interacting with their environment. It is because self-organizing biological systems – such as the brain – tend to minimize the entropy of their states (Friston, 2010). For neuronal systems, this means minimising the average surprise experienced through environmental interactions: Simply stated, the brain generates predictions of its sensory inputs based on generative models of the world. Where sensory evidence contradicts these predictions, a prediction error signal is generated and the generative models are updated to improve future predictions.

Mathematically this can be cast in a set of equations. Here, brain dynamics are assumed to be ergodic processes with long-term averages equal to their ensemble average. The conditional entropy H(y|m) of a neuronal input y is then characterized as the average surprise; i.e., the negative log-evidence (− ln p(y|m)) associated with sensory data, given a generative model m embodied by the brain:

$$H\left(y|m\right)={\lim }_{T\to \infty }\frac{1}{T}{\displaystyle {\int }_0^T}-lnp\left(y|m\right)\mathit{dt}.$$ (6)

Now, let p(ϑ|y,m) be a true posterior probability associated with the cause ϑ of sampled sensory inputs y under the generative model m. The cause ϑ could be any external factor such as visual stimuli or an internal input from a cortical neuron. The brain tries to approximate p(ϑ|y,m) regarding a recognition density q(ϑ; μ) shaped by prior beliefs.

The difference between p(ϑ|y, m) and q(ϑ;μ) is commonly quantified by the Kullback-Leibler divergence D_KL:

$$D_{\mathit{KL}}\left(q\left(\vartheta ;\mu \right)||p\left(\vartheta |y,m\right)\right)={\displaystyle {\int }_{\vartheta }}q\left(\vartheta ;\mu \right)ln\frac{q\left(\vartheta ;\mu \right)}{p\left(\vartheta |y,m\right)}\mathit{d\vartheta }.$$ (7)

We also know from the Bayes' rule that:

$$p\left(\vartheta |y,m\right)=\frac{p\left(y,\vartheta |m\right)}{p\left(y|m\right)},$$ (8)

where p(y,ϑ|m) is the probability of the joint occurrence of the input y and its cause ϑ, and p(y|m) is the marginal likelihood of observing y given the model m. Eq. (7) can therefore be split into two components leading to the general form of free-energy:

(9)

where F(μ,y) is free-energy and H(y|m) denotes the conditional entropy or average surprise. Note that ‘free-energy’ as used here stems from the variational Bayesian paradigm (Bishop, 2006) and should not be confused with ‘thermodynamic free-energy’ – although they can be related formally (Sengupta et al., 2013).

Due to the Gibb's inequality (or alternatively, Jensen's inequality), the quantity D_KL is always non-negative. Therefore, free-energy is always greater than surprise. Under some simplifying assumptions, this free-energy can be equated with the sum of squared prediction-error multiplied by the precision of that prediction-error. Taken together this amounts to a normative description of dynamic brain behavior that can be modelled as a gradient descent on free-energy or prediction error in a relatively straightforward fashion (see Eq. (5)). Note that surprise is a function of sensory inputs only, but free-energy depends on both internal states in the brain through sufficient statistics μ (i.e., quantities which fully parametrise the recognition density q(ϑ; μ) in Eq. (7)) and sensory data. In many situations (e.g., a Gaussian recognition density) it is sufficient to specify the mean or expectation of the recognition density, which is usually denoted by μ. Furthermore, free-energy depends on action α via its effects on sensations that are actively sampled (i.e., y = y(α)).

The foregoing suggests that the optimum bound on surprise is the free-energy F(μ,y). By minimising free-energy, the Bayesian brain can implicitly minimise surprise. At the same time, the difference between the true posterior beliefs and the expectations are resolved; thereby minimising prediction error. The resolution of prediction errors thus corresponds to updating prior beliefs about causes (i.e., perception), while actively sampling sensations (to match predictions) through interaction with the environment (i.e., action).

The next section takes the concepts of Bayesian inference and free-energy further by briefly reviewing hierarchical dynamic models and how they might be implemented in the brain. The resulting hierarchical scheme provides the theoretical underpinnings for our discussion of focal epilepsy and functional brain connectivity.

2.3. Hierarchical Bayesian inference cascades in the brain

In the previous section, we assumed the existence of some generative models that define the brain's prior beliefs about how sensations are caused. Here we consider the nature of these models and their implications for neuroanatomy and neuronal message passing. In brief, it is generally assumed that the generative model has a hierarchical structure. A multi-layer Bayesian inference network is necessary to model hierarchical nonlinear mappings between causes and observations encountered in the natural world. Furthermore, the implicit (hierarchical) simplification of causal structure calls on a much smaller number of computational units (Chalasani, 2013). In hierarchical models, manifold causes are decomposed into a web or chain of ‘hidden’ causes that become progressively more abstract towards the higher levels. In other words, the higher levels of the hierarchy (e.g., association cortex) deal with multi-dimensional sensory input, while lower levels (e.g., primary visual cortex) encode less abstract causes (e.g., lines and shapes of objects causing visual sensory samples).

Suppose an agent observes a dynamic sensory input y given an external cause ϑ with the prior p(ϑ). A generative model provides a probabilistic description of how that input is caused: p(y,ϑ) = p(y|ϑ)p(ϑ). In this case, hierarchical dynamic models offer a state-space description that decomposes p(y,ϑ) into a hierarchy of causal states v_i and hidden dynamical states x_i (i = 1 , … , N, N being the number of levels in the model) (Friston, 2010), where ϑ = (x_i,v_i,θ_i). These models are expressed in Eqs. (10a), (10b), (10c), (11). Note that although all variables are time dependent (e.g. x_i(t)), this explicit dependence is not shown for simplicity of expression.

$$\mathit{Level}1\left\{\begin{array}{c}y=g_1\left(x_1,v_1,{\theta }_1\right)+z_1\\ \dot{x_1}=f_1\left(x_1,v_1,{\theta }_1\right)+w_1\end{array}\right)$$ (10a)

$$\mathit{Level}2\left\{\begin{array}{c}{v}_1=g_2\left(x_2,v_2,{\theta }_2\right)+z_2\\ \dot{x_2}=f_2\left(x_2,v_2,{\theta }_2\right)+w_2\end{array}\right)$$ (10b)

$$\mathit{Level}N\left\{\begin{array}{c}{v}_{N-1}=g_N\left(x_N,v_N,{\theta }_N\right)+z_N\\ \dot{x_N}=f_N\left(x_N,v_N,{\theta }_N\right)+w_N\end{array}\right)$$ (10c)

where z_i and w_i are independent Gaussian observation noise and state noise processes, respectively:

$$\left[\begin{array}{c}{z}_i\\ w_i\end{array}\right]~N(0,\Pi {\left({\lambda }_i\right)}^{-1}).$$ (11)

The continuous nonlinear functions g_i and f_i are parametrized by θ_i at the ith level and model the predicted responses and hidden states, respectively. The precision parameters λ_i model the (inverse) amplitude of random fluctuations and hence, determine the precision Π(λ_i) or reliability of predictions at each level. In this setting, changing hidden states and causes to minimise free-energy corresponds to hierarchical perceptual inference, while changing the parameters to minimise free-energy over time corresponds to learning.

Hierarchical models provide a Markov chain of levels, where all necessary information for driving the ith layer is provided by the layer below. An important aspect of hierarchical dynamic models is that higher-level causes can also influence lower-level predictions, as the state-space of hierarchical dynamic models is formed by the hidden states of the interconnected levels.

Note that the generative model associated with Eqs. (10a), (10b), (10c) would be very complicated and constitutes a complete description of functional brain architectures. Conceptually, we are interested in the key role that precision plays in mediating the coupling between hierarchical levels of such models. Practically, the implicit dynamics in Eqs. (10a), (10b), (10c) inspire simplified forms for modelling observed neuronal activity; for example, the bilinear approximations used in dynamic causal models (DCMs). Having said this, the biophysical modelling of neuronal dynamics with DCM does not try to estimate the generative models that may be used in the brain; although recent advances using canonical microcircuits – as the basis of neuronal modelling (Bastos et al., 2015) – represent an attempt to move in this direction.

2.4. Free-energy and brain connectivity

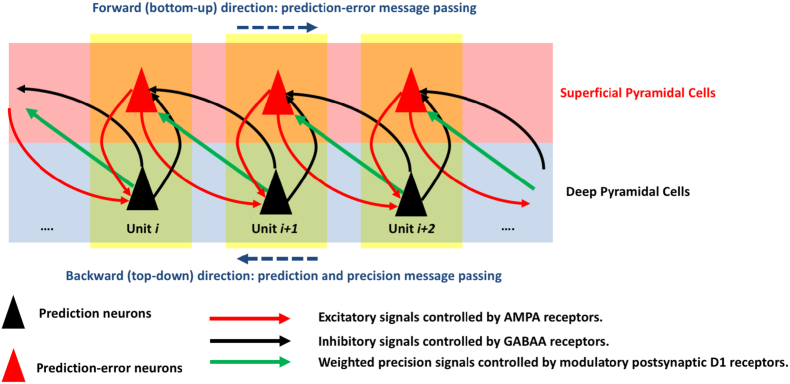
The minimisation of free-energy can be effectively modelled in computational neuroscience using the predictive coding framework (Friston, 2010). In predictive coding, ‘top-down’, ‘backward’ or ‘descending’ connections convey predictions from higher processing levels to lower ones, whereas ‘bottom-up’, ‘forward’ or ‘ascending’ connections convey prediction-errors in the opposite direction (Fig. 1). From a neurobiological point of view, superficial (supragranular) and deep (infragranular) pyramidal cells in the cortex are considered as sources of forward (prediction-error) and backward (prediction) signalling, respectively (for review see Bastos et al. (2012)). See also Kanai et al. (2015) for a discussion of how optimal precision weighting could be mediated in the brain; in the setting of visual attention and feature selection.

Fig. 1.

A simplified schematic of the hierarchical predictive coding in the cortex. This schematic is based on Fig. 1 in Edwards et al. (2012), published under the terms of Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0). Each yellow box represents a cortical column as a predictive coding unit. In this scheme, pyramidal cells are divided into two classes of prediction (black triangles) and prediction-error (red triangles). Predictive coding is then implemented according to a hierarchical scheme: ‘top-down’, ‘backward’ or ‘descending’ neuronal connections (black arrows) transfer predictions from higher processing levels to lower ones, whereas ‘bottom-up’, ‘forward’ or ‘ascending’ neuronal connections (red arrows) convey prediction-errors in the opposite direction. The term ‘prediction-error’ here refers to the (precision-weighted) difference between expectations and predictions at each unit. The precision-weights (green arrows) are controlled by postsynaptic neuromodulation (e.g. conferred by D1-dopamine receptors). The internal feedback loop within each unit constitutes ‘intrinsic’ connectivity, whereas between-unit interactions lead to ‘extrinsic’ connectivity. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

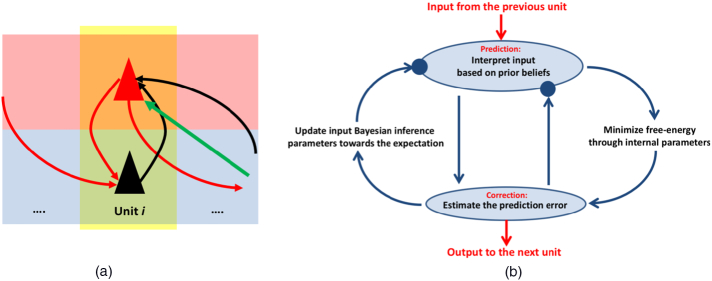
The units depicted in Fig. 1, Fig. 2 are not limited to locally connected neural circuits, but at different spatial scales, from neurons and macrocolumns through to macroscopic brain regions Park and Friston (2013). See also Towlson et al. (2013) for a good discussion on whether brain networks are scale invariant – i.e., we expect topological similarity between microscale and macroscale brain networks.

Fig. 2.

(a) A typical hierarchical processing unit presented in Fig. 1 with an input from its previous layer (incoming red arrow on the left) and an output to its next layer (outgoing red arrow on the right). The precision-weighting signal is illustrated by a green arrow. According to this model, the intrinsic connectivity of local microcircuits and extrinsic connectivity between cortical regions become integrated: Abnormal precision signalling can lead to aberrant intrinsic connectivity and increased local functional connectivity, with decreased extrinsic connectivity, as observed for example in focal epilepsy. (b) A normal free-energy minimisation cycle associated with the hierarchical processing unit presented in (a). The input and output signals (red arrows) of panel (a) are also illustrated in this cycle. The blue circles show where precision (i.e., neuronal excitability or postsynaptic gain) may be subverted by focal epilepsy. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Long-range connections are of excitatory nature and therefore, mediated by the neurotransmitter glutamate (mainly, through two types of the sector: AMPA and NMDA) that are in turn modulated by short-range GABAergic neurons (Bastos et al., 2012, Litvak et al., 2015, Penny, 2012). Therefore, the red-colour arrows in Fig. 1, Fig. 2 will play an important role in modelling long-range connections. In our neuronal model, we consider no set (anatomical) distance between neuronal ‘units’ – thus, unit i and unit i + 1 in Fig. 1 may be ‘long-range neighbours’ (e.g., two remote cortical areas).

Crucially, the ascending prediction-errors are determined by the difference between prediction and sensory input, weighted by a precision term (controlled by postsynaptic gain; e.g. mediated by postsynaptic dopamine receptor D1) (Edwards et al., 2012). Fig. 2 illustrates the prediction-error update process at each hierarchical layer.

In this neurobiological formulation of predictive coding, there is an intimate relationship between neuronal computation and local, as well as global connectivity. Hierarchical implementation of recurrent message passing (Fig. 1) equips brain dynamics with multiple causal interactions; including both intrinsic connections (coupling between cortical subpopulations) and extrinsic connections (passing messages between areas along the cortical hierarchy). The integration of these intrinsic and extrinsic neuronal architectures provides a basis for the development of stable functional networks with certain local (within-region) and global (between-region) network properties. The ensuing computational framework may help understand how localised aberrant connectivity (e.g. localised hypersynchrony in an epileptogenic area of the cortex) is linked to connectivity changes between brain areas (e.g. increased functional segregation seen in focal epilepsy).

3. Abnormal brain networks in focal epilepsy: disrupted free-energy minimisation?

Epilepsy describes a wide array of primary neurological conditions that share a predisposition to recurrent epileptic seizures. These seizures are disruptions in normal neurological function caused by abnormal, often hypersynchronous activity in the brain. Where this activity apparently arises from a specific area of the brain, the epilepsy can be described as focal. Even within the group of focal epilepsies, the causes are varied: In a set of childhood ‘benign seizure susceptibility syndromes’ (Panayiotopoulos et al., 2008), focal seizure arises from a recognizable set of brain areas without associated focal lesions (e.g. in benign epilepsy with centrotemporal spikes, BECTS). On the other hand, in most adult patients with focal epilepsies the pathophysiology is directly related to localised brain lesions. Seizures in the latter group are often drug treatment resistant and associated with a high degree of morbidity, including cognitive impairments (Rayner et al., 2016).

Despite the focal onset of individual seizures, focal epilepsies are thought to involve widespread functional brain network abnormalities beyond the apparently epileptogenic zone and even during interictal, ‘resting state’ activity (Berg et al., 2010). Reported changes at the macroscopic network level include increased segregation within distributed functional networks (van Diessen et al., 2014). In fact, there is increasing evidence from neuroimaging studies for the engagement of a shared set of brain areas that are recruited during interictal states – despite the heterogeneous nature of focal epilepsy (Laufs et al., 2011). These altered patterns of functional connectivity may be caused by synaptic changes induced by seizure activity and thus reflect the severity and duration of disease. This speaks to their potential use as biomarker for progressive network dysfunction in focal epilepsies (Yaffe et al., 2015) – leading to a more mechanistic understanding of the impact of epilepsy on wider brain function (Smith and Schevon, 2016).

Widespread functional connectivity alterations are observed interictally in focal epilepsies arising from identified neocortical lesions (e.g. focal cortical dysplasias, Englot et al. (2015)), from archicortical lesions (e.g. hippocampal sclerosis, Coito et al. (2016)), and idiopathic focal epilepsies without identifiable lesions (e.g. benign epilepsy with centrotemporal spikes, Adebimpe et al. (2015)). The overlap between networks affected across these different focal epilepsies suggest that functional connectivity changes are not only the result of anatomical connections of the epileptic focus to its specific cortical targets, but rather represents a shift in functional dynamics of the cortical network as a whole. This implies that cortico-cortical connectivity is altered and may not directly involve the epileptogenic focus. This speaks to our previous work, where we postulate that the epileptogenic focus may isolate itself from wider brain networks, also in the interictal state (Pedersen et al., 2015). The putative synaptic changes underlying cortico-cortical network abnormalities seen across the focal epilepsies are the focus of our current treatment.

We argue that macroscopic changes of brain functional connectivity observed in a range of focal epilepsy syndromes may stem from a disrupted cycle of free-energy minimization at the level of individual cortical columns and levels of cortical hierarchies. Thus, we are not trying to explain the generation of seizures, but the associated (and likely secondary) effects on whole brain dynamics apparent in interictal measurements of ongoing brain activity described above. While some of these effects may be mediated through cortico-subcortical loops, we suggest that they can be modelled as coupling changes between populations within the cortex. The ensuing model absorbs both direct synaptic connections between cortical areas, and statistical dependencies mediated through shared cortico-subcortical loops into aberrant (cortico-cortical) effective connectivity. As outlined above, the minimization cycle involves passing predictions and prediction errors between levels of the cortical hierarchy, in a way that depends upon the relative precision or postsynaptic gain that predominates at each level. Here, precision encodes the expected confidence or reliability of prediction-errors and can be regarded as a measure of signal-to-noise. Crucially, precision itself has to be estimated and optimized during perceptual (and active) inference. In other words, each hierarchical processing unit has to predict both the expected pattern of the neuronal input it samples and the reliability or precision of the evidence that is elicited. At a physiological level, precision is thought to be encoded by the synaptic gain or excitability of superficial pyramidal populations encoding prediction-error, which depends on neuromodulation, via e.g. the dopaminergic system. Precise prediction-errors are thus afforded a greater influence over higher-level representations generating top-down predictions.

Any pathophysiology that disrupts the modulation or control of cortical excitability will have profound implications for perceptual inference (Boly et al., 2011). Physiologically, aberrant prediction-error update in the Bayesian brain would manifest as a blockade on recurrent message passing among different hierarchical levels and a reduction of globally coherent hierarchical neuronal coupling. Persistent reoccurrence of these abnormal changes may result in a loss of global integration between widespread brain functional networks. In other words, predictive coding provides a computational framework within which to understand how pathophysiological failures of intrinsic connectivity and neuromodulation would lead to false inference and perceptual and motor symptoms.

Several neurobiological changes are purported to underlie localized seizure susceptibility in seizure onset zones in focal epilepsy (e.g. excitation-inhibition imbalance, abnormal local neuronal circuitry, modulation of neuronal responses through abnormal glial cell homeostatic function). Many of these microscopic changes, at the mesoscale may converge to result in abnormal precision control of pyramidal cell responses, or abnormal synaptic gain. If otherwise normal prediction-error signalling at an ensemble of hierarchical Bayesian processing units is modulated by pathological precision, it essentially clamps the associated message-passing representations to a particular value. Such an overly precise representation becomes impervious to influences from ascending prediction-errors. In other words, it blocks belief-updating at higher levels of the hierarchy.

Local abnormalities in the function of a cortical area in focal epilepsy may therefore explain abnormally increased segregation even in interictal, macroscopic functional networks. From an electrophysiological perspective, this would be manifest as a reduction in ascending and descending afferent extrinsic (between-layer) connectivity, reflecting the fact that processing in the level(s) of the localized pathology is impervious to ascending prediction-errors or descending predictions. A macroscopic demonstration of this altered functional connectivity in focal epilepsy would be the emergence of state-specific brain network abnormalities that may be a result of recurrent seizure suppression over the disease's progression.

Evidence of such effects can be found in several measures, but would be most clear in analyses that can reveal directed connectivity. Recently, DCM has emerged as a flexible model-based analysis method for electrophysiological data that allows inference on the causal relationship between a network of coupled sources, both at the macro- and mesoscale. Indeed, provisional DCM evidence from patients with impaired levels of consciousness demonstrates a loss of descending connectivity from prefrontal to temporal regions during an auditory mismatch negativity paradigm (Boly et al., 2011). DCM effectively integrates observation at different scales. While there are several DCM studies of epilepsy, most have focused on single sources and changes in excitability during seizure at the level of local microcircuits.

One might predict that DCM of electrophysiological measurements, or even of resting state fMRI time series in focal epilepsy may show similar failures of extrinsic connectivity across common epileptic brain nodes. Extending our view of persistent dysfunction in the epileptic brain to coupling abnormalities between hierarchically organized sources may (1) aid a mechanistic understanding of varied cognitive comorbidities seen in epilepsy, and (2) be a potentially important way to develop an individualized and non-invasive prognostic biomarker for patients with focal epilepsy by classifying them in accordance to their persistent brain functional abnormalities.

As an interim summary, we postulate that disturbances in local connectivity, mediated through an excessively precise prediction-error signal, compromises effective extrinsic connectivity between hierarchically coupled cortical sources. This gives rise to increased local and decreased global functional connectivity, observable at the macroscale in focal epilepsy. This locally abnormal activity may also cause further synaptic changes leading to the emergence of abnormal coupling between other cortical areas, and thus exert a wider impact on Bayesian inference circuitry. In fact, ‘commonly observed’ brain areas in focal epilepsy such as insular, piriform and cingulate cortices may subserve hubs with abnormal precision control. Many of these features would cause measurable changes in brain function, many of which would relate naturally to analysis using dynamic causal modelling as we will discuss below.

4. A testable framework using dynamic causal modelling

The following testable framework allows for inference on mesoscopic and macroscopic connectivity changes at both individual and group levels and could be divided into three successive steps:

• A)Functional connectivity analysis: detection of ‘common’ brain networks in focal epilepsy

Persistent functional connectivity changes in focal epilepsy can be evaluated using inter-ictal fMRI or EEG-fMRI. Using graph theory-based measures of functional connectivity, abnormalities shared between patients are characterized as a set of affected network nodes, which affords a focus for more detailed analysis of effective connectivity. For this approach, networks of interest need to be identified to minimize model complexity and maximize the prior plausibility of DCM. Nodes can be identified in several ways. These can be based on existing robust networks identifiable from resting state data (e.g. the default node network), networks that are known to be involved in aspects of the symptomatology of the epilepsy condition at hand (e.g. language related network in BECTS, Vannest et al. (2017)), or regions implicated in other neuroimaging studies. Target regions include the fronto-insula cortex (ipsilateral), superior temporal gyrus (ipsilateral), posterior cingulate cortex (left and right), the piriform cortex (ipsilateral) (Fahoum et al., 2012, Laufs et al., 2011, Pedersen et al., 2016) and the suspected seizure onset zone.

• B)Effective connectivity analysis: Detection of causal relations within common networks

Effective connectivity can be estimated from a variety of neuronal signals, including resting state fMRI using cross spectral DCM on a subset of network nodes (Friston et al., 2014). DCM allows for the fitting of network models to functional signals using different, competing model architectures. Bayesian model comparison, then allows statistical inference, as to which model has most likely produced the data. For each individual subject, specific effective connectivity network architectures can therefore be compared: architectures with and without hierarchical forward and backward connections; with and without abnormal intrinsic connectivity within seizure onset zones; with and without changes in extrinsic connectivity of specific regions of interest, such as the posterior cingulate cortex, or the fronto-insular cortices. Shared effective connectivity network architectures can then be identified using fixed effects Bayesian model selection. The assumption here is that all participants share the same underlying functional architecture.

• C)Parametric empirical Bayesian modelling of group effects

Applying recent advances on integrated (empirical Bayesian) modelling of group effects on DCMs (Litvak et al., 2015), one can test significant effects of individual subject-specific parameters (such as age of epilepsy onset, duration of disease, frequency of seizures, degree of cognitive problems) on the connectivity estimates. This can be done both in fMRI data, using the network architecture identified above and making inference on macroscale networks, or in EEG data where available, allowing inference on mesoscale, local dynamics.

The hierarchical (cortical) architectures implied by generative models in the brain (i.e., Eqs. (10a), (10b), (10c)) are used for understanding of aberrant precision control in the genesis of interictal activity using DCM. However, it should be noted that DCM is not, at present, capable of inferring the precise architectures implied by generative models with the general form of Eqs. (10a), (10b), (10c). Rather, the form of message passing implied by a hierarchical generative model places constraints on the effective connectivity one would expect to mediate normal and interictal dynamics in the brain. Put simply, Eqs. (10a), (10b), (10c) prescribe a generic neuronal message passing that is usually understood in terms of predictive coding (although equivalent variational message passing schemes exist in the context of a discrete state space generative models (Friston et al., 2016a, Friston et al., 2016b)). These schemes involve passing predictions and prediction-errors between hierarchical levels of cortical brain architectures; where the influence of ascending prediction-errors is controlled by precision. Physiologically, this means we would expect extrinsic (long range) connections in DCM to convey predictions and prediction-errors, while intrinsic (within region) DCM connections primarily reflect the precision or gain afforded to prediction-errors. This means a sufficient description of interictal activity could be cast purely in terms of aberrant precision control, reflected in abnormal intrinsic (self) connectivity in standard (bilinear) DCMs of cortical hierarchies. Clearly, the level of detail afforded by a DCM makes it difficult to map directly onto the highly nonlinear and structured connectivity (predictive coding) architectures that would be required to invert models with the general form of Eqs. (10a), (10b), (10c). For example, most current DCMs for fMRI do not distinguish between forward and backward connections and have a very limited parameterisation of intrinsic connections. This is because DCM lumps together multiple neuronal populations within any one region, which precludes lamina-specific connectivity and a proper distinction between inter and intralaminar connections. Having said this, a crude approximation of the pathophysiology suggested by our theoretical treatment suggests a special focus on intrinsic connectivity as the mediator – or signature – of interictal pathophysiology. Furthermore, there are ongoing efforts to make DCMs sufficiently detailed, so that they can be related directly to the predictive coding schemes described above. See Bastos et al., 2012, Bastos et al., 2015 for a particular example in the dynamic causal modelling of electromagnetic activity and Fogelson et al. (2014) and Ranlund et al. (2016), for applications in the context of schizophrenia research. Finally, there have been recent advances in the dynamic causal modelling of fMRI data which may be especially relevant for the current thesis; namely, the ability to model haemodynamics using the same canonical microcircuits that underlie predictive coding: see Friston et al. (2017).

Such an approach would allow for (1) the identification of shared network abnormalities within a patient group with focal epilepsy when compared to controls, (2) the characterization of the network abnormality in terms of an effective connectivity architecture with dissociated forward and backward sources, and (3) the analysis of subject-specific effects of disease variables specifically on the presumptive causal network structures (i.e. synaptic connection strengths underlying the functional connectivity).

The DCM framework provides robust tools that allow inference on network configurations from neuroimaging data. Using Bayesian model reduction (BMR), even very large model spaces – encompassing many possible network configurations – can be ranked for Bayesian model comparison in a matter of seconds, given an inverted ‘full’ DCM that contains all possible connections (which takes a few minutes to invert). Furthermore, where the true model architecture is not known, Bayesian model averaging will provide the best available parameter estimates, accounting for uncertainty over model architectures. Taken together, these tools therefore allow (1) efficient estimation of both parameters and model evidence to allow for modelling of individual patient networks, and therefore (2) exploration of large model spaces to reduce biasing the analysis towards a subset of hypotheses. Of particular interest here are recent developments for hierarchical modelling of distributed networks with DCM. Here, the hierarchy relates to the difference between within-epoch, between-epoch and between-subject effects that may be very useful for tracking changes in coupling over seconds or minutes (i.e., hierarchical modelling of between-epoch effects) and, crucially, identifying pathophysiology through group differences in connectivity (i.e., hierarchical modelling of between-subject effects). See Friston et al., 2015, Friston et al., 2016a, Friston et al., 2016b and Litvak et al. (2015) for a discussion of these technical developments.

5. Predictions and therapeutic interventions

The approach outlined here focuses on identifying pathophysiology underlying persistent network abnormalities in focal epilepsy. Seizure frequency, or epileptiform discharges seen on clinical EEG may not themselves correspond closely with the overall burden on brain function posed by the epilepsy. This has direct clinical relevance, particularly for the potentially associated cognitive burden. Identifying non-invasive network measures associated with abnormal inference, and therefore presumably cognitive problems may become a useful clinical tool to aid the prognosis and guide the need for further intervention and therapeutic support.

In terms of therapeutic interventions, hierarchical predictive coding speaks to several possibilities. If hierarchical processing depends sensitively on the encoding of precision and associated neuromodulatory gain control, then it may be possible to harness endogenous mechanisms to rebalance hierarchical precision or gain. For example, interventions that induce attention or sensory attenuation, should (in theory) change precision and postsynaptic gain using endogenous mechanisms that, if judiciously induced at the appropriate hierarchical level, could afford a mechanism for rebalancing. Appropriate cognitive-behavioral therapy, pharmacological neuromodulation, or even transcranial and deep-brain electrical stimulation may become relevant therapies for cognitive improvements in focal epilepsy.

6. Time to consider the free-energy principle for epilepsy?

Understanding the relationship between symptoms and the underlying dynamic network properties of the epileptic brain remains a major challenge in human epilepsy research, particularly when considering the cognitive impact of the disorder (Badawy et al., 2012). The free-energy framework, together with dynamic causal modelling approaches to estimating effective connectivity may offer a new approach for neuroimaging to specifically develop and address hypotheses regarding the network pathomechanisms underlying epileptic phenotypes.

Persistent functional network abnormalities in the brain, commonly observed across the heterogeneous spectrum of focal epilepsy can be modelled and explained using effective connectivity within the free-energy framework. In the context of hierarchical Bayesian inference, the pathophysiology of focal epilepsy may render them unable to pass on prediction-errors to higher neuronal levels that update the generative models. This would cause more broadly an increased segregation of functional brain nodes in focal epilepsy as a secondary effect of the local deficiency in recurrent neuronal message passing. The description of focal epilepsy as a disease of excessive surprise (or precision) in the Bayesian brain fits well with the false inference implications of this pathophysiology and together with dynamic causal modelling, may be developed further into a tool to identify and characterize such abnormalities.