Microscopic Interpretation and Generalization of the Bloch-Torrey Equation for Diffusion Magnetic Resonance

Abstract

In order to bridge microscopic molecular motion with macroscopic diffusion MR signal in complex structures, we propose a general stochastic model for molecular motion in a magnetic field. The Fokker-Planck equation of this model governs the probability density function describing the diffusion-magnetization propagator. From the propagator we derive a generalized version of the Bloch-Torrey equation and the relation to the random phase approach. This derivation does not require assumptions such as a spatially constant diffusion coefficient, or ad-hoc selection of a propagator. In particular, the boundary conditions that implicitly incorporate the microstructure into the diffusion MR signal can now be included explicitly through a spatially varying diffusion coefficient. While our generalization is reduced to the conventional Bloch-Torrey equation for piecewise constant diffusion coefficients, it also predicts scenarios in which an additional term to the equation is required to fully describe the MR signal.

1. Introduction

Measuring molecular self-diffusion in magnetic resonance (MR) experiments is an important tool for understanding the geometrical structure of materials ranging from porous media to brain tissue. Translational diffusion within an inhomogeneous magnetic field causes dephasing in a spin-echo experiment [1]. The macroscopic MR signal decay is related to the average overall molecular spin phases [2]. The molecular displacement depends on random thermal forces (Brownian motion), however it is also affected by the boundaries dictated by the geometric structure of the specimen, such as cellular membranes or the edges of pores, which modulate the motion of molecules. The goal of diffusion MR is ultimately to recover information about geometrical structure from the macroscopic, voxel scale, MR signal [3]. This structure can be encoded through effective diffusion coefficients, or Probability Density Functions (PDF), which are defined over a large population of molecules.

The leading approach to relate the microstructure to the macroscopic MR signal is the Bloch–Torrey (BT) equation [4], in which the phenomenological Bloch equation [5] is expanded by accounting for the behavior of a population of spins, explicitly modeled by the diffusion coefficient, D, yielding

$$\frac{\partial }{\partial t}\langle \mathbf{m}\rangle =\gamma (\langle \mathbf{m}\rangle \times \mathbf{H})-\nabla (\mathbf{v}\langle \mathbf{m}\rangle )+\nabla (D\nabla \langle \mathbf{m}\rangle ),$$ (1)

where 〈m〉 is the average magnetization (throughout the paper, boldface describes three-dimensional vectors), H is the applied magnetic field², γ is the gyromagnetic ratio, and v is the velocity of the spins due to the flow of the medium within which the spins are embedded [6]. The complete equation also includes T₁ and T₂ weighted terms: $-\frac{\langle m_x\rangle \widehat{\mathbf{x}}+\langle m_y\rangle \widehat{\mathbf{y}}}{T_2}-\frac{\langle m_z\rangle -\langle m_0\rangle }{T_1}\widehat{\mathbf{z}}$, where T₁ is the longitudinal (spin–lattice) relaxation time, T₂ is the transverse (spin–spin) relaxation time [5], and 〈m₀〉 is the thermal equilibrium magnetization of the sample in the presence of a magnetic field. In our analysis we assume that T₁ and T₂ are spatially invariant, in which case these relaxation mechanisms affect all the nuclei in the same way and their contribution can be factored out by comparing the diffusion-weighted signal to a reference signal (e.g., without a diffusion gradient). In what follows, we will omit these relaxation terms, concentrating on the diffusion related terms.

The macroscopic MR signal is obtained by integrating the solution of the BT equation over the whole sample or over a given voxel. The BT equation provides an explicit description of the combined effects of diffusion, flow and spin dephasing, whereas the microstructure is incorporated implicitly through boundary conditions imposed on interfaces between various tissue components or solid-fluid phases in porous media. This makes analytical and even numerical solutions of the BT equation challenging [7–9]. In particular, analytical approaches that solve the BT equation, such as the Multiple Correlation Function (MCF) framework, are only efficient for simple geometries [10–13].

For a constant diffusion coefficient, the solution to the BT equation can be related to an alternative formulation for modeling the diffusion MR signal, known as random phase approach [2, 10, 14–17]. It relies on the PDF of the spin dephasing within a voxel. In the simplest case of free diffusion, the propagator is Gaussian that implies a Gaussian distribution of the spin dephasing. However, the microstructure of a sample can strongly affect diffusion and thus the form of the propagator and the PDF of the dephasing. Nevertheless, the Gaussian assumption is the basis of many diffusion MR methods, such as diffusion tensor imaging (DTI) [18]. Other phase averaging methods, such as q-space imaging (QSI) [19] and diffusion spectrum imaging (DSI) [20], also assume constant diffusion coefficients within voxels. However, assumptions of free diffusion or even a constant diffusion coefficient may not be valid in biological applications. Spatial heterogeneities can result in space and time dependent diffusion coefficients both on a microscopic cellular level (nucleus, plasma membrane) and on a coarser tissue level (intracellular/extracellular diffusion, tumoral regions, etc.) One therefore needs to quantify the effects of spatially dependent diffusion coefficients onto MRI measurements.

For this purpose, we introduce a general microscopic model, which describes the interactions of a single molecule with its environment in terms of molecular displacement, flow, and spin precession. From this model, we derive the Fokker-Planck equation, which describes the time evolution of the transition probability of the spins, which we refer to as the diffusion-magnetization propagator. We use this propagator to derive a generalized form of the BT equation for any space and/or time dependent diffusion coefficient D. The microstructure is incorporated explicitly through the spatial dependence of D (e.g., with lower diffusivity across membranes or zero diffusivity on obstacles), eliminating the need for boundary conditions. We then identify the set of assumptions under which the conventional BT equation remains valid for a space-dependent diffusion coefficient. Finally, we relate the derived propagator to the microscopic random phase approach [1, 2] for cases of space dependent diffusion coefficients. Figure 1 presents a flow chart of our derivation, highlighting the importance of the diffusion-magnetization propagator as the connection between the microscopic and macroscopic scales.

Figure 1.

The derivation flow chart. We start by defining a microscopic stochastic model for the motion of a single molecule. Next we derive the Fokker-Planck equation for the probability density function, which we call the diffusion-magnetization propagator. We use this propagator to model the macroscopic signal in two ways: (i) by averaging over all the phases of the molecules, called the random phase approach, and (ii) by deriving a generalized Bloch–Torrey (BT) equation. Explicit derivation of the diffusion-magnetization propagator provides the missing link between the microscopic domain and the macroscopic MR signal.

2. The microscopic model

Molecular motion in liquid is a process known as self diffusion. It is caused by random molecular collisions, driven by thermal energy. At the microscopic scale, it is not possible to predict which way a particular molecule will move at a given time. We assume that the forces acting on each molecule and the medium in which they move can be modeled using the following stochastic equations:

$$\frac{d\mathbf{r}}{dt}=\mathit{\sigma }(\mathbf{r},t)\mathbf{f}(t)+\mathit{\mu }(\mathbf{r},t),$$ (2)

$$\frac{d{m}_l}{dt}=\gamma {(\mathbf{m}\times \mathbf{H}(\mathbf{r},t))}_l=i\sum _{j=1}^3{\mathrm{\Lambda }}_{lj}(\mathbf{r},t)m_j.$$ (3)

In this microscopic model, Eq. (2) is a Langevin equation that describes the velocity of a single molecule in a position r at time t [21]. This equation includes two mechanisms: 1) thermal collisions of a molecule with its environment, which are modeled by a Gaussian white noise f(t), with zero mean and delta correlated covariance: 〈f(t)〉 = 0 and 〈f(t₁)f(t₂)〉 = δ(t₁ − t₂); and 2) flow and drift μ(r, t) that can be caused by an external force. The matrix σ(r, t) in the stochastic term models the time correlation of the process, allowing non-Gaussian dynamics [22]. This matrix reflects the interaction of the molecules with the environment, which depends on the underlying deterministic geometry, as well as the temperature and viscosity of the medium. This matrix is naturally related to the diffusion tensor $D(\mathbf{r},t)=\frac{1}{2}\mathit{\sigma }(\mathbf{r},t){\mathit{\sigma }}^T(\mathbf{r},t)$. In turn, Eq. (3) describes how the magnetic moment m of each spin precesses with the Larmor frequency, in the presence of a magnetic field, H, which can be space and time dependent [1, 2, 5]. The component m_l in m is the magnetic moment in the direction l. It is useful to describe the microscopic model in a matrix representation by considering the antisymmetric and self-adjoint matrix Λ,

$$\mathrm{\Lambda }=-i\gamma \left(\begin{array}{ccc}0& H_z& -H_y\\ -H_z& 0& H_x\\ H_y& -H_x& 0\end{array}\right).$$ (4)

Then, by defining a(t) = (m(t), r(t)), Eqs. (2–3) can be combined to a matrix form:

$$\frac{d\mathbf{a}}{dt}=\mathbf{A}[\mathbf{a},t]+B[\mathbf{a},t]\mathbf{\eta }(t),$$ (5)

where

$$\mathbf{A}[\mathbf{a},t]=\left[\begin{array}{c}i\mathrm{\Lambda }(\mathbf{r},t)\mathbf{m}\\ \mathit{\mu }(\mathbf{r},t)\end{array}\right],B[\mathbf{a},t]=\left[\begin{array}{cc}I& 0\\ 0& \mathit{\sigma }(\mathbf{r},t)\end{array}\right],\mathbf{\eta }(t)=\left[\begin{array}{c}0\\ \mathbf{f}(t)\end{array}\right],$$

and the initial condition is a(t₀) = a₀ = (m₀, r₀).

The microscopic stochastic model describes the behavior of each single molecule. In order to understand the behavior of a mesoscopic concentration of molecules, we need to average over all the trajectories of molecules. The Stratonovich’s Fokker-Planck equation for this stochastic model reads [21]:

$${\partial }_{t}P(\mathbf{a},t\mid {\mathbf{a}}_0,t_0)=-\sum _i{\partial }_i{A}_i(\mathbf{a},t)P(\mathbf{a},t\mid {\mathbf{a}}_0,t_0)+\frac{1}{2}\sum _{i,j,k}{\partial }_i{B}_{ik}(\mathbf{a},t){\partial }_j\left(B_{jk}{(\mathbf{a},t)}^{T}P(\mathbf{a},t\mid {\mathbf{a}}_0,t_0)\right)$$ (6)

(an equivalent Itô formalism is derived in Appendix A, see [23] for a discussion of the Itô versus Stratonovich derivations). The index i runs over the spatial coordinate of r(t) and m(t) (i.e., i runs from 1 to 6 in three dimensions). Substituting the expressions for A and B, we arrive to the following Fokker-Planck equation:

$${\partial }_{t}P=-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}P)-\nabla (\mathit{\mu }P)+\nabla (D\nabla P)+\frac{1}{2}\nabla (P\nabla D),$$ (7)

where we define ${\nabla }_{\mathbf{m}}={\sum }_{i=1}^3\frac{\partial }{\partial m_i}$. The equation is completed by the usual initial condition P(a, t = t₀|a₀, t₀) = δ(a − a₀), where δ(·) is the Dirac distribution. The solution P(a, t|a₀, t₀) is a diffusion-magnetization propagator describing the conditional probability of finding a molecule with magnetic moment m and position r at time t, given that there was a molecule with magnetic moment m₀ and position r₀ at time t₀. This is a generalization of the diffusion propagator [15, 21], since it accounts both for molecular displacement and for magnetization changes. We note that the Fokker-Planck equation (7) is associated with isotropic D, while its anisotropic version is provided in Appendix A. As mentioned earlier, the structural boundary conditions can be included explicitly through the diffusion tensor D and through the flow and drift term μ, as will be illustrated later in the numerical simulation.

3. Generalized Bloch-Torrey equation

Given the diffusion-magnetization propagator (Eq. (7)), we can now derive the equation for the average magnetization 〈m〉(r, t), by averaging over the magnetic moment m with respect to the propagator P(a, t|a₀, t₀) (a detailed calculation and a generalization to anisotropic D can be found in Appendix B):

$$\frac{\partial }{\partial t}\langle \mathbf{m}\rangle (\mathbf{r},t)=i\mathrm{\Lambda }\langle \mathbf{m}\rangle -\nabla (\mathit{\mu }\langle \mathbf{m}\rangle )+\nabla (D\nabla \langle \mathbf{m}\rangle )+\frac{1}{2}\nabla (\langle \mathbf{m}\rangle \nabla D).$$ (8)

The MR signal is obtained by integrating 〈m〉 over a given voxel. Comparing Eq. (8) with Eq. (1), we can see that Eq. (8) is a generalized form of the BT equation that contains one additional term, $\frac{1}{2}\nabla (\langle \mathbf{m}\rangle \nabla D)$. This term accounts for changes in the density of molecules that may occur due to a space or time dependent diffusion coefficient.

We emphasize that a straighforward inclusion of a space-dependent diffusion coefficient into the conventional BT equation (1), which can be obtained by assuming a generalized phenomenological Fick’s law, is consistent neither with the Stratonovich, nor with the Itô interpretation of the microscopic diffusion model (2–3). In particular, the fundamental relation between the BT equation (in such an extension) and the random phase averaging can be lost. Note that the conventional form of the Bloch-Torrey equation (based on the Fick’s law) might be recovered by using the Hänggi-Klimontovich interpretation [24, 25]. The advantage of our approach is that we start from the microscopic diffusion model and then derive the associated BT equation. In this way, the relation to the random phase averaging is preserved, as shown below. Finally, we stress that the choice of the stochastic interpretation should be dictated by physics at the microscopic scales that results in inhomogeneous diffusion at mesoscopic scales [26]. An experimental justification of an appropriate interpretation presents a very interesting perspective. To better understand the contribution of the extra term, we first explore the cases in which the term is canceled, resulting in equivalence between the generalized and conventional BT equations.

3.1. Piecewise constant diffusion coefficient

Clearly, for a constant D, the extra term is nulled. Below, we show that the additional term is also canceled when D is a piecewise constant. For simplicity, consider a one-dimensional system of compartments (ℓ_j, ℓ_j+1) with zero drift and a piecewise constant diffusion coefficient

$$D(x)=\sum _j{D}_j[\mathrm{\Theta }(x-{\ell }_j)-\mathrm{\Theta }(x-{\ell }_{j+1})],$$

where D_j is the constant diffusion coefficient in the j-th compartment, and Θ(x) is the Heaviside step function. In this case, the term is nulled within each compartment, whereas integrating Eq. (8) over a small region near each boundary yields the flux continuity as the boundary condition (see Appendix C). In principle, under the assumption of an infinitely thin boundary, i.e, a sharp transition between compartments, the local D may be defined by the structure of the histology-based data, and the coefficients D and the external drift μ can account for boundary conditions of this structure. In turn, if the diffusion coefficient varies less sharply across the boundary, the extra term corrects the effective boundary condition by accounting for a finite thickness of the boundary (see Appendix C).

3.2. Inhomogeneous diffusion coefficient in steady state

If D is not a piecewise constant, for example, if the boundaries found from the histology-based data are not sharp, the extra term is nulled only when both following conditions hold: (1) there exists an equilibrium distribution at steady state; and (2) this equilibrium distribution is unique. Under these assumptions the extra term in the generalized BT equation is compensated by the external drift μ(r, t) in Eq. (2), which takes the explicit form of (see Appendix D)

$$\mathit{\mu }=D\nabla \text{ln}(V{\rho }_{eq}(\mathbf{r}))+\frac{\nabla D}{2}+\frac{{\mathbf{J}}_{eq}}{{\rho }_{eq}(\mathbf{r})},$$ (9)

where J_eq is the probability flux, and we define ρ_eq(r|r₀, t₀) = P(r, t → ∞|r₀, t₀) = ρ_eq(r) in a volume element V. Therefore ρ_eq(r) is determined by both the local diffusion coefficient, D, and the external drift, μ. Substituting Eq. (9) in the generalized BT equation (8), and assuming ρ_eq ≠ 0, the extra term is canceled. Therefore, we arrive at the conventional BT equation (1), where v from Eq.(1) takes the form of [27, 28]

$$\mathbf{v}(\mathbf{r},t)=\frac{{\mathbf{J}}_{eq}(t)}{{\rho }_{eq}(\mathbf{r})}+D\nabla \text{ln}(V{\rho }_{eq}(\mathbf{r})).$$ (10)

We see that v(r, t) is now composed of two terms, the first can be identified as a flow term and the second as a drift term, which maintains equilibrium by compensating for the density changes created by inhomogeneous diffusion. Note that the emergence of a drift due to inhomogeneous diffusion has been observed in a single particle tracking experiment [29]. Interestingly, imposing the Boltzmann equilibrium distribution on ρ_eq leads to a version of the fluctuation dissipation theorem (see Appendix E). In summary, the derivation of the BT equation in the steady state shows that in cases of inhomogeneous diffusion, the conventional BT equation is valid only under the aforementioned conditions. In biological systems these conditions may not be satisfied [6, 30, 31]. Therefore, in these systems, the generalized BT equation may give a better representation of the forward model.

4. The generalized random phase approach

Given the diffusion-magnetization propagator in Eq. (7), we can also derive and explore the random phase approach which is the basis for most diffusion MR applications today. In the random phase approach, the measured macroscopic signal E is related to the ensemble average over all the random phases acquired by individual molecules due to their displacements [2]. It can be formally written as a Feynman path integral over all trajectories r(t) started from r₀ at t₀:

$$\begin{array}{l}E(t)=\langle e^{i\varphi (t)}\rangle \\ =\underset{N\to \infty }{lim}\int P(\mathbf{r}(t_i),t_i\mid \mathbf{r}(t_{i-1}),t_{i-1})e^{i\varphi (t)}\rho ({\mathbf{r}}_0,t_0)\mathcal{D}\mathbf{r},\end{array}$$ (11)

where ρ(r₀, t₀) is the initial density at time t₀, and the PDF P(r(t), t|r(t₀) = r₀, t₀) plays an important role as the weighting factor of a random trajectory r(t) to the average of the accumulated phase ϕ(t) acquired up to time t by a single particle as a consequence of its motion in the magnetic field. The symbol $\mathcal{D}\mathbf{r}={\displaystyle \prod _{i=1}^N}d{\mathbf{r}}_{t_i}$ refers to integration over all intermediate time steps between t₀ and t_N = t, such that t_i = t₀ + iΔt, and $\mathrm{\Delta }t=\frac{t}{N}$. The phase ϕ(t) is a functional of the trajectory r(t) started from r₀.

Using our microscopic model, we can derive the diffusion equation that accounts for a given diffusion MR experiment, and thus we can identify the source of the phase/displacement distribution. For this purpose, we consider a conventional pulsed gradient spin-echo diffusion MR experiment, where H(r, t) = (H₀ +G(t)r(t)) ẑ is a magnetic field along the ẑ axis, H₀ is the static magnetic field, and G(t) is a linear time-dependent magnetic field gradient (known as the diffusion gradient) with an arbitrary waveform vanishing at the origin. In this case, the magnetic moment changes with time only in the x and y components. The phase shift accumulated due to the gradient field by a single molecule moving along a given trajectory, r = r(t), is

$$\varphi (t)=\gamma \underset{0}{\overset{t}{\int }}\mathbf{H}(\mathbf{r}(\tau ),\tau )d\tau =\gamma H_{0}t+\gamma \underset{0}{\overset{t}{\int }}\mathbf{G}(\tau )·\mathbf{r}(\tau )d\tau .$$

It is convenient to work with the components in the rotating frame, the so-called transverse magnetization m_±(t) = m_x(t)±im_y(t). To obtain the net diffusion-attenuated MR signal, we need to average the contributions of individual molecules in all possible initial positions and trajectories [1, 2, 10, 15]. Using our microscopic model (Eqs. (2–3)), we define the magnetic moment of a single molecule as a function of the dephasing, ϕ, which can in general include some real deterministic function R(t)

$$m_{+}(t)=R(t)e^{i\varphi (t)}.$$ (12)

Since our microscopic model is defined in the Stratonovich calculus, it is easy to show that under this transformation, R(t) = R(0) = R is a constant which depends only on the initial condition of the spins (see Appendix F). From Eq. (12) it is also clear that m₊(t = 0) = R. Therefore, the average magnetization over time and space is

$$\langle m_{+}\rangle (t)=\underset{N\to \infty }{lim}\int P(\mathbf{a}(t_i),t_i\mid \mathbf{a}(t_{i-1}),t_{i-1})R{e}^{i\varphi (t)}\rho ({\mathbf{r}}_0,t_0)\mathcal{D}\mathbf{r}\mathcal{D}{m}_{\pm }=m_{+}(t=0)\langle e^{i\varphi (t)}\rangle ,$$ (13)

where the probability P(a(t_i), t_i|a(t_i−1), t_i−1) is calculated from Eq. (7) at short time, the m_z component is traced out, and we assume a uniform distribution of spins at t₀ due to a uniform rf pulse. Similar to Eq. (11), the magnetic signal measured in Eq. (13) is the ensemble average over all the accumulated phases of the molecule’s trajectories, providing an analytic relation between the diffusion-magnetization propagator and the MR signal modeled by the random phase approach.

We note that originally, the PDF in the derivation by Carr and Purcell [2] was determined ad-hoc. The same ad-hoc PDF with the assumption of a constant diffusion coefficient within the voxel is also the building block of the familiar q-space formalism [15] and other advanced methods, which aim to improve the sampling of the microstructure by using the phase spectrum [32]. Moreover, the same representation was used to develop the matrix multiplication method [14], which provides analytical solutions for some specific geometries. Our analysis above, on the other hand, reveals the connection between the BT equation for a general form of D and the random phase approach through the derived Fokker-Planck equation. This connection and the explicit extra term in the generalized BT equation can help in developing approximations and simplified assumptions in order to analyze Eq. (11) in complex geometries; see for example [16, 33, 34].

5. Methods

We illustrate the difference between the generalized and conventional BT equations (Eq. (1) and Eq. (8)) using synthetic data from a two-dimensional system. Simulations of diffusion MR measurements (with a magnetic field in the ẑ direction) were achieved by choosing the spatially varying parameters, D, μ, and H [30, 35–37]. For in-vivo MR, these parameters generally vary on the micron length scale associated with cells, and clusters of cells. For our explicit illustration, we assumed no external force acting on the system such that the entire structure is encoded through D only. We compare two systems, one with a constant diffusion coefficient, D = D₀, and one with inhomogeneous diffusion with a parabolic shape D(x, y) = D₀(x² + y²)/ℓ² over a structural unit of size 2ℓ (i.e., x and y vary between −ℓ and ℓ), repeated periodically in both directions. We simulated two signals: one using the conventional BT equation, the other using the generalized BT equation. Specifically, we solved Eqs. (1) and (8) in two dimensions, in the presence of a parabolic diffusion coefficient, using the finite differences method, which approximates the computational domain by a square lattice. The edges of the lattice, i.e., the borders of the voxel itself, were defined with a pseudo periodic boundary condition [8]. The spatial dependence of D dictates the transition probabilities between lattice sites (note that D = 0 corresponds to no transition, i.e a solid wall). Single pulsed field gradient spin-echo experiments [38] are simulated with increasing gradient pulse amplitude, G = 10 − 70 mT/m, yielding a range of b-values of 30−1700 s/mm² depending on the diffusion time applied. Other parameters were: the duration of the gradient pulse, δ = 5 ms, the free diffusion coefficient of water D₀ = 2.3×10⁻³ mm²/s, structural unit size 0.02 × 0.02 mm₂, and two diffusion times, Δ = 50 ms (Fig. 2(a–b)) and Δ = 200 ms (Fig. 2(c)). The total number of grid points was 61 × 61. From the diffusion MR simulation, we also calculated an apparent diffusion coefficient by linearly fitting the logarithm of the average magnetic signal over a range of b-values.

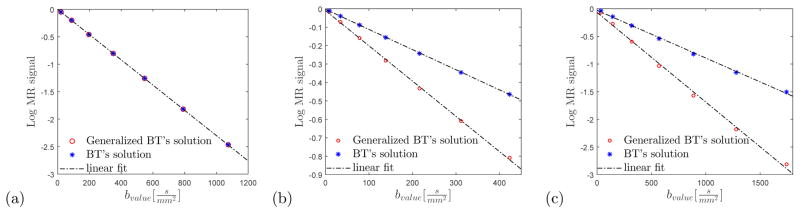
Figure 2.

Comparison of the generalized and conventional Bloch-Torrey (BT) equations. The logarithm of the averaged magnetic signal (normalized by the b-value=0 signal) as a function of the b-value is plotted for (a) a constant diffusion coefficient and (b,c) a parabolic shaped diffusion coefficient, at short (b) and long (c) diffusion times. The signal for the conventional BT equation (Eq. (1)) is plotted using blue stars, and the signal for the generalized BT equation (Eq. (8)) is plotted using red circles. A linear fit (dashed line) of the two curves presents the apparent diffusion coefficients (the slope of the lines). In (b) and (c) the two curves differ, suggesting that in inhomogeneous diffusion there is an additional decay that is not accounted for by the conventional BT equation.

6. Results

Figure 2(a) shows the magnitude of the simulated signal for constant D. As predicted, the simulated signals for the generalized BT (red circles) and the conventional BT (blue stars) were identical. Figure 2(b–c) presents the simulated signal for the parabolic shaped D. We can see that the simulated signal for the generalized BT decays faster than the signal for the conventional BT.

The goal of this simulation is to show that the extra term, when it exists, is not negligible. If we fit the results to a straight line and calculate the corresponding apparent diffusion coefficients as if the underlying tissue is homogeneous, then the difference is significant: the one with the extra term is ~ 1.21 × 10⁻³ mm²/s, and the other, calculated using the conventional BT equation is ~ 0.73 × 10⁻³ mm²/s. Figure 2(c) presents the signal for the parabolic D for a longer diffusion time (Δ = 200 ms). It shows that even in the long time limit the averaged diffusion coefficient converges to a different value when taking into account the additional term in the generalized BT equation.

7. Discussion

We have presented a simple microscopic stochastic model of molecular motion under a spatially and temporally varying magnetic field. The model analytically bridges the microscopic description of molecular motion with the macroscopic MR signal, allowing the simulation of complex microstructures with inhomogeneous diffusion coefficients, anisotropic diffusion, and restricted geometries.

One of the important results of our derivation is a generalization of the BT equation to a form that has an additional term, which accounts for inhomogeneous diffusion. Through our derivation, we prove that the conventional BT equation is valid for constant or piecewise constant diffusion coefficients, or under the assumption of the existence and uniqueness of the equilibrium density. However, in complex biological systems, these assumptions may not be valid, and the generalized BT equation would provide a more accurate description of the diffusion MR signal.

The BT equation is an important theoretical pillar of diffusion MRI, with extensive research taking place in the past 60 years [3, 10]. A solution to this equation for free diffusion and a piecewise constant diffusion coefficient in simple geometries was derived under different boundary conditions [4, 6, 10, 12, 33, 39]. A solution for more complex geometries may be achieved using numerical simulation [7–9]; however it requires additional assumptions, such as uniqueness and existence of the equilibrium distribution, which affect the BT equation and its boundary conditions, but may not be satisfied in general. Our generalized BT equation can improve the interpretation of diffusion MR experiments by avoiding some assumptions that otherwise might oversimplify complex systems. Moreover, modeling structural features of the medium through space-dependent diffusion coefficient allows one to withdraw boundary conditions that present major challenges in the analysis of the conventional BT equation. In particular, the inclusion of an interface layer with lower diffusivity can replace transmission boundary conditions [40], while the introduction of a boundary layer with either enhanced T₂ relaxation or localized internal gradients can model surface relaxation. Note that inhomogeneous D was previously considered [41] by representing microstructure as a spatial disorder, D(r), which is modeled following the effective medium theory. Here, we do not assume the spatial changes in D to be random and small, leaving it to be a general function which can be space and time dependent.

The validity of the assumptions regarding the existence and uniqueness of an equilibrium density is an open question [6, 30, 31] that merits additional considerations. The existence of an equilibrium density is easily justified in simple stationary examples, yet it might not be true in living tissue, where compartments may dynamically change their shape and size, and where the water consistency of intracellular and extracellular spaces is modulated by complex biological processes, such as membrane permeability and exchange, molecular transport, aquaporins, and inflammation. Due to the dynamic nature of biological systems, it is likely that the density is not static as well.

For a complex system the conditions on the equilibrium may be satisfied at one scale (in time and space), but not at the other. In fact, in multiscale structures (such as living tissues), physical description and governing mathematical equations can change from scale to scale. For instance, density (ρ_eq), diffusion (D) and drift (μ) may be constant at the lowest scales but become time and space dependent at higher scales, requiring strict and cross-scale assumptions in order to yield an equilibrium. In fact, the explicit relation (9) suggests that to achieve an equilibrium in inhomogeneous diffusion, there should be a drift force that exactly balances the change of density that is dictated by the additional term in the generalized BT equation. While such forces may be easily identified and verified at low scales and simple examples [26], it is not clear if they can exist in a dynamic and multi-scale specimen such as living tissue. Therefore, one cannot assume in general the existence of time independent equilibrium state of the system, especially if the structure of the system evolves with time (e.g., living tissue). For instance, non-equilibrium scenarios might be more appropriate for diffusion imaging of brain metabolites. It should also be mentioned that some dynamical properties, such as the time dependence of the instantaneous diffusion coefficient at long diffusion times, which was verified using coarse graining analysis, can also be measured from the macroscopic MR signal [31].

In addition to the existence of a steady state, cancellation of the extra term requires uniqueness of the equilibrium density. However, by definition, if the equilibrium density depends on the initial conditions, then the equilibrium density is no longer unique. Dependence on the initial condition may be expected in dynamic systems, or in open systems interacting with its surrounding environment [6, 30]. Clearly many biological systems are dynamic (e.g., cellular metabolism, changes in cellular shapes and sizes, exchange of molecules across compartments). However, dynamics may have different time scales, and further work is required to establish which dynamics are on a time scale that would effectively cancel the uniqueness of the density equilibrium and thus affect a diffusion MRI measurement.

An additional key element in our analysis is the derivation of the Fokker-Planck equation (7), which accounts for the joint effects of magnetization and diffusion. The access to its solution, the diffusion-magnetization propagator, reveals the analytical connection between the microscopic molecular model, the generalized BT equation, and the random phase approach. The relation between the random phase approach and the BT approach has been established long ago, e.g., Das and Saha [17] combined relaxation and diffusion, but, similar to Hahn’s approach [1], they only considered Gaussian diffusion. Later, the relation between the two approaches was rediscussed and generalized [10, 16]. Mathematically, the relation between the random phase and the BT equation may also be formulated using the Feynman-Kac formula [10, 42, 43]. This formulation suggests that the BT equation is similar to a backward Fokker-Planck equation [44]. When the coefficients of the BT equation do not depend on space and time, the backward and forward Fokker-Planck equations are identical. In turn, when the coefficients are time and space dependent, the connection between the BT equation and the random phase approach using the Feynman-Kac formula is more complex. Here, we derived the relation between these approaches using the general case of the forward Fokker-Planck equation with inhomogeneous coefficients D and μ.

The Langevin equation we used for the microscopic model originates from basic physical principles and has been considered previously, in different contexts, as the generating process of molecular diffusion [15, 17, 22]. We chose to use the Stratonovich microscopic description to prove the equivalence to the random phase approach. In future work, the microscopic model can be further generalized to non-Markovian systems which may also take into account interactions between pores [45, 46]. The model can be generalized further, for example, by including hydrodynamic flow or considering more general Louiville dynamics of spins [47]. While our simulations demonstrated the effect of inhomogeneous diffusion in space, they are equally applicable to dynamic diffusion changes over time. It is also worth noting that the extra term predicts that inhomogeneous diffusion still affects the signal, even if the magnetization is homogeneous. Therefore, this term may also affect T₂ weighted measurements.

When T₁ and T₂ are spatially invariant, they affect all the nuclei in the same way and their contribution can be factored out by comparing the diffusion-weighted signal to a reference signal (e.g., without a diffusion gradient). This standard scheme is not applicable for spatially dependent T₁ and/or T₂ relaxation that can potentially lead to intricate links with the spatially dependent diffusion coefficient. In general, the T₂ relaxation mechanism is mathematically equivalent to random disappearance of the transverse magnetic moment of a particle. Such phenomena are well studied in stochastic theory and can be modeled at the microscopic level by introducing an exponentially distributed lifetime of a particle (the T₂ relaxation time being the mean lifetime). This formulation could be extended to spatially dependent T₂ as well. In our case, the description is more subtle because the particle is preserved while its magnetic moment exponentially “decays”. Moreover, the effect would be different along the x̂, ŷ, and ẑ components. Accounting for the T₁ relaxation involves further complications because while the x̂ and ŷ components vanish, the ẑ component does not vanish but approaches an equilibrium value.

Another important observation is the way our approach handles surface relaxation. The Robin boundary condition imposed to the conventional Bloch-Torrey equation is an effective description of the surface relaxation due to magnetic impurities on the surface. The same phenomenon can be modeled in our framework by introducing a boundary layer, either with enhanced T₂ relaxation, or with an extra magnetic field (e.g., susceptibility-induced internal gradients). In the former case, the generalization would be similar to the generalization due to spatially dependent T₂, which was discussed in the previous paragraph. In the latter case, the matrix Λ (Eq. 4) would include both the externally applied gradient over the whole voxel and the internal gradients localized near the relaxing boundary. The exact relation of our framework to surface relaxation as well as a rigorous description of the links between inhomogeneous diffusion and inhomogeneous T₂ or T₁ are left for future work.

In this work we presented the forward problem of predicting the MR signal for inhomogeneous diffusion. Future studies should investigate the inverse problem, in particular, the ability to infer, based on the generalized BT equation, an appropriate diffusion tensor to describe a more complex underlying geometry. The currently available MR technology gives access only to average quantities at the millimeter scale. As a result, a large number of possible different diffusion tensor configurations could be mapped to the same measured signal. Solving this ill-posed inverse problem would require stabilizing the model fit by reformulation with, for example, the inclusion of an application dependent prior knowledge or a regularizer.

Appendix A. The Fokker-Planck equation

In the Stratonovich calculus, the propagator corresponding to Eqs. (2, 3) satisfies [21]

$${\partial }_{t}P=-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}P)-\nabla (\mathit{\mu }P)+\frac{1}{2}\nabla (P\mathit{\sigma }\nabla \mathit{\sigma })+\nabla (D\nabla P).$$ (A.1)

In the isotropic case, since σ∇σ = ∇D, we can write the equation with the extra term as follows:

$${\partial }_{t}P=-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}P)-\nabla (\mathit{\mu }P)+\frac{1}{2}\nabla (P\nabla D)+\nabla (D\nabla P).$$

For completeness, we also derive the microscopic stochastic equation in the Itô form using the Wong–Zakai corrections [21]

$$\frac{d\mathbf{a}}{dt}={\mathbf{A}}^I[\mathbf{a}(t),t]+B^I[\mathbf{a}(t),t]\mathbf{\eta }(t),$$

where the Itô coefficients denoted by A^I and B^I are related to the Stratonovich coefficients as

$$B^I=B,{\mathbf{A}}_k^I={\mathbf{A}}_k+\frac{1}{2}\sum _{ij}{B}_{ij}{\partial }_i{B}_{kj}=\left[\begin{array}{c}i\mathrm{\Lambda }\mathbf{m}(t)\\ \mathit{\mu }(\mathbf{r},t)+\frac{1}{2}\mathit{\sigma }\nabla \mathit{\sigma }\end{array}\right].$$

Using this relation we can derive the Fokker-Planck equation from the Itô formalism

$$\begin{array}{l}{\partial }_{t}P=-([{\nabla }_{\mathbf{m}},\nabla ]A^{I}P)+\frac{1}{2}\nabla \nabla (\mathit{\sigma }{\mathit{\sigma }}^{T}P)\\ =-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}P)-\nabla (\mathit{\mu }P)-\frac{1}{2}\nabla (P\mathit{\sigma }\nabla {\mathit{\sigma }}^T)+\frac{1}{2}\nabla \nabla (\mathit{\sigma }{\mathit{\sigma }}^{T}P)\\ =-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}P)-\nabla (\mathit{\mu }P)+\frac{1}{2}\nabla (P\mathit{\sigma }\nabla \mathit{\sigma })+\nabla (D\nabla P)\\ =-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}P)-\nabla (\mathit{\mu }P)+\nabla (P\sqrt{D}\nabla \sqrt{D})+\nabla (D\nabla P).\end{array}$$

The transition to the second line is due to the symmetry of the matrix $\mathit{\sigma }={\mathit{\sigma }}^T=\sqrt{2D}$.

Appendix B. Derivation of the generalized BT equation

In the main text we presented the generalized BT equation:

$$\frac{\partial }{\partial t}\langle \mathbf{m}\rangle =i\mathrm{\Lambda }\langle \mathbf{m}\rangle -\nabla (\mathit{\mu }\langle \mathbf{m}\rangle )+\nabla (D\nabla \langle \mathbf{m}\rangle )+\frac{1}{2}\nabla (\langle \mathbf{m}\rangle \nabla D).$$ (B.1)

Here, we provide a detailed derivation. Taking the Fokker-Planck equation (Eq. (A.1)), multiplying it by m, and then integrating over it, we get

$$\int \rho ({\mathbf{a}}_0,t_0)\frac{\partial P}{\partial t}\mathbf{m}d\mathbf{m}d{\mathbf{a}}_0=\int \rho ({\mathbf{a}}_0,t_0)\left[\nabla (D\nabla P)+\frac{1}{2}\nabla (P\mathit{\sigma }\nabla \mathit{\sigma })-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}P)-\nabla (\mathit{\mu }P)\right]\mathbf{m}d\mathbf{m}d{\mathbf{a}}_0,$$

where the probability P = P(a, t|a₀t₀) is defined in a volume V, and ρ(a₀, t₀) is the initial probability density at time t₀. Looking at the left hand side, and defining P̄(a, t) = ∫ ρ(a₀, t₀)P(a, t|a₀, t₀)da₀, we get

$$\int \rho ({\mathbf{a}}_0,t_0)\frac{\partial P(\mathbf{a},t\mid {\mathbf{a}}_0,t_0)}{\partial t}\mathbf{m}d\mathbf{m}d{\mathbf{a}}_0=\frac{\partial }{\partial t}\int \overline{P}(\mathbf{a},t)\mathbf{m}d\mathbf{m}=\frac{\partial }{\partial t}\langle \mathbf{m}\rangle ,$$

where m and a₀ are integration variables and therefore do not depend on time. The right hand side is

$$\begin{array}{l}\int \left[\nabla (D\nabla \overline{P})+\frac{1}{2}\nabla (\overline{P}\mathit{\sigma }\nabla \mathit{\sigma })-{\nabla }_{\mathbf{m}}(i\mathrm{\Lambda }\mathbf{m}\overline{P})-\nabla (\mathit{\mu }\overline{P})\right]\mathbf{m}d\mathbf{m}\\ =\nabla \left(D\nabla \int \overline{P}\mathbf{m}d\mathbf{m}\right)+\frac{1}{2}\nabla \left(\int \overline{P}\mathbf{m}d\mathbf{m}\mathit{\sigma }\nabla \mathit{\sigma }\right)\\ +\int (i\mathrm{\Lambda }\mathbf{m}\overline{P}){\nabla }_{\mathbf{m}}\mathbf{m}d\mathbf{m}-\nabla \left(\mu \int \overline{P}\mathbf{m}d\mathbf{m}\right)\\ =\nabla (D\nabla \langle \mathbf{m}\rangle )+\frac{1}{2}\nabla (\langle \mathbf{m}\rangle \mathit{\sigma }\nabla \mathit{\sigma })+i\mathrm{\Lambda }\langle \mathbf{m}\rangle -\nabla (\mathit{\mu }\langle \mathbf{m}\rangle ).\end{array}$$

The surface term in the integration by parts is zero since m · (m × H) = 0. Equating the two sides, we get the generalized BT equation (B.1) for the average magnetization. In the case of isotropic diffusion, one can substitute, σ∇σ = ∇D. For completeness, the phenomenological relaxation terms can be added:

$$\frac{\partial }{\partial t}\langle \mathbf{m}\rangle =i\mathrm{\Lambda }\langle \mathbf{m}\rangle +\nabla (D\nabla \langle \mathbf{m}\rangle )+\nabla (\langle \mathbf{m}\rangle \sqrt{D}\nabla \sqrt{D})-\nabla (\mathit{\mu }\langle \mathbf{m}\rangle )-\frac{\langle m_x\rangle \widehat{\mathbf{x}}+\langle m_y\rangle \widehat{\mathbf{y}}}{T_2}-\frac{\langle m_z\rangle -\langle m_0\rangle }{T_1}\widehat{\mathbf{z}},$$ (B.2)

where we use the relation $\mathit{\sigma }={\mathit{\sigma }}^T=\sqrt{2D}$. When D is not spatially dependent, the additional term is zero, and the equation becomes identical to the BT equation [4, 6].

Appendix C. The effect of the additional term on eventual boundary condition

In this section, the effect of the additional term in the generalized BT equation will be analyzed. For simplicity, we will consider here a one-dimensional system, whereas the generalization to higher dimensions is straighforward. The generalized BT equation in one dimension is

$$\frac{\partial }{\partial t}\langle \mathbf{m}\rangle =i\mathrm{\Lambda }(x)\langle \mathbf{m}\rangle -\frac{\partial }{\partial x}(\mu \langle \mathbf{m}\rangle )+\frac{\partial }{\partial x}\left(D\frac{\partial }{\partial x}\langle \mathbf{m}\rangle \right)+\frac{1}{2}\frac{\partial }{\partial x}\left(\langle \mathbf{m}\rangle \frac{\partial }{\partial x}D\right),$$ (C.1)

where the notation Λ(x) highlights that the magnetic field is a function of x. Let us assume μ = 0 and first consider the piecewise constant diffusion coefficient:

$$D(x)=D_0-(D_0-D_1)\left[\mathrm{\Theta }(x)-\mathrm{\Theta }(x-\ell )\right],$$ (C.2)

where Θ(x) is the Heaviside step function, D₀,D₁ are positive constants, and ℓ > 0 is a point on the x-axis, such that

$$\begin{array}{ll}\frac{\partial }{\partial t}\langle \mathbf{m}\rangle =i\mathrm{\Lambda }(x)\langle \mathbf{m}\rangle +D_0\frac{{\partial }^2}{\partial x^2}\langle \mathbf{m}\rangle \hfill & x<0\text{or}x>\ell ,\hfill \\ \frac{\partial }{\partial t}\langle \mathbf{m}\rangle =i\mathrm{\Lambda }(x)\langle \mathbf{m}\rangle +D_1\frac{{\partial }^2}{\partial x^2}\langle \mathbf{m}\rangle \hfill & 0<x<\ell .\hfill \end{array}$$ (C.3)

In this case, the additional term disappears, and the interface condition coupling two BT equations can be found in a standard way. For this purpose, we can integrate Eq. (C.3) over a small region [ℓ−ε, ℓ+ε] around the boundary point ℓ, assuming the magnetization is continuous at this point:

$$\frac{\partial }{\partial t}\langle \mathbf{m}\rangle (\ell ,t)2\epsilon \approx i\mathrm{\Lambda }(\ell )\langle \mathbf{m}\rangle (\ell ,t)2\epsilon +D_0\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell +\epsilon ,t)-D_1\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell -\epsilon ,t).$$

The limit ε → 0 leads to the usual condition of flux conservation across the boundary:

$$D_0\underset{\epsilon \to 0}{lim}\langle \mathbf{m}\rangle (\ell +\epsilon ,t)=D_1\underset{\epsilon \to 0}{lim}\langle \mathbf{m}\rangle (\ell -\epsilon ,t).$$ (C.4)

In order to see the effect of the additional term, we replace the unrealistic sharp drop in the diffusion coefficient in Eq. (C.2) by a smooth transition over a small region of size ε:

$$D(x)=D_0+(D_1-D_0)\left[{\mathrm{\Theta }}_{\epsilon }(x)-{\mathrm{\Theta }}_{\epsilon }(x-\ell )\right],$$ (C.5)

where

$${\mathrm{\Theta }}_{\epsilon }(x)=\frac{1}{1+exp(-x/\epsilon )}.$$ (C.6)

In contrast to the above analysis, in which ε was just an auxiliary small parameter, here 2ε plays the role of the characteristic width of the boundary region. In the limit ε → 0, one retrieves the Heaviside function Θ(x).

Now, the integral of the generalized BT equation (C.1) over the boundary region [ℓ − ε, ℓ + ε] yields

$$\begin{array}{l}\frac{\partial }{\partial t}\langle \mathbf{m}\rangle (\ell ,t)2\epsilon \approx i\mathrm{\Lambda }(\ell )\langle \mathbf{m}\rangle (\ell ,t)2\epsilon +\\ D_0\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell +\epsilon ,t)-D_1\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell -\epsilon ,t)\\ -{\frac{1}{2}(D_0-D_1)\left(\langle \mathbf{m}\rangle \frac{\partial }{\partial x}[{\mathrm{\Theta }}_{\epsilon }(x)-{\mathrm{\Theta }}_{\epsilon }(x-\ell )]\right)|}_{\ell -\epsilon }^{\ell +\epsilon }.\end{array}$$ (C.7)

The derivative in the last term reads

$$\frac{\partial }{\partial x}\left[{\mathrm{\Theta }}_{\epsilon }(x)-{\mathrm{\Theta }}_{\epsilon }(x-\ell )\right]=\frac{1}{4\epsilon {\text{cosh}}^2(\frac{x}{2\epsilon })}-\frac{1}{4\epsilon {\text{cosh}}^2(\frac{x-\ell }{2\epsilon })}.$$ (C.8)

Substituting this expression into the last term in Eq. (C.7), we get

$$\begin{array}{l}{\frac{1}{2}(D_0-D_1)\left(\langle \mathbf{m}\rangle \left(\frac{1}{4\epsilon {\text{cosh}}^2(\frac{x}{2\epsilon })}-\frac{1}{4\epsilon {\text{cosh}}^2(\frac{x-\ell }{2\epsilon })}\right)\right)|}_{\ell -\epsilon }^{\ell +\epsilon }\\ =\frac{1}{2}(D_0-D_1)\left(\frac{\langle \mathbf{m}\rangle (\ell +\epsilon ,t)}{4\epsilon {\text{cosh}}^2(\frac{1}{2}+\frac{\ell }{2\epsilon })}-\frac{\langle \mathbf{m}\rangle (\ell =\epsilon ,t)}{4\epsilon {\text{cosh}}^2(-\frac{1}{2}+\frac{\ell }{2\epsilon })}\right)\\ -\frac{1}{2}(D_0-D_1)\left(\frac{\langle \mathbf{m}\rangle (\ell +\epsilon ,t)-\langle \mathbf{m}\rangle (\ell -\epsilon ,t)}{4\epsilon {\text{cosh}}^2(\frac{1}{2})}\right).\end{array}$$

For a boundary at point ℓ to be well defined, its characteristic width 2ε should be much smaller than other physical distances of the problem, in particular, the distance ℓ between two boundaries. As a consequence, the first two terms in the above relation are exponentially small and can be neglected. Substituting these results into Eq. (C.7) and dropping the terms of order ε yields the following condition:

$$0=D_0\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell +\epsilon ,t)-D_1\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell -\epsilon ,t)-\frac{1}{2}(D_0-D_1)\left(\frac{\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell +\epsilon ,t)+\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell -\epsilon ,t)}{4{\text{cosh}}^2(\frac{1}{2})}\right),$$

from which

$$\left(D_0-\frac{D_0-D_1}{8{\text{cosh}}^2(\frac{1}{2})}\right)\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell +\epsilon ,t)=\left(D_1-\frac{D_1-D_0}{8{\text{cosh}}^2(\frac{1}{2})}\right)\frac{\partial }{\partial x}\langle \mathbf{m}\rangle (\ell -\epsilon ,t).$$

This is an effective boundary condition accounting for a smooth drop of the diffusion coefficient across the boundary of width 2ε. This relation can be compared to the usual boundary condition (C.4) at a sharp boundary.

Appendix D. The steady state solution

We derive the explicit condition on μ, on which the extra term disappears. We first derive the diffusion propagator from the diffusion-magnetization propagator by integrating over the magnetic moments, such that

$$P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)=\int P(\mathbf{a},t\mid {\mathbf{a}}_0,t_0)\rho ({\mathbf{m}}_0,t_0)d\mathbf{m}d{\mathbf{m}}_0,$$

where ρ(m₀, t₀) is the initial distribution of spins, which we assume to be uniform due to a uniform rf pulse at time t₀. Performing an integration over m and m₀ leads to the following diffusion equation:

$${\partial }_{t}P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)=\nabla (D\nabla P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0))+\nabla (P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)\sqrt{D}\nabla \sqrt{D})-\nabla (\mathit{\mu }P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)),$$ (D.1)

where the term that depends on the magnetic moment is zero on the boundary due to the steady state constant magnetic field. This equation can be written as the continuity equation

$${\partial }_{t}P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)=-\nabla \mathbf{J}(\mathbf{r},t\mid {\mathbf{r}}_0,t_0),$$ (D.2)

with the probability flux defined as

$$\mathbf{J}(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)=\mathit{\mu }P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)-D\nabla P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)-P(\mathbf{r},t\mid {\mathbf{r}}_0,t_0)\sqrt{D}\nabla \sqrt{D}.$$ (D.3)

At the steady state, ∂_tP(r, t|r₀, t₀) = 0, and the steady state probability flux,

$${\mathbf{J}}_{eq}(t\mid {\mathbf{r}}_0,t_0)=\mathit{\mu }{\rho }_{eq}-D\nabla {\rho }_{eq}-{\rho }_{eq}\sqrt{D}\nabla \sqrt{D},$$ (D.4)

does not depend on r, according to Eq. (D.2). Here we assumed the existence of an equilibrium density, ρ_eq = ρ_eq(r|r₀, t₀) = P(r, t → ∞|r₀, t₀). We can extract the following expression for μ from Eq. (D.4):

$$\mathit{\mu }=D\nabla \text{ln}(V{\rho }_{eq})+\sqrt{D}\nabla \sqrt{D}+\frac{{\mathbf{J}}_{eq}}{{\rho }_{eq}},$$ (D.5)

where a volume element V is added to get a dimensionless quantity (it disappears, anyway, because of the gradient operator). The steady state flux can depend on times t and t₀, and on the initial position r₀, whereas μ(r, t) depends on the current position r and time t, and not on the initial condition. Hence, Eq. (D.5) holds only if the equilibrium density is unique, ρ_eq(r|r₀, t₀) = ρ_eq(r). The requirement of uniqueness can be relaxed in the specific case when the steady state flux is J_eq(t|r₀, t₀) = −D(r, t)∇ρ_eq(r|r₀, t₀), which would require that ∇ρ_eq(r|r₀, t₀) exactly cancels out the spatial dependence of D(r, t). In this case, Eq. (D.4) implies $\mathit{\mu }=\sqrt{D}\nabla \sqrt{D}$, i.e no external drift or flow exists.

Appendix E. The Einstein-Smoluchowski relation

The Einstein-Smoluchowski relation can be derived by assuming Boltzmann equilibrium distribution ρ_eq = exp(−βU(r)), where F(r) = μb = −∇U, b is a friction constant, and β = 1/(k_BT) (k_B being the Boltzmann constant, and T the absolute temperature), such that,

$${\mathbf{J}}_{eq}(t)=\mathit{\mu }{\rho }_{eq}+D\beta {\rho }_{eq}\nabla U-{\rho }_{eq}\sqrt{D}\nabla \sqrt{D}={\rho }_{eq}\left(\mathit{\mu }+D\beta \nabla U-\sqrt{D}\nabla \sqrt{D}\right).$$

Furthermore, stationary equilibrium requires no net flux of particles (or of probability) in the system. This property should hold when the system asymptotically comes to rest, as long as there is no production or consumption of particles through chemical reactions. Therefore J_eq(t) = 0, which will lead to

$$(1-bD\beta )\mathit{\mu }=\sqrt{D}\nabla \sqrt{D}.$$ (E.1)

This relation is known as the Einstein-Smoluchowski relation, which is a form of the fluctuation-dissipation theorem. Substituting it back into the Fokker-Planck equation, we get the Smoluchowski equation:

$${\partial }_{t}P=\nabla (D\nabla P)-\nabla (bD\beta \mathit{\mu }P)=\nabla (D(\nabla -\beta \mathbf{F})P),$$

see also in [27, 28].

Appendix F. The validity of the transformation for the derivation of the random phase approach

In Eq. (12) we introduced the following transformation:

$$m_{+}=R(t)exp(i\varphi (t)).$$ (F.1)

In the Stratonovich calculus, a regular chain rule holds:

$$\frac{d{m}_{+}(t)}{dt}=\frac{dR(t)}{dt}\text{exp}(i\varphi (t))+i\frac{d\varphi (t)}{dt}{m}_{+}(t).$$ (F.2)

We know from Eq. (3) in the main text that

$$\frac{d{m}_{+}(t)}{dt}=i\gamma (H_0+\mathbf{G}(t)·\mathbf{r}(t))m_{+}(t)=i\frac{d\varphi (t)}{dt}{m}_{+}(t).$$ (F.3)

In order to have a well defined transformation, a condition is dictated on R(t) by equating Eq. (F.2) and Eq. (F.3):

$$\frac{dR(t)}{dt}=0,$$

with the solution R(t) = R(0) = R. We see that R(t) is constant, which depends only on the initial condition of m. Therefore, under this condition, the transformation is valid.