A numerical analysis of a semi-dry coupling configuration in photoacoustic computed tomography for infant brain imaging

Abstract

In the application of photoacoustic human infant brain imaging, debubbled ultrasound gel or water is commonly used as a couplant for ultrasonic transducers due to their acoustic properties. The main challenge in using such a couplant is its discomfort for the patient. In this study, we explore the feasibility of a semi-dry coupling configuration to be used in photoacoustic computed tomography (PACT) systems. The coupling system includes an inflatable container consisting of a thin layer of Aqualene with ultrasound gel or water inside of it. Finite element method (FEM) is used for static and dynamic structural analysis of the proposed configuration to be used in PACT for infant brain imaging. The outcome of the analysis is an optimum thickness of Aqualene in order to meet the weight tolerance requirement with the least attenuation and best impedance match to recommend for an experimental setting.

1. Introduction

The rate of growth of the brain during infancy, the most critical developmental period, is incomparable with that of any other developmental periods [1], [2]. A better understanding of the infantile brain change helps early detection of abnormalities and provides ideal opportunities for prevention and reduction of neurological and mental disorders in the most modifiable stage of the central nervous system. Among different neuroimaging methods for studying the infant brain [3], [4], [5], [6], [7], [8], [9], [10], photoacoustic (PA) imaging is a noninvasive modality that can potentially simultaneously provide high-resolution images of brain vasculatures and hemodynamics [11], [12], [13], [14], [15], [16]. With this method, improving an infant or child's compliance during neuroimaging sessions within a clinical setting would be possible. The PA imaging methodology involves a pulsed laser light source, ultrasonic transducers and an acoustic couplant layer between the imaging target and transducers. Transmission from an ultrasonic sensor is best received with a couplant to minimize degradation and signal loss, such as gaps or air bubbles [17], [18].

Acoustic couplants can be characterized in the following groups: liquids, gels, and dry couplants. Liquids and gels generally have lower acoustic impedances than dry couplant materials, and help reduce the large impedance mismatch between air and solid materials [19]. Water has a low acoustic attenuation and impedance which makes it a desirable PA coupling material, and is commonly used for PA imaging applications. However, due to the viscosities of liquids and gels, they tend to fall due to gravity, or dry out over a long period of time [20]. Liquid and gel couplants may sometimes lead to corrosion or a reduction in mechanical properties with the material being tested [21]. Coupling gels could also lead to potential bacterial growth if not cleaned properly [22]. These are some of the challenges that have led to studies exploring dry coupling materials as alternatives to avoid liquid/gel coupling in PA imaging. Dry coupling materials are desirable for applications in which the material would be needed for an extended period of time, such as daily usage for patients, and are generally preferred over liquid or gel couplants [23]. Reduced reflectance and low transmission loss of acoustic energy is needed for efficient dry coupling. Reduced reflectance is a result of the acoustic impedance of the couplant that needs to be close to that of the tissue [24], such that the acoustic energy is not lost due to high impedance mismatch between air and the couplant material [25].

Elastomers have been studied as the most popular dry couplant which have impedance values most similar to water. Additionally, they are most similar in overall performance to wet couplants [20]. There are several dry couplants that are polymeric materials, which are divided into three main categories: thermoplastics, thermosets, and elastomers. Crosslinked molecular chains are found in thermosets and elastomer materials, the major difference being that the molecular chains are not as heavily crosslinked in elastomers, and there is more freedom for the chains to relax after removal of a load [26]. Table 1 compares acoustic attenuation and impedance of water against several other polymeric materials [24], [27], [28], [29].

Table 1.

Acoustic impedance and attenuation of polymeric materials in literature [24], [27], [28], [29]].

Material	Impedance (MRayl)	Attenuation (dB/cm @ 5 MHZ)
Sylgard 184 (Silicone Elastomer)	1.03	–
Aqualene	1.46	2.8
Water	1.48	0.054
Acrylic, Clear	2.32	11.3
UHMWP	2.33	8
Polyurethane	2.36	27.6–100
Polypropylene	2.40	5.1
Polystyrene	2.52	1.8
Polycarbonate	2.75	23.2
Polyester	2.86	10–20
Epoxy	2.86	15–20
Nylon 6-6	2.90	12.9
Teflon	3.00	3.9

Although the represented materials do not have an attenuation low enough to match water, Aqualene is a material that closely matches water in impedance compared to other materials.

Dry couplants are preferred for PA imaging, due to the stability and structural support that water cannot provide, while still obtaining water's acoustic characteristics, specifically low attenuation and impedance matching. In this study, we explore the feasibility of a semi-dry coupling system including an inflatable container which consists of a thin layer of Aqualene with US gel or water inside of it to be used in a PACT system for infant brain imaging. If a rigid membrane is used as the couplant, the gap between the membrane and the infant's head will significantly attenuate the signal. If the membrane is purely flexible, such as Aqualene, the transducers will not be placed in a fixed position, hence the image will not be correctly reconstructed. The semi-dry configuration proposed here is chosen to utilize the flexibility of the dry coupling material while incorporating water to minimize the air gap between the inner and outer layers to obtain the best acoustic signal. Finite element method (FEM) is used for static and dynamic structural analysis of the proposed configuration. The outcome of the analysis is an optimum thickness of Aqualene in order to meet the weight tolerance requirement with the least attenuation and impedance.

2. Materials and method

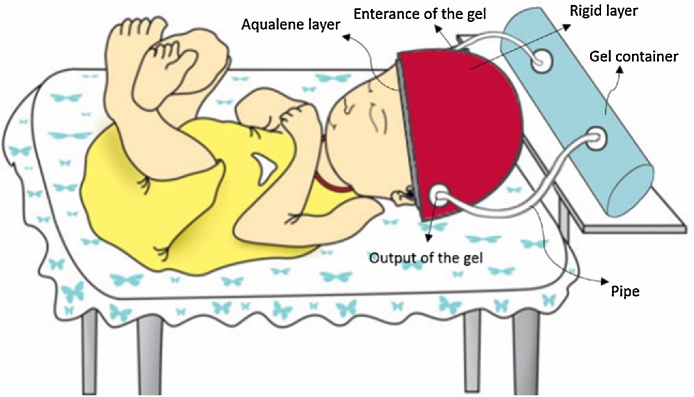
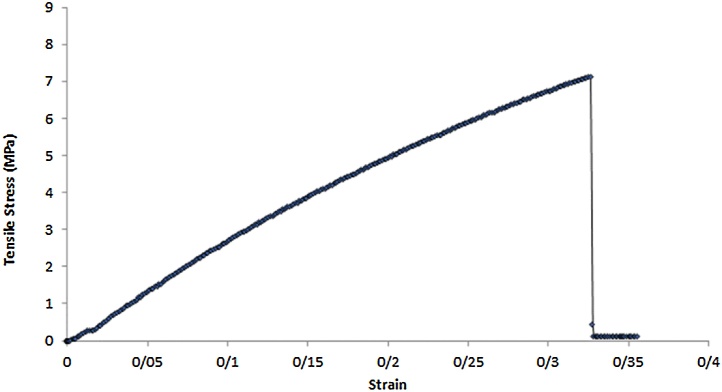
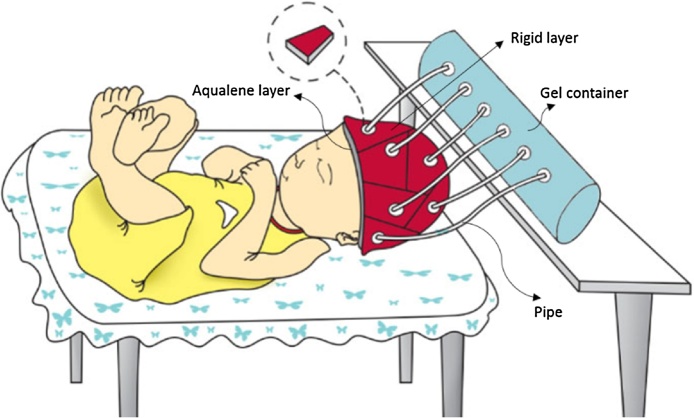
The analytical setup of the semi-dry coupling methodology mainly consists of a hemispherical cap designed for the head of an infant on which the US transducers are placed, the inflatable membrane, a pump and US gel/water. The cap comprises of two polymeric materials with two openings that allow water or US gel to flow between them, thus providing a semi-dry coupling set up. Fig. 1 represents the setup that was used for the theoretical analyses. In this cap, the outer layer and the inner layer were defined as a rigid layer and a deformable layer, respectively. The main purpose of the outer layer is to provide a closed space to contain the water surrounding the inner layer. Given that all the analyses were performed on the inner layer, the only criteria that was considered for the outer layer was that it needed to be rigid. Thus, the inner and outer layers chosen were Aqualene [29] and polyethylene [30], respectively. The specifications of these layers are presented in Table 2, Table 3. Table 2 lists the values cited from literature, and Table 3 lists the values that were determined experimentally for Aqualene. The only mechanical property information supported for Aqualene was the tensile strength and Young's modulus, which were listed as 3.3 MPa and 1580 MPa [31], respectively. Given the material was cited as an elastomer, and its incredibly high Young's Modulus that is not typical of elastomeric materials, five samples of Aqualene were tested at Wayne State University in the Department of Biomedical Engineering to obtain accurate mechanical property values. The samples were tested on a Mark-10 ESM301 from Wagner Instruments for tensile strength and strain at break, and the Young's Modulus was calculated from these values. The average Young's Modulus from the tested samples was 22.5 MPa. Fig. 2 shows the stress-strain curve of one of the samples with its experimental material properties listed in Table 3.

Fig. 1.

Set up of the theoretical analyses evaluated in this study (the ultrasound transducers that are not shown here, will be evenly distributed on the cap).

Table 2.

Material properties of the inner layer (Aqualene) and the outer layer (Polyethylene) [29], [30]].

Material properties	Polyethylene	Aqualene
Density (g/cm3)	0.96	0.92
Coefficient of thermal expansion (c−1)	2.4 × 10−4	3 × 10−3
Reference temperature (°C)	22	22
Poisson’s ratio	0.4	0.34

Table 3.

Material properties of Aqualene determined experimentally.

Width (mm)	12
Thickness (mm)	2
Length (mm)	55
Estimated Tensile stress (MPa)	7.02
Estimated Strain at Break	0.32
Estimated Calculated Modulus (MPa)	21.99

Fig. 2.

One of the five Aqualene samples that was experimentally tested for its tensile strength and strain at break. The values for this sample are listed in Table 3.

Additionally, the optical properties of Aqualene are also considered to prove its validity for this application. Simple optical properties characterization experiments were performed at Wayne State University in the Department of Biomedical Engineering. Observations showed that the very thin layer of Aqualene did not impact the light from scattering and absorption standpoints. The material is translucent, and only 0.2% light intensity reduction at a wavelength of 532 nm for 2 mm thickness was observed. No scattering effect on the light (comparing the beam size before and after the Aqualene layer) was observed during experimentation.

For the analysis, in order to displace the air between the inner layer of the cap and the head of the infant, the inner layer must be tangent to the surface of the infant's head with the least amount of pressure applied to prevent any damage to the head. Due to the lack of symmetry of the infant’s head and to achieve more precise results, a three-dimensional model of a one month-old infant's head is used. The model was constructed from CT Scan slices using the Mimics and Geomagic software programs provided by Shahid Sadoughi University of Medical Sciences and Health Services, Yazd, Iran. Two models were designed for the analytical simulations using the Abaqus and CATIA software programs.

In the first model, the cap was designed with Abaqus in a hemispherical shape. The diameter of Aqualene (inner layer) for the cap was set to 19.4 cm and the distance between the forehead and the back of the head set to 18.6 cm. The range of the distance to the skin was 4–10 mm for Aqualene. In this model, since the geometrical characteristics such as the diameter and the shape of Aqualene were constant, the only variable factor was thickness; thus, the thicknesses of Aqualene were changed from 0.4 mm to 1 mm, leading to three modes to be evaluated in Model 1. In the second model the CATIA software was used. The cap consisted of two layers; the materials were the same as in the first model. The cap design had the approximate shape of an infant's head with the thickness of Aqualene set to 0.4 mm. The range in diameter was 161–191 mm, and the range in distance between the skin and Aqualene was 2.3–3.5 mm.

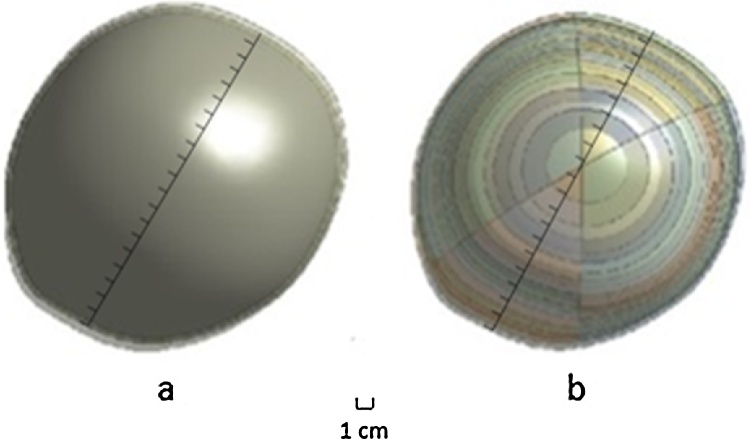
To analyze the data on the deformation of any part of Aqualene during loading, two more modes were analyzed to explore how the deformation changed at each of the distinct parts represented in Fig. 3 In the first mode, the surface of Aqualene was analyzed (a). In the second mode, Aqualene divided into 40 segments, where 10 distinct parts divided into four sections (b), was analyzed.

Fig. 3.

Presentation of two modes of Model 2, i.e., a and b. The modes are explained in the text.

For both models, the ANSYS Workbench Release 15.0 software is used. The Hypermesh software is used to create the mesh and was imported into the ANSYS program using Fluid Structure Interaction (FSI) method to perform the analysis. FSI is a branch of mechanics, generated from a mutual cross effect between hydrodynamics and solid mechanics which studies the behavior of solids in the flow field and the influence of deformation or movement on the flow field. With this fluid structure coupling problem solving method, Computational Fluid Xerography (CFX) and mechanical solvers run simultaneously exchanging data with one-way steady-state transfer from CFX to a structural system [32]. This study generates pressure distribution maps under working conditions using CFX evaluation of water and deformation under several load conditions for the inner layer. The properties of water from the ANSYS program can be seen in Table 4.

Table 4.

Properties of water used in simulations.

Density (kg m−3)	997
Specific heat type (J kg−1 k−1)	4181.7
Dynamic viscosity (Kg m−1 s−1)	8.899 × 10−4
Thermal conductivity (W m−1 K−1)	0.6069
Absorption coefficient (m−1)	1
Scattering coefficient (m−1)	0
Thermal expansivity (k−1)	2.57 × 10−4

3. Results

The simulation results are given for the modes discussed in the materials and method section.

3.1. Model1

For model 1, a hemispherical cap placed on a 3D model of the head of a one-month-old infant is analyzed. In this model, by exerting boundary conditions, the skin and a narrow slice of the cap where the inner and outer layers touch each other, are considered as a fixed support. Loading on the inner layer is carried out as a wide uniformly distributed load equal to the fluid pressure of water exerted on the inner layer. The simulation was performed for different pressures and thicknesses of the inner layer. The thickness was set to 1 mm and reduced to different values in order to evaluate how the deformation would change as a result of the pressures applied to each thickness. In the following, the modes defined in Model 1 are described.

3.1.1. Mode 1 of model 1

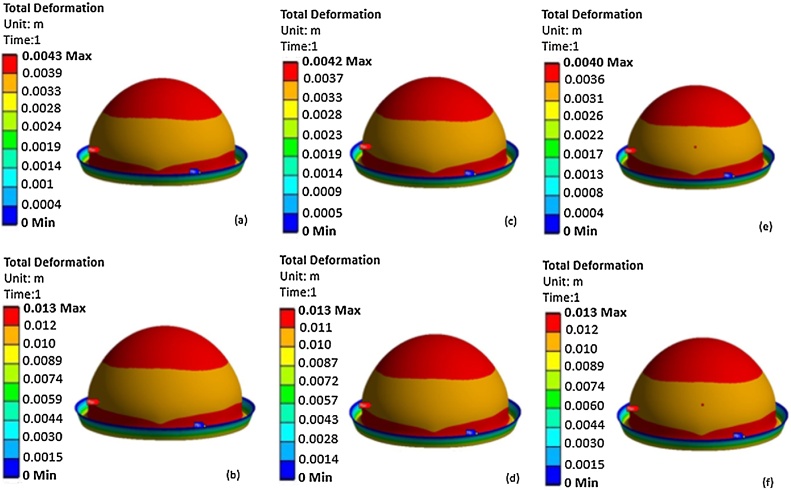
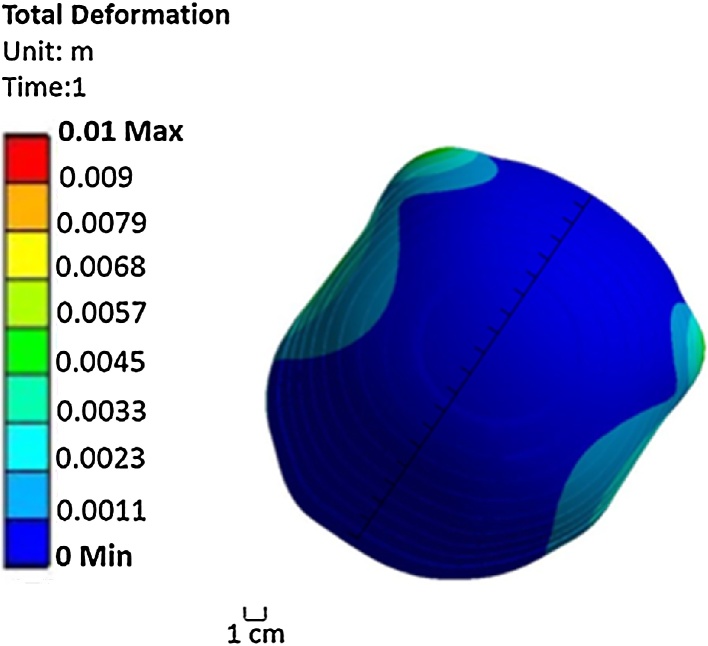
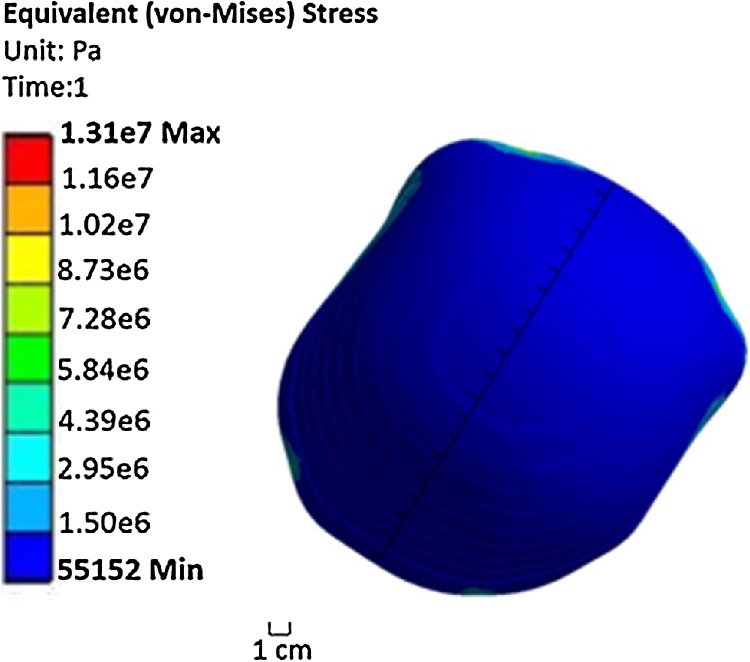
The thickness of the inner layer (Aqualene) was set to 1 mm, the pressure of the fluid in the space between the two layers was changed from p1 = 7 kPa to p2 = 22 kPa, and the distance between the skin and Aqualene changed from 4 mm to 10 mm. p1 was set to 7 kPa because, this was the pressure at which Aqualene touched the infant’s head. p2 was set to 22 kPa because this was the pressure at which all points of Aqualene covered the infant's head. Fig. 4a and b present the contour of deformation caused by exerting pressures of 7 KPa and 22 kPa, respectively. However, the difference of 15 kPa from the two pressures that was applied to some regions of the infant's head exceeded the limit at which the maximum pressure of 11.5 KPa could be applied without causing any damage. This pressure is computed as a result of the maximum allowable force of 50 lbs and an average area of an infant’s head [33]. The approximate area was calculated from Eq. (1), in which the mean of the head circumference measurements was incorporated, i.e., the mean circumference was 35.18 cm, and the area was 29.56 in² (see Table 5) [34]. Fig. 5a and b present the contour of equivalent (von-Mises) stress by exerting pressures of 7 kPa and 22 kPa, respectively. According to these figures, the maximum stresses were 0.644 MPa and 1.93 MPa, which were well below the tensile strength of Aqualene. Thus, the material is able to withstand the pressures applied without being damaged.

Fig. 4.

Analytical results of the deformation of Model 1 at the pressures applied to each thickness for each mode. (a) p1 of Mode 1, (b) p2 of Mode 1, c) p1 of Mode 2, d) p2 of Mode 2, e) p1 of Mode 3, f) p2 of Mode 3.

Table 5.

Percentile Head Circumferences (cm) for Males and Females at Birth [34].

Gender	3rd	5th	10th	25th	50th	75th	90th	95th	97th
Male	31.48	32.14	33.08	34.46	35.81	37.00	37.97	38.51	38.85
Female	31.93	32.25	32.75	33.65	34.71	35.85	36.95	37.65	38.12

Fig. 5.

Analytical results of equivalent(von-Mises) stress of Model 1 at the pressures applied to each thickness for each mode. (a) p1 of Mode 1, (b) p2 of Mode 1, c) p1 of Mode 2, d) p2 of Mode 2, e) p1 of Mode 3, f) p2 of Mode 3.

3.1.2. Mode 2 of model 1

The thickness of Aqualene was set to 0.6 mm, and the pressure of the fluid in the space between the two layers was changed from p1 = 6.8 kPa to p3 = 21 kPa. p1 was set to 6.8 kPa since it was the pressure at which Aqualene touched the infant's head. Similar to Mode 1, p2 was set to 21 kPa because this was the pressure at which all points of Aqualene covered the infant's head. Fig. 4c and d demonstrate the contour of deformation caused by exerting pressures of 6.8 kPa and 21 kPa, respectively. However, the difference of 14.2 kPa from the two pressures that was applied to some regions of the infant's head exceeded the limit at which the maximum pressure of 11.5 KPa could be applied without causing any damage. Fig. 5c and d present the contour of equivalent (von-Mises) stress by exerting pressures of 6.8 kPa and 21 kPa, respectively. According to these figures, the maximum stresses were 0.625 MPa and 1.9 MPa, which were well below the tensile strength of Aqualene. Thus, the material is able to withstand the pressures applied without being damaged.

3.1.3. Mode 3 of Model 1

The thickness of Aqualene was set to 0.4 mm, and the pressure of the fluid in the space between the two layers was changed from p1 = 6.5 kPa to p3 = 21.5 kPa. p1 was set to 6.5 kPa since it was the pressure at which Aqualene touched the infant's head. Similar to Mode 1 and Mode 2, p2 was set to 21.5 kPa because this was the pressure at which all points of Aqualene covered the infant's head. Fig. 4e and f present the contour of deformation caused by exerting pressures of 6.5 kPa and 21.5 kPa, respectively. However, the difference of 15 kPa from the two pressures that was applied to some regions of the infant’s head exceeded the limit at which the maximum pressure of 11.5 KPa could be applied without causing any damage. Fig. 5 and f present the contour of equivalent (von-Mises) stress by exerting pressures of 6.5 kPa and 21.5 kPa, respectively. According to these figures, the maximum stresses were 0.598 MPa and 1.98 MPa, which were well below the tensile strength of Aqualene. Thus, the material is able to withstand the pressures applied without being damaged.

In each case, by exerting a pressure p1, the area of Aqualene adjacent to the forehead and the back of the infant's head are the first places to touch the infant's head. It is not possible to increase the exerting pressure to infant's head, p1, more than 11.5 kPa, 0.2 kPa (safety margin) less than the maximum pressure calculated from Eq. (2) as 11.7 kPa. Thus, the limit was set to 11.5 kPa from p1 as a safety factor for each mode. According to Fig. 4, all points of Aqualene touch the head when exerting pressures that exceed 11.5 kPa from the starting pressure of p1.

A = 2πr² (1)

3 P = F/A (2)

Eq. (2) is used to compute the average pressure, such that P is the pressure applied to the infant's head, F is the maximum force that can be applied to the infant’s head, and A is the area of the hemisphere representing the infant's head.

Furthermore, since the distance between the head and Aqualene is not the same at all points and the top of the head has the greatest distance in this model, by exerting the maximum calculated pressure in the three modes mentioned above, it cannot be expected that all parts of Aqualene touch the head uniformly. This is due to certain areas exceeding the maximum pressure of 11.5 kPa that can be applied to the infant's head. Therefore, the cap should be designed in a way to minimize the distance of Aqualene to the infant's head (Model 2), and to analyze the effects of exerting both a uniform and non-uniform pressure (two modes) to determine that Aqualene approaches the surface of the head uniformly.

3.2. Model 2

In this model, the design of the cap is changed, and two modes are designed to analyze the effects of a uniform and non-uniform pressure as the fluid pressure, respectively.

3.2.1. Mode a of model 2

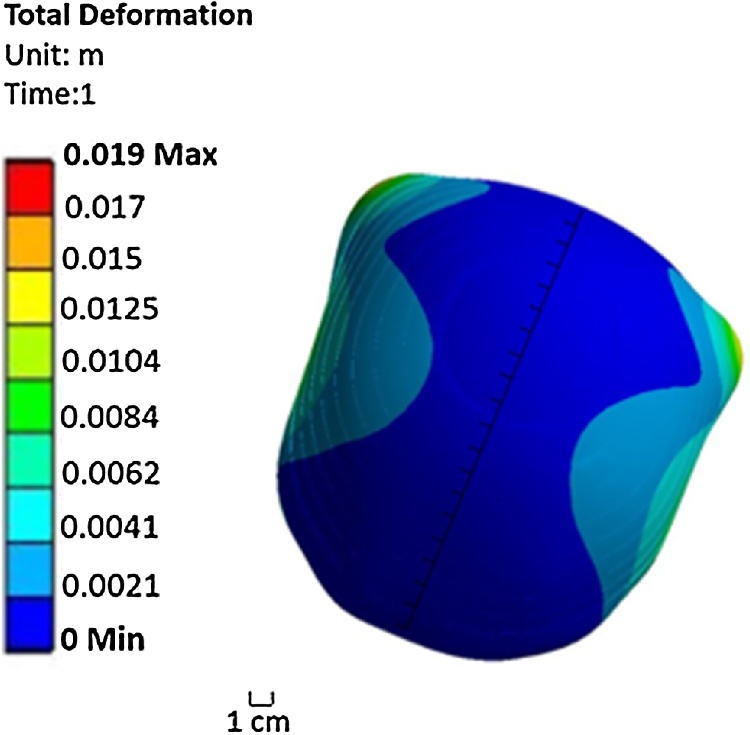
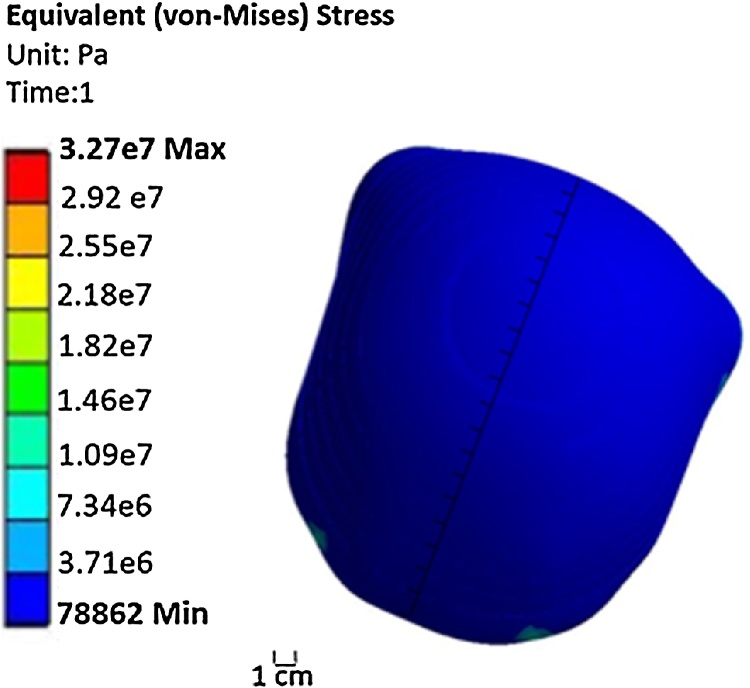
In order to maintain a pressure equivalent to the fluid rate once the water has been distributed throughout the area of the cap uniformly, a pressure of 10 kPa is required to be applied to the inner layer (Aqualene). The thickness of Aqualene was set to 0.4 mm, and the distance between Aqualene and the skin ranges from 2.3 mm to 3.5 mm. This range was determined from the geometry of the three-dimensional model of the head and Aqualene. Fig. 6 shows the contour of deformation caused by exerting a pressure of 10 kPa to Aqualene. The majority of the points represented have a deformation that is uniformly distributed. However, not all points of Aqualene touch the head at the same time within the range of 2.3–3.5 mm. Because of this, a non-uniform pressure is applied for the second mode of Model 2. Additionally, the contour of equivalent (von-Mises) stress in Fig. 7 has a maximum stress distribution of 1.5 MPa throughout the inner layer of the cap (Aqualene). This is well below the tensile strength of Aqualene. Thus, the material is able to withstand the maximum pressures applied.

Fig. 6.

Contour of deformation generated by exerting a pressure of 10 kPa for Mode a of Model 2.

Fig. 7.

Contour of equivalent (von-Mises) stress generated by exerting a pressure of 10 kPa for Mode a of Model 2.

The results of Mode a suggest that it is not possible to make all parts of Aqualene touch the surface of the head at the same time by simply changing the design of the cap and exerting a uniform pressure. Therefore, Mode b explores dividing Aqualene to 40 arbitrary parts with a non-uniform pressure applied to obtain a uniform deformation in which all points of Aqualene touch the infant's head at the same time.

3.2.2. Mode b of model 2

A non-uniform pressure was applied to Aqualene, with the thickness of Aqualene set to 0.4 mm. The distribution of the non-uniform pressure is listed in Table 6. The values in Table 6 show the external pressure for each of the 10 parts at each partition, such that there are 40 total segments evaluated. For each partition, the part indices are written such that the first part is at the top of the cap and the 10th part is at the bottom of the cap. Similar to Mode a, the distance between the inner layer and the skin ranges from 2.3 mm to 3.5 mm. Fig. 8 shows the contour of deformation caused by exerting the non-uniform pressure from Table 6 in which a nearly complete uniform distribution of deformation of 2.1 mm to 3.5 mm is achieved with all points of Aqualene touching the surface of the infant's head at the same time. Additionally, the contour of equivalent (von-Mises) stress in Fig. 9 has a maximum stress distribution of 3.7 MPa throughout the inner layer of the cap (Aqualene). This is well below the tensile strength of Aqualene. Thus, the material is able to withstand the maximum pressures applied. In Fig. 8, the back corners of Aqualene have a higher deformation. However, in reality this situation will not occur because the outer layer surrounds the inner layer and will prevent it from expanding past the outer layer boundary. Additionally, there is a small region by the ears where the deformation of Aqualene exceeds 3.5 mm. For this region, the thickness of Aqualene in that specific area can be adjusted to meet the range of Aqualene and the skin as represented in all remaining areas.

Table 6.

Distribution of non-uniform pressure from Mode b. The values are listed in units of kPa. The partitions of Aqualene on the infant’s head are as follows: the first is the left side, the second is the right side, the third is the front side, and the fourth is the back side.

Slice	1st partition	2nd partition	3rd partition	4th partition
1	29	29	5	7
2	29	29	5	7
3	29	29	5	7
4	29	29	5	7
5	29	29	5	7
6	7.8	8.4	5	7
7	7.8	8.4	5	7
8	7.8	8.4	4.8	7
9	7.8	8.4	4.8	6
10	7.8	8.4	4.8	6

Fig. 8.

Contour of deformation generated by exerting a non-uniform pressure on each of the 40 parts of Mode b of Model 2.

Fig. 9.

Contour of equivalent(von-Mises) stress generated by exerting a non-uniform pressure on each of the 40 parts of Mode b of Model 2.

4. Discussion

The purpose of this study was to prove the feasibility of the proposed semi-dry coupling methodology in PACT systems through numerical simulations which considered two different geometries for the cap. The coupling incorporated a thin inner layer of Aqualene with water between the inner and outer layers. Aqualene is used due to its impedance and material characteristics; its impedance nearly matches that of water, and its chemical composition, allows it to have an extended rubbery state resulting from controlled crosslinking at high temperatures and pressures [29]. Also, to displace the air between Aqualene and the infant's head, a water flow was set between the outer and inner layers. Thus, the pressure of the fluid removed the air gap [35].The simultaneous evaluation of deformation of Aqualene and the pressure exerted on the infant's head had a significant importance analytically. The deformation of Aqualene was mainly due to the material properties of Aqualene itself, such as its mechanical properties and chemical composition. The geometry of the cap had a significant influence on the pressure exerted on the infant’s head. The small range of pressure (11.5 kPa) that could be applied to the infant’s head presented some limitations in our analysis. This led to two different designs. The results of these designs demonstrated that the deformation throughout the cap for both models varied in different areas.

In the analysis of the first model, the distance between Aqualene and the skin was not uniform due to the hemisphere-shape of the cap, which led to some inconclusive results. Thus, three solutions were considered for the analysis of the second model: designing the model in the approximate shape of the head, taking into account the low thickness of Aqualene, and considering the effects of a non-uniform pressure applied to Aqualene by arbitrarily adding a number of sections to the cap design. The reason behind each solution is as follows:

4.1. First solution

Given the first model of the cap was hemispherical, the distance between the skin and Aqualene in areas above the head varied from areas adjacent to the forehead and the back of the head. The CFX evaluation demonstrated that by reducing the thickness of Aqualene from 1 mm to 0.4 mm, the deformation under several load conditions resulted in pressures exceeding the maximum limit that could be applied to the infant's head. As a result, the second model of the cap was changed into the approximate form of a head, hence the distance between the skin and Aqualene did not vary significantly at all the points considered and the cap touched the head more uniformly.

4.2. Second solution

Given that two of the most important properties of couplants in photoacoustic imaging are impedance and acoustic attenuation, Aqualene was the dry couplant material that nearly matched water in impedance. However, the acoustic attenuation of Aqualene among all other dry couplants considered was still significantly higher than water [28]. Thus, reducing the thickness of Aqualene from 1 mm to 0.4 mm was important and helped reduce the effects of its higher acoustic attenuation factor [24].

4.3. Third solution

In order to obtain a uniform deformation of Aqualene by exerting an acceptable pressure that can be applied to the infant's head, it is not possible to simply rely on a uniform pressure of the fluid. By considering the effect of a non-uniform pressure distributed to the inner layer from a theoretical perspective, analytical simulations demonstrated the effects of integrating arbitrary sections to the design of the cap. These effects are represented in Table 6 and Fig. 8. The slices are defined in Mode b of the second model, and their effects clearly represent how the pressure must be uniformly distributed due to the design structure. Thus, more desirable results can be achieved theoretically.

The results from the third solution present an important point regarding the non-uniform pressure applied to the inner layer. Because one thin sheet of Aqualene was used in the second model, a non-uniform pressure had to be applied with the integrated arbitrary sections to the design. In order to apply this solution experimentally, the design of the cap has to evolve into a beehive-shape, with a few sectioned areas of different sizes. Each section would have its own inner layer of Aqualene with water or US gel as the fluid flowing between the inner and outer layers. The pressures applied to each section would be different because of their own geometries, and would lead to an overall non-uniform pressure. The proposed set up is shown in Fig. 10.

Fig. 10.

Cartoon demonstrating the sectioned configuration (beehive-shape) design for the cap.

5. Conclusion

Due to the limitations found with liquid coupling in PA imaging, and limitations of dry coupling, here we studied the feasibility of a semi-dry coupling methodology to be used in PACT systems for infant brain imaging. Aqualene was chosen as the couplant layer due to its mechanical integrity, chemistry, and its acoustic properties. The deformation of Aqualene was analyzed from a theoretical perspective through numerical simulations that explored the effects of several factors.

Therefore, the practical system that we propose would incorporate Aqualene as the couplant (inner layer). Aqualene can be used as a thin sheet or as a powder. As a powder, it can be formed and casted to the approximate shape of an infant's head. Aqualene is also flexible, and can be integrated in several sections such that ultimately a non-uniform pressure can be applied throughout the entire cap. A thorough representation of data must be considered to get the best approximation for the cap design, incorporating a variety of geographical zones and genetics of several infants. The CT Scan information of all the infants studied will ultimately be used to simulate an average three-dimensional model used to make a phantom and produce the cap to prove its functionality and feasibility. The cap will be molded with a thickness of 0.4 mm to account for its mechanical and acoustic properties, specifically its acoustic attenuation factor. Additionally, it should be noted that water or US gel will flow between Aqualene and the rigid outer layer selected to accomplish the semi-dry coupling methodology.

By incorporating a more robust cap design that better represents the head of the infant, selecting a thickness of the inner layer that is more feasible mechanically and acoustically, and considering the analytical results that demonstrate the effects of non-uniform pressure, there is a stronger foundation in applying these recommendations to a physical part that can be utilized experimentally.

Conflict of interest

The authors declare no conflicts of interest.

Biographies

Najme Meimani is a graduate student in Mechanical Engineering at the University of Isfahan, Iran. She received her bachelor’s degree in Mechanical Engineering at Yazd University, Iran. She has over six years of research experience in the electro mechanics field. Since 2012, she started research in biomedical engineering, specifically simulation, and has been designing some innovative instruments in ophthalmology and heart surgery. She works with many programs, including CATIA, Abaqus, Ansys, and Matlab. Recently she has been working on simulation of Acoustic Radiation Force Impulse (ARFI) imaging at Tehran University of Medical Science.

Nina Abani In 2013, Nina received a B.S.E in Materials Science & Engineering from the University of Michigan. She works at Hi-Lex Controls, Inc. as a product engineer in Rochester Hills, Michigan since 2013. She is also a graduate student in Materials Science & Engineering at Wayne State University since 2015. During her time at the University of Michigan, she worked as a research assistant at the Advanced Life Support Laboratory and the Laboratory for Nanostructured Energy Conversion Devices. She also worked as a Research Experience for Undergraduates (REU) intern in the Plastics Research Group at Ford Motor Company.

Juri Gelovani clinical training has been in neurology, neurosurgery, neurotraumatology and neuroimaging. During the course of his career, he has served as a neurology and neuroimaging consultant in obstetrics and gynecology and neonatology. Dr. Gelovani is the pioneer of molecular-genetic in vivo imaging. His research interests include molecular PET imaging of cancer and the central nervous system using newly developed radiotracers, genomics and proteomics for cancer therapy, adoptive immunotherapy and regenerative stem cell therapies. He holds more than 15 patents, has published more than 160 papers and book chapters, and edited a major book in molecular imaging in oncology. Additionally, several diagnostic imaging compounds he developed are currently in clinical trials in cancer patients.

Mohammad R.N. Avanaki In 2012, Mohammad received a Ph.D. with Outstanding Achievement in Medical Optical Imaging and Computing from the University of Kent in the United Kingdom. His bachelor's and master's degrees with honors are in electronics engineering. In 2014, he completed a three-year postdoctoral fellowship at Washington University in St. Louis, in the OILab. He is currently an assistant professor in the Biomedical Engineering, Dermatology and Neurology departments of Wayne State University and Scientific member of Karmanos Cancer Institute. He is also serving as the chair of bio-instrumentation track.