Abstract
Super-resolution microscopy provides direct insight into fundamental biological processes occurring at length scales smaller than light’s diffraction limit. The analysis of data at such scales has brought statistical and machine learning methods into the mainstream. Here we provide a survey of data analysis methods starting from an overview of basic statistical techniques underlying the analysis of super-resolution and, more broadly, imaging data. We subsequently break down the analysis of super-resolution data into four problems: the localization problem, the counting problem, the linking problem, and what we’ve termed the interpretation problem.
Graphical abstract
1. A GLANCE AT SUPER-RESOLUTION
Processes fundamental to life, including DNA transcription, RNA translation, protein folding, and assembly of proteins into larger complexes, occur at length scales smaller than the diffraction limit of light used to probe them (<200 nm).
For this reason, up until a decade ago, these processes were largely inaccessible to conventional microscopy methods. Key technical achievements by way of experiments, from structured illumination methods1,2 to manipulations of fluorophore photophysics,3–5 have peered into this previously impenetrable scale with several techniques now providing detailed in vivo 3D images as shown in Figure 1.6
Figure 1.
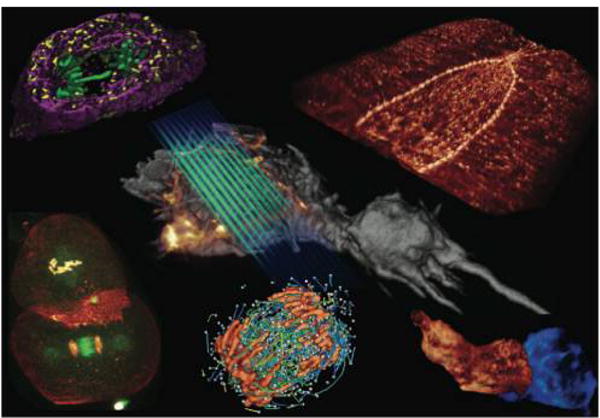
Recent optical microscopy methods like lattice light sheet resolve structures within cells.6 In addition to imaging an entire structure, single particle tracking is also possible with this technology providing simultaneous information on both the “environment” and “dynamics” of tagged biomolecules. Reproduced with permission from ref 6. Copyright 2014, American Association for the Advancement of Science.
On the experimental front, many technical challenges remain including the following: high density labeling; poor time resolution at the expense of high spatial resolution; challenges with fluorophore activation and complex photophysics; overexpression of select proteins altering cell homeostasis; and high light intensity, some ~104 times higher than that under which cells have evolved for methods such as photoactivated localization microscopy.7 Despite these challenges, experiments have begun to resolve the spatiotemporal dynamics and organization of cellular components within their native environment, revealing, for instance, the intricacy of yeast DNA transfer from mother to daughter cell8 and the stochastic assembly of chemoreceptors on E. coli’s surface.9 What is more, recent advances in optics have mitigated the spatial-temporal resolution trade-off providing greater in vivo resolution in 3D.6,10–18 Advances continue to accrue, with the latest techniques reaching spatial resolutions of ~1 nm and temporal resolutions on the order of μs.19
Ten years have passed since the inception of super-resolution microscopy and the variety of data collected has presented new modeling challenges.20 Initial data analysis methods, such as mean square displacement analyses, were directly motivated from the analysis of bulk ensemble data largely inspired by Occam’s razor. Thus, such methods did not explicitly take advantage of the richness of single molecule data sets such as their temporal ordering or even their intrinsic heterogeneity.
A large fraction of this review is devoted to later “data-driven” efforts, deeply inspired from the fields of machine learning and inference, and increasingly available through an array of open-source software,21–25 to turn the thousand-word picture provided by super-resolution methods into a quantitative narrative.
Here, we first review the basic physics of super-resolution methods (section 2) and tools of data-driven modeling (section 3). Subsequent sections tackle specific challenges present along the way: the localization problem (section 4), the counting problem (section 5), the linking problem (section 6), and what we’ve termed the interpretation problem (section 7).
2. BEATING THE DIFFRACTION LIMIT: AN INTRODUCTION
2.1. Why Fluorescence Microscopy?
Upon excitation of a sample within a specific wavelength range (the absorption spectrum), a fluorophore emits light at a longer wavelength (the emission spectrum). The excitation wave-length may be filtered away leaving behind only the emission from the fluorescent components. In this way, fluorescence brings improved contrast to microscopy.
The first fluorescence microscopes, developed by the Carl Zeiss company and others in the early 20th century, relied either on the autofluorescence of various tissues or chemical dyes and stains such as fluorescein.26 An important milestone in increasing the ability to fluorescently label a given biological structure was achieved by Coons et al. in the 1940s, who demonstrated that antibodies, raised to bind a specific antigen with high specificity, could be attached to fluorescent dyes, thus realizing a method to fluorescently label any antigen of interest.27 The subsequent discovery of the green fluorescent protein,28 together with advances in molecular biology techniques, then allowed the expression of proteins directly fused to fluorescent markers by the end of the 20th century.29
At the same time, the detection of the signal from single fluorophores (rather than larger labeled structures) was achieved by progressive improvements in instrumentation.30,31 This powerful combination of new advanced optical techniques with fluorescent protein tags, which could be detected in live cells at the single molecule level, set the stage for a new era of measurements in cell biology and biophysics.18
2.2. Point Spread Functions and the Diffraction Limit
Although labeling techniques have greatly improved over the last century, fundamental physical reasons have limited the resolution achievable by optical microscopy. Historically, this resolution has been defined as the ability to distinguish two close objects.
As early as 1834, Airy derived the profile of the diffraction pattern, or point spread function (PSF), of a point source of radiation imaged through a telescope, now known as the Airy disk.32 He established that “the image of a star will not be a point but a bright circle surrounded by a series of bright rings. The angular diameter of these will depend on nothing but the aperture of the telescope, and will be [sic] inversely as the aperture”.32 More precisely, for a telescope of aperture a imaging at a wavelength λ, the intensity I at an angle θ from the optical axis, relative to the intensity I0 at the center, is given by
| (1) |
where x = (2π/λ)a sin θ and J1 is the first order Bessel function of the first kind. Rings appear at the maxima x = x1, x2, … of I(x). In the limit of small angles (i.e., θ ≈ sin θ), these maxima correspond to θi = λxi/(2πa). Thus, the angular diameters of the rings are indeed inversely proportional to the aperture a (Figure 2).
Figure 2.
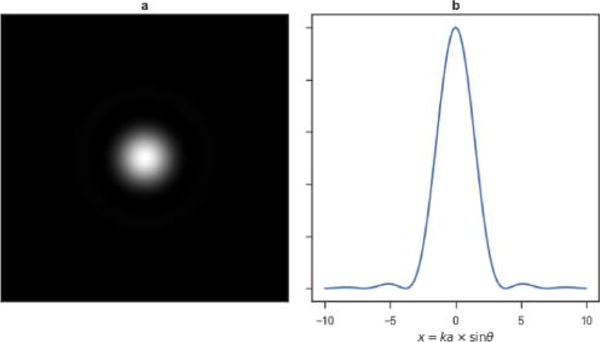
Point emitter generates an Airy spot (a) with an intensity profile (b) given by eq 1. The wavenumber k, used in (b), is 2π/λ. The intensity profile and diffraction spots were plotted using a simple Python script.
A few decades later, Abbe showed that a similar result held for optical microscopy: a point source imaged at a wavelength λ through a microscope objective of numerical aperture NA, defined as the product of the index of refraction of the medium between the objective and the sample, n, and the sine of the half angular aperture of the objective, θ, yields a spot of size d ≈ λ/2NA in the transverse direction and 2λ/NA2 in the axial direction33 (Figure 3).
Figure 3.
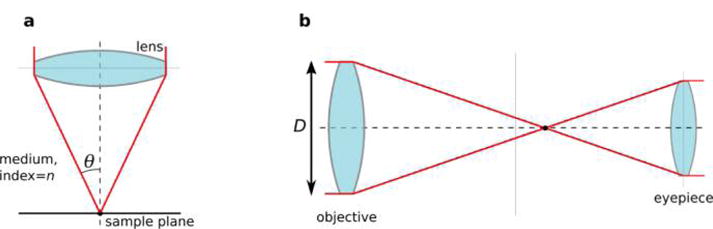
Microscope seen as a telescope. (a) A microscope’s resolution is determined by the numerical aperture NA of its objective, which is defined as the product of the index of refraction of the medium between the objective and the sample, n, and the sine of the half angular aperture, θ. (b) A telescope’s angular resolution is determined by its (physical) aperture, D. The intensity profile and diffraction spots were plotted using a simple Python script.
Whether in astronomy or microscopy, it is the finite extent of the image of a point source that limits our ability to separate two objects nearby. In 1879, Rayleigh suggested a rule, now called the Rayleigh criterion, whereas two diffraction spots could be considered as resolved if their centers were further apart than the center of a spot is from its first zero in intensity34 (Figure 4). He emphasized that this rule was simply suggested as an approximation “in view of the necessary uncertainty as to what exactly is meant by resolution”, though this rule still remains in use today.35 In fact, it is generally agreed in astronomy that spots up to ~20% closer are resolvable.35
Figure 4.

Fully resolved (a), barely resolved (b), and nonresolved (c) Airy diffraction spots. The intensity profile and diffraction spots were plotted using a simple Python script.
Nowadays, super-resolution imaging continues to leverage ideas and tools from astronomy, both on the experimental36 and analysis side.37
Even though the Rayleigh criterion may not be strictly accurate, the resolution of a microscope is certainly inversely correlated with the size of the diffraction spot. As this spot has a size of d = λ/2NA in the transverse direction and d = 2λ/NA2 in the axial direction, improvements to the resolution are achieved by working at a shorter wavelength or larger numerical aperture.
The room for improvement from changes in the wavelength is limited by the spectrum of visible light, λ = 400 to 700 nm. Electron microscopy achieves a much higher, near-atomic resolution by operating at a pm-scale wavelength, but this comes at the cost of invasive sample preparations, radiation damage to the sample, and low contrast.38
The numerical aperture NA = n sin θ has also reached its practical limits: now, oil immersion objectives (n ≈ 1.5) with half angular apertures of more than 60° achieve NA ≈ 1.4. Few (easy to work with) liquids have higher indices of refraction. Taking these improvements together, the smallest spot size that can be achieved is thus around 150 nm in the transverse direction and 400 nm in the axial direction (Figure 5).
Figure 5.
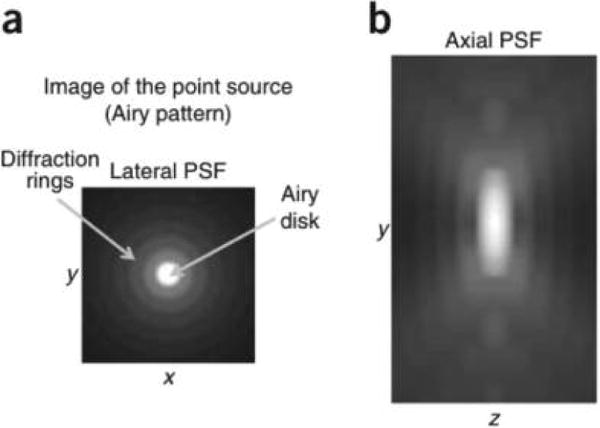
Projections of an example 3D PSF on (a) the x−y plane and (b) the y−z plane.39 Reproduced with permission from ref 39. Copyright 2011, Nature Publishing Group.
2.3. Beyond the Diffraction Limit
Objects may be distinguished from one another at a subdiffraction scale by using a combination of methods including structured illumination, stochastic fluorophore activation, and basic data processing.
As an example of the latter, if we approximate the imaging system as a linear system, i.e., where the measured image can be obtained by applying a linear operator (e.g., convolution by the PSF) to the original sample (e.g., the emitter’s original intensity distribution), it is in principle possible to mathematically invert (“deconvolve”) the imaging operator to reconstruct a higher resolution image, by solving a system of linear equations. Unfortunately, theoretical results indicate that the performance of such an approach is strongly limited by noise.40,41 Nonetheless, in the context of microscopy, this idea was first implemented by Agard et al.42 and may achieve a 2-fold improvement.43
Furthermore, Rayleigh’s criterion does not limit the ability to determine to very high accuracy the position of a single point emitter. For example, the center of a single spot can be estimated to a precision length smaller than the size of the spot itself by fitting the emission pattern to a known PSF, or an approximation of it, such as a Gaussian. The central limit theorem then suggests that the accuracy of such a calculation should be proportional to the inverse square root of the number of observed photons.
By determining the approximate position of emitters over a time series of fluorescence images, where the low density of fluorescent markers ensured their spatial separation, Morrison et al. tracked the diffusion of individual low-density receptors on cell membranes, with a resolution of ~25 nm, well below the diffraction limit.44,45
Even as early as in 1995, Betzig suggested that such a localization strategy may be applicable in more densely labeled samples as well, provided that “unique optical characteristics” could be imparted on individual fluorophores.46 Such “unique characteristics” would allow distinguishing the signals arising from each of the fluorophores; thus, the fluorophores underlying each diffraction spot could then be localized with subdiffraction accuracy.46
Betzig’s original suggestion was to discriminate certain molecules that would exhibit a random spread in their zero phonon absorption line width.46 However, it was instead the serendipitous discovery of a photoconvertible fluorescent protein, that is, a fluorescent protein whose emission spectrum can be modified by a light-induced chemical modification,47 as well as the development of optically switchable constructs based on organic dyes,48 that provided the critical advance toward the realization of this proposal in biological samples.
Briefly, the light-induced conversion of probes to a fluorescent state at a slow enough rate ensures that only a few probes are emitting at any given time even if the sample itself is densely labeled, thus generating the sparsity needed for localization in dense environments.3–5 Both labeling approaches were shown to be amenable to this technique: the approach based on fluorescent proteins was named (fluorescence) photoactivated localization microscopy ((F)PALM);4,5 and the approach based on organic dyes, stochastic optical reconstruction microscopy (STORM)3).
While this review will primarily focus on techniques that rely on the stochasticity of photoconversion to temporally separate the emission of different fluorophores, it is also possible to exploit another physical phenomenon to enforce this separation. Specifically, as early as in 1994, Hell et al. noted that while the diffraction limit imposes a lower bound on the size of excitation spots, it is possible to decrease the size of this spot by “deexcitation” (stimulated emission depletion, STED) of the fluorophores located on its edges.49 Specifically, this deexcitation is carried out by alternatively exciting fluorophores within a small region of the sample and immediately illuminating a doughnut-shaped area around this region with a depletion laser, bringing the fluorophores back to their ground state. The intensity profile of this second region is also diffraction limited; however, given enough time, only the fluorophores close to the exact center of the doughnut (where the deexcitation intensity is zero) stay active. Measuring the fluorescence of these remaining fluorophores thus realizes a point spread function that is effectively smaller than the diffraction limit.
A similar approach, relying on the readout of fluorescence along thin stripes rather than small spots, was also developed, under the name of saturated structured-illumination microscopy (SSIM).2 This method relies on the observation that high spatial frequencies in the fluorophore distribution can be “brought back” to a lower frequency under illumination by a similarly high frequency pattern (i.e., by observing the beats between the two patterns).50 Using linear optics (structured illumination microscopy, SIM), the illumination pattern itself is diffraction-limited, and thus the resolution improvement of SIM is limited to a factor of 2 over diffraction-limited microscopy; however, the nonlinearity offered by the saturation method described above allows the generation of higher-frequency patterns and thus further gains in resolution.2
Ultimately, the fundamental basis for any of these techniques is to note that the diffraction limit was derived under certain “standard”, but not absolute, hypotheses: that all fluorophore positions must be recovered from a single image and that the signal captured depends linearly on the excitation. Attacking the first condition, by spreading the information across multiple frames, is the approach taken by stochastic photoconversion. STED and SSIM, additionally, also violate the second condition, by operating in a nonlinear regime.
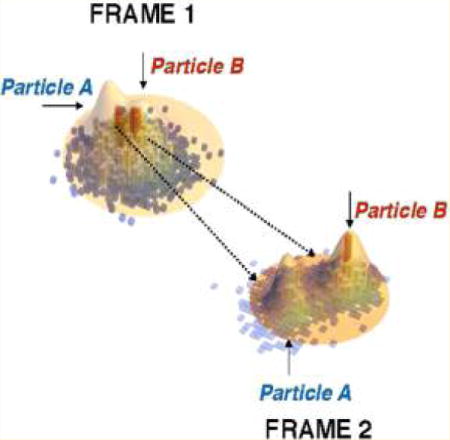
The large improvement in resolution afforded by structured illumination and stochastic activation of fluorophores, together termed super-resolution microscopy, immediately opened the door to a large number of discoveries. As early as in 2007, Shroff et al. demonstrated the ability of two-color super-resolution to resolve the relative positions of pairs of proteins assembled in adhesion complexes, the attachment points between the cytoskeleton of migrating cells and their substrates, which otherwise seem entirely colocalized in diffraction limited microscopy (Figure 6).51
Figure 6.
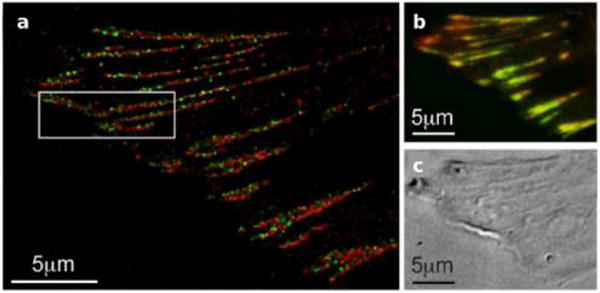
Two-color PALM can be used to address fundamental questions on molecular organization. (a) Adhesion proteins paxilin (green) and zyxin (red) are shown by two-color PALM to adopt different spatial distributions even though they appear colocalized in (b) diffraction limited microscopy. (c) A differential interference contrast image of the image shown in (b).51 Reproduced with permission from Hari Shroff, Catherine G. Galbraith, James A. Galbraith, Helen White, Jennifer Gillette, Scott Olenych, Michael W. Davidson, and Eric Betzig. “Dual-color superresolution imaging of genetically expressed probes within individual adhesion complexes.” Proceedings of the National Academy of Sciences 104, no. 51 (Dec 18, 2007): 20308−20313. Copyright (2007), National Academy of Sciences, U. S. A.
3. DATA-DRIVEN MODELING: KEY CONCEPTS
In the previous section, we discussed the basic physics underlying super-resolution microscopy. Here, we frame the foundational statistical ideas necessary for a quantitative treatment of super-resolution microscopy data that we will use in later portions of this review without exhaustively reviewing all tools or aiming at mathematical rigor.
While the methods and tools presented here are often established in statistics, examples drawn from optical microscopy will be used to motivate the ensuing discussion. We begin with a high-level description of two model building approaches: forward and inverse methods. Forward model-building approaches, whose first step is to posit physical models motivated by observation and first-principles,52 are broadly used in physics and chemistry. By contrast to forward modeling, inverse modeling approaches or “inference” use the data to learn the model under some assumptions.
The list below summarizes the essence of the data-driven, inverse, methods.
Propose model(s): Models or hypotheses are proposed. This includes proposing models for the system of interest such as whether motion of a particle is “directed” or “diffusive” and models for the measurement noise–such as photon statistics–treated in greater detail in section 3.1.1, which affects static53–55 and dynamic22,25,56–58 quantities throughout optical microscopy. Models proposed can be parametric or nonparametric models (as defined in section 3.1.2).
Inference/Data-mining: After a model form is selected, model parameters are inferred, or estimated, from the data. We review both frequentist and Bayesian inference methods (sections 3.2.1 and 3.2.2) and refer the reader to a recent review for information theoretic inference schemes.59
Reject or select model(s): After a model has been parametrized, we compare the model’s prediction(s) and consistency with existing or new data using hypothesis testing. Often the model’s consistency with the data is used to compare candidate models, a topic more broadly referred to as the model selection problem, discussed in section 3.3.
3.1. Deciding How to Propose Models
Models proposed often come along with assumptions about the system and its noise. These assumptions may be only locally valid. That is, while simple models of normal, confined, or directed diffusion12,60 may be valid over a small region of space or time, these models may not hold over the entire data set. In this case, locally valid models may be stitched or otherwise combined to describe the heterogeneity inherent to live cells.61–66 Indeed, systematic strategies for combining simpler models are an area of active research in statistics and machine learning67–69 that we will discuss in greater depth in section 7.3).
As a practical example, combining simple models together is important as is evident from single particle trajectories whose dynamics may be affected by molecular crowding,70–74 binding,63,75–79 or active transport.80–84 While an anomalous diffusion model may appear more appropriate for such in vivo dynamics, normal diffusion models are often still warranted for such apparently anomalous diffusive processes since, for instance, temporal and spatial resolution now experimentally resolvable can measure short diffusive trajectory segments before events typically leading to anomalous diffusion become manifest.61,63,65,66,85–88
Once models are obtained and parametrized, models provide a mathematical framework in which to address quantitative questions and test basic model hypotheses.
3.1.1. Signal versus Noise
Fluorescence microscopy data sets are intrinsically noisy. For example, the sample may exhibit background autofluorescence, the camera may introduce shot noise, experimental apparatus may drift during data acquisition, and molecules of interest may move faster than the acquisition rate.
The importance of accounting for measurement noise inherent to optical microscopy has been highlighted in the recent literature.24,88–93 For instance, it is now becoming more widely appreciated that neglecting measurement noise in single particle tracking (SPT) can be mistakenly interpreted as a signature of anomalous diffusion.22
In particular, inverse approaches, where models are directly drawn from the data, strongly rely on criteria to distinguish signal from noise. These approaches are particularly sensitive to noise models,61,86,94–96 and for this reason, it is often best to simultaneously infer the model for the system of interest together with the noise model in a self-consistent fashion. The hidden Markov model that we describe in greater depth in section 3.4.1 is one such example.
For now, we begin with a motivating example of noise encountered in attempting to localize a point emitter whose true spatial location, r, is assumed to be fixed (Figure 7). An estimate of the true spatial location r may be obtained, for example, as the center of a Gaussian PSF fitted to the 2D photon count histogram (a standard approach in super-resolution microscopy53–55).
Figure 7.
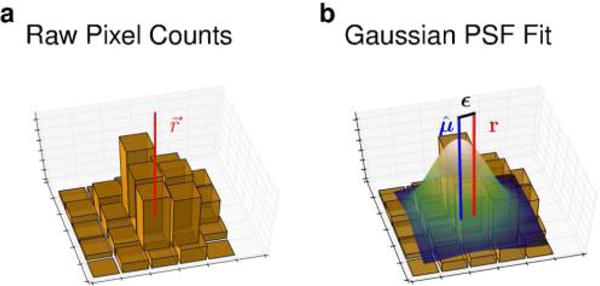
Measurement error affects particle localization. (a) 2D histograms contain photon numbers detected (by a CCD camera, say) along the x and y coordinates with the true molecular position (r) indicated by the point at which the solid vertical red line intersects with the x,y-plane. (b) In order to localize a static point emitter, the histogram may be fit to a PSF (e.g., a Gaussian or an Airy function) illustrated by a color surface contour. The estimate of the emitter’s position, μ, shown by a solid vertical blue line, is approximated from the PSF. The difference between μ and r is the localization error ε. Factors such as photon count, exposure time, pixel size and background autofluorescence all contribute to ε.
A careful description of the various methods for extracting from the data (section 4) will highlight how finite photon counts, camera pixelation, camera-type specific noise, and background autofluorescence all contribute to the noise,54,56 and cause the estimated position to differ from the true molecular position by an error ε, that is,
| (2) |
The error ε, illustrated in Figure 7, is typically assumed, in static imaging applications, to be a random variable of mean zero.53,54
Beyond the type of noise that we have surveyed here that arises in inferring models from static structures, we briefly mention noise sources that arise from molecular motion during imaging such as “motion blur” or “dynamic [measurement] error”22,56 discussed in greater depth in sections 6.5 and 7 and illustrated in Figure 8.
Figure 8.
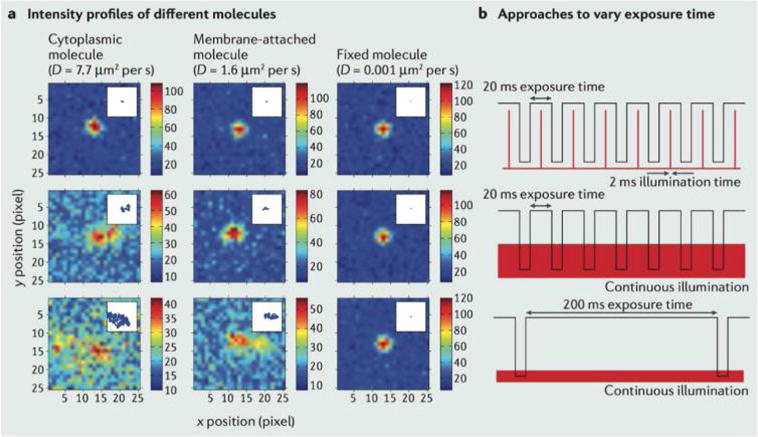
Motion and optics affect measurement noise. The simulated images illustrate how thermal motion, inherent to nanoscale measurements, affect the intensity profile of three molecules with different (given) diffusion coefficients D (describing the diffusion of cytoplasmic, membrane- attached and fixed/immobile molecules) shown in the columns of panel (a). (a) The estimated point spread function (PSF) measured for different molecules under alternate illumination strategies (shown in the rows). The color bar displays the number of photons collected. (b) The illumination strategies are stroboscopic (top), continuous illumination with short camera exposure time (middle), continuous illumination with long camera exposure time (bottom). The two-state signals shown denote the state of the shutter (open/closed) and laser (on/off). The localization precision (accuracy and uncertainty) is affected by how accurately the PSF can be inferred from digital images produced by tagged molecules. The plots from panel (a) demonstrate how some molecular and sampling parameters affect measurement noise statistics when the PSF is used to infer the molecular position. “Smearing” of the PSF, induced by motion blur when a simulated molecule spans an area covered by different pixels in a single frame, introduces a new source of position uncertainty (in addition to the localization noise described in Figure 7). Reproduced with permission from ref 97. Copyright 2013, Nature Publishing Group.
Motion blur presents important theoretical challenges: (i) it complicates the task of localizing particles, whose localization may no longer be adequately modeled using temporally uncorrelated Gaussian noise22,25,54–56,58 (section 4)); (ii) it complicates linking localized point emitters across frames into a single particle trajectory (section 6); and (iii) it fundamentally alters the interpretation of kinetic data12,15,22,25,58,86,95,98–100 (section 7). As a more concrete example of the latter, the point emitter’s motion within a single image frame statistically couples measurement noise to the molecule’s thermal fluctuations,22,25,58 which is a coupling often ignored.54,55,60
Faster data acquisition may not necessarily reduce dynamical noise since, as is described in the stochastic process time series literature,101,102 improved temporal resolution comes hand-in-hand with increased measurement noise (section 6.5). As a result, recent literature has begun addressing the problem of disentangling measurement noise from thermal noise in high frequency (above 10 kHz) single molecule measurements.103–105
Noise is unavoidable and the mathematical frameworks we present in subsequent sections present principled strategies for incorporating knowledge of noise statistics into the process of model inference.
3.1.2. Parametric vs Nonparametric Modeling Frameworks
Once a model for both the system of interest and its associated noise are selected, the next step is to infer all model parameters. The main feature distinguishing parametric from nonparametric models is the number of parameters or, more precisely, how this number depends on the amount of data available.
Parametric methods have a fixed number of parameters, independent of the amount of data.106 In other words, a parametric model’s functional form, M, is prespecified and its parameters, θ = {θ1, θ2, ⋯, θK}, are K numbers to be determined from the data, D = {D1, D2, ⋯, DN}. Thus, rigid assumptions on the nature of the model are made before data is even considered. Despite this apparent shortcoming, parametric models also present important advantages: they are easily interpretable and parameters can be estimated “efficiently”, where efficiency is measured in terms of an estimator’s parameter variance relative to the Cramér-Rao lower bound (CRLB).54,107
As an example of a parametric model, we assume that we are modeling the data as independent identically distributed (iid) draws from a 1D Gaussian density indexed by its parameters θ ≡ (μ, σ). The model, captured by the conditional probability of the data given the model, is
| (3) |
Having just selected a parametric family for p(Di|θ) we may now use the data to provide an estimate for θ denoted by .
The model above makes a number of implicit assumptions. For example, it assumes a priori that there are no statistical dependencies between measurements; noise is time-independent, the density of the random variables are unimodal, the mean of the random variables equals the mode of the distribution, etc. These a priori specifications highlight the type of rigid structure that is often imposed by a parametric model.
By contrast, the phrase “nonparametric model” implies that a model is not initially characterized by a finite, fixed number of parameters.106,108 Nonparametric methods are advantageous as they provide the flexibility to account for features arising in the data that were not a priori known. For example, if the process under consideration is characterized by a fixed, albeit multimodal density, where the number of modes is unknown in advance, a nonparametric model, such as a kernel density estimator,109 would reveal the more complex shape of the density characterizing the data generating process as more data becomes available. By contrast, a parametric approach would likely misbehave since the multimodal aspect of the data was not explicitly accounted for in advance.
Although nonparametric approaches are more general, they do not avoid modeling assumptions106,108 and infinite amounts of data do not necessarily “automatically guide one to the correct model”. More concretely, the iid assumption, which can be verified by statistical methods110–112 discussed in section 3.3), may still be incorrectly invoked by a multimodal (mixture) model. In particular, the “identical” aspect of iid is often suspect, as the distribution from which each observation is sampled may change over time due to, for example, drift in the alignment of optical components.
3.2. Inference
Parametric and nonparametric models alike contain parameters that we must learn, or infer, from the data. Here we review two approaches to parameter inference, frequentist or Bayesian, and we refer the reader to Tavakoli et al.59 and Pressé et al.113 for information theoretic approaches.
3.2.1. Frequentist Inference
The term “frequentist” in the statistics literature implies that there exists a fixed parameter θ responsible for generating the observations. The frequentist approach can be summarized as follows: (i) “probabilities” refer to limiting relative frequencies of events and are objective properties and (ii) parameters of the data generating process are fixed (typically unknown) constants.106
Maximum likelihood is a common frequentist approach to parameter estimation and it yields a maximum likelihood estimate (MLE) for an unknown parameter.106,110,114
Briefly, in maximum likelihood estimation, we begin by writing down a likelihood, the probability of the sequence of observations given a model,
conjectured to have given rise to the these observations. For shorthand, we drop the M dependence such that p(D1, D2, …, DN|M, θ) = p(D1, D2, …, DN|θ). We then maximize the data’s likelihood with respect to the parameter vector θ associated with the posited model M.
For example, for iid observations where , the MLE for θ is
| (4) |
where the MLE, , maximizes the log likelihood function l(θ|D). While both the likelihood and its logarithm yield identical MLEs, likelihoods are typically small quantities and logarithms are used to avoid numerical underflow problems.
To make our example specific, suppose we want to estimate the emission rate of a fluorophore, r, from a single count of the number of photons emitted, n, in time interval ΔT. Our model assumes that all photons emitted are collected and that the number of photons emitted per time interval is Poisson distributed. Under these model assumptions, the likelihood of observing n photons given our model is
| (5) |
By maximizing the likelihood, eq 5, with respect to the rate, r, we obtain an estimate for the rate in terms of known quantities, . Any other value of r would decrease the likelihood of observing n photons in the interval ΔT.
3.2.1.1. Time Series Analysis and Likelihoods
Likelihood ideas readily accommodate time series data as they respect the natural time ordering of observation. This feature of likelihood methods is especially useful in treating temporally correlated observations that arise in tracking superresolved particles or even counting fluorophores within a region of interest.12,14,15,21,66,85–88,115
For example, consider the simplified case where the data consists of a series of coordinates at different points in time D = {r1, r2, …, rN}. Here, the likelihood over the full joint distribution of the time ordered data, p(D|θ), is given by
| (6) |
While we’ve assumed in writing D = {r1, r2, …, rN} that the data provided positions with no associated uncertainty, we discuss noise in greater depth thoughout this review.
Accurately computing the likelihood and maximizing it with respect to all model parameters, such as all conditional probabilities that appear in eq 6, is difficult because of the large number of conditional probabilities that appear when N is large.110 The Markov assumption for first-order Markov processes, that the probability of sampling ri at time point i only depends on the state of the system in the immediate past (i − 1), is therefore commonly invoked in SPT analysis in order to reduce the number of parameters that must be inferred. From this point on, whenever we refer to Markov processes or the Markov assumption we assume they are first-order. While the validity of the Markov assumption can also be checked,110 there are information theoretic reasons for a priori preferring Markov models, discussed elsewhere.113,116
Under the Markov assumption, eq 6 reduces to the more tractable form
| (7) |
with the Markov process’ conditional density, p(ri |ri−1, θ), often called the “transition density”.
As a more concrete example for which the transition densities take specific functional forms, suppose the model, M, coincides with simple normal diffusion and observations are uniformly spaced Δt time units apart. For this example, the transition density of a time series measured without noise, p(ri |ri−1, θ) is available in closed-form and is a Gaussian density with mean ri−1 and, for standard SPT models, covariance matrix 2DΔt where D is a diagonal matrix of diffusion coefficients.
In more general Markovian time series models, obtaining the transition density often requires solving the Fokker–Planck equation associated with the posited model M for the model’s transition density.117,118 Since the Fokker–Planck equation may lack a closed-form solution, the transition density may therefore not have an analytical form adding to the computational cost of likelihood maximization. While it is true that individual likelihoods are simple, their products can become very complicated and significantly increase the computational burden. In and of itself that should not be a prohibitively expensive computational issue. However, given the size of the computational burden already needed for processes such as linking algorithms, an increase due to the need to solve numerically elaborate likelihoods might well be the proverbial “straw that breaks the camel’s back”.
While some popular Markovian motion models arising in super-resolution trajectory analysis (section 7.1) admit closed-form transition densities,25,86 others do not. For this reason, we mention that approximating a likelihood may introduce biased parameter estimates which, in turn, may affect the outcome of model goodness-of-fit tests (section 3.3) used to check the consistency of the model with the data.
3.2.1.2. Confidence Intervals
The precision of a parameter’s MLE is quantified by the concept of confidence interval (or a confidence set if multiple parameters are estimated). In order to introduce this concept, we briefly return to the example shown in Figure 7 where we suppose that an emitter, fixed in space, does not photobleach. Under this circumstance, we repeatedly image the molecule, and for each of the N independent images measured, a different number of photons are collected due to the inherently stochastic emission properties of the fluorophore, as well as other noise sources.
As a result of these variations, different images produce different empirical PSF fits. These fits yield the following hypothetical estimates of a molecule’s position
For each estimated mean, , we may then compute confidence intervals at the level of 1 − α where α ∈ [0,1] (and where α = 0.05 is typically used, which corresponds to computing the 95% confidence interval).
Confidence intervals are functions of the observed (random) data and the assumed model. Within a frequentist inference framework, the true fixed parameter either does or does not fall within the confidence interval106 (i.e., with probability 1 or 0 since the frequentist parameter is not random), but the width of the confidence interval does give an indication of the “quality” of the measurement. It should be noted that, despite being very useful in accounting for random errors, confidence intervals critically depend on the assumed model and can fail if this model is wrong or if undetected systematic errors exist.
In our example, one could compute the collection of confidence intervals associated with each of the estimates . By definition, if the data was indeed generated from the specified model, then a fraction 1 − α (e.g., 95%) of these confidence intervals will contain the true (unknown but fixed) molecular position, r.
As mentioned earlier, maximum likelihood methods are popular in part because, in the limit of infinite sample size, they asymptotically achieve the CRLB.54,119–121 In the non-asymptotic regime, it is ultimately the shape and breadth of the full likelihood function around its maximum which provides an estimate for the quality of the MLE.
3.2.1.3. Other Frequentist Estimators
Maximum likelihood is not the only type of frequentist method. Among other frequentist methods, we can mention least-squares regression53 which reduce to maximum likelihood under the assumption of Gaussian uncorrelated noise, generalized moment-type methods110 (which match select model moments to the data), and general least-squares (which minimize the distance of a parametrized function from the data).
While typically less efficient (as measured by the CRLB) than likelihood maximization,110 both moment and least-squares methods can be attractive, because computing the exact likelihood can be complicated or intractable in some models since the full joint distribution may not be known or easily computable. Hence, an approach only requiring specification of a few moments or minimizing the distance to a parametric function may be preferred.
3.2.1.4. Fundamental Assumptions of Frequentist Inference
We end this section on frequentist inference with a note on the assumption that the parameter to be inferred is “fixed”. While this may appear as an advantage, heterogeneity inherent to live cells may require the assumption of having a single fixed parameter vector describing all data to be relaxed.
What is more, in live cell super-resolution applications, in vivo conditions can never be exactly reproduced and thus each experiment is never a true iid draw as described in our hypothetical example used to illustrate the confidence interval concept.
This being said, a collection of point parameter MLEs can still be useful in quantifying live cell heterogeneity. For example, once the MLE of an assumed model and data set are obtained, this MLE can be used to verify the model’s consistency with the data. If the model is deemed consistent, the MLE can be used to compute a theoretical CRLB or to simulate new observations in order to compute “bootstrap estimates” of the MLE parameter’s confidence interval.106,122 The simplest indication of heterogeneity would then be suggested by nonoverlapping confidence intervals.
3.2.2. Bayesian Inference
Bayesian methods, now widely used across biophysics,61,65,96,123–127 are defined by the following key properties:106 (i) a probability describes a degree of belief, not a limiting frequency, (ii) distributions for parameters generating the data can be defined even if parameters themselves are fixed constants, and (iii) inferences about parameters are obtained from “posterior probability” distributions.
While frequentist methods yield parameter “point estimates” or MLEs, Bayesian methods return a full distribution over unknown parameters (the posteriors) for the same amount of data. Because the posterior is a joint distribution over all parameters, it can also quantify relationships between parameters. Therefore, while frequentist methods treat the data as a random variable, Bayesian methods treat data in addition to model parameters, as random variables.128
In frequentist reasoning, the likelihood played a central role. By contrast, in Bayesian inference, it is the posterior, p(θ|D, M). That is, the probability of the model parameters having considered the data (and the model’s structure, M). Again, for shorthand, we drop the M dependence of the posterior.
We can construct the posterior using the likelihood as well as the prior over the model, p(θ), by invoking Bayes’ theorem as follows
where p(D) is obtained by normalization from
| (8) |
where p(D, θ) is the joint probability of the model and the data.
For parametric models, the integral in eq 8 represents an integration over the model’s parameters. However, for multiple possible candidate models, we first need to sum over all models and, subsequently, integrate over their respective parameters.
We may even compare models, say Ml for different values of l selected from a broader set of models M by integrating over all parameters assigned to that model
| (9) |
Then marginal posteriors, p(Ml|D), across different l’s can be compared to select between different candidate models irrespective of their precise parameter values.124
For an increasing number, N, of data points, the likelihood function itself dictates the shape of the posterior distribution. Thus, a proper choice of likelihood function, even in Bayesian inference, is critical (Figure 9).
Figure 9.
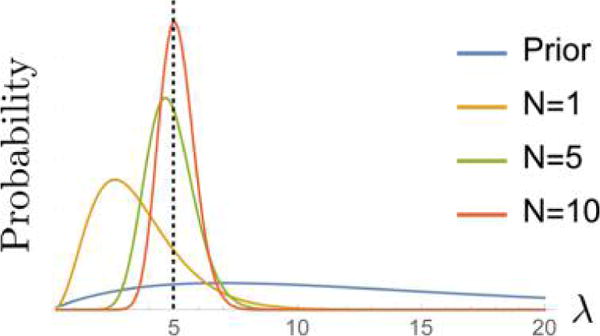
Posterior often becomes sharper as more data is used. Here data are sampled from a Poisson distribution with λ = 5 (designated by the dotted line) with D = {2, 8, 5, 3, 5, 2, 5, 10, 6, 4}. The prior (eq 12 with α = 2, β = 1/7) is plotted along with the resulting posterior informed by N = 1, N = 5, and N = 10 data points.
3.2.2.1. Priors
Parameter estimates obtained by maximizing a posterior generally converge to the MLE in the limit of infinite data108 (Figure 9). However, with finite data sets, faced in all data-driven modeling efforts, the prior can cause Bayesian and MLE estimates for parameter values to differ substantially (with Bayesian parameter point estimates coinciding with the maximum of the posterior distribution). This suggests that, for scarce data, a judicious choice of prior is important.
An extreme realization of limited data is found in traditional statistical mechanics where a (canonical) distribution over arbitrarily many degrees of freedom for particles follows from just a single point observation (the average energy) with vanishingly small error.113,129,130 While more data is typically assumed available in biophysics, data may still be quite limited. For example, in single particle tracking, individual tracks may be shortened due to photobleaching or by having particles move in and out of focus.61 Priors can be tailored to address many issues arising from data sparsity thereby conferring an important advantage to Bayesian methods and, in particular, the analysis of super-resolution data. For this reason, we discuss two different prior types: informative and uninformative.128,131
3.2.2.2. Uninformative Priors
The constant, uniform prior, inspired by Laplace’s principle of insufficient reason for mutually exclusive hypotheses, such as coin flips, is the simplest uninformative prior.
For a prior, p(θ), constant over a reasonable range, the likelihood and posterior have precisely the same dependence on model parameters, θ,
| (10) |
As a result, in this simple case, the likelihood can be treated as a model posterior.
A counterintuitive implication of assuming uninformative priors follows from the observation that uniformity of a prior over a model parameter, say θ, implies some structure, and thus knowledge, on the distribution of a related variable, say eθ.128 Conversely, if we assume that the variable eθ is uniform on the [0, 1] interval, the variable θ is concentrated at 1.
This problem is addressed by invoking priors invariant under coordinate transformations, such as the Jeffreys prior,132–134 which is sometimes used in the biophysical literature.135–138
3.2.2.3. Informative Priors
Bayes’ theorem, the recipe by which priors, p(θ), are updated into posteriors, p(θ|D), upon the availability of data, directly motivate another prior form.
Specifically, if we insist that priors and posteriors be of the same “mathematical form”, then the form of the likelihood sets the form of the prior. Such a prior, which when multiplied by its likelihood generates a posterior of the same form as the prior, is called a conjugate prior.
An immediate advantage of using conjugate priors is that, when additional independent data (say D2 beyond D1) are incorporated into a posterior, the new posterior p(θ|D2, D1), obtained by multiplying the old posterior, p(θ|D1), by the likelihood, is again guaranteed to have the same form as old posterior and the prior
| (11) |
Priors, say p(θ|γ), may depend on additional parameters, γ, called hyperparameters distinct from the model parameters θ. These hyperparameters, in turn, can also be distributed according to a hyperprior distribution, p(γ|η), thereby establishing a parameter hierarchy.
As a specific example of a parameter hierarchy, an observable (say the FRET intensity) can be function of the state of a protein, which depends on transition rates to that state (model parameters), which, in turn, depends on prior parameters (hyperparameters) determining how transition rates are assumed to be a priori distributed. We will see examples of such hierarchies in the context of later discussions on nonparametric Bayesian methods (section 3.4).
We illustrate the concept of conjugacy by returning to our earlier single emitter example. The prior conjugate to the Poisson distribution with parameter λ, where λ plays the role of rΔT (eq 5), is the gamma distribution
| (12) |
which contains two hyperparameters, α and β. After a single observation of n1 emission events in time ΔT, the posterior is
| (13) |
while, after N independent measurements, with D = {n1, ⋯nN}, we have
| (14) |
Figure 9 illustrates both how the posterior is dominated by the likelihood provided N is large and how an arbitrary hyperparameter choice becomes less important for large enough N.
Single molecule photobleaching provides yet another illustrative example64 and allows us to introduce the topic of inference of a probability distribution relevant to our later discussion on Bayesian nonparametrics.
Here we consider the probability that a molecule has an inactive fluorophore (one that never turns on), a basic problem facing quantitative super-resolution image analysis.139 Let θ be the probability that a fluorophore is active (and detected). Correspondingly, 1 − θ is the probability that the fluorophore never turns on. The probability that y molecules among a total of n molecules in a complex turn on is then binomially distributed
| (15) |
Over multiple measurements (each over a region of interest with one complex having n total molecules) with outcome yi, we obtain the following likelihood:
| (16) |
One choice for p(θ) is the beta distribution, the conjugate prior to the binomial
| (17) |
whose multivariate generalization is the Dirichlet distribution, which can be further generalized to the infinite-dimensional case (the Dirichlet process) that we will revisit on multiple occasions.
By construction (i.e., by conjugacy), our posterior now takes the form of the beta distribution
| (18) |
Given these data, the estimated mean, , obtained by maximizing this posterior, called the maximum a posteriori estimate, is now
| (19) |
which is, perhaps unsurprisingly, a weighted sum over the data and prior expectation (the first and second terms, respectively, on the right-hand side).
Conjugate priors do have obvious mathematical appeal and yield analytically tractable forms for posteriors (eq 18), but they are restrictive. Numerical methods to sample posteriors, including Gibbs sampling and related Markov chain Monte Carlo (MCMC) methods,140,141 continue to be used64 and developed142 for biophysical problems and have somewhat reduced the historical analytical advantage of conjugate priors. However, the advantage conferred by the tractability of conjugate priors has turned out to be major advantage for more complex inference problems such as those involving Dirichlet processes (section 3.4).
3.2.2.4. Credible Intervals
The analog of a frequentist confidence interval is a Bayesian credible interval. Likewise in higher dimensions, the Bayesian analog of the confidence set is the credible region. A Bayesian 1 − α credible region is any subset of parameter space over which the integral of the posterior distribution probability is equal to 1 − α.143 For a more concrete 1D example, suppose that we compute the posterior over a 1D Gaussian random variable. The probability of the Gaussian’s mean parameter falling between a given lower bound a and upper bound b would be the area of the posterior density over [a, b]. Any interval having a probability of 1 − α is a valid 1 − α credible interval.
3.3. Reject or Select Model Based on Empirical Evidence
3.3.1. Frequentist Goodness-of-Fit Testing
Before physically interpreting models, we should verify whether various model assumptions are consistent with the data. Checking a model’s distribution, and its implied statistical dependencies, against measured data falls under the category of “goodness-of-fit tests”.106,114,144
3.3.1.1. Example of Goodness-of-Fit Testing for iid Random Variables
A classic example of a goodness-of-fit test is the well-known Kolmogorov–Smirnov (KS) test,144 which we describe here. We assume that N iid samples of a scalar random variable X are drawn from an unknown distribution F. The empirical cumulative distribution function (ECDF) is defined as where IA is the indicator function of event A. That is, the ECDF evaluated at v is the fraction of times the random variable was equal to or less than v.
In the classic KS framework, the statistical model assumes a known distribution F0. The KS test checks the null hypothesis, H0: F = F0 against the alternative hypothesis Ha: F ≠ F0. To decide between hypotheses, one computes the “test statistic” for iid samples . If TN is greater than a critical value (determined for any desired test accuracy144) one rejects the null hypothesis and places less confidence in the model. From a frequentist point of view, the test can be understood as follows: if we generate samples of size N from the distribution F0, their ECDF will typically not match the cumulative distribution function (CDF) of F0 exactly but will be at some “distance” (as quantified by the KS test statistic) from it; we then ask, how likely is it that this distance is as large as the one computed for our data set? If such a large distance occurs with a probability less than α, then the null hypothesis is rejected.
As we will discuss in section 3.3.4, more complex models will tend to fit the data better. The KS test does not penalize a model for complexity in any way, it simply checks for consistency of a model’s distribution against the empirically observed data. This should be contrasted with model selection criteria (section 3.3.4) which attempt to balance model complexity and “predictive scores” (such as the likelihood).114
3.3.1.2. Goodness-of-Fit Testing in Time Series Analysis
The basic idea behind the KS goodness-of-fit test has been extended to multivariate random variables and to random variables exhibiting time dependence (i.e., time series).111,112
While many other goodness-of-fit tests, including the chisquare and Cramér-von Mises tests,144 exist, here we briefly illustrate how the ideas behind the KS can be generalized to time series data. We consider the case of scalar time series data D = {r1, r2, … rT }.
If a Markovian model, with prespecified parameter vector θ0, is assumed, we can introduce the Rosenblatt transform145 also known as the “probability integral transform” (PIT)111,112 defined by dx for observation i.
The sequence of Zi’s is now iid, despite the fact that the sequence was derived from a time series exhibiting statistical dependence or possibly even nonstationary behavior.86,111 All of the same tests used for iid variables, such as the KS test above, can be invoked to test the consistency of the model θ0 with the data.
While we have discussed a scalar Markovian time series, the PIT can be extended to multivariate non-Markovian series provided the joint density (i.e., the likelihood) can be accurately computed.111,112
Goodness-of-fit testing readily apply to 3D trajectories of particles. For instance, in recent work on mRNA motion in the cytoplasm of live yeast cells,86 goodness-of-fit testing was used to reject the hypothesis that time series coordinates are statistically independent. This rejection ultimately motivated new spatiotemporally correlated models as well as new models for measurement noise that identified novel kinetic signatures of molecular motor induced transport.86
3.3.2. Bayesian Hypothesis Testing
Previously, we demonstrated how goodness-of-fit testing could be used to verify the consistency of a model’s statistical assumptions against the data. Such an absolute consistency check on a model’s specific parameter values is accomplished by formulating hypotheses or “events” such as, H0: θ = θ0 and H1: θ ≠ θ0. Events can also be something with more of a “model comparison flavor”, such as H0: θ = θ0 and H1: θ = θ1.
Here we consider the case where the model M is fixed and we test H0: θ = θ0 and H1: θ ≠ θ0. In this type of binary testing, the Hi are events such that individual event probabilities sum to one, . The posterior probability of the null, H0, hypothesis is
| (20) |
| (21) |
where the integral in the denominator is an integral over all θ ≠ θ0.
While generalizing the ideas here to test multiple hypotheses is straightforward,114 it is the selection of priors and choice of models that makes Bayesian hypothesis testing technically complicated.106 To be more specific, eq 21 selects between values of the parameters θ of a single model but does not, in itself, provide information on whether the model itself is correct at all (and thus whether this selection is meaningful).
Before discussing model selection in greater depth (section 3.3.4), we now briefly describe an important model, the hidden Markov model (HMM), that motivates modeling approaches used across biophysics146 that we will revisit on multiple occasions.
3.3.3. Hidden Markov Models
HMMs146–149 have been used so far in a number of problems, chief among them force spectroscopy and single molecule FRET (smFRET) data analysis.149–155
To introduce the HMM, we begin by considering a sequence of observations D = y = {y1, y2, …, yN} and assume that these give us indirect information about the “latent” or hidden states (variables) si at every time point i, that alone describe the system dynamics. Hidden states and observations are then related by the probability of making the observation yi given the state of the system si, p(yi|si) assuming observations are uncorrelated in time.
The HMM then starts with a parametric form for p(yi|si) (the emission probability), the number of states K, and the data D. From this input, the HMM infers the set of parameters, θ, which includes (i) the “emission parameters” that parametrize p(yi|si), (ii) initial state probabilities, and (iii) the transition rates, i.e., transition probabilities p(si|sj) for all (i, j) pairs, that describe the jump process between states assumed Markovian.
In discrete time, the likelihood used to describe the data for an HMM model is
| (22) |
where s = {s1, …, sN} and i is the time index.
In general, we are not interested in knowing the full distribution p(y, s|θ); instead we only care about the marginal likelihood p(y|θ) which describes the observation probability given the model, no matter what state the system occupied at each point in time. In other words, since we do not know what state the system is at any time point, we must sum over the si.
The HMM itself can be represented by the following sampling scheme
| (23) |
That is p(s1) is the distribution from which s1 is sampled. Then for any i > 1, p(si|si−1) is the conditional distribution from which si, conditioned on si−1, is sampled, while its observation yi is sampled from the conditional p(yi|si, θ).
We then maximize the likelihood for this HMM model, eq 22, over each parameter θ. Multiple methods are available to maximize HMM-generated likelihood functions numerically.156 Most commonly, these include the Viterbi algorithm149,157 and forwar–backward algorithms in combination with expectation maximization.147,158
3.3.3.1. Aggregated Markov Models
Aggregated Markov models (AMMs)159–161 are a special case of HMMs where many hidden states have identical output. For instance, for Gaussian p(yi|si), two or more states have identical Gaussian means.
This special category of HMMs was introduced to biophysics in the analysis of ion-channel patch clamp experiments159,162–164 where the number of microscopic channel states exceeded the typically binary output of patch clamp experiments. Since then, AMMs have also been successfully applied to smFRET, where a low FRET state may also arise from different microscopic states (e.g., blinking of fluorophore photophysics or an internal state of the labeled protein)151 and, recently, to address the single molecule counting problem using super-resolution imaging data.21
In AMMs, experimentally indistinguishable states are lumped together into an “aggregate of states” belonging to an “observability class”, say “bright” and “dark” in the case of smFRET.
Limiting ourselves, for simplicity, to just two aggregates, 1 and 2, we may write a rate matrix Q as follows
| (24) |
The submatrices Qij, describe the transitions from aggregate i to aggregate j and the kl element of Qij describes transitions from the microscopic state k in aggregate i to microscopic state l in aggregate j.
AMMs are subsequently treated in much the same as HMMs. That is a likelihood is constructed and maximized with respect to the model parameters. In continuous time and ignoring noise, the likelihood of observing the sequence of aggregates D = {a1, a2, …, aN} is
| (25) |
where the ith element of the column vector, , represents the initial probability of being in state i from the a1 aggregate and
| (26) |
The row vector, 1T, in eq 25, is a mathematical device used to sum over all final microscopic states of the aggregate, aN, observed at the last time point as we do not know in which microscopic state the system finds itself in within the Nth measurement.
Just as with HMMs, the θ parameters include all transitions between microscopic states across all aggregates as well as initial probabilities for each state within each observability class and any emission parameters used. As there are fewer observability classes in AMMs than there are microscopic states, many parameters from AMMs may be unidentifiable165 and thus may need to be prespecified.
AMMs and HMMs can be generalized to include the possibility of missed (unobserved) transitions21,166 – for instance when transitions happen on time scales that approach or exceed the data acquisition frequency–and can readily apply to discrete or continuous time.
One fundamental shortcoming of either HMMs or AMMs is their explicit reliance on a predetermined number of states. This is true of many modeling strategies that predetermine the model “complexity”.
The next section on model selection addresses the challenge of finding the model of the right complexity.
3.3.4. Model Selection
We assume that models under consideration have passed tests, ensuring the interpretive value of the model, and that we are interested in selecting the best (or preferred) predictive or descriptive candidate model among these without excessively overfitting.114
Here we review the basic ideas behind well-established model selection criteria that can be naively described as finding the best model by balancing a “predictive component” (often quantified by a likelihood) and a “complexity penalty” (often quantified by a function of the number of parameters in a model).
In this article, we do not review cross validation type techniques for accessing the predictive ability of models. In cross validation some fraction of the data is kept in reserve in order to see how the prediction performs. Cross validation is used mostly in “man supervised learning” applications, for example “deep learning” of gigantic labeled color image data sets. With such data sets we often have a good idea of what the ground truth is. In super-resolution image analysis the genuine “ground truth” is much harder to come by, except in simulations.
3.3.4.1. Information-Theoretic Model Selection Criteria
While many information theoretic methods exist167–169 and have recently been reviewed elsewhere,59 here we focus on the Akaike Information Criterion (AIC).170–173 The AIC starts from the idea that, while it may not be possible to find the true (hypothetical) model, it may be possible to find one that minimizes the difference in the “information content” between the true (hypothetical) model and the preferred candidate model. The preferred model should provide a good fit to existing data, the training set, and provide predictive power on alternate data sets, the validation set.
While the derivation of the AIC is involved,59,114 the AIC expression itself is simple
| (27) |
where denotes the MLE of a given model.
Minimizing the AIC, which is equivalent to maximizing the likelihood subject to a penalty on parameter numbers, K, generates the preferred model. The AIC itself is an asymptotic result valid in the large data set limit though higher order corrections exist.114 The penalty term, 2K, is derived, not imposed by hand. Also, as we will see, it is a weaker penalty than that of the Bayesian information criterion that we now describe.
As a concrete example, suppose goodness-of-fit testing cannot rule out the possibility that the model itself is an undetermined sum of exponentials obscured by noise. The AIC would then be used to find the number of exponential components required without overfitting the data. Additional examples motivated from the biophysical literature are provided by Tavakoli et al.59
3.3.4.2. Bayesian Information Criterion
While the mathematical form for the Bayesian (or Schwartz) information criterion (BIC)174 used in model selection, that we will see shortly, may appear similar to the AIC, eq 27, it is conceptually very different. It follows from Bayesian logic with no recourse to information theory.59,114,175–177 As before, the derivation itself is involved and discussed in detail in Tavakoli et al.59
Unlike the AIC, the BIC searches for a true model173,178 that exists regardless of the number of data points N available used to find this model. That is, the model itself is assumed to be of fixed, albeit unknown, complexity, by contrast to the AIC which seeks an approximate model and is therefore more willing to grow the model complexity along with the size of the data set, N, available.
Briefly put, the BIC starts from a posterior for a model class with a fixed number of parameters, K, just as we had seen with our exponential example earlier. Following the logic of eq 9, we consider the average posterior that comes from summing over parameter values for each of the K parameters generating a marginal posterior.
If a candidate model contains too many parameters, then many of these parameters (integrated over all values that they can be assigned) will result in a small marginal posterior for that particular parameter number. By contrast, if too few parameters are present in the posterior, the model itself will be insufficiently complex to capture the data, and this will also yield small marginal posteriors.
From this logic follows the BIC
| (28) |
which differs from the AIC, eq 27, in the complexity penalty term (second term on the right-hand side).
While the logic underlying both AIC and BIC is different, both AIC and BIC are used interchangeably in practice, and their performance is problem-specific59 (Figure 10). For instance, since the AIC tends to overfit small features it may underperform for slightly nonlinear models (which may have fewer parameters) and that may be obscured by noise but may be preferred for highly nonlinear models (with a correspondingly larger number of parameters) as small features may no longer be due to noise.172
Figure 10.
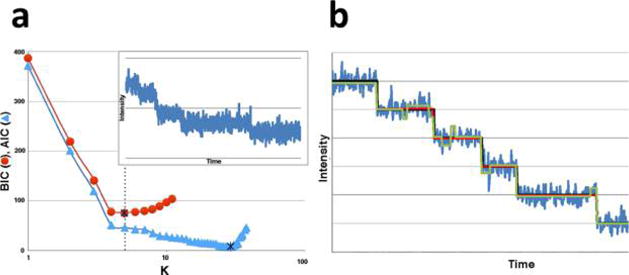
AIC and BIC are often both applied to step-finding. (a) We generated 1000 data points with a background noise level of standard deviation σb = 20. On top of the background, we arbitrarily added 6 dwells (5 points where the mean of the process suddenly changes) with noise around the signal having a standard deviation of σs = 5 (see inset). At this high noise level, and for this particular application, the BIC outperforms the AIC and the minimum of the BIC is at the theoretical value of 5 (dotted line). This is because the AIC overinterprets noise. All noise is Gaussian and uncorrelated. (b) Here we show another synthetic time trace with hidden steps, generated in the same manner as the data set in (a). The AIC (green) finds a model that overfits the true model (black), while the BIC (red) does not. However, as we increase the number of steps (while keeping the total number of data points fixed), the AIC does eventually outperform the BIC. This is to be expected. The AIC assumes the model could be unbounded in complexity and therefore does not penalize additional steps (model parameters) as much. The BIC, by contrast, assumes that there exists a true model of finite complexity. The data set for this simulation was generated via a Python implementation of the Gillespie algorithm, while both the BIC and AIC were implemented via elementary Python scripts.
3.4. Overview of Bayesian Nonparametrics
Bayesian nonparametrics is a relatively recent (1973) approach to statistical modeling179 that fundamentally integrates the model selection step into the model-building process. In other words, it builds models whose complexity reflect that of the data.179–181 This is especially important to super-resolution and, more broadly, single molecule data analysis, as few model features, such as the number of states in an HMM, are initially known.
As we previously discussed, nonparametric approaches do make parametric assumptions. For instance, a particular nonparametric model may assume that measurements are iid. However, beyond these parametric constraints, nonparametric approaches allow for a possibly infinite number of parameters.
3.4.1. Dirichlet Process
The prior process, the analog of the prior used in parametric Bayesian inference, is of major importance in Bayesian nonparametrics. The most widely used of these processes is the Dirichlet process (DP) prior,179 along with its various representations,67,68,182 such as the “Chinese restaurant” process and the stick-breaking construction.181,183
Just as a prior in parametric statistics samples parameter values, the DP samples probability distributions. Probability density estimation,184 clustering,185 HMMs,183 and Markovian switching linear dynamical systems (SLDS),68 have all been generalized to the nonparametric case by exploiting the DP.
We introduce the DP with a parametric example and begin by considering probabilities of outcomes, π = {π1, π2, …, πK} with Σk πk = 1 and πk ≥ 0 for all k, distributed according to a Dirichlet distribution, π|α ~ Dirichlet (α1, …, αK). In other words
| (29) |
The Dirichlet distribution is conjugate to the multinomial distribution.
To build a posterior from the prior above, we introduce a multinomial likelihood with populations n = {n1, n2, …, nK} distributed over K unique bins
| (30) |
The resulting posterior obtained from the prior, eq 29, and likelihood, eq 30, is now
| (31) |
The multinomial shown above is a starting point for many inference problems. For example, eq 31 may represent the posterior probability of weights in mixture models, such as sums of Gaussians, and is used in clustering problems.184
To be more specific, the finite mixture model can be represented using the following sampling scheme with yi denoting the ith observation
| (32) |
Here si is the (latent or unobservable) cluster integer label, F(·) is a distribution governing the yi random variables assigned to cluster parametrizes F and the prior over the unobservable ’s are governed by the so-called “base distribution” H.184
Equation 32, formalizes the logic that if a model is a sum of Gaussians (i.e., a sum of , with each component indexed si with parameters , we draw an observation by first selecting a mixture component (according to the weight of each component, multinomial(π1, … πK)) and subsequently sampling a value from that particular mixture component (i.e., a Gaussian).
In the absence of prior knowledge on the expected mixture components, we set all αk to α/K and, under these assumptions, we can write down the probability of belonging to cluster (or mixture component) j184
| (33) |
where nj is the number of observations assigned to cluster “j” and .
The DP is the infinite dimensional (K → ∞) generalization of the Dirichlet prior distribution and is used in infinite mixture models.184 In infinite mixture models, the prior probability of occupying a pre-existing mixture components is
| (34) |
whereas the probability of creating a new component is
| (35) |
Before moving forward, some comments are in order. When doing classic finite mixture modeling, we needed to predefine the number of mixture components, K. Each K component has a prior probability given by eq 33; if we change K (and as a result change the yi cluster assignments), one is faced with a model selection problem. In the DP mixture model, the data determines the number of active clusters/states as well as the parameters needed to describe the data in an à la carte fashion within a single Bayesian posterior.
In both finite and infinite mixture models, the quality of the clustering strongly depends on the base distribution, H, since this distribution governs the θ which determines the similarity (or dissimilarity) between the probability distributions, F(·), associated with different clusters.
3.4.1.1. Infinite Mixture Models
Previously, in eq 32, we showed how to sample a priori mixture weights for finite mixture models. For infinite mixture components, we may combine the first two as well as the last two expressions of eq 32 and obtain
| (36) |
where α is the “concentration parameter” quantifying the preference for creating new clusters184 while H is a judiciously selected68,179,186 “base distribution” that plays the same role here as it did for finite mixture models in setting θk. G is the DP’s sample and it is a random distribution that can be represented as follows
| (37) |
where the Kronecker delta, , denotes a mass point for parameter value θk 67,187 and F*G denotes
| (38) |
It can be shown that the mean of the random distribution G is given by and its variance is (H(1–H))/(α + 1).108 Thus, as α increases, G approaches H. Hence the concentration parameter can be thought of as constraining the similarity between G and H.
While we have just described infinite mixture models, we have not yet described how to draw samples from the DP. DP itself is often represented by the “stick-breaking construction” which is easily implemented computationally182
Following this procedure, we find that G ~ DP(α, H).108
The analogy to stick-breaking here is motivated by imagining that we begin with a stick of unit length. We break it at a location, v1, sampled from a beta distribution v1 ~ beta(1, α). We set π1 = v1. The remainder of the stick has length (1–v1). We then assign to π1 a value of θ1 sampled from H and reiterate to get π2, so the πk are all sampled according to the stick-breaking construction. In practice, we terminate the stick breaking process when the remaining stick length falls below a prespecified cutoff. In the statistics literature, the resulting distribution for π is known as the Griffiths–Engen–McClosky (GEM) distribution.188
The DP powerfully generalizes previously finite models, such as the hidden Markov model,67 ubiquitously used across single molecule biophysics189 that we discuss in greater depth in section 7.3.2.
4. THE LOCALIZATION PROBLEM
The localization problem is the first step in the analysis of a super-resolution data set and involves finding the position of a fluorescent molecule, x0 = (x0, y0), from an image I. The image itself is thought of as a matrix, whose elements describe individual intensities at each pixel.
In order to localize a fluorophore, we must have a model describing the expected mean number of photons per frame in pixel x given the fluorophore location at position x0, λ(x; x0). Typically, λ(x; x0) is given by the point spread function of the imaging system. The intensity at each pixel at location x is itself distributed randomly, according to a distribution p(I(x)|λ(x; x0)), due to shot noise and readout noise.
We begin by describing readout noise (section 4.1) and follow with a discussion on identifying “regions of interest” (ROIs) containing fluorophores (section 4.2). Once positively identified, we draw from our discussion on maximum likelihood in order to describe inference frameworks used in localization in section 4.3. While theoretically attractive, maximum likelihood methods may be computationally expensive and require good noise models to outperform simpler approaches. For this reason, we describe performance criteria of localization methods ultimately used to judge whether the computational cost of a method is warranted in section 4.4. Sections 4.5 and 4.6 describe simpler localization strategies, including least-squares fit. Subsequent sections tackle generalizations of the methods discussed thus far: 3D super-resolution in section 4.7, simultaneous fitting of multiple emitters in section 4.8, and deconvolution-style approaches in section 4.9. Finally, we end with a note on drift correction in super-resolution (section 4.10) without which the best localization methods are of limited value.
4.1. Readout Noise in Single Molecule Experiments
Intuitively, one can expect photon shot noise to be partly responsible for reducing the accuracy of localization methods. Indeed, localization must be achieved with few photons per frame as the total photon budget of most fluorophores, meaning the number of photons collected before the fluorophore undergoes irreversible photobleaching, is limited to hundreds or thousands of photons.4,190 While greater brightnesses can be achieved by using quantum dots as fluorescent markers,191 they remain more challenging to deliver into cells and present toxicity concerns.192
Perhaps more unexpectedly, accurate localization also requires a model describing how a fluorophore’s emitted photons are converted into a camera readout. For instance, at a given illumination level, assuming an average number of photons strike the sample per frame per unit area, one may naively expect the camera’s readout at a given pixel, I = I(x), to be a Gaussian random variable identical for all pixels, or at least well approximated by such a description. In fact, as we now discuss, both Gaussian and identical assumptions are violated in practice.
Since few photons hit each camera pixel on any given frame, the Poisson limit theorem states that given the average number of photons λ for this pixel, the distribution of the actual number Np of such photons follows a Poisson distribution (“shot noise”)
| (39) |
where for notational simplicity, we let λ = λ(x; x0).
The total noise of the measurement arises from the convolution of this shot noise by a camera readout noise, that is neither necessarily normally distributed, nor pixel-independent.193 In other words, the readout I at a camera pixel is distributed according to a distribution p(I|Np) that is non-normal and pixel-dependent. As later described, we will use both knowledge of p(Np|λ) and p(I|Np) to address the localization problem.194
4.1.1. Camera Specific Readout
Two technologies, with different readout distributions, are widely used for single molecule imaging:194 the older EMCCD (electron-multiplication charge coupled device), where the electrons produced by a photon hitting a pixel are collected and amplified by chip-wide electronics, and the more recent sCMOS (scientific complementary metal oxide semiconductor), which offer higher sensitivity and read rates, at the cost of pixel-to-pixel noise variation (“fixed pattern noise”), by performing signal amplification at the pixel and column level.194
The noise distribution of an EMCCD camera follows from its amplification mechanism195 where a photon hitting a pixel is converted into electrons. Chip-wide multiple charge-carrier multiplication (CCM) stages then amplify this electronic signal serially, one pixel at a time.
Specifically, each electron entering a stage has a low probability p of giving rise to an output of two electrons; otherwise, no amplification takes place and a single electron is output with high probability 1 – p. Repeating this process across a large number of stages yield an exponentially distributed number of electrons arising from this single photon195
| (40) |
where the multiplication factor m is itself weakly pixel-dependent, due to manufacturing imperfections. The distribution of the output from the amplification stage for Np photons simultaneously hitting a single pixel is the Np-fold convolution of the one-photon distribution196,197
| (41) |
After amplification, the electronic readout stage itself introduces both Gaussian noise, of standard deviation σ, which needs to be convolved to this distribution, and an offset in the number of counts (“dark count”), c0, considered constant.196
The other technology, sCMOS cameras, offer higher sensitivity and readout rates by attaching an individual amplification stage to each pixel. This different amplification technology yields the following normally distributed readout
| (42) |
but the gain m, offset c0, and variance σ2 all vary (relatively) strongly from pixel to pixel (Figure 11).198
Figure 11.

Pixel dependent noise, if known, can be used to refine localization analysis. The left panel displays a simulated “variance map”, where the colorbar indicates the encoding of the noise level, similar to one that could be measured on an sCMOS camera. The color indicates that a single (red) pixel has higher variance, σ, than its neighbors. A MLE for the emitters’ location, shown in the middle panel, that ignores the pixel dependent variance, does not correctly identify the emitter locations that we placed on two parallel lines in this simulation; instead, an artifactual excess of events is detected at the “hot” pixel. On the right panel, we see that the MLE tailored for sCMOS cameras (“MLE-sCMOS”), which does take the variance map into account, avoids this artifact.198 Reproduced with permission from ref 198. Copyright 2013, Nature Publishing Group.
From the distribution camera readouts for a given number of photons, p(I|Np), and the distribution of photon counts, p(Np|λ), we may compute the probability distribution of the camera readout I given λ, by marginalizing over the unobservable number of photons Np
| (43) |
As we will see in the next section, this distribution is essential for our goal of estimating x0 (on which λ depends).
As earlier mentioned, numerical estimation of this sum (which also matches experimental observations) demonstrates that p(I|λ) is highly skewed for EMCCD cameras,196 thus violating the normally distributed noise assumption (Figure 12). In the case of sCMOS cameras, numerical estimation of the sum in eq 43 also yields a non-normal distribution p(I|λ); moreover, and more importantly, this distribution changes from pixel to pixel due to the variability of m, c0, and σ2.198
Figure 12.
Probability density of EMCCD camera readout counts can be highly non-Gaussian. Here we numerically evaluated eq 43 via a simple Python script for different mean photon numbers, λ (0.32, 1.75, 7.0) and multiplication levels m (9.8, 28). The dark count c0 and readout noise standard deviation, σ, were set to 1000 and 10, respectively.
In principle, one may also infer m and c0 directly from p(I|λ). With these two parameters at hand, and furthermore knowing, from Eqs (41) and (42), that the mean of I is a linear function of Np, we can obtain an estimate of Np at each pixel given I. This estimate is useful in evaluating the localization accuracy of the methods we will later explore in section 4.6.2. However, the central quantity, moving forward, is p(I |λ).
4.2. Detecting Single Molecules
We have previously described how the camera readout, I, is related to the illumination level, λ, through the distribution p(I|λ). As we will discuss in section 4.6, physical models of spatial localization allow us to estimate, for given fluorophore parameters Θ, the value of λ at each pixel x, λ(x;Θ). The fluorophore parameters Θ minimally include the position of the fluorophore (as we had described earlier), but may also include its brightness,45 orientation,199 velocity,200 or other properties.
From p(I|λ) and λ(x;Θ) we obtain a distribution of images conditioned on Θ
| (44) |
where we have assumed that readout noise is uncorrelated across pixels.
We may, in principle, fit the entire image and simultaneously localize a large number of fluorophores. This is a difficult task, which we will address in section 4.8. Alternatively, we may crop out ROIs centered around “emission-like” patterns, as a prelude to their further analysis.45,201 Mathematically, this is equivalent to marginalizing over the positions outside of the ROI, i.e., ignoring the dependence of the image within the ROI on the positions outside of it. We explain this here with the caveat that, even today, the selection of these ROIs is often treated in an ad hoc manner, with limited theoretical justification.202
4.2.1. Laplacian of Gaussian Filter
One may expect that ROIs could be chosen by locating pixels whose intensity go beyond some preset threshold. Such an approach cannot achieve high identification levels of relevant regions, in particular due to the presence of large amplitude and low spatial frequency background noise. Instead, a commonly used approach (and one of the few for which a theoretical basis has been offered) is to enhance features of a characteristic size σ (chosen to be that of a diffraction-limited spot) by convolution of the raw image I(x) = I(x, y) with a Laplacian of Gaussian kernel K(x, y),203
| (45) |
i.e., the convolved image I′(x) is
| (46) |
In this convolved image, features of a characteristic size σ have been “enhanced” to appear as sharp peaks. Peaks with a value greater than a given threshold can then be selected as originating from a single molecule and deserving further processing. This threshold is usually empirically chosen,203 for example by picking as many peaks as possible while avoiding peaks that “look like” noise (as tested during the following processing stages).
However, if we have a good model of the background noise, we can also estimate (by simulation) the distribution of peak values that would be obtained from convolving an image only constituted of background noise, and then choose a threshold value that satisfies a user-specified false-positive p-value (that is, such that the probability of observing peaks with a value greater than the threshold in a convolved pure noise image is p).204
Briefly, the theoretical justification for eq 45 relies on matched filter theory.205 Matched filter theory indicates that, if we are in the presence of additive white noise (i.e., if the differences between the observations and the true values consititute a random signal with constant spectral power density), the best linear filter to retrieve the original distribution is the convolution by the spatially reversed PSF itself (I′(x) = I(x) PSF(−x)). In Fourier space, such a filter corresponds to multiplication by the conjugate of the Fourier transform of the PSF. Furthermore, empirical observations establish that the spectral power density (the square of the magnitude of the Fourier transform) of background fluorescence noise, not to be confused with camera readout noise, in an image approximately follows a power-law, , with s ≈ 2 (where denotes the Fourier transform).203 Thus, in order to apply the matched filter result, we first need to transform our data so that it exhibits white noise (whitening); this is done by multiplying the data, in Fourier space, by the filter H(k) = |k|s/2 (so that . The combination of both steps (whitening and convolution by the spatially reversed PSF) corresponds to the multiplication, in Fourier space, by the filter
| (47) |
(where the overbar indicates complex conjugation). In the case where s = 2 and the PSF is modeled as a Gaussian, eq 47 indeed corresponds to the Laplacian of Gaussian filter described in eq 47.203
Since super-resolution data sets often contain many consecutive frames, additional improvements beyond whitening filters may be used. For instance, since background fluorescence varies slowly over time, it is possible to empirically decrease the influence of background fluorescence by working on difference images, that is, the difference in intensity between a frame and the next one.4 The switching-on of a molecule then appears as a positive peak in the data, whereas its disappearance is a negative peak, both of which may be further selected using the whitened matched filter (eq 45).4
4.2.2. Errors in Emitter Identification
The output of this initial analysis is a list of ROIs, where a single molecule is assumed to have been fluorescent. Metrics, which we now introduce, can be used to quantify the quality of the list. For any method, such metrics are typically calculated from synthetic data, where the ground truth is a priori known, which is not the case with real data. Therefore, the metrics provide only an estimate of the method result quality. If the data treated is substantially different than the synthetic data the metrics were calculated on, this estimate may be quite inaccurate.
These metrics below are expressed in terms of two kinds of possible errors: some molecules may have been missed by the detection algorithm (false negatives, FN), and some regions of interest may have mistakenly been drawn somewhere where there was, in fact, no molecule (false positives, FP).206
If we denote TP the number of true positives (correctly drawn regions of interest), two fundamental measures of accuracy are possible: the precision (quantifying false positives)
| (48) |
and the recall (quantifying false negatives)
| (49) |
In order to directly rank different methods, it is convenient to combine these two measures into a single quantity. Such quantities include the Jaccard index202,206
| (50) |
or the F1-score (or F-measure)207
| (51) |
Modern localization methods are typically able to achieve high precision (p ≳ 95%) while still having limited, though widely varying, recalls (r ≈ 25% to 75%);202 this latter value thus also limits the achievable Jaccard index and F1-score.
4.3. Maximum Likelihood Localization
Having segmented our image into regions and identified whether such regions contain a single molecule, we now turn to the problem of localization within an ROI using maximum likelihood, described earlier in section 3.2.1.
Specifically, the MLE given by eq 4 finds parameters Θ maximizing the probability of observing I over the N × N pixels
| (52) |
where the probability, p(I|Θ), above is understood as the product over each pixel x of the probability of observing the actual pixel value I(x), expressed as a function of the fluorophore parameters Θ, i.e.
| (53) |
where we have adopted the common assumption of pixel independence.
The maximization of eq 52 can be carried using out-of-the-box numerical approaches, such as gradient descent;54 practical implementations of such a method in a super-resolution context (which achieve the CRLB) are available for both EMCCD and sCMOS cameras.55,194,208
The actual value of the CRLB (5 to 50 nm) depends strongly on a number of experimental parameters, most importantly the number of photons that can actually be collected.55,194,208
Despite the theoretical optimality of the MLE (in the CRLB, or mean-squared error, sense), the necessarily imperfect knowledge we have about the imaging system (background fluorescence, the PSF, the camera noise) reduces its performance. In fact, PSF mis-specification or imperfections degrade the performance of the method and may even lead to overly optimistic accuracy estimations.55,121,209 It thus remains useful to study simpler approaches, which can take advantage of empirical corrections.
4.4. Additional Super-Resolution Performance Metrics
While the Jaccard index, eq 50, and the mean-square error of a single molecule’s localization are good performance metrics, even perfect localization cannot reconstruct a biological structure that is poorly labeled.4
To assess the quality of a reconstruction, Fourier ring correlation (FRC), a method originally developed for cryoelectron microscopy, is employed.210,211 Briefly, in this method, the collected single molecule events are randomly split into two data sets, which are used to create two independent reconstructions I1 and I2 of the structure. The “consistency” between these two reconstructions is then used as a quantification of their resolution.210,211 This consistency is obtained, as the name implies, by computing the Fourier transforms, and , of the images, and computing the normalized correlation between “rings” of constant spatial frequency magnitude |k| = k,
| (54) |
where denotes the complex conjugate of .
This formula yields, for each magnitude of spatial frequency, the degree of correlation, normalized between −1 and +1, to which the features of that characteristic size are correlated between the two independent reconstructions. In fact, it is this separation of length scales that motivates the use of correlation in Fourier space.
For relatively large sized structures, using a random half of the events does not greatly diminish the quality of the reconstruction; thus, the two reconstructions should be highly correlated. Conversely, for structures too small to be well resolved, there is no reason to expect the two reconstructions to be highly correlated and, consequently, the FRC should be smaller.
We may then select a conventional threshold FRC (typically, FRC(q) = 1/7) and report as “the resolution” the corresponding characteristic size beyond which the threshold is exceeded.210,211 Interestingly, this measure tends to indicate that nowadays, the main factor limiting the resolution of reconstructed static structures is typically the labeling density rather than the accuracy of the single molecule localization itself.210,211
4.5. Simplified Localization Approaches
We have seen that while maximum likelihood localization is theoretically the method that achieves the lowest mean-squared error, imperfect knowledge of the imaging system characteristics may make other localization methods preferable. Additionally, maximum likelihood calculations are typically computationally expensive and implementations often run on specialized hardware such as graphical processing units (GPUs).55,198 Thus, it remains useful to study simpler, possibly less model-dependent, approaches.
4.5.1. Centroid Localization Method
An intuitive, simple, and extremely fast approach to the localization problem is to compute the average of the pixel coordinates x = (x, y) within a ROI, weighted by their intensities I(x).201
In such a method, it is crucially important to first subtract away any background fluorescence Ib from the ROI,212 such that the estimated localization is
| (55) |
where the sum is over the region of interest. Background subtraction is important because in its absence, the weighted average eq 55 becomes a weighted average between the true centroid and the ROIs geometric center.
However, even with this correction, the method remains unsuitable for high-resolution localization.212 One simple reason is that, even under the reasonable assumption that the physical PSF is symmetric (and thus its centroid should yield the fluorophore position), this is not the case for the camera readout, which is measured on a discrete pixel grid. Even worse, the centroid of the camera readout does not necessarily coincide with the centroid of the physical PSF (again due to pixelation).212 Still, the extreme simplicity of the method has led to its use as a minimal baseline against which other approaches can be compared.202
4.5.2. Finding the Point of Radial Symmetry
The centroid method we just described attempts to localize an event with subpixel resolution by identifying its “geometric center”. Other definitions of “geometric center” have been proposed, most notably the radial symmetry approach.213,214 Briefly, this approach attempts to find the point that best approximates a “radial center of symmetry” for the image.
In this method, the gradient of the signal is calculated either at each pixel215 or at each point where four adjacent pixels (or, in the 3D case,214 eight adjacent voxels) meet.213,215 The line defined by this point and gradient pair is taken as approximating a local axis of symmetry for the image. If all such lines were to intersect with each other at a single point, such a point would be a reasonable definition of the radial symmetry center. Because this is not the case, the radial symmetry center is instead defined as the point that minimizes its total distance to all such lines,215 possibly with an appropriate weighting factor.213,214
Specifically, it is reasonable to weight lines inversely proportionately to their distance from the center of the image. Since this center is yet unknown, the weighting is instead done using the inverse distance to the centroid (as computed above).213,214 Most importantly, an analytical expression can be derived to compute the radial symmetry center thus defined;213,214 as such, this method is extremely rapid.
While simulations indicate that this method yields high, close to CRLB-level localization accuracy of single events at a high speed,202,213,215 they also show that its performance degrades extremely quickly for high-density data, being unable to correctly localize events that were not well separated from the others.202
4.5.3. Correlation
As discussed earlier, the good performance of the Laplacian of Gaussian kernel for event detection was justified on the basis of simple noise and PSF models (section 4.2). We now extend this approach to tackle the localization problem itself.
In this approach, a peak’s position is determined by computing the correlation between the image and the model PSF (although using the Laplacian of the PSF may work better from a theoretical point of view, as discussed above, it is the PSF itself that is typically used), and finding the position at which this correlation is maximal. The same background removal approaches as for centroid calculations may be used;212 however, they are less important, as adding a constant background to the image simply shifts the filtered image by a constant and thus does not affect the maximum’s position.
The correlation of two images is only defined for integer coordinates, so additional work is needed to obtain a subpixel localization. A simple way to do so is to fit the values of the correlation in the vicinity of the maximum with a continuous, peaked model function (e.g., a parabola)212 and use the maximum of the latter. A more sophisticated approach is to compute this correlation after Fourier-resampling both the image and the model PSF to a higher resolution. Such a resampling is achieved by taking the Fourier transform of the image, zero-padding it to a higher spatial frequency, and taking the Fourier transform back. Correlation in real space corresponds to point-wise product in Fourier space; thus, the desired procedure amounts to computing the point-wise product of the Fourier transforms of the image and the PSF, zero-pad it, Fourier transform the padded product back into real space, and then select those coordinates at which the correlation attains its maximum.216,217 To sidestep the computational cost of the Fourier transforms that upsampling requires, such methods are typically first run with a limited upsampling to yield a low resolution localization and then run again with higher upsampling but only in a small neighborhood around the position selected by the first iteration.216,217
An important advantage of correlation-based localization is that it can be directly used for any experimentally measured PSF. For example, in particle tracking (an early application of subpixel localization212), one can use the image of a molecule in one frame as the model PSF for the next frame.212 In superresolution experiments, this approach has been suggested to analyze thick-sample data, which typically exhibits highly distorted PSFs217 in the absence of specialized optical corrections.36 In this case, the distorted, sample-specific PSF is measured at the beginning of the experiment by imaging a point-source at different depths; detected events are then localized by correlation with this PSF.217
4.6. Least-Squares Fitting and Model PSFs
The previous section covered methods that require limited assumptions regarding the PSF; for instance, that it be radially symmetric or invariant across the data set. Here instead we focus on an approach, least-squares fitting, that demands no such assumptions but that does require a form of the PSF.
While, in theory, maximum likelihood achieves the optimal mean square error when an accurate PSF model is available (section 4.3), the least-squares method is widely used44,45 because of the good performance of readily available, fast, and robust algorithms.202,204 Although we will first focus on the common case of fitting a Gaussian PSF model, we will then discuss possible corrections to this model.
4.6.1. Gaussian PSF Least-Squares Fitting
Since the theory of least-squares fitting, as with maximum likelihood (section 4.3), can be described independently of the model PSF’s exact functional form, we will, for simplicity, assume a Gaussian PSF. This choice is one of the earliest in use, offers mathematical simplicity, and maintains good performance.
Specifically, we model the image I0 arising from a fluorophore as a two-dimensional Gaussian as follows
| (56) |
The unknown amplitude A, center x0 and standard deviation σ, as well as the unknown, locally constant mean background Ib, are parameters collectively regrouped as Θ, the fluorophore characteristics, that we now want to infer. Furthermore, despite the subtraction of the background Ib, the measured image still differs from the model by a noise term of mean zero. Next, it is also possible to assume that some parameters are a priori known such as σ or Ib, for example, they may be independently estimated from the image intensity far away from the fluorophore.218 It is also possible to improve this model by averaging the PSF over each pixel.3
One may then infer the remaining set of parameters minimizing the sum of squared differences between the observed intensity and model provided by eq 56, weighted by the signal variance at each pixel. Numerically, this is a classic least-squares minimization, for which fast and robust implementations, such as the Levenberg-Marquart algorithm,193 are available.
The maximum likelihood framework (section 4.3) and least-squares fitting are identical, even for non-normal PSFs, if the noise at each pixel is assumed to be independent and drawn from the same normal distribution with unspecified variance
| (57) |
where l denotes the log-likelihood.
4.6.2. Least-Squares Fitting Localization Accuracy
Thompson et al. provided a theoretical analysis of least-squares fitting accuracy in the presence of normally distributed background noise as well as photon counting noise (section 4.1), as a function of the PSF’s standard deviation (the “spot size”) s, the pixel size a, the number of photons in the event Np and the standard deviation of the background noise b (Figure 13).53
Figure 13.

Image of a point source by a microscope can be approximated as a Gaussian of standard deviation s. Collecting this image on a camera further pixelates it with pixel size a. The noisy intensity profile was generated using a simple Python script.
For simplicity, we limit ourselves to rederiving Thompson’s results in the case of a 1D model and assume that for a fluorophore at position x: (i) the expected number of photons at the ith pixel (i.e., the PSF model) is Ni(x); (ii) the variance is (i.e., the sum, in quadrature, of the photon counting noise, Ni(x), and the background noise, b2); and (iii) the detected photon number at that same pixel is yi. By definition, the fitted position, , is obtained by minimizing the weighted sum of square residuals, i.e.
| (58) |
By expanding Ni(x) in the above to first order in around the true underlying position and solving for , we directly derive the mean square error of the fitted center’s position
| (59) |
While this sum can be evaluated numerically, we can also simplify it under reasonable approximations. We ignore, for now, the effects of pixelation (a → 0). In this case, under a Gaussian PSF model, the expected number of photons at pixel i is , and the sum in eq 59 can be replaced by an integral.
In general, this integral is not analytically tractable but it can be asymptotically evaluated in two limits: (i) dominant photon-counting noise and (ii) dominant background noise . These two cases respectively yield
| (60) |
and
| (61) |
Since each expression dominates the other in the limit where it has been derived, the authors suggested the following interpolation formula53
| (62) |
The pixelation noise’s main effect (arising from a nonzero a) is to increase the photon counting noise term ⟨(Δx)2⟩1. Specifically, the PSF’s spatial variance, s2, appearing in this term should be increased by the spatial variance of a square pixel of size a, which is a2/12.53 The final expression for the uncertainty of Gaussian fitting is thus
| (63) |
Although eq 63 is widely used to report localization accuracies,4,5,219 the summation in eq 59 can also be evaluated numerically.53 This numerical estimate indicates that eq 63 actually overestimates the localization accuracy (in the relevant regime of parameters) by approximately 10%.53 This is a discrepancy that has also been reported from experimental comparisons.3
An interesting consequence of eq 59 is that the mean square error is minimal for a nonzero pixel size a (∂(Δx)2/∂ a = 0). In other words, it is counter-productive to make the pixel size as small as possible. Instead, its optimal size is close to the spot size s. Intuitively, this is due to the compromise between the higher spatial information gained from each pixel when the pixels are smaller and the averaging out of background noise when the pixels are larger.
In practice, Gaussian PSF fitting has been shown to achieve nanometer-resolution. For example, Yildiz et al. have used this approach to show that the motion of fluorescently labeled myosin V enzymes along their tracks occurs in steps of variable size that can be grouped in consecutive pairs whose sizes add up to 74 nm (fluorescence imaging with one-nanometer accuracy, FIONA).219
4.6.3. Applicability of Least-Squares to Non-Normal Noise
While the assumption of identically and normally distributed noise is reasonable in many applications of least-squares fitting, which is the source of its versatility and the reason many efficient algorithms have been developed, it is clearly violated in super-resolution, as described in section 4.1.
Although many super-resolution analysis discount non-normal noise, here we discuss a variance-stabilizing transformation204 that mitigates the effect of ignoring non-normal noise.
For simplicity, we consider only the effect of Poisson (shot) noise, whose variance is equal to its mean. Since the variance of the noise changes across the fitted ROI, the assumption of identical noise distribution is violated.
In order to correct for this nonuniformity, we exploit the following (numerical) observation, known as the Anscombe transform: if X is Poisson-distributed with both mean and variance equal to m ≥ 4, then is approximately normally distributed with mean and, more importantly, unit variance.220 Thus, applying this transformation to an image corrupted by Poisson noise yields an image with (approximately) uniform Gaussian noise and the classical least-squares algorithm may then be applied. Of course, the fit should not be done using the original PSF model but, likewise, the Anscombe-transformed model.204
Note that this correction assumes that the image data is correctly expressed in units of photon counts, which requires a calibration of the readout-to-photons conversion factor as discussed in section 4.1. Additionally, more sophisticated transforms (e.g., the generalized Anscombe transform221) may be used to handle more realistic non-Poisson noise models.
While, to our knowledge, the effect of a variance-stabilizing transformation for the accuracy of least-squares fitting has not been evaluated independently of other improvements, the SimpleSTORM package, which relies on it as a preprocessing step before least-squares fitting,204 was shown to exhibit a relatively strong performance.202,204
4.6.4. Corrections to the Point Spread Function
Although we have mentioned, and it is widely quoted,53,201 that the diffraction pattern of a point source is an Airy disc (section 2.2), and chose to approximate this pattern with a Gaussian peak both for maximum likelihood and for least-squares fitting, we now revisit this claim.
When imaging using a high-NA objective, as commonly done in super-resolution applications, the PSF of a freely rotating fluorophore, directly derived from first-principles, is in fact closer to a Gaussian function than to an Airy function222 thus justifying, a posteriori, the use of Gaussians for least-squares fitting.
A rotationally constrained fluorophore, which may occur, or conversely be avoided, e.g., due to the labeling strategy used,199,223 presents additional complications. Such a constraint breaks radial symmetry, in which case the PSF may present two “lobes”.199,222 If a rotationally free model, such as a Gaussian, is used to fit data sets lacking radial symmetry, simulations indicate that maximum likelihood estimation can lead to substantial errors (dozens of nanometers), in particular in the case of defocused molecules (e.g., for 3D measurements).222,224 Conversely, orientational information may be derived from properly fitting the observed PSF to a model PSF for anisotropic emission.199
In the opposite extreme, highly mobile fluorophores, which move by a significant fraction of a pixel size during the time it takes to acquire a single frame,200 may distort the effective molecular PSF, which is now a weighted average of the PSF at each position visited by the molecule. Once more, ignoring this distortion leads to poor localization accuracy, whereas using a PSF model that takes motion into account not only restores the original localization accuracy but also provides information on the instantaneous molecular velocity200 and additional information on motion models discussed in section 6.5.
We end with a note on the nonuniformity of a sample’s refraction index which introduces additional PSF aberrations, especially for thick samples.36 This effect is has so far been treated experimentally by using adaptive optics (e.g., deformable mirrors) to properly shape the PSF.36
4.7. 3D Localization
4.7.1. Cylindrical Lens 3D
While our discussion, so far, has been limited to localizing single molecules in a 2D plane, most biological samples are three-dimensional and, as a consequence, there is considerable interest in obtaining volumetric fluorescence data.
In classical microscopy, this can be achieved by selectively exciting, and thus collecting, fluorescence from a single plane (multiphoton microscopy225 or selective plane illumination microscopy (SPIM)226). However, such techniques remain essentially limited by diffraction. Instead, true 3D super-resolution can be achieved by encoding information about the depth of a molecule in its PSF.
Fundamentally, the techniques we have discussed up until now fit a PSF that encodes lateral but not vertical information. In other words, in 2D, the value of the PSF measured by the camera at position (x, y) when the emitter is at position (x0, y0) depends only on the distance between the two positions, i.e., PSF = PSF(x–x0, y–y0). In 3D, the dependence on the true position z0 cannot be expressed in terms of translation and the PSF would need to be of the form PSF(x−x0, y−y0, z0).
As early as in 1994, Kao et al. introduced a cylindrical lens in the optical path of their particle tracking setup and observed a depth-dependent PSF.227 This depth-dependent PSF progressively switches from being a vertically oriented ellipse for molecules above the focal plane to a horizontally oriented one on the other side. Thus, the lengths of the PSF’s two axes, wx and wy, could be estimated and converted to a depth value using a calibration table. Specifically, the relative difference between the two widths, defined as R = (wy−wx) /(wx+wy), was matched with a calibration curves Rcal(z) in order to read out the depth z while the (x, y) position was obtained by least-squares fitting to a parabolic PSF (section 4.6).
The cylindrical lens approach was adapted for super-resolution by Huang et al.228 who took advantage of the advent of more general nonlinear fitting procedures, allowing the determination of wx and wy by least-squares fit along with the in-plane position. That is, the model PSF was chosen as a Gaussian with the following parameters that need to be fitted: the position of the center and the amplitude of the PSF, similarly to the two-dimensional case along with the PSF width and height wx and wy treated as independent parameters. The authors found, purely empirically, that the fitted wx and wy could be accurately mapped back to the molecule depth z via the use of a calibration curve obtained by measuring the PSF of point sources positioned at different depths, as follows: the depth z is chosen to minimize the Euclidean distance between the point and the curve.
Instead of estimating depth based on ellipticity calibration curves, we may immediately adapt all methods described for 2D localization to the 3D case by simply including the depth z in the set of parameters Θ.217,229 All theoretical results regarding such methods, such as the CRLB accuracy limit (section 4.3), are then applicable. For example, we demonstrated earlier that in the presence of a highly distorted, but experimentally well characterized PSFs, the position of the maximum in the ROI’s correlation with the PSF generated good localization performance (section 4.5.3). This method is, in fact, especially applicable to 3D imaging of thick samples, as the PSF of events localized deep into the cell can be distorted by severe optical aberrations.217
4.7.2. Other Approaches for Encoding Depth Information in the PSF
While the cylindrical lens approach is relatively simple from an experimental viewpoint, it only requires introducing a cylindrical lens in the optical path, it encodes depth information at the cost of lateral resolution, as it distorts the PSF. Additionally, as discussed earlier in section 4.6.4, other phenomena can lead to elliptical distortion of the PSF, leading to spurious apparent changes in depth. Hence, additional ways to encode depth information have been proposed.229
For example, the biplane-PALM approach relies on simultaneously imaging two planes, a few hundred nanometers from each other on the same camera.229 This can be achieved by imaging on one-half of the camera chip the “standard” focused image and, on the other half, a slightly defocused image, obtained by splitting the collected light and reprojecting it onto the camera after a longer light path. A ROI corresponding to a single event now coincides with a pair of spots, one on each plane, that may once more be fitted by least-squares either to an experimental PSF, also measured over the two planes, or a theoretically derived one.229 As a fluorophore is displaced along the z axis, it does not get defocused to the same degree in the two planes; this difference in defocusing thus encodes the depth information. In its first implementation, a depth resolution of 75 nm was achieved.229
Additional z-resolution can be provided by more sophisticated procedures. For example, a spatial light modulator can be used to shape the 3D PSF into a double-helix, such that individual events are now observed as pairs of close peaks, whose relative position encode depth information.10 This technique, to which all the previous fitting discussions apply, exhibits a low theoretical maximal resolution (CRLB) of approximately 15 nm.230 Interferometric PALM (iPALM) provides an even more sophisticated procedure to encode depth information231 in which the measured image is split over three cameras, each of which measure an interference pattern between two images that are phase-shifted with respect to one another. The relative intensities of a same peak across all three cameras allow the experimenter to compute this phase shift and thus infer the event depth, with an experimentally demonstrated resolution of approximately 10 nm.231
4.8. Simultaneous Localization of Multiple Molecules
The fundamental breakthrough from which super-resolution microscopy emerged, namely achieving temporal separation of events too close to be resolved spatially, is also an important limitation. As described so far, a super-resolution acquisition scheme must ensure that only a few molecules are activated per frame, thus imposing lengthy acquisition times for densely labeled samples.
However, just as we have described various ways in which the coordinates of a single molecule can be retrieved if a model PSF is known, we could, in theory, write down an emission model for two, or more, close molecules with overlapping PSFs (given their coordinates x0 and x1), and then fit a ROI to such a model. This approach was pioneered by astronomers who were interested in separating images of stars in “crowded fields” (e.g., stars in distant galaxies, which appear very close to each other) and have since long ago developed such algorithms.232 One of these algorithms, DAOPHOT (Dominion Astrophysical Observatory photometry),232 was directly adapted for super-resolution microscopy, under the name of DAOSTORM.37
There are a few difficulties that are associated with the simultaneous fitting of multiple molecules at a time. The first is computational; the greater the molecules simultaneously fit, the greater the number of parameters, rendering the least-squares or maximum likelihood optimization more challenging numerically.
Fortunately, it is clear that even when PSFs are slightly overlapping, it remains acceptable to cut the image into smaller regions, that are approximately statistically independent from each other, and fit them one at a time. This approximation was used by another super-resolution package developed at the same time, MFA (multiple-emitter fitting analysis).233 More accurately, one can also draw such regions to be bounded by areas of the image where the intensity is relatively low and are thus unlikely to contain a molecule (the approach of DAOPHOT/DAOSTORM). Again, in such cases, the problem of fitting PSFs in a region becomes independent from the fitting in another region,37 in a manner similar to how we drew ROIs for single-emitter fitting but this time with multiple fluorophores per ROI.
More importantly, simultaneous fitting of many fluorophores also presents a model selection problem: allowing for more fluorophores always result in a better (or at least, not worse) fit of a collection of spots (either the fitting algorithm can exploit the additional degrees of freedom to eliminate some residuals of the fit or, at worst, it can always set the brightness of the additional fluorophores to a very small value, thus not worsening the fit). Thus, additional criteria are necessary to prevent overfitting.
While general model selection methods were presented in section 3.3.4, here we present two more model selection strategies specifically adapted to the problem of multiemitter fitting used by DAOSTORM37 and by MFA.233
DAOSTORM first uses a peak detection algorithm (such as the one discussed in section 4.2.1) in order to find candidate regions that may correspond to a molecule. This set of candidates is then fit, by MLE, to a multiemitter model. The residuals of the fit (i.e., the difference between the original image and the one that a set of fluorophores at positions given by the fit would yield) are then iteratively reinserted into the original peak detection algorithm.37 Thus, it is the sensitivity of the peak detection algorithm that provides a stopping criterion against the addition of extraneous fluorophores to the fit.
Model selection by MFA233 relies instead on computing the log-likelihood ratio, LLR;
| (64) |
The numerator, , is the likelihood of the estimates given the image, assuming that each pixel’s signal is independently obtained from a Poisson-distributed source with mean equal to the sum of the PSFs at this pixel (eq 53). The denominator, is the maximum value that the above-mentioned likelihood could ever attain, which it does in the case where the expected mean intensity at each pixel matches the actually observed intensity. In other words, it is the product over the pixels of the probability of observing the actual camera output if the mean expected intensity at that pixel was set to be equal to that output.
Having evaluated the “goodness” of each model (as measured by its LLR), we now need to estimate, for each model, how well the model matches the data, as compared to how well it would match random data sets generated from the model itself. Such a comparison penalizes overfitting, as the marginal improvement to the LLR, for each additional parameter, decreases sharply once the “correct” number of parameters is reached, whereas such a transition does not occur for random data sets.
More specifically, we need to estimate the probability p that the LLR of a data set generated from the model be lower than the LLR of the real data. In other words, we need the value of the cumulative distribution for the LLR, evaluated at the LLR of the real data. According to Wilks’ theorem, this distribution can be approximated by a χ2 distribution with a number of degrees of freedom equal to the difference between the number of pixels and the number of fitting parameters.234 We thus obtain p simply by evaluating the cumulative distribution function of the above-mentioned χ2 distribution.233 Having done so for each of the models in contention, the model with the highest such probability is then selected.
4.9. Deconvolution-Based Super-Resolution
We have so far focused on reconstructing coordinates of each single event with subdiffraction accuracy. However, subdiffraction imaging may be achieved by other means. For example, deconvolution microscopy achieves a 2-fold improvement over diffraction-limited microscopy by approximating the inverse (in a linear operator sense) of the “imaging operator”, i.e., the operator that convolves a distribution of point emitters by the imaging system’s PSF.42
Here, we discuss adaptations of deconvolution-style approaches to data sets collected using single molecule localization-style techniques where additional information is encoded in temporal fluctuations of the fluorescence (i.e., stochastic switching of the fluorophores).
4.9.1. Compressed Sensing
Contrary to localization methods discussed thus far, here we do not initially attempt to reconstruct a list of molecular positions. Instead, we want to reconstruct a higher resolution image than the one from which we started.
More specifically, we seek a “fluorophore density map” on a discrete grid s, where each “pixel” on the grid may be smaller than the raw image, I, physical pixels. Instead of considering s and I as matrices, we will consider them as vectors of entries (for example, by concatenating the physical columns of pixels in the image), respectively of size N and n. In this formalism, convolution by the PSF, which is a linear operator, can be understood as multiplication by a matrix A, of size (N, n),
| (65) |
Each row of the matrix A corresponds to a possible fluorophore position and each entry in the row corresponds to a physical pixel indicating how much a fluorophore at the row-encoded position would increase the intensity at that physical pixel.
Localization methods discussed so far correspond approximately to a setup where we know (or have a good model of) A (i.e., how much a fluorophore at any position affects the intensity measured at any position–in other words, the PSF) and seek to obtain s (i.e., the fluorophore density map). We will focus on the same formulation first. However, we will later see that we can also attempt to recover A and s simultaneously.
The usual caveats of deconvolution microscopy, namely the sensitivity of s to noise and to inaccurate knowledge of A still apply. Moreover, as there are many more (discretized) fluorophore positions than image pixels (N ≫ n), the problem is underdetermined. However, in the context of a super-resolution data set, we have the additional information that we expect only a few fluorescent proteins to be “on” on each frame; that is, we have a sparsity prior on s (we expect most of its entries to be zero).
This class of problems (searching for approximate and sparse solutions to an underdetermined linear system) is known as compressed sensing and is well described in the mathematical literature.235 For example, Zhu et al. showed that in the presence of photon counting noise, a solution can be obtained by searching for the vector s with minimum l1 norm (i.e., sum of absolute values of components) among all those for which the l2 norm of the residual vector, I − A·s (i.e., sum of squared errors), is no larger than a noise-level dependent threshold.236 Such a vector can then be found using standard algorithms.237
Such a deconvolution yields, for each frame of the image stack, a sparse list of discretized molecular positions. All such lists can then be merged together to obtain a final list of molecular positions. Although the original implementation of this idea236 yielded a relatively poor localization accuracy of ~60 nm, it was able to recover highly overlapping events, i.e. it allowed a very fast imaging rate (6 to 15-fold faster than for single-event fitting, 2 to 3-fold faster than for a multiemitter fitting such as DAOSTORM).
4.9.2. Exploiting Fluorophore Temporal Fluctuations
Instead of using an experimental protocol designed to achieve temporally sparse photoactivation of fluorophores, it is also possible to rely on the natural blinking and bleaching of fluorophores, that occurs (to varying degrees depending on the fluorophore) even under continuous illumination.
For example, a simple way to exploit the fluorophore blinking is to compute the difference between consecutive frames of a regular fluorescence movie. In these difference images, the spontaneous switching-on of a fluorophore appears as a positive peak, whereas turning-off events, or photobleaching, appear as a negative one. Standard localization algorithms (e.g., PSF fitting) can then be directly applied to such images, yielding a super-resolution approach that does not require the use of photoconvertible markers (bleaching/blinking-assisted localization microscopy, BaLM).238 More interestingly, it is possible to exploit the fact that these temporal fluctuations in fluorescence intensity are uncorrelated between molecules (as each fluorophore undergoes stochastic switching independently from the others).
Dertinger et al. noticed that due to this stochasticity, pixels where the emission of two blinking fluorophores (quantum dots, in their case) overlap exhibit lower temporal coherence than pixels which capture the emission of a single quantum dot.239 This observation yields a simple and elegant method, named super-resolution optical fluctuation imaging (SOFI), to obtain a superresolved image I.239 At each pixel, one simply plots the value of the temporal correlation of this pixel’s signal for a well-chosen time lag τ
| (66) |
where ⟨·⟩t denotes an average over time.
Lidke et al. exploited temporal fluctuations in order to generalize the model proposed in eq 65.191 Remember that we originally wrote I = A·s, where I is the image (a size n vector), s the discretized fluorophore density (a size N vector), and A the imaging operator (an N by n matrix). In this generalization, the time dependency, over T frames, of I and s, was also taken into account; these two variables are now matrices respectively of size (n, T) and (N, T), where each row encodes respectively the time-varying image intensity at a pixel and the time-varying active fluorophore density at a position. The shape of A is unchanged, and we still have
| (67) |
However, in this analysis, we will also consider the imaging operator A as an unknown.
The problem may thus appear severely under-determined, as we are trying to reconstruct N × T + n × N parameters (A and s) while having only n × T measurements (I). However, we can exploit the fact that in our target reconstruction, each row of s should represent the time-varying intensity of a single fluorophore at a fixed position; conversely, a reconstruction will be poor if some rows of s encode the time-varying mixture of the intensities of multiple fluorophores. From the central limit theorem, the values of s adopted by a mixture are necessarily “more normally distributed” than intensity values of a single fluorophore. In other words, a weighted sum of multiple iid random variables is more normally distributed than each individual variable. Thus, we can restate our objective as follows: we seek the solution of eq 67 for which the rows of s are “as non-normally distributed as possible”. In order to quantify the “non-normality” of the distribution of values a row of s takes, we compute the entropy of the distribution, H = −Σs p(s)log p(s). Because the normal distribution has the maximal entropy among all distributions for a given mean and variance, we thus seek the solution (A, s) of eq 67 for which the total entropy of s (the sum of the entropies of each row of s) is minimal.191 This minimization problem is known as independent component analysis, and can be solved using the standard FastICA algorithm.240
The outputs of this analysis are both matrices A and s with A giving the PSF associated with each of the fluorophores while s indicates, for each fluorophore, the frames on which it is active. This analysis does not directly yield superresolved coordinates; it simply separates the PSFs of each fluorophores (into columns of A) starting from a data set where they were spatially and temporally overlapping. Each of these PSFs can then be fit to obtain a superresolved coordinate for each fluorophore using any of the methods we have discussed so far.191
4.9.3. Bayesian Deconvolution Approach for Fluorescence Time Series
Bayesian methods may also be used to obtain both spatial (A, following our earlier notation) and spatiotemporal (s) information. For example, Cox et al. simultaneously fitted the full set of fluorophore positions, the state histories (bright, transiently dark, or irreversibly photo-bleached) for each fluorophore, as well as the transitions rates between these states (Bayesian analysis of blinking and bleaching, 3B).241
This Bayesian formulation can be seen as another approach to tackling eq 67: instead of reducing the problem to independent component analysis, the time-evolution of the fluorophores (i.e., each row of s) is modeled as a Markov chain between the three above-mentioned states. The true underlying fluorophore spatial distribution is then selected as the one maximizing the likelihood that the entire image stack arises from that distribution. This likelihood is computed by integrating over all possible temporal evolutions (which is done using the forward algorithm).193,241 Instead of yielding a maximum likelihood estimate, one can also sample (by Markov chain Monte Carlo) spatial fluorophore distributions from the posterior derived from this likelihood,193,241 thus yielding a super-resolved image where the intensity at each position encodes the confidence level about the presence or absence of a fluorophore there. This method is extremely demanding computationally, to the point that cloud-based implementations have been developed.242
4.9.4. Richardson-Lucy Deconvolution for Fluorescence Time Series
Mukamel et al. also proposed a simpler deconvolution method (deconSTORM) taking temporal correlations into account.243 Again, the final output of such a method is not a list of coordinates, but simply an image with a higher resolution. Specifically, Mukamel et al. based their work on Richardson-Lucy deconvolution.
Briefly, Richardson-Lucy deconvolution is an iterative approach, whereby the estimated deconvolved image at iteration k is derived from the estimate at the previous iteration , as well as the measured image I, the PSF (assumed known, under a Poisson noise model), and a prior distribution on the true image p(·), which is, in the classical form of the algorithm, kept constant throughout iterations
| (68) |
Mukamel et al. proposed to deconvolve a time series of images by running the iterations of Richardson-Lucy deconvolution in parallel; that is, at each iteration, a new deconvolution of each frame is computed. More importantly, instead of keeping the same image prior throughout the iterations, they used a different prior for each frame and updated this prior at each iteration
| (69) |
Specifically, when running an iteration, the prior for the frame at time t was chosen so that the a priori probability of observing a bright pixel at a given position in that frame is increased whenever the same pixel was also bright in an earlier frame (already reconstructed during this iteration); the closer (temporally) this frame was, the stronger the contribution to the prior. In other words, each frame is deconvolved with a series of priors that, at each iteration, favors a reconstruction similar to reconstructions of the preceding frames.243
4.9.5. Recovering Molecular Localizations from Deconvolution-Style Approaches
We have presented deconvolution-style approaches to obtain a superresolved image without first localizing single molecules. But both methods, deconvolution and localization, may be used in tandem. That is, an initial deconvolution step identifying candidate single molecule positions (from local maxima of the deconvolved image), may be used as initial guesses in a subsequent localization step. Such an approach was implemented in the FALCON algorithm244 that may be understood as a variant of multiemitter fitting (section 4.8), where the model selection step (finding the correct number of fluorophores to fit) is accomplished by an initial deconvolution.
4.10. Drift Corrections
In the absence of active correction, different microscope components drift by dozens of nanometers relative to each other during the acquisition of a single molecule localization data set.3,4 This drift affects positions of measured events.
Thus, in order to combine all the localization events obtained in that data set into a single high-resolution image, it is necessary to either (i) actively correct for this drift by measuring it in real time and displacing the sample in a compensatory manner or (ii) to estimate the drift in order to subtract it from the fitted positions.
In practice, the second option (drift estimation and subtraction) is typically chosen, as it is a purely mathematical operation, that does not require any modification to the instrument itself. In order to do so, we may track bright fiducial markers (e.g., gold nanoparticles or fluorescent beads) on the coverslip. This can be achieved by using the same localization algorithms as used for “real” events.3,4 As the fiducial marker concentration can be chosen to be very sparse, tracking markers from one frame to the next is straightforward. Additionally, the high level of brightness of these fiducially ensures that they are at least as well, and typically better, localized than the events themselves, i.e., they are not a limiting factor for localization accuracy.
Since fiducials are typically bound to the coverslip, such that their motion relative to the camera matches the sample drift relative to the camera, they are less suitable for thick-sample 3D single molecule localization microscopy. From the instrumentation point of view, the use of fiducial markers in a thick sample data set requires repeatedly switching between the imaging planes and the fiducial (i.e., coverslip) plane.217 To avoid the need for such a movement, which complicates the experimental setup and may lead to additional drift itself, one may abandon the use of fiducials and instead rely on correlating event time-slices. In this approach, groups of events are formed by stacking consecutive frames until reaching a set number of events. The cross-correlation between event positions in one group and those in the next then exhibits a peak at a position that encodes the average displacement of the events between the two groups–in other words, the sample drift–as long as the reasonable assumption that both groups are randomly sampled from the entire structure holds.245,246
Neither of these methods can correct drift that occurs on the same time scale as the frame rate as drift estimation requires averaging over a large number of events. In order to increase the rate at which drift information is collected, McGorty et al. proposed instead to use a correlation drift estimator on the bright field image itself (that is, the drift is estimated by finding the shift that maximizes the correlation between a bright field frame and the previous bright field frame).247 Of course, it is not possible to simultaneously collect a bright field image in the visible wavelength and single molecule fluorescence in the same wavelength, as the former would swamp the latter; McGorty et al. thus collected the bright field image in the infrared spectrum. Such an approach allowed them to achieve real-time drift correction, with a 10 nm in-plane and 20 nm axial stability, at rates of a few hertz and over minutes of acquisition.247
5. THE COUNTING PROBLEM
Whether two fluorescent events occurring in close spatial and temporal proximity actually come from the same fluorescent protein is an important question that was raised since early PALM experiments.4,5
One reason motivating this question is technical: “stacking” multiple frames together, by summing their intensities before fitting them, ensures that all photons associated with a single labeled protein are used, thereby improving the reconstructed image’s final quality.4
The question was less relevant in STORM, which relies on blinking organic dyes, as multiple dye-labeled antibodies typically bind to the same target.3 Each labeled site is thus associated with dozens or hundreds of fluorescence events. Thus, proper assignment of each event to its original label is essentially impossible.248
By contrast, in PALM, given a number of fluorescent events arising from a single diffraction limited spot, it was reasonable to ask whether one may enumerate the proteins, or, alternatively, quantify the protein density, that gave rise to the fluorescent signal. Furthermore, if the number of fluorescent events originated from a group of proteins that formed a complex, with each subunit individually labeled, it may then be possible to quantify protein complex stoichiometry.
Inferring protein complex stoichiometry in vivo is an important problem. Many protein complexes involved in essential cellular tasks contain multiple copies of various proteins. For example, E. coli’s flagellar motor is composed of dozens of proteins all appearing in dozens of copies.249
What is more, protein complex stoichiometry may well be dynamical since a pool of freely diffusing protein subunits available to a protein complex changes over time.250,251 The FliM bacterial flagellar switch protein251 is a typical example.
Furthermore, determining a complex’s stoichiometry can also help understand a complex’s operation. For example, asymmetric cell division (sporulation) of B. subtilis creates a smaller daughter cell (the forespore) that initially contains only 30% of its copy of the chromosome; the remaining 70% must be translocated from the larger daughter cell by SpoIIIE, a hexameric, membrane-anchored DNA translocase.252,253 It was originally thought, based on similarities with bacterial conjugation systems, that SpoIIIE forms a single aqueous channel between the mother cell and forespore.252 Later studies suggested, on the contrary, that the septum is closed and two SpoIIIE hexamers jointly form a channel across both membranes through which the DNA passes, based on inability of GFP expressed specifically in the mother cell to diffuse to the forespore.253 Since both models predict different SpoIIIE copy numbers at the translocation septum, they could be resolved by accurately counting of SpoIIIE monomers.
Finally, at the cellular level, proteins and protein complexes can form higher order structures and super-resolution can provide deeper insight into the biological effect of such structures from the spatiotemporal ordering of its constituent proteins. For instance, E. coli’s chemotactic clusters–which allow the sensing of gradients of small molecules–involve tens of thousands of receptor proteins.254 These clusters are positioned in an apparently periodic fashion on the membrane.9 It had been suggested, from time-lapse fluorescence microscopy, that receptor proteins are in fact inserted at random in the cell membrane but later migrate to pre-existing anchor sites.9 Other models proposed that this periodicity arises spontaneously from the stochastic nucleation and merging of clusters.9 Greenfield et al. suggested that studying the protein number distribution per cluster could offer insights in the mechanism by which they are formed.9 We will revisit the type of insight afforded by super-resolution to this question later.
5.1. Counting from Fluorescence Intensity
Proteins localized in small clusters can be counted without the need to spatially resolve them. To do so, we may estimate the number of photons collected and divide through by the mean number of photons emitted by each fluorophore. This mean number (the fluorophore’s photon budget) depends not only on the excitation used but also, more crucially, on specific cellular conditions, in addition to other properties such as possible fluorophore interactions.
As an example of this early approach, if clusters contain few fluorophores, a histogram of the cluster brightnesses may exhibit discrete peaks at multiples of a base value.255 In such a case, this base value likely corresponds to the intensity of a single labeled protein and peaks observed at two, three, or more times this intensity correspond to clusters of two, three, or more proteins.255
In a different approach, a calibration curve relating fluorescence intensity to fluorophore number is constructed by engineering arrays of, say, 12, 24, and 36 fluorophore binding sites and measuring the fluorescence intensity for each number of bound markers.256 Crucially, such a method can be used to establish the existence of a nonlinear relationship between fluorophore count and fluorescence intensity, that can be caused, for example, by interactions among fluorophores.256
The precision of methods relying on total observed intensity is relatively low and relying on a standard mean fluorophore brightness is not without risks. For example, in 2006, Joglekar et al. GFP-labeled a number of yeast kinetochore proteins (where the kinetochore is the structure that links centromeric DNA to spindle microtubules).257 They relied on the fluorescence of a single protein within the complex, Cse4, as a GFP fluorescence standard as that protein was thought to exist in a single copy per complex.257 However, later studies demonstrated that this assumption was incorrect: Cse4 may be present in 4 to 8 copies per centromere and the reported counts of all other proteins were thus underestimated by the same ratio.258,259 Such a difference disqualified earlier arguments indicating that Cse4 may be present in too small a quantity to maintain the necessary attachment points.258,259
Further biochemical studies (protection assays) suggested that one of these proteins (centromere protein A, CENP-A) was, in fact, present at the levels suggested in the Joglekar study.260 This time, it was argued that the larger numbers observed by the Coffman and Lawrimore studies258,259 arose from the inclusion in their counts of “unincorporated” labeled CENP-As, i.e., those not part of the structure itself but simply lingering in the structure’s vicinity, possibly due to lower incorporation efficiency of labeled CENP-A. Since biochemical studies are not devoid of artifacts either, this controversy remains open to this day,261 and should serve as a reminder that the biological question is not to know how many fluorescent proteins are present somewhere but how many of the underlying proteins are actually participating in the process of interest.
5.2. Counting by Photobleaching Using Diffraction Limited Data
An alternative approach is to rely on the stochastic photo-bleaching of single fluorophores.250 More precisely, we rely on the observation that the times at which multiple active fluorescent proteins appearing within the same diffraction spot eventually photobleach are stochastic and thus likely different from one another. Thus, a time series of the total fluorescence signal will exhibit a stepwise decrease250 with possible double-sized steps if two fluorophores simultaneously photobleach within the time scale of data acquisition.
So long as a majority of steps are resolvable, most steps should coincide with the photobleaching of a single fluorophore (or reversible transitions to and from dark states for blinking fluorophores). This is especially true toward the end of the photobleaching trace where the odds of two simultaneous photobleaching events are comparatively low. Thus, given an estimate for the single fluorophore intensity drop, the number of labeled proteins present at the start of the trace can be estimated as the ratio between the initial intensity and the fluorescence drop arising from a single photobleaching event.
Leake et al. applied this method to study MotB, a component of the stator of E. coli’s flagellar motor, concluding that 22 ± 6 copies were present per complex.250 However, this method also suffers from low precision as the noise level at the start of the trace is high and the initial intensity is therefore poorly defined.
Instead of trying to resolve fluorescence decrease steps, which may be challenging, one may compare the evolution over time of the total intensity of a collection of fluorophore spots (which is decreased by any photobleaching event) to the evolution of the number of spots, within that same collection, which have not completely photobleached yet (which decreases only when all the fluorophores within a given spot have photobleached). The slower the decrease of the number of spots relative to the decrease of the intensity, the larger the number of fluorophores per spot.262 Yet another approach is to count molecules by means of photon arrival statistics.263,264 This technique exploits the photon antibunching effect, which essentially states that a single emitting quantum system (a fluorophore in this case) emits photons one at a time. Therefore, if the temporal resolution of the detector is sufficiently fine, photons detected at the same time can only originate from different emitters. In its most recent implementation,264 photon counting statistics were gathered and then a nonlinear regression with a Levenberg–Marquardt algorithm was used to back out the number of emitters, i.e., molecules of interest. However, this method is limited to counting up to 20 or so molecules, largely because of error introduced by blinking and photobleaching effects.
A more promising albeit more difficult approach is to attempt to identify and count all individual photobleaching steps, and use their number as an estimate of the protein count.196 For example, Ulbrich et al. studied the composition of a membrane-bound receptor in X. laevis oocytes, that was known to form tetramers.196 The number of steps in each photobleaching step was visually estimated. Interestingly, the distribution of the number of steps resolved (1–4) is well fitted by a binomial distribution, consistent with a model that only about 80% of the labels are ever fluorescent.
In the sections that follow we will explore theoretical approaches that have been proposed to locate photobleaching steps that can be resolved.
5.2.1. Hidden Markov Modeling of Photobleaching Time Series
Even before Ulbrich’s original experiments, Messina et al. proposed to determine the number, N, of fluorophores using HMMs, discussed earlier in section 3.3.3, where each state coincides with a combination of states for each individual fluorophore.265
The large number of states in this model is suitably shrunk by exploiting the fact that states with the same number of bright fluorophores are indistinguishable, leading to a formulation where each state corresponds to a number n of active fluorophores. For instance, the transition from a state with n active fluorophores to n − 1 has a rate equal to n times the transition rate to the dark state (as any of the n fluorophores could go dark) and, similarly, the transition from the state with n active fluorophores to n+1 has a rate equal to (N−n) times the recovery rate from the dark state (as any of those (N−n) fluorophores could recover).265
Standard maximum likelihood techniques193 were then applied to compute the likelihood corresponding to each total number of fluorophores N. As there is no penalization for overfitting, this likelihood can only increase for increasing N; however, it is expected to plateau once the true number of underlying fluorophores is reached.
This method’s original implementation was applied to time-correlated single photon counting experiments; that is, a setup where stochastic arrival times of each individual photon is measured,265 rather than the more common setup where an average intensity is measured by integration over a longer period. In such a case, the source of noise arises from the existence of “background” photons not associated with a fluorophore of interest,176 as well as from the stochasticity of the arrival times of the “true” photons. However, the approach of Messina et al. can also be directly adapted to the case where an average intensity is measured.146 The authors suggest that up to 30 fluorescent dyes may be counted using such a technique.265
5.2.2. Step-Finding Algorithms in Counting by Photo-bleaching
Without characterizing the kinetics of photo-bleaching, it is also possible to rely on classical step-finding algorithms to count the number of photobleaching events in a time trace.96,266,267 The problem of locating sharp discontinuous changes in noisy data, the purview of step-finding algorithms, is a general problem across science that has been investigated across single molecule biophysics.59 As always, a precise understanding of the noise characteristics in the data-generating process is required to accurately locate steps (Figure 14).
Figure 14.
Step-finding algorithms are widely applied across biophysics. (a) In this synthetic time trace containing 15 steps, the fluorescent signal-to- noise ratio decreases with time by an approximate factor of 3. Methods assuming constant noise statistics tend to overfit the start of the trace where the noise level is high (yellow line). A step-finding algorithm that does take into account variable noise performs significantly better (red line which overlaps with the theoretical noiseless trace used to generate this synthetic data).96 (b) An example of a real data trace (red line) showing an RNA hairpin zipping and unzipping (data was obtained through force spectroscopy).268 The offset green line are the steps found using a step-finding algorithm assuming constant noise.269 The time trace in (a) was created via a simple Gillespie algorithm with variable noise ratio. The code implementation of the method in ref 96 can be found online at https://github.com/lavrys/Photobleach. The code for the algorithm that does not take into account variable noise can be found at https://github.com/knyquist/KV_SIC. Adapted with permission from “Single Molecule Conformational Memory Extraction: P5ab RNA Hairpin.” (J. Phys. Chem. B 2014, 118, 6597−6603).268 Copyright 2014, American Chemical Society.
5.2.2.1. Edge-Preserving Smoothing
Many step-finding algorithms start from an initial filtering or downsampling of the data.270 Although linear filters, where each data point is replaced by a weighted average of the neighboring data points within a specified window, are easily implemented, they also tend to blur or smooth out true transitions in the data. In particular, multiple temporally close transitions may become “merged” into a single transition.271
To avoid this effect, Chung and Kennedy271 proposed (for the purpose of resolving state transitions in patch-clamp experiments) a nonlinear filter, whereby the weight given to a neighboring point during the filtering depends on how well it predicts the current observation, an approach known in the image-processing field as edge-preserving smoothing.
More precisely, for each data point y(t) in a trace, we consider 2K “predictors” of “order” −K, −(K − 1), …, −1, +1, …, K − 1, K, namely the averages of the i (1 ≤ i ≤ K) previous or i future data points
| (69a) |
The squared error below provides a metric quantifying the predictor’s quality
| (70) |
The Chung-Kennedy filter is then computed by weighting the predictor of order i by the inverse pth power of the average badness of the predictors of the same order i but considered over the M preceding (for negative orders) or following (for positive orders) data points
| (70a) |
(where the denominator is simply a normalization factor).
This filter possesses three parameters (K, M, and p), which are tuned empirically. The authors demonstrate that an appropriate choice of the parameters leads to a reduction of the noise without distorting sharp transitions.271 More quantitatively, the effect of various filters on the quality of various step-finding algorithms has been the subject of a comparative study by Carter et al.270 finding that a properly (manually) tuned Chung-Kennedy filter exhibited better performance than mean or median filtering.
5.2.2.2. Segmenting the Trace
Regardless of whether (and how) the data is smoothed to facilitate step-finding, the essential part of step-finding is to segment a trace into “approximately constant” regions separated by a step. Two approaches are possible: “bottom-up”, where small regions are merged together on the basis of value closeness, and “top-down”, where the whole trace is progressively split into separate regions.
An example of the bottom-up approach was proposed by McGuire et al.266 Briefly, starting from the beginning of a trace, data points are progressively added to a running window until the value of the fluorescence moves outside of a small range centered at the current window mean. When this occurs, the current window is terminated and a new window started. After running this process on the whole trace, it is repeated on the resulting “leveled” trace until the levels have converged. This whole process is then iterated (starting from the “leveled” trace) using progressively wider window ranges.266
Conversely, an example of a “top-down” approach is provided by a mathematical idealization of the white noise assumption: the goal is to find the piecewise constant signal , containing N discontinuities (steps), that minimizes the mean square error, . Because it is computationally intractable to test all possible combinations of step numbers and their coinciding locations, the number of locations scaling as the number of time points raised to a power equal to the number of change points, Kalafut and Visscher272 proposed to iteratively add change points one after another, each of them at the position that decreases the mean square error the most. At each iteration, one only needs to check, for each time point, the decrease in mean square error if the next change point was inserted there. Even a naive implementation of this approach only exhibits a complexity proportional to the product of the number of time points by the number of change points. We note however that recent theoretical developments have provided efficient exact algorithms to solve this problem through a careful pruning of the solution tree.273,274
As a fit’s mean square error can only decrease as more steps are added, “top-down” approaches additionally require an explicit penalty against overfitting. Kalafut and Visscher propose the use of the Bayesian information criterion (BIC), discussed briefly in section 3.3.4.272 However, as acknowledged by the authors, this does typically tend to overfit the data.272
For particular applications, it is always possible to create better step-finding algorithms directly informed by the physics that dictates the noise properties of the problem.
For example, a Bayesian algorithm specifically applied to counting by photobleaching is presented by Tsekouras et al.96 In this method, priors and likelihoods are specifically informed by the physics dictating that noise properties should vary stochastically, on the basis of the number of active fluorophores, and that the number of overlapping blinking and photobleaching events have different a priori expectations based on the length of the time trace and the stochastic nature of the photobleaching process.
With this information at hand, Tsekouras et al. arrive at a “top-down” method, more precisely, a marginal posterior for the entire trace, that can be used as a criterion to locate photobleaching steps. The method succeeds in avoiding the overfitting problem arising from assumptions of constant noise across a data set and, according to the authors, scores correctly dozens or even hundreds of steps, provided enough data points are present between successive steps to avoid small number statistics problems (Figure 15).
Figure 15.
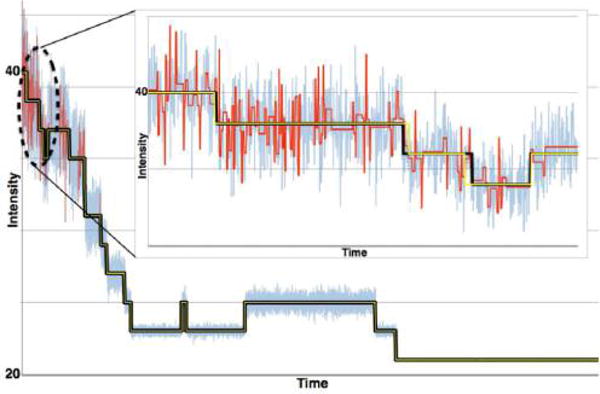
Successful Bayesian step-finding algorithms used in photobleaching use priors informed by the fluorophore photophysics. Here we present a noisy synthetic photobleaching time trace (blue) and the underlying true noiseless signal (black) for a set of 10 fluorophores that eventually all photobleach. Too many steps are found from an algorithm that assumes a constant noise profile (red) grossly overfitting the start of the trace where the noise level is at its highest. Results (yellow) of the Bayesian algorithm proposed by Tsekouras et al.,96 which is tailored to photobleaching and assumes that noise grows along with the number of active fluorophores, are much more accurate. Inset: a blow-up of the first 1000 data points in this time trace where noise is highest and constant-noise algorithms overfit. The data set was created with a simple Gillespie algorithm using a variable signal-to-noise ratio. The code implementation of the method in ref 96 can be found online at https://github.com/lavrys/Photobleach. The code for the algorithm that does not take into account variable noise can be found at https://github.com/knyquist/KV_SIC.
5.3. Counting by Blinking Correction
As suggested earlier, super-resolution microscopy, and PALM in particular, are seemingly well suited for counting, as the molecular photoactivation times are, by design, as temporally separated as possible. Thus, the number of fluorescence events or bursts detected within a diffraction-limited spot should, in theory, match the number of active fluorophores within that spot. This is only in principle true if fluorophores do not blink.
However, even in the presence of blinking, counting remains possible so long as consecutive bursts originating from the blinking of a single fluorophore can be grouped together. Indeed, threshold methods–described in greater detail below–were used, for example, to study the size distribution of E. coli’s chemotactic cluster.9
5.3.1. Threshold Methods for Counting from PALM Data
In the very first implementation of PALM, Betzig et al.4 acknowledged the need for such a grouping and applied a purely empirical threshold (“blinking correction time”) to merge events appearing within the neighboring pixels and separated by no more than three dark frames, in essence applying a very simple form of the nearest-neighbor solution to the linking problem which we discuss in section 6.
Annibale et al.275 further studied the blinking kinetics of the widely used mEos2 photoactivatable fluorescent protein (PA-FP), imaged on a coverslip in vitro. By lowering the fluorophore density, the authors could ensure that each fluorescent event corresponded indeed to a single fluorophore (further confirmed by the absence of multistep photo-bleaching).275 The authors found that roughly half of the molecules reactivated after entering a dark state, i.e., blinked. Recovery times from the dark state were found to be multiexponentially distributed (similar to observations on other PA-FPs276) and regularly lasted as long as tens of seconds. This observation thus raised the concern that earlier studies may have misinterpreted large number of blinking events as evidence for protein oligomerization.275
The authors thus proposed two methods to correct for this blinking. Either the blinking correction time could be empirically increased or, perhaps more interestingly, the authors found that recovery from the dark state could be accelerated, and thus the blinking correction time kept low, through continuous illumination by the photoactivation laser. Thus, they recommended the use of a continuous photo-activation scheme, rather than a pulsed activation scheme where the photoactivation laser is alternatively turned on for a brief period of time, then kept off while the fluorescence of the activated subset is collected.275
In order to maximize the accuracy of the estimated number of events, Lee et al. offered an alternative selection strategy for selecting the blinking correction time.277 First, the authors suggested a scheme by which the photoactivation laser power is tuned in order to ensure a near-constant number of photoactivation events per unit time. Such a strategy ensures maximal separation between active active fluorophores in times and thus minimizes the probability that two fluorophores be simultaneously active.
In short, the scheme was devised by first considering the total number of molecules, N(t), yet to be photoactivated at time t with instantaneous activation rate k(t) which was found to be proportional to the photoactivation laser power, P(t). The number of molecules that photoactivate between times t and t + dt is dN = k(t) N(t) dt; thus, the number of molecules that photoactivate per frame could be kept constant by solving
| (71) |
and selecting a k(t) (or equivalently P(t)) that enforces a constant dN/dt.277 The authors subsequently generated a simulated time series corresponding to the blinking behavior of various fluorophore numbers. The number of events in each time series was then counted by using various possible values for the blinking correction time; the blinking correction time that achieved, for each given underlying number of fluorophores, the minimum mean bias was then tabulated. As could be expected, the more fluorophores in a single spot, the smaller the correction time that achieved unbiased counting. Since the correct number of fluorophores is initially unknown, the authors proposed to start from an arbitrary count, pick the corresponding correction time, count using that correction time and iterate. Overall, this approach was shown to exhibit an error of a few percent when counting up to a hundred molecules.277
While this method introduces a blinking correction time (i.e., a threshold), it does not attempt to produce a “grouping” of events correctly identifying whether two events truly arose from the same molecule. In general, such a grouping may be impossible to attain, as the blinks arising from multiple molecules may be interlaced, or even overlap each other (Figure 16). In such a case, “undercounting” (the incorrect merging of events corresponding to two different fluorophores) is unavoidable. Instead, the blinking correction time was chosen (by using the simulations described above) so that these undercounts are exactly compensated by “overcounts” which are cases where a single fluorophore took a time longer than the blinking correction time to recover from its dark state.277
Figure 16.
It is impossible to regroup blinking events belonging to a single fluorophore using thresholds when signals from different fluorophores overlap or superpose. For illustrative purposes only, we depict the signal from one hypothetical PA-FP in orange and another in blue. Although methods based on grouping events using a blinking correction time cannot identify which event belongs to which fluorophore in such cases, this does not preclude them from yielding an accurate count.
5.3.1.1. Stochastic Counting Methods from PALM Data
While the above method277 relied on calibrated photophysical (blinking and photobleaching) rates for the fluorophores, it is also possible to learn blinking and photobleaching rates self-consistently from the data itself and, simultaneously, avoid thresholds altogether.21 The reason to avoid using calibrated photophysical rates is clear: each protein complex exists within its own unique microenvironment within the cell and rates may differ from one environment to the next.
In order to infer both photophysical rates and the number of fluorophores within an ROI self-consistently, Rollins et al.21 introduced an aggregate Markov model (AMM) (section 3.3.3), and used likelihood maximization to infer photophysical rates and protein counts.21
Figure 17 shows the state of an individual fluorophore. The states fall under two categories called aggregates: bright and dark. Only the active state that emits photons belongs to the bright aggregate. All other states (inactive, dark and photo-bleached) belong to the dark aggregate. The AMM is appropriate here as, for a N-fluorophore system (N unknown), there are many states that make up the dark aggregate, bright aggregate and, more generally, the 2-fold, 3-fold, …, N-fold bright aggregate if 2, 3, …, N fluorophores are simultaneously active.
Figure 17.
Fluorophores may exist in many states but all single fluorophore states fall under two aggregated states: bright and dark. Here there are three states—inactive (I), photobleached (B), and dark (D)—making up the dark aggregate and only one state, active (A), making up the bright aggregate. For this example, with a single dark state there are four rates that fully characterize the photophysics, {ka, kd, kr, kb}. Reproduced with permission from Geoffrey C. Rollins, Jae Yen Shin, Carlos Bustamante, and Steve Pressé. “Stochastic approach to the molecular counting problem in superresolution microscopy.” Proceedings of the National Academy of Sciences 112, no. 2 (Dec 22, 2014): E110-E118.
Just as we had seen in section 3.3.3, the rates can be cast in the form of a rate matrix Q that governs the switching between the AMM states. Assuming for simplicity only two aggregated states (such that at most a single fluorophore can be active at any given time), Q takes the form
| (72) |
where, just as we had introduced earlier in eq 24, the Qij are submatrices with d and b denoting dark and bright state, respectively. From this transition matrix, a likelihood can be constructed based on the aggregate state occupied at each time point and from this likelihood, photophysical rates and fluorophore numbers can be inferred (Figure 18). The authors generalized their treatment in that same paper to treat missed events, that is, dwells in aggregate states (i.e., dark or bright states) shorter than the data acquisition time (Figure 19).
Figure 18.
Results of the method described by Rollins et al.21 employed on synthetic data sets. (a) Synthetic time traces were generated using Gillespie algorithm with photophysical rates kb = 1.0, kd = 10.0, kr = 0.1, ka = 0.5 (see Figure 17) for each of 5 fluorophores. In maximizing the likelihood, photophysical rates as well as the fluorophore numbers may be simultaneously inferred. The results of this inference (shown as histograms) closely match the theoretical expected answer (dotted line) despite the fact that overlapping events were very probable for this choice of photophysical parameters. (b) Same as in (a), except that the effect of missed events has been taken into consideration, resulting in a substantial improvement in accuracy. Assumptions made in creating these data sets are discussed in the original publication, ref 21. Adapted with permission from Geoffrey C. Rollins, Jae Yen Shin, Carlos Bustamante, and Steve Pressé. “Stochastic approach to the molecular counting problem in superresolution microscopy.” Proceedings of the National Academy of Sciences 112, no. 2 (Dec 22, 2014): E110–E118.
Figure 19.
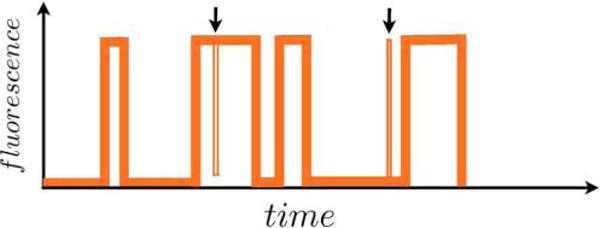
Events of duration shorter than the data acquisition interval can be missed when collecting data, introducing error into the analysis. If a fluorophore blinks faster than the data acquisition rate, the resulting brief dip or rise in fluorescence intensity (denoted with arrows above) will be missed when collecting data. Such missed transitions can be accounted for in inferring photophysical parameters and fluorophore counts.21
5.4. Limitations of Counting
Biological constraints complicate the counting problem. For instance, even if all proteins are labeled and are expressed in their native amount (which has been made possible by the advent of widespread genome editing systems), not all fluorophores mature,196,278 nor will all photoconvertible fluorescent proteins successfully photoconvert.139 Fundamentally, no algorithm can count proteins that never appear.
Various approaches have been proposed to quantify the percentage of proteins that properly activate. For example, by expressing a labeled human glycine receptor GlyR, whose known stoichiometry of three α and two β subunits could be used as a reference, in X. laevis oocytes and counting them either by stepwise photobleaching or by blinking correction, Durisic et al. found that across a wide range of photoconvertible fluorescent proteins, only 40 to 80% of the proteins successfully photoconverted.139 Likewise, Wang et al. expressed a dozen different fluorescent proteins in E. coli and compared the number of events collected in a PALM experiment, corrected through division by the mean number of blinks per molecule, to an estimate of the actual number of fluorescent proteins expressed, obtained by quantitative Western blotting.190 They found an even lower detection efficiency for fluorescent proteins: only between 1% and 20% of them successfully photoconverted. Such limitations need to be taken into account while comparing the accuracy of counting methods: minor gains in the theoretical accuracy of counting will only matter if the global accuracy of the count is not limited by experimental considerations.
6. THE LINKING PROBLEM
Tracking and, in particular SPT, can be broken down into three analysis steps typically performed independently: localization, linking, and interpretation. While the study of static structures only require particle localization, dynamics requires both linking and interpretation.
Inferring dynamics from super-resolution is difficult as there is a trade-off between spatial and temporal super-resolution.279 Spatial super-resolution requires long exposure times in order to collect enough photons to accurately localize particles. These long exposure times make it difficult to interpolate the positions of particles moving rapidly through space as photons are being emitted at different positions yielding a ”smeared” PSF. Shorter exposure times are not necessarily the answer as too few photons may be collected.
Accurate particle linking, often also called data association, which connects a particle’s position across different time frames is therefore an important theoretical challenge. On its own, linking does not characterize the motion of particles, i.e., determine whether the motion is diffusive or directed, although motion models can often facilitate linking. Nor does linking interpolate the dynamics between frames. The latter two issues are relegated to section 7 on the interpretation problem.
Of the three major SPT components—localization, linking, and interpretation—linking is the least developed. However, it is a critical component: poor linking introduces errors that can derail the subsequent interpretation of the dynamics and is often the limiting factor in determining the quality of tracking algorithms.212,280
6.1. Overview of Linking Methods
Linking methods may be considered local or global.281,282 Local approaches work one particle at a time, by linking a single particle in one frame to a single particle in the next. On the other hand, global approaches take many or all particles in each frame into consideration, linking them to a corresponding number of particles in the next. Global approaches perform better when the density of particles to be tracked is high,281 though this often comes at a heavy computationally cost (Figure 20a)).
Figure 20.
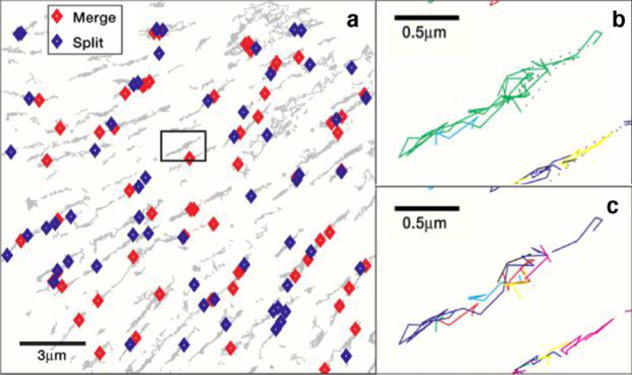
Algorithms that take into consideration multiple frames are more computationally demanding but achieve better results than those taking only successive frames into account. (a) The dynamics of cell-surface receptors were followed and rare merging (blue diamond) and splitting (red diamond) events were monitored. Global rather than local linking methods are needed here to quantify such events which−despite their rarity−are critical in understanding signal transduction.283 (b and c) Comparison between (b) an algorithm that takes into account information across space and time and (c) an algorithm that only considers two frames at a time. The latter algorithm yields many shorter, broken trajectories by failing to link segments (different colors). Dotted lines represent virtual detections, i.e., locations traced by a particle temporarily disappeared. See Danuser283 for details. Reproduced with permission from ref 283. Copyright 2011, Cell Press.
Another way to categorize linking methods is to consider the relative weight they ascribe to spatial versus temporal information281,282 (Figure 20b). For instance, to save on computational cost, many methods only consider two successive frames at any given time in order to link, in the most general case, all particle positions in one frame to all particle positions in the next, thereby maximizing the weight of spatial and minimizing the weight of temporal information. Other methods take into consideration multiple frames, thus assigning more weight to temporal information. Such multi-frame integration is correspondingly more difficult and may be one of the primary areas where there is room for improvement in increasing tracking method reliabilities, as studies in human vision have shown integration to be critical for improved performance.282
As we will discuss, methods that are spatially focused and local, such as simple nearest neighbor (NN) linking methods (section 6.4.1), are overall inferior to global, more temporally focused methods, such as multiple hypothesis tracking (MHT; section 6.4.5.3), which directly address several problems mentioned in the next section, such as missed events or abrupt motion changes, at the expense of computational cost. Furthermore, as we will see, methods that exploit knowledge (theoretical or measured) about particle motion in a specific environment, such as whether particles could move via diffusion alone or via combination of diffusion and directed transport, can exhibit superior performance as long as the model is well specified.
6.2. Cell versus Particle Linking
We briefly highlight the differences between particle and cell tracking. By contrast to particles, most cell tracking methods take advantage of the high contrast of the cells with respect to background.284 Such methods include template matching284 which is only good for very similar cell shapes, as it tries to match a model cell image to the acquired image cell and deformable models.285,286 Both approaches achieve linking by identifying similar-looking or similar-shaped cells across different frames. For example, in the deformable model approach, an initial image or shape is assigned to a cell depending on how that cell looks in the first frame and an approximate image or shape is sought in subsequent frames.286 By contrast to cell tracking, more challenging global rather than local linking strategies are more useful for particle tracking, in part because particles look identical and are diffraction limited.
6.3. Problems Facing Linking Methods
Difficulties in linking arise not only from the data’s diffraction limited nature but also from measurement noise, as often quantified by the signal-to-noise ratio (SNR).287 Sources of noise and additional complications involved in linking include the following: photon shot noise, thermal fluctuations, optical alignment drift, occlusion, chromatic aberration, spatial overlap, systematic position errors due to, for example, fluorophore orientation and pixel nonuniformity, inter-and intra-trajectory inhomogeneities, merging, splitting, appearance, and disappearance of particles282,287–289 (Figure 21).
Figure 21.
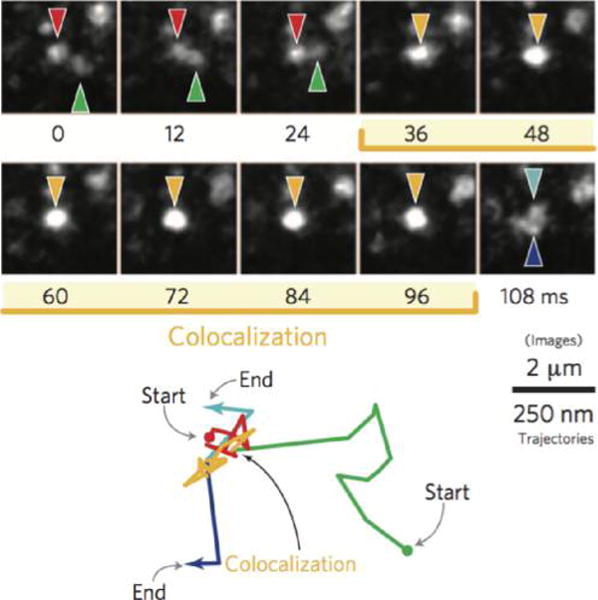
Particles may merge and/or split, leading to trajectories that are temporarily joined. This presents new challenges in identifying pre- and post- colocalization track segments for the same particle. Top: example of a trajectory segment where two formyl peptide receptor290 particles (denoted by the green and red arrows at 0, 12 and 24 ms) merge (at 36 ms) and remain colocalized until 96 ms (yellow arrow), only to split again at 108 ms (blue and gray arrows). Bottom: Particle trajectories followed above. Trajectories colored to match the corresponding colored arrows in the figure above. Adapted with permission from ref 290. Copyright 2014, Nature Publishing Group.
Sources of error in the linking of diffraction-limited particles include not only experimental considerations, but also the choice of models for noise and motion–and the stitching of these models–and the choice of algorithms (local versus global, localization while linking, high cost etc.).287 For instance, algorithms which localize prior to linking propagate error into the linking step by assuming, say, a Gaussian PSF for fast-moving particles.200 Such error may be minimized by jointly performing the localization and linking steps in a self-consistent fashion.291
In subsequent sections we discuss methods of linking. We refer the readers to Mont et al.292 for newly defined metrics quantifying the linking quality.
6.4. Linking Methods
Addressing the challenges discussed in the last section requires principled and often problem-specific linking strategies. We now describe basic linking methods and offer an introduction to their mathematical underpinnings.
6.4.1. Nearest Neighbor Linking
Nearest neighbor (NN) linking is an example of a local spatially focused method. NN methods are simple to implement but inappropriate at high particle density, when particles move at different speeds, split, merge, appear or disappear.293
All NN algorithms try to match a localized particle in one frame to the nearest localized particle in the next frame. Note that “nearest” in this context can refer not only to spatial distance but also to intensity, volume, orientation or combinations thereof. If a combination is used, a suitable coefficient tuning the relative importance of disparate information types must be specified.
More precisely, given a set of N positions, {r1, …, rN}, predicted by the algorithm (either by doing a brute force vicinity search294 or one informed by a model of particle motion295) and a set of N′ experimentally localized measurements of positions, {m1, …, mN′}, both referring to the same time frame t, the goal is to find a one-to-one correspondence between them. This correspondence is represented by the N × N′ association matrix A whose elements aij take the value 1 if ri and mj match and zero otherwise.296
When particles appear or disappear, N may not equal N′ and some estimates or measurements remain unmatched. In this case, “dummy” estimates or measurements are included.296 A NN algorithm then optimizes A by minimizing the total displacement Φ
| (73) |
where d denotes a measure of distance, usually (but not always) simply the Euclidean distance between predicted and measured positions.
In order to reduce computational cost, local assumptions are made. For instance, matches between true particles are only considered if d < dmax where dmax is some maximum distance beyond which a particle could not have moved. If a match between a dummy and a true particle is considered, d is set equal to dmax.
NN algorithms have been used to investigate, among other systems, ligand-gated ion channels such as P2X1297 and 5HT3A,298 Tat (twin-arginine translocation) pathway components in Streptomyces bacteria,294 or the motion (free, hindered, hop, or corralled diffusion) of membrane proteins within cellular or biomimetic membrane compartments.299–302 Local degree of confinement within those compartments is determined by membrane protein motion experiments. In such experiments, NN methods work well, because for some cases, motion models (diffusion on membranes) are well characterized and because the objects of interest are sparse. Sparsity may happen naturally though it is often engineered, for example, by photobleaching the bulk of active fluorophores.
6.4.1.1. Residual Tracking
A special case of NN, residual tracking303 is a method introduced for cases where we expect many particles to be fused or, at the very least, in close proximity even if the overall particle density is low. We begin by constructing all possible links that particles in one frame can have to particles in the next. Each one of these associations is called a hypothesis. To rank order these hypotheses, we consider all fluorescence intensities at time t at position (x, y) in a 2D image, . In theory, such fluorescences are obtained from (i) the sum of a constant background fluorescence, bt; (ii) the fluorescence of the ith particle, Pt, i extending across some pixels that include location (x, y); and (iii) a stochastic acquisition noise term Nt
| (74) |
The key idea of this method is to make the residual Rt, defined below, approach zero
| (75) |
Residual tracking is computationally efficient but seriously limited because it considers only successive frames.
NN methods have clear limitations. They are prone to error if more than one particle is likely to find itself within d, i.e., for dense samples, and even more so because the calculation of d depends on the model chosen.
6.4.2. Overview of Filters
We have just described a local, spatial method. We now broaden our discussion to filters incorporating past temporal information in linking that goes beyond the previous frame.296 This is by contrast to other methods, such as multiple hypothesis tracking (MHT) discussed in section 6.4.5.3, which incorporate numerous frames, past and future, in addition to spatial information all at once.
Filters are sequential Bayesian methods using motion models to create an estimate of the future position of a particle, subsequently updated using current actual measurements. Because of their reliance on motion models, inhomogeneities requiring complex motion models, present difficulties for such approaches. A detailed discussion of the Kalman filter, probably the most commonly used filter, will be relegated to section 7.2.4.
Filtering approaches can be either global, more commonly called joint in the filtering literature,296 i.e., applied to all the particles in an image frame at once, or local, a.k.a. independent, i.e., applied to one particle at a time. All filtering methods can in theory be used as joint or independent filters, but in practice only the Kalman filter and the particle filter are ever used as independent filters. All filtering methods, especially if used by themselves, assume only small changes in number of detected particles per frame.
Filtering algorithms, often used as part of a broader tracking data analysis scheme, see for example section 6.4.5.1, have also been used by themselves, for example in linking frames for gene carrying particles (viruses, drugs, etc.)304 and viral296 particles.
6.4.2.1. Joint Filters: Spatiotemporal Filtering
Unlike independent filters, joint filters296 link all particles in one frame to all particles in the next. This avoids those conflicts that plague independent filters but is correspondingly more computationally expensive. The simplest joint filter is the spatiotemporal filter, which can be thought of as a generalization of the Kalman filter, discussed in section 7.2.4.
To be more specific, for spatiotemporal filters296 we assume, in analogy to HMMs (section 3.3.3), that, at time t, a particle has a hidden state rt represented by a noisy measurement mt. The goal is to estimate rt from the data. The spatiotemporal filter achieves this for all particles in a frame, i.e., it is a global linking method, by recursively finding the posterior, p(rt|m1→t), where the index 1 → t denotes all frames from frame 1 to frame t. To find the posterior, we first specify the following quantities: p(rt|rt−1), dictated by the motion model to describe the evolution of the hidden state; p(mt|rt), representing the relation between observation and state; and an initial prior p(r0). Using these quantities, a two-step recursive Bayesian approach yields the posterior
| (76) |
| (77) |
where in the last expression, we invoked Bayes’ theorem and assumed measurements are independent. While in general the integral of eq 76 cannot be evaluated analytically, under some Gaussian approximation the formalism reduces to the well-known Kalman filter296 (section 7.2.4). This is because the Kalman filter performs exactly the task of creating a prediction p(rt|m1→t−1) for the particle position, then compares with the measurements, and finally yields a result by combining the prediction and the difference between prediction and measurements, called the innovation. In the Kalman filter, prediction and innovation must be combined linearly via some gain matrix; the Gaussian approximation is required to mathematically justify the gain matrix form.
Alternatively, for non-Gaussian p(rt|rt−1) and p(mt|rt), the integral of eq 76 can be estimated by sampling the integrand, typically via MCMC. This method is called the particle filter. What is more, inconsistencies in the performance of filters across an image have been addressed using a modified sampling scheme called the boosted particle filter.
Finally in the special case where there are only a few particles that look and behave very similarly per frame, it is possible to use a mixture of particle filters to approximate the posterior p(rt|m1→t). For example, two particle filters, each corresponding to a different motion model, can be constructed and then the posterior estimated as a weighted sum of the samplings from each filter.296
6.4.2.2. Independent Particle Filters
Independent particle filters use one particle filter for each particle. That is, only a single particle is linked between two successive frames. Computational requirements for independent particle filters are therefore low. However, independent particle filters fail if particles pass so close to each other that the corresponding filters both choose the same particle, i.e., conflict. When filters conflict, one solution is to find sets of trajectories that minimize the number of appearing and disappearing particles.296 Drawing from graph theory, each particle position can be thought of as a vertex and each link between two positions as an edge. When particles conflict, some vertices have more than two edges, while others may have one or none in which case they are called orphan vertices. Godinez et al.296 propose a method to minimize orphan vertices by creating candidate links between them following a logic very similar to NN linking discussed in section 6.4.1. The need to find some procedure to resolve conflicts is the main disadvantage of independent particle filters.
It is theoretically possible to use filters other than the particle filter to follow each particle, so that we can, for example, have independent Kalman filters. However, no implementations of such filters have–to our knowledg–ever been constructed, since the risk (filter conflict) outweighs the reward (easing of the computational burden). Independent particle filters is the only exception because particle filter sequential Monte Carlo sampling already imposes a heavy computational burden so easing it becomes a priority.
6.4.3. Energy Minimization
In linking by energy minimization, we begin with a set of frames and stack them in the order in which they were acquired thereby forming a 3D volume. The linking problem, that is, finding trajectories within this 3D volume, is reduced to a global minimization of an objective function defined on this volume that can be thought of as an energy.293 Energy minimization methods are global and consider both temporal and spatial information in the linking process. By contrast to filters and MHT, discussed in section 6.4.5.3, energy minimization methods are non-Bayesian. More specifically, while filter methods only incorporate time up to the frame currently being processed and MHT considers, in principle, all possible trajectories across all space and time, energy minimization methods are more computationally efficient.282
High accuracy combined with low computational cost have made energy minimization methods popular for linking, especially for cases with smooth, long tracks. For instance, they have been used to track low-density lipoproteins transported inside endosomes and adenovirus-2 particles moving along microtubules,305 viruses transporting across membranes,306 diffusion of proteins in chromatin structures,307 changing distributions of Vipp1 proteins, essential for photo-synthesis, in cyanobacteria308 and lac repressors in DNA in a study of DNA repair mechanisms related to antibiotic resistance in bacteria.309
The effectiveness of energy minimization methods depends on one’s choice of objective function (i.e., energy). For instance, objective functions may be phenomenologically motivated based, in whole or in part, on physical properties such as the fluorescence signal to be linked305,310,311 (Figure 22). For example, we may define a distance metric such as eq 73, albeit for all particles as opposed to one particle, that may be further regularized by the quadratic difference in fluorescence intensity moments of order 0 and 2.305 In a similar example, trajectories were constructed by following high gray intensity curves.310 In yet another similar example combining NN and energy minimization, Bonneau et al. tracked glycine receptors in neurons but linked brightness rather than distance globally for the particles.311 Track fragments across the 3D volume were linked in such a way as to minimize 3D volume geodesics albeit constrained by physical motion models, such as the local diffusion coefficient.311
Figure 22.
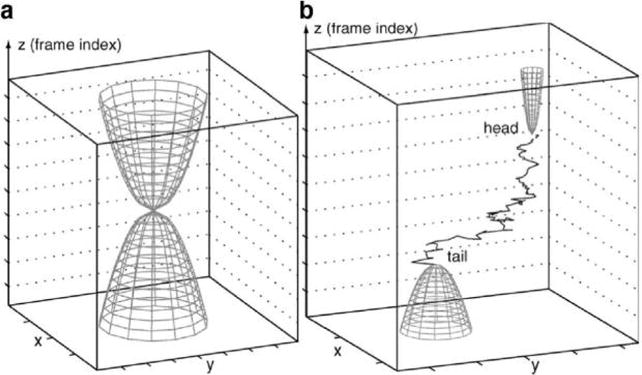
Motion models can be used to limit the search area for linking algorithms.311 (a) The two parabolas represent the past and future volumes in which a particle localized at their intersection may be found on the basis of a motion model. Limiting the search volume reduces the computational cost of the method. (b) Once a trajectory segment has been determined, it is possible to use different motion models in different spatiotemporal areas of the trajectory, as shown by the different shapes of the paraboloid search regions. In this case motion in the later end of the trajectory (designated “head”) is considerably more constrained than motion in the early part of the trajectory (designated “tail”). Reproduced with permission from ref 311. Copyright 2005, IEEE Computer Society.
Objective functions can also be motivated by mathematical principles. For example, Shafique and Shah312 draw heavily from graph theory, constructing a graph where localized particles in all frames are vertices and links are edges. They invoke tools from graph theory in order to maximize trajectory length while ensuring that the optimal trajectory set minimizes orphan vertices, i.e., maximizing graph cover.313 These graph theoretic inspired methods can tolerate cost functions that are not optimized for the problem or that are ad hoc to a greater or lesser degree. They are therefore more general than physics-based energy minimization methods and avoid having to go to great lengths to pick suitable motion model based cost functions.
A method, detailed elsewhere,314 that brings together phenomenological objective functions and graph theoretic methods has been used in studies of the tumor necrosis factor 1 crucial in inflammation,315 integrin and talin protein dynamics in cellular focal adhesions,316 and enzymes that are suspected of promoting tumor generation.314
6.4.3.1. Linking via Message Passing between Frames
This new method is an attempt to fix the problems energy minimization methods encounter when particle density is high and works best for such high particle densities (Figure 23).
Figure 23.
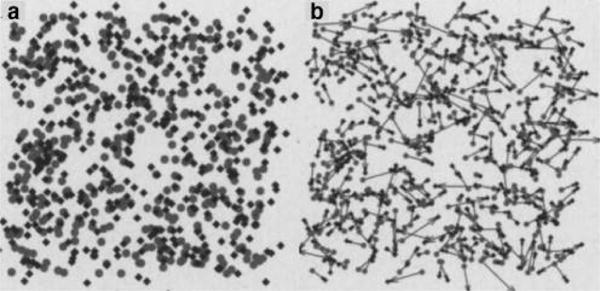
Biological images can be cluttered to the point where near-neighbor algorithms are bound to fail. (a) Superposition of two successive frames in synthetic data mimicking particle transport via turbulent fluid flow. Particles in the first and second frame represented as light-colored spheres and dark-colored diamonds, respectively. (b) Trajectory track segments derived for particles in these two frames via the “passing messages between frames” method.291 It is obvious that nearest-neighbor algorithms would not work well for this data. Reproduced with permission from Michael Chertkov, Lukas Kroc, F. Krzakala, M. Vergassola, and L. Zdeborová. “Inference in particle tracking experiments by passing messages between images.” Proceedings of the National Academy of Sciences 107, no. 17 (Apr 27, 2010): 7663−7668.
The method starts by formulating the linking problem as a weighted complete bipartite graph.291 Subsequent mathematical mapping detailed elsewhere291 reduces the linking problem to what is known as the message-passing formulation of belief propagation. This normally is a computationally very expensive method, but it can be approximated by a MCMC algorithm which reduces computational cost by multiple orders of magnitude, making the method tractable.
A general criticism that can be made of all energy minimization methods is that they rely on trajectories that are long and regular, which is not always realized in biophysics where observed trajectories are jagged and short due to fast changes in motion or photobleaching.
6.4.4. Multiple-Target Tracking
While filters (section 6.4.2) are Bayesian and operate one frame at a time, multiple-target tracking (MTT)317 is a non-Bayesian linking method that also works one frame at a time. It has the advantage of being much less computationally expensive than filters. MTT links particles to the next frame starting from localized particles at the current frame in addition to knowledge of motion model and photophysical parameters drawn from previous frames for each trajectory (Figure 24).
Figure 24.
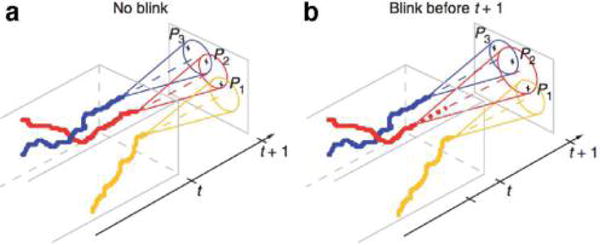
Effects of blinking, or temporary disappearance of particles, present linking challenges. (a) No blinking. Three trajectories are associated with three localized points (P1, P2, and P3). Motion models constrain the possible areas within which each of the localized points terminating the trajectory could have moved, but ambiguity nevertheless exists. Thus, P1 can potentially be the terminal point for either red and yellow trajectories, and similarly for P2. The problem can only be resolved because P3 belongs to the blue trajectory, meaning that P2 and P1 must belong to the red and yellow trajectories, respectively. (b) Blinking in the red trajectory before the current frame. Because no particle was detected for the red trajectory at frame t, the potential area in which the particle may be found in frame t + 1 is correspondingly larger. However, assignment of localized points at frame t + 1 to trajectories is still resolvable. On the contrary, combinations of blinks or, alternatively, blinks lasting longer than one time frame can lead to important misassignments.317 Adapted with permission from ref 317. Copyright 2008, Nature Publishing Group.
More specifically, in order to link existing trajectories to localized points (particles) in the new frame, an area where the particle would be expected in the new frame must be determined. This area is calculated based on a Brownian motion diffusion model, although the method can be adapted for other motion models, with the position of the particle in the last frame as initial condition and bounded by some predetermined distance. If a single particle is found within that area it is added to the trajectory. If there is overlap, i.e., there are more than one candidate particles in the area, MTT compares the likelihood for each possible linking as a function of the positions, intensities and blinking probabilities of the particles involved. If there are any unconnected particles in the area, particles are relocalized and the procedure repeated.
MTT is computationally inexpensive but is much less powerful than algorithms that take many frames, past and future into consideration, like MHT (section 6.4.5.3); it is also much less effective if the particles being tracked behave very similarly because if their trajectories cross it is prone to misidentifications. Initially demonstrated on tracks created by the motion of epidermal growth factors in the plasma membrane of cells,317 it has since been used to study actin dendritic spines318 and enhanceosome assembly in embryonic stem cells.85
6.4.5. Bayesian Nonfilter Methods
Here we briefly highlight a group of Bayesian linking methods devised for frames where particle density is high (which causes filters (section 6.4.2) to fail) and particle motion is not smooth (which causes energy minimization (section 6.4.3) methods to fail).293 These methods, informed by priors derived from models of motion or knowledge of particular system, are particularly useful in biophysics, where jagged motion and high particle densities are often encountered293 but can fail if motion models are inadequate, or probability distribution assumptions do not hold314 (Figure 25).
Figure 25.
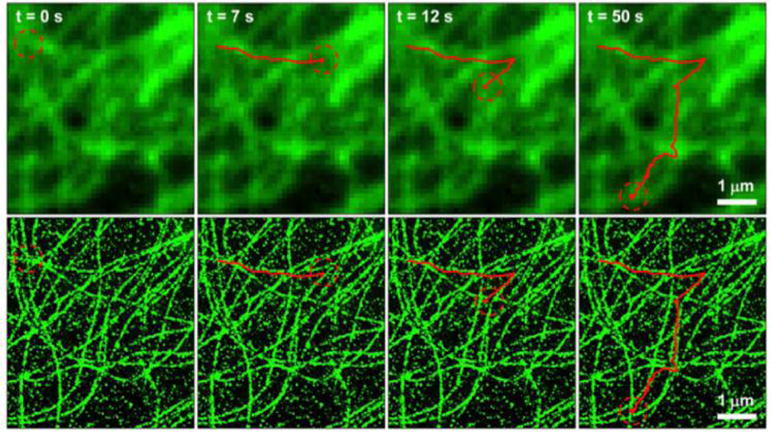
Contextual information on a tagged particle’s microenvironment may be used in linking. In the top panels above, a lysosome (red trajectory) was transported by molecular motors on a microtubule network (green background). By using super-resolution to image the microtubule network with high precision (lower panels), it became possible to closely match a lysosome trajectory to a particular microtubule and quantify when the lysosome detached or switched between microtubules.319 Reproduced with permission from Štefan Bálint, Ione Verdeny Vilanova, Ángel Sandoval Álvarez, and Melike Lakadamyali. “Correlative live-cell and superresolution microscopy reveals cargo transport dynamics at microtubule intersections.” Proceedings of the National Academy of Sciences 110, no. 9 (Feb 26, 2013): 3375−3380.
6.4.5.1. Interacting Multiple Model
Kalman filters, discussed in section 7.2.4, assume a single motion model. By contrast, the interacting multiple model (IMuM)320 uses multiple Kalman filters each with a different, competing, motion model to estimate particle positions in the next frame. The Kalman filter that wins the competition sets the motion model for that particle in that frame alone; in the next frame the Kalman filters compete anew. In this way IMuM avoids any assumption of smooth motion, reflects the fact that particles in biological settings can switch between types of motion relatively quickly and also avoids the very high computational cost of the MHT (section 6.4.5.3).
More specifically, similar to filters, IMuM computes the posterior p(rt|m1→t) by assuming that the system can be reduced to a set of j switching linear models with additive Gaussian noise profiles of the general form
| (78) |
where j is the index of the model that is active at time t, is the state transition matrix, is an “observation matrix” relating the hidden position to the measurement, and (η, ε) are the “process” and “measurement” noise vectors respectively, described in greater depth in section 7.2.4. Both noise vectors are assumed to be uncorrelated white zero mean Gaussian processes.
As there are too many possible sequences of motion models to consider for the problem to be computationally tractable across all frames, IMuM considers only two successive frames i, i+1 at a time. That is, IMuM calculates position predictions for the (i+1)th frame from each motion model via a Kalman filter employing that motion model. Once the predicted positions for each motion model have been constructed, the motion model whose predictions for each particle best matches a measurement is determined by maximizing the likelihood of the innovation for the Kalman filters for each particle in each frame.
IMuM yields good results but only when the linearity and Gaussianity assumptions that underlie the Kalman filter are justified. It also has a disadvantage compared to methods such as the MHT since it does not consider future temporal information.
6.4.5.2. Linking with iHMMs
Here we mention a non-parametric Bayesian method that appeared almost a decade ago.321 Prohibitively expensive computationally at the time it was first presented, it now shows promise. This method relies on iHMMs (section 7.3.2), and thus can grow in complexity as the amount of available data increases. To be more precise, previous methods, such as IMuM (section 6.4.5.1), prespecify the number of motion models or state space. To accommodate the complexity of large data sets, large state spaces would be needed, thereby increasing the computational burden. iHMMs only grow the state space as needed and thus we argue that they are well suited for cases where large numbers of particles may be moving with a variety of motion models in heterogeneous environments, as is the case, for example, of different transcription factors diffusing in the nucleus.322
6.4.5.3. Multiple Hypothesis Tracking
Multiple-hypothesis tracking (MHT), first proposed by Reid,323 is perhaps the most advanced among available methods. It is intended to tackle the major problems of particle motion heterogeneity:280 high particle density, particle merging, splitting, and temporary disappearances.
In principle, MHT, starts from all particle positions localized across time frames (past and future), thereby constructing all possible trajectories that could arise when linking all frames.
In practice, this is not computationally feasible, and thus a greedy algorithm is often used to stitch locally optimal links across frames. Greedy algorithms are more efficient, but pay a price in that some potential trajectories are never considered. Here we describe one such implementation by Jaqaman et al.280
In the first step of this implementation, particles in one frame can link to at most one particle in the previous or next frame. Taking all such possible links for each particle in a frame, short candidate segments linking just two localized particle positions are created. Segments are also constructed for particles in one frame linking to nothing in the previous or next frame, these links corresponding to a particle appearance and disappearance, respectively. Some of these candidate two-particle trajectory segments are mutually exclusive, i.e., conflict.
In the second step each possible two-particle trajectory segment is assigned a cost, and in any group of conflicting segments, only the lowest cost segment is retained.
In the third step, these two-particle trajectory segments across all frames are themselves linked in five ways: end of one segment to the start of the other, for continuation; end-to-middle, for particle merging; middle-to-start, for particle splitting; end-to-nothing, for trajectory ending; and nothing-to-start for new trajectory initiation. This trajectory segment linking creates large numbers of potential trajectories, many of which conflict. Trajectories that do not conflict are regrouped as a candidate tracking hypothesis. Step four assigns a cost function, which may be Bayesian or otherwise motivated, to each hypothesis and the lowest cost hypothesis is selected, similar to energy minimization methods (section 6.4.3).
This implementation of MHT has been used to follow the motion of the macrophage trans-membrane CD36 receptors;280 the formation of clathrin-coated pits;280,324 microtubule dynamics;325 and AAA+ ATPase motor cytoplasmic dynein dynamics.326
Chenouard et al.287 extended the previous treatment by turning MHT into a Bayesian framework. Briefly, for reasons of computational efficiency, they built tracking hypotheses between frames k and k + d by considering all possible positions that a particle could take in each of these frames. To further limit computational cost, they stored hypotheses as tree graphs, and in the first step of MHT, they do not explicitly consider particle splitting, merging, appearance, and disappearance when constructing trajectories.
This reduction of the computational burden is necessary in view of two new features this implementation of MHT introduces, both of which are computationally costly.
The first new feature enters in the second step of MHT. When linking a measurement A in frame k to a measurement B in frame k + 1, the algorithm assumes a particle has moved from A to B via a combination of diffusion and directed transport and assigns each of these a Kalman filter (section 7.2.4). Then the algorithm employs an iHMM (section 7.3.2) to set the specific motion parameter models used in the two Kalman filters and among conflicting trajectory segments retains the one with the most likely parameter values.
The second feature enters in the third and fourth steps of the MHT. Instead of creating trajectories by linking only trajectory segments whose starts or ends are in adjacent frames, the algorithm links trajectory segments even if they are separated by several frames. This compensates for the algorithm ignoring particle appearances and disappearances in step one. Trajectory segments involving such “hops” across frames, realized in the tree graph formalism via virtual detections, are assigned a cost on the basis of a model based on the photophysics of particle disappearance for the particular system.
Once trajectories have been created up to the predetermined tree depth, i.e., frame k + d, the most likely tracking hypothesis in a single frame, i.e., k+1, is obtained by maximizing the full joint probability up to the k + d frame (Figure 26).
Figure 26.
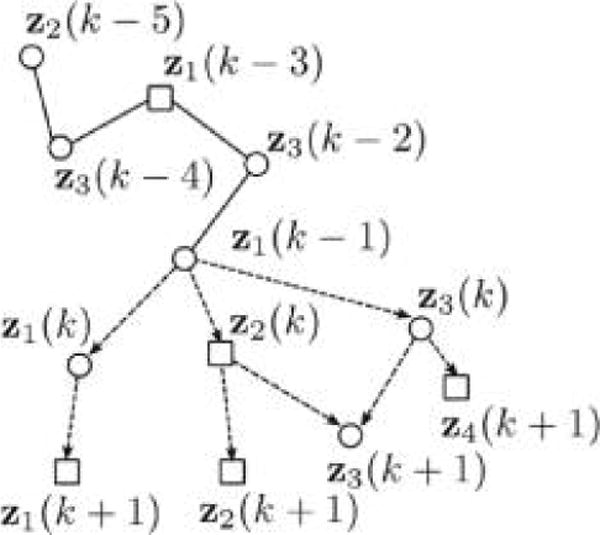
A tree can be constructed by linking particle positions. Here a trajectory that has been established from time frame k − 5 to k − 1 is examined for possible extensions to time frames k and k + 1. z refers to a measurement (circle) or a predicted virtual particle position (square). In the zi(j) notation j is the time frame and i enumerates the possible particle locations, real or virtual. All possible track extensions are considered, whether they consist of real detected particles or virtual detections. See Chenouard et al.287 for details. Reproduced with permission from ref 287. Copyright 2013, IEEE Computer Society.
Although computationally heavy and rarely used thus far, this implementation of MHT shows great promise due to the thoroughness of the tree-graph approach and the highly customizable extra features that allow for significant expansion the method. For example, it is possible to inform the iHMM with additional motion models or extend the tree graph approach to account for particle splitting and merging, which are not considered thus far.
6.5. Temporal Super-Resolution
Temporal super-resolution, which is to localize particle positions at time intervals t across frames collected at longer times, can also be thought of as the ultimate solution to the “connect-the-dots” problem. The “connect-the-dots” problem is the mirror image of the interpretation problem. In the interpretation problem we ask “given a particle trajectory, what can I learn about how the particle moves (i.e., the motion model) between observations?”. In the “connect-the-dots” problem, we ask “given some imperfect idea of the particle motion, how can we best connect localizations of the same particle in adjacent frames?”. The “connect-the-dots” problem can be seen as part of linking in that a motion model can guide us in making the correct links, i.e., correctly identifying which observations across frames belong to the same particle. It can also be seen as part of an iterative approach to both linking and the interpretation problem: if we assume a naive motion model and link observations to get initial trajectories, we can then interpret those trajectories to change the motion model and get higher quality links and better trajectories, then interpret those and so on. In this context, temporal super-resolution is important because it would allow us to sample the particle motion at such small intervals that any uncertainty as to the motion model would disappear. In such a situation, linking would be trivial, interpretation much easier, and “connecting-the-dots” unnecessary.
The connect-the-dots problem has yet to attract the intense attention that spatial super-resolution enjoys. While biology’s traditional focus has been on structure, counting and localization, a clearer picture of dynamics may help address fundamental questions such as the mechanism of transport between nucleus and cytoplasm327 or protein folding pathways.328
As we described earlier, spatial super-resolution, requiring hundreds of photons to localize particles with tens of nanometers resolution, comes at the cost of temporal super-resolution, i.e., time resolution less than μs or faster, that we refer to as the spatial-temporal trade-off arising from a fluuorophore’s limited photon budget.279
Whereas the spatial PSF is typically a Gaussian, a fluorophore passing through an ROI appears in that ROI as a box-shaped pulse in time that may last for more or sometimes less than a single frame329 (Figure 27). Thus, any method relying on a Gaussian noise pulse in time introduces error.
Figure 27.

Temporal and spatial blur have different PSFs. While spatial blur (left) can be well approximated by a Gaussian, temporal blur (right) is a “box-shaped” pulse that cannot reliably be considered Gaussian. Algorithms that make Gaussian assumptions may therefore fail when used to temporally localize particles.329 Reproduced with permission from ref 329. Copyright 2005, IEEE Computer Society.
The photons arising from this pulse are spread out over a spatial region, i.e., are blurred, either because the particle is moving fast compared to the frame rate or because of errors caused during localization by the use of PSF functions that are not appropriate for fast moving particles.200 Another reason for this blurring, which contains the temporal superresolved image we seek, is that the camera frame rate may be slower than typical frequencies of motion where few photons are released per pixel in turn complicating, in a manner known as aliasing, the “connect-the-dots” problem (Figure 28).
Figure 28.
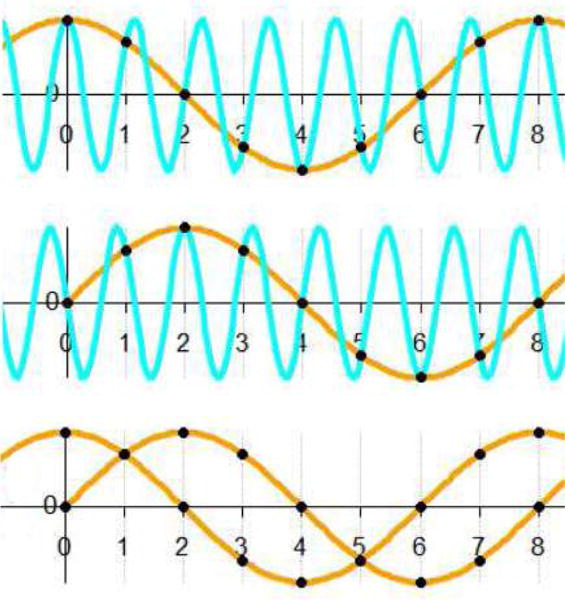
Sampling rates and “connect-the-dots” schemes can bias interpretation. Consider two particles that are undergoing oscillatory motion with the same amplitude and frequency but are slightly off-phase (top and middle, blue curves). At a frame rate less than the period of the particle motion, observations (top and middle, yellow curves) suggest an oscillatory model with the same amplitude but a different frequency. This effect, where some motion characteristics are inferred correctly while others are not, is called “aliasing” and is a key challenge of temporal super-resolution.
Existing theoretical methods increasing temporal super-resolution are often motivated by machine vision or other applications.329 However, methods developed for many machine vision applications often implicitly assume an abundance of photons to be detected, contrary to shot noise expected in super-resolution, and may rely, either in whole330 or in part,329 on increasing the number of cameras or optimizing a camera sampling scheme.329,330
However, there are methods from machine vision more appropriate for SPT. Briefly, a (Bayesian) inference approach used by Borman and Stevenson331 relies on the notion that frames collected at high data acquisition have low spatial resolution but high temporal resolution while frames obtained by integrating the fast frames yield low temporal resolution but high spatial resolution. This algorithm exploits information at both frame rates to achieve both high spatial and temporal localization at once. In order to do this, it introduces a highly under-determined association matrix that relates position of objects (i.e., particle localizations in super-resolution) in high resolution frames to many possible object histories (i.e., particle trajectories in super-resolution) allowed by the low resolution frames. Motion models and observation models, an analog of an emission probability in HMMs, are subsequently used to reduce the indeterminacy.
It has been shown that indeterminacy can be further reduced by exploiting two effects:332 the fact that some parts of the image remain static and that low-resolution pixels affect only those high-resolution pixels with which there is spatial and temporal overlap.
At present, temporal resolution lags far behind spatial resolution. While spatial resolution is pushing into the nanometer scale, temporal resolution rarely goes beyond the millisecond scale. As a result, we cannot follow particle motion directly and instead must infer its parameters (velocity, diffusion coefficient, etc.) from the trajectories we construct: this is the purview of the interpretation problem.
7. THE INTERPRETATION PROBLEM
Stacks of in vivo optical images are the starting point for the analysis of dynamics inside cells.61,65,66,85,86,88,95,126,333
Previously, we discussed that particle tracking involves particle localization and linking. Unless stated otherwise, in this section we start from the assumption that we have performed both localization and linking with minimal error and that the observed trajectory originates from a single molecule (a realistic assumption when the fluorescent label density is relatively low).
The possibility that linking or localization errors may be large, as may be expected in crowded environments or if fluorescence efficiencies depend on the local cellular environment, or that linking or localization may be performed jointly while inferring motion models from single particle tracks goes beyond the scope of this section.
Rather, here we are focused on time series analysis or what we’ve termed the “interpretation problem”. That is, the inference of motion models and their parameters, such as velocities, forces, diffusivities, binding interaction strengths, from previously localized and linked single particle trajectories.
We begin this section by reviewing established or “legacy” SPT time series analysis approaches, section 7.1, and discuss some of their fundamental limitations. For instance, we spend some time discussing mean square displacement (MSD) methods, arguably the most commonly used technique in SPT data analysis,60,65,89,299,334 which dates back to the turn of the 20th century335 and provides average information on particle trajectories.
We follow this discussion on methods that do not average down the information, as MSD does, and explicitly account for noise, section 7.2, where a tracked particle’s “true” position, {r1, r2, … rT}, may differ from the “measured position”, {m1, m2, … mT}. In particular we will spend some time discussing the classic Kalman filter.
We will finally extend our discussion to nonparametric approaches, briefly introduced in section 3.4, further developed herein, section 7.3.
The motivation for moving toward nonparametric model formulations in time series analysis is clear: the heterogeneity of a cell’s environment often warrants more complex models. For example, we may want to treat abrupt changes in motion models that may arise from spontaneous molecular changes or interactions with heterogeneous environments61,63,66,95 or, alternatively, use information on these environments to inform motion models.
For instance, high spatial (10 nm) and temporal (10 μs) resolution 3D SPT measurements were recently combined with conventional two-photon scanning microscopy to obtain useful “contextual” information on the changing environment in which tagged nanoparticles diffused.14,15 This new imaging approach showed that the motion of a 3D trajectory of a fluorescently tagged nanoparticle, mimicking a virus, was heavily influenced by larger 3D surface structures that were not otherwise captured by standard SPT motion models (Figure 29).
Figure 29.
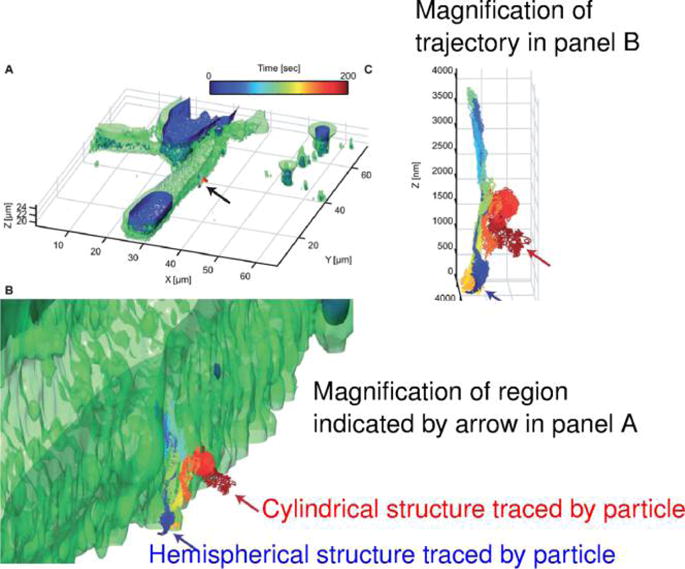
Multiscale super-resolution image data reveals critical contextual information. The plot displays a 3D multiresolution microscopy measurement of a particle approaching the membrane of a fibroblast cell. The fast diffusing nanoparticle was tracked using a 3D SPT module (the moving particle was kept in the focus of the objective via a piezoelectric stage and an optical feedback loop running at 100 kHz). The background (cell membrane, nucleus, etc.) was tracked with a conventional two-photon scanning fluorescence microscope. Valuable “contextual information” along single particle tracks is obtained from the combination of these two modalities. The arrows show trajectory segments where the nanoparticle traced out structured protrusions on the cell boundary.15 Reproduced with permission from ref 15. Copyright 2015, Royal Society of Chemistry.
7.1. Legacy Time Series Analysis Methods
Mean square displacement (MSD)22,60,65,89,299,334∓336 ideas are often used to determine whether a particle is “immobile” or which type of diffusion, such as “normal” or “standard”, “confined”, “directed”, or “anomalous”, is most probable.60 If the particle diffuses normally, that is, the motion is Brownian and characterized by a single diffusion coefficient, then the MSD of the molecule’s position (rt) at absolute time t, ⟨r(τ)2⟩, defined as
| (79) |
is proportional to τ, as the number of observations, N, tend to infinity, where τ represents a relative “time lag” between data points, N represents the number of observations in the trajectory, and denotes the Euclidean (or L2) distance squared. For other types of diffusive behaviors, beyond normal diffusion, eq 79 is no longer simply proportional to τ for large N. Rather, Table 1 lists MSD curves, represented graphically in Figure 30, expected for different diffusive behaviors (using notation from Park et al.60). The other diffusive behaviors can be derived from specific motion models57,299,337 such as stochastic differential equation (SDE) models discussed in section 7.2.1.
Table 1.
Mean Square Displacement (MSD) Curves Continue to Be Used to Drawn Ensemble Information from SPT Measurements60,65a
| qualitative diffusion type | MSD Signature | |
|---|---|---|
| normal diffusion | ⟨r(τ)2⟩ = | 2dDτ |
| confined/corralled diffusion | ⟨r(τ)2⟩ = | C1(1 − C2 exp(−C3τ)) |
| immobile/stationary | ⟨r(τ)2⟩ < | σloc2 |
| directed diffusion (constant velocity v) | ⟨r(τ)2⟩ = | 2dDτ + v2τ2 |
| anomalous subdiffusion (α < 1) | ⟨r(τ)2⟩ = | Cτα |
In the right column, we find the predicted theoretical MSD trend associated with ideal sampling (“ideal” is used since both infinite sample sizes and no measurement noise effects are included) where the Ci’s coincide with constants determined from the assumed dynamical model, α is an anomalous exponent, D corresponds to the normal diffusion coefficient, d to the dimension of the trajectory (e.g. such as two or three common in SPT), and σloc2 corresponds to the measurement/localization noise variance.
Figure 30.
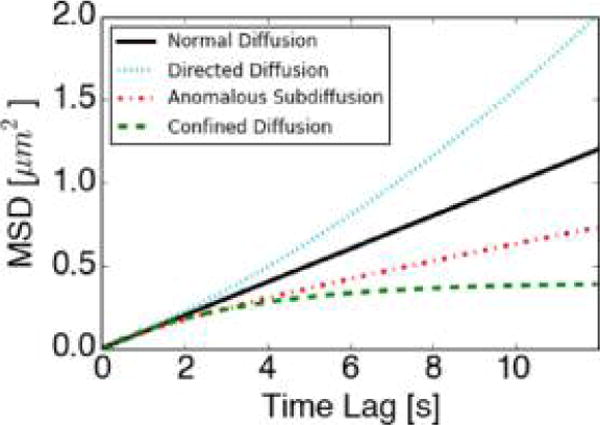
Idealized MSD curves. The theoretical limits of some common motion models used in single particle tracking (SPT). Graphical illustration of information contained in Table 1.
Despite their widespread use, we now discuss several documented issues associated with using MSD curves to analyze finite length trajectories.22,66,86,90,93,334
7.1.1. Issues Facing Legacy Methods
Many of the problems faced by MSD that we now discuss are also faced by other traditional SPT analysis methods such as power spectral56,90,338 and velocity autocorrelation58,338 methods.
7.1.1.1. Issue 1: The Stationarity Assumption
The assumption of stationarity110—the dependence of trajectory statistics on relative time differences and not absolute time—is one systematic shortcoming facing all three methods mentioned above.
This assumption breaks down in many SPT applications for a variety of reasons; for example, if a system is initialized far from equilibrium and eventually reaches steady state during the course of data acquisition.
Stationarity can also be violated if parameters governing the motion of the tagged particle change abruptly. This is especially problematic in vivo since microenvironments sampled by the tagged particle may change in both time and space and, even within a single trajectory, the dynamics of a tagged particle can abruptly change61,65,66,339,340 or drift slowly over time.86 As a concrete example, the diffusion of some receptor proteins may be suddenly perturbed by the appearance of a clathrin-coated pit that traps the protein.341
As another example, the stationarity assumption may also be violated when the background fluorescence varies across microenvironments sampled by the tagged particle, hence altering the effective measurement noise66,86,93 or when multiple trajectories−each with differing fluorescence intensities−are averaged into a single MSD thereby introducing “heterogeneous measurement noise”.
7.1.1.2. Issue 2: Spatial and Temporal Coarse Graining
Even if stationarity holds, the MSD of eq 79 coarse-grains spatial locations and averages down time. Yet time averaging can be avoided by using likelihood methods that both respect the data’s natural time ordering (see eq 6) and can be used to infer quantities such as the directionality of velocities and forces acting on tagged particles.22,86∓88 This type of coarse graining is also a problem facing power spectral methods56,90,338 and velocity autocorrelation techniques.58,338
7.1.1.3. Issue 3: Temporal Correlations Introduced by Averaging
As previously described, MSD curves are obtained by time averaging. Since the same data are used to produce correlations at two different times, say ⟨r(τ)2⟩ and ⟨r(τ′)2⟩, the process of time averaging produces highly correlated quantities.22,334 This high statistical correlation is particularly unattractive if the amount of data is low since correlations within data reduce the effective sample size. To mitigate these problems, ad hoc measures, such as restricting τ values to less than some predetermined fraction of N,12,85 are invoked in an effort to reduce correlations though such methods typically ignore the fact that true temporal correlations (such as in the case of correlated measurement noise) may exist.22,93 Indeed, MSDs for normal diffusion with correlated measurement noise may be confounded with MSDs arising from anomalous diffusion.22
7.2. Beyond Traditional SPT Analyses
In the previous section we discussed key challenges facing traditional SPT trajectory analysis tools and never explicitly dealt with noise as it is averaged away when computing mean quantities.
Here, we provide a brief overview of recent promising SPT trajectory analyses that overcome many of the issues highlighted in section 7.1.1 and motivate data-driven models that explicitly account for effects such as temporal and spatial heterogeneity characteristic of live cell measurements.
Many methods we discuss, including stochastic differential equation (SDE) models and hidden Markov model (HMM) inspired methods, were first introduced to disciplines such as statistics, control theory, and mathematical finance and have begun to make their way into super-resolution data analysis. Sections 7.2.1−7.2.4, presented with a high-level didactic flavor with SPT applications discussed as appropriate, build the background needed to understand the more complex “regime switching” time series models later surveyed, section 7.3.
7.2.1. Stochastic differential equation models
The MSD expressions shown in Table 1, with the exception of anomalous diffusion, can be derived from the following parametric stochastic differential equation (SDE) describing particle position, rt, at time t
| (80) |
where D denotes the diffusion coefficient, Bt denotes standard Brownian motion (i.e., the white noise), and (v − κ rt) denotes the instantaneous particle velocity where κ allows for linear variation in the velocity field and can be thought of as proportional to the spring constant of a harmonic potential. This SDE assumes overdamped dynamics, i.e., a stochastic dynamical model neglecting inertial effects.
The particle dynamics are summarized by the parameter vector θ ≡ (v, κ, D) where κ and D are square matrices of the same dimension as the position vector. Values for the parameter values reproducing the limits of Table 1 are shown in Table 2.
Table 2.
| qualitative diffusion type | SDE constraints in eq 80 |
|---|---|
| standard diffusion | D > 0, κ = 0, v = 0 |
| confined/corralled diffusion | D > 0, κ > 0 |
| immobile/stationary | D = 0, v = 0, κ = 0 |
| directed diffusion (constant velocity v) | D > 0, v ≠0 |
The SDE of eq 80 is the starting point for many likelihood formulations that respect natural time ordering. For simplicity of demonstration only, we ignore measurement noise effects and use the Markovian SDE to write the likelihood p(D|θ) of measurements D = {r1, r2, …, rN} as follows
| (81) |
where p(ri+1|ri, θ) is the transition density.
Importantly, this transition density is obtained by solving the Fokker−Planck117 equation associated with the SDE of eq 80 which, for the linear SDE provided, may be computed exactly.25,86,118
Eq 81, and its construction from SDEs, motivates our later discussions on diffusion as well as the Kalman filters, Sec. (7.2.4), where we discuss how to extend eq 81 to include not only measurement noise, as we did with HMMs (section 3.3.3), but also “process” noise, such as error in localization.
7.2.2. Hidden Markov-Type Models in SPT
In section 7.1.1 we described the challenge of traditional ensemble methods, such as MSD, in dealing with tagged particles that may undergo abrupt changes in dynamics. While the parametric SDE described in eq 80 only contained a single diffusion coefficient, and thus describes the dynamics of a particle in a single “diffusive state”, a recent promising Bayesian method named “vbSPT” (variational Bayes single particle tracking) generalizes the treatment above to an arbitrary number of diffusive states. More concretely, from SPT trajectories, vbSPT (i) determines the number of diffusive state and assigns each data point to a state (called “segmentation”); (ii) parametrizes the diffusion coefficient for each state;61 and (iii) quantifies the transition probabilities between states. vbSPT does so by first performing an initial HMM analysis on a preset list of candidate diffusive states and subsequently comparing their “maximum evidence”, defined by Persson et al.,61 as a model selection criterion.
While measurement noise effects ignored in vbSPT may lead to spurious state assignments,62 vbSPT is still helpful in analyzing data where trajectories are expected to come from “purely diffusive” shorter trajectory segments (Figure 31).
Figure 31.
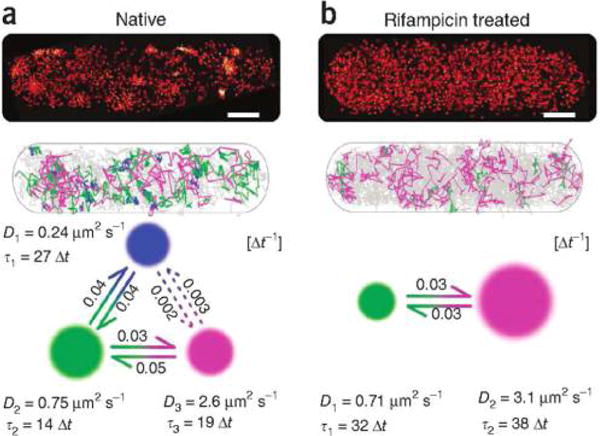
vbSPT is used to determine the number of diffusive states arising from changes in interaction of RNA helper protein (Hfq) in E. coli treated with rifampicin. (a) Trajectories sample three different diffusion coefficients identified as differently colored trajectories in the untreated cell. The transition probabilities linking each diffusive state along with each state’s diffusion coefficient is inferred and represented in the kinetic scheme shown below. (b) The slowest diffusive state from (a) vanishes for E. coli treated with rifampicin, a transcription inhibitor, suggesting that this state coincided with an interaction of Hfq with RNA. Throughout this figure, Δt = 300 Hz. In addition, the scale bar indicates 0.5 μm. See details in Chenouard et al.61 Reproduced with permission from ref 61. Copyright 2013, Nature Publishing Group.
As we discuss shortly, recent advances in nonparametric Bayesian methods67,68,108,179∓181 can help avoid prespecifying the number of candidate states, by simultaneously inferring the number of states and parametrizing the model, and help broaden the types of models considered beyond diffusion. Before these topics are addressed, we highlight recent techniques for dealing with measurement noise in experimental SPT data.
7.2.3. Simple Example of Measurement Noise in SPT
We motivate our discussion on the Kalman filter in the next section by discussing a simpler model incorporating both “static” measurement noise (the localization noise due photon statistics) and “dynamic” measurement noise (position estimation errors due to finite camera exposure time).22,56,58,342
To illustrate the effect of both noise sources, we begin with a simplified form of the SDE model, eq 80, presented earlier22
| (82) |
| (83) |
where denotes the position measurement taken at frame i under the assumption of discrete time measurements, tE is the camera’s exposure time, and is the “static” measurement error with each draw of this noise being an iid mean zero Gaussian with variance σloc2. The integral is needed since molecules continuously move and emit photons as the camera’s shutter remains open. Also, while the above assume constant uniform illumination, the expressions are straightforwardly adapted22 to treat different types of illumination used in microscopy including stroboscopic97 and time lapse (where the illumination laser is not continuous, in order to reduce photobleaching at the expense of temporal resolution).95
Our goal is to use a likelihood in order to infer all model parameters. In the absence of blinking317 or photoactivation,343 one way to move forward is to define
| (84) |
While from eq 82, Δi has zero mean, the covariances shown below are nonzero22
| (85) |
where Δt = ti+1 − ti and the motion blur coefficient, ρ, is 1/6 for the case of continuous illumination though it can be adjusted for other “shutter functions”.22
The result of eq 85 implies that we can now use a Gaussian likelihood, p(D|θ), for D independent differenced measure- ments Δi, with a value of ρ inserted into the covariance as an input rather than the measurements themselves in order to infer θ =(D, σloc2).89,102
7.2.4. Kalman Filtering in Time Series Modeling and Tracking
In the previous subsection, we discussed approaches for analyzing simple parametric diffusion models accounting for the statistical effects of measurement noise (including both static localization and dynamic motion blur errors) through exact likelihood based frameworks.22,89
As discussed in section 3, models with exact likelihoods simplify parameter estimation, goodness-of-fit hypothesis testing and confidence interval estimation. However, phenomena encountered in live cell SPT studies, such as molecular confinement57,60,299,344 or spatially varying forces,86∓88 motivate new models that go beyond eq 82.
The Kalman filter (KF)110,345 directly addresses more complex problems even providing an alternative strategy to evaluating exact likelihoods for several parametric models relevant to SPT.25,86,346
7.2.4.1. Parametric Models Amenable to Kalman Filtering
The standard KF can process the following parametric discrete time model110
| (86) |
| (87) |
In the above, the “state vector” at time t, rt, is of size r. It can be any quantity characterizing the system dynamics, such as position, velocity or angular orientation, though we will focus on position for concreteness.
The “measurement vector”, of size m, is represented by mt while xt, a vector of size k, is a vector assumed to be known precisely (i.e., without measurement error). F, A, and H are matrices of dimensions r× r, m× k, and m× r, respectively.
The vector ηt of size r is often referred to as “process noise” in control theory and signal processing.345 It is a zero mean random variable usually attributed to unresolved “thermal fluctuations” or any other source that directly affects the dynamics of rt.
By contrast, the vector εt of size m is the “measurement noise” that does not affect the dynamics of rt. Rather, εt prevents us from directly observing the precise instantaneous value of rt.
While it is possible to treat more general cases of correlated ηt and εt,345 here we assume that process and measurement noise vectors satisfy
| (88) |
| (89) |
The KF algorithm can then be used for any parametric model, M, that can be expressed using the {F, H, Q, R, A} form where, to avoid introducing technical complications associated with unidentifiable parameter, H is often assumed known in many SPT and single molecule applications.86,103,104,347
7.2.4.2. Simple Example of the {F, H, Q, R, A} Form
We provide an example demonstrating how we may translate a generic state-space model into the {F, H, Q, R, A} form required by the KF algorithm. We show this for an order p autoregressive (linear state space) model, denoted by AR(p) which can be used in SPT when trajectories exhibit complex temporal “memory”.346
Once p is selected, a task which, in itself, may be cast as a model selection problem, the AR(p) is defined by the following relations
| (90) |
| (91) |
The parameter vector here is simply (μ, σ2, ϕ1, ϕ2, … ϕp) though the model can be augmented to account for correlated noise as well (“autoregressive moving average model”) which we ignore here.
For p = 2, say, the AR(2) model can be expressed using the {F, H, Q, R, A} matrices required of the KF algorithm110
While we have only dealt with discrete time models, the procedure may also be adapted to treat continuous time SDEs of the form provided in eq 80.86,110
7.2.4.3. The KF Algorithm in a Nutshell
Here we briefly review the basics of the KF algorithm in order to discuss its broader relevance to tracking in super-resolution.
Briefly, the KF yields a “state estimate”, i.e., the true position of the particle at time t, rt, given all measurements up to time t, (m1, …, mt−1, mt), as well as all previous state estimates. As we now discuss, based on the description of the KF provided by Bishop et al.,348 the KF returns the state estimate of minimal variance (Figure 32). We should note that in this pedagogical description we take, without loss of generality, xt in eq 87 to be zero at all times.
Figure 32.
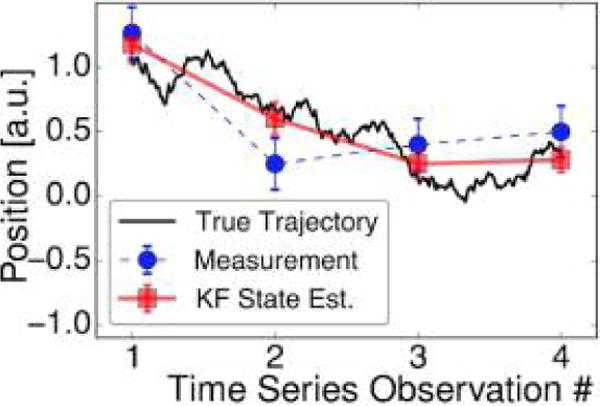
Traditional application of the Kalman Filter (KF). The underlying trajectory evolving in continuous time is shown by the solid black line. The observed or measurement data consists of discretely sampled data corrupted by measurement noise shown with blue circles along with their corresponding 95% confidence interval. The KF exploits knowledge of the model, its parameters and noise measurement in order to obtain improved estimates of position. The data set was created via an implementation of an Ornstein−Uhlenbeck stochastic differential equation, while processing was performed by a simple implementation of the KF, both in MATLAB.
In order to accomplish its task, the KF begins from the state estimate superscripted with a minus sign to indicate that this state estimate is informed by all measurements before time t; this is called the “KF prediction”.
We can also define a deviation of this estimate from its true (unknown) value
| (92) |
with coinciding covariance
| (93) |
Thus, given initial conditions for and , we can use eqs 86 and 87 to compute both and .
In its simplest realization, the goal of the KF is to find the estimate the unknown rt, , from a combination of and a correction, called an “innovation”, as follows
| (94) |
where the innovation, , is preceded by a matrix, K. This matrix, known as the “gain”, is derived from information encoded in the model parameters and will be determined shortly. A simple justification for eq 94 is described elsewhere in ref 349.
The matrix K is selected in order to guarantee the smallest possible covariance
| (95) |
where now where is defined in eq 94. By taking the expectation of , we then minimize the resulting Pt to obtain Kt expressed in terms of the {F, H, Q, R, A} and .
From this Kt, we now obtain a and minimal value for Pt. If t is the last time step, we are done and we have now obtained the full estimate for the sequence of states, . Otherwise, we use rt^ to estimate and Pt to estimate and continue onto the next time step.
7.2.4.4. Some Extensions of the KF
If the random vectors (i.e., ηt, εt, and ri) of the dynamical model may be treated as multivariate Gaussian random variables, then we may compute an exact likelihood of the observable measurement time series conditioned on the model and parameter vector. This likelihood is denoted by p(m1, m2, …, mT |M, θ);110 although ri does not explicitly appear in the likelihood, both the measurement noise and the dynamics of the latent state variable ri are encoded by M and θ. That is, the latent state dynamics induce temporal correlation structure in measurement time series. Despite the temporal correlation in the data, given a noisily measured times series {m1, m2, …, mT}, one can obtain the exact MLE (i.e., no approximations of the likelihood required) of a state space model of the form given in eqs 86 and 87) simply by maximizing the log likelihood expression
| (96) |
Each candidate value of θ (for a fixed measurement sequence and M) can be used to evaluate a “cost function”. This cost function can be efficiently evaluated for multiple θ values with the aid of the KF algorithm110 and aims at approximating the statistical properties of the entire measurement time series. The value of θ maximizing the expression above, which can be obtained by a variety of nonlinear optimization routines such as Newton’s method or a Nelder−Mead search, is the exact MLE in multivariate Gaussian models which can be written in the form of eqs 86 and 87.110
This “off-line” learning application of the KF is commonly used in econometrics110 but is less frequently used in mechanical engineering and tracking. In the latter domains, one often assumes (or a proxy) is known or given and simply uses the KF in “on-line learning” applications to recursively make estimates of ri as measurements are collected over time.345
7.3. Bayesian Nonparametric SPT Analysis
Powerful nonparametric Bayesian methods, briefly introduced in section 3.4, have been used in time series analysis67∓69 and show promise in live cell SPT trajectory analysis when model features, such as the number of diffusion coefficients sampled by a moving particle during the course of its trajectory, are a priori unknown.
These tools are especially helpful in capturing behaviors with spatially varying forces, autoregressive temporal correlation and measurement noise.68 In this subsection, we provide back- ground to understand the so-called hierarchical Dirichlet process switching linear dynamical system (HDP-SLDS)68 since this technique shows promise in the analysis of optical microscopy trajectories.
HDP-SLDS is useful as the number of “modes” (or Markovian states), the time points at which the system hops from one state to the next (the change points), and the parameters needed to parametrize the model are learned in a data-driven fashion.67,68 As we have previously mentioned, this holistic model inference strategy, devoid of the postprocessing model selection step, is preferred and especially useful to the study of dynamics in living systems.
The relatively recent HDP-SLDS and other nonparametric Bayesian methods extending finite state HMMs have already found their way into single molecule and SPT data analysis applications.62,64,66
In this subsection, we briefly review the difference between switching linear dynamical systems (SLDS) and HMMs (section 7.3.1) and introduce the concept of the hierarchical Dirichlet processes (HDPs),67 section 7.3.2. HDP-SLDS approaches are discussed in section 7.3.3 with details relegated to ref 186.
7.3.1. Moving beyond Standard HMMs
Before we discuss nonparametric realizations of the SLDS or HMM, we briefly review these key models.
In short, in standard HMMs (detailed in section 3.3.3), dynamics are encoded by the latent variables or states (si) which are unobservable (Figure 33). However, once the latent states are estimated or given, the temporal order of the measurements is irrelevant to estimating the state’s “emission probability distribution”. That is, those parameters that set the probability distribution of the measurement mi given the state si at each time point, p(mi|si). To each state si is associated a unique parameter vector θi inferred from the data.
Figure 33.
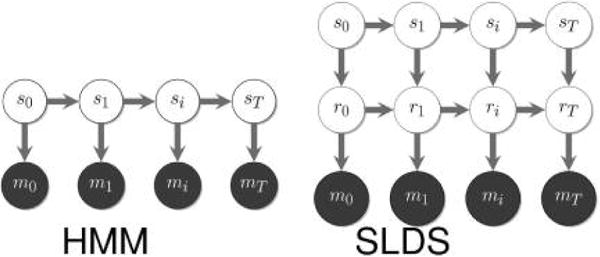
Dependencies of HMM and Markovian SLDS models. In both HMM and SLDS, unobservable states (latent variables) are denoted by white circles. The observations are denoted by filled circles. The subscripts index time and arrows connecting variables indicates conditional statistical dependencies between variables. For instance in the HMM, the latent variables determine the observations. While observations themselves do not affect observations at different times, the same is not true of the states. That is, once the states of the HMM are determined, past observed measurements no longer help predict subsequent measurements. The SLDS adds an additional layer of latent variables which determine the “position” estimates (rt). By contrast to the HMM, in the SLDSs, both “position” estimates (rt) and state estimates can be used to predict future observation.
Switching linear dynamical system (SLDS) extend the standard HMM.68 In this review, we focus on Markovian SLDSs related to the interacting multiple model used in linking problems320 discussed earlier.
In the SLDS, the positions, ri, are thought of as latent states and they themselves are controlled by an additional layer of latent variables (the “control” states), si. Both layers are required to explain the measurement (Figure 33). The SLDS associates to each si a parameter vector θ = (v, κ, D, R).
If κi and R are zero for all states, differencing time adjacent measurements (as we did in section 7.2.3) from a common state would yield an iid sequence for which a classic HMM framework could be invoked to construct a likelihood and infer parameters. This approach was used by Persson et al.61
However, if either κi or R contain nonzero entries, as would be expected in live cell SPT where R is always nonzero and the parameter κi characterizes molecular interaction and/or confinement forces,25,57,344 complex temporal correlations cannot be eliminated by differencing measurements. Despite this complication, ideas underlying the KF can nonetheless be successfully leveraged to compute marginal likelihoods, such as p(D|θ), and used in SPT trajectory analysis.62,66
For both SLDSs and HMMs discussed here we have worked under the assumption that the number of states is specified. Yet, as we’ve also argued it is rarely clear for studies of dynamics inside cells how many states we should start with. For this reason, we now turn to nonparametric Bayesian techniques for generalizing finite state HMMs and SLDs to include an “infinite number of states” and let the data, confined by the model prior, introduce new states if warranted.
7.3.2. Infinite State Space Time Series Models via Hierarchical Dirichlet Processes
As we’ve discussed, a technical limitation facing classic HMMs is their reliance on a predefined number of states. To overcome this challenge, we introduce the infinite hidden Markov model (iHMM).350
Prior to doing this, we reproduce for convenience the HMM model below
| (97) |
Since the HMM is a frequentist model, it has no prior on the transition probabilities. Suppose we did want to introduce a prior on these transition probabilities at every time point. One possible prior would be a multinomial to determine to which state the transition probability brings us. To then select a prior on the weight of each transition probability, a convenient choice would the conjugate to the multinomial, namely the Dirichlet distribution (section 3.4).
So far, none of our discussion is nonparametric as we have specified how many states, and thus how many transition probabilities we have. To generalize our discussion we need the infinite-dimensional generalization of the Dirichlet distribution, namely the Dirichlet process (DP).
Here, the DP prior is used to construct an HMM transition matrix, p(st|st−1),67,68,351 starting from st−1 and transitioning to any of an infinite number of states.
As discussed in section 3.4, the DP depends on two prespecified hyperparameters. The base distribution, H, and the concentration parameter, α, which, roughly speaking, fixes how closely a draw from the DP approximates H.
If H is a continuous distribution, as is often the case for nonparametric mixture models, the HMM or SLDS encounter a serious technical challenge as any algorithm that samples state transitions from a DP prior does not “share states”,67 i.e., it will never resample the same transition probability.
On the other hand if H is discrete and finite, then we are back our parametric case. Instead what we need is an H which is discrete and infinite.
To do this, we introduce the hierarchical DP (HDP),67 defined as follows
where γ is a hyperparameter that plays the role of a concentration parameter on the prior of the base distribution of the DP and G is a distribution over transition probabilities. Since H is now guaranteed to be a discrete distribution, it solves the “state sharing” problem discussed above while at the same time reaping the benefits of a continuous base measure H indexing the states.67
While MCMC sampling may be used to infer iHMM parameters,158 recent methods66,352 have improved computa- tional efficiency by, for example, limiting the number of states sampled at each time point.352 Although this makes implementation easier, iHMMs have just barely begun to be explored in biophysics, more specifically smFRET and photobleaching.189
Similarly to HMMs, SLDSs can also be generalized to the nonparametric case. The infinite state space SLDS models, HDP-SLDS68,186 have recently been used to improve “state switching” detection by explicitly accounting for measurement noise and confinement forces in simulated SPT trajectories62 and uncover nonlinear dynamics in chromatids of live yeast cells.66
We refer the interested reader to refs 68 and 186 for the technical details of the HDP-SLDS and other infinite state dynamical models. While the mathematics are demanding, the problems solved by nonparametric methods help motivate the effort to become better acquainted with them. To this end, below we provide a simple simulated example of the power of nonparametric methods.
7.3.3. Motivating Example for Using Nonparametric Bayesian Methods
We consider a particle evolving in a time dependent harmonic potential, motivated by recent work where harmonic wells appear and disappear at different spatial locations mimicking the diffusion of biomolecules recently observed in neurons,87,353 where standard analysis tools assuming stationary potentials or a fixed number of states fail.
We first simulate a process having three kinetic states visited by a particle. Our goal will be to determine the number of states, all parameters associated with them and the times at which state changes occur from the simulated data.
All states are governed by a Ornstein−Uhlenbeck model, where particles diffuse within a harmonic potential, of the type shown in eq 80. The states are distinguished by unique parameter sets θ where each state i has a vi which changes the location of the potential well’s minimum and particle diffusion coefficient, Di.
Our three state model is
| (98) |
In other words, state ζ has the same θ vector as state α, but with Dζ replacing Dα. In the transition from state ζ to state γ, v also changes. Throughout this simple example we use dimensionless quantities.
The top left panel of Figure 34 illustrates one such simulated 2D trajectory. The vertical red line indicates the location where the transition in v, and thus the hop from one potential surface to another (with the drift term in the SDE is given by −∇U), occurs.
Figure 34.
Nonparametric Bayesian analysis is helpful to SPT trajectory analysis. (a) Position trajectory of a 2D simulation illustrating nonlinear time dependent kinetics; the bottom portion of the plot displays the true state label as well as the number of states (and label) inferred by the HDP-SLDS algorithm.68 The vertical red line denotes the point at which the potential abruptly changes; potential before and after this change are plotted in rightmost panels. (b) The potential energy surface governing the particle dynamics before an abrupt state change in the position of the potential energy’s global minimum location at t = 40 s. The x and y coordinates of the measured position are plotted; the portion of the trajectory governed by the potential plotted in this panel is colored in red. (c) Potential energy surface of trajectory after an abrupt state change in the position corresponding to the potential energy’s minimum location at t = 40 s. The x and y coordinates of the measured position are plotted; the portion of the trajectory subject to the potential plotted in this panel is colored in black. (d) The MSD curve of the simulated trajectory exhibiting transitions between three types of diffusive motion; the MSD was computed using all measurements shown in the top left panel. See text for additional discussion. The data set for this simulation was created by a simple Gillespie algorithm while the labels and number of states were found via a simple MATLAB implementation of the HDP-SLDS algorithm.68 Standard MATLAB functions were used to calculate the MSD.
The true state labels are shown below the trajectories in the top left panel and the two harmonic wells governing state γ and ζ are shown in the right panels of Figure 34.
The bottom left panel shows the MSD curve computed using the observed 2D trajectory that would likely be classified “anomalous” using the guidelines of classic SPT analysis (Figure 30) rather than a stochastic switching between three different confined diffusion models. While the agreement between the estimated and true states is excellent, much of the success hinges on careful prior selections.62,66 The same is true of all Bayesian methods where priors properly informed by the physics of the problem provide a systematic way to improve inference.96
While the example above may appear contrived, it may apply for instance to the diffusion of cargo transiently trapped in clathrin-coated pits.341 In this scenario, after a cargo molecule is trapped, it experiences “confined diffusion” until the pit vanishes or endocytosis occurs. If a pit vanishes, a new pit (a new potential minimum) may recruit the cargo. Since the HDP-SLDS model is not limited to a finite number of states, the approach can handle pits of different sizes, free-diffusion (unbound) states, as well as more realistic scenarios.
This flexibility fundamentally speaks to the power of the HDP-SLDS modeling approach68 as alternatives to anomalous diffusion in describing complex kinetics observed in vivo.
8. CONCLUDING REMARKS
Ten years after the publication of the seminal papers on super-resolution,3∓5 single molecule super-resolution microscopy has become a standard lab technique now widely available across major imaging facilities. It has been used to study a number of biological targets just below the resolution of diffraction-limited microscopy, such as microtubules,319 mitochondria,354 and the nucleopore complex.355,356 Theoretical developments in interpreting super-resolution experiments, and single molecule experiments more broadly, have ushered data-driven methods into the physics and chemistry mainstream.59 While studies in live cells are motivating more general theoretical approaches borrowing heavily from statistical advances179 now feasible due to computing power, quantitative analysis efforts have also helped identify clear challenges standing in the way of greater modeling accuracy. Novel experimental methods have begun addressing some of these challenges such as phototoxicity6 and image distortions in thick heterogeneous samples357 though other key challenges such as labeling density358 and environment-dependent photophysical properties359 remain.
As this is a review of analysis methods, we highlight three broad directions that have been the focus of recent theoretical efforts. The first is on joint methods that simultaneously, and thus self-consistently, solve many problems at once such as problems in interpretation and counting21 or localization and linking.320 Such efforts reduce the number of user-dependent postprocessing steps albeit at a heavier computational cost. The second introduces problem-specific models,360 priors (whether theoretically96 or experimentally319 motivated), and algorithms287,291 suited to the particularities of the physical (or photophysical) challenge to reduce the computational burden and improve the prediction accuracy. The third is focused on generalizing models to accommodate the data’s complexity.67,68
The picture of life emerging from breakthrough experimental techniques and analysis methods is one far richer in structural features, dynamics, and stochasticity than we could have conceived of even a decade ago. We envision a future in imaging where a combination of experiments and principled analysis provide a compelling narrative into the chaotic journey of life from the level of single molecules upward.
Acknowledgments
C.B. and A.L. acknowledge support from the Nanomachines program (KC1203) funded by the Director, Office of Science, Office of Basic Energy Sciences of the U.S. Department of Energy (DOE) contract no. DE-AC02-05CH11231 (step-finding algorithms), by the National Institute of Health grants R01GM071552 and R01GM032543 (fluorescent protein characterization), and by the Howard Hughes Medical Institute (fluorescent protein counting). S.P. acknowledges the support of NSF MCB 1412259 as well as startup from IUPUI and ASU. C.C. was supported by internal R&D funds from Ursa Analytics, Inc. We thank Ioannis Sgouralis for many helpful suggestions.
Biographies
Antony Lee obtained his B.S. and M.S. in physics from the École Polytechnique in Palaiseau, France. He is now a graduate student in the group of Carlos Bustamante, at the University of California, Berkeley. During his Ph.D., he developed techniques for counting proteins and probing protein−protein interactions using super-resolution microscopy. He also used optical tweezers to study the dynamics of transcription elongation by E. coli RNA polymerase.
Konstantinos Tsekouras is a postdoctoral researcher in the Pressé group at ASU. Dr. Tsekouras received his B.S. degree in physics from the National and Kapodistrian University of Athens and his M.S. and Ph.D. degrees from Rice University. He works on the modeling of biophysical and physiological systems and on the development of data- driven inference methods that increase the amount of information that can be extracted from experimental data.
Christopher Calderon is the President and founder of Ursa Analytics, Inc. Dr. Calderon received his B.S. in Chemical Engineering from Purdue University and his Ph.D. in Chemical Engineering from Princeton University. He was an NSF VIGRE postdoctoral fellow jointly appointed to the Departments of Statistics and Computational & Applied Mathematics at Rice University and was a visiting fellow at Lawrence Berkeley National Laboratory. Dr. Calderon currently directs an R&D company focused on developing new computational statistics algorithms applied to image analysis and signal processing applications. His company participates in academic collaborations focused on developing new algorithms and open-source software for optical microscopy data analysis applications. Industrial efforts at Ursa Analytics are focused on developing supervised and unsupervised machine learning algorithms deployed on embedded hardware.
Carlos Bustamante is Professor of Molecular and Cell Biology, Physics, and Chemistry at the University of California, Berkeley and a Howard Hughes Medical Institute Investigator. Dr. Bustamante received his B.S. degree in biology from the Universidad Peruana Cayetano Heredia, his M.S. degree in biochemistry from the Universidad Nacional Mayor de San Marcos, and his Ph.D. in biophysics from the University of California, Berkeley. The laboratory of Dr. Bustamante develops and applies single-molecule manipulation and detection methods, such as optical tweezers, magnetic tweezers, and single molecule fluorescence microscopy to characterize the dynamics and the mechanochemical properties of various molecular motors that interact with DNA, RNA, or proteins. His lab also uses and develops novel methods for super-resolution microscopy to study the organization and function of protein complexes in cells. Dr. Bustamante is a Fellow of the American Physical Society, an elected member of the National Academy of Sciences and the Chilean Academy of Science, and a member of the Board of Directors of the American Association for the Advancement of Science. He is the recipient of the 2012 Raymond and Beverly Sackler International Prize in Biophysics for his seminal contributions to single molecule biophysics.
Steve Pressé is an Associate Professor of Physics and Associate Professor in the School of Molecular Sciences at Arizona State University. He obtained his B.Sc. in Chemistry at McGill and his Ph.D. at MIT in the area of chemical physics and a postdoc from UCSF in biophysics. Dr. Pressé is the recipient of awards including an FQRNT postgraduate fellowship and, most recently, an NSF CAREER. His lab works on the following: statistical mechanical modeling of biological phenomena, the application and development of statistical tools to the analysis of imaging and spectroscopy data, and bacterial dynamics and hydrodynamics.
Footnotes
ORCID
Steve Pressé: 0000-0002-5408-0718
Notes
The authors declare no competing financial interest.
References
- 1.Klar T, Jakobs S, Dyba M, Egner A, Hell S. Fluorescence Microscopy With Diffraction Resolution Barrier Broken by Stimulated Emission. Proc Natl Acad Sci USA. 2000;97:8206–8210. doi: 10.1073/pnas.97.15.8206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gustafsson M. Nonlinear Structured-Illumination Microscopy: Wide-Field Fluorescence Imaging With Theoretically Unlimited Resolution. Proc Natl Acad Sci USA. 2005;102:13081–13086. doi: 10.1073/pnas.0406877102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rust M, Bates M, Zhuang X. Sub-Diffraction-Limit Imaging by Stochastic Optical Reconstruction Microscopy (STORM) Nat Methods. 2006;3:793–796. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Betzig E, Patterson G, Sougrat R, Lindwasser O, Olenych S, Bonifacino J, Davidson M, Lippincott-Schwartz J, Hess H. Imaging Intracellular Fluorescent Proteins at Nanometer Resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 5.Hess S, Girirajan T, Mason M. Ultra-High Resolution Imaging by Fluorescence Photoactivation Localization Microscopy. Biophys J. 2006;91:4258–4272. doi: 10.1529/biophysj.106.091116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen B, Legant W, Wang K, Shao L, Milkie D, Davidson M, Janetopoulos C, Wu X, Hammer J, Liu Z, et al. Lattice Light- Sheet Microscopy: Imaging Molecules to Embryos at High Spatiotemporal Resolution. Science. 2014;(346):1257998. doi: 10.1126/science.1257998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Waldchen S, Lehmann J, Klein T, van de Linde S, Sauer M. Light-Induced Cell Damage in Live-Cell Super-Resolution Microscopy. Sci Rep. 2015;5 doi: 10.1038/srep15348. 1534810.1038/srep15348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shin J, Lopez-Garrido J, Lee S, Diaz-Celis C, Fleming T, Bustamante C, Pogliano K. Visualization and FunctionalDissection of Coaxial Paired SpoIIIE Channels Across the Sporulation Septum. eLife. 2015;4:e06474. doi: 10.7554/eLife.06474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Greenfield D, McEvoy A, Shroff H, Crooks G, Wingreen N, Betzig E, Liphardt J. Self-Organization of the Escherichia Coli Chemotaxis Network Imaged With Super-Resolution Light Microscopy. PLoS Biol. 2009;7 doi: 10.1371/journal.pbio.1000137. e100013710.1371/journal.pbio.1000137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pavani S, Thompson M, Biteen J, Lord S, Liu N, Twieg R, Piestun R, Moerner W. Three-Dimensional, Single-Molecule Fluorescence Imaging Beyond the Diffraction Limit by Using a Double-Helix Point Spread Function. Proc Natl Acad Sci USA. 2009;106:2995–2999. doi: 10.1073/pnas.0900245106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wells N, Lessard G, Goodwin P, Phipps M, Cutler P, Lidke D, Wilson B, Werner J. Time-Resolved Three-Dimensional Molecular Tracking in Live Cells. Nano Lett. 2010;10:4732–4737. doi: 10.1021/nl103247v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thompson M, Casolari J, Badieirostami M, Brown P, Moerner W. Three-Dimensional Tracking of Single mRNA Particles in Saccharomyces Cerevisiae Using a Double-Helix Point Spread Function. Proc Natl Acad Sci USA. 2010;107:17864–17871. doi: 10.1073/pnas.1012868107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ram S, Kim D, Ober RJ, Ward ES. 3D Single Molecule Tracking With Multifocal Plane Microscopy Reveals Rapid Intercellular Transferrin Transport at Epithelial Cell Barriers. Biophys J. 2012;103:1594–1603. doi: 10.1016/j.bpj.2012.08.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Welsher K, Yang H. Multi-Resolution 3D Visualization of the Early Stages of Cellular Uptake of Peptide-Coated Nanoparticles. Nat Nanotechnol. 2014;9:198–203. doi: 10.1038/nnano.2014.12. [DOI] [PubMed] [Google Scholar]
- 15.Welsher K, Yang H. Imaging the Behavior of Molecules in Biological Systems: Breaking the 3D Speed Barrier With 3D Multi- Resolution Microscopy. Faraday Discuss. 2015;184:359–379. doi: 10.1039/c5fd00090d. [DOI] [PubMed] [Google Scholar]
- 16.Li D, Shao L, Chen BC, Zhang X, Zhang M, Moses B, Milkie DE, Beach JR, Hammer JA, Pasham M, et al. Extended- Resolution Structured Illumination Imaging of Endocytic and Cytoskeletal Dynamics. Science. 2015;349:aab3500. doi: 10.1126/science.aab3500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shechtman Y, Weiss L, Backer A, Sahl S, Moerner W. Precise 3D Scan-Free Multiple-Particle Tracking Over Large Axial Ranges With Tetrapod Point Spread Functions. Nano Lett. 2015;15:4194–4199. doi: 10.1021/acs.nanolett.5b01396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lippincott-Schwartz J. Profile of Eric Betzig, Stefan Hell, and W. E. Moerner, 2014 Nobel Laureates in Chemistry. Proc Natl Acad Sci USA. 2015;112:2630–2632. doi: 10.1073/pnas.1500784112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Balzarotti F, Eilers Y, Gwosch K, Gynnå A, Westphal V, Stefani F, Elf J, Hell S. Nanometer resolution imaging tracking of fluorescent molecules with minimal photon fluxes. Science. 2017;355:606–612. doi: 10.1126/science.aak9913. [DOI] [PubMed] [Google Scholar]
- 20.Gunawardena J. Models in Biology: Accurate Descriptions of Our Pathetic Thinking. BMC Biol. 2014;12:29–40. doi: 10.1186/1741-7007-12-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rollins G, Shin J, Bustamante C, Pressé S. Stochastic Approach to the Molecular Counting Problem in Superresolution Microscopy. Proc Natl Acad Sci U S A. 2015;112:E110–118. doi: 10.1073/pnas.1408071112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Berglund A. Statistics of Camera-Based Single-Particle Tracking. Phys Rev E. 2010;82:011917. doi: 10.1103/PhysRevE.82.011917. [DOI] [PubMed] [Google Scholar]
- 23.de Chaumont F, Dallongeville S, Chenouard N, Hervé N, Pop S, Provoost T, Meas-Yedid V, Pankajakshan P, Lecomte T, Le Montagner Y, et al. Icy: an Open Bioimage Informatics Platform for Extended Reproducible Research. Nat Methods. 2012;9:690–696. doi: 10.1038/nmeth.2075. [DOI] [PubMed] [Google Scholar]
- 24.Lindén M, Ćurić V, Boucharin A, Fange D, Elf J. Simulated Single Molecule Microscopy With SMeagol. Bioinformatics. 2016;32:2394–2395. doi: 10.1093/bioinformatics/btw109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Calderon C. Motion Blur Filtering: A Statistical Approach for Extracting Confinement Forces and Diffusivity From a Single Blurred Trajectory. Phys Rev E: Stat Phys, Plasmas, Fluids, Relat Interdiscip Top. 2016;93:053303. doi: 10.1103/PhysRevE.93.053303. [DOI] [PubMed] [Google Scholar]
- 26.Masters B. The Development of Fluorescence Microscopy. In Encyclopedia of LifeSciences. 2010:1–9. [Google Scholar]
- 27.Coons A, Creech H, Jones R. Immunological Properties of an Antibody Containing a Fluorescent Group. Exp Biol Med. 1941;47:200–202. [Google Scholar]
- 28.Shimomura O, Johnson F, Saiga Y. Extraction Purification and Properties of Aequorin a Bioluminescent Protein From the Luminous Hydromedusan, Aequorea. J Cell Comp Physiol. 1962;59:223–239. doi: 10.1002/jcp.1030590302. [DOI] [PubMed] [Google Scholar]
- 29.Tsien R. The Green Fluorescent Protein. Annu Rev Biochem. 1998;67:509–544. doi: 10.1146/annurev.biochem.67.1.509. [DOI] [PubMed] [Google Scholar]
- 30.Moerner W, Kador L. Optical Detection Spectroscopy of Single Molecules in a Solid. Phys Rev Lett. 1989;62:2535–2538. doi: 10.1103/PhysRevLett.62.2535. [DOI] [PubMed] [Google Scholar]
- 31.Shera EB, Seitzinger NK, Davis LM, Keller RA, Soper SA. Detection of Single Fluorescent Molecules. Chem Phys Lett. 1990;174:553–557. [Google Scholar]
- 32.Airy G. On the Diffraction of an Object-Glass With a Circular Aperture. Trans Camb Philos Soc. 1834;5:283–291. [Google Scholar]
- 33.Abbe E. Beiträge zur Theorie des Mikroskops und der Mikroskopischen Wahrnehmung. Arch Mikrosk Anat. 1873;9:413–418. [Google Scholar]
- 34.Rayleigh L. Investigations in Optics With Special Reference to the Spectroscope. Philos Mag Series 5. 1879;8:261–274. [Google Scholar]
- 35.Hecht E. Optics. 4th. Addison-Wesley; Boston: 2002. [Google Scholar]
- 36.Izeddin I, El Beheiry M, Andilla J, Ciepielewski D, Darzacq X, Dahan M. PSF Shaping Using Adaptive Optics for Three- Dimensional Single-Molecule Super-Resolution Imaging Tracking. Opt Express. 2012;20:4957–4967. doi: 10.1364/OE.20.004957. [DOI] [PubMed] [Google Scholar]
- 37.Holden S, Uphoff S, Kapanidis A. DAOSTORM: an Algorithm for High-Density Super-Resolution Microscopy. Nat Methods. 2011;8:279–280. doi: 10.1038/nmeth0411-279. [DOI] [PubMed] [Google Scholar]
- 38.Kourkoutis L, Plitzko J, Baumeister W. Electron Microscopy of Biological Materials at the Nanometer Scale. Annu Rev Mater Res. 2012;42:33–58. [Google Scholar]
- 39.Cole R, Jinadasa T, Brown C. Measuring Interpreting Point Spread Functions to Determine Confocal Microscope Resolution Ensure Quality Control. Nat Protoc. 2011;6:1929–41. doi: 10.1038/nprot.2011.407. [DOI] [PubMed] [Google Scholar]
- 40.Carroll R, Hall P. Optimal Rates of Convergence for Deconvolving a Density. J Am Stat Assoc. 1988;83:1184–1186. [Google Scholar]
- 41.Fan J. On the Optimal Rates of Convergence for Non-parametric Deconvolution Problems. Ann Stat. 1991;19:1257–1272. [Google Scholar]
- 42.Agard D, Sedat J. Three-Dimensional Architecture of a Polytene Nucleus. Nature. 1983;302:676–681. doi: 10.1038/302676a0. [DOI] [PubMed] [Google Scholar]
- 43.Schermelleh L, Heintzmann R, Leonhardt H. A Guide to Super-Resolution Fluorescence Microscopy. J Cell Biol. 2010;190:165–175. doi: 10.1083/jcb.201002018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Morrison I, Anderson C, Georgiou G, Cherry R. Measuring Diffusion Coefficients of Labelled Particles on Cell Surfaces by Digital Fluorescence Microscopy. Biochem Soc Trans. 1990;18:938–938. doi: 10.1042/bst0180938. [DOI] [PubMed] [Google Scholar]
- 45.Anderson C, Georgiou G, Morrison I, Stevenson G, Cherry R. Tracking of Cell Surface Receptors by Fluorescence Digital Imaging Microscopy Using a Charge-Coupled Device Camera. Low- Density Lipoprotein Influenza Virus Receptor Mobility at 4 Degrees C. J Cell Sci. 1992;101:415–425. doi: 10.1242/jcs.101.2.415. [DOI] [PubMed] [Google Scholar]
- 46.Betzig E. Proposed Method for Molecular Optical Imaging. Opt Lett. 1995;20:237–239. doi: 10.1364/ol.20.000237. [DOI] [PubMed] [Google Scholar]
- 47.Ando R, Hama H, Yamamoto-Hino M, Mizuno H, Miyawaki A. An Optical Marker Based on the UV-Induced Green-to- Red Photoconversion of a Fluorescent Protein. Proc Natl Acad Sci USA. 2002;99:12651–12656. doi: 10.1073/pnas.202320599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bates M, Blosser TR, Zhuang X. Short-Range Spectroscopic Ruler Based on a Single-Molecule Optical Switch. Phys Rev Lett. 2005;94:108101. doi: 10.1103/PhysRevLett.94.108101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hell S, Wichmann J. Breaking the Diffraction Resolution Limit By Stimulated-Emission - Stimulated-Emission-Depletion Fluorescence Microscopy. Opt Lett. 1994;19:780–782. doi: 10.1364/ol.19.000780. [DOI] [PubMed] [Google Scholar]
- 50.Jost A, Heintzmann R. Superresolution Multidimensional Imaging With Structured Illumination Microscopy. Annu Rev Mater Res. 2013;43:261–282. [Google Scholar]
- 51.Shroff H, Galbraith C, Galbraith J, White H, Gillette J, Olenych S, Davidson M, Betzig E. Dual-Color Superresolution Imaging of Genetically Expressed Probes Within Individual Adhesion Complexes. Proc Natl Acad Sci U S A. 2007;104:20308–20313. doi: 10.1073/pnas.0710517105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Komatsuzaki T, Kawakami M, Takahashi S, Yang H, Silbey R, editors. Advances in Chemical Physics Vol 146 Single Molecule Biophysics: Experiments and Theories. John Wiley & Sons; New York: 2011. [Google Scholar]
- 53.Thompson R, Larson D, Webb W. Precise Nanometer Localization Analysis for Individual Fluorescent Probes. Biophys J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ober R, Ram S, Ward E. Localization Accuracy in Single- Molecule Microscopy. Biophys J. 2004;86:1185–1200. doi: 10.1016/S0006-3495(04)74193-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Smith C, Joseph N, Rieger B, Lidke K. Fast, Single-Molecule Localization That Achieves Theoretically Minimum Uncertainty. Nat Methods. 2010;7:373–375. doi: 10.1038/nmeth.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Savin T, Doyle P. Static and Dynamic Errors in Particle Tracking Microrheology. Biophys J. 2005;88:623–38. doi: 10.1529/biophysj.104.042457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Destainville N, Salomé L. Quantification and Correction of Systematic Errors Due to Detector Time-Averaging in Single-Molecule Tracking Experiments. Biophys J. 2006;90:L17–19. doi: 10.1529/biophysj.105.075176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Backlund M, Joyner R, Moerner W. Chromosomal Locus Tracking With Proper Accounting of Static and Dynamic Errors. Phys Rev E. 2015;91:062716. doi: 10.1103/PhysRevE.91.062716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Tavakoli M, Taylor J, Li C, Komatsuzaki T, Pressé S. Single Molecule Data Analysis: An Introduction. Adv Chem Phys. 2016 [Google Scholar]
- 60.Park HY, Buxbaum AR, Singer RH. Single mRNA Tracking in Live Cells. Methods Enzymol. 2010;472:387–406. doi: 10.1016/S0076-6879(10)72003-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Persson F, Lindén M, Unoson C, Elf J. Extracting Intracellular Diffusion States and Transition Rates From Single- Molecule Tracking Data. Nat Methods. 2013;10:265–269. doi: 10.1038/nmeth.2367. [DOI] [PubMed] [Google Scholar]
- 62.Calderon C. Data-Driven Techniques for Detecting Dynamical State Changes in Noisily Measured 3D Single-Molecule Trajectories. Molecules. 2014;19:18381–18398. doi: 10.3390/molecules191118381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tsekouras K, Siegel A, Day R, Pressé S. Inferring Diffusion Dynamics From FCS in Heterogeneous Nuclear Environments. Biophys J. 2015;109:7–17. doi: 10.1016/j.bpj.2015.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hines K. A Primer on Bayesian Inference for Biophysical Systems. Biophys J. 2015;108:2103–2113. doi: 10.1016/j.bpj.2015.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Monnier N, Barry Z, Park H, Su K, Katz Z, English B, Dey A, Pan K, Cheeseman I, Singer R, et al. Inferring Transient Particle Transport Dynamics in Live Cells. Nat Methods. 2015;12:838–840. doi: 10.1038/nmeth.3483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Calderon C, Bloom K. Inferring Latent States and Refining Force Estimates via Hierarchical Dirichlet Process Modeling in Single Particle Tracking Experiments. PLoS One. 2015;10:e0137633. doi: 10.1371/journal.pone.0137633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Teh Y, Jordan M, Beal M, Blei D. Hierarchical Dirichlet Processes. J Am Stat Assoc. 2006;101:1566–1581. [Google Scholar]
- 68.Fox E, Sudderth E, Jordan M, Willsky A. Bayesian Nonparametric Inference of Switching Dynamic Linear Models. IEEE Trans Signal Process. 2011;59:1569–1585. [Google Scholar]
- 69.Fox E, Hughes M, Sudderth E, Jordan M. Joint Modeling of Multiple Time Series via the Beta Process With Application to Motion Capture Segmentation. Ann Appl Stat. 2014;8:1281–1313. [Google Scholar]
- 70.Banks D, Fradin C. Anomalous Diffusion of Proteins Due to Molecular Crowding. Biophys J. 2005;89:2960–2971. doi: 10.1529/biophysj.104.051078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Feder T, Brust-Mascher I, Slattery J, Baird B, Webb W. Constrained Diffusion or Immobile Fraction on Cell Surfaces: a New Interpretation. Biophys J. 1996;70:2767–2773. doi: 10.1016/S0006-3495(96)79846-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Konopka M, Shkel I, Cayley S, Record M, Weisshaar J. Crowding and Confinement Effects on Protein Diffusion in Vivo. J Bacteriol. 2006;188:6115–6123. doi: 10.1128/JB.01982-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.McGuffee S, Elcock A. Diffusion, Crowding & Protein Stability in a Dynamic Molecular Model of the Bacterial Cytoplasm. PLoS Comput Biol. 2010;6:e1000694. doi: 10.1371/journal.pcbi.1000694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Tolić-Nørrelykke I, Munteanu E, Thon G, Oddershede L, Berg-Sørensen K. Anomalous Diffusion in Living Yeast Cells. Phys Rev Lett. 2004;93:078102. doi: 10.1103/PhysRevLett.93.078102. [DOI] [PubMed] [Google Scholar]
- 75.Wachsmuth M, Waldeck W, Langowski J. Anomalous Diffusion of Fluorescent Probes Inside Living Cell Nuclei Investigated by Spatially-Resolved Fluorescence Correlation Spectroscopy. J Mol Biol. 2000;298:677–689. doi: 10.1006/jmbi.2000.3692. [DOI] [PubMed] [Google Scholar]
- 76.Saxton M. A Biological Interpretation of Transient Anomalous Subdiffusion. I. Qualitative Model. Biophys J. 2007;92:1178–1191. doi: 10.1529/biophysj.106.092619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Siegel A, Hays N, Day R. Unraveling Transcription Factor Interactions With Heterochromatin Protein Using Fluorescence Lifetime Imaging Microscopy and Fluorescence Correlation Spectroscopy. J Biomed Opt. 2013;18:025002. doi: 10.1117/1.JBO.18.2.025002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Parry B, Surovtsev I, Cabeen M, O’Hern C, Dufresne E, Jacobs-Wagner C. The Bacterial Cytoplasm Has Glass-Like Properties and Is Fluidized by Metabolic Activity. Cell. 2014;156:183–194. doi: 10.1016/j.cell.2013.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Schwille P, Korlach J, Webb W. Fluorescence Correlation Spectroscopy With Single-Molecule Sensitivity on Cell and Model Membranes. Cytometry. 1999;36:176–182. doi: 10.1002/(sici)1097-0320(19990701)36:3<176::aid-cyto5>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 80.Caspi A, Granek R, Elbaum M. Enhanced Diffusion in Active Intracellular Transport. Phys Rev Lett. 2000;85:5655–5658. doi: 10.1103/PhysRevLett.85.5655. [DOI] [PubMed] [Google Scholar]
- 81.Bruno L, Levi V, Brunstein M, Despósito M. Transition to Superdiffusive Behavior in Intracellular Actin-Based Transport Mediated by Molecular Motors. Phys Rev E. 2009;80:011912. doi: 10.1103/PhysRevE.80.011912. [DOI] [PubMed] [Google Scholar]
- 82.Bressloff P, Newby J. Stochastic Models of Intracellular Transport. Rev Mod Phys. 2013;85:135–196. [Google Scholar]
- 83.Regner B, Vucinić D, Domnisoru C, Bartol T, Hetzer M, Tartakovsky D, Sejnowski T. Anomalous Diffusion of Single Particles in Cytoplasm. Biophys J. 2013;104:1652–1660. doi: 10.1016/j.bpj.2013.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Wu J, Berland K. Propagators and Time-Dependent Diffusion Coefficients for Anomalous Diffusion. Biophys J. 2008;95:2049–2052. doi: 10.1529/biophysj.107.121608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Chen J, Zhang Z, Li L, Chen BC, Revyakin A, Hajj B, Legant W, Dahan M, Lionnet T, Betzig E, et al. Single-Molecule Dynamics of Enhanceosome Assembly in Embryonic Stem Cells. Cell. 2014;156:1274–1285. doi: 10.1016/j.cell.2014.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Calderon C, Thompson M, Casolari J, Paffenroth R, Moerner W. Quantifying Transient 3D Dynamical Phenomena of Single mRNA Particles in Live Yeast Cell Measurements. J Phys Chem B. 2013;117:15701–15713. doi: 10.1021/jp4064214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Masson J, Dionne P, Salvatico C, Renner M, Specht C, Triller A, Dahan M. Mapping the Energy and Diffusion Landscapes of Membrane Proteins at the Cell Surface Using High-Density Single- Molecule Imaging Bayesian Inference: Application to the Multiscale Dynamics of Glycine Receptors in the Neuronal Membrane. Biophys J. 2014;106:74–83. doi: 10.1016/j.bpj.2013.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Holcman D, Hoze N, Schuss Z. Analysis and Interpretation of Superresolution Single-Particle Trajectories. Biophys J. 2015;109:1761–1771. doi: 10.1016/j.bpj.2015.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Michalet X, Berglund A. Optimal Diffusion Coefficient Estimation in Single-Particle Tracking. Phys Rev E. 2012;85:061916. doi: 10.1103/PhysRevE.85.061916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Vestergaard C, Blainey P, Flyvbjerg H. Optimal Estimation of Diffusion Coefficients From Single-Particle Trajectories. Phys Rev E. 2014;89:022726. doi: 10.1103/PhysRevE.89.022726. [DOI] [PubMed] [Google Scholar]
- 91.Wang Q, Moerner W. An Adaptive Anti-Brownian Electrokinetic Trap With Real-Time Information on Single-Molecule Diffusivity and Mobility. ACS Nano. 2011;5:5792–5799. doi: 10.1021/nn2014968. [DOI] [PubMed] [Google Scholar]
- 92.Wang Q, Moerner W. Single-Molecule Motions Enable Direct Visualization of Biomolecular Interactions in Solution. Nat Methods. 2014;11:555–558. doi: 10.1038/nmeth.2882. [DOI] [PubMed] [Google Scholar]
- 93.Relich P, Olah M, Cutler P, Lidke K. Estimation of the Diffusion Constant From Intermittent Trajectories With Variable Position Uncertainties. Phys Rev E: Stat Phys Plasmas, Fluids, Relat Interdiscip Top. 2016;93:042401. doi: 10.1103/PhysRevE.93.042401. [DOI] [PubMed] [Google Scholar]
- 94.Calderon CP, Chen W-H, Lin K-J, Harris NC, Kiang C-H. Quantifying DNA Melting Transitions Using Single-Molecule Force Spectroscopy. J Phys: Condens Matter. 2009;21:034114. doi: 10.1088/0953-8984/21/3/034114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Knight S, Xie L, Deng W, Guglielmi B, Witkowsky L, Bosanac L, Zhang E, El Beheiry M, Masson J, Dahan M, et al. Dynamics of CRISPR-Cas9 Genome Interrogation in Living Cells. Science. 2015;350:823–826. doi: 10.1126/science.aac6572. [DOI] [PubMed] [Google Scholar]
- 96.Tsekouras K, Custer TC, Jashnsaz H, Walter NG, Pressé S. A Novel Method to Accurately Locate and Count Large Numbers of Steps by Photobleaching. Mol Biol Cell. 2016;27:3601–3615. doi: 10.1091/mbc.E16-06-0404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Gahlmann A, Moerner W. Exploring Bacterial Cell Biology With Single-Molecule Tracking and Super-Resolution Imaging. Nat Rev Microbiol. 2013;12:9–22. doi: 10.1038/nrmicro3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Ashley T, Andersson S. Method for Simultaneous Localization and Parameter Estimation in Particle Tracking Experiments. Phys Rev E. 2015;92:052707. doi: 10.1103/PhysRevE.92.052707. [DOI] [PubMed] [Google Scholar]
- 99.Hoze N, Holcman D. Recovering a Stochastic Process From Super-Resolution Noisy Ensembles of Single-Particle Trajectories. Phys Rev E. 2015;92 doi: 10.1103/PhysRevE.92.052109. [DOI] [PubMed] [Google Scholar]
- 100.Rowland DJ, Tuson HH, Biteen JS. Resolving Fast and Confined Diffusion in Bacteria With Image Correlation Spectroscopy. Biophys J. 2016;110:2241–51. doi: 10.1016/j.bpj.2016.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Zhang L, Mykland P, Ait-Sahalia Y. A Tale of Two Time Scales: Determining Integrated Volatility With Noisy High-Frequency Data. J Am Stat Assoc. 2005;100:1394–1411. [Google Scholar]
- 102.Aït-Sahalia Y, Fan J, Xiu D. High-Frequency Covariance Estimates With Noisy and Asynchronous Financial Data. J Am Stat Assoc. 2010;105:1504–1517. [Google Scholar]
- 103.Calderon C, Harris N, Kiang C, Cox D. Quantifying Multiscale Noise Sources in Single-Molecule Time Series. J Phys Chem B. 2009;113:138–148. doi: 10.1021/jp807908c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Fernandez V, Kosuri P, Parot V, Fernandez J. Extended Kalman Filter Estimates the Contour Length of a Protein in Single Molecule Atomic Force Microscopy Experiments. Rev Sci Instrum. 2009;80:113104. doi: 10.1063/1.3252982. [DOI] [PubMed] [Google Scholar]
- 105.Žoldák G, Stigler J, Pelz B, Li H, Rief M. Ultrafast Folding Kinetics and Cooperativity of Villin Headpiece in Single-Molecule Force Spectroscopy. Proc Natl Acad Sci U S A. 2013;110:18156–18161. doi: 10.1073/pnas.1311495110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Wasserman L. All of Statistics: a Concise Course in Statistical Inference. Springer Science & Business Media; Berlin: 2013. [Google Scholar]
- 107.van der Vaart A. Asymptotic Statistics. Cambridge University Press; Cambridge, U.K: 1998. [Google Scholar]
- 108.Ghosh R, Ramamoorthi J. Bayesian Nonparametrics. Springer- Verlag; New York: 2010. [Google Scholar]
- 109.Scott D. Multivariate Density Estimation: Theory, Practice, and Visualization. John Wiley & Sons; New York: 1992. [Google Scholar]
- 110.Hamilton J. Time Series Analysis. Princeton University Press; Princeton, NJ: 1994. [Google Scholar]
- 111.Hong Y, Li H. Nonparametric Specification Testing for Continuous-Time Models With Applications to Term Structure of Interest Rates. Rev Fin Studies. 2005;18:37–84. [Google Scholar]
- 112.Diebold F, Gunther T, Tay A. Evaluating Density Forecasts With Applications to Financial Risk Management. Int Econ Rev. 1998;39:863–883. [Google Scholar]
- 113.Pressé S, Ghosh K, Lee J, Dill K. Principles of Maximum Entropy and Maximum Caliber in Statistical Physics. Rev Mod Phys. 2013;85:1115–1141. [Google Scholar]
- 114.Claeskens G, Hjort N. Model Selection and Model Averaging. Cambridge University Press; Cambridge, U.K: 2008. [Google Scholar]
- 115.Arhel N, Genovesio A, Kim K, Miko S, Perret E, Olivo- Marin J, Shorte S, Charneau P. Quantitative Four-Dimensional Tracking of Cytoplasmic and Nuclear HIV-1 Complexes. Nat Methods. 2006;3:817–824. doi: 10.1038/nmeth928. [DOI] [PubMed] [Google Scholar]
- 116.Ge H, Pressé S, Ghosh K, Dill KA. Markov Processes Follow From the Principle of Maximum Caliber. J Chem Phys. 2012;136:064108. doi: 10.1063/1.3681941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Risken H. The Fokker-Planck Equation. Springer-Verlag; Berlin: 1996. [Google Scholar]
- 118.Prakasa Rao B. Statistical Inference for Diffusion Type Processes. Arnold Publishers: London; 1999. [Google Scholar]
- 119.Rao CR. Information and Accuracy Attainable in the Estimation of Statistical Parameters. Bull Calcutta Math Soc. 1945;37:81–91. [Google Scholar]
- 120.Cramér H. Mathematical Methods of Statistics. Princeton University Press; Princeton, NJ: 1946. [Google Scholar]
- 121.Abraham A, Ram S, Chao J, Ward E, Ober R. Quantitative Study of Single Molecule Location Estimation Techniques. Opt Express. 2009;17:23352–23373. doi: 10.1364/OE.17.023352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Tang C, Chen S. Parameter Estimation and Bias Correction for Diffusion Processes. J Econometr. 2009;149:65–81. [Google Scholar]
- 123.Kou S, Xie X, Liu J. Bayesian Analysis of Single-Molecule Experimental Data. Appl Statist. 2005;54:469–506. [Google Scholar]
- 124.Monnier N, Guo S, Mori M, He J, Lénárt P, Bathe M. Bayesian Approach to MSD-Based Analysis of Particle Motion in Live Cells. Biophys J. 2012;103:616–626. doi: 10.1016/j.bpj.2012.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Bronson J, Fei J, Hofman J, Gonzalez R, Jr, Wiggins C. Learning Rates and States From Biophysical Time Series: A Bayesian Approach to Model Selection and Single-Molecule FRET Data. Biophys J. 2009;97:3196–3205. doi: 10.1016/j.bpj.2009.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Tuerkcan S, Alexandrou A, Masson J. A Bayesian Inference Scheme to Extract Diffusivity and Potential Fields From Confined Single-Molecule Trajectories. Biophys J. 2012;102:2288–2298. doi: 10.1016/j.bpj.2012.01.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Witkoskie J, Cao J. Single Molecule Kinetics. II. Numerical Bayesian Approach. J Chem Phys. 2004;121:6373–6379. doi: 10.1063/1.1785784. [DOI] [PubMed] [Google Scholar]
- 128.Lee P. Bayesian Statistics: An Introduction. John Wiley & Sons; New York: 2012. [Google Scholar]
- 129.Jaynes E. Information Theory and Statistical Mechanics. Phys Rev. 1957;106:620–630. [Google Scholar]
- 130.Jaynes E. Information Theory and Statistical Mechanics. II. Phys Rev. 1957;108:171–190. [Google Scholar]
- 131.Gelman A. In Encyclopedia of Environ- metrics. Vol. 3. Wiley Online Library; New York; 2002. Prior Distribution; pp. 1634–1637. [Google Scholar]
- 132.Jeffreys H. Proc R Soc London, Ser A. 1946;186:453–461. doi: 10.1098/rspa.1946.0056. [DOI] [PubMed] [Google Scholar]
- 133.Jeffreys H. The Theory of Probability. Oxford University Press; Oxford, U.K.: p. 1939. [Google Scholar]
- 134.Eno D. Ph D thesis. Virginia Polytechnic Institute and State University; Blacksburg, VA: 1999. Noninformative Prior Bayesian Analysis for Statistical Calibration Problems. [Google Scholar]
- 135.Fisher C, Ullman O, Stultz C. Comparative Studies of Disordered Proteins With Similar Sequences: Application to Aβ40 and Aβ42. Biophys J. 2013;104:1546–1555. doi: 10.1016/j.bpj.2013.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Ensign D, Pande V. Bayesian Detection of Intensity Changes in Single Molecule and Molecular Dynamics Trajectories. J Phys Chem B. 2010;114:280–292. doi: 10.1021/jp906786b. [DOI] [PubMed] [Google Scholar]
- 137.Ensign D, Pande V, Andersen H, Boxer S. Bayesian Statistics and Single-Molecule Trajectories. Stanford University Press; Stanford, CA: 2010. [Google Scholar]
- 138.Ensign D, Pande V. Bayesian Single-Exponential Kinetics in Single-Molecule Experiments and Simulations. J Phys Chem B. 2009;113:12410–12423. doi: 10.1021/jp903107c. [DOI] [PubMed] [Google Scholar]
- 139.Durisic N, Laparra-Cuervo L, Sandoval-Álvarez A, Borbely J, Lakadamyali M. Single-Molecule Evaluation of Fluorescent Protein Photoactivation Efficiency Using an in Vivo Nanotemplate. Nat Methods. 2014;11:156–62. doi: 10.1038/nmeth.2784. [DOI] [PubMed] [Google Scholar]
- 140.Hastings W. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika. 1970;57:97–109. [Google Scholar]
- 141.Smith A, Roberts G. Bayesian Computation Via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods. J R Stat Soc B. 1993;55:3–23. [Google Scholar]
- 142.Beckers M, Drechsler F, Eilert T, Nagy J, Michaelis J. Quantitative Structural Information From Single-Molecule FRET. Faraday Discuss. 2015;184:117–129. doi: 10.1039/c5fd00110b. [DOI] [PubMed] [Google Scholar]
- 143.Berger J. Statistical Decision Theory and Bayesian Analysis. Springer; New York: 1985. [Google Scholar]
- 144.Lehmann E, Romano J. Testing Statistical Hypotheses. Springer-Verlag; New York: 2005. [Google Scholar]
- 145.Rosenblatt M. Remarks on a Multivariate Transformation. Ann Math Stat. 1952;23:470–472. [Google Scholar]
- 146.McKinney SA, Joo C, Ha T. Analysis of Single-Molecule FRET Trajectories Using Hidden Markov Modeling. Biophys J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Rabiner L. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proc IEEE. 1989;77:257–286. [Google Scholar]
- 148.McCallum A, Freitag D, Pereira F. Maximum Entropy Markov Models for Information Extraction and Segmentation. Proceedings of the 17th International Conference on Machine Learning. 2000:591–598. [Google Scholar]
- 149.Liu Y, Park J, Dahmen KA, Chemla YR, Ha TA. Comparative Study of Multivariate Univariate Hidden Markov Modelings in Time-Binned Single-Molecule FRET Data Analysis. J Phys Chem B. 2010;114:5386–5403. doi: 10.1021/jp9057669. [DOI] [PubMed] [Google Scholar]
- 150.Pirchi M, Ziv G, Riven I, Cohen SS, Zohar N, Barak Y, Haran G. Single-Molecule Fluorescence Spectroscopy Maps the Folding Landscape of a Large Protein. Nat Commun. 2011;2:493. doi: 10.1038/ncomms1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Chung HS, Gopich IV. Fast Single-Molecule FRET Spectroscopy: Theory and Experiment. Phys Chem Chem Phys. 2014;16:18644–18657. doi: 10.1039/c4cp02489c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Keller B, Kobitski A, Jaschke A, Nienhaus G, Noé F. Complex RNA Folding Kinetics Revealed by Single-Molecule FRET and Hidden Markov Models. J Am Chem Soc. 2014;136:4534–4543. doi: 10.1021/ja4098719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Blanco M, Walter N. Analysis of Complex Single-Molecule FRET Time Trajectories. Methods Enzymol. 2010;472:153–178. doi: 10.1016/S0076-6879(10)72011-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Elms PJ, Chodera JD, Bustamante C, Marqusee S. The Molten Globule State Is Unusually Deformable Under Mechanical Force. Proc Natl Acad Sci U S A. 2012;109:3796–3801. doi: 10.1073/pnas.1115519109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Lee T. Extracting Kinetics Information From Single-Molecule Fluorescence Resonance Energy Transfer Data Using Hidden Markov Models. J Phys Chem B. 2009;113:11535–11542. doi: 10.1021/jp903831z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Kelly D, Dillingham M, Hudson A, Wiesner K. A New Method for Inferring Hidden Markov Models From Noisy Time Sequences. PLoS One. 2012;7:e29703. doi: 10.1371/journal.pone.0029703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Forney GD. The Viterbi Algorithm. Proc IEEE. 1973;61:268–278. [Google Scholar]
- 158.Bishop C. Pattern Recognition and Machine Learning. Springer; Berlin: 2006. [Google Scholar]
- 159.Qin F, Auerbach A, Sachs F. Maximum Likelihood Estimation of Aggregated Markov Processes. Proc R Soc London Ser B. 1997;264:375–383. doi: 10.1098/rspb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Ball F, Rice J. Stochastic Models for Ion Channels: Introduction and Bibliography. Math Biosci. 1992;112:189–206. doi: 10.1016/0025-5564(92)90023-p. [DOI] [PubMed] [Google Scholar]
- 161.Qin F, Auerbach A, Sachs F. A Direct Optimization Approach to Hidden Markov Modeling for Single Channel Kinetics. Biophys J. 2000;79:1915–1927. doi: 10.1016/S0006-3495(00)76441-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Colquhoun D, Hawkes AG. On the Stochastic Properties of Bursts of Single Ion Channel Openings of Clusters of Bursts. Philos Trans R Soc B. 1982;300:1–59. doi: 10.1098/rstb.1982.0156. [DOI] [PubMed] [Google Scholar]
- 163.Horn R, Lange K. Estimating Kinetic Constants From Single Channel Data. Biophys J. 1983;43:207–223. doi: 10.1016/S0006-3495(83)84341-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Qin F, Auerbach A, Sachs F. Estimating Single-Channel Kinetic Parameters From Idealized Patch-Clamp Data Containing Missed Events. Biophys J. 1996;70:264–280. doi: 10.1016/S0006-3495(96)79568-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Kienker P. Equivalence of Aggregated Markov Models of Ion- Channel Gating. Proc R Soc London, Ser B. 1989;236:269–309. doi: 10.1098/rspb.1989.0024. [DOI] [PubMed] [Google Scholar]
- 166.Roux B, Sauve R. A General Solution to the Time Interval Omission Problem Applied to Single Channel Analysis. Biophys J. 1985;48:149–158. doi: 10.1016/S0006-3495(85)83768-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Rissanen J. Fisher Information and Stochastic Complexity. IEEE Trans Inf Theory. 1996;42:40–47. [Google Scholar]
- 168.Balasubramanian V. Advances in minimum description length: Theory and applications. MIT Press; Cambridge, MA: 2005. MDL, Bayesian Inference, and the Geometry of the Space of Probability Distributions; pp. 81–98. [Google Scholar]
- 169.Myung I, Balasubramanian V, Pitt M. Counting Probability Distributions: Differential Geometry and Model Selection. Proc Natl Acad Sci U S A. 2000;97:11170–11175. doi: 10.1073/pnas.170283897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Shibata R. Selection of the Order of an Autoregressive Model by Akaike’S Information Criterion. Biometrika. 1976;63:117–126. [Google Scholar]
- 171.Nishii R. Asymptotic Properties of Criteria for Selection of Variables in Multiple Regression. Ann Stat. 1984;12:758–765. [Google Scholar]
- 172.Vrieze S. Model Selection and Psychological Theory: A Discussion of the Differences Between the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) Psychol Meth. 2012;17:228–243. doi: 10.1037/a0027127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Kuha JA. AIC and BIC Comparisons of Assumptions and Performance. Socio Meth Res. 2004;33:188–229. [Google Scholar]
- 174.Schwarz G. Estimating the Dimension of a Model. Ann Stat. 1978;6:461–464. [Google Scholar]
- 175.Chen S, Gopalakrishnan PS. Environment and Channel Change Detection and Clustering via the Bayesian Information Criterion. Proc DARPA Broadcast News Transcription and Under- standing Workshop. 1998;8:127–132. [Google Scholar]
- 176.Andrec M, Levy R, Talaga D. Direct Determination of Kinetic Rates From Single-Molecule Photon Arrival Trajectories Using Hidden Markov Models. J Phys Chem A. 2003;107:7454–7464. doi: 10.1021/jp035514+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Chen J, Chen Z. Extended Bayesian Information Criteria for Model Selection With Large Model Spaces. Biometrika. 2008;95:759–771. [Google Scholar]
- 178.Atkinson A. Likelihood Ratios, Posterior Odds and Information Criteria. J Econometr. 1981;16:15–20. [Google Scholar]
- 179.Ferguson T. A Bayesian Analysis of Some Nonparametric Problems. Ann Stat. 1973;1:209–230. [Google Scholar]
- 180.Orbanz P, Teh Y. Encyclopedia of Machine Learning. Springer; New York: 2011. Bayesian Nonparametric Models. [Google Scholar]
- 181.Teh Y. Encyclopedia of Machine Learning. Springer; New York: 2011. Dirichlet Process. [Google Scholar]
- 182.Phadia E. Prior Processes and Their Applications. Springer; New York: 2013. [Google Scholar]
- 183.Teh Y, Jordan M, Beal M, Blei D. Hierarchical Dirichlet Processes. J Am Stat Assoc. 2006;101:1566–1581. [Google Scholar]
- 184.Neal R. Markov Chain Sampling Methods for Dirichlet Process Mixture Models. J Comp Graph Stat. 2000;9:249–265. [Google Scholar]
- 185.Kim S, Tadesse M, Vannucci M. Variable Selection in Clustering via Dirichlet Process Mixture Models. Biometrika. 2006;93:877–893. [Google Scholar]
- 186.Fox E, Sudderth E, Jordan M, Willsky A. Bayesian Nonparametric Methods for Learning Markov Switching Processes. IEEE Signal Process Mag. 2010;27:43–54. [Google Scholar]
- 187.Sethuraman J. A Constructive Definition of Dirichlet Priors. Stat Sin. 1994;4:639–650. [Google Scholar]
- 188.Pitman J. Poisson-Dirichlet and GEM Invariant Distributions for Split-and-Merge Transformations of an Interval Partition. Comb Probab Comput. 2002;11:501–514. [Google Scholar]
- 189.Hines K, Bankston J, Aldrich R. Analyzing Single-Molecule Time Series via Nonparametric Bayesian Inference. Biophys J. 2015;108:540–556. doi: 10.1016/j.bpj.2014.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Wang S, Moffitt J, Dempsey G, Xie X, Zhuang X. Characterization and Development of Photoactivatable Fluorescent Proteins for Single-Molecule-Based Superresolution Imaging. Proc Natl Acad Sci U S A. 2014;111:8452–8457. doi: 10.1073/pnas.1406593111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Lidke K, Rieger B, Jovin T, Heintzmann R. Super- resolution by Localization of Quantum Dots Using Blinking Statistics. Opt Express. 2005;13:7052–7062. doi: 10.1364/opex.13.007052. [DOI] [PubMed] [Google Scholar]
- 192.Alivisatos A, Gu W, Larabell C. Quantum Dots as Cellular Probes. Annu Rev Biomed Eng. 2005;7:55–76. doi: 10.1146/annurev.bioeng.7.060804.100432. [DOI] [PubMed] [Google Scholar]
- 193.Press W, Teukolsky S, Vetterling W, Flannery B. Numerical Recipes 3rd ed: The Art of Scientific Computing. Cambridge University Press; Cambridge, UK: 2007. [Google Scholar]
- 194.Huang Z, Zhu H, Long F, Ma H, Qin L, Liu Y, Ding J, Zhang Z, Luo Q, Zeng S. Localization-Based Super-Resolution Microscopy With an sCMOS Camera. Opt Express. 2011;19:19156–19168. doi: 10.1364/OE.19.019156. [DOI] [PubMed] [Google Scholar]
- 195.Hynecek J, Nishiwaki T. Excess Noise and Other Important Characteristics of Low Light Level Imaging Using Charge Multiplying CCDs. IEEE Trans Electron Devices. 2003;50:239–245. [Google Scholar]
- 196.Ulbrich M, Isacoff E. Subunit Counting in Membrane-Bound Proteins. Nat Methods. 2007;4:319–321. doi: 10.1038/NMETH1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197.Pertsinidis A, Zhang Y, Chu S. Subnanometre Single- Molecule Localization, Registration and Distance Measurements. Nature. 2010;466:647–651. doi: 10.1038/nature09163. [DOI] [PubMed] [Google Scholar]
- 198.Huang F, Hartwich T, Rivera-Molina F, Lin Y, Duim W, Long J, Uchil P, Myers J, Baird M, Mothes W, et al. Video-Rate Nanoscopy Using sCMOS Camera-Specific Single-Molecule Localization Algorithms. Nat Methods. 2013;10:653–658. doi: 10.1038/nmeth.2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Backlund M, Lew M, Backer A, Sahl S, Moerner W. The Role of Molecular Dipole Orientation in Single-Molecule Fluorescence Microscopy and Implications for Super-Resolution Imaging. Chem- PhysChem. 2014;15:587–599. doi: 10.1002/cphc.201300880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Rowland DJ, Biteen JS. Top-Hat and Asymmetric Gaussian-Based Fitting Functions for Quantifying Directional Single- Molecule Motion. ChemPhysChem. 2014;15:712–720. doi: 10.1002/cphc.201300774. [DOI] [PubMed] [Google Scholar]
- 201.Ghosh R, Webb W. Automated Detection and Tracking of Individual and Clustered Cell Surface Low Density Lipoprotein Receptor Molecules. Biophys J. 1994;66:1301–1318. doi: 10.1016/S0006-3495(94)80939-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Sage D, Kirshner H, Pengo T, Stuurman N, Min J, Manley S, Unser M. Quantitative Evaluation of Software Packages for Single-Molecule Localization Microscopy. Nat Methods. 2015;12:717–724. doi: 10.1038/nmeth.3442. [DOI] [PubMed] [Google Scholar]
- 203.Sage D, Neumann F, Hediger F, Gasser S, Unser M. Automatic Tracking of Individual Fluorescence Particles: Application to the Study of Chromosome Dynamics. IEEE Trans Image Process. 2005;14:1372–1383. doi: 10.1109/tip.2005.852787. [DOI] [PubMed] [Google Scholar]
- 204.Köthe U, Herrmannsdörfer F, Kats I, Hamprecht F. SimpleSTORM: A Fast, Self-Calibrating Reconstruction Algorithm for Localization Microscopy. Histochem Cell Biol. 2014;141:613–627. doi: 10.1007/s00418-014-1211-4. [DOI] [PubMed] [Google Scholar]
- 205.Turin G. Introduction An to Matched Filters. IEEE Trans Inf Theory. 1960;6 31110.1109/TIT.1960.1057571. [Google Scholar]
- 206.Coltharp C, Kessler R, Xiao J. Accurate Construction of Photoactivated Localization Microscopy (PALM) Images for Quantitative Measurements. PLoS One. 2012;7 doi: 10.1371/journal.pone.0051725. e5172510.1371/ journal.pone.0051725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 207.Křížek P, Raška I, Hagen GM. Minimizing Detection Errors in Single Molecule Localization Microscopy. Opt Express. 2011;19:3226–3235. doi: 10.1364/OE.19.003226. [DOI] [PubMed] [Google Scholar]
- 208.Mortensen K, Churchman L, Spudich J, Flyvbjerg H. Optimized Localization Analysis for Single-Molecule Tracking and Super-Resolution Microscopy. Nat Methods. 2010;7:377–381. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 209.Starr R, Stahlheber S, Small A. Fast Maximum Likelihood Algorithm for Localization of Fluorescent Molecules. Opt Lett. 2012;37:413–415. doi: 10.1364/OL.37.000413. [DOI] [PubMed] [Google Scholar]
- 210.Nieuwenhuizen R, Lidke K, Bates M, Puig D, Grünwald D, Stallinga S, Rieger B. Measuring Image Resolution in Optical Nanoscopy. Nat Methods. 2013;10:557–562. doi: 10.1038/nmeth.2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Banterle N, Bui K, Lemke E, Beck M. Fourier Ring Correlation as a Resolution Criterion for Super-Resolution Microscopy. J Struct Biol. 2013;183:363–367. doi: 10.1016/j.jsb.2013.05.004. [DOI] [PubMed] [Google Scholar]
- 212.Cheezum M, Walker W, Guilford W. Quantitative Comparison of Algorithms for Tracking Single Fluorescent Particles. Biophys J. 2001;81:2378–2388. doi: 10.1016/S0006-3495(01)75884-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213.Parthasarathy R. Rapid, Accurate Particle Tracking by Calculation of Radial Symmetry Centers. Nat Methods. 2012;9:724–726. doi: 10.1038/nmeth.2071. [DOI] [PubMed] [Google Scholar]
- 214.Liu S, Li J, Zhang Z, Wang Z, Tian Z, Wang G, Pang D. Fast and High-Accuracy Localization for Three-Dimensional Single- Particle Tracking. Sci Rep. 2013;3:2462. doi: 10.1038/srep02462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 215.Ma H, Long F, Zeng S, Huang Z. Fast and Precise Algorithm Based on Maximum Radial Symmetry for Single Molecule Localization. Opt Lett. 2012;37:2481–2483. doi: 10.1364/OL.37.002481. [DOI] [PubMed] [Google Scholar]
- 216.Guizar-Sicairos M, Thurman S, Fienup J. Efficient Subpixel Image Registration Algorithms. Opt Lett. 2008;33:156–158. doi: 10.1364/ol.33.000156. [DOI] [PubMed] [Google Scholar]
- 217.York A, Ghitani A, Vaziri A, Davidson M, Shroff H. Confined Activation and Subdiffractive Localization Enables Whole- Cell PALM With Genetically Expressed Probes. Nat Methods. 2011;8:327–333. doi: 10.1038/nmeth.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 218.Hess S, Gould T, Gudheti M, Maas S, Mills K, Zimmerberg J. Dynamic Clustered Distribution of Hemagglutinin Resolved at 40 nm in Living Cell Membranes Discriminates Between Raft Theories. Proc Natl Acad Sci U S A. 2007;104:17370–17375. doi: 10.1073/pnas.0708066104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219.Yildiz A, Forkey J, McKinney S, Ha T, Goldman Y, Selvin P. Myosin V Walks Hand-Over-Hand: Single Fluorophore Imaging With 1.5-nm Localization. Science. 2003;300:2061–2065. doi: 10.1126/science.1084398. [DOI] [PubMed] [Google Scholar]
- 220.Anscombe F. The Transformation of Poisson, Binomial and Negative-Binomial Data. Biometrika. 1948;35:246. [Google Scholar]
- 221.Murtagh F, Starck J-L, Bijaoui A. Image Restoration With Noise Suppression Using a Multiresolution Support. Astron Astrophys Suppl Ser. 1995;112:179–189. [Google Scholar]
- 222.Stallinga S, Rieger B. Accuracy of the Gaussian Point Spread Function Model in 2D Localization Microscopy. Opt Express. 2010;18:24461–24476. doi: 10.1364/OE.18.024461. [DOI] [PubMed] [Google Scholar]
- 223.Vaughan J, Jia S, Zhuang X. Ultrabright Photoactivatable Fluorophores Created by Reductive Caging. Nat Methods. 2012;9:1181–1184. doi: 10.1038/nmeth.2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 224.Engelhardt J, Keller J, Hoyer P, Reuss M, Staudt T, Hell S. Molecular Orientation Affects Localization Accuracy in Super- resolution Far-Field Fluorescence Microscopy. Nano Lett. 2011;11:209–213. doi: 10.1021/nl103472b. [DOI] [PubMed] [Google Scholar]
- 225.Zipfel W, Williams R, Webb W. Nonlinear Magic: Multiphoton Microscopy in the Biosciences. Nat Biotechnol. 2003;21:1369–1377. doi: 10.1038/nbt899. [DOI] [PubMed] [Google Scholar]
- 226.Huisken J, Swoger J, Del Bene F, Wittbrodt J, Stelzer E. Optical Sectioning Deep Inside Live Embryos by Selective Plane Illumination Microscopy. Science. 2004;305:1007–1009. doi: 10.1126/science.1100035. [DOI] [PubMed] [Google Scholar]
- 227.Kao H, Verkman S. Tracking of Single Fluorescent Particles in Three Dimensions: Use of Cylindrical Optics to Encode Particle Position. Biophys J. 1994;67:1291–1300. doi: 10.1016/S0006-3495(94)80601-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 228.Huang B, Wang W, Bates M, Zhuang X. Three- Dimensional Super-Resolution Reconstruction Microscopy. Science. 2008;319:810–813. doi: 10.1126/science.1153529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 229.Juette M, Gould T, Lessard M, Mlodzianoski M, Nagpure B, Bennett B, Hess S, Bewersdorf J. Three-Dimensional Sub-100 nm Resolution Fluorescence Microscopy of Thick Samples. Nat Methods. 2008;5:527–529. doi: 10.1038/nmeth.1211. [DOI] [PubMed] [Google Scholar]
- 230.Pavani S, Piestun R. Three Dimensional Tracking of Fluorescent Microparticles Using a Photon-Limited Double-Helix Response System. Opt Express. 2008;16:22048–22057. doi: 10.1364/oe.16.022048. [DOI] [PubMed] [Google Scholar]
- 231.Shtengel G, Galbraith J, Galbraith C, Lippincott-Schwartz J, Gillette J, Manley S, Sougrat R, Waterman C, Kanchanawong P, Davidson M, et al. Interferometric Fluorescent Super-Resolution Microscopy Resolves 3D Cellular Ultrastructure. Proc Natl Acad Sci U S A. 2009;106:3125–3130. doi: 10.1073/pnas.0813131106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 232.Stetson P. AOPHOT: A Computer Program for Crowded- Field Stellar Photometry. Publ Astron Soc Pac. 1987;99:191–222. [Google Scholar]
- 233.Huang F, Schwartz S, Byars J, Lidke K. Simultaneous Multiple-Emitter Fitting for Single Molecule Super-Resolution Imaging. Biomed Opt Express. 2011;2:1377–1393. doi: 10.1364/BOE.2.001377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 234.Wilks S. The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses. Ann Math Stat. 1938;9:60–62. [Google Scholar]
- 235.Candès E, Romberg J, Tao T. Stable Signal Recovery From Incomplete and Inaccurate Measurements. Comm Pure Appl Math. 2006;59:1207–1223. [Google Scholar]
- 236.Zhu L, Zhang W, Elnatan D, Huang B. Faster STORM Using Compressed Sensing. Nat Methods. 2012;9:721–723. doi: 10.1038/nmeth.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 237.Grant M, Boyd S, Ye Y. Global optimization. Springer; New York: 2006. Disciplined Convex Programming; pp. 155–210. [Google Scholar]
- 238.Burnette D, Sengupta P, Dai Y, Lippincott-Schwartz J, Kachar B. Bleaching/Blinking Assisted Localization Microscopy for Superresolution Imaging Using Standard Fluorescent Molecules. Proc Natl Acad Sci U S A. 2011;108:21081–21086. doi: 10.1073/pnas.1117430109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 239.Dertinger T, Colyer R, Iyer G, Weiss S, Enderlein J. Fast and Background-Free 3D Super-Resolution Optiocal Fluctuation Imaging (SOFI) Proc Natl Acad Sci U S A. 2009;106:22287–22292. doi: 10.1073/pnas.0907866106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 240.Hyvarinen A. Fast and Robust Fixed-Point Algorithm for Independent Component Analysis. IEEE Trans Neur Net. 1999;10:626–634. doi: 10.1109/72.761722. [DOI] [PubMed] [Google Scholar]
- 241.Cox S, Rosten E, Monypenny J, Jovanovic-Talisman T, Burnette D, Lippincott-Schwartz J, Jones G, Heintzmann R. Bayesian Localization Microscopy Reveals Nanoscale Podosome Dynamics. Nat Methods. 2011;9:195–200. doi: 10.1038/nmeth.1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242.Hu Y, Nan X, Sengupta P, Lippincott-Schwartz J, Cang H. Accelerating 3B Single-Molecule Super-Resolution Microscopy With Cloud Computing. Nat Methods. 2013;10:96–97. doi: 10.1038/nmeth.2335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 243.Mukamel E, Babcock H, Zhuang X. Statistical Deconvolu- tion for Superresolution Fluorescence Microscopy. Biophys J. 2012;102:2391–2400. doi: 10.1016/j.bpj.2012.03.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 244.Min J, Vonesch C, Kirshner H, Carlini L, Olivier N, Holden S, Manley S, Ye J, Unser M. FALCON: Fast and Unbiased Reconstruction of High-Density Super-Resolution Microscopy Data. Sci Rep. 2014;4:4577. doi: 10.1038/srep04577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 245.Bates M, Huang B, Dempsey GT, Zhuang X. Multicolor Super-Resolution Imaging With Photo-Switchable Fluorescent Probes. Science. 2007;317:1749–1753. doi: 10.1126/science.1146598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 246.Mlodzianoski M, Schreiner J, Callahan S, Smolková K, Dlasková A, Šantorová J, Ježek P, Bewersdorf J. Sample Drift Correction in 3D Fluorescence Photoactivation Localization Microscopy. Opt Express. 2011;19:15009–15019. doi: 10.1364/OE.19.015009. [DOI] [PubMed] [Google Scholar]
- 247.McGorty R, Kamiyama D, Huang B. Active Microscope Stabilization in Three Dimensions Using Image Correlation. Opt Nanoscopy. 2013;2:3. doi: 10.1186/2192-2853-2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 248.Nieuwenhuizen R, Bates M, Szymborska A, Lidke K, Rieger B, Stallinga S. Quantitative Localization Microscopy: Effects of Photophysics and Labeling Stoichiometry. PLoS One. 2015;10:0127989. doi: 10.1371/journal.pone.0127989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 249.Berg H. The Rotary Motor of Bacterial Flagella. Annu Rev Biochem. 2003;72:19–54. doi: 10.1146/annurev.biochem.72.121801.161737. [DOI] [PubMed] [Google Scholar]
- 250.Leake M, Chandler J, Wadhams G, Bai F, Berry R, Armitage J. Stoichiometry and Turnover in Single, Functioning Membrane Protein Complexes. Nature. 2006;443:355–358. doi: 10.1038/nature05135. [DOI] [PubMed] [Google Scholar]
- 251.Delalez NJ, Wadhams GH, Rosser G, Xue Q, Brown MT, Dobbie IM, Berry RM, Leake MC, Armitage JP. Signal- Dependent Turnover of the Bacterial Flagellar Switch Protein FliM. Proc Natl Acad Sci U S A. 2010;107:11347–11351. doi: 10.1073/pnas.1000284107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 252.Wu L, Lewis P, Allmansberger R, Hauser P, Errington J. A Conjugation-Like Mechanism for Prespore Chromosome Partitioning During Sporulation in Bacillus Subtilis. Genes Dev. 1995;9:1316–1326. doi: 10.1101/gad.9.11.1316. [DOI] [PubMed] [Google Scholar]
- 253.Liu N, Dutton R, Pogliano K. Evidence That the SpoIIIE DNA Translocase Participates in Membrane Fusion During Cytokinesis and Engulfment. Mol Microbiol. 2006;59:1097–1113. doi: 10.1111/j.1365-2958.2005.05004.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 254.Baker M, Wolanin P, Stock J. Signal Transduction in Bacterial Chemotaxis. BioEssays. 2006;28:9–22. doi: 10.1002/bies.20343. [DOI] [PubMed] [Google Scholar]
- 255.Gross D, Webb W. Molecular Counting of Low-Density Lipoprotein Particles as Individuals and Small Clusters on Cell Surfaces. Biophys J. 1986;49:901–11. doi: 10.1016/S0006-3495(86)83718-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 256.Burton BM, Marquis KA, Sullivan NL, Rapoport TA, Rudner DZ. The ATPase SpoIIIE Transports DNA Across Fused Septal Membranes During Sporulation in Bacillus Subtilis. Cell. 2007;131:1301–1312. doi: 10.1016/j.cell.2007.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 257.Joglekar A, Bouck D, Molk J, Bloom K, Salmon E. Molecular Architecture of a Kinetochore-Microtubule Attachment Site. Nat Cell Biol. 2006;8:581–5. doi: 10.1038/ncb1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 258.Coffman V, Wu P, Parthun M, Wu J. CENP-A Exceeds Microtubule Attachment Sites in Centromere Clusters of Both Budding and Fission Yeast. J Cell Biol. 2011;195:563–572. doi: 10.1083/jcb.201106078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 259.Lawrimore J, Bloom K, Salmon E. Point Centromeres Contain More Than a Single Centromere-Specific Cse4 (CENP-A) Nucleosome. J Cell Biol. 2011;195:573–582. doi: 10.1083/jcb.201106036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 260.Henikoff S, Henikoff J. Point” Centromeres of Saccharomyces Harbor Single Centromere-Specific Nucleosomes. Genetics. 2012;190:1575–1577. doi: 10.1534/genetics.111.137711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 261.McKinley K, Cheeseman I. The Molecular Basis for Centromere Identity and Function. Nat Rev Mol Cell Biol. 2015;17:16–29. doi: 10.1038/nrm.2015.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 262.Liesche C, Grußmayer K, Ludwig M, Wörz S, Rohr K, Herten D, Beaudouin J, Eils R. Automated Analysis of Single- Molecule Photobleaching Data by Statistical Modeling of Spot Populations. Biophys J. 2015;109:2352–2362. doi: 10.1016/j.bpj.2015.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 263.Ambrose W, Goodwin P, Enderlein J, Semin D, Martin J, Keller R. Fluorescence photon antibunching from single molecules on a surface. Chem Phys Lett. 1997;269:365–370. [Google Scholar]
- 264.Kurz A, Schmied J, Grußmayer K, Holzmeister P, Tinnefeld P, Herten D-P. Counting Fluorescent Dye Molecules on DNA Origami by Means of Photon Statistics. Small. 2013;9:4061–4068. doi: 10.1002/smll.201300619. [DOI] [PubMed] [Google Scholar]
- 265.Messina T, Kim H, Giurleo J, Talaga D. Hidden Markov Model Analysis of Multichromophore Photobleaching. J Phys Chem B. 2006;110:16366–16376. doi: 10.1021/jp063367k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 266.McGuire H, Aurousseau M, Bowie D, Bluncks R. Automating Single Subunit Counting of Membrane Proteins in Mammalian Cells. J Biol Chem. 2012;287:35912–35921. doi: 10.1074/jbc.M112.402057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 267.Chen Y, Deffenbaugh N, Anderson C, Hancock W. Molecular Counting by Photobleaching in Protein Complexes With Many Subunits: Best Practices and Application to the Cellulose Synthesis Complex. Mol Biol Cell. 2014;25:3630–3642. doi: 10.1091/mbc.E14-06-1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 268.Pressé S, Peterson J, Lee J, Elms P, MacCallum J, Marqusee S, Bustamante C, Dill K. Single Molecule Conformational Memory Extraction: P5ab RNA Hairpin. J Phys Chem B. 2014;118:6597–6603. doi: 10.1021/jp500611f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 269.Little MA, Jones NS. Generalized Methods and Solvers for Noise Removal From Piecewise Constant Signals. I. Background Theory. Proc R Soc London Ser A. 2011;467:3088–3114. doi: 10.1098/rspa.2010.0671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 270.Carter BC, Vershinin M, Gross SP. A Comparison of Step-Detection Methods: How Well Can You Do? Biophys J. 2008;94:306–319. doi: 10.1529/biophysj.107.110601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 271.Chung S, Kennedy R. Forward-Backward Non-Linear Filtering Technique for Extracting Small Biological Signals From Noise. J Neurosci Methods. 1991;40:71–86. doi: 10.1016/0165-0270(91)90118-j. [DOI] [PubMed] [Google Scholar]
- 272.Kalafut B, Visscher K. An Objective Model-Independent Method for Detection of Non-Uniform Steps in Noisy Signals. Comput Phys Commun. 2008;179:716–723. [Google Scholar]
- 273.Killick R, Fearnhead P, Eckley I. Optimal Detection of Changepoints With a Linear Computational Cost. J Am Stat Assoc. 2012;107:1590–1598. [Google Scholar]
- 274.Rigaill G. A Pruned Dynamic Programming Algorithm to Recover the Best Segmentations With 1 to Kmax Change-Points. J Soc Fr Statistique. 2015;156:180–205. [Google Scholar]
- 275.Annibale P, Scarselli M, Kodiyan A, Radenovic A. Photoactivatable Fluorescent Protein mEos2 Displays Repeated Photoactivation After a Long-Lived Dark State in the Red Photoconverted Form. J Phys Chem Lett. 2010;1:1506–1510. [Google Scholar]
- 276.Dickson R, Cubitt B, Tsien R, Moerner W. On/Off Blinking and Switching Behaviour of Single Molecules of Green Fluorescent Protein. Nature. 1997;388:355–358. doi: 10.1038/41048. [DOI] [PubMed] [Google Scholar]
- 277.Lee S, Shin J, Lee A, Bustamante C. Counting Single Photoactivatable Fluorescent Molecules by Photoactivated Localization Microscopy (PALM) Proc Natl Acad Sci U S A. 2012;109:17436–17441. doi: 10.1073/pnas.1215175109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 278.Shaner NC, Steinbach PA, Tsien RY. A Guide to Choosing Fluorescent Proteins. Nat Methods. 2005;2:905–909. doi: 10.1038/nmeth819. [DOI] [PubMed] [Google Scholar]
- 279.Fernández-Suárez M, Ting A. Fluorescent Probes for Super-Resolution Imaging in Living Cells. Nat Rev Mol Cell Biol. 2008;9:929–943. doi: 10.1038/nrm2531. [DOI] [PubMed] [Google Scholar]
- 280.Jaqaman K, Loerke D, Mettlen M, Kuwata H, Grinstein S, Schmid S, Danuser G. Robust Single-Particle Tracking in Live- Cell Time-Lapse Sequences. Nat Methods. 2008;5:695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 281.Chenouard N, Smal I, de Chaumont F, Maška M, Sbalzarini I, Gong Y, Cardinale J, Carthel C, Coraluppi S, Winter M, et al. Objective Comparison of Particle Tracking Methods. Nat Methods. 2014;11:281–289. doi: 10.1038/nmeth.2808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 282.Meijering E, Smal I, Danuser G. Tracking in Molecular Bioimaging. IEEE Signal Process Mag. 2006;23:46–53. [Google Scholar]
- 283.Danuser G. Computer Vision in Cell Biology. Cell. 2011;147:973–978. doi: 10.1016/j.cell.2011.11.001. [DOI] [PubMed] [Google Scholar]
- 284.Meijering E, Dzyubachyk O, Smal I. Methods for Cell and Particle Tracking. Methods Enzymol. 2012;504:183–200. doi: 10.1016/B978-0-12-391857-4.00009-4. [DOI] [PubMed] [Google Scholar]
- 285.McInerney T, Terzopoulos D. Deformable Models in Medical Image Analysis: a Survey. Med Image Anal. 1996;1:91–108. doi: 10.1016/s1361-8415(96)80007-7. [DOI] [PubMed] [Google Scholar]
- 286.Dufour A, Thibeaux R, Labruyere E, Guillen N, Olivo- Marin JC. 3-D Active Meshes: Fast Discrete Deformable Models for Cell Tracking in 3-D Time-Lapse Microscopy. IEEE Trans Image Process. 2011;20:1925–1937. doi: 10.1109/TIP.2010.2099125. [DOI] [PubMed] [Google Scholar]
- 287.Chenouard N, Bloch I, Olivo-Marin J. Multiple Hypothesis Tracking for Cluttered Biological Image Sequences. IEEE Trans Pattern Anal Mach Intell. 2013;35:2736–3750. doi: 10.1109/TPAMI.2013.97. [DOI] [PubMed] [Google Scholar]
- 288.Kalaidzidis Y. Intracellular Objects Tracking. Eur J Cell Biol. 2007;86:569–578. doi: 10.1016/j.ejcb.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 289.Shroff H, Galbraith C, Galbraith J, Betzig E. Live-Cell Photoactivated Localization Microscopy of Nanoscale Adhesion Dynamics. Nat Methods. 2008;5:417–423. doi: 10.1038/nmeth.1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 290.Kusumi A, Tsunoyama T, Hirosawa K, Kasai R, Fujiwara T. Tracking Single Molecules at Work in Living Cells. Nat Chem Biol. 2014;10:524–532. doi: 10.1038/nchembio.1558. [DOI] [PubMed] [Google Scholar]
- 291.Chertkov M, Kroc L, Krzakala F, Vergassola M, Zdeborová L. Inference in Particle Tracking Experiments by passing Messages Between Images. Proc Natl Acad Sci U S A. 2010;107:7663–7668. doi: 10.1073/pnas.0910994107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 292.Mont A, Calderon C, Poore A. A New Computational Method for Ambiguity Assessment of Solutions to Assignment Problems Arising in Target Tracking. Proc SPIE. 2014;9092:90920J. [Google Scholar]
- 293.Chenouard N, Dufour A, Olivo-Marin J. Tracking Algorithms Chase Down Pathogens. Biotechnol J. 2009;4:838–845. doi: 10.1002/biot.200900030. [DOI] [PubMed] [Google Scholar]
- 294.Celler K, van Wezel G, Willemse J. Single Particle Tracking of Dynamically Localizing TatA Complexes in Streptomyces Coelicolor. Biochem Biophys Res Commun. 2013;438:38–42. doi: 10.1016/j.bbrc.2013.07.016. [DOI] [PubMed] [Google Scholar]
- 295.Barden A, Goler A, Humphreys S, Tabatabaei S, Lochner M, Ruepp M, Jack T, Simonin J, Thompson A, Jones J, et al. Tracking Individual Membrane Proteins and Their Biochemistry: The Power of Direct Observation. Neuropharmacology. 2015;98:22–30. doi: 10.1016/j.neuropharm.2015.05.003. [DOI] [PubMed] [Google Scholar]
- 296.Godinez W, Lampe M, Wörz S, Müller B, Eils R, Rohr K. Deterministic and Probabilistic Approaches for Tracking Virus Particles in Time-Lapse Fluorescence Microscopy Image Sequences. Med Image Anal. 2009;13:325–42. doi: 10.1016/j.media.2008.12.004. [DOI] [PubMed] [Google Scholar]
- 297.Ruepp M-D, Brozik JA, de Esch IJP, Farndale RW, Murrell-Lagnado RD, Thompson AJ. A Fluorescent Approach for Identifying P2X1 Ligands. Neuropharmacology. 2015;98:13–21. doi: 10.1016/j.neuropharm.2015.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 298.Jack T, Simonin J, Ruepp M-D, Thompson AJ, Gertsch J, Lochner M. Characterizing New Fluorescent Tools for Studying 5- HT3 Receptor Pharmacology. Neuropharmacology. 2015;90:63–73. doi: 10.1016/j.neuropharm.2014.11.007. [DOI] [PubMed] [Google Scholar]
- 299.Kusumi A, Sako Y, Yamamoto M. Confined Lateral Diffusion of Membrane Receptors as Studied by Single Particle Tracking (Nanovid Microscopy). Effects of Calcium-Induced Differentiation in Cultured Epithelial Cells. Biophys J. 1993;65:2021–40. doi: 10.1016/S0006-3495(93)81253-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 300.Saxton MJ, Jacobson K. Single-Particle Tracking: Applications to Membrane Dynamics. Annu Rev Biophys Biomol Struct. 1997;26:373–399. doi: 10.1146/annurev.biophys.26.1.373. [DOI] [PubMed] [Google Scholar]
- 301.Poudel KR, Keller DJ, Brozik JA. Single Particle Tracking Reveals Corralling of a Transmembrane Protein in a Double- Cushioned Lipid Bilayer Assembly. Langmuir. 2011;27:320–327. doi: 10.1021/la104133m. [DOI] [PubMed] [Google Scholar]
- 302.Poudel KR, Keller DJ, Brozik JA. The Effect of a Phase Transition on Single Molecule Tracks of Annexin V in Cushioned DMPC Assemblies. Soft Matter. 2012;8:11285–11293. [Google Scholar]
- 303.Chenouard N, Bloch I, Olivo-Marin J. Feature-Aided Particle Tracking. 15th IEEE International Conference on Image Processing. 15th IEEE International Conference on Image Processing. 2008:1796–1799. doi: 10.1109/ICIP.2008.4712125. [DOI] [Google Scholar]
- 304.Ruthardt N, Bräuchle C. Visualizing Uptake and Intracellular Trafficking of Gene Carriers by Single-Particle Tracking. In: Bielke W, Erbacher C, editors. Nucleic Acid Transfection. Springer; Berlin: 2010. pp. 283–304. Topics in Current Chemistry 296. [DOI] [PubMed] [Google Scholar]
- 305.Sbalzarini I, Koumoutsakos P. Feature Point Tracking and Trajectory Analysis for Video Imaging in Cell Biology. J Struct Biol. 2005;151:182–195. doi: 10.1016/j.jsb.2005.06.002. [DOI] [PubMed] [Google Scholar]
- 306.Ewers H, Smith AE, Sbalzarini IF, Lilie H, Koumoutsakos P, Helenius A. Single-Particle Tracking of Murine Polyoma Virus-Like Particles on Live Cells and Artificial Membranes. Proc Natl Acad Sci U S A. 2005;102:15110–15115. doi: 10.1073/pnas.0504407102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 307.Bancaud A, Huet S, Daigle N, Mozziconacci J, Beaudouin J, Ellenberg J. Molecular Crowding Affects Diffusion and Binding of Nuclear Proteins in Heterochromatin and Reveals the Fractal Organization of Chromatin. EMBO J. 2009;28:3785–3798. doi: 10.1038/emboj.2009.340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 308.Bryan SJ, Burroughs NJ, Shevela D, Yu J, Rupprecht E, Liu LN, Mastroianni G, Xue Q, Llorente-Garcia I, Leake MC, et al. Localisation and Interactions of the Vipp1 Protein in Cyanobacteria. Mol Microbiol. 2014;94:1179–1195. doi: 10.1111/mmi.12826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 309.Wollman AJM, Syeda AH, McGlynn P, Leake MC. Single-Molecule Observation of DNA Replication Repair Pathways in E. coli. In: Leake MC, editor. Biophysics of Infection. Springer International Publishing; Berlin: 2016. pp. 5–16. Advances in Experimental Medicine and Biology 915. [DOI] [PubMed] [Google Scholar]
- 310.Xue Q, Leake MA. Novel Multiple Particle Tracking Algorithm for Noisy in Vivo Data by Minimal Path Optimization Within the Spatio-Temporal Vol. I. ISBI09: Proceedings of the Sixth IEEE international conference on Symposium on Biomedical Imaging; IEEE Press: Piscataway, NJ. 2009; pp. 1158–1161. [Google Scholar]
- 311.Bonneau S, Dahan M, Cohen L. Single Quantum Dot Tracking Based on Perceptual Grouping Using Minimal Paths in a Spatiotemporal Volume. IEEE Trans Image Process. 2005;14:1384–1395. doi: 10.1109/tip.2005.852794. [DOI] [PubMed] [Google Scholar]
- 312.Shafique K, Shah M. A Noniterative Greedy Algorithm for Multiframe Point Correspondence. IEEE Trans Pattern Anal Mach Intell. 2005;27:51–65. doi: 10.1109/TPAMI.2005.1. [DOI] [PubMed] [Google Scholar]
- 313.West DB. Introduction to Graph Theory. Vol. 2 Prentice Hall; Upper Saddle River, NJ: 2001. [Google Scholar]
- 314.Racine V, Hertzog A, Jouanneau J, Salamero J, Kervrann C, Sibarita J. Multiple-Target Tracking of 3D Fluorescent Objects Based on Simulated Annealing. 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro. 2006:1020–1023. [Google Scholar]
- 315.Heidbreder M, Zander C, Malkusch S, Widera D, Kaltschmidt B, Kaltschmidt C, Nair D, Choquet D, Sibarita J-B, Heilemann M. TNF-α Influences the Lateral Dynamics of TNF Receptor I in Living Cells. Biochim Biophys Acta Mol Cell Res. 2012;1823:1984–1989. doi: 10.1016/j.bbamcr.2012.06.026. [DOI] [PubMed] [Google Scholar]
- 316.Rossier O, Octeau V, Sibarita JB, Leduc C, Tessier B, Nair D, Gatterdam V, Destaing O, Albiges-Rizo C, Tampé R, et al. Integrins β 1 and β 3 Exhibit Distinct Dynamic Nanoscale Organizations Inside Focal Adhesions. Nat Cell Biol. 2012;14:1057–1067. doi: 10.1038/ncb2588. [DOI] [PubMed] [Google Scholar]
- 317.Sergé A, Bertaux N, Rigneault H, Marguet D. Dynamic Multiple-Target Tracing to Probe Spatiotemporal Cartography of Cell Membranes. Nat Methods. 2008;5:687–694. doi: 10.1038/nmeth.1233. [DOI] [PubMed] [Google Scholar]
- 318.Izeddin I, Specht CG, Lelek M, Darzacq X, Triller A, Zimmer C, Dahan M. Super-Resolution Dynamic Imaging of Dendritic Spines Using a Low-Affinity Photoconvertible Actin Probe. PLoS One. 2011;6:e15611. doi: 10.1371/journal.pone.0015611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 319.Bálint Š, Vilanova I, Álvarez Á, Lakadamyali M. Correlative Live-Cell and Superresolution Microscopy Reveals Cargo Transport Dynamics at Microtubule Intersections. Proc Natl Acad Sci U S A. 2013;110:3375–3380. doi: 10.1073/pnas.1219206110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 320.Genovesio A, Liedl T, Emiliani V, Parak W, Coppey- Moisan M, Olivo-Marin J. Multiple Particle Tracking in 3-D+T Microscopy: Method and Application to the Tracking of Endocytosed Quantum Dots. IEEE Trans Image Process. 2006;15:1062–1070. doi: 10.1109/tip.2006.872323. [DOI] [PubMed] [Google Scholar]
- 321.Fox EB, Sudderth EB, Willsky AS. Hierarchical Dirichlet Processes for Tracking Maneuvering Targets. 10th International Conference on Information Fusion. 2007 [Google Scholar]
- 322.Izeddin I, Rácamier V, Bosanac L, Cissé II, Boudarene L, Dugast-Darzacq C, Proux F, Bénichou O, Voituriez R, Bensaude O, et al. Single-Molecule Tracking in Live Cells Reveals Distinct Target-Search Strategies of Transcription Factors in the Nucleus. eLife. 2014;3:e02230. doi: 10.7554/eLife.02230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 323.Reid D. An Algorithm for Tracking Multiple Targets. IEEE Trans Autom Control. 1979;24:843–854. [Google Scholar]
- 324.Loerke D, Mettlen M, Yarar D, Jaqaman K, Jaqaman H, Danuser G, Schmid SL. Cargo and Dynamin Regulate Clathrin- Coated Pit Maturation. PLoS Biol. 2009;7:e1000057. doi: 10.1371/journal.pbio.1000057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 325.Matov A, Applegate K, Kumar P, Thoma C, Krek W, Danuser G, Wittmann T. Analysis of Microtubule Dynamic Instability Using a Plus-End Growth Marker. Nat Methods. 2010;7:761–768. doi: 10.1038/nmeth.1493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 326.Firestone AJ, Weinger JS, Maldonado M, Barlan K, Langston LD, O’Donnell M, Gelfand VI, Kapoor TM, Chen JK. Small-Molecule Inhibitors of the AAA+ ATPase Motor Cytoplasmic Dynein. Nature. 2012;484:125–129. doi: 10.1038/nature10936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 327.Pollard TD. No Question About Exciting Questions in Cell Biology. PLoS Biol. 2013;11 doi: 10.1371/journal.pbio.1001734. e100173410.1371/journal.pbio.1001734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 328.Dill KA, MacCallum JL. The Protein-Folding Problem, 50 Years On. Science. 2012;338:1042–1046. doi: 10.1126/science.1219021. [DOI] [PubMed] [Google Scholar]
- 329.Shechtman E, Caspi Y, Irani M. Space-Time Super- Resolution. IEEE Trans Pattern Anal Mach Intell. 2005;27:531–545. doi: 10.1109/TPAMI.2005.85. [DOI] [PubMed] [Google Scholar]
- 330.Agrawal A, Gupta M, Veeraraghavan A, Narasimhan S. Optimal Coded Sampling for Temporal Super-Resolution. IEEE Conference on Computer Vision and Pattern Recognition (CVPR) IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2010:599–606. doi: 10.1109/CVPR.2010.5540161. [DOI] [Google Scholar]
- 331.Borman S, Stevenson R. Simultaneous Multi-Frame MAP Super-Resolution Video Enhancement Using Spatio-Temporal Priors. 1999 International Conference on Image Processing. 6th International Conference on Image Processing (ICIP’99) 1999;3:469–473. doi: 10.1109/ICIP.1999.817158. [DOI] [Google Scholar]
- 332.Mudenagudi U, Banerjee S, Kalra PK. Space-Time Super- Resolution Using Graph-Cut Optimization. IEEE Trans Pattern Anal Mach Intell. 2011;33:995–1008. doi: 10.1109/TPAMI.2010.167. [DOI] [PubMed] [Google Scholar]
- 333.Beheiry ME, Dahan M, Masson J-B. InferenceMAP: Mapping of Single-Molecule Dynamics With Bayesian Inference. Nat Methods. 2015;12:594–595. doi: 10.1038/nmeth.3441. [DOI] [PubMed] [Google Scholar]
- 334.Qian H, Sheetz M, Elson E. Single Particle Tracking. Analysis of Diffusion and Flow in Two-Dimensional Systems. Biophys J. 1991;60:910–921. doi: 10.1016/S0006-3495(91)82125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 335.Einstein A. On the Movement of Small Particles Suspended in a Stationary Liquid Demanded by the Molecular-Kinetic Theory of Heat. Ann Phys (Berlin, Ger) 1905;322:549–560. [Google Scholar]
- 336.Langevin P. Sur la Théorie du Mouvement Brownien. C R Acad Sci Paris. 1908;146:530–533. [Google Scholar]
- 337.Pressé S. A Data-Driven Alternative to the Fractional Fokker- Planck Equation. J Stat Mech : Theory Exp. 2015;2015:P07009. [Google Scholar]
- 338.Metzler R, Jeon J, Cherstvy A, Barkai E. Anomalous Diffusion Models and Their Properties: Non-Stationarity, Non-Ergodicity and Ageing at the Centenary of Single Particle Tracking. Phys Chem Chem Phys. 2014;16:24128–24164. doi: 10.1039/c4cp03465a. [DOI] [PubMed] [Google Scholar]
- 339.Fusco D, Accornero N, Lavoie B, Shenoy S, Blanchard J, Singer R, Bertrand E. Single mRNA Molecules Demonstrate Probabilistic Movement in Living Mammalian Cells. Curr Biol. 2003;13:161–167. doi: 10.1016/s0960-9822(02)01436-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 340.Montiel D, Cang H, Yang H. Quantitative Characterization of Changes in Dynamical Behavior for Single-Particle Tracking Studies. J Phys Chem B. 2006;110:19763–19770. doi: 10.1021/jp062024j. [DOI] [PubMed] [Google Scholar]
- 341.Weigel A, Tamkun M, Krapf D. Quantifying the Dynamic Interactions Between a Clathrin-Coated Pit and Cargo Molecules. Proc Natl Acad Sci U S A. 2013;110:E4591–4600. doi: 10.1073/pnas.1315202110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 342.Ritchie K, Shan X, Kondo J, Iwasawa K, Fujiwara T, Kusumi A. Detection of Non-Brownian Diffusion in the Cell Membrane in Single Molecule Tracking. Biophys J. 2005;88:2266–2277. doi: 10.1529/biophysj.104.054106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 343.Manley S, Gillette J, Patterson G, Shroff H, Hess H, Betzig E, Lippincott-Schwartz J. High-Density Mapping of Single- Molecule Trajectories With Photoactivated Localization Microscopy. Nat Methods. 2008;5:155–157. doi: 10.1038/nmeth.1176. [DOI] [PubMed] [Google Scholar]
- 344.Calderon C. Correcting for Bias of Molecular Confinement Parameters Induced by Small-Time-Series Sample Sizes in Single- Molecule Trajectories Containing Measurement Noise. Phys Rev E. 2013;88:012707. doi: 10.1103/PhysRevE.88.012707. [DOI] [PubMed] [Google Scholar]
- 345.Anderson B, Moore J. Optimal Filtering. Prentice-Hall; Englewood Cliffs, NJ: 1979. [Google Scholar]
- 346.Jaqaman K, Dorn J, Jelson G, Tytell J, Sorger P, Danuser G. Comparative Autoregressive Moving Average Analysis of Kinetochore Microtubule Dynamics in Yeast. Biophys J. 2006;91:2312–2325. doi: 10.1529/biophysj.106.080333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 347.Wu P-H, Agarwal A, Hess H, Khargonekar PP, Tseng Y. Analysis of Video-Based Microscopic Particle Trajectories Using Kalman Filtering. Biophys J. 2010;98:2822–30. doi: 10.1016/j.bpj.2010.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 348.Bishop G, Welch G, Allen BD. Tracking: Beyond 15 minutes of Thought. SIGGRAPH Course Pack. 2001;11 [Google Scholar]
- 349.Brown RG, Hwang PY. Introduction to Random Signals and Applied Kalman Filtering: With MATLAB Exercises and Solutions. Vol. 1 Wiley; New York: 1997. [Google Scholar]
- 350.Beal M, Ghahramani Z, Rasmussen C. The Infinite Hidden Markov Model. Advances in Neural Information Processing Systems. 2001 [Google Scholar]
- 351.Fox E, Sudderth E, Jordan M, Willsky A. An HDP-HMM for Systems With State Persistence. Proceedings of the 25th International Conference on Machine Learning. 2008:312–319. doi: 10.1145/1390156.1390196. [DOI] [Google Scholar]
- 352.Van Gael J, Saatci Y, Teh YW, Ghahramani Z. Beam Sampling for the Infinite Hidden Markov Model. Proceedings of the 25th International Conference on Machine Learning. 2008:1088–1095. [Google Scholar]
- 353.Hoze N, Holcman D. Residence Times of Receptors in Dendritic Spines Analyzed by Simulations in Empirical Domains. Biophys J. 2014;107:3008–3017. doi: 10.1016/j.bpj.2014.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 354.Rosenbloom AB, Lee S-H, To M, Lee A, Shin JY, Bustamante C. Optimized Two-Color Super Resolution Imaging of Drp1 During Mitochondrial Fission With a Slow-Switching Dronpa Variant. Proc Natl Acad Sci U S A. 2014;111:13093–13098. doi: 10.1073/pnas.1320044111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 355.Löschberger A, van de Linde S, Dabauvalle M-C, Rieger B, Heilemann M, Krohne G, Sauer M. Super-Resolution Imaging Visualizes the Eightfold Symmetry of gp210 Proteins Around the Nuclear Pore Complex and Resolves the Central Channel With Nanometer Resolution. J Cell Sci. 2012;125:570–575. doi: 10.1242/jcs.098822. [DOI] [PubMed] [Google Scholar]
- 356.Szymborska A, de Marco A, Daigle N, Cordes VC, Briggs JA, Ellenberg J. Nuclear Pore Scaffold Structure Analyzed by Super-Resolution Microscopy and Particle Averaging. Science. 2013;341:655–658. doi: 10.1126/science.1240672. [DOI] [PubMed] [Google Scholar]
- 357.Bartsch TF, Kochanczyk MD, Lissek EN, Lange JR, Florin EL. Nanoscopic Imaging of Thick Heterogeneous Soft-Matter Structures in Aqueous Solution. Nat Commun. 2016;7 doi: 10.1038/ncomms12729. 1272910.1038/ncomms12729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 358.van de Linde S, Wolter S, Heilemann M, Sauer M. The Effect of Photoswitching Kinetics and Labeling Densities on Super- Resolution Fluorescence Imaging. J Biotechnol. 2010;149:260–266. doi: 10.1016/j.jbiotec.2010.02.010. [DOI] [PubMed] [Google Scholar]
- 359.Ha T, Tinnefeld P. Photophysics of Fluorescence Probes for Single Molecule Biophysics and Super-Resolution Imaging. Annu Rev Phys Chem. 2012;63:595–617. doi: 10.1146/annurev-physchem-032210-103340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 360.Masson J, Dionne P, Salvatico C, Renner M, Specht C, Triller A, Dahan M. Mapping the Energy and Diffusion Landscapes of Membrane Proteins at the Cell Surface Using High-Density Single- Molecule Imaging and Bayesian Inference: Application to the Multiscale Dynamics of Glycine Receptors in the Neuronal Membrane. Biophys J. 2014;106:74–83. doi: 10.1016/j.bpj.2013.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]


