Skip to main content
PMC home page
NIST Author Manuscripts logoLink to NIST Author Manuscripts
. Author manuscript; available in PMC: 2018 Jan 25.
Published in final edited form as: ACS Appl Mater Interfaces. 2017 Jan 9;9(3):2642–2649. doi: 10.1021/acsami.6b13620

Spatially Resolved Ferroelectric Domain-Switching-Controlled Magnetism in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 Multiferroic Heterostructure

Peisen Li †,‡,§, Yonggang Zhao †,‡, Sen Zhang †,‡, Aitian Chen †,‡, Dalai Li ||, Jing Ma ⊥, Yan Liu †,‡, Daniel T Pierce #, John Unguris #, Hong-Guang Piao ∇, Huiyun Zhang †, Meihong Zhu †, Xiaozhong Zhang ∇, Xiufeng Han ||, Mengchun Pan §, Ce-Wen Nan ⊥
PMCID: PMC5488254  NIHMSID: NIHMS856000  PMID: 28025891

Abstract

Intrinsic spatial inhomogeneity or phase separation in cuprates, manganites, etc., related to electronic and/or magnetic properties, has attracted much attention due to its significance in fundamental physics and applications. Here we use scanning Kerr microscopy and scanning electron microscopy with polarization analysis with in situ electric fields to reveal the existence of intrinsic spatial inhomogeneity of the magnetic response to an electric field on a mesoscale with the coexistence of looplike (nonvolatile) and butterfly-like (volatile) behaviors in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 ferromagnetic/ferroelectric (FM/FE) multiferroic heterostructures. Both the experimental results and micromagnetic simulations suggest that these two behaviors come from the 109° and the 71°/180° FE domain switching, respectively, which have a spatial distribution. This FE domain-switching-controlled magnetism is significant for understanding the nature of FM/FE coupling on the mesoscale and provides a path for designing magnetoelectric devices through domain engineering.

Keywords: electric field control of magnetism, ferroelectric domain switching, spatially resolved, scanning Kerr microscopy, SEMPA

Graphical Abstract

graphic file with name nihms856000u1.jpg

INTRODUCTION

Intrinsic spatial inhomogeneity or phase separation, which involves spatial inhomogeneity of electronic and/or magnetic properties, has attracted much attention because of its significance in science and technology.1–4 For example, it is believed to be one of the key issues to understand the mechanisms of high-temperature superconductivity in cup-rates4,5 and colossal magnetoresistance in manganites.2,3 Spatially resolved techniques have provided important information for understanding the phenomena of intrinsic spatial inhomogeneity or phase separation,4,6–8 which exists in many systems.1–5 In multiferroic materials, the coupling between ferroelectric (FE) and ferromagnetic (FM) orders also gives rise to intrinsic spatial inhomogeneity due to the complexity of the FE (domain structure and domain switching) that is coupled to the FM. Moreover, multiferroic materials provide an avenue to electric field control of magnetism and have been extensively studied because electric field control of magnetism at room temperature is one of the cornerstones of novel electric writing magnetic memories.9–12

Recently, in artificial FM/FE multiferroic heterostructures, it has been demonstrated that magnetization can be controlled by electric fields via strain-mediated magnetoelectric coupling, 13–17 which is likely to emerge as a niche application in the short term because it can operate well at room temperature.18 Most of the early attempts for electric field control of magnetism in the strain-mediated FM/FE systems are based on the piezoelectric effect. The bipolar electric field control of magnetization exhibits a reversible and symmetric butterfly-like behavior, which can be understood as tuning the magnetic anisotropy via the converse magnetostriction effect19–21 or controlling the saturation magnetization based on octahedral disorder sensitive to the piezostrain of the FE substrate.22 However, this butterfly-like behavior indicates that the magnetization changes were not retained after removal of the applied electric fields, which is disadvantageous for novel electric writing, magnetic reading memories. Clearly, non-volatile electric field control of magnetism is highly desired.

Encouragingly, there have been several reports on the nonvolatile electric field control of macroscopic magnetic properties in FM/FE systems, revealing the key role of FE domains and their switching.13,23–25 For example, Wu et al. demonstrated a permanent magnetization change in Ni/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (011) (Ni/PMN-PT) via a non-180° FE polarization reorientation process.23 Additionally, Zhang et al. reported nonvolatile electric field control of magnetism in the Co40Fe40B20 (CoFeB)/PMN-PT (001) system and demonstrated that it is closely related to 109° FE domain switching.24 Moreover, besides 109° FE domain switching, 71° and 180° FE domain switching was also observed by piezoresponse force microscopy (PFM) and high-resolution X-ray diffraction reciprocal space mapping (XRD-RSM) for the rhombohedral (R) phase.24,26,27 An interesting and fundamental question arises as what are the effects of different FE domain switches on magnetism. The 109° FE domain switching is expected to induce a 90° rotation of the magnetic easy axis, while the 71° and 180° FE domain switching are not expected to change the magnetic easy axis.24 Therefore, it is likely that there exists an intrinsic spatial inhomogeneity of magnetic response to electric field. The macroscopic magnetic properties, revealed by magnetic measurements without spatial resolution, are composed of contributions induced by the 109°, 71°, and 180° FE domain switches. To clarify this issue, spatially resolved magnetic characterizations on the mesoscale with in situ electric fields are required. To date, there have been only a few reports on the electric field control of magnetism in the FM/FE multiferroic heterostructures with mesoscale spatial resolution.28–35 For example, Lahtinen et al. proved that the magnetic domain configuration is an exact copy of the FE domain structure in a CoFe/BaTiO3 (001) heterostructure by polarization microscopy and the magneto-optic Kerr effect (MOKE).31 Using X-ray magnetic circular dichroism (XMCD)–photoemission electron microscopy (PEEM), Buzzi et al. revealed that the strain-mediated magnetoelectric coupling under unipolar electric fields is highly dependent on the initial states of the FE domains in Ni/PMN-PT (011).33

In this paper, we study electric field control of magnetism in CoFeB/PMN-PT (001) at the mesoscale using spatially resolved techniques including scanning Kerr microscopy (SKM) and scanning electron microscopy with polarization analysis (SEMPA) with in situ electric fields. Two spatially resolved techniques were chosen because the SKM could reveal the magnetic moment information projected only in the detection direction, while SEMPA can measure the in-plane magnetic moment vector and has a much higher spatial resolution. Mesoscale magnetization response to external electric fields (M–E) with looplike (nonvolatile) and butterfly-like (volatile) behaviors were observed in different regions, demonstrating the intrinsic spatial inhomogeneity of magnetic response to the electric field. The regions of looplike response showed an in-plane 90° rotation of the local magnetic moments, while in the regions of butterfly-like response the local magnetic moments remain unchanged. Micromagnetic simulations are consistent with the looplike and butterfly-like M–E behavior resulting from the spatial distribution in the PMN-PT of regions of 109° FE domain switching and regions of 71° or 180° domain switching, respectively.

RESULTS AND DISCUSSION

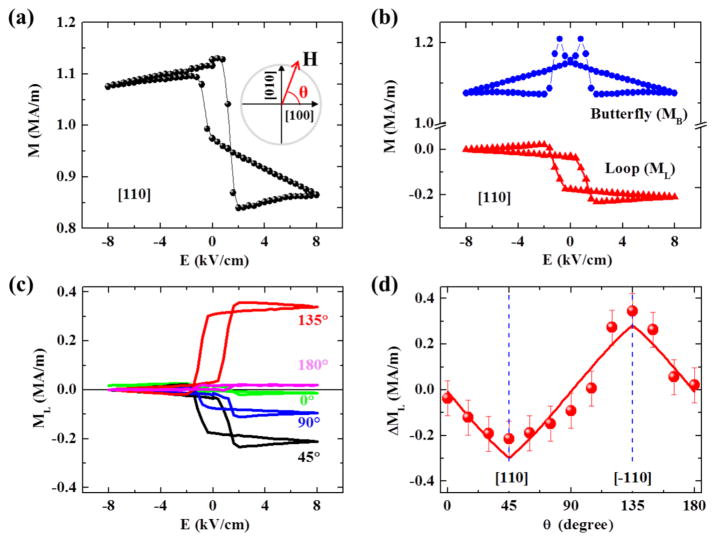
Heterostructures were prepared by sputtering amorphous CoFeB film on PMN-PT (001) substrates with the edges along the [100] and [010] directions of the PMN-PT (Figure S1a). We first measured the macroscopic magnetic properties with in situ electric fields applied across the FM/FE structure after magnetizing the sample by a 100 mT field along the measurement direction and then removing the magnetic field. Figure 1a shows the change of magnetization along the [110] direction with electric field (M–E curve), with a 1 mT external magnetic field applied along [110] to define the measurement direction. We observe a looplike behavior with a reversible and sharp magnetization switching when the electric field exceeds the coercive field (Ec) of PMN-PT (about 1.5 kV cm−1 at room temperature, as shown in Figure S2). It is noteworthy that the magnetization decreases slowly after the electric field exceeds Ec, independent of the electric field polarity, which indicates the contribution of the butterfly-like behavior. Compared with the change of magnetization along the [110] direction with electric field, the result for the [1̄10] direction displays a complementary curve, as shown in Figure S3a. Similar to the separation of the bipolar looplike nonvolatile strain and butterfly-like volatile strain from the strain versus electric field curves,27 the butterfly-like and the looplike M–E curves in Figure 1b were separated based on the different symmetries of the two curves (Supporting Information S3). The coexistence of two types of M–E curves here is different from the previously reported coexistence of loop and butterfly M–E behaviors in the Pr0.5Ca0.5MnO3/Pb(Mg1/3Nb2/3)0.67Ti0.33O3 system, which originates from the competition between charge-mediated interactions (responsible for the loop M–E behavior) and strain-mediated interactions (responsible for the butterfly M–E behavior).36 In our sample, the charge-mediated interaction is negligible because the 20 nm thickness of the FM is much larger than the effective length of the FE field effect, which is only 1–2 unit cells near the interface for metals.37

Figure 1.

Figure 1

Open in a new tab

Macroscopic magnetization controlled by electric field. (a) M–E curves measured at 300 K along the [110] direction with a 1 mT external magnetic field. A simplified version of the crystal axes, magnetic field (H), and the angle θ is shown in the inset. (b) The looplike (ML, red triangles) and butterfly-like (MB, blue circles) electric-field-controlled magnetization (M–E) hysteresis curves obtained from panel a. (c) Angle dependence of ML–E curves obtained with steps of 45° at 300 K. (d) Angle dependence of the nonvolatile manipulation magnitude ΔML and the fitting curve (red line, Supporting Information S7). The error bars in panel d are the standard error derived from multiple measurements, which includes error in the sample alignment for each measurement. Error bars in panels a–c are smaller than the point markers.

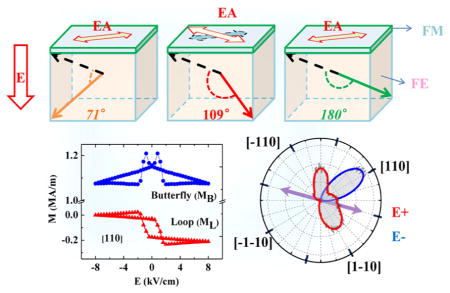
To understand the mechanism of electric field control of magnetism in CoFeB/PMN-PT (001), we also measured the change of the magnetization along different directions with electric field. Figure 1c shows the evolution of looplike ML–E curves at various angles (θ) increasing from 0° to 180° in 45° steps. Here, θ is the angle between the 1 mT magnetic field defining the measurement direction and the [100] direction (Figure S1a). Apparently, the looplike nonvolatile bipolar electric field control of magnetism is anisotropic and strongly depends on the measurement direction. For θ = 45°, the positive electric fields tend to decrease the magnetization, while the negative electric fields tend to increase it, which is opposite to the θ = 135° case. To gain further insight into the mechanism underlying the angular anisotropy of the looplike ML–E curves, we plot the angular dependence of magnetization difference ΔML (ML(+8 kV cm−1) − ML(−8 kVcm−1)) in Figure 1d. The electric-field-induced manipulation is maximum in the [110] and [1̄10] directions, while it is close to zero in the [100] and [010] directions. This is further demonstrated by the electric field control of magnetic hysteresis (M–H) curves along the different directions (Figure S4), which shows that the M–H hysteresis curves in the [110] direction under ±4 kV cm−1 exhibit a change that is opposite to that in the [1̄10] direction, while there is no obvious change of M–H in the [100] direction under ±4 kVcm−1. Furthermore, as shown in Figure 1d, the modulation changes monotonically between the [110] and [1̄10] directions. The anisotropy of the looplike ML–E curves, Figure 1c,d, is consistent with an in-plane 90° rotation of magnetic moment and will be discussed later.24

The fact that the change of magnetization with electric field can be separated into the butterfly-like and looplike M–E curves suggests two distinct contributions to the electric field control of magnetism in the CoFeB/PMN-PT (001). One possible scenario is that the different contributions from 109°, 71°, and 180° switching of FE domains lead to the intrinsic spatial inhomogeneity of magnetic response to the electric field. To clarify this issue, we made spatially resolved measurements of electric-field-controlled magnetism using SKM and SEMPA with in situ electric fields.

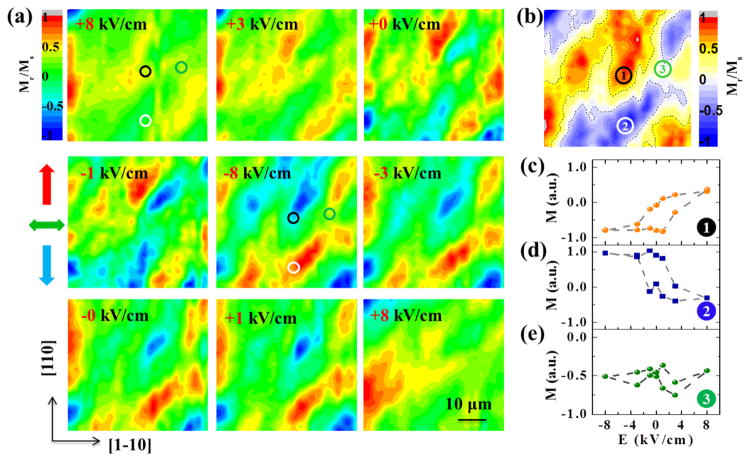
Before the SKM measurement, shown schematically in Figure S1b, the sample was magnetized by a 100 mT magnetic field along the [110] direction, and then the magnetic field was removed. Figure 2a shows the mapping results of Mr/Ms (remanent magnetization/saturation magnetization) along the [110] direction under different in situ electric fields. Red, blue, and green colors in the Mr/Ms images represent three kinds of magnetic moment orientations in our sample, i.e., parallel, antiparallel, and perpendicular to the [110] direction, respectively, as indicated by the colored arrows on the left of Figure 2a. In order to get the magnetic response to electric field for different regions, we plot the difference between the images at +8 kV cm−1 and −8 kVcm−1 obtained from Figure 2a and show the result in Figure 2b, which reveals three typical kinds of changes with electric field, displayed in red, light yellow, and blue. To study the typical magnetic responses to electric field, we focused on the three representative regions marked by 1, 2, and 3 in Figure 2b. For region 1, the magnetic moment is along the [11̄0]/[1̄10] direction at +8 kV cm−1 and does not change much as the electric field decreases to −1 kVcm−1, but the magnetic moment rotates to the [ 11¯0] direction at −8 kVcm−1 with the color changing from about green to blue as shown in Figure 2a. When changing the electric field from −8 kVcm−1 to +8 kV cm−1, the magnetic moment is retained until the electric field is larger than +1 kV cm−1, suggesting that the local magnetic moment in region 1 displays a nonvolatile electrical modulation of magnetization. In contrast, region 2 shows a color change from green to red, indicating that the magnetic moment rotates from the [11̄0]/[1̄10] to the [110] direction antiparallel to that of region 1. For region 3, the direction of the magnetic moment does not change with electric field. The local magnetic moment responses to the electric field in the three regions of Figure 2a are shown in Figure 2c–e. Clearly, the M–E behaviors of regions 1 and 2 are similar and show looplike electric-field-controlled magnetism. It is notable that significant switching of magnetic moment occurs only when the electric field exceeds the coercive field (Ec) of PMN-PT. For region 3 in Figure 2e, the magnetic moment changes slightly and the electric-field-controlled magnetism is reversible and volatile, similar to a butterfly-like M–E behavior. The effect in region 3 is weak compared to that in regions 1 and 2. This is consistent with the result of XRD-RSM that the volatile strain (0.1%) is much smaller than the nonvolatile strain (0.29%) (Figure S3j,k of ref 24). We also used an AC-mode MOKE technique to measure the local M–E in different regions; the results show looplike and butterfly-like behaviors (Supporting Information S5). In addition, the changes of the local magnetic anisotropy with electric field in the three regions were investigated by rotation magneto-optic Kerr effect (Rot-MOKE) magnetometry. 38 As shown in Figure S6, the magnetic anisotropies of both region 1 and region 2 are different at ±8 kVcm−1 while they are roughly the same at ±8 kVcm−1 for region 3. Specifically, compared with positive electric field, for negative electric field the anisotropy is larger and the magnetic easy axis rotates toward the [110] direction in regions 1 and 2. This result further supports the suggestion that there are two types of electric-field-controlled magnetism in different mesoscale regions, indicating spatial inhomogeneity of magnetic response to electric field.

Figure 2.

Figure 2

Open in a new tab

Electric field control of magnetism with SKM. (a) Scanning MOKE maps of Mr/Ms in a 50 × 50 μm2 area under different static electric fields. The in-plane longitudinal MOKE was aligned to the [110] direction of PMN-PT substrates. The colored arrows at the left represent the different magnetic moment orientations. (b) The difference of SKM images under ±8 kVcm−1 (M+8–M–8) deduced from panel a. The dotted lines are a guide for the eye to distinguish three types of contrasts. (c–e) The local static electric-field-controlled magnetization (M–E) curves for the different regions numbered in panel b. The uncertainty in the measurement is smaller than the point size.

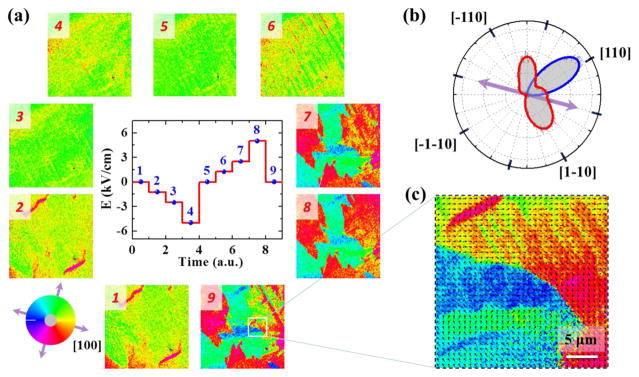
SEMPA can measure the in-plane magnetic moment vector at the surface of a magnetic thin film,39 and it has been demonstrated that SEMPA with in situ electric fields is helpful for elucidating the FM domain rotation process.40 In order to get more insight into the electric-field-controlled magnetism in different mesoscale regions in our samples, we used SEMPA to measure the variation of the in-plane magnetic moment vector with electric field. Figure 3a shows the SEMPA images of a 125 × 125 μm2 area of CoFeB/PMN-PT under different electric fields, with the magnetic moment directions indicated by the color wheel. SEMPA images show uniform green color (images 3–6) upon applying negative electric fields and sweeping through zero to +1 kV cm−1, suggesting a nonvolatile, single magnetic domain structure with the magnetic moment along the [110] direction. In contrast, multidomain structure appears when electric field exceeds the coercive field of PMN-PT, as shown by the multicolored states in images 7, 8, and 9. From the pixel-by-pixel information on the direction of the magnetic moments in an image, an angular distribution of the magnetization can be created for the entire image. The angular distribution of the magnetization from image 5 in Figure 3a (at zero field after negative poling) is shown by the blue curve in Figure 3b. Similarly, the angular distribution from image 9 (at zero field after positive poling) is shown by the red curve. After negative poling, the magnetic moments are predominantly along the [110] direction. After positive poling, much of the magnetization has switched by 90° to the [11̄0] direction. There is, however, a peak in the angular distribution after positive poling between the [110] and the [1̄10] directions whose origin is less clear. The peak could originate from averaging moments in the [110] and the [1̄10] directions on the microscale below the spatial resolution of the large images in Figure 3a, or alternatively the peak could be due to a competing anisotropy in the CoFeB film. A higher magnification image of a region of image 9 of Figure 3a is shown in Figure 3c where wide variations in the magnetization directions are apparent. In fact, at small length scales, it is evident that there are variations beyond a simple 90° rotation of the magnetization. This is not unexpected because there is always a competition between the intralayer exchange in the FM film which acts to maintain the magnetization direction and the magnetoelastic coupling which acts to change it. Still, the major change in the magnetization produced by electric fields is a 90° rotation, as shown by the 90° separation of the main peaks in Figure 3b.

Figure 3.

Figure 3

Open in a new tab

Electric field control of magnetism with SEMPA. (a) Nine SEMPA images of the CoFeB magnetization under electric fields. The measurement sequence is shown in the central inset. The magnetic moment direction is defined by the color wheel and crystal directions as shown in the left inset. (b) The angular distribution of the magnetization in image 5 of panel a after negative poling is depicted by the blue curve. The angular distribution of the magnetization in image 9 after positive poling is depicted by the red curve. (c) A higher-resolution SEMPA image of a selected area of image 9 after positive electric field poling. The arrows along with the color wheel show the local magnetization direction.

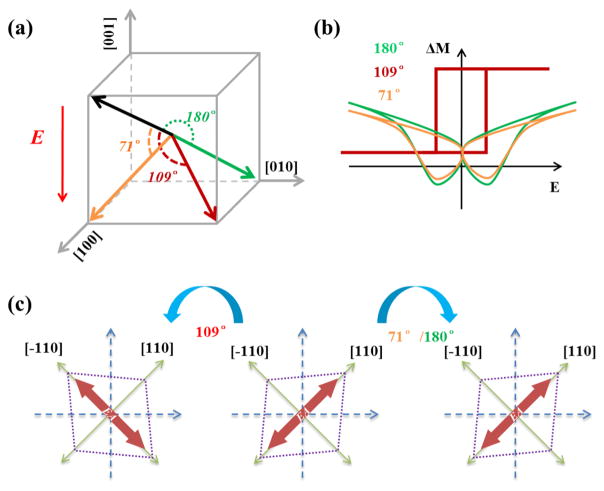
The observation of two different types of M–E behavior and anisotropy suggests that there are two different kinds of strain response induced by electric fields in our system. In addition, magnetization switching of the looplike M–E curves occurs around the coercive field of PMN-PT, suggesting FE domain switching plays a key role. The PMN-PT used in this work is near the region of the morphotropic phase boundary. The main structure is the rhombohedral (R) phase;41 therefore, the spontaneous FE polarization is along one of the 〈111〉 axes and there are eight equivalent polarization directions. Taking a FE domain with an initial polarization along the [111] direction as an example, the polarization can be switched by 71°, 109°, and 180° domain switching processes,26 as shown in Figure 4a. The R phase shows a rhombic distortion with a long diagonal along a 〈110〉 direction parallel to the component of the FE polarization in the (001) surface plane of the PMN-PT crystal, providing a local anisotropic strain in the long diagonal direction. Similar to the CoFe/BaTiO3 system,31 the local magnetic anisotropy of the CoFeB is influenced by the underlying FE domain through the strain-mediated magnetoelectric coupling. Because of the positive magnetostriction coefficient of CoFeB thin films and the absence of magnetocrystalline anisotropy in CoFeB,42 the magnetic moments prefer to align along the in-plane component of the FE polarization, i.e., a 〈110〉 direction, as demonstrated by the SKM and SEMPA results (see Figures 2 and 3). Application of an external electric field reorganizes the FE domain structure of PMN-PT through domain-switching processes, thereby modulating the magnetization via the strain effect with looplike and butterfly-like M–E behaviors, as shown by experimental data in Figure 1b and schematically in Figure 4b. Figure 4c shows the two types of strain coupling induced by the FE domain switching of PMN-PT (001). (i) For the 109° domain switching, the elongated diagonal of rhombic distortion changes from the [110] axis to the [1̄10] axis thereby changing the strain and rotating the magnetic easy axis from the [110] to the [1̄10] direction. In this case, the magnetic anisotropy and consequently the in-plane magnetization of the CoFeB film can be controlled by electric fields resulting in the looplike M–E behavior. (ii) For the 71°/180° domain switching, although the direction of elongated diagonal does not change, the domain switching produces a change of strain with a butterfly-like strain versus electric field curve. Therefore, the electric-field-controlled magnetism shows the butterfly-like M–E behavior. Thus, the two different strain couplings originating from the 109° and 71°/180° domain switching cause the looplike and butterfly-like M–E behaviors, respectively, i.e., the CoFeB film above the 109° domain switching regions shows the looplike electric-field-controlled magnetism while the M–E behavior of the CoFeB film above the 71°/180° domain switching regions is butterfly-like (schematically shown in Figure 4b). In this picture, the spatial distribution of electric-field-controlled magnetism originates from the different type of FE domain switching in different regions.

Figure 4.

Figure 4

Open in a new tab

Schematic of the FE-domain-switching-controlled magnetism. Schematic of (a) three FE domain switching processes of PMN-PT and (b) picture of the related M–E curves. (c) The top view looking down [001] of distortions and related in-plane magnetic easy axes (EA, red arrows) for the different FE domain switching processes, starting from a FE polarization along the [111] direction.

For the looplike M–E behavior, it has been demonstrated that magnetic moments tend to stay along the [110] direction at −8 kVcm−1 because most of the FE domains align in the [110] direction to reduce the ferroelastic energy after −8 kV cm−1 poling.24,27 The angle dependence of the nonvolatile magnetization change by electric fields (Figure 1d) could be explained by the 90° rotation of magnetic moments. In this case, the manipulation magnitude, ΔML, can be expressed as ΔMMax(|sin(θ − 45°)| − |cos(θ − 45°)|), where ΔMMax is the maximum of ΔML and is about 0.29 MA m−1 for this sample. It can be seen from Figure 1d that the equation fits the experimental data well. Details of the above analysis are described in Supporting Information S7.

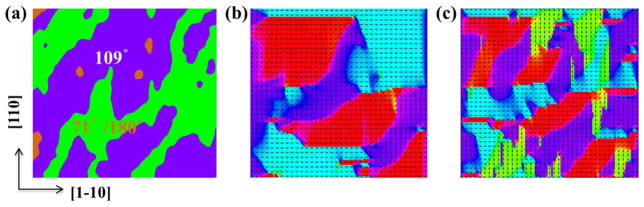
We used micromagnetic simulations to model the above picture of magnetization switching.43 The types of FE domain switching can be deduced from the difference of SKM images under positive and negative electric fields (Figure 2b), whereby the 109° domain switching is indicated by the red/blue regions and 71°/180° domain switching by the light yellow region. The deduced FE domain switching is shown in Figure 5a. The initial magnetic moment configuration of the +8 kV cm−1 state is based on Figure 2a. Micromagnetic simulation was carried out to separate the regions with magnetic moments along the [1̄10] from those along the [11̄0] because the SKM result in Figure 2a cannot distinguish regions with magnetic moments along these two directions; the result is shown in Figure 5b. Then we varied the magnetic anisotropy in the simulation, based on the FE domain switching derived from Figure 5a, to model the effect of a −8 kVcm−1 electric field. Figure 5c shows the resulting simulated magnetic moment configuration, indicating that the magnetic moment rotates by 90° in-plane with some small transition regions when responding to the 109° FE domain switching, but there are not many changes in the regions of 71°/180° FE domain switching. This is consistent with a picture in which the looplike M–E behavior is induced by 109° FE domain switching and the butterfly-like M–E behavior is induced by 71°/180° FE domain switching.

Figure 5.

Figure 5

Open in a new tab

Micromagnetic simulation of the FE-domain-switching-controlled magnetism. (a) The map of the FE-domain switching deduced from Figure 2b. (b) Initial state obtained by micromagnetic simulation for the +8 kV cm−1 state to separate the regions with magnetic moments along the [1̄10] from those along the [11̄0] based on Figure 2a. (c) Micromagnetic simulation results after electric field switching to the −8 kVcm−1 state.

CONCLUSION

We have demonstrated the intrinsic spatial inhomogeneity of the magnetic response to an electric field on the mesoscale with the coexistence of looplike (nonvolatile) and butterfly-like (volatile) behaviors in CoFeB/PMN-PT (001) by using SKM and SEMPA with in situ electric fields. Separate regions exhibiting looplike and butterfly-like magnetization response were observed. This intrinsic spatial inhomogeneity of M–E effect is closely related to the rich features of FE domain structures and domain-switching processes of PMN-PT as evidenced by changes at the FE coercive electric field. The experimental results and micromagnetic simulations can be understood in a consistent picture in which the looplike behavior comes from the 109° FE domain switching while the butterfly-like behavior comes from the 71°/180° FE domain switching. This work provides an example of intrinsic spatial inhomogeneity or phase separation in the magnetic response to an electric field in FM/FE heterostructures demonstrating the ubiquitous nature of such intrinsic spatial inhomogeneity or phase separation. Our increased understanding of electric field control of magnetism in FM/FE structures on the mesoscale provides a path for electric field control of magnetism through domain engineering, which is significant for future straintronic device applications based on electric-field-controlled magnetism.

METHODS

Sample Preparation

A 20 nm thick amorphous Co40Fe40B20 (nominal target composition) magnetic film with a 10 nm thick tantalum (Ta) protection layer was directly deposited on a 0.5 mm thick Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (PMN-PT) (001) single-crystal substrate using an ultrahigh vacuum magnetron sputtering system with a base pressure of 1 × 10−6 Pa. The amorphous property of CoFeB and crystalline property of PMN-PT have been studied with XRD and transmission electron microscopy (TEM) in our previous report.44 For the sample measured with SEMPA, the PMN-PT was only 0.2 mm thick so that larger electric fields could be applied. Au layers with a 300 nm thickness were sputtered on both the top and bottom sides of the FM-FE structure as the electrodes for the M–E measurements. For the MOKE and SEMPA measurements, the Au layer was sputtered only on the back side of the FE.

Magnetization Measurements

Electric field control of macroscopic magnetization was measured with in situ electric fields applied across the FM/FE heterostructure after magnetizing the sample by a 100 mT field along the measurement direction and then removing the magnetic field. Measurements of the spatial distribution of electricfield-controlled magnetism were performed on a scanning MOKE system with a diode laser operated at a 660 nm wavelength. We used a 100 mT magnetic field to get an initial magnetic state, and then the magnetic field was removed before the electric-field-dependent SKM mapping.

SEMPA Measurement

We used a modified scanning electron microscopy (SEM) instrument to image the FM domain structure of the CoFeB/PMN-PT sample. The magnetic information comes from the spin polarization of the low-energy secondary electrons. Secondary electrons emitted from a FM domain have a spin polarization proportional to the magnetization in the domain. Thus, an SEM instrument modified to measure the polarization of the secondary electrons provides a measurement of the magnetization in the region probed by the incident electron beam. This high-resolution magnetic imaging technique, called scanning electron microscopy with polarization analysis, was used to image the magnetization in the CoFeB film.39 A typical SEMPA measurement consists of a simultaneously measured intensity image showing the topography and polarization images along two axes. The third component of polarization can be measured with a second spin analyzer. The spin polarization measurements can be combined into a vector image in which the direction is indicated by the color.

Micromagnetic Simulation

Micromagnetic simulations were carried out using the object-oriented micromagnetic framework (OOMMF) software.43 To simulate the FM domain state at −8 kV cm−1, the initial FM domain state and initial local magnetoelastic anisotropies obtained from the SKM image at +8 kV cm−1 in Figure 2a were used as input. The effect of the electric field was introduced by changing the directions of the local magnetoelastic anisotropies during the FE domain-switching process (Figure 5a). The local magnetoelastic anisotropy field (μ0Hσ = 15 mT) was obtained through Hσ = 3λ·Y·S/Ms, where S is the local strain induced by the FE rhombic distortion. The value of S is 0.2% for PMN-PT as deduced from the inplane distortion difference for the [110] and [11̄0] direction shown in Figure 3f of ref 24. The Young’s modulus, Y, and magnetostriction coefficient, λ, are 160 GPa and 2 × 10−5 for CoFeB, respectively;42 the saturation magnetization, Ms, is 1.2 MA m−1; and the uniform exchange constant, A, is 2.8 × 10−11 J m−1.45

Supplementary Material

Supp1

Acknowledgments

This work was supported by the 973 project of the Ministry of Science and Technology of China (Grant 2015CB921402), National Science Foundation of China (Grants 51572150, 11134007, 11234007, 51471093, 11604384, 11474183, 11304385, and 51332001), and Research Project of National University of Defense Technology (Grant JC15-03-02).

References

  • 1.Ortix C, Lorenzana J, Di Castro C. Coarse Grained Models in Coulomb Frustrated Phase Separation. J Phys: Condens Matter. 2008;20:434229. doi: 10.1103/PhysRevLett.100.246402. [DOI] [PubMed] [Google Scholar]
  • 2.Moreo A, Yunoki S, Dagotto E. Phase Separation Scenario for Manganese Oxides and Related Materials. Science. 1999;283:2034. doi: 10.1126/science.283.5410.2034. [DOI] [PubMed] [Google Scholar]
  • 3.Dagotto E. Complexity in Strongly Correlated Electronic Systems. Science. 2005;309:257. doi: 10.1126/science.1107559. [DOI] [PubMed] [Google Scholar]
  • 4.Campi G, Bianconi A, Poccia N, Bianconi G, Barba L, Arrighetti G, Innocenti D, Karpinski J, Zhigadlo ND, Kazakov SM, Burghammer M, Zimmermann M, Sprung M, Ricci A. Inhomogeneity of Charge-Density-Wave Order and Quenched Disorder in a High-Tc Superconductor. Nature. 2015;525:359. doi: 10.1038/nature14987. [DOI] [PubMed] [Google Scholar]
  • 5.Bianconi A, Poccia N. Superstripes and Complexity in High-Temperature Superconductors. J Supercond Novel Magn. 2012;25:1403. [Google Scholar]
  • 6.Fäth M, Freisem S, Menovsky AA, Tomioka Y, Aarts J, Mydosh JA. Spatially Inhomogeneous Metal-Insulator Transition in Doped Manganites. Science. 1999;285:1540. doi: 10.1126/science.285.5433.1540. [DOI] [PubMed] [Google Scholar]
  • 7.Murakami Y, Kasai JJ, Kim H, Mamishin S, Shindo D, Mori S, Tonomura A. Ferromagnetic Domain Nucleation and Growth in Colossal Magnetoresistive Manganite. Nat Nanotechnol. 2010;5:37. doi: 10.1038/nnano.2009.342. [DOI] [PubMed] [Google Scholar]
  • 8.Renner C, Aeppli G, Kim BG, Soh YA, Cheong SW. Atomic-Scale Images of Charge Ordering in a Mixed-Valence Manganite. Nature. 2002;416:518. doi: 10.1038/416518a. [DOI] [PubMed] [Google Scholar]
  • 9.Spaldin NA, Fiebig M. The Renaissance of Magnetoelectric Multiferroics. Science. 2005;309:391. doi: 10.1126/science.1113357. [DOI] [PubMed] [Google Scholar]
  • 10.Bibes M, Barthelemy A. Multiferroics: Towards a Magnetoelectric Memory. Nat Mater. 2008;7:425. doi: 10.1038/nmat2189. [DOI] [PubMed] [Google Scholar]
  • 11.Hu JM, Li Z, Chen LQ, Nan CW. High-Density Magnetoresistive Random Access Memory Operating at Ultralow Voltage at Room Temperature. Nat Commun. 2011;2:553. doi: 10.1038/ncomms1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Li P, Chen A, Li D, Zhao Y, Zhang S, Yang L, Liu Y, Zhu M, Zhang H, Han X. Electric Field Manipulation of Magnetization Rotation and Tunneling Magnetoresistance of Magnetic Tunnel Junctions at Room Temperature. Adv Mater. 2014;26:4320. doi: 10.1002/adma.201400617. [DOI] [PubMed] [Google Scholar]
  • 13.Eerenstein W, Wiora M, Prieto JL, Scott JF, Mathur ND. Giant Sharp and Persistent Converse Magnetoelectric Effects in Multiferroic Epitaxial Heterostructures. Nat Mater. 2007;6:348. doi: 10.1038/nmat1886. [DOI] [PubMed] [Google Scholar]
  • 14.Chen A, Zhao Y. Research Update: Electrical Manipulation of Magnetism through Strain-Mediated Magnetoelectric Coupling in Multiferroic Heterostructures. APL Mater. 2016;4:032303. [Google Scholar]
  • 15.Ma J, Hu JM, Li Z, Nan CW. Recent Progress in Multiferroic Magnetoelectric Composites: from Bulk to Thin Films. Adv Mater. 2011;23:1062. doi: 10.1002/adma.201003636. [DOI] [PubMed] [Google Scholar]
  • 16.Liu M, Zhou Z, Nan T, Howe BM, Brown GJ, Sun NX. Voltage Tuning of Ferromagnetic Resonance with Bistable Magnetization Switching in Energy-Efficient Magnetoelectric Composites. Adv Mater. 2013;25:1435. doi: 10.1002/adma.201203792. [DOI] [PubMed] [Google Scholar]
  • 17.Chen A, Zhao Y, Li P, Zhang X, Peng R, Huang H, Zou L, Zheng X, Zhang S, Miao P, Lu Y, Cai J, Nan CW. Angular Dependence of Exchange Bias and Magnetization Reversal Controlled by Electric-Field-Induced Competing Anisotropies. Adv Mater. 2016;28:363. doi: 10.1002/adma.201503176. [DOI] [PubMed] [Google Scholar]
  • 18.Eerenstein W, Mathur ND, Scott JF. Multiferroic and Magnetoelectric Materials. Nature. 2006;442:759. doi: 10.1038/nature05023. [DOI] [PubMed] [Google Scholar]
  • 19.Yang JJ, Zhao YG, Tian HF, Luo LB, Zhang HY, He YJ, Luo HS. Electric Field Manipulation of Magnetization at Room Temperature in Multiferroic CoFe2O4/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 Heterostructures. Appl Phys Lett. 2009;94:212504. [Google Scholar]
  • 20.Geprags S, Brandlmaier A, Opel M, Gross R, Goennenwein S. Electric Field Controlled Manipulation of the Magnetization in Ni/BaTiO3 Hybrid Structures. Appl Phys Lett. 2010;96:142509. [Google Scholar]
  • 21.Zhang S, Zhao Y, Xiao X, Wu Y, Rizwan S, Yang L, Li P, Wang J, Zhu M, Zhang H, Jin X, Han X. Giant Electrical Modulation of Magnetization in Co40Fe40B20/Pb - (Mg1/3Nb2/3)0.7Ti0.3O3(011) Heterostructure. Sci Rep. 2014;4:3727. doi: 10.1038/srep03727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Thiele C, Dorr K, Bilani O, Rodel J, Schultz L. Influence of Strain on the Magnetization and Magnetoelectric Effect in La0.7A0.3MnO3/PMN-PT (001) (A = Sr, Ca) Phys Rev B: Condens Matter Mater Phys. 2007;75:054408. [Google Scholar]
  • 23.Wu T, Bur A, Zhao P, Mohanchandra KP, Wong K, Wang KL, Lynch CS, Carman AGP. Giant Electric-Field-Induced Reversible and Permanent Magnetization Reorientation on Magnetoelectric. Appl Phys Lett. 2011;98:012504. [Google Scholar]
  • 24.Zhang S, Zhao YG, Li PS, Yang JJ, Rizwan S, Zhang JX, Seidel J, Qu TL, Yang YJ, Luo ZL, He Q, Zou T, Chen QP, Wang JW, Yang LF, Sun Y, Wu YZ, Xiao X, Jin XF, Huang J, Gao C, Han XF, Ramesh R. Electric-Field Control of Nonvolatile Magnetization in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 Structure at Room Temperature. Phys Rev Lett. 2012;108:137203. doi: 10.1103/PhysRevLett.108.137203. [DOI] [PubMed] [Google Scholar]
  • 25.Liu M, Howe BM, Grazulis L, Mahalingam K, Nan T, Sun NX, Brown GJ. Voltage-Impulse-Induced Non-Volatile Ferroelastic Switching of Ferromagnetic Resonance for Reconfigurable Magnetoelectric Microwave Devices. Adv Mater. 2013;25:4886. doi: 10.1002/adma.201301989. [DOI] [PubMed] [Google Scholar]
  • 26.Zhao T, Scholl A, Zavaliche F, Lee K, Barry M, Doran A, Cruz MP, Chu YH, Ederer C, Spaldin NA, Das RR, Kim DM, Baek SH, Eom CB, Ramesh R. Electrical Control of Antiferromagnetic Domains in Multiferroic BiFeO3 Films at Room Temperature. Nat Mater. 2006;5:823. doi: 10.1038/nmat1731. [DOI] [PubMed] [Google Scholar]
  • 27.Yang L, Zhao Y, Zhang S, Li P, Gao Y, Yang Y, Huang H, Miao P, Liu Y, Chen A, Nan CW, Gao C. Bipolar Loop-Like Non-Volatile Strain in the (001)-Oriented Pb(Mg1/3Nb2/3)O3-PbTiO3 Single Crystals. Sci Rep. 2014;4:4591. doi: 10.1038/srep04591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Chung T, Carman GP, Mohanchandra KP. Reversible Magnetic Domain-Wall Motion under an Electric Field in a Magnetoelectric Thin Film. Appl Phys Lett. 2008;92:112509. [Google Scholar]
  • 29.Chung T, Keller S, Carman GP. Electric-Field-Induced Reversible Magnetic Single-Domain Evolution in a Magnetoelectric Thin Film. Appl Phys Lett. 2009;94:132501. [Google Scholar]
  • 30.Brintlinger T, Lim S, Baloch KH, Alexander P, Qi Y, Barry J, Melngailis J, Salamanca-Riba L, Takeuchi I, Cumings J. In Situ Observation of Reversible Nanomagnetic Switching Induced by Electric Fields. Nano Lett. 2010;10:1219. doi: 10.1021/nl9036406. [DOI] [PubMed] [Google Scholar]
  • 31.Lahtinen THE, Tuomi JO, van Dijken S. Pattern Transfer and Electric-Field-Induced Magnetic Domain Formation in Multiferroic Heterostructures. Adv Mater. 2011;23:3187. doi: 10.1002/adma.201100426. [DOI] [PubMed] [Google Scholar]
  • 32.Lahtinen THE, Franke KJA, van Dijken S. Electric-Field Control of Magnetic Domain Wall Motion and Local Magnetization Reversal. Sci Rep. 2012;2:258. doi: 10.1038/srep00258. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Buzzi M, Chopdekar RV, Hockel JL, Bur A, Wu T, Pilet N, Warnicke P, Carman GP, Heyderman LJ, Nolting F. Single Domain Spin Manipulation by Electric Fields in Strain Coupled Artificial Multiferroic Nanostructures. Phys Rev Lett. 2013;111:027204. doi: 10.1103/PhysRevLett.111.027204. [DOI] [PubMed] [Google Scholar]
  • 34.Ghidini M, Maccherozzi F, Moya X, Phillips LC, Yan W, Soussi J, Métallier N, Vickers ME, Steinke NJ, Mansell R, Barnes CHW, Dhesi SS, Mathur ND. Perpendicular Local Magnetization under Voltage Control in Ni Films on Ferroelectric BaTiO3 Substrates. Adv Mater. 2015;27:1460. doi: 10.1002/adma.201404799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Gao Y, Hu J, Wu L, Nan CW. Dynamic In Situ Visualization of Voltage-Driven Magnetic Domain Evolution in Multiferroic Heterostructures. J Phys: Condens Matter. 2015;27:504005. doi: 10.1088/0953-8984/27/50/504005. [DOI] [PubMed] [Google Scholar]
  • 36.Zhu QX, Wang W, Yang SW, Li XM, Wang Y, Habermeier HU, Luo HS, Chan HLW, Li XG, Zheng RK. Coaction and Competition between the Ferroelectric Field Effect and the Strain Effect in Pr0.5Ca0.5MnO3 Film/0.67Pb(Mg1/3Nb2/3)O3-0.33PbTiO3 Crystal Heterostructures. Appl Phys Lett. 2012;101:172906. [Google Scholar]
  • 37.Vaz CAF. Electric Field Control of Magnetism in Multiferroic Heterostructures. J Phys: Condens Matter. 2012;24:333201. doi: 10.1088/0953-8984/24/33/333201. [DOI] [PubMed] [Google Scholar]
  • 38.Mattheis R, Quednau G. Determination of the Anisotropy Field Strength in Ultra-Thin Magnetic Films Using Longitudinal MOKE and a Rotating. J Magn Magn Mater. 1999;205:143. [Google Scholar]
  • 39.Scheinfein MR, Unguris J, Kelley MH, Pierce DT, Celotta RJ. Scanning Electron Microscopy with Polarization Analysis (SEMPA) Rev Sci Instrum. 1990;61:2501. [Google Scholar]
  • 40.Trassin M, Clarkson JD, Bowden SR, Liu J, Heron JT, Paull RJ, Arenholz E, Pierce DT, Unguris J. Interfacial Coupling in Multiferroic/Ferromagnet Heterostructures. Phys Rev B: Condens Matter Mater Phys. 2013;87:134426. [Google Scholar]
  • 41.Noheda B, Cox D, Shirane G, Gao J, Ye ZG. Phase Diagram of the Ferroelectric Relaxor (1-x)PbMg1/3Nb2/3O3-xPbTiO3. Phys Rev B: Condens Matter Mater Phys. 2002;66:054104. [Google Scholar]
  • 42.Lei N, Devolder T, Agnus G, Aubert P, Daniel L, Kim J, Zhao W, Trypiniotis T, Cowburn RP, Chappert C, Ravelosona D, Lecoeur P. Strain-Controlled Magnetic Domain Wall Propagation in Hybrid Piezoelectric/Ferromagnetic Structures. Nat Commun. 2013;4:1378. doi: 10.1038/ncomms2386. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Donahue MJ, Porter DG. Interagency Report NISTIR 6376. National Institute of Standards and Technology; Gaithersburg, MD: 1999. OOMMF User’s Guide, version 1.0. http://math.nist.gov/oommf. [Google Scholar]
  • 44.Zhang S. Springer Theses. XVI. Springer; New York: 2014. Electric Field Control of Magnetization and Electronic Transport in Ferromagnetic/Ferroelectric Heterostructures. [Google Scholar]
  • 45.Bilzer C, Devolder T, Kim JV, Counil G, Chappert C, Cardoso S, Freitas PP. Study of the Dynamic Magnetic Properties of Soft CoFeB Films. J Appl Phys. 2006;100:053903. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp1
NIHMS856000-supplement-Supp1.pdf (481.4KB, pdf)

RESOURCES