Sub-cellular modeling of platelet transport in blood flow through microchannels with constriction

Abstract

Platelet transport through arterial constrictions is one of the controlling processes influencing their adhesive functions and the formation of thrombi. We perform high-fidelity mesoscopic simulations of blood flow in microchannels with constriction, resembling arterial stenoses. The wall shear rates inside the constrictions reach levels as high as ≈8000 s⁻¹, similar to those encountered in moderate atherosclerotic plaques. Both red blood cells and platelets are resolved at sub-cellular resolution using the Dissipative Particle Dynamics (DPD) method. We perform a systematic study on the red blood cell and platelet transport by considering different levels of constriction, blood hematocrit and flow rates. We find that higher levels of constriction and wall shear rates lead to significantly enhanced margination of platelets, which may explain the experimental observations of enhanced post-stenosis platelet aggregation. We also observe similar margination effects for stiff particles of spherical shapes such as leukocytes. To our knowledge, such numerical simulations of dense blood through complex geometries have not been performed before, and our quantitative findings could shed new light on the associated physiological processes such as ATP release, plasma skimming, and thrombus formation.

1 Introduction

Platelet aggregation at sites of vascular injury is essential for hemostasis and arterial thrombosis. Several studies have shown that both biochemical and hemodynamic factors contribute to thrombus formation at a vulnerable vessel wall.¹ The hemodynamics and local shear gradients, which occur with changes in vessel geometry (due to possible stenoses) or as a consequence of thrombus formation itself, have been proven to have a significant role in the formation and progression of thrombi.^2,3 One of the major pathological thromboses results from the rupture of atherosclerotic plaques in coronary arteries, which could obstruct the vessel lumen.⁴ Arterial thrombosis in the coronary arteries due to rupture of vulnerable plaques is the principal pathological process leading to acute myocardial infarction, sudden death, and ischemic stroke.

Blood is a dense suspension of both deformable cells and rigid particles in plasma; the main constituent of blood is the red blood cells (RBCs) that make up approximately 35–50% of the blood’s volume and are mainly responsible for its complex rheology. Platelets are non-nucleated blood cells that have a non-deformable discoid shape in their unactivated resting form. They have a diameter of approximately 2 μm, thickness of 0.5 μm, and a number density of 150 000–400 000 mm⁻³. Despite the small number of circulating platelets in the vascular network, their role is extremely crucial in hemostasis and thrombosis. The process of clot formation and growth at a site of injury on a blood vessel wall involves a number of simultaneous processes including: flow dynamics, multiple chemical reactions of the coagulation cascade and species transport, platelet activation and adhesion. Initiation of thrombosis is triggered by a disruption in endothelial cells and the exposure of the blood to the subendothelial collagen and extravascular cells. For efficient platelet adhesion to a site of injury or existing thrombus, it must be sufficiently close to that site for platelet–subendothelium or platelet–platelet bonds to form. An increased concentration of platelets near the walls known as platelet margination occurs in the presence of RBCs at hematocrit levels of more than ≈10%. This shear induced platelet diffusion has been confirmed in in vivo⁵ and in vitro⁶ experiments, and has been explained in several theoretical and numerical studies.^7–10 At high shear rates platelet adhesion to the wall is essentially mediated by a large multimeric protein called von Willebrand Factor (vWF). The mechanism of this enhanced adhesion was studied before^11,12 and is attributed to shear-induced unfolding and elongation of vWF fibers at a critical shear rate, which in turn exposes more A1 binding sites for platelets to adhere. This enhanced vWF-mediated platelet adhesion was confirmed in the experiment of Westein et al.,¹³ where microchannels with different levels of constriction and wall shear rates as high as 8000 s⁻¹ were considered.

Many of the above processes occur when an atherosclerotic plaque ruptures in an artery and then produces a thrombus that quickly grows to occlude the vessel. Therefore, microfluidic channels with constrictions have been devised to mimic atherosclerotic plaques by generating significantly high wall shear rates in the stenotic region to study the mechanisms by which fluid dynamics influences clot formation and its stability,^13,14 whereas other devices were built in several experiments^15,16 to study the blood transport, rheology and ATP release from RBCs under high shear stress conditions. Faivre et al.¹⁵ found the geometrical focusing of RBCs downstream of a constriction, and showed that rapid variation of the geometry coupled with the deformability of the red cells can dramatically modify their spatial distribution in the channel. Their experimental study, however, did not consider the transport and dynamics of more stiff particles such as platelets, which is the subject of the present work.

Numerical simulations of blood flow in complex geometries are relatively scarce, and in a few studies 2D or dilute suspensions of blood in microvessels have been addressed.^17,18 Other computational studies are limited to blood flow in straight channels with the inclusion of platelets or microparticles as drug carriers.^19–22 Skorczewski et al.¹⁷ presented two-dimensional lattice-Boltzmann immersed boundary computations of blood flow in a channel with a bump representing thrombus to investigate the motion of platelets near a vessel wall and close to an intravascular thrombus. Wang et al.¹⁸ studied the flow of semi-dilute blood and platelet trajectories in a microvessel with the presence of thrombus. These studies show that the RBCs can have a strong effect on the motion of platelets near the vessel wall, and platelets near the wall tumble more slowly than platelets in a flow without RBCs. The tumbling dynamics of near-wall platelets is important as it brings them closer to the vessel wall injury for possible adhesion. Soares et al.²³ used Dissipative Particle Dynamics (DPD) to study the flow of platelets suspension in a stenotic geometry. In their study, platelets were considered in plasma at zero hematocrit, and their dynamics were investigated as they passed through the constriction.

One of our goals in this study is to perform high-fidelity simulations of blood (plasma, RBCs and platelets) in microfluidic channels taking into account important contributing factors such as constriction geometry, flow rate or equivalently wall shear stress, blood hematocrit, and cell deformability. We will focus on platelet distribution and transport as they pass through the constriction, and the results will complement the experimental study of Faivre et al. Studying a larger population of platelets will give us insights on the overall behavior of platelet transport and their distribution inside and in postconstriction regions where the shear rates can get as high as the ones encountered in atherosclerotic plaques.

2 Numerical methods

We employ DPD, a mesoscopic particle-based hydrodynamics approach,^24,25 to model fluid and suspending cells in the microfluidic channels. Further, a coarse-grained representation of cell membrane is used for both RBCs^26,27 and platelets. The DPD representation of red cells in blood was extensively used and validated in the previous studies for suspensions of both healthy²⁸ and disease cells²⁹ (e.g., malaria and sickle cells). Using the same model, Lei et al. systematically investigated the flow of blood and its non-Newtonian behavior through small tubes (diameters 10–150 μm).³⁰ The current study uses the previous models to extend it to whole blood in a complex geometry where platelets are also included.

2.1 Hydrodynamics

The pairwise interactions between DPD particles ensure the conservation of momentum of the DPD system. Moreover, since these interactions depend only on the relative positions and velocities, the resulting DPD fluids are Galilean invariant. Therefore, DPD can provide the correct hydrodynamic behavior of fluids at the mesoscale, and it has been successfully applied to study complex fluids.^28,31

In the standard DPD method, the pairwise forces consist (in the basic form) of three components: (i) conservative force ${\mathbf{f}}_{ij}^{\mathrm{C}}=a_{\mathrm{c}}(1-r_{ij}/r_{\mathrm{c}}){\widehat{\mathbf{r}}}_{ij}$; (ii) dissipative force, ${\mathbf{f}}_{ij}^{\mathrm{D}}=\gamma {\omega }_{\mathrm{d}}(r_{ij})({\widehat{\mathbf{r}}}_{ij}·{\widehat{\mathbf{v}}}_{ij}){\widehat{\mathbf{r}}}_{ij}$; and (iii) random force, ${\mathbf{f}}_{ij}^{\mathrm{R}}=\sigma {\omega }_{\mathrm{r}}(r_{ij})({\zeta }_{ij}/\sqrt{\mathrm{\Delta }t}){\widehat{\mathbf{r}}}_{ij}$. Hence, the total force on particle i is given by ${\mathbf{f}}_i={\displaystyle \sum _{i\ne j}}\left({\mathbf{f}}_{ij}^{\mathrm{C}}+{\mathbf{f}}_{ij}^{\mathrm{D}}+{\mathbf{f}}_{ij}^{\mathrm{R}}\right)$, where the sum acts over all particles j within a cut-off radius r_c, and a_c, γ, σ are the conservative, dissipative, random coefficients, respectively, r_ij is the distance with the corresponding unit vector r̂_ij, v̂_ij is the difference between the two velocities, ζ_ij is a Gaussian random number with zero mean and unit variance, and Δt is the simulation timestep size. The parameters γ and σ and the weight functions are coupled through the fluctuation– dissipation theorem and are related by ω_d = ω_r² and σ² = 2γk_BT, where k_B is the Boltzmann constant and T is the temperature of the system. The weight function ω_r(r_ij) is given by

$${\omega }_{\mathrm{r}}(r_{ij})=\{\begin{array}{ll}{\left(1-\frac{r_{ij}}{r_{\mathrm{c}}}\right)}^k\hfill & r_{ij}<r_{\mathrm{c}}\hfill \\ 0\hfill & r_{ij}\ge r_{\mathrm{c}}\hfill \end{array},$$ (1)

with k = 1 in the original DPD form, whereas other values of k have been used to increase the fluid viscosity.³² More details on the basic formulation of the DPD method can be found in ref. 24 and 25. Equations of motion for each particle of mass m_i are written by (dr_i = v_idt; dv_i = f_i/m_idt) and integrated using a velocity-Verlet algorithm.³³ Table 1 presents the DPD parameters used for the fluid (representing plasma) particles throughout this study.

Table 1.

DPD fluid parameters used in simulations. n is the fluid’s number density, a_c is the conservative force coefficient, γ is the dissipative force coefficient, k is the weight function exponent, and η is the fluid’s dynamic viscosity. In all simulations, we set the particle mass m = 1, and the thermal energy k_BT = 0.092 in DPD units (see Appendix for conversion to the physical units)

n	rc	ac	γ	k	η
4.0	1.58	5.0	20.0	0.15	148.0

2.2 Cell mechanics and the fluid–cell interactions

In this study we use a coarse-grained representation of the cell membrane structure (lipid bilayer + cytoskeleton), which was introduced in the work of Fedosov et al.²⁷ The membrane is defined as a set of N_v DPD particles with Cartesian coordinates x_i, i ∈ 1,…,N_v in a two-dimensional triangulated network created by connecting the particles with wormlike chain (WLC) bonds. The free energy of the system is given by

$$V_{\mathrm{t}}=V_{\mathrm{s}}+V_{\mathrm{b}}+V_{\mathrm{a}}+V_{\mathrm{v}},$$ (2)

where V_s is the stored elastic energy associated with the bonds, V_b is the bending energy, and V_a and V_v are the energies due to cell surface area and volume constraints, respectively. Following Fedosov et al., we combine a wormlike chain (WLC) potential, V_WLC, with a long-range repulsive force potential, V_POW, to achieve the strain-hardening behavior of RBC membrane. For the coarse-grained membrane with N_s bonds, the potential of bond j depends on its length l_j, and V_s is the sum of all N_s bonds: $V_{\mathrm{s}}={\displaystyle \sum _{j\in 1,\dots ,N_{\mathrm{s}}}}\left[V_{\text{WLC}}\left(l_j\right)+V_{\text{POW}}\left(l_j\right)\right]$. The bond energies are defined as

$$V_{\text{WLC}}+V_{\text{POW}}=\frac{k_{\mathrm{B}}T{l}_{max}}{4p}\frac{3x^2-2x^3}{1-x}+\frac{k_{\mathrm{p}}}{l},$$ (3)

where x = l/l_max with l_max the maximum bond length (equilibrium length is l₀), p is the persistence length, and k_p is the repulsive force coefficient. The persistence length and k_p are computed by balancing the forces at equilibrium and from their relation to the macroscopic shear modulus μ_s:

$${\mu }_{\mathrm{s}}=\frac{\sqrt{3}{k}_{\mathrm{B}}T}{4p{l}_{max}{x}_0}\left(\frac{x_0}{2{(1-x_0)}^3}-\frac{1}{4{(1-x_0)}^2}+\frac{1}{4}\right)+\frac{\sqrt{3}{k}_{\mathrm{p}}}{2{l_0}^2}.$$ (4)

The bending energy is defined as

$$V_{\mathrm{b}}=\sum _{j\in 1,\dots ,N_{\mathrm{s}}}{k}_{\mathrm{b}}\left[1-cos({\theta }_j-{\theta }_0)\right],$$ (5)

where k_b is the bending constant and $k_{\mathrm{b}}=2k_{\mathrm{c}}/\sqrt{3}$, with k_c the bending rigidity of the bilayer, θ_j is the instantaneous angle between two adjacent triangles having the common edge j, and θ₀ is the spontaneous angle, which is set to zero in our simulations.

The energies associated with the area and volume conservation constraints are

$$V_{\mathrm{a}}=\frac{k_{\mathrm{A}}{\left(A_{\text{cell}}-A_0^{\text{tot}}\right)}^2}{2A_0^{\text{tot}}}+\sum _{j\in 1,\dots ,N_{\mathrm{t}}}\frac{k_{\mathrm{a}}{\left(A_j-A_0\right)}^2}{2A_0},$$ (6a)

$$V_{\mathrm{v}}=\frac{k_{\mathrm{V}}{(V_{\text{cell}}-V_0^{\text{tot}})}^2}{2V_0^{\text{tot}}},$$ (6b)

where k_A, k_a and k_V are the global area, local area and volume constraint coefficients, respectively, N_t is the number of triangles in the mesh, A_j is the current area of triangle j, A₀ is the equilibrium value of the triangle area, and $A_0^{\text{tot}}$ and $V_0^{\text{tot}}$ are the desired cell area and volume. In practice, we use high values for the constraints coefficients to enforce area and volume incompressibility. The membrane parameters used in eqn (3)–(6) are given in Table 2 for both RBCs and platelets. All parameters are calibrated against the optical tweezer experiments.²⁷ These values are varied consistently in our simulations depending on the coarse-graining level such that the elastic properties of the RBC membrane remain unchanged. Note that platelets are nondeformable in their resting form and thus, we use values two orders of magnitude higher for their shear modulus and bending rigidity than RBCs.

Table 2.

DPD parameters for RBCs and platelets: N_v is the number of DPD particles on the membrane, l_m is the maximum bond extension, l₀ is the equilibrium bond length, k_c is the bending rigidity, μ_s is the shear modulus, $A_0^{\text{tot}}$ and $V_0^{\text{tot}}$ are the targeted cell area and volume, respectively, k_A + k_a is the combined area constraint coefficient, and k_V is the volume constraint coefficient (see Appendix)

Cell	Nv	lm/l0	kc	μs	$A_0^{\text{tot}}(V_0^{\text{tot}})$	kA + ka (kV)
RBC	362	2.2	6.667	100.0	134 (94)	4900 (104)
Platelet	42	1.12	100.0	104	16.9 (4.2)	5 × 104 (106)

Further, the fluid–cell interactions are accounted for through viscous friction using the dissipative and random DPD forces. The repulsive-force coefficient for the coupling interactions is set to zero. The strength of the dissipative force γ is computed such that no-slip condition on the cell surface is enforced. Further details of the DPD model for the fluid–cell and cell–cell interactions are given in the Appendix.

2.3 Simulation setup

The simulation domain is composed of straight channel section with a constriction at the center as shown in Fig. 1(a). The constriction is modeled by the segment of a circle adjusted to achieve 50% and 75% occlusion. The domain is periodic in the axial x and perpendicular z directions. RBCs in their resting form are biconcave (plotted in Fig. 1(b)) with diameter of 7.82 μm,³⁴ whereas platelets are oblate spheroids with diameter of 2 μm and aspect ratio of 0.3³⁵ (plotted in Fig. 1(c)). The coarse-grained RBC membrane is described by 362 DPD particles, whereas the platelet membrane contains 42 DPD particles.

Fig. 1.

(a) Schematic of a microchannel with 75% degree constriction. Top: 3D presentation of the channel where the walls are triangulated. Bottom: 2D view of the same geometry in the x–y plane. Channel dimensions are 195 × 30 × 30 micron, and the constriction length is 40 μm. (b) Coarsegrained model of RBC membrane with 362 DPD particles forming a triangulated grid. (c) Coarse-grained model of platelet membrane with 42 DPD particles.

The wall boundaries in the simulation domain are treated as pseudo-planes similar to the work of Lei et al.³⁶ Specifically, particles within one cut-off distance from the wall are reflected in a bounce-forward scheme. Further, in order to impose the no-slip condition, a predefined force that compensates for the missing particles on the opposite side of the wall is applied to the particles both in wall normal and tangential directions. In this scheme, it is important to have a planar description of the geometry, and thus the whole geometry is triangulated similar to Fig. 1(a).

To drive the flow (simple fluid or blood) in a straight channel, we apply a constant body force to each particle. This will yield a parabolic profile for simple fluids or a plug-like profile for blood. The application of uniform body force, however, fails to achieve the correct density and velocity profiles in stenotic geometries as shown in the recent study by Yazdani et al.³⁷ Thus, we follow their work to compute a tailored-body force driver for DPD particles by obtaining the pressure gradient field from the numerical solution of Navier–Stokes (N–S) equations for the same geometry and Reynolds number (with proper scaling from NS to DPD units), where the Reynolds number is defined as

$$Re=\frac{\overline{u}H}{\nu },$$ (7)

where ū is the mean velocity, H is the height of the straight section of the channel, and ν is the kinematic viscosity of the plasma. Further, the characteristic shear rate is defined as γ̇_w = 6ū/H, which corresponds to the wall shear rate of a parabolic Poiseuille flow with the same mean velocity ū, and is varied in our simulations to address its effect on platelet transport. In addition, the cell Reynolds number defined based on RBC diameter is Re_cell = γ̇_wD_RBC²/ν ≈ 0.025, which renders the inertia effect negligible.

In order to relate the DPD parameters with the physical values, we need to first define length and time scales. The length scale in our simulations is chosen to be [L] = 10⁻⁶ m. If the suspending fluid contains platelets only (i.e. platelet rich plasma), then a time scale can be defined through the fluid viscosity since platelets are considered rigid, and is given by

$$[t]={[L]}^2\frac{{\nu }^{\mathrm{M}}}{{\nu }^{\mathrm{P}}}(\mathrm{s}),$$ (8)

where superscripts M and P denote the model (DPD) and physical units, respectively. In case of blood, different flow rates result in different RBC deformations, and this imposes a new time scale based on the RBC relaxation time

$$[t]=[L]\frac{{\eta }^{\mathrm{P}}}{{\eta }^{\mathrm{M}}}\frac{{\mu }_{\mathrm{s}}^{\mathrm{M}}}{{\mu }_{\mathrm{s}}^{\mathrm{P}}}(\mathrm{s}),$$ (9)

where μ_s is the RBC membrane shear modulus. The detailed calculations of the time scales and the parameters mapping from physical to model units are given in the Appendix.

3 Results

To examine the tailored body-force method used to drive the blood flow we first test the mean velocity field from DPD simulations for a representative geometry with 75% occlusion as shown in Fig. 2 (for the video refer to the ESI^†). The driving force field is derived from the numerical solution of N–S equations for the same geometry and Re = 0.35. The results clearly show that the maximum velocity (wall shear rate) occurs at the throat of the constriction. Further, the velocity profiles at different axial locations follow a plug-like shape for the blood at hematocrit 25%.

Fig. 2.

(a) Snapshot of the blood simulation in a microchannel with 75% degree constriction. The channel height is 30 μm, and blood is at 25% hematocrit. Red cells represent the deformable red blood cells and black ellipsoidal cells are nondeformable platelets in their resting form. Following Yazdani et al.,³⁷ the driving body force is the non-uniform pressure gradient derived from numerical solution Navier–Stokes equation at Re = 0.35 for the same geometry (video for this simulation is provided in ESI^†). (b) Left: Velocity contours and streamlines for the flow of blood in the 75%-constriction microchannel; right: profiles of streamwise velocity component at five different locations along the microchannel length specified by the same colors. A plug-like velocity profile is achieved for the blood except at the throat.

At the beginning of the simulations, RBCs are placed randomly within the channel, and platelets are distributed uniformly across the channel height. RBC-wall hydrodynamic interactions cause a lift owing to deformability of RBCs, which drives them away from the wall.³⁸ As the simulations progress, this cross-stream migration of RBCs, leads to a RBC depleted region or cell-free layer (CFL) near the walls. The velocity profiles follow parabolic curves in the near-wall region, whereas we observe plug-flow profiles with a nearly flat velocity in the center due to the RBC core of the flow shown in Fig. 2(b). We note that velocity profiles downstream of the constriction differ from the upstream profile, where the difference is more pronounced close to the constriction’s outlet (solid blue curve in Fig. 2(b)). This difference is due to the RBC focusing towards the center of the channel, and the enhancement of the CFL thickness post-constriction. We observe that the velocity recovers further downstream in the microchannel as RBC core region expands and cell distribution becomes similar to the distribution upstream of the constriction (shown in Fig. 3). The recovery length is estimated to be ΔL ≈ 60 μm downstream of the constriction, and is expected to be longer as flow rate increases.

Fig. 3.

Profiles of RBC concentration (hematocrit) at different locations along the 75% constriction (inlet, middle and outlet) as well as further downstream of the constriction (red dashed line considered at x = 160 μm). Here, the average hematocrit of blood is 25%.

Fig. 3 shows the spatial distribution of RBCs at the inlet, in the middle and downstream of a 75% constriction. The profiles downstream are considered at the outlet of constriction and at x = 160 μm. This result shows that geometrical constriction coupled with deformability of RBCs can enhance the cell-free layer (CFL) for a fixed flow rate (e.g., CFL thickness δ ≈ 2.5 micron at inlet as opposed to ≈5.0 micron at outlet). Similarly, geometrical focusing of RBCs towards the center of the microchannel was observed experimentally by Faivre et al.¹⁵ As cells move further downstream of the channel, the upstream CFL thickness will be recovered due to the RBC pair collisions and lateral migration. We also note that RBC concentration drops at the center of constriction, which is caused by the increase in RBC velocities. Further, the CFL thickness drops as the channel narrows down (δ ≈ 0.4 micron at the throat of the constriction). In the following sections we present the results on the platelet distributions and transport with the presence of the constriction.

3.1 Cell distributions

To obtain the profiles in Fig. 3–8, first DPD simulations were performed long enough (for t* ≈ 4000 DPD time units or ≈0.72 s) to achieve steady state conditions, where no more variations in velocity and hematocrit profiles were detected. Sampling of RBCs and platelets concentration was performed for the last Δt* ≈ 400, and these time-averaged concentration profiles were spatially averaged (along z-dir) and plotted against the channel height y. The bin width in the following histogram plots is 0.5 μm.

Fig. 8.

The effect of blood hematocrit on platelets concentration downstream of a constriction: (a) profiles of platelets concentration downstream of a 75% constriction; (b) profiles of platelets concentration downstream of a 50% constriction. The mean hematocrit of blood varies from 0 to 25%, and the upstream wall shear rate remains the same for all cases at γ̇_w = 500 s⁻¹.

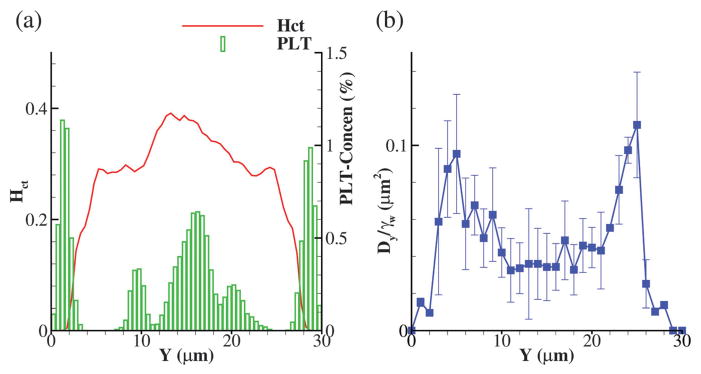
Before presenting the results for complex geometries, we perform a short analysis of blood flow in a straight channel with no constriction and make comparisons with similar numerical and experimental studies. Fig. 4(a) shows the hematocrit and platelet concentration profiles in a straight channel of 30 μm height where the wall shear rate is kept at γ̇_w = 500 s⁻¹. Similar RBC and platelet distributions were obtained in the boundary integral simulations of Zhao et al.⁷ and Lattice-Boltzmann/spectrin-link simulations of Mehrabadi et al.³⁹ with CFL thickness δ ≈ 2.5 μm. Note that the asymmetry in platelet concentration profile is due to the slight nonuniform initial distribution of platelets in the domain, which is hard to control precisely.

Fig. 4.

(a) Profiles of hematocrit and platelet concentration for blood flow through a straight microchannel. (b) Profile of effective diffusivity D_y scaled by the wall shear rate γ̇_w = 500 s⁻¹. Here, the average hematocrit of blood is 25%.

By analyzing platelets’ trajectories in the microchannel, we are able to estimate the RBC-enhanced diffusion of platelets by assuming that the motion of platelets in blood flow can be estimated as a standard diffusion process. The shear-induced diffusivity can be estimated from mean square displacements of platelets 〈Δy²〉(t) = 〈[y(t) − y(0)]²〉 ~ 2D_yt at long time once diffusive motion has been established. Here 〈Δy²〉(t) grows linearly with time and its slope defines the effective diffusion constant D_y.⁷ Alternatively, we can estimate diffusion coefficient from the following equation

$$D_y(y)=\frac{\langle \delta y^2(y)\rangle }{2\mathrm{\Delta }t},$$ (10)

where 〈δy²(y)〉 is the time average of the variance of platelets jumps during time step Δt used for resolving their trajectories. Taking Δt large enough (1000 DPD time steps or approximately ≈10⁻⁴ s in this study), the resulting diffusion coefficient will be equivalent to the slope of mean square displacement linear growth with time.^39,40 Fig. 4(b) presents platelets diffusion (scaled by the wall shear rate γ̇_w = 500 s⁻¹) across the channel height, where the error bars show its standard deviation. The effective diffusion increases away from the wall and across the CFL edge and decreases close to the center of the channel in the RBC core region. Similar trend was observed in the work of Mehrabadi et al. Further, the effective diffusion in the RBC core region is estimated to be D_y ≈ 2 × 10⁻⁷ cm² s⁻¹, which is very close to the estimated experimental value of Turitto and Weiss⁴¹ and reported numerical values of Zhao et al. and Mehrabadi et al.

3.1.1 Effect of geometry and wall shear rate

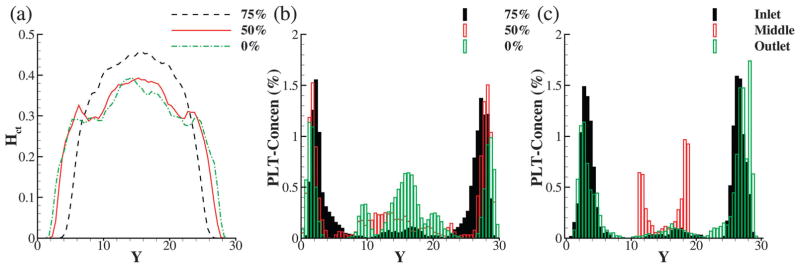
We first present RBC and platelet concentrations downstream of constrictions at different levels in Fig. 5. The average hematocrit and volume concentration of platelets are 25% and 0.25% (equivalent to 400 000 platelets in 1 mm³ of blood), respectively. The upstream wall shear rate is fixed at γ̇_w = 500 s⁻¹, and it reaches up to ≈8000 and 2000 s⁻¹ in the 75% and 50% constrictions, respectively. The hematocrit profiles in Fig. 5(a) show a significant increase in CFL thickness downstream of the 75% constriction compared to the profile in a straight channel, which in turn leads to a significantly enhanced platelet margination post-constriction as shown in Fig. 5(b) (black histograms). However, the hematocrit profile for 50% constriction shows only a marginal increase in CFL thickness downstream, accompanied with milder enhancement in platelet margination.

Fig. 5.

Effect of constriction geometry on RBC and platelet distribution: (a) profiles of RBC concentration downstream of a constriction at 75 and 50% and plotted against the profile of H_ct for a straight channel. The mean hematocrit of the blood is 25%; (b) platelet volume concentration for the same simulations as in (a); (c) platelet concentrations at the inlet, center and outlet of a 75% constriction.

The lateral migration of platelets in confined blood flow has been previously studied and is attributed to the hydrodynamic pair collisions of rigid platelets with soft RBCs.^7,42 This shearinduced platelet margination is generally a rather slow process, which is the reason for the high platelet concentration in the center of the channel for the cases of straight channel and 50% constriction (shown by red and green histograms in Fig. 5(b)). In order to measure margination enhancement in different geometries, we integrate platelets concentration profiles in the CFL region given in Fig. 7. We observe that after the same duration of simulation time (≈0.72 s), almost 83.6% of platelets marginate in the 75% constriction channel, compared to 41.3% margination in the straight channel. Hence, there is a two-fold enhancement in the platelet migration. This number is estimated to be about 63.6% for the case of 50% channel constriction.

Fig. 7.

Fractions of marginated platelets downstream of a constriction (after 0.72 s) vs. constriction levels (■; lower axis), and vs. wall shear rates (▲; upper axis).

It is also interesting to see platelet transport throughout the constriction, which is depicted in Fig. 5(c) by showing concentration profiles at inlet, center and outlet of the 75% constriction. It can be noted that near-wall platelet concentration is high at both inlet and outlet suggesting that margination is enhanced throughout the length of the constriction irrespective of the axial location. Similar to the hematocrit profile in Fig. 3, the reduction in platelet concentration at the center of constriction can be explained by the conservation of mass.

This enhanced margination inside the constriction can be explained by the increase in the collision frequency between platelets and RBCs. The collision frequency depends both on the particles density and the local shear rate. In the case of 75% constriction, besides the increase in RBC density close to the edge of CFL, the wall shear rate increases by a factor of 4. This combined effect leads to a significant enhancement in platelet migration. In the case of 50% constriction, however, the RBC core region remains almost unaffected compared to the flow in the straight channel (see Fig. 5(a)). Thus, the two-fold increase of wall shear rate in the constriction may be the only source of the observed mild enhancement in platelet migration.

Fig. 6 shows the effect of increasing flow rate or wall shear rate on cell distributions downstream of the 50% constriction. The hematocrit profiles in Fig. 6(a) do not show any significant variation in the CFL and RBC core regions upon increasing the flow rate. However, interestingly, platelet concentration profiles in Fig. 6(b) show an enhancement in margination. Fig. 7 shows the percentage of marginated platelets upon increasing the shear rate. At the base flow rate, wall shear rate inside the constriction reaches as high as γ̇_w ≈ 2000 s⁻¹. We have already estimated that 63.6% of platelets migrate to the wall downstream. At the flow rates 1.5 and 2.0 times higher than the base flow rate, the maximum wall shear rate in the constriction increases to γ̇_w ≈ 3000 and 4000 s⁻¹, respectively. This in turn, will increase the collision frequencies in the constriction and we observe an increase in the fractions of marginated platelets reaching up to 72.7% and 80.7%, respectively. This enhancement at twice higher flow rate is comparable to the results for 75% constriction where γ̇_w ≈ 8000 s⁻¹, which suggests that hydrodynamic shear gradients and pair collisions play a significant role in the platelets wall migration.

Fig. 6.

Wall shear rate effect on RBC and platelet distribution downstream of a 50% constriction: (a) profiles of RBC concentration at the base, 1.5 and twice higher flow rates. Upstream wall shear rate at the base flow rate is γ̇_w = 500 s⁻¹, and the mean hematocrit of blood is 25% in all cases; (b) platelet volume concentration for the same simulations as in (a).

3.1.2 Effect of blood hematocrit

Fig. 8 shows the platelets concentration profiles downstream of a constriction where the mean blood hematocrit varies from 0 to 25%. In the case of zero hematocrit where no soft RBCs are present, it is clear that platelets tend to concentrate at the center of the channel due to the geometrical focusing effect of the constrictions (green histograms). As we introduce RBCs to blood flow, due to heterogenous pair collisions between platelets and RBCs, platelets drift toward the walls and are trapped in the CFL region. Further, the near-wall peaks shift toward the wall with increasing hematocrit, where the height of the peaks increase with increasing hematocrit. The degree of margination of the platelets is higher for 75% constriction than 50% for all values of hematocrit (H_ct > 0) tested here.

3.2 Platelet transport through microchannel and constriction

We first plot the trajectories of all platelets throughout the microchannel in Fig. 9. We observe two distinct sets of trajectories for both 50 and 75% constrictions as shown by (x_p − t*) curves; those platelets that are closer to the walls transport with lower speed as noted by the smaller slope in their (x_p − t*) profiles, whereas the platelets closer to the center of the channel have higher velocities. Note that the peaks in y_p trajectories occur when near-wall platelets pass through the constriction. Further, we observe the lateral migration of the platelets from the channel center toward the walls shown by (y_p − t*) curves in Fig. 9(b) and (d), which is accompanied by the drop in velocities reflected in their (x_p − t*) trajectories. This lateral drift (shown by green curves) could occur smoothly and be gradual (Fig. 9(b)), or may be more abrupt as the platelet travels through the constriction (Fig. 9(d)).

Fig. 9.

Trajectories of platelets inside a microchannel with 50% constriction (top row) and 75% constriction (bottom row), where X_p and Y_p are axial and vertical positions of the platelet’s center of mass, respectively, and t* is the DPD time unit; (a) and (c) axial positions vs. time for all platelets; (b) and (d) trajectories of three representative platelets: axial positions (dashed lines and left axis); vertical positions (solid lines and right axis).

We also plot contours of relative platelet concentration (C_plt/〈C_plt〉) in the channel, averaged in time and space (along z-axis) in Fig. 10. Interestingly, we observe locally enhanced platelet presence post-constriction (at x ≈ 110 μm) for 75% constriction in Fig. 10(a) as opposed to 50% constriction in Fig. 10(b). It appears that some platelets tend to decelerate and spend a brief period of time in that region. Similar platelet motion was observed in the experimental work of Tovar-Lopez et al.¹⁴ However, unlike their experiment, we do not observe any regions of recirculation in our simulations probably due to differences in the shape of the constriction and the low-Re flow regime tested in our simulations. The other observation is the non-monotonic trend in near-wall platelet concentration through the constriction; the relative concentration first decreases from the inlet toward the apex followed by the increase at the outlet. This trend is more pronounced as the degree of constriction increases. Further, there is a slight dispersion of the platelet concentration at the exit of the constriction compared to the inlet which may not be clearly distinguished in Fig. 5(c). Bark and Ku⁴³ used a continuum description of platelet concentration based on a phenomenological mass transport model. They found a monotonic decrease of nearwall platelet concentration inside a 84%stenosis at Re = 1, which could be due to the fact that their model does not take into account the focusing of RBCs post-constriction, and platelet diffusion coefficient is taken constant throughout the stenosis.

Fig. 10.

Contours of relative platelet concentration in channels with (a) 75% and (b) 50% constriction. The color map is the same for both figures.

Understanding the transport behavior and dynamics of platelets inside a constriction is important because it affects platelets adhesion efficiency at the site of injury. More specifically, the platelet’s dynamics i.e., tumbling vs. sliding motions, in the CFL region strongly affects the minimum particle distance to the wall and the probability of contact between platelet’s receptors and wall ligands. Fig. 11 presents a snapshot of RBCs and platelets in 50% constriction, where the H_ct is 25%. We observe that near-wall platelets primarily undergo either sliding or tumbling motion. The tumbling of platelets near the vessel wall, however, is strongly influenced by the presence of RBCs and enhanced confinement effects in the CFL region such that full tumbling motions are mostly restricted.

Fig. 11.

Snapshot of the platelet dynamics in a 50% constriction (video for this simulation is provided in ESI^†). Red arrows show representative sliding and tumbling platelets passing through the constriction.

The probability distribution of minimum platelet distance from the wall inside the constriction is given in Fig. 12. We find that the probability is the highest right adjacent to the wall even though the tumbling motion is significantly hindered. This result is due to the drop in CFL thickness and the increasing confinement, which make near-wall platelets slide for most of the time they are traveling inside the constriction. This will, in turn, increase the chances of contact between the platelet’s receptors and vWF ligands at distances ΔY < 200 nm.

Fig. 12.

Probability distribution for minimum distance of platelet’s surface from the wall inside the constrictions. Red bars are slightly shifted to the right for clarity.

In order to further analyze different modes of dynamics of platelets in the constriction we select a few platelets and plot their trajectories through the 50% constriction in Fig. 13(a), while their minimum distance from the wall is monitored in Fig. 13(b) as they pass through the constriction. These selected trajectories represent the majority of platelets’ dynamics throughout the microchannel. We note the platelets that are initially located closer to the channel center experience the local curvature of flow velocity as they enter the constriction, thereby acquire a drift velocity (platelet no. 1 & 2). Further collisions with RBCs in the core region will induce extra drift velocity toward the wall. It is interesting to note that these two platelets migrate to the opposite sides of the channel height even though they were initially released from the same vertical location as shown in Fig. 13(a). Platelets that are located in the CFL region upstream of the constriction, however, will remain close to the wall as they pass through the constriction (platelets no. 3 & 4). Platelet no. 3 stays very close to the wall and keeps sliding as it passes through the constriction (shown by the red curve in Fig. 13(b)). Platelet no. 4, however, is farther away from the wall as it enters the constriction and undergoes a tumbling motion indicated by the drop in ΔY_min at X_p ≈ 77 μm in Fig. 13(b) that brings it closer to the wall. It then slides briefly before it tumbles away from the wall as it exits the constriction.

Fig. 13.

(a) Trajectories of four representative platelets inside a microchannel with 50% constriction (wall boundaries are shown with gray lines), where X_p and Y_p are axial and vertical positions of the platelet’s center of mass, respectively. (b) Minimum distance to the walls for platelets in (a) passing through the constriction (60 < X_p < 105 μm). The minimum distance is calculated based on the closest point on platelet’s surface from the wall.

Using a microfluidic device, Tovar-Lopez et al.¹⁴ investigated platelet transport through an asymmetric constriction. They were able to perfuse two streams of blood through the channel and demonstrated that by progressively biasing and resolving the fluid streams, only 15–25% of the blood stream proximal to the stenosis geometry contributes to aggregate development. The contours of platelet concentrations in Fig. 10 and trajectories in Fig. 13 also indicate that only platelets in the close proximity of the constriction tend to further migrate toward the wall, which increases their chances of adhesion.

4 Discussion and summary

We performed a high-fidelity computational study of blood flow through constrictions in microchannels. The shear gradients in such geometries are similar to blood flow in atherosclerotic plaques. Quantifying the transport and margination of platelets as well as RBC distributions are particularly important in these geometries as they affect platelet aggregation and thrombus formation following the plaque rupture. The DPD numerical framework is a Lagrangian approach, which consistently takes fluctuations into account. Particle representation of the cell membrane uses WLC springs, and can capture the accurate cell deformations at lower cost compared with the continuum models.

Our focus here has been a systematic study of the effects of geometry shapes, wall shear rates and blood hematocrits on platelet distribution inside and post constriction. This study complements a previous in vitro experiment that looked at concentrations of RBCs pre and post constrictions.¹⁵ We observed the geometrical focusing of RBCs toward the center of the channel post constrictions leading to increase in CFL thickness. More importantly, platelets as hard ellipsoidal cells tend to migrate strongly toward the wall. We obtained an enhancement in margination at higher degrees of constriction and higher flow rates (wall shear rates).

Most of the margination results in this study may be explained by the balance between wall-induced hydrodynamic lift away from the wall, and hydrodynamic pair collisions.^40,42,44 The outermost layer of RBC core region experiences a lift velocity due to the hydrodynamic interaction with the wall where U_lift ∝ S_yy/h². Here S_yy is the particle stresslet normal to the wall and h is the distance of RBC centroid away from the wall. For large enough values of h, the stresslet is almost a linear function of the shear rate. Further, the effective repulsive velocity from homogeneous collisions (i.e., RBC–RBC) is proportional to the collision frequency, which scales linearly with shear rate. These two competing effects have the same linear scaling with the shear rate and thus, the cell-free layer thickness remains almost insensitive to shear rate as shown in Fig. 6. Stiff particles, however, undergo larger cross-stream displacement than deformable particles in heterogeneous pair collisions⁴² (e.g., platelet–RBC). As the shear rate increases upon increasing the flow rate or the degree of constriction, the frequency of heterogenous collisions increases, which in turn enhances platelet’s lateral drift toward the wall as shown by platelet trajectories in Fig. 13 and average platelet concentration contours in Fig. 10.

Although platelet transport has been the focus of this study, it is interesting to know how spherical particles behave in such geometries. Fig. 14 presents the concentration profile of rigid spherical particles having the same volume of platelets downstream of 75% constriction. The platelet concentration is plotted for comparison. This result suggests that spherical particles undergo similar enhanced margination downstream of constrictions. Noting that leukocytes are also spherical and nearly rigid with larger size, this result suggests the advantages of using microfluidic devices with constriction to separate stiff particles from softer RBCs in blood.

Fig. 14.

Concentration profiles of stiff spherical particles and platelets downstream of 75% constriction. The mean hematocrit of blood is 25%. Fraction of marginated particles is 83.6% for platelets and 79% for spherical particles.

At high shear rates, initial platelet adhesion and arrest is primarily through binding between platelet’s GPIbα receptors and vWF multimer’s A1 domain. vWF is a large multimer with a mean length in the range of 175–350 nm.^45,46 However, this length is highly uncertain and may vary due to conformational changes at different shear rates. The present results are relevant primarily to vascular constrictions such as stenosis, however, they can be used to explain platelet deposition onto the thrombus as well. These results suggest that a combined effect of the bulging shape of thrombus/geometrical centering of RBCs, and the hydrodynamic interaction of RBCs with platelets tend to enhance platelet deposition onto the thrombus. At high blood hematocrits, platelets tend to slide very close to the wall increasing their adhesion probabilities, whereas at lower blood hematocrits, tumbling motions may bring the platelets closer to the wall.

In conclusion, we have established a mesoscopic particlebased model which is able to quantify flow of blood and its particulates in complex geometries while resolving the cells hydrodynamic interactions. Future applications of the present model will be focused on platelet adhesion and translocation in such geometries under high-shear rate environments such as in atherosclerotic plaques.

Appendix

Fluid–cell and cell–cell interactions

Fluid–cell interactions are achieved achieved through viscous friction using the dissipative and random DPD forces. The repulsive-force coefficient for the coupling interactions is set to zero. The dissipative coefficient γ is computed such that no-slip condition on cell surface is enforced. The derivation of γ is based on the idealized case of linear shear flow over a patch of RBC membrane. The total shear force exerted by the fluid on a patch of area A is Aηγ̇. In DPD discrete form, we distribute a number of particles on the wall to mimic the membrane vertices. The force on a single wall particle exerted by the fluid can be found as follows

$$F_{\mathrm{s}}={\int }_{v_{\mathrm{h}}}ng(r){\mathbf{f}}^{\mathrm{D}}\mathrm{d}V,$$ (11)

where f^D is the DPD dissipative force between fluid particles and membrane vertices, n is the fluid number density, g(r) is the radial distribution function of fluid particles with respect to the membrane particles, and v_h is the half sphere volume of fluid above the wall. The total shear force on area A is equal to N_vF_s, where N_v is the number of wall particles on the patch with area A. Further, since the repulsive conservative force is zero, the radial distribution function is uniform i.e., g(r) = 1. The dissipative coefficient γ can then be computed through the equality of N_vF_s = Aηγ̇. Table 3 presents the parameters used for fluid–cell interactions in this study.

Table 3.

DPD parameters for fluid–cell interaction forces

Cell	rc	ac	γ	k
RBC	1.5	0.0	48.4	0.2
Platelet	1.5	0.0	10.0	0.2

In order to prevent cells overlap we typically use stronger conservative repulsive forces between DPD particles on RBC and platelet membranes. For more effective prevention of cells overlap, it is also possible to use a Morse potential in the form of

$$V_{\mathrm{M}}(r)=D_{\mathrm{e}}[{\mathrm{e}}^{2\beta (r_0-r)}-2{\mathrm{e}}^{\beta (r_0-r)}],$$ (12)

where r is the separation distance, r₀ is the zero force distance, D_e is the well depth of the potential, and β characterizes the interaction range. By properly setting the parameters we can ensure strong repulsive forces between cell membrane particles and prevent their overlap. We present the Morse potential parameters used for cell–cell interactions in Table 4 noting that the cutoff radius for all the Morse interactions is set as r_cM = 1.

Table 4.

Morse potential parameters for cell–cell interactions

Type	De	β	r0
RBC–RBC	5.0	2.0	0.95
RBC–platelet	10.0	2.0	1.0
Platelet–platelet	10.0	2.0	1.0

Mapping to physical units

Assuming the length scale of the DPD system to be [L] = 10⁻⁶ m, the time scale [t] can be evaluated by eqn (8) if hematocrit H_ct = 0 (e.g. platelet rich plasma) or by eqn (9), otherwise. Here, for brevity, we only consider flow of blood and we use eqn (9):

$$[t]={10}^{-6}\frac{1.2\times {10}^{-3}}{148}\frac{100}{4.5\times {10}^{-6}}=1.802\times {10}^{-4}\mathrm{s},$$ (13)

where we used the viscosity of plasma η^P = 1.2 × 10⁻⁶ Pa s, and the RBC shear modulus⁴⁷ ${\mu }_{\mathrm{s}}^{\mathrm{P}}=4.5\times {10}^{-6}{\text{Nm}}^{-1}$. The force scale is related to the RBC membrane relaxation time and is defined by the membrane shear modulus as

$$[F]=[L]\frac{{\mu }_{\mathrm{s}}^{\mathrm{P}}}{{\mu }_{\mathrm{s}}^{\mathrm{M}}}={10}^{-6}\frac{4.5\times {10}^{-6}}{100}=4.5\times {10}^{-14}\mathrm{N}.$$ (14)

Further, the DPD system thermal energy (energy scale) is computed by

$$\begin{array}{l}[E]\equiv {(k_{\mathrm{B}}T)}^{\mathrm{M}}=\frac{{\mu }_{\mathrm{s}}^{\mathrm{P}}}{{\mu }_{\mathrm{s}}^{\mathrm{M}}}{[L]}^2=\frac{4.5\times {10}^{-6}\times {10}^{-12}}{100}\\ =4.5\times {10}^{20}\equiv 10.87{(k_{\mathrm{B}}T)}^{\mathrm{P}},\end{array}$$ (15)

where k_B = 1.3806 × 10⁻²³ J K⁻¹ is the Boltzmann constant, and T = 300 K is considered for the room temperature. The thermal energy of the DPD system remains fixed, and the RBC membrane bending rigidity taken⁴⁸ k_c ≈ 72(k_BT)^P, which is scaled to 6.667 in DPD units.