Increased Detection of Genetic Loci Associated With Risk Predictors of Osteoporotic Fracture Using a Pleiotropic cFDR Method

Abstract

Although GWAS have been successful in identifying some osteoporosis associated loci, the findings explain only a small fraction of the total genetic variance. In this study we use a recently developed novel pleiotropic conditional false discovery rate (cFDR) method to identify novel genetic loci associated with two risk traits for osteoporotic fracture (the clinical outcome and end result of osteoporosis), Height (HT) and Femoral Neck (FNK) BMD. The cFDR method allows us to improve the detection of associated variants by incorporating any potentially shared genetic mechanisms between the two associated traits. We analyzed the summary statistics from two GWAS meta-analyses for single nucleotide polymorphisms (SNPs) that are associated with HT and FNK BMD. Using the cFDR method, we show enrichment in the identification of SNPs associated with each trait conditioned on their strength of association with the second trait. The findings revealed 18 SNPs that are associated with both HT and FNK BMD, 4 of which had not previously been reported to play a role in bone health. The novel SNPs located at KIF1B and the intergenic region between FERD3L and TWISTNB are noteworthy as these genes may be associated with processes that are functionally important in bone metabolism. By leveraging GWAS results from related phenotypes we identified several novel loci that may contribute to the proportion of variability explained for each trait, although we cannot speculate about these potential contributions to heritability based on this analysis alone.

Introduction

Incidence of osteoporosis is a common occurrence among older adults that is characterized by reduced bone mineral density (BMD), deficiencies in the structure of bone tissue, as well as an increased susceptibility to low trauma fractures. According to the Centers for Disease Control (CDC), it is estimated that at least 16% of US adults above the age of 65 exhibit clinical symptoms of osteoporosis at either the lumbar spine or femoral neck [1]. BMD is a highly heritable trait as the effect of genetics is estimated to account for as much as 75% of the variance in BMD at the site of the femoral neck [2]. Despite the fact that previous genome-wide association studies (GWAS) have identified more than 60 genetic loci associated with BMD [3, 4], these loci in total explain <10% of BMD heritability [5]. The large proportion of unexplained heritability suggests that further endeavors and innovative approaches are needed to identify novel genes/variants important for osteoporosis risk.

There is ample evidence to show that many complex phenotypes, including BMD, are likely to be influenced by numerous loci with small to modest effect sizes, and that even with the meta-analysis approach the traditional GWAS may still lack the sufficient power to detect the majority of these associations [6]. The main limitation of the standard GWAS is that they generally test for association among a large number of variants using a relatively small number of subjects. While it may be true that GWAS typically explore the association with common SNPs and that part of the missing heritability may be attributed to those variants that are rare, most of this unexplained variability is still due to low power resulting from a lack of adequate sample size in combination with small effect sizes [6]. To explain a greater proportion of the phenotypic heritability we must adopt novel statistical methods that can increase the effective sample size by using more information embedded in the existing data sets and samples.

Previous studies have suggested that many genetic loci contain variants that influence several different traits [7] – a situation referred to as pleiotropy. Although the true extent of pleiotropy in the human genome remains unknown it is currently estimated that at least 5% of SNPs and 17% of genes are involved in pleiotropic effects [7]. The presence of pleiotropy in the genome implies that traits correlated with one another may also have overlapping genetic determinants. We hypothesized that by incorporating the pleiotropic effects among related disease risk factors, we could identify novel genetic loci that are associated with the risk of osteoporotic fracture. This is because we can greatly enlarge the sample sizes for detecting pleiotropic loci by effectively and efficiently combining existing samples dedicated to the studies of individual traits.

Recently, Andreassen et al [8] proposed a novel genetic pleiotropy-informed conditional false discovery rate (cFDR) method for GWAS analysis. This method can incorporate the summary statistics from GWAS studies for two related traits to test variants for association with one phenotype conditional on different strengths of association with the second. A major advantage of the cFDR method is that it allows us to focus specifically on the subset of variants with a given strength of association in the conditional phenotype. Therefore, this method can greatly lessen the burden of multiple testing and subsequently improve the detection of trait-associated variants. Andreassen et al innovatively applied this method and successfully discovered novel loci that are associated with two genetically similar mental health diseases, Schizophrenia and Bipolar Disorder. Since it was originally developed, the cFDR method has become a commonly used approach to identify pleiotropic variants associated with correlated traits [9–11].

In this study, we applied the cFDR method on GWAS summary statistics data from two large meta-analysis studies [12, 13] with an aim to identify novel variants having pleiotropic effects on two correlated traits related to risk of osteoporotic fracture namely, height (HT) and femoral neck (FNK) BMD [14, 15]. It was previously believed that bone density did not influence height and could only decrease height through bone deformities, however current studies have suggested otherwise. Studies have found that maximal height tends to occur around the age of 30–35, which coincides with the time of peak bone mass [16]. Additionally, lower bone mineral density has a greater influence on height loss in the femur than the lumbar spine [16]. Based on intuition, it seems reasonable to expect lumbar density to have the greater influence since a weak spine would lead to poor posture and in turn result in reduced height. Therefore, these findings suggest that bone mineral density may influence height beyond the impact of bone strength on posture and that BMD may affect the length of the bones as well.

While the majority of studies have looked at the association of BMD with change in height or with BMI (a function of height), there are few studies that have looked at correlation between BMD and height directly. The phenotypic correlation between BMD and height in adults is estimated to be around 0.2–0.3 [17]. Although the correlation between BMD and height may be only moderate, this relationship suggests the possibility of pleiotropic effects through overlapping genetic mechanisms. We believe that taken together these findings justify the hypothesis that there may be pleiotropic SNPs exerting an effect on both traits.

Recent findings have determined the number of gene regions associated with HT to be in excess of 400 [18], while other GWAS studies have identified dozens of loci that are both associated with FNK BMD and thought to be involved in bone health [3, 4]. Despite these discoveries, to date researchers have only been able to explain a small proportion of the heritability in both HT and FNK BMD. The objective of this study is to better characterize the genetic mechanisms that underlie these traits, and to better understand how they impact overall bone health and development.

Materials and Methods

GWAS Datasets

The dataset containing the results for association with HT was taken from a GWAS meta-analysis of 253,288 subjects performed by the Genetic Investigation of Anthropometric Traits (GIANT) Consortium [12]. This was a meta-analysis to determine the strength of association between HT and more than 2 million genotyped or imputed SNPs. The data contained summary statistics, providing the p-values for association and direction of effect for each variant after controlling for genomic inflation at both the individual study level and again following the meta-analysis.

The dataset containing the results for association with FNK BMD was from a GWAS meta-analysis involving 53,236 subjects performed by the Genetic Factors for Osteoporosis (GEFOS) Consortium [13]. This meta-analysis used whole genome sequencing, whole exome sequencing and deep imputation of genotype data to identify variants associated with three BMD traits; FNK BMD, Lumbar Spine BMD, and Forearm BMD. This data also contained summary statistics, showing the associations between the three traits and more than 10 million SNPs. To our knowledge, this meta-analysis is the largest currently published in the field of bone health.

Although the FNK BMD data contains approximately five times the number of SNPs as the HT data, there is no evidence to suggest a sample size bias in the applied methods. Additionally, it is often necessary to adjust GWAS results using genomic control to ensure that the variance estimates for each SNP are not inflated due to population structure. However, for each of the two original datasets the authors had previously applied genomic control and therefore it was not necessary to re-apply the adjustment in this analysis.

Data Preparation

We began by first annotating and mapping SNPs to genes for the two GWAS studies and then combining the summary statistics for the 984,907 SNPs that were common. This was followed by a linkage disequilibrium (LD) based pruning method to remove large correlations between pairs of variants. The pruning algorithm begins with a window of 50 SNPs where LD is calculated between each pair of SNPs, and if pairs have an R² value greater than 0.2 then one of that pair is removed. The LD threshold of 0.2 used in this pruning method is the standard cutoff value used in other applications of the cFDR method throughout the literature. We used a minor allele frequency (MAF) pruning strategy where for pairs with R²>0.2 the SNP with the smaller MAF was removed. Following this initial removal of SNPs, the window slides 5 SNPs forward and the process repeats until there are no pairs of SNPs that are in high LD. The dataset was pruned using the HapMap 3 genotypes. At the end of the pruning process, there were 119,950 variants remaining to be used in the analysis.

Statistical Analysis

We first define some basic terminology that is necessary to understand the applied statistical methods. In the cFDR analysis, “principal trait” refers to the phenotype for which the association is being tested and “conditional trait” denotes the second phenotype. The term “pleiotropic enrichment” refers to an increase in the number of loci associated with the principal trait when restricting the analysis to include only the SNPs with stronger levels of association in the conditional trait. We further detail the assessment of pleiotropic enrichment and calculation of the cFDR statistic below.

Stratified Plots for Pleiotropic Enrichment

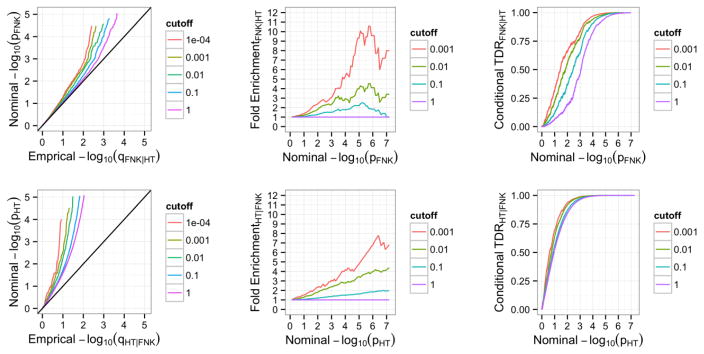
We present conditional Q-Q plots based on varying levels of significance in the conditional trait to compare the observed distribution of the p-values in the principal trait to the uniform [0,1] distribution of p-values expected when there is no significant enrichment. We plot the Q-Q curve for the quantiles of nominal −log₁₀(p) values for association of the subset of variants that are below each significance threshold in the conditional trait. The nominal −log₁₀(p) values are plotted on the y-axis and the quantiles of the nominal p-values are plotted on the x-axis. Pleiotropic enrichment is assessed by the degree of leftward shift from the expected distribution of p-values under no enrichment (diagonal line) that is observed when restricting the analysis to include SNPs with a greater strength of association in the conditional trait. The degree of spacing between conditional Q-Q plots contains important information about the extent of pleiotropy between the two traits. Larger spacing between conditional Q-Q plots indicates a greater extent of pleiotropic genes shared between traits.

The presence of pleiotropic effects suggests that the proportion of SNPs associated with the principal trait at any given significance level varies based on the level of association in the conditional trait. We present fold-enrichment plots of −log₁₀(p) values to compare the proportion of SNPs reaching each level of association for the conditional subsets versus the group including all SNPs. We are most interested in the fold-enrichment for SNPs reaching the level of genome-wide significance, denoted as −log₁₀(p) ≥ 7.3. The existence of pleiotropy is observed as an upward shift in the level of fold-enrichment when restricting the subset to SNPs with stronger levels of association in the conditional trait.

Additionally, the subsets of SNPs with the strongest level of enrichment are more likely to be associated with the principal trait. Therefore, the change in enrichment level across the different cutoff groups is associated with an increase in the True Discovery Rate (1 - FDR). The TDR is estimated as 1 – (p/q), where p is a given p-value of association and q is the quantile calculated as the number of SNPs with p-values less than or equal to p divided by the total number of SNPs in the group. For each ordering (FNK|HT and HT|FNK) we present stratified TDR plots of −log₁₀(p) values to compare the TDR for the conditional subsets versus the group including all SNPs.

Calculation of Conditional FDR

The calculation of the cFDR extends from the single phenotype case, where the unconditional false discovery rate for a set of variants is characterized as the probability of a false positive association. The cFDR expands this idea to the two phenotype case and is defined as the probability that a SNP has a false positive association with the principal trait given that the p-values for association with both the principal and conditional phenotypes are at least as small as the observed p-values.

$$\mathit{cFDR}\left(p_i|p_j\right)=Pr\left(H_0^{(i)}|P_i\le p_i,P_j\le p_j\right)$$ (1)

The cFDR is expressed as cFDR(p_i|p_j) where p_i represents the observed strength of association for a particular variant with the principal phenotype and p_j represents the observed significance level for that same SNP with the conditional phenotype. The term $H_0^{(i)}$ represents the null hypothesis that there is no association between a particular SNP and the principal trait.

Using the summary statistics from the pruned dataset, the conditional false discovery rates for each variant were computed following the steps outlined by Andreassen et al [8]. We computed the cFDR for each variant in the case where HT is the principal phenotype conditioned on strength of association with FNK BMD (HT|FNK BMD) as well as the reverse (FNK BMD|HT). In order to determine if the cFDR method results in the enrichment of associated SNPs, we successively restricted the subset of SNPs being tested based on the level of significance for the association of each variant with the conditional trait using the following criteria for P_j ≤ p_j; P_j ≤ 1 (all SNPs), P_j ≤ 0.1, P_j ≤ 0.01, P_j ≤ 0.001, P_j ≤ 0.0001. SNPs were determined to be significantly associated with the principal phenotype when the cFDR was computed to be smaller than 0.05.

After computing the cFDR for each variant with both orderings of the two traits, we computed the conjunction cFDR (ccFDR) value to identify loci that are associated with both traits. The ccFDR is defined as the probability that a given SNP has a false positive association with both traits and was calculated as the maximum cFDR value between the two orderings of the traits.

$$\mathit{ccFDR}=max\left({\mathit{cFDR}}_{i\mid j},{\mathit{cFDR}}_{j\mid i}\right)$$ (3)

All SNPs with a ccFDR value smaller than 0.05 were considered to be significantly associated with both traits, and we present a conjunction Manhattan plot to illustrate the locations of pleiotropic genetic variants.

Functional Term Enrichment Analysis

In order to evaluate the potential functions of the trait associated loci identified by cFDR, we used a hypergeometric test to perform functional term enrichment analyses with the GO terms database provided by the Gene Ontology Consortium. The program GOEAST was used to determine the GO terms that are enriched among the genes mapped to SNPs with significant cFDR values. Using the GO term enrichment analysis we characterize trait-associated loci based on their known biological processes and molecular functions. This analysis allows us to validate our findings by determining gene sets that are significantly associated with bone metabolic processes. The functional term enrichment analysis was performed for the set of SNPs with cFDR smaller than 0.05 for FNK BMD as well as for the set of SNPs with cFDR smaller than 0.01 for HT. The differing significance thresholds for inclusion of SNPs in the functional term enrichment analysis are tailored to the empirical findings for each trait. There are many more genetic loci that influence HT than other complex traits, and therefore we chose to use a more stringent selection criteria to limit the analysis to a smaller subset of SNPs with higher significance levels.

Results

Assessment of Pleiotropic Enrichment

The conditional Q-Q plot for FNK BMD given nominal p-values of association with HT (Fig 1) shows some enrichment across varying significance thresholds for HT. The presence of leftward shift when restricting the analysis to include the SNPs that have more significant associations with HT indicates an increase in the number of true associations for a given HT p-value. Based on the fold-enrichment plot (Fig 1) we observe an 8-fold increase in the proportion of SNPs reaching the genome wide significance level when comparing the subset with the most stringent conditional association to the group with all SNPs.

Figure 1. Stratified plots to assess pleiotropic enrichment.

Stratified QQ plots of nominal versus empirical -log₁₀ p-values for Upper Left: FNK BMD as a function of significance of the association with HT, and Lower Left: HT as a function of significance of the association with FNK BMD. The diagonal line represents the null hypothesis of no enrichment. Fold-enrichment plots of enrichment versus nominal -log₁₀ p-values for Upper Middle: FNK BMD as a function of significance of the association with HT, and Lower Middle: HT as a function of significance of the association with FNK BMD. The purple line with slope of zero represents all SNPs. Stratified True Discovery Rate (TDR) plots of the conditional TDR versus nominal -log₁₀ p-values for Upper Right: FNK BMD conditional on strength of association with HT, and Lower Right: HT conditional on strength of association with FNK BMD.

Enrichment is also observed for HT given FNK BMD (Fig 1) though clearly there are many more genetic factors contributing to the heritability of HT compared to FNK BMD, as evidenced by the earlier departure from the null line at all conditional thresholds. These earlier deflections indicate a greater proportion of true associations for any given FNK BMD nominal p-value. The fold-enrichment plot (Fig 1) shows approximately a 7-fold increase in the proportion of SNPs associated with the principal trait at the genome wide significance level between the group of SNPs with strongest association in the conditional trait and the group with all SNPs.

The increase in pleiotropic enrichment across subsets of SNPs is associated with an increase in conditional TDR, which is defined as one minus conditional FDR [8]. The increase in TDR across groups is shown for FNK BMD conditioned on HT as well as HT conditioned on FNK BMD (Fig 1). The TDR plots indicate that there is a much larger fold-increase across pleiotropic groups for FNK BMD conditional on HT than HT conditional on FNK BMD, as evidenced by a larger degree of spacing between the different groups.

FNK BMD loci identified with cFDR

Conditional on their association with HT, we identified a total of 46 significant SNPs (cFDR < 0.05) for FNK BMD variation (Supplementary Table 1), which were mapped to 16 different chromosomes. In the original meta-analysis for FNK BMD [13], 27 of these 46 SNPs had p-values smaller than 1×10⁻⁵ while 9 SNPs reached genome-wide significance at 5×10⁻⁸. The 46 SNPs identified to be associated with FNK BMD are enriched in the intergenic (43.5%) and intronic (54.3%) genomic regions. Furthermore, 11 of these variants are enriched in the gene ontology (GO) term “skeletal system development”, although no other GO terms are highly enriched for the FNK BMD associated loci (Table 1).

Table 1.

Functional Term Enrichment Analysis

GO Term	Gene Count	P-value	FDR
FNK BMD loci
Skeletal System Development	6	2.5×10−5	0.03542
HT loci
Skeletal System Development	67	3.8×10−11	6.7×10−8
Ossification	31	4.2×10−8	7.8×10−5
Bone Development	32	6.0×10−8	1.1×10−4
Osteoblast Differentiation	17	2.3×10−7	4.2×10−4
Cartilage Development	25	9.6×10−9	1.8×10−5

HT gene loci identified with cFDR

We identified a total of 4,599 SNPs significantly (cFDR < 0.05) associated with HT given their association with FNK BMD, which were located on all the 22 chromosomes. Of these 4,599 SNPs, 1,439 had p-values smaller than 1×10⁻⁵ while 750 reached genome-wide significance at 5×10⁻⁸ in the original meta-analysis for HT [12]. Of the SNPs identified by the cFDR analysis, four were located at HMGA2, one at QSOX2, eight at CYP19A1, and four at ZBTB38. All these four genetic loci have been shown to be associated with the HT trait in previous GWAS height studies [18–22]. Similar to the FNK BMD trait, most of the identified SNPs reside in the intronic (41.1%) and intergenic (54.9%) regions while a small proportion are located in the untranslated regions (1.61%) or nearby transcription start sites (2.11%).

When performing the functional term enrichment analysis of these results we included 2,570 SNPs that were retained after LD pruning and had cFDR < 0.01 (Supplementary Table 2). This analysis indicated a large number of HT loci were enriched in several skeletal metabolism related functional terms (Table 1), such as “skeletal system development”, “ossification”, “bone development”, “osteoblast differentiation”, and “cartilage development”.

Pleiotropic gene loci for both FNK BMD and HT

To identify genetic loci that are associated with both HT and FNK BMD, we computed the conjunction cFDR (ccFDR) value, which is defined as the probability that a given SNP has a false positive association with both the principal and conditional traits. The ccFDR analysis identified 18 independent pleiotropic loci that were significantly (ccFDR < 0.05) associated with both traits (Fig 2 and Table 2). Of the 18 identified pleiotropic variants, 4 of these were novel findings, as they are not previously mentioned in any BMD or HT related research. All of these 4 novel SNPs, rs17400878 (KIF1B), rs10950710 (FERD3L and TWISTNB), rs10510109 (BTBD16 and PLEKHA1), and rs7193150 (GPR139 and GP2) had p-values larger than 1×10⁻⁵ and thus may be easily missed/ignored in individual GWAS analysis, but ccFDR values smaller than 0.05 due to the presence of pleiotropic effects (Table 2).

Figure 2. Manhattan plot of conjunction -log₁₀ FDR values for FNK BMD and HT.

The red line marking the conjunction -log₁₀ FDR value of 1.3 corresponds to ccFDR < 0.05. The figure shows the chromosomal locations of identified pleiotropic loci.

Table 2.

Conjunction cFDR: Pleiotropic Loci in FNK BMD and HT

SNP	Role	Chr	Neighbor Gene	Raw P-Value		cFDR		ccFDR
				FNK	HT	FNK|HT	HT|FNK
rs6494633a	intronic	15q22.33	SMAD3	7.59E-06	1.40E-04	2.12E-03	4.80E-04	2.12E-03
rs2289263a	intronic	15q22.33	SMAD3	3.79E-04	1.30E-07	2.84E-02	2.23E-06	2.84E-02
rs3759579a	upstream	14q32.32	MARK3	3.31E-05	2.60E-07	3.56E-03	1.73E-06	3.56E-03
rs12050772a	intronic	15q21.2	CYP19A1	1.29E-04	6.60E-09	1.09E-02	1.04E-07	1.09E-02
rs6040061a	intronic	20p12.2	JAG1	9.52E-05	3.20E-03	4.22E-02	1.95E-02	4.22E-02
rs13137552a	intergenic	4q22.1	DMP1 IBSP	6.36E-05	1.00E-03	2.09E-02	6.00E-03	2.09E-02
rs9905128a	intergenic	17q24.3	PRKAR1A	4.33E-06	9.90E-05	1.28E-03	3.63E-04	1.28E-03
rs10793939a	intergenic	9q34.11	FUBP3	6.14E-05	7.20E-10	6.98E-03	1.42E-08	6.98E-03
rs17277372b	intronic	1q24.3	DNM3	7.80E-07	9.20E-25	3.74E-05	1.38E-23	3.74E-05
rs2741856b	intergenic	17q21.31	MEOX1 SOST	1.34E-09	1.50E-08	6.32E-07	1.05E-07	6.32E-07
rs6715538b	intronic	2p16.2	SPTBN1	1.06E-04	5.20E-04	2.88E-02	3.69E-03	2.88E-02
rs11952384b	intronic	5q14.3	MEF2C-AS1	3.82E-07	3.10E-10	1.21E-04	4.03E-09	1.21E-04
rs10474292b	intergenic	5q14.3	MEF2C-AS1 MIR3660	3.14E-08	2.80E-09	1.22E-05	2.24E-08	1.22E-05
rs10280461b	intergenic	7p14.1	EPDR STARD3NL	1.28E-06	1.10E-08	1.44E-04	4.68E-08	1.44E-04
rs17400878c	intronic	1p36.22	KIF1B	3.19E-04	3.60E-07	2.41E-02	4.96E-06	2.41E-02
rs10950710c	intergenic	7p21.1	FERD3L TWISTNB	2.54E-04	5.10E-05	4.32E-02	6.18E-04	4.32E-02
rs10510109c	intergenic	10q26.13	BTBD16 PLEKHA1	2.64E-05	7.50E-03	2.22E-02	3.28E-02	3.28E-02
rs7193150c	intergenic	16p12.3	GPR139 GP2	5.54E-05	6.80E-03	4.00E-02	4.31E-02	4.31E-02

Note:

^aThis SNP or other SNPs in LD was/were previously reported to be associated with bone development

^bThis gene is previously reported to be associated with bone development but the SNP is not

^cThis SNP and gene have neither been reported to be associated with bone development, FNK BMD, HT, or other related traits

On the other hand, 8 of these 18 variants, rs6494633 (SMAD3), rs2289263 (SMAD3), rs3759579 (MARK3), rs12050772 (CYP19A1), rs6040061 (JAG1), rs13137552 (DMP1 and IBSP), rs9905128 (PRKAR1A), and rs10793939 (FUBP3) were reported in previous association studies for BMD [3, 23–27] and additional 6 SNPs, rs17277372 (DNM3), rs2741856 (MEOX1 and SOST), rs6715538 (SPTBN1), rs11952384 (MEF2C-AS1), rs10474292 (MEF2C-AS1 and MIR3660), and rs10280461 (EPDR and STARD3NL) were not identified by previous research but are located at or near the genes that are associated with osteoporosis and other bone related traits [24, 26].

Discussion

In this analysis we combined the summary statistics from two GWAS meta-analyses to exploit the pleiotropic effects of variants that are associated with HT and FNK BMD. Compared to a standard single phenotype analysis, simultaneously analyzing multiple related traits allows for the increased discovery of trait-associated variants without requiring additional and larger datasets for individual traits [8]. Additionally, it allows us to further explore the common genetic mechanisms between related phenotypes. The detection of novel susceptibility loci with pleiotropic effects may lead to a better understanding of disease origin/mechanisms and have a critical impact on the clinical treatment and prevention of related complex phenotypes simultaneously.

We applied a recently developed cFDR approach to the pleiotropic analysis. This method exploits the idea that a variant with significant effects in two associated traits is more likely to be a true effect, and therefore has a higher probability of being detected in multiple independent studies. This technique allows for an increase in effective sample size and therefore a subsequent increase in power to detect true associations for more variants with small to intermediate effect sizes. In the original implementation of the cFDR method, the authors used a model-based approach to show that when pleiotropic effects exist between correlated traits, a large proportion of variants that are significant for one trait are also significant for the second trait leading to an increase in detection power [8]. Through simulation, the authors showed that compared with the unconditional FDR for a single trait analysis, using the cFDR method resulted in an increase of 15–20 times the number of non-null SNPs discovered for a local FDR smaller than 0.05 [8].

It is important to note that the cFDR method has an underlying assumption that the study samples for both traits are independent. In this analysis, the study samples are not completely independent as some cohorts were included in the meta-analysis for both traits. After comparing the sample sizes for the shared cohorts we found that approximately 7% of the HT study individuals were included in the FNK BMD meta-analysis and 34% of the FNK BMD subjects were included in the HT study sample. When there are overlapping samples the increase in effective sample size is not as great as what would be expected when the studies are independent. Although there is a well outlined procedure for calculating the effective sample size for a case/control extension of cFDR when control subjects are shared between studies, it is unclear how this method can be generalized to determine the effective sample size for quantitative traits with overlapping samples [28]. While the overall gain in power may be reduced due to the shared samples, there is still an improvement in terms of significant novel SNPs compared to single trait analysis.

Based on the fundamental idea of cFDR that variants having significant effects in both traits are more likely to have a true effect, an alternative approach to detecting novel pleiotropic loci is to perform a meta-analysis of FNK BMD and HT. While the traditional meta-analysis approach can also provide an increase in statistical power, there are clear advantages to using the cFDR method when the traits of interest are correlated. In comparison to the meta-analysis approach, which only allows for detection of loci with the same direction of allelic effects in both traits, the cFDR method allows for the detection of loci regardless of their effect directions [6].

In the current study, we identified 18 pleiotropic SNPs that are associated with both HT and FNK BMD. Eight of these SNPs were previously identified to be associated with BMD and are also located at genes known to play important roles in influencing bone health. The two pleiotropic SNPs (rs6494633 and rs2289263) located at SMAD3, an osteoporosis candidate gene [29], are known to be associated with BMI, Osteoarthritis, and rheumatoid arthritis [23]. There was one pleiotropic SNP (rs13137552) located at DMP1 that is known to be associated with osteoporosis [3], and the DMP1 gene plays a key role in the regulation of mineralization in the bone as well as osteogenic gene expression [26]. The two SNPs rs3759579 and rs12050772 are also known to be associated with BMD and are located at MARK3 and CYP19A1 respectively, two additional genes that are linked to bone health [3, 24, 26, 27]. In addition, the SNP located at the JAG1 locus (rs6040061) is associated with BMD in three independent cohorts of European descent [25]. Finally, the two SNPs rs9905128 (PRKAR1A) and rs10793939 (FUBP3) were previously identified to be associated with bone health in the GEFOS2 cohort [4].

The identified SNPs located at loci 1q24.3 (DNM3) [30], 2p16.2 (SPTBN1) [3, 4, 31, 32], 5q14.3 (MEF2C) [33], 7p14.1 (EPDR1 and STARD3NL) [3, 34], and 17q21.31 (MEOX1 and SOST) [35] are not mentioned in previous bone GWAS studies, but they are located at or near genes that are associated with BMD. This subset of variants accounts for 33% of all associated pleiotropic variants identified in this analysis. The 14 pleiotropic SNPs that were either identified in previous studies or located near genes known to play a role in bone health may furnish empirical partial validation for the cFDR method to successfully identify disease associated genetic loci.

More importantly, we identified 4 novel BMD-HT associated loci that have not been reported in previous BMD or height related GWAS. The SNPs located at loci 1p36.22 (KIF1B), 7p21.1 (FERD3L and TWISTNB), 10q26.13 (BTBD16 and PLEKHA1), and 16p12.3 (GPR139 and GP2) along with the genes they are located at or near have not been discussed in other bone research. The subset of SNPs located at these loci account for 22% of all associated pleiotropic variants identified in the analysis. The novel loci on 1p36.22 (KIF1B) and 7p21.1 (FERD3L and TWISTNB) are particularly interesting.

The SNP rs17400878 (1p36.22) is located in the intronic region of the KIF1B gene, which encodes proteins that transport mitochondria and synaptic vesicle precursors [36]. Based on a mouse model, impaired transport of synaptic vesicle precursors and muscle weakness could be caused by heterozygosity of the KIF1B gene [36]. In a separate study, silencing the KIF1B gene inhibited expression of membranal MT1-MMP (membrane type 1-matrix metalloproteinase) [37]. MMPs play a functional role in the initiation of bone resorption [38] as well as osteoclast recruitment and differentiation [39]. MT1-MMP activates latent TGF-beta, a protein believed to prolong the life span of osteoblasts by delaying the transformation from osteoblasts into osteocytes [40]. Therefore, the MT1-MMP preserves osteoblasts by activating TGF-beta. Taken together, all the evidence suggests that the genetic variants in KIF1B gene may contribute to the variation in BMD via influencing expression of MT1-MMP and TGF-beta.

The SNP rs10950710 (7p21.1) is an intergenic variant located close to the FERD3L (Fer3-like bHLH transcription factor) and TWISTNB (TWIST Neighbor) genes. FERD3L and TWISTNB are associated with craniosynostoses [41, 42]. Craniosynostosis is a genetic disease that causes premature closure of the cranial sutures in an infant’s skull, resulting in changes in the growth pattern of the bone. Recently, a 9.0 Mb deletion in 7p21.1-p21.3 (chr7:10,661,799–19,661,326, hg19) which encompasses rs10950710 was detected in a case of Craniosynostosis using a microarray-based comparative genomic hybridization (array-CGH) [42]. Additionally, in an earlier study a 2.5 Mb deletion in 7p21 was detected in patients with a Craniosynostosis related phenotype, Saethre-Chotzen syndrome, by in silico analysis [41]. To our knowledge there have not been any animal models or functional validation experiments for this signal.

Despite these novel findings, there are several important limitations of the applied method due to the cross sectional design of the study. Firstly, we cannot use GWAS summary statistics data to estimate the contribution of the novel findings to the proportion of variability explained in the traits of interest. In order to determine how much the novel SNPs add to either trait’s variance we would need to analyze the raw genotype data for both traits, which is unavailable. Additionally, we cannot differentiate between the two pleiotropic cases where either a single locus directly affects both traits, or the locus affects only one trait and the change in one phenotype in turn impacts the second trait. However, given longitudinal data this question could be addressed using the cross-lagged panel model or other causal modeling approaches [43]. A third limitation is that when using GWAS summary statistics data there is no way to decompose the apparent association to determine which trait contributes more influence to each pleiotropic signal.

We also acknowledge that the cFDR approach cannot be used for the definitive identification of causal variants. The purpose of this type of association analysis is to address the missing heritability problem that persists in genetic association studies by identifying some novel SNPs that add to the total proportion of variability explained. We aim to introduce some novel findings without being overly speculative about their importance and functional roles. The goal of this specific study was to identify potential novel loci (and substantiate some earlier-identified genes) to stimulate further functional validation studies. Those novel and shared common pleiotropic genes identified in this analysis should be followed up in future fine mapping studies and functional mechanistic experiments of the GWAS associated regions to determine their clinical significance.

In summary, by incorporating pleiotropic effects into a conditional analysis we showed there is significant pleiotropy between BMD and HT, two traits closely related to risk of osteoporotic fracture. We detected several novel pleiotropic loci for BMD and HT and our results provide insight into the shared genetic influences of height and BMD as well as the ways in which the trait-associated loci impact bone health.

Highlights.

• Used pleiotropic cFDR method to detect novel loci associated with two risk predictors for osteoporotic fracture, Height and Femoral BMD

• Showed enrichment of SNPs associated with the first trait conditional on their strength of association with the second trait

• Simultaneously analyzed GWAS summary statistics from single trait GWAS analysis for both phenotypes

• Identified several novel potential pleiotropic loci that may be involved in bone processes