Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2017 Apr 24;44(8):3456–3464. doi: 10.1002/2017GL073048

Global observations of magnetospheric high‐m poloidal waves during the 22 June 2015 magnetic storm

G Le 1,✉, P J Chi 2, R J Strangeway 2, C T Russell 2, J A Slavin 3, K Takahashi 4, H J Singer 5, B J Anderson 4, K Bromund 1, D Fischer 6, E L Kepko 1, W Magnes 6, R Nakamura 6, F Plaschke 6, R B Torbert 7
PMCID: PMC5488625  PMID: 28713180

Abstract

We report global observations of high‐m poloidal waves during the recovery phase of the 22 June 2015 magnetic storm from a constellation of widely spaced satellites of five missions including Magnetospheric Multiscale (MMS), Van Allen Probes, Time History of Events and Macroscale Interactions during Substorm (THEMIS), Cluster, and Geostationary Operational Environmental Satellites (GOES). The combined observations demonstrate the global spatial extent of storm time poloidal waves. MMS observations confirm high azimuthal wave numbers (m ~ 100). Mode identification indicates the waves are associated with the second harmonic of field line resonances. The wave frequencies exhibit a decreasing trend as L increases, distinguishing them from the single‐frequency global poloidal modes normally observed during quiet times. Detailed examination of the instantaneous frequency reveals discrete spatial structures with step‐like frequency changes along L. Each discrete L shell has a steady wave frequency and spans about 1 R E, suggesting that there exist a discrete number of drift‐bounce resonance regions across L shells during storm times.

Keywords: high‐m poloidal waves, field line resonances, magnetic storm, ULF waves, magnetospheric multiscale mission

Key Points

  • Observed long‐lasting high‐m poloidal waves associated with second harmonics of field line resonances during a major magnetic storm

  • Demonstrated global spatial extent of storm time poloidal FLR region using observations from a constellation of widely spaced satellites

  • Revealed discrete spatial structures of resonant L shells with step‐like frequency changes

1. Introduction

Magnetospheric ultra‐low‐frequency (ULF) pulsations with high azimuthal wave numbers (m > ~15), or small azimuthal wavelengths, are typically of the poloidal mode with periods 100 s or longer, which is the field line resonance (FLR) eigenmode with magnetic field perturbations in the radial direction and electric field perturbations in the azimuthal direction [Sugiura and Wilson, 1964]. Although disturbances both external and internal to the magnetosphere can drive magnetospheric ULF waves, internal plasma instabilities caused by non‐Maxwellian ion distributions or phase space density radial gradient are generally regarded to be the energy source of high‐m poloidal waves. They include the drift‐bounce resonant instability due to pressure gradients and the magnetic field gradient and curvature [Southwood et al., 1969; Chen and Hasegawa, 1988, 1991] and drift mirror instability due to temperature anisotropy [Hasegawa and Chen, 1989; Chen and Hasegawa, 1991]. Ring current populations are considered to be the dominant energy source for storm time poloidal waves. High‐m poloidal waves have received considerable attention recently because they can exchange energy with energetic particles and thus are of potential importance to the dynamics of the inner magnetosphere [Zong et al., 2009].

Since high‐m waves are difficult to detect on the ground due to the atmospheric screening effect, satellite observations are essential to study these waves [Hughes and Southwood, 1976; Kokubun et al., 1989]. Statistical surveys of satellite data indicate that poloidal waves frequently occur in the outer ring current region (L ~ 5–9) in both geomagnetically quiet and active times and have been observed at all local times [Kokubun et al., 1989; Anderson et al., 1990; Zhu and Kivelson, 1991; Hudson et al., 2004; Liu et al., 2009; Dai et al., 2015]. The azimuthal wave numbers for poloidal waves were first determined directly using measurements from two or three spacecraft with small azimuthal separations and confirmed to be high m (~40–120) [Hughes et al., 1979; Takahashi et al., 1985a]. More recently, multiple satellite missions have provided more opportunities for direct determination of m numbers and occurrence statistics [e.g., Eriksson et al., 2005; Schäfer et al., 2007; Liu et al., 2009; Le et al., 2011; Takahashi et al., 2013; Chi and Le, 2015].

Although previous surveys have established the global occurrence of high‐m poloidal waves, they rarely provide information about the radial and azimuthal extent of the waves at the time of occurrence. These wave characteristics are tied to their generation mechanisms. Determining the spatial extent of the waves requires extended coverage of wave region by multiple satellites with simultaneous measurements. Studies of large‐scale properties of high‐m waves using widely spaced satellites have been scarce. Zong et al. [2009] studied shock‐excited waves using nine satellites and observed both poloidal and toroidal waves with comparable intensity at L = 4.4, but only toroidal waves at geosynchronous orbit. Korotova et al. [2016] observed poloidal waves that occurred simultaneously over a local time extent of ~10 h during the recovering phase of a magnetic storm. In this paper, we report a rare example in which storm time high‐m poloidal waves are observed globally by 15 satellites from five missions including Magnetospheric Multiscale (MMS), Van Allen Probes, Time History of Events and Macroscale Interactions during Substorm (THEMIS), Cluster, and Geostationary Operational Environmental Satellites (GOES), covering L values between ~4 and 12 as well as local times from the morning, noon, afternoon, and postdusk local time sectors. The long‐lasting waves occur on 23–25 June, during the recovery phase of a major magnetic storm that started on 22 June 2015. In the next sections, we will present global observations of wave properties and discuss their implications for wave generation.

2. Observations

A strong and long‐lasting magnetic storm was triggered on 22 June 2015 by joint forces of three coronal mass ejections from the Sun [Liu et al., 2015]. Figure 1 shows the IMF and solar wind conditions from ACE as well as the SYM‐H index (the 1 min high‐resolution global storm index) for 22 through 25 June. The storm main phase lasted for about 1/2 day, and the Dst minimum reached to −207 nT at the end of the storm main phase, ~0425 UT on 23 June. The recovery phase lasted for about 1 week. The event of interest occurred in the early recovery phase, from ~14 UT on 23 June to the end of 25 June. During this interval, 15 satellites from MMS, Van Allen Probes, GOES, Cluster, and THEMIS missions all observed, at times, poloidal waves in the frequency band ~3–30 mHz.

Figure 1.

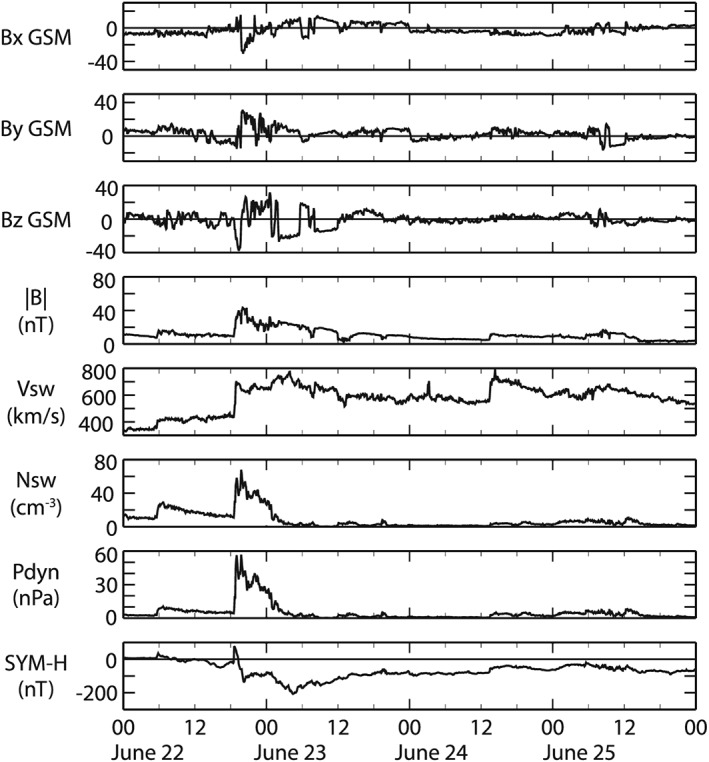
Figure 1

Open in a new tab

The IMF and solar wind data from ACE as well as the SYM‐H index for the 22 June 2015 storm.

Figure 2 presents an overview of the global occurrence characteristics of the poloidal waves as observed by the fleet of satellites during the early recovery phase. The dynamic power spectrograms for the poloidal component of the magnetic field cover the time period in the recovery phase, from 12 UT on 23 June to the end of 25 June. For MMS, Cluster, and THEMIS (A/D/E) missions, we only show the spectrogram from one of the satellites for each mission because of the similarity among the closely spaced satellites. The poloidal component, b ν , is radially outward and perpendicular to the background magnetic field (calculated by moving averages with a 5 min window). The wave power displayed is associated with the first difference of the poloidal magnetic field component. The gaps in the spectrograms correspond mostly to the times when the satellites are either outside the magnetosphere or inside L = 2 and also to a few short intervals of bad data points.

Figure 2.

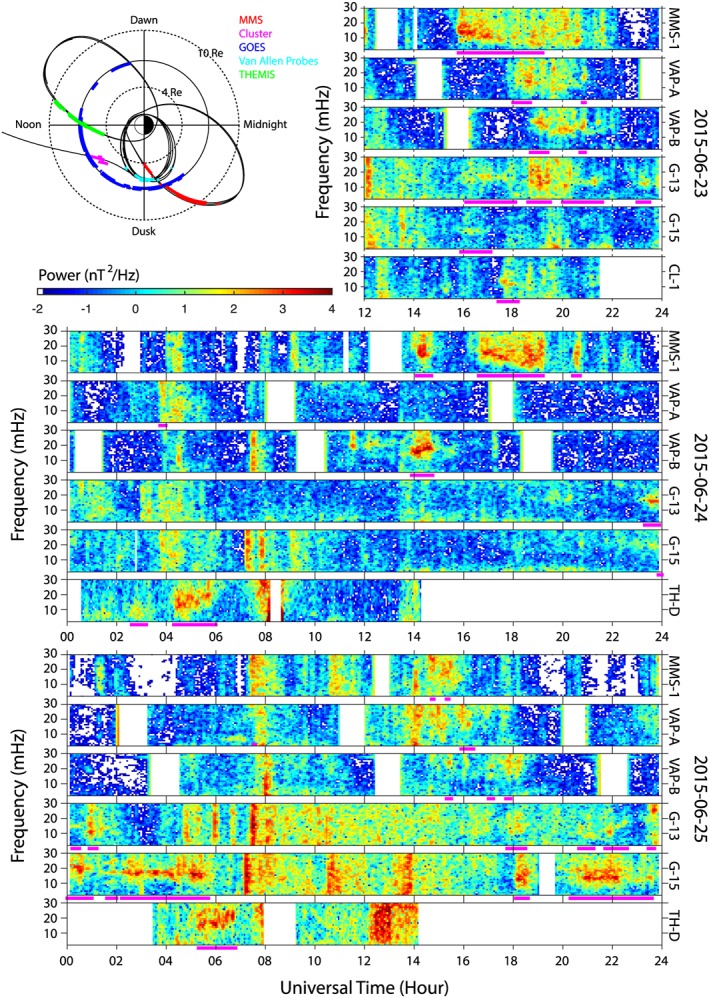
Figure 2

Open in a new tab

Spectrograms of poloidal component of the magnetic field (b ν) observed by MMS, Val Allen Probes, GOES 13/15, Cluster, and THEMIS from 1200 UT, 23 June to the end of 25 June. Horizontal bars indicate the poloidal wave intervals. In the top left panel, the black traces are the satellite orbits, and color‐coded segments are the locations of the wave intervals.

We identify the poloidal wave intervals in the data based on the narrowbanded peaks in ~3–30 mHz frequency range in the spectrograms and mark them as horizontal bars under each spectrogram. If the spectral peaks are present in both poloidal and toroidal components, the waves are considered to be poloidal mode only if the poloidal wave power is stronger than the toroidal power. It is evident in the spectrograms that all the satellites observed poloidal waves at times during this interval. The waves were first observed by MMS and GOES at ~1550 UT on June 23 and later by all other spacecraft. We believe that the wave onset time is ~1550 UT.

The locations of the satellites are shown in top left panel of Figure 2. The thin black traces are the trajectories of the satellites mapped to the magnetic equator along the dipole field lines in solar magnetic (SM) coordinates. The two dashed circles are for L = 4 and L = 10, respectively. In the orbit plot, the colored segments along the orbit tracks are the satellite locations corresponding to the poloidal wave intervals identified in the spectrograms. They include the wave intervals from all 15 satellites, but the same color is used for all satellites in the same mission. The distribution of these wave intervals shows that the poloidal waves have been observed in the region with L values from ~4 to 12 within a large local time range spanning the entire dayside and into the premidnight sector. In particular, MMS observed the waves in the same region in three consecutive orbits on June 23–25. These observations, and those from the other missions during these 3 days, strongly suggest that the wave activities persisted for the entire period.

The highly precise magnetic field measurements by MMS can well resolve the phase shifts in the poloidal magnetic field components (b ν) among the four satellites despite their close separations, allowing for the determination of the azimuthal wave numbers (m) of the waves. Figure 3 (first to third rows) shows the time series for 45 minutes of the wave magnetic field from MMS (1545–1630 UT on 23 June), including the compressional (b μ), poloidal (b ν), and azimuthal (b φ) components. The poloidal waves are highly compressional and consist of wave packets with variable amplitudes. The magnetic fields observed by the four satellites appear to be almost identical, but small and clear time lags are found among the satellites. For any two satellites that are separated longitudinally, the azimuthal phase shift of the wave can be measured due to such separation. Four MMS satellites can provide six of such measurements. Figure 3 (fourth row) show the observed phase shifts (time lags) as a function of longitudinal separations for the six pairs formed by MMS satellites for three selected waves intervals. The time lag is determined by cross‐correlation analysis of the poloidal components (b ν) observed by each pair. The red lines are the least squares fits. The fitted slopes in the three examples are −28, −12, and −24, and the wave periods are 74 s, 72 s, and 72 s, respectively. These results imply that the m numbers of the adjacent poloidal waves are −135, −62, and −119, respectively. The negative sign of the wave number indicates that the azimuthal wave vector k is directed westward, which is in the same direction of the proton drift. The estimated values of m numbers, on the order of 100, confirm that they are indeed high‐m poloidal waves.

Figure 3.

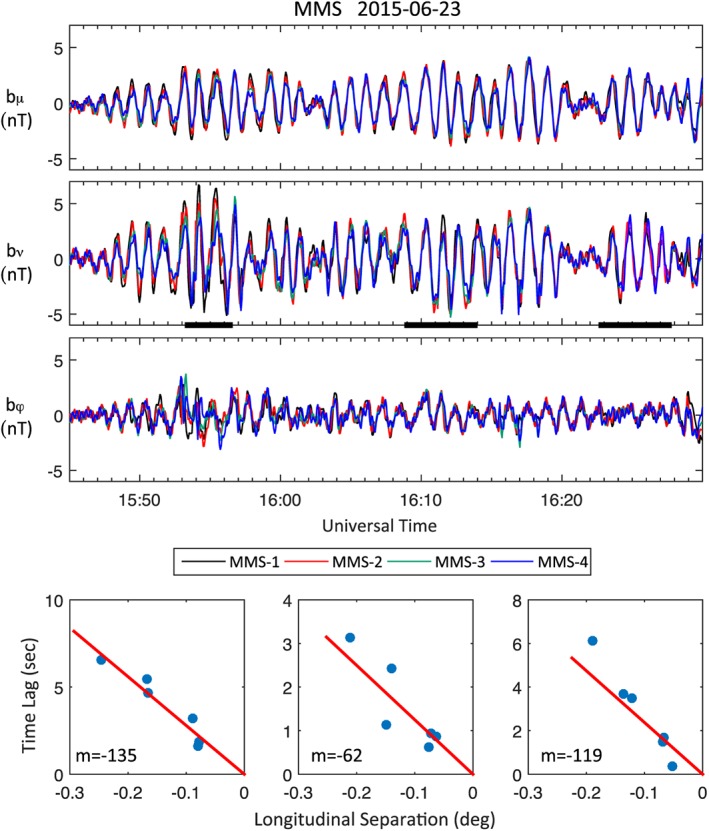
Figure 3

Open in a new tab

(first to third rows) MMS wave magnetic field in field‐aligned (μ), poloidal (ν), and toroidal (φ) directions. The three horizontal bars indicate the time intervals selected for estimating the azimuthal wavenumbers. (fourth row) The observed time lags in b ν versus longitudinal separations between MMS satellites.

The identification of even or odd modes of the standing field line resonance can be directly inferred from the phase difference between the magnetic and electric field perturbations [Singer et al., 1982; Takahashi et al., 2011]. For a field line with two footpoints in the northern and southern ionosphere, the odd harmonics of field line resonance will have the magnetic field nodes (b ν = 0) and electric field antinodes (maximum E φ) at the equator. For even harmonics, the electric field nodes (E φ = 0) and magnetic field antinodes (maximum b ν) are at the equator. A field line resonance always involves a 90° phase difference between E φ and b ν everywhere along the field line, but the sign of this phase difference varies with the observer's location and the harmonic number. For a spacecraft located slightly north of the equator, b ν lags E φ for the even harmonic, whereas b ν leads E φ for the odd harmonic. Figure 4 shows two 10 min intervals of the magnetic field and electric field perturbations observed by Van Allen Probes, which were located slightly north of the equator. The magnetic wave b ν lagged the electric wave E φ by 90°, indicating clearly the wave is associated with an even harmonic. The observed frequency is in the range of ~10–20 mHz at Van Allen Probes near the apogee. The analysis of the toroidal component of the waves (not shown) indicates that the observed poloidal frequency is that of the second harmonic. This is also consistent with previous Van Allen Probes observations of the second harmonic FLR frequencies at similar locations [Nosé et al., 2015].

Figure 4.

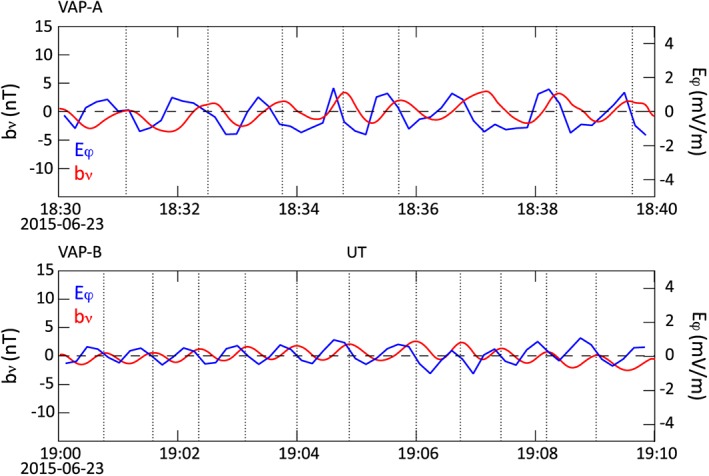
Figure 4

Open in a new tab

Poloidal component of the magnetic field (red) and azimuthal component of the electric field (blue) for two wave intervals observed by Van Allen Probes A and B, respectively. Vertical dotted lines are placed at peaks of b v for guides only.

Although the observed high‐m poloidal waves were present over a large region in the inner magnetosphere, we observed noticeable spatial variations of wave frequencies. In the spectrograms in Figure 2, we note that the wave frequencies change (either increase or decrease) with time. This is most evident in the MMS data where intense waves were observed over an extended period across a large range of L values. Apparently, the wave frequencies are a function of L as they decrease with increasing L values consistently, as shown in Figure 5a. The points in Figure 5a represent the average frequencies of the wave packets within the poloidal wave intervals identified in Figure 2. If a wave interval is longer than 20 min, multiple points are plotted, each for a 20 min segment.

Figure 5.

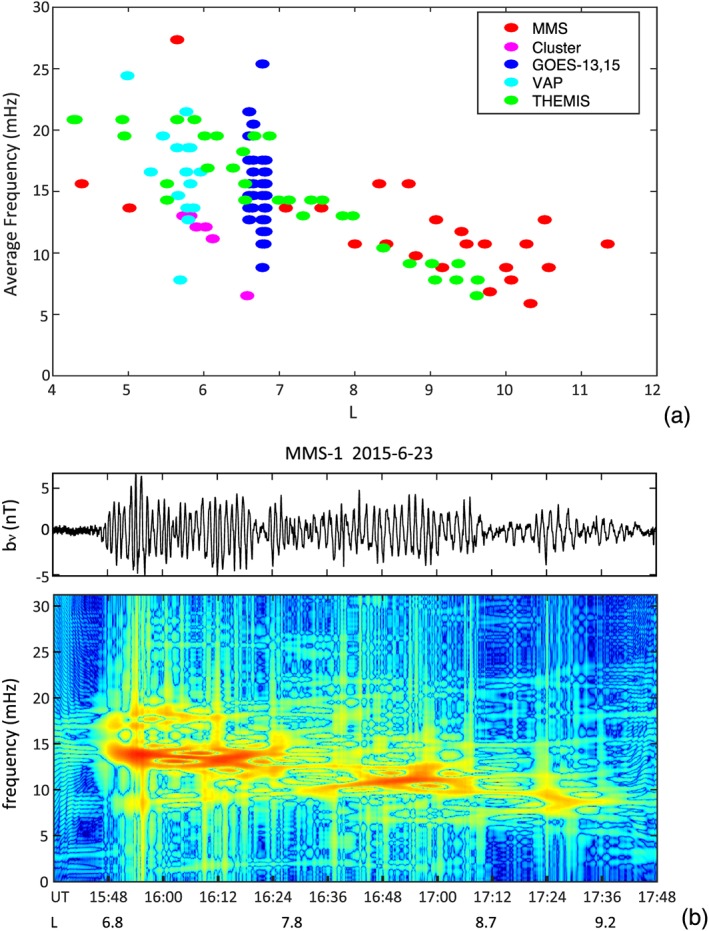
Figure 5

Open in a new tab

(a) average wave frequency as a function of L. (b) poloidal component of (top) the magnetic field and (bottom) the instantaneous wave frequencies estimated from Wigner‐Ville distribution for the outbound pass of MMS‐1 on 23 June 2015, covering the region with L from ~6.8 to ~9.2 in postdusk local times.

A detailed analysis of the instantaneous wave frequency reveals discrete poloidal mode structures along L. In Figure 5b (top) shows nearly 2 h of b ν from the outbound pass of MMS‐1 on 23 June 2015, covering the region with L from ~6.8 to ~9.2 in postdusk local times. Figure 5b (bottom) is the time‐frequency representation estimated from the Wigner‐Ville Distribution (WVD). Chi and Russell [2008] provide detailed discussions about WVD and its application to different types of ULF waves. Since WVD does not contain a windowing function, as those in Fourier and wavelet frameworks, by correlating the signal with a time‐ and frequency‐translated version of itself, it provides the highest possible resolution in the time‐frequency plane. This approach is very effective in detecting changing characteristics of nonstationary signals and also comes with a well‐known trade‐off of the interference terms that can be seen in the spectrogram. The instantaneous frequencies as shown in Figure 5b (bottom) suggest that there are discrete structures of poloidal waves along the spacecraft orbit; i.e., the wave frequency changes discretely with L. Inside each discrete structure, the wave frequency is nearly constant, and the frequency abruptly changes when the spacecraft moves to the next structure. Each discrete structure has a radial extent of ~1 R E. The Van Allen Probes also observed similar discrete frequency structures at L values between 5.7 and 6.1 (not shown). To our knowledge, this is the first observation of discrete structures of poloidal waves in the radial direction.

Spatial variations in the azimuthal direction are also apparent, as the waves are stronger in the dusk and postdusk sectors. This is most evident in the spectrograms of MMS, Van Allen Probes, and GOES data. The most intense waves occurred in ~18–21 LT sector where the partial ring current peaks during storm times.

3. Discussion and Conclusions

Using the observations from widely spaced satellites associated with five missions, we examine high‐m poloidal waves that occurred during the recovery phase of 22 June 2015 magnetic storm. Our observations reveal distinct features in the spatial characteristics of storm time high‐m poloidal waves, which are new and not available from any previous statistical surveys. First, our multisatellite observations have clearly demonstrated that storm time high‐m poloidal waves can occur “globally”; i.e., the region of field line resonance has a large spatial extent in the inner magnetosphere which spans many L shells and local time sectors. The resonance region in our observations is much more extended than previously reported cases with 1.5–8 h in the azimuthal extent [Engebretson et al., 1992] and up to 1.7 R E radial extent [Singer et al., 1982; Takahashi et al., 1985b]. This global extent of the resonance region should not be confused with the global distributions of the wave occurrence rates obtained from statistical surveys based on single‐satellite observations [e.g., Hudson et al., 2004; Liu et al., 2009; Dai et al., 2015]. While these statistical surveys established the global occurrence of the waves, the spatial distribution of the wave occurrence rate does not imply a similar spatial extent of the resonance region at any given time.

Second, the spatial structures within the resonance region for storm time high‐m poloidal waves provide new insight into their generation mechanisms. For toroidal mode waves with magnetic field perturbations in the azimuthal direction, ideal MHD predicts that field line resonance is radially singular and each field line oscillates independently with its own eigenfrequency [Chen and Hasegawa, 1974; Southwood, 1974; Cheng et al., 1993; Denton et al., 2003]. Thus, the frequency of toroidal waves changes with L in the magnetosphere due to the gradual changes in the length of the field line and the plasma mass density. On the other hand, poloidal mode waves have field lines that oscillate radially, meaning that their frequency cannot change with L easily. Phase mixing and efficient damping of the waves would occur if radial oscillations of neighboring L shells were not in sync. Observations indeed show that poloidal mode waves often exhibit nearly constant frequency across L shells [e.g., Takahashi et al., 1987; Chi and Le, 2015]. For example, in our previous observations at low altitudes using Space Technology 5 data, we found that high‐m poloidal mode waves could maintain a steady Pc5 frequency across L shells from L ~ 4 to 8 [Chi and Le, 2015]. The mechanism often invoked to explain such constant frequency for poloidal waves is the so‐called global poloidal mode theory in which a poloidal mode can be trapped in a region where the poloidal frequency has a dip with respect to L [Vetoulis and Chen, 1994, 1996; Denton and Vetoulis, 1998]. Using spacecraft observations of poloidal wave events (all observed during quiet times), Denton et al. [2003] calculated the poloidal frequency as a function of L and confirmed that these waves did occur in association with the poloidal frequency dip.

The frequency characteristics of the storm time poloidal waves presented in this study are quite peculiar. On one hand, it is evident that the frequency of the poloidal waves exhibits a decreasing trend as a function of L (Figure 5a), which is different from the single‐frequency global poloidal mode waves observed during quiet times. On the other hand, the poloidal waves also exhibit discrete structures in L, where the frequency remains constant in each discrete structure and changes only when entering into another discrete structure. The radial extent of the discrete structures is ~1 R E. These observations show new features that have not been reported before, probably because Fourier analysis does not offer adequate temporal and frequency resolution in the power spectrogram. The likely explanation for such observations is that during storm times, there are ample supplies of energetic particles that can provide free energy to poloidal waves at the local FLR frequency for a wide range of L shells. As these waves oscillate in the poloidal direction and interact with their counterparts in neighboring L shells, waves will rapidly undergo destructive interference if they are at different frequencies. In other words, poloidal waves in neighboring L shells need to oscillate at a constant frequency to be able to survive. However, they can maintain a constant frequency only within a limited range of L shells to be compatible with locally excited poloidal FLRs. Our observations also clearly demonstrate the difference in the radial profile of wave frequency between storm time and quiet time poloidal waves. Future studies should contrast the plasma and energetic particle characteristics associated with storm time and quiet time poloidal mode waves to understand their generation mechanisms and provide guidance to numerical modeling and simulations.

In summary, we present multimission, global observations of high‐m poloidal waves during the recovery phase of the major magnetic storm starting on 22 June 2015. The data came from a constellation of 15 satellites from five missions including MMS, Van Allen Probes, THEMIS, Cluster, and GOES, covering L values between ~4 and 12 as well as all local times. The observations by such a constellation of widely spaced satellites demonstrate that storm time high‐m poloidal waves are long lasting and can occur globally. Highly accurate magnetic field data from the four MMS satellites enable us to detect the azimuthal phase shifts and determine the m numbers to be ~100. Simultaneous measurements of electric and magnetic fields from Van Allen Probes have enabled us to determine that the poloidal waves are associated with the second harmonic FLR. The wave frequencies range from 8 to 22 mHz, with a decreasing trend as the L value increases. The L‐dependent frequencies indicate that they are of different type from the global poloidal mode, which is common during periods of low geomagnetic activity and would be nearly monochromatic across different L shells. The storm time high‐m poloidal waves in our observations show discrete spatial structures. Each structure has a steady wave frequency and spans about 1 R E in the radial direction, suggesting that there exist a discrete number of drift‐bounce resonance regions across L shells for storm time global poloidal waves.

Acknowledgments

We thank Vassilis Angelopoulos for useful discussions of THEMIS data. We thank the JHU/APL Van Allen Probes team for providing the magnetic field and electric field data. Science work at JHU/APL was supported by NASA grant NNX14AB97G. We acknowledge use of NASA/GSFC's Space Physics Data Facility's CDAWeb service for obtaining the ACE interplanetary magnetic field data, ACE solar wind plasma data, the SYM‐H index, the magnetic field data from Cluster and THEMIS, and the magnetic and electric field data from Van Allen Probes. We acknowledge use of NOAA Space Weather Prediction Center for obtaining GOES magnetometer data. MMS data are available at CDAWeb and MMS Science Data Center at https://lasp.colorado.edu/mms/sdc/public/. We thank the entire team of NASA's MMS mission for the dedication and expertise in its successful development and operations.

Le, G. , et al. (2017), Global observations of magnetospheric high‐m poloidal waves during the 22 June 2015 magnetic storm, Geophys. Res. Lett., 44, 3456–3464, doi:10.1002/2017GL073048.

References

  1. Anderson, B. J. , Engebretson M. J., Rounds S. P., Zanetti L. J., and Potemra T. A. (1990), A statistical study of Pc 3–5 pulsations observed by the AMPTE/CCE Magnetic Fields Experiment: 1. Occurrence distributions, J. Geophys. Res., 95(A7), 10495–10523, doi:10.1029/JA095iA07p10495. [Google Scholar]
  2. Chen, L. , and Hasegawa A. (1974), A theory of long‐period magnetic pulsations: 1. Steady state excitation of field line resonance, J. Geophys. Res., 79(7), 1024–1032. [Google Scholar]
  3. Chen, L. , and Hasegawa A. (1988), On magnetospheric hydromagnetic waves excited by energetic ring‐current particles, J. Geophys. Res., 93(A8), 8763–8767, doi:10.1029/JA093iA08p08763. [Google Scholar]
  4. Chen, L. , and Hasegawa A. (1991), Kinetic theory of geomagnetic pulsations: 1. Internal excitations by energetic particles, J. Geophys. Res., 96(A2), 1503–1512, doi:10.1029/90JA02346. [Google Scholar]
  5. Cheng, C. Z. , Chang T. C., Lin C. A., and Tsai W. H. (1993), Magnetohydrodynamic theory of field line resonances in the magnetosphere, J. Geophys. Res., 98(A7), 11339–11347, doi:10.1029/93JA00505. [Google Scholar]
  6. Chi, P. J. , and Le G. (2015), Observations of magnetospheric high‐m poloidal waves by ST‐5 satellites in low Earth orbit during geomagnetically quiet times, J. Geophys. Res. Space Physics, 120, 4776–4783, doi:10.1002/2015JA021145. [Google Scholar]
  7. Chi, P. J. , and Russell C. T. (2008), Use of the Wigner‐Ville distribution in interpreting and identifying ULF waves in triaxial magnetic records, J. Geophys. Res., 113, A01218, doi:10.1029/2007JA012469. [Google Scholar]
  8. Dai, L. , et al. (2015), Storm time occurrence and spatial distribution of Pc4 poloidal ULF waves in the inner magnetosphere: A Van Allen Probes statistical study, J. Geophys. Res. Space Physics, 120, 4748–4762, doi:10.1002/2015JA021134. [Google Scholar]
  9. Denton, R. E. , and Vetoulis G. (1998), Global poloidal mode, J. Geophys. Res., 103(A4), 6729–6739, doi:10.1029/97JA03594. [Google Scholar]
  10. Denton, R. E. , Lessard M. R., and Kistler L. M. (2003), Radial localization of magnetospheric guided poloidal Pc 4–5 waves, J. Geophys. Res., 108(A3), 1105, doi:10.1029/2002JA009679. [Google Scholar]
  11. Engebretson, M. J. , Murr D. L., Erickson K. N., Strangeway R. J., Klumpar D. M., Fuselier S. A., Zanetti L. J., and Potemra T. A. (1992), The spatial extent of radial magnetic pulsation events observed in the dayside near synchronous orbit, J. Geophys. Res., 97(A9), 13741–13758, doi:10.1029/92JA00992. [Google Scholar]
  12. Eriksson, P. T. I. , Blomberg L. G., Walker A. D. M., and Glassmeier K.‐H. (2005), Poloidal ULF oscillations in the dayside magnetosphere: A Cluster study, Ann. Geophys., 23, 2679–2686, doi:10.5194/angeo‐23‐2679‐2005. [Google Scholar]
  13. Hasegawa, A. , and Chen L. (1989), Theory of the drift mirror instability, in Plasma Waves and Instabilities at Comets and in Magnetospheres, edited by Tsurutani B. T. and Oya H., pp. 173–177, AGU, Washington, D. C., doi:10.1029/GM053p0173. [Google Scholar]
  14. Hudson, M. , Denton R., Lessard M., Miftakhova E., and Anderson R. (2004), A study of Pc‐5 ULF oscillations, Ann. Geophys., 22, 289–302. [Google Scholar]
  15. Hughes, W. J. , and Southwood D. J. (1976), The screening of micropulsation signals by the atmosphere and ionosphere, J. Geophys. Res., 81(19), 3234–3240. [Google Scholar]
  16. Hughes, W. J. , McPherron R. L., Barfield J. N., and Mauk B. H. (1979), A compressional Pc4 pulsation observed by three satellites in geostationary orbit near local midnight, Planet. Space Sci., 27, 821–840. [Google Scholar]
  17. Kokubun, S. , Erickson K. N., Fritz T. A., and McPherron R. L. (1989), Local time asymmetry of Pc 4–5 pulsations and associated particle modulations at synchronous orbit, J. Geophys. Res., 94(A6), 6607–6625, doi:10.1029/JA094iA06p06607. [Google Scholar]
  18. Korotova, G. I. , Sibeck D. G., Engebretson M. J., Wygant J. R., Thaller S., Spence H. E., Kletzing C. A., Angelopoulos V., and Redmon R. J. (2016), Multipoint spacecraft observations of long‐lasting poloidal Pc4 pulsations in the dayside magnetosphere on May 1–2, 2014, Ann. Geophys., 34, 985–998, doi:10.5194/angeo‐34‐985‐2016. [Google Scholar]
  19. Le, G. , Chi P. J., Strangeway R. J., and Slavin J. A. (2011), Observations of a unique type of ULF wave by low‐altitude Space Technology 5 satellites, J. Geophys. Res., 116, A08203, doi:10.1029/2011JA016574. [Google Scholar]
  20. Liu, W. , Sarris T. E., Li X., Elkington S. R., Ergun R., Angelopoulos V., Bonnell J., and Glassmeier K. H. (2009), Electric and magnetic field observations of Pc4 and Pc5 pulsations in the inner magnetosphere: A statistical study, J. Geophys. Res., 114, A12206, doi:10.1029/2009JA014243. [Google Scholar]
  21. Liu, Y. D. , Hu H., Wang R., Yang Z., Zhu B., Liu Y. A., Luhmann J. G., and Richardson J. D. (2015), Plasma and magnetic field characteristics of solar coronal mass ejections in relation to geomagnetic storm intensity and variability, Astrophys. J. Lett., 809(2), doi:10.1088/2041‐8205/809/2/L34. [Google Scholar]
  22. Nosé, M. , et al. (2015), Formation of the oxygen torus in the inner magnetosphere: Van Allen Probes observations, J. Geophys. Res. Space Physics, 120, 1182–1196, doi:10.1002/2014JA020593. [Google Scholar]
  23. Schäfer, S. , Glassmeier K. H., Eriksson P. T. I., Pierrard V., Fornaçon K. H., and Blomberg L. G. (2007), Spatial and temporal characteristics of poloidal waves in the terrestrial plasmasphere: A CLUSTER case study, Ann. Geophys., 25, 1011–1024, doi:10.5194/angeo‐25‐1011‐2007. [Google Scholar]
  24. Singer, H. J. , Hughes W. J., and Russell C. T. (1982), Standing hydromagnetic waves observed by ISEE 1 and 2: Radial extent and harmonic, J. Geophys. Res., 87(A5), 3519–3529, doi:10.1029/JA087iA05p03519. [Google Scholar]
  25. Sugiura, M. , and Wilson C. R. (1964), Oscillation of the geomagnetic field lines and associated magnetic perturbations at conjugate points, J. Geophys. Res., 69(7), 1211–1216, doi:10.1029/JZ069i007p01211. [Google Scholar]
  26. Southwood, D. J. (1974), Some features of field line resonances in the magnetosphere, Planet. Space Sci., 22, 483–491. [Google Scholar]
  27. Southwood, D. J. , Dungey J. W., and Etherington R. J. (1969), Bounce resonant interaction between pulsations and trapped particles, Planet. Space Sci., 17(3), 349–361, doi:10.1016/0032‐0633(69)90068‐3. [Google Scholar]
  28. Takahashi, K. , Higbie P. R., and Baker D. N. (1985a), Azimuthal propagation and frequency characteristic of compressional Pc 5 waves observed at geostationary orbit, J. Geophys. Res., 90(A2), 1473–1485, doi:10.1029/JA090iA02p01473. [Google Scholar]
  29. Takahashi, K. , Russell C. T., and Anderson R. R. (1985b), ISEE 1 and 2 observation of the spatial structure of a compressional Pc 5 wave, Geophys. Res. Lett., 12, 613, doi:10.1029/GL012i009p00613. [Google Scholar]
  30. Takahashi, K. , Fennell J. F., Amata E., and Higbie P. R. (1987), Field‐aligned structure of the storm time Pc 5 wave of November 14–15, 1979, J. Geophys. Res., 92(A6), 5857–5864, doi:10.1029/JA092iA06p05857. [Google Scholar]
  31. Takahashi, K. , Glassmeier K.‐H., Angelopoulos V., Bonnell J., Nishimura Y., Singer H. J., and Russell C. T. (2011), Multisatellite observations of a giant pulsation event, J. Geophys. Res., 116, A11223, doi:10.1029/2011JA016955. [Google Scholar]
  32. Takahashi, K. , Hartinger M. D., Angelopoulos V., Glassmeier K.‐H., and Singer H. J. (2013), Multispacecraft observations of fundamental poloidal waves without ground magnetic signatures, J. Geophys. Res. Space Physics, 118, 4319–4334, doi:10.1002/jgra.50405. [Google Scholar]
  33. Vetoulis, G. , and Chen L. (1994), Global structures of Alfvén‐ballooning modes in magnetospheric plasmas, Geophys. Res. Lett., 21, 2091–2094, doi:10.1029/94GL01703. [Google Scholar]
  34. Vetoulis, G. , and Chen L. (1996), Kinetic theory of geomagnetic pulsations: 3. Global analysis of drift Alfvén‐ballooning modes, J. Geophys. Res., 101(A7), 15441–15456, doi:10.1029/96JA00494. [Google Scholar]
  35. Zong, Q.‐G. , Zhou X.‐Z., Wang Y. F., Li X., Song P., Baker D. N., Fritz T. A., Daly P. W., Dunlop M., and Pedersen A. (2009), Energetic electron response to ULF waves induced by interplanetary shocks in the outer radiation belt, J. Geophys. Res., 114, A10204, doi:10.1029/2009JA014393. [Google Scholar]
  36. Zhu, X. , and Kivelson M. G. (1991), Compressional ULF waves in the outer magnetosphere: 1. Statistical study, J. Geophys. Res., 96(A11), 19451–19467, doi:10.1029/91JA01860. [Google Scholar]

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES