Abstract
Tissues use feedback circuits in which cells send signals to each other to control their growth and survival. We show that such feedback circuits are inherently unstable to mutants that misread the signal level: Mutants have a growth advantage to take over the tissue, and cannot be eliminated by known cell‐intrinsic mechanisms. To resolve this, we propose that tissues have biphasic responses in and the signal is toxic at both high and low levels, such as glucotoxicity of beta cells, excitotoxicity in neurons, and toxicity of growth factors to T cells. This gives most of these mutants a frequency‐dependent selective disadvantage, which leads to their elimination. However, the biphasic mechanisms create a new unstable fixed point in the feedback circuit beyond which runaway processes can occur, leading to risk of diseases such as diabetes and neurodegenerative disease. Hence, glucotoxicity, which is a dangerous cause of diabetes, may have a protective anti‐mutant effect. Biphasic responses in tissues may provide an evolutionary stable strategy that avoids invasion by commonly occurring mutants, but at the same time cause vulnerability to disease.
Keywords: calcium homeostasis, design principles, evolutionary dynamics, mathematical models of disease, stem‐cell homeostasis, tissue homeostasis
Subject Categories: Quantitative Biology & Dynamical Systems, Signal Transduction
Introduction
Maintaining proper tissue size is a fundamental problem for multicellular organisms. To do so, cells must precisely coordinate their proliferation and death rates, because an imbalance in these rates leads to either excessive growth or degeneration. Moreover, cells must coordinate their growth in the face of fluctuations, such as injury, or changes in the target size of the tissue, such as during development. This coordination requires feedback control.
Feedback circuits for controlling tissue size regulate cell growth by a signal that is affected by the size of the tissue. Thus, when the tissue is too small, the growth rate is positive, and when it is too large, the growth rate is negative. Only when the tissue reaches a desired size are the proliferation and death rates equal and the system reaches steady state. An example of such a feedback is the control of the concentration of T cells by IL‐2 produced by the T cells (Hart et al, 2014). Another example occurs in endocrine tissues whose growth is regulated by the physiological variable that they control (Karin et al, 2016), such as in the control of beta‐cell mass by blood glucose. These physiological feedback circuits can show dynamical compensation mechanisms that make them robust with respect to variation in parameters, such as insulin resistance in the case of glucose control (Karin et al, 2016). Feedback is also found in tissues that are renewed by proliferating stem cells (Lander et al, 2009), such as skeletal muscle and olfactory epithelium.
For such feedback circuits to function properly, each cell must respond precisely to the input signal. These responses depend on the activity and expression of receptors, signaling pathways, and regulatory proteins and are thus susceptible to mutations. When a mutant cell with a dysregulated proliferative or apoptotic response arises, it may invade the population and thus break the homeostatic control. Mutant takeover leads to aberrant tissue size and function. Thus, mechanisms must be in place to prevent such takeover.
One mechanism for protection from mutant invasion is cell intrinsic and concerns the paradoxical activation of apoptosis by c‐myc (Lowe et al, 2004). C‐myc is a transcription factor that drives proliferation in many cell types (Bouchard et al, 1998), yet it paradoxically induces apoptosis when overexpressed (Evan et al, 1992). This paradoxical induction of apoptosis plays an important role in tumor suppression because it eliminates transformed cells (Harrington et al, 1994; Lowe et al, 2004).
Here, we extend the idea of cell‐intrinsic elimination of mutants to the level of circuits of communicating cells. We show that tissue feedback circuits are inherently sensitive to takeover by common types of mutants that misread the feedback signal, such as receptor loss‐of‐function or receptor locked‐on mutations. The feedback loop gives these mutants a growth advantage relative to wild‐type cells. We propose that mutant invasion can be prevented by a biphasic response mechanism, in which the signal is toxic to the cells at both low and high levels. Biphasic control gives the mutants a selective disadvantage compared to wild‐type cells, and the mutants are hence eliminated.
Biphasic control of growth is prevalent in physiological systems. Examples include the control of beta‐cell mass by glucose (Robertson et al, 2003), the control of mammary gland mass by estrogen (Lewis‐Wambi & Jordan, 2009), the control of neuronal survival by glutamate (Hardingham & Bading, 2003), epidermal growth factor signaling (Högnason et al, 2001), and the control of T‐cell concentration by IL2 and by antigen level (Critchfield et al, 1994; Hart et al, 2014). Biphasic control was also demonstrated for mechanical signaling—the control of epithelial cell proliferation by mechanical stretch through Piezo1 (Gudipaty et al, 2017). In all of these cases, signal is toxic at both high and low levels.
As mentioned above, we find that biphasic control can protect the tissue from invasion by commonly occurring mutants that mis‐sense the feedback signal. However, we show that this protective mechanism comes at a cost. The biphasic response introduces an unstable fixed point. If the input signal fluctuates beyond this unstable fixed point, a runaway phenomenon occurs in which cells are eliminated and signal diverges, potentially leading to disease. We discuss this tradeoff between stability to mutant invasion and risk of disease in several systems, including beta‐cell control of glucose, parathyroid control of calcium, stem‐cell differentiation, and excitotoxicity in neurons.
Results
Tissue homeostasis circuits are inherently vulnerable to invasion by sensing mutants
Feedback circuits that control tissue size act to balance the proliferation and removal rates of the cells. The cells adjust their growth rate (proliferation minus death/removal) as function of an input y, which in turn is affected by the size of the tissue (Figs 1A and B, and EV1A and B).
Figure 1. Biphasic control can resist mutant invasion of feedback circuits.
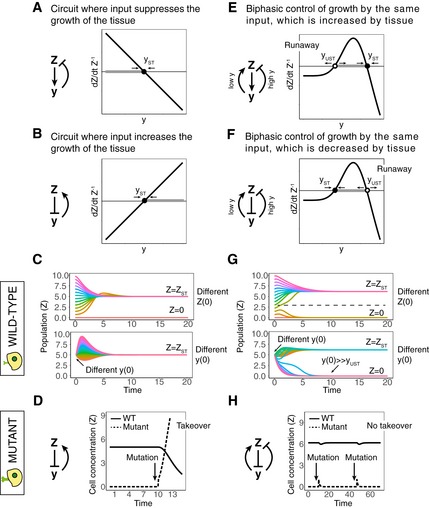
- A monophasic feedback circuit in which cells Z generate an input y that inhibits their growth rate. The population is at steady state Z = Z ST when y = y ST.
- A monophasic feedback circuit where cells Z decrease an input y, which increases their growth rate. The population is at steady state Z = Z ST when y = y ST.
- Trajectories of Z from different initial concentrations of cells (Z) (i) or y (ii) for the circuit of (B). The healthy concentration Z = Z ST is reached regardless of initial concentration of Z, as long as it is nonzero, and regardless of the initial concentration of y.
- An arrow marks the time when a mutant with a strong activation of the sensing of y arises (for the circuit depicted in B). This mutant has a selective advantage and takes over the population.
- A biphasic feedback circuit where Z generates a signal y, which, in turn, decreases the growth rate of Z at high concentrations and increases the growth rate of Z at low concentrations. The population is at steady state Z = Z ST when y = y ST, and there is also an unstable fixed point at y UST < y ST.
- A biphasic feedback circuit where cells Z inhibit y, which, in turn, decreases the growth rate of Z at high concentrations and increases the growth rate of Z at low concentrations. The population is at steady state Z = Z ST when y = y ST, and there is also an unstable fixed point at y UST > y ST.
- Trajectories of Z from different initial concentrations of Z (i) or y (ii) for the circuit depicted in (F). The healthy concentration Z = Z ST is not reached for small values of Z (Z << Z ST) or large values of y (y >> y UST).
- The arrows mark the times when a mutant with a strong activation of the sensing of y arises (for the biphasic circuit depicted in F). This mutant has a selective disadvantage and is thus eliminated.
Figure EV1. Phase plots of alternative tissue feedback circuits.
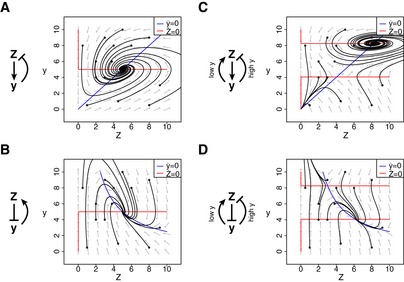
- A monophasic feedback circuit in which cells Z generate an input y that inhibits their growth rate. Trajectories from different initial concentrations of Z,y reach steady state at Z = Z ST , y = y ST.
- A monophasic feedback circuit in which cells Z inhibit y which increases their growth rate. Trajectories from different initial concentrations of Z,y reach steady state at Z = Z ST , y = y ST.
- A biphasic feedback circuit where Z generates a signal y, which, in turn, decreases the growth rate of Z at high concentrations and increases the growth rate of Z at low concentrations. Trajectories from different initial concentrations of Z,y either reach steady state at Z = Z ST , y = y ST, or, at low initial Z or high initial y, result in population collapse Z→0
- A biphasic feedback circuit where cells Z inhibit y, which, in turn, decreases the growth rate of Z at high concentrations and increases the growth rate of Z at low concentrations. Trajectories from different initial concentrations of Z,y either reach steady state at Z = Z ST , y = y ST, or, at low initial Z or low initial y, result in population collapse Z→0.
There are two possible cases. In the first case, the signal y increases with tissue size Z (i.e., Z activates y), and y inhibits the growth rate of the cells (Figs 1A and EV1A). If there are too many cells, y is large and growth rate is negative leading to reduction in tissue size. If there are too few cells, the opposite occurs and the tissue grows. This feedback loop guides the tissue to steady state at the point where growth rate is zero, at y = y ST.
In the second case, the signal y decreases with tissue size (Z inhibits y) and y increases the growth rate of the cells (Figs 1B and EV1B). The same considerations show that the tissue stably settles at y = y ST. These feedback circuits thus provide a stable tissue size, because different initial cell populations and different initial concentrations of y all converge on the same final population Z ST (Fig 1C). At the same time, the circuits also provide a stable signal level y = y ST.
We propose that such generic feedback circuits are susceptible to invasion by mutants that misread the signal. When such a mutant arises at steady state, it senses the actual signal level y ST as a larger or smaller value y MUT. In the case of Fig 1A, if the mutation causes a misreading of the signal as too low, as for example in a receptor‐inactivating mutation, the feedback loop provides the mutant with a growth advantage and the mutant will take over the population. As a result, the tissue will show aberrant growth and, when the mutant is at high enough frequency, will show a level of y that is too high, y > y ST.
In the case of Fig 1B, if the mutation causes a misreading of the signal as too high, as for example in a locked‐on receptor mutation, the feedback loop provides the mutant with a growth advantage (Fig EV2A). The mutant will take over the population (Fig 1D). As a result, the tissue will show aberrant growth and, when the mutant is at high enough frequency, will show a level of y that is too low, y < y ST (because in this case the tissue acts to reduce y). In both cases, sensing mutants can take over the population and only reach equilibrium again at an aberrant tissue size, leading to a breakdown of homeostatic control. Importantly, the same conclusion holds whether the growth of the cells is modeled as logistic or exponential (see Appendix Section S1), and when y acts in delay (see Appendix Section S2).
Figure EV2. Sensing mutations modulate the effect of input on growth rate.

- A monophasic feedback circuit in which cells Z inhibit y which increases their growth rate (solid line). A threefold activating mutation causes a shift in the response curve (dashed line), so the mutant mis‐senses the level of y to a higher level where the mutant has a positive growth rate.
- A biphasic feedback circuit where cells Z inhibit y, which, in turn, decreases the growth rate of Z at high concentrations and increases the growth rate of Z at low concentrations (solid line). A threefold activating mutation causes a shift in the response curve (dashed line), so the mutant mis‐senses the level of y to a higher level where the mutant has a negative growth rate.
Biphasic response can protect against mutant invasion but can cause vulnerability to disease
To overcome the problem of mutant invasion, the sensing mutants need to have a selective disadvantage. One way to do this is an alternative implementation of the feedback circuit, in which y affects the growth rate of Z in a biphasic manner (Figs 1E and F, and EV1C and D). The word biphasic means that the growth rate curve has an inverse‐U shape, with a rising and a falling phase—y stimulates the growth of Z at low concentrations and inhibits the growth of Z at high concentrations, so the signal is toxic (negative growth rate) at both low and high levels of y.
As with the monophasic circuits, here there are also two possible cases. In the first case, the signal y increases with tissue size Z (i.e., Z activates y). This circuit has a stable fixed point at y = y ST and an unstable fixed point at y = y UST where y UST < y ST (Figs 1E and EV1C). In the second case, the signal y decreases with tissue size (Z inhibits y). This circuit also has a stable fixed point at y = y ST and an unstable fixed point at y = y UST, but here y UST > y ST (Figs 1F and EV1D).
In comparison with the monophasic circuits depicted in Fig 1A and B, the biphasic circuits have fewer types of sensing mutations with a fitness advantage. In particular, they are protected from invasion by loss‐of‐sensing mutants and locked‐on sensing mutants. Whereas in the monophasic circuit of Fig 1A, loss‐of‐sensing mutations invade the population, in Fig 1E, the biphasic response gives these mutants a negative growth rate. They are thus eliminated. Similarly, whereas locked‐on sensing mutants invade the monophasic circuit of Fig 1B, in the biphasic case of Fig 1F, they are eliminated (Fig EV2B). Thus, mutants with strong inactivation (or strong activation) in the response to y have a fitness disadvantage (Fig 1H). This robustness to mutants is very important since such mutations may be common. For example, many constitutively active mutations of diverse G‐coupled protein receptors have been observed (Seifert & Wenzel‐Seifert, 2002), and it is common for mutations to lead to loss of function (Eyre‐Walker & Keightley, 2007; Sarkisyan et al, 2016). Mutations with intermediate effects may be rarer; for example, a study in yeast (González et al, 2015) showed that mutations that destroy protein function are much more common than those that reduce its activity to an intermediate level.
The elimination of sensing mutants by the biphasic mechanism is frequency dependent: Mutants are eliminated if they have low frequency compared with wild‐type cells. The reason for this is that when mutants are rare, the tissues maintain a proper signal y ST which the mutants mis‐sense as y MUT and therefore have a fitness disadvantage. On the other hand, if the mis‐sensing mutant appears at high enough frequency, it is prevalent enough to change the level of y and force it to reach an improper level that it mis‐reads as y ST. In this case, the population of mis‐sensing mutants will be at steady state and will not be eliminated.
Biphasic circuits still have a range of mild‐effect mutants with a growth advantage. These mutants mis‐interpret the normal signal y ST as a different value lying in the gray‐shaded regions of Fig 1E and F, namely y MUT lies between y ST and y UST. Later, we discuss mechanisms that can reduce the growth advantage of these mild mutants.
The biphasic mechanism of resistance to mutants, however, comes at a cost in terms of the robustness of the circuit to perturbations in the input y. The biphasic response curve crosses zero twice and therefore introduces a new unstable fixed point, denoted by a white circle in Fig 1E and F. The stable fixed point (full black circle) still exists, and the circuit can maintain the cell concentration constant in the face of small fluctuations around this fixed point. However, large fluctuations in signal y that exceed the unstable fixed point, or large fluctuations in Z, may lead to negative growth rate and to the risk of the elimination of the cell population (Fig 1G). Beyond the unstable fixed point, a runaway phenomenon occurs in which the cell population shrinks, leading to change in y that pushes it deeper into the unstable region, leading to faster shrinkage and so on. This runaway phenomenon has the hallmarks of certain disease as described below.
To summarize so far, circuits with biphasic control avoid invasion by mutants with strong activation or inactivation of sensing. This robustness is useful because such mutations have a severe effect if they take over the population. This mechanism has two vulnerabilities: Mutations with mild effect on sensing may still invade, and an unstable fixed point introduced by the biphasic control provides risk of runaway behavior if signal fluctuates too widely. We next provide several examples of biphasic control.
Glucotoxicity can protect from mutant beta cells, but can cause diabetes
The first example occurs in the endocrine circuit that regulates blood glucose by pancreatic beta cells (Fig 2). Fasting blood glucose (y) is maintained within a tight range around approximately y ST = 5 mM, and blood glucose dynamics are precise in response to perturbations (Allard et al, 2003; Ferrannini et al, 1985). To achieve this tight regulation, beta cells (Z) secrete insulin, which reduces glucose by increasing its uptake by peripheral tissues and decreasing its endogenous production. Thus, in this case, Z inhibits y (the case of Fig 1B and E).
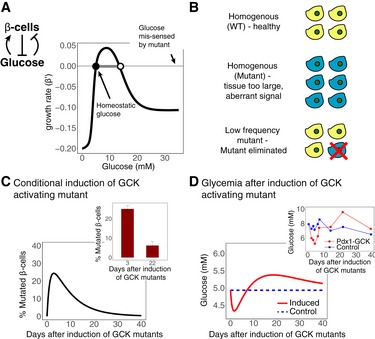
Figure 2. Frequency‐dependent selection of mutant pancreatic beta cells.
-
AFeedback circuit in which beta cells secrete insulin, which lowers blood glucose levels. Blood glucose levels, in turn, affect beta‐cell growth rate in a biphasic manner, with beta‐cell growth being negative at both low and high glucose concentrations. The system is stable at the homeostatic glucose concentration at 5 mM. It also has an unstable fixed point at a higher glucose concentration. A mutant with a sixfold increase in glucokinase affinity senses the glucose level y as y MUT = 6y. This mis‐sensing shifts its stable and unstable fixed points to lower glucose concentrations.
-
BBiphasic control leads to frequency‐dependent selection of the sensing mutant. The cell population in the tissue reaches a stable steady state only when it is homogenous with respect to the sensing of y. When a mutant with low frequency arises somatically, it is eliminated from the tissue; in contrast, if it is transmitted in the germ line, it will spawn a tissue with aberrant size.
-
C, DMathematical simulation of a tamoxifen‐induced conditional knock‐in of a sixfold activating GCK mutant in beta cells. (C) The percentage of beta cells with mutated GCK increases to ˜25% after 3 days, but then decreases and is eliminated after a few weeks. (D) Glucose levels initially decrease after the tamoxifen injection, but return to normal after a few weeks. Insets: Experimental results of Tornovsky‐Babeay et al (2014).
The response of beta‐cell growth to glucose is biphasic (Figs 2A and EV3A). Both low and high levels of glucose are toxic to beta cells. The response curve therefore has a stable fixed point at y = 5 mM (Karin et al, 2016), and it also has an unstable fixed point at a higher glucose concentration. The toxicity at high levels of glucose is known as glucotoxicity (Efanova et al, 1998; Del Prato, 2009; Bensellam et al, 2012).
Figure EV3. Schematic diagrams for tissue homeostasis circuits.
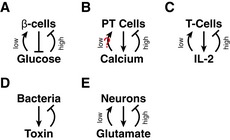
- Plasma glucose inhibits beta cell death at low concentrations and is toxic for beta cells at high concentrations. Beta cells, in turn, secrete insulin which reduces the level of plasma glucose.
- Plasma calcium inhibits parathyroid cell proliferation at high concentrations and may potentially stimulate parathyroid cell growth at low concentrations. Parathyroid cells, in turn, secrete PTH which increases the level of plasma calcium.
- T cells secrete IL‐2, which affects both T‐cell death and proliferation such that growth is negative at high and low concentrations of IL‐2.
- Secrete‐and‐sense circuit engineered by You et al (2004), where a death promoter in bacteria is under the control of a molecule secreted by the bacteria.
- Neurons secrete glutamate. Glutamate is toxic to neurons at high concentrations and promotes neuronal survival at low concentrations.
The unstable fixed point caused by glucotoxicity is puzzling, because, as described by Topp et al (2000), it provides a potential susceptibility to the system. If glucose levels exceed the unstable fixed point for extended periods (e.g., due to insulin resistance), beta cells will have negative growth rate and be removed, leading to an increase in glucose and a vicious cycle which can eliminate the beta‐cell population. This process has been suggested to lead to type II diabetes (Topp et al, 2000; De Gaetano et al, 2008; Ha et al, 2016).
Glucotoxicity of beta cells is therefore detrimental, because it adds instability to perturbations in blood glucose. Since glucotoxicity is mediated by reactive oxygen species, it could have been mitigated by antioxidants, but antioxidants and oxidative stress protective genes are expressed at an exceptionally low level in beta cells (Robertson et al, 2003). This raises the question of why beta cells have not evolved to resist glucotoxicity. Here, we suggest that glucotoxicity may have a biological function: It eliminates beta‐cell mutants with impaired glucose sensing.
Mutants that affect glucose sensing can occur at many steps in the glucose sensing and insulin secretion process. These steps include glucose import, phosphorylation and metabolism, closure of KATP channels, and opening of voltage‐dependent calcium channels (MacDonald et al, 2005). Many mutations are known to affect glucose sensing by beta cells (Fajans et al, 2001; James et al, 2009), among them autosomal dominant mutations in the enzyme glucokinase (GCK) (Froguel et al, 1993; Glaser et al, 1998; Fajans et al, 2001; Matschinsky, 2002; James et al, 2009).
We focus on GCK because it performs the rate‐limiting step in glucose sensing. GCK is a hexokinase isozyme expressed in beta cells that phosphorylates the glucose that is transported into the cells. It has a half‐maximal activation at K = 8.4 mM glucose and a Hill coefficient of n = 1.8 (Matschinsky, 2002). Hence, its activity level at the homeostatic set point of 5 mM glucose is ~30% of maximal activation. Glucose sensing is also affected by the expression level of GCK (Wang & Iynedjian, 1997). Germ line mutations in GCK result in low and high blood glucose levels for activating and inactivating mutations, respectively (Matschinsky, 2002). GCK mutations also affect the rates of beta‐cell death and proliferation (Porat et al, 2011; Tornovsky‐Babeay et al, 2014). This means that somatic mutations in GCK cause impaired glucose sensing that may alter circuit function.
Our theory makes a specific prediction on the fate of GCK mutations in beta cells, namely that their survival will be dependent on their frequency in the tissue (Fig 2B). We predict that a strong activating mutation in GCK will be lost when the majority of the population is wild type, because the mutants will be eliminated by the biphasic mechanism: Glucose level is set by the wild‐type tissue to be 5 mM, but the mutants mis‐sense a much higher level and succumb to glucotoxicity. In contrast, when the mutation is transmitted through the germ line, it is expected to survive and instead pull the blood glucose level to a low point, which the mutants interpret incorrectly as 5 mM.
This frequency‐dependent survival was observed in an experiment by Tornovsky‐Babeay et al (2014), which studied a strong (~6‐fold) activating mutation of GCK (Y214C). This mutation, when transmitted via germ line, and thus to all beta cells, results in large and hyperfunctional islets and severe hypoglycemia (Cuesta‐Munoz et al, 2004) as occurs in rare human patients. The experimenters conditionally expressed this mutation in beta cells of adult mice, such that only a subset of the beta cells expressed the transgene (~25%: 3 days after conditional expression). Both the proliferation and apoptosis rates increased in the cells expressing the transgene, but the increase in apoptosis rate was higher and after 22 days only 5% of the cells that expressed the transgene were left. Thus, the mutated cells were eliminated, whereas the wild‐type cells remained.
We simulated this experiment using the biphasic control circuit (Fig 2B–D, see Appendix Section S3 for simulation details). The results of the simulation are consistent with the experimental observations—despite having a higher proliferation rate, the population of induced mutants was eliminated by their even higher apoptosis rate (Fig 2C). This elimination restores blood glucose levels to baseline after an initial hypoglycemia (Fig 2D), in agreement with the experimental blood glucose measurements (Fig 2C and D).
Resistance to mutant invasion is enhanced by low proliferation, low cell number, and spatial compartments
We have thus seen that strong hypersensing mutants are eliminated from the beta‐cell population. We now address the question of sensitivity to mild sensing mutants. These mutants misread the signal at a level that lies between the stable and unstable fixed points, , leading to a growth advantage (shaded area of Fig 2A).
Using evolutionary dynamics theory (Nowak, 2006), we quantify the probability that such sensing mutants will invade the population of beta cells during a normal life span. The analysis results in several design principles to reduce the probability of such invasion.
To make simple approximation, we approximate the growth rate of beta cells when as constant, where is the proliferation rate and is the death rate in this range (. We also approximate by a constant the probability that a ‐fold activating mutant will arise after a cell division, . The population of beta cells is sub‐divided into compartments—pancreatic islets of Langerhans—each consisting of about beta cells (Leslie & Robbins, 1995). We define the evolutionary stability of the circuit as the probability that no mutant will invade a single pancreatic islet by time t. This probability is given by a Moran process term (Appendix Sections S4 and S5):
| (1) |
where is the range of inputs to which the circuit is stable given by the relative distance between the stable and unstable fixed points (dynamic stability of the circuit), is the number of beta cells in each islet, is beta‐cell turnover rate, and is the ratio of proliferation to removal for the mutants.
We can now approximate the evolutionary stability of the glucose homeostasis circuit using (equation (1)). Typical parameters are which corresponds to glucotoxicity around 10 mM glucose (Maedler et al, 2006) and (Stolovich‐Rain et al, 2012). For an average beta‐cell turnover of (Meier et al, 2008; Saisho et al, 2013) and mutation probability with a target size of 100 bp, μ0 = 10−7, the evolutionary stability of the circuit is . For a 70‐year life span, the stability is , so that ~0.6% of the pancreatic islets have an invading mutant by 70 years for these parameters. Note that we have only analyzed here mutations that are due to cell division and excluded other possible sources of somatic mutation, which may increase the overall number of islets with invading mutants. Increasing the mutation rate by 10‐fold leads to ~6–7% of islets being taken over by an invading mutant.
The analysis shows that evolutionary stability is in a tradeoff with dynamic stability. The circuit can be made more dynamically stable by pushing the unstable fixed point to higher glucose (increasing δ). This, however, increases the range of mild mutants that can invade (Fig 3A–C). At the extreme, one can push the unstable fixed point to infinity and end up with a monostable circuit, which is susceptible to all activating mutations in sensing.
Figure 3. Tradeoff between evolutionary stability and dynamical stability.

- A monophasic feedback circuit where cells Z inhibit y which increases their growth rate. This circuit has low evolutionary stability—any mutant that mis‐senses y to a higher value may invade the population
- For every initial value of Z > 0 or y, the circuit converges to the homeostatic set point. Nullclines are indicated by red and blue lines in the phase plots.
- A biphasic feedback circuit where Z inhibits y, which, in turn, decreases the growth rate of Z at high concentrations and increases the growth rate of Z at low concentrations. This circuit has high dynamical stability (large y UST ‐y ST) and high evolutionary stability, but mild activating mutants may invade the population.
- Large perturbations in either Z or y may result in the elimination of the cell population Z due to a runaway process. Nullclines are indicated by red and blue lines in the phase plots.
- A biphasic feedback circuit with lower dynamical stability (small y UST ‐y ST) and higher evolutionary stability, since only few mild activating mutants may invade the population (gray region).
- Small perturbations in either Z or y may result in the elimination of the cell population Z due to a runaway process. Nullclines are indicated by red and blue lines in the phase plots.
Similarly, evolutionary stability is in tradeoff with the response time of the circuit. The response time to a glucose perturbation depends on the growth rate of the cells, which is, for . To make the response time more rapid, either should increase, but this will make the circuit less evolutionarily stable [decrease according to (equation (1))]. The intuitive reason for this tradeoff is that fast response requires faster proliferation, but this gives mutants a bigger growth advantage. We conclude that if mutations that activate glucose sensing are sufficiently likely, glucotoxicity may be selected for despite its harmful potential for diabetes.
Evolutionary stability of the parathyroid gland
Another prediction of (equation (1)) is that changes in the parameters, such as a large increase in cell proliferation rate, can lead to invasion by mild sensing mutants. We hypothesize that this occurs in the circuit that controls calcium homeostasis, leading to the disease known as tertiary hyperparathyroidism.
The parathyroid (PT) gland (Z) controls plasma calcium (y) by secreting parathyroid hormone (PTH) which increases calcium production. This circuit is analogous to the glucose homeostasis circuit discussed previously—calcium controls both the secretion of PTH and the mass dynamics of the PT gland (Naveh‐Many et al, 1995; Wada et al, 1997; Mizobuchi et al, 2007). The signs of the circuit are opposite to the glucose circuit, because Z acts to increase y. It is unclear whether this circuit has biphasic control, so the circuit is similar to either one of the circuits in Fig 1A or Fig 1E (Fig EV3B).
This circuit is sensitive to invasion by deactivating mutants in calcium sensing (mis‐sensing calcium as lower than it actually is). Under normal conditions, however, the PT gland has a very low turnover (very small ) (Bilezikian et al, 2001). Therefore, these mutants have a low probability to arise and invade due to the rarity of cell divisions.
However, in cases of increased demand for PTH, which occurs in hypocalcaemia such as that caused by renal failure, excessive proliferation of the parathyroid cells takes place ( increases). Such conditions are termed secondary hyperparathyroidism (SHPT). In such conditions, we expect, from (equation (1)), that mutants will arise and have a large probability to invade the PT gland.
Indeed, the invasion of mutants with calcium‐sensing inactivation often occurs in secondary hyperparathyroidism (Gogusev et al, 1997; Yano et al, 2000; Fraser, 2009). The invasion of such mutants alters the calcium homeostatic set point (Malberti, 1999) and leads to tertiary hyperparathyroidism. The new set point is mildly higher calcium, which is due to the mis‐sensing of the mutants. The common mutations that lead to tertiary hyperparathyroidism are known to cause only an intermediate reduction in the expression of the calcium‐sensing receptor (Yano et al, 2000) and not a strong inactivation. This is what we expect if calcium controls PT gland growth in a biphasic manner, eliminating the strong deactivating mutations.
Biphasic control in secrete‐and‐sense circuits in T cells and bacteria
As an additional example, we consider the evolutionary stability of a motif suggested to control cell populations known as secrete and sense (You et al, 2004). An experimental characterization of such a circuit in vitro employed the control of T‐cell population size by IL2, a cytokine secreted by the T cells (Hart et al, 2014). In this circuit, y = IL2 increases both the death rate and proliferation rate of the cells at different rates, similar to the circuit depicted in Fig 1E. The resulting overall growth rate is biphasic, with negative growth rate at low (y < y UST) and high (y > y ST) concentrations of IL2 (Fig EV3C). This causes the population to have a stable fixed point at y = y ST and an unstable fixed point at y = y UST. Initial seeding of T cells in plates across 4 decades of concentration led to convergence after 7 days to the same steady‐state population to within a factor of 2 (Hart et al, 2014). This steady‐state population was much lower than the carrying capacity of the system and resulted from vigorous balance of cell proliferation and death. Seeding with too few T cells, or experimental reduction in IL2, led to the elimination of the T cells. The present analysis suggests that the biphasic effects of IL2 can protect against loss‐of‐sensing mutants in IL2 signaling. This suggests an experiment in which such mutants are predicted to be eliminated if present at low concentrations within a wild‐type population, but to take over if present at high numbers (frequency‐dependent selection).
A secrete‐and‐sense circuit has also been synthetically engineered in bacteria by You et al (2004), by placing a death gene under control of a quorum sensing signal so the gene is activated when quorum signal is strong, similar to the circuit depicted in Fig 1A (Fig EV3D). This circuit maintains cell concentration constant. However, homeostatic control is rapidly lost (Balagadde, 2005) since selection favors mutants which inactivate the synthetic signaling pathway, in accord with the present predictions.
Evolutionary stable strategies in tissues with stem cells
The cases discussed so far have a population of dividing cells that is under size control. Many tissues, however, are made of nondividing differentiated cells that originate from a pool of stem cells. We consider the case of tissues in which the differentiated cells are constantly removed and must be replenished, such as blood cells and the epithelia of lungs and skin. In these cases, tissue size control requires feedback from the differentiated cells back to the stem cells (Bullough, 1975). The dividing stem‐cell population is sensitive to takeover by mutants. Here, we suggest that a biphasic control mechanism can provide protection from invasion of mutants also in this case (Fig 4).
Figure 4. Biphasic control can provide mutant resistance to stem‐cell homeostatic circuits.
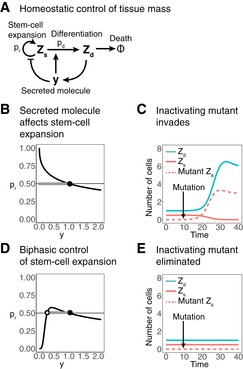
- Homeostatic control of a population of cells Z d, which differentiate from a population of dividing stem cells Z s. Differentiated cells secrete a factor y which increases the differentiation rate p d of Z s and therefore decreases the rate of stem‐cell expansion p r = 1−p d.
- In a monophasic model, stem‐cell expansion rate decreases with y. The system has a stable fixed point at the concentration of y where p r = 0.5.
- A mutated stem cell with a strong inactivation of the sensing of y has a growth advantage (differentiates less), and therefore, it invades the stem‐cell population. As a result, both the stem‐cell pool and the number of terminally differentiated cells increase.
- Biphasic control of stem‐cell expansion, where stem‐cell expansion is low both at high and low concentrations of y. The system has a stable fixed point at the concentration of y where p r = 0.5 and an unstable fixed point at some lower concentration of y.
- A mutated stem cell with a strong inactivation on y sensing now has a growth disadvantage and is therefore eliminated from the stem‐cell population.
We demonstrate the effect of biphasic control by considering a monophasic circuit presented by Buzi et al (2015). In this circuit, differentiated cells secrete a molecule y that affects the differentiation probability of the stem cells (Fig 4A and B). The molecule y increases the differentiation rate of the stem cells and thus limits their expansion rate. This type of feedback has been demonstrated for many tissues, such as blood, skin, skeletal muscle, olfactory epithelium, bone, hair, and more (Lander et al, 2009; Buzi et al, 2015). In many of these tissues, the secreted molecule belongs to the TGF‐β family (Lander et al, 2009). The dynamic equations for the stem cells Z s and differentiated cells Z d are as follows:
| (2) |
| (3) |
| (4) |
where is the stem‐cell division rate, is the differentiated cell removal rate, is the probability that a stem cell that divided will not differentiate, and is the probability that it will (). The differentiated cells secrete molecule y that increases differentiation rate —forming a negative feedback loop (because differentiation is akin to loss of stem cells, leading to less differentiated tissue in the long term). Too many differentiated cells lead to a high level of y and to a decrease in the stem‐cell population, leading to a reduction back to tissue size set point . This monophasic circuit thus maintains a stable, constant population of differentiated cells (Buzi et al, 2015).
As above, this monophasic circuit is susceptible to invasion by loss‐of‐sensing mutations: stem cells that cannot sense y or that mis‐sense y as too low. Within a single compartment, such a sensing mutant cannot coexist with wild‐type stem cells. As this mutant stem cell differentiates less than the wild‐type stem cells, it self‐renews more often and has an evolutionary advantage over other stem cells. It is likely to invade the compartment and disrupt tissue homeostasis (Fig 4C). Invasion of the mutant means an exponential growth in both (mutant) stem cell and differentiated cell populations.
We find that adding a biphasic response curve can increase the evolutionary stability of this circuit (Fig 4D and E). In such biphasic control, y stimulates the growth of the stem cells at low concentrations and also stimulates differentiation at high concentrations (and thus inhibits renewal at high concentrations). Therefore, stem cells with a strong inactivating mutants that mis‐sense y as too low grow less than wild type and thus have a selective disadvantage relative to other stem cells and are eliminated from the stem‐cell population. The TGF‐β feedback has indeed been demonstrated to have biphasic control in several cell types (Battegay et al, 1990; McAnulty et al, 1997; Cordeiro et al, 2000; Fosslien, 2009).
Neuronal excitotoxicity as an additional putative case for evolutionary stability/disease tradeoff
Several other diseases are associated with a biphasic response of cells to their input. Glutamate, a common neurotransmitter, has a biphasic effect on neurons—it increases neuronal survival at intermediate concentrations and causes neuronal death at low and high levels (Lipton & Nakanishi, 1999; Fig EV3E). The latter effect is called neuronal excitotoxicity. Excitotoxicity is associated with neurodegenerative diseases such as Alzheimer's, Parkinson's, and Huntington's (Coyle & Puttfarcken, 1993; Dong et al, 2009).
We speculate that the biphasic effect of glutamate on neuronal survival may be beneficial for the elimination of neurons with improper sensing. Such defective neurons may arise due to somatic mutation in the brain, either in mature neurons (Lodato et al, 2015) or in neuronal progenitors (Poduri et al, 2013). In order to evaluate the role of the biphasic effect of glutamate on neuronal evolutionary stability, it is necessary to better characterize the homeostatic feedback circuits that control neuronal mass dynamics.
Discussion
In this study, we raise the question of the stability of circuits that control tissue size with respect to invasion by mutants. We consider feedback circuits that provide size control by regulating cell growth according to an input signal proportional to the number of cells. We show that such feedback mechanisms can be invaded by commonly occurring mutants, which have loss‐of‐sensing or locked‐on sensing of the input signal. Invasion leads to aberrant tissue size and function. We find that these common mutants can be eliminated by a biphasic control mechanism. In biphasic control, the signal is toxic at both high and low levels, giving the mutants a selective disadvantage. The biphasic protection mechanism comes at a cost: It introduces an unstable fixed point that can cause a runaway phenomenon under strong fluctuations in the input signal, potentially leading to disease. This study thus provides an explanation for several well‐studied toxicity phenomena associated with diseases, by suggesting that they have a beneficial function of protecting tissues from invasion by common mutants.
The biphasic control mechanism protects against strong sensing mutations, such as loss‐of‐function or locked‐on receptors. These strong mutations presumably have a large mutational target size and are thus the most commonly arising mutations in a tissue. The control mechanism is sensitive, however, to a range of mild sensing mutations. These mutations cause the cell to mis‐interpret the signal level, to a level that lies between the desired steady‐state level y ST and the unstable fixed point y UST (Fig 1). It is likely that such mild mutations are more rare than loss‐of‐function or locked‐on mutations. The vulnerability to these mild mutations might explain the recurrence of a few specific point mutations of mild effect in sensing pathways in cancer, presumably because mutations of larger effect are eliminated (Hanahan & Weinberg, 2011).
There is a tradeoff between evolutionary stability—the range of mild mutations that can invade, and dynamic stability—the position of the unstable fixed point. The closer the y ST is to y UST, the higher the evolutionary stability and the lower the dynamical stability. As y UST approaches y ST, we expect to see critical slowing down of the dynamics of the system and a general loss of resilience to perturbations (Scheffer et al, 2009). Such critical slowing down was shown to occur in populations of yeast in response to dilution (Dai et al, 2012) as well as in genetic circuits (Axelrod et al, 2015).
This study maps the concept of evolutionary stable strategies (ESS) from evolutionary ecology (Smith & Price, 1973) to the level of cell circuits in tissues. In ecology, an ESS is defined when a population of organisms with that strategy cannot be invaded by any other strategy. In the present study, a mis‐sensing mutant is analogous to the invading strategy. In this sense, the biphasic mechanism is evolutionarily stable with respect to strong mutations. It is unstable to a range of mild mutations. The evolutionary instability to mild mutations can be reduced using compartments with small cell numbers, low turnover rates, and proximity of the stable and unstable fixed points, as described by equation (1).
As in ESS in ecology, selection of sensing mutants is frequency dependent: If the entire population is mutant, it can survive. But a single‐mutant cell on a background of wild‐type cells is eliminated by the biphasic mechanism. Experiments show the predicted frequency‐dependent selection of a strong glucokinase mutant in beta cells: When present at low frequency, the mutants are eliminated; when present in the germ line, they survive and cause hypoglycemia.
Many of the biphasic toxicity phenomena considered here are mediated by excess production of reactive oxygen species (ROS) which leads to apoptosis (Coyle & Puttfarcken, 1993; Hildeman et al, 1999; Schulz et al, 2002; Robertson, 2004). ROS are implicated in both beta‐cell glucotoxicity and neuronal excitotoxicity. Such toxicity can be mitigated by antioxidants, which reduce ROS levels (Skulachev, 1998). Thus, the level of antioxidants may, in principle, tune the tradeoff between evolutionary stability and dynamic stability described here. High antioxidants can reduce the toxicity of high signal level and thus push the unstable fixed point farther from the stable fixed point. This can reduce the risk of disease, but increase susceptibility to invasion by mild mutants. This tradeoff may provide a viewpoint to understand the conflicting effects of antioxidants on health (Bjelakovic et al, 2012; Sayin et al, 2014; Le Gal et al, 2015).
In this study, we discussed circuits where a tissue regulates its own size. Some tissues, however, regulate the size of other tissues. For example, the ovaries regulate mammary epithelial mass by secreting estrogen, and the pituitary gland regulates the mass of the thyroid and adrenal glands by secreting TSH and ACTH, respectively. Depending on the feedback loops at play, such circuits may be susceptible to mutant invasion both in the regulating and regulated tissue. The considerations of this study indicate that biphasic control reduces the susceptibility to invading mutants in these cases as well. We therefore predict biphasic responses also when tissues regulate each other. For example, estrogen controls mammary growth in a biphasic manner (Lewis‐Wambi & Jordan, 2009), therefore reducing the target range of mutants with a fitness advantage in the mammary epithelium.
Finally, biphasic control raises the question of how tissues can start growing. Consider the tissue in Fig 1E, in which Z produces y. If initially y = 0, Z = ε, then the tissue has negative growth rate and cannot grow to reach Z = Z ST. This can be resolved if y is determined externally during tissue development. For example, during gestation, metabolites and factors are supplied to the fetus externally by the mother at levels close to y ST. Another possibility is that tissue development is determined by a different program that is later suppressed.
In summary, we show that physiological feedback circuits are inherently vulnerable to takeover by mutants that mis‐sense the feedback signal. Biphasic mechanisms, in which the signal is toxic at both high and low levels to the relevant tissue, can protect against such mutant invasion. We therefore hypothesize that phenomena such as glucotoxicity and excitotoxicity may reflect the bad side of a good anti‐mutant strategy (Stearns & Medzhitov, 2016). Characterizing physiological homeostatic circuits and the tradeoffs they face in quantitative detail may thus lead to a better understanding of diabetes (Topp et al, 2000), neurodegenerative diseases (Doble, 1999; Lipton & Nakanishi, 1999), and possibly other pathologies associated with biphasic control.
Materials and Methods
Circuits with monophasic and biphasic control
To simulate the circuits of Fig 1 in the main text, we used a circuit where a cell mass Z either increases the level of its input y (Fig 1A and E) or decreases the level of y (Fig 1B and F). The equation used for Z is follows:
| (5) |
where λ + is the y‐dependent proliferation rate of Z, and λ ‐ is the y‐dependent removal rate of Z.
In Fig 1C, D, G and H, we simulated two cases—a monophasic circuit, where y increases the growth rate of Z, and a biphasic circuit, where y increases the growth rate of Z at low concentrations and decreases the growth rate of Z at high concentrations. The monophasic circuit was simulated using the growth rate equations:
| (6) |
| (7) |
and the biphasic circuit was simulated by using the growth rate equations:
| (8) |
| (9) |
These circuits were also used to simulate the phase plots in Fig 3A and B. For Fig 3C, we used the following circuit:
| (10) |
| (11) |
We used the following equation for the dependence of y on Z:
| (12) |
This equation means that Z increases the degradation rate of y, and at steady state, we get . We chose the parameters.
Mutant invasion simulation
We simulated the effect of a mutation by adding a term Z mut such that:
| (13) |
Z mut represents the mass of cells with a (given) k‐fold sensing mutation on y, so the growth rate of Z mut is given as follows:
| (14) |
Note that for the monophasic circuit simulated in Fig 1, the removal rate does not depend on , and therefore, it is not affected by the sensing mutation (only is affected). We simulated the invasion of a fourfold sensing mutant in Fig 1D and H by setting at specific time intervals in the simulation (t = 10 for the monophasic circuit and t = 10, t = 47 for the biphasic circuit). The initial values for the simulations were for the monophasic circuit in Fig 1D, and for the biphasic circuit in Fig 1H.
Circuits of communicating stem cells
In this study, we presented two circuits that regulate the functional mass of differentiated cells, based on the model that is presented in Buzi et al (2015). For the monophasic circuit, the equations are as follows:
| (15) |
| (16) |
| (17) |
| (18) |
where is the stem‐cell division rate, is the differentiated cell removal rate, is the probability that a stem cell that divided will not differentiate, and 1 − p r is the probability that it will differentiate. The population is the population of stem cells with a k‐fold sensing mutation. The monophasic replication rate p r (y), which is depicted in Fig 3B, was set as follows:
| (19) |
The exact function used is not important, since as long as it is monotonically decreasing, an invading mutant will take over. In the biphasic case, the replication rate used is as follows:
| (20) |
The simulation of invading mutants is the same as for Fig 1 (which is explained in the mutant invasion simulation section). For the simulations, we set , and with the initial conditions . A mutation event was set such that at .
Author contributions
OK and UA conceived and performed the research. OK and UA wrote the manuscript.
Conflict of interest
The authors declare that they have no conflict of interest.
Supporting information
Appendix
Expanded View Figures PDF
Review Process File
Acknowledgements
This work was supported by the Israel Science Foundation (1349/15) and the Minerva Foundation. UA is the incumbent of the Abisch‐Frenkel Professorial Chair. OK is supported by the Azrieli Center for Systems Biology grant.
Mol Syst Biol. (2017) 13: 933
References
- Allard P, Delvin EE, Paradis G, Hanley JA, O'Loughlin J, Lavallée C, Levy E, Lambert M (2003) Distribution of fasting plasma insulin, free fatty acids, and glucose concentrations and of homeostasis model assessment of insulin resistance in a representative sample of Quebec children and adolescents. Clin Chem 49: 644–649 [DOI] [PubMed] [Google Scholar]
- Axelrod K, Sanchez A, Gore J (2015) Phenotypic states become increasingly sensitive to perturbations near a bifurcation in a synthetic gene network. eLife 4: e07935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balagadde FK (2005) Long‐term monitoring of bacteria undergoing programmed population control in a microchemostat. Science 309: 137–140 [DOI] [PubMed] [Google Scholar]
- Battegay EJ, Raines EW, Seifert RA, Bowen‐Pope DF, Ross R (1990) TGF‐beta induces bimodal proliferation of connective tissue cells via complex control of an autocrine PDGF loop. Cell 63: 515–524 [DOI] [PubMed] [Google Scholar]
- Bensellam M, Laybutt DR, Jonas J‐C (2012) The molecular mechanisms of pancreatic β‐cell glucotoxicity: recent findings and future research directions. Mol Cell Endocrinol 364: 1–27 [DOI] [PubMed] [Google Scholar]
- Bilezikian JP, Marcus R, Levine MA. (eds) (2001) The parathyroids: basic and clinical concepts, 2nd edn San Diego, CA: Academic Press; [Google Scholar]
- Bjelakovic G, Nikolova D, Gluud LL, Simonetti RG, Gluud C (2012) Antioxidant supplements for prevention of mortality in healthy participants and patients with various diseases. Cochrane Database Syst Rev CD007176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouchard C, Staller P, Eilers M (1998) Control of cell proliferation by Myc. Trends Cell Biol 8: 202–206 [DOI] [PubMed] [Google Scholar]
- Bullough WS (1975) Mitotic control in adult mammalian tissues. Biol Rev 50: 99–127 [DOI] [PubMed] [Google Scholar]
- Buzi G, Lander AD, Khammash M (2015) Cell lineage branching as a strategy for proliferative control. BMC Biol 13: 13–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordeiro MF, Bhattacharya SS, Schultz GS, Khaw PT (2000) TGF‐beta1, ‐beta2, and ‐beta3 in vitro: biphasic effects on Tenon's fibroblast contraction, proliferation, and migration. Invest Ophthalmol Vis Sci 41: 756–763 [PubMed] [Google Scholar]
- Coyle J, Puttfarcken P (1993) Oxidative stress, glutamate, and neurodegenerative disorders. Science 262: 689–695 [DOI] [PubMed] [Google Scholar]
- Critchfield JM, Racke MK, Zúñiga‐Pflücker JC, Cannella B, Raine CS, Goverman J, Lenardo MJ (1994) T cell deletion in high antigen dose therapy of autoimmune encephalomyelitis. Science 263: 1139–1143 [DOI] [PubMed] [Google Scholar]
- Cuesta‐Munoz AL, Huopio H, Otonkoski T, Gomez‐Zumaquero JM, Nanto‐Salonen K, Rahier J, Lopez‐Enriquez S, Garcia‐Gimeno MA, Sanz P, Soriguer FC, Laakso M (2004) Severe persistent hyperinsulinemic hypoglycemia due to a de novo glucokinase mutation. Diabetes 53: 2164–2168 [DOI] [PubMed] [Google Scholar]
- Dai L, Vorselen D, Korolev KS, Gore J (2012) Generic indicators for loss of resilience before a tipping point leading to population collapse. Science 336: 1175–1177 [DOI] [PubMed] [Google Scholar]
- De Gaetano A, Hardy T, Beck B, Abu‐Raddad E, Palumbo P, Bue‐Valleskey J, Porksen N (2008) Mathematical models of diabetes progression. Am J Physiol Endocrinol Metab 295: E1462–E1479 [DOI] [PubMed] [Google Scholar]
- Del Prato S (2009) Role of glucotoxicity and lipotoxicity in the pathophysiology of Type 2 diabetes mellitus and emerging treatment strategies. Diabet Med 26: 1185–1192 [DOI] [PubMed] [Google Scholar]
- Doble A (1999) The role of excitotoxicity in neurodegenerative disease: implications for therapy. Pharmacol Ther 81: 163–221 [DOI] [PubMed] [Google Scholar]
- Dong X, Wang Y, Qin Z (2009) Molecular mechanisms of excitotoxicity and their relevance to pathogenesis of neurodegenerative diseases. Acta Pharmacol Sin 30: 379–387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efanova IB, Zaitsev SV, Zhivotovsky B, Köhler M, Efendić S, Orrenius S, Berggren PO (1998) Glucose and tolbutamide induce apoptosis in pancreatic beta‐cells. A process dependent on intracellular Ca2+ concentration. J Biol Chem 273: 33501–33507 [DOI] [PubMed] [Google Scholar]
- Evan GI, Wyllie AH, Gilbert CS, Littlewood TD, Land H, Brooks M, Waters CM, Penn LZ, Hancock DC (1992) Induction of apoptosis in fibroblasts by c‐myc protein. Cell 69: 119–128 [DOI] [PubMed] [Google Scholar]
- Eyre‐Walker A, Keightley PD (2007) The distribution of fitness effects of new mutations. Nat Rev Genet 8: 610–618 [DOI] [PubMed] [Google Scholar]
- Fajans SS, Bell GI, Polonsky KS (2001) Molecular mechanisms and clinical pathophysiology of maturity‐onset diabetes of the young. N Engl J Med 345: 971–980 [DOI] [PubMed] [Google Scholar]
- Ferrannini E, Bjorkman O, Reichard GA, Pilo A, Olsson M, Wahren J, DeFronzo RA (1985) The disposal of an oral glucose load in healthy subjects: a quantitative study. Diabetes 34: 580–588 [DOI] [PubMed] [Google Scholar]
- Fosslien E (2009) The hormetic morphogen theory of curvature and the morphogenesis and pathology of tubular and other curved structures. Dose Response 7: 307–331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser WD (2009) Hyperparathyroidism. Lancet 374: 145–158 [DOI] [PubMed] [Google Scholar]
- Froguel P, Zouali H, Vionnet N, Velho G, Vaxillaire M, Sun F, Lesage S, Stoffel M, Takeda J, Passa P (1993) Familial hyperglycemia due to mutations in glucokinase. Definition of a subtype of diabetes mellitus. N Engl J Med 328: 697–702 [DOI] [PubMed] [Google Scholar]
- Glaser B, Kesavan P, Heyman M, Davis E, Cuesta A, Buchs A, Stanley CA, Thornton PS, Permutt MA, Matschinsky FM, Herold KC (1998) Familial hyperinsulinism caused by an activating glucokinase mutation. N Engl J Med 338: 226–230 [DOI] [PubMed] [Google Scholar]
- Gogusev J, Duchambon P, Hory B, Giovannini M, Goureau Y, Sarfati E, Drüeke TB (1997) Depressed expression of calcium receptor in parathyroid gland tissue of patients with hyperparathyroidism. Kidney Int 51: 328–336 [DOI] [PubMed] [Google Scholar]
- González C, Ray JCJ, Manhart M, Adams RM, Nevozhay D, Morozov AV, Balázsi G (2015) Stress‐response balance drives the evolution of a network module and its host genome. Mol Syst Biol 11: 827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gudipaty SA, Lindblom J, Loftus PD, Redd MJ, Edes K, Davey CF, Krishnegowda V, Rosenblatt J (2017) Mechanical stretch triggers rapid epithelial cell division through Piezo1. Nature 543: 118–121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ha J, Satin LS, Sherman AS (2016) A mathematical model of the pathogenesis, prevention, and reversal of type 2 diabetes. Endocrinology 157: 624–635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanahan D, Weinberg RA (2011) Hallmarks of cancer: the next generation. Cell 144: 646–674 [DOI] [PubMed] [Google Scholar]
- Hardingham GE, Bading H (2003) The yin and yang of NMDA receptor signalling. Trends Neurosci 26: 81–89 [DOI] [PubMed] [Google Scholar]
- Harrington EA, Fanidi A, Evan GI (1994) Oncogenes and cell death. Curr Opin Genet Dev 4: 120–129 [DOI] [PubMed] [Google Scholar]
- Hart Y, Reich‐Zeliger S, Antebi YE, Zaretsky I, Mayo AE, Alon U, Friedman N (2014) Paradoxical signaling by a secreted molecule leads to homeostasis of cell levels. Cell 158: 1022–1032 [DOI] [PubMed] [Google Scholar]
- Hildeman DA, Mitchell T, Teague TK, Henson P, Day BJ, Kappler J, Marrack PC (1999) Reactive oxygen species regulate activation‐induced T cell apoptosis. Immunity 10: 735–744 [DOI] [PubMed] [Google Scholar]
- Högnason T, Chatterjee S, Vartanian T, Ratan RR, Ernewein KM, Habib AA (2001) Epidermal growth factor receptor induced apoptosis: potentiation by inhibition of Ras signaling. FEBS Lett 491: 9–15 [DOI] [PubMed] [Google Scholar]
- James C, Kapoor RR, Ismail D, Hussain K (2009) The genetic basis of congenital hyperinsulinism. J Med Genet 46: 289–299 [DOI] [PubMed] [Google Scholar]
- Karin O, Swisa A, Glaser B, Dor Y, Alon U (2016) Dynamical compensation in physiological circuits. Mol Syst Biol 12: 886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander AD, Gokoffski KK, Wan FYM, Nie Q, Calof AL (2009) Cell lineages and the logic of proliferative control. PLoS Biol 7: e1000015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Gal K, Ibrahim MX, Wiel C, Sayin VI, Akula MK, Karlsson C, Dalin MG, Akyurek LM, Lindahl P, Nilsson J, Bergo MO (2015) Antioxidants can increase melanoma metastasis in mice. Sci Transl Med 7: 308re8. [DOI] [PubMed] [Google Scholar]
- Leslie RDG, Robbins DC (1995) Diabetes: clinical science in practice Cambridge. New York, NY: Cambridge University Press; [Google Scholar]
- Lewis‐Wambi JS, Jordan VC (2009) Estrogen regulation of apoptosis: how can one hormone stimulate and inhibit? Breast Cancer Res 11: 206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipton SA, Nakanishi N (1999) Shakespeare in love—with NMDA receptors? Nat Med 5: 270–271 [DOI] [PubMed] [Google Scholar]
- Lodato MA, Woodworth MB, Lee S, Evrony GD, Mehta BK, Karger A, Lee S, Chittenden TW, D'Gama AM, Cai X, Luquette LJ, Lee E, Park PJ, Walsh CA (2015) Somatic mutation in single human neurons tracks developmental and transcriptional history. Science 350: 94–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe SW, Cepero E, Evan G (2004) Intrinsic tumour suppression. Nature 432: 307–315 [DOI] [PubMed] [Google Scholar]
- MacDonald PE, Joseph JW, Rorsman P (2005) Glucose‐sensing mechanisms in pancreatic ‐cells. Philos Trans R Soc B Biol Sci 360: 2211–2225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maedler K, Schumann DM, Schulthess F, Oberholzer J, Bosco D, Berney T, Donath MY (2006) Aging correlates with decreased beta‐cell proliferative capacity and enhanced sensitivity to apoptosis: a potential role for Fas and pancreatic duodenal homeobox‐1. Diabetes 55: 2455–2462 [DOI] [PubMed] [Google Scholar]
- Malberti F (1999) The PTH‐calcium curve and the set point of calcium in primary and secondary hyperparathyroidism. Nephrol Dial Transplant 14: 2398–2406 [DOI] [PubMed] [Google Scholar]
- Matschinsky FM (2002) Regulation of pancreatic beta‐cell glucokinase: from basics to therapeutics. Diabetes 51(Suppl 3): S394–S404 [DOI] [PubMed] [Google Scholar]
- McAnulty RJ, Hernández‐Rodriguez NA, Mutsaers SE, Coker RK, Laurent GJ (1997) Indomethacin suppresses the anti‐proliferative effects of transforming growth factor‐beta isoforms on fibroblast cell cultures. Biochem J 321(Pt 3): 639–643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier JJ, Butler AE, Saisho Y, Monchamp T, Galasso R, Bhushan A, Rizza RA, Butler PC (2008) Cell replication is the primary mechanism subserving the postnatal expansion of ‐cell mass in humans. Diabetes 57: 1584–1594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizobuchi M, Ogata H, Hatamura I, Saji F, Koiwa F, Kinugasa E, Koshikawa S, Akizawa T (2007) Activation of calcium‐sensing receptor accelerates apoptosis in hyperplastic parathyroid cells. Biochem Biophys Res Commun 362: 11–16 [DOI] [PubMed] [Google Scholar]
- Naveh‐Many T, Rahamimov R, Livni N, Silver J (1995) Parathyroid cell proliferation in normal and chronic renal failure rats. The effects of calcium, phosphate, and vitamin D. J Clin Invest 96: 1786–1793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak MA (2006) Evolutionary dynamics: exploring the equations of life Cambridge. Mass: Belknap Press of Harvard University Press; [Google Scholar]
- Poduri A, Evrony GD, Cai X, Walsh CA (2013) Somatic mutation, genomic variation, and neurological disease. Science 341: 1237758–1237758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porat S, Weinberg‐Corem N, Tornovsky‐Babaey S, Schyr‐Ben‐Haroush R, Hija A, Stolovich‐Rain M, Dadon D, Granot Z, Ben‐Hur V, White P, Girard CA, Karni R, Kaestner KH, Ashcroft FM, Magnuson MA, Saada A, Grimsby J, Glaser B, Dor Y (2011) Control of pancreatic β cell regeneration by glucose metabolism. Cell Metab 13: 440–449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson RP, Harmon J, Tran PO, Tanaka Y, Takahashi H (2003) Glucose toxicity in beta‐cells: type 2 diabetes, good radicals gone bad, and the glutathione connection. Diabetes 52: 581–587 [DOI] [PubMed] [Google Scholar]
- Robertson RP (2004) Chronic oxidative stress as a central mechanism for glucose toxicity in pancreatic islet beta cells in diabetes. J Biol Chem 279: 42351–42354 [DOI] [PubMed] [Google Scholar]
- Saisho Y, Butler AE, Manesso E, Elashoff D, Rizza RA, Butler PC (2013) Cell mass and turnover in humans: effects of obesity and aging. Diabetes Care 36: 111–117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarkisyan KS, Bolotin DA, Meer MV, Usmanova DR, Mishin AS, Sharonov GV, Ivankov DN, Bozhanova NG, Baranov MS, Soylemez O, Bogatyreva NS, Vlasov PK, Egorov ES, Logacheva MD, Kondrashov AS, Chudakov DM, Putintseva EV, Mamedov IZ, Tawfik DS, Lukyanov KA et al (2016) Local fitness landscape of the green fluorescent protein. Nature 533: 397–401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sayin VI, Ibrahim MX, Larsson E, Nilsson JA, Lindahl P, Bergo MO (2014) Antioxidants accelerate lung cancer progression in mice. Sci Transl Med 6: 221ra15 [DOI] [PubMed] [Google Scholar]
- Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, Dakos V, Held H, van Nes EH, Rietkerk M, Sugihara G (2009) Early‐warning signals for critical transitions. Nature 461: 53–59 [DOI] [PubMed] [Google Scholar]
- Schulz JB, Henshaw DR, Siwek D, Jenkins BG, Ferrante RJ, Cipolloni PB, Kowall NW, Rosen BR, Beal MF (2002) Involvement of free radicals in excitotoxicity in vivo . J Neurochem 64: 2239–2247 [DOI] [PubMed] [Google Scholar]
- Seifert R, Wenzel‐Seifert K (2002) Constitutive activity of G‐protein‐coupled receptors: cause of disease and common property of wild‐type receptors. Naunyn Schmiedebergs Arch Pharmacol 366: 381–416 [DOI] [PubMed] [Google Scholar]
- Skulachev VP (1998) Cytochrome c in the apoptotic and antioxidant cascades. FEBS Lett 423: 275–280 [DOI] [PubMed] [Google Scholar]
- Smith JM, Price GR (1973) The logic of animal conflict. Nature 246: 15–18 [Google Scholar]
- Stearns SC, Medzhitov R (2016) Evolutionary medicine Sunderland, MA: Sinauer Associates, Inc., Publishers; [Google Scholar]
- Stolovich‐Rain M, Hija A, Grimsby J, Glaser B, Dor Y (2012) Pancreatic beta cells in very old mice retain capacity for compensatory proliferation. J Biol Chem 287: 27407–27414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Topp B, Promislow K, deVries G, Miura RM, Finegood DT (2000) A model of beta‐cell mass, insulin, and glucose kinetics: pathways to diabetes. J Theor Biol 206: 605–619 [DOI] [PubMed] [Google Scholar]
- Tornovsky‐Babeay S, Dadon D, Ziv O, Tzipilevich E, Kadosh T, Schyr‐Ben Haroush R, Hija A, Stolovich‐Rain M, Furth‐Lavi J, Granot Z, Porat S, Philipson LH, Herold KC, Bhatti TR, Stanley C, Ashcroft FM, In't Veld P, Saada A, Magnuson MA, Glaser B et al (2014) Type 2 diabetes and congenital hyperinsulinism cause DNA double‐strand breaks and p53 activity in β cells. Cell Metab 19: 109–121 [DOI] [PubMed] [Google Scholar]
- Wada M, Furuya Y, Sakiyama J, Kobayashi N, Miyata S, Ishii H, Nagano N (1997) The calcimimetic compound NPS R‐568 suppresses parathyroid cell proliferation in rats with renal insufficiency. Control of parathyroid cell growth via a calcium receptor. J Clin Invest 100: 2977–2983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Iynedjian PB (1997) Modulation of glucose responsiveness of insulinoma beta‐cells by graded overexpression of glucokinase. Proc Natl Acad Sci USA 94: 4372–4377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yano S, Sugimoto T, Tsukamoto T, Chihara K, Kobayashi A, Kitazawa S, Maeda S, Kitazawa R (2000) Association of decreased calcium‐sensing receptor expression with proliferation of parathyroid cells in secondary hyperparathyroidism. Kidney Int 58: 1980–1986 [DOI] [PubMed] [Google Scholar]
- You L, Cox RS, Weiss R, Arnold FH (2004) Programmed population control by cell–cell communication and regulated killing. Nature 428: 868–871 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix
Expanded View Figures PDF
Review Process File


