Convergence, divergence, and reconvergence in a feedforward network improves neural speed and accuracy

Summary

One of the proposed canonical circuit motifs employed by the brain is a feedforward network where parallel signals converge, diverge, and reconverge. Here we investigate a network with this architecture in the Drosophila olfactory system. We focus on a glomerulus whose receptor neurons converge in an all-to-all manner onto six projection neurons that then reconverge onto higher-order neurons. We find that both convergence and reconvergence improve the ability of a decoder to detect a stimulus based on a single neuron’s spike train. The first transformation implements averaging, and it improves peak detection accuracy but not speed; the second transformation implements coincidence detection, and it improves speed but not peak accuracy. In each case, the integration time and threshold of the postsynaptic cell are matched to the statistics of convergent spike trains.

Introduction

The maximum rate of information flow grows with the number of parallel channels in a transmission line (Stein, 1967). This allows for the transmission of more information over a fixed time window or, equivalently, the need for less time to transmit a fixed amount of information. Accordingly, sensation typically begins with a large array of peripheral sensors. For example, vision begins with a large array of photoreceptors, and hearing begins with a large array of hair cells (Sterling and Laughlin, 2015).

The olfactory system represents another example of this strategy. The detailed architecture of the olfactory system has been most fully characterized in Drosophila (Figure 1A), but the vertebrate olfactory system has a similar architecture (Bargmann, 2006). Each Drosophila odorant receptor is expressed by ~40 olfactory receptor neurons (ORNs) in each antenna, on average. All the ORNs that express the same receptor have similar odor response properties (de Bruyne et al., 1999; de Bruyne et al., 2001), and they project their axons to the same glomerulus in the brain (Vosshall et al., 2000). There they converge onto postsynaptic projection neurons (PNs). Each PN pools input from every single ORN in its cognate glomerulus (Kazama and Wilson, 2009). Given the theoretical benefits of pooling from parallel channels, we would expect to detect a near-threshold odor stimulus more quickly and accurately based on a single PN spike train, as compared to a single ORN spike train.

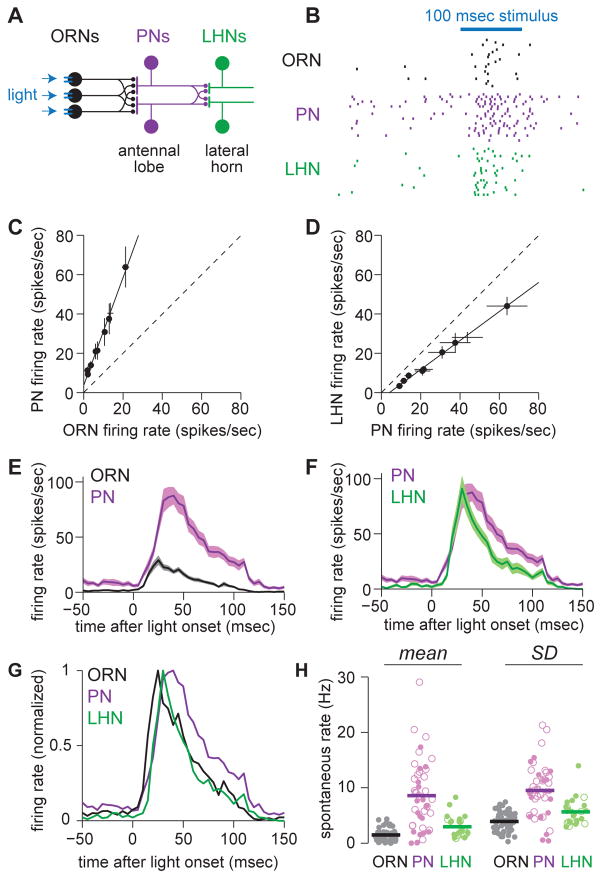
Figure 1. Sensory processing across three layers of olfactory circuitry.

(A) Schematic of feedforward circuitry from a single olfactory glomerulus (DA1). About 40 ORNs in each antenna project to this glomerulus. Each ORN axon diverges to contact all the PNs in this glomerulus, and conversely each PN receives convergent input from all 40 ORNs. PN axons then reconverge onto LHNs. ORNs express channelrhodopsin-2, and we use light to inject a brief packet of spikes into the ORNs.

(B) Rasters showing spikes in a DA1 ORN, a DA1 PN, and a postsynaptic LHN in response to repeated presentations of the primary stimulus used throughout this study (a 100 msec flash).

(C) ORN and PN firing rates evoked by a range of optogenetic stimuli of different intensities. Each symbol represents a different stimulus. The open circle denotes the primary stimulus used throughout this study. Dashed line denotes unity slope.

(D) As in (C), but for PN and LHN firing rates. PN-LHN gain is lower than ORN-PN gain (ANCOVA, p = 7.6 × 10⁻¹³).

(E) Mean firing rate over time in ORNs and PNs (± s.e.m. across cells, n=58 ORNs and 44 PNs).

(F) As in (E) but comparing PNs and LHNs (n=25 LHNs).

(G) Mean firing rates from (E,F) normalized to their peak.

(H) Spontaneous firing rates, mean (left) and standard deviation (right). Each symbol is a different recording (open circles are cell-attached recordings, filled circles are whole-cell current clamp recordings). Mean rates are higher in PNs than in ORNs (t-test, p = 2.4×10⁻¹³) or LHNs (t-test, p = 5.1×10⁻⁵). Standard deviations are also higher in PNs than in ORNs (t-test, 3.7×10⁻¹³) or LHNs (t-test, 3.0×10⁻⁴).

The benefits of pooling from parallel channels are not necessarily limited to the periphery: pooling could also be useful in central circuits. Specifically, a signal might diverge onto many neurons, whose activity then converges at a later stage. This could allow the brain to reduce noise accumulated independently in transmission along the parallel channels (Alonso et al., 1996; Faisal et al., 2008). Divergent neural architecture is widespread in central sensory circuits. For example, in the retina, each photoreceptor signal diverges onto many postsynaptic bipolar cells (Cohen and Sterling, 1990). In the cochlea, each hair cell signal diverges onto many postsynaptic ganglion cells (Liberman, 1980). In the Drosophila olfactory system, each ORN axon diverges to synapse onto all the identical “sister” PNs in the same glomerulus (Kazama and Wilson, 2009). However, it is difficult to show that the neurons that receive divergent signals actually reconverge onto a common postsynaptic neuron. Even if they do, the effect of pooling will not be straightforward, because these convergent inputs may be correlated as a consequence of having diverged upstream.

Here we use a single olfactory coding channel in Drosophila as a setting to investigate these questions. We study a population of ~40 ORNs that diverge and converge, in an all-to-all manner, onto six postsynaptic PNs. We show that these sister PNs reconverge onto a specific class of lateral horn neurons (LHNs). We investigate how the representation of a near-threshold stimulus is transformed at the ORN-to-PN step, and again at the PN-to-LHN step. We find that the function of convergence is different in the two cases: the first step implements averaging, and the second step implements coincidence detection. In each case, the integrative properties of the postsynaptic cell match the statistics of their convergent presynaptic spike trains.

Results

Sensory processing across three layers of olfactory circuitry

Our approach in this study was to inject a brief packet of spikes into the ORNs presynaptic to one glomerulus, and to trace this signal through three synaptically-connected layers: from ORNs to PNs, and then from PNs to LHNs (Figure 1A). We selected glomerulus DA1 for these experiments because we have good genetic access to the DA1 ORNs and their downstream PNs and LHNs in the brain. The benefits of pooling many ORNs might be most obvious for near-threshold stimuli, and so in this study we chose to focus on stimuli that elicit only about one spike per trial per ORN. It can be difficult to control odor stimuli near threshold, so we used an optogenetic approach instead. We expressed the light-activated cation channel channelrhodopsin-2 in DA1 ORNs, and we stimulated these neurons by flashing light on one antenna. To measure spikes in DA1 ORNs, we made in vivo extracellular recordings. In separate experiments, we made genetically-targeted in vivo patch-clamp recordings from PNs postsynaptic to glomerulus DA1, and from a specific class of LHNs that are postsynaptic to these PNs (Figure S1, Figure S2).

In pilot experiments, we identified a set of flash parameters that could reliably evoke small numbers of spikes in ORNs. Varying the duration and intensity of the flash evoked different numbers of spikes (Figure S3). In most of this study, we focus for simplicity on a single stimulus, a flash that elicited an average of 1.7 spikes per ORN per trial (Figure 1B). The onset of an odor can elicit a similar number of ORN spikes in the same time window. Thus, this ORN response likely resembles spiking patterns that occur in nature (Figure S4).

Overall, there was a linear relationship between ORN and PN spike counts in this near-threshold regime. PN spike rates were consistently about three-fold larger than ORN spike rates (Figure 1C). When we compared PN and LHN spike counts, we found that the input-output curve was again linear, but the slope was significantly lower, just below unity (Figure 1D).

ORN responses were more transient than the stimulus itself (Figure 1E). (ORN responses to a prolonged pulse of real odor can also adapt over time; Figure S4). As compared to ORN responses, PN responses were more prolonged (Figure 1E). However, LHN responses were more transient than those of PNs (Figure 1F,G). This implies that there are mechanisms that cause LHNs to respond preferentially to the onset of PN activity.

In short, a brief and minimal a packet of spikes is transformed in complementary ways as it travels through the first two feedforward layers of this system. The first transformation is high-gain and broadens the time course of the spike packet. The second transformation is lower gain and compresses the spike packet in time.

Multilayered circuitry improves accuracy and speed

Importantly, ORNs, PNs, and LHNs all fire spontaneously even in the absence of a stimulus. This poses a classic signal detection problem. Stimulus detection is only accurate if spontaneous firing is reliably different from stimulus-evoked firing (van Drongelen et al., 1978). Notably, for the three types of synaptically connected neurons we are focusing on here, spontaneous rates are significantly different (Figure 1H). Can we detect a weak stimulus more rapidly and accurately on the basis of spike trains from an ORN, a PN, or an LHN? To address this question, we took the perspective of an observer trying to determine whether a stimulus was present or not during a given window of time, on the basis of individual spike trains.

To carry out this analysis, we must first decide on the time window over which the observer can count spikes. In Drosophila, behavioral responses to odor can occur with latencies as short as ~80 msec (Bhandawat et al., 2010; Gaudry et al., 2013). Therefore, we began by counting spikes over an 80 msec window (Figure 2A).

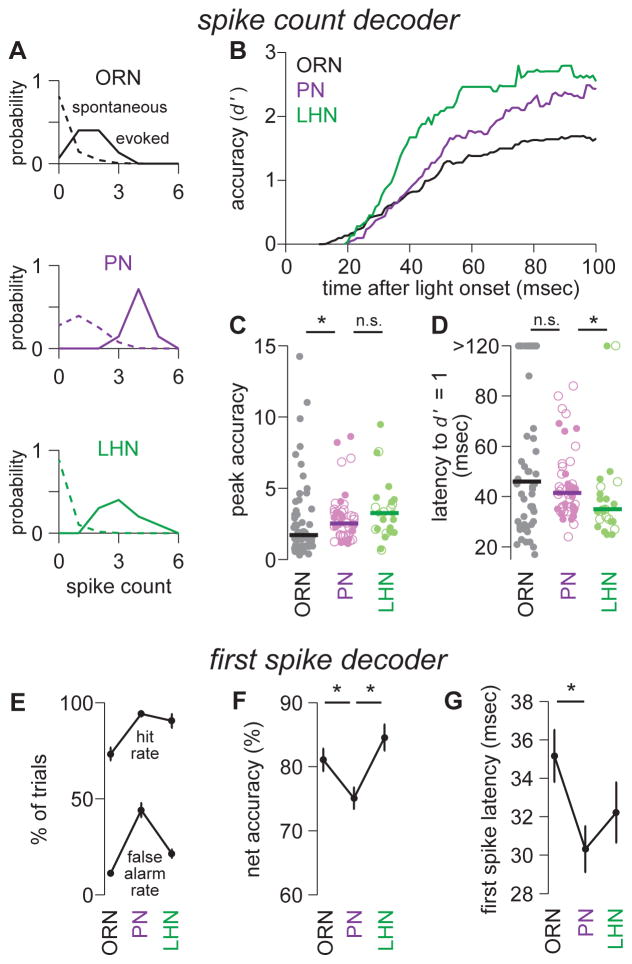
Figure 2. Multilayered circuitry improves accuracy and speed.

(A) Spike count histograms for 80 msec time windows containing a stimulus (solid) or no stimulus (dashed). Data are accumulated across multiple trials for a typical ORN, PN, and LHN. The accuracy of stimulus detection is assessed using the metric d′. This value is the separation between the means of the two distributions (μ_evoked - μ_spontaneous) normalized by the root of the average variance of the two distributions (√(½ (σ²_evoked + σ²_spontaneous)).

(B) Median accuracy (d′) over time for ORNs, PNs, and LHNs. An 80 msec window was slid forward in time, and resulting d′ values were plotted at the end point of each window. This and all subsequent panels in this figure are computed on the same data set (n=58 ORNs, 44 PNs, 25 LHNs).

(C) Peak accuracy (d′) for individual ORNs, PNs, and LHNs. PNs are significantly different from ORNs (Wilcoxon rank-sum test, p = 0.013), but not significantly different from LHNs (Wilcoxon rank-sum test, p = 0.25). Solid bars denote medians. (PN detection accuracy is actually lower than our theoretical expectation, due to high spontaneous activity in PNs; see Figure S8.)

(D) Latency to baseline detection accuracy (d′ =1) for individual ORNs, PNs, and LHNs. Latency is similar for ORNs and PNs (Wilcoxon rank-sum test, p = 0.33), but shorter for LHNs than for PNs (Wilcoxon rank-sum test, p = 0.015). Solid bars denote medians.

(E) Mean hit rates and false alarm rates for a decoder operating with a threshold of a single spike (± s.e.m. across cells). The hit rate is the percentage of trials with at least one spike during the stimulus period. The false alarm rate is the percentage of trials with at least one spike during a period of equal length (100 msec) when no stimulus was presented.

(F) Mean net accuracy for the decoder in E (± s.e.m. across cells). Net accuracy is worse for PNs than for ORNs (t-test, p = 0.018) or LHNs (t-test, p = 0.00077). Net accuracy is the average of the hit rate and the correct rejection rate.

(G) Mean first spike latency (i.e., the detection latency for the decoder in E), ± s.e.m. across cells. Latency is shorter in PNs than in ORNs (t-test, p = 0.0092). Latency is not significantly different in PNs and LHNs (t-test, p = 0.32). Different methods of measuring first spike latency produced slightly different values but did not change the qualitative differences between cell types (see Supplemental Experimental Procedures, Data Analysis).

To quantify detection accuracy, we used the metric d′ (Supplemental Experimental Procedures). This metric describes the separation between spontaneous firing rates and stimulus-evoked firing rates. Because we are interested in how accuracy grows over time, we performed this analysis in 80 msec windows that progressively slid forward, and we plotted detection accuracy (d′) versus the ending time of the window (Figure 2B).

We found that peak accuracy is significantly higher for a typical PN than for a typical ORN (Figure 2C). However, a PN only outperforms an ORN at a relatively long latency from stimulus onset (Figure 2B). This is because these PNs have significantly higher (and more variable) spontaneous spike rates than their presynaptic ORNs do (Figure 1H). Higher and more variable spontaneous rates mean that an observer needs to wait longer—to count more evoked spikes—before it can reliably detect the stimulus. As a result, a typical PN reaches a baseline level of accuracy (d′ = 1) at the same time that a typical ORN does (Figure 2D).

Peak LHN accuracy is similar to peak PN accuracy (Figure 2B,C). However, LHN accuracy rises more quickly, so that a baseline level of accuracy (d′ = 1) is achieved significantly faster (Figure 2D). This is because spontaneous spike rates are significantly lower in an LHN than in a PN. A decoder of LHN activity therefore needs to count evoked spikes for a shorter interval in order to be confident that a stimulus is present.

Of course, the latency of the behavioral response represents an upper bound on the time to decode the activity of ORNs, PNs, and LHNs. Events downstream from the olfactory system must occupy a substantial fraction of the behavioral latency. We therefore also considered the lower bound of decoding time—the time to wait for a single stimulus-evoked spike. Specifically, we measured the percentage of trials that yielded a correct detection (at least one spike during the stimulus period) or a false alarm (at least one spike during a period of equal length when no stimulus was presented).

By this alternate measure, a PN had a higher correct detection rate but also a higher rate of false alarms, as compared to an ORN (Figure 2E) and therefore a significantly lower net accuracy (Figure 2F). However, the average first spike in a PN was significantly faster than the average first spike in an ORN (Figure 2G). This latter result is rather striking, especially because there is a delay of ~4.5 msec between an ORN spike and the start of an excitatory postsynaptic potential (EPSP) in a PN (Kazama and Wilson, 2008).

Compared to a PN, an LHN had a lower rate of false alarms (Figure 2E), and therefore a significantly higher net accuracy (Figure 2F). This result reinforces the conclusion that early LHN spikes are more informative than early PN spikes (Figure 2B). Moreover, the average first spike in an LHN was almost as fast as the average first spike in a PN (Figure 2G). Again, this speed is notable, given the delay of 1.3 msec between a PN spike and the start of an EPSP in an LHN (see data on paired PN-LHN recordings below; see also Fisek and Wilson, 2014; Kohl et al., 2013).

In summary, single-neuron accuracy (d′) improves at each step in this circuit, but the nature of the improvement is different for the two steps. Compared to ORNs, PNs can perform more accurately when an observer is given a relatively long time to count spikes, but the PN’s first spike—despite occurring earlier, on average—carries less information because of the PN’s higher (and more variable) spontaneous firing rate. Compared to PNs, LHNs can perform more accurately at short latencies after stimulus onset. The first LHN spike is no faster than the first PN spike, but it carries more information, because of the LHN’s lower (and less variable) spontaneous firing rate. Single LHNs can perform better than single PNs do because single LHNs pool input from multiple sister PNs (see below).

In the remainder of this study, we investigate the mechanisms that create the progressive improvement in stimulus detection performance from ORNs to PNs to LHNs. Specifically, we focus on three factors: the statistics of convergent presynaptic spike trains, the effective integration time of the postsynaptic cell, and the threshold of the postsynaptic cell. For simplicity and consistency, we use one stimulus throughout this study, but we found that other stimuli in the near-threshold regime (Figure 1C,D) produced qualitatively similar results (but note that the situation is different for stronger stimuli, see Figure S3).

A decoder of ORN activity benefits from a long integration time and low spike count threshold

In the above analysis, we have invoked a hypothetical decoder that receives input from a single ORN, PN, or LHN. Our goal was to compare how informative these single neurons are about the presence of a stimulus on a single-trial basis. Here we will use a hypothetical decoder for a different purpose. Our goal is to ask how a postsynaptic neuron might most usefully decode spikes from a pool of ORNs. Specifically, what happens to detection accuracy and speed when we vary the integration time and threshold of the decoder? Then, we will ask how well PN properties are matched to the properties of this idealized hypothetical decoder of ORNs.

We first investigated the effects of varying integration time. We can define the “integration time” of a decoder as the time over which one input spike summates effectively with subsequent input spikes. Our hypothetical decoder simply counts spikes within a specified time window, so the integration time is just the width of this time interval. As before (Figure 2B), we used spike counts to compute a time-varying estimate of detection accuracy (d′). Whereas previously we had measured detection accuracy based on single ORNs, we here assembled pools of 40 ORNs by combining ORN recordings drawn from our data set, so as to emulate the input to a single PN (Figure 3A). This assembly is justified because ORNs spike independently (that is, ORNs have no noise correlations; Figure S5; Kazama and Wilson, 2009). Exact estimates of the number of DA1 ORNs vary, but a pool size of ~40 is implied by genetic labeling experiments (see Supplemental Experimental Procedures).

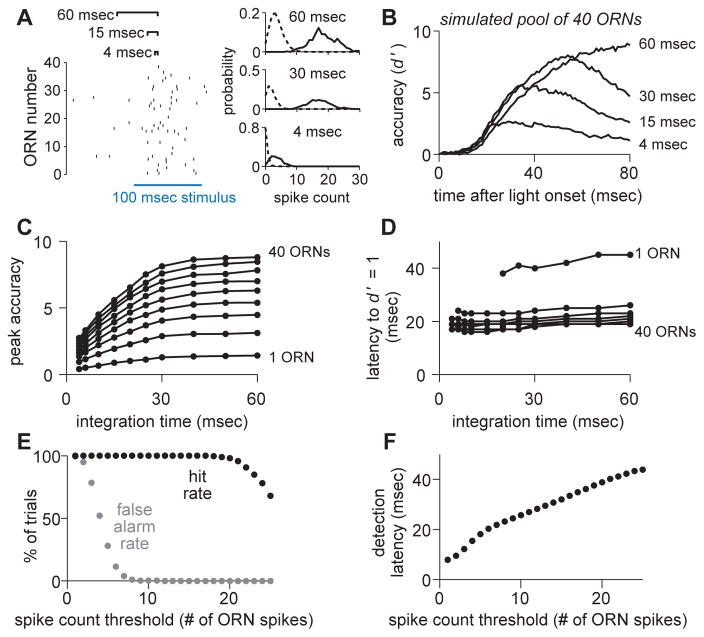
Figure 3. A decoder of ORN activity benefits from a long integration time and low threshold.

(A) Comparing different integration windows by counting ORN population spikes in sliding windows of variable length (i.e., a variable integration time). At each time point, we construct spike count histograms and measure the separation between spontaneous and evoked activity (stimulus detection accuracy) using d′.

(B) Mean accuracy (d′) over time for simulated populations of 40 ORNs. Increasing integration time increased peak accuracy. Populations were assembled by randomly selecting (without replacement) single trials from all of our ORN data (n = 58 ORN recordings, see Supplemental Experimental Procedures).

(C) Peak accuracy for various integration times (mean over 2000 simulations of each ORN pool size). ORN pool sizes plotted are: 1, 5, 10, 15, 20, 25, 30, 35, and 40.

(D) As in C, but for latency to baseline accuracy (d′ = 1).

(E) Performance of a binary classifier (operating over 30 msec integration windows), for a range of spike count thresholds.

(F) Detection latencies for the binary classifier in E, for a range of spike count thresholds.

As one might expect, longer integration times improved peak accuracy (Figure 3B,C), because the decoder averaged over more ORN spikes. Peak accuracy saturated with an integration time of about 30 msec. Longer integration times did not improve accuracy further because the ORN response is transient.

Increasing integration time also slightly lengthened the latency to reach a given level of accuracy (Figure 3B,D). As integration time increases, the onset of evoked activity is blurred, and so to reliably detect a stimulus, the decoder needs to wait for more evoked spikes. However, the increase in latency is relatively small.

The overall effect of varying integration time was robust to the size of the ORN pool (Figure 3C,D). In short, this analysis argues that it would be useful for a decoder to integrate ORN population activity over at least 30 msec, because this yields a large improvement in accuracy, with only a modest impairment of speed.

The above analysis (d′) does not employ a threshold—it simply measures the separation between spontaneous and evoked firing rates. To investigate the effect of a threshold, we implemented a binary classifier: we slid a 30 msec integration window forward from the time of stimulus onset, and if the number of spikes in the window exceeded threshold, we counted it as a correct detection and noted the time. To measure the rate of false alarms, we repeated the same procedure during epochs when no stimulus was present. We define the “spike count threshold” as the number of presynaptic spikes necessary for the decoder to detect the stimulus. With a pool of 40 ORNs, there was a large range of thresholds that elicited perfect detection accuracy (Figure 3E). Lower thresholds yielded faster detection (Figure 3F), because they require waiting for fewer spikes. A spike count threshold of about 8 ORN spikes yielded the fastest detection without sacrificing accuracy.

To summarize, this analysis reveals two useful properties in a hypothetical (linear) decoder of ORN population activity. First, peak accuracy is maximized when ORN spikes are integrated over at least 30 msec. This is a relatively long integration time, compared to the integration time of LHNs (see below), and compared to behavioral latencies. Second, given a decoder integrating on a 30-msec timescale, a spike count threshold of ~8 ORN spikes maximizes speed while not sacrificing accuracy. This is a low threshold, in the sense that it represents a small percentage (~20%) of the full population of 40 active ORNs.

PNs have a long integration time and a low spike count threshold

Next, we compared PNs with the idealized decoders described above, again focusing on integration time and threshold. One way to estimate PN integration time is to compare the dynamics of ORN and PN firing rates, and fit the transformation with a linear filter (Figure 4A, Supplemental Experimental Procedures). We found that the best-fitting filter had a duration of 23 msec (Figure 4A). Another relevant fact is that the unitary EPSP at ORN-to-PN synapses has a time constant of roughly 30 msec (Kazama and Wilson, 2008). Taken together, these facts imply that a PN integrates ORN spikes over a window of approximately 20–30 msec. This estimate is in rough agreement with the integration time of the idealized decoder described above.

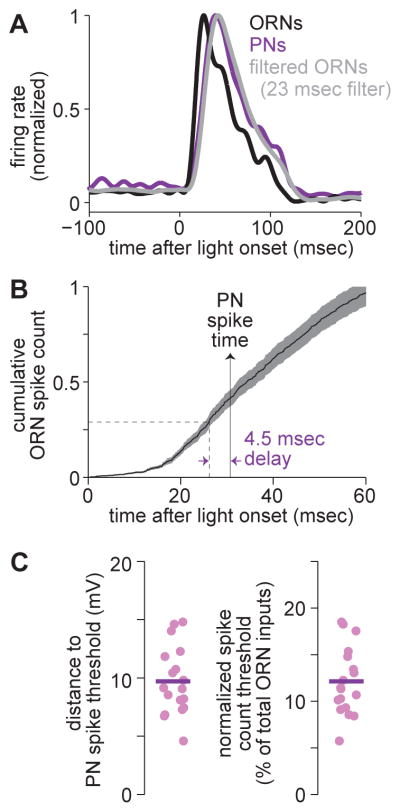
Figure 4. PNs have a long integration time and a low spike count threshold.

(A) Normalized firing rates for ORNs and PNs (reproduced from Figure 1G). Convolving the ORN response with a rectangular filter having a width of 23 msec yields a good fit to the PN response.

(B) Mean cumulative ORN spike count (± s.e.m. across cells, n = 58). The vertical solid line with the arrow denotes mean time to first evoked PN spike (from Figure 2G). After accounting for the 4.5 msec transmission delay between ORN spikes and PN EPSP onset, the horizontal dashed line identifies that 0.28 spikes/ORN have occurred prior to the typical first PN spike. This is equivalent to about 11 spikes per 40 ORNs.

(C) Distance to spike threshold. Left: distance in units of voltage, measured as the difference between the average threshold of spontaneous PN spikes and the average PN voltage overall (n = 18 PN recordings). Right: same data expressed as the percentage of all ORNs that must spike once to drive the PN to threshold (assuming a unitary EPSP amplitude of 2 mV and 40 ORNs, see Supplemental Experimental Procedures).

How does the spike count threshold of PNs compare to that of the idealized decoders described above? In other words, how many closely-spaced ORN spikes are needed to drive the PN to fire a spike? As a first approach to this question, we asked how many ORN spikes have typically occurred by the time of the first stimulus-evoked PN spike. The average time of the first evoked PN spike is 30 msec (Figure 2G). From this measurement, we subtracted a delay of 4.5 msec, representing axonal conduction and synaptic transmission (Kazama and Wilson, 2008). We then asked how many ORN spikes had accumulated, on average, by this time. This value was 0.28 spikes per ORN (Figure 4B), or one spike in 28% of the ORN pool. Given a pool of 40 active ORNs, this implies a spike in about 11 ORNs.

The PN’s spike count threshold can also be estimated directly from current clamp recordings. Here we can think of the spike count threshold as the number of closely-spaced ORN EPSPs needed to drive the PN to fire a spike. We measured the average voltage at which a spontaneous PN spike initiates, as well as the average PN voltage overall (in the absence of any stimulus). The difference between these values is the distance to spike threshold, which was about 10 mV on average (Figure 4C). If an ORN spike depolarizes the PN by about 2 mV (Supplemental Experimental Procedures), then 5 synchronous ORN spikes would be needed to generate a spike in the PN, if summation were linear. This represents a small fraction (about 13%) of the total population of 40 active ORNs (Figure 4C).

Broadly speaking, these two methods for estimating the PN spike count threshold yield similar results. The PN should typically fire a spike as soon as a small percentage of the ORN pool responds to the stimulus—a percentage we estimate at 13 to 28%. This estimate is in rough agreement with the spike count threshold of the idealized decoder described above. In addition, this result is closely related to the finding that the ORN-to-PN firing rate relationship has a high gain (Figure 1D): both follow from the fact that the average ORN spike has a relatively potent effect on the PN membrane potential.

Recall that the typical first stimulus-evoked PN spike is fast, insofar as it actually precedes the typical first spike in any given ORN (Figure 2G). This depends critically on the fact that PNs have a low spike count threshold. A model fit to known properties of PNs and their input synapses can reproduce this fast first spike latency in PNs, but only if each ORN spike has a potent effect on the PN voltage, and only if the number of convergent ORNs is high (Figure S6).

In short, PNs are well-suited to harness the power of ORN convergence for accuracy and speed. Their long integration time and low spike count threshold are usefully matched to the statistical properties of ORN spike trains. As a consequence, PNs effectively average out ORN noise, and they also rapidly track firing rate increases in the ORN population.

Individual lateral horn neurons pool input from sister PNs

We next turn to the decoding of PN activity by LHNs. Six uniglomerular PNs are postsynaptic to glomerulus DA1 (Caron et al., 2013; Datta et al., 2008) and project axons to the lateral horn. The axons of “sister” PNs overlap spatially in the lateral horn (Kazama and Wilson, 2009; Marin et al., 2002; Wong et al., 2002), suggesting they may converge on some of the same LHNs. As a first step toward understanding how LHNs interpret PN activity, we set out to determine if this is true.

Previous studies have identified and characterized several clusters of LHNs that receive direct excitation from DA1 PNs (Kohl et al., 2013; Ruta et al., 2010). Among these LHN clusters, one has especially strong responses to the most potent odor for DA1 ORNs (cis-vaccenyl acetate; van der Goes van Naters and Carlson, 2007). This particular LHN cluster has been given various names (DC1, aSP-f, and aSP5; Cachero et al., 2010; Kohl et al., 2013; Ruta et al., 2010; Yu et al., 2010).

To determine whether the LHNs in this cluster receive convergent input from sister DA1 PNs, we performed simultaneous paired PN-LHN recordings (Figure 5A). In each paired recording, we delivered a brief depolarizing current pulse to trigger a PN spike, and we looked for a time-locked excitatory postsynaptic potential (EPSP) in the LHN (Figure 5B,C). In a morphologically and physiologically distinct subtype of LHNs within this cluster (Figure S1, Figure S2), we reliably observed EPSPs with a consistent short latency from the PN spike, indicating a monosynaptic connection (5/5 pairs). All the LHNs referred to in this study belong to this subtype.

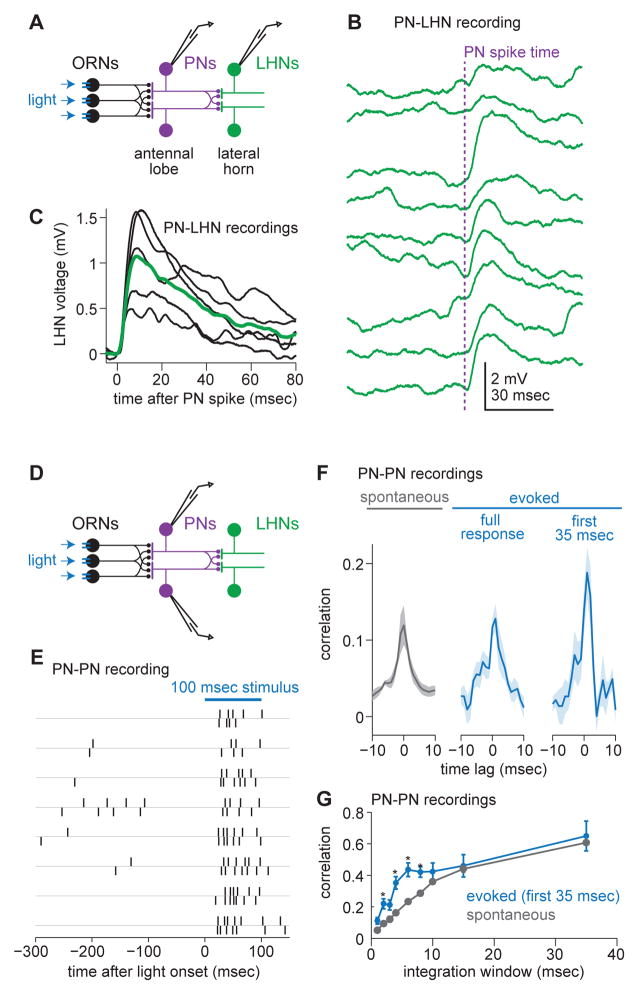
Figure 5. Individual lateral horn neurons pool input from sister PNs and stimulus onset increases short-timescale correlations among sisters.

(A) Schematic of a paired PN-LHN recording.

(B) Examples of unitary EPSPs recorded from a single LHN (green) in response to a single PN spike evoked by current injection (PN spike time indicated by vertical dashed line). Traces are ordered chronologically, top to bottom.

(C) Mean EPSPs (black) for each paired recording. Overlaid is the grand average unitary EPSP over all 5 pairs. Before averaging, EPSPs are aligned to the time of the PN spike (specifically, the onset of the PN spike waveform; see Supplemental Experimental Procedures). On average, the latency between the PN spike and EPSP onset is 1.3 ± 0.2 msec (mean ± SEM across recordings; measured as the time that the trial-averaged EPSP in an LHN takes to reach 5% of its peak).

(D) Schematic of a paired PN-PN recording.

(E) Rasters from two simultaneously recorded DA1 PNs.

(F) Cross-correlation functions (shift-subtracted) for spontaneous and stimulus-evoked activity (mean ± s.e.m. over pairs, n = 8 DA1 PN pairs). Stimulus evoked activity is shown for two time windows, one encompassing the full response (120 msec), and one that includes only the first 35 msec of the response.

(G) Correlation coefficient (shift-subtracted) for PN pairs over various integration windows (mean ± s.e.m. over pairs). There is a significant effect integration window size on the correlation coefficient (ANOVA, p = 0.0061). For short integration windows, correlation coefficients are higher during evoked activity than during spontaneous activity (* denotes p < 0.02, paired t-test).

Given a direct PN-to-LHN connection in 5/5 paired recordings, it is almost certain that each LHN receives convergent input from multiple DA1 PNs. If in reality there was a connection from only one of the six PNs, the chance of seeing a connection in 5/5 samples is 0.01%. Thus, we can conclude that each LHN receives convergent input from at least two DA1 PNs, and possibly all six.

Stimulus onset increases short-timescale correlations among sister PNs

Because these LHNs pool convergent input from multiple sister PNs, it is important to characterize the relationship between sister PN spike trains. With this goal in mind, we made paired recordings from DA1 PNs (Figure 5D). Inspection of paired rasters showed that sister PN spikes were notably correlated—i.e., sister PNs were more likely to fire in quick succession than one would predict by chance, based on the mean firing rates of these neurons (Figure 5E). This correlation arises because each PN receives divergent input from every individual ORN that targets its glomerulus (Kazama and Wilson, 2009).

To quantify this effect, we computed shift-subtracted cross-correlation functions (Supplemental Experimental Procedures). For DA1 ORNs, this function was flat (Figure S5), indicating that ORNs are statistically independent. For DA1 PNs, the result was a positive correlation (Figure 5F). PN correlations depended on timescale, with significantly larger correlations at long timescales (Figure 5G).

Notably, in the first 35 msec after stimulus onset, PN correlations were considerably higher than they were in the absence of a stimulus (Figure 5F). The stimulus-induced increase in correlations was mainly restricted to short timescales (Figure 5G). This phenomenon can be explained by how correlated synaptic inputs interact with spike threshold (de la Rocha et al., 2007) and is consistent with a previous report of correlations among sister PNs in a different glomerulus (Kazama and Wilson, 2009).

A decoder of PN population activity faces a speed-accuracy tradeoff

The above analyses show that the statistics of PN activity depend on timescale. Thus, for a decoder of PN activity, accuracy and speed should both depend on integration time. To explore the effect of systematically varying integration time, we again turned to a hypothetical decoder. First, we computed detection accuracy based on spike counts from single PNs (Figure 6A). We varied the duration of the integration window over which we counted spikes (Figure 6B). As one might expect, there was a tradeoff between peak accuracy and speed (Figure 6C,D). A longer integration time produced higher peak accuracy, but only at long latencies. The reason is that accurate detection cannot occur until the number of counted spikes per window exceeds the number of expectable spontaneous spikes per window. Thus, longer windows delay the time point when peak accuracy can be reached.

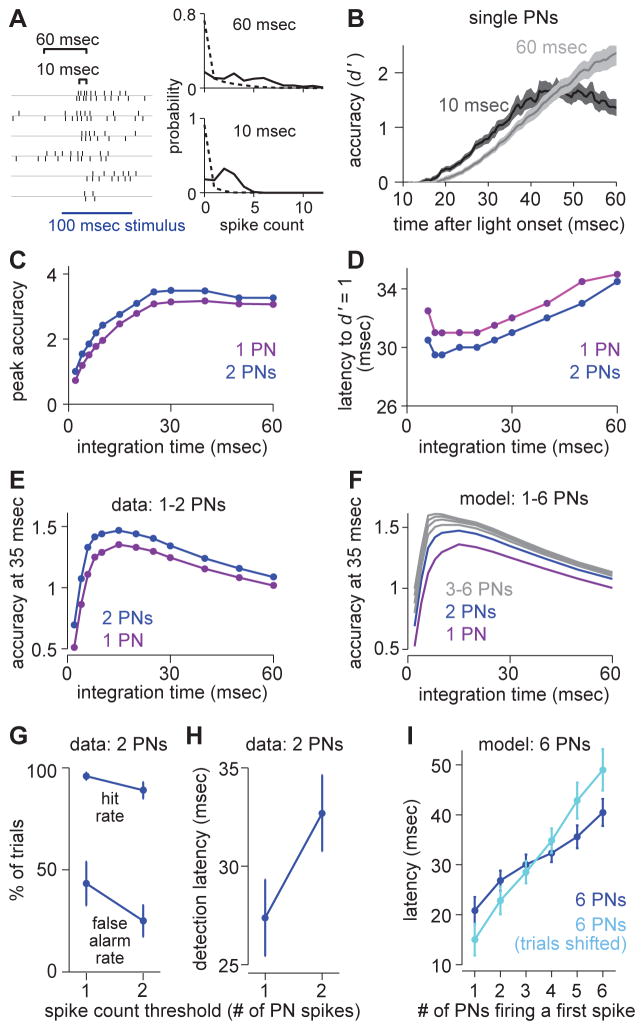
Figure 6. A decoder of PN population activity faces a speed-accuracy tradeoff.

(A) Comparing different integration windows by counting spikes from pairs of PNs (or single PNs) in sliding windows of variable length (i.e., a variable integration time). At each time point, we construct spike count histograms and measure the separation between spontaneous and evoked activity (stimulus detection accuracy) using d′.

(B) Accuracy (d′) over time based on spike trains from a single PN (mean ± s.e.m. over PNs).

(C) Peak detection accuracy versus integration time, averaged over all PN pairs or the single PNs included in these pairs. Accuracy (single PNs) increases with integration time (ANOVA, p = 7.2 × 10⁻⁴). Accuracy is higher for PN pairs than for single PNs (ANOVA, p = 0.0142). This and all subsequent panels in this figure are computed on the same data set (n = 8 PN pairs).

(D) Mean latency to baseline accuracy (d′ = 1) versus integration time. Latency increases with integration time (single PNs, ANOVA, p = 5.6 × 10⁻⁴). Latencies are shorter for PN pairs than for single PNs (ANOVA, p = 0.0090). Latency is not calculated for windows of 4 msec or shorter, because several (single) PNs never reach baseline accuracy.

(E) Mean accuracy versus integration time, evaluated at 35 msec after stimulus onset. Accuracy is maximal for decoders that integrate over 10–20 msec. Accuracy is higher for PN pairs than for single PNs (ANOVA, p = 6.0 × 10⁻⁴). The improvement in accuracy with pairs is significantly greater for short timescales than for long timescales (ANOVA, interaction between population size and integration time: p = 0.0045).

(F) Same as E but for modeled PN populations ranging in size from 1 PN to 6 PNs. Spike counts in PN populations were simulated based on distributions from paired PN data (Supplemental Experimental Procedures).

(G) Hit rates and false alarm rates for a binary classifier (with a 10-ms integration window, mean ± s.e.m), for two different thresholds (one spike or two spikes, pooled over a pair of sister PNs). The higher threshold produces a higher net accuracy (paired t-test, p = 0.0189).

(H) Detection latencies for the binary classifier in G, for the same two thresholds. The higher threshold imposes a speed cost of about 5 msec (paired t-test, p = 0.0073).

(I) In a modeled population of 6 PNs, mean latency for a given number of these PNs to fire a first spike after stimulus onset. First PN spike distributions were simulated based on distributions from paired PN data (Supplemental Experimental Procedures). When trials were shifted to remove correlations, latencies became longer for higher thresholds.

We next considered data from PN pairs. PN pairs consistently outperformed single PNs, in terms of both peak accuracy and speed (Figure 6C,D). To begin to link these observations to LHN responses, we focused on the time point 35 msec after stimulus onset, about the time of the first LHN spike (Figure 2G). Given this response latency, the ideal integration time was 10 – 20 msec for a decoder of one or two PNs (Figure 6E). To extrapolate to a pool of six PNs, we constructed a model that preserved pairwise correlations among PNs (Figure 5G; Supplemental Experimental Procedures). Adding more and more PNs had the greatest benefit for short integration times, and shifted the ideal integration time to shorter intervals (Figure 6F). This is because correlations between PNs were greatest at short timescales (Figure 5G, Figure S7).

To recap, a hypothetical decoder of PNs faces a speed-accuracy tradeoff in its choice of integration times. Long integration times maximize peak accuracy, while short integration times maximize speed. However, the accuracy reduction of a short integration time is mitigated by adding sister PNs to the pool, and indeed the relative benefit of pooling across multiple PNs is greatest for short integration times. The speed-accuracy tradeoff faced by a decoder of PNs is similar to that faced by a decoder of ORNs (Figure 3C,D), but it is more pronounced.

Next, to investigate the effect of varying the spike count threshold, we returned to our binary classifier. As before (in Figure 3E,F), we slid an integration window forward from the time of stimulus onset, and if the number of stimulus-evoked spikes within the window exceeded the threshold, we counted a correct detection. False alarms were measured on stretches of data when no stimulus was presented. We used a narrow integration window (10 msec) because this window is best for a decoder that is forced to respond by the time of the first LHN spike (Figure 6E,F).

In this narrow time window, a single PN rarely fires more than twice, so we focused on thresholds of one or two PN spikes. For a decoder pooling from two sister PNs, raising the threshold from one spike to two spikes reduced false positives (Figure 6G) but also delayed detection (Figure 6H). However, correlations should make it possible to cross a high threshold sooner because they increase the likelihood that multiple PNs will spike in the same brief time window. This result is clearest in a model pool of six PNs (Supplemental Experimental Procedures): here, the speed cost of a high threshold was lower when correlations were present (Figure 6I).

In summary, a hypothetical decoder of PNs faces a speed-accuracy tradeoff in its choice of spike count threshold. Raising the threshold improves accuracy but delays the time of threshold crossing. However, the speed cost of a high threshold is mitigated by the fact that sister PN spikes are correlated.

LHNs operate with a high, but dynamic, spike count threshold

Given this tradeoff between speed and accuracy, how can LHNs be so fast but also accurate? LHNs suppress spontaneous spikes (Figure 1H) and thereby improve accuracy at short latencies (Figure 2F). Nonetheless, the first spike latency of an LHN is not significantly longer than that of a PN (Figure 2G). How is this achieved?

The average amount of depolarization needed to trigger a spontaneous LHN spike is about 10 mV (Figure 7A). If a PN spike depolarizes the LHN by about 1 mV (Figure 5C), then 10 synchronous PN spikes would be needed to generate a spike in the LHN, assuming linear summation. Recall that only 5 synchronous ORN spikes are needed to drive a PN spike, according to our analogous PN analysis (see above). The difference between PN and LHN spike count threshold is even larger if we normalize these numbers by the size of the presynaptic pool. Whereas PNs require only a small percentage of their feedforward inputs to spike, we estimate that LHNs require all of their feedforward inputs to spike (Figure 7B). Thus, in relative terms, the LHN spike count threshold is high, at least during epochs of spontaneous activity. This helps explain why the spontaneous firing rate is so low in LHNs.

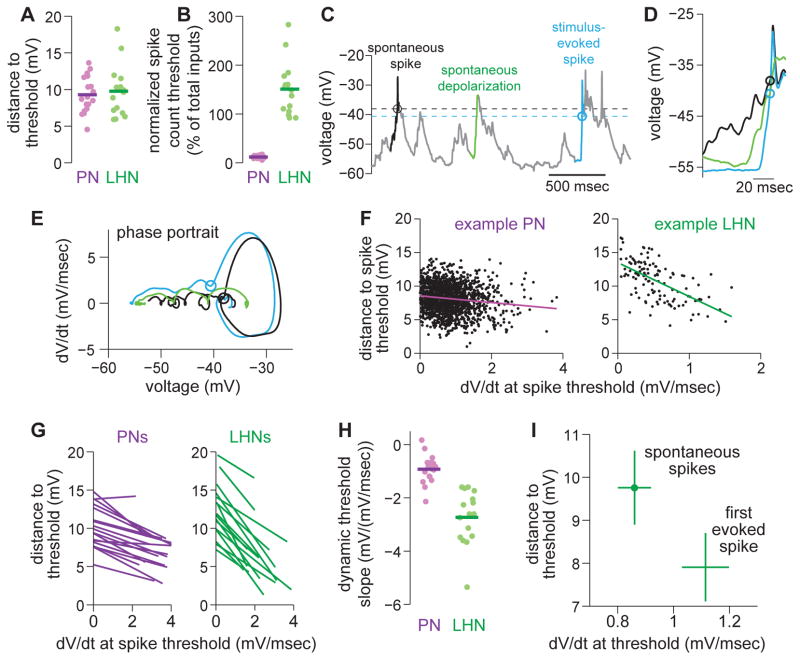
Figure 7. LHNs operate with a high, but dynamic, spike count threshold.

(A) Distance to spike threshold for PNs and LHNs. Each symbol is a different recording. This and subsequent group-data panels in this figure are computed on the same data set (n = 18 PNs and 16 LHNs).

(B) Same but normalized by the estimated typical EPSP amplitude for each cell type (2 mV for PNs, 1.08mV for LHNs, see Figure 5C and Supplemental Experimental Procedures) and also normalized by the size of the presynaptic pool (here assumed to be 40 ORNs and 6 PNs). This value represents the percentage of the total presynaptic pool that must spike nearly-synchronously to drive the postsynaptic cell above threshold.

(C) A typical whole-cell current clamp recording from an LHN highlighting two spikes (black and blue), and also a depolarization that does not evoke a spike (green). Circles and dashed lines denote spike thresholds.

(D) Brief snippets of voltage surrounding the two spikes and the non-spiking depolarization (from C).

(E) Phase portrait (dV/dt vs. V) for these three snippets.

(F) Distance to spike threshold versus rate of depolarization for all spikes (spontaneous and stimulus-evoked) recorded from a typical PN and LHN.

(G) Linear regression fits (like those in F) for all PNs and LHNs. Each line represents a different recording.

(H) Slopes of linear regression fits from G for all PNs and LHNs. Distance to threshold depends on dV/dt more strongly in LHNs than in PNs (t-test, p = 1.9 × 10⁻⁷).

(I) Distance to threshold versus dV/dt in LHNs. Spikes in two categories were analyzed—namely, spontaneous spikes and the first stimulus-evoked spike. Distance to threshold is significantly lower for the first stimulus-evoked spike (paired t-test, p = 6.2 × 10⁻⁴). dV/dt is also significantly higher for the first stimulus-evoked spike (paired t-test, p = 0.0024).

Given the high spike count threshold in LHNs, how can the first LHN spike be so fast (Figure 2G)? Inspection of the LHN voltage trace revealed that the spike threshold is not static—it varies from moment to moment (Figure 7C–E). In particular, whereas spontaneous spikes initiated at relatively high thresholds (Figure 7A), stimulus-evoked spikes typically initiated at lower thresholds (Figure 7C–E).

At stimulus onset, the peak rate of membrane depolarization was often much larger than during epochs of spontaneous activity. It is well-known that fast membrane depolarization can lower the spike threshold in some types of neurons; this phenomenon has been termed a “dynamic threshold” (Azouz and Gray, 2000; Wickens and Wilson, 1998). Indeed, we found that faster depolarizations consistently produced lower thresholds in LHNs (Figure 7F–G). By contrast, in PNs, threshold was significantly less dependent on the rate of depolarization (Figure 7F–H). Stimulus onset lowered the threshold for LHN spikes by about 20%, on average (Figure 7I).

The dynamic threshold helps explain how LHNs can maintain a fast response while still suppressing spontaneous activity. When PN spikes arrive at a relatively slow rate (i.e. in the absence of a stimulus), we estimate that an LHN must wait to receive about 10 closely-spaced PN spikes before it can fire (Figure 7B,I). Thus, spontaneous activity is suppressed in LHNs. But when PN spikes arrive in quick succession (i.e. at stimulus onset, when spike rates and noise correlations are highest), we estimate that LHNs need only receive about 8 PN spikes before they can fire (Figure 7I). In essence, the dynamic threshold in LHNs should allow them to mitigate the speed-accuracy tradeoff: LHNs can set a high spike count threshold to improve accuracy, while lowering the threshold at stimulus onset to maintain speed.

Beyond the dynamic threshold mechanism, there may be other mechanisms at work that bring the LHN to threshold rapidly. The average first spike latency in an LHN is actually faster than our estimate of the latency to accumulate first spikes in six sister PNs (compare Figure 2G and Figure 6I). It is possible that there are higher-order correlations among sister PNs that we cannot discern. These correlations could make the first spikes elicited by all six sister PNs even more synchronized; in this scenario, the sixth PN spike would occur with shorter latency than we predict in Figure 6I. An additional possibility is that EPSPs might sum supra-linearly in LHN dendrites.

The dynamic threshold shortens the LHN integration window

For an idealized decoder of PN spike trains, detecting the stimulus rapidly requires a short integration time (Figure 6). If the postsynaptic firing rate is simply proportional to the membrane potential, and if EPSPs summate linearly, then the integration time is specified by the duration of a unitary EPSP. By this logic, the integration time in an LHN seems long, given that the average EPSP has a time constant of ~40 msec (Figure 5C). However, the dynamic threshold in an LHN will shorten its effective integration time (Azouz and Gray, 2000). To see why this is true, consider the effect of summing six EPSPs in an LHN, with variable arrival intervals between EPSPs (Figure 8A). As these intervals decrease, the peak of the compound EPSP grows gradually. However, the rising slope of the compound EPSP grows more sharply (Figure 8B). Thus, insofar as spiking depends on dV/dt, the cell’s effective integration time is narrower. This mechanism can contribute to “coincidence detector” or “differentiator” behavior, whereby a neuron responds preferentially to short presynaptic inter-spike intervals (Lundstrom et al., 2009; Slee et al., 2005).

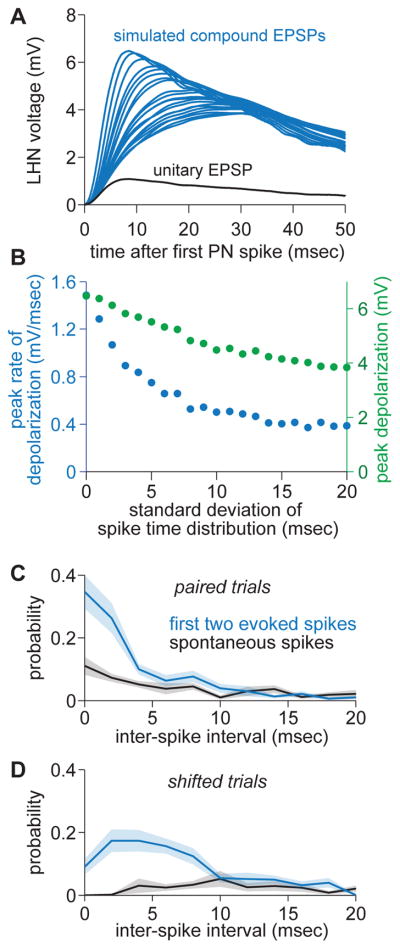
Figure 8. The dynamic threshold shortens the LHN integration window.

(A) Simulated compound EPSPs in an LHN in response to 6 PN spikes with variable inter-spike intervals. A single unitary EPSP is shown in black for comparison. EPSP summation is assumed to be linear.

(B) Comparison of the peak depolarization (green) and the peak rate of depolarization (blue) for the simulated compound EPSPs shown in A. The peak rate of depolarization falls off faster than does the peak depolarization.

(C) In a pair of PNs, probability distributions of inter-spike intervals for the first two stimulus-evoked PN spikes, or the first two spontaneous PN spikes (measured from an arbitrarily chosen time point during spontaneous activity). The x-axis is truncated at 20 msec.

(D) Same but for trial-shifted distributions, meaning correlations between sister PN pairs have been eliminated.

It is instructive to compare the dynamics of dV/dt in an LHN (Figure 8A,B) with the timescale of spike coincidences in sister PNs. Stimulus onset dramatically increases the relative prevalence of short inter-spike intervals in sister PNs (Figure 8C). This is partly because the stimulus simply increases firing rates, and partly because correlations increase at stimulus onset (Figure 5F). This latter effect is clearly relevant because if we eliminate correlations by shifting trials, we eliminate most of the shortest inter-spike intervals (Figure 8D). An ideal decoder would respond preferentially to short inter-spike intervals, because they are highly predictive of a stimulus, with proportionately less weight assigned to longer inter-spike intervals, which are less predictive. A dynamic threshold narrows the neuron’s integration window, and so it should move the LHN in the direction of this ideal decoder.

Discussion

Here, we show that PNs and LHNs receive spike trains with different statistical properties. Our results argue that the properties of neurons within each layer—specifically, their integration time and threshold—are well-suited to the statistics of the input they receive. These findings suggest a framework for thinking about other circuits where signals converge, diverge, and re-converge.

Different integration times for different input spike train statistics

The speed and accuracy of spike train decoding depends critically on the timescale over which spikes are integrated. We can define the “integration time” of a decoder as the time over which one presynaptic spike can summate effectively with subsequent spikes. In general, increasing the integration time of a decoder should improve detection accuracy, because more spikes can be averaged together. Indeed, we show that it is useful for a decoder to integrate ORN spikes over at least ~30 msec, because accuracy is best at long timescales, and there is little cost in terms of speed. Accordingly, we found that PNs do indeed integrate ORN spikes over ~30 msec. This represents a relatively long integration time, equal to a substantial fraction of the behavioral latency. A similarly long integration time has been measured in pheromone-sensitive PNs in moths, based on a paired-pulse experimental design (Tabuchi et al., 2013).

There is a long history to the idea that the brain must average the spike trains of convergent ORNs (Cleland and Linster, 2005; van Drongelen et al., 1978). This idea is supported by the finding that vertebrate olfactory bulb neurons generally have better reliability and lower odor detection thresholds, as compared to ORNs (Duchamp-Viret et al., 1989; Meeks et al., 2010; Rospars et al., 2013; Tan et al., 2010). The same is true of central and peripheral neurons in the moth pheromone-processing system (Boeckh and Boeckh, 1979; Rospars et al., 2014). Here we show explicitly that a long integration time is useful for a hypothetical decoder of ORN activity, and we demonstrate that PNs behave as integrators that summate ORN spikes over a relatively long time window.

In contrast, a decoder of PN spikes incurs a relatively high cost if it employs a long integration time, because PNs have high spontaneous rates and correlated spike times. Integration times beyond ~10 msec diminish the decoder’s stimulus detection speed (due to high spontaneous activity in PNs) and impair the ability of the decoder to average out noise between PNs (due to increasing correlations at long timescales). Accordingly, LHNs are endowed with a mechanism that shortens their effective integration time—the dynamic spike threshold.

Different thresholds for different input spike train statistics

A binary classifier is defined by a threshold as well as an integration window, and its performance depends critically on the choice of threshold. We have formulated this problem in terms of the “spike count threshold” of a postsynaptic neuron, which we define as the number of closely-spaced presynaptic spikes needed to drive a postsynaptic spike. In general, a binary classifier faces a speed-accuracy tradeoff in its choice of threshold: lower thresholds yield faster first spike latencies but also poorer accuracy, due to high false alarm rates.

Our results draw attention to two factors that can affect this tradeoff: spontaneous activity and correlations between neurons. First, if spontaneous activity and correlations are both low, then the accuracy cost of a low threshold is diminished. Second, if presynaptic spike trains are correlated, speed can be achieved with a high threshold (Middleton et al., 2009). These two factors are most relevant to a decoder of ORNs and a decoder of PNs, respectively.

ORNs are uncorrelated; the DA1 ORNs also have low spontaneous firing rates. Thus, a hypothetical decoder that integrates over time (and over many ORNs) can achieve a relatively low and constant level of baseline activity. This enables the decoder’s threshold to be set at a low value without sacrificing accuracy. Accordingly, we found that the spike count threshold in a PN is relatively low. This enables PNs to respond rapidly, responding preferentially to those ORNs that happened to spike earliest. A similar inference has been reached for pheromone-sensitive ORNs and PNs in the moth (Rospars et al., 2014). (As an aside, we note that PN noise is considerably higher than we would predict for a hypothetical decoder that simply pools ORN spike trains; this additional noise is likely due to noisy input from local interneurons; see Figure S8.)

As compared to their presynaptic ORNs, the DA1 PNs have relatively high spontaneous firing rates, and their spontaneous spikes are correlated. As a consequence, an accurate decoder of PN spikes must have a high threshold. Accordingly, we found that LHNs do indeed have a high spike count threshold. In principle, a high threshold will delay detection. However, in this case, the speed-accuracy tradeoff is mitigated by the correlations among sister PNs. These correlations allow a decoder to set a high threshold without sacrificing too much speed. PN correlations also increase at stimulus onset, which further improves both accuracy and speed. Indeed, we find that LHNs respond to a stimulus remarkably rapidly.

LHNs also have a dynamic threshold, meaning that they are not linear decoders. Because the spike threshold in LHNs depends on the rate of change of its membrane potential, not all incoming spikes are treated equally. This allows LHNs to mitigate the speed-accuracy tradeoff that faces a linear decoder. In the absence of a stimulus, the spike count threshold is high, which suppresses spontaneous activity. At stimulus onset, the threshold drops, which should yield both a speed benefit and an accuracy benefit.

A high and dynamic threshold makes this type of LHN a “coincidence detector”. Similar coincidence detector properties are found in layer IV visual cortical neurons. Interestingly, like LHNs, these neurons receive correlated convergent feedforward signals—in this case, from thalamic neurons, whose correlations derive from divergent retinal projections (Alonso et al., 1996). In both LHNs and layer IV cortical neurons, therefore, presynaptic spike train statistics and postsynaptic properties are seemingly well-matched.

Integrators and differentiators

It is useful to think of PNs as integrators and LHNs as differentiators. PNs average presynaptic spikes over a relatively long time window, and their spike threshold is fairly static. By contrast, the LHN spike threshold depends more steeply on dV/dt, and as a consequence, effective integration time is shortened in LHNs.

In general, an integrator is a neuron whose firing rate depends mainly on the mean input current. Conversely, a differentiator is a neuron whose firing rate depends mainly on the variance of the input current. There is a continuous spectrum of behaviors from differentiation to integration (Ratte et al., 2013; Ratte et al., 2015). Our results extend this literature by showing how the intrinsic properties of a neuron—whether integrator or differentiator—may be usefully matched to population spiking statistics of its inputs.

The mechanisms that distinguish integrators from differentiators can be recapitulated in Hodgkin-Huxley models of spiking neurons (Azouz and Gray, 2000; Lundstrom et al., 2008). In particular, lowering the level of the voltage-gated Na⁺ conductance promotes differentiation. If the Na⁺ conductance is low enough, the level of Na⁺ channel inactivation can become a limiting factor in spike initiation. In this regime, the spike threshold becomes sensitive to the speed of subthreshold depolarization, because channel activation is faster than inactivation. Fast depolarization allows activation to win out over inactivation, and spike threshold falls. Conversely, slow depolarization allows inactivation to keep pace with activation, and spike threshold rises.

Spike timing correlation and synchrony

Neurons that are tuned to the same sensory features often exhibit “noise correlations”—i.e., correlated spontaneous activity, and correlated trial-to-trial fluctuations in stimulus-evoked activity. From the perspective of an idealized decoder, correlations can be either harmful or helpful. When two neurons are functionally identical, positive correlations will generally be harmful (Averbeck et al., 2006). Many studies have measured correlations in population codes and developed a theory of their origin and function (Averbeck et al., 2006; Cohen and Kohn, 2011). However, comparatively few studies have investigated how correlated activity influences downstream circuitry, mainly because of the difficulty in identifying downstream targets of correlated populations. Here, we have the rare opportunity to directly investigate both a pool of correlated neurons (sister PNs) and some of the postsynaptic recipients of their convergent axons (LHNs).

We found that correlations between PNs exhibited two properties that ameliorate their adverse effects. First, correlations are smaller for shorter timescales of analysis. This widely observed phenomenon (Bair et al., 2001; Cohen and Kohn, 2011; Giridhar et al., 2011) indicates that millisecond-timescale spike precision is largely independent from PN to PN. The consequence of this finding is that short-timescale decoders will benefit more from pooling PNs than do long-timescale decoders (Figure 6F, Figure S7).

Second, correlations increase at the onset of a stimulus, although only at short timescales. This phenomenon likely arises from a feedforward mechanism—namely, the interaction between correlated excitatory synaptic currents and the spike threshold in the postsynaptic neuron (de la Rocha et al., 2007). These short time-scale correlations carry information about the presence of a stimulus, but require a decoder tuned to short integration windows.

LHNs, the true biological decoders of PN activity, are indeed tuned to short integration windows by virtue of their dynamic threshold. This means that PN correlations, as viewed by an LHN, are relatively small and stimulus-dependent. LHNs thus minimize the deleterious (stimulus-independent) and maximize the advantageous (stimulus-dependent) effects of correlated inputs.

Convergence, divergence, and reconvergence may represent a general mechanism for distilling information from a large population of neurons into an individual cell, while remaining relatively immune to accumulated noise and preserving speed. At successive layers of a feedforward network, convergence can allow a single cell to explicitly represent information that was only implicit in earlier layers. Under the correct conditions, a signal injected into the front end of the network will propagate securely, while spurious noise injected into any individual neuron will tend to die out. Finally, as the signal propagates, temporal compression of the spike packet can counteract the delays necessarily involved with transmission between layers. In this manner, some fundamental constraints on neural computations (noise, delays) can be counteracted.

Experimental Procedures

Fly Stocks

In virtually all experiments, the genotype used was Mz19-Gal4,UAS-CD8:GFP;JK1029-VP16-AD,ChaDBD/UAS-ChR2. A handful of recordings were conducted in different but related genotypes (see Supplemental Experimental Procedures). All experiments were performed in males. Mz19-Gal4 drives expression in DA1 PNs (Tanaka et al., 2004). JK1029-VP16-AD,ChaDBD drives strong expression in several clusters of LHNs receiving DA1 PN input (Kohl et al., 2013), as well as strong expression in DA1 ORNs. See Supplemental Experimental Procedures for details.

Electrophysiology

In vivo extracellular ORN recordings were performed using saline-filled sharp quartz electrodes. In vivo PN and LHN patch-clamp recordings were performed from GFP-labeled somata under visual control as described previously (Fisek and Wilson, 2014). See Supplemental Experimental Procedures for details.

Optogenetic Stimulation

ORNs were stimulated with blue light (470 nm) produced by an LED coupled to an optical fiber. The end of the fiber was precisely aligned to the antenna ipsilateral to the recorded neuron. The contralateral antenna was not stimulated. See Supplemental Experimental Procedures for details.

Spike Detection

Spikes were detected using custom-written MATLAB routines. See Supplemental Experimental Procedures for details.

Data Inclusion

Five whole-cell PN recordings were omitted because their activity fell far outside the distribution expected on the basis of cell-attached PN recordings, which constitute a useful benchmark because they are non-invasive. See Supplemental Experimental Procedures for details.

Data Analysis, Simulating Populations of >2 PNs, PN Integrate-and-fire Model, and Statistics

See Supplemental Experimental Procedures for details.