Abstract
Third variable effects elucidate the relation between two other variables, and can describe why they are related or under what conditions they are related. This article demonstrates methods to analyze two third-variable effects: moderation and mediation. The utility of examining moderation and mediation effects in school psychology is described and current use of the analyses in applied school psychology research is reviewed and evaluated. Proper statistical methods to test the effects are presented, and different effect size measures for the models are provided. Extensions of the basic moderator and mediator models are also described.
Keywords: Mediation, Moderation, Interaction effect
Across disciplines, researchers are recognizing the advantage of integrating more sophisticated methodology into their statistical toolkits. Advanced statistical models allow the investigation of complex research hypotheses that may better approximate the multifaceted reality from which data are drawn, permitting for example, the investigation of differential growth trajectories of behavioral change, nested data structures such as individuals within schools, or multivariate processes that underlie or modify other bivariate relations. This latter class of models, sometimes referred to as third variable effect models, has received particular emphasis recently because these models allow for an understanding of the factors that may modify or inform the relation of two other variables. However, the utility of these methods is limited if their implementation does not reflect best practices currently advocated in the methodological literature.
The purpose of this paper is to describe two third-variable effect models, specifically mediation analysis and moderation analysis, for the school psychology audience and to present current methodological recommendations for their implementation in applied research. We first describe the utility of implementing the models in school psychology research and provide an example application of the models. We then conduct a literature review of how mediation analysis and moderation analysis have been applied in three top school psychology journals over the past 23 years to gauge current practice. We follow with a presentation of the basic mediation and moderation models, illustrating the most recent recommendations for their statistical estimation, and briefly discuss advanced models that involve the effects.
Why study mediation and moderation?
Although evaluating bivariate relations between variables can lend insight into whether a hypothesized relation holds or whether a program appears to work, it cannot address questions of why, how, and for whom the relation holds, or the program works. Investigating third variables such as moderators and mediators permits the investigation of such questions, informing both theory and evidence-based practice in school psychology. A moderator variable is a third variable (Z) that changes the relation between a predictor (X) and an outcome (Y), thereby affecting the strength and/or direction of the relation between the two variables. Moderators demonstrate the generalizability of the relation between X and Y, illustrating the context(s) under which the relation holds. Moderation effects are often referred to as statistical “interactions” in the social science literature; the terms are interchangeable and refer to the same phenomenon. A mediator variable (M) is a third variable that explains how or why two other variables (i.e., X and Y) are related. In a mediation model, the independent variable (X) predicts the mediator variable (M) which in turn predicts the outcome (Y). Thus, a mediator is intermediate in the relation between X and Y. By modeling an intermediate variable in the X–Y relation, the overall effect between X and Y can be decomposed into component parts called the direct effect of X on Y and the indirect effect of X on Y through M (i.e., the mediated effect). Investigating both direct and indirect effects often provides more insight than simply evaluating the bivariate X–Y relation alone, and researchers have proposed several different ways to statistically test mediation using the component parts.
Studying mechanisms of change by investigating mediator variables has the potential to direct and refine the development of evidence-based interventions because it can shed light on how an intervention achieves its effects (or alternatively why it fails to achieve effects). Additionally, studying contextual effects by investigating moderator variables has the potential to extend the generalizability and external validity of evidence-based treatment programs to different cultural groups or in different settings. By analyzing mediation and moderation effects in this way, researchers can promote theory refinement and positively affect practice.
Investigating mediation and moderation effects also works toward fulfilling several recent federal mandates and legislation in education. Legislative movements such as the No Child Left Behind Act (U.S. Department of Education, 2002) and the reauthorization of the Individuals With Disabilities Education Improvement Act (IDEA, 2004) dictate the use of evidence-based practice in the assessment and intervention of students in both general and special education. Investigating moderators in the development of evidence-based programs can preemptively direct practice by targeting individuals that are likely to respond to treatment or individuals that may need additional support (Kazdin & Nock, 2003). This is particularly important given the recent movements towards the Response-to-Intervention (RTI) model of identification and intervention, where education and placement decisions are based on the degree to which specific students respond to evidence-based treatment. Additionally, analyzing mediation in the development and evaluation of evidence-based programs can identify the effectiveness of individual components of treatment packages. Thus, the investigation of mediation and moderation effects can refine treatment or intervention programs by removing components that do not work, and/or promoting components that do work.
Example application of mediation and moderation analysis in school psychology
Most school-based treatment or intervention programs, regardless of the target outcome, consist of a molar treatment package that consists of various treatment components which have some hypothesized connection to the primary outcome of interest (Shadish, Cook, & Campbell, 2001). Programs aim to manipulate these various components in an effort to change the outcome variable. Statistical mediation analysis can be implemented to evaluate hypothesized mechanisms of change in such intervention processes. Consider a reading program that is aimed at increasing overall reading competence in elementary school students with learning disabilities. Program researchers may hypothesize that oral reading fluency underlies the acquisition of reading competence, such that the program aims to improve fluency which, in turn, influences tests scores. One can formally test this hypothesis with a mediation analysis where oral reading fluency is modeled as a mediator of the relation between the reading program and reading competency. The bottom panel of Fig. 1 shows a conceptual diagram of the mediation analysis, where squares in the figure correspond to observed variables in the model and single-headed directional arrows indicate regression coefficients. By investigating statistical mediation, a researcher can examine underlying hypotheses for why or how the reading intervention works. Note that mediation hypotheses cannot be tested or falsified through a simple examination of bivariate correlations or research that only investigates reading fluency as a primary outcome.
Fig. 1.
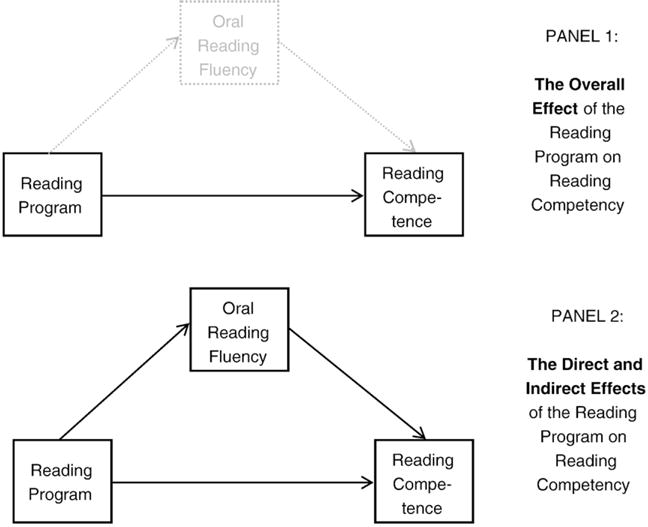
Conceptual path diagram of the mediation reading program example.
If the reading treatment program from the previous example was specifically aimed at improving reading skills in students with learning disabilities, researchers may be interested in determining whether the program generalizes to students in the broader school population. A researcher could formally test this hypothesis by examining differential treatment effects of the program by learning disability status in a statistical moderation analysis. Fig. 2 shows a conceptual diagram of a moderation analysis. The arrow that connects the Reading Program box to the Reading Competence box represents the effect of the reading program on reading competence (e.g., a regression coefficient), and the arrow from the LD Status box to the arrow denotes the moderating effect that learning disability status has on this association. Non-significant results from such a moderation analysis would indicate that the program generalized to the larger school population; whereas significant results would indicate that the program affected students with and without learning disabilities differently.
Fig. 2.
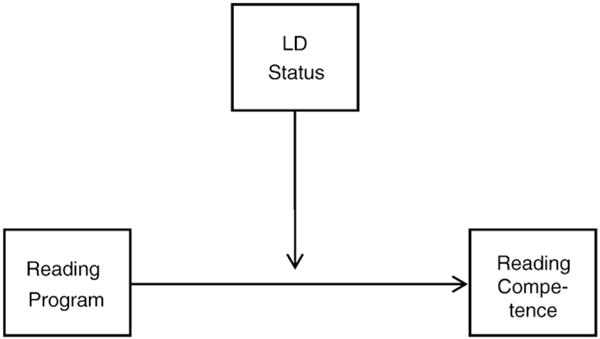
Conceptual path diagram of the moderation reading program example.
Literature review
To guide our presentation of methods for this paper, we conducted a literature review to examine how school psychologists have used and applied mediation and moderation models in their research over the past 23 years. We examined articles in three predominant journals: (a) Journal of School Psychology, (b) School Psychology Review, and (c) School Psychology Quarterly. The full text of these journals was searched between 1986 and 2008 across four sources: Science Direct, Psych Info, and EBSCO Psychology and the Behavioral Sciences, respectively. Search terms for each journal were mediation, mediator, indirect effect, moderation, moderator, interaction term, and statistical interaction. The term “interaction” was not explicitly searched for by itself to avoid a deluge of articles involving personal or social interactions. Thus the results from this search are not exhaustive and should only be used to obtain a general point of reference to the current state of practice of statistical mediation and moderation analysis in school psychology.
The literature survey identified 48 studies that examined mediation and 50 studies that examined moderation resulting in a pool of 98 articles. Seven of these studies investigated both mediation and moderation and were counted twice due to interest in separate methodological aspects of each technique. Thus, 91 separate articles were identified within the literature review. Fig. 3 displays a frequency histogram of publication date for the articles examined. The noticeable negative skew in the graph illustrates increased use of both mediation and moderation over time, likely fostered by seminal methodological publications on the methods in later years (e.g., Aiken & West, 1991; MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002).
Fig. 3.
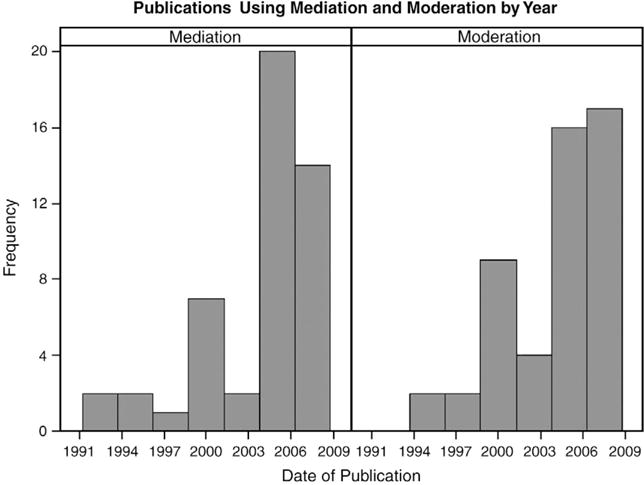
Frequency histogram of moderation and mediation publications in selected school psychology journals over time.
Articles were coded based on the method used to analyze data to understand how the each of the models was used and evaluated. Articles that tested mediation were broken down into those that used (a) a causal step approach (Baron & Kenny, 1986), (b) normal theory point estimation (Sobel, 1982), and (c) structural equation modeling (SEM). Articles that used SEM were further coded into those that used a test of overall model fit to test mediation versus those that directly estimated a mediated effect point estimate. Articles that tested moderation were broken down into those that used (a) moderated multiple regression (i.e. Aiken & West, 1991), (b) ANOVA, and (c) moderated multiple regression in hierarchal linear models (i.e. models controlling for multilevel data). Table 1 illustrates descriptive statistics from the review as well as the median sample size employed in each method.
Table 1.
Literature survey results: methods used to test mediation and moderation effects.
| Model type | Method used | Frequency | % of studies | Median sample size |
|---|---|---|---|---|
| Mediation | 48* | 49* | 360* | |
| Causal steps | 15 | 31.25 | 173 | |
| Indirect effect | 21 | 43.75 | 520 | |
| SEM-model fit | 3 | 6.25 | 282 | |
| SEM-indirect | 9 | 18.75 | 349 | |
| Moderation | 50* | 51* | 342.5* | |
| ANOVA | 8 | 16 | 102 | |
| Regression | 32 | 64 | 342.5 | |
| HLM | 9 | 18 | 509 |
Note: descriptive statistics are reported separately for mediation and moderation analyses.
Indicates descriptive statistics for the overall sample of studies identified.
Eight of the studies (8%) in the review were manipulated program evaluations with three examining mediation and five examining moderation. Programs that were evaluated included various academic and behavior prevention and intervention programs, parenting programs, and a subjective well-being intervention program. Of the studies in the review, 52 (53%) were cross-sectional, with approximately half of those investigating mediation. Thirty two of the studies (32%) used two waves of data in their analysis, and 15 of the studies (15%) used three or more waves of data. Although substantive areas of the studies varied widely, patterns emerged that were consistent with general school psychology research. Roughly half of the review articles investigated (n=45) academic achievement as a key outcome variable. Other studies examined predictors of negative interpersonal interactions and classroom behavior, social relations among adolescents and children, school climate, subjective well-being and school engagement, cognitive processes, and Attention Deficit Hyperactivity Disorder. Given the purpose of this paper, no formal method of categorization was developed to evaluate substantive area of interest. Thus the preceding must be considered in light of the fact that these are rather arbitrary and nonexclusive categories.
Evaluating results from the literature review reveals key points. First, the use and application of moderation analysis appears generally based on best practices, namely moderated multiple regression. This is not unexpected given that key methodological resources on the method were published many years ago (e.g., Aiken & West, 1991; Cohen & Cohen, 1983). Conversely, it appears that the use and application of statistical mediation analysis consists primarily of outdated methods, namely using underpowered methods (e.g., causal steps approach and normal theory point estimation) to examine mediation. Given this discrepancy and the larger need to address appropriate analyses for investigating mediation, we first review the proper methods to test moderation effects and focus the remainder of the article on describing contemporary statistical methods to test mediation.
Moderation analysis
What is a moderator?
As stated earlier, a moderator is a third variable (Z) that changes the relation between a predictor (X) and an outcome (Y), thereby affecting the strength and/or direction of the relation between the two variables. The moderator (typically a covariate or secondary predictor of interest) interacts with the primary predictor variable to influence the outcome, such that any effects of the primary predictor on the dependent variable are conditional on, or dependent on, values of the moderator. In a regression context, this dependency yields different bivariate regression lines predicting Y from X for different values of the moderator variable, Z. In an ANOVA context (or alternatively in a regression with categorical predictor variables), this dependency can be illustrated by non-parallel lines for moderator-based subgroups. Moderators may enhance, reduce, or directionally change the effect of the predictor on an outcome, such that the effects of one variable depend on levels of the other variable in analysis. In the presence of moderation, the main effects are no longer additive and need to be interpreted with reference to the moderator variable, because the outcome variable is explained by the simultaneous effect of the variables.
In general, moderator effects are one of two types: ordinal or disordinal interactions (Cohen et al., 2003). In plots of the data, ordinal interactions are illustrated by lines that do not cross one another in the plot, whereas disordinal interactions are illustrated by lines that do cross in the plot (see Fig. 4). Ordinal interactions may be of two subtypes. A synergistic interaction effect occurs when a change in the level of the moderator variable enhances the bivariate relation between X and Y (Cohen et al., 2003). A buffering interaction effect occurs when a change in the level of the moderator variable reduces the magnitude of the bivariate relation between X and Y. Fig. 4 illustrates two such examples, where Panel 2 corresponds to a synergistic interaction such that the effect of treatment is greater for students with learning disabilities versus those with none, and Panel 3 corresponds to a buffering interaction such that the effect of treatment is less for students with learning disabilities versus those with none. Detailed descriptions of different moderator effects and a framework for their estimation and interpretation were originally presented in Aiken and West (1991). More recently, Aguinis (2004) has also written a book on moderator effects.
Fig. 4.
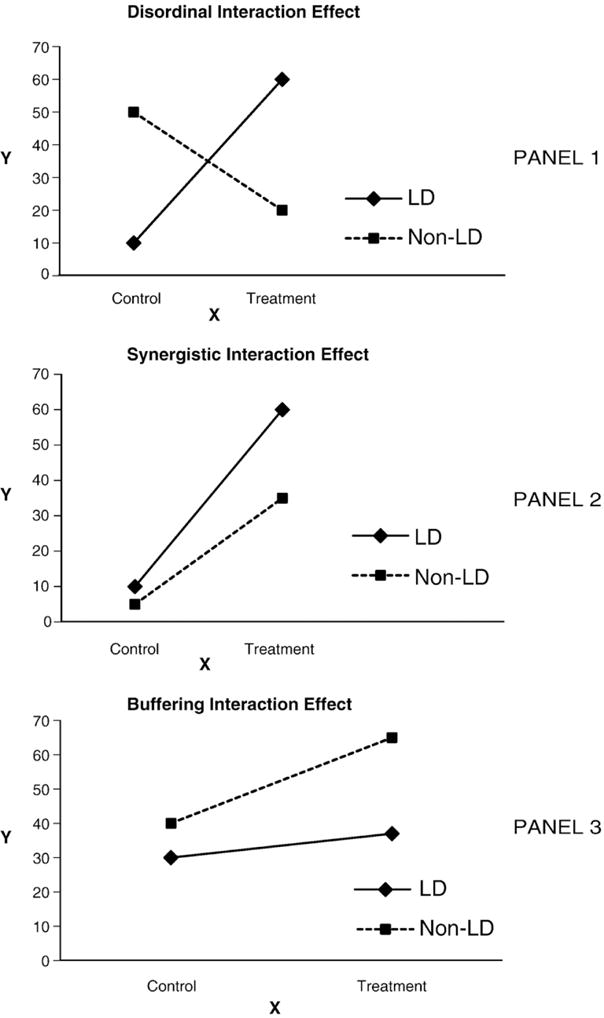
Differentiating interaction effects. The solid line in each graph across the panels pertains to the X–Y relation at one level of the moderator variable (i.e., learning disabled). The dashed line in each graph across the panels pertains to the X–Y relation at the other level of the moderator variable (i.e., not learning disabled).
Estimating the basic moderation model
To demonstrate estimation of the basic moderation model, we provide a numerical example for the aforementioned hypothetical school psychology study where the efficacy of a reading program is potentially influenced by a student’s learning disability status. The data for the numerical example are presented in Table 2. Throughout this section the reading program acts as the primary predictor variable (i.e., X), learning disability status acts as the moderator variable (i.e., Z), and reading performance serves as the outcome variable (i.e., Y).
Table 2.
Dataset for numerical examples (N=20).
| Subject # | Reading program (X) | Learning disability status (Z) | Oral reading fluency (M) | Reading performance (Y) | Program×LD status interaction (XZ) |
|---|---|---|---|---|---|
| 1 | .5 | .5 | .799 | 2.532 | .25 |
| 2 | −.5 | −.5 | −1.781 | −.124 | .25 |
| 3 | −.5 | −.5 | −2.219 | 1.170 | .25 |
| 4 | .5 | −.5 | .177 | −.583 | −.25 |
| 5 | −.5 | −.5 | −2.331 | −1.627 | .25 |
| 6 | .5 | .5 | .438 | .522 | .25 |
| 7 | .5 | −.5 | 1.402 | −1.238 | −.25 |
| 8 | −.5 | .5 | −.607 | −2.140 | −.25 |
| 9 | .5 | .5 | .801 | 1.412 | .25 |
| 10 | .5 | .5 | 1.657 | 1.248 | .25 |
| 11 | −.5 | −.5 | −.268 | .197 | .25 |
| 12 | −.5 | .5 | −1.485 | −.843 | −.25 |
| 13 | −.5 | .5 | −.755 | −1.469 | −.25 |
| 14 | −.5 | .5 | −1.531 | −.001 | −.25 |
| 15 | −.5 | −.5 | −.672 | .713 | .25 |
| 16 | .5 | −.5 | 2.662 | .640 | −.25 |
| 17 | .5 | −.5 | 1.201 | 1.078 | −.25 |
| 18 | .5 | −.5 | .915 | .937 | −.25 |
| 19 | −.5 | .5 | −.986 | −.915 | −.25 |
| 20 | .5 | .5 | 2.582 | −.602 | .25 |
Note. For the reading program variable a value of −.5 corresponds to the control group and a value of .5 corresponds to the treatment group. For the learning disability status variable a value of −.5 corresponds to students with no learning disabilities and a value of .5 corresponds to students with a learning disability.
The basic moderation model is estimated with the following multiple regression equation
| (1) |
where Ŷ is the predicted value of a student’s reading performance, X represents group assignment to the reading program (i.e., treatment vs. control), Z corresponds to a student’s learning disability status (i.e., learning disabled vs. not learning disabled), and XZ is the interaction term formed by multiplying the reading program and learning disability codes. Recall that coding schemes such as dummy coding or effects coding are a way of representing nominal or ordinal variables in a regression model (Cohen et al., 2003). For details on implementing different coding schemes to accommodate categorical variables in a multiple regression model, see Cohen et al. (2003) or Aiken and West (1991).
Eq. (1) is the preferred statistical method for testing moderation effects with observed (i.e., not latent) variables because it allows for categorical or continuous predictors and it provides tests of the main effects and the interaction effect (Aguinis, 2004; Aiken & West, 1991). Note that inclusion of the main effects (i.e., the lower order predictors X and Z) is critical because the failure to include non-significant lower order terms in analysis confounds effects in the model. Effects are confounded because the variance associated with the lower order terms is not independent of the variance associated with the interaction term. If the lower order main effects are not included in the regression model, they are not statistically partialled out of the interaction, and the significance of the interaction term may be artificially inflated (Aiken & West, 1991).
The multiple regression equation corresponding to the reading program example is as follows
| (2) |
The regression coefficients in the equation quantify the effect of the variable on reading performance while controlling for the effect of other variables in the model. Sample estimates of the population regression parameters (i.e., the βs) in the moderation model are denoted by in the following paragraphs. For example, is the regression coefficient relating the reading program to reading performance controlling for both a student’s learning disability status and the interaction of the reading program and learning disability status; , (t=−.311, p=.760) is the regression coefficient relating learning disability status to reading performance controlling for the effects of the reading program and the interaction of the reading program and learning disability status in the model; and is the regression coefficient relating the interactive effective of the reading program and students’ learning disability status on reading performance controlling for each effect independently. Finally, represents the intercept in the equation, or the predicted reading score value when all predictors in the model equal zero. The coefficient corresponding to the interactive effect of the reading program and learning disability status is considered a higher-order term in the model as it is created by multiplying other variables in the equation.
Fig. 5 depicts the moderated multiple regression equation for the numerical example as a path diagram, where double-headed curved lines denote correlations among the predictor variables. Sample estimates of the regression coefficients and their corresponding significance levels appear above the paths to which they correspond. Note that the model in Fig. 5 is somewhat different from the depiction of an interaction effect in Fig. 2. Fig. 2 is conceptual in nature, whereas Fig. 5 corresponds to the moderated multiple regression in Eq. (2).
Fig. 5.
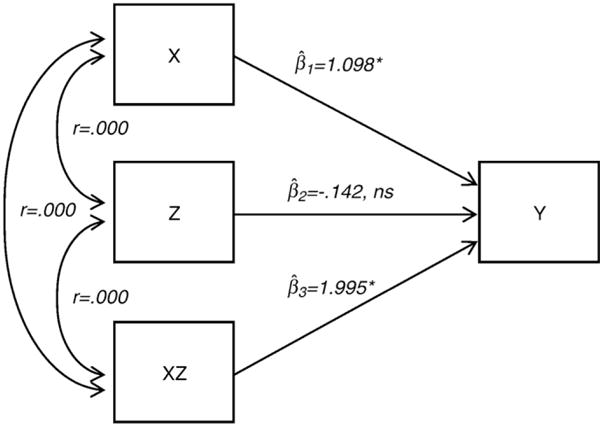
The basic moderation model. X=the independent variable, Y=the dependent variable, Z=the moderator variable, XZ=the interaction of the independent and moderator variables, = the effect of the independent variable on the outcome controlling for Z and XZ, = the effect of the moderator on the outcome controlling for X and XZ, and = the effect of the XZ interaction on the outcome controlling for the lower order effects. *Corresponds to p<.05 and ns corresponds to not significant. Correlations among the predictor variables are approximately zero because of the balanced design in the example.
Testing for moderation
A t-test of the regression coefficient associated with the XZ interaction term (i.e., ) is one way to determine if there is statistical moderation. If the coefficient is significant, then there is a significant moderation effect. The parameter estimate, its standard error, and the significance level of the coefficient associated with the interaction are provided in any standard output of a regression analysis in conventional statistical software packages such as SAS or SPSS. As shown in the numerical example, the regression coefficient associated with the interactive effect of the reading program and students’ learning disability status on reading performance was significant at an alpha level of .05 . The significant finding suggests that the efficacy of the reading program on students’ reading performance was affected by, or moderated by, their learning disability status (i.e., there was significant moderation).
In lieu of the t-test, one can also use an R2 change test (denoted R2Δ) to evaluate moderation (Aguinis, 2004; Aiken & West, 1991). The R2Δtest, which is distributed as an F-statistic, quantifies variance accounted for by the XZ interaction, above and beyond the variance accounted for in the model without the interaction term. The F-statistic for the R2Δ change is computed with the following equation
| (3) |
where is the R2 associated with the model that includes the main effects and the interaction term (i.e., Eq. (1)), is the R2 associated with a regression model that includes only the main effects for X and Z, k2 is the number of predictors in the equation that includes the interaction term, k1 is the number of predictors in the equation that includes only the main effects, and N is the sample size. The R2Δ is easily requested in conventional statistical software packages, so there is no need to compute the statistic by hand. Results from the R2Δ test of moderation will be identical to results from a t-test of the interaction term in Eq. (1), such that the square root of the R2Δ F-statistic will equal the value of the t-statistic, and the p-values of the two tests will be identical. Returning to the numerical example, the R2Δ statistic comparing a model with only the reading program and learning disability status predicting reading performance (R2 =.221) to a model with both predictors and their interaction (R2 =.400) is R2Δ=.179(F=3.980, p=.044). Note that the square root of the F-statistic equals the value of the t-statistic for the interaction term in Eq. (2) (i.e., ), and the p-values from the two tests are identical (i.e., p=0.44).
Multicollinearity and centering predictor variables in moderation analysis
Entering the product of X and Z into the moderated multiple regression equation to model the effect of their interaction on the outcome introduces multicollinearity, such that X and Z and highly correlated with the XZ product term. The implication of this multicollinearity is that standard errors of the regression coefficients become inflated, resulting in unstable estimates. Much of this excessive correlation is due to scaling of the variables (i.e., differences in the means). Multicollinearity due to such scaling is termed non-essential multicollinearity and can be reduced by centering the predictor variables (i.e., subtracting the mean from each score; Aiken & West, 1991). Centering the predictors about their mean also improves interpretation of lower order terms in the equation (Aiken & West).
In a balanced design where there are equal sample sizes across groups, a researcher can mean center dummy coded dichotomous variables by subtracting the mean of the codes (i.e., the mean of 0 and 1=.5) from each observation to yield effect codes with the values of −.5 and .5. Note that one can also center in unbalanced designs where the sample size across groups is unequal, but the resulting codes will no longer be .5 and −.5. The researcher can mean center continuous predictor variables by computing the mean of the predictor (e.g., X or Z) and subtracting this value from each observed score in the data for that variable (Aiken & West, 1991)
| (4) |
| (5) |
Mean centering the interaction term is achieved by forming the product of the two centered variables in Eqs. (4) and (5)
| (6) |
Note that this approach to centering of the interaction term is not equivalent to first forming the product of the observed X and Z variables, computing the mean of the XZ term and then subtracting this from the observed values. The proper way to mean center the interaction is as described in Eq. (6).
Mean centering predictor variables aids interpretation of lower order coefficients (i.e., X and Z) in a moderation analysis because the transformation moves the zero point of the predictors to a meaningful location (the mean of each variable). By moving the zero point of the predictors to their means, the intercept in the moderation model becomes the expected value of the outcome variable at the average of all the predictor variables. The interpretation of the β1 parameter becomes the regression of Y on X at the mean of Z, or alternatively the average regression of Y on X across all values of Z. Returning to the numerical example, the coefficient represents the average effect of the reading program on student reading performance across students with and without learning disabilities. Similarly, the interpretation of the β2 parameter becomes the regression of Y on Z at the mean of X, or alternatively the average regression of Y on Z across all values of X. In the numerical example, the coefficient represents the average effect of learning disability status on student reading performance across the treatment and the control groups. The interpretation of the higher-order interaction term parameter, β3, remains the same across centered and uncentered solutions: the interactive effect of X and Z on Y.
Interpreting moderation effects
The main effect of the primary predictor does not fully characterize the relation between X and Y in the presence of significant moderation. Instead, the relation between X and Y must be analyzed at different values of the moderator variable, Z, to fully understand the association. Plotting the interaction aids interpretation of the interaction effect and provides a way to investigate how the relation between Y and X changes across levels of the moderator variable. Fig. 6 demonstrates a plot of the interaction for the numerical reading program example and illustrates that students with a learning disability have greater positive reading gains from the program than do students without a learning disability. Specifically, students with a learning disability have lower reading performance at baseline relative to non-learning disabled controls and show better reading performance after participating in the treatment.
Fig. 6.
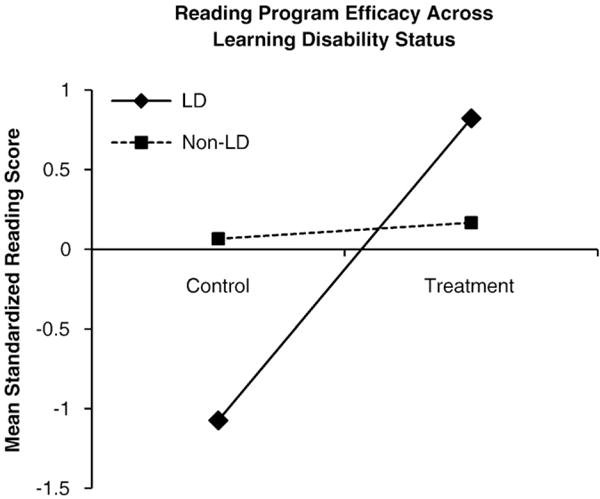
Plot of the interaction for the numerical reading program example.
When plotting interactions, specific values of the moderator variable, Z, must be chosen at which to graph the regression of Y on X. For categorical moderator variables, values of Z should correspond to the codes for the groups that you wish to plot (as shown in the plot of the numerical example). For continuous moderator variables, when theory or other important criteria provide meaningful values of Z, those values can be chosen. In cases where specific values of Z are less meaningful, Aiken and West (1991) recommend plotting simple slopes for scores at ±1 standard deviation from the mean of Z and at the mean of Z itself. These values represent a range in which most observed scores should fall in a normal distribution. However, it is important to make sure the data actually contain score values at ±1 standard deviation from the mean, otherwise the graph represents an extrapolation beyond the data.
Rearranging the terms in Eq. (1) facilitates plotting of the interaction (Aiken & West, 1991) and illustrates how the slope of Y on X is dependent on the value of the moderator variable, Z
| (7) |
If there is no interaction effect then the β3 coefficient equals zero and drops out of the equation. If there is no β3 coefficient in Eq. (7), then the regression of Y on X depends wholly on β1. Contrast this to a case where there is a non-zero interaction effect (i.e., β3 is less than or greater than zero). If β3 is non-zero then the term remains in the equation and the X–Y relation depends on both β1 and β3. The larger the absolute value of β3, the more the relation between X and Y is affected by the moderator variable.
Regression slopes that correspond to the prediction of Y from X at a single value of Z are termed simple slopes. The estimation and interpretation of simple slopes is described in detail in Aiken and West (1991). Tests of statistical significance for these simple slopes, or simple effects, are available and indicate whether the regression of Y on X at a given value of Z significantly differs from zero (see pp. 14–18 in Aiken & West). Aiken and West also demonstrate how comparisons may be made among the simple effects to examine which pairs of slopes significantly differ from one another. Note that for continuous moderators, the presence of a significant XZ interaction implies that simple slopes vary across values of Z (Aiken & West, 1991). The simple slope equation for students with learning disabilities (i.e., X=.5) in the numerical example is
| (8) |
and the simple slope equation for students without learning disabilities (i.e., X=−.5) in the numerical example is
| (9) |
These simple regression equations are consistent with the graph of the interaction in Fig. 6 that showed students with learning disabilities obtain better benefits from the reading program than do students without learning disabilities. That is, the regression coefficient associated with students who have learning disabilities is larger than that of the regression coefficient associated with students who do not have a learning disability.
It is important to note that the moderation example demonstrated in this article makes use of unstandardized coefficients from the regression model. Although standardized coefficients are sometimes advocated as a means to compare the magnitude of effects across samples, there are several statistical and interpretational issues that preclude presentation of standardized coefficients in a moderation analysis. First, the utility of comparing standardized coefficients across studies (in the presence or absence of an interaction effect) is itself questionable as the coefficients depend on the variance of the sample from which they are derived. Problems with these comparisons escalate with an increase in multicollinearity among the predictor variables. Second, standardization introduces additional error variance into the regression coefficient due to the inclusion of the variances of X and Y as a stochastic scaling adjustment in computation. Moreover, unlike unstandardized regression coefficients, the numerical value of the interaction term changes across centered and uncentered solutions in a moderation analysis. Values of any simple slopes and their associated level of significance also change. Finally, SAS and SPSS do not properly standardize the interaction term in analysis, treating it as an individual variable rather than the product of two random coefficients. For all of these reasons, it is inappropriate to report and interpret standardized coefficients when an interaction is present in a multiple regression model.
Effect sizes in moderation models
Estimates of effect size describe the practical significance of an effect, independent of sample size. Effect size measures are important when interpreting analysis results because they can inform non-significant findings and can enhance understanding of the practical utility of statistically significant effects. It is increasingly common that journal outlets require the reporting of effect size in addition to the results from null hypothesis significance tests. Squared partial correlation coefficients, or partial r2 measures, are an example of effect size measures for moderation analysis (and more generally multiple regression analysis) and are equivalent to the R2Δ described earlier.
R2Δ illustrates the unique portion of variance explained by a predictor in the criterion variable that is not explained by other predictors in the model (Cohen et al., 2003). Although originally only shown for the interaction effect in the Testing for Moderation section of the paper, R2Δ can be computed for any effect in the moderation model such as the effect of X on Y, the effect of Z on Y, or the effect of the interaction of X and Z on Y. When assessing Partial r2 values for the numerical example were .266, .006, and .230 for the effect of X, Z, and the XZ interaction, respectively. Cohen (1988) defined small, moderate, and large effect sizes of squared partial correlation coefficients (such as the R2Δ) as .02, .13, and .26, respectively. Partial r2 effect size measures can be requested as output options from a regression analysis in standard statistical software packages and may be useful to report in analysis.
Power in moderation models
Power is often low in moderation analyses because of the small effect sizes that are typically observed in the social sciences (Aiken & West, 1991; Stone-Romero & Liakhovitski, 2002). Reviews of substantive literature in the social sciences demonstrate that interaction effects in real data typically explain between 1% and 3% of the variance in the dependent variable (Champoux & Peters, 1987). Thus, interactions explaining even 1% of the variance may be meaningful (Abelson, 1985; Evans, 1985; McClelland & Judd, 1993). To maximize the power of detecting moderator effects, researchers may use the largest sample available, consider the use of extreme groups to increase variance in the design (e.g., oversample participants that are either very high-scoring or very low-scoring on a non-manipulated independent variable), and choose measures that have high reliability (Aiken & West; Stone-Romero & Liakhovitski).
Assumptions of the moderation model
Several statistical assumptions underlie the moderation model. Most of these assumptions correspond to those associated with ordinary least squares regression, such as correct model specification, error-free measurement, and normally distributed residuals (Cohen et al., 2003). One of the major assumptions of the moderated multiple regression model is homogeneity of error variance, also called homoscedascity. Homoscedascity requires that the residual variance that remains after predicting Y from X is constant across values of the moderator variable, Z, such that the predicted scores, Ŷ, are distributed similarly along the simple slopes. Bartlett’s M statistic provides a formal statistical test of whether homogeneity of error variance has been violated (non-significant results indicate that no violation has occurred). The statistical test is available in both SAS and SPSS. In the presence of heteroskedastic error variance, there are nonparametric tests available to test for moderation in both ANOVA (e.g., the Kruskal–Wallis test; Kruskal & Wallis, 1952) and regression frameworks (e.g, nonparametric regression; e.g., Takezawa, 2005).
Advanced moderation models
The interaction effects described here represent the basic moderation model. Models that incorporate more complex, higher-order moderator effects are also possible. For example, it may be of interest to model three-way interaction effects where the effect of a two-way interaction on an outcome can be explored across levels of a fourth variable in the model. As well, curvilinear by linear interactions may also be investigated where quadratic terms are entered into the equation. Although the methods described here for the basic moderation model extend to these more complex scenarios, interpretation of effects becomes increasingly challenging with the introduction of more than one moderator variable or the presence of curvilinear relations (Aiken & West, 1991).
Mediation analysis
What is a mediator?
As previously described, a mediator is a third variable that explains how or why two other variables are related. The mediation model is a three variable model where an independent variable (X) predicts a mediator variable (M), which in turn predicts an outcome (Y). The mediator intervenes in the relation between X and Y illustrating the mechanism through which the two variables are related. By modeling an intermediary variable in the X–Y relation, the researcher is able to decompose the bivariate relation between the two variables into direct and indirect (i.e., mediated) effects. If the mediator accounts for the total effect of X on Y, such that there is no relation between the variables once the mediator is partialled out of their relation and the direct effect is equal to zero, then the mediating process is termed complete mediation. If instead a direct effect of X on Y remains once the mediator is partialled out of the X–Y relation, then the mediating process is termed partial mediation (e.g., Shrout & Bolger, 2002).
Differentiating mediators from other third variable effects
There are several other third variables that also elucidate the relation between two other variables, but these variables are not mediators (MacKinnon, Krull, & Lockwood, 2000). A confounder is a variable that is related to other variables, such that it artificially enhances their relation. The difference between a confounder and a mediator variable is that a confounder is not intermediate in a causal sequence, as is hypothesized in the mediation model. An example of a confounder variable is prior subject knowledge in a study that evaluates the effectiveness of different learning strategies. If prior subject knowledge is not accounted for, it may artificially enhance or detract from the effects of a given learning approach making the bivariate relation noticeably change from what it would be otherwise.
A covariate is a variable that is related to a predictor and outcome variable but does not appreciably change the bivariate relation between the two when included in a model. Covariates are often used in analysis to reduce unexplained variability in an outcome variable. Like a confounder, a covariate is not hypothesized to occur in a causal sequence between X and Y. Examples of covariates might be demographic variables such as gender or socioeconomic status.
Estimating the basic mediation model
To demonstrate estimation of the basic mediation model, data from a numerical example are evaluated (see Table 2), where the aforementioned reading program was hypothesized to achieve its effects by increasing the oral reading fluency of subjects. Throughout the following sections the reading program is the primary predictor variable (i.e., X), oral reading fluency is the mediator variable (i.e., M), and reading performance is the outcome variable (i.e., Y). Fig. 1 shows a path diagram of this mediation model.
The basic mediation model is defined by three equations. First, the overall effect of X (the primary predictor variable) on Y is
| (10) |
where Ŷ is the predicted value of a student’s reading performance, X represents group assignment to the reading program (i.e., treatment vs. control), β0Y is the regression intercept, and β1Y is the slope coefficient representing the relation between the program and reading performance. The overall effect represents the relationship between X and Y without consideration of the mediator. The top panel of Fig. 1 shows this overall effect (specifically the β1Y regression coefficient) as a solid line. The dashed lines in Panel 1 of the Figure indicate that although there is an implicit underlying process by which X and Y are related in the mediation model, this process is not directly estimated in the overall effect regression equation. Instead, the overall effect regression equation in the top panel of the Figure combines the direct and indirect effect into a single regression coefficient. This overall effect is important because it plays a role in defining some of the test statistics and effect sizes in the mediation model.
The mediation model uses two regression equations to decompose the overall effect into its direct and indirect components as follows
| (11) |
| (12) |
where M̂ is the predicted value of a student’s oral reading fluency, M corresponds to a student’s observed oral reading fluency, β0Y* and β0M are regression intercepts, and the β1Y*, β2Y, and β1M terms are regression slopes. The asterisks in Eq. (11) denote the fact that the coefficients are different from those in Eq. (10). Specifically in Eq. (11), β1Y* represents the influence of X on Y partialling out the mediator, whereas β1Y in Eq. (10) is not a partial regression coefficient; it is simply the bivariate relationship between X and Y not controlling for other variables.
Returning to the small data set in Table 2, the estimates of the previous equations are
| (13) |
| (14) |
| (15) |
The regression coefficients in the equations quantify various effects of predictors on the mediator and outcome variables. Specifically, in Eq. (13) where reading performance is only predicted by the reading program, is the regression coefficient corresponding to the overall effect (i.e., the total effect) of the reading program on reading performance. In Eq. (14) where reading performance is predicted by both the reading program and oral reading fluency, is the regression coefficient relating the direct effect of the reading program (X) to reading performance (Y), controlling for oral reading fluency (M), and is the regression coefficient relating oral reading fluency to reading performance, controlling for the effect of the reading program. Turning to the equation where the mediator is the outcome variable, is the regression coefficient relating the reading program to oral reading fluency. Finally, , and represent the intercepts in each equation; these terms do not play a role in a mediation analysis. Various coefficients from the three mediation regression equations are used to define different statistical tests of mediation, which are outlined in subsequent sections. Fig. 7 illustrates the mediation regression equations and the estimates from the numerical example in a path diagram. Recall that in path diagrams squares correspond to observed variables in the model and single-headed directional arrows indicate regression coefficients. In line with the numerical example for the moderation model, sample estimates of the regression coefficients and their corresponding significance levels appear above the paths to which they correspond in the Figure.
Fig. 7.
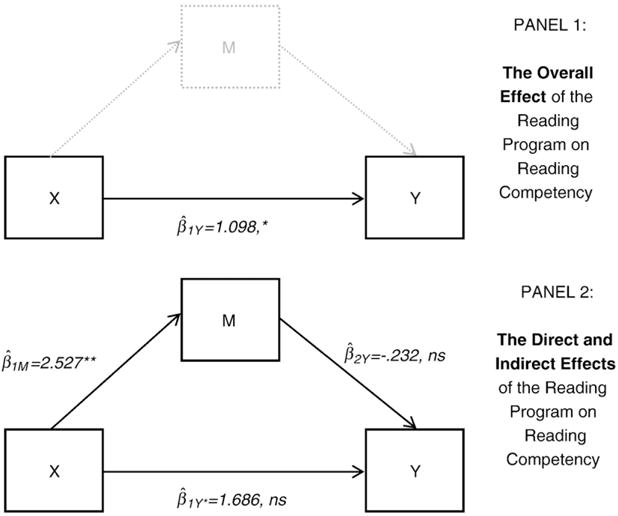
The basic mediation model. X=the independent variable, Y=the dependent variable, M=the mediator variable, =the effect of the independent variable on the mediator, =the effect of the mediator on the outcome controlling for X, and =the direct effect of the X on Y controlling for M. *Corresponds to p<.05, **corresponds to p<.001 and ns corresponds to not significant.
Causal steps
Several different methods have been proposed to test mediation. Early articles on mediation analysis illustrated causal step methods to test for mediation, where the mediation regression equations were evaluated sequentially (e.g., Baron & Kenny, 1986; Judd & Kenny, 1981). First, a significant overall effect of the independent variable (X) on the dependent variable (Y) is required. In other words, the regression coefficient in Eq. (10) must be significant. Second, the mediator (M) must affect Y, and X must affect M. Thus the β2Y and β1M slope coefficients from Eqs. (11) and (12) must also both be significant for mediation to hold. Finally, the magnitude of the overall effect of X on Y must be greater than the direct effect of X on Y that remains after partialling out the mediator. If all of these criteria are satisfied, then there is evidence for mediation. Recall that this was the most common approach to testing mediation hypotheses found in our previous literature review.
Although researchers frequently use the causal steps approach, it has several critical limitations. First, the method is underpowered (MacKinnon et al., 2002). The low power is primarily due to the requirement that X and Y are significantly related. Fritz and MacKinnon (2007) showed that with small effect sizes of mediation regression parameters (i.e., and ), 20,886 subjects are needed to detect effects with .8 power in complete mediation models. Results from the literature review presented at the beginning of this article indicate that the median sample size of mediation studies conducted with causal steps methodology in the school psychology domain is 173, substantially below the optimal sample size. Second, the causal steps method does not provide a point estimate of the mediated effect, and thus precludes formation of confidence intervals or evaluation of standard errors. Finally, the requirement that there be a significant overall effect of X on Y in order for there to be significant mediation is debatable (MacKinnon & Fairchild, 2009). Although the overall effect of X on Y is unquestionably of interest in most studies, it is not a test of mediation. There are several scenarios in which significant mediation can occur without a significant overall effect of X on Y (e.g., mediation effects that differ in sign or in magnitude across different subgroups).
Difference in coefficients
The difference in coefficients estimator quantifies the reduction in the overall effect of the independent variable on the dependent variable after accounting for the mediator. A researcher forms the estimate by subtracting the direct effect of X on Y when M is partialled out of the relation (i.e., ), from the overall effect of X on Y when M is not included in the model (i.e., ). Consulting the path diagram in Fig. 7, the estimator takes the path connecting X and Y in Panel 1 of the Figure, or the coefficient that results from simply regressing Y on X, and subtracts the path connecting X and Y in Panel 2 of the Figure, or the coefficient that results from regressing Y on both X and M. The logic behind the estimator is that, if the mediator accounts for all or part of the relation between X and Y, then when it is accounted for in their relation the magnitude of their association should reduce. Significance testing of the mediated effect point estimate is conducted by dividing the difference in coefficients by an estimate of its normal theory standard error (e.g., McGuigan & Langholtz, 1988). Although the difference in coefficients may be an intuitive framework to understand the logic of mediation, the estimator does not easily generalize to more complicated models such as those that involve estimating effects on categorical variables or multiple mediators. There are preferable estimators of the mediated effect.
Product of coefficients
The product of coefficients estimator is derived from the estimation of indirect effects in path analysis, where the effects of one variable on another are transmitted through an intermediary predictor variable. The product of coefficients estimator of mediation is more flexible than the difference in coefficients, extending to more complex mediation models such as those with multiple outcomes. Alwin and Hauser (1975) describe how indirect effects “tell us how much of a given effect occurs because the manipulation of the antecedent variable of interest leads to changes in other variables which in turn change the consequent variable” (p.39). Applied to mediation, this means that the mediated effect depends on the extent to which the independent variable changes the mediator and on the extent to which the mediator subsequently affects the outcome variable. With this logic, the product of coefficients estimator multiplies the coefficient connecting the X and M variables in Fig. 7 by the coefficient connecting the M and Y variables in the Figure. Thus, the product of coefficients estimator defines the mediated effect as . As with the difference in coefficients estimator, significance testing of the mediated effect point estimate is conducted by dividing the product of coefficients by an estimate of its normal theory standard error (Sobel, 1982). This standard error is
| (16) |
where is the sampling variance (i.e., squared standard error) of the coefficient and is the sampling variance of the coefficient. The product of coefficients estimate of the mediated effect for the reading program example is (2.527)(−.232)=−.586. The standard errors of the two coefficients are .347 and .339, respectively. Substituting the regression coefficients and their standard errors into Eq. (16) yields . Dividing the point estimate by its standard error gives a z statistic of z=−.687, which is not significant (p=.493).
Asymmetric confidence limits and resampling
Although both the difference in coefficients and the product of coefficients estimators allow for null hypothesis significance testing and confidence interval estimation, both have conservative Type 1 error rates and limited power to detect mediation in small sample sizes (MacKinnon et al., 2002). Conventional standard error estimators based on normality assumptions (e.g., Eq. (16)) do not accurately capture the sampling distribution of the mediated effect and thus are limited in making accurate statistical inferences. Normal theory standard errors are imperfect for mediation because the sampling distribution of the product of two normally distributed variables (e.g., the regression coefficients used to compute the mediated effect ) is not normally distributed. Rather, the sampling distributions of the mediated effect are often asymmetric and kurtotic. The implication of this asymmetry is that critical values associated with a given level of confidence from the standard normal distribution, or the z-score value at which an estimate will be considered significant, are no longer associated with the correct area under the curve. For example, 1.96 is no longer the z-value that is associated with p=.05 in a two-tailed test. Methodologists have derived the sampling distribution of the product of two normally distributed variables (Meeker, Cornwell, & Aroian, 1981), so it is possible to obtain adjusted critical values that yield correct p-values. Using statistical tests for mediation based on adjusted critical values that account for asymmetry in the distribution of the mediated effect will have greater power because they more accurately capture the shape of the sampling distribution.
An automated computer program (PRODCLIN; MacKinnon, Fritz, Williams, & Lockwood, 2007) has been developed to estimate asymmetric confidence limits for the mediated effect, , based on Meeker et al.’s (1981) derivations and is freely accessible at http://www.public.asu.edu/~davidpm/ripl/Prodclin/. The program computes asymmetric confidence limits for any mediated effect with a single mediator and a single outcome variable. The user need only provide sample estimates of the coefficient, the coefficient, and their respective standard errors. All of these estimates are provided in the output of any standard statistical software package such as SAS or SPSS. Inputting sample estimates of the and regression coefficients from the previous numerical example into the PRODCLIN program yields asymmetric confidence limits of [−2.316, 1.083] for the mediated effect. Because zero falls within the interval, we know that the estimate is not significant.
The PRODCLIN program does not extend beyond the single mediator model in which a single mediated effect is estimated for a continuous outcome variable. Thus asymmetric confidence limits based on the distribution of the product are the preferred method to estimate mediation in the basic single mediator model only, or to describe individual mediated effects in a multiple mediator model with continuous outcomes. When more complex mediation models are estimated, such as those that consider more than one dependent variable or more than one mediator variable, asymmetric confidence intervals for the mediated effect can be formed with resampling methods such as the bootstrap (see Efron & Tibshirani, 1993). Bootstrapping procedures form empirical confidence limits for the mediated effect using the sampling distribution of the data itself. The conventional method of bootstrapping is called the “percentile bootstrap”. In short, bootstrapping utilizes the sample data as a population from which random samples of size N are drawn with replacement a large number of times. Estimates of mediation are then computed in each of the bootstrapped samples and an empirical sampling distribution of the mediated effect estimates is formed. The collection of mediation effects from the bootstrap samples forms a frequency distribution, and the 5th and 95th percentiles from this frequency distribution serve as the confidence interval limits for the mediated effect. The percentile bootstrap (as well as more advanced resampling methods such as the bias-corrected bootstrap) is available in several different SEM software packages, including AMOS, EQS, LISREL, and MPLUS. In packages like SAS or SPSS, automated macros to obtain bootstrap confidence limits for the mediated effect can be created. Several such macros for a variety of different mediation models are available for use at Dr. Kris Preacher’s website: http://quantpsy.org.
Mediation analysis in program evaluation
Mediation analysis is especially useful in program evaluation where it is used to understand the underlying mechanisms of a program. Whether a manipulation was effective or unsuccessful, mediation analysis is able to identify components of the program that contributed to its success or failure. By evaluating specific components of a program that produce intended or unintended change, mediation analysis can identify: (a) supportive elements, or those components that encouraged intended behavior, (b) ineffective elements, or those components that did not contribute to changing the behavioral outcome, and/or (c) iatrogenic elements, or those components that promoted unintended effects of the program. To that end, it is important to differentiate overall program effect hypotheses from mediation hypotheses. Although testing the overall relation between X and Y is vital in its own right, a non-significant overall program effect does not preclude a statistically significant mediation effect (MacKinnon & Fairchild, 2009). This emphasizes why the causal steps approach to investigating mediation, which requires a significant overall effect of X on Y, is limiting. By identifying the successful and unsuccessful components of a program, interventions can be iteratively refined to be more efficient and cost effective.
When considered in the context of program evaluation, component paths in the mediation model have distinct interpretations. The path relating the program to the mediator variable (i.e., ) corresponds to the action theory of the model, defining what components of the program are designed to manipulate mechanisms of change (Chen, 1990; MacKinnon, 2008). This part of the model outlines pieces of the program curriculum related to hypothesized mediator(s) and illustrates how the intervention intends to change the mediating variable(s). The path relating the mediator variable to the outcome (i.e., ) corresponds to the conceptual theory of the model, describing how hypothesized mediators are theoretically linked to outcomes of interest (Chen, 1990; MacKinnon, 2008). Relationships examined in this part of the model are driven by previous research or theory presented in the literature that explain motivations for, or antecedents of, behavioral outcomes.
Power in mediation models
The power to detect mediation effects is conventionally lower than the power to detect main effects because the magnitude of the mediated effect is bounded by the individual coefficients from which it is formed. Recent research has shown that causal steps tests for mediation and normal theory point estimators of the mediated effect are underpowered (Fritz & MacKinnon, 2007; MacKinnon et al., 2002). As presented earlier, with small effect sizes for the mediation regression parameters (i.e., and ), the causal steps method requires 20,886 subjects to achieve .80 power (Fritz & MacKinnon). Although the sample size requirement for normal theory standard error estimators is smaller, the methods are still underpowered relative to newer methods that account for asymmetry in the sampling distribution of the mediated effect. Methodological work has shown that asymmetric confidence limits based on the distribution of the product and resampling methods such as the percentile bootstrap and the bias-corrected bootstrap give the best combination of low Type 1 error rates and power to detect effects in mediation models (Fritz & MacKinnon; MacKinnon et al.). Consequently, these methods should be implemented to test mediation hypotheses in substantive research.
Effect size in mediation models
Currently, effect size measures for mediation have only been outlined for the single mediator model. Effect sizes of two types have been described: (a) measures for individual paths of the mediation model and (b) measures for the mediated effect itself. Effect size measures for individual paths in the model are useful for understanding what parts of the model work and what parts need to be improved. One such measure, squared correlations (or squared partial correlations), quantify the amount of variance explained in the mediation model that is uniquely attributable to a single piece of the design (as described in the Effect Sizes in Moderation Models section). By identifying the relative contribution of individual paths in the mediation model, programs can be iteratively refined to promote stronger components and to remove or reduce weaker ones. Squared correlations and squared partial correlations from the numerical example are: , , and . More specifically, represents the squared correlation between the M and X variables in the model, corresponds to the squared partial correlation between the M and Y variables with the influence of X removed, and denotes the squared partial correlation between X and Y variables in the model with the influence of M removed. The measures illustrate that the weakest part of the mediation model is the b2Y coefficient, demonstrating that oral reading fluency (i.e., the mediator) is only weakly related to reading performance (i.e., the outcome variable). However, recall that there was significant moderation in the reading example dataset, such that learning disability status impacted the efficacy of the reading program. Rather than oral reading fluency truly being unrelated to reading performance, it may be possible that learning disability status also moderates the impact of oral reading fluency on reading performance. Ignoring this moderation effect can attenuate the overall relation between the variables. Squared partial correlation effect size measures for the mediation model are further discussed and statistically evaluated in Fairchild, MacKinnon, Taborga, and Taylor (2009).
Two effect size measures for the overall mediated effect have been developed and evaluated: an R2 mediated measure and the proportion mediated. The R2 mediated measure quantifies the proportion of variance in the outcome that is common to both X and M but can be attributable to neither predictor alone (Fairchild et al., 2009). In this way, the measure is able to illustrate the practical significance of a mediated effect. The R2 mediated effect size measure is computed by using squared bivariate correlations and the overall model R2 from a model where Y is predicted from both X and M, as follows
| (17) |
where is the squared correlation between the outcome and the mediator, is the overall model R2 from the regression equation where Y is predicted from X and M (i.e., Eq. (11)), and is the squared correlation between the outcome and the independent variable (i.e., X). The R2 mediated effect size measure for the numerical example is .109−(.239−.217)=.087. Applying Cohen’s (1988) benchmark values for R2Δ (i.e., .02, .13, and 26), the effect size of the non-significant mediated effect in the example is in the small range. Although the R2 mediated measure can be used with smaller sample sizes, it is possible that estimates from the measure can be negative in some circumstances (a mathematical artifact of the equation).
The proportion mediated effect size is an intuitive measure that quantifies the proportion of a total effect that is mediated (e.g., Ditlevsen, Christensen, Lynch, Damsgaard, & Keiding, 2005). The proportion mediated has also been used as a test of mediation itself in some research studies (e.g., Foshee et al., 1998). The measure is computed by taking the ratio of the mediated effect to the total effect, as follows
| (18) |
The estimate of the proportion mediated effect for the numerical example is: (2.527*−.189)/[(2.527*−.189)+1.477]=−.244. The estimate is negative for the example simply because the direct and indirect effects in the model are of opposite sign. Such mediation models are sometimes called inconsistent mediation models. Discussion of inconsistent mediation models is beyond the scope of this paper, but MacKinnon (2008) describes the phenomenon in detail for readers who are interested. To improve interpretability of the proportion mediated estimate in such circumstances, Alwin and Hauser (1975) recommend taking the absolute value of the regression coefficients before computing the effect size measure. Doing so for the numerical example yields a proportion mediated effect of .244, or approximately 24%. Because absolute values were used in computation, interpretation of the measure changes slightly and becomes the proportion of the absolute overall effect that is mediated. So for the numerical example, 24% of the absolute overall effect is mediated. Although the proportion mediated was computed here, there is evidence that the effect size measure should only be used with sample sizes that are greater than or equal to 500 due to instability in the estimate (MacKinnon, Fairchild, Yoon, & Ryu, 2007). Thus, presentation of the effect size estimate with the numerical example data where N=20 is for illustrative purposes only. At present, there are no suggested benchmarks to formally gauge the magnitude of the proportion mediation. Because there are various advantages and disadvantages to each mediation effect size measure, it may be useful to implement more than one to gain the clearest picture of effects in a mediation model.
Assumptions
A number of assumptions underlie estimation of the mediation model. The majority of these assumptions attend to those associated with ordinary least squares regression (OLS), namely: (a) correct specification of the model’s functional form, (b) no omitted variables from the model, (c) no measurement error, (d) homoscedascity of residuals, (e) uncorrelated error terms across equations, and (f) normally distributed residuals (Cohen et al., 2003). Beyond these OLS estimation assumptions, mediation analyses also assume correct causal ordering of the variables, no reverse causality effects, and no XM interaction.
Causal inference in mediation analysis
Issues of causality and limitations of causal inference in the statistical mediation model have been widely discussed in the literature. Model-implied causal relations are plausible when both the independent variable and the mediator are experimentally manipulated, but this scenario is unusual. Non-randomized studies make interpretation of causal relations in the mediation model tentative, and statistical frameworks such as structural equation modeling do not guard against this limitation. Random assignment of the independent variable allows for the causal effect estimation of the β1M path in the mediation model, but unless subjects are also randomly assigned to levels of the mediator, the β2Y and β1Y paths in the model are not causal parameters. Because measurement of the mediating variable occurs subsequent to the assignment of treatment conditions, values of the mediating variable may be confounded with the unknown assignment mechanism. Consequently, in non-experimental contexts, it is critical to have a strong theoretical rationale for relations among variables in the mediation model.
Advanced mediation models
Although many interesting research questions can be evaluated with the basic single mediator model, research studies often introduce design elements or variable attributes that are not accommodated by the conventional single mediator model. In the following sections, we briefly describe several advanced mediation models that extend to some of these situations. All of these models require additional considerations in their statistical estimation that go beyond those described for the single mediator model. Citations for methodological articles on each model are provided to direct further reading.
Multilevel mediation models
In many prevention or intervention studies, particularly in school-based settings, individual participants are clustered within larger groups such as a classroom, school, or a school district. In these situations, the assumption of independent observations underlying conventional statistical models such as ANOVA and regression is violated, and Type 1 error rates of the models are often increased (see the Peugh article in this issue). Methods to estimate multilevel mediation models that accurately model dependency among observations in the data are available (e.g., Kenny, Korchmaros, & Bolger, 2003; Krull & MacKinnon, 2001) and should be implemented in these cases. These methods are often appropriate when a program is randomized at the group level (such as a school) and the mediator and outcome variables are measured at the individual level (such as students).
Mediation in SEM
When modeling more than one dependent variable, a detailed modeling approach is required due to the possibility of correlated dependent variables and/or correlated error terms. Path analysis, a variation of structural equation modeling (SEM), is an extension of multiple regression that simultaneously estimates the equations in a mediation model. In SEM, the fit of an observed covariance matrix of the variables is compared to a model-implied covariance matrix, and goodness-of-fit statistics are calculated to analyze discrepancies between the two. Though more than one mediated effect may be estimated in these models, methods described for the single mediator model can be implemented to test individual mediated effects. Tests of overall fit of the model can also provide evidence for a hypothesized mediation relation, or relations (James, Mulaik, & Brett, 2006; MacKinnon, 2008).
Categorical mediation models
It may also be of interest to explore mediation effects on a categorical outcome variable, such as whether students pass a grade level, or whether they drop out of school. In both circumstances, a researcher uses information from available predictor variables to predict whether a student passes or does not pass, or alternatively whether a student remains in or drops out of school. Because in these cases the dependent variable takes on only two possible values, one models the probability that the given event will occur. When modeling the probability of an event occurrence, the use of standard OLS regression procedures can lead to incorrect conclusions because assumptions underlying the model are violated. Instead, logistic or probit regression frameworks should be utilized. MacKinnon, Lockwood, Brown, Wang, & Hoffman (2007) describe and compare methods to test mediation in these types of models.
Simultaneously analyzing mediation and moderation effects
Combining the mediation and moderation models into a single framework allows the investigation of complex research hypotheses. There are many different types of relations that can be explored in such models. For example, is the mechanism by which a program or manipulation achieves its effects the same across different groups? This question asks if a mediated effect differs across levels of a moderator variable, and the analysis that addresses this question has been often referred to as moderated mediation in the literature. It may also be of interest to ask if the reason an overall effect is moderated can be explained by a mediation process. This question considers whether the presence of an interaction effect can be explained by a mediating mechanism, a phenomenon that has been called mediated moderation in the literature. Finally, it may be informative to examine moderation in individual paths of the mediation model to investigate contextual effects in different pieces of the model. Plotting simple mediated effects in these models to understand the mediation relation at different levels of the moderator variable has been proposed in the literature (Tein et al., 2004). Several other sources explain these modeling extensions and present methods for testing all such hypotheses (Edwards & Lambert, 2007; Fairchild & MacKinnon, 2009; MacKinnon, 2008; Preacher, Rucker, & Hayes, 2007).
Longitudinal mediation models
Cross-sectional data only provide a snapshot of concurrent relations, limiting the ability to compute unbiased estimates of the mediated effect (Cole & Maxwell, 2003; Gollob & Reichardt, 1991; Maxwell & Cole, 2007). Since mediation seeks to explain the mechanisms by which a causal effect occurs, and causes must precede effects in time, it makes sense that longitudinal data are well suited to test mediation. There are several benefits of utilizing longitudinal data to examine mediation, including an increased power relative to cross-sectional designs (due to the ability to reduce within-subject variability) and the ability to investigate the assumption of correct causal ordering of the X to M to Y relation.
Two-wave longitudinal mediation models that examine pre–post data can quantify the overall amount of change, but these models do not accommodate questions about intra-individual variability of change or potential curvilinear change because doing so requires at least three waves of data. Three models are generally used to assess change in 2-wave longitudinal models: (a) difference score models, (b) residualized change scores, and (c) ANCOVA (analysis of covariance). Models with two waves of data are often considered half-longitudinal mediation models because some relations in the data are cross-sectional (e.g., both M and Y are measured at post-test). MacKinnon (2008) describes two-wave longitudinal mediation models in detail.
Longitudinal data with three or more time points allow for the investigation of change over time in mediating processes as well as true longitudinal mediation relations where the independent variable, the mediator, and the outcome occur in sequential time points. Most of these models require estimation in a structural equation modeling software program due to the complexity of model parameters. Latent growth curve models are an example of such models and provide the flexibility to investigate heterogeneity in mediational growth processes across participants. Cheong, MacKinnon, and Khoo (2003), Maxwell and Cole (2007), and Cole and Maxwell (2003) all describe methods to test longitudinal mediation models with three or more waves of data. MacKinnon (2008) also illustrates these models.
Multiple mediator models
Most behaviors are affected by multiple variables, so it is sensible that there are multiple mediator models of behavioral outcomes. Models that consider the effect of more than one mediator in a relationship are called multiple mediator models. Multiple mediator models are a straightforward extension of the single mediator case, but their interpretation can be more difficult when considering the large number of possible relations among variables in the model. Such models introduce the idea of a total mediated effect, or the sum of all individual mediated effects together. There are multiple mediator models where the effects of the mediator variables occur in sequence, such that one mediator temporally precedes another. In addition, it is possible to estimate models where the effects of several mediators are “stacked”, such that the mediators are hypothesized to affect an outcome contemporaneously. In these models, statistical contrasts among different mediated effects in the model can be used to determine whether two mediation effects significantly differ from one another. MacKinnon (2008) provides detailed guidance on how to estimate these models, and Taylor, MacKinnon, and Tein (2008) describe three-path mediation analysis (appropriate for serial mediation) in detail.
Concluding remarks
The investigation of third variables such as moderators and mediators contributes to understanding why or under what conditions two variables are related. When conducted correctly, these analyses have the potential to inform the evaluation of prevention and intervention programs, as well as to refine program curricula. Given recent federal mandates for evidence-based practice in education and beyond, these models will likely continue to be valuable to the school psychologist and other substantive researchers in the future. Investigators can conduct both the basic moderation and mediation models in a multiple regression analysis framework using conventional statistical software packages such as SAS or SPSS. Varied methodological resources that extend these basic models are also available and enable the exploration of interesting and advanced research hypotheses that involve moderator and mediator effects. Though such extensions often require estimation in structural equation modeling software to accommodate complex data structures, core assumptions of the models and their underlying basic frameworks remain as described here.
This paper sought to describe contemporary methods for testing moderation and mediation effects in school psychology. We described the basic moderation and mediation models for the substantive researcher, and demonstrated methods to estimate and explore effects in the models. The literature review conducted at the beginning of this paper illustrated that, although school psychology researchers generally implemented proper methods to conduct moderation analyses, investigators have been using imperfect methods to test mediation effects. Thus in an effort to facilitate the examination of valuable mediation research hypotheses in school psychology, we offer specific recommendations for conducting statistical mediation analyses to conclude this article.
The product of coefficients estimator of mediation is the most generalizable estimator of the mediated effect and should be implemented in substantive research. Because the sampling distribution of the mediated effect is asymmetric, the utility of normal theory variance estimators of mediation which do not accurately capture the asymmetry in the mediated effect sampling distribution is limited. Asymmetric confidence limits based on resampling methods, as well as those based on the distribution of the product of two random variables, have greater power and more accurate Type 1 error rates relative to normal theory methods and should be utilized. In addition to significance testing of the mediated effect, there are several effect size measures available to describe effects in a single mediator model. Such measures provide useful information on the magnitude of mediation effects that are independent of sample size or statistical significance and should be reported when possible. When available, longitudinal data should be used to examine mediation hypotheses as assumptions of the mediation model are more feasible (and testable) in this context. The product of coefficients estimator and asymmetric confidence limits for the mediated effect as described in the paper can be equivalently applied to longitudinal data where X, M, and Y come from sequential time points. Finally, although the original causal steps approach to testing mediation (i.e., Baron & Kenny, 1986; Judd & Kenny, 1981) required an overall significant effect of X and Y to provide evidence for mediation, the requirement is restrictive and is not itself a test of mediation. Non-significant overall effects do not preclude the investigation of mediation. This is especially critical to recognize in program evaluation where investigating mediation in spite of a non-significant overall program effect will likely promote understanding of what parts of the program contributed to its failure or detracted from its success.
Appendix A
SPSS code to compute the basic mediation and moderation models
-
*
Comments in the code are denoted by lines that start with an asterisk (∗). These comments are not commands, but provide guidance or additional notes for the reader. We do not recommend cutting and pasting the comments into SPSS command lines as they contain special characters in some circumstances.
-
*
Throughout the Appendix, X references the independent variable, Z references the moderator variable, XZ references the product of the independent variable and the moderator, M references the mediator variable, and Y references the dependent variable (i.e., the outcome).
-
*
The XZ interaction variable was computed prior to running analysis by creating a new variable that multiplied values of X and Z for each subject in the data.
-
*
The researcher can substitute out all or any variable names to correspond with variable names that appear in his or her own data, as well as alter the code to request additional statistics if desired. This demonstration only serves to illustrate the basic structure of the single mediator model and the moderation model.
-
*
The following code illustrates how to estimate a basic single mediator model. Recall that three regression equations defined the single mediator model.
-
*First estimate a regression equation where Y is predicted only from X. This model corresponds to Eq. (8) in the manuscript, and provides an estimate of the overall effect of X on Y (i.e., the coefficient).
- REGRESSION
- /STATISTICS COEFF CI
- /DEPENDENT Y
- /METHOD=ENTER X.
-
*Second, estimate a regression equation where Y is predicted from both X and M. This model corresponds to Eq. (9) in the manuscript, and provides an estimate of both the direct effect of X on Y once M is partialled (i.e., the coefficient), and the effect of M on Y (i.e., the coefficient).
- REGRESSION
- /STATISTICS COEFF CI
- /DEPENDENT Y
- /METHOD=ENTER X M.
-
*Third, estimate a regression equation where M is predicted from X. This model corresponds to Eq. (10) in the manuscript and provides an estimate of the effect of X on M (i.e., the coefficient).
- REGRESSION
- /STATISTICS COEFF CI
- /DEPENDENT M
- /METHOD=ENTER X.
-
*
An estimate of mediation can be computed by multiplying the and coefficients from Models 2 and 3. Recall that these parameter estimates and their respective standard errors from the model output can be used to estimate asymmetrical confidence limits for the mediated effect in PRODCLIN.
*** THIS COMPLETES ESTIMATION OF THE SINGLE MEDIATOR MODEL.***
-
*
The following code illustrates how to estimate the basic moderation model. Recall that one regression equation defined the moderation model.
-
*Estimate a regression equation where Y is predicted from X, Z, and the XZ product (recall the interaction term variable must be created before running analysis). This model corresponds to Eq. (1) in the manuscript, and will yield the , , and coefficients, respectively.
- REGRESSION
- /STATISTICS COEFF CI
- /DEPENDENT Y
- /METHOD=ENTER X Z XZ.
-
*
An estimate of moderation is provided by the coefficient in the output. The p-value associated with this coefficient will demonstrate whether there is significant moderation.
***** THIS COMPLETES ESTIMATION OF THE MODERATION MODEL. *****
References
- Abelson RP. A variance explanation paradox: When a little is a lot. Psychological Bulletin. 1985;97:129–133. [Google Scholar]
- Aguinis H. Regression analysis for categorical moderators. New York, NY: The Guilford Press; 2004. [Google Scholar]
- Aiken LS, West SG. Multiple regression: Testing and interpreting interactions. Thousand Oaks, CA: Sage Publications; 1991. [Google Scholar]
- Alwin DF, Hauser RM. The decomposition of effects in path analysis. American Sociological Review. 1975;40:37–47. [Google Scholar]
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Champoux JE, Peters WS. Form, effect size, and power in moderated regression analysis. Journal of Occupational Psychology. 1987;60:243–255. [Google Scholar]
- Chen HT. Theory driven evaluations. Newbury Park, CA: Sage; 1990. [Google Scholar]
- Cheong J, MacKinnon DP, Khoo S-T. Investigation of mediational processes using parallel process latent growth curve modeling. Structural Equation Modeling. 2003;10:238–262. doi: 10.1207/S15328007SEM1002_5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. New York, NY: Lawrence Erlbaum Associates; 1988. [Google Scholar]
- Cohen J, Cohen P. Applied multiple regression/correlation analysis for the behavioral sciences. 2nd. Hillsdale, NJ: Erlbaum; 1983. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioural sciences. 3rd. Mahwah, NJ: Lawrence Earlbaum Associates; 2003. [Google Scholar]
- Cole DA, Maxwell SE. Testing mediational models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Ditlevsen S, Christensen U, Lynch J, Damsgaard MT, Keiding N. The mediation proportion: A structural equation approach for estimating the proportion of exposure effect on outcome explained by an intermediate variable. Epidemiology. 2005;16:114–120. doi: 10.1097/01.ede.0000147107.76079.07. [DOI] [PubMed] [Google Scholar]
- Edwards JR, Lambert LS. Methods for integrating moderation and mediation: A general analytical framework using moderated path analysis. Psychological Methods. 2007;12:1–22. doi: 10.1037/1082-989X.12.1.1. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ. An introduction to the bootstrap. London: Chapman & Hall; 1993. [Google Scholar]
- Evans MG. A Monte Carlo study of the effects of correlated method variance in moderated multiple regression analysis. Organizational Behavior and Human Decisions Processes. 1985;36:305–323. [Google Scholar]
- Fairchild AJ, MacKinnon DP. A general model for testing mediation and moderation effects. Prevention Science. 2009;10:87–99. doi: 10.1007/s11121-008-0109-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairchild AJ, MacKinnon DP, Taborga MP, Taylor AB. R2 effect size measures for mediation analysis. Behavioral Research Methods. 2009;41:486–498. doi: 10.3758/BRM.41.2.486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foshee VA, Bauman KE, Arriaga XB, Helms RW, Koch GG, Linder GF. An evaluation of safe dates, an adolescent dating violence prevention program. American Journal of Public Health. 1998;88(1):45–50. doi: 10.2105/ajph.88.1.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz MS, MacKinnon DP. Required sample size to detect the mediated effect. Psychological Science. 2007;18:233–239. doi: 10.1111/j.1467-9280.2007.01882.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollob HF, Reichardt CS. Interpreting and estimating indirect effects assuming time lags really matter. In: Collins LM, Horn JL, editors. Best methods for the analysis of change: Recent advances, unanswered questions, future directions. Washington, D. C: American Psychological Association; 1991. pp. 243–259. [Google Scholar]
- Individuals with Disabilities Education Act (IDEA), 20 U.S.C. § 1414 et seq.
- James LR, Mulaik SA, Brett JM. A tale of two methods. Organizational Research Methods. 2006;9:233–244. [Google Scholar]
- Judd CM, Kenny DA. Process analysis: Estimating mediation in treatment evaluations. Evaluation Review. 1981;5:602–619. [Google Scholar]
- Kazdin A, Nock M. Delineating mechanisms of change in child and adolescent therapy: Methodological issues and research recommendations. Journal of Child Psychology and Psychiatry. 2003;44:1116–1129. doi: 10.1111/1469-7610.00195. [DOI] [PubMed] [Google Scholar]
- Kenny DA, Korchmaros JD, Bolger N. Lower level mediation in multilevel models. Psychological Methods. 2003;8:115–128. doi: 10.1037/1082-989x.8.2.115. [DOI] [PubMed] [Google Scholar]
- Krull JL, MacKinnon DP. Multilevel modeling of individual and group level mediated effects. Multivariate Behavioral Research. 2001;36:249–277. doi: 10.1207/S15327906MBR3602_06. [DOI] [PubMed] [Google Scholar]
- Kruskal WH, Wallis WA. Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association. 1952;47:583–621. [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. Mahwah, NJ: Earlbaum; 2008. [Google Scholar]
- MacKinnon DP, Fairchild AJ. Current directions in mediation analysis. Current Directions in Psychology. 2009;18:16–20. doi: 10.1111/j.1467-8721.2009.01598.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence intervals for the indirect effect: Program PRODCLIN. Behavior Research Methods. 2007;39:384–389. doi: 10.3758/bf03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Brown CH, Wang W, Hoffman JM. The intermediate endpoint effect in logistic and probit regression. Clinical Trials. 2007;4:499–513. doi: 10.1177/1740774507083434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Krull JL, Lockwood CM. Equivalence of the mediation, confounding, and suppression effect. Prevention Science. 2000;1(4):173–181. doi: 10.1023/a:1026595011371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test the significance of mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Fairchild AJ, Yoon M, Ryu E. Evaluation of the proportion mediated effect size measure of mediation Unpublished manuscript 2007 [Google Scholar]
- Maxwell SE, Cole DA. A bias in cross-sectional analyses of longitudinal mediation. Psychological Methods. 2007;12:23–44. doi: 10.1037/1082-989X.12.1.23. [DOI] [PubMed] [Google Scholar]
- McClelland GH, Judd CM. Statistical difficulties of detecting interactions and moderator effects. Psychological Bulletin. 1993;114:376–390. doi: 10.1037/0033-2909.114.2.376. [DOI] [PubMed] [Google Scholar]
- McGuigan K, Langholtz B. A note on testing mediation paths using ordinary least-squares regression. 1988 Unpublished note. [Google Scholar]
- Meeker WQ, Jr, Cornwell LW, Aroian LA. In: The product of two normally distributed random variablesSelected tables in mathematical statistics. Kennedy WJ, Odeh RE, editors. VII. Providence, RI: American Mathematical Society; 1981. [Google Scholar]
- Preacher KJ, Rucker DD, Hayes RF. Addressing moderated mediation hypotheses: Theory, methods, and prescriptions. Multivariate Behavioral Research. 2007;42:185–227. doi: 10.1080/00273170701341316. [DOI] [PubMed] [Google Scholar]
- Shadish W, Cook T, Campbell D. Experimental and quasi-experimental designs for generalized causal inference. Boston: Houghton-Mifflin; 2001. [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods. 2002;7(4):422–445. [PubMed] [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology. 1982;13:290–312. [Google Scholar]
- Stone-Romero EF, Liakhovitski D. Strategies for detecting moderator variables: A review of conceptual and empirical issues. Research in Personnel and Human Resources Management. 2002;21:333–372. [Google Scholar]
- Takezawa K. Introduction to nonparametric regression. Hoboken, NJ: Wiley; 2005. [Google Scholar]
- Taylor AB, MacKinnon DP, Tein J-Y. Tests of the three-path mediated effect. Organizational Research Methods. 2008;11:241–269. [Google Scholar]
- Tein J, Sandler IN, MacKinnon DP, Wolchik SA. How did it work? Who did it work for? Mediation in the context of a moderated prevention effect for children of divorce. Journal of Consulting and Clinical Psychology. 2004;72:617–624. doi: 10.1037/0022-006X.72.4.617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- U.S. Department of Education. No child left behind: A desktop reference. Washington DC: Education Publications; 2002. PDF available at www.ed.gov/admins/lead/account/cvlbreference/index.html. [Google Scholar]


