Ecosystem-based management and the wealth of ecosystems

Significance

Ecosystems store vast quantities of wealth, but difficulties measuring wealth held in ecosystems prevent its inclusion in accounting systems. Ecosystem-based management endeavors to manage ecosystems holistically. However, ecosystem-based management lacks headline indicators to evaluate performance. We unify the inclusive wealth and ecosystem-based management paradigms, allowing apples-to-apples comparisons between the wealth of the ecosystem and other forms of wealth, while providing a headline performance index for evaluating the performance of ecosystem-based management. We project that the Baltic Sea fishery ecosystem yields increasing stores of wealth over the next 50 y under the ecosystem-based management-inspired multispecies maximum sustainable yield management beginning in 2017, whereas the previous single-species management generally results in declining wealth.

Abstract

We merge inclusive wealth theory with ecosystem-based management (EBM) to address two challenges in the science of sustainable management of ecosystems. First, we generalize natural capital theory to approximate realized shadow prices for multiple interacting natural capital stocks (species) making up an ecosystem. These prices enable ecosystem components to be better included in wealth-based sustainability measures. We show that ecosystems are best envisioned as portfolios of assets, where the portfolio’s performance depends on the performance of the underlying assets influenced by their interactions. Second, changes in ecosystem wealth provide an attractive headline index for EBM, regardless of whether ecosystem wealth is ultimately included in a broader wealth index. We apply our approach to the Baltic Sea ecosystem, focusing on the interacting community of three commercially important fish species: cod, herring, and sprat. Our results incorporate supporting services embodied in the shadow price of a species through its trophic interactions. Prey fish have greater shadow prices than expected based on market value, and predatory fish have lower shadow prices than expected based on market value. These results are because correctly measured shadow prices reflect interdependence and limits to substitution. We project that ecosystem wealth in the Baltic Sea fishery ecosystem generally increases conditional on the EBM-inspired multispecies maximum sustainable yield management beginning in 2017, whereas continuing the current single-species management generally results in declining wealth.

The influential management consultant Peter Drucker is credited with saying “what gets measured, gets managed.”* Ecosystem-based management (EBM) is frequently upheld as a holistic management alternative to traditional, decoupled, single-species management approaches (2, 3). However, implementation of EBM lags, in part, because of the lack of a conceptually sound framework and measurable headline indicator for assessing management tradeoffs among multiple species, their habitat, and human wants and needs from the ecosystem. Instead, managers are often faced with a proliferation of potentially contradictory measures, making it difficult to measure the performance of managed ecosystems. Furthermore, the proliferation of indicators undercuts the holistic aims of EBM and often leads to “ecological” vs. “economic” arguments appealing to distinct indicators. A headline “bioeconomic” indicator that measures the value to society created through a more inclusive management approach is critical to help make good on the promise of EBM and provide policymakers, tasked with implementation of EBM, with a concrete measure of progress. Such an indicator can be developed by linking EBM with bioeconomic modeling and concepts and measures from sustainability assessment.

Writing concerning societal wellbeing, Stiglitz et al. (4) note that “[w]hat we measure affects what we do, and if our measurements are flawed, our decisions may be distorted.” Arrow et al. (5), Dasgupta (6), and Barbier (7) argue that sustainability requires maintaining the capacity for future human wellbeing (including but not limited to market consumption), which requires constant or increasing “wealth”—the price-weighted sum of all societal capital stocks valued at appropriate asset prices. Wealth accounting (8–10) (e.g., inclusive, comprehensive, or genuine wealth) has a long history in economics (11) and provides a rigorous economic paradigm for measuring sustainability (5, 12–15). There is broad acknowledgment that ecosystems are important stores of wealth. For example, the 2014 Inclusive Wealth report suggests that 28% of global wealth is contained in ecosystems, which may be an underestimate (9). Resolving EBM’s need for a headline indicator of a system’s ecological–economic sustainability and national accountant’s need for accurate prices at which to value ecosystems is important for environmental stewardship and sustainability (16). At the core of this problem is the accurate measurement of natural capital asset prices, also known as “shadow prices” (17).

We contribute to the EBM, wealth accounting, and natural capital literatures by extending (18, 19) to accurately measure natural capital asset prices in systems with multiple interacting stocks of natural capital. The extension enables a wealth metric that can guide resource management at local scales by generating a headline EBM index—the change in natural capital wealth in an ecosystem—while providing appropriate data for national accounts. Although the theory of wealth accounting was developed in the context of national accounts, it may be exceedingly valuable at the ecosystem management scale (20–22). Moreover, we show that properly derived and measured natural capital asset prices (shadow prices) reflect the localized limits of substitution among ecosystem components. Shadow prices capture ecological and economic interactions between capital stocks, implying that a wealth index need not be merely a weak sustainability index (23, 24) but is capable of capturing the limits and opportunities of substitution, thereby advancing Barbier’s (7) “capital sustainability” concept. Our empirical analysis provides a roadmap for the application of natural capital asset measurement and wealth accounting in more complex EBM contexts.

Valuing an Ecosystem Full of Natural Capital

Operationalizing wealth accounting requires natural capital asset prices or shadow prices (6, 8, 9, 14, 17). The Systems of Environmental–Economic Accounting framework (7, 13, 25) suggests that entire ecosystems can be valued as assets. However, ecosystems are better viewed as a fund or portfolio of distinct but interacting natural assets (26, 27). The performance of the ecosystem fund is a function of the performance of the underlying assets. Unlike a financial fund, the capital stocks held in an ecosystem fund directly interact and affect each other’s performance. As with financial assets, the way that the assets in an ecosystem are jointly managed is critical to their valuation—thereby linking EBM with ecosystem wealth accounting. Management interventions typically operate differentially on components of an ecosystem and may have complex feedbacks through the ecosystem. It is important to disaggregate the bundled ecosystem portfolio into the most important or material assets to track the wealth held in an ecosystem and assess management’s influence on changes in ecosystem wealth through time.

Fenichel and Abbott (FA) (19) and Fenichel et al. (18) adapted Jorgenson’s (28) capital asset pricing approach to a single stock of natural capital to provide “apples-to-apples” comparisons between traditional capital asset prices and natural capital asset prices. FA enables valuation of natural capital assets under a given management approach without requiring the analyst to assume an optimized policy. FA prices are scarcity measures and account for modeled feedbacks from human behavior and institutions. These features allow resource managers to use wealth accounting approaches to examine how management changes affect capital asset values apart from any change in the immediate state of the ecosystem. The FA approach can be extended to measure shadow prices for an ecosystem with $N$ interacting stocks of natural capital with each stock indexed by $i$ (derivation is in SI Text):

$$p^i\left(\mathit{s}\right)=\frac{M{D}^i\left(\mathit{s},\mathit{x}\left(\mathit{s}\right)\right)+\left(\frac{\partial p^i}{\partial s^i}{\dot{s}}^i+{\displaystyle \sum _{j\ne i}^N\frac{\partial p^j}{\partial s^i}{\dot{s}}^j}\right)+{\displaystyle \sum _{j\ne i}^N{p}^j\frac{\partial {\dot{s}}^j}{\partial s^i}}}{\delta -\left[M{G}^i\left(\mathit{s}\right)-MH{I}^i\left(\mathit{s},\mathit{x}\left(\mathit{s}\right)\right)\right]}.$$ [1]

Eq. 1 takes the same general form as the FA single-stock natural capital asset pricing equation (18). The left-hand side, $p^i\left(\mathit{s}\right)$, is the shadow price for natural capital stock $s^i\in \mathit{s}$, where $\mathit{s}$ is an N-length vector of capital stocks. The shadow price measures the extra current and discounted future benefits arising from conserving an additional unit of a natural capital stock, its marginal social value, given the current institutions and assumed management plan. As in FA, the shadow price is a function of the marginal dividends, $M{D}^i$, an index of net benefit flows to society from an additional unit of natural capital stock i; a series of price and stock effects $((\partial p^i/\partial s^i){\dot{s}}^i+{{\displaystyle \sum }}_{j\ne i}^N(\partial p^j/\partial s^i){\dot{s}}^j)+{{\displaystyle \sum }}_{j\ne i}^N{p}^j\partial {\dot{s}}^j/\partial s^i$, which we discuss momentarily; a “baseline” discount rate $\delta$ ; a marginal growth rate of natural resource $i$, $M{G}^i$; and a rate of marginal human impact, $MH{I}^i$. As in FA, $MD$, $MG$, and $MHI$ are functions of the stocks of natural capital and humans’ institutionally conditioned responses to these stocks—the economic program $\mathit{x}\left(\mathit{s}\right)$.

Despite Eq. 1 taking the same general form as FA’s single-stock natural capital asset price equation, there are three important differences. First, the shadow price of natural capital stock $i$ is a function of the entire N-length vector of stocks, $\mathit{s}$. The shadow price of a stock of natural capital depends, in general, on the state of the entire ecosystem. Second, although FA described the economic program as a scalar function of a single capital stock, here we generalize it as a mapping from an N-length vector of stocks to an $L$-length vector of human actions: $\mathit{x}\left(\mathit{s}\right)$. This vector-valued function captures all human feedbacks that are relevant to benefits flows $(MD$) or human impacts to natural capital stocks in the ecosystem ($MHI$) and allows for multiple inputs and joint production, which are common in ecosystems (29).

The third change compared to FA has the greatest ramifications for linking wealth accounting and EBM. The terms following $MD$ in the numerator of Eq. 1 are complicated relative to those in FA. These terms capture expectations of the influence of conserving an increment of natural capital i on the future productivity of the ecosystem fund in delivering valued services (i.e., capital gains) given the biophysical dynamics and economic program. The second numerator term $\left((\partial p^i/\partial s^i){\dot{s}}^i+{\displaystyle {\sum }_{j\ne i}^N(\partial p^j/\partial s^i){\dot{s}}^j}\right)$ reflects the effects of investment in $s^i$ on capital gains through its effects on the shadow prices of all assets in the ecosystem fund (i.e., “price effects”). In FA’s single-stock case, this term collapses to $dp/dt=\dot{p}=(\partial p/\partial s)\dot{s}$. The third numerator term in Eq. 1, ${\displaystyle {\sum }_{j\ne i}^N{p}^j\left(\partial {\dot{s}}^j/\partial s^i\right)}$, captures an effect that is only present in multiasset systems: the effects of an investment in $s^i$ on the physical growth of other natural capital stocks in the fund (i.e., “cross-stock effects”). Together, price effects and cross-stock effects enable shadow prices to capture nonlinear substitution possibilities and complementarities among stocks as their quantities change. These substitution possibilities can arise from consumption, production, or ecological interactions, and it is these substitution and complementarity relationships that are at the core of the sustainability problem (7, 30).

Headline Indicator for EBM

The potential present and future wellbeing stored in a set of capital stocks at time t, $\mathit{s}\left(t\right)$, can be expressed as the net present value (NPV) of dividend flows, D, from natural and other capital stocks: $V\left(\mathit{s}\left(t\right)\right)={\displaystyle {\int }_t^{\infty }{e}^{–\delta \left(\tau -t\right)}D\left(\mathit{s}\left(\tau \right),\mathit{x}\left(\mathit{s}\left(\tau \right)\right)\right)d\tau }$. The quantity $V$ incorporates the trajectory of human behavior and stocks through time according to the ecological dynamics and economic program. Although changes in $V$ are the ultimate theoretical basis for assessing welfare (23, 31), it can be convenient to work with a linear accounting index known as inclusive wealth (6, 8, 9): $IW\left(t\right)={\displaystyle {\sum }_{i=1}^N{p}^i\left(t\right)s^i\left(t\right)}$. For a discrete time interval $\mathrm{\Delta }t$, let $\mathrm{\Delta }IW={\displaystyle {\sum }_{i=1}^N{\overline{p}}^i\mathrm{\Delta }{s}^i}$, where ${\overline{p}}^i$ is a weighted average of the asset price for stock $i$ at the beginning and end of the accounting period (21). Dasgupta (23), Dasgupta and Maler (32), and Arrow et al. (5) show that $\mathrm{\Delta }V/\mathrm{\Delta }t\approx \mathrm{\Delta }IW/\mathrm{\Delta }t$ for a sufficiently short time period. A necessary condition for sustainability over $\mathrm{\Delta }t$ is that $\mathrm{\Delta }V\approx \mathrm{\Delta }IW\ge 0$, because this condition ensures maintenance of the potential to provide valued service flows today and in the future. Our approach to calculating natural capital shadow prices leads to direct computation of $\mathrm{\Delta }IW$ and $\mathrm{\Delta }V$. Furthermore, when the shadow prices come from Eq. 1, $\mathrm{\Delta }IW$ or $\mathrm{\Delta }V$ provides a headline ecological–economic index of the sustainable management of an ecosystem under EBM and a quantity for national accountants to use to value changes in ecosystems.

A general concern with green accounting and especially inclusive wealth is that species and abiotic components of ecosystems are not perfect substitutes. On the surface, the linear-in-stocks form of $IW$ suggests that declines in asset $s^i$ can be indefinitely substituted at a constant rate for investments in another capital stock $s^j$, such that $IW$ is unchanged. This view (24) may originate from and be sustained by efforts to calculate inclusive wealth using adjusted market prices to illustrate the $IW$ concept (10). However, recognizing from Eq. 1 that $IW={\displaystyle {\sum }_{i=1}^N{p}^i\left(\mathit{s}\right)s^i}$, the inclusive wealth index is actually nonlinear in stocks. Therefore, stocks are not necessarily perfect substitutes—assuming that shadow prices are updated between evaluation points to reflect changes in substitutability. As stocks change, their shadow prices change along with the shadow prices of other stocks. If $\partial p^i/\partial s^j>0$, then $s^i$ and $s^j$ are capital complements. When stocks are capital complements, increasing one stock raises the value of the other. For example, increases in a prey stock make a predator stock more productive and hence, more valuable, whereas an increase in predator stocks creates a need for more prey and hence, makes prey more valuable. If $\partial p^i/\partial s^j<0$, then $s^i$ and $s^j$ are capital substitutes. Stocks of natural capital are substitutes when increases in one stock reduce the value of the other. For example, two species that fill similar roles in an ecological–economic system (e.g., two competing prey species) may be capital substitutes. However, the substitutability or complementarity of capital stocks depends on more than their ecological interactions; the interactions of capital stocks in the provision of dividends, $MD$, and human responses to changes in the ecosystem portfolio $\mathit{x}\left(\mathit{s}\right)$ also matter. Overall, these capital substitutes and complement relationships reflect joint ecological–economic interactions and relative scarcity within the ecosystem. The ability to capture these interactions makes $\mathrm{\Delta }IW$ and $\mathrm{\Delta }V$ strong candidates as headline indicators for EBM.

Case Study

To illustrate the usefulness of $\mathrm{\Delta }IW$ and $\mathrm{\Delta }V$ as indicators of sustainable management for EBM and respond to recent calls for assessing marine natural capital (33), we compute shadow prices for the three most ecologically and economically important natural capital stocks in the Baltic Sea commercial fishery: cod (Gadus morhua), herring (Clupea herengus), and sprat (Sprattus sprattus). Predatory cod shapes this ecosystem (34). By contrast, prey availability, including herring and sprat, influences cod’s consumption rates and growth, thus creating a feedback loop that strongly ties these three species together. For simplicity, we assume that environmental factors are invariant, and we do not consider the sensitivity of cod to the salt water inflows from the North Sea. Tahvonen et al. (35) show that stochasticity is not critical to maximum sustained yield in this system.

Cod, sprat, and herring generate ∼80% of the Polish Baltic Sea fleet’s revenue, which is representative of other Baltic Sea nations (36). For the case study, we focus on net revenue, a monetary index for an important benefit flow in this system, but the methodology could include a broader set of benefit flows, beyond food provision, in other applications. It is important to consider how changes over time in net revenue and stocks are affected by and affect ecosystem structure, fishers’ responses to regulations, and feedbacks among the fish species (37). In 2014, Poland began managing all three species with binding individual vessel-level allocations, which are shares of the total allowable catch (TAC) for each stock. The shares are set as the fraction of the assessed fish stock in each year. Joint production (29) best describes the fishery, because the three species are jointly harvested (38). The allocation system, ex-vessel prices, fishing costs, and the market economy that drive fishers to attempt to maximize net revenue together constitute the economic program, which is almost certainly inefficient. In this multispecies fishery, we assume limited ability to target particular species, so that the economic program—the supply of effort in the fishery—can be written as a scalar function $x\left(\mathit{s}\right)$, where $x\left(\mathit{s}\right)$ is a function of all three stocks. If effort could be perfectly targeted (39), then $\mathit{x}\left(\mathit{s}\right)$ could be a three-element vector of the effort levels targeting each stock. Fig. 1 shows the historical stock performance and projected biomass starting from 2013, assuming single-species management and the business as usual (BAU) TAC allocation regime based on the single-species stock assessments vs. an alternative, recently accepted, multispecies maximum sustainable yield (MMSY) TAC allocation regime (EC 2016/1139) that follows EBM principles (40, 41).

Fig. 1.

Historical stock biomass (solid lines), predicted stock biomass under single-species BAU (dashed lines), and forecasted stock biomass under the EBM MMSY (dot-dash lines) from the multispecies interaction model.

Natural Capital Prices in an Ecosystem “Fund.”

We estimate three interconnected shadow price functions, one for each fish stock. To illustrate the three-to-one shadow price function, we hold two stocks constant (Fig. 2). As expected, the price curves for each species slope downward in own stock; prices increase as quantity declines, reflecting the relative scarcity of each stock. The shape of these price curves is affected by cross-stock effects seen by comparing the position of the price curves at alternative stock levels for the other two species.

Fig. 2.

Shadow prices when the two other species are fixed at the 2013 (solid lines) and equilibrium (dashed lines) levels for the single-species BAU (red) and EBM MMSY (blue) scenarios. Black curves show sensitivity for the BAU case when other stocks are held at 80% (dot-dash lines) and 110% (dotted lines) of equilibrium levels. Black dots show 2013 ex-vessel prices (y axis) at 2013 stock levels (x axis). SS, steady states.

The price curves show that a species in an ecosystem can be an asset, having a positive shadow price, or a liability, having a negative shadow price, depending on its abundance (42). In such cases, the label of “asset” or “liability” applies to the marginal value; a species may provide overall benefits, although its marginal value in conservation is negative. The shadow price of cod is positive at 2013 stock levels but negative at the system’s BAU steady state, whereas the shadow prices for prey fish are positive at the BAU steady state but negative at 2013 levels. At 2013 levels, cod are scarce, so scarce that their implicit value in conservation for reproduction (the shadow price) exceeds the ex-vessel price of harvesting the cod (illustrated by the black dots in Fig. 2). However, in the BAU equilibrium, the shadow price for cod is negative, suggesting that the BAU strategy fails to adequately account for the predation effects on the prey stock, resulting in an overinvestment in cod. In contrast to BAU management, the MMSY management program maintains all three stocks as assets, with positive shadow prices, in equilibrium (Fig. 2).

The price curves for herring and sprat reflect their direct value for their respective fisheries as well as their indirect value as “inputs” to or “supporting services” for the growth and sustenance of cod stocks. In 2013, herring and sprat stocks are above their steady-state levels. This abundance paired with low cod stocks that cannot benefit from additional prey saturation drive the 2013 shadow values of prey stocks below zero. Prey stocks decline in equilibrium, which in combination with growth in the cod population, ensures that they become assets in the long run.

Whether stocks are capital substitutes or complements ultimately depends on the complex interplay of trophic interactions, how changes in species abundance affect harvester behavior, and the way that stocks enter the MD function. To examine these patterns in the Baltic, we map shadow price contours for herring and cod (Fig. 3) under the BAU scenario. Upward (downward) sloping contours indicate complementary (substitute) relationships between the stocks on the axes (SI Text). The complementary and substitute relationships reflected in the shadow prices are strongly influenced by ecological relationships as well as economic and behavioral factors. It is these kinds of relationships that EBM is charged with balancing (43).

Fig. 3.

Contours of shadow prices (single-species BAU scenario). Shadow prices are calculated by fixing the cod stock at the steady state in A, the sprat stock at the steady state (SS) in B and D, and the herring stock at the steady state in C. The arrows are the increasing direction of shadow prices.

In the Baltic Sea case, the substitutability or complementarity between species is tightly linked to trophic interactions. The prey species, herring and sprat (Fig. 3A), have the downward sloping contours of capital substitutes. As the stock of herring declines, increasing its shadow price, a compensating increase in sprat drives the shadow price of herring back to its previous level. Sprat and herring are substitutes to fishers in the linear profit function entering D and substitutes as prey for cod. The slopes of the contours are not constant, implying that the extent of substitutability between herring and sprat varies depending on relative abundances. The shadow price reflects the imperfect ecological and economic niche overlap. This nonconstant shadow price relationship means that declines in sprat cannot be made up with a fixed ratio increase in herring and vice versa.

Cod and either prey species have upward sloping contour lines, implying complementarity, an extreme lack of substitutability (Fig. 3 B–D). Increasing abundance of prey species enhances the asset value of cod and vice versa. Although cod and prey are substitutes in terms of their immediate contribution to fishing profits, the predator–prey ecological relationship drives their capital complementarity through supporting ecosystem services, which come through the MG, cross-stock, and cross-price terms. Specifically, the wealth gains from investing in cod are enhanced with an accompanying increase in a prey stock. The marginal social value of cod stock increases faster with increases in sprat than with increases in herring, which is illustrated by the flatter contours in Fig. 3C relative to Fig. 3D.

Changes in Baltic Sea Wealth.

Consider how management coupled with ecological dynamics stores wealth in the Baltic Sea fish populations. As noted above, nondeclining intertemporal wellbeing, $\mathrm{\Delta }V\ge 0$, is a necessary condition for sustainability (23), where the change in wealth, $\mathrm{\Delta }IW$, serves as an approximation for $\mathrm{\Delta }V$ when $\mathrm{\Delta }V$ is not measurable (44). The theoretical equivalence of $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ holds for relatively short intervals where the shadow prices of assets are effectively constant. When shadow prices change significantly over evaluation intervals, a weighted average of before and after prices is more appropriate; however, finding the optimal weighting to minimize the divergence between $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ may quickly become intractable for highly nonlinear systems (21). We measure the potential divergence between $\mathrm{\Delta }V$ and $\mathrm{\Delta }\mathrm{I}W$ using a first-order midpoint approximation for the shadow price in $\mathrm{\Delta }IW$ [i.e., $\mathrm{\Delta }IW=0.5(p_{t-1}+p_t)(s_t-s_{t-1})$].

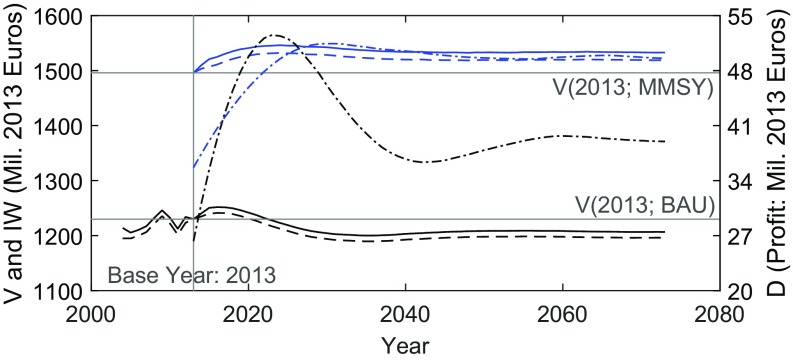
We calculate $V$ and $IW$ (the latter indexed to $V$ for the base year 2013) under BAU (black lines in Fig. 4) and EBM-based MMSY (blue lines in Fig. 4) scenarios. We also plot the paths of benefits flows ($D$) (dot-dash lines in Fig. 4). $V$, as the NPV of future $D$, acts as a “leading indicator” for fluctuations in benefits flows from the ecosystem, anticipating future declines in wellbeing in terms of reduced $D$ (31). The $IW$ and $V$ indices qualitatively track over the range of the data, and the signs of the slopes (changes) generally align. For the historical (pre-2013) period, the sign of $\mathrm{\Delta }IW$ does not match that of $\mathrm{\Delta }V$ on a year to year basis in two of the years. Nevertheless, the $\mathrm{\Delta }V\hspace{0.17em}\text{and}\hspace{0.17em}\mathrm{\Delta }IW$ over the historical period generally tell a consistent story of increasing wealth and intertemporal wellbeing, suggesting that past management generally passes a sustainability test. The post-2013 forecasts show that the sign of $\mathrm{\Delta }IW$ matches that of $\mathrm{\Delta }V$ 100% of the time for the BAU and the MMSY scenarios, suggesting that $\mathrm{\Delta }IW$ is a strong proxy for $\mathrm{\Delta }V$ in the Baltic Sea ecosystem over the range of historical and simulated data.

Fig. 4.

$V\left(t\right)$ (solid lines), $IW\left(t\right)=\mathrm{\Delta }IW+IW(t-1)$ indexed to 2013 so that $IW\left(2013\right)=V\left(2013\right)$ (dashed lines), and profit $D\left(t\right)$ (dot-dash lines) as a function of time for single-species BAU (black) and EBM-based MMSY scenarios (blue). Historical data (pre-2013) are also shown in black.

Viewed over a 60-y horizon (2013–2073), which leads to a system steady state, the analysis of $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ for the single-species BAU scenario suggests that this management may be suspect on sustainability grounds. By contrast, if MMSY was implemented in 2013, we project that $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ would be positive relative to 2013. Furthermore, moving from BAU to MMSY management in 2013 instantaneously increases $V$, suggesting that MMSY management is preferred on efficiency and sustainability grounds. The MMSY scenario is in line with recently proposed and accepted changes to the Baltic Sea fisheries regulations set to begin in 2017 (EC 2016/1139) that take into account interactions between species and shift toward EBM. Single-species BAU management ultimately leads to a greater cod stock. The MMSY scenario leads to fewer cod but greater prey fish abundance. Changes in the inclusive wealth and intertemporal wellbeing indices capture the dual roles of herring and sprat in their roles in directed fisheries and as ecological inputs in the production of cod. Capturing these direct and indirect roles of species in decision-making is an important tenant of EBM.

Although the Baltic Sea fishery ecosystem is more likely to be sustainable under the EBM MMSY regime than the single-species BAU regime, neither is strictly sustainable across all intervals of the 60-y forecast. Because of the nonmonotonicity of $V$ and $IW$ over time, there are intervals where wealth declines, which is inconsistent with wealth or welfare-based notions of sustainability. Furthermore, theoretically, the equivalence between $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ can deteriorate over longer time intervals (greater $\mathrm{\Delta }t$) when stocks and shadow prices are in flux. In this case, although BAU and MMSY $IW$ trajectories track $V$ remarkably well on a year to year basis, small quantitative deviations between $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ emerge immediately after 2013, opening a wedge between V and IW. Such divergences can lead to deviations in the sign of $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ over multiyear periods when the path of $V$ and hence, $IW$ is nonmonotonic—as evidenced here by different signs for $\mathrm{\Delta }V$ and $\mathrm{\Delta }IW$ (relative to 2013) over the period 2020–2023 in the BAU case. The gap emerges between the indices, because the linear price averaging embodied in $IW$ is not sufficiently precise when there is rapid change in the system and price curves are not sufficiently linear over the region of system change.

Discussion

Measurement is a necessary condition for effective management, but it is not sufficient. One must also synthesize and weigh the tradeoffs reflected in the measurements themselves. Failure to do so risks leaving decision-makers adrift in a sea of indicators. Assessing progress toward sustainable management requires informing managers about the consequences to present and future stakeholders of investment and divestment decisions across a complex fund of interacting species and their habitats—demanding a fundamentally integrative decision approach. Assessing the change in the wealth stored in an ecosystem facilitates the aims of EBM by breaking down artificial barriers between economic and ecological indicators. Our case study reveals that wealth generally rises (falls) under the EBM (single-species management). Under EBM, cod, which provides the product of greatest commercial value, is maintained at a lower level than under the single-species management scenario, but prey fish, which provide a lower-valued commercial product, are maintained at a greater level—in part for their role in sustaining cod stocks. This insight comes from balancing complex interactions and nonlinear production processes—precisely the mission of EBM.

Our example responds to calls for a headline EBM indicator in fisheries and marine systems (33). However, this framework and pricing approach are applicable across many domains (18, 45). Furthermore, grounding EBM in the theory of sustainability assessment could raise support for EBM in new domains other than those where it has already gained significant acceptance.

There is broad interest in valuing ecosystems as unitary stocks. However, changes in the wealth of ecosystems cannot be valued without considering changes in the value of the constituent stocks that make up the ecosystem. It is reasonable and useful to include the value of the “ecosystem fund” into regional or national wealth accounts, filling an important gap in the sustainability accounting literature (46, 47). However, the wealth stored in ecosystems is only a portion of the wealth of humanity, which also includes human and built capital. Linking natural capital accounting to broader wealth accounting efforts is ultimately essential to fully assess sustainability and guide decision-making.

Limited substitutability and complementarities are at the heart of the sustainability question (7, 30, 48). Correctly measured shadow prices capture the limits of substitutability and important complementarities. The linearity of wealth-based indicators combined with the use of fixed shadow prices occasionally have led to misconceptions that wealth-based indicators impose an assumption that capital stocks are perfect substitutes for one another—that it is a weak sustainability index (12, 16, 24). However, the shadow prices resulting from Eq. 1 are functions of the underlying capital stocks, and the interactions among stocks are reflected through cross-price and cross-stock effects and MG and MHI terms. Wealth metrics are not measures of weak sustainability. Shadow prices and associated changes in wealth reflect the limits of substitution if derived from a coupled systems modeling approach that adequately incorporates ecological and economic knowledge. Our case study shows that ecological interactions can dictate whether stocks are capital substitutes or capital complements; therefore, ecological relationships take on an even more vital role in natural capital asset prices in systems with interacting stocks than they did in FA’s single-asset approach (18, 19). Although our case study focuses on the substitutability between stocks of natural capital and provisioning services, the framework can be extended to the analysis of substitutability between stocks of natural and human or produced capital and can incorporate a broader set of services. Indeed, there is nothing in theory or practice that requires first nesting stocks of interest within a system into the bins of natural, human, and produced capital. An advantage of our approach is that the measures of substitutability between capital stocks emerge endogenously from the structure of the bioeconomic model rather than being imposed arbitrarily. EBM essentially charges decision-makers with the responsibility of managing a complex fund of natural assets in a way that yields sustainable benefits to stakeholders. This Olympian task can be facilitated by providing managers with informed measurements of substitution possibilities within their purview and an approach to assess tradeoffs. Shadow prices for natural capital, derived from integrative bioeconomic models and embedded within a wealth accounting framework, provide the essential bridge from measurement to management.

Methods

The vector of shadow prices, $p^i$, associated with $\mathit{s}$ can be recovered using similar approximation techniques as in ref. 18. The derivation of natural capital asset prices for multiple interacting stocks and the numerical method to approximate the suggested shadow prices are explained in SI Text. We implemented an empirical analysis of the Baltic Sea fishery ecosystem based on ref. 40 using a curve-fitting method detailed in SI Text. The recovery of natural capital asset prices is performed using the R package {capn} (environment.yale.edu/profile/eli-fenichel/software).

We capture predator–prey dynamics and regulation-constrained vessel responses in the Baltic Sea fishery with a modified version of the ecological–economic vessel-level fishing choice model in ref. 40. We assume that Polish management is representative of the Baltic Sea and scale results based on Poland’s fleet to the system. In the model (details are in SI Text, and parameterization in Tables S1–S7), the fishing fleet consists of 411 vessels that optimize individual behavior subject to regulations, feasibility constraints (maximum days that the vessel can spend at sea), owned capital, production structure, and individual technical efficiency. The economic component allows estimation of the profit-seeking response to the quota allocations based on the established harvest control rule. The biological submodel describes the feedback within the ecosystem based on interacting components derived from established food web links. We first build a detailed age-structured model with eight age classes and predator–prey relationships for each stock. Then, we use approximation techniques to compress the dynamics to focus on the three natural capital stocks (Fig. S1).

Table S1.

Maturity rates and weights at age in stock (56). NA stands for not applicable

Age, y	1	2	3	4	5	6	7	≥8
Maturity, % of mature stock
Cod	0.00	0.13	0.36	0.83	0.94	0.96	0.96	0.98
Sprat	0.17	0.93	1.00	1.00	1.00	1.00	1.00	1.00
Herring	0.00	0.70	0.90	1.00	1.00	1.00	1.00	1.00
Average weight 2008–2013, g
Cod	NA	179	366	827	997	1,279	1,898	2,216
Sprat	5	9	10	11	11	11	12	12
Herring	13	22	28	32	37	41	46	51

NA, not applicable.

Table S7.

Fixed biomass at age shares based on the 2008–2013 data from ref. 56

Age, y	1	2	3	4	5	6	7	≥8
Cod	Not included	0.158	0.234	0.311	0.166	0.074	0.034	0.023
Sprat	0.293	0.310	0.181	0.095	0.064	0.031	0.014	0.012
Herring	0.184	0.216	0.176	0.140	0.108	0.077	0.043	0.056

Fig. S1.

The figure compares the original (circles) and smoothed (curves) simulations. A shows the ecological system, and B shows net revenue.

Table S2.

Recruitment function coefficients (SEs) based on 1974–2014 data

Species	αi: Intrinsic growth rate	βi: Density dependence	γi: Environmental impact
Cod	0.382*** (0.086)	−1.32 × 10−3*** (2.78 × 10−4)	0.304*** (0.052)
Sprat	4.745* (0.253)	−4.22 × 10−4*** (2.35 × 10−4)	NA
Herring	3.574*** (0.134)	−6.74 × 10−4*** (1.32 × 10−4)	NA

Cod recruitment dependent on environmental conditions is described by the average deep water salinity (*10% of significance level; ***1% of significance level). The source data are from ref. 56. NA, not applicable.

SI Text

Derivation of Natural Capital Asset Prices for Multiple Interacting Stocks.

Let $s^i\left(t\right)$ be the $i$ th natural capital stock of an $N$ stock ecosystem, and let $d{s}^i/dt$ describe the change in the capital stock i through time:

$$\frac{d{s}^i}{dt}={\dot{s}}^i=G^i(\mathit{s}\left(t\right))-f^i(\mathit{s},\mathit{x}(\mathit{s}\left(t\right))),\hspace{0.17em}i=1,\cdots ,N,$$ [S1]

where superscripts are indices;, $\mathit{s}\left(t\right)=\left(s^1\left(t\right),s^2\left(t\right),\cdots ,s^N\left(t\right)\right)$ is a vector of multiple (natural) capital stocks at time $t$, and $G^i$ is a growth function for stock $i$, which can be a function of other natural capital stocks. For example, in a biological system, $G$ includes prey–predator relationships. The function $f^i$ is an anthropogenic impact function (e.g., harvesting behavior) on stock $i$. The vector $\mathit{x}$ represents human feedback responses shaped by governing institutions. Specifically, define $M\left(\mathit{s},\mathbf{\Omega }\right)$ as a time-autonomous economic program that accounts for the vector of capital stocks and a vector of parameters defining institutional arrangements, $\mathbf{\Omega }$ (19, 23), that maps into a vector-valued function $M:\left(\mathit{s}\left(t\right),\mathbf{\Omega }\right)\to \mathit{x}\left(\mathit{s}\left(t\right);\mathbf{\Omega }\right)$, where the length of $\mathit{x}$ is $L$ and is not necessarily equal to the length of $\mathit{s}$. We suppress the parameter vector $\mathbf{\Omega }$ when doing so does not cause confusion. To clarify, in a fishery, $f^i$ may be harvest of species $i$, whereas $\mathit{x}$ may include decisions, such as time at sea and gear choices, that combine with stock $s^i$ to lead to $f^i$.

Define $D\left(\mathit{s}\left(t\right),\mathit{x}\left(\mathit{s}\left(t\right)\right)\right)$ as an index of the net benefits or dividends flowing to society at time $t$. Suppressing the dependence on time, assume that $D\left(\mathit{s},\mathit{x}\left(\mathit{s}\right)\right)$ is measured in stable monetary terms, so that discounting at a constant exponential rate is justified (49). At a time $t$, the present value of net benefits is

$$V\left(\mathit{s}\left(t\right)\right)=\underset{t}{\overset{\infty }{{\displaystyle \int }}}{e}^{-\delta \left(\tau -t\right)}D\left(\mathit{s}\left(\tau \right),\mathit{x}\left(\mathit{s}\left(\tau \right)\right)\right)d\tau .$$ [S2]

The term $\delta$ is the social discount rate (e.g., the US Office of Management and Budget rate of 3%) (50). Substituting $\mathit{x}\left(\mathit{s}\right)$, it is possible to redefine $D$ over the stock vector $\mathit{s}$, so that $D^{\ast }\left(\mathit{s}\left(\tau \right)\right)\equiv D(\mathit{s}\left(\tau \right),\mathit{x}(\mathit{s}\left(\tau \right)))$, where the asterisk indicates the elimination of $\mathit{x}$. We slightly abuse notation and assume that the partial derivative of $D$ includes the feedback through the economic program: $D_{s^i}^{\ast }=D_{s^i}(\mathit{s}\left(\tau \right),\mathit{x}(\mathit{s}\left(\tau \right)))=\partial D/\partial s^i+\left({\nabla }_{\mathit{x}}D\right)\prime d\mathit{x}/d{s}^i$, where ${\nabla }_{\mathit{x}}D$ is the gradient vector of $D$ with respect to $\mathit{x}$, $d\mathit{x}/d{s}^i$ is the $(L\times 1$) derivative vector of $\mathit{x}$ with respect to $s^i$, and $\prime$ indicates transpose. A similar substitution of the economic program into $f^i$ yields $f^i\left(\mathit{s},x\left(\mathit{s}\right)\right)=f^{i\ast }\left(\mathit{s}\right),\hspace{0.17em}\text{so}\hspace{0.17em}\text{that}\hspace{0.17em}{f}_{s^i}^i=\partial f^i/\partial s^i+\left({\nabla }_{\mathit{x}}{f}^i\right)\prime d\mathit{x}/d{s}^i=f_{s^i}^{i\ast }$. To be clear, the first step is substituting in the economic program. Therefore, although the second term looks like it comes from a total derivative, it is in fact just an application of the chain rule.

Substitution of the economic program into $D$, the assumption of an infinite time horizon, and assuming that the resource dynamics (Eq. S1) and economic program are time-autonomous enable $V$ to be expressed solely as a function of $\mathit{s}\left(t\right)$. The shadow price of stock $i$ at time $t$ for a given economic program is

$$p^i(\mathit{s}\left(t\right))\equiv \frac{\partial V\left(\mathit{s}\left(t\right)\right)}{\partial s^i\left(t\right)}.$$ [S3]

Note that $p^i$ is a function of all stocks, $\mathit{s}$, rather than a single stock. Each stock can impact $D$, the stock dynamics, and the feedback rules embodied in $\mathit{x}$. The asset price of $p^i$ includes cross-stock effects (Eq. 1).

Following the works by Dasgupta and Maler (32) and Arrow et al. (44) and adopting the definition (Eq. S3), we differentiate $V\left(\mathit{s}\left(t\right)\right)$ with respect to $t$ and express it as

$$\frac{dV}{dt}=\delta V-D\left(\mathit{s},\mathit{x}\left(\mathit{s}\right)\right)={\left({\nabla }_{\mathbf{s}}V\right)}^{\prime }\frac{d\mathit{s}}{dt}=\mathit{p}\left(\mathit{s}\right)\prime \frac{d\mathit{s}}{dt},$$ [S4]

where ${\nabla }_{\mathbf{s}}V$ is a ($N\times 1)$ gradient vector, $d\mathit{s}/dt$ is an ($N\times 1)$ Jacobian matrix, and $\mathit{p}=\left(p^1\left(\mathit{s}\right),p^2\left(\mathit{s}\right),\cdots ,p^N\left(\mathit{s}\right)\right)$ is an ($N\times 1)$ shadow price vector. Eq. S4 states that the time rate of change of the present value of benefits is equal solely to the effect from changes in the natural capital stocks evaluated at appropriate prices (19) or $dIW/dt=\mathit{p}\prime \dot{\mathit{s}}=dV/dt$. Rearranging the terms in Eq. S4,

$$\delta V=D\left(\mathit{s},\mathit{x}\left(\mathit{s}\right)\right)+\mathit{p}\left(\mathit{s}\right)\prime \dot{\mathit{s}}=H\left(\mathit{s},\mathit{x},\mathit{p}\right)=H^{\ast }(\mathit{s},\mathit{p}).$$ [S5]

$H^{\ast }(\mathit{s},\mathit{p})$ is the current value Hamiltonian as evaluated along the economic program $\mathit{x}\left(\mathit{s}\right)$, and it is composed of the flow of current benefits, $D\left(\mathit{s},x\left(\mathit{s}\right)\right)$, and the value of increments to the stocks, $\mathit{p}\prime \dot{\mathit{s}}$.

Dividing by $\delta$ on both sides, Eq. S5 yields

$$V\left(\mathit{s}\right)={\delta }^{-1}\left(D\left(\mathit{s},\mathit{x}\left(\mathit{s}\right)\right)+\mathit{p}\left(\mathit{s}\right)\prime \dot{\mathit{s}}\right),$$ [S6]

which Shapiro and Stiglitz (51) call the fundamental asset equation. Differentiating Eq. S6 with respect to $s^i$,

$$p^i\left(\mathit{s}\right)=\frac{D_{s^i}(\mathit{s},\mathit{x}\left(\mathit{s}\right))+\left(\frac{\partial p^i}{\partial s^i}{\dot{s}}^i+{\displaystyle \sum _{j\ne i}^N\frac{\partial p^j}{\partial s^i}{\dot{s}}^j}\right)+{\displaystyle \sum _{j\ne i}^N{p}^j\frac{\partial {\dot{s}}^j}{\partial s^i}}}{\delta -\left(G_{s^i}^i\left(\mathit{s}\right)-f_{s^i}^i\left(\mathit{s},\mathit{x}\left(\mathit{s}\right)\right)\right)}.$$ [S7]

After creating the definitions $M{D}^i\equiv D_{s^i}$, $M{G}^i\equiv G_{s^i}^i$, and $MH{I}^i\equiv f_{s^i}^i$ to preserve consistency with ref. 18, Eq. S7 is identical to Eq. 1.

The cross-price term, $\partial p^j/\partial s^i$, determines whether two stocks are capital complements or substitutes. Assuming that increasing stock $i$ raises the value of $V\left(\mathit{s}\right)$ (i.e., stock $i$ is an asset), then stocks $i$ and $j$ are only complements if $V_{s^i{s}^j}\left(\mathit{s}\right)=\partial p^i\left(\mathit{s}\right)/\partial s^j>0$. That is, endowing the system with more of stock $j$ makes stock $i$ more valuable. The reverse would be true if the stocks were substitutes, because the idea that stock $j$ is a substitute for $i$ implies that it can replace stock $i$, thereby lowering stock $i$’s marginal value. We explore the slope of the level sets of the shadow price of $p^i=V_{s^i}$ in stocks $i$ and $j$ by invoking the implicit function theorem: $d{s}^j/d{s}^i=-\left(V_{s^i{s}^i}/V_{s^i{s}^j}\right)$, where $V_{s^i{s}^i}=\partial p^i/\partial s^i$ and $V_{s^i{s}^j}=\partial p^i/\partial s^j$. Assuming that $\partial p^i/\partial s^i<0$, a result that Fig. 2 shows holds in our case study, then $\partial p^i\left(\mathit{s}\right)/\partial s^j>0$ implies upward sloping contours in state space for the case of complements. The reverse is true for the case of substitutes. However, the value of $\partial p^i/\partial s^j$ must be recovered jointly with shadow prices, and the shadow prices themselves are not obvious ex ante.

Approximating Shadow Prices.

We use a polynomial approximation approach following refs. 18, 52, and 53 to approximate solutions to Eqs. S2 and S3. The function approximation uses a linear combination of a series of nonlinear basis functions evaluated at a finite number of points in state space (53). We use Chebyshev polynomials for the basis functions. Chebyshev polynomials are used, because they have desirable orthogonality properties that enable them to provide the lowest error approximations to unknown functions, while also offering multiple differentiability (54, 55).

First, we located the evaluation nodes by specifying M univariate evaluation points for each of the N state variables and then calculated $D$ and ${\dot{s}}^i$ at all combinations of these points. The evaluation nodes were selected by finding the $M$ roots of each unidimensional Chebyshev polynomial on the bounded approximation interval of each state variable. Node coordinates were then combined to locate a node in multidimensional space. We define ${\phi }^i$ as the $M\times \left(q^i+1\right)$ univariate basis matrix of $q^i$ th degree over bounded ranges for each state variable. We expand the univariate bases matrices to allow for approximation over the bounded ${\mathrm{ℝ}}^N$ domain by finding the tensor product across dimensions to form an $M^N\times {\displaystyle {\prod }_{i=1}^N(q^i+1)}$ basis matrix: $\mathrm{\Phi }\left(\mathit{S}\right)={\phi }^N\otimes {\phi }^{N-1}\otimes \cdots \otimes {\phi }^1$, where $\mathit{S}$ is the $M^N\times N$ matrix of evaluation points (i.e., all grid nodes of $M$ evaluation points for all N state variables), and ⊗ is the Kronecker product.

Second, we let $V^k\left(\mathit{S}\right)\approx {\mathrm{\Phi }}^k\left(\mathit{S}\right)\mathit{\beta }$, where $k=1,\dots ,M^N$ indexes the $M^N$ distinct capital stock vectors (i.e., individual evaluation points in an N-dimensional grid) formed by the tensor product basis, ${\mathrm{\Phi }}^k\left(\mathit{S}\right)$ is the kth row of $\mathrm{\Phi }\left(\mathit{S}\right)$, and $\mathit{\beta }$ is a ${\displaystyle {\prod }_{i=1}^N(q^i+1)}\times 1$ vector of unknown approximation coefficients. Stacking these $M^S$ vector equations, we obtain the matrix equation:

$$V\left(\mathit{S}\right)=\left[\begin{array}{c}{\text{V}}^1\left(\mathit{S}\right)\\ \begin{array}{c}⋮\\ {\text{V}}^k\left(\mathit{S}\right)\\ ⋮\end{array}\\ {\text{V}}^{{\text{M}}^{\text{N}}}\left(\mathit{S}\right)\end{array}\right]\approx \left[\begin{array}{c}{\mathrm{\Phi }}^1\left(\mathit{S}\right)\\ \begin{array}{c}⋮\\ {\mathrm{\Phi }}^k\left(\mathit{S}\right)\\ ⋮\end{array}\\ {\mathrm{\Phi }}^{M^N}\left(\mathit{S}\right)\end{array}\right]\mathit{\beta }=\mathrm{\Phi }\left(\mathit{S}\right)\mathit{\beta }.$$ [S8]

Using Eq. S5 and the fact that $\partial V/\partial s^i\left(\mathit{S}\right)=p^i\left(\mathit{S}\right)\approx (\partial \mathrm{\Phi }\left(\mathit{S}\right)/\partial s^i)\mathit{\beta }$, we obtain $\delta \mathrm{\Phi }\left(\mathit{S}\right)\mathit{\beta }\approx D\left(\mathit{S}\right)+{\displaystyle {\sum }_{i=1}^{S}diag\left({\dot{s}}^i\right)(\partial \mathrm{\Phi }\left(\mathit{S}\right)/\partial s^i)\mathit{\beta }}$. Now let $M^N>{\displaystyle {\prod }_{i=1}^N(q^i+1)}$, so that it is not possible to satisfy the equality exactly at all approximation points. If we minimize the sum of squared approximation errors, then the resulting solution for $\mathit{\beta }$ is

$$\mathit{\beta }={\left(\text{Ψ}{\left(\mathit{S}\right)}^{\prime }\text{Ψ}\left(\mathit{S}\right)\right)}^{-1}\text{Ψ}{\left(\mathit{S}\right)}^{\prime }D\left(\mathit{S}\right),$$ [S9]

where $\mathrm{\Psi }\left(\mathit{S}\right)=\delta \mathrm{\Phi }\left(\mathit{S}\right)-{\displaystyle {\sum }_{i=1}^{N}diag\left({\dot{s}}^i\right)\partial \mathrm{\Phi }\left(\mathit{S}\right)/\partial s^i}$.

With solutions for $\mathit{\beta }$ in hand, we now have the ability to calculate the shadow prices at any vector of capital stocks in the approximation domain $\mathit{s}$ through evaluation of the partial derivative of the basis vector: $p^i\left(\mathit{s}\right)\approx (\partial \mathrm{\Phi }\left(\mathit{s}\right)/\partial s^i)\mathit{\beta }$. We implement the approximation using the R package {capn}, which is available at environment.yale.edu/profile/eli-fenichel/software.

Baltic Sea Model Adaptation Details.

We adopt Hutniczak’s (40) ecological–economic model of the Baltic Sea fishery that contains multiple agent and species interactions and follow her description of institutional arrangements. In this model, changes in the ecosystem result from species growth, predation, and individual fishing vessels’ behaviors under a set of regulatory rules. Regulators annually set species-specific TACs based on single-species stock assessments and target fishing mortalities. Harvest allocations are distributed among vessels in the form of individual nontransferable quotas. We assume that vessels in the fishing fleet seek to maximize current net revenue through harvest choices—subject to regulations, physical constraints, owned capital, production structure, individual technical efficiency, and available stock abundance.

The biological component of the model includes age-structured submodels for cod, herring, and sprat linked through predation as described in appendix A of ref. 40. The International Council for the Exploration of the Sea (ICES) provides annual stock assessments for major Baltic Sea species. The model parameters (tables A1, A3, A4, and A6 of ref. 40) are updated based on the Report of the Baltic Fisheries Assessment Working Group (56) and available in Tables S1–S3.

Table S3.

Harvest parameters estimated from data from ref. 56 for years 2008–2013

Age, y	1	2	3	4	5	6	7	≥8
Selectivity—cod	NA	0.072 (0.014)	0.325 (0.031)	0.297 (0.028)	0.355 (0.024)	0.331 (0.051)	0.280 (0.064)	0.270* (0.085)
Selectivity—sprat	0.085 (0.009)	0.170 (0.012)	0.209 (0.016)	0.231 (0.012)	0.247 (0.011)	0.261 (0.017)	0.221 (0.025)	0.227 (0.027)
Selectivity—herring	0.026 (0.004)	0.056 (0.006)	0.093 (0.007)	0.119 (0.011)	0.130 (0.011)	0.150 (0.017)	0.189 (0.018)	0.174 (0.015)
Discard multiplier—cod	NA	2.038 (0.190)	1.314 (0.057)	1.152 (0.021)	1.122 (0.026)	1.059 (0.027)	1.028 (0.022)	1.014 (0.016)

SEs are in parentheses. All estimates are significant at the 99% confidence level, except those indicated (*significant at the 95% confidence level). NA, not applicable.

The largest and only conceptual change in the current biological model relative to ref. 40 is that we follow the Report of the Benchmark Workshop on Baltic Multispecies Assessment (57) approach, and we estimate weight of cod recruitment (w_a,t; a = 2) as a function of parental weight (w_SSB) in addition to weight of adult cod (w_a,t; a ≥ 3) as a function of the amount of prey available, with $a$ indicating age.

$$w_{a,t}={\psi }_1+{\psi }_2\text{ln}\left(w_{SSB,t-2}\right);a\in \left[2\right]$$ [S10a]

$$w_{a,t}=w_{a-1,t-1}\left({\theta }_{a-1}+\frac{{\left({\displaystyle \sum _{i\in \left(z,h\right)}{\displaystyle \sum _{a=1}^8{y}_{i,a,t}}}\right)}^n}{{\left({\displaystyle \sum _{i\in \left(z,h\right)}{\displaystyle \sum _{a=1}^8{y}_{i,a,t}}}\right)}^n+{K_{sh}}^n}\right);a\in \left[\mathrm{3,8}\right].$$ [S10b]

The subscripts $z$ and $h$ indicate prey species (sprat and herring, respectively); furthermore, $y$ is the biomass, $K_{sh}$ is the half-saturation constant, $n$ is a functional response constant, and Greek letters are estimated parameters. Eqs. S10a and S10b are jointly estimated by generalize methods of moments with robust SEs using cod weight based on 1991–2014 data (56). Estimated parameters are provided in Table S4, and details on constants can be found in the work by Hutniczak (40).

Table S4.

Cod growth function coefficients estimated from the 2008–2013 data from ref. 56

Coefficient	ψ1	ψ2	ϑ2	ϑ3	ϑ4+
Value	0.215***	0.119***	1.464***	1.717***	0.803***
SEs	−0.002	−0.009	−0.022	−0.013	−0.006

^***At 1% of significance level.

The commercial harvest model closely follows the work by Hutniczak (40). Vessels operate as decision-making units that seek to maximize net revenue constrained by quota allocations, stock levels, and vessel characteristics, including technical efficiency constraints, through adjusting fishing behavior. The input requirement, the amount of effort required to land the chosen species composition in units of days at sea, is estimated with one-way fixed effects to account for the heterogeneity in fleet input efficiency, and estimation results are given in Table S5. This method offers the advantage of enabling us to account for effects, such as costly targeting and joint production. Landing price data calculated in 2013 Euros (EUR) are provided in Table S6. Data come from the Polish Fisheries Monitoring Centre in Gdynia, the Polish Marine Institute in Gdynia, and the 2015 Annual Economic Report on the European Union (EU) Fishing Fleet (36).*

Table S5.

Input requirement coefficients

Coefficient	Vessels ≥12 m		Vessels 8–11.99 m
${\alpha }_c$	0.162 (0.026)	***	0.311 (0.029)	***
${\alpha }_h$	0.164 (0.033)	***	0.017 (0.029)
${\alpha }_s$	0.154 (0.034)	***	NA
${\alpha }_o$	0.109 (0.025)	***	0.115 (0.029)	***
${\alpha }_k$	−1.031 (0.464)	**	−0.098 (0.211)
${\alpha }_{cc}$	0.042 (0.007)	***	0.058 (0.007)	***
${\alpha }_{ch}$	−0.004 (0.002)	*	−0.012 (0.003)	***
${\alpha }_{cs}$	−0.006 (0.003)	**	NA
${\alpha }_{co}$	−0.010 (0.002)	***	−0.041 (0.004)	***
${\alpha }_{hh}$	0.046 (0.008)	***	−0.001 (0.008)
${\alpha }_{hs}$	−0.011 (0.003)	***	NA
${\alpha }_{ho}$	−0.009 (0.003)	***	−0.020 (0.003)
${\alpha }_{ss}$	0.051 (0.009)	***	NA
${\alpha }_{so}$	−0.011 (0.003)	***	NA
${\alpha }_{oo}$	0.026 (0.006)	***	0.042 (0.006)	***
${\alpha }_{kk}$	0.651 (0.934)		−0.049 (0.428)
${\alpha }_{kc}$	−0.074 (0.017)	***	−0.018 (0.015)
${\alpha }_{kh}$	−0.048 (0.028)	*	0.028(0.016)	*
${\alpha }_{ks}$	0.014 (0.023)		NA
${\alpha }_{ko}$	−0.021 (0.025)		−0.025 (0.017)
Fixed effects
Individual	Yes		Yes
Time	No		No

NA, not applicable.

^*At 10% of significance level.

^**At 5% of significance level.

^***At 1% of significance level.

Table S6.

Summary of the landing price data in 2013 Euros per 1 kg fresh weight

Vessel length, m	Cod	Herring	Sprat	Other
8–9.99	1.261	0.427	0.318	1.164
10–11.99	1.280	0.388	0.358	0.610
12–17.99	1.147	0.370	0.274	0.434
18–23.99	1.104	0.340	0.270	0.431
≥24	1.055	0.362	0.275	0.527

The source data are from ref. 36.

We forecast two target fishing mortality scenarios. First, we consider BAU, which models historical and current policy. The fishing mortality rates associated with this case are 0.30, 0.26, and 0.29 for cod, herring, and sprat, respectively. Second, we adopt the MMSY approach suggested by the ICES (57) and planned for implementation in 2017. The mortality rates for this case are 0.55, 0.3, and 0.3 for cod, herring and sprat, respectively (40).

Data Generation.

To implement the shadow price approximation approach, we generate an $M^N\times (2N+1)$ matrix of simulated (pseudo)data. There are $M^N$ evaluation nodes, $N$ columns of stock levels (three in our case study), $N$ columns of changes in stock with respect to time ${\dot{s}}^i$ (three in the case study), and a column of dividend flows, $D$. The $M^N\times (2N+1)$ matrix must span over all regions of the state space for which we wish to calculate shadow prices (i.e., all combinations of stocks for each species). In practice, such data are rarely available, because observational time series data from ecological–economic systems rarely sample very broadly through the state space. “Pseudodata” generated by models can fill this gap—while also ensuring that the resulting data are consistent with the underlying bioeconomic model of the system (37).

Before generating the pseudodata, we must establish the domain that those data fill. This domain must be defined sufficiently broadly, so that it fully captures the system dynamics originating from any stock level for which one wants to produce a shadow price. We established the steady-state stock vector by simulating from 2013 initial conditions. By year 50 (2063), the stocks of the three species are stable at [cod, herring, sprat] = [439, 1,163, 1,252] thousand metric tons under the BAU scenario and [cod, herring, sprat] = [364, 1,585, 1,864] thousand metric tons under the MMSY scenario. In addition to these steady-state vectors, we also considered the range of the transition path to the steady state from the observed 2013 stocks [cod, herring, sprat] = [175, 1,303, 1,753] thousand metric tons as well as the recent range of the stocks in defining the domain for generating pseudodata.

For herring, we set the lower bound at 60% of the BAU steady-state biomass (698 thousand metric tons) and the upper bound at 140% of the BAU steady-state biomass (1,628 thousand metric tons). For sprat, we set the lower bound at 60% of the BAU steady-state biomass (751 thousand metric tons) and the upper bound at 160% of the BAU steady-state biomass (2,128 thousand metric tons). A greater relative range was used for sprat because of the large initial stock size. These ranges do a good job of capturing the full future projected trajectory and a large fraction of the historical stock sizes. The 2013 stock of cod and the recent historical cod biomass have been substantially lower than the steady state. Therefore, we set the lower cod bound at 130 thousand metric tons and the upper cod bound at 800 thousand metric tons, which capture both the recent history and projection values. The lower and upper bounds of domains also safely cover the range of the MMSY scenario.

Having established the domain, we generate a 20th-order three-dimensional Chebyshev polynomial defined over the domain for each of the three species and use the combined roots of these polynomials to establish 8,000 points at which to simulate the model. At each of these 8,000 simulation nodes, we simulate profit, $D,$ and growth rates, ${\dot{s}}^i$. We use fixed biomass at age shares based on 2008–2013 averages to map the full age-structured model into a biomass dynamic model (Table S7). For estimates requiring a two period lag (e.g., cod recruitment), we use the same biomass at t − 1 and t.

The bioeconomic simulation model solves for net revenue maximizing fishing effort for all individual Polish fishing vessels active in 2012. Then, for $D$, we sum over the fleet at each simulation node. We scale these predictions using multipliers, assuming that the Polish fleet is representative of the other fleets fishing in the Baltic Sea, to translate these sample results on fishing behavior and economic returns to the entire Baltic Sea fleet. We use fixed shares based on 2012 TAC distribution between EU members: 0.30 for cod, 0.28 for herring, and 0.29 for sprat. Our shares approach is justified, because allocation among EU members is based on the principle of relative stability, which implies that each country receives a fixed share of each TAC (58), and similarity of the composition of EU fleets participating in the Baltic Sea harvest (36). The results for the Polish fleet indicate that TAC utilization can vary considerably with changing individual quotas and biomass levels. The underutilization of TAC occurring in our model is an expected response to varying harvest conditions that cause lack of profitability for some quota combinations. Annual ICES reports show that historical TAC utilization was ∼39–89% (2010–2015^†) for cod, ∼35–109% (1989–2015) for herring, and ∼41–103% (1987–2015) for sprat between 2008 and 2012. Our simulation results suggest that the TAC utilizations from our simulation model fall within realistic ranges.

The 8,000 simulation nodes create a somewhat “bumpy” surface linking the status of the three species, the economic program $\mathit{x}\left(\mathit{s}\right)$, and hence, simulated profit $D$ and growth rate ${\dot{s}}^i$. These irregularities create numerical issues for shadow price approximation because of their tendency to produce locally unstable estimates of derivatives. This bumpiness occurs, because the simulation compresses the decisions of 411 representative vessels over a state space of 24 age categories for three species down to three dimensions. The discrete changes of vessel behavior across this large, but finite, number of vessels at critical stock thresholds create small but nontrivial discontinuities in overall effort predictions from the simulations. The bumpiness of the implied surface can be viewed as a surface with discrete jumps that lead to the Gibbs–Wilbraham phenomenon (59). The Gibbs–Wilbraham phenomenon is an overshoot in the convergence of a functional approximation (i.e., Gibbs oscillations) in the neighborhood of a discontinuity of the function being approximated (60). High-dimensional Chebyshev approximations can be particularly vulnerable to Gibbs oscillations when fitted to a discrete sample of nodes (59).

To avoid these numerical problems, we avoid approximating the shadow prices on the raw pseudodata, but instead, we fit smooth, locally well-fitting surfaces for $D$ and ${\dot{s}}_i$ and use the predictions from these fitted surfaces for the approximation of shadow prices. To accomplish this smoothing, we use the linear spline local fitting method applied to the 8,000 simulation nodes. This method performs well and demands fewer parameters compared with other options. The bandwidths are selected using cross-validation for each $D$ and ${\dot{s}}^i$ linear spline. Adopting the fitted splines, we smooth the simulated population dynamics of each species using a linear approximation [$s^i\left(t+1\right)\approx s^i\left(t\right)+{\widehat{\dot{s}}}^i\left(t\right)$] and predicted profit [$\widehat{D}\left(t\right)$], where carets indicate the function relationship based on the splines. The percentage root mean square errors of three ${\dot{s}}^i$ (cod, herring, and sprat) and $D$ are 5.78, 1.63, 0.48, and 0.71%, respectively, for the BAU and 1.07, 1.62, 0.56, and 0.51%, respectively, for the MMSY. This smoothing process provides reasonable derivatives, while capturing the overwhelming majority of information contained in the pseudodata. We compare simulation results from the original model with the smoothed model based on the linear splines, which are repeated from Fig. 1 (Fig. S1). An alternative to our smoothing approach would be to use a denser set of simulation nodes for the shadow price approximation. This alternative would further smooth the surface, allowing the shadow price approximation to occur without additional intermediate steps. However, generating the pseudodata requires that each of the 411 vessels solve a constrained optimization problem at each time step. It currently takes 21.7 h to generate the 8,000 nodes using 40 processors (48 gigabytes of random access memory) on the high-performance Omega computing cluster at the Yale Center for Research Computing. Our approach of fitting a smoothed model on a smaller set of nodes provides a computationally efficient approach that likely will be necessary for ecosystem management models with dimensions beyond our three-species model.