Manipulating the ABCs of self-assembly via low-χ block polymer design

Significance

Molecular sequence and interactions dictate the mesoscale structure of all self-assembling soft materials. Block polymers harness this relationship to access a rich variety of nanostructured materials but typically require energetically unfavorable (high-χ) interactions between blocks. Contrary to this convention, we demonstrate that ABC triblock terpolymers featuring low-χ interactions between end blocks can self-assemble into a unique mixed morphology that subverts the demands of chain connectivity. As a consequence of block–block mixing, the characteristic length scales of these self-assembled structures exhibit an unusual trend: As the total polymer size increases, the domain spacing decreases. These developments expand the vocabulary of block polymer design and open additional avenues for manipulating the self-assembly of synthetic macromolecules.

Abstract

Block polymer self-assembly typically translates molecular chain connectivity into mesoscale structure by exploiting incompatible blocks with large interaction parameters (χ_ij). In this article, we demonstrate that the converse approach, encoding low-χ interactions in ABC bottlebrush triblock terpolymers (χ_AC $\mathrm{\lesssim }$ 0), promotes organization into a unique mixed-domain lamellar morphology, which we designate LAM_P. Transmission electron microscopy indicates that LAM_P exhibits ACBC domain connectivity, in contrast to conventional three-domain lamellae (LAM₃) with ABCB periods. Complementary small-angle X-ray scattering experiments reveal a strongly decreasing domain spacing with increasing total molar mass. Self-consistent field theory reinforces these observations and predicts that LAM_P is thermodynamically stable below a critical χ_AC, above which LAM₃ emerges. Both experiments and theory expose close analogies to ABA′ triblock copolymer phase behavior, collectively suggesting that low-χ interactions between chemically similar or distinct blocks intimately influence self-assembly. These conclusions provide fresh opportunities for block polymer design with potential consequences spanning all self-assembling soft materials.

Block polymers are a diverse class of soft materials capable of self-assembling into complex periodic nanostructures. Synthetic command over composition, dispersity, sequence, and molecular architecture enables control over the mesoscopic order and macroscopic thermal, mechanical, rheological, and transport properties (1–4). The phase behavior of “simple” linear AB diblock copolymers is universally parameterized by the segregation strength χ_ABN and relative volume fraction f, where χ_AB represents the effective Flory–Huggins binary interaction parameter and N is the total volume-averaged degree of polymerization. Mixing behavior, captured through the mean-field concept of χ_AB, is central to block polymer self-assembly: the competing demands of minimizing interfacial energy and maximizing configurational entropy only favor microphase separation when A–B interactions are repulsive (χ_AB > 0) (5, 6). Extension to higher-order multiblock polymers introduces additional interaction parameters (χ_ij) that impact self-assembly and properties (7). For example, introducing a mutually incompatible C block (χ_AC > 0, χ_BC > 0) generates a host of new morphologies dictated by the chain connectivity (ABC, ACB, or BAC) and intrinsic χ_ij-values (8, 9). In this rich phase space, designing multiblock polymers with a combination of miscible and immiscible blocks can also access new structures and impart useful functions (10, 11). Perhaps the best-known examples of such systems are linear ABA′ triblock copolymers (χ_AB > 0, χ_AA′ ≈ 0): their high-value industrial applications as thermoplastic elastomers are entirely enabled by A/A′ mixing and chain connectivity, which together create physically cross-linked materials with excellent processability and mechanical properties (12). The self-assembly of yet more complex systems, including ABA′C tetrablock polymers (13, 14) and A_n(BA′)_m heteroarm star polymers (15), is also crucially determined by A/A′ miscibility. These examples illuminate interesting parallels and contrasts between block polymer phase behavior and protein self-assembly. Nature delivers exquisite control over protein folding by precisely tailoring amino acid sequences and intramolecular interactions that are often attractive (e.g., hydrogen bonding), whereas block polymer design to date exploits simple molecular connectivity and primarily repulsive interactions (χ > 0) to induce microphase separation.

Previous reports have investigated the role of negligible (χ ∼ 0) or attractive (χ < 0) intermolecular interactions on the phase behavior of various homopolymer (AB/A′) (16, 17) and block polymer (AB/A′C) (18, 19) blends. In contrast, studies in which the macromolecules themselves are intramolecularly encoded with miscible blocks are to the best of our knowledge limited to the aforementioned A/A′ self-similar interactions. In this report, we study ABC bottlebrush triblock terpolymers with grafted poly(_D,L-lactide), poly(styrene), and poly(ethylene oxide) side chains (LSO), featuring low-χ interactions (χ_AC $\mathrm{\lesssim }$ 0) between distinct A and C end blocks. These materials generate a unique mixed morphology with atypical mesoscopic domain connectivity, which we denote LAM_P. Additionally, under certain conditions of molecular asymmetry, another consequence of low-χ design manifests in decreasing domain spacing with increasing total molar mass. Valuable insight into the molecular origins of this unusual behavior is achieved by comparison with analogous ABA′ brush triblock copolymers––grafted poly(_D,L-lactide)-block-poly(styrene)-block-poly(_D,L-lactide) (LSL′)––and self-consistent field theory (SCFT). The experimental and theoretical conclusions described herein regarding low-χ block polymers reveal unexpected breadth in self-assembly and should create new opportunities for molecular and materials design.

Results and Discussion

Synthesis and Structure of Low-χ Block Polymers.

ABC and ABA′ brush triblock polymers containing grafted poly(_D,L-lactide) (PLA, A block), polystyrene (PS, B block), and poly(ethylene oxide) (PEO, C block) side chains were synthesized by ring-opening metathesis polymerization (ROMP) (20–22). The living nature and synthetic utility of ROMP enable the formation of well-defined block polymers with precisely controlled molar mass, narrow molar mass dispersity, and diverse pendant functionalities. Synthetic details (SI Appendix, Scheme S1), characterization data (SI Appendix, Tables S1 and S2), and size-exclusion chromatograms (SI Appendix, Figs. S1–S3) for all samples are provided. Fig. 1 illustrates the molecular structure of the LSO and LSL′ brush triblock polymers studied herein and highlights the relative interaction parameters dictated by block chemistry and sequence. Both LSO and LSL′ feature low-χ interactions between the end blocks (χ_AC, χ_AA′ $\mathrm{\lesssim }$ 0), which in particular distinguish LSO from typical frustrated ABC triblock polymers that include similar relative χ-values but highly unfavorable A/C interactions (χ_AC >> 0) (9, 23). N_A, N_B, and (N_C or N_A′) indicate the number-average degrees of polymerization through the polynorbornene backbone for blocks containing PLA, PS, and (PEO or PLA) grafts, respectively. All LSO and LSL′ triblock polymers were annealed at 140 °C under modest applied pressure, and the ordered structures that developed were identified by synchrotron small-angle X-ray scattering (SAXS) (e.g., see SI Appendix, Fig. S4).

Fig. 1.

Molecular structures and relative interaction parameters for (A) LSO and (B) LSL′ brush triblock polymers.

SCFT.

SCFT, generally regarded as the state of the art for block polymer melts (24), was used to model our polymers and provide insight into their self-assembly. The standard model for branched polymers was modified to account for the strong steric interactions that occur in bottlebrushes due to the high grafting density of the side chains, as was done previously for similar bottlebrush block polymers (25). Gaussian chains were used to represent the N = N_A + N_B + N_C (LSO) or N = N_A + N_B + N_A′ (LSL′) side chains, and the volumes and unperturbed end-to-end lengths of the side chains were set to known literature values (26, 27). For the backbone, a worm-like chain of fixed persistence length was used to handle the strong lateral tension that occurs due to side-chain crowding. The interactions between the three side-chain species (PLA, PS, and PEO) were represented in the Hamiltonian by standard Flory–Huggins terms controlled by χ_LS, χ_SO, and χ_LO. The equilibrium lamellar period (d*) was obtained by minimizing the free energy (F). Additional SCFT details, including values for all parameters (SI Appendix, Table S3) and a schematic of chain dimensions (SI Appendix, Scheme S2), are provided.

Unique Domain Connectivity.

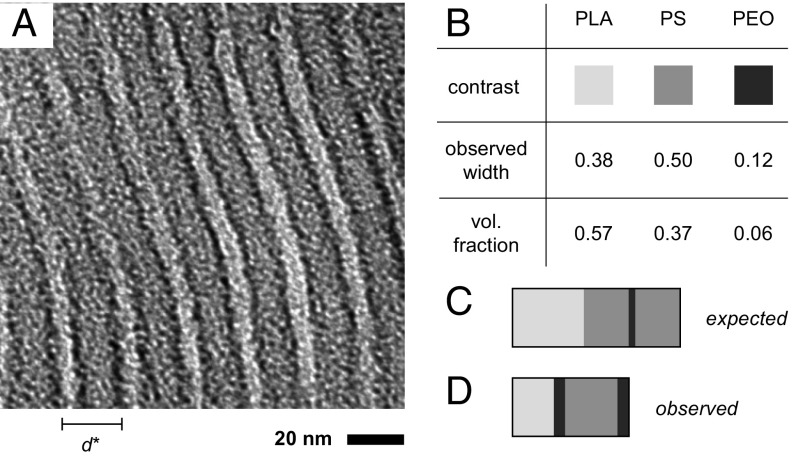
We begin by presenting data and calculations corresponding to LSO brush triblock terpolymers (Fig. 1A), then draw close analogies to LSL′ (Fig. 1B) phase behavior. All LSO materials self-assemble into well-ordered lamellar morphologies. Transmission electron micrographs of thin sections of LSO* (N_A = 28, N_B = 27, N_C = 5) stained over ruthenium tetroxide (RuO₄) vapor reveal a three-color, four-layer lamellar morphology (Fig. 2A). (Additional images are provided in the SI Appendix, Fig. S5.) Exposing L, S, and O to RuO₄ vapor results in unstained, slightly stained, and strongly stained domains, respectively, as deduced from literature results: PS is selectively stained in PLA/PS mixtures (28, 29), and PEO is stained to a greater extent than PS (30, 31). Surprisingly, the extent of staining and layer widths observed by transmission electron microscopy (TEM) are completely inconsistent with both the side-chain volume fractions measured by ¹H NMR (f_L = 0.57, f_S = 0.37, f_O = 0.06) (Fig. 2B) and the ABCB connectivity required by the expected three-domain microstructure, LAM₃ (Fig. 2C) (8, 9). The conflict between LAM₃ and the pattern observed by TEM can only be resolved by invoking partial mixing between the A and C end blocks, apparently driven by low-χ interactions (χ_AC$\mathrm{\lesssim }$0). The resulting morphology exhibits mesoscopic ACBC connectivity (Fig. 2D), consistent with the observed staining pattern. Because the three blocks are not well-segregated, the side-chain volume fractions are not required to equal the relative domain widths. Reflecting the crucial role of partial mixing, this unique morphology is herein designated LAM_P.

Fig. 2.

(A) TEM of LSO* stained with RuO₄. (B) Relative contrast from the stain, relative widths of corresponding layers observed by TEM, and side-chain volume fractions measured by ¹H NMR. (C) One LAM₃ period with the expected ABCB domain connectivity and layer widths based on data in B. (D) One LAM_P period observed in A, exhibiting mesoscopic ACBC domain connectivity.

SCFT fully supports the distinction between LAM₃ (Fig. 3A) and LAM_P (Fig. 3B), controlled primarily by the relative and absolute interaction parameters. Composition profiles for LSO* were calculated over one lamellar period using realistic PLA–PS (χ_AB ≡ χ_LS) and PS–PEO (χ_BC ≡ χ_SO) values estimated in the literature: χ_LS = 0.080 (32) and χ_SO = 0.049 (33) at 140 °C, renormalized to a common monomer reference volume (118 ų). (We note that literature χ-values obtained by fitting experimental data to mean-field approximations are often inaccurate, potentially affecting the agreement between experiment and theory (34).) PLA–PEO interactions (χ_AC ≡ χ_LO) were arbitrarily varied in the simulations, and LAM₃ is correctly predicted to occur at moderate to large χ_AC (Fig. 3C), in broad agreement with previous experimental and theoretical studies of frustrated ABC triblock terpolymers (35–37). In contrast, LAM_P exclusively emerges when χ_AC is sufficiently small to favor partial A/C block–block mixing (Fig. 3D). Using this collection of physical parameters, a first-order phase transition between LAM₃ and LAM_P was predicted to occur at a critical value χ^C = 0.009 (Fig. 3E). The mesoscopic ACBC domain connectivity and relative domain widths predicted for LAM_P perfectly match the pattern observed in Fig. 2A and reinforce the microscopic origins of mixing deduced from TEM.

Fig. 3.

Illustrations and SCFT data distinguishing LAM₃ and LAM_P morphologies. In A–D, the light-, medium-, and dark-gray layers represent PLA, PS, and PEO (or mixed PLA/PEO) domains, respectively. (A and B) LSO chain packing in (A) LAM₃ and (B) LAM_P. (C and D) SCFT composition profiles for LSO* within one normalized lamellar period (z/d₀), where ϕ(z) is the relative segment concentration of each component. (C) χ_AC > χ^C: LAM₃ with d* = 43.5 nm. (D) χ_AC < χ^C: LAM_P with d* = 25.6 nm. (E) SCFT calculations of the normalized free energy (Top) and domain spacing (Bottom) versus χ_AC ≡ χ_LO for LSO*. The transition from mixed (LAM_P) to unmixed (LAM₃) morphologies is first order, occurring at a critical value χ^C (dotted line); for χ_AB = 0.080 and χ_BC = 0.049, χ^C = 0.009.

Decreasing Domain Spacing with Increasing Total Molar Mass.

A series of LSO brush triblock terpolymers with fixed N_A = 26 and N_B = 24 (guaranteed by a common parent diblock) and variable N_C (SI Appendix, Scheme S3) highlights additional consequences of block–block mixing. N_C was varied in increments of two or four backbone repeat units, from N_C = 0 (LSO-0) to N_C = 20 (LSO-20) (SI Appendix, Table S1). (Note that, due to the high molar mass of each PEO macromonomer, the total molar mass varies by >45,000 g/mol across this series.) SAXS measurements reveal an unusual trend: as the total molar mass (M) increases over the range of compositions where LAM_P forms (0 < f_O ≤ 0.20), the lamellar period (d*) strongly decreases: d* ∼ M^−0.87 (Fig. 4A). For comparison, Fig. 4A also includes literature data for linear poly(isoprene-b-styrene-b-ethylene oxide) (ISO) and poly(styrene-b-isoprene-b-ethylene oxide) (SIO) triblock terpolymers similarly synthesized by varying the O block length from a common parent diblock. The domain spacing trends observed for both ISO and SIO series typify the expected increase in lamellar period with increasing M: α_ISO ≈ 0.90 (38, 39) and α_SIO ≈ 0.56 (40). Clearly, α_LSO is strikingly different. Additional data illustrating the unusual negative trend for LSO are summarized in the SI Appendix, Table S4. Schematic illustrations of assigned structures (SI Appendix, Fig. S6), indexed 2D SAXS data (SI Appendix, Fig. S7), 1D azimuthally averaged intensity reductions (SI Appendix, Fig. S8), and TEM images (SI Appendix, Fig. S9) are also provided.

Fig. 4.

(A) Lamellar periods (d*) versus normalized molar mass for brush LSO (this work) and linear ISO and SIO triblock terpolymers (literature data). Calculated exponents (best fit) to the power law d* ∼ M^α are included for comparison. (B and C) Consequences of varying end-block length N_X in LSL′ and LSO. (B) Domain spacing d*. (C) Apparent PLA glass transition temperatures (T_g); for all samples, a single T_g (T_g,PEO < T_g ≤ T_g,PLA) was observed.

A series of LSL′ brush triblock copolymers was similarly synthesized from identical macromonomers, generating an analogous series with variable end-block length from a parent LS diblock (N_A = 30, N_B = 28). Like LSO, this LSL′ series exhibits decreasing lamellar periods with increasing end-block length (i.e., increasing total molar mass) (Fig. 4B). Additional morphological data for LSL′ are provided in the SI Appendix, Table S5 and Figs. S10 and S11. Differential scanning calorimetry data for LSL′ and LSO are compared in Fig. 4C and provide quantitative evidence of block–block mixing in LSO. For all LSO samples, a single glass transition temperature (T_g) was observed between T_g,PLA (55 °C) and T_g,PEO (−70 °C) (SI Appendix, Fig. S12). As N_C (and therefore the weight fraction of PEO) increases, T_g decreases, consistent with continued dilution of mixed A/C domains by the low-T_g component. The presence of only one T_g in polymer blends is generally regarded as evidence for miscibility (41, 42) and is consistent with the behavior of PLA and PEO homopolymers, which mix over wide ranges of molar masses and blend compositions (43, 44). In the analogous LSL′ series, a single T_g corresponding to the PLA block is observed that does not change as N_A′ increases, because mixed domains inherently remain pure PLA (SI Appendix, Fig. S13).

Role of Low-χ Interactions.

We have investigated herein the impact of low-χ block–block interactions on structure and physical properties by studying densely grafted ABC and ABA′ brush triblock polymers. The LSO polymers described above self-assemble into lamellae with unique domain connectivity (ACBC), which we denote LAM_P. In contrast, linear ABC triblock terpolymers (e.g., ISO and SIO) have been extensively studied and typically form two- or three-domain lamellar morphologies (LAM₂ or LAM₃) depending on block lengths and relative interaction parameters. In the conventional LAM₃ morphology generated by both ISO and SIO, the mesoscopic domain connectivity (ABCB) necessarily reflects the underlying molecular sequence. In other words, the self-assembly of ABC… multiblock polymers into lamellae (i.e., structures periodic in one dimension) typically requires A, B, C, … domains to be connected in that order due to the covalent linkages between blocks. The crucial differences distinguishing LSO and ostensibly similar ISO/SIO triblocks could potentially be attributed to either the polymer architecture (brush vs. linear) or block–block interactions. We note that architecture-induced segmental mixing has been demonstrated in ABC heteroarm star terpolymers, wherein forming low-energy morphologies may force one arm to transit across an incompatible domain (χ > 0) (45, 46). However, these architecture effects do not pertain to brush LSO because the blocks are connected end-to-end in the same way as linear ABC triblock terpolymers. The data presented in Figs. 2‒4 instead indicate that block–block interactions, captured through the mean-field concept of Flory–Huggins binary interaction parameters (χ_ij), are the dominant factors governing the unique behavior of LSO.

Both the relative and absolute magnitudes of each χ_ij, convolved with the molecular sequence, underpin the self-assembly of multiblock polymers. For example, given I, S, and O blocks with χ_IO > χ_IS ≈ χ_SO (47, 48), SIO connectivity imposes costly high-χ interactions between adjacent blocks (χ_BC > χ_AB ≈ χ_AC), whereas ISO connectivity alleviates this penalty by not inherently requiring I/O (A/C) interfaces. ISO and SIO phase diagrams are consequently distinct due to so-called frustration. The influence of each χ_ij is less understood. In contrast to (SI/IS)O materials where every χ_ij >> 0, the LSO polymers studied herein feature low χ_AC between the end blocks (χ_LO $\mathrm{\lesssim }$ 0). Actual literature estimates for χ_LO range from 0.0038 to −0.161 depending on end groups and measurement techniques (49, 50). Combining any −0.161 < χ_LO < 0.0038 with the aforementioned literature values χ_LS = 0.080 and χ_SO = 0.049 yields a frustrated system. SCFT simulations (Fig. 3) suggest that the magnitude of χ_LO, beyond simple frustration effects, dictates the unique LAM_P self-assembly observed in Fig. 2. Calculations for LSO indicate that LAM_P is stable when χ_LO < χ^C, which marks a first-order phase transition between LAM_P and LAM₃ (Fig. 3E). The predicted value of χ^C is sensitive to physical parameters including the statistical segment lengths and χ_ij and is consequently difficult to quantitatively associate with experiments. Using the aforementioned literature values corresponding to L, S, and O pairwise interactions, we estimate χ^C ∼ 0.009, which sets an approximate upper bound on the value of χ_LO because no evidence of LAM₃ is experimentally observed. Experiment and theory collectively suggest that low-χ interactions (χ_AC $\mathrm{\lesssim }$ 0) underpin the self-assembly of LSO to LAM_P.

Molecular Asymmetry Effects.

The pronounced decrease in domain spacing observed for LSO and LSL′ upon increasing N_C or N_A′ (at constant N_A, N_B) also emerges as a consequence of the low-χ design, involving molecular asymmetry, block–block mixing, and screening effects. SCFT simulations of linear ABA′ triblock copolymers have previously revealed that asymmetry in A/A′ block lengths can induce a decrease in domain spacing (51). The explanation is twofold. First, A/A′ asymmetry lowers the stretching energy in A domains (52), which can be understood by imagining equivalent A block lengths and then transferring material from one end to the other; as asymmetry increases, the overall A segment distribution shifts away from the interface, increasing d*. Second, when the end blocks are sufficiently asymmetric, a significant proportion of the shorter A blocks can pull out into B domains (Fig. 5A). Although chain pullout incurs an enthalpic penalty (χ_AB > 0), this effect is more than compensated by relaxation of the B block, which is entropically favored and further increases d*. The synthesis of ABA′ triblocks from a common diblock precursor exhibits the same trend: growing longer A′ blocks decreases molecular asymmetry and correspondingly lowers d*. Experimental studies of linear ABA′ triblock copolymers have corroborated this theory of end-block asymmetry (53, 54), and the LSL′ and LSO brush triblock polymers studied herein exhibit strikingly similar behavior. We conclude that architecture is not a critical molecular design parameter dictating the trends in d* (Fig. 4); instead, the close parallels between the self-assembly of ABA′ triblock copolymers and appropriately designed ABC triblock terpolymers implicate block–block mixing. ABA′ samples (linear or brush) clearly have mixed A/A′ domains before chain pullout, and a negligible χ_LO in LSO should also promote end-block mixing. Application of the stretching energy and chain pullout concepts developed to rationalize ABA′ self-assembly therefore also captures the essence of ABC systems (Fig. 5B). Molar mass dispersity additionally favors pullout of shorter end blocks (A′ or C), whereas longer ones remain anchored in mixed domains.

Fig. 5.

Illustration of chain pullout to explain the trends in d* for LSL′ and LSO brush triblock polymers with varying end-block length (equivalently, varying molecular asymmetry). Linear chains are depicted to aid visualization. As the end-block length N_X increases from a fixed parent LS diblock, d* decreases (here, D* ≡ d*/d*_LS, where d*_LS is the period of the parent LS diblock)_. (A) X = A′ (LSL′): short PLA end blocks pull out of PLA domains into PS domains. (B) X = C (LSO): short PEO end blocks pull out of mixed PLA/PEO domains into PS domains.

Informed SCFT simulations of LSO indicate the stability of LAM_P over a wide range of N_C (SI Appendix, Fig. S14). In addition, simulations incorporating an exponential distribution of end-block dispersity for both LSO and LSL′ (SI Appendix, Tables S6 and S7) show good agreement between the predicted and measured magnitudes of d*. The simulations capture a sharp initial decrease in d* when the backbone lengths of the third block are short (N_C, N_A′ ≤ 7), reinforcing the significance of molecular asymmetry and chain pullout. As the end-block lengths continue to increase, however, the predicted values of d* monotonically increase, in contrast to the experimental trends. These disparities may reflect (i) inaccuracies in the χ_ij values used (34), (ii) larger dispersities in N_C and N_A′ than anticipated by theory, or (iii) potential nonequilibrium effects, as discussed below.

Screening Unfavorable Block–Block Interactions.

In LSO, the effects of molecular asymmetry and chain pullout are amplified by the screening of high-χ block–block interactions. The most unfavorable contacts in LSO (L/S) can be partially mitigated by inserting PEO between PLA and PS domains near the interface, because χ_LS > χ_SO and χ_LO $\mathrm{\lesssim }$ 0. This possibility is naturally permitted in the disordered state, but upon self-assembly to the conventional LAM₃ morphology, chain connectivity necessarily creates energetically costly PLA/PS interfaces. Screening L/S contacts in LAM₃ would typically require altering the block sequence to LOS, an impossible task postsynthesis, but LAM_P restores this opportunity by incorporating partial mixing between the end blocks. This phenomenon decouples the molecular block sequence from the self-assembled domain pattern. Screening unfavorable block–block interactions in LSO likely also contributes to the molecular origins of the domain spacing trend. As PEO inserts between PLA and PS blocks at the interface, it should expand the intermolecular distance in the plane of the lamellae and therefore contract the lamellar period (i.e., d*). Similar mixing consequences have been observed in block polymer/homopolymer blends in which the homopolymer localizes at the block–block interfaces (55–57).

Dispersity, Crystallization, and Architecture.

Comparing LSO, LSL′, and linear (IS/SI)O reinforces the importance of low-χ interactions and refutes other potential explanations for the unique mesoscopic ACBC domain connectivity and domain spacing trend. Dispersity differences among the blocks can be discounted because all samples across the LSO, LSL′, ISO, and SIO series depicted in Fig. 4 were synthesized by living polymerizations (either ROMP or anionic polymerization) from parent diblock precursors. Because O comprises the C block in each ABC series, PEO clearly does not inherently cause domain contraction with increasing O block lengths or weight fractions. Furthermore, we see little evidence of extensive PEO crystallization from variable-temperature wide-angle X-ray scattering data, which indicate that all LSO LAM_P samples contain low crystalline weight fractions (<10 wt %) (SI Appendix, Figs. S15 and S16). Densification upon PEO crystallization and concomitant domain contraction is therefore unlikely. The higher molar mass O blocks in linear ISO and SIO would presumably accentuate this effect, yet both ISO and SIO show strong increases in d* with N_C. Comparing LSO and LSL′ provides further evidence that crystallization is not responsible for the unusual trend in d*: Whereas both LSO and LSL′ exhibit decreasing d* with increasing end-block lengths, LSL′ has no crystallizable components.

We expect that the phenomena described above, illustrating the physical consequences of designing polymers with certain miscible blocks, are general to the class of soft materials with χ_AB, χ_BC >> |χ_AC| ≈ 0. Although bottlebrush polymers were used in the present study, SCFT calculations predict identical behavior for analogous linear triblock terpolymers with the same absolute and relative χ-parameters (SI Appendix, Fig. S17). Although bottlebrush polymers experience some steric-induced stiffening compared to linear polymers (58, 59), our results suggest that brush LSO and LSL′ are actually relatively flexible. The backbone flexibility should enable brush LS(O/L′) to adopt looping midblock configurations (Figs. 3 and 5), just like linear AB(C/A′) triblocks with compatible end blocks (60, 61). Informed SCFT calculations indicate that the effective backbone persistence length of brush LSO and LSL′ corresponds to ∼5 norbornene repeat units (25). Because the B midblocks of LSO and LSL′ are much longer than 5 units (N_B ≥ 24), they should readily form loops, although undoubtedly less than the 40% predicted for flexible (linear) triblocks (62). Our results, placed in the context of recent work on bottlebrush block polymer self-assembly, suggest that polymer architecture is not a major factor controlling the formation of partially mixed morphologies. Instead, the primary driving force appears to be the magnitude of χ_AC. Designed low-χ interactions emerge as tools to manipulate block polymer self-assembly.

Potential Nonequilibrium Behavior.

Although SCFT calculations suggest that LAM_P is at equilibrium with experimentally relevant values of χ and f, experimental proof is currently limited by our inability to access the order–disorder transition temperature (T_ODT). SAXS data obtained upon heating a LAM_P sample (LSO with N_A = 25, N_B = 22, N_C = 5) from 25 to 200 °C indicate that LAM_P is thermally stable throughout the entire experimentally accessible temperature range (SI Appendix, Fig. S18). Consistent with other reports of high-molar-mass bottlebrush polymers (25, 63), no T_ODT is observed below the onset of decomposition, preventing careful annealing and quench studies originating from the disordered state. Because SCFT is an equilibrium theory, any deviations from equilibrium would affect the agreement between experimentally measured results and predicted behavior.

To further probe potential nonequilibrium effects and because morphologies for multiblock polymers can be sensitive to processing conditions (64, 65), an LSO brush triblock terpolymer (N_A = 25, N_B = 22, N_C = 5) was annealed in four different ways: thermal annealing under pressure, thermal annealing without pressure, drop casting, and channel die alignment. All approaches afforded self-assembled morphologies with virtually identical LAM_P geometry and periodicity (±0.5 nm) (SI Appendix, Fig. S19). These results are reported while acknowledging studies of linear multiblock polymers that highlight the potential influence of processing path on the formation of kinetically trapped structures (66, 67), which may be mistaken for equilibrium. Previously, ABC block polymer morphologies containing partially mixed regions have indeed been predicted (68) and observed (69) as metastable defect states kinetically trapped upon casting from preferential solvents, but these examples were easily annihilated during the type of extended thermal treatments performed herein to anneal LSO. Equilibrium or not, the morphological attributes of LAM_P are long-lived, in contrast to and notably distinct from prior materials.

Conclusion

The insights gained herein from both experiment and theory illustrate the profound influence low-χ interactions exert on self-assembly. Proper selection of χ_ij and f can generate unusual morphologies characterized by partial block mixing (LAM_P), decouple molecular sequence from mesoscopic connectivity, and provide counterintuitive control over domain spacing. Whereas high-χ block polymers have been the subject of widespread interest, low-χ systems remain relatively unexplored, yet the latter generate fascinating physics that are anticipated to gain importance as sequence complexity further evolves. Expanding the block polymer design toolkit to include low-χ interactions creates new opportunities to tailor mesoscale structure and should find utility in the future design of functional materials.