Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2017 Jun 5;114(25):6605–6610. doi: 10.1073/pnas.1702671114

Sensorimotor integration on a rapid time scale

Jinhong Luo a,1, Ninad B Kothari a, Cynthia F Moss a
PMCID: PMC5488944  PMID: 28584095

Significance

Humans and other animals continuously monitor sensory information to inform the selection of motor commands for adaptive behaviors. Acoustic communication, for example, utilizes auditory feedback to fine-tune vocal production parameters. Because most animal species produce vocalizations that last several hundred milliseconds, it is difficult to dissect the temporal dynamics of audio-vocal feedback control. Here we took advantage of the brief echolocation signals of bats and mapped out the time course of vocal adjustments to background noise on a millisecond time scale. The high temporal resolution data provided the foundation for the model of audio-vocal volume control. We discovered that temporal summation, a shared auditory process across the animal kingdom, lies at the core of adaptive vocal volume control.

Keywords: echolocation, environmental noise, motor control, sensorimotor integration, vocal production

Abstract

Sensing is fundamental to the control of movement: From grasping objects to speech production, sensing guides action. So far, most of our knowledge about sensorimotor integration comes from visually guided reaching and oculomotor integration, in which the time course and trajectories of movements can be measured at a high temporal resolution. By contrast, production of vocalizations by humans and animals involves complex and variable actions, and each syllable often lasts a few hundreds of milliseconds, making it difficult to infer underlying neural processes. Here, we measured and modeled the transfer of sensory information into motor commands for vocal amplitude control in response to background noise, also known as the Lombard effect. We exploited the brief vocalizations of echolocating bats to trace the time course of the Lombard effect on a millisecond time scale. Empirical studies revealed that the Lombard effect features a response latency of a mere 30 ms and provided the foundation for the quantitative audiomotor model of the Lombard effect. We show that the Lombard effect operates by continuously integrating the sound pressure level of background noise through temporal summation to guide the extremely rapid vocal-motor adjustments. These findings can now be extended to models and measures of audiomotor integration in other animals, including humans.

Sensing plays a critical role in the control of movement. In humans, natural behaviors, from grasping a coffee mug to producing intelligible speech, all rely on the guidance of sensing. Similarly, sensory signals lie at the core of most animal behaviors. However, the brain mechanisms underlying sensorimotor integration are not well understood. This is particularly true regarding the control of vocalizations, which are used by a wide range of animal species for communication. At present, a dominant model for motor control is derived from the state feedback control (SFC) theory, which successfully accounts for a wide range of motor behaviors, such as visually guided arm movement (1) and speech production (2). SFC models posit that motor control is based on a comparison of sensory prediction generated from an internal forward model with actual sensory feedback, and sensory feedback is used to train and update the internal forward model. According to this SFC model, sensory feedback is not directly used to guide motor commands, due to its noisy and delayed characteristics, and this notion has been supported by a large body of experimental and theoretical work (1–7). These stand in contrast to motor reflexes, which are movements in direct response to sensory signals. Note, motor reflexes can be graded in response magnitude and can be modulated by cognitive processes (8, 9). One well-known example is the pupillary light reflex, an adjustment in pupil diameter in response to light intensity (10).

The Lombard effect refers to an animal’s increase in vocal signal amplitude in response to an increase in background noise (11). Evidence of the Lombard effect comes from studies of mammals (including humans), birds, frogs, and fish (12–16). Despite over a century of research, the brain mechanisms of the Lombard effect remain elusive. At present, the dominant hypothesis is that the Lombard effect shares the same brain circuits underlying the Fletcher effect (13, 17), an increase in sound-level production in response to a reduction in auditory feedback amplitude (17). Under this hypothesis, the SFC model should account for the Lombard effect. In other words, the Lombard effect should operate through the comparison of predicted vocal amplitude from an internal forward model with the auditory feedback amplitude. Because background noise interferes with the feedback amplitude of an animal’s vocalizations, the magnitude of the Lombard effect grows stronger with increasing background noise. Here, to the contrary, we show that the Lombard effect is a direct response to background noise and features an extremely short latency of about 30 ms. Thus, the Lombard effect can be better described as a reflex.

Results

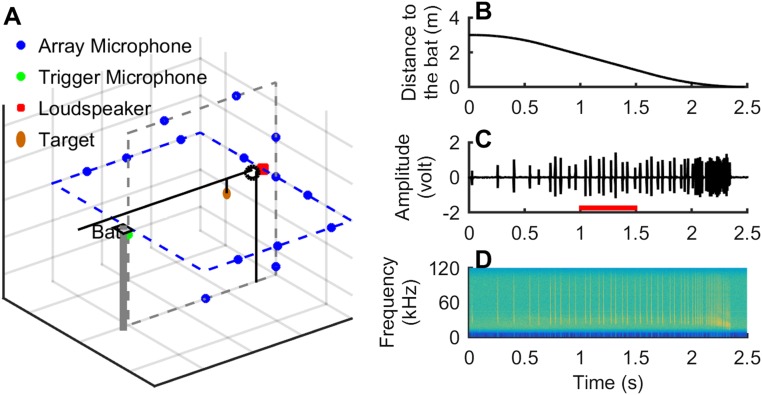
The echolocating big brown bat, Eptesicus fuscus, produces vocalizations of a few milliseconds in duration, which offers the opportunity to investigate the Lombard effect on a millisecond time scale and to generate data for a quantitative sensorimotor model that differentiates between SFC and reflex hypotheses. This modeling effort depends on detailed analysis of the time course of the Lombard effect. In this study, we trained individual adult bats (five individuals) to rest on a platform and track an approaching tethered insect by echolocation and recorded the bat’s echolocation signals with an array of 14 microphones (Fig. 1A). For each trial, the tethered insect was delivered to the bat via a motorized pulley system and traveled a distance of 3 m in about 2.5 s. The distance between the bat and the tethered insect over the time course of a trial is shown in Fig. 1B. One example of the bat’s sonar tracking behavior is shown in Fig. 1 C and D. In the middle of a trial, around 1 s after the tethered insect began its trajectory toward the bat, either a silent sound file (with all samples set to zero) or a 5- to 100-kHz broadband white noise of varying temporal structure was randomly broadcast from a loudspeaker positioned 3.5 m away in front of the bat (Fig. 1A, illustrated by the red square). The sound recording, noise broadcast, and motorized pulley system controlling prey delivery to the bat were all synchronized. High-speed demonstration videos of bats tracking approaching prey targets in silence and in noise are provided in Movie S1.

Fig. 1.

Fig. 1.

Open in a new tab

Experimental setup and testing paradigm. (A) Experimental setup showing the platform where the bat rests, the prey target (insect), and the sound recording and noise broadcast system. (B) The time-distance function of the computer-controlled prey target. (C and D) The waveform and spectrogram of the echolocation call sequence of a bat tracking the approaching prey target, showing a systematic decrease in the interval between neighboring calls from the start to the end and a clear buzz (high repetition rate and a large decrease in the end frequency) shortly before the bat contacts the prey. The time of the noise presentation relative to the bat’s sonar behavior is indicated by a red bar at the bottom in C.

Time Course of the Lombard Effect on a Millisecond Scale.

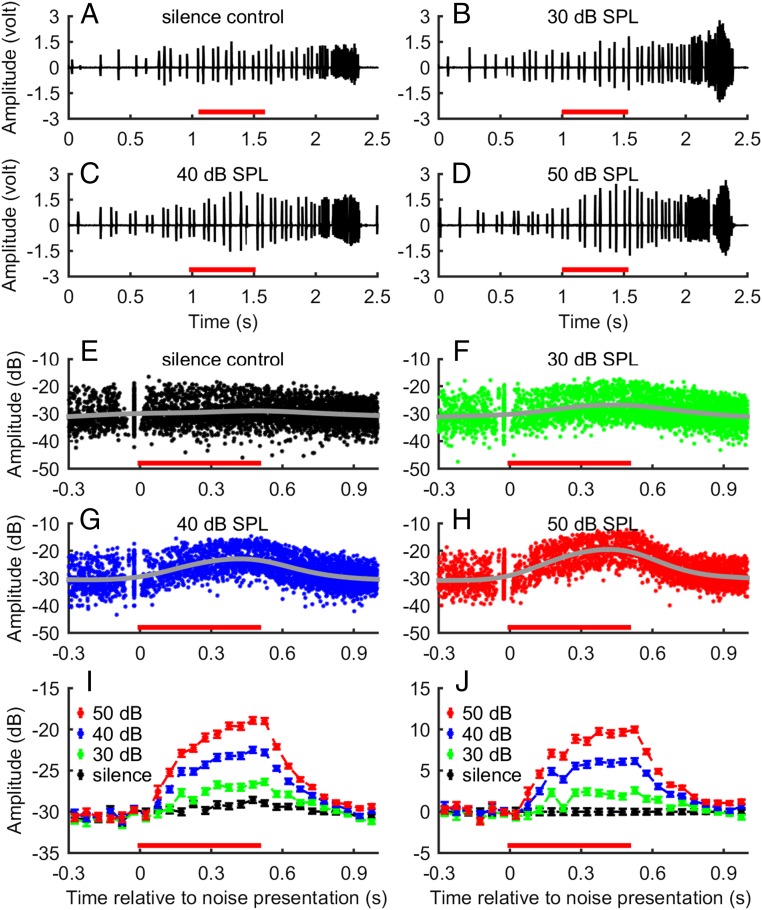
In the first experiment, we presented the bats with 500-ms broadband noise at 30 dB, 40 dB, and 50 dB SPL (sound pressure level relative to 20 μPa), along with a silence control. One example of the echolocation behavior from each condition is shown in Fig. 2 A–D. The time course of the noise, relative to the sonar behavior of the bat, is indicated by a red bar at the bottom of each figure panel. These examples show that the peak amplitude of the calls in both 40-dB and 50-dB noise conditions exhibited a gradual increase after the noise started, and a gradual decrease after the noise ended. In contrast, there is little variation in the peak amplitude of calls in the silence control. The same phenomenon of noise-related changes in call amplitude can be seen in the scatter plots of the root-mean-square (RMS) call amplitude from all five bats per condition, after aligning the sonar calls in time relative to the noise onset (Fig. 2 E–H). The gray line in each panel represents the spline fitting, showing the average trend. To compare differences in the call amplitude over the time course statistically, we combined data points from each neighboring 50-ms time window. Fig. 2 I and J shows the mean ± SEM for each time window and each noise condition and the normalized mean ± SEM, respectively. The normalized means were calculated by taking the differences in means between the noise conditions and the silence control to account for the inherent time-related changes in call amplitude when bats were tracking the approaching insect. Before the noise was broadcast, there was little variation in call amplitude across conditions, with a maximum difference in the averaged call amplitude of 1.1 dB. After the noise started, bats produced gradually more intense calls until reaching a plateau. After the noise ended, the call amplitude decreased gradually and returned to the baseline level of silence control. The rising and the plateau (maximum) of the call amplitude depended on the noise level: the higher the noise level, the steeper the initial rise and the greater the maximum increase.

Fig. 2.

Fig. 2.

Open in a new tab

Millisecond-level time course of call amplitude control by bats in response to ambient noise. (A–D) Examples of the time course of the call amplitude of a bat in silence control and in 30-, 40-, and 50-dB SPL noise conditions. Noise-related changes in call amplitude can be observed in the 40- and 50-dB noise conditions. (E–H) Scatter plot of the call amplitude for data pooled from all five bats and time-aligned to the noise onset. The gray line represents the spline fit and shows the average trend of the data over time. Shortly before the noise starts, many calls occurred almost at the same time and were surrounded by a white gap both before and after. These isolated calls were the calls used as the trigger for the noise broadcast, and the white gaps represent the intervals between sonar calls. (I) Mean ± SEM of the call amplitude after combining neighboring calls every 50-ms nonoverlapping time window. The middle time point was used to construct the new time axis. For example, 25 ms was the new time axis to represent the combined data between 0 and 50 ms. (J) Normalized mean ± SEM after subtracting the mean call amplitude in the noise conditions by the mean call amplitude in the silence control that represented the paradigm-related influence. For all panels, the red bar at the bottom shows the time course of noise presentation.

These data allowed us to estimate the response latency of call amplitude adjustment. For the averaged data in the time window between 50 and 100 ms after noise onset (referenced at 75 ms, Fig. 2J), the bats produced 2.2 ± 0.7 dB higher-amplitude calls in the 50-dB noise condition (T test, P < 0.001, df = 162); whereas there was no change in call amplitude at 25 ms after noise onset (−0.35 ± 0.47 dB; T test, P = 0.62, df = 150), which suggests that the response latency lies between 25 and 75 ms.

Real-Time Transfer of Background Noise into Vocal-Motor Control.

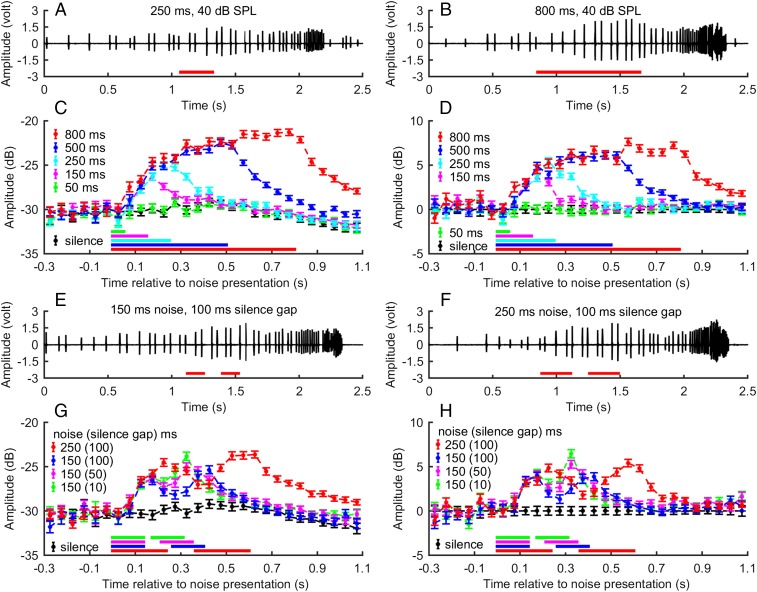
To test the hypothesis that the noise-induced call amplitude changes are a result of the bat’s real-time processing of the background noise and not simply triggered by the onset of the noise, we collected additional data using two paradigms in three additional experiments. In the first paradigm, we presented bats with noise of different durations: 50, 150, 250, and 800 ms. In the second paradigm, we presented bats with two repeated noise elements of either 150 or 250 ms duration, separated by a silence gap of either 10, 50, or 100 ms. The noise amplitude was 40 dB SPL across all these conditions. We found that the call amplitude is determined by both the duration of the noise and the duration of the silence gap (Fig. 3). Call amplitude adjustments in all noise conditions showed the same pattern of a gradual increase after the noise started, remaining constant if the noise was longer than about 300 ms and gradually decreasing after the noise ended. The gapped noise paradigm offers strong support for the real-time processing hypothesis, as not only the peak of the call adjustment time course was determined by the noise duration (as in paradigm 1), but also the valley of the time course was directly affected by the duration of the silence gap. The longer the silence gap, the greater the decrease in call amplitude. Once the noise started again, the animals increased call amplitude again before dropping to the baseline amplitude.

Fig. 3.

Fig. 3.

Open in a new tab

Time course of call amplitude of bats in response to noise of varying temporal pattern. (A and B) Examples of the time course of call amplitude of a bat exposed to noise of 250 ms duration and 800 ms duration, respectively. The maximum call amplitude in the 800-ms noise condition is greater than in the 250-ms noise condition. (C) Mean ± SEM of call amplitude for data pooled every 50-ms nonoverlapping time window and time-aligned to the noise onset of data from all bats. Noise conditions of different duration are color-coded. (D) The normalized mean ± SEM of data shown in C to account for the paradigm-related call amplitude changes over time. (E and F) Examples of the time course of call amplitude of a bat exposed to two repeated noise elements of 150 and 250 ms, separated by 100 ms silence. A drop in call amplitude between the two noise elements can be observed in both conditions. (G) Mean ± SEM of call amplitude for data pooled every 50-ms time window and time-aligned to the noise onset of data from all bats. Noise conditions of varying noise element duration and silence gap are color-coded. (H) The normalized mean ± SEM of data shown in G to account for the paradigm-related call amplitude changes over time. Note that both before and shortly after the noise began the call amplitudes largely overlap across different noise conditions (C, D, G, and H), which not only highlights the robustness of the Lombard effect, but also implies limited audio-vocal processing time of the Lombard effect. For all conditions, the bar(s) at the bottom of each panel show the time of noise presentation. When multiple bars are present in the same panel, the color of the bar codes the noise condition.

A Computational Model for the Lombard Effect.

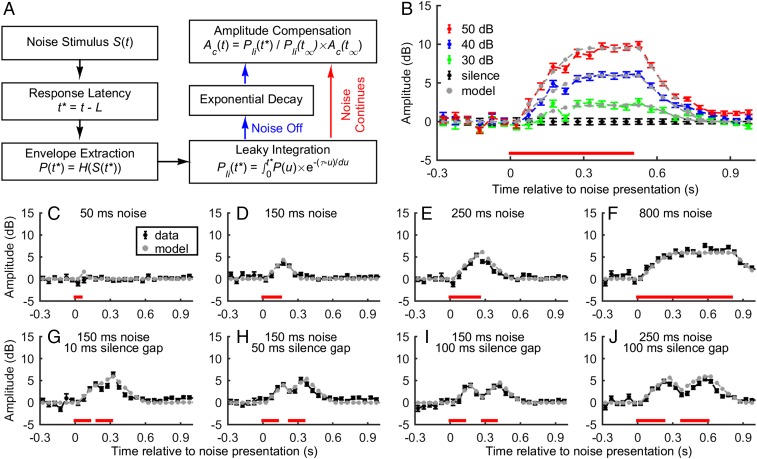
Here we present a computational model that accounts for the noise-induced changes in call amplitude (Fig. 4A). The proposed model contains three free parameters: time constant (τ, in ms), response latency (L, in ms), and the maximum increase in call amplitude for a given noise level [Ac(t∞), in dB]. The time constant determines the maximum integration time for the background noise. The response latency determines how fast the noise information is reflected by a change in call amplitude. The maximum increase in call amplitude represents the compensation goal for a given noise level.

Fig. 4.

Fig. 4.

Open in a new tab

A computational model for the Lombard effect. (A) The model takes the white noise as the input, followed by envelope extraction, leaky integration, and scaling. There are three free parameters: the response latency (ms), time constant (ms), and maximum compensation (dB). (B) Data from the 500-ms continuous noise conditions were used to find the optimal combination of the three model parameters through minimizing the sum of squared errors. The corresponding model predictions are colored in gray. (C–J) A comparison of the model prediction, based on the three parameters optimized from the 40-dB SPL noise condition (267 ms of time constant, 30 ms of response latency, and 5.9 dB of maximum compensation), and the data. The model precisely predicts the time course of the call amplitude for all conditions. For B–J, the red bar at the bottom shows the time course of noise presentation.

This model works as follows. First, after the background noise enters the auditory system, the envelope of the sound pressure level is extracted. Second, the pressure envelope is temporally integrated over the effective noise duration, and this process is leaky. The effective noise duration equals the time elapsed after the noise began minus the response latency. Subsequently, the integrated pressure envelope is continuously transformed into call amplitude compensation if the noise continues. If the noise ends, the integrated pressure envelope follows an exponential decay function that shares the same time constant with the leaky integration process, and then the output is continuously transformed into vocal amplitude compensation (Fig. 4A).

We used mean vocal-level adjustment data in the 500-ms noise condition of experiment 1 to search for the three free parameters for the model. (Note that median vocal adjustment values differed by less than 0.1 dB from the mean, on average; Table S1). Predictions based on the combinations of the three parameters that resulted in the best fit, i.e., the smallest sum of squared errors, are shown in Fig. 4B. The optimal time constant and response latency were 267 and 30 ms for the 40-dB noise condition; and 252 and 33 ms for the 50-dB noise conditions, respectively. Thus, the differences in the vocal amplitude compensation between the 40- and 50-dB noise conditions were driven nearly entirely by the third parameter, the maximum increase in call amplitude (5.9 dB vs. 9.8 dB). One important parameter returned by the model is the response latency of about 30 ms, which is remarkably short. Fig. 4 C–J shows that the model accounts for the data from the other eight experimental conditions quite well. The absolute differences between the model prediction and the data for these conditions were 0.6 ± 0.45 dB. In other words, once the three parameters are established, the fine time course of the Lombard effect can be predicted precisely.

Table S1.

Time course of the Lombard effect in the 500-ms continuous noise conditions

Relative time of noise presentation (ms) 30 dB SPL 40 dB SPL 50 dB SPL
Mean vocal-level adjustment (dB) Median vocal-level adjustment (dB) Mean vocal-level adjustment (dB) Median vocal-level adjustment (dB) Mean vocal-level adjustment (dB) Median vocal-level adjustment (dB)
−275 −0.06 0.06 0.69 0.90 0.23 −0.02
−225 −0.41 0.00 0.12 −0.20 0.76 0.37
−175 0.07 0.14 0.15 0.15 0.20 −0.01
−125 −0.94 −0.69 −0.34 0.40 −1.14 −0.32
−75 −0.05 0.05 0.34 0.43 0.57 0.42
−25 −0.26 −0.07 0.10 −0.03 −0.04 −0.06
25 −0.53 −0.66 −0.35 −0.74 −0.35 −0.68
75 −0.40 −0.77 0.85 1.21 2.21 2.28
125 0.24 0.57 2.50 3.15 4.55 5.16
175 2.33 2.14 4.90 4.98 7.10 8.89
225 0.45 −0.44 3.93 3.76 6.75 7.12
275 2.31 1.55 5.55 5.45 8.86 9.96
325 2.43 2.08 5.75 6.09 8.56 9.38
375 2.27 1.93 6.10 5.83 9.75 10.63
425 2.06 1.21 5.87 5.74 9.45 10.45
475 1.85 1.33 6.07 5.62 9.64 10.79
525 2.58 1.98 6.15 5.53 9.97 9.67
575 1.57 0.69 4.68 4.08 7.29 6.99
625 1.46 0.91 3.07 2.95 4.91 4.82
675 0.46 0.27 2.12 2.11 3.28 3.50
725 1.08 −0.13 1.91 1.28 2.91 2.53
775 0.51 −0.13 1.29 0.91 1.84 1.66
825 0.19 −0.76 0.88 0.19 1.19 0.41
875 −0.06 0.01 0.48 0.40 1.08 1.08
925 −0.22 −0.73 0.12 −0.35 1.06 0.27
975 −0.66 −0.82 0.65 0.97 1.22 0.54
Open in a new tab

Note, there is little difference in the magnitude of the Lombard effect between the means and the medians.

Discussion

Taking advantage of the echolocating bat’s adaptive sonar behavior, we have successfully traced the time course of the Lombard effect. Importantly, we have demonstrated that background noise level is continuously monitored to guide the vocal amplitude control, as revealed by the noise-gap paradigm, in which vocal amplitude adjustments were affected by both the duration of the noise element and the silence gap (Fig. 3). The success of our model in accounting for the fine time course of the Lombard effect offers theoretical support that background noise is directly used to guide vocal amplitude control. Specifically, our model clearly shows that neither internal forward model predictions nor a comparison of these predictions with background noise is required, as would be expected by the SFC models or by the Fletcher effect hypothesis. Furthermore, this study also revealed that transforming sensory inputs into vocal-motor control underlying the Lombard effect is extremely rapid, with a latency of about 30 ms.

How can the Lombard effect operate so rapidly? The Lombard effect response latency of 30 ms is even shorter than the auditory laryngeal reflex, an increase in fundamental frequency in response to the presentation of a click, with a latency of ∼50 ms in humans (18). Nevertheless, the 30-ms response latency is well within the physiological limit of audio-vocal integration, as the acoustic crycothyroid muscle reflex can be as short as 6 ms (19). Our model shows that the short response latency of the Lombard effect is probably due to the very few audio-vocal processes involved: Envelope extraction, leaky integration, and scaling. Because both envelope extraction and leaky integration can be accomplished by the peripheral auditory system (20, 21), it is likely that the initiation of the Lombard effect does not require higher auditory centers. The output from the peripheral auditory system can be directly sent to the vocal-motor system of the brainstem to guide the vocal amplitude adjustments, as indicated by the finding that decerebrate cats show the Lombard effect (22).

Why have past studies overestimated the response latency for the Lombard effect? The Lombard effect was first described over a century ago and is among the most widely studied audio-vocal integration phenomena. The response latency of the Lombard effect was estimated to be about 150–175 ms for humans (23, 24), 150 ms for birds (25), and less than 150 ms for bats (26). There are at least two possible explanations for the overestimation. First, the duration of the vocalizations under investigation sets the finest latency measurement resolution. For the human and bird experiments (23–25), the vocalizations studied were about 150 ms long, which constrains the lower latency limit of the Lombard effect that can be measured. Second, estimations based on statistical assessment are by nature overestimations, because all experimental data are intrinsically noisy. For example, using the data from the 500-ms continuous noise experiment (experiment 1) we estimated the response latency for the Lombard effect to be between 25 and 75 ms because calls were 2.2 ± 0.7 dB more intense for the 75-ms call group statistically, but not for the 25-ms call group.

In addition to explaining the extremely short vocal response latency to noise, our model offers a mechanistic explanation of the Lombard effect that applies to all vertebrates. This stems from the fact that two basic auditory processes, envelope extraction and leaky integration, are fundamental to the vertebrate auditory system. Specifically, both envelope extraction and leaky integration underlie the process of temporal summation, which has been demonstrated for fish (27), frogs (28), birds (29), and mammals (20). Thus, the basic auditory system of vertebrates is wired to show the Lombard effect.

The fact that background noise is directly used to guide vocal amplitude adjustments, and the short response latency of about 30 ms, suggests that the Lombard effect can be described as a reflex. Thus, the Lombard effect is fundamentally different from the Fletcher effect and does not require a comparison of internal forward model predictions with the sensory feedback. Our results are in line with the data from an earlier study on another bat species (Rhinolophus ferrumequinum) that exhibited the Lombard effect in the first call after noise onset (26). However, the term reflex should not be interpreted as that the Lombard effect is a fixed response to background noise. In fact, the Lombard effect in humans is affected by both the communication context (30) and content (31) and can be inhibited through training (32). These studies highlight that cognitive processes can modulate the Lombard effect.

Materials and Methods

Five adult big brown bats (Eptesicus fuscus), four males and one female, were trained to rest on a platform and track an approaching tethered insect by echolocation (Fig. 1A). Echolocation calls of the bat were recorded by an array of 14 microphones (DX500, Petterson Elektroniks, with the horn on) that covered about −65 to + 65 degrees horizontally and −30 to +45 degrees vertically. The insect was tethered to a pulley motor system whose speed was computer-controlled. Details of the motor system can be found in Kothari et al., 2014 (33). In this experiment, the tethered insect started at a distance of 3 m from the bat and traveled for a time period of about 2.5 s for each trial. The time-distance function of the prey target is shown in Fig. 1B. Between the time window of 0.5 and 2 s, the prey target traveled at a constant speed of about 1.5 m/s. In the noise treatment conditions, we presented 5- to 100-kHz broadband white noise from a loudspeaker (Fig. 1A, illustrated by the red square) around 1 s after a trail started, which thus allowed us to analyze calls both before and after the noise presentation that were still within the time window in which the tethered insect was traveling at a constant speed. The exact time delay of noise onset was randomly jittered by 0.2 s maximally. For three of the four experiments, the start of the noise presentation was amplitude-triggered by the vocalizations of the bat recorded by the trigger microphone under the platform (Fig. 1A, illustrated by the green circle). In the fourth experiment, we disabled the trigger so that the noise started at a time delay of 0.8 s within a noise treatment trial. Experimental procedures were approved by the Johns Hopkins University Institutional Animal Care and Use Committee.

Sound recording, noise broadcast, and the motor system for insect target control were all synchronized. Specifically, for each trial, a transistor–transistor logic (TTL) signal was generated by the motor system and represented as the digital start trigger for the sound recording system (National Instruments, PXIe 8135, with two data acquisition card PXIe 6358 consisting of 16 analog input channels and 8 analog output channels). The sound recording and noise presentation was synchronized by directly recording the noise with one of the analog recording channels, with custom-written programs in LABVIEW (National Instruments, LABVIEW 2015 Professional Development System). The bat’s echolocation calls were recorded at a sample rate of 250 kHz, and the noise was generated at a sample rate of 2.5 MHz. The noise was presented with a custom-made electrostatic loudspeaker, which has a relative flat frequency response (± 5 dB) between 20 and 90 kHz that is the main frequency range of the bats’ echolocation calls. The presented noise level was directly measured with a free-field measurement microphone (7016, 1/4 inch Condenser microphone, ACO Pacific; with protection grid removed) placed at the position of the bat and directed toward the loudspeaker. Each array microphone was directed to the platform with a laser beamer. We localized the spatial position of the array microphones by playing and recording chirp sequences (5- to 25-kHz FM sweeps) through a loudspeaker placed at different locations. The exact location of the speaker was recorded by a motion tracking system containing three high-speed cameras (MX T40, Vicon Motion Systems). The distance between the platform and each microphone was confirmed by direct measurements from a laser distance meter (GLR 500, Bosch).

We collected sound recordings of individual bats from four experiments in total. In the first experiment, we presented bats with 500-ms-long white noise at 30-, 40-, and 50-dB SPL level. In the second experiment, we presented bats with white noise of different noise durations: 50, 150, and 250 ms. In the third experiment, we presented bats with two repeated noise elements of 150 ms duration each that were separated by silence gaps of 10, 50, and 100 ms. In the fourth experiment, we presented the bats with either 800 ms noise or two repeated noise elements of 250 ms duration that were separated by a silence gap of 100 ms. Each experiment had its own silence control. For the last three experiments, the noise amplitude was 40 dB SPL. During the data collection, presentations of the treatments were randomized, and the experimenter was not aware of the exact treatment. For each recording day, typically 20–30 trials were run for each bat in about 30 min. A minimum of 4 d was devoted to data collection for each experiment to contain a minimum of 30 trials per condition per bat.

Sound analysis was performed with custom-written programs in MATLAB (R2015a, MathWorks), based on Luo et al. (16, 34, 35). We first checked the waveform of the echolocation call sequence for each trial and excluded the trials in which the bat did not track the prey target, as indicated by no decrease in the pulse-interval over time, which were rare cases (<5% of the total trails). Then, we accounted for the frequency response of the microphones by filtering the recorded calls with each microphone’s compensatory impulse response (32nd-order finite-impulse response filter) and high-pass–filtered all recordings at 10 kHz. Because of the spectral notch of the microphones at around 75 kHz, we low-pass–filtered the recordings at 70 kHz. Subsequently, we identified echolocation calls from the microphone that was directed toward the bat (central microphone, 0-degree azimuth and elevation), from which each echolocation call was cut with a fixed time window of 5 ms before the call and 5 ms after the call. Then we estimated the call duration (−20 dB relative to the peak amplitude) and the RMS amplitude over the duration. Through cross-correlation, calls in all other channels were readily available for analysis after compensating for the frequency- and distance-specific transmission loss. The quality of the sound analysis program was manually checked by displaying the waveform and spectrogram at varying stages of the analysis and its high quality was confirmed. Each analyzed call represented the call of the maximum RMS amplitude of the 14 recorded calls from the 14 microphones, so that the influence of the changes in calling direction of the bat on signal parameter estimation is minimized.

We used the Global Optimization Toolbox from MATLAB to search for the free parameters of the model. Optimization for each of the three noise conditions (30, 40, and 50 dB SPL) was run repeatedly until the optimization output did not improve anymore. Specifically, we used the mean vocal-level adjustments, as shown in Fig. 2J, to search for the free parameters of the model. Nevertheless, we wish to point out that we also computed median level adjustments, and there was little difference between the mean and median vocal-level adjustments (<0.1 dB on average; Table S1). Mathematical processes of the model and the simulation details are provided as MATLAB scripts in Dataset S1. In short, the computational model takes the background noise (i.e., the sound pressure level of the noise over the entire time course) and the three free parameters as inputs. The outputs are predictions of the amplitude adjustments (Fig. 4A).

There was individual variation in the compensation magnitude of the Lombard effect, and different individuals contributed different number or percentage of calls (i.e., sample size) to the population analysis (ranging from 13 to 25%; Table S2). To assess how much the differential sample size of individual bats affected the population analysis, we compared the mean call amplitude of our population data with the mean call amplitude from bootstrapped data, in which each bat contributed equally to the population analysis [bootstat = bootstrp(1000, @mean, ind_data); MATLAB R2015a], using the data from experiment 1. We found that there was a negligible effect of the differential sample size on the estimation of the mean call amplitude compensation at the population level across the three noise conditions. The differences in maximum increase in call amplitude (based on data within time window of 250–500 ms) between the empirical and bootstrapped data were 0.11, 0.14, and 0.14 dB for the 30-, 40-, and 50-dB noise conditions, respectively.

Table S2.

Number of calls from individual bats and percentage contribution to the population analysis

Noise level Silence 30 dB 40 dB 50 dB
Bat 1 Call number 932 910 875 768
Percentage 24.6% 26.5% 25.6% 24.6%
Bat 2 Call number 659 535 594 407
Percentage 17.4% 15.6% 17.4% 13.1%
Bat 3 Call number 704 604 553 577
Percentage 18.6% 17.6% 16.2% 18.5%
Bat 4 Call number 663 620 610 564
Percentage 17.5% 18.1% 17.9% 18.1%
Bat 5 Call number 811 714 749 749
Percentage 21.4% 20.8% 21.9% 24.0%
Open in a new tab

Data are from experiment 1, in which either a silent sound file or 500-ms continuous noise was broadcast at different noise levels.

Supplementary Material

Supplementary File
Download video file (14.6MB, mp4)
Supplementary File
pnas.1702671114.sd01.pdf (38.7KB, pdf)

Acknowledgments

We thank Melville Wohlgemuth for suggestions during animal training, Klemen Koselj and Lutz Wiegrebe for suggestions to the model, and James Garmon for engineering supports. Two anonymous reviewers provided valuable comments for improving the manuscript. This project is funded by National Science Foundation (IOS-1010193), the Human Frontiers Science Program (RGP0040), the National Science Foundation (IOS-1460149), the Office of Naval Research (N00014-12-1-0339), and the Air Force Office of Scientific Research (FA9550-14-1-039) (to C.F.M.), and by a long-term postdoctoral fellowship from Human Frontier Science Program (to J.L.) (LT000279/2016-L).

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1702671114/-/DCSupplemental.

References

  • 1.Shadmehr R, Krakauer JW. A computational neuroanatomy for motor control. Exp Brain Res. 2008;185:359–381. doi: 10.1007/s00221-008-1280-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Hickok G, Houde J, Rong F. Sensorimotor integration in speech processing: Computational basis and neural organization. Neuron. 2011;69:407–422. doi: 10.1016/j.neuron.2011.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Wolpert DM, Miall RC. Forward models for physiological motor control. Neural Netw. 1996;9:1265–1279. doi: 10.1016/s0893-6080(96)00035-4. [DOI] [PubMed] [Google Scholar]
  • 4.Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science. 1995;269:1880–1882. doi: 10.1126/science.7569931. [DOI] [PubMed] [Google Scholar]
  • 5.Hickok G. Computational neuroanatomy of speech production. Nat Rev Neurosci. 2012;13:135–145. doi: 10.1038/nrn3158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Houde JF, Nagarajan SS. Speech production as state feedback control. Front Hum Neurosci. 2011;5:82. doi: 10.3389/fnhum.2011.00082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Tourville JA, Guenther FH. The DIVA model: A neural theory of speech acquisition and production. Lang Cogn Process. 2011;26:952–981. doi: 10.1080/01690960903498424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Binda P, Pereverzeva M, Murray SO. Attention to bright surfaces enhances the pupillary light reflex. J Neurosci. 2013;33:2199–2204. doi: 10.1523/JNEUROSCI.3440-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Steinhauer SR, Condray R, Kasparek A. Cognitive modulation of midbrain function: Task-induced reduction of the pupillary light reflex. Int J Psychophysiol. 2000;39:21–30. doi: 10.1016/s0167-8760(00)00119-7. [DOI] [PubMed] [Google Scholar]
  • 10.Campbell FW, Gregory AH. Effect of size of pupil on visual acuity. Nature. 1960;187:1121–1123. doi: 10.1038/1871121c0. [DOI] [PubMed] [Google Scholar]
  • 11.Lombard E. Le signe de l’elevation de la voix. Ann Mal Oreille Larynx Nez Pharynx. 1911;37:101–119. [Google Scholar]
  • 12.Brumm H, Zollinger SA. The evolution of the Lombard effect: 100 years of psychoacoustic research. Behaviour. 2011;148:1173–1198. [Google Scholar]
  • 13.Hotchkin C, Parks S. The Lombard effect and other noise-induced vocal modifications: Insight from mammalian communication systems. Biol Rev Camb Philos Soc. 2013;88:809–824. doi: 10.1111/brv.12026. [DOI] [PubMed] [Google Scholar]
  • 14.Holt DE, Johnston CE. Evidence of the Lombard effect in fishes. Behav Ecol. 2014;25:819–826. [Google Scholar]
  • 15.Shen JX, Xu ZM. The Lombard effect in male ultrasonic frogs: Regulating antiphonal signal frequency and amplitude in noise. Sci Rep. 2016;6:27103. doi: 10.1038/srep27103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Luo J, Goerlitz HR, Brumm H, Wiegrebe L. Linking the sender to the receiver: Vocal adjustments by bats to maintain signal detection in noise. Sci Rep. 2015;5:18556. doi: 10.1038/srep18556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Lane H, Tranel B. The Lombard sign and the role of hearing in speech. J Speech Lang Hear. 1971;14:677–709. [Google Scholar]
  • 18.Sapir S, McClean MD, Larson CR. Human laryngeal responses to auditory stimulation. J Acoust Soc Am. 1983;73:315–321. doi: 10.1121/1.388812. [DOI] [PubMed] [Google Scholar]
  • 19.Jen PH-S, Ostwald J. Response of cricothyroid muscles to frequency-modulated sounds in FM bats, Myotis lucifugus. Nature. 1977;265:77–78. doi: 10.1038/265077a0. [DOI] [PubMed] [Google Scholar]
  • 20.Heil P, Neubauer H. A unifying basis of auditory thresholds based on temporal summation. Proc Natl Acad Sci USA. 2003;100:6151–6156. doi: 10.1073/pnas.1030017100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Heil P, Neubauer H, Tetschke M, Irvine DR. A probabilistic model of absolute auditory thresholds and its possible physiological basis. In: Moore BCJ, et al., editors. Basic Aspects of Hearing: Physiology and Perception. Springer; New York: 2013. pp. 21–29. [DOI] [PubMed] [Google Scholar]
  • 22.Nonaka S, Takahashi R, Enomoto K, Katada A, Unno T. Lombard reflex during PAG-induced vocalization in decerebrate cats. Neurosci Res. 1997;29:283–289. doi: 10.1016/s0168-0102(97)00097-7. [DOI] [PubMed] [Google Scholar]
  • 23.Heinks-Maldonado TH, Houde JF. Compensatory responses to brief perturbations of speech amplitude. Acoust Res Lett Online. 2005;6:131–137. [Google Scholar]
  • 24.Bauer JJ, Mittal J, Larson CR, Hain TC. Vocal responses to unanticipated perturbations in voice loudness feedback: An automatic mechanism for stabilizing voice amplitude. J Acoust Soc Am. 2006;119:2363–2371. doi: 10.1121/1.2173513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Osmanski MS, Dooling RJ. The effect of altered auditory feedback on control of vocal production in budgerigars (Melopsittacus undulatus) J Acoust Soc Am. 2009;126:911–919. doi: 10.1121/1.3158928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Hage SR, Jiang T, Berquist SW, Feng J, Metzner W. Ambient noise induces independent shifts in call frequency and amplitude within the Lombard effect in echolocating bats. Proc Natl Acad Sci USA. 2013;110:4063–4068. doi: 10.1073/pnas.1211533110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Fay RR, Coombs S. Neural mechanisms in sound detection and temporal summation. Hear Res. 1983;10:69–92. doi: 10.1016/0378-5955(83)90018-7. [DOI] [PubMed] [Google Scholar]
  • 28.Schwartz JJ, Wells KD. Interspecific acoustic interactions of the neotropical treefrog Hyla ebraccata. Behav Ecol Sociobiol. 1984;14:211–224. [Google Scholar]
  • 29.Dooling RJ, Searcy MH. Temporal integration of acoustic signals by the budgerigar (Melopsittacus undulatus) J Acoust Soc Am. 1985;77:1917–1920. doi: 10.1121/1.391835. [DOI] [PubMed] [Google Scholar]
  • 30.Garnier M, Henrich N, Dubois D. Influence of sound immersion and communicative interaction on the Lombard effect. J Speech Lang Hear Res. 2010;53:588–608. doi: 10.1044/1092-4388(2009/08-0138). [DOI] [PubMed] [Google Scholar]
  • 31.Patel R, Schell KW. The influence of linguistic content on the Lombard effect. J Speech Lang Hear Res. 2008;51:209–220. doi: 10.1044/1092-4388(2008/016). [DOI] [PubMed] [Google Scholar]
  • 32.Pick HL, Jr, Siegel GM, Fox PW, Garber SR, Kearney JK. Inhibiting the Lombard effect. J Acoust Soc Am. 1989;85:894–900. doi: 10.1121/1.397561. [DOI] [PubMed] [Google Scholar]
  • 33.Kothari NB, Wohlgemuth MJ, Hulgard K, Surlykke A, Moss CF. Timing matters: Sonar call groups facilitate target localization in bats. Front Physiol. 2014;5:168. doi: 10.3389/fphys.2014.00168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Luo J, Wiegrebe L. Biomechanical control of vocal plasticity in an echolocating bat. J Exp Biol. 2016;219:878–886. doi: 10.1242/jeb.134957. [DOI] [PubMed] [Google Scholar]
  • 35.Luo J, Lingner A, Firzlaff U, Wiegrebe L. The Lombard effect emerges early in young bats: Implications for the development of audio-vocal integration. J Exp Biol. 2017;220:1032–1037. doi: 10.1242/jeb.151050. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File
Download video file (14.6MB, mp4)
Supplementary File
pnas.1702671114.sd01.pdf (38.7KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES