Population data indicate that thyroid regulation is consistent with an equilibrium-point model, but not with a set-point model

Although it is believed that normal thyroid hormone levels are set points, representing individually pre-determined reference levels, in this paper, we discuss how analysis of the population distribution of Free Thyroxine/Thyroid Simulating Hormone (FT4/TSH) levels supports a model of homeostasis in which these levels represent the equilibrium points of the physiologic processes of homeostasis alone.

This discussion follows on from our previous work¹ in which we differentiated the curve describing the population distribution of FT4/TSH levels (the ‘population curve’) from the curve describing the physiologic relationship of TSH suppression by FT4 (the ‘TSH curve’). We demonstrated¹ that the population curve theoretically could have a positive, neutral or negative slope depending on the pattern of population inter-individual variation in the TSH curve and the ‘T4 curve’ (the curve describing the stimulation of FT4 by TSH). The fact that the empiric population curve resembles the TSH curve, in also having a negative slope, indicates that in the population inter-individual variation in TSH curves is less than the inter-individual variation in T4 curves. We discuss here how the negative slope of the population curve also provides evidence as to the nature of FT4 homeostasis.

The prevailing model of homeostasis,² and particularly as it applies to FT4 levels,³ is a ‘set point’ model. All set-point models require an obvious set point (a physical/physiologic reference signal) or a hidden set point (a “mathematical” reference signal based on some internal property of the system). Apart from the means to specify such a set point, such physiology also requires that the body has the means to identify the desired level of the parameter to be so specified, a means to sense an ‘error signal’ (a deviation from this set point), and a linked ‘corrective’ process.²

Thus there has arisen a conception that the body aims for a particular but variable FT4 value,³ and that hypothalamus-pituitary function is controlled to attain and maintain this target level.³ Research has been directed at identifying individuals' personal set points, rather than relying on population ranges, so that thyroid disorders may be better diagnosed and treated.⁴

In contrast, an equilibrium or balance model requires no reference level; the level of a parameter in this model reflects the balance point of the physiologic processes acting on the parameter. In the case of FT4 levels the balance point is that which results from the closed control-loop of FT4 and TSH, i.e. the TSH and T4 curves, each based on proportional control.

In the set point model of FT4 regulation, given that the set point is a reference point set independently of the thyroid, it must be possible for 2 individuals to be identical in terms of thyroid gland sensitivity to TSH (i.e., to have identical T4 curves) but have different FT4 set points. The prevailing set point model of regulation model requires that the hypothalamus/pituitary attains the appropriate different set point levels by maintaining the different appropriate levels of TSH. As the T4 curve has a positive slope, the individual with the higher FT4 set point must have the higher prevailing TSH level.

If we extend this to a population with inter-individual variation in FT4 set points and T4 curves, we can divide this population into different groups. For the purposes of this analysis we compare the half with higher set points with the half with lower set points. Because of the independence of each individual's T4 set point from his/her T4 curve, these 2 halves must be identical in terms of their T4 curve distributions. Therefore the half with the higher FT4 set points must, by the same logic as above, have (on average) higher prevailing TSH levels.

However, the population curve has a negative slope reflecting the fact that in the population individuals with higher FT4 have (on average) lower TSH levels. Therefore the set point model cannot be valid.

By contrast an equilibrium point model of FT4 regulation, on account of not requiring independence of the FT4 level and the T4 curve, can generate a population in which higher FT4 values are associated with (on average) lower TSH values.

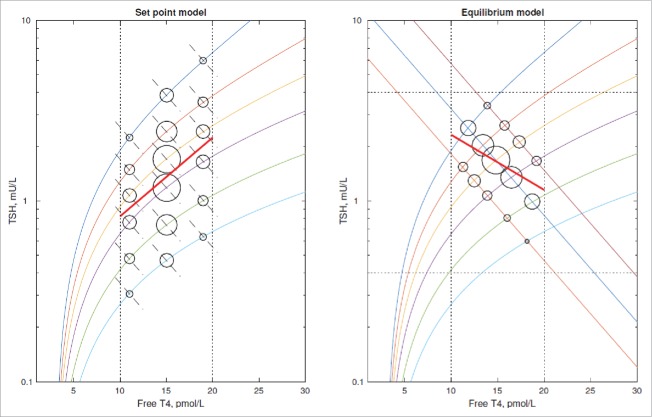
A mathematical representation of the above argument is shown in Figure 1. We show a representation of the population distribution of normal T4 curves. The panel representing the set point model shows the FT4 levels being driven by TSH curves, adjusted by mechanisms unimportant to this discussion, to match the set point levels. In contrast the panel representing the equilibrium point model shows the FT4 values lying at the intersection of the given T4 and TSH curves.

Figure 1.

Comparison of the set point model and equilibrium point model in terms of population distribution of FT4/TSH levels. The area of the circles indicates the number of individuals with FT4/TSH levels at that point i.e., in this case the clustering of individuals around the mean. The multiple lines with a positive slope represent the inter-individual variation in T4 curves and the lines with negative slope represent the inter-individual variation in TSH curves. These latter lines are shown as dashed in the set point model to indicate their ability to be adjusted so as to attain the set point FT4. The set point model implies a line of best fit (bold line) with a positive slope but it is possible for an equilibrium point model to generate a line of best fit with a negative slope.

The set point model implies that the FT4 level is set externally to thyroid gland physiology and thus is independent of the T4 curve. Therefore the distribution of FT4 levels on each of the T4 curves is identical to the population distribution. On each of the T4 curves, higher FT4 levels are accompanied by and driven by higher TSH levels. The population curve in this situation must have a positive slope (Fig. 1).

In an equilibrium model of FT4 regulation it is not necessary that the distribution of FT4 levels be identical on each T4 curve. If the distribution of TSH curves is restricted as compared with the distribution of T4 curves a negatively sloped population curve is generated (Fig. 1).

To maintain the set point model one could propose that the the dominant controller of FT4 levels is not TSH, or that the 2 halves of the population are sufficiently different in terms of the T4 curve distribution that a negative population curve is generated. Both proposals are implausible. There is no described physiology whereby the FT4 /TSH feedback loop is not the major controller of thyroid physiology, and any putative discrepancy in T4 curve distribution would have to go beyond merely compensating for the different set points, as such compensation would result in a population curve with zero rather than a negative slope.

Triiodothyronine (T3) physiology does not save the thyroid set point model. The physiologic T3/TSH relationships are similar but not as tight as the T4/TSH relationships,⁴ and the population T3 correlation with TSH is similar to the population T4 correlation in being negative.⁵ Thus T3 homeostasis also behaves as an equilibrium.

The validity of all of the previously described physiologic processes concerning FT4 homeostasis, the hereditary nature of FT4 levels,³ their intra-individual stability³ as compared with the population range, and their variation in response to physiologic and pathological stimuli,³ as well as the importance of deiodinases, hormone transporters, transcription factors, and other processes of thyroid hormone metabolism are not challenged by this paper- they are equally valid in set point and equilibrium point models.

Other work regarding the physiologic effects of different hormone levels within the normal range, the effects of genetic polymorphisms of genes controlling physiologic processes,⁴ and the effects of changing the mass of the thyroid or pituitary on FT4 levels⁴ also suggest that thyroid hormone levels are equilibrium points.

In summary we have shown that the analysis of statistical population data can provide information, not available from empiric experimentation, concerning fundamental physiologic processes. The equilibrium model of thyroid regulation is simple, consistent with evolutionary principles, and consistent in the most parsimonious way with all of the data from physiologic and population studies.

The principles of this analysis are applicable to the analysis of other physiologic processes.