Unsupervised Learning for Robust Respiratory Signal Estimation from X-Ray Fluoroscopy

Abstract

Respiratory signals are required for image gating and motion compensation in minimally invasive interventions. In X-ray fluoroscopy, extraction of a respiratory signal can be challenging due to characteristics of interventional imaging, in particular injection of contrast agent and automatic exposure control. We present a novel method for respiratory signal extraction based on dimensionality reduction that can tolerate these events. Images are divided into patches of multiple sizes. Low-dimensional embeddings are generated for each patch using illumination-invariant kernel PCA. Patches with respiratory information are selected automatically by agglomerative clustering. The signals from this respiratory cluster are combined robustly to a single respiratory signal.

In the experiments, we evaluate our method on a variety of scenarios. If the diaphragm is visible, we track its superior-inferior motion as ground truth. Our method has a correlation coefficient of more than 91% with the ground truth irrespective of whether or not contrast agent injection or automatic exposure control occur. Additionally, we show that very similar signals are estimated from biplane sequences and from sequences without visible diaphragm. Since all these cases are handled automatically, the method is robust enough to be considered for use in a clinical setting.

I. Introduction

Catheter-based interventions are minimally invasive procedures to diagnose and treat a wide array of diseases. These include cardiovascular interventions to treat structural heart disease and cardiac rhythm disorders, as well as interventional radiological procedures such as transarterial chemoembolization to treat liver tumors. Catheterization is commonly guided using X-ray fluoroscopy images acquired with a C-arm system. Fluoroscopy visualizes interventional devices and bones well, but soft tissue has poor contrast. Injection of iodinated contrast agent can help to visualize anatomic structures. However, contrast agent in high doses is potentially harmful and is applied sparingly, especially during pediatric procedures. Another approach to visualize soft tissue is augmented fluoroscopy. Structures of interest are segmented in a 3-D modality, e.g., MR or CT, and overlaid in realtime on top of the fluoroscopic images [1], [2]. These overlays are usually static, but newer approaches try to compensate for patient motion by animating the overlays according to the motion visible in the X-ray images, in particular respiratory motion [3], [4], to increase accuracy and reduce procedure times.

To realize this motion compensation in augmented fluoroscopy, motion modeling is a promising approach [5]. Motion models require a respiratory surrogate signal, which could be provided by the proposed method. There are other situations when it is highly desirable to automatically extract the respiratory state of the patient from fluoroscopic images. For example, even if only a static overlay is used, it is only accurate in a single phase of the respiratory cycle, which can be detected and highlighted using the respiratory signal. Furthermore, for registration between the X-ray coordinate system and the 3-D modality used for overlay creation, the respiratory state should be the same in all the involved images. Motion estimation in X-ray images also benefits from respiratory information [6]. Another potential clinical application of our method is radiation therapy in the lung or abdomen, where tumors are affected by respiratory motion. Image-based surrogate signals could be used in a motion model to predict the tumor motion and to adapt the treatment beam accordingly [7].

External devices to measure respiratory signals are available, for example spirometer [8], belts with pressure sensors [9], or range imaging devices [10]. These devices require additional setup time and must be synchronized or registered with the X-ray system. Consequently, they are not commonly used. Image-based estimation of the respiratory signal does not have these drawbacks, but has to face multiple challenges in fluoroscopy. First of all, the contrast of soft tissue is low. Thus, it might be hard to detect the respiratory state, especially if collimation is used. No assumptions about C-arm angulation, table position, or imaging parameters should be made, as the physician or the system can vary them during the intervention and the respiratory signal estimation should work in all cases. In particular, automatic exposure control (AEC) changes the brightness of the images, which invalidates many assumptions on intensity. Other challenges are injection of contrast agent and movement of interventional devices, which cause strong local intensity changes in the image that are not related to respiratory motion.

In the literature, several algorithms for respiratory signal extraction have been proposed. The intensity changes of a region of interest (ROI) over time can constitute a respiratory signal [11], but the ROI must be chosen manually for each C-arm and table position. A popular idea is diaphragm tracking, e.g., [3], [4], [12], [13], but it is problematic in X-ray due to collimation and varying C-arm angulations. The above methods have some built-in assumptions about the X-ray images that are often violated. In recent years, manifold learning has been the dominating paradigm for respiratory signal extraction from medical images, for example in MR [14], ultrasound [14], SPECT [15], [16], and X-ray [17], [18], [19]. In the domain of X-ray fluoroscopy, Fischer et al. applied incremental manifold learning to extract the respiratory signal in realtime [17]. As this method depends on global intensity comparisons, it is not robust to automatic exposure control or contrast agent injection. Panayiotou et al. extracted tubular regions from fluoroscopic images before dimensionality reduction [18]. According to their experiments, the technique is robust to contrast agent. However, it is designed and evaluated only for retrospective gating, i.e., its performance is unclear for realtime motion compensation. In contrast to [18], Ma et al. suppressed tubular structures before applying principal component analysis (PCA) [19], and showed that it gives better results.

In this article, we propose a new method for respiratory signal extraction from X-ray fluoroscopy images. It is based on unsupervised learning and designed to be robust and widely applicable for the challenging case of interventional imaging, where fluoroscopic images are acquired with different and small fields of view, C-arm angles, and AEC. Additional challenges result from interactions of the physician, for example injection of contrast agent and insertion and movement of interventional devices. To handle this variety, we propose to extract many respiratory signals from each image using a patch-based approach. Two unsupervised learning methods are combined for respiratory signal extraction, namely dimensionality reduction and clustering. Dimensionality reduction, in particular kernel PCA, creates a set of proposal signals from the patches. We show that intensity variations occur frequently in fluoroscopic images and make kernel PCA invariant to these changes. The proposal signals from all the patches are clustered to find the respiratory information and to combine the information from all the patches such that outliers can be tolerated. Finally, we evaluate the method extensively on clinical X-ray sequences. We compare the performance on contrasted and non-contrasted images, different zoom levels, and biplane acquisitions. We show that our method performs robustly and accurately in these cases and that it is fast enough for interventional use.

II. Methods

An overview visualization of our method is given in Fig. 2. The images are divided into non-overlapping patches. On each patch, dimensionality reduction is applied to compute a low-dimensional embedding. Using clustering and robust combination of signals, a joint respiratory signal is created from the low-dimensional embeddings. Each of these steps is detailed in the following sections.

Fig. 2.

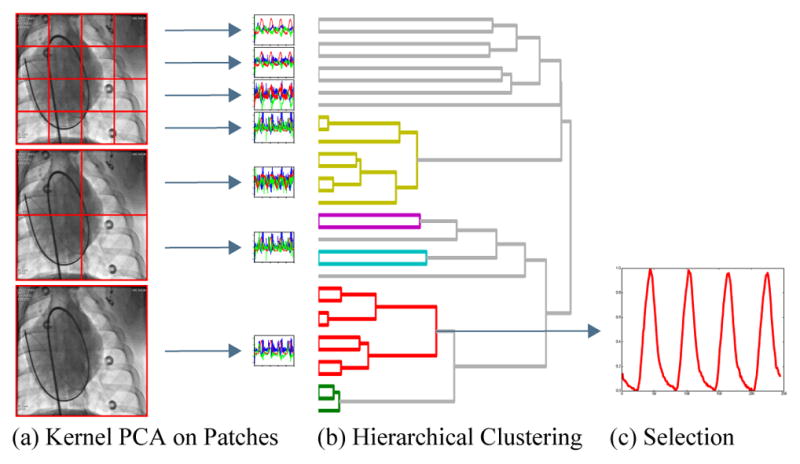
Illustration of the proposed respiratory signal estimation. From the medical image, non-overlapping patches are extracted at multiple resolutions (a). Kernel PCA is applied to each patch leading to a set of low-dimensional embeddings, where each color represents a different dimension. Hierarchical clustering, represented by a dendrogram, finds similar signals (b). The respiratory cluster is identified and the corresponding signals are combined and normalized to give the respiratory signal (c).

The notation in this paper is as follows: lower case and upper case letters denote scalar values (e.g., p, T, ε), bold lower case letters represent vectors (e.g., y, e), and bold upper case letters denote matrices (e.g., K). Upper case calligraphic letters are sets (e.g., 𝒞). Upper indices in parentheses select a certain point in time from a set of variables (e.g., y^(t)). Upper indices in brackets indicate the patch number (e.g., ρ^[p]) and upper indices in braces indicate the eigenvalues or eigenvectors (e.g., λ^{i}, e^{i}) of a matrix. Lower indices denote a vector component, (e.g., s_i).

A. Background

Respiratory signal extraction is generally divided into two phases, the learning phase and the application phase. In the learning phase, a set of training images y^(t), t ∈ {1, …, T} is used to learn the mapping from the image space to the respiratory signal s^(t) ∈ ℝ^D_s, where D_s is the dimension of the respiratory signal. In the application phase, the respiratory signal is estimated from newly acquired images using the previously learned mapping in realtime. Some authors only consider the learning phase, which can be used without the application phase for retrospective analysis of image sequences.

Dimensionality reduction is an approach that is well-suited for respiratory signal extraction. The main intuition is that the high-dimensional image data actually lies on a smooth, low-dimensional subspace. This is well justified for medical imaging, because the images are acquired in a controlled environment. In particular for interventional fluoroscopic images, the main sources of variation are cardiac and respiratory motion. For respiratory signal extraction, dimensionality reduction is usually applied directly to the vectorized X-ray images y ∈ ℝ^D_y. For an image of size D_u×D_v, the dimension of the vectorized representation is D_y = D_u · D_v. Potentially, the images are processed [19] or masks are applied [18] before vectorization. A mapping, specific to the C-arm angulation, the table position, and the patient, is learned from the image data itself in an unsupervised manner.

B. Kernel PCA

Our respiratory signal extraction method uses kernel PCA (KPCA) [20], which is a nonlinear extension of PCA. It is based on the kernel matrix K, where the entries of the matrix are defined as K_ij = k(y⁽ⁱ⁾, y^(j)). The function k is a Mercer kernel, such that it corresponds to the dot product in a feature space. If k is linear, the result of kernel PCA is identical to conventional PCA and the feature space is the image space. Learning of the mapping involves computing the eigendecomposition of the kernel matrix

$${\lambda }^{\{i\}}{\mathit{e}}^{\{i\}}=\mathit{K}{\mathit{e}}^{\{i\}},$$ (1)

where λ^{i} are the eigenvalues and e^{i} the eigenvectors of K, sorted by decreasing eigenvalues. To map training samples or previously unseen samples y to the principle component i, the projection on the respective eigenvector is computed

$${\mathit{s}}_i=\frac{1}{{\lambda }^{\{i\}}}\sum _{t=1}^T{\mathit{e}}_t^{\{i\}}k\left({\mathit{y}}^{(t)},\mathit{y}\right),$$ (2)

where s ∈ ℝ^D_s is a D_s-dimensional embedding signal. The division by λ^{i} normalizes the variance of each component i to 1. Respiratory motion is represented in one of the first dimensions of s, since it is one of the major sources of intensity variation.

C. Correlation Kernel

Most dimensionality reduction methods depend on the magnitude of the input data, e.g., by computing intensity differences [21], [22] or by reconstructing intensities of a sample from its neighbors [23] or from the low-dimensional embedding (PCA). This is susceptible to intensity variations caused by automatic exposure control. The same is true for common kernels used in kernel PCA, e.g., radial basis function, polynomial, or sigmoid kernel. For robustness against intensity variations, we use a normalized cross-correlation (NCC) kernel

$$k_{\text{NCC}}\left({\mathit{y}}^{(i)},{\mathit{y}}^{(j)}\right)=\frac{1}{D_{\mathit{y}}}\frac{{\left({\mathit{y}}^{(i)}-{\overline{\mathit{y}}}^{(i)}\right)}^{\top }\left({\mathit{y}}^{(j)}-{\overline{\mathit{y}}}^{(j)}\right)}{{\sigma }_{{\mathit{y}}^{(i)}}{\sigma }_{{\mathit{y}}^{(j)}}},$$ (3)

where ȳ is the mean and σ_y is the standard deviation of y. The output of k_NCC is normalized between [−1, 1]. This correlation kernel is identical to the linear kernel with input images normalized to ȳ = 0 and σ_y = 1. This enables to choose PCA or kernel PCA for dimensionality reduction, depending on the problem setup. The complexity of kernel PCA is dominated by the number of training samples T, while PCA is dominated by the image dimensionality D_y. For images, T is usually much smaller than D_y. However, if dimensionality reduction is applied to small patches, then T ≈ D_y and it might be faster to use conventional PCA. For sake of simplicity, we always use kernel PCA in this paper.

D. Patch-based Processing

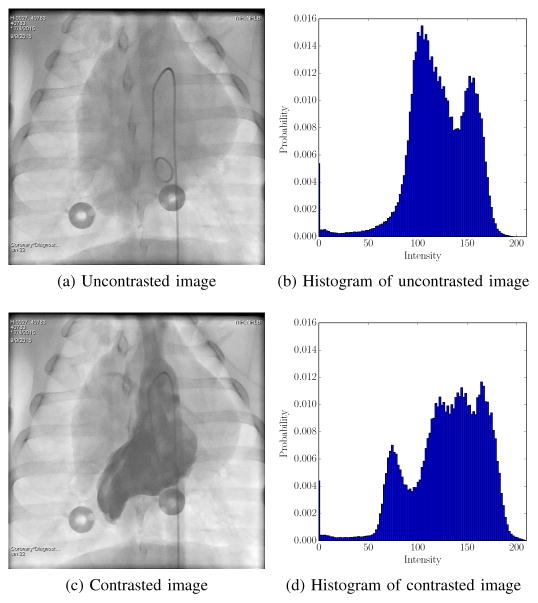
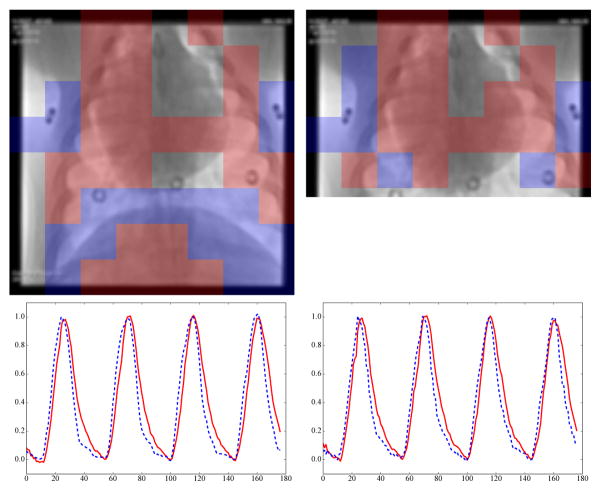
The correlation kernel provides global intensity invariance. However, AEC also leads to local intensity variations. AEC employs vendor-specific criteria to stabilize the intensity distribution in a certain region of interest. It is triggered by a change in the average attenuation in this region due to motion or contrast agent. This leads to intensity changes outside the region of interest which are not related to motion, as illustrated in Fig. 3. Both images are approximately in the same respiratory state, but one of them contains contrast agent. In the histograms, the contrast agent is visible as an additional peak of low image intensities. In addition, the remaining histogram is shifted to the right, because AEC increases the X-ray tube power. Global intensity normalization is challenging in this case due to the additional peak caused by the contrast agent.

Fig. 3.

Comparison of images with and without contrast agent. The contrast agent strongly attenuates the X-rays, which is visible as an additional peak at intensity 75 in the histogram Fig. 3d. In consequence, AEC increases the X-ray tube power, which shifts the rest of the histogram to the right.

With patch-based processing, even local illumination variations can be tolerated. To use as much information from the images as possible, we extract patches at multiple resolutions. A minimal patch size Q × Q is specified as a parameter of the method. The number of resolutions R is determined automatically by increasing the patch size by factors of 2 until the patch is too big to fit in the image Q · 2^R−1 > min (D_v, D_u). Non-overlapping patches ρ are extracted from the images y at each resolution. For an image of size D_u × D_v, this leads to $P={\sum }_{r=1}^R\lfloor D_u/Q/2^{r-1}\rfloor ·\lfloor D_v/Q/2^{r-1}\rfloor$ patches ρ^[p], p ∈ {1, …, P }. Kernel PCA is applied to each patch independently.

The major advantage of patch-based processing is that many respiratory signals are estimated from a single image. This allows to combine the signals intelligently and to tolerate outliers. Even if some of the patches are corrupted, for example due to contrast agent or interventional devices, a good signal can still be generate from the remaining patches. Global methods do not have such a recovery mechanism if the single global signal that they estimate is incorrect due to local corruptions of the image.

E. Signal Combination

From the previous steps, we have P signals s^[p], each D_s-dimensional. It is unknown which dimensions or which patches contain respiratory information. In addition, the sign of corresponding signals might be flipped relative to each other. These ambiguities of sign and ordering are inherent in dimensionality reduction and must be removed in the learning phase.

To remove the ambiguity of ordering, we use clustering. The input samples for clustering are the 1-D signals from all possible patches and dimensions, S = P ·D_s overall. A matrix M ∈ ℝ^S×T is defined as the input of clustering

$$\left(\begin{array}{cccc}{\mathit{s}}_1^{[1](1)}& {\mathit{s}}_1^{[1](2)}& \cdots & {\mathit{s}}_1^{[1](T)}\\ {\mathit{s}}_2^{[1](1)}& {\mathit{s}}_2^{[1](2)}& \cdots & {\mathit{s}}_2^{[1](T)}\\ ⋮& ⋮& \cdots & ⋮\\ {\mathit{s}}_{D_{\mathit{s}}}^{[1](1)}& {\mathit{s}}_{D_{\mathit{s}}}^{[1](2)}& \cdots & {\mathit{s}}_{D_{\mathit{s}}}^{[1](T)}\\ {\mathit{s}}_1^{[2](1)}& {\mathit{s}}_1^{[2](2)}& \cdots & {\mathit{s}}_1^{[2](T)}\\ ⋮& ⋮& \cdots & ⋮\\ {\mathit{s}}_{D_{\mathit{s}}}^{[P](1)}& {\mathit{s}}_{D_{\mathit{s}}}^{[P](2)}& \cdots & {\mathit{s}}_{D_{\mathit{s}}}^{[P](T)}\end{array}\right),$$ (4)

where each of the S rows is an input sample to clustering, containing the T time points as features. We use agglomerative clustering to find clusters of similar signals. Agglomerative clustering is a variant of hierarchical clustering, where samples are recursively agglomerated until all samples are combined. This results in a tree representation, where the root contains all samples and the leafs single samples. Clusters of varying size appear on intermediate levels of the tree. There are different ways to build the tree and extract clusters, for details see [24]. We use average linkage, where the distance between clusters is defined as the average of all sample distances. A nice property of hierarchical clustering is that the number of clusters does not need to be specified a priori. Instead, all clusters with an average distance smaller than ε are extracted from the tree. ε is a cluster similarity threshold, i.e., two clusters are combined if the average distance between the samples of the clusters are below ε. In our implementation, we additionally require that the largest cluster contains at least Δ number of samples. This ensures that the respiratory signal is supported by multiple patches. If this is not the case, ε is doubled until a sufficiently large cluster is found. However, for high values of ε, less similar signals end up in the same cluster, which might deteriorate the respiratory signal. Depending on the clinical application, it might be preferable to notify the user that a proper respiratory signal could not be found.

Hierarchical clustering works with all kinds of distance measures. To be tolerant w.r.t. to the possible sign flip in the signals, our distance measure is based on the normalized cross correlation between the signals

$$d(\mathit{a},\mathit{b})=1-\mid k_{\text{NCC}}(\mathit{a},\mathit{b})\mid ,$$ (5)

where a, b are two arbitrary 1-D signals, i.e., rows of M. With this normalized distance measure, it is easy to set a generally applicable ε.

The result of the clustering are C clusters 𝒞_c, 𝒞_c1 ∩ 𝒞_c2 = ∅, ${\cup }_{c=1}^C{\mathcal{C}}_c=\{1,\dots ,S\}$, i.e., each row index of M is part of exactly one cluster. The clusters are sorted by decreasing cluster size. Note that not all signals from step (b) in Fig. 2 contribute to the signal in (c), because only one respiratory cluster is selected. Additionally, the signal in (c) does not necessarily have the same color, representing the dimension of the component, or sign as the corresponding signal in (a), which shows that the ordering and sign ambiguities are removed during clustering.

After clustering, we can compute a prototype signal for each cluster. All the signals assigned to a cluster are aligned using the sign of the NCC, which removes the sign ambiguity. The aligned signals are combined using the median

$${\mathit{s}}_c^{(t)}=\underset{i\in {\mathcal{C}}_c}{\text{median}}{M}_{it}$$ (6)

to yield a global C-dimensional surrogate s^(t). Each time point t of ${\mathit{s}}_c^{(t)}$ is the median over multiple rows of M. The median operator is robust to outliers and fast to compute. This robustness is necessary because outliers can occur in the application phase due to events like injection of contrast agent or usage of interventional devices, which are common in interventional fluoroscopy. The mean and mode operator were also investigated to perform this signal combination. The mean is not robust enough. The mode would have a similar robustness, but is slower because it does not have a closed-form solution. In addition, we tried to reject outlier signals based on the appearance of the patches. Even though most outliers can be detected this way, the resulting signals are similar. In our experience, the number of outliers is small enough to have little impact after the median operator. However, the algorithm would have been slower and more complex.

F. Selection of Respiratory Dimension and Normalization

The dimension with respiratory information must be selected from the global surrogate signal ${\mathit{s}}_c^{(t)}$, c ∈ {1, …, C} computed in Eq. (6). The criteria for selection are two general properties of respiratory motion. The first criterion is the breathing frequency, which is assumed to be above 0.1 Hz and below 1 Hz. Dimensions of ${\mathit{s}}_c^{(t)}$ with a peak frequency outside of this range are removed. The second criterion exploits that respiratory motion affects large parts of the torso, which means it is visible in many patches. Thus, the remaining dimensions of ${\mathit{s}}_c^{(t)}$ are sorted by cluster size and the largest is chosen.

We normalize the respiratory signal to the interval [0, 1] based on the median of the minimal and maximal peaks of the signal in the learning phase. By convention, 0 corresponds to full exhalation and 1 to full inhalation. Due to the sign ambiguity of dimensionality reduction, this is not guaranteed automatically. The issue of global sign is commonly neglected in the literature [14], [15], [17], [18], [19], [25], [26], with the exception of [16], because it does not affect the commonly used correlation measures for evaluating algorithm performance. To determine the sign, we use a heuristic that is based on the intuition that more time is spent in exhalation than in inhalation [16]. As the mean value of the unnormalized respiratory signal is close to 0, the absolute maximum value is ensured to be larger than the absolute minimum value. However, to apply the algorithm in a clinical setting, a more robust method to determine the global sign would be required.

G. Application Phase

The application phase involves fewer steps than the learning phase and all of them can be computed efficiently. Only patches that contribute to the respiratory cluster are processed. Kernel PCA is applied to each of them, i.e., a simple projection onto the eigenvectors that were computed in training. The signals can be aligned quickly, because any sign changes are known from the learning phase. Then the median operator is applied to combine all the signals from the cluster, see Eq. (6).

III. Experiments

A. Experimental setup

The images were acquired on flat-panel X-ray C-arm systems (Artis, Siemens Healthcare, Forchheim, Germany) from multiple sites. The dataset comprises ventilated pigs, pigs with manual ventilation, and humans. All experiments were approved by institutional review board (for humans) or animal care and use committee (for animals). Overall, our experiments contain 60 sequences of a length of 53 – 587 images. The mean sequence length is 214 images and the median length 199 images. The framerate is 10 – 15 Hz and the pixel spacing is 0.154 – 0.432 mm. The original image size is 512 × 512 – 1024 × 1024, but we downsample the images by multiples of 2 to have a size close to 128 × 128 pixels since methods based on dimensionality reduction do not require a high resolution and the runtime is reduced drastically. Subsets of these images are used for each experiment depending on their properties, e.g., all sequences with contrast agent are used in Section III-C and all images with biplane imaging are used in Section III-D.

We implement several methods as comparison to our proposed method, which we call Multi-Resolution KPCA in the experiments. The most basic method is the application of PCA to the images. This is related to the approach of Ma et al., except that we do not apply morphological closing before PCA because our images do not contain coronaries [19]. It is also similar to the methods of Panayiotou et al., but without focus on tubular structures [18]. As a representative of manifold learning, we use Isomap [14], [17]. Additionally, we implement the two major contributions of this article individually, specifically, patch-based processing (Multi-Resolution PCA) and illumination-invariant kernel PCA (KPCA). Thus, we can analyze the impact of each step individually. Furthermore, we try our method without multi-resolution information, i.e., only patches at the specified patch size Q are extracted (Patch KPCA). The post-processing of Section II-F is applied to all methods to avoid a bias towards our method. Instead of clusters and their size, the embedding dimensions and their explained variances are used in Isomap, PCA, and KPCA for selection of the respiratory dimension.

The methods are trained on the first 45 images of each sequence if not stated otherwise. With the framerates of our dataset, this corresponds to 3–4.5 s, which is sufficient for 1–2 breathing cycles. The hyper-parameters for all methods were determined visually. The same parameters are used for all experiments. The patch size for patch-based methods is Q = 16. The dimensionality of the surrogate signals is D_s = 3. The cluster similarity threshold is ε = 0.05, while the minimum number of samples in a cluster is set to Δ = 8. The number of neighbors for building the neighborhood graph in Isomap is 10.

All the methods are implemented in Python using its scientific libraries. In particular, kernel PCA and Isomap are based on scikit-learn [27]. The implementation only uses the CPU, i.e., the GPU is not used for acceleration. The experiments are executed on a consumer notebook with an Intel Core i7-3720QM CPU and 8 GB of RAM.

B. Comparison to Diaphragm Tracking

For quantitative evaluation, the diaphragm motion in superior-inferior direction is used as ground truth. It is a good surrogate of the respiratory state because it corresponds to internal breathing motion. Diaphragm tracking itself is not a practical method for respiratory signal estimation in fluoroscopy since the visibility of the diaphragm cannot be guaranteed under all circumstances. To track the diaphragm, we apply template matching with manual corrections where necessary, which is appropriate since it only serves as the ground truth. The correlation coefficient is used to compare the outputs of the investigated methods with the ground truth signal. The experiment is performed on 25 sequences, all without injection of contrast agent.

C. Influence of Contrast Agent

We conduct special experiments to investigate the effect of contrast agent injection. Again, the estimated respiratory signals are compared to the superior-inferior motion of the diaphragm. 21 sequences comprising contrast agent injection in the left ventricle (6), pulmonary arteries (10), coronaries (2), and aorta (3) are processed. On average, 55% of the frames are contrasted in these sequences. In the first version of the experiment, the methods learn on a subsequence without contrast agent and are applied to the subsequence in which contrast agent is injected. In the second version, the subsequences for learning and application are reversed. If the signal extraction should be universally applicable without requiring special attention by the physician, both cases are important.

D. Comparison of Biplane Signals

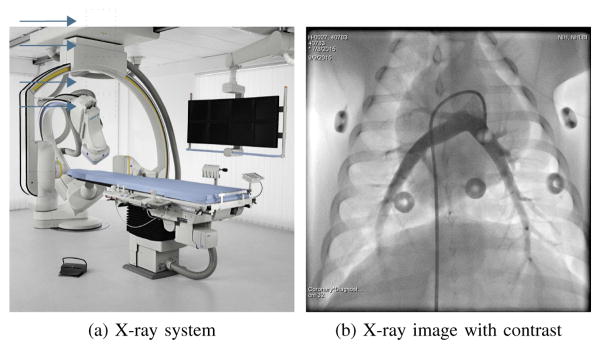
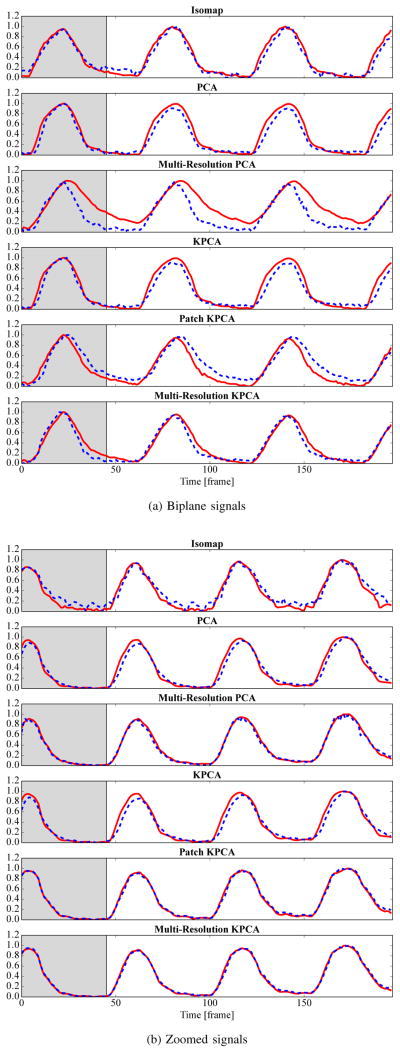
In biplane imaging, the C-arm systems has two X-ray sources and detector planes (plane A and B) and is able to alternately acquire images from two views, see Fig. 1a. As both views show the same patient, the estimated respiratory signals should be identical. In practice, plane B often has a smaller detector. Additionally, it does not show the patient in anterior-posterior projection, thus the image content and the motion directions are different. In this experiment, we check the similarity of the respiratory signals from both views for the investigated methods using the correlation coefficient on 2·10 biplane sequences. Exemplary biplane images are shown in Fig. 4.

Fig. 1.

A biplane X-ray system used for interventional applications (Fig. 1a) and an X-ray image of a pig with contrast agent injection in the pulmonary arteries (Fig. 1b).

Fig. 4.

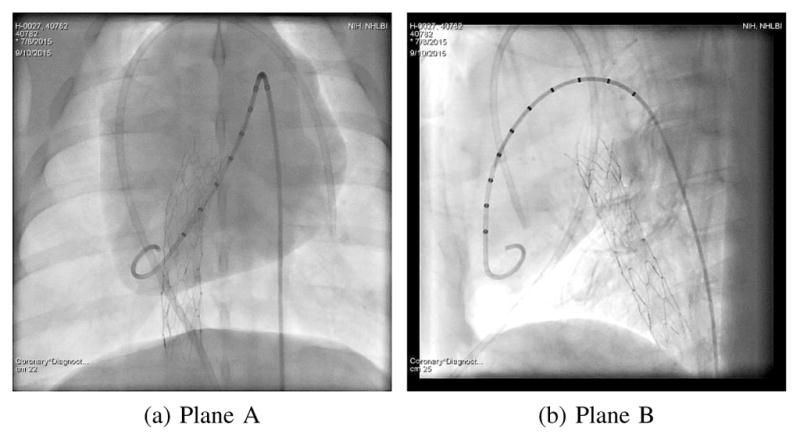
Simultaneously acquired biplane images from an X-ray system as in Fig. 1a should lead to identical respiratory signals.

E. Evaluation of Zooming

For X-ray images with a large field of view, respiratory signal extraction is easy. If the diaphragm is visible, many methods explicitly track the diaphragm or implicitly make use of the high-contrast structure that moves according to respiratory motion. However, there are many circumstances where the diaphragm is not in the field of view. In particular, collimation and zooming are used heavily by physicians to reduce the radiation exposure of the patient. Here, we evaluate the tolerance w.r.t. smaller fields of view. A region of interest (ROI) that excludes the diaphragm is defined. We can still use the diaphragm motion extracted from the full images as a reference signal. In addition, we compare the respiratory signal that each method estimates from the full image with the respiratory signal from the ROI using the correlation coefficient. The same 25 sequences as in Section III-B are used.

F. Runtime Measurement

The runtime of the methods is important because the usefulness of retrospective respiratory signal extraction is limited in an interventional setting. The duration of the learning phase and the duration of application phase is measured separately. Learning needs to be executed only once per C-arm angulation and table position. The accumulated duration of processing all the T training images is reported. The application phase is more time-critical, since it is executed once for each newly acquired X-ray image. The time for processing a single image is given. Additionally, the runtime of each step of our proposed algorithm is analyzed in more detail. The experiment is conducted for the same 25 sequences used in Section III-B.

G. Influence of Patch Size

The patch size is an important parameter of this algorithm. It potentially has a large influence on the robustness, accuracy, and runtime. Therefore, we perform the experiments on diaphragm tracking (Section III-B) and runtime (Section III-F) for varying patch sizes (Q ∈ {8, 16, 24, 32, 64}). For the patch size 64, only 5 patches per image are available. Thus, we reduced the minimum cluster size Δ to 2 for this case. To determine the contribution of the multi-resolution approach, we perform the experiment for Patch KPCA and Multi-Resolution KPCA.

H. Influence of Minimum Cluster Size

The behavior of clustering depends on the minimum cluster size Δ and the cluster similarity threshold ε. Jointly, they influence how many samples are clustered and how similar they need to be. The starting value of ε = 0.05 is small such that in the ideal case, the samples are very similar. In this experiment, we vary the minimum cluster size (Δ ∈ {4, 8, 16, 32, 64}) to analyze how the algorithm performance varies due to clustering. The experiments are conducted on the same data as Section III-B.

I. Analysis of Irregular Respiration

A common assumption is that respiration is periodic, which is valid for the 47 sequences of pigs on an automatic ventilator. These pigs have a constant breathing depth and frequency. In many interventions, the subjects are not on a ventilator, which leads to an increased variability in respiration. In our datasets, there are 8 sequences of manually ventilated pigs and 5 sequences of free-breathing humans. Out of the 47 sequences of ventilated pigs, the diaphragm is only visible in 33 sequences, which are used here because we can extract the ground truth signal. We analyze the behavior of our algorithm in these two cases quantitatively and qualitatively.

J. Analysis of Algorithm Statistics

The proposed method has an adaptive behavior mainly due to clustering. We report and analyze statistics on this adaptivity. For example, the clustering selects a subset of patches from different resolutions and selects one of the D_s dimensions of the low-dimensional embedding signal. For clustering itself, we are interested in the cluster size, which reflects the spatial support of the respiratory signal. In addition, we measure how often an increase in ε is required to get a sufficiently large respiratory cluster. The statistics are calculated on 67 sequences from Section III-B and Section III-C. Note that the sequences from Section III-C are used twice with different subsequences for training.

IV. Results

The results of the experiments that compare to a ground truth signal based on diaphragm tracking are summarized in Table I, while the correlation coefficient between different versions of the same sequence are given in Table II.

TABLE I.

Comparison to Diaphragm Tracking on Fluoroscopic Images (Mean of NCC in % ± Standard Deviation)

	No Contrast	Zoom	Apply Contrast	Learn Contrast
Isomap	97 ± 3.6	91 ± 8.0	93 ± 6.3	75 ± 25
PCA	96 ± 8.6	92 ± 4.8	95 ± 4.1	83 ± 17
Multi-Resolution PCA	91 ± 7.5	89 ± 7.1	86 ± 13	65 ± 28
KPCA	97 ± 1.6	92 ± 5.0	97 ± 2.2	91 ± 13
Patch KPCA	92 ± 5.6	90 ± 7.6	97 ± 2.6	95 ± 6.5
Multi-Resolution KPCA	93 ± 5.5	92 ± 4.9	98 ± 1.9	98 ± 2.0

TABLE II.

Comparison of Respiratory Signals on Corresponding Images (Mean of NCC in % ± Standard Deviation)

	Biplane	Zoom
Isomap	93 ± 10	97 ± 1.7
PCA	96 ± 8.2	95 ± 9.0
Multi-Resolution PCA	92 ± 9.6	99 ± 3.2
KPCA	97 ± 7.1	97 ± 2.3
Patch KPCA	98 ± 1.8	98 ± 3.4
Multi-Resolution KPCA	98 ± 1.4	99 ± 1.6

A. Comparison to Diaphragm Tracking

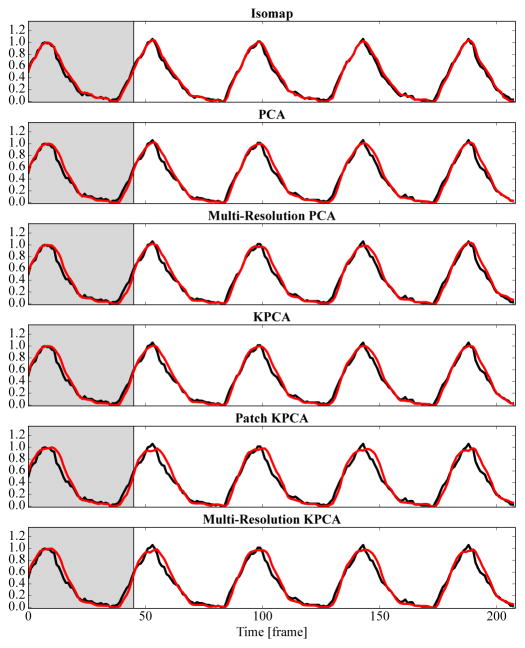
All methods have a high correlation coefficient of more than 0.9 with the diaphragm tracking signal, see the left column of Table I. The global methods PCA with 0.96, Isomap with 0.97, and kernel PCA with 0.97 are better than the patch-based methods. Exemplary respiratory signals are shown in Fig. 5. As indicated by the high correlation, all methods visually agree well with diaphragm tracking.

Fig. 5.

The reference respiratory signal created from diaphragm tracking (–) and the output of each method ( ) are shown. For this simple sequence without contrast agent injection, all methods deliver good results. The gray background indicates the learning phase. The vertical axis is normalized to 0–1. Best viewed in color.

B. Influence of Contrast Agent

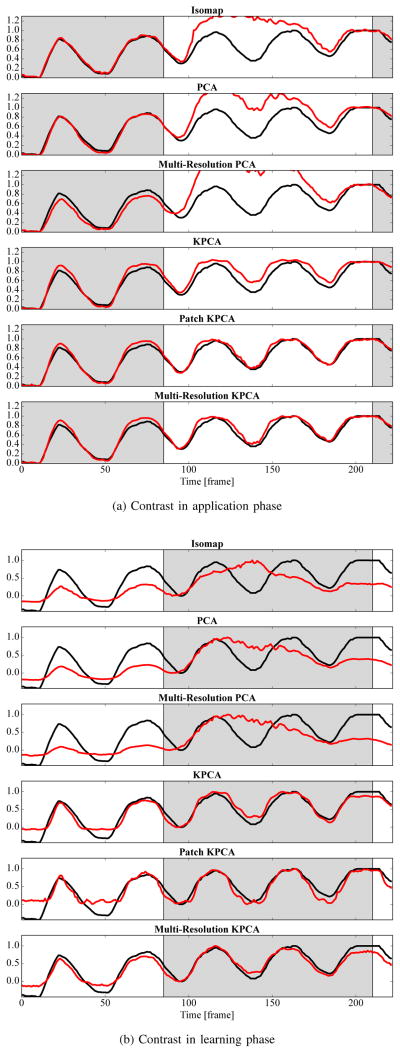
If respiratory signal extraction is trained on uncontrasted images and applied to contrasted images, most methods still perform well quantitatively. The reason is that the contrast agent rarely overlaps with the diaphragm, which is the main indicator for the respiratory signal. In addition, the amount of injected contrast agent is often sufficiently low such that AEC does not heavily change the intensities. The highest correlation coefficient is observed for KPCA with 0.97 and for Patch and Multi-Resolution KPCA with 0.97 and 0.98, respectively. For these methods, the results are at least as good as for the experiment without contrast agent. The correlation of Isomap and Multi-Resolution PCA decreases considerably. If the mapping is trained on contrasted images, previous methods track the contrast agent inflow instead of respiration. The correlation coefficient of the state-of-the-art methods PCA and Isomap is only 0.83 and 0.75, respectively. Multi-Resolution PCA deteriorates to 0.66 and kernel PCA to 0.91. Only the proposed combination of patches and kernel PCA still has an unchanged high correlation coefficient of 0.98. The possible effect of contrast agent on the respiratory signals is visualized in Fig. 6. In this sequence, contrast agent is injected in the left ventricle, which is such a large structure that it triggers AEC. The methods based on absolute intensity values are heavily disturbed by the resulting global change of image intensities. Quantitatively, the correlation coefficient in Fig. 6a is 0.78 for Isomap, 0.84 for PCA, 0.71 for Multi-Resolution PCA, 0.98 for KPCA, and 0.99 for Multi-Resolution KPCA. The effect is even worse when the injection happens during the learning phase, see Fig. 6b.

Fig. 6.

Respiratory signals extracted by all methods ( ) for an exemplary sequence with contrast agent injection. The gray background indicates the learning phase. In Fig. 6a, the contrast agent is injected in the application phase and in Fig. 6b in the learning phase. Diaphragm tracking is shown as a reference signal (–) in each plot. Best viewed in color.

C. Comparison of Biplane Signals

The correlation coefficient between signals from plane A and plane B is over 0.95 for all methods except Multi-Resolution PCA and Isomap. Multi-Resolution PCA has a correlation coefficient of only 0.92. The main reason for this low correlation is that some of the biplane sequences contain contrast agent, which Multi-Resolution PCA and Isomap do not tolerate well. With 0.98, the best correlation coefficient is achieved using our proposed Multi-Resolution KPCA. The quantitative results are summarized in the left column of Table II. A qualitative example for biplane signals is shown in Fig. 7a from a sequence without contrast agent injection. All methods have similar signals for plane A and B, except for Multi-Resolution PCA.

Fig. 7.

In Fig. 7a, signals from plane A ( ) and plane B ( ) are juxtaposed. In Fig. 7b, the signals are extracted from the full image ( ) and a region of interest that excludes the diaphragm ( ). The gray background indicates the learning phase. Best viewed in color.

D. Evaluation of Zooming

As listed in the zoom column of Table I, the average correlation coefficient of the output of all methods with the diaphragm is in a relatively small range. The worst result is achieved by Multi-Resolution PCA with 0.89 and the best result by Multi-Resolution KPCA with 0.92. For the relative comparison of signals from the full image and the zoomed image, all methods agree very well. In all cases, the average correlation coefficient is above 0.95. For the patch-based methods, the signals are nearly identical and the average correlation coefficient is above 0.98. The quantitative results are summarized in the right column of Table II. In Fig. 7b, the signals from the full image and the zoomed image excluding the diaphragm can be seen for an exemplary sequence. The main differences between the full and the zoomed signals are the level of noise or small baseline drifts. For the patch-based methods, these effects cannot be observed. Note that in Fig. 7, Multi-Resolution PCA is better than the baseline methods in Fig. 7b and KPCA is better in Fig. 7a, but Multi-Resolution KPCA combines the advantages of both.

E. Runtime Measurement

For the learning phase, the runtime is in an acceptable range for all methods. Isomap with 0.05 s and KPCA alone with 0.01 s are very fast, since their runtime depends mostly on the number of training images T and not the dimensionality D_y. The patch-based methods are quite slow with 0.12–0.36 s. The reason is that P PCAs or kernel PCAs are performed instead of 1. For the application phase, all methods can handle typical X-ray framerates of up to 15 Hz. Multi-Resolution KPCA is slowest with 8.4 ms per image, while PCA is fastest with 0.3 ms. All runtimes are summarized in Table III.

TABLE III.

Runtime of Respiratory Signal Extraction (Mean ± Standard Deviation)

	Learning time [s]	Application time [ms]
Isomap	0.05 ± 0.00	1.52 ± 0.91
PCA	0.08 ± 0.06	0.32 ± 0.03
Multi-Resolution PCA	0.36 ± 0.05	1.70 ± 1.06
KPCA	0.01 ± 0.00	6.09 ± 0.17
Patch KPCA	0.12 ± 0.01	4.92 ± 1.29
Multi-Resolution KPCA	0.25 ± 0.03	8.43 ± 1.90

We analyze the runtime of the proposed Multi-Resolution KPCA in more detail. During training, preprocessing of the images and alignment and normalization of the respiratory signal are negligible with less than 1% each. Patch extraction from the images takes 14% of the time and clustering 10%. With 73%, the majority of the time is spent to compute the kernel PCA for each patch. During the application phase, the distribution of the runtime is more balanced. Approximately 50% of the time is needed to extract the patches, and the other 50% to compute the projection onto the kernel PCA eigenvectors. The time spent for preprocessing the images, and combining the signals from the patches is negligible. To sum up, the operations that must be performed for each patch have the largest share of the runtime. For an image size of 128 × 128 and a patch size of Q = 16, for example, P = 85 patches are extracted and as many kernel PCAs are required.

F. Influence of Patch Size

The correlation with the diaphragm only changes slightly with the patch size Q. For Multi-Resolution KPCA, it is 0.94 for Q = 8, 0.93 for Q = 16, 0.94 for Q = 24, 0.91 for Q = 32, and 0.92 for Q = 64. For Patch KPCA, the correlation for small patch sizes has similar values. It is 0.93 for Q = 8, 0.92 for Q = 16, and 0.94 for Q = 24. For the larger patch sizes of Q = 32 and Q = 64, the correlation drops to 0.87. For both methods, smaller patch sizes below Q = 32 are better. The multi-resolution approach is more stable w.r.t. changed patch sizes or larger patches. In general, larger patches can capture respiratory motion more accurately, since they are less affected by structures moving in or out of the patch. However, the brightness correction due to kernel PCA is less local, and the extracted signals become less robust.

The runtime of the method decreases with increasing patch size and with decreasing image size. For Q = 8, the runtime is 22 ms per image in the application phase on average. This is reduced to 4.4 ms per image in the application phase for Q = 32. For the whole learning phase, 0.08 – 0.81 s are required, which is slightly worse than other methods.

G. Influence of Minimum Cluster Size

There is little dependence of the result on the minimum cluster size Δ. For Δ ∈ {4, 8, 16}, the correlation coefficient is always 0.93. The reason is that Δ only affects the result if the largest cluster is smaller than Δ, which never occurred for these values of Δ in the 25 sequences of this experiment. For Δ = 32, the correlation coefficient increases slightly to 0.94. For Δ = 64, it deteriorates to 0.88, which indicates that patches uncorrelated to the diaphragm are included in some sequences due to the mechanism that increases ε.

H. Analysis of Irregular Respiration

On the ventilated sequences, the average correlation coefficient for the proposed method is 0.95 ± 0.05. For manual ventilation or free-breathing data, the correlation coefficient is 0.96±0.05. Irregular breathing does not have a negative effect on the quantitative results.

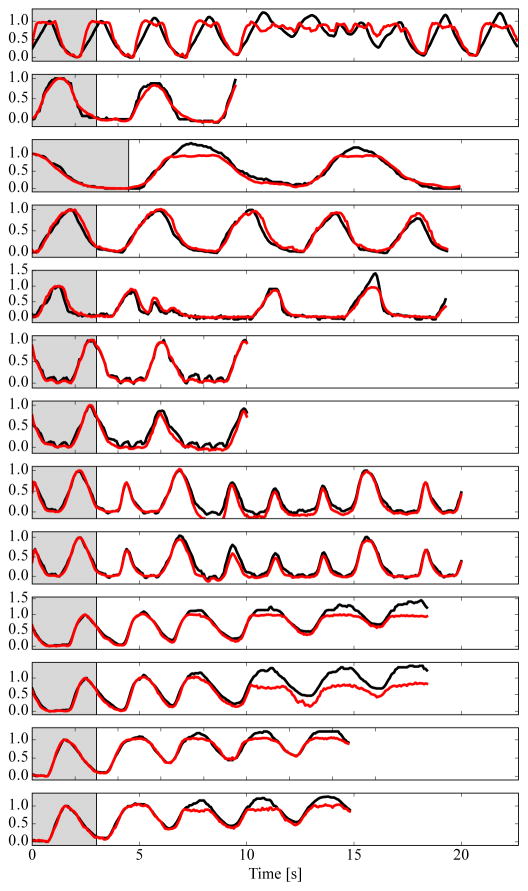
Qualitative plots of all 13 non-ventilated sequences are shown in Fig. 8. Multiple breathing frequencies and changes in breathing frequency are handled well. Changes in breathing depth are only represented well if the breathing amplitude is lower in the test data than in the training data, e.g., sequence 5, 8, and 9. In contrast, increasingly deep inhalations as in sequences 10, 11, and 13 are not tracked sufficiently in the respiratory signal.

Fig. 8.

Respiratory signals extracted by the proposed methods ( ) on free-breathing humans (top 5 sequences) and manually ventilated pigs (bottom 8 sequences). The gray background indicates the learning phase. Diaphragm tracking is shown as a reference signal (–) in each plot. Best viewed in color.

I. Analysis of Algorithm Statistics

There are D_s = 3 possible dimensions of the low-dimensional embeddings that can be selected for each patch as explained in Section II-E. The first dimension is chosen 99% of the time. In the remaining cases, the second dimension is chosen. The first and second component of the same patch are never in the same cluster due to the orthogonality constraint of the PCA. The dimensions of the low-dimensional embeddings are sorted by eigenvalues. This sorting corresponds to the amount of variation in the patches that is explained by the dimension. Thus, if a patch contains respiratory information, it is the most important source of variation in that patch with a large probability.

Since patches can be selected from multiple resolutions, i.e., patch sizes, it is interesting how often each resolution is actually used. In all but one sequence, there are 4 resolutions. The smallest patch size of Q = 16 constitutes 71% of the patches used for respiratory signal extraction. The next larger patches of size 32 × 32 pixels are responsible for 22% of the selected samples, and the patches of size 64 × 64 for the remaining 7%. The full image is never used. An overview of the patch size distribution is given in in Fig. 9. This bias towards smaller patches is caused by the higher number of small patches compared to larger patches. When related to the total number of patches per resolution, see the bars in Fig. 9, the proportion is similar for the three small patch sizes. This proportion also reflects, for each resolution, how much of the image is covered with patches that contribute to the final respiratory signal. Overlapping patches from different resolutions quite often contribute to the same cluster. For a patch in the respiratory cluster, on average 2.3 out of the possible 4 contained patches from the next smaller size are also included in the cluster.

Fig. 9.

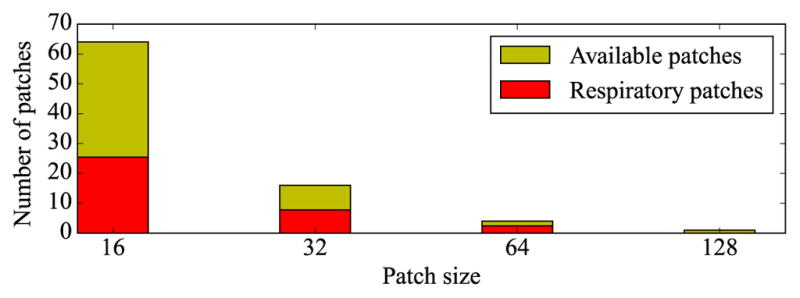
Average number of patches used in the respiratory cluster for each patch size ( ). For comparison, the total number of available patches in each image is given for each patch size ( ). Best viewed in color.

The number of used patches that support the respiratory signals is directly related to the size of the respiratory cluster. The size of this cluster ranges from 9 to 80. The mean and standard deviation is 36 ± 18. Note that the maximum cluster size for 4 resolutions is 255, which would include all of the 3 low-dimensional signals from all 85 patches. The minimum possible cluster size is 8 due to the constraint imposed by Δ. This lower threshold was enforced in 3 out of the 67 sequences by increasing ε to 0.1.

V. Discussion

Our experiments show that dimensionality reduction in general is a prudent approach to respiratory signal extraction. It does not rely on tracking of high-contrast structures like catheters or the diaphragm, which are not always available. It is applicable independent of the field of view or C-arm angulation, as shown by our experiments on biplane and zoomed images. The learning phase to train the mapping from image space to signal space is a drawback. It is a comprehensible requirement, since it is hard to tell at which position in the respiratory cycle an image was acquired if a full cycle has not yet been observed. However, it is not necessary to acquire additional images for training. The respiratory signal is just not available before enough images are acquired in a new C-arm position. This creates the requirement for a short learning phase, since it must be repeated for each C-arm angulation and table position. It is possible to reuse previously learned mappings if the same C-arm position is used in a later stage of the procedure.

It is not surprising that the global methods have the best results in the basic diaphragm tracking experiment (Section IV-A). This experiment is a best-case scenario, where the diaphragm is visible as a high-contrast structure for guiding the respiratory signal extraction and there are no confounding disturbances from other high-contrast structures. This high-contrast structure has a big influence on the objective functions of Isomap, PCA, and KPCA. Consequently, the respiratory signals of these methods follow the diaphragm motion accurately. Patch-based methods on the other hand are not dominated by the diaphragm because they average information from at least Δ patches. The root cause of the lower correlation of the patch-based methods is a small phase shift relative to the ground truth, which occurs in some sequences. There are two empirical indications to support these claims. First, in Section IV-D, the same sequences as in Section IV-A are processed on a ROI excluding the diaphragm. The advantage of the global methods disappears completely. Second, if a phase shift of up to 3 images is allowed in Section IV-A, the average correlation of PCA and the patch-based methods is above 0.97 as well. What is more, it indicates that there is a temporal offset of the respiratory motion in different regions of the thorax. This is also visible in Fig. 10.

Fig. 10.

Patches automatically selected by clustering (largest cluster , second largest cluster ). On the left, the complete images are processed. On the right, a ROI without the diaphragm is used. Almost the same patches are chosen to contain respiratory information.

The averaging behavior is also the reason why the patch-based methods have better results in the relative zooming experiments. The patch-based methods did not focus so much on the diaphragm for the full images, so the extracted respiratory signal is not much different if the diaphragm is not visible. In Fig. 10, the patch locations that contribute to the respiratory signal are shown for Patch KPCA. The color identifies the largest cluster, the second largest cluster is shown in . The patches are overlaid onto the first image of the processed sequence for the full image and the zoomed version. In both versions and for both clusters, similar patches are chosen by clustering. The corresponding respiratory signals for each cluster are shown below the images. The signal is delayed by ~ 133 ms relative to the signal, corresponding to the phase shift mentioned in the previous paragraph. Incidentally, the patches at the diaphragm border are not in the largest cluster, i.e., they do not contribute to the respiratory signal used in the quantitative evaluation.

We experimentally evaluated the sensitivity of the proposed method w.r.t. parameter changes. For the patch size Q (Section IV-F) and the minimum cluster size Δ (Section IV-G), the method was found to have a small sensitivity. Even though there are a multiple parameters that can be adapted, the exact values are not crucial to achieve good results.

The biggest differences between the state of the art and the proposed method is visible for the experiments involving contrast agent (Section IV-B). If contrast agent is present during training, the performance of the state-of-the-art methods deteriorates heavily. The reason is that the flow of contrast agent changes pixel intensities drastically and the dimensionality reduction methods focus on that variation. This effect is suppressed by patch-based processing, since the contrast agent only appears in parts of the image. If contrast agent is injected during the application phase, the performance degradation is not as bad. On many sequences, the baseline methods still provide reasonable respiratory signals. However, if the contrast agent happens to appear in a region that showed high respiratory motion during training or if strong exposure changes are made by AEC, the signals will be destroyed, see Fig. 3. Only the combination of patch-based processing and brightness invariance is robust to large local variations in signal intensity. Sequences containing contrast agent cannot be neglected in the analysis. Although one goal of augmented fluoroscopy is to reduce the use of contrast agent, contrast agent is still often necessary to confirm the clinical outcome. It is also a way to validate the overlay and its motion compensation. When injecting contrast agent, physicians can see the structure of interest in X-ray and in the overlay. The motion compensation would appear unreliable if these two representations do not align or worse if sudden atypical motions occur in the overlay. Additionally, there are other high-contrast structures that are frequently used in minimally-invasive interventions, such as catheters, needles, and stents, which would have a similar effect on respiratory signal extraction methods. In general, robustness is relevant for image analysis methods to avoid unexpected behavior during clinical use.

Besides dimensionality reduction, there are some other relationships to previous respiratory signal extraction methods. One previous method based on hierarchical manifold learning [28] also combines multiple signals computed from patches [25]. Our method has some important differences. It is invariant to intensity variations due to the correlation kernel. Not all of the image patches are used, but only those that carry respiratory information as chosen by clustering. Together with using the median instead of the mean to combine multiple signals, this greatly improves the robustness against outliers. In our experiments, there is little difference in accuracy between Patch KPCA, where only patches of small size are used, and Multi-Resolution KPCA, where all patches are used. However, there is a large difference to Multi-Resolution PCA, which does not include brightness invariance. This shows that the use of multiple resolutions, as in hierarchical manifold learning, is not as important as local brightness invariance. A disadvantage of our method is that the signals of the patches are not aligned intrinsically. However, the choice of patch size is not critical and the signals are aligned automatically during clustering. Of course, hierarchical manifold learning could be improved as well w.r.t. brightness invariance and outlier robustness.

Another related idea occurs in the masked PCA method of Panayiotou et al. [18]. It also selects only parts of the images to extract the respiratory signal. Their assumption is that tubular structures carry respiratory information, which are identified using vesselness filtering. There is no further justification for this assumption, and it could not be confirmed by other authors [19]. We speculate that the tubular structures are only helpful for cardiac signal extraction, which is estimated additionally in [18]. This coincides with the finding in [18] that hierarchical manifold learning and masked PCA are not significantly different for respiratory gating. In our method, the patch selection is driven by clustering, i.e., the size of the clusters. This assumes that respiratory motion affects many patches and is a dominant source of variation.

VI. Conclusion and Outlook

We have presented a method for robust respiratory signal extraction from fluoroscopic sequences. We extended state-of-the-art methods based on dimensionality reduction with patch-based processing and brightness invariance. With the contributions presented in this paper, we can increase the robustness against many disturbances occurring in interventional imaging, such as contrast agent injection, automatic exposure control, and interventional devices. Only unsupervised learning is necessary to achieve a patient-specific respiratory signal, which can be extracted in realtime after a short learning phase.

Three main drawbacks still remain for methods based on dimensionality reduction. Firstly, the learning phase delays the availability of the respiratory signal. Incremental learning might be an option to shorten it [17]. Secondly, the mapping is only valid for a single C-arm and table position. This restricts the applicability, e.g., rotational scans as in C-arm CT are not feasible. Local PCA has already been proposed to circumvent this problem [26]. Some fluoroscopy-guided interventions frequently change the C-arm and table position, so mappings must be stored for each position or relearned each time. Thirdly, the global sign of the respiratory signal is undetermined. Heuristics as used here only work for some applications, e.g., if the learning phase is long [16] or for ventilated patients. Possible solutions for this problem could be manual indication of the global sign by the physician, or a binary classification approach based on supervised learning. Future work will be to handle these problems and apply the respiratory signal for motion compensation in augmented fluoroscopy.