Abstract
One of the key elements in Dynamic Contrast Enhanced (DCE) Image Analysis is the Arterial Input Function (AIF). Traditionally, in DCE studies a global AIF sampled from a major artery or vein is used for estimating the vascular permeability parameters; however, not addressing dispersion and delay of the AIF at the tissue level can lead to biased estimates of these parameters. To find less biased estimates of vascular permeability parameters, a vascular model of the cerebral vascular system is proposed that considers effects of dispersion of the Arterial Input Function (AIF) in the vessel branches, as well as extravasation of the contrast agent to the extravascular-extracellular space. Profiles of the contrast agent concentration were simulated for different branching levels of the vascular structure, combined with the effects of vascular leakage. To estimate the permeability parameters, the extended model was applied to these simulated signals and also to DCE-T1 (Dynamic Contrast Enhanced–T1) images of patients with Glioblastoma Multiforme tumors. The simulation study showed that compared to the case of solving the pharmacokinetic equation with a global AIF, using the local AIF that is corrected by the vascular model can give less biased estimates of the permeability parameters (Ktrans, vp and Kb). Applying the extended model to signals sampled from different areas of the DCE-T1 image showed that it is able to explain the contrast agent concentration profile both in the normal areas and the tumor area where effects of vascular leakage exist. Differences in the values of the permeability parameters estimated in these images using the local and global AIFs followed the same trend as the simulation study. These results demonstrate that the vascular model can be a useful tool for obtaining more accurate estimation of parameters in DCE studies.
Keywords: Arterial Input Function, Vascular Modeling, Dynamic Contrast Enhanced Imaging, Vascular Permeability, Cerebral Tumors, DCE-MRI
Graphical Abstract
We have introduced a model of the brain vascular system for simultaneously describing blood flow and contrast agent extravasation to the extravascular extracellular space, to be used for estimating the local arterial input function (AIF) and permeability parameters. Simulations show that using this model-corrected local AIF instead of the global AIF can lead to less biased estimates of the permeability parameters in pharmacokinetic models. Testing the two AIFs on DCE-T1 images of cerebral tumors showed similar trends in the estimated values of the permeability parameters as the simulated signals.
INTRODUCTION
One of the challenges in Dynamic Contrast Enhanced (DCE) studies is estimation of the time trace of local plasma Contrast Agent (CA) concentration or the Arterial Input Function (AIF) at the tissue level. We previously introduced a vascular transfer function of the brain that could model delay and dispersion of the CA concentration profile at different levels of the vascular branching tree. This transfer function is based on laws of fluid dynamics and vascular morphology. Previously, Gall et al (1) and Kellner et al (2) had used a similar approach and derived a vascular tree model to explain delay and dispersion of the Arterial Spin Labeling (ASL) bolus (3); they also used this model for estimating the residue function for brain tissue in perfusion measurements (4). These models assume that there is no leakage of the contrast agent to the extravascular-extracellular space. We used this transfer function to derive a model and by applying it to DCE-CT images and using the estimated model parameters, created an arrival time map of the brain [**].
In the MRI field, Dynamic Susceptibility Contrast (DSC) Imaging is the method of choice for perfusion studies in which Mean Transit Time (MTT), Cerebral Blood Flow (CBF) and Cerebral Blood Volume (CBV) are estimated (5); DSC is based on changes of the T2* signal in the dynamic images (6). In DCE-MRI studies, dynamic series of T1-weighted images are acquired and are mainly used for estimation of vascular permeability parameters such as vascular transfer rate constant (Ktrans), vascular plasma volume (vp), and extracellular-extravascular space (EES) volume (ve) (7–9). Estimation of the permeability parameters can be done using pharmacokinetic models and one of these which is widely used is the Standard Model (SM) or Extended Tofts model (10). One of the main components in this model is the AIF. Theoretically this should be the local AIF that is sampled directly at the inlet to the tissue being studied; however, in practice usually the AIF sampled from a major artery is used (11) which results in eliminating the effects of dispersion and delay of the AIF (12). Inaccurate estimation of the AIF at the tissue level for use in permeability and perfusion analyses could substantially add bias to the estimated hemodynamic and permeability maps. Calamante et al used independent component analysis to show that delay and dispersion of the AIF can cause underestimation of the CBF and overestimation of the MTT in DSC studies (13). In their study, they showed that although the delay can be corrected using the information of the arrival time of the bolus to the tissue, correcting for the dispersion should be done using a vasculature model. Lee et al used a model of tissue microcirculation based on tracer kinetics and Bayesian probability theory to estimate the localized AIF in DSC images and used that to estimate perfusion parameters (14); Permeability parameters found by employing these local AIFs showed strong correlation with those measured by quantitative Positron Emission Tomography (PET) with H2[15O].
In the DCE-MR area, Fluckiger et al presented a method for blind estimation of the local AIF based on the Alternating Minimization with Model (AMM) method (15); to estimate the local AIF, they constrained it with a model containing three gamma-variate curves. Their results show that compared to using the local AIF, the current method of using arterially measured AIFs biases the resulting parameters high, especially in regions where more dispersion of the AIF is expected. In one approach, to eliminate the need of direct AIF measurement, Yankeelov et al proposed a method for quantitative analysis of DCE-MRI by comparing the CA concentration profile of tissues of interest to that of a reference region. Using this method, Ktrans and ve were estimated but a validation of the final results was not performed (16).
In this paper, to address the effects of extravasation, we extend our Basic Vascular Model (BVM) that we previously introduced [**]. by combining it with the SM. Next, by simulating the AIF at different levels of the vascular system and also adding effects of vascular leakage to the simulated CA concentration profiles, we compare the results of using our model-corrected local AIF for estimating the permeability parameters with the Standard Model, to those estimated when using the global AIF. Finally we perform the same comparison using DCE-MR images of a patient with a cerebral tumor.
MATERIALS AND METHODS
All modeling and calculations were done in MATLAB (MATLAB Release 2010b, The MathWorks, Inc., Natick, Massachusetts, United States).
The Basic Vascular Model
Transfer function of the vascular pathway
We previously introduced a model to address dispersion and delay of the CA profile when flowing from a main artery down to the lower levels of the vascular tree in the brain(17) [**].. This model is mainly based on a previously derived equation for describing the transfer function of a single vessel with laminar flow (3, 17). The transfer function is a function of t0n, the time required for the fluid on the central axis of the tube to pass through the a vessel at the nth branching level:
| (1) |
Where:
| (2) |
Here, D0n is the length and v0n the maximum velocity of blood in the vessel (or the velocity along the central axis) at the nth level. The interesting point about this transfer function is that it can describe each vessel segment based on only one parameter (t0n). This parameter is not related to the injection time of the contrast agent and based on Equation 2, depends only on the blood velocity in the vessel and its length. We will refer to t0n as the branch delay which is a characteristic of each branch, assuming that blood flow is constant. We selected the maximum value of n=6 based on the study done by Wright et al where they measured the number of arterial branching levels in the different brain regions using magnetic resonance angiography (18).
Under certain assumptions, the delay time, t0n of each segment in the vascular tree can be considered equal [**]. and in this case the transfer function of all the sequential branches can be considered identical. In this case the parametric equation of the transfer function from the opening of a main branch to the end of one of the sub-branches at the nth level of vascular tree can be expressed as:
| (3) |
Where “* n“ denotes n repeated convolutions. Here g is a gain factor compensating for the fractional volume of the vessels in the tissue.
By sampling the CA profile from a voxel in the DCE image series, and also by sampling the AIF in a voxel representing the circle of Willis, we can write the following equation:
| (4) |
AIFL(t) is the local AIF in the tissue. If the vessels are intact and do not have CA leakage, the CA profile sampled from a voxel in the DCE images can represent the AIFL(t). It should be noted that in this equation, the effects of the capillaries on dispersing the AIF has not been considered. To find the transfer function that can best describe the relation between the AIF and AIFL(t) for each voxel in the image, we developed a procedure based on the Nelder-Mead simplex search method of Lagarias et al.(19) as a non-linear fitting method with the sum of squared errors as the cost function, along with Akaike Information Criterion (AIC) (20) to find the best configuration of the transfer function (based on the number of branching layers, n) that can transform the AIF to the AIFL(t). Since initially it is not known that the selected voxel belongs to which branching level of the vascular tree, the fitting procedure is repeated separately for six configurations of one to six layers of branching, to find the following set of parameters for the transfer function for each configuration:
| (5) |
After finding the best fit transfer function for each configuration of the vascular tree, using the fitting residual values, the best model is selected using the AIC to represent the transfer function that transfers the AIF to the selected AIFL(t)[**].
The model described above (Basic Vascular Model or BVM) has been designed to explain dispersion and delay of the AIF in the vascular tree with no extravasation in any of the vessels. As we will explain in the following sections, the model in its current form will not be able to explain the profile of the CA concentration when the signal is sampled from areas with leaky vessels.
Extending the Basic Vascular Model
When the tissue concentration signal is sampled from voxels in image areas containing vessels with no leakage, the signal mainly represents the CA concentration profile in the intravascular space. This profile is generally a dispersed form of the AIF in major vessels; however, when the CA leaks into the extravascular space, the sampled tissue concentration signal will follow a different trend. Based on this observation, to address the changes of the CA profile in areas with leaky vasculature and to find a more accurate estimation of the intravascular (plasma) CA concentration profile in these vessels, we modified the BVM to include effects of leakage of the CA to the extravascular space.
Adding Permeability Parameters to the Basic Vascular Model
One of the models describing tracer kinetics is the Extended Tofts Model or Standard Model (SM). According to the SM which is a two compartmental model (12, 21), the relationship between Ct(t) (tissue concentration profile of the CA) and Cp(t) (plasma concentration profile of the CA) can be described follows:
| (6) |
In this equation, the tissue concentration of CA, Ct(t) is composed of two main components: The first term on the right, represents the component of the signal that is due to leakage of the CA to the extravascular space and is dependent on the forward (Ktrans) and inverse (kb) transfer rate constants. The second term, vpCp(t) basically represents the time trace of the plasma CA concentration in the vessels that feed the tissue from which Ct(t) is being sampled. Depending on the type of the vasculature leakage, some of the permeability parameters may not be taken into account and Equation 6 may follow different models of vascular extravasation as described below (9, 22):
Model I: Impermeable vasculature where the Blood Brain Barrier is intact (Ktrans = 0, kb= 0, vp≠ 0).
Model II: Moderate influx which is observed as leakage without efflux (Ktrans ≠ 0, kb= 0, vp≠ 0).
Model III: Fast leakage which leads to bidirectional exchange (Ktrans ≠ 0, kb≠0, vp≠ 0).
Figure 1 shows a schematic diagram of the signal components of the extended Tofts model and their relation. AIF(t) is the CA profile sampled at the location of one of the major arteries. The cube in this figure represents an imaginary voxel in the image where the tissue CA concentration profile Ct(t), is being sampled from Cp(t) is the plasma CA concentration in the vessel (or vessels) feeding the tissue in the voxel.
Figure 1.
Schematic diagram showing the main components of the pharmacokinetic model and their location. AIF(t) is the CA profile sampled at the location of one of the major arteries. The cube in this figure represents an imaginary voxel in the image where the tissue CA concentration profile, Ct(t), is being sampled from. Cp(t) is assumed to be the plasma CA concentration in the vessel (or vessels) feeding the tissue in the voxel.
As we noted in the introduction section, in conventional methods of calculating the permeability parameters using the pharmacokinetic model, for the profile of Cp(t), the CA profile sampled from one of the major arteries (in the image) or even veins (such as the superior sagittal sinus) is usually used; however, this is not a correct representative of the CA profile in tissue since it does not address dispersion of the CA profile at different levels of the vascular tree and can lead to biased estimates of the permeability parameters. In image areas with non-leaky vessels, the sampled profile basically represents only the intravascular CA concentration which can be described with the BVM [**].. To find an equation for describing the intravascular CA concentration profile in leaky vessels, we added a new feature to the vascular transfer function that we defined by Equation 3. If in Equation 6 we replace the plasma CA concentration profile, Cp(t) with the local interpretation of the AIF in tissue, the pharmacokinetic model can be written as:
| (7) |
And by replacing AIFL(t) from Equation 4 we have:
| (8) |
or
| (9) |
Where
| (10) |
The transfer function hE(t), describes transformation of the AIF profile to the measured tissue concentration signal at different locations of the vascular structure, with or without leakage of the vessels. In the case where the vessels are intact (non-leaky), Ktrans will be zero and the measured signal will be basically the intravascular plasma concentration of the CA in the tissue which can be described by convolving the AIF with h(t)1 to n. In the case where the vessels are leaky, Ct(t) is the superposition of the intravascular and extravascular components of the signal which are the two main components of this equation.
To find the best function that transfers the AIF to the tissue concentration signal, in addition to the six configurations of the vascular tree (as in the BVM), three configurations of the SM (9, 22) (Models I, II and III) are also considered. Therefore for each signal, 18 different combinations of the transfer function are studied and using the fitting residues for each, the best transfer function describing transformation of the AIF to the tissue CA concentration profile is selected using the AIC. After finding the curve that best fits to the sampled signal, using the parameters found in the fitting procedure and also the two main components of this transfer function, the transfer functions describing the extravascular and intravascular components of the tissue concentration signal can be constructed and by convolving them with the AIF profile, each can be described as below:
| (11) |
| (12) |
Here and are the intravascular and extravascular components of the tissue CA concentration profile and h(t)est is the estimated vascular transfer function.
Subjects
Three treatment naïve patients with Glioblastoma Multiforme (GBM) were scanned using the procedure described below. The study was approved by the Henry Ford Health System Institutional Review Board and written informed consent was obtained from all subjects.
DCE-MR Image Acquisition
DCE-MR image acquisition was performed on a 3T GE Excite HD MR system (GE Healthcare, Waukesha WI) using a standard eight-channel phased-array RF coil. Before CA administration, T1 mapping was obtained using DESPOT1 (23). With TE/TR = 0.84/5.8ms, 256×256 matrix size, 240 mm FOV, sixteen slices with 5 mm thickness and six flip angles of 2°, 5°, 10°, 15°, 20°, and 25°. These images were used to create the pre-contrast T1 maps that were used as the baseline values for the 3D Spoiled Gradient Echo (SPGRE) DCE-T1 procedure (9). The 3D SPGRE DCE-T1 sequence included 70 image volumes acquired 5.9s apart, all with a 20° flip angle, TE/TR = 0.84/5.8 ms, 256×256 matrix size, 240 mm FOV, sixteen slices with 5 mm thickness. Total data acquisition was 6.8 min. Contrast agent (Magnevist; Bayer Healthcare Pharmaceuticals, Wayne, NJ) was administered intravenously by power injection 20s after the start of the DCE-T1 sequence, at a dose of 0.1 mmol/kg with a rate of 4 mL/s.
It has been shown that changes in the relaxivity (ΔR1) are linearly related to contrast agent concentration in tissue (24, 25); we previously derived an equation for extracting ΔR1 signals from T1-weighted SPGRE MRI data (9). If TE is selected such that TE ≪ T2*, the effects of T2* in the ΔR1 calculated from the SPGRE DCE-T1 data can be minimized (9) which is the condition we had for acquiring our DCE-T1 images. By applying this equation to our DCE-T1 data we produced the ΔR1 maps for this image sequence. The voxelwise ΔR1 signals in these images were used for estimation of the permeability parameters using the SM. To adjust the equations for DCE-MR applications, we replace Ct(t) with (1 − Hct)ΔR1t(t) and AIF(t) with ΔR1a(t) in equation 9:
| (13) |
Comparison of Performance of the BVM and the Extended Model in Normal and Leaky vessels
To compare the performance of the BVM with its extended form for describing the CA concentration profile in brain areas with leaky or non-leaky vessels, we studied the tissue CA concentration signals sampled from two regions of the brain in a patient with GBM: One from the normal tissue and the other from the tumor area. For each model, based on the procedure explained in the methods section, we separately used the BVM and the extended model to find the best transfer function describing the transformation of the AIF to the CA concentration profile in each of these regions.
Applying the Extended Model to DCE-T1 Images for Estimation of the Permeability Parameters
When using the extended model for estimation of the transfer function, for each voxel in the image, in addition to the parameters describing the vascular structure connecting the major artery and the vessels passing through that voxel, the permeability parameters can also directly be estimated as a byproduct of the method. Depending on the model of leakiness that is being considered, at each branching level, the transfer function can have one (vp), two (vp, Ktrans) or three (vp, Ktrans, Kb) parameters to represent one of the three configurations of the SM. After estimating all 18 transfer functions based on the fitting procedure and selecting the best fitted model, the permeability parameters can be estimated using the parameters of the best fit model.
We previously reported another method that we had established for estimating permeability parameters (9) in DCE-T1 images. This method was also based on finding the best set of permeability parameters describing the three configurations of the SM. In this method, initially for each configuration, the best set of parameters that related the global AIF to the tissue CA concentration in each voxel was estimated using the simplex method. Next, using the F-test (26), the best configuration was selected and the parameters satisfying that configuration of the SM were selected as the permeability parameters for that voxel. The difference between this method and using the extended model is basically using the global AIF vs. the local AIF for solving the SM or Tofts equation. To compare the results, and to evaluate the results of employing the local AIF for estimating permeability parameters, we estimated the permeability parameter maps from the DCE-T1 images of the brain of a patient with GBM, using both methods.
Simulation Study
One of our main goals for developing the vascular model is to estimate the permeability parameters more accurately. We hypothesized that by employing the local AIF and using that for solving the pharmacokinetic model, we will be able to find more accurate estimates of the permeability parameters. To test this hypothesis, we simulated the three models of vascular leakage at different branching levels of the vessels and compared the estimated values of the permeability parameters when using the global AIF vs. the local AIF found by the vascular model. Our assumption was that the artery or arteriole that feeds the capillary bed can be from any of the six branching levels. Although this is not necessarily true, we did this to make our simulation more robust.
In the first step, using the AIF sampled from the circle of Willis in the ΔR1 image series estimated from the DCE MRI series of a human subject (with image acquisition parameters described in the previous section), we simulated curves of the dispersed AIF at six levels of the vascular system using our vascular model with values close to those in the arteries of the human brain. This provided the dispersed and delayed CA concentration profile at each of these layers. For model I, which is considered to be the model with no vascular leakage, the only parameter that we accounted for was the fractional plasma volume, vp. Using four different values of vp (0.01, 0.02, 0.04 and 0.1), tissue concentration signals were simulated at each level of the vascular branching structure. For simulating the signals for Model II, the forward transfer rate constant (Ktrans) was added to the equation to simulate leakage of the vessels. We did the simulation for a fixed value of the fractional plasma volume (vp = 0.01) and two values of the forward transvascular transfer rate (Ktrans= 0.001 (1/min) and 0.005 (1/min)). And finally, the tissue concentration signal was simulated using model III of the Pharmacokinetic model in which a third parameter, Kb was added. Similar to the other two models, we estimated these three parameters using the two methods and compared the results. The simulation was done using Ktrans = 0.005 and vp = 0.01 and two values for Kb (0.2 and 0.5).
RESULTS
Applying the BVM to MRI data
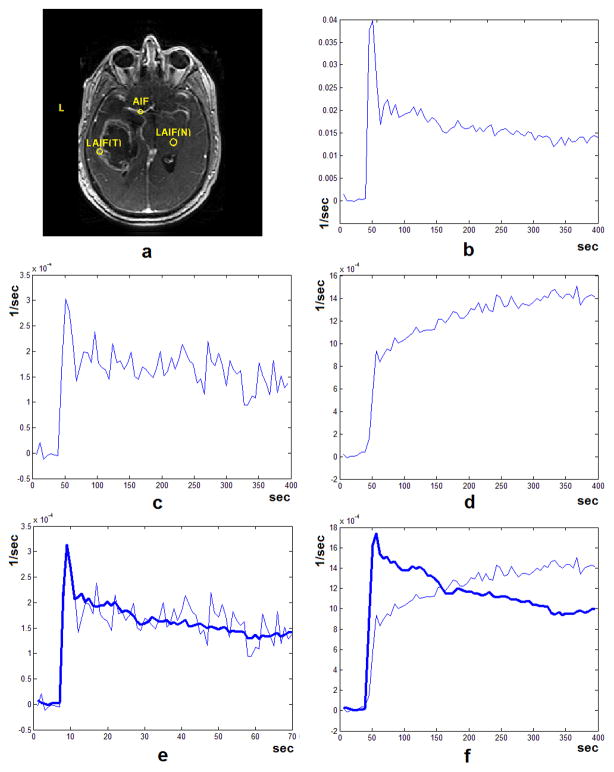
Figure 2-a shows one slice of a DCE-T1 image from a patient with Glioblastoma Multiforme after injection of the CA. Figure 2-b shows the CA concentration profile (ΔR1(t)) sampled from the voxels in the circle of Willis (as marked in Figure 2-a) and Figure 2-c shows the CA profile from an ROI sampled from the normal white matter area. Using the procedure explained in the methods section, we found the best transfer function (based on the BVM) explaining the transformation of the AIF to this local AIF. By convolving the AIF in Figure 2-b with this transfer function, the bold curve in Figure 2-e is estimated. To explore the performance of this model in other areas of the brain, we sampled a signal from an ROI in the tumor area as seen in Figure 1-a. The CA concentration profile sampled from this ROI can be seen in Figure 2-d. The tail of this profile does not follow the trend that is seen in the CA profile in the normal area. After applying the method above to this signal and finding the best fit, the bold curve in Figure 2-f is estimated. As seen here, the BVM can only describe changes in the CA profile in intact vessels with no leakage and in cases where leakage vascular exists, it does not perform correctly.
Figure 2.
(a) One slice of a post contrast injection DCE-MRI image from a patient with Glioblastoma Multiforme with three ROIs from a major artery (AIF), normal tissue (LAIF(N)) and the tumor area (LAIF(T)). The CA profile sampled from the major artery (b) normal tissue (c, non-leaky vasculature) and the tumor area (d, leaky vasculature) from the DCE-MR image series. Using our vascular model, the transfer function that gave the best fit for each of the two CA profiles and the resulting local AIF was found. As seen here, in the case of non-leaky vasculature, after reconstruction using the best fit transfer function, the resulting local AIF can give a good estimation of the signal sampled from the tissue (e). But in the case of the signal sampled from the tumor area (f), the best fit signal cannot follow the trend of the AIF and the best fit model is erroneously selected as the sixth level to minimize the residual error of the fitting procedure. The Sum of Squared Errors (SSE) for the fitted curves in (e) and (f) are 4.86 E-8 and 9.29 E-006 respectively.
Applying the Extended Model to MRI data
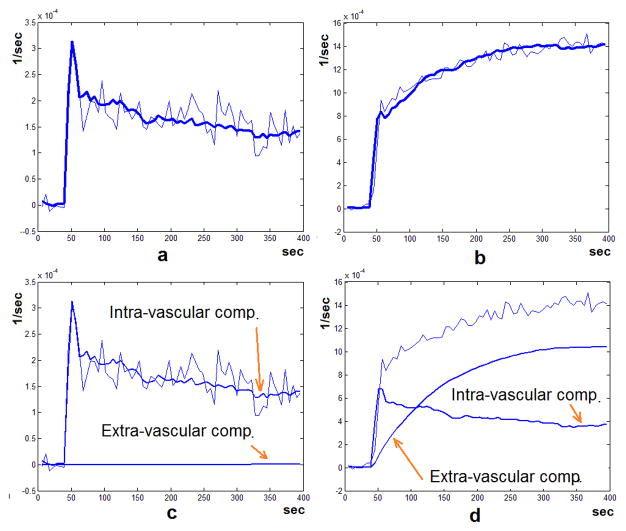
To test the extended model, we applied it to the CA concentration profile sampled from the tumor area (Figure 2-a). The bold curve in Figure 3-b shows the tissue CA concentration profile that was reconstructed by convolving the best selected transfer function with the AIF. As seen in this figure, this profile matches the original data very well. We applied the extended model to the CA profile sampled from the normal tissue and repeated the same procedure on it. Figure 3-a shows the reconstructed profile. This profile is the same as the profile found using the basic vascular model. Using the estimated parameters of the transfer function, the tissue concentration profile was decomposed into the intravascular and extravascular components. These can be seen in Figure 3-c and Figure 3-d. When the signal is sampled from the normal tissue, the extravascular component appears to be non-existent and is seen as a flat line. But for the signal sampled from the tumor area, these two components are separated as two different profiles: The intra-vascular signal and the extra-vascular signal representing leakage of the CA to the EES.
Figure 3.
The profiles representing the tissue CA concentration (thin line) and the reconstructed profile after fitting and model selection (bold line) from (a) the normal tissue and (b) the tumor area as described in Figure 2. (c) and (d) show intra-vascular and extra-vascular components of the reconstructed tissue concentration profiles, based on the decomposition done by the Extended Vascular Model. As seen here, in the case where the signal sampled from the normal tissue (c), the extra-vascular component is a flat line, indicating no leakage to the extra-vascular space. But when the signal in sampled from the tumor (d) the intra-vascular and extra-vascular components are separated which can indicate the flow or extravasation properties of the vessels in the sampled region independently. The Sum of Squared Errors (SSE) for the fitted curves in (a) and (b) are 4.86 E-8 and 2.98 E-7 respectively.
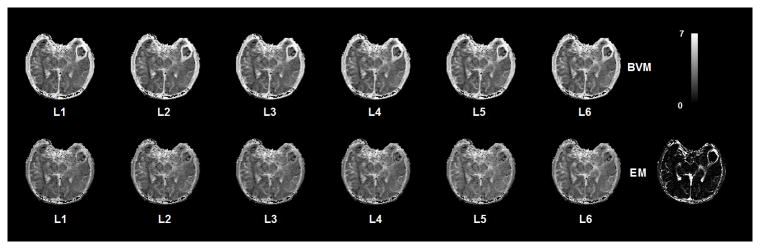
We applied both models to all voxels in a slice of the DCE-T1 image series of the same patient. Figure 4 shows residual maps from the fitting procedure using the two models for different levels of the vascular tree. The residual values in the tumor area are much lower for the extended model which means that this model can explain the trend of the CA profile in the leaky vasculature areas much better than the BVM. Finding the best fit in the lower levels can be due to the tumor being fed through a major artery in the lower branching levels.
Figure 4.
Maps of the fitting residual values using the BVM and the Extended Model (EM) in a set of DCE MR Images. Every voxel in each map represents the residue of the best fit function at each branching level of the vascular structure. For better representation of these maps, they have been scaled to log (108 SSE) which SSE is the Sum of Squared Errors of the fitting process. In areas of the brain outside the tumor, the residual values are almost identical for the EVM and BVM at each branching level which indicates that the EVM can explain dispersion and delay of the AIF in non-leaky vessels similar to the BVM. As seen here, the residual values in the tumor area are much lower for the EVM which means that this model can explain the trend of the CA profile in the leaky vasculature areas much better than the BVM. Finding the best fit for the tumor at the 4th level can be due to the tumor being fed through a vessel at the 4th branching level.
Estimation of Permeability Parameters in DCE-MR Imaging Using the Extended Model
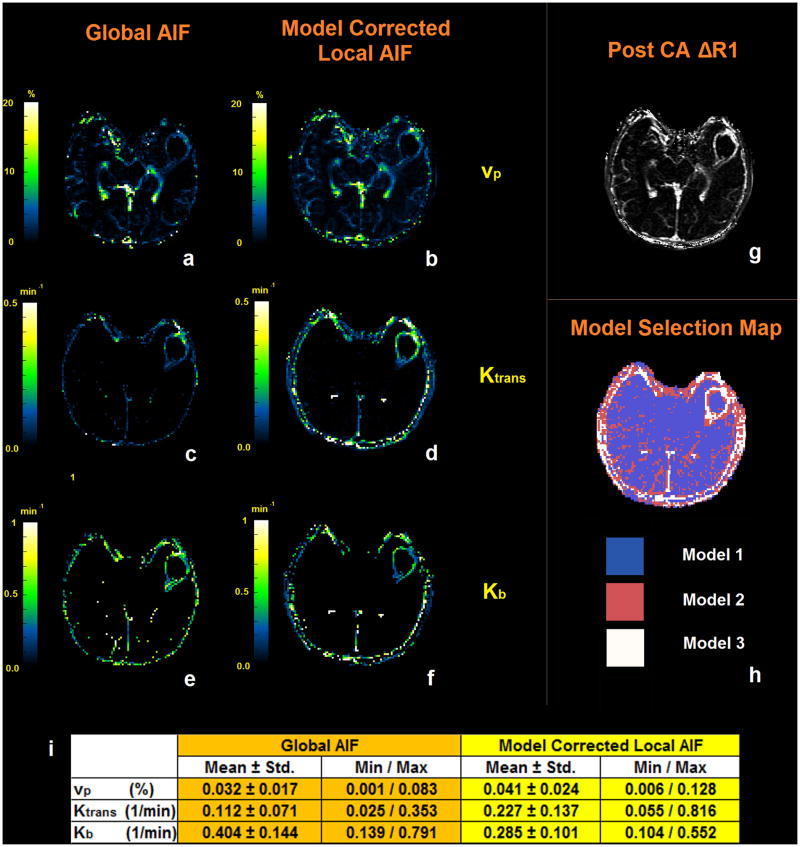
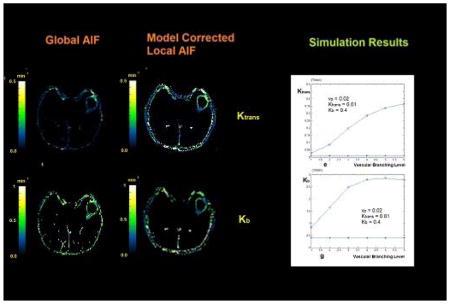
Figures 5-a, 5-c and 5-e show the three permeability maps (vp, Ktrans, Kb) that were estimated by solving the pharmacokinetic model using the global AIF for the DCE-MR series of the slice shown in Figure 5-g. Figures 5-b, 5-d and 5-f show the same maps that were estimated using the local AIF found by the extended model. As seen in the vp map, in the non-leaky areas the values found by the two methods are very close; however, the vp values in figure 5-a show lower values in the tumor area compared to Figure 5-b. This can be interpreted as an underestimation of the plasma volume fraction in leaky areas when the global AIF is used. The outcome of the simulation study described in the next section confirms these results. Comparison of the corresponding Ktrans and Kb maps when the extended model is used, show that the values of Ktrans and Kb when using the global AIF are both underestimated. The total time for processing one slice of the DCE-MR images was approximately 3 hours on an Intel Core i7, 2.70 GHz processor. This included 18 repetitions of the transfer function fitting algorithm for each voxel and finally selecting the best fit transfer function.
Figure 5.
(a, c and e) The three permeability maps (vp, Ktrans, Kb) estimated by solving the pharmacokinetic model using the global AIF for the DCE-MR series of the slice shown in (g). (b, d and f) permeability maps estimated using the Local AIF found by the vascular model. (h) Model selection map estimated using the residual sum of squares from the fitting procedure and finding the minimum AIC. (i) The mean, standard deviation, minimum and maximum values of vp, Ktrans and Kb measured in the voxels representing the tumor.
Simulation Study
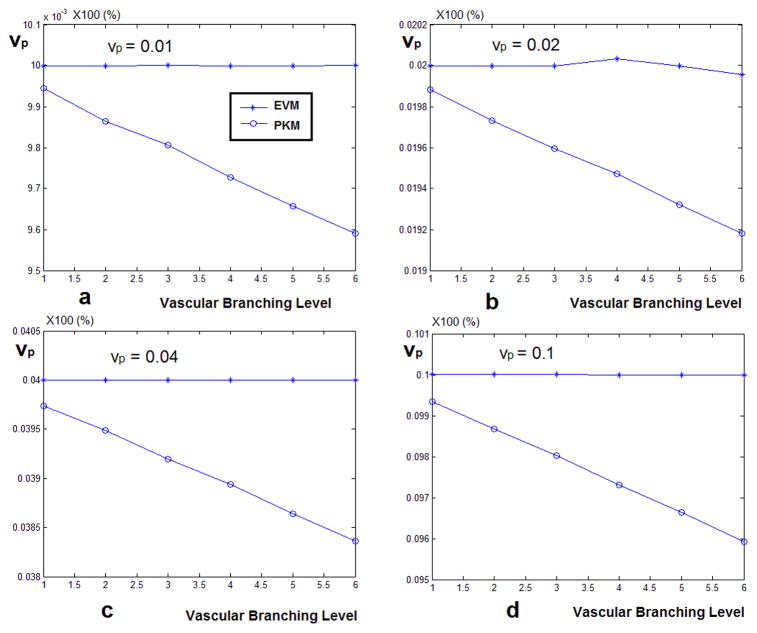
In Figure 6 the results of estimating vp using the two methods are presented. The signals were simulated for four values of vp (0.01, 0.02, 0.04 and 0.1). The observation in all these graphs is that when the global AIF is used, starting from the first level of vascular branching, the value of vp gets underestimated and the gap between the estimated value and the nominal value increases as the tissue concentration signal gets more dispersed. But the values estimated by the model corrected local AIF remain very close to the nominal value at all levels of the vascular branching.
Figure 6.
(a) The vp values estimated by solving the PKM equation using the global AIF and local AIF estimated by the vascular model. When the model corrected local AIF is used, the estimated values of vp is much closer to the nominal value compared to using the global AIF which leads to underestimation of vp. (b)–(d) show the estimated values of vp for simulating a fractional plasma volume of 0.02, 0.04 and 0.1
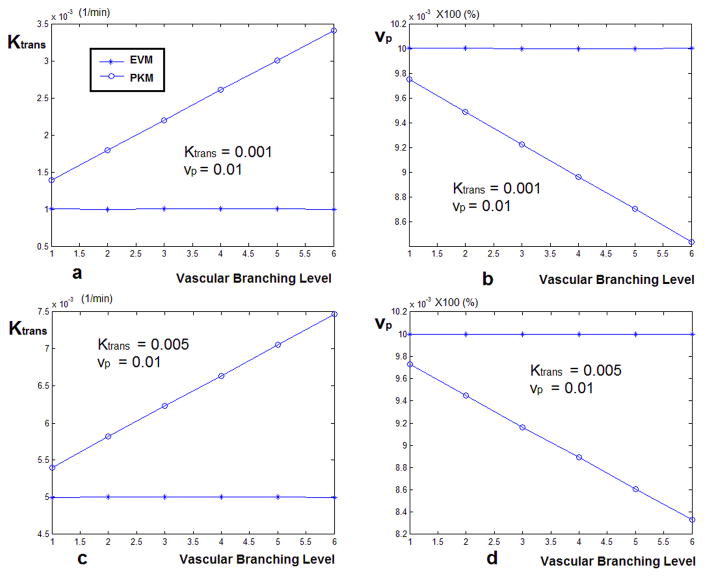
The plots in Figure 7 show the estimated values of Ktrans and vp in the case of simulating model II, calculated using the global AIF and the model corrected local AIF, assuming that they are sampled from six different levels of the vascular tree. Figure 7-a and 7-b show the case where vp = 0.01 and Ktrans = 0.001 (1/min) and Figures 7-c and 7-d represent vp=0.01 and Ktrans = 0.005 (1/min). As seen here, in both configurations, the Ktrans values found using the global AIF are overestimated at all branching levels and as the vascular levels increase, this value increases as well. In the case of the estimated vp (similar to the case of the first configuration of the Pharmacokinetic model) when using the global AIF, the fractional plasma volume is underestimated starting from the first level and is underestimated by about 80% the nominal value when it gets to the last level. In the case of using the extended model, the estimated value of vp is always accurate.
Figure 7.
Estimated values of Ktrans and vp calculated by solving the Pharmacokinetic model using the global AIF and the local AIF estimated by the vascular model for simulated signals. These signals were created assuming that they are sampled from six different levels of the vascular tree. Also, leakage was added to the vessels based on the second configuration of the pharmacokinetic model where only Ktrans and vp exist in the equation. Figures (a) and (b) show the case where vp = 0.01 and Ktrans = 0.001 (1/min) and (c) and (d) represent vp=0.01 and Ktrans = 0.005 (1/min). As seen here, in both configurations, the Ktrans values found using the global AIF are over estimated at all branching levels and as the vascular levels increase, this value increases as well. In the case of Ktrans = 0.001, the over estimation is about 9 times the nominal value and in the case of Ktrans = 0.005, this is about 3 times. In contrast, for the case of using the vascular model, the estimated value of Ktrans is equal to the nominal value. In the case of vp, similar to the case of the first configuration of the Pharmacokinetic model, in the case of using the global AIF, the fractional plasma volume is underestimated from the first level and is underestimated by about half the nominal value. In the case of using the local AIF, the estimated value of vp is always accurate.
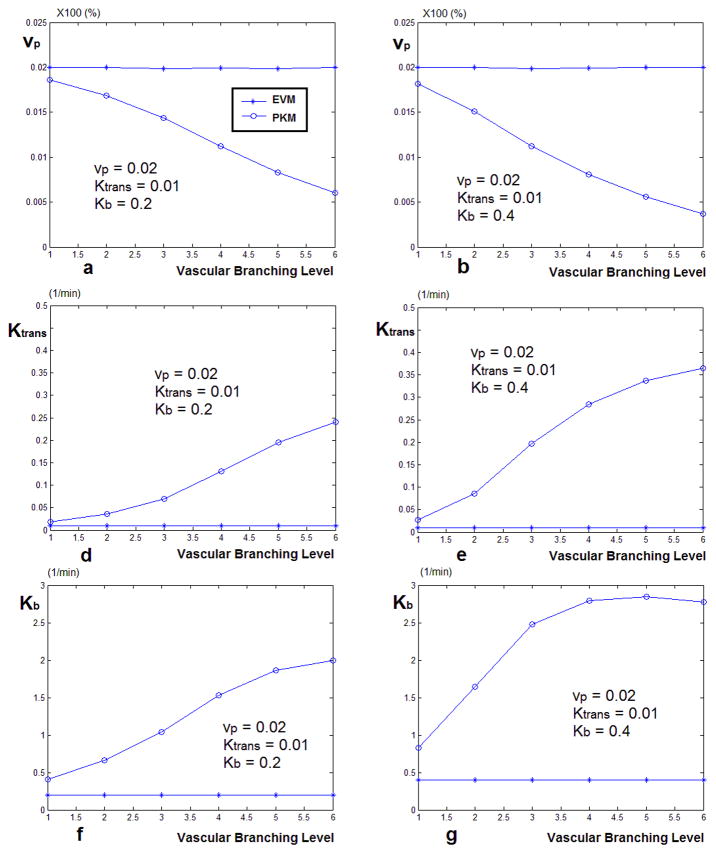
The graphs comparing the estimated values of Ktrans, Kb and vp, using the two AIFs for two sets of Model III simulated signals are plotted in Figure 8. As seen in both signal sets, the value of vp, Ktrans and Kb estimated by the local AIF is the same as the nominal value. In this case of using the global AIF, the value of Ktrans can be overestimated as much as 20 times and Kb and high as 6 times the nominal value.
Figure 8.
Estimated values of vp, Ktrans and Kb, using the PKM and global AIF vs. The local AIF corrected by the vascular model. The curves on the left (a, d, f) represent the case where Kb = 0.2 and the curves on the right represent Kb = 0.5. In both cases Ktrans = 0.005 and vp = 0.01. As seen in both cases, the value of vp estimated by vascular model is almost the same as the nominal value. The values of Ktrans and Kb are estimated close to the nominal value and even though at some of the branching levels they deviate from that value but it is much less than the case of the estimates done using the AIF. In this case, the value of Ktrans can be overestimated as much as 20 times and Kb and high as 6 times the nominal value.
DISCUSSION AND CONCLUSION
We introduced a model of the brain vascular system that explains dispersion and delay of the AIF at different levels of the vascular structure, combined with the effects of extravasation of the CA to the extravascular space. This model is an extension of a previous model of the vessels (BVM) which did not include effects of extravasation. The results of applying these models to DCE-T1 images of patients with GBM show that the extended vascular model is able to explain the CA concentration profile at different levels of the vascular tree in areas of the brain, with or without leakage of the vessels. Also simulation results showed that for solving the Tofts equation, if the local AIF provided by the vascular model is used instead of the global AIF, permeability parameters can be estimated more accurately.
The advantage of using the vascular model for solving the pharmacokinetic model as described by Tofts equation is that it can provide an estimate the local AIF found in each voxel which can lead to more accurate estimation of the permeability parameters. One by-product of using this model is that it can be used for decomposing the tissue concentration signal of the CA into the intra and extra-vascular components which are basically the flow and leakage components of the signal. Extracting the extra-vascular component of the signal can lead to estimation of the permeability parameters with fewer data points and using shorter scan times. Overall, this model has the potential to address many open problems in DCE-MRI and DSC-MRI and also in DCE-CT applications where this model can be used for simultaneous measurement of permeability and perfusion parameters. It should be noted that although this model in its current form gives a reasonable estimate of the local AIF, a more complete model should take into account the effects of the capillaries on the dispersion which can be added in future studies. However, the model in its current form is a big step forward towards finding less biased estimates of the permeability parameters. Another point is that in our model we selected the maximum number of branching levels as six levels; although there is the possibility of existence of branches having higher number of bifurcations, in such events, n = 6 would be selected as the best configuration of the function. One of the drawbacks of this method is the relatively long processing time due to the 18 configurations of the model that are being fit to the data. One solution to solving this would be to use adaptive models for this part of the methods.
In the simulation study, although the full range of parameters was not considered, the results show that when the local AIF is used, the estimated parameters are less biased compared to the case of using the global AIF. Although in this study the transfer function based on the extended model was used for simulating the tissue concentration signals and for transforming the AIF, however, based on our model, we expect the simulated signals to be a reasonable estimation of the signals is real tissue. The accuracy of the results show the reliability of this model for estimating the permeability parameters by decomposing the tissue concentration signal to the intravascular and extravascular components which is the main advantage compared to using the global AIF. Comparing these simulation results with the results obtained from processing the DCE-MRI data from the tumor patients confirms that when the global AIF is used for solving the pharmacokinetic equation, the permeability parameters estimated in the tumor area are overestimated or underestimated with the same trend as the simulation study. These results confirm the findings by Fluckiger et al when they used a local AIF for measuring the permeability parameters (15).
One issue with any suggested model in DCE studies is clinically validating the estimated parameters in the human brain (27). Although there have been attempts to address this issue by developing phantoms to simulate perfusion, most of these systems fail to establish and accurately replicate physiologically relevant capillary permeability and exchange performance. One approach to solving this problem has been using concepts of physics and transport phenomena for better understanding of contrast agent kinetics. In one approach, Peladeau-Pigeon and Coolens (27) used the results of a Computational Fluid Dynamics (CFD) simulation and DCE-CT data obtained from a flow phantom to test Tofts (28) enhanced model and Fick’s principle (29) The phantom used in this study contained a single tube. Our simulation is a similar approach for simulating such a physical model; however, effects of dispersion due to vascular branching and flow have also been incorporated in our model. Although, validation of the results for in vivo human data is not possible, in the next step, to further investigate the accuracy of these results, these methods will be applied to DCE-T1 images of animals. Assessment of the accuracy of either method for estimating the permeability parameters can be investigated using methods such as histology or autoradiography; however, the results of the simulation study lean towards accuracy of the values found by the extended model.
In conclusion, we have introduced a model of the brain vasculature that describes the flow of blood in the brain vessels and also leakage of the CA to the extracellular extravascular space. This model can be used to estimate the local AIF in brain areas with vessels with or without leakage of the CA. Our simulations show that using the local AIF estimated by this model for solving the SM can give less biased estimations of the permeability parameters compared to using the global AIF. Using this model on DCE-MR images of cerebral tumors for estimating the permeability parameters yielded similar results as the simulations. One application of this model can be simultaneous estimation of the intravascular component of the CA concentration signal and the permeability parameters in areas with vascular extravasation. To validate the accuracy of the method for estimating the permeability parameters, it should be applied to DCE images of animals. Further additions to this model can include effects of the capillaries on dispersion of the AIF so that this model can be used for more accurate estimation of perfusion parameters in DCE-CT and DSC-MR images.
Acknowledgments
Support: Research reported in this manuscript was supported by the National Institutes of Health under award number RO1NS64134.
Abbreviations
- CA
Contrast Agent
- AIF
Arterial Input Function
- ASL
Arterial Spin Labeling
- DCE-CT
Dynamic Contrast Enhanced Computed Tomography
- DCE-MR
Dynamic Contrast Enhanced Magnetic Resonance
- DSC
Dynamic Susceptibility Contrast
- MTT
Mean Transit Time
- CBF
Cerebral Blood Flow
- CBV
Cerebral Blood Volume
- Ktrans
Vascular transfer rate constant
- vp
Vascular plasma volume
- kb
Inverse transfer rate constants
- ve
extracellular-extravascular space volume
- PET
Positron Emission Tomography
- AMM
Alternating Minimization with Model
- BVM
Basic Vascular Model
- EM
Extended Model
- AIC
Akaike Information Criterion
- MRA
Magnetic Resonance Angiography
- SM
Standard Model
- DESPOT1
Driven Equilibrium Single Pulse Observation of T1
- GBM
Glioblastoma Multiforme
- SPGRE
Spoiled Gradient Echo
- EES
Extravascular Extracellular Space
- CFD
Computational Fluid Dynamics
Footnotes
Siamak P. Nejad-Davarani, Hassan Bagher-Ebadian, James R. Ewing, Douglas C. Noll, Tom Mikkelsen, Michael Chopp, Quan Jiang. A Parametric Model of the Brain Vascular System for Estimation of the Arterial Input Function (AIF) at the Tissue Level. Submitted to NMR in Biomedicine
DISCLOSURE/CONFLICT OF INTEREST
The authors declare that they have no conflicts of interest in the research.
References
- 1.Gall P, Guether M, Kiselev V. Model of Blood Transport Couples Delay and Dispersion and Predicts ASL Bolus Measurements. ISMRM 18; Stockholm, Sweeden. 2010. p. 1736. [Google Scholar]
- 2.Kellner E, Gall P, Gunther M, Reisert M, Mader I, Fleysher R, et al. Blood tracer kinetics in the arterial tree. Plos One. 2014;9(10):e109230. doi: 10.1371/journal.pone.0109230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gall P, Petersen ET, Golay X, Kiselev V. Delay and Dispersion in DSC Perfusion Derived from a Vascular Tree Model Predicts ASL Measurements. ISMRM 16; Toronto, Canada. 2008. p. 627. [Google Scholar]
- 4.Gall P, Kiselev V. On the Form of the Residue Function for Brain Tissue. ISMRM 18; Stockholm, Sweeden. 2010. p. 1795. [Google Scholar]
- 5.Sourbron S, Ingrisch M, Siefert A, Reiser M, Herrmann K. Quantification of cerebral blood flow, cerebral blood volume, and blood-brain-barrier leakage with DCE-MRI. Magn Reson Med. 2009 Jul;62(1):205–17. doi: 10.1002/mrm.22005. Epub 2009/05/19. eng. [DOI] [PubMed] [Google Scholar]
- 6.Guzman-de-Villoria JA, Fernandez-Garcia P, Mateos-Perez JM, Desco M. Studying cerebral perfusion using magnetic susceptibility techniques: technique and applications. Radiologia. 2012 May-Jun;54(3):208–20. doi: 10.1016/j.rx.2011.06.003. Epub 2011/09/20. Estudio de la perfusion cerebral mediante tecnicas de susceptibilidad magnetica: tecnica y aplicaciones. spa. [DOI] [PubMed] [Google Scholar]
- 7.Chan AA, Nelson SJ. Simplified gamma-variate fitting of perfusion curves. IEEE International Symposium on Biomedical Imaging: Nano to Macro; 2004; p. 4. [Google Scholar]
- 8.Nestorov I. Whole-body physiologically based pharmacokinetic models. Expert opinion on drug metabolism & toxicology. 2007 Apr;3(2):235–49. doi: 10.1517/17425255.3.2.235. Epub 2007/04/13. eng. [DOI] [PubMed] [Google Scholar]
- 9.Bagher-Ebadian H, Jain R, Nejad-Davarani SP, Mikkelsen T, Lu M, Jiang Q, et al. Model selection for DCE-T1 studies in glioblastoma. Magn Reson Med. 2012 Jul;68(1):241–51. doi: 10.1002/mrm.23211. Epub 2011/12/01. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tofts PS, Brix G, Buckley DL, Evelhoch JL, Henderson E, Knopp MV, et al. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. Journal of magnetic resonance imaging : JMRI. 1999 Sep;10(3):223–32. doi: 10.1002/(sici)1522-2586(199909)10:3<223::aid-jmri2>3.0.co;2-s. Epub 1999/10/03. eng. [DOI] [PubMed] [Google Scholar]
- 11.Calamante F. Arterial input function in perfusion MRI: A comprehensive review. Progress in nuclear magnetic resonance spectroscopy. 2013 Oct;74:1–32. doi: 10.1016/j.pnmrs.2013.04.002. Epub 2013/10/03. eng. [DOI] [PubMed] [Google Scholar]
- 12.Sourbron SP, Buckley DL. Classic models for dynamic contrast-enhanced MRI. NMR in biomedicine. 2013 Aug;26(8):1004–27. doi: 10.1002/nbm.2940. Epub 2013/05/16. eng. [DOI] [PubMed] [Google Scholar]
- 13.Calamante F, Gadian DG, Connelly A. Delay and dispersion effects in dynamic susceptibility contrast MRI: simulations using singular value decomposition. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2000 Sep;44(3):466–73. doi: 10.1002/1522-2594(200009)44:3<466::aid-mrm18>3.0.co;2-m. Epub 2000/09/07. eng. [DOI] [PubMed] [Google Scholar]
- 14.Lee JJ, Bretthorst GL, Derdeyn CP, Powers WJ, Videen TO, Snyder AZ, et al. Dynamic susceptibility contrast MRI with localized arterial input functions. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2010 May;63(5):1305–14. doi: 10.1002/mrm.22338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fluckiger JU, Schabel MC, DiBella EV. Toward local arterial input functions in dynamic contrast-enhanced MRI. Journal of magnetic resonance imaging : JMRI. 2010 Oct;32(4):924–34. doi: 10.1002/jmri.22339. [DOI] [PubMed] [Google Scholar]
- 16.Yankeelov TE, Luci JJ, Lepage M, Li R, Debusk L, Lin PC, et al. Quantitative pharmacokinetic analysis of DCE-MRI data without an arterial input function: a reference region model. Magnetic resonance imaging. 2005 May;23(4):519–29. doi: 10.1016/j.mri.2005.02.013. [DOI] [PubMed] [Google Scholar]
- 17.Nejad Davarani SP, Bagher-Ebadian H, Ewing JR, Chopp M, Noll D, Jiang Q, editors. WorldComp’12. Las Vegas, Nevada, USA: 2012. Analytical Model of the Brain Vascular System for Estimation of the Arterial Input Function (AIF) at the Tissue Level. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wright SN, Kochunov P, Mut F, Bergamino M, Brown KM, Mazziotta JC, et al. Digital reconstruction and morphometric analysis of human brain arterial vasculature from magnetic resonance angiography. NeuroImage. 2013 May 28;82C:170–81. doi: 10.1016/j.neuroimage.2013.05.089. Epub 2013/06/04. Eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM Journal of Optimization. 1998;9:36. [Google Scholar]
- 20.Posada D, Buckley TR. Model selection and model averaging in phylogenetics: advantages of akaike information criterion and bayesian approaches over likelihood ratio tests. Systematic biology. 2004 Oct;53(5):793–808. doi: 10.1080/10635150490522304. Epub 2004/11/17. eng. [DOI] [PubMed] [Google Scholar]
- 21.O’Connor JP, Tofts PS, Miles KA, Parkes LM, Thompson G, Jackson A. Dynamic contrast-enhanced imaging techniques: CT and MRI. The British journal of radiology. 2011 Dec;84(Spec No 2):S112–20. doi: 10.1259/bjr/55166688. Epub 2012/05/25. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ewing JR, Bagher-Ebadian H. Model selection in measures of vascular parameters using dynamic contrast-enhanced MRI: experimental and clinical applications. NMR in biomedicine. 2013 Aug;26(8):1028–41. doi: 10.1002/nbm.2996. Epub 2013/07/25. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Deoni SC, Peters TM, Rutt BK. High-resolution T1 and T2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2005 Jan;53(1):237–41. doi: 10.1002/mrm.20314. Epub 2005/02/04. eng. [DOI] [PubMed] [Google Scholar]
- 24.Strich G, Hagan PL, Gerber KH, Slutsky RA. Tissue distribution and magnetic resonance spin lattice relaxation effects of gadolinium-DTPA. Radiology. 1985 Mar;154(3):723–6. doi: 10.1148/radiology.154.3.3969477. Epub 1985/03/01. eng. [DOI] [PubMed] [Google Scholar]
- 25.Bagher-Ebadian H, Paudyal R, Nagaraja TN, Croxen RL, Fenstermacher JD, Ewing JR. MRI estimation of gadolinium and albumin effects on water proton. NeuroImage. 2011 Jan;54( Suppl 1):S176–9. doi: 10.1016/j.neuroimage.2010.05.032. Epub 2010/05/25. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lomax RG. An introduction to statistical concepts. 2. Mahwah, N.J: Lawrence Erlbaum Associates Publishers; 2007. p. xi.p. 472. [Google Scholar]
- 27.Peladeau-Pigeon M, Coolens C. Computational fluid dynamics modelling of perfusion measurements in dynamic contrast-enhanced computed tomography: development, validation and clinical applications. Physics in medicine and biology. 2013 Sep 7;58(17):6111–31. doi: 10.1088/0031-9155/58/17/6111. Epub 2013/08/15. eng. [DOI] [PubMed] [Google Scholar]
- 28.Sourbron SP, Buckley DL. On the scope and interpretation of the Tofts models for DCE-MRI. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2011 Sep;66(3):735–45. doi: 10.1002/mrm.22861. Epub 2011/03/09. eng. [DOI] [PubMed] [Google Scholar]
- 29.Truskey GA, Yuan F, Katz DF. Transport phenomena in biological systems. 2. Upper Saddle River, N.J: Pearson Prentice Hall; 2009. p. xxiii.p. 860. [Google Scholar]