Abstract
In this paper, we introduce a novel model of the brain vascular system, which is developed based on laws of fluid dynamics and vascular morphology. This model is used to address dispersion and delay of the Arterial Input Function (AIF) at different levels of the vascular structure and to estimate the local AIF in DCE images. We developed a method based on the Simplex algorithm and Akaike Information Criterion for estimating the likelihood of the contrast agent concentration signal sampled in DCE images to belong to different layers of the vascular tree or being a combination of different signal levels from different nodes of this structure. To evaluate this method, we tested the method on simulated local AIF signals at different levels of this structure. Even down to an SNR of 5.5 our method was able to accurately detect the branching level of the simulated signals. When two signals with the same power levels were combined, our method was able to separate the base signals of the composite AIF at the 50% threshold. We applied this method to Dynamic Contract Enhanced Computed Tomography (DCE-CT) data and using the parameters estimated by our method, we created an arrival time map of the brain. Our model corrected AIFcan be used for solving the pharmacokinetic equations for more accurate estimation of vascular permeability parameters in DCE imaging studies.
Keywords: Arterial Input Function, Vascular Modeling, Dynamic Contrast Enhanced Imaging, Vascular Permeability, Perfusion, Laminar Flow
Graphical Abstract
We have presented a model of the cerebral vascular system based on vascular morphology and laws of fluid dynamics, to be used for estimating the local arterial input function in DSC and DCE MRI and DCE-CT studies. Using this local arterial input function can reduce errors in estimation of permeability and perfusion parameters in these studies. The model was tested on DCE-CT images by creating an arrival time map using the model parameters, which matched the expected values in the brain.
INTRODUCTION
Estimating the Arterial Input Function (AIF) of a Contrast Agent (CA), the time-concentration curve in plasma, especially at the tissue level, has long presented a challenge in Dynamic Contrast Enhanced Magnetic Resonance (DCE-MR), Dynamic Contrast Enhanced Computed Tomography (DCE-CT) and Dynamic Susceptibility Contrast (DSC) imaging studies. The AIF is used for estimating Mean Transit Time (MTT), Cerebral Blood Flow (CBF), Cerebral Blood Volume (CBV), vascular transfer rate constant (Ktrans), vascular plasma volume (vp), and extracellular-extravascular space (ve) in DSC and DCE studies (1, 2). Using an inaccurate AIF profile in permeability and perfusion analyses could substantially add bias to the estimated hemodynamic and permeability maps. This is one of the main reasons for finding the Arterial Input Function (AIF) at the tissue level or in other words, the local AIF. One of approaches towards solving this problem is modeling the vascular system in the brain and using that to find the dynamics of blood flow at the capillary (tissue) level.
Many researchers have attempted to model vasculature for applications in DSC and DCE studies. Depending on the applications, there have been different approaches to this problem, each having their advantages and shortcomings. One approach has been modeling the blood circulatory system of the whole body and finding the flow at different locations in the vascular system. In this category, Sherwin et al built a one dimensional network based on space-time variables and linear and non-linear modeling (3). Another modeling approach is based on having a three-dimensional arterial tree embedded in a one-dimensional representation of the arterial system (4). Bagher-Ebadian et al suggested a model and algorithm based on the blood-circulatory system, for estimating the CA time-concentration curve in arterial plasma after an intravenous bolus injection (5, 6). Although these models allow performing quantitative and qualitative studies about local and global hemodynamic quantities, none of the models above have addressed the model of the flow at the capillary (tissue) level in the brain.
In one study Calamante et al proposed using Independent Component Analysis (ICA) in perfusion studies as a tool to define a local AIF for obtaining more accurate quantification of CBF in DSC-MRI studies (7). The method for finding the local AIF was based on a semi-manual approach and user input was required for choosing the components and also there was no method for validating the local AIF. Mouridsen et al defined a physiological estimation of microvasculature which was used for estimation of cerebral perfusion with Bayesian methods (8). In this study, it was assumed that the AIF has a Gamma variate Probability Density Function (PDF). Assuming Gamma Variate or exponential decay functions for the local AIF have been used in other studies as well (9, 10). Cebral et al used a method based on MR angiograms to develop detailed assessment of blood flow patterns from direct in vivo measurements of vessel anatomy and flow rates using finite element methods (11). The focus of this research was only on major arteries and small arteries were not modeled.
There have been a considerable number of studies for modeling changes in the AIF for Arterial Spin Labeling (ASL) applications. Some have used Gaussian kernels (12) or variations of it (13) for modeling dispersion of the AIF which provide plausible smoothening of the AIF box-car shape along the arterial pathway. Hernandez et al. previously presented a one dimensional model for ASL applications that takes into account the effects of transit times by modeling displacement and decay of the inversion tag between the tagging and imaging locations (14). In another study, Kazan et al. modeled the effects of dispersion in Arterial Spin Labeling (ASL) (15) using the mass transport equation. In another study Gallichan and Jezzard modeled dispersion of the AIF using laminar (parabolic) and pulsatile flow of blood in major arteries (16). This model was designed only for ASL applications and also it considered only a single tube with no branching, which is not the case in vascular structures. Later Chapelle et al. used a variation of this model with adding a gamma-variate kernel to address dispersion in ASL (17). Although these studies have suggested practical approaches for addressing changes of the ASL bolus, none of them have considered the effects of multiple pathways of flow through the vasculature for modeling the overall dispersion. One of the approaches that has used laws of fluid dynamics for estimating the changes in the bolus profile is a method proposed by Gall et al (18). They introduced a framework for solving the deconvolution problem in DSC using a functional form of the residue function and also for estimating the changes in the bolus profile in ASL applications. In this framework, the function was derived based on the laws of laminar flow and a vascular tree model. Their results of using this function showed excellent agreement with data measured using ASL in early branches of the vascular tree.
The methods discussed above show different models for the AIF but most of these models either represent the input function only at the level of the major arteries (such as the carotid artery) or if they have an estimation of the input function at a lower level, the model does not represent all the major parameters that affect the AIF at the capillary level. Here, using an approach similar to the work done by Gall et al (18) and Kellner et al (19), we introduce an analytical model of dispersion in major arteries at different levels of branching based on laws of fluid dynamics and morphological properties of the vessels. Next, using this model and Akaike Information Criterion (AIC), we introduce a method for estimating the structure of the vascular tree at different locations in DCE images.
MATERIALS AND METHODS
Implementation of the vasculature model
The model which we have proposed, explains dispersion of the AIF based on two different sources: Dispersion in a single vessel due to laminar flow and dispersion due to branching of the vessels down to the capillaries and multiple arrival times of blood in the tissue due to different vascular pathways of different lengths. All modeling and visualization was done in MATLAB (MATLAB Release 2010b, The MathWorks, Inc., Natick, Massachusetts, United States).
Parametric expression of dispersion in single tube
The average Reynolds number (Re) for the Carotid Artery has been calculated to be 266 and 911 for mean and peak flow rates respectively (20) and since this is less than 4000, we consider the flow of blood in the brain vessels other than the capillaries being laminar. In laminar flow, the velocity of the fluid in a tube is dependent on the radial distance to the center of the tube and can be characterized as (21):
| (1) |
where v0 is the velocity of blood along the central axis of the vessel with a radius of R.v is the blood velocity at the radial distance r from this axis. In this study, considering the time resolution of DCE imaging, the effects of pulsatile flow of blood in the vessels are ignored and it is assumed that flow has reached a steady state; thus, from this point on, v0 will represent the maximum blood velocity in each vessel. Based on Equation 1, in an approach similar to the work by Gall et al (22) and Kellner et al (19), we have derived a transfer function that describes the distortion of the contrast agent profile, after passing through a single vessel (details are presented in the Appendix):
| (2) |
where
| (3) |
D0 is the length of the vessel and since v0 is the maximum velocity of blood in the vessel, t0 is the shortest time that the contrast agent takes to pass through the vessel and under the assumption of steady flow in the vascular system, it can be considered a characteristic of the vessel.
Dispersion due to the cascade of vessels
In the case where a cascade of vessels exists, the overall transfer function of the vessels from the input node to any node in the system is the convolution of the transfer functions of the individual vessels in the pathway. In such a system, the transfer function of each vessel can be written as follows:
| (4) |
| (5) |
| (6) |
| (7) |
In these functions, t01 to t0n are the time delays of each individual vessel along the vascular route, from the opening of the main artery down to the nth branching layer. The transfer function of the vessels from the main input to the nth level of sub-branches can be written as:
| (8) |
Fractal geometry of the vessels
Based on Murray’s branching law of vessels, when an artery bifurcates, the radii of the daughter vessels are related to the radius of the parent vessel through (23, 24):
| (9) |
If we assume that the two daughter branches are similar, the radius of these daughter vessels and the parent vessel will be related through:
| (10) |
Therefore the maximum velocity of blood in each of the daughter vessels (v0d) will be times that of the parent vessel (v0d ). Also if we assume that the length of the daughter branches is:
| (11) |
the delay time of the daughter vessels (t0d) will be equal to the delay time of the parent vessel (t0p). The benefit of employing these assumptions is that while they are close to reality (25) it can reduce the number of parameters that describe a vascular tree; instead of having an individual t0 for each branch, one t0 can describe the entire tree from the major artery down to the arterioles. In this case, if h(t)1 is the transfer function of each branch the general equation for the transfer function of the vascular tree will be:
| (12) |
Where “*n” denotes n repeated convolutions.
Simulating the CA concentration profile at different levels of the vascular structure
To explore the feasibility of using our method for estimating the vascular transfer function parameters in DCE images, we first performed a simulation of the CA concentration profiles. Initially we implemented a vascular morphological model as in Figure 1, with parameters comparable to real life values. The diameter of the common carotid artery in healthy adults has been estimated to be (26) 6.0 ± 0.8 mm and the mean velocity of blood passing through the Internal Carotid Artery (ICA) has been measured to be 32.7 ± 3.0 cm/s in healthy adults (26). These values were used as the starting points of our model implementation. Based on the findings of Wright et al. the mean and standard deviation of the branch lengths in the brain is 25.02 ± 2.71 mm (19.35 mm-30.14 mm). The length of the main branch of our model was set to 4 cm based on these reported values. The model starts with one main artery; this artery bifurcates and two daughter vessels are created with the length and radius described in the previous section.
Figure 1.
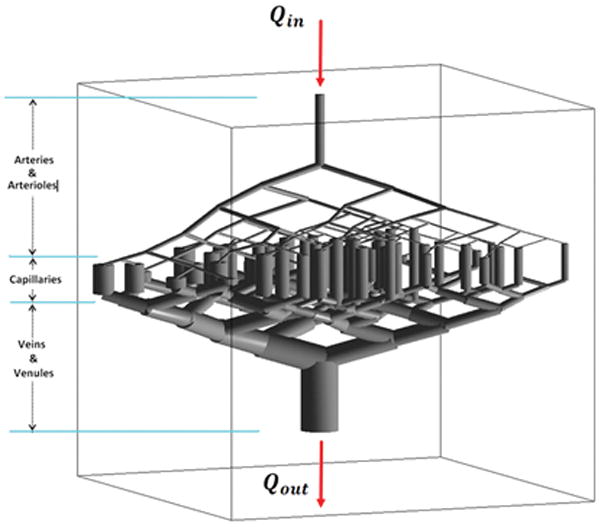
Morphological structure of the vascular model; branching of arteries and arterioles has been simulated down to six levels. As seen here, the veins and venules have larger volume and diameter compared to arteries and arterioles. The volumetric flow rate of blood entering this model equals the efferent flow. Every segment of the capillary bed is modeled as a single tube vessel in which the flow is non-laminar.
Using the same procedure, the daughter branches can be created recursively till they reach the capillary level. The three main arterial branches originating from the circle of Willis are the Anterior Cerebral Artery (ACA), Middle Cerebral Artery (MCA) and Posterior Cerebral Artery (PCA) (27). Each of these major vascular trees feeds a different part of the brain, but since they all originate from the circle of Willis, considering the relatively low time resolution of the imaging modalities, we assumed that the CA concentration profile of the blood entering these three branches is similar. According to the measurements done by Wright et al. (28), the maximum number of bifurcations in these trees are 6.15 ± 1.53 (ACA), 8.80 ± 1.40 (MCA), and 5.93 ± 1.66 (PCA). Using these initial values and branching rules, our model was implemented with six levels of branching down to the capillary level as in Figure 1; the veins and venules were implemented as the mirror image of the arteries and arterioles, albeit with a larger radius such that the overall volume of the veins and venules be four times that of the arteries and arterioles (21).
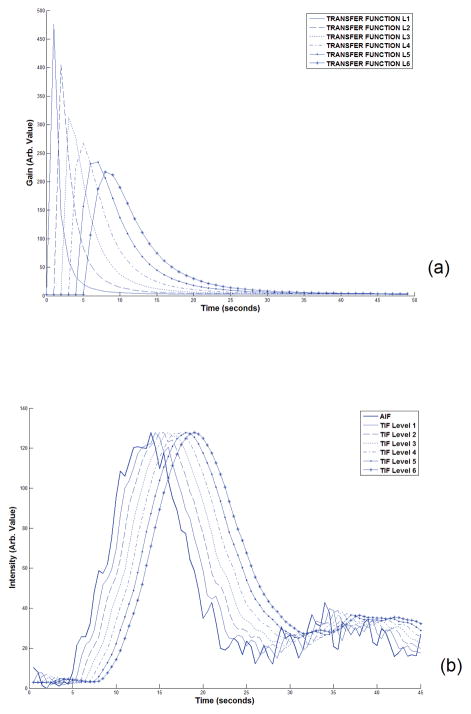
The flow rate in the vessels in this model was calculated by finding the resistance of every branch based on Poiseuille’s law (21) and converting the model to an analogous electric circuit and finding the electric current in all branches based on Ohm’s law (29). After finding the velocity of blood in all branches of the model, the time delay (t0) of each branch was calculated using Equation 3 and the vascular transfer function between the opening of the main artery and every node was estimated based on Equation 12. Figure 2-a shows the transfer functions between the opening of the main artery to the end of each of the vessels in the vascular structure, down to the sixth layer of branching in one vascular line. Using the profile of the contrast agent in the carotid artery of a human subject in a DCE-CT image series (acquired by the procedure which will be described in the following sections) and these six transfer functions, the local AIF at every node was calculated as plotted in Figure 2-b. For better visual comparison of these curves, the peaks are all scaled to the same level as the AIF. By moving to higher levels of the vascular tree, the arrival time of the CA profile increases and it also gets more dispersed.
Figure 2.
(a) The transfer functions of vessels from the opening of the main artery down to the 6th level of the vascular branching. As seen here, as the level increases, the arrival time and dispersion both increase. (b). Plots of the main AIF (bold curve) of a human subject along with the local AIF at six levels of our vascular model estimated by convolving the main AIF with the transfer function at each level. The AIF was sampled from the first 45 seconds of the DCE-CT image series in the voxels showing the Internal Carotid Artery of a human subject after the bolus injection of the CA. For easier comparison of the profile of these curves, the peaks are scaled to the peak of the AIF. As seen here, by moving to the higher levels of the vascular structure, the arrival time delay gets longer and the curves get more dispersed.
Estimating the vascular level of a DCE signal
In this section we describe the method we have used for solving the inverse problem which is estimating the values of the time delay (t0) of the vascular tree based on the CA profile sampled in the brain tissue which can be both for the simulated data and data from DCE images.
Fitting the data to the models
Every voxel in the image volume belongs to one part of the vascular tree or the capillary bed; however, except for a few major vessels, it is not visually possible to follow the level of vessels in the branch hierarchy. The goal is to determine the likelihood of each voxel belonging to different branching levels of the vascular tree structure. The first step is to estimate a transfer function (according to Equation 12) that when convolved with a global AIF, can result in the CA concentration profile of that voxel. For practical purposes, to compensate for the signal reduction due to volumetric fraction of vessels in tissue, a gain factor g was added to the transfer function:
| (13) |
The global AIF profile is defined as AIF(t) and the measured tissue concentration signal of an arbitrary voxel in the brain image as CA(t). The relationship between these two can be defined as:
| (14) |
where x is the branching level of the vessels in that voxel which generally speaking, is initially an unknown value and one of the goals is to determine the possible value (or values) of x for that voxel. It should be noted that in this equation, the effects of the capillary bed on dispersing the AIF have been neglected. Using the simplex algorithm (30) as a non-linear fitting method and the sum of squared errors as the cost function, for every possible configuration of the transfer function h(t)1 to 2, h(t)1 to 3, … or h(t)1 to 6), the best function transforming the reference AIF(t) to CA(t) is found. This results in six different configurations of the transfer function where each is described by [g, t0, n] where n varies from 1 to 6 and represents the branching level of the vessel. It should be noted that the parameters estimated for every configuration of the transfer function are not dependent on the parameters from other configurations and are estimated independently every time the fitting procedure is repeated.
Model selection and model averaging using Akaike Information Criterion (AIC)
After finding the six best transfer functions (one for each of the six branching layer configurations) or the model configurations for every voxel, the problem of determining the contribution of each model configuration should be addressed; this is necessary since each voxel might be representing a combination of vessels from different layers of the vascular structure; or if it is the representative of only one vessel or tissue type, the branching level of the vessel at that voxel needs to be estimated. In our study, we used Akaike Information Criterion (AIC) for model selection and model averaging (31). The AIC value can be calculated using the residual sum of squares (RSS) for each of the six models being investigated using the following equation:
| (15) |
Here n is defined as the number of observations which in our study represents the number of image timepoints. k is the number of model configuration parameters which in our application, is two for each model configuration. We define AICmin as the AIC for the model configuration with the best fit. To calculate the Akaike weights, we first define a new variable Δi that represents the difference between the AIC values in these six model configurations with the lowest AIC value:
| (16) |
Using these values, the Akaike weight (wi) for each model configuration is estimated:
| (17) |
For each voxel, the estimated Akaike weights are considered to be the probability of model configuration i (i=1 to 6) being the best model that describes the transfer function between the opening of the main artery and that voxel. Using the Akaike weights and the estimated values of the model parameters for each configuration of the model, an average transfer function is calculated which we name h(t)est Using this transfer function, the local AIF can be estimated as follows:
| (18) |
In our model, we have not included the effects of the capillaries on the AIF and therefore the transfer function that is estimated using the method explained above will give an estimation of the transfer functions of the arteries and arterioles feeding the capillary bed which is the reason that in this equation we have referred to it as AIFL(t).
Delay maps
As explained before, every transfer function is described with a set of parameters [g, t0, n]. In the case of dealing with only one model configuration, the total delay time from the main artery opening to the voxel being studied (or the arrival time of the contrast agent) can be calculated as n × t0; however, in this study since multiple model configurations are used, by applying the rules of model averaging using AIC (32), the delay time (CA arrival time) of each voxel is estimated by calculating a weighted sum of the delay times of all model configurations, with the weights being the Akaike weights of that voxel:
| (19) |
Where t0i is the t0 of model configuration with i branching levels. The benefit of using this model averaging method (32) for calculating the delay time is that voxels representing tissues that are being supplied by more than one branching level of the vascular system will have all those vessels accounted for and the delay time will be a weighted average of all the possible delay times from different vascular pathways. This approach can also address the concept of collateral flow. Previously, Brix et al used a similar weighted model approach for finding the best approximating model from three nested compartmental pharmacokinetic model for analysis of tissue microcirculation (33).
Model evaluation using DCE-CT imaging
The next step of vascular model development was evaluating the performance of the model using human DCE data. After studying different dynamic imaging modalities, DCE-CT imaging was selected as this modality. Compared to DCE-MRI, DCE-CT images have lower Signal to Noise Ratio (SNR) and Contrast to Noise Ratio (CNR) (34). However, other characteristics of this modality made it a better choice for our study: the signal intensity of the CT images is linearly dependent on the CA concentration (35) and also, the temporal resolution of this modality is much higher (~10 times more) than DCE-MR images (0.5 sec vs. 5 sec). In addition, CT images have better spatial resolution (36).
The study was approved by the Henry Ford Health System institutional review board and written informed consent was obtained from the subject. DCE-CT images were acquired on a GE LightSpeed VCT scanner with image matrix size of 512×512 (24×24 cm FOV) and eight slices (5mm slice thickness) with 99 imagepacks (89 image sets sampled every 0.5 seconds for the first 44 seconds, 1 image acquired at the 50 second time point, followed by 9 image sets acquired every 16 seconds for a total scan time of 194 seconds). 50ml of iodinated CA with a concentration of 0.5ml/Kg was injected as a bolus using a power injector at a rate of 4cc/sec starting five seconds after start of image acquisition; cine scan was done for 50 sec. The dynamic images were baseline corrected to make their intensity linearly dependent on the CA concentration. Also, to increase the SNR, especially in the tissue regions, the neighboring voxels were averaged and the images downsized to 128×128. After these pre-processing steps, the CT images were ready to be used for testing the model using the same approach explained in the previous sections.
RESULTS
Simulation Results
Estimation of the level of the simulated CA concentration profiles
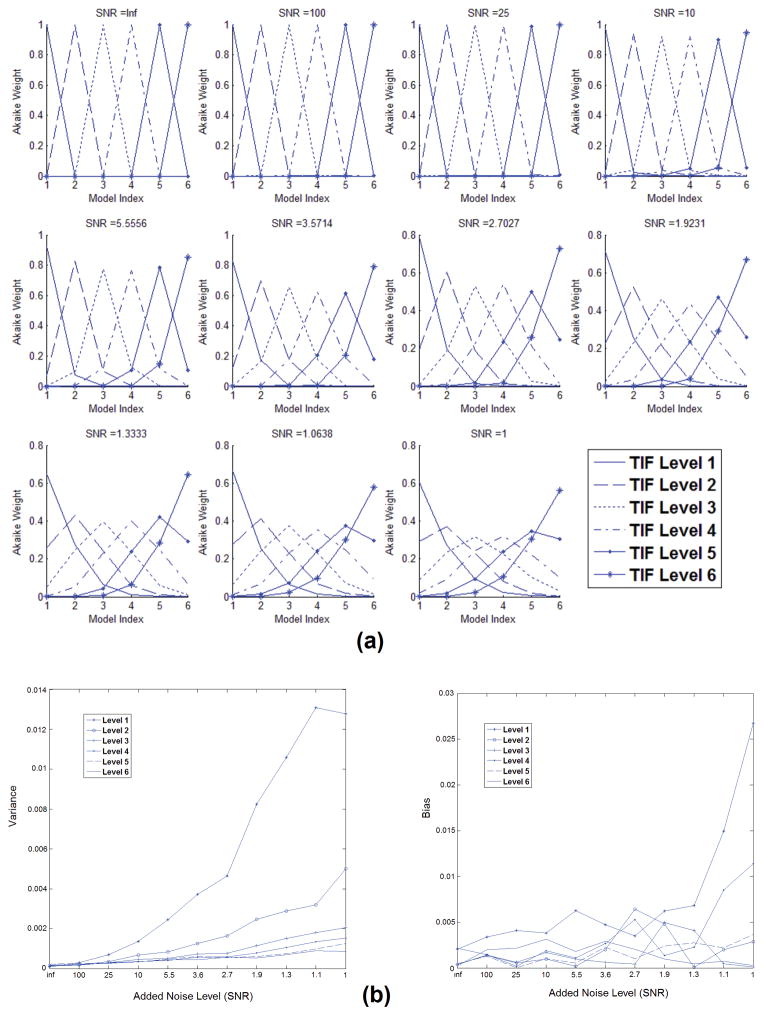
The goal of the first part of our simulation was to explore the ability of our method for finding the correct transfer function of the vascular structure based on the AIF and the simulated CA concentration profiles as we explained previously. The different model configurations were fit to each of the six profiles using the fitting procedure and the model selection methods that we described. The likelihood of these profiles belonging to each of the different model configurations was estimated using the fitting residue value and the Akaike method. The effect of noise on the performance of the model was evaluated by adding different levels of noise to the simulated profiles. Figure 3-a shows the results of these simulations. As seen here, the added noise level is varied between 0% to 100% and at each of these levels the likelihood of selecting the correct level of the vascular structures has been estimated. Up to the 18% noise level, the likelihood of selecting the correct level of the profile is almost 1 for all cases. As this noise level increases, the accuracy of the system decreases and this likelihood gets less; however, in the 100% noise level, the likelihood of selecting the correct level index does not go below 0.3.
Figure 3.
(a) Akaike weights of each of the simulated signals after model averaging. The plots show the likelihood of each of the simulated local AIFs being selected as the level of branching that they were simulated for. As seen here, even at the 18% noise level, the likelihood of picking the correct branching level of the signal is almost 1 for all cases. As the noise level increases, the accuracy of the system decreases and the likelihood of picking the correct model configuration gets less; however, in the 100% noise level, the likelihood of picking the correct level index does not go below 0.3. (b) Bias and variance of the estimated parameters for the six cionfigurations of the model for 11 levels of gaussian noise added to the signal. These values are estimated with the procedure described above and for 300 repetitions at each noise level. When the vascular structure has only one level, only one time delay is estimated and the curves represent the values of that parameter. For higher levels of vascular branching, in the graph we used the sum of the estimated values of these parameters. As seen here, for all levels of noise, the estimates of these parameters remain very close to the original values of these parameters. One of the sources of bias can be the temporal resolution of the simulated signals.
In Figure 3-b, the bias and variance of the estimated parameters are plotted. These values are estimated with the procedure described above. In these graphs, each data point shows the bias and variance of the values for each noise level. As seen here, for all levels of noise, the estimates of these parameters remain very close to the original values of these parameters. One of the reasons for the bias in the estimated values can be the temporal resolution of the simulated data.
Decomposing the simulated composite profile
When applying our method to the DCE-CT images, it is likely that the signal sampled from a typical voxel in the image represents a composite of vessel segments from more than one level of the vascular tree which can also be the result of collateral flow in cranial vasculature. To simulate these conditions, and to explore the feasibility of our method for detecting these signals, the superposition of the CA profile from different levels of the model was created and decomposed by the fitting algorithm and by applying the AIC method as we explained before.
Figure 4 shows a schematic diagram of our model simulation in the case when two signals are combined. Here, the square represents a hypothetical voxel in which vessels from both the second and sixth levels pass through. The temporal signal sampled in this voxel is the weighted sum of the signals from the two vessel segments and depending on the effective volume of each of them in this voxel, the level of contribution of each signal is adjusted from 0% to 100%. Also, we added different levels of noise to the composite signal (0% to 100%) and explored the feasibility of our method to decompose these signals in presence of noise.
Figure 4.
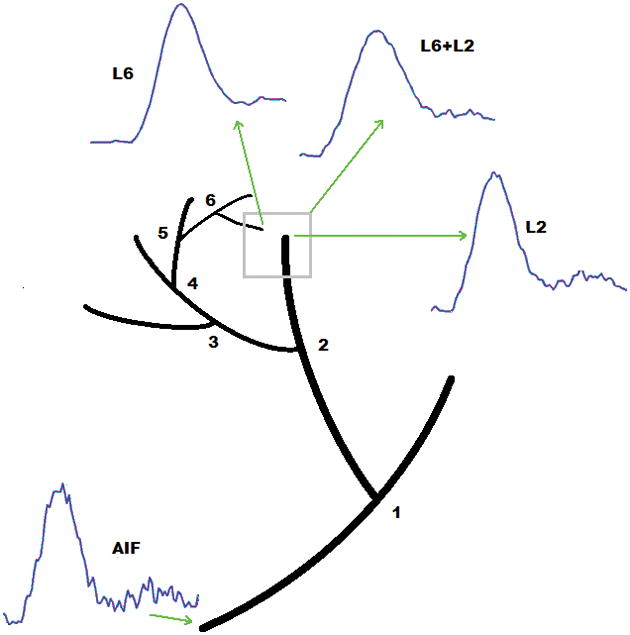
Schematic figure showing a typical AIF from one of the major cerebral arteries of a human subject in DCE-CT images and the simulated local AIFs at the second (L2) and sixth level (L6) of our vascular model. In this figure the effect of one voxel representing vessels from two different levels has been simulated. In this case the signal sampled from this voxel would be the superposition of the two signals (L6+L2). Using this configuration, we have studied the feasibility of our method to distinguish and separate the signals that form the composite signal.
Figure 5 shows the curves representing the Akaike weights of the composite signals after decomposition by the method explained above. Each curve represents the average of results from 300 repetitions at each noise level. As seen here, at noise levels lower than 50%, almost all these curves meet at the 50% contribution level point which matches our expectation. One observation in these curves is that in cases where the contribution of either signal is not close to 50%, when no noise is added to the signals or the noise level is small, the Akaike weights tend to get saturated to 1 or 0; this is due to the large difference in the residue values of the fitting procedure for the two signals in the absence of noise. But when noise is added, since the residues will have large values, the Akaike weights will not get saturated in these cases. When the difference between the levels of the two signals increases, this saturation effect will become more evident, even in the presence of noise. These results show that in the no-noise situation, the AIC does not act as an unbiased estimator.
Figure 5.
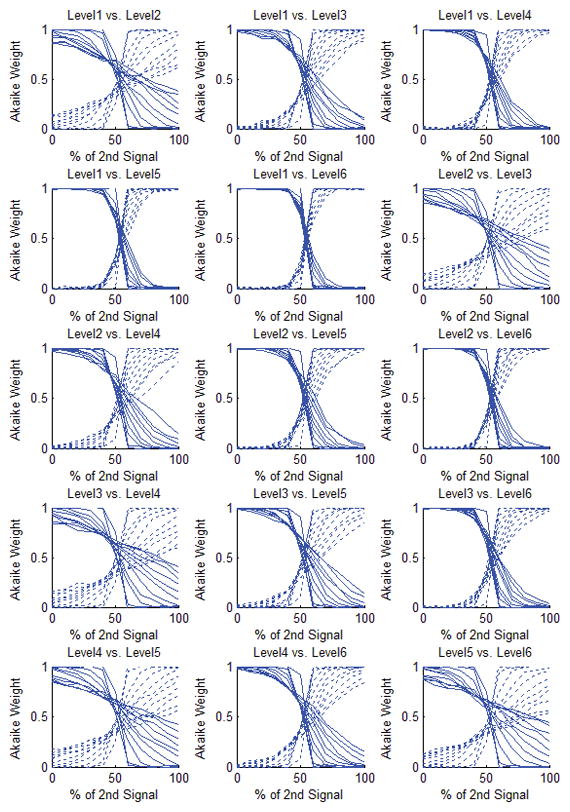
Akaike weights of the simulated composite signals after decomposition. Each curve represents the average of results of 300 repetitions at each noise level. The composite signal is basically the weighted sum of the two simulated signals (the x-axis represents the percentage of contribution of the second signal in the composite signal) from different layers of the vascular structure. In each of the boxes above, each plot represents one noise level: In the upper half of the box, from left to right, each dotted line indicates 0% to 100% noise level (SNR = Inf, 100, 25, 10, 5.5, 3.6, 2.7, 1.9, 1.3, 1.1, 1) added to the composite signal and the solid lines correspond to 100% to 0% noise levels respectively. In the absence of noise, the switching point for all of these cases occurs at the 50% level which is what is expected. However, in the case that the model configuration levels are consecutive, when the noise level is increased, this switching point moves towards higher values, in favor of the model with fewer parameters. The worst case is seen in level 5 vs. level 6 when the noise level is 100%. However, even in this case even up to 52% noise level, the cutoff threshold is still around 50%.
Results of applying the model to DCE-CT images
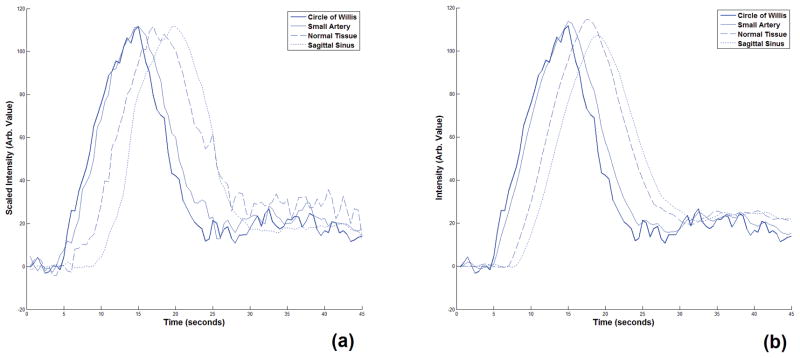
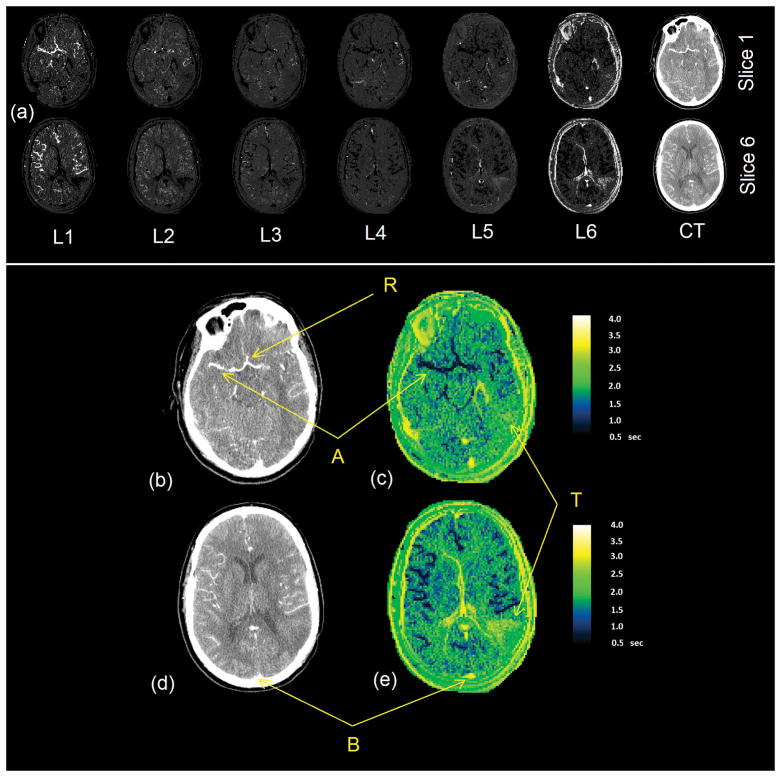
Figure 6 shows the tissue concentration signals sampled from four different regions (circle of Willis, a small artery which was the sub-branch the middle cerebral artery, a region of the normal tissue and the superior sagittal sinus) and the corresponding tissue input signals estimated by Equation 18. These curves show that the proposed method can describe the transfer function for the arteries and capillaries very well and the reconstructed signal matches the tissue concentration signal sampled from the tissue with healthy vessels. Figure 7-a shows the six Akaike weight maps for two slices of a DCE-CT image volume. As seen in this figure, in the Akaike map of the first model configuration, the voxels that represent the major artery that the AIF has been sampled from have the highest Akaike weight which has a value very close to 1. As the model configuration index increases, the voxels with the highest value shift from the major arteries to other cerebral regions. In the map corresponding to model configurations 5 and 6, the voxels showing the major veins such as the sagittal sinus have the highest likelihood of belonging to this model configuration. The reason for this is that the transfer function was not designed to describe the changes of the CA concentration profile in the veins and venules and since in the model fitting step these configurations give the lowest fitting residue, they are selected at the best fitting model configurations.
Figure 6.
(a) CA concentration signals sampled from four regions of a DCE-CT image of the human brain. These regions are the circle of Willis, a small artery which is a sub-branch of the middle cerebral artery, a region in the normal tissue and the superior sagittal sinus. These signals are scaled to show the relative dispersion and delay of the CA profiles more clearly. (b) The reconstructed CA concentration signals corresponding to the signals in (a) that were created using our proposed fitting and model selection method. As seen here, unlike the results for the other vessels, since our model was not designed for veins and venules, the reconstructed CA concentration signal representing the sagittal sinus does not match the signal sampled from this region.
Figure 7.
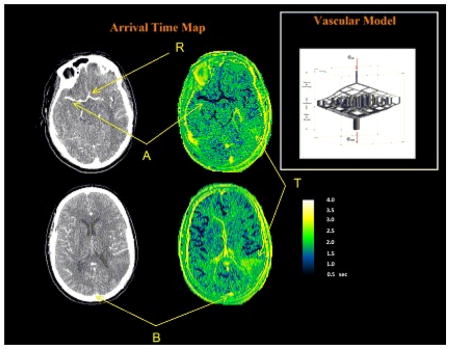
(a) Akaike weight maps of two slices of the CT image based on the six levels (configurations) of the vascular tree model. The intensity of each voxel in the images L1 through L6 images show the likelihood of that voxel belonging to that level in the vascular tree. Based on the Akaike method, the sum of the intensities of every voxel across the six images is one. The images on the right column are the CT images of the same slice, a few seconds after injection of the contrast agent. As seen in these CT images, all the major vessels have been enhanced in intensity but there is no distinction between the arteries and veins since they are all enhanced. (b,d) Enlarged images of the two sections of post injection CT images in (a) and (d,e) the delay maps (in seconds) created using our method. ‘R’ is the reference point for measuring the glocal AIF. ‘A’ is the location of one of the main arteries and ‘B’ shows the Superior Sagittal Sinus. ‘T’ shows the location of the tumor.
These probability maps were used to create the blood flow delay maps of the brain as seen in Figure 7-c and 7-e. Point R in this figure shows the reference point where the global AIF was sampled (same profile as the AIF in Figure 2). This AIF was used to estimate the transfer function between R and all the voxels in the image. As seen here, the estimated delay time is different at different parts of the brain: The arteries such as the main arteries marked as A have a short delay time and other areas of the brain have longer delay times and have values up to 4 seconds which is a good approximation of the mean transit time of the blood flow in the brain (37). As explained above, the profile in veins (such the Superior Sagittal Sinus marked as B) cannot be explained using this model and the estimated delay times in these regions are not valid. As seen in Figure 7-e, the tumor (T) shows a longer delay time. This long delay time in the tumor area is an overestimation of the actual value. One reason for this can be the extravasation of the CA to the extracellular-extravascular space which results in changes of the CA concentration profile in this area such that it that cannot be explained solely by dispersion and delay. This issue will be addressed in an accompanying paper [*].
DISCUSSION AND CONCLUSION
In this study, the first system investigation was performed on a novel vascular model that we have developed for studying the changes of the AIF at different levels of the vascular structure, using a transfer function of a single vessel. Our investigation is based on a combination of simplex (for fitting) and AIC (for model selection) methods and we did a simulation study to test our methods and also studied the application of our method in DCE-CT images of the human brain. Our model can analytically explain dispersion of the contrast agent profile at different levels of the vascular tree in the brain without any assumptions about the profile of the contrast agent, using systems analysis methods. The simulation results showed high accuracy in finding the level of the CA profile in the vascular tree and the contribution of CA profiles at different levels of the vascular tree. Applying this model to DCE-CT images of the human brain exhibited that the arrival time of the contrast agent at each voxel matched the expected data.
Our novel semi-empirical model of the brain vascular system is based on laws of fluid dynamics and morphology of the vascular structure in the brain. Our approach is similar to the framework proposed by Gall et al (18) and Kellner et al (19). One advantage of this model is that it does not make any assumptions about the profile of the contrast agent (such as it being a gamma variate or Gaussian function, etc.). The vascular model in its current form, does not include all aspects of the laws of fluid dynamics and vascular physiology such as turbulence at the bifurcation points in the vessels; but considering the data modalities and also the time resolution of our dynamic experiments, it can explain dispersion in the brain vasculature very well. However, this model assumes no leakage of the CA from the vessels into the extravascular space; leakage can change the profile of the measured tissue response signal. To address leakage, permeability and diffusion parameters should be incorporated into the model. As an extension of our model, we have included and studied the effects of some these parameters in our model. These will be reported in a separate paper. The number of parameters that are directly estimated using the vascular model two which are basically the delays of the vascular segments and a scaling factor; however other parameters can be indirectly estimated using the estimated transfer function.
Our vascular model has demonstrated its application for studying the changes of the AIF at different levels of the vascular structure and for improving the measurement of arrival time of the contrast agent in the dynamic contrast enhanced perfusion measurements. Kellner et al (19) have described two approaches for measuring the tracer in the vessel segment with laminar flow: the snapshot method where the CA volume in measured instantaneously and the flow-type method where local velocity contribution to the labeled CA volume is considered. Although the flow-type model provides better theoretical approach, fitting the flow-type model and snapshot model to the ASL data showed that the transfer function of the snapshot model gave better fits to the data than the flow-type model. On the other hand, the expected bolus dispersions using these two models differ only slightly after passing through a few bifurcations (19).
The interesting point about the vascular transfer function is that it can describe dispersion in a single vessel with only one parameter. Our model mainly describes arteries, arterioles and capillaries and in order to describe the veins, venules and capillaries, more parameters should be added to the model to address the dispersion of the CA profile in the veins more accurately. However, considering the fact that the total volume fraction of capillaries, veins and venules consist only about 3% of the total brain volume (38), the likelihood of selecting a voxel representing a vein is low. For this reason and also to avoid the unnecessary increase of the complexity of our model at this point, we did not include that in our analysis. Despite this, since the transfer function of the veins and venules is the closest to that of the highest level of arterioles in our model, these vessels show the best fit to the transfer functions describing these vessels; the results as seen in the final Akaike weight maps (Figure 7-a) show the major veins (such as the inferior and superior sagittal sinus) having the highest likelihood at the highest model level which confirms this point.
The good performance of the model fitting and selection method in the simulation studies in presence of noise shows its robustness for finding the vascular branching level of signals for non-simulated data. In the second part of this paper [*], this model will be translated to DCE-MR experiments for estimating permeability parameters in these images. To extend this model to be used for perfusion studies, the Tissue Input Function (TIF) should be estimated and for this reason, the effect of capillaries should be added to the model.
One application of this model and methods introduced in this paper is tissue characterization; based on the vascularity of the tissue, the CA profile can change and this can be used to classify it. As was noted, modeling abnormal vasculature in the brain such as those in tumors can add to the options for possible equations of the transfer function and by using the same procedure as described in this study, different types of tissue can be characterized in the DCE images based on the parameters of the model which will be part of the future work.
In conclusion, we have developed a model of the vascular system of the brain that explains dispersion of the CA profile in different locations of the brain vascular system and has been tested using DCE-CT and simulated data. Even though at this point only healthy arteries, arterioles have been modeled in our model, our model in its current form can give a good estimate of the transfer functions of most vessels in the brain. Further steps in this research will involve adding parameters to the model to describe certain effect of capillaries and also vascular pathologies that could be used for more accurate estimation of perfusion and permeability characteristics of vessels in DCE images.
Acknowledgments
Support: Research reported in this manuscript was supported by the National Institutes of Health under award number RO1NS64134.
Abbreviations
- AIF
Arterial Input Function
- CA
Contrast Agent
- DCE-MR
Dynamic Contrast Enhanced Magnetic Resonance
- DCE-CT
Dynamic Contrast Enhanced Computed Tomography
- DSC
Dynamic Susceptibility Contrast
- MTT
Mean Transit Time
- CBF
Cerebral Blood Flow
- CBV
Cerebral Blood Volume
- Ktrans
Vascular transfer rate constant
- vp
Vascular plasma volume
- ve
Extracellular-extravascular volume
- TIF
Tissue Input Function
Probability Density Function
- ASL
Arterial Spin Labeling
- ICA
Internal Carotid Artery
- ACA
Anterior Cerebral Artery
- MCA
Middle Cerebral Artery
- PCA
Posterior Cerebral Artery
- AIC
Akaike Information Criterion
- RSS
Residual Sum of Squares
APPENDIX
Derivation of the transfer function of a single vessel with laminar low
To derive an equation for the transfer function of a vessel, we start by finding the volume of the Contrast Agent (CA) and the total volume of the fluid exiting a vessel with the length of D0, as a function of time. Initially, CA is introduced to the entrance of the vessel in the form of a step function and after flowing through the vessel it forms a parabola. The equation of the surface of the parabola is written as:
| (A.1) |
Where R is the radius of the vessel, r the radial distance of the parabola surface from the axis of the vessel and z is the distance from the opening of the vessel. After time t0 = D0/v0, the tip of the parabola reaches the end of the vessel and at time t = D/v0 it reaches the plane z = D (assuming that the fluid continues to flow in a cylindrical form). The volume of the CA enclosed between the between the planes D0 and D can be calculated as:
| (A.2) |
Prior to time t = t0 there is no CA exiting the vessel so the average CA concentration is zero during this time. The total volume of fluid exiting the vessel between the times t0 and t can be calculated as:
| (A.3) |
To find CA concentration of the fluid exiting the vessel, the volume of the CA exiting the vessel in an infinitesimal time should be divided by the total volume of fluid exiting the vessel in the same time:
| (A.4) |
And since this is the response to the unit step function, the transfer function equation can be found by differeniatig this with respect to time:
| (A.5) |
Footnotes
DISCLOSURE/CONFLICT OF INTEREST
The authors declare that they have no conflicts of interest in the research.
References
- 1.Chan AA, Nelson SJ. Simplified gamma-variate fitting of perfusion curves. IEEE International Symposium on Biomedical Imaging: Nano to Macro. 2004;2004:4. [Google Scholar]
- 2.Nestorov I. Whole-body physiologically based pharmacokinetic models. Expert opinion on drug metabolism & toxicology. 2007 Apr;3(2):235–49. doi: 10.1517/17425255.3.2.235. Epub 2007/04/13. eng. [DOI] [PubMed] [Google Scholar]
- 3.Sherwin SJ, Franke V, Peiró J, Parker KH. One-dimensional modelling of a vascular network in space-time variables. J Eng Math. 2003;47:217–50. [Google Scholar]
- 4.Blanco PJ, Pivello MR, Urquiza SA, Feijoo RA. On the potentialities of 3D-1D coupled models in hemodynamics simulations. Journal of biomechanics. 2009 May 11;42(7):919–30. doi: 10.1016/j.jbiomech.2009.01.034. Epub 2009/03/10. eng. [DOI] [PubMed] [Google Scholar]
- 5.Bagher-Ebadian H, Jafari-Khouzani K, Soltanian-Zadeh H, Ewing JR. International Society of Magnetic Resonance in Medicine. Vol. 16. Toronto, Canada: 2008. A Blood Circulatory Model to Estimate the Arterial Input Function in MR Brain Perfusion Studies. [Google Scholar]
- 6.Noorizadeh A, Bagher-Ebadian H, Faghihi R, Narang J, Jain R, Ewing JR. Input Function Detection in MR Brain Perfusion Using a Blood Circulatory Model Based Algorithm. International Society of Magnetic Resonance in Medicine Annual Meeting; Stockholm, Sweden. 2010. [Google Scholar]
- 7.Calamante F, Morup M, Hansen LK. Defining a local arterial input function for perfusion MRI using independent component analysis. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2004 Oct;52(4):789–97. doi: 10.1002/mrm.20227. Epub 2004/09/25. eng. [DOI] [PubMed] [Google Scholar]
- 8.Mouridsen K, Friston K, Hjort N, Gyldensted L, Ostergaard L, Kiebel S. Bayesian estimation of cerebral perfusion using a physiological model of microvasculature. NeuroImage. 2006 Nov 1;33(2):570–9. doi: 10.1016/j.neuroimage.2006.06.015. Epub 2006/09/15. eng. [DOI] [PubMed] [Google Scholar]
- 9.Calamante F, Gadian DG, Connelly A. Quantification of bolus-tracking MRI: Improved characterization of the tissue residue function using Tikhonov regularization. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2003 Dec;50(6):1237–47. doi: 10.1002/mrm.10643. Epub 2003/12/04. eng. [DOI] [PubMed] [Google Scholar]
- 10.Calamante F, Gadian DG, Connelly A. Delay and dispersion effects in dynamic susceptibility contrast MRI: simulations using singular value decomposition. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2000 Sep;44(3):466–73. doi: 10.1002/1522-2594(200009)44:3<466::aid-mrm18>3.0.co;2-m. Epub 2000/09/07. eng. [DOI] [PubMed] [Google Scholar]
- 11.Cebral JR, Yim PJ, Lohner R, Soto O, Choyke PL. Blood flow modeling in carotid arteries with computational fluid dynamics and MR imaging. Acad Radiol. 2002 Nov;9(11):1286–99. doi: 10.1016/s1076-6332(03)80562-7. Epub 2002/11/27. eng. [DOI] [PubMed] [Google Scholar]
- 12.Hrabe J, Lewis DP. Two analytical solutions for a model of pulsed arterial spin labeling with randomized blood arrival times. J Magn Reson. 2004 Mar;167(1):49–55. doi: 10.1016/j.jmr.2003.11.002. Epub 2004/02/28. eng. [DOI] [PubMed] [Google Scholar]
- 13.Ozyurt O, Dincer A, Ozturk C. A modified version of Hrabe-Lewis model to acocunt dispersion of labeled bolus in arterial spin labeling. 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. p. 4065. [Google Scholar]
- 14.Hernandez-Garcia L, Lee GR, Vazquez AL, Yip CY, Noll DC. Quantification of perfusion fMRI using a numerical model of arterial spin labeling that accounts for dynamic transit time effects. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2005 Oct;54(4):955–64. doi: 10.1002/mrm.20613. [DOI] [PubMed] [Google Scholar]
- 15.Kazan SM, Chappell MA, Payne SJ. Modeling the effects of flow dispersion in arterial spin labeling. IEEE transactions on bio-medical engineering. 2009 Jun;56(6):1635–43. doi: 10.1109/TBME.2009.2016977. Epub 2009/03/25. eng. [DOI] [PubMed] [Google Scholar]
- 16.Gallichan D, Jezzard P. Modeling the effects of dispersion and pulsatility of blood flow in pulsed arterial spin labeling. Magn Reson Med. 2008 Jul;60(1):53–63. doi: 10.1002/mrm.21654. Epub 2008/06/27. eng. [DOI] [PubMed] [Google Scholar]
- 17.Chappell MA, Woolrich MW, Kazan S, Jezzard P, Payne SJ, MacIntosh BJ. Modeling dispersion in arterial spin labeling: validation using dynamic angiographic measurements. Magn Reson Med. 2013 Feb;69(2):563–70. doi: 10.1002/mrm.24260. Epub 2012/04/11. eng. [DOI] [PubMed] [Google Scholar]
- 18.Gall P, Guether M, Kiselev V. Model of Blood Transport Couples Delay and Dispersion and Predicts ASL Bolus Measurements. ISMRM 18; Stockholm, Sweeden. 2010. p. 1736. [Google Scholar]
- 19.Kellner E, Gall P, Gunther M, Reisert M, Mader I, Fleysher R, et al. Blood tracer kinetics in the arterial tree. Plos One. 2014;9(10):e109230. doi: 10.1371/journal.pone.0109230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lee SE, Lee SW, Fischer PF, Bassiouny HS, Loth F. Direct numerical simulation of transitional flow in a stenosed carotid bifurcation. Journal of biomechanics. 2008 Aug 7;41(11):2551–61. doi: 10.1016/j.jbiomech.2008.03.038. Epub 2008/07/29. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Truskey GA, Yuan F, Katz DF. Transport phenomena in biological systems. 2. Upper Saddle River, N.J: Pearson Prentice Hall; 2009. p. xxiii.p. 860. [Google Scholar]
- 22.Gall P, Petersen ET, Golay X, Kiselev V. Delay and Dispersion in DSC Perfusion Derived from a Vascular Tree Model Predicts ASL Measurements. ISMRM 16; Toronto, Canada. 2008. p. 627. [Google Scholar]
- 23.Murray CD. The Physiological Principle of Minimum Work: I. The Vascular System and the Cost of Blood Volume. Proc Natl Acad Sci U S A. 1926 Mar;12(3):207–14. doi: 10.1073/pnas.12.3.207. Epub 1926/03/01. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sherman TF. On connecting large vessels to small. The meaning of Murray’s law. The Journal of general physiology. 1981 Oct;78(4):431–53. doi: 10.1085/jgp.78.4.431. Epub 1981/10/01. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Turner R. How much cortex can a vein drain? Downstream dilution of activation-related cerebral blood oxygenation changes. NeuroImage. 2002 Aug;16(4):1062–7. doi: 10.1006/nimg.2002.1082. [DOI] [PubMed] [Google Scholar]
- 26.Ferrara LA, Mancini M, Iannuzzi R, Marotta T, Gaeta I, Pasanisi F, et al. Carotid diameter and blood flow velocities in cerebral circulation in hypertensive patients. Stroke; a journal of cerebral circulation. 1995 Mar;26(3):418–21. doi: 10.1161/01.str.26.3.418. Epub 1995/03/01. eng. [DOI] [PubMed] [Google Scholar]
- 27.Uflacker R. Atlas of vascular anatomy : an angiographic approach. 2. Philadelphia: Lippincott Williams & Wilkins; 2007. p. xiv.p. 905. [Google Scholar]
- 28.Wright SN, Kochunov P, Mut F, Bergamino M, Brown KM, Mazziotta JC, et al. Digital reconstruction and morphometric analysis of human brain arterial vasculature from magnetic resonance angiography. NeuroImage. 2013 May 28;82C:170–81. doi: 10.1016/j.neuroimage.2013.05.089. Epub 2013/06/04. Eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Esposito A. A Simplified Method for Analyzing Circuits by Analogy. Machine Design. 1969 Oct;:173–7. [Google Scholar]
- 30.Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM Journal of Optimization. 1998;9(1):36. [Google Scholar]
- 31.Posada D, Buckley TR. Model selection and model averaging in phylogenetics: advantages of akaike information criterion and bayesian approaches over likelihood ratio tests. Systematic biology. 2004 Oct;53(5):793–808. doi: 10.1080/10635150490522304. Epub 2004/11/17. eng. [DOI] [PubMed] [Google Scholar]
- 32.Burnham KP, Anderson DR. Model selection and inference : a practical information-theoretic approach. New York: Springer; 1998. p. xix.p. 353. [Google Scholar]
- 33.Brix G, Zwick S, Kiessling F, Griebel J. Pharmacokinetic analysis of tissue microcirculation using nested models: multimodel inference and parameter identifiability. Medical physics. 2009 Jul;36(7):2923–33. doi: 10.1118/1.3147145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ogura A, Miyai A, Maeda F, Hongoh T, Kikumoto R. Comparison of contrast resolution between dynamic MRI and dynamic CT in liver scanning. Nihon Hoshasen Gijutsu Gakkai zasshi. 2002 Feb;58(2):286–91. doi: 10.6009/jjrt.kj00001364261. [DOI] [PubMed] [Google Scholar]
- 35.Kudo K, Terae S, Katoh C, Oka M, Shiga T, Tamaki N, et al. Quantitative cerebral blood flow measurement with dynamic perfusion CT using the vascular-pixel elimination method: comparison with H2(15)O positron emission tomography. AJNR American journal of neuroradiology. 2003 Mar;24(3):419–26. Epub 2003/03/15. eng. [PMC free article] [PubMed] [Google Scholar]
- 36.O’Connor JP, Tofts PS, Miles KA, Parkes LM, Thompson G, Jackson A. Dynamic contrast-enhanced imaging techniques: CT and MRI. The British journal of radiology. 2011 Dec;84(Spec No 2):S112–20. doi: 10.1259/bjr/55166688. Epub 2012/05/25. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ibaraki M, Ito H, Shimosegawa E, Toyoshima H, Ishigame K, Takahashi K, et al. Cerebral vascular mean transit time in healthy humans: a comparative study with PET and dynamic susceptibility contrast-enhanced MRI. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism. 2007 Feb;27(2):404–13. doi: 10.1038/sj.jcbfm.9600337. Epub 2006/06/01. eng. [DOI] [PubMed] [Google Scholar]
- 38.Ito H, Kanno I, Iida H, Hatazawa J, Shimosegawa E, Tamura H, et al. Arterial fraction of cerebral blood volume in humans measured by positron emission tomography. Annals of nuclear medicine. 2001 Apr;15(2):111–6. doi: 10.1007/BF02988600. Epub 2001/07/13. eng. [DOI] [PubMed] [Google Scholar]