The Size of AOT Reverse Micelles

Abstract

Reverse micelles (RMs) made from water and sodium bis(2-ethylhexyl) sulfosuccinate (AOT) are commonly studied experimentally as models of aqueous microenvironments. They are small enough for individual RMs to also be studied by molecular dynamics (MD) simulation, which yields detailed insight into their structure and properties. Although RM size is determined by the water loading ratio (i.e. the molar ratio of water to AOT), experimental measurements of RM size are imprecise and inconsistent, which is problematic when seeking to understand the relationship between water loading ratio and RM size, and when designing models for study by MD simulation. Therefore, a systematic study of RM size was performed by MD simulation with the aims of determining the size of an RM for a given water loading ratio, and of reconciling the results with experimental measurements. Results for a water loading ratio of 7.5 indicate that the interaction energy between AOT anions and other system components is at a minimum when there are 62 AOT anions in each RM. The minimum is due to a combination of attractive and repulsive electrostatic interactions that vary with RM size and the dielectric effect of available water. Overall, the results agree with a detailed analysis of previously published experimental data over a wide range of water loading ratios, and help reconcile seemingly discrepant experimental results. In addition, water loss and gain from an RM is observed and the mechanism of water exchange is outlined. This kind of RM model, which faithfully reproduces experimental results, is essential for reliable insights into the properties of RM-encapsulated materials.

Graphical Abstract

INTRODUCTION

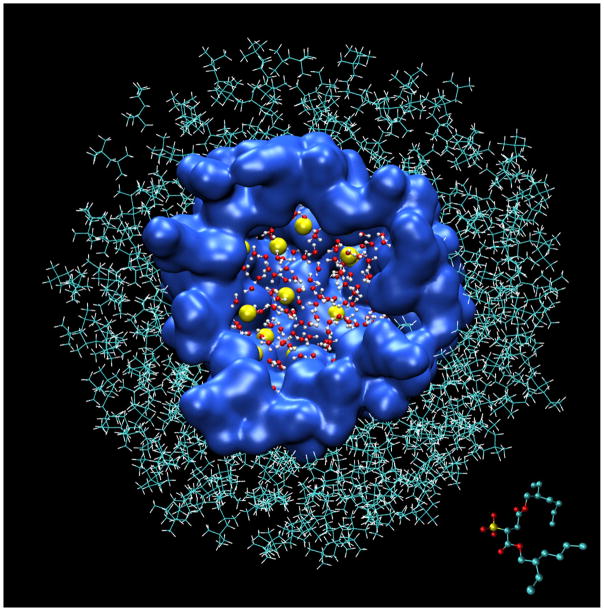
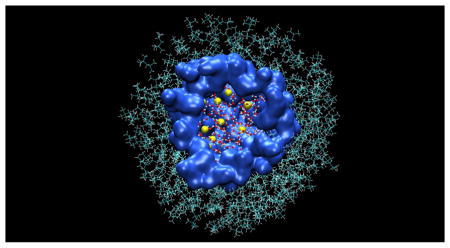
Reverse micelles (RMs), composed of water and surfactant suspended in a nonpolar solvent, are popular experimental systems for the study of biological materials under conditions where they are physically confined with limited amounts of water. As such, they are frequently used as experimental models of crowded biological microenvironments such as membranous organelles, intercellular spaces, and the interior of macromolecular chaperones.^1–3 While RMs can be made with diverse surfactant types, sodium bis(2-ethylhexyl) sulfosuccinate (aka aerosol OT or AOT) is popular because it readily forms RMs without a cosurfactant that are chemically stable, optically transparent, and capable of encapsulating relatively large amounts of water (Figure 1).

Figure 1.

Cross section of an RM model with W₀ = 7.5 and 62 AOT. Water molecules are rendered as CPK models, sodium cations as yellow van der Walls spheres with a radius of 0.6 Å, AOT anions as a blue surface, and isooctane as lines. A single AOT anion is rendered as a CPK model in the lower right corner.

RM size in ternary AOT-based systems is determined by the water loading ratio (i.e. the mole ratio of water to surfactant, or W₀),⁴ and the radius polydispersity (γ) of 0.065 – 0.30 reported for these systems^5–12 suggests that their size distributions are narrow. However, the absolute size of RMs is not a simple or direct measurement, and experimental estimates of AOT RM size vary by as much as 35% for any given W₀ value,¹³ particularly when these estimates are from techniques that rely on fundamentally different properties of an RM such as scattering intensities and transport rates. The uncertainty about RM size is especially problematic when performing molecular dynamics (MD) simulations for insight into the structure and organization of RMs because the number of molecular components in most simulations is fixed.¹⁴ The question of RM size remains unresolved despite numerous MD simulation studies with continuum solvent,^15–17 coarse-grained surfactant,^18–22 and all-atom models.^13,23 Indeed, RM simulations of W₀ = 7.5 have been recently described with as few as 70 AOT molecules per RM,²⁴ (n_AOT) and as many as 106.²⁵ Moreover, the question is a general one, with similar questions arising in studies of reverse micelles made with cetyltrimethylammonium bromide and other surfactants.^14,26 In the case of AOT, One approach to answering the question of RM size via simulation has been to allow RMs to self-assemble from randomly distributed components. However, this approach is computationally expensive, and has thus far yielded systems with unexpectedly large indices of polydispersity.²⁷

Therefore, this study was undertaken to obtain a more precise and complete understanding of RM size, and address two main questions: what is the physicochemical basis for the relationship between W₀ and RM size, and how can fundamentally different kinds of experimental data be reconciled? We address the first question with MD simulations by examining the interaction energies within RMs across a range of sizes, and comparing the simulation results to previously published experimental data. The results of this horizontal study (at constant W₀ = 7.5) are also extrapolated vertically (across a range of W₀) to further test them against experimental data. We address the second question by examining the nature of the experimental data available. We find that structural insights provided by these simulations help reconcile many of the apparent discrepancies in available experimental data.

METHODS

Simulations

Simulations were performed as NPT ensembles with NAMD 2.9,²⁸ the CHARMM27 all atom force field for proteins and lipids,²⁹ and TIP3P water.³⁰ Parameters for the AOT anion and isooctane (isoO) were obtained from previously published studies.^23,25,31,32 Long-range electrostatic forces were calculated with the Particle Mesh Ewald method³³ and an interaction cutoff of 12 Å was applied within periodic boundary conditions. Van der Waals (VdW) forces were smoothly shifted to zero between 10 Å and 12 Å. Equations of motion were integrated with the Verlet method and a time step of 2 fs. Langevin dynamics with a damping coefficient of 5 ps⁻¹ was used to keep the temperature at 300 °K. The pressure was maintained at 1 atm using a Nosé-Hoover-Langevin piston.³⁴

Simulation systems were constructed by selecting a W₀ value and the number of surfactant molecules (n_AOT) to include in the system. These parameters determine the number of water molecules (n_water) to include, and the systems are denoted below as RM_X where X = n_AOT and ranged from 34 to 106. A spherical cluster of n_water + n_AOT water molecules was extracted from a well-equilibrated simulation of pure water at 300 °K and 1 atm. AOT molecules were added by replacing n_AOT randomly selected water molecules with sodium cations, and distributing the anionic portions randomly on the surface of the cluster with SO₃ groups oriented inward. These water/AOT clusters were placed in the center of a truncated octahedron of sufficient size to contain 2536 molecules of isoO (n_ISO) – a number chosen so that the isoO mass was 83% of the total system mass for the largest RM and thus, within the RM-forming portion of the AOT/water/isoO phase diagram.²⁵ Compositions of systems are listed in Table 1.

Table 1.

Compositions of simulated systems^*

System	nAOT	nwater	natoms	fiso (%)	rw (Å)	s (Å)
WD	-	255	66701	98	12.3	95
RM34	34	255	68945	94	12.3	98
RM46	46	345	70007	92	13.6	98.5
RM50	50	375	70361	91	13.9	98.7
RM54	54	405	70715	90	14.4	98.9
RM58	58	435	71069	90	14.8	99
RM60	60	450	71246	89	14.9	99.1
RM62	62	465	71423	89	15.1	99.2
RM64	64	480	71600	89	15.3	99.3
RM66	66	495	71777	88	15.4	99.4
RM68	68	510	71954	88	15.6	99.5
RM70	70	525	72131	88	15.7	99.6
RM74	74	555	72485	87	16.1	99.7
RM78	78	585	72839	87	16.4	99.8
RM82	82	615	73193	86	16.7	100
RM94	94	705	74255	84	17.4	100.4
RM106	106	795	75317	83	18.2	100.9

^*n_AOT and n_water are the numbers of AOT and water molecules. n_atoms is the total number of atoms in each system. f_iso is the mass fraction of isoO as a percentage of mass of all components in the system. r_W is the average distance from the center of the RM to the outermost water molecule. s is edge length of the truncated octahedron unit cell.

Simulation systems were equilibrated in four stages, each stage consisting of 0.01 ns minimization and 1 ns of NPT simulation. In stage one, all atoms except those in the isoO solvent were fixed in position. In stage two, the hydrocarbon tails of the AOT anions were unfixed. In stage three, the remaining portions of the AOT anions were unfixed. In stage four, all molecules in the system were unfixed. A separate simulation of a water droplet in isoO (without AOT) was equilibrated with only the latter two stages. Equilibrated systems were propagated for 30 ns with coordinates and energies saved every 0.001 ns. Only the final 15 ns of each trajectory were used for the data analysis. The entire process – system assembly, equilibration, and 30 ns simulation – was repeated twice for each system with a different water cluster and sodium cation substitutions to assess the reproducibility of results. A separate RM₆₂ system was propagated for 100 ns to examine the time required for convergence.³⁵

Analysis

Interaction energies for each saved coordinate set were calculated using VMD³⁶ and the same parameters used to create the trajectory (VMD and NAMD therefore yield identical energies for the same structure). Four energies were calculated for individual members of each molecular species: its interaction with all other components of the same molecular species, and its overall interaction with each of the other three molecular species. These energies were averaged over all members of each species, and over all saved coordinate sets, for each simulation.

Most RMs quickly became ellipsoid in shape. Therefore, analysis of the distribution of components in terms of radial density profiles was problematic, and local nearest distance metrics were substituted in which the SO₃ groups demarcated the boundary between polar and apolar phases. The distance of various atoms and groups from this boundary surface was calculated.³⁷ Each atom/group was assigned to a 1 Å layer, based on its distance to the nearest SO₃ headgroup. The thickness of the surfactant layer (r_AOT) is the distance from the boundary to the AOT terminal CH₃ groups, plus the radius of an SO₃ head group (3.1 Å) and the radius of a CH₃ group (2.3 Å). The various radii and distances referenced in this work are summarized in Table 2.

Table 2.

Radius definitions

Symbol	Definition
rW	Average distance from the center of the RM to the outermost water molecule (used only in table 1)
rh	Hydrodynamic radius of RM complexes
rAOT	Thickness of the surfactant shell
rg	Radius of gyration of RM complexes
r0	VdW radius of a water oxygen
rcore	Radius of the core containing water, sodium cations, and approximately half the volume of SO3 groups

The radius of gyration (n_g) of simulated RM complexes was calculated as the root mean square distance between atom pairs according to equation 1:

$$r_g^2=\frac{1}{2n^2}\sum _{i=1}^n\sum _{j=1}^n\langle {(r_{ij})}^2\rangle =\frac{1}{n}\sum _{i=1}^n\langle {(r_{ic})}^2\rangle$$ (1)

where n is the number of atoms, n_ij is the distance between atom i and j, and r_ic is the distance between atom i and the center of mass of the RM. To facilitate the comparison of r_g values from simulations with r_g values obtained from SAXS, only sodium, oxygen, and sulfur atoms were included in the calculation of r_g, because carbon and hydrogen atoms in AOT scatter X-rays to the same degree as the atoms in isoO, and do not create the electron contrast detected by SAXS.

RM shape was characterized by modeling the aqueous core consisting of water and sodium cations as an ellipsoid with the same mass and moments of inertia.^18,22 The principal moments of inertia (I₁, I₂, and I₃) were calculated by determining the eigenvalues of the inertia tensor. For ellipsoids, the relations between semi-axes and principal moments of inertia are given by equations 2 – 4. The semi-axes a, b, and c of the ellipsoid systems were determined by solving equations 2–4 for a, b, and c:

$$I_1=\frac{1}{5}{m}_{aq}(a^2+b^2)$$ (2)

$$I_2=\frac{1}{5}{m}_{aq}(a^2+c^2)$$ (3)

$$I_3=\frac{1}{5}{m}_{aq}(b^2+c^2)$$ (4)

where m_aq is the combined mass of the water molecules and sodium cations. Because these calculations are based on the coordinates of atomic centers, and neglect the volume of the outermost water molecules, the VdW radius of a water oxygen (r_o = 1.4Å) was added to each semi-axis, yielding a′, b′, and c′. Eccentricity, e, is a commonly used measure of the degree to which shape deviates from spherical.^23,24,38 It was calculated from the semi-axes by

$$e=\sqrt{1-\frac{{c^{\prime }}^2}{{a^{\prime }}^2}}$$ (5)

where e = 0 for a perfect sphere and approaches 1 for disc-like and rod-like shapes.

As RMs became ellipsoid, the hydrodynamic radius (r_h) of simulated RM complexes was determined according to equation 6:

$$r_h={(a^{\prime }{c^{\prime }}^2)}^{1/3}+r_{\mathit{AOT}}$$ (6)

where r_h is equal to the radius of sphere that has the same volume as the ellipsoidal RMs.³⁹

RESULTS

Equilibration

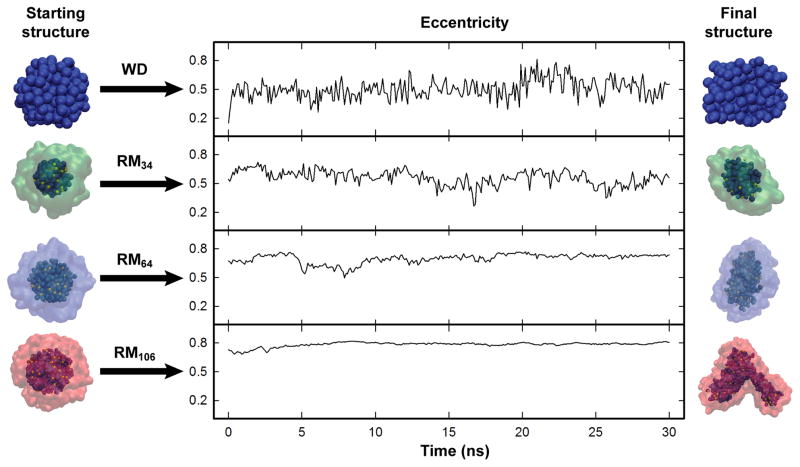
The stability of system energy over time is a common criterion by which NPT simulations are judged to be suitably equilibrated. By this criterion, the water droplet and all 16 RM systems reached stable energies within 10 ns. However, simulated systems did not all reach a stable shape within this time, and some of the systems required nearly 15 ns to reach stable eccentricity values (Figure 2). Therefore, all simulations were run for 30 ns, but only the last 15 ns were deemed to be equilibrated and used for analysis.

Figure 2.

Eccentricity vs time for the WD, RM₃₄, RM₆₄, and RM₁₀₆ systems. On either end of each graph, the initial and final structures are illustrated by representing water molecules as blue spheres, sodium cations as yellow spheres, and AOT anions as a surface. The starting structures were energy minimized before marking time “0” in the eccentricity graphs. Note that the final structure of the RM₁₀₆ system is highly distorted. This degree of distortion was not reflected in the eccentricity calculations, fission into smaller systems appeared imminent. There were no shape distortions suggesting imminent fission observed in any of the smaller systems.

Trajectory analysis

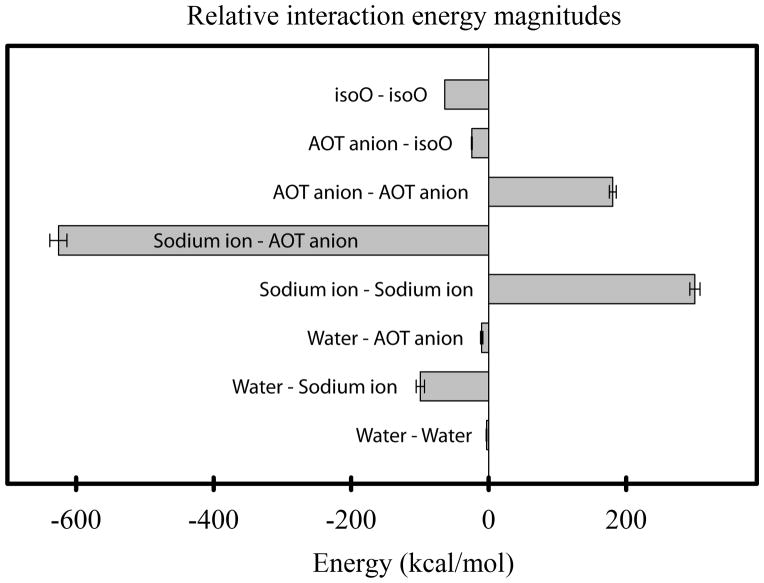
The overall energy of each RM system varied with system size, so most energy terms have been normalized by n_AOT to facilitate comparisons. Representative values for the various nonbonded interaction energies in the RM₆₂ system are illustrated in Figure 3. The largest single term was the attractive electrostatic interaction between sodium cations and AOT anions. This attractive interaction was only partially balanced by repulsive interactions between cations and between anions. Relatively small negative energies were found for nonbonded isoO–isoO, AOT anion–isoO, water–AOT anion, water–sodium and water–water interactions.

Figure 3.

The relative magnitudes of all pairwise non-bonded interaction energies for an RM₆₂ system, normalized by n_AOT .

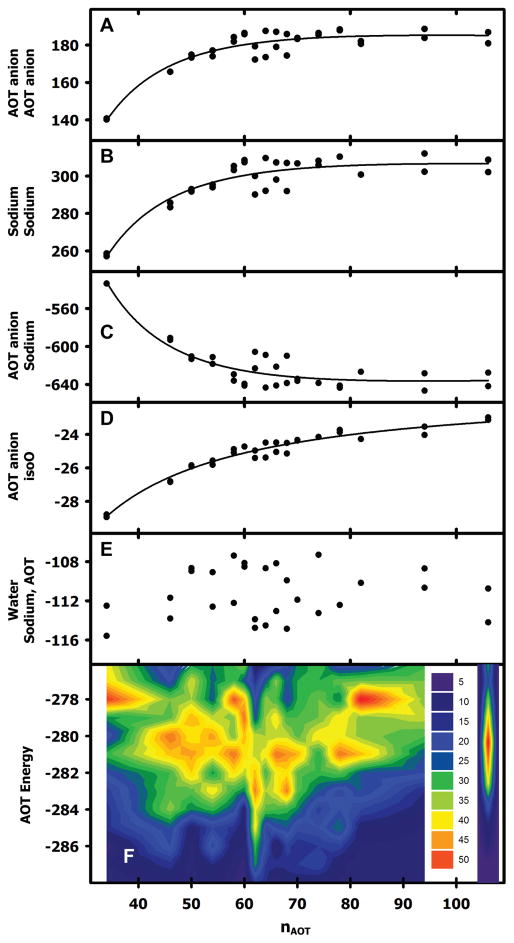
Interaction energies involving AOT headgroups and sodium cations both became more positive with RM size, suggesting that these repulsive interactions favor smaller RMs at constant W₀ (Figures 4A,B). In contrast, interaction energies between sodium cations and AOT anions became more negative with RM size, suggesting that these attractive interactions favor larger RMs at constant W₀ (Figure 4C). Water-water and isoO-isoO interaction energies were −3 kcal/mol and −64 kcal/mol, respectively, and independent of system size (Figure 3). The interaction energies between AOT anions and isoO became slightly more positive with RM size (Figure 4D), while those between sodium cations and with AOT anions exhibited no strong trend (Figure 4E).

Figure 4.

RM system nonbonded interaction energies in kcal/mole normalized by n_AOT. (A) AOT anion – AOT anion interaction energies with an inverse second order fit. (B) Sodium cation – Sodium cation interaction energies with an inverse second order fit. (C) AOT anion – Sodium cation interaction energies with an inverse second order fit. (D) AOT anion – isoO interaction energies with an inverse second order fit. (E) The sum of water – AOT anion and water – Sodium cation interaction energies. There are two results for each system in panels A-E from the two independent 30 ns simulations, that sometimes superimpose. (F) AOT energy (defined in the text, i.e. the sum of the energies depicted in panels A-E) with a quadratic fit to all data except the RM₁₀₆ system (indicated in open circles). The value of n_AOT at the minimum is 60.9 (vertical red arrow). All energies are normalized by n_AOT. The two results for each system are from the two independent 30 ns simulations. (G) Histograms of the AOT energies combined into a contour graph. Autocorrelation times for the AOT energies were generally less than 100 ps. Therefore, energies were calculated at 100 ps intervals for the two 15 ps simulations for each system, divided into 1 kcal/mol bins, and color-coded according to bin counts as indicated.

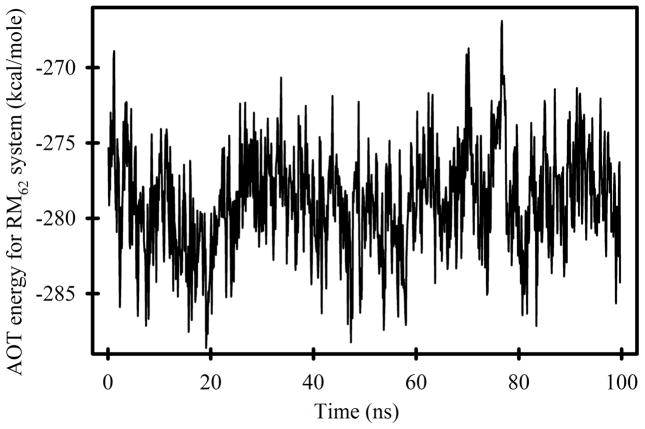
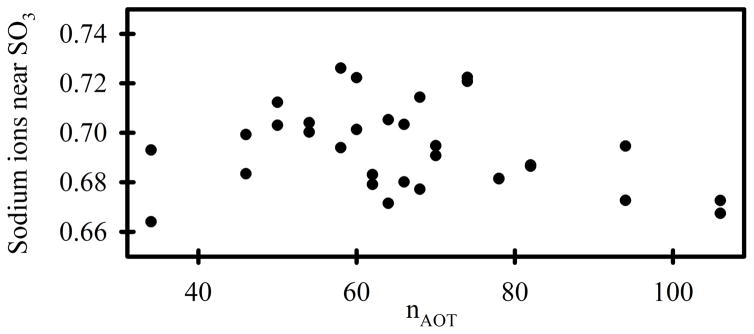
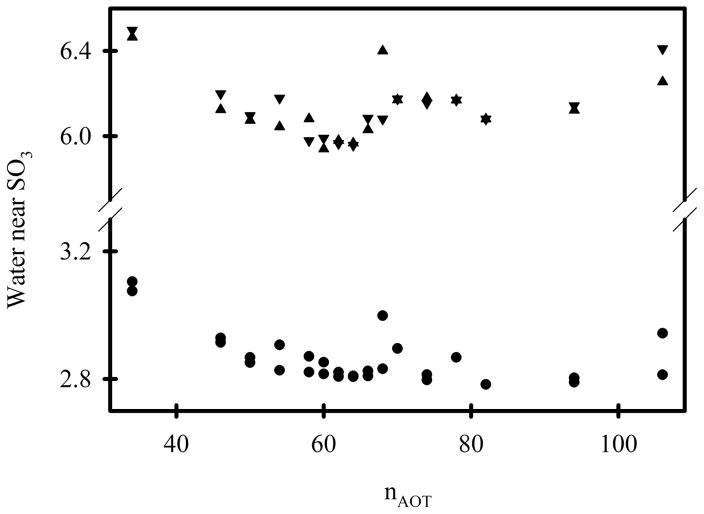
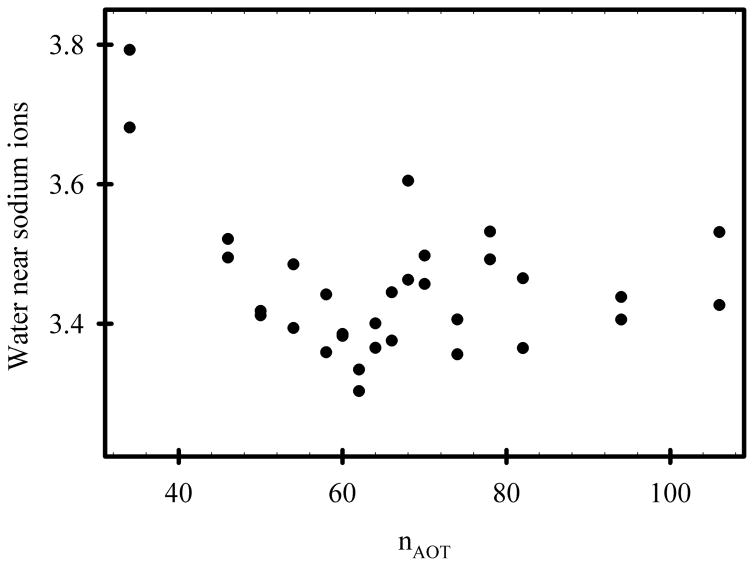
The sum of the energies depicted in Figures 4A-E represent the energies of interaction between sodium AOT and all other system components. This “AOT energy” exhibits a minimum in the range of n_AOT = 62 to 68 (Figure 4F). However, the data from RM₁₀₆ systems is anomalous. Together with the anomalous shape of this system (Figure 2, lower panel), it appears that they are unstable for reasons that are not reflected in the AOT energy. Fission into smaller systems appears imminent, and this behavior was not observed for any of the smaller systems. If the AOT energies in Figure 4F are fit while excluding the RM₁₀₆ system, the minimum value corresponds to n_AOT = 60.9. Histograms of the AOT energy at 100 ps intervals for both 15 ns simulations of each system were created for each of the systems and combined into a contour graph (Figure 4G). There are several noteworthy features in this graph. First, the RM₆₂ system makes far more frequent excursions to energies < −284 kcal/mol than any other system. There is no correlation between these low energies and the number of sodium cations in the immediate vicinity of AOT head groups (Figure 5), or the number of water molecules in the immediate vicinity of AOT head groups (Figure 6). However, the RM₆₂ system had the smallest number of water molecules in the immediate vicinity of sodium cations (Figure 7). To test whether AOT energies in the RM₆₂ system were representative of simulations over longer times, it was propagated for 100 ns (Figure 8). No systematic drift in AOT energy was observed.

Figure 5.

The average number of sodium cations within 3Å of the SO₃⁻ groups. The two results for each value of n_AOT were derived from the two independent 30 ns simulations.

Figure 6.

The average number of water molecules within 3Å (circles) and 5Å (triangles) of the SO₃⁻ groups. The two results for each value of n_AOT were derived from the two independent 30 ns simulations.

Figure 7.

The average number of water molecules within 3Å of sodium cations. The two results for each value of n_AOT were derived from the two independent 30 ns simulations.

Figure 8.

AOT energies over 100 ns for an RM₆₂ system.

Second, there appear to be discrete preferred energy levels among the various systems, particularly at −283, −281, and −278 kcal/mol. The systems are not trapped at these levels, since autocorrelation times for the energy values are <100 ps. Several systems frequent more than one of these preferred levels, and systems differing in n_AOT by only 2 can frequent quite different levels (e.g. RM₆₂ and RM₆₀). The existence of such discrete levels suggests that geometric factors may influence system energy, such as those that stabilize 60-mer viral capsids.

Third, there is a clear trend for higher AOT energies as n_AOT values become either smaller or larger than 62. However, the data from RM₁₀₆ systems is anomalous (extreme right portion of Figure 4F). These systems were included in this study because of previously published on a system of this size.²⁵ However, their anomalous shape (Figure 2, lower panel) suggests that they are unstable for reasons not reflected in the AOT energy. Fission into smaller systems appears imminent, and this behavior was not observed for any of the smaller systems.

Altogether, these results suggest that when W₀ = 7.5, RM₆₂ systems assume a relatively low energy state more frequently that other RM systems, and that the structural basis for this low energy state is that screening of sodium cation – AOT anion interactions by water is reduced.

RM Structure and Organization

Deviations from a spherical shape became larger with increased RM size, while fluctuations in eccentricity became smaller (Figure 2). If the size of an RM is not appropriate for a given W₀, shape distortion may occur because it is inherently unstable, without any indication of this distortion in the eccentricity value. For example, the RM₁₀₆ system, illustrated in Figure 3, has a stable eccentricity value, but a highly distorted shape.

Nearest distance metrics indicate that water and sodium cations preferentially situate 2.5 Å closer to the center of the micelle than the SO₃ headgroups, but another layer of water and sodium cations situate 2.5 Å farther from the center than these groups (Figure 9). This pattern is a reflection of AOT anion penetration into the aqueous core of the RM, and displacement of water and sodium cations to the outside. It should be noted that an intermolecular distance of 2.5 Å is insufficient space for water molecules to situate between the ions. This observation, and the overall dominance of the interaction energy between sodium cations and AOT anions, is consistent with the aforementioned conclusion that RM stability is determined by the proximity of charged species and the extent to which water is available to screen the electrostatic interactions.

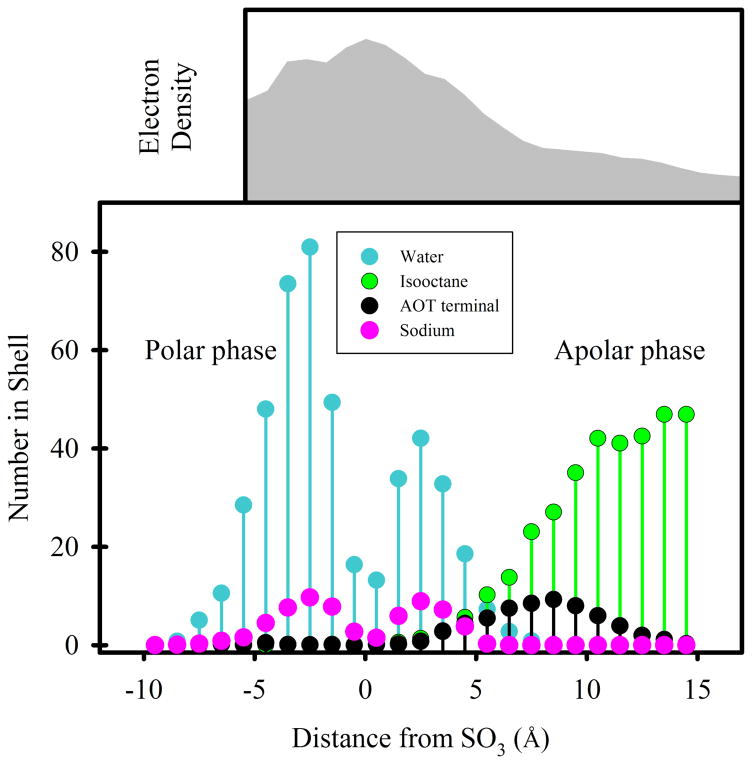
Figure 9.

Distribution of components in an RM₆₂ system. Lower panel: Nearest distance metrics analysis³⁷ with distance to the nearest SO₃ group on the horizontal axis. The polar phase is comprised primarily of water (blue) and sodium cations (magenta). The apolar phase is comprised of AOT chains (black) and isoO (green). The AOT terminal methyl groups are indicated to enable the determination of r_AOT as described in the text. Upper panel: a radial electron density profile approximated by weighting an ordinary radial density profile by atomic numbers. The horizontal axis is roughly aligned with the distance scale of the lower panel. The vertical axis is arbitrary.

Figure 9 also shows that the distribution of isoO exhibits substantial overlap with the distribution of AOT chains, which is relevant to the observation in Figure 4D that interaction energies between AOT and isoO become more positive with RM size (discussed below). Finally, Figure 9 indicates that very few waters are more than 8Å inside of the SO₃ groups. It should be noted that this distance is not a useful measure of the aqueous core radius because the RM has an ellipsoidal shape, and because AOT headgroups penetrate into the aqueous core of the RM.

Mass exchange

No loss or gain of sodium cations or AOT anions was observed over the course of the 30 ns simulations, but multiple water molecules both exited the RM into the isoO phase, and re-entered the RMs from the isoO phase. The number of water molecules gained and lost for all systems are listed in Table 3. There was no discernable difference in the first or second halves of the simulations, no apparent correlation between RM size and the rates of water gain/loss, and no tendency for a net change in n_water. In stark contrast, no molecules were lost from a pure water droplet in isoO over the same interval. This observation suggested that AOT anions were responsible for facilitating water transit in and out of the RM core. Although no attempt was made to estimate the magnitude of energy barrier that regulates water transfer, it was noted that the non-bonded interaction energy of a water molecule was −21 kcal/mol in the RM core, and −2.5 kcal/mol in the isoO phase. At various points in surfactant layer, the energy was approximately −10 kcal/mol. Thus, AOT anions appear to facilitate water transit in and out of the RM core by creating a population of water molecules at the interface with intermediate energies.

Table 3.

Water losses and gains for simulated RM systems^*

System	Loss	Gain	Net
WD	0	0	-
RM34	7	6	−1
RM46	5	5	0
RM50	6	5	−1
RM54	7	4	−3
RM58	7	7	0
RM60	6	6	0
RM62	8	7	−1
RM64	7	5	−2
RM66	6	6	0
RM68	11	11	0
RM70	9	7	−2
RM74	6	6	0
RM78	7	7	0
RM82	12	11	−1
RM94	8	7	−1
RM106	8	7	−1

^*counts are for the entire 30-ns simulations

Experimental correlation

A large number of experimental studies have been published that provide information about RM size. Some cannot be compared to the present results because they do not provide data for W₀<12. Some DLS results must be excluded because the AOT concentration ([AOT]) used was greater than 200 mM and such concentrations appear to distort the results of DLS experiments.⁴⁰ Since [AOT] = 140 mM in the simulations, only DLS studies performed with 100mM < [AOT] < 200 mM were compared.⁴⁰ However, there are 11 published studies of RM size that may be compared to the simulation results reported herein.

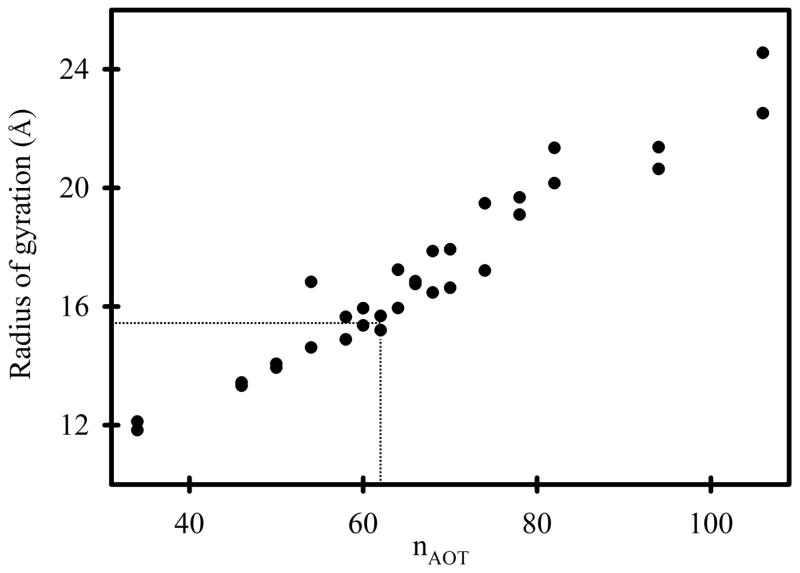
Amararene et al.⁶ reported SAXS results for RMs with W₀ values ranging from 3 to 30. Linear interpolation of their results for W₀ = 7.5 yields r_g = 16 ± 1Å. Yano et al.^41,42 reported SAXS results for RMs with W₀ values ranging from 3.5 to 24.4. Linear interpolation of their results for W₀ = 7.5 yields r_g = 17 ± 1 Å. From the RM₆₂ simulation and equation 2 we obtained r_g = 15.7 Å (Figure 10), in close agreement with both experimental results. SAXS measurements have also been reported by Hirai et al., who reported a sharp discontinuity in the relationship between r_g and W₀ at W₀ = 10.. Linear interpolation of their results for W₀ < 10 yields r_g = 26 Å for W₀ = 7.5,⁴³ considerably larger than the other two aforementioned SAXS studies. However, a linear extrapolation of their results for W₀ > 10 yields r_g = 18 Å for W₀ = 7.5, which is in agreement with the other SAXS studies and with the simulation results reported herein.

Figure 10.

Radius of gyration vs n_AOT for simulated RM systems. The two results for each value of n_AOT were derived from the two independent 30 ns simulations. The average radius of gyration for the RM₆₂ system is 15.7 Å, and indicated with dotted lines.

When comparing SAXS and simulation results, it must be emphasized that conclusions about r_g are model dependent; whether the scattering entities are modeled as solid or hollow spheres has a significant influence on the results. A radial electron density profile for the RM₆₂ system,^23,24 approximated by weighting an ordinary radial density profile by atomic numbers, suggests that three regions with different X-ray scattering tendencies are present: an oxygen-rich region in the center, a transition region 10–15 Å from the RM center, and a relatively low density carbon-rich region beyond the transition region (Figure 9, upper panel). Some support for both solid and hollow models may be found in this graph, but the transition region – broadened as it is by eccentricity – suggests that nonspherical models must be considered for accurate results, and that simulations are needed to determine the n_AOT for an RM from an r_g measurement.

Eicke and Rehak reported LS measurements for RMs with W₀ values ranging from 2.78 to 44.44 and derived average apparent molecular weight estimates, from which values of n_AOT may be calculated. Exponential interpolation of their results for W₀ = 7.5 yields n_AOT = 64, which is in good agreement with the simulation results.

Numerous estimates of the hydrodynamic radius have been derived from experimental measurement of transport rates.^40,44–49 Linear interpolations of these results for W₀ = 7.5 yield values for r_h ranging from 26 to 31 Å (Table 4). In some of these experimental studies, the thickness of AOT anion layer, r_AOT, was used to interconvert r_h and a “water pool radius”.^6,46,50 However, estimates of r_AOT used for this purpose ranged from 7 – 15 Å,^{6,8,46,47,49,51} and most were based on assumptions that the simulations show to be inaccurate (e.g. an extended conformation or a radial orientation for the aliphatic AOT chains). Nearest distance metrics (Figure 9) show that the density of CH₃ groups at the end of AOT (i.e. AOT terminal) anions is maximal 8.5 Å outside of the SO₃ groups. Therefore, the thickness of AOT anion layer appears to be 8.5 Å plus the radius of an SO₃ head group (~3.1 Å) and the radius of a CH₃ group (~2.3 Å), or r_AOT ≈ 13.9 Å. To calculate r_h, the semi-axes a and c of the RM₆₂ aqueous core were determined as 31.4, 14.5, and 12.3 Å respectively by solving equations 2–4 for a′, b′, and c′. Therefore, the simulations suggest that r_h = 30.7 Å (the sum of (a′ c′²)^1/3, ~16.8 Å and the r_AOT, which is within the range of published experimental values.

Table 4.

Interpolated values of r_h for W₀ = 7.5 from published experimental studies and the value of r_h from the RM₆₂ simulations.^*

rh (Å)	Technique	Reference
26	FRAPP	Chatenay et al.44
27	DLS	Bohidar and Behboudnia40
28	DLS	Vasquez et al.45
31	Viscosity measurements	Kinugasa et al.46**
29	FCS	Pal et al.47
30	DLS	Nazario et al.48
31	PCS	Zulauf and Eicke49
30	MD simulations	Eskici and Axelsen

^*DLS – dynamic light scattering. FRAPP – fluorescence recovery after fringe pattern photobleaching. FCS – fluorescence correlation spectroscopy. PCS – photon correlation spectroscopy.

^**r_h was estimated from Kinugasa et al.⁴⁶ by assuming r_AOT = 13.9 Å.

Extrapolation to other values of W₀

The size of an RM “core” is here defined as the locus of points representing the centers of the AOT sulfonate head groups (r_core). This core would contain n_water water molecules, n_AOT sodium cations, and approximately half the volume of the n_AOT SO₃ groups. Assuming an overall density of ρ, the approximate volume of such a core is given by

$$V_{\mathit{core}}\cong \frac{n_{\mathit{AOT}}(W_0{m}_{\mathit{water}}+m_{\mathit{sodium}}+m_{\mathit{sulfate}}/2)}{\rho }$$ (7-a)

where m_water, m_sodium, and m_sulfonate are the molar masses of water, sodium cations, and sulfonate anions, respectively. Given an average molecular volume for core components, v̄, equation 7-a simplifies to

$$V_{\mathit{core}}\cong n_{\mathit{AOT}}\left(W_0+\frac{3}{2}\right)\overline{v}=\frac{4}{3}\pi r_{\mathit{core}}^3$$ (7-b)

given the key assumption that the RM core is spherical in shape. The surface area of this core, A_core, is given by

$$A_{\mathit{core}}=a_{\mathit{AOT}}{n}_{\mathit{AOT}}=4\pi r_{\mathit{core}}^2$$ (7-c)

where a_AOT is the surface area covered by an AOT anion, and its volume-to-surface-area ratio is given by

$$\frac{V_{\mathit{core}}}{A_{\mathit{core}}}\cong \frac{r_{\mathit{core}}}{3}=\overline{v}\frac{\left(W_0+\frac{3}{2}\right)}{a_{\mathit{AOT}}}$$ (7-d)

Equation 7-d illustrates the basis for a linear relationship between W₀ and r_core, and the use of linear extrapolations when calculating intermediate results in tabulated data. It follows that the number of AOT per RM is given by

$$n_{\mathit{AOT}}=\frac{4\pi r_{\mathit{core}}^2}{a_{\mathit{AOT}}}=36\pi {\left(W_0+\frac{3}{2}\right)}^2\frac{{\overline{v}}^2}{a_{\mathit{AOT}}^3}$$ (7-e)

Given W₀ = 7.5, n_AOT = 62 (from this study), and ρ = 1.1 g/cm³ (estimated from 2014 Du et al),⁵² equation 7-a yields V_core 18,414 Ų. Equation 7-b yields v̄ = 33 ų per molecule, and r_core = 16.4 Å. Equation 7-c yields a_AOT = 54.4 Ų, close to the published estimate of 55 Ų.

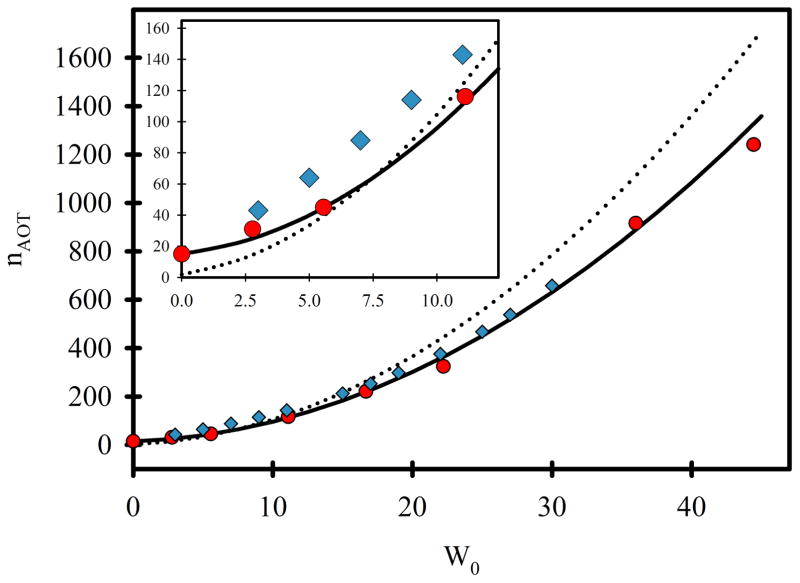
A graph of n_AOT versus W₀ (equation 7-e, Figure 11, dotted line) compared to the published experimental data of Eicke and Rehak (red dots)⁵³ and of Amararene et al. (blue diamonds)⁶ shows that agreement away from W₀ = 7.5 is poor. In particular, equation 7-e fails to predict the experimentally observed value of n_AOT = 15 for W₀ = 0, and it overestimates n_AOT by 37% for W₀ = 45. This discrepancy suggests that a “dry” term must be added to equation 7-e in the form of $n_{\mathit{AOT}}^0=13.6$ to correct for the number of AOT molecules in a water-free RM. With that correction, and an increase in a_AOT to 59.1 Ų, equation 7-f agrees with the entire range of results from Eicke and Rehak, and the results of Amararene et al. beyond W₀ = 15 (Figure 11, solid line).

Figure 11.

Extrapolated results for various W₀ and comparison with experimental studies. Solid line – n_AOT values obtained from equation 7-f which include the $n_{\mathit{AOT}}^0$ “dry” term and a slightly larger value of a_AOT . Dotted line – n_AOT values obtained from equation 7-e. Red circles – the published experimental data of Eicke and Rehak.⁵³ Blue diamonds – the published experimental results of Amararene et al.⁶

$$n_{\mathit{AOT}}=36\pi {\left(W_0+\frac{3}{2}\right)}^2\frac{{\overline{v}}^2}{a_{\mathit{AOT}}^3}+n_{\mathit{AOT}}^0$$ (7-f)

RM preparations may be characterized experimentally by a radius polydispersity index (γ), and reported values range from 0.065 to 0.30,^5–12 although only the value of γ = 0.15 from Amararene et al. was measured in isoO.⁶ This index may be converted into a standard deviation for the distribution of radii using equation 8:

$${\gamma }^2=\frac{\langle {r_{\mathit{core}}}^2\rangle -{\langle r_{\mathit{core}}\rangle }^2}{\langle {r_{\mathit{core}}}^2\rangle }=\frac{{\sigma }^2}{\langle {r_g}^2\rangle }or{\sigma }^2=\frac{{\gamma }^2{\langle r_{\mathit{core}}\rangle }^2}{1-{\gamma }^2}$$ (8)

where σ is the standard deviation of r_core. Assuming that γ = 0.15, equation 8 suggests that σ = 2.5 Å for r_core, while equation 7-f suggests that n_AOT ranges from 43 to 79 for RMs with r_core = 16.6 ± 2.5 Å.

DISCUSSION

The chief result of this investigation is quantitative insight into the relationship between W₀ and the size of a RM in the commonly used water/AOT/isooctane system. It has long been appreciated that there is a linear relationship between W₀ and RM radius, justified largely in geometric terms (as per eq. 7-d) above. However, widely divergent slopes have been proposed for this relationship, and it has not been clear how to infer the number of AOT molecules in an RM from the radius information that such slopes provide. The results in this study suggest that RMs with a W₀ = 7.5 most likely contain 62 AOT molecules per RM, which is in agreement with published experimental measurements of SAXS, light scattering, and transport rates after considering the nature of the information provided by these techniques. From this benchmark, n_AOT for W₀ ranging from 0 to 45 may be predicted from equation 7-f, also in excellent agreement with experimental results. Finally, our analysis suggests that systems with W₀ = 7.5 should have a second moment distribution of radii that corresponding to n_AOT from 43 to 79 (calculated using equations 7f and 8).

A second important result from this study is a physicochemical explanation for the relationship between W₀ and n_AOT, and for the expectation that each value of W₀ has a value of n_AOT where the AOT energy is a minimum. The AOT energy has three main components: (1) the electrostatic repulsion between anionic AOT head groups (Figure 4A), (2) the electrostatic repulsion between sodium cations (Figure 4B), (3) the electrostatic attraction between sodium cations and anionic AOT head groups (Figure 4C). To some extent, the interaction energies between the AOT anion and isoO also favor smaller RMs at constant W₀ (Figure 4D). These energies are primarily due to VdW interactions, which may increase in magnitude in smaller RMs because curvature – and hence, the wedge-shaped gaps in the AOT layer into which isoO may penetrate – is greater in smaller RMs. The fits to the data in Figure 4 help illustrate trends in the data, such as the tendency for repulsive interactions to favor smaller RMs, and for attractive interactions to favor larger RMs at constant W₀. Overall, results indicate that the size of an RM is determined primarily by a balance between these attractive and repulsive interactions, and the availability of water to screen them (Figure 7).

A third result from this study is the ability to reconcile experimental results that are reported in units that are difficult to interconvert, such as radius-of-gyration, hydrodynamic radius, and aggregation number. Widely discrepant experimental results have been noted for some time,^13,23,27 but upon close examination some of these discrepancies may be attributed to differences in solvents⁴⁶ or temperature.²⁷ Other discrepancies are due to linear interpolation between n_AOT vs W₀ when a nonlinear interpolation is needed, or to a comparison of r_g and r_core without suitable conversion.¹³ Most of the remaining studies may be reconciled by a well-informed estimation of the surfactant layer thickness. The value of r_AOT ≈ 13.9 Å suggested by the simulations helps reconcile published values with each other and revise previously calculated values for r_core . In general, simulations are essential for interpreting experimentally derived values such as r_g and r_h in terms of the n_AOT for an RM.

A fourth result is insight into the shape and internal organization of an RM. Deviations from spherical shape observed in these simulations are significant to an understanding of RM size and other characteristics observed in experimental studies. For example, the simulations show that the distributions of water and AOT overlap to a large extent, so that n_AOT and hence, the size of an RM in terms of the number of its component molecules, is not easily derived from any of the experimentally derived radii defined in Table 2.

A fifth result is insight into the mechanism of water exchange between RMs. Intermicellar exchange has been demonstrated experimentally, but has not been reported in previous all-atom RM simulations.^{23–25,27,45} It has been suggested that the mechanism of intermicellar water exchange involves sequential fusion and fission of RMs,⁵⁴ or channels forming during micellar collisions.^55,56 However, the simulations demonstrate that the AOT anion facilitates the loss and gain of individual water molecules from an RM, most likely by creating a population of water molecules with an energy that is intermediate between the aqueous and isooctane phases. This population is evident from the nearest distance metrics which show extensive overlap of the water, AOT anion, and isoO distributions (Figure 9).

It should be noted that the simulations in this study were performed nominally at 300K, but they are being compared to experimental studies at 293 or 298K. While it would have been a simple matter to adjust the simulation temperature to the temperatures of the experiments, the simulation parameters have been optimized for 300K. There is no simple way to adjust a parameter set so that is valid at other temperatures. More importantly, perhaps, there may be no need to make this adjustment because experimentally determined r_h values did not change over temperatures ranging from 288°K to 318°K.^48,49 The accuracy of common parameter sets has also been questioned because of the high concentrations found in RM systems,⁵⁷ although the reported inaccuracies were manifest in properties not examined in this study.

Finally, this study provides a starting point for the accurate simulation of materials encapsulated in RMs. There are significant differences in the interpretation of RM properties, with or without protein inside, in the literature. Although many experimental studies are interpreted with the assumption of an idealized spherical geometry of the RM, most computational studies support the conclusion that encapsulated materials do not experience the conditions of a hard spherical confinement.^25,32 Moreover, encapsulated material will likely increase the volume and surface area of an RM. The need for extra surfactant to cover the increased surface area may be met by (1) the coalescence of RMs with same W₀ ratio, which would result in a larger RM with same W₀ ratio (2) the acquisition of surfactant from other RMs, which would result in a smaller W₀, (3) the replacement of water with the encapsulated material, which would negate the need for additional surfactant but result in a smaller W₀, or (4) situating portions of the encapsulated material at the interface to substitute for surfactant. In any of these possibilities, the AOT energy would be determined by not only by electrostatic interactions between surfactant, sodium cations, and water but also by the physicochemical characteristics of the encapsulated material. Simulation studies of encapsulation are needed to explore these possibilities.

CONCLUSION

An RM with W₀ = 7.5 appears to be most stable when n_AOT = 62, and this relationship is determined by a balance of electrostatic forces that are modulated by the dielectric effect of encapsulated water. Most importantly, the RM₆₂ system corresponds precisely to most of the experimental data available for RMs made with AOT and a W₀ = 7.5. From this benchmark value, n_AOT may be calculated for a wide range of W₀ values in close agreement with experimental data. The information obtained from simulations about RM structure and organization enables helps reconcile many of the seemingly inconsistent experimental results about RM size.