Hybrid Resonators and Highly Tunable Terahertz Metamaterials Enabled by Vanadium Dioxide (VO₂)

Abstract

Hybrid metamaterials that exhibit reconfigurable responses under external stimulus, such as electric fields and light radiation, have only recently been demonstrated by combining active media with patterned metallic structures. Nevertheless, hybrid terahertz (THz) metamaterials whose spectral performance can be dynamically tuned over a large scale remain rare. Compared with most active media (for instance, silicon) that provide limited activity, vanadium dioxide (VO₂), which exhibits an insulator-to-metal transition, has been recently explored to facilitate dynamically tunable metamaterials. More importantly, the phase transition yields a three orders of magnitude increase in THz electrical conductivity, which suggests the potential for creating VO₂ based hybrid resonators that operate at THz frequencies. Here, we show that an integration of VO₂ structures and conventional metallic resonating components can enable a class of highly tunable THz metamaterials. Considering the widely studied phase-transition dynamics in VO₂, the proposed hybrid metamaterials are capable of offering ultrafast modulation of THz radiation.

Introduction

Metamaterials represent a new class of engineered materials that are generally composed of an array of subwavelength ‘artificial atoms’ that provide an unprecedented ability for electromagnetic wave manipulation. Recent developments have been focused on functionalizing metamaterials by endowed them with tunability at the ‘atomic’ level^1–3. Various active media (e.g., semiconductors^4–10, liquid crystals^11–18, ferromagnetic¹⁹ and ferroelectric²⁰ materials and graphene^21–24) that are capable of providing variable dielectric or magnetic properties have been introduced into metamaterial systems to facilitate a reconfigurable response. In particular, tunable terahertz (THz) metamaterials^{6–10, 17, 18, 25–29} have received considerable attention due to their ability to provide highly efficient manipulation of THz radiation. Nevertheless, effective tuning of hybrid THz metamaterials has been considerably constrained by the limited range in the active material properties that can be achieved in practice. For example, the response modulation observed in refs 6, 7 was attributed to the electrically triggered carrier density change of 10¹⁶ cm⁻³ in n-type GaAs and the optical pumping induced conductivity varying up to 10² Ω⁻¹ cm⁻¹ in silicon, respectively. Furthermore, despite the radically different regulating mechanism, only mild responses to an applied electric field were identified in graphene²⁸ and nematic liquid crystal¹⁷ integrated tunable THz metamaterials.

Vanadium dioxide (VO₂), a classical transition metal oxide that undergoes an insulator-to-metal transition (IMT) near room temperature (T _IMT ~ 67 °C), has been intensively studied with respect to the fundamental physics involved during the transition process, e.g., the femtosecond structural dynamics³⁰, and the potential applications, e.g., next generation transistors³¹. As an active medium that has been demonstrated to be sensitive to thermal, optical and electric fields, VO₂ was recently utilized to enable active metamaterials at both THz^32–38 and optical frequencies^39–43. For instance, taking advantage of the hysteresis characteristic of VO₂, Driscoll and coworkers have demonstrated electrically controlled frequency tuning as well as the memory effect of a VO₂ integrated THz metamaterial³². From a different standpoint, Liu and coworkers have reported the observation of a THz-field-induced IMT in VO₂ metamaterials³⁷, in which the split ring resonators (SRRs) offer both the locally-enhanced nonlinearity and the globally macroscopic observation of the IMT dynamics. A close examination of the reported THz properties of VO₂ reveals that IMT leads to an approximately three orders of magnitude increase in the conductivity (σ₁) and, more importantly, when VO₂ is in its fully metallic state σ₁ reaches ~4 × 10³ Ω⁻¹ cm⁻¹, which is just one order of magnitude lower than that of gold. In stark contrast to the methodology previously adopted to introduce active media for the achievement of tunability, the sufficiently high conductivity of VO₂ actually enables the material to support strong THz resonances that can be exploited to achieve highly tunable THz devices. Recently, a temperature controlled THz metamaterial consisting of VO₂ cut-wires was reported with large transmission amplitude modulation⁴⁴.

In this study, by integrating structured VO₂ with conventional metallic resonating components, we propose and demonstrate a series of hybrid highly tunable terahertz metamaterials. Furthermore, the work reported here provides a path forward to the design of VO₂ based THz metadevices. Besides the dramatic manipulation of the response, we also envision that the unique characteristics of the phase transition of VO₂, including the hysteresis and ultrafast dynamics, may provide a paradigm that can be extended to sophisticated control of THz radiation.

Results

Despite the elusive microscopic mechanism behind the phase transition, VO₂ indeed provides a huge contrast in material properties between its insulator and metallic phases. For instance, Kim and coworkers have reported that the exceedingly large conductivity change during IMT of VO₂ can be utilized to build high-speed next-generation transistors³¹. It should be noted that in this type of electronic application, the electrical current filaments that arise from a localized transition are responsible for the observed resistance magnitude jumps in the voltage-current curves. Optically, VO₂ during transition should be treated as a composite material with permittivity that can be described by effective medium approximations. Indeed, using scanning near-field infrared microscopy, Qazilbash and coworkers have illustrated the percolation progress at the nanometer scale in VO₂ thin films, i.e., the portion of metallic state experiences gradual growth with increasing temperature until a complete transition is achieved⁴⁵. Consequently, the interactions between VO₂ films and THz waves are in general dominated by their macroscopic material properties. Various groups have reported the temperature-dependent THz conductivity (σ₁) of VO₂ thin films deposited on a sapphire substrate^{37, 46}. An approximately three orders of magnitude increase in σ₁ indicates the potential of VO₂ as an active medium for tunable metamaterials, while, more importantly, the high conductivity exhibited in the metallic state indicates the possibility of further creating hybrid VO₂/metal THz resonators and metamaterials with a high degree of tunability.

In this paper, we propose a hybridization of VO₂ microstructures with conventional metallic resonating components that will enable highly-active THz metamaterials. Schematics of the four types of VO₂ integrated hybrid metamaterials that will be considered here are illustrated in Fig. 1. In particular, the IMT property of VO₂ is expected to enable THz radiation manipulation through various mechanisms. Here we consider four different examples, which include tuning the resonance of gap-loaded SRRs (Fig. 1(a)), producing Fano resonances in asymmetric VO₂/Au double-bars (Fig. 1(b)), creating a perfect absorber effect in Au-cross/VO₂ sandwich structures (Fig. 1(c)), and Au/VO₂ coupled strips capable of supporting a magnetic resonance (Fig. 1(d)). The corresponding unit cell is depicted as an inset at the left-top corner of each figure. It should be noted that, although sputtering based growth of VO₂ on different substrates has been reported, crystalline sapphire wafers are preferred to obtain high quality VO₂ thin films because of the beneficial lattice matching effect⁴⁷. Therefore, without loss of generality, sapphire is assumed as the substrate with a permittivity of 10.5 for all simulations in this work. By fitting the measured THz spectroscopy results reported in ref. 37, we obtain the material properties of VO₂ as a function of σ₁ and utilize them to explore the tuning behavior in the proposed hybrid resonators during the IMT process (details available in Methods).

Figure 1.

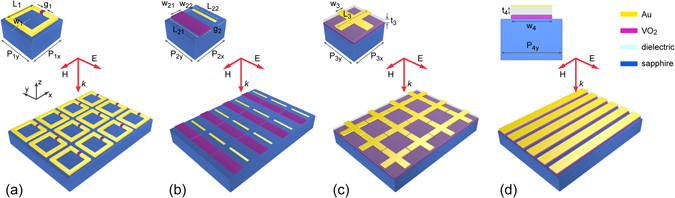
Vanadium dioxide enables hybrid THz metamaterials. Schematic showing four different metamaterial examples, each consisting of an array of hybrid resonators. These metamaterial designs include (a) gap-loaded split ring resonators (SRRs), (b) asymmetric VO₂/Au double-bars, (c) Au-cross/VO₂ absorber structures, and (d) Au/VO₂ paired-strips. The geometrical parameters (all unit in μm) are: P _1x = P _1y = 30, L ₁ = 25, w ₁ = 3 and g ₁ = 1.5; P _2x = 75, P _2y = 72, L ₂₁ = 70, L ₂₂ = 55, w ₂₁ = 25, w ₂₂ = 5, and g ₂ = 20; P _3x = P _3y = 100, L ₃ = 95, w ₃ = 20 and t ₃ = 8; P _4y = 90, w ₄ = 60 and t ₄ = 12. The thickness of VO₂ in (a) is 200 nm and that in (b), (d) and (d) is 3 μm. The thickness of gold in all designs is 200 nm.

It has been widely reported that the resonance associated with SRRs, the most-studied and intriguing meta-atom structure, can be efficiently regulated by varying the dielectric environment in the vicinity of their gaps owing to the highly localized field enhancement. Consequently, we first consider an array of SRRs with VO₂ islands loaded in their gaps, as depicted in Fig. 1(a). The transmission spectra corresponding to a THz plane wave incident on the structure for a series of VO₂ conductivity values are illustrated in Fig. 2(a). In the case where σ₁ = 10 Ω⁻¹ cm⁻¹, which corresponds to VO₂ at room temperature³⁷, a transmission dip indicating a sharp resonance is identified around 0.8 THz. It is evident that the transmission around this resonance increases dramatically with a corresponding increase in σ₁, while the gradual emergence of a transmission dip around 1.7 THz indicates the onset of a new resonance mode. This is clearly revealed by the electric field distributions (Fig. 2(c)) at the resonances frequencies, i.e., 0.74 and 1.74 THz. To better display the transmission tuning behavior due to the change in the localized material properties in the gap, a semi-log plot of the σ₁-dependent THz transmission spectra in the frequency range of interest is shown in Fig. 2(b), which unambiguously indicates a drastic but continuous spectrum tuning before saturation. Furthermore, by monitoring the local field, we study the field enhancement (|E|) in the SRR gap and display the results as a function of σ₁ in Fig. 2(d). The significant decrease of the on-resonance in-gap field enhancement in the semi-log plots further discloses the tuning effect arising from the phase transition of the critically-placed VO₂. In other words, the tunability exhibited in Fig. 2 is based upon the change in the electrical properties of the SRRs. Beyond that, as we discussed above, the highly conductive metallic-phase VO₂ can actually support strong THz resonance. As depicted in Fig. 1(b–d), hereinafter we present three types of hybrid resonators for versatile THz metamaterials that exhibit remarkable response modulation enabled by the phase transition of VO₂.

Figure 2.

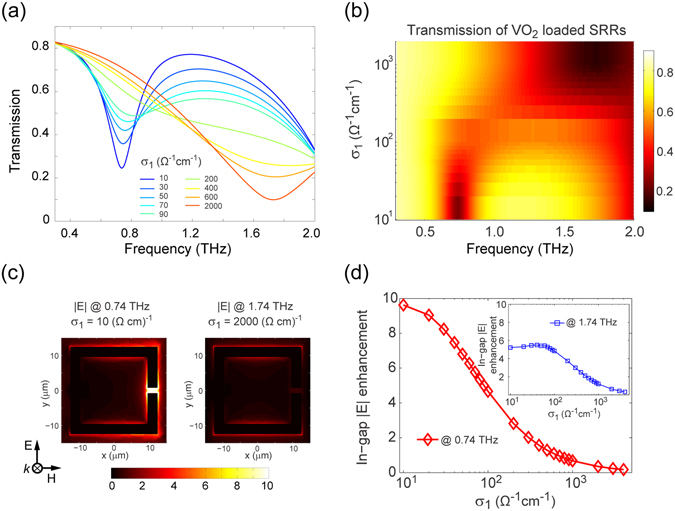
Active performance of the THz metamaterial consisting of an array of SRRs with VO₂ loaded in their gaps. (a) Simulated transmission spectra for a series of VO₂ conductivity (σ₁) values. (b) A semi-log two-dimensional plot of the transmission spectra. (c) The electric field distribution for the first resonance at 0.74 THz when σ₁ = 10 Ω⁻¹ cm⁻¹ and the second resonance at 1.74 THz when σ₁ = 2000 Ω⁻¹ cm⁻¹. (d) The in-gap electric field enhancement as a function of σ₁ at 0.74 THz. The field enhancement at 1.74 THz is shown in the inset. All data for |E| was normalized to the electric field magnitude of the incident wave.

Optical Fano resonances, which typically give rise to an asymmetric line-shape of the scattering spectrum, have recently been intensively studied due to their potential applications in optoelectronic devices such as sensors, lasers and switches. In general, the interference between different parts of a Fano system is responsible for the asymmetric resonance profile, leading to the unique enhanced light-matter interactions. Owing to their unprecedented flexibility in manipulating electromagnetic waves, metamaterials are ‘predisposed’ to possessing Fano resonances⁴⁸. Various meta-atoms, such as asymmetric SRRs⁴⁹, SRR-bar structures⁵⁰, dolmen structures⁵¹, gold heptamers⁵², and so on, have been utilized to realize Fano resonances from microwave to optical frequencies. Among those with different structural complexity, the asymmetric double-bar design^{53, 54}, based upon the interference between dipole and quadrupole modes, is more attractive due to its rather simple structure that can support Fano resonances at optical frequencies. By taking advantage of the Fano resonance enabled enhanced nonlinear effect, Moritake and coauthors have demonstrated the controllable fluorescence emission of a quantum dot (QD) embedded in a gold asymmetric double-bar metamaterial⁵⁵.

Fano systems that can be tuned in a dynamic fashion have been reported with, however, limited tuning capability^{50, 56}. As the schematic in Fig. 1(b) illustrates, we propose that a metamaterial consisting of an array of asymmetric VO₂/Au double-bar resonators is a good candidate for demonstrating active tuning of THz Fano resonances. Figure 3(a) and (b) show simulated transmission and absorption spectra, respectively, of the hybrid metamaterial at a series of conductivity values σ₁ for VO₂. It can be seen that by increasing the value of σ₁, a Fano resonance with asymmetric line-shape is gradually identified within the frequency range of interest. Specifically, with VO₂ in its insulator phase, the dipole resonance of the gold bar produces a sharp transmission dip around 0.95 THz, while, when VO₂ is highly conductive, the absorption peak appearing around 0.8 THz clearly reveals the characteristic asymmetric profile of a Fano resonance. It can easily be concluded that the VO₂ bar in its metallic phase supports a dipolar resonance (not shown), whereas the observed Fano resonance arises from the interference between the asymmetric VO₂/gold double bars. This Fano resonance mode is expected to form non-radiative magnetic resonance and, accordingly, leads to an enhanced magnetic field in the gap between the bars. At σ₁ = 2000 Ω⁻¹ cm⁻¹, this is readily identified from the magnetic field distribution at the frequency of the absorption peak (0.79 THz) shown in Fig. 3(c). To further confirm the observed Fano resonance mode, the dependence of the in-gap |H_z| enhancement as a function of σ₁ is shown in Fig. 3(d), while the dispersion of the in-gap |H_z| is depicted in the inset. The results indicate that a Fano resonance starts to emerge when σ₁ is greater than 100 Ω⁻¹ cm⁻¹ and, with VO₂ in its metallic phase, the hybrid system can support a relatively high quality factor Fano resonance. By exhibiting the strong and continuously controllable Fano-like interference, the proposed hybrid asymmetric system promises the potential to achieve controllable slow-light, sensing and other nonlinear THz devices.

Figure 3.

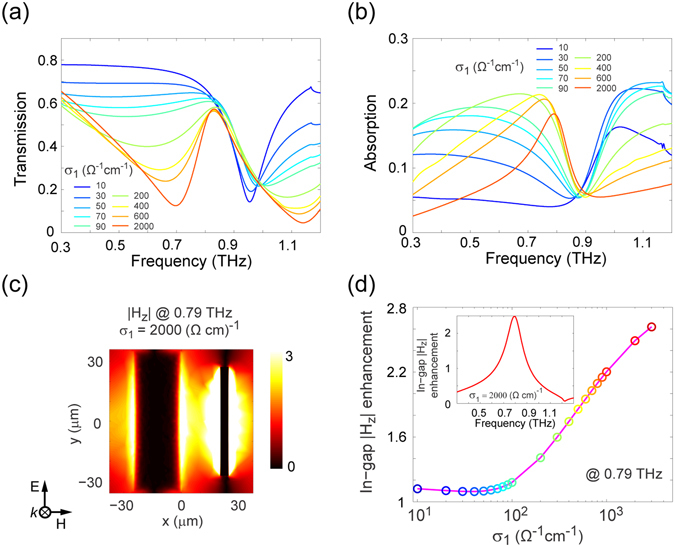
Asymmetric VO₂/Au double-bar resonator based hybrid metamaterial for a tunable THz Fano resonance. Simulated (a) transmission and (b) absorption spectra of the hybrid metamaterial for a series of conductivity values σ₁. (c) Magnetic field distribution at 0.79 THz when σ₁ = 2000 Ω⁻¹ cm⁻¹. (d) The in-gap |H_z| enhancement as a function of σ₁ at 0.79 THz. The case for σ₁ = 2000 Ω⁻¹ cm⁻¹ as a function of frequency is shown in the inset. All data for |H_z| was normalized to the magnetic field magnitude of the incident wave.

Metamaterial absorbers that can achieve unity absorptivity have attracted considerable attention since the first experimental demonstration⁵⁷. Potential applications including, but are not limited to, IR camouflage, thermophotovoltaics, electromagnetic modulators and enhanced nonlinearity. At THz frequencies, in addition to the more conventional microelectromechanical systems (MEMS) based method^{58, 59}, liquid crystal enabled tunable metamaterial absorber designs have been recently reported¹⁷. In Fig. 1(c), we illustrate a hybrid metamaterial absorber in which a SiO₂ film serves as the spacer between an Au-cross array and the VO₂ film that functions as a ground plane in the metallic phase. Figure 4(a) shows the σ₁ dependence of the absorption spectra resulting from the metamaterial system, while the corresponding absorption properties of the VO₂ and gold cross are illustrated in Fig. 4(b). These results reveal that, when the VO₂ film is in the metallic phase, the optimized structure behaves like a perfect absorber with the achievement of unity absorptivity around 0.82 THz. More importantly, the absorption properties of the system closely depend on the conducting characteristics of the VO₂ ground plane, which enables the creation of THz absorbers with dynamically tunable properties. To have a complete picture of the hybrid metamaterial absorber, in Fig. 4(c) we plot the corresponding power transmittance (T) and reflectance (R) at 0.82 THz as well as two more frequencies that are far from the resonance as a function of σ₁. For the sake of comparison, T and R data for the bare VO₂ film on a substrate are also provided. It can be seen that T (R) of the system at 0.82 THz is low (high) even when the VO₂ is in its insulator phase, which can be attributed to the intrinsic electric resonance of the Au-cross. As the value of σ₁ is increased, R at 0.82 THz dramatically decreases until both T and R reach near-zero values when σ₁ → 1000 Ω⁻¹ cm⁻¹. For frequencies far away from the resonance (e.g., 0.40 and 1.20 THz), T decreases but R increases with increasing σ₁, resulting from the fact that a rather weak interaction between the Au-cross and the VO₂ film is expected. As these results suggest, all scattering parameters of the proposed metamaterial absorber can be purposely controlled, which is distinctly different from the reported tunable absorber devices^{17, 59} with fixed opaque ground plane and can therefore be highly beneficial for sophisticated manipulation of THz radiation. To confirm the perfect absorber mode, a vector plot of electric current density on the Au-cross and the VO₂ film surface are shown in Fig. 4(e) and (f), respectively. The antiparallel induced currents on the two surfaces are evidence of a magnetic resonance, as is further illustrated in the magnetic field distribution in Fig. 4(g).

Figure 4.

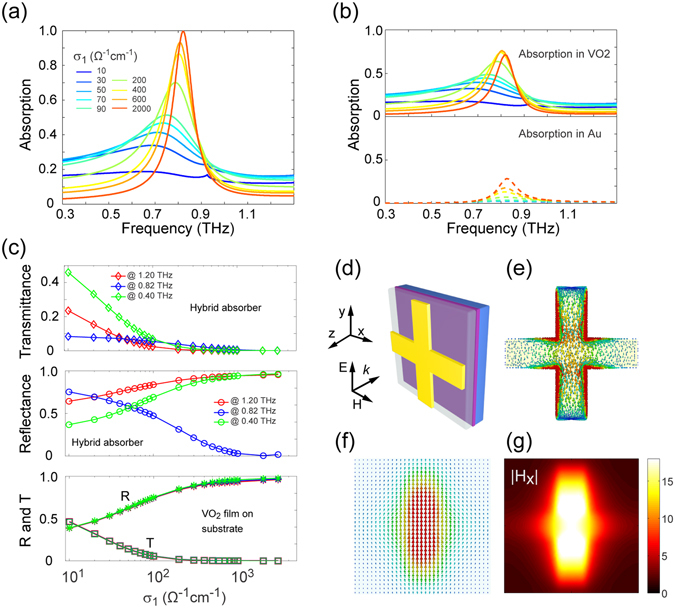
VO₂ based tunable THz metamaterial absorber. Simulated (a) absorption spectra of the hybrid metamaterial and (b) the absorption in the VO₂ and gold material. (c) Transmittance (T) and reflectance (R) of the hybrid metamaterial and a bare 3-μm-thick VO₂ film on a substrate at the resonance frequency (0.82 THz) and two more frequencies far from the resonance (0.40 and 1.20 THz). (d) Schematic of the metamaterial absorber unit cell. A vector plot of electric current density on the surface of (e) the gold cross and (f) the VO₂ film. (g) Distribution of the x-component of the normalized magnetic field (|H_x|) in the spacer.

Given the fact that the response of natural materials to the magnetic component of an electromagnetic wave vanishes at THz frequencies and above, the ability of metamaterials to create artificial magnetism is of paramount importance. Indeed, the ability of metamaterials to support magnetic resonances has facilitated the achievement of various exotic phenomena, including negative refraction, cloak based invisibility, and the perfect absorber effect. Compared with SRRs, which are the primary metamaterial resonator utilized for achieving artificial magnetism at radio frequencies, the paired-strip design consisting of two conductive strips separated by a dielectric spacer has been employed to realize strong magnetic responses at optical frequencies⁶⁰, because of its planar structure that is more amenable to micro- and nano-fabrication.

A hybrid metamaterial composed of a one-dimensional array of VO₂/gold paired-strips is proposed (see Fig. 1(d)) to implement tunable magnetism at THz frequencies. First of all, the simulated transmission spectra shown in Fig. 5(a) indicate the largely controllable response of the system due to the IMT of VO₂. In particular, when σ₁ is greater than 300 Ω⁻¹ cm⁻¹, two transmission dips are identified around 1.03 and 1.41 THz, at where, however, the hybrid metamaterial with insulating VO₂ (σ₁ = 10 Ω⁻¹ cm⁻¹) is relatively transparent to the THz wave. In order to understand the underlying physical mechanism, the normalized magnetic field (|H_x|) at the geometric center of the spacer is obtained at the resonances from a field probe and plotted as a function of σ₁ in Fig. 5(b). Clearly, the magnetic field within the VO₂/gold paired-strips is increasingly enhanced when there is a corresponding increase in σ₁. In addition, as shown in Fig. 5(c), compared with the case with VO₂ in the insulating state (σ₁ = 10 Ω⁻¹ cm⁻¹), a broadband and pronounced enhancement of |H_x| in the spacer is observed when σ₁ = 2000 Ω⁻¹ cm⁻¹. Moreover, Fig. 5(d) shows the evolution of the magnetic field distribution in a cross-section plane orthogonal to the strips for different values of σ₁. As σ₁ is increased, a corresponding increase in the magnetic field confinement in the space between the VO₂ and gold elements is observed. A comparison between the two figures in the most-right column of Fig. 5(d) unambiguously reveals the distinct mode of the two resonances arising from the permittivity difference between the substrate (sapphire) and superstrate (air).

Figure 5.

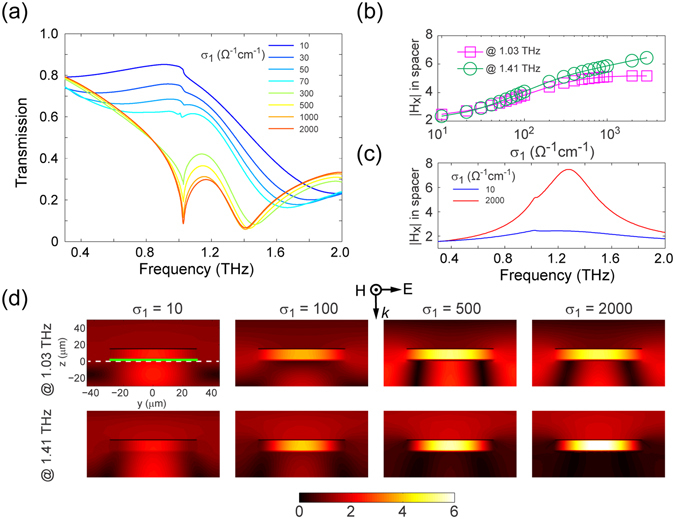
Au/VO₂ paired-strip based active magnetic THz metamaterial. (a) Simulated transmission spectra. (b) The x-component of magnetic field (|H_x|) at the geometric center of the spacer as a function of σ₁. (c) The dispersion of (|H_x|) when σ₁ = 10 and 2000 Ω⁻¹ cm⁻¹. (d) The distribution of magnetic field at the two resonances (i.e., 1.03 and 1.41 THz) for a series of σ₁ values. The white dashed line indicates the surface of the substrate and the green line represents the VO₂ film. All field data was normalized to the magnetic field magnitude of the incident wave.

Discussion

Exhibiting lattice rearrangement or deformation at the atomic level, phase-transition materials have shown the capability of providing a large change in refractive index over a broad frequency range and consequently have been utilized to enable active photonic systems. Beyond the large conductivity variations that can be achieved during the IMT, as a classical transition metal oxide VO₂ also exhibits hysteresis, a property associated with the first-order structural transition. Taking advantage of this hysteretic behavior, researches have demonstrated the memory process in VO₂ integrated hybrid metamaterials^{32, 43}. We emphasize that, though for simplicity no hysteretic characteristics have been taken into account in our designs, the proposed hybrid metamaterials are expected to manifest system history dependent THz responses, including the controllable memory effect. Besides temperature, other field regulation methods such as optical pumping, electric current and electric field induced phase transition of VO₂ have been reported. In contrast to methods based upon thermal effects, optically-induced and field-effect-induced IMT can adjust VO₂’s material parameters at a subpicosecond level. Consequently, the proposed hybrid metamaterials have the potential for ultrafast modulation of THz radiation.

Although it has been challenging to grow thick single phase VO₂ due to the existence of a large number of states in the material, a variety of preparation procedures including pulsed laser deposition (PLD), molecular beam epitaxy (MBE), and sputtering have been utilized to achieve crystalline VO₂ thin films. In particular, radio frequency (RF) sputtering, a relatively straightforward approach that requires controllable conditions (including an Ar and O₂ mixture environment, substrate temperature and RF power) has been implemented to obtain high quality VO₂ films^61–63. Furthermore, we note that VO₂ films with acceptable quality have been successfully grown on different substrates such as gold⁴³ and glass⁴⁴, which would offer more flexibility in the design of hybrid THz metamaterials. For instance, the metallic substrate may allow the metal/VO₂/metal configuration to enable, for example, negative refraction⁶⁴ and giant chirality⁶⁵ at THz frequencies.

In summary, we have demonstrated that the integration of VO₂ structures with conventional metallic resonating components can enable a class of highly tunable THz metamaterials. By presenting a series of proof-of-concept designs, we show that the insulator-to-metal transition of VO₂ can facilitate dramatic response tuning of gap-loaded SRRs. More importantly, it was shown that the IMT of VO₂ can also enable hybrid metamaterials exhibiting active Fano resonances, the perfect absorber effect, and artificial magnetism at THz frequencies. These responses can be dynamically tuned over a large scale, owing to the dramatic change in the THz electrical conductivity of VO₂ enabled by its IMT. Considering the reported subpicosecond response times of VO₂ under external stimulus, the proposed hybrid metamaterial systems may open up new avenues for highly tunable ultrafast THz devices.

Methods

The permittivity of VO₂ in the THz region can be described by the following Drude model: $\epsilon \left(\omega \right)={\epsilon }_{\infty }-\frac{{({\omega }_{\mathrm{p}}({\sigma }_1))}^2}{{\omega }^2+i\gamma \omega }$, where ε _∞ is the permittivity at high frequency, ω _p(σ ₁) is the conductivity dependent plasmon frequency and γ is the collision frequency⁴⁶. On the other hand, both ${\omega }_{\mathrm{p}}^2$ and σ ₁ are proportional to the free carrier density. Therefore, the plasmon frequency at ${\sigma }_1^{\prime }$ can be approximately expressed as ${\omega }_{\mathrm{p}}^2\left({\sigma }_1^{\prime }\right)=\left(\frac{{\sigma }_1^{\prime }}{{\sigma }_1}\right){\omega }_{\mathrm{p}}^2\left({\sigma }_1\right)$. By fitting the measured THz spectra shown in ref. 37, we determined that when σ ₁ = 3 × 10³ Ω⁻¹ cm⁻¹ (ε _∞ = 12), the corresponding ω _p = 1.40 × 10¹⁵ rad/s, while γ = 5.75 × 10¹³ rad/s is assumed to be independent of σ ₁. These Drude model parameters agree well with the experimental results reported by other groups⁴⁶. In addition, considering the roughly 1 μm thick skin depth of metallic-phase VO₂ around 1.0 THz, 3-μm-thick VO₂ structures were utilized to construct the hybrid resonators. Full-wave simulations were implemented using the commercial finite integration package CST Microwave Studio. For each type of hybrid metamaterial, a unit cell of the structure was simulated by employing periodic boundary conditions.

Data availability

The data that support the findings of this study are available from the corresponding author on request.

Author Contributions

S.W. and L.K. conceived the idea and performed the numerical simulations. S.W., L.K. and D.H.W. contributed to the interpretation of results and participated in the preparation of manuscript.

Competing Interests

The authors declare that they have no competing interests.