Ab initio simulations of protein-folding pathways by molecular dynamics with the united-residue model of polypeptide chains

Abstract

We report the application of Langevin dynamics to the physics-based united-residue (UNRES) force field developed in our laboratory. Ten trajectories were run on seven proteins [PDB ID codes 1BDD (α; 46 residues), 1GAB (α; 47 residues), 1LQ7 (α; 67 residues), 1CLB (α; 75 residues), 1E0L (β; 28 residues), and 1E0G (α+β; 48 residues), and 1IGD (α+β; 61 residues)] with the UNRES force field parameterized by using our recently developed method for obtaining a hierarchical structure of the energy landscape. All α-helical proteins and 1E0G folded to the native-like structures, whereas 1IGD and 1E0L yielded mostly nonnative α-helical folds although the native-like structures are lowest in energy for these two proteins, which can be attributed to neglecting the entropy factor in the current parameterization of UNRES. Average folding times for successful folding simulations were of the order of nanoseconds, whereas even the ultrafast-folding proteins fold only in microseconds, which implies that the UNRES time scale is approximately three orders of magnitude larger than the experimental time scale because the fast motions of the secondary degrees of freedom are averaged out. Folding with Langevin dynamics required 2–10 h of CPU time on average with a single AMD Athlon MP 2800+ processor depending on the size of the protein. With the advantage of parallel processing, this process leads to the possibility to explore thousands of folding pathways and to predict not only the native structure but also the folding scenario of a protein together with its quantitative kinetic and thermodynamic characteristics.

There are two protein-folding problems in contemporary computational biology. The first problem is to predict protein structure from sequence, and the second one is to predict protein-folding pathways. There are many approximate methods to attack the folding problem, which belong to two broad categories of physics and knowledge-based methods (1–3). Molecular dynamics (MD) is the only computational method that provides a time-dependent analysis of a system in molecular biology and, consequently, can be implemented to solve the second protein-folding problem.

Ideally, both the protein and the surrounding solvent should be represented at the all-atom level (4) because this approach is the closest to experiment. However, there are two severe limitations to such a treatment, namely the multidimensionality of the system (typically, >10⁴ degrees of freedom with explicit solvent) and the small values of the time step in integrating the equations of motion (of the order of femtoseconds). Because of these two limitations, explicit-solvent all-atom MD algorithms can simulate events in the range of 10^-9 to 10^-8 s for typical proteins and 10^-6 s for very small proteins (4–6). These time scales are at least one order of magnitude smaller than the folding times of proteins (4). Consequently, all-atom simulations of real-size proteins are usually limited to unfolding the native structure of the proteins, followed by subsequent refolding (4, 5), or by umbrella-sampling methods, in which selected reaction coordinates (usually the fraction of native contacts and the radius of gyration) are controlled along the folding pathway (7). Such approaches combined with experimental data provide valuable insights into the folding pathways (4).

One famous example of a successful explicit-solvent all-atom MD simulation is that of Duan and Kollman (8) on the 36-residue villin headpiece. They observed short-living folding intermediates in a 1-μs-long run. The advent of distributed computing provides hope that this approach could be extended to larger systems in the future (9). Recently, a stochastic difference equation approach (10, 11) has been devised to study the folding pathways at the all-atom level. However, this method requires a priori knowledge of both the unfolded and folded states.

The dimensionality of a system containing the protein and the surrounding solvent can be reduced when the solvent is treated implicitly. The free energy of interaction of a solvent with a biomolecule is usually described by the generalized Born model (12). With the implicit-solvent approach, ab initio folding simulations seem feasible for small proteins. One such example is the simulation of the B domain of staphylococcal protein A (a 46-residue protein) using the all-atom amber force field and the generalized Born model, carried out by Jang et al. (13). However, even the use of implicit-solvent models does not reach the time scales necessary for folding larger proteins.

Reduced (mesoscopic) models of proteins, in which each amino acid residue is represented by only a few interaction sites, offer additional extensions of the time scale. This approach is used mainly to study general characteristics of protein folding rather than to predict folding pathways of real proteins (14, 15). Quite often, the interaction potentials are intentionally biased toward the experimental structure (the Gō-like models) (16, 17). The models that have been applied with some success in folding simulations of real proteins by using MD can be termed semimesoscopic, because the backbone is represented at the all-atom level, whereas the side chains are treated as united-interaction sites (18, 19). Also, Monte Carlo dynamics with lattice mesoscopic models and knowledge-based potentials is applied with success to study folding of real proteins (20). A physics-based mesoscopic model and MD algorithm based on generalized Lagrange equations of motion were developed recently for nucleic acids by Rudnicki et al. (21)

For the past several years, we have been developing a physics-based united-residue (UNRES) force field (22–26). Each amino acid residue is represented by only two interaction sites, which makes the model simple enough to carry out large-scale simulations. The advantage of UNRES compared with other mesoscopic protein force fields is that it has been derived carefully as a potential of mean force of the UNRES chain (24) and ultimately parameterized (25, 26) based on the concept of a hierarchical protein energy landscape (18).

In connection with the efficient conformational space annealing (CSA) (27) method of global optimization, UNRES is able to predict the structures of real-size proteins without ancillary information from structural databases (26, 28). Therefore, UNRES seems to be a good mesoscopic force field for studying the folding pathways of proteins in real time. Therefore, we recently (M.K., A.L., H.A.S., and A. Jagielska, unpublished data) implemented the use of this force field in MD. In this article, we provide an overview of dynamics with the UNRES force field and the initial application of the method to simulate ab initio folding pathways of a set of proteins of different sizes and fold types.

Methods

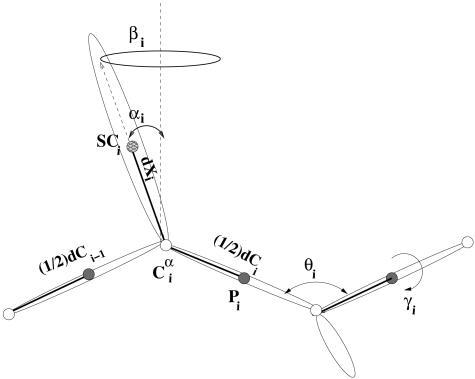
UNRES Force Field. In the UNRES model (22–26), a polypeptide chain is represented as a sequence of α-carbon (C^α) atoms. The C^α atoms are linked together by backbone virtual bonds (designated as dCs), which constitute the backbone. United side chains (SCs) are connected to the backbone by the virtual bonds (dXs). United peptide (p) groups are in the centers of the dCs. The centers of mass of the side chains are at the ends of the dXs (Fig. 1). The interaction sites are the united p groups in the middle of the dCs, and the SCs at the ends of the dXs. The p group centers represent only the C′, O, N, and H atoms of the peptide groups, whereas the C^α atoms are included in the SC centers. Consequently, the positions of the C^α atoms are geometric points and not interaction sites.

Fig. 1.

UNRES model of the polypeptide chain. Filled circles represent p groups, and open circles represent the C^α atoms, which serve as geometric points. Ellipsoids represent side chains, with their centers of mass at the SCs. The p groups are located halfway between two consecutive C^α vectors or dCs. The SCs are located at the end of the C^α···SC vectors or the dXs. The variables to change the conformation of the polypeptide chain are the virtual-bond angles θ, the virtual-bond dihedral angles γ, and the angles α_SC and β_SC, which define the location of a side chain with respect to the backbone.

UNRES is a physics-based force field that is derived as a restricted free-energy function of a polypeptide chain. The restricted free energy is defined as the free energy of a given coarse-grain conformation obtained by integrating the Boltzmann factor of the all-atom (i.e., the polypeptide chain-plus-solvent) energy over the degrees of freedom that are neglected in the UNRES model (24). The complete UNRES potential-energy function is expressed by Eq. 1.

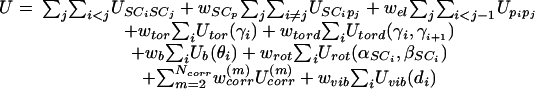[1]

The terms U_SCiSCj correspond to the mean free energy of hydrophobic (hydrophilic) interactions between the side chains. These terms implicitly contain the contributions from the interactions of the side chain with the solvent. The terms U_SCipj correspond to the excluded-volume potential of the side-chain–peptide group interactions. The terms U_pipj represent the energy of average electrostatic interactions between backbone peptide groups. The terms U_tor and U_tord are the torsional and double-torsional potentials, respectively, for the rotation about a given virtual bond or two consecutive virtual bonds. The terms U_b and U_rot are the virtual-angle-bending and side-chain-rotamer potentials. The terms U^(m) _corr correspond to the correlations (of order m) between peptide-group electrostatic and backbone-local interactions. The terms U_vib(d_i), d_i being the length of the ith virtual bond introduced in this work, are simple harmonic potentials. The w values represent weights of the various energy terms. They were determined in our earlier work (25, 26) by our hierarchical method for optimizing the energy landscape that is aimed at lowering energy as more and more native-like structural elements are formed in a specific order, which is intended to be identified in a rough way with the folding pathway. This feature distinguishes our approach from methods that are aimed at lowering energy with increasing bulk similarity to the native structure expressed, e.g., as the rms deviation (rmsd) from the native structure (29, 30). The weight w_vib was arbitrarily set at 1. In this work, we used our recently derived 4P force field (26) based on optimizing the energy landscapes of PDB ID codes 1GAB (31) (a 47-residue α-protein), 1E0L (32) (a 28-residue β-protein), 1E0G (33) [a 48-residue (α+β) protein], and 1IGD (34) [a 61-residue (α+β) protein].

MD with the UNRES Model. We implement the Lagrange formalism and gather the virtual-bond vectors shown in Fig. 1 into a vector of generalized coordinates q = (dC_o, dC₁,..., dC_n, dX₁, dX₂,..., dX_n)^T. The vector dC_o specifies the position of the first C^α atom of the chain, dC_i specifies the 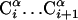virtual-bond vector, and dX_i specifies the 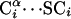virtual-bond vector. These coordinates have the sense of local Cartesian coordinates and not curvilinear coordinates such as virtual-bond angles and virtual-bond-dihedral angles. The vectors q̇ and q̈ denote generalized velocities and generalized accelerations, respectively. We assume that the virtual bonds are elastic rods with mass distribution that scales with the length of a rod. The Cartesian coordinates of the interacting sites x = (r_p1, r_p2,..., r_pn-1, r_SC1, r_SC2,..., r_SCn)^T are related to the generalized coordinates by a linear transformation x = Aq, where A is a constant matrix such that a_i(k),j = 0 [i(k) being a Cartesian coordinate of site k] if the coordinates up to j correspond to virtual-bond vectors of the part of the chain to the right of site k, a_i(k),j = 1 if the coordinates correspond to the virtual-bond vectors to the left of site k or to a C^α···SC virtual bond containing the side chain with index k, and a_i(k),j = 1/2 if the coordinates correspond to the virtual-bond vector containing the peptide group with index i(k). The same relationship holds between the time derivatives of x and q.

In matrix notation, the complete equations of motion for Langevin dynamics with the UNRES force field can be written as Eq. 2,

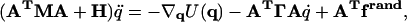[2]

where M is the diagonal matrix of masses of the sites (p groups and SCs) such that m_ii is the mass of the site corresponding to the ith generalized coordinate, H (a diagonal matrix) is the part of the inertia matrix corresponding to the internal stretching motion of the virtual bonds with h_ii = (1/12)m_p (m_p being the mass of a peptide group) for peptide groups and h_ii = (1/3)m_SCj(i) (m_SCj(i) being the mass of the side chain corresponding to the ith generalized coordinate) for side chains, Γ is the diagonal friction tensor (represented by the friction matrix) acting on the interacting sites such that γ_ii is the coefficient of the site corresponding to the ith coordinate, f ^rand is the vector of random forces acting on interacting sites, U is the UNRES potential energy defined by Eq. 1, and ▿_q denotes the gradient in q. We use Eq. 3 to compute friction coefficients,

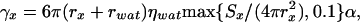[3]

where r_x is the radius of a peptide group or a side chain, r_wat is the radius of a water molecule taken here as 1.4 Å, η_wat is the viscosity of water, and S_x is the solvent-accessible surface area. We adapted the algorithm from the tinker package (ref. 35; http://dasher.wustl.edu/tinker) to calculate the surface area. Because the surface areas of the UNRES sites often happen to decrease to 0, we set a lower limit of 0.1 on the ratio of the solvent-exposed surface area of a site to its full surface area (Eq. 3). The scaling factor α should be between 0.001 (low-friction limit) to 0.1 (overdamped limit) according to other works on united-residue Langevin dynamics (14). In this work, we set α = 0.01.

The vector f ^rand consists of random forces acting on the interaction sites, the components of which at a given step of integration are calculated from the normal distribution according to Eq. 4 (14, 16, 36),

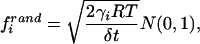[4]

where f^rand_i is the ith component of the random force vector f ^rand, γ_i is the friction coefficient associated with the ith coordinate of the interaction sites, R is the universal gas constant, T is the absolute temperature, δt is the integration time step, and N(0, 1) is the normal distribution with zero mean and unit variance. Together, the stochastic and friction forces constitute a thermostat that maintains the average temperature at the preset value.

We use the velocity Verlet algorithm (37) with variable time step for the UNRES model to integrate the equations of motion. For the Langevin dynamics simulations, we developed its modified version, which can be written as Eqs. 5 and 6, respectively.

Step 1 is (updating coordinates):

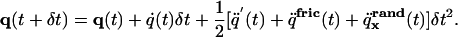[5]

Step 2 is (updating velocities):

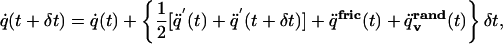[6]

with

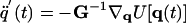[7]

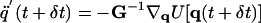[8]

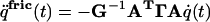[9]

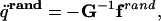[10]

where the matrix G is defined as A^TMA + H. The subscripts x and v at q̈^rand indicate that the random forces are sampled independently to compute the new coordinates and velocities, respectively.

We also adapted a more sophisticated stochastic velocity Verlet algorithm (38, 39) in which the stochastic and friction forces are integrated analytically in a given time step; however, it is prohibitively expensive, because the friction matrix in UNRES coordinates (A^TΓA) is not diagonal. Moreover, it does not perform better than the simple and cheap algorithm defined by Eqs. 5 and 6.

We set the time step at 4.89 fs to yield stable trajectories. However, this is only a formal time step, and because of the reduction of the number of the degrees of freedom in UNRES, the time step is several times larger compared with all-atom MD.

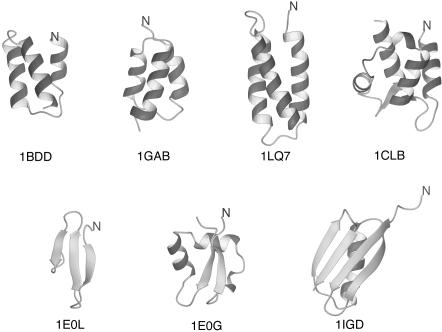
Test Systems and Procedures. We chose the following proteins to test the approach: PDB ID codes 1BDD (40) (also referred to as protein A), 1GAB (31), 1LQ7 (41), 1CLB (42) (α-proteins), 1E0L (32) (a β-protein), and 1E0G (33) and 1IGD (34) (α+β proteins). The native structures of all proteins studied are global energy minima with the 4P force field (26). The experimental structures of all test proteins are shown in Fig. 2.

Fig. 2.

Experimental structures of the proteins used to run UNRES/MD simulations. The N termini are marked for tracing purposes.

We carried out two types of simulations: (i) simulations in which a system was coupled to the Berendsen thermostat, but no explicit friction or stochastic forces were present, and (ii) full-blown Langevin simulations in which friction and stochastic forces were present explicitly. We set the coupling constant to the thermal bath at 0.0489 ps in simulations with the Berendsen thermostat. We set the working temperature at 800 K; this value was established empirically to achieve a compromise between quick folding time and long-enough stability of the native-like structures. Because the force field used here was parameterized without taking into account the physical folding temperature of any of the training proteins, the folding temperatures for this force field need not correspond to physical temperatures. For each protein and each simulation procedure (the Berendsen thermostat or Langevin dynamics), we ran 10 independent trajectories, each starting from a completely extended structure. The duration of a run was from ≈10 to ≈20 ns.

To characterize the MD runs for trajectories that resulted in native-like structures, we computed the folding time (τ_f) defined as the time at which the rmsd from the corresponding experimental structures decreases below a given cut-off value, ρ_cut. The values of ρ_cut were 3.5 Å for 1E0L, 4 Å for 1BDD and 1GAB, 5 Å for 1LQ7, 5.5 Å for 1CLB and 1E0G, and 6 Å for 1IGD. For 1E0G, additionally, we set ρ′_cut = 3.5 Å on the nonlocal β-sheet fragment (Fig. 2).

Results and Discussion

Table 1 summarizes the characteristics of the trajectories defined in the preceding sections, the CPU times per nanosecond, the lowest C^α rmsd values from the experimental structures, the lowest potential energies obtained in MD searches of all proteins studied, and the rmsd and potential-energy values for the lowest-energy structures obtained in CSA searches from our earlier work (26). It should be noted that native-like structures of all proteins studied are global minima of their energy surfaces, as found by the CSA method (Table 1). It can be seen that native-like structures were obtained in at least one trajectory for all α-proteins, although for 1LQ7 only one and two trajectories converged to the native structure for the Berendsen and Langevin simulations, respectively.

Table 1. Summary of folding of test proteins with UNRES/MD only for those proteins that produced native-like structure during simulations.

PDB ID code (no. of residues)		τf,† ns			ρmin,‡ Å	ρCSA,§ Å	Emin,¶ Kcal/mol	ECSA,∥ Kcal/mol	CPU,** min
	N*	Min	Max	Ave
1BDD (46)	10 (9)	0.3 (0.4)	4.8 (10.6)	1.8 (3.0)	2.7 (2.7)	5.5	-409 (-414)	-597	19 (38)
IGAB (47)	3 (3)	0.4 (0.4)	1.5 (9.8)	0.8 (3.9)	1.9 (2.7)	2.9	-461 (-501)	-669	22 (45)
1LQ7 (67)	1 (2)	2.1 (2.6)	2.1 (7.4)	2.1 (5.0)	1.7 (1.7)	2.3	-658 (-652)	-937	44 (99)
1CLB (75)	5 (5)	0.3 (0.4)	4.5 (3.6)	1.9 (2.3)	4.0 (4.0)	5.1	-740 (-709)	-1053	48 (111)
1E0G (48)	6 (3)	0.1 (2.7)	16.3 (8.1)	8.8 (5.0)	3.9 (3.2)	4.1	-405 (-380)	-632	17 (39)

Data for the Berendsen simulation are given for each protein. Langevin simulation data are given in parentheses.

^*Number of trajectories (of 10) that yielded native-like structures

^†Minimum (Min), maximum (Max), and average (Ave) folding time over all trajectories

^‡Minimum rmsd value over all trajectories

^§rmsd of the lowest-energy structure found by the CSA method

^¶Minimum potential energy over all trajectories

^∥Lowest energy found by the CSA method

^**CPU time per 1 ns of simulations on a single AMD Athlon MP 2800+ processor

For the successful simulations, the average folding times are of the order of nanoseconds, whereas it is known from experiment that the folding time is of the order of microseconds even for the fastest folders (6). This result confirms our observation (M.K., A.L., and H.A.S., unpublished data) that the time scale of UNRES dynamics is approximately three orders of magnitude larger than that of all-atom dynamics, owing to averaging the secondary degrees of freedom, which usually correspond to fast motions. Except for 1E0G, the folding time is shorter for simulations with the Berendsen thermostat compared with the Langevin dynamics simulations even with low-friction coefficients. The reason for this result is most probably that there are no explicit stochastic and friction forces [the latter oppose especially concerted motion of larger fragments (36) such as, e.g., α-helices] in simulations with the Berendsen thermostat, and maintaining the average temperature is achieved by scaling down the velocities. It can also be seen (Table 1) that the CPU time required per 1 ns of Berendsen dynamics is up to two times shorter than that required for Langevin dynamics, which is caused by the fact that more algebraic operations are involved in a single step of Langevin dynamics compared with the Berendsen dynamics.

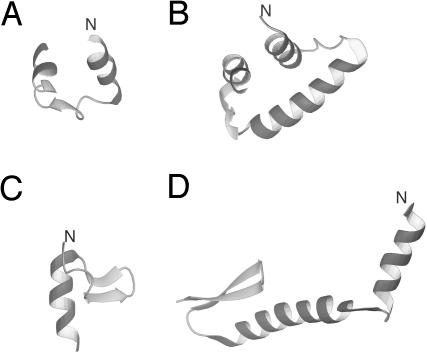
Of the three β and α+β proteins, only 1E0G folded to the native structure, whereas 1E0L and 1IGD did not. The most persistent structures obtained in MD simulations of 1E0L and 1IGD were α-helical; for 1E0L this was an HTH motif and for 1IGD, a distorted three-helix bundle (these structures are shown in Fig. 3 A and B, respectively). Short-lived structures appeared with one of the hairpins of 1E0L and with the C-terminal hairpin for 1IGD but only in a few runs; examples of such structures are shown in Fig. 3 C and D, respectively. Such partially folded structures appeared early in a run (after <1 ns) and then changed to fully α-helical structures that persisted until the end of a run. It therefore can be safely stated that the failure to fold 1E0L and 1IGD was not caused by insufficient simulation time.

Fig. 3.

Examples of misfolded structures of 1E0L and 1IGD obtained during MD simulations. (A and B) The persistent all-helical structures of 1E0L and 1IGD, respectively. (C) A short-lived most native-like structure of 1E0L. (D) A short-lived most native-like structure of 1IGD.

The fact that some of the proteins considered do not fold to the native structures in MD simulations, although their global minima are native-like, can be understood easily. When parameterizing the force field, we used the CSA method for the generation of the decoy sets. The CSA method considers only energy minima and is focused strictly on structures with a low potential energy. From Table 1 it can be seen that the lowest potential energies attained in MD runs are at least ≈160 kcal/mol higher than the lowest potential energies found by the CSA method (27). This difference occurs because of thermal motion that is ignored when using global optimizers such as CSA, which implement local energy minimization. Our present method of hierarchical optimization of a protein energy landscape (25, 26) uses the CSA method to generate decoys and, consequently, largely ignores the entropy factor. It should be noted that both 1E0L and 1IGD contain β-hairpins, the formation of which involves a particularly severe decrease of entropy because of the formation of long-range contacts compared with the formation of an α-helix. The successful folding of 1E0G can be explained by the fact that the strands are stabilized by packing to α-helices; this feature was even implemented when deriving the 4P force field by the hierarchical method (26). Analysis of successful folding trajectories of 1E0G fully confirms this observation.

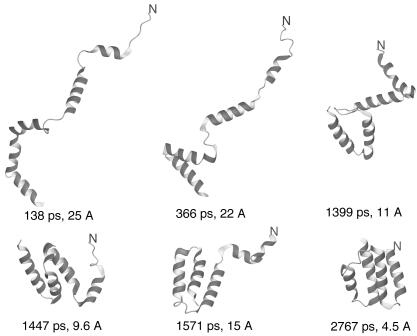
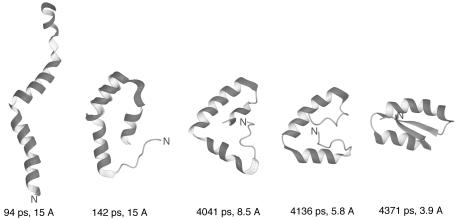
In Fig. 4, we present a sample Langevin dynamics trajectory of 1CLB with the 4P force field. The very initial stage of folding when α-helical segments are formed in the initially fully extended chain is not shown for the sake of clarity of presentation. This initial stage takes <100 ps, on average, in the folding simulations of the model Ala₁₀ polypeptide (M.K., A.L., H.A.S., and A. Jagielska, unpublished data). It can be seen in Fig. 4 that folding occurs in a stepwise manner starting from the formation of loose α-helices, through the formation of the C-terminal EF-hand motif followed by the formation of the C-terminal three-helix bundle and, finally, the formation of the N-terminal α-helix and its packing to the final structure composed of two EF-hand motifs.

Fig. 4.

Example of a fast folding pathway of 1CLB obtained in Langevin dynamics simulations. The N terminus of the chain is marked for tracing purposes.

An example of a successful folding trajectory of 1E0G (an α+β protein) is presented in Fig. 5. It can be seen that folding starts with the formation of α-helical fragments in the whole chain including those parts that form the β-sheet in the native structure. These very early structures have a bent helix in the middle part, which is the beginning of the formation of the native HTH motif. Subsequently, the initially helical N-terminal and the C-terminal parts start to pack against the middle helices and straighten. This intermediate stage persists through most of the folding trajectory. Late in folding, the strands start to pack to form a β-sheet; Fig. 5 shows that initially incorrect packing, which would lead to a parallel β-sheet, appeared. Last, the protein leaves the short-lived misfolded intermediate and forms the native-like structure. It seems that the stable β-sheet formed here because favorable interactions induce extended conformation in the N- and the C-terminal parts of the chain.

Fig. 5.

Example of a folding pathway of 1E0G obtained in Langevin dynamics simulations. The N terminus of the chain is marked for tracing purposes.

Table 1 shows that even for the largest protein considered, 1CLB, it takes only 40 h on a single AMD Athlon MP 2800+ processor to run 20 ns of Langevin simulations. It should be noted that the largest folding time for 1CLB with the 4P force field was 3.6 ns of simulations; therefore, 20 ns is enough for extensive folding simulations. Consequently, it is possible to simulate the folding pathways of proteins in real time with the UNRES/MD approach.

Conclusions

We applied the MD method with the UNRES model of polypeptide chains to a set of test proteins with sizes of 28–75 aa and different folding types. The force field used in the study was parameterized by using the decoy set generated by the CSA method (27), i.e., not tuned to MD simulations. MD runs for α-proteins successfully yielded native-like structures in most cases, although not all trajectories converged to native-like structures. However, we found that the two proteins containing β-hairpins [1E0L (a three-stranded antiparallel β-sheet) and 1IGD (an α+β protein)] did not converge to the native structures, and α-helices were persistently formed instead of β-hairpins, although the global energy minima of these proteins are native-like with this force field (and CSA search procedure) in our previous study (25, 26). We attribute this result to the fact that the decoy sets used in force-field parameterization consisted of energy minima, and therefore the entropy factor was largely unaccounted for in parameterization. Therefore, the UNRES force field must now be reparameterized for MD simulations. With the advantage of MD-generated ensembles, not only qualitative information about the sequence of folding events but also quantitative kinetic and thermodynamic characteristic of folding can now be included.

Even given the limitation of the current force field, it can be stated safely that the UNRES/MD approach will enable us to carry out simulations of protein folding in real time. First, although simplified, UNRES is fully based on the physics of protein interactions and, unlike the Gō-like potential, need not be parameterized every time to fold a specific protein. Second, the reduction of the number of degrees of freedom results in both reduction of computational cost and lengthening of the time scale; it took only a few hours of computer time to fold 1CLB (a 75-residue protein). Based on the comparison of all-atom and UNRES MD using a mean first-passage time analysis of the model Ala₁₀ polypeptide (M.K., A.L., H.A.S., and A. Jagielska, unpublished data), UNRES provides a three- to four-order-of-magnitude speed-up relative to implicit- and explicit-solvent all-atom MD simulations: (i) because of averaging over secondary degrees of freedom, the UNRES time scale is approximately four times larger than the all-atom time scale (M.K., A.L., H.A.S., and A. Jagielska, unpublished data), and (ii) for the same reason, the cost of computing the UNRES energy is by orders of magnitude lower than the cost of computing the all-atom energy. Therefore, with the advantage of parallel processing, it is possible to run even thousands of folding trajectories of a protein in a few hours of real time, which will enable us to explore folding pathways and derive the distribution of folding times. It can be noted also that all-atom folding pathways can be obtained by converting the key coarse-grained structures into an all-atom representation using the method developed in our laboratory (43, 44) and carrying out limited all-atom MD simulations for each of them; for example the “milestone” method developed recently by Faradjian and Elber (11) seems to be very appropriate for this task.