A comprehensive allometric analysis of 2nd digit length to 4th digit length in humans

Abstract

It has been widely reported that men have a lower ratio of the 2nd and 4th human finger lengths (2D : 4D). Size-scaling ratios, however, have the seldom-appreciated potential for providing biased estimates. Using an information-theoretic approach, we compared 12 candidate models, with different assumptions and error structures, for scaling untransformed 2D to 4D lengths from 154 men and 262 women. In each hand, the two-parameter power function and the straight line with intercept models, both with normal, homoscedastic error, were superior to the other models and essentially equivalent to each other for normalizing 2D to 4D lengths. The conventional 2D : 4D ratio biased relative 2D length low for the generally bigger hands of men, and vice versa for women, thereby leading to an artefactual indication that mean relative 2D length is lower in men than women. Conversely, use of the more appropriate allometric or linear regression models revealed that mean relative 2D length was, in fact, greater in men than women. We conclude that 2D does not vary in direct proportion to 4D for both men and women, rendering the use of the simple 2D : 4D ratio inappropriate for size-scaling purposes and intergroup comparisons.

1. Introduction

Relative index finger length (2D : 4D), calculated as the ratio between the length of the 2nd (2D) and 4th (4D) fingers, has interested researchers for more than a century [1]. In the human hand, three phenotypes have been defined: index shorter than ring finger (i.e. 2D < 4D), index and ring finger being equal in length (i.e. 2D = 4D) and index longer than ring finger (i.e. 2D > 4D) [2].

The 2D : 4D ratio has been reported to be associated with a broad range of human characteristics, such as behavioural traits, fertility, handedness, sexual orientation, sex-related diseases and sports performance [3–9], although effect sizes are generally low to moderate. Sex differences in the 2D : 4D ratio have been investigated extensively [7] where men tend to have a lower 2D : 4D ratio than women [10]. In an important study on mice, endocrine signalling examined during a narrow window of embryonic exposure to differential levels of androgens and oestrogens was found to be associated with the 2D : 4D ratio [11]. Nevertheless, an important question is whether the index is independent of its denominator, which is an essential requirement for the accuracy of the 2D : 4D ratio, and indeed any index which normalizes one variable for another variable [12].

In the biological sciences, the construction of a simple ratio, of the form Y/X, is a common approach used to derive a standardized variable of an examined trait where the numerator, the criterion variable, is typically divided by a denominator, the predictor variable [12]. For example, oxygen uptake is conventionally normalized per-ratio standards to body weight in human samples [13]. Likewise, left ventricular ejection fraction is calculated as the ratio of stroke volume to end-diastolic volume and represents the traditional measure of contractility of the mammalian heart [14]. Additionally, previous studies in evolutionary biology revealed that the neocortex ratio, which is the resultant of the neocortex to brain size ratio, carries information about the number of social relationships in primates [15]. Nevertheless, the empirical and theoretical shortcomings of simple ratios as size-adjustment approaches are noteworthy [12,13,16–19]. Since a size-proportion ratio seldom normalizes the Y variable consistently across the measurement range of the X variable [12], the unappreciated residual size-correlation inherent to ratiometric indices has, in general, led researchers to formulate untenable biological explanations [18,19].

When a ratio is still substantially correlated with its denominator then, as we have demonstrated with a number of other physiological ratios [20], biased inferences can result. Another indicator of the inappropriateness of ratios is a substantial non-zero Y-intercept in the linear relationship between numerator and denominator [19], and such a non-zero intercept has been reported for 2D : 4D [10,21]. While there have been attempts to partition out the confounding effects of differences in the length of 4D to obtain unbiased interpretations of the 2D : 4D ratio [21], a thorough allometric scrutiny of this morphometric index has not been published to date.

Since Julian Huxley's seminal study on the chela size of the Uca pugnax in 1924 [22], methods for allometric scaling have entailed, to a great extent, logarithmic transformations of the original measurements [23]. Nonetheless, logarithmic modelling might introduce an undetected systematic bias into calculations [24], and, importantly, yields a mathematical function not describing the biological relationship between the examined observations in the arithmetic domain [23]. Recent advances in the analytical procedures for studies of allometry and scaling now permit a more comprehensive appraisal of linear and nonlinear regression models based on the underlying assumptions and nature of random error [25].

Therefore, we aimed to compare, using a formal information-theoretic approach, 12 candidate models for scaling untransformed 2D and 4D lengths, and ascertain how different model selections influence the quantification of sex differences in relative index finger length in humans.

2. Material and methods

The study sample of 416 participants comprised data collected directly by the researchers from 154 men and 262 women (electronic supplementary material, files 1 and 2). The study design, methods and ethics procedures used to obtain the data have been previously described [21]. This study also adhered to the ethics and research governance procedures at Teesside University. Separate analyses were conducted for the right and left hands. Measures of centrality and dispersion were expressed as mean ± standard deviation (s.d.).

Type I regression procedures [26] and the analytical framework outlined in a recently published article on methods for allometric analysis [25] were used to examine the morphometric relationship between the fingers (electronic supplementary material, file 3). Briefly, we performed nonlinear regression analyses of untransformed observations using the Model Procedure in SAS v. 9.4 to fit three sets of four models, involving two straight lines and two power functions, with multiplicative, lognormal, heteroscedastic error and additive, normal, homoscedastic or heteroscedastic error, respectively [25]. Parameter estimates for each model were solved using an iterative protocol based on the Marquardt procedure [25]. Participants' sex was also included as a categorical covariate in the statistical models. A common slope was fitted for the whole sample when the effect of the sex × 4D interaction term was found not to be substantial. Sex differences in the slope would indicate a fundamentally different relationship between 2D and 4D and preclude comparisons between men and women [27]. The Akaike information criterion (AIC) was adopted to assess the relative quality of each candidate model [28]. The ΔAIC from the estimated best model (i.e. the model with the lowest AIC value; ΔAIC = 0) was judged according to the following scale: 0–2, essentially equivalent; 2–7, plausible alternative; 7–14, weak support; greater than 14, no empirical support [28]. Parameter estimates were interpreted from the best/essentially equivalent models for the examined data. Regression parameters are reported as point estimates and 95% confidence limits (CL). All statistical analyses were conducted using SAS (PROC MODEL, SAS^® v. 9.4; SAS Institute, Inc., Cary, NC, USA), and graphs were produced using IBM Statistical Package for the Social Sciences (SPSS) Statistics v. 23.0 (SPSS, Chicago, IL, USA).

3. Results

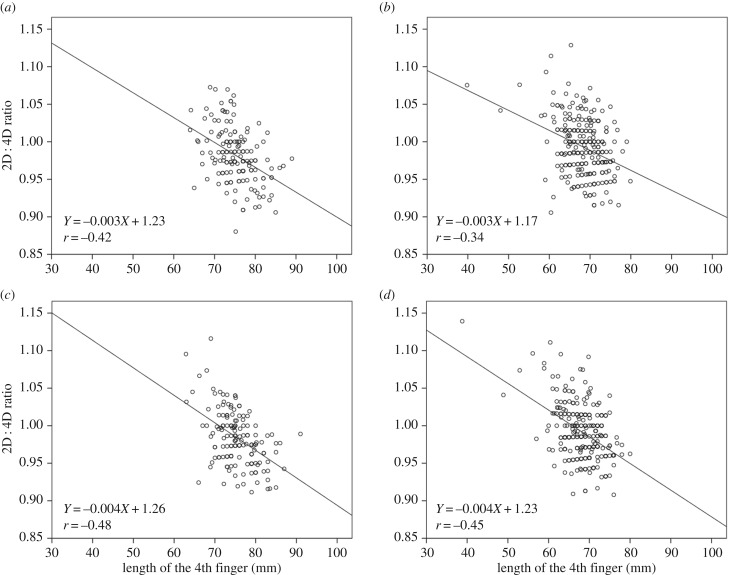
As expected, mean lengths of 2D and 4D were larger in men than women, irrespective of the examined hand (table 1). For the right hand, the substantial, inverse correlations between the 2D : 4D ratio and 4D in both sexes indicated that the ratiometric index is not normalizing for 4D length uniformly across the measurement range (figure 1a,b). The correlation coefficients (95%CL) describing the relationship between the index and its denominator were found to be −0.42 (−0.56 to −0.27) and −0.34 (−0.45 to −0.22) in men and women, respectively. The mean 2D : 4D ratio was greater in women (0.993 ± 0.037) than in men (0.982 ± 0.037), with the 95%CL for this sex difference being 0.004 to 0.019.

Table 1.

Descriptive characteristics of the study participants (n = 416). Values are expressed as mean ± s.d., with range in parentheses.

variable	men (n = 154)	women (n = 262)
right hand
2nd finger length, mm	73.82 ± 4.19 (61.00 to 87.00)	67.77 ± 4.60 (42.80 to 79.00)
4th finger length, mm	75.27 ± 4.61 (64.00 to 89.00)	68.31 ± 4.76 (39.80 to 79.90)
2D : 4D ratio	0.982 ± 0.037	0.993 ± 0.037
2D : 4D normalized indexa	0.993 ± 0.034	0.986 ± 0.035
2D : 4D normalized indexb	0.994 ± 0.033	0.986 ± 0.035
2D : 4D normalized indexc	2.328 ± 0.079	2.310 ± 0.081
adjusted 2nd finger length, mma	70.37 ± 2.40	69.79 ± 2.46
adjusted 2nd finger length, mmb	70.34 ± 2.51	69.82 ± 2.38
left hand
2nd finger length, mm	74.13 ± 4.10 (61.00 to 90.00)	67.46 ± 4.36 (44.20 to 78.00)
4th finger length, mm	75.42 ± 4.73 (62.90 to 91.00)	68.08 ± 4.79 (38.80 to 80.00)
2D : 4D ratio	0.984 ± 0.036	0.992 ± 0.037
2D : 4D normalized indexa	1.000 ± 0.032	0.983 ± 0.033
2D : 4D normalized indexb	0.996 ± 0.032	0.985 ± 0.034
2D : 4D normalized indexc	2.775 ± 0.090	2.730 ± 0.091
adjusted 2nd finger length, mma	70.67 ± 2.28	69.49 ± 2.32
adjusted 2nd finger length, mmb	70.64 ± 2.36	69.51 ± 2.24

^aTwo-parameter power function with normal, homoscedastic error.

^bStraight line with intercept and normal, homoscedastic error.

^cPower function ratio. The normalized indices (footnotes a and b) were derived directly from the model residuals [12] in raw arithmetic space, with the 2D : 4D ratio or 2D as the dependent variable and 4D and sex as predictors. Each participant's residual was added to the predicted mean ratio for each sex at the mean 4D length in the whole sample, to obtain an adjusted 2D : 4D ‘ratio’ or 2D free from the influence of 4D length. The normalized index (footnote c) was directly derived from the ratio of 2D to 4D raised to the power of 0.80 and 0.76 in the right and left hand, respectively.

Figure 1.

Scatterplots showing the negative correlation between the 2D : 4D ratio and the length of the 4D for men (a,c), and women (b,d) in the right and left hand, respectively.

Following our formal comparisons, in the right hand, the two-parameter power function with normal, homoscedastic error, of the form Y = a·X^b, was found to be the best out of 12 competing models (table 2). The allometric exponent (b) describing the nonlinear relationship between 2D and 4D was 0.80 (0.74 to 0.85). A ratio index is free of bias only if this exponent is 1. The 95%CL for the difference in exponent between males and females was −0.21 to 0.02. Using this most appropriate size-scaling model, women displayed a lower and not higher, mean 2D : 4D than men (table 1). The model with straight line, intercept and normal homoscedastic error was found to be ‘essentially equivalent' to the best model: Y = 13.59 + 0.79X. The 95%CL for the Y-intercept was 10.19 to 16.99. Table 2 reveals that the three-parameter power function (relaxing the constraint of a zero Y-intercept in the two-parameter model) was also ‘essentially equivalent'.

Table 2.

Statistical models fitted to untransformed data for scaling 2D (mm) to 4D (mm) in the right hand. AIC, Akaike's information criterion; ΔAIC, Akaike difference.

model	AIC	ΔAIC	inference
Straight line, no intercept, with lognormal heteroscedastic error	1984.1	61.0	no empirical support
Straight line, no intercept, with normal, heteroscedastic error	1983.7	60.6	no empirical support
Failed to converge. Convergence criterion changed to 0.011
Straight line, no intercept, with normal, homoscedastic error	1979.9	56.8	no empirical support
Three-parameter power function with normal, heteroscedastic error	1929.0	5.9	plausible alternative
Failed to converge. Convergence criterion changed to 0.014
Two-parameter power function with normal, heteroscedastic error	1928.8	5.7	plausible alternative
Failed to converge. Convergence criterion changed to 0.013
Straight line, intercept, with lognormal heteroscedastic error	1928.1	5.1	plausible alternative
Straight line, intercept, with normal, heteroscedastic error	1927.3	4.3	plausible alternative
Failed to converge. Convergence criterion changed to 0.01
Three-parameter power function with lognormal, heteroscedastic error	1926.5	3.5	plausible alternative
Failed to converge. Equation rearranged and converged
Two-parameter power function with lognormal, heteroscedastic error	1925.9	2.8	plausible alternative
Straight line, intercept, with normal, homoscedastic error	1924.6	1.6	essentially equivalent
Three-parameter power function with normal, homoscedastic error	1923.8	0.8	essentially equivalent
Failed to converge. Equation rearranged and converged
Two-parameter power function with normal, homoscedastic error	1923.1	0	best

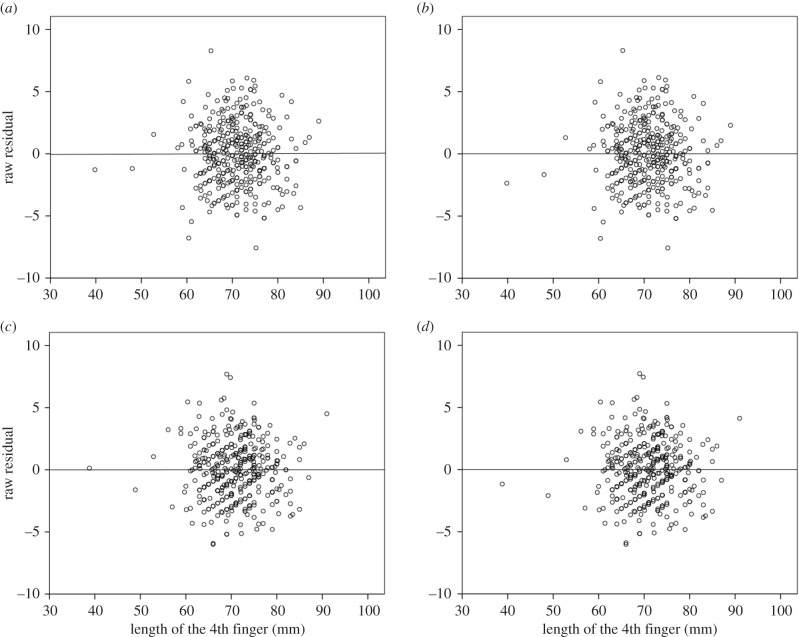
In the left hand, we found negative correlations between 2D : 4D and 4D of similar magnitudes to those observed in the right hand (figure 1c,d). The correlation coefficient between the 2D : 4D ratio and 4D was −0.48 (−0.62 to −0.33) in men, and −0.45 (−0.56 to −0.35) in women. Again, women had a greater mean 2D : 4D ratio than men (0.992 ± 0.037 versus 0.984 ± 0.036), with the 95%CL for this difference being 0.001 to 0.016. The AIC criteria revealed the rectilinear function with intercept and normal, homoscedastic error (Y = 16.10 + 0.75X) to be the best model in the set of candidates (table 3). The 95% confidence interval for the positive Y-intercept was 12.96 to 19.25. The 95%CL for the difference in the regression slope between the sexes was −0.17 to 0.03. The two-parameter power function with normal, homoscedastic error was found to be ‘essentially equivalent’ to the best model, with an allometric exponent of 0.76 (0.71 to 0.80). The 95%CL for the sex difference in the exponent was −0.17 to 0.04. The adjusted mean 2D : 4D estimates from the best/essentially equivalent models were found, again, to be lower among women than men (table 1). In line with AIC outcomes, the model residuals were well behaved in both hands (figure 2).

Table 3.

Statistical models fitted to untransformed data for scaling 2D (mm) to 4D (mm) in the left hand. AIC, Akaike's information criterion; ΔAIC, Akaike difference.

model	AIC	ΔAIC	inference
Straight line, no intercept, with lognormal heteroscedastic error	1978.0	103.8	no empirical support
Straight line, no intercept, with normal, heteroscedastic error	1971.1	96.9	no empirical support
Failed to converge. Convergence criterion changed to 0.013
Straight line, no intercept, with normal, homoscedastic error	1962.3	88.1	no empirical support
Three-parameter power function with normal, heteroscedastic error	1882.0	7.8	weak support
Failed to converge. Convergence criterion changed to 0.014
Three-parameter power function with lognormal, heteroscedastic error	1880.8	6.6	plausible alternative
Two-parameter power function with normal, heteroscedastic error	1880.5	6.3	plausible alternative
Failed to converge. Equation rearranged and converged
Straight line, intercept, with lognormal heteroscedastic error	1879.1	4.9	plausible alternative
Two-parameter power function with lognormal, heteroscedastic error	1878.8	4.6	plausible alternative
Straight line, intercept, with normal, heteroscedastic error	1877.8	3.6	plausible alternative
Failed to converge. Convergence criterion changed to 0.014
Three-parameter power function with normal, homoscedastic error	1876.3	2.1	plausible alternative
Failed to converge. Equation rearranged and converged
Two-parameter power function with normal, homoscedastic error	1874.3	0.1	essentially equivalent
Straight line, intercept, with normal, homoscedastic error	1874.2	0	best

Figure 2.

Raw residuals against the untransformed 4D measures from the two-parameter power function (a,c) and linear regression (b,d) model with normal, homoscedastic error in the right and left hand, respectively.

4. Discussion

Although the 2D : 4D ratio has been selected to study the association between differences in relative index finger length and biological traits, the substantial residual dependency of the 2D : 4D ratio on its denominator (4D) hinders the understanding of the true relationship between the 2D and 4D in human samples (figure 1). Accordingly, the traditional approach of normalizing 2D for differences in 4D length as simple ratio statistics fails to serve this purpose in an unbiased manner across the typical measurement range of finger lengths in both men and women.

Notably, the outcomes of the British Broadcasting Corporation (BBC) study were seemingly interpreted as an additional line of evidence supporting the description of a sexual dimorphism based on sex differences in the 4D linear regression slope [10]. Nevertheless, the Y-intercept value, and not the linear regression slope, is the criterion parameter in linear regression models indicating the validity of a ratio statistics [19]. Not only did the inverse association between the 2D : 4D ratio and 4D we observed highlight the spurious size-dependence of the index (figure 1), but the uncontrolled confounding effects of morphological differences in 4D length illustrated the degree of bias in 2D : 4D estimates. Since the underlying assumptions of ratios were found to be violated [12,19], the notion of a sexually dimorphic index established on the previously reported sex differences in the 2D on 4D linear regression slope [10] is, therefore, untenable.

In the human fetus, the differentiation in the growth patterns of the fingers appears at a gestational age of approximately nine weeks [29]. The mechanistic interplay between androgen and oestrogen signalling regulates the network of genes involved in chondrocyte proliferation and, therefore, the morphological relationship between the fingers [11]. Notwithstanding these mechanisms, the mathematical flaws of the 2D : 4D ratio alter the magnitude of sex differences in relative index finger length and, consequently, lead to erroneous interpretations. The molecular pathways obviously shed light on the absolute differences in the length of the fingers between the sexes [11], whereas any interpretations about casual associations grounded on the biased size-proportion 2D : 4D ratio are limited by non-biological factors introducing artefactual variability.

The large ΔAIC for the ratio standards models (straight line, no intercept) in both hands demonstrated that these models have essentially no support (tables 2 and 3). In particular, our study provides a comprehensive and novel approach for deriving 2D : 4D measures standardized for differences in the 4D working directly in the raw arithmetic data space. After simple allometric or linear regression-standards normalization, the mean 2D : 4D estimates from the best models were found to be higher in men than women, irrespective of the examined hand and modelling approach (table 1). Nonetheless, the drawbacks of power-function ratios are well established [12]. While power-function ratios might turn out to successfully eliminate size correlations, they paradoxically introduce size-related distortions in distributional patterns compared to modelling morphometric relationships using raw data [12]. Accordingly, the adjusted 2D : 4D ratios and adjusted 2D length we derived from the model residuals were both independent of 4D length and materially unaffected by distributional distortions [12]. The adjusted 2D : 4D indices were derived according to the empirical and theoretical assumptions regarding the use of residuals, which reflect the true biological variability of the observed values independent of body size [12]. Our approach involved modelling the 2D : 4D ratio as the dependent variable, adjusting for 4D length using the residuals method [12], and then obtaining an adjusted ratio free from the influence of 4D length. Importantly, this size-adjustment approach is mathematically equivalent to modelling 2D length as the dependent variable [30], with the advantage of providing a properly adjusted ratio index rather than an expression of 2D length free from the influence of 4D length. The mathematical equivalence and concordance between these analyses ultimately substantiate the failure of simple ratio models (tables 2 and 3) to provide unbiased 2D : 4D estimates (figure 1) [12,30]. Furthermore, the measurement of 2D and 4D lengths carried out by trained anthropologists is another key strength of the present study that minimizes any random variability in the examined data [21]. Our results reflect a long-standing wealth of evidence in the biological literature, whereby relationships between morphometric variables seldom vary in a directly proportional fashion [12,13,16– 19].

We, therefore, point out that the formulation of this index as a simple ratio might cloud any potential associations between the relative length of the fingers and other human traits, particularly sex differences. To date, the formulations of simple ratios as the 2D : 4D have been superseded by more comprehensive and accurate allometric analyses for addressing size-scaling problems [25]. If the relationship between the 2D and 4D was found to be directly proportional, for a given value of 4D the 2D : 4D ratio would have predicted the same value of the outcome compared with what we observed after proper modelling of differences in the denominator of the index.

Our study demonstrates that, in human samples, failure to statistically control for the true covariation patterns associated with the 4D in the 2D : 4D ratio provides biased estimates of differences between the sexes and, consequently, a spuriously sexually dimorphic index.

Data accessibility

The raw data supporting this article and statistical codes used to perform nonlinear regression analyses have been provided as part of the electronic supplementary material.

Authors' contributions

L.L., A.M.B. and G.A. contributed to the design of the paper, conducted statistical analyses, wrote and revised the manuscript. L.K. and J.F. provided the examined data and contributed to the manuscript revision. K.L.W. contributed to the revision of the manuscript. All authors approved the final version of the manuscript and agree to be accountable for the content herein.

Competing interests

We declare no competing interests with regard to this publication.

Funding

No funding was received to conduct and/or prepare this manuscript.