Island Rule, quantitative genetics and brain–body size evolution in Homo floresiensis

Abstract

Colonization of islands often activate a complex chain of adaptive events that, over a relatively short evolutionary time, may drive strong shifts in body size, a pattern known as the Island Rule. It is arguably difficult to perform a direct analysis of the natural selection forces behind such a change in body size. Here, we used quantitative evolutionary genetic models, coupled with simulations and pattern-oriented modelling, to analyse the evolution of brain and body size in Homo floresiensis, a diminutive hominin species that appeared around 700 kya and survived up to relatively recent times (60–90 kya) on Flores Island, Indonesia. The hypothesis of neutral evolution was rejected in 97% of the simulations, and estimated selection gradients are within the range found in living natural populations. We showed that insularity may have triggered slightly different evolutionary trajectories for body and brain size, which means explaining the exceedingly small cranial volume of H. floresiensis requires additional selective forces acting on brain size alone. Our analyses also support previous conclusions that H. floresiensis may be most likely derived from an early Indonesian H. erectus, which is coherent with currently accepted biogeographical scenario for Homo expansion out of Africa.

1. Introduction

Several studies since the early 1960s have investigated shifts in body size in insular environments, a pattern known as Island Rule, in a comparative and macroecological context [1–8]. These studies evaluated the patterns leading to insular dwarfing or gigantism by correlating body size shifts between insular species and their mainland relatives to several island characteristics. These factors may trigger a complex chain of adaptive events that, over relatively short evolutionary time, also drive shifts in body size [9]. It is arguably difficult to perform a direct analysis of the natural selection forces behind body size differentiation, mainly because the kind of detailed information about island colonization scenarios, such as the timing of isolation and the genetic–demographic parameters necessary to evaluate the strength of selection, are often hard to collect. However, if such data are available, the study of the Island Rule may move from the mere description of a pattern, to the analysis of its process, which is one of the main challenges in the macroecology research agenda [10,11].

The diminutive Hobbit man, Homo floresiensis, was described in 2004 as a small-bodied, exceptionally small-brained hominid that appeared on Flores Island some 700 kya, and survived up to 90–60 kya. Flores Man stands out as one of the most exciting, yet controversial, discoveries in the history of research on human evolution [12–14]. In a sense, most of the controversy on H. floresiensis regards the possibility that it just represents a population of H. erectus that underwent insular dwarfism. Despite initial discussions [15], most studies now recognize H. floresiensis as a valid species, although explaining its unusual morphology, and especially its exceptionally small brain, by insular dwarfism alone is far from universally accepted.

The magnitude of body (and brain) size dwarfism in H. floresiensis is within the range of reduction in insular primates [16–18], and the Island Rule applies to other species in the fossil record of Flores [19]. However, some studies have suggested that H. floresiensis may be anatomically closer to early, small-bodied African forms of Homo, such as H. habilis and H. rudolfensis [20]. For instance, two recent cladistics analyses based on cranial characters provided conflicting results, either supporting that H. floresiensis belongs to the H. erectus clade [21] or suggesting an older ancestry, closer to basal African early Homo (although the H. erectus ancestry cannot be ruled out from these analyses, [22]). If H. floresiensis originated from an early Homo, its small body and brain needs not to be explained by the Island Rule, and would just reflect deeper ancestry followed by little evolutionary change. However, assuming an early Homo ancestry would have deep implications for the so-called ‘Out of Africa I’ hypothesis, which portrays H. erectus or related forms as the first hominin to leave Africa [23]. On the other hand, assuming H. floresiensis really derives from H. erectus, it remains to be understood how insularity drove body size shifts in Flores Man, and how it affected its brain size and cognitive ability [24].

Given the available information about genetic and demographic parameters in humans, as well as about colonization of Flores and the hominin fossil record, it is now possible to investigate the potential for insular dwarfism in H. floresiensis using classical quantitative evolutionary genetic models [25]. Here, we used simulations to evaluate the multiple possible trajectories of body and brain size dwarfing between H. erectus and H. floresiensis, under a wide range of demographic and genetic parameters. We started by testing the hypothesis that the differentiation between the two species was due to neutral evolution, under alternative colonization scenarios of Flores Island. Given that we consistently rejected this hypothesis, we moved beyond estimating the strength of natural selection, and assessed its plausibility by comparison to extant natural populations. Finally, we evaluated how natural selection on body size leads to a correlated response in brain size, and whether dwarfism per se explains the exceptionally small brain of H. floresiensis. We found that dwarfing in H. floresiensis is best explained by strong directional selection over a relatively short time, and that, in agreement with a recent study based on an allometric analyses of brain–body size variation in fossil hominids [26], body size reduction alone would produce a larger brain than observed in Flores Man.

2. Material and methods

(a). Species data

Our goal was to analyse the differences in body weight, in kilogram, and brain volume, in cubic centimetres (which we refer to as body size and brain size throughout the paper) between H. floresiensis and its potential ancestor, which likely was a form of H. erectus [26,27]. This species was present in the region at about 1 Ma, whereas australopiths or earlier forms of Homo are more than 1 Myr older and have never been found outside Africa. On the other hand, anatomically modern humans arrived in Indonesia much later than the earliest dates currently available for H. floresiensis (which is around 700 kya, [13,14]). This means taking brain and body size values of H. erectus (sensu lato) as the ancestor of Flores Man is the most parsimonious assumption and was our starting hypothesis since. Even so, given ongoing discussion and uncertainty surrounding H. floresensis ancestry [20–22], we also explored the likelihood that the brain of Flores Man was small just because it derived from a relatively small-brained ancestor such as H. habilis (see electronic supplementary material, text S1).

We assumed a mean initial body size value of 27 kg for H. floresiensis and about 50 kg for H. erectus [28,29]. These values (as well as brain size; see below) were transformed to natural logarithms to stabilize variance and normalize the statistical distribution of the traits for allometric analyses of brain–body size relationships [30–32]. Of course, there is uncertainty in these values for the ancestor and descendent populations, especially in the sense of assuming the skull of H. floresiensis (LB1) to be a somewhat ‘typical’ specimen [28]. We started each simulation by randomly sampling the initial body size value from a normal distribution with these means and 0.05 standard deviations in ln-scale [32], which corresponds to the coefficient of variation of 5% in the original scale (so that, on average, the variation within a species such as H. erectus, with on average 50 kg, falls between 45 and 55 kg in 95% of the simulations [28–34]). As for brain size, we used the most recent estimate for H. floresiensis brain volume, which is 426 cm³ [27], and mean ancestral values for H. erectus ranging from about 750 cm³ (around the mean values of early H. erectus, including Dmanisi forms classified by some as H. georgicus) up to 1000 cm³ (the mean brain volume of late H. erectus in China [33,34]).

(b). Quantitative evolutionary genetics models

We applied quantitative evolutionary genetics models to evaluate patterns in body size evolution in H. floresiensis. First, we used the mutation-drift equilibrium (MDE) [35] model, in which population divergence under neutral evolution is given by

2.1

where S² is the variance among populations, given by the squared difference between the means (in this case of two species or populations), N_e is the effective population size, h² is the heritability of the trait, 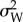is the within population phenotypic variance and t is the time since the divergence between the two species (in terms of number of generations). The F-value must be compared with a neutral expectation given by the F-distribution with 1 and infinite degrees of freedom, with non-significant F-values indicating neutral evolution (under a two-tailed test, F-values below 2.5% and above 97.5% of the F-distribution indicate stabilizing or directional selection, respectively).

As we consistently rejected neutrality (see Results), we used Lande's [36] model, whose goal is to estimate the strength of natural selection necessary to differentiate the mean values of the two species on a logarithmic scale (z) with a given within populations standard deviation σ, over a given time interval t:

2.2

Under this model, selection is modelled by truncation, and the b value actually represents the number of standard deviations from the mean phenotype in a normal distribution of phenotypes, so that the 1 − p-value associated with b gives the proportion of a population not reproducing per generation (while the rest of individuals are assumed to have equal fitness), in order to drive the differences between the two means (i.e. the selective mortality). The parameter b from equation (2.2) can be used to estimate the selection differential S in one generation by

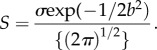2.3

In turn, S is used to derive the selection gradient β, describing the relationship between fitness and trait values [37], as

2.4

When traits are expressed in the ln-scale, this selection gradient β is equivalent to β_µ, the mean-standardized selection gradient, which represents the relative selection intensity on the trait in comparison to the selection on fitness [37]. The parameter β_µ is more appropriate than selection differentials to estimate selection in natural populations, making it easier to compare the minimum selection intensity necessary to differentiate H. floresiensis from its ancestor with previous empirical estimates [37–40].

We further used quantitative genetic models to investigate the patterns of correlated evolution between brain and body size, and how this links to dwarfism under the Island Rule. We started with the assumption that brain size reduction tracked body size decrease, without any selective pressures intervening on brain volume per se, or even counteracting it (but see [29] for an alternative model). Under this model of correlated evolution, the slope of brain size reduction α would be a function of the heritabilities of the two traits (i.e. brain and body sizes) and the genetic correlation r between them, as well as their standard deviations

2.5

where h_b and σ_b are the square-root of heritability and standard deviation of brain size within populations, respectively, and h_w and σ_w are the same parameters calculated for body size. The slope α can finally be used to calculate the expected brain size (EBS) and the expected ancestor brain size (EABS) for H. floresiensis by means of regression.

The model described in equation (2.5) assumes that brain size evolution occurred as a correlated response to body size evolution. However, it is possible to investigate the simultaneous selective pressures necessary to produce the differentiation between H. floresiensis and its ancestor for both traits. We used the multivariate extension of Lande's [36] model (see also [30,31]) to derive the vector of selection gradients β by

2.6

where G is the genetic covariance matrix and ΔZ is the vector of differences between body and brain size in the ln-scale between H. floresiensis and simulated ancestral values (see below).

(c). Genetic and demographic parameters

The application of quantitative genetic models requires knowledge of several population genetics parameters that may be difficult to estimate for fossil (or even current) species or populations, which is indeed one of the main criticisms of their application [41]. Previous attempts assumed values based on a few empirical estimates or ‘best guesses’ and tried evaluating how robust or consistent the outcomes were [42–44]. Studies about Homo provide a more realistic range of parameters to be used in the equations, as shown in table 1.

Table 1.

Range of parameters used in the quantitative genetic analysis of body size differentiation of H. floresiensis and the results of pattern-oriented modelling (POM) for brain–body size evolution, including mean parameter values and their standard deviations that gives the values of expected brain size (EBS) close of the observed in H. floresiensis' LB1 (400–450 cm³), and the standardized regression slope (equivalent to a partial multiple correlation) between each parameter in Lande's [30] equation and the expected brain size (b(EBS)). Significance of deviation from mean parameters was established by a randomization test.

model parameters	mean parameters	range in simulations	POM
			mean parameter	b(EBS)
heritability of body size	0.725	0.60–0.85	0.724 ± 0.072*	0.194
heritability of brain size	0.875	0.80–0.95	0.882 ± 0.042**	−0.095
CV of body size (log scale)	0.05	0.04–0.06	0.047 ± 0.005**	0.496
CV of brain size (log scale)	0.10	0.08–0.12	0.105 ± 0.011**	−0.451
effective population size, Ne	1525	50–3000
time (generations)	6000	2000–10 000
brain–body size correlation	0.445	0.32–0.60	0.449 ± 0.035**	−0.319
ancestral body size (kg)	50	45–55	50.6 ± 2.35*	0.535
ancestral brain size (cm3)*	875	750–1000	833 ± 65**	−0.317

*p < 0.05; **p < 0.01.

The heritability of body size is usually high within humans, but varies depending on how it is evaluated, ranging from about 0.6 up to 0.85 in most studies [45,46]. Heritability of brain size tends to be even higher, and usually above 0.8 and sometimes very close to 1.0 [47–50].

There is also a difference in the coefficients of variation among populations for these traits. We assumed for ln-transformed body size an average intraspecific standard deviation σ = 0.05 [32], which corresponds to the coefficient of variation in the original scale and that was set to range between 0.04 and 0.06 in our simulations (so that, on average, the variation within a species such as H. erectus, with on average 50 kg, falls between 45 and 55 kg in 95% of the simulations, thereby matching empirical observations [28]). For brain size, there seems to be a slightly larger variance in Homo natural populations. Considering the upper and lower limits usually found in H. sapiens (approx. 1000–1700), a coefficient of almost 40% would be found. Yet, values within population values tend to be smaller, with σ ranging from 0.08 to 0.12 [50,51].

Brain–body size correlations depend on the taxonomic level, being typically high in among species comparisons and in large groups (i.e. mammals), but much lower when dealing with a smaller phylogenetic scope. Although evolutionary brain–body size correlations are usually higher than 0.8 [52], the correlation in equation (2.5) should be the additive genetic correlated response in a segregating population. A recent meta-analysis for the brain–body size relationship [53] found a weighted average equal to 0.556 ± 0.035 (excluding estimates based on small sample sizes) for the phenotypic correlation between these two traits. We used this value in the correlated evolution models by considering the proportionality between phenotypic (P) and genetic (G) covariance matrices as G ∼ h²·P [54,55], where h² is the mean heritability of the two traits. By assuming h² = 0.8 for brain and body size (see the section on upper and lower limits described above), the mean genetic correlation is estimated at 0.445, varying between 0.32 and 0.6 for the minimum and maximum combinations of h² values for the two traits. This range matches previous estimates, and the mean is very close to the value reported by Holloway [50], who provided mean phenotypic correlations between brain and body size (both length and weight) around 0.44 for brain–body size, ranging from 0.37 to 0.52. Grabowski [29] recently estimated high evolutionary integration between these traits in modern humans (derived from genetic covariance matrix G) with a slightly larger correlation coefficient, equal to 0.532 (M Grabowski 2017, personal communication).

Population size on islands varies a lot under different island colonization scenarios, but given the evolutionary context we investigated upon, we assumed that in H. floresiensis the carrying capacity was quickly achieved, and therefore used a single population size value per species. Estimates of population density in hunter–gatherers range from 0.01 to about 3 individuals km⁻² [56]. More refined estimates by Binford [57] for tropical forest human populations fall within this wide interval, ranging from 0.016 and 0.92 individuals km⁻². Therefore, we assumed Binford's estimates as the upper and lower limits of density distribution (http://intersci.ss.uci.edu/wiki/index.php/Binford_hunter-gatherer_data). The application of MDE requires knowledge of the effective population size (N_e), which can confidently be approximated to 25% of census size [58]. Assuming that Flores is about 13 400 km² [59] and population density values typical for hunter–gatherers in tropical forests, we defined upper and lower of N_e for our simulations as 50–3000. Note that these estimates are probably low, especially considering that fossil evidence shows a long-term persistence of H. floresiensis, from 700 kya up to at least 50 kya. However, using low N_e values provides a conservative approach in that it favours the hypothesis of differentiation by drift over selection. Moreover, after dwarfing, populations of H. floresiensis could have been larger by virtue of the lower absolute metabolic requirements of small-bodied individuals [59]. Island size itself certainly varied over time, changing the area available for occupation, which should have been larger during marine low-stands typical of glacial times.

Revised dates suggest that the skull of H. floresiensis LB1 was at least 60 kya old [60] and some new fossils were dated at 700 kya [13], about 300 ky after initial colonization of Flores Island [14]. These estimates help to set upper and lower limits for the number of generations for divergence between the two mean trait values of interest here. This is probably the most difficult parameter to estimate, especially because of known variation in patterns of tempo and mode of body size evolution on islands [61]. We started by applying a range of 50 kya to 300 kya for the time because the divergence from H. erectus, because the new findings for H. floresiensis [13] at 700 mya now set a maximum divergence time at about 300 kya after the initial colonization of Flores about 1 mya. Even so, the selective pressure driving dwarfism are deemed to be fast, occurring in a punctuational mode very quickly after island occupation [61,62]. Thus, combining these limits for divergence time with an average generation length of ca 30 years [63,64] gives lower and upper limits of approximately 2000–10 000 generations for the divergence between H. floresiensis and H. erectus.

(d). Simulation parameters and pattern-oriented modelling

We relied upon studies about living Homo populations to get realistic population genetics parameter ranges (table 1; see electronic supplementary material, appendix S1 for a detailed description and the literature sources). However, uncertainty in designing the parameters space remains important. Fortunately, it is computationally feasible assuming a range of values around each parameter large enough to allow evaluating a posteriori how confident we are about natural selection (as opposed to genetic drift) as the main evolutionary mechanism driving the differentiation between H. floresiensis and H. erectus, and to see whether realistic selection strengths are able to produce such differentiation. To this aim, we evaluated which parameter combination produces the brain size observed in H. floresiensis, and how variation in parameter values affects the distribution of EBSs. We did this by using a pattern-oriented modelling (POM; [65,66]) approach. Under POM, we first observed the distribution of EBS under the full range of parameters, and then calculated the means of h², σ, r only for those simulations that resulted in EBS values within the 400–450 cm³ range (i.e. around the observed brain size of LB1), comparing these means to those obtained across the full range of simulations.

We initially used 50 000 random parameter combinations to calculate the statistics in equations (2.1)–(2.6), sampling within the ranges given above. We also used the same range of parameters h² and σ to calculate the α in brain–body size correlated evolution (equation (2.5)). This slope α was used to calculate the EBS based on the ancestral size (with a mean body size of 50 kg) and randomly selecting ancestral brain values in the range 750–1000 cm³, defining the intercept of the regression model. A multiple regression of EBS against values of h², σ, r and ancestral brain and body size across the simulations enables the evaluation of the importance of each individual parameter, and its contribution to the change in EBS value.

We also used the same α to answer an alternative question: what was the most likely expected ancestral brain size (EABS), starting from a 27 kg, 426 cm³ brain H. floresiensis individual [26]? The EABS is thus independent of any further assumption about the ancestor brain size (i.e. given that body size variation from late and early H. erectus is quite small) and depends only on quantitative genetic parameters such as heritabilities, population variation in brain and body size, and the genetic correlation between these two traits.

An R script [67] performing all simulations and calculations described above is available (see the electronic supplementary material for results).

3. Results

(a). Natural selection and genetic drift on body size evolution

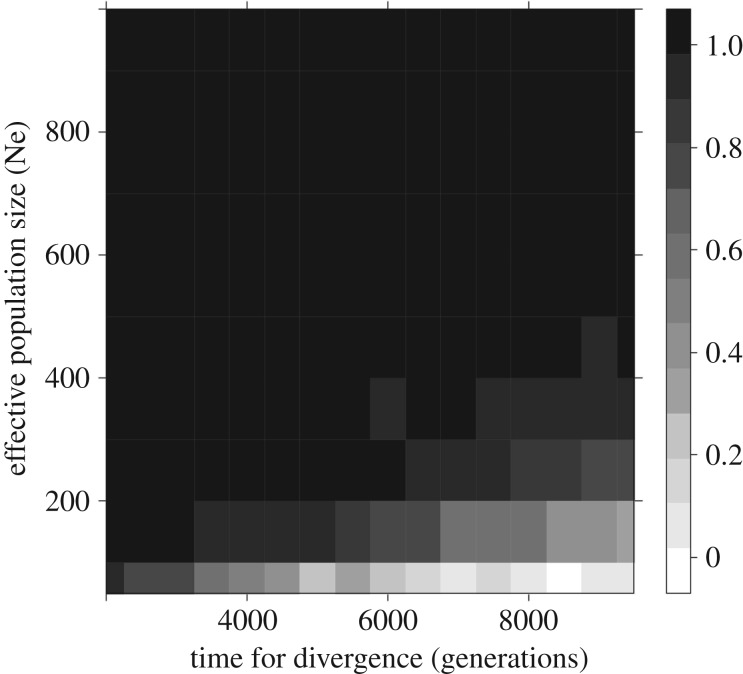
As anticipated above, the hypothesis of neutral evolution intervening on H. erectus to H. floresiensis body size evolution was rejected in 97% of the 50 000 simulations according to MDE model, except when an effective population size N_e as low as less than 100 individuals is combined with time for divergence exceeding 9000 generations (figure 1). At N_e > 200 neutrality is rejected with a frequency of 100% with time for divergence less than 5000 generations long. Thus, MDE convincingly suggests that directional selection is involved in the phenotypic differentiation between H. erectus and H. floresiensis under most colonization scenarios.

Figure 1.

Mapping the frequency of rejecting the neutrality hypothesis for the differentiation of body size between H. erectus and H. floresiensis according to Turelli's MDE model, along time for divergence and effective population size.

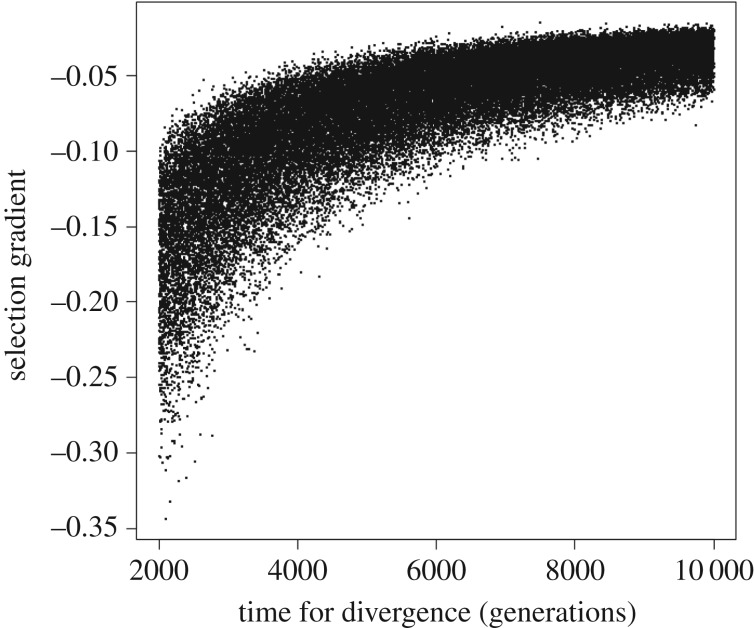
Under Lande's [36] model, the mean value of truncation selection threshold b was equal to 3.138 ± 0.155 phenotypic standard deviations, which corresponds to a minimum selective mortality of about 8.48 × 10⁻⁴ per generation (95% CI between 4.01 × 10⁻⁴ and 2.71 × 10⁻³) against the largest individuals. The median corresponding selection gradient β_µ was equal to −0.059 (95% CI ranging between −0.026 and −0.183). The strength of natural selection is related to time for divergence (figure 2), but even for a divergence time of 2000 generations, the values of β_µ are always much smaller than −1.

Figure 2.

Relationship of selection gradient β (approximating mean-standardized selection gradient β_µ) for the differentiation of body size between H. erectus and H. floresiensis with time for divergence in the simulations.

(b). Brain–body size correlated evolution

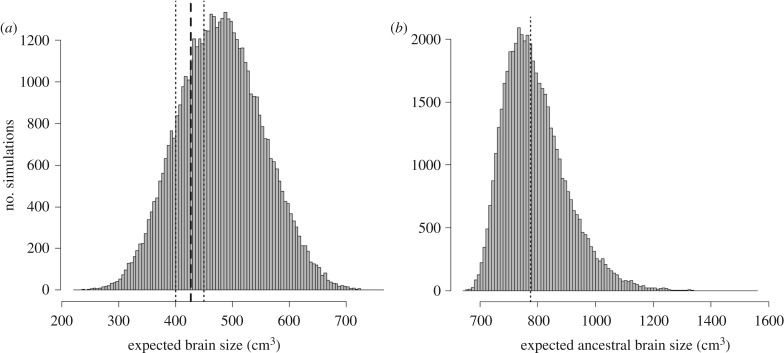
Under the range of parameters used in the simulations, there is a wide possible variation in EBS, with a mean of 479 ± 73 cm³ (figure 3a). Although the 426 cm³ estimated for LB1 brain size is within this relatively wide interval, the mean EBS values from the simulations are slightly larger than 426 cm³. The distribution of expected ancestral brain size (EABS) peaks at around 750 cm³ (median 775, with 95% CI from 628 to 1050), although larger values close to the lower limit found in H. sapiens, or the upper limits for H. erectus, that is around 1000–1100 cm³, are present within the EABS distribution (figure 3b).

Figure 3.

Distribution of expected brain size (EBS, in cubic centimetres) of Homo floresiensis under correlated evolution with body size evolution from H. erectus with ancestral brain sizes ranging from 750 cm³ to 1000 cm³ (a). Distribution of expected ancestral brain sizes (EABS) leading to the evolution of brain and body size values of H. floresiensis (b).

The POM approach allows a more direct evaluation of which combination of parameters tends to generate that subset of EBS closest to LB1 brain size. A total of 21.3% simulations gives EBS values in the range of 400–450 cm³. Overall, the mean parameters in these POM samples significantly differ from the overall mean parameters across the simulations, according to a randomization test, despite the small absolute differences generated, except for ancestral brain size (table 1).

Genetic correlation, heritabilities and population variability in equation (2.5), as well as ancestral brain size, together explained 79% of the variation in EBS, with the highest effect observed for variation in ancestral brain size (table 1). By inspecting the directions of these coefficients, it is possible to evaluate how changing parameters in equation (2.5) will change the EBS values. More interestingly, the ancestral body size within the expected range of EBS between 400 and 450 cm³ is normally distributed around 50 kg, and the brain size of simulations is skewed towards values perfectly fitting the range of early H. erectus, peaking at about 750–800 cm³.

Finally, bivariate models that compare H. floresiensis with ancestral values for body and brain size show that independent selection gradients driving brain size evolution are necessary to explain the phenotype of H. floresiensis. The median value of β between generations is −0.067 for body size (close to those median of values in figure 2), but values for brain size are indeed different from zero (as assumed by equation (2.5)) and equal to −0.016. This indicates the selection gradient for body size is about four times larger than for brain size.

4. Discussion and conclusion

(a). Natural selection and neutral evolution in Homo floresiensis body size

The quantitative evolutionary genetic models used here to analyse the phenotypic differentiation between H. floresiensis and a putative H. erectus-like ancestor are similar to previous findings [18,26] which were based on allometric scaling analyses of fossil hominids. Previous reports indicated that the Island Rule applies in primates [16,17]. Yet, we found the pattern for brain size evolution in H. floresiensis is slightly different than for its body size, suggesting that insularity may cause different evolutionary trajectories in these two traits.

First and most importantly, our analyses show that, assuming an H. erectus ancestry, it is highly unlikely that the shift in body size in H. floresiensis is due to neutral evolution alone. Of course, directional selection is expected under the Island Rule, considering the effects of both biotic interactions and resource use driving different aspects of species life history [5–7,9]. Our analyses show that the strength of selection necessary to drive such population differentiation is comfortably within the range observed in other evolutionary analyses.

The minimum directional selection forces driving dwarfism in H. floresiensis are also relatively low according to Lande's [36] model, as found in previous studies, with truncation of less than 0.1% of the population with the largest body size being enough to drive the difference. Hereford et al. ([38]; see also [37,39,40]) estimated bias-corrected medians for absolute values of β_µ in morphological traits to be close to 0.3 (see their table 1), although higher values (up to 1.0) are not uncommon, showing that relatively high selection strengths are commonplace in natural populations. The distribution of β_µ for the differentiation between H. erectus and H. floresiensis stays well within these limits. Even under the hypothesis that insular dwarfism occurred in as little time as 2000 generations, the selection gradient required (i.e. β_µ around −0.17; figure 2) still appears to be within the ranges commonly observed in natural populations, suggesting that a reduction of about 50% in body size (i.e. from about 50 kg in H. erectus to 27 kg in H. floresiensis) would increase fitness by approximately 8.5% [37,40]. This is not strong selection across a few generations, but it is important to highlight that it should be maintained continuously throughout a relatively long-time period of hundreds of generations, or should be much higher during shorter periods of environmental stress. Anyway, it is possible to conclude that strong directional selection on body size (and on brain size as well, see below) is a plausible explanation for the dwarfing observed in H. floresiensis.

The relative likelihood of directional selection as opposed to neutral evolution in driving body size differentiation in H. floresiensis stands on the assumptions about the ancestral states and time for speciation. Thus, our results do not say any final word on the ancestry of Flores Man (see electronic electronic supplementary material, table S1 and figures S1 and S2). However, our analyses consistently support a relatively large-bodied hominid as the ancestor to H. floresiensis, in the sense that evolutionary rates and selection strength necessary to drive such population differentiation expected under Island Rule are within the range observed in other evolutionary analyses. With plausible selection strengths, we feel it is not parsimonious to invoke an older and/or smaller-bodied African ancestor to explain H. floresiensis phenotype, especially if this implies revising the entire ‘Out of Africa I’ scenario.

(b). Patterns of brain–body size evolution

An important issue about H. floresiensis is its exceptionally small brain size, and whether the Island Rule is a sufficient explanation for it [18,26,68]. Previous studies showed that, even if body size reduction in Flores Man is plausibly within the range of reduction found in other insular primates, the effect of body size reduction alone would allometrically produce a brain larger than LB1 [26]. We achieved a similar conclusion here by estimating directly H. floresiensis EBS under quantitative genetic models, assuming a wide range of variation in heritabilities, standard deviation and brain–body size correlations.

It is important to notice that we initially applied Lande's [30] correlated evolution model because we were modelling selective forces driving body size evolution due to ecological constraints under the Island Rule. However, alternative models where selective forces act directly on brain size, also exist (see [29,69]). Because of the complex social life that characterizes our own genus and of the high energetic consumption of the brain [70–72], it is expected that additional selective pressures for reduction in brain size alone, with a β_µ of around 1.5% (but around 5% in 2000 generations) per generation, occurring in addition to (or even driving) those for reduced body size, could have taken place in H. floresiensis evolution [29]. Indeed, multivariate analysis based on responses mediated by G-matrix supported these conclusions, although independent selection strengths in brain size alone are about four times smaller than in body size evolution.

Previous studies [73] applied an ontogenetic scaling model to fossil dwarf insular hippopotamuses of Madagascar found that their brains were some 30% smaller than expected for their body size. They concluded that brain size evolution should be seen as independent from body size evolution in insular mammals, and extended their reasoning to explain the exceptionally small endocranial volume of H. floresiensis. However, in hominins there could be counteracting forces to brain size reduction, so far as cognitive functions are strongly related to brain size, and cultural and behavioural aspects remain important. Stone tools associated with H. floresiensis are well-developed, leaving room for the alternatives that either brain plasticity in H. floresiensis was enough to maintain good functioning despite its small size, or that more complex brain functional reorganization intervened to maintain cognitive functions intact despite brain size reduction [26,74,75].

(c). Concluding remarks

Our analyses support the Island Rule as the most parsimonious explanation for the reduced brain and body sizes in Flores Man. Because they are based on patterns of brain and body size evolution alone, rather than on a more complex set of morphological traits, we are not in the position to choose among alternative candidate taxa as ancestors of H. floresiensis. However, EBS and EABS distributions from our simulations support the previous conclusion [21,26] that H. floresiensis may most likely be derived from an early Indonesian H. erectus-like hominin. This is indeed consistent with recent findings in Flores revealing that H. floresiensis was already established as a species about 700 kya, and with the outcomes of a spatially explicitly phenotypic evolution model [76] suggesting there is more similarity between early forms of H. erectus out of Africa (such as Dmanisi fossils) and Indonesian H. erectus than with any African H. erectus.

The framework we provide here enables assessment of how evolutionary mechanisms, especially directional selection, could drive population divergence between insular and continental forms, trying to link better patterns and processes in macroecology. It is worthwhile noticing that a general application of such methods to other groups of organisms, in a comparative framework, may be still challenging. We used here genetic and population parameters, as well as demographic and colonization scenarios, based on relatively well known estimates for H. sapiens. Despite some uncertainties, there is an overall consensus about the ‘Out of Africa I’ scenario that led H. erectus from African to Indonesia (providing biogeographic support to the status of H. erectus as a possible ancestor of H. floresiensis).

The models for evolutionary analyses presented here, perhaps further coupled with molecular approaches now used for evaluating adaptive radiation and speciation patterns, may become an additional approach to deal with phenotypic differentiation and provide a new research avenue in island biogeography. We hope our findings will stimulate researchers to explore the factors driving body size and brain size variation in a multivariate path of life-history and ecological processes, improving our understanding of insular dwarfism, in H. floresiensis as well as in other species, under ever more realistic evolutionary scenarios.

Ethics

We declare all ethical procedures were followed during this study.

Data accessibility

All data necessary to reproduce the results in this paper can be found in the electronic supplementary material, appendix.

Authors' contributions

J.A.F.D.-F. conceived the study and conducted all simulations; J.A.F.D.-F. and P.R. discussed the results and interpretations, and equally contributed to writing the manuscript.

Competing interests

We declare we have no competing interests.

Funding

Work by J.A.F.D.-F. on macroecology and macroevolution have been continuously supported by CNPq productivity grants and is developed in the context of National Institutes for Science and Technology (INCT) in Ecology, Evolution and Biodiversity Conservation, supported by MCTIC/CNpq (proc. 465610/2014-5) and FAPEG.