Full Information Maximum Likelihood Estimation for Latent Variable Interactions With Incomplete Indicators

Abstract

Researchers have developed missing data handling techniques for estimating interaction effects in multiple regression. Extending to latent variable interactions, we investigated full information maximum likelihood (FIML) estimation to handle incompletely observed indicators for product indicator (PI) and latent moderated structural equations (LMS) methods. Drawing on the analytic work on missing data handling techniques in multiple regression with interaction effects, we compared the performance of FIML for PI and LMS analytically. We performed a simulation study to compare FIML for PI and LMS. We recommend using FIML for LMS when the indicators are missing completely at random (MCAR) or missing at random (MAR) and when they are normally distributed. FIML for LMS produces unbiased parameter estimates with small variances, correct Type I error rates, and high statistical power of interaction effects. We illustrated the use of these methods by analyzing the interaction effect between advanced cancer patients’ depression and change of inner peace well-being on future hopelessness levels.

Missing data represent “one of the most important statistical and design problems in research” (Azar, 2002, p. 70). Inappropriate handling of missing data can result in substantially biased parameter estimates and invalid statistical inferences. Missing data can be classified into three types based on missingness mechanisms: missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR) (Enders, 2010; Little & Rubin, 2002; Van Buuren, 2012). MCAR assumes that the probability of missingness does not depend on any observed or missing values. MAR assumes that the probability of missingness depends on the observed values but not on the missing values. MNAR assumes that the probability of missingness depends on the missing values. In the past decades, there has been an increasing interest in missing data handling approaches for all these mechanisms. For example, multiple imputation and full information maximum likelihood estimation handle MAR data, and selection modeling and pattern mixture modeling are employed when the data are MNAR (Enders, 2010; Little & Rubin, 2002). Most of these approaches assume linear relationships among variables. In recent years, researchers have developed and investigated missing data handling techniques for estimating interaction effects in multiple regression (Bartlett, Seaman, White, & Carpenter, 2015; Doove, Van Buuren, & Dusseldorp, 2014; Enders, Baraldi, & Cham, 2014; Kim, Sugar, & Belin, 2015; Seaman, Bartlett, & White, 2012; vonHippel, 2009). Specifically, these approaches handle incompletely observed predictors in multiple regression with interaction effects.

On the other hand, there is a lack of research on proper approaches to handle incompletely observed indicators in latent variable interactions when the predictors are not measured directly, but are represented by a confirmatory factor model with indicators in latent variable interactions. To address this issue, we investigated full information maximum likelihood (FIML) estimation for two latent variable interaction methods: product indicator (PI; Kenny & Judd, 1984) and latent moderated structural equations (LMS; Klein & Moosbrugger, 2000; Moosbrugger, Schermelleh-Engel, & Klein, 1997; Schermelleh-Engel, Klein, & Moosbrugger, 1998). We investigate three variants of the PI method: constrained product indicator (CPI; Jöreskog & Yang, 1996; Kenny & Judd, 1984), generalized appended product indicator (GAPI; Wall & Amemiya, 2001), and unconstrained product indicator (UPI; Marsh, Wen, & Hau, 2004). These latent variable interaction methods are available in the major SEM software packages; Mplus (Muthén & Muthén, 1998–2015), R package lavaan (Rosseel, 2012), and LISREL (Jöreskog & Sörbom, 2015) can be used for PI; Mplus and R package nlsem (Umbach et al., 2015) can be used for LMS. We conducted a simulation study to investigate whether FIML produces unbiased parameter estimates, which leads to valid statistical inferences for these methods.

The structure of the manuscript is the following. First, we reviewed three approaches to handle incompletely observed predictors in multiple regression with interaction effects that were relevant to FIML for latent variable interaction methods: listwise deletion, “just another variable” (JAV) multiple imputation, and FIML estimation. We evaluated them theoretically and in light of published simulation studies. We discussed other missing data handling approaches in the General Discussion section. Second, we introduced the latent variable interaction methods (PI and LMS) and provided the details of how FIML handles incompletely observed indicators in each method. Third, we conducted a simulation study to investigate how FIML performed under various conditions, including sample sizes, interaction effect sizes, missing data rates, and missing data mechanisms. Fourth, we applied these methods to a substantive example with incompletely observed indicators. Finally, we discussed our results and findings. Throughout the manuscript, we focused on the situation where the predictors (or indicators of predictors) had missing values. We discussed the situation where the outcome (or indicators of outcome) had missing values in the General Discussion section.

Multiple regression with interaction effects

Without loss of generality, we consider the interaction effect between two predictors ξ₁ and ξ₂ of outcome η (Equation [1]):

$$\eta ={\gamma }_0+{\gamma }_1{\xi }_1+{\gamma }_2{\xi }_2+{\gamma }_3{\xi }_1{\xi }_2+\zeta$$ (1)

where ξ₁ ξ₂ is the interaction term (product of ξ₁ and ξ₂); ζ is the disturbance; γ₀ is the intercept; γ₁, γ₂, and γ₃ are the regression coefficients. In this section, we described and evaluated three approaches to handle incompletely observed predictors in multiple regression with interaction effects.

Listwise deletion

In listwise deletion (or complete-case analysis), participants are eliminated from the analysis when they have missing values in any variables (ξ₁, ξ₂, η). Little’s (1992) theoretical work has shown that listwise deletion leads to unbiased γ₀, γ₁, γ₂, γ₃ estimates and valid statistical inferences in two situations: (a) predictors are MCAR, and/or (b) the missingness of a predictor depends on the observed values of other predictors. These two conditions are more restrictive than MAR. Another important disadvantage is that, compared to JAV and FIML (discussed later), both which use all observed data, listwise deletion often has lower statistical power due to reduced sample sizes. Simulation studies by Enders et al. (2014) and Seaman et al. (2012) have shown that when ξ₁ and/or ξ₂ are MCAR, listwise deletion results in unbiased γ₀, γ₁, γ₂, γ₃ estimates. However, the lower-order effect (γ₀, γ₁, γ₂) estimates have larger variances compared to those by JAV and FIML. When ξ₁ and/or ξ₂ are MAR, listwise deletion can produce biased γ₀, γ₁, γ₂, γ₃ estimates with smaller variances compared to those by JAV and FIML. Therefore, listwise deletion is not recommended. We do not consider this approach for latent variable interactions.

Just another variable

Just another variable (JAV) is a Bayesian parametric multiple imputation approach (Bartlett et al., 2015; Enders et al., 2014; Kim et al., 2015; Seaman et al., 2012; von Hippel, 2009). Without loss of generality, consider that ξ₁ is incompletely observed and ξ₂ and η are completely observed in Equation (1). When ξ₁ has missing values, the interaction term ξ₁ ξ₂ is also incompletely observed. JAV assumes that the conditional distribution of the incompletely observed variables (ξ₁ and ξ₁ ξ₂) on the completely observed η and ξ₂ is multivariate normal (MVN; Equation [2]):

$$\left(\begin{array}{c}{\xi }_1\\ {\xi }_1{\xi }_2\end{array}\right)~\text{MVN}\left[\left(\begin{array}{c}{\beta }_{10}+{\beta }_{11}\eta +{\beta }_{12}{\xi }_2\\ {\beta }_{20}+{\beta }_{21}\eta +{\beta }_{22}{\xi }_2\end{array}\right),\left(\begin{array}{cc}{\tau }_{11}& {\tau }_{21}\\ {\tau }_{21}& {\tau }_{22}\end{array}\right)\right]$$ (2)

where ξ₁ and ξ₁ ξ₂ are linearly conditional on η and ξ₂ with parameters βs and τs; βs are the regression coefficients; τs are the residual variances and covariances; JAV is an iterative process between two steps. In the first step, missing values of ξ₁ and ξ₁ ξ₂ are imputed using Equation (2). We use the observed values of η and ξ₂ and the estimates of βs and τs to impute ξ₁ and ξ₁ ξ₂. In the second step, the estimates of βs and τs are updated by random draws from the β and τ matrices in Equation (2), which are based on the observed values of η and ξ₂, imputed values of ξ₁ and ξ₁ ξ₂, and the specified prior distributions of βs and τs.¹ Data sets with imputed values are created after every specified number of cycles. Data augmentation algorithm (Enders 2010; Little & Rubin, 2002) or multivariate imputation via chained equations algorithm (Van Buuren, 2012) can be employed in the imputation processes.² After creating multiple complete data sets with imputed values, we estimate the interaction model in Equation (1) for each data set. Each data set shall provide different sets of regression coefficient estimates and statistical inferences of the regression coefficients. These sets of results are combined (pooled) to one set of regression coefficients estimates and statistical inferences (Enders, 2010; Little & Rubin, 2002).

Theoretical work by Bartlett et al. (2015) and Seaman et al. (2012) has shown that JAV only produces consistent γ₀, γ₁, γ₂, γ₃ estimates when ξ₁ is MCAR. The key reason is that ξ₁ ξ₂ is nonlinearly related to ξ₂. In fact, the distribution of ξ₁ ξ₂ is a nonlinear function that involves ξ₂ (Aroian, 1944; Bohrnstedt & Goldberger, 1969). Therefore, the imputation model for ξ₁ ξ₂ in Equation (2) is misspecified. Another reason is that the distribution of ξ₁ ξ₂ is nonnormal, which also violates the assumption of the conditional distribution of ξ₁ ξ₂. Given these reasons, Seaman et al. (2012) have shown that the estimates of βs and τs are only consistent when ξ₁ is MCAR. Only consistent estimates of βs and τs produce imputed values of ξ₁ and ξ₁ ξ ₂ that result in consistent γ₀, γ₁, γ₂, γ₃ estimates. In addition to the theoretical work, simulation studies by Bartlett et al. (2015), Enders et al. (2014), Kimet al. (2015), and Seaman et al. (2012) have investigated the biases and variances of γ₀, γ₁, γ₂, γ₃ estimates. When ξ₁ is MCAR, JAV produces unbiased γ₀, γ₁, γ₂, γ₃ estimates. Moreover, the lower-order effect estimates have smaller variances compared to those obtained by listwise deletion. When ξ₁ is MAR and normal, JAV produces unbiased γ₃ estimates. When ξ₁ is MAR and nonnormal, JAV can result in biased γ₃ and lower-order effect estimates with larger variances compared to those produced by listwise deletion. The bias of γ₃ becomes more pronounced with the increase of interaction effect size.

Full information maximum likelihood estimation

Without loss of generality, we continue to consider the same scenario that ξ₁ is incompletely observed and ξ₂ and η are completely observed. Full information maximum likelihood estimation (FIML) maximizes the sample log-likelihood function (Equation [3]) to estimate γ₀, γ₁, γ₂, and γ₃.

$$l=\sum _{i=1}^{N}ln\left(f({\mathbf{w}}_i)\right)$$ (3)

where l is the sample log-likelihood function; ${\sum }_{i=1}^N(·)$ is the summation function across cases 1 to N; ln(·) is the natural logarithm function; f(w_i) is the probability density function for the vector of variables w for case i. When all variables are completely observed in Equation (1), w = (η, ξ₁, ξ₂, ξ₁ξ₂). FIML allows cases with missing values on some variables. In other words, it utilizes all observed variables for each case, and thus the name “full information.” Equation (3) implies that we need to specify the distributions for w (i.e., specify f (w_i)). FIML assumes that all variables (η, ξ₁, ξ₂, ξ₁ ξ₂) are linearly related with each other and are multivariate normally distributed. When ξ₁ and ξ₁ ξ₂ are incompletely observed, FIML assumes that their conditional distribution on η and ξ₂ is multivariate normal. The sample log-likelihood function in Equation (3) can be rewritten as Equation (4):

$$l=\sum _{i=1}^N\left(-\frac{k_i}{2}ln(2\pi )-\frac{1}{2}ln\mid {\mathbf{\sum }}_i\mid -\frac{1}{2}{\left({\mathbf{w}}_i-{\mathit{\mu }}_i\right)}^{\mathrm{T}}{\mathbf{\sum }}_i^{-1}\left({\mathbf{w}}_i-{\mathit{\mu }}_i\right)\right),$$ (4)

where (·)^T is the matrix transpose function; | · | is the determinant function; (·)⁻¹ is the matrix inverse function; k_i is the number of completely observed variables for case i; μ_i and Σ_i are the elements of the model-implied mean vector and covariance matrix that correspond to the observed data (w_i) for case i. The log-likelihood function is maximized to obtain the FIML parameter estimates.

FIML is closely related to JAV. Both assume that the incompletely observed variables (ξ₁ and ξ₁ ξ₂) are linearly related to the completely observed variables (η and ξ₂). Both make the same assumption about the conditional distribution of ξ₁ and ξ₁ ξ₂. In fact, JAV is equivalent to FIML asymptotically (Little & Rubin, 2002, p. 201). The theoretical justification by Bartlett et al. (2015) and Seaman et al. (2012) that JAV can only produce consistent γ₀, γ₁, γ₂, γ₃ estimates when ξ₁ is MCAR is generalizable and applicable to FIML asymptotically. This is also supported by Yuan’s (2009) and Yuan and Savalei’s (2014) theoretical work. In the more general settings to multiple regression with interaction effects, they have shown that FIML estimation that maximizes Equation (4) does not produce consistent covariance estimates of the variables when the MAR variables (here, ξ₁ and ξ₁ ξ₂) and the completely observed variables accounting for the missingness (here, η and ξ₂) are nonlinearly related. As a result, γ₀, γ₁, γ₂, γ₃ estimates, which are derived from these covariance estimates, are not consistent. The simulation studies by Enders et al. (2014) have shown that the biases and variances of γ₀, γ₁, γ₂, γ₃ estimates are nearly the same between FIML and JAV when sample size ≥ 200. The results further support the equivalence between FIML and JAV for multiple regression with interaction effects.

Latent variable interactions

Multiple regression makes two assumptions about the predictors ξ₁ and ξ₂. First, it is assumed that ξ₁ and ξ₂ are perfectly reliable. Second, the underlying constructs of ξ₁ and ξ₂ are represented by a single variable. When ξ₁ and ξ₂ are not perfectly reliable and the underlying constructs are represented by confirmatory factor models, latent variable interaction methods are appropriate to model the interaction effects between ξ₁ and ξ₂ on outcome η. In this section, we introduced two methods to model latent variable interactions: product indicator (PI) and latent moderated structural equations (LMS). For each method, we described and evaluated how FIML handles the incompletely observed indicators of ξ₁ and ξ₂. For simplicity of the presentation, we treated outcome η as a single variable, although in both PI and LMS, η could be a factor with multiple indicators.

Product indicator

In latent variable interactions, the interaction term ξ₁ ξ₂ is the product of factors ξ₁ and ξ₂. Unlike multiple regression, we cannot multiply ξ₁ and ξ₂ to form the interaction term. To represent ξ₁ ξ₂, product indicator (PI) multiplies the indicators of ξ₁ and ξ₂ (product indicators) as indicators of ξ₁ ξ₂. There are three main issues when specifying the models in PI. The first issue is the selection of product indicators of ξ₁ ξ₂. Consider a widely studied situation where ξ₁ and ξ₂ have three indicators each (X₁, X₂, X₃ and X₄, X₅, X₆) (e.g., Cham, West, Ma, & Aiken, 2012; Kelava et al., 2011; Marsh et al., 2004; Wall & Amemiya, 2001), so there are nine possible product indicators (X₁X₄, X₁X₅, X₁X₆, X₂X₄, X₂X₅, X₂X₆, X₃X₄, X₃X₅, X₃X₆). Simulation studies suggest creating three product indicators using the three most reliable indicators of ξ₁ and ξ₂, respectively (Jackman, Leite, & Cochrane, 2011; Marsh et al., 2004; Wu, Wen, Marsh, & Hau, 2013). This produces unbiased γ₃ estimates with unbiased estimated standard errors. It also reduces the complexity of model specification in SEM software, and it can be employed in scenarios with any number of indicators of ξ₁ and ξ₂.³ The second issue is centering the indicators of ξ₁ and ξ₂ in the presence of missing values. Centering indicators at their means and then computing the product indicators can simplify the model specification by fixing the latent intercepts of the indicators and product indicators to zero. This greatly increases the chances of successful model convergence (Algina & Moulder, 2001). When the indicators of ξ₁ and ξ₂ have missing values, we suggest using the FIML estimated means of the indicators. Adopting these two solutions and assuming all indicators have equal reliabilities, the measurement model of ξ₁, ξ₂, and ξ₁ ξ₂ can be expressed as in Equation (5):

$$\left(\begin{array}{c}{X}_1\\ X_2\\ X_3\\ X_4\\ X_5\\ X_6\\ X_1{X}_4\\ X_2{X}_5\\ X_3{X}_6\end{array}\right)=\left(\begin{array}{ccc}{\lambda }_{X1}& 0& 0\\ {\lambda }_{X2}& 0& 0\\ {\lambda }_{X3}& 0& 0\\ 0& {\lambda }_{X4}& 0\\ 0& {\lambda }_{X5}& 0\\ 0& {\lambda }_{X6}& 0\\ 0& 0& {\lambda }_{X1X4}\\ 0& 0& {\lambda }_{X2X5}\\ 0& 0& {\gamma }_{X3X6}\end{array}\right)\left(\begin{array}{c}{\xi }_1\\ {\xi }_2\\ {\xi }_1{\xi }_2\end{array}\right)+\left(\begin{array}{c}{\delta }_{X1}\\ {\delta }_{X2}\\ {\delta }_{X3}\\ {\delta }_{X4}\\ {\delta }_{X5}\\ {\delta }_{X6}\\ {\delta }_{X1X4}\\ {\delta }_{X2X5}\\ {\delta }_{X3X6}\end{array}\right),$$ (5)

where λs are the factor loadings; δs are the unique factors, which are set to be uncorrelated with all other unique factors. The subscripts of λs and δs correspond to the indicators. The third issue is the choice of PI method out of its three variants: constrained product indicator (CPI), generalized appended product indicator (GAPI), and unconstrained product indicator (UPI). The three variants of PI add model constraints related to ξ₁ ξ₂, which provide more information to describe the distribution of ξ₁ ξ₂ (Aroian, 1944; Bohrnstedt & Goldberger, 1969; Jöreskog & Yang, 1996). Table 1 summarizes the constraints for each PI variant (see also Cham et al., 2012; Kelava et al., 2011). CPI has the most constraints, followed by GAPI and UPI. Simulation studies find that CPI produces unbiased γ₃ estimates with higher statistical power than GAPI and UPI when the indicators of ξ₁ and ξ₂ are normally distributed. When these indicators are nonnormally distributed, CPI produces biased γ₃ estimates. GAPI and UPI produce unbiased γ₃ estimates when sample size ≥ 500 (Cham et al., 2012; see also Coenders, Batista-Foguet, & Saris, 2008; Marsh et al., 2004; Wall & Amemiya, 2001). Note that these simulation studies only investigate the situation where the indicators of ξ₁ and ξ₂ are completely observed.

Table 1.

Model constraints of product indicator methods.

Model constraint	Constrained product indicator (CPI)	Generalized appended product indicator (GAPI)	Unconstrained product indicator (UPI)
Mean of ξ1ξ2	√	√	√
Variance and covariances of ξ1ξ2	√	×	×
Factor loadings of product indicators	√	√	×
Unique factor variances of product indicators	√	√	×
Unique factor covariances of product indicators	√	√	√

When the indicators of ξ₁ and/or ξ₂ have missing values, FIML can be used with PI (Zhang, 2010). FIML for PI is an extension of FIML for multiple regression with interaction effects. The sample log-likelihood function is the same as Equations (3) and (4); w is a vector of indicators of ξ₁ and ξ₂, product indicators of ξ₁ξ₂, and outcome η. In our example, w = (X₁, X₂, X₃, X₄, X₅, X₆, X₁X₄, X₂X₅, X₃X₆, η). We expect that the results for JAV and FIML for multiple regression with interaction effects are generalizable to FIML for PI; FIML for PI only produces consistent γ₀, γ₁, γ₂, γ₃ estimates when the indicators of ξ₁ are MCAR. The first and the key reason is that FIML for PI also maximizes the sample log-likelihood function, which incorrectly assumes that the product indicators are linearly related to the indicators of ξ₁ and ξ₂. When the indicators of ξ₁ are MAR, FIML estimation produces inconsistent covariance estimates of w (Yuan, 2009; Yuan & Savalei, 2014). As a result, γ₀, γ₁, γ₂, γ₃ estimates are not consistent. Second, FIML for PI incorrectly assumes that the conditional distribution of the product indicators on the completely observed elements in w is multivariate normal. Similar to the distribution of ξ₁ξ₂, the distribution of product indicators is nonnormal and nonlinearly related to the indicators of ξ₁ and ξ₂ (Aroian, 1944; Bohrnstedt & Goldberger, 1969). Third, η is nonnormally distributed even when the indicators of ξ₁ and ξ₂ are multivariate normally distributed (Klein & Moosbrugger, 2000; more later). Our expectation is supported by the simulation studies by Zhang (2010) that have investigated FIML for CPI and UPI. When the indicators of ξ₁ and ξ₂ are MCAR, CPI and UPI produce unbiased γ₃ estimates under normality of indicators. Only UPI produces unbiased γ₃ estimates under nonnormality of the indicators. When the indicators are MAR, CPI and UPI lead to biased γ₃ estimates in all indicator distribution conditions. The bias increases as the missing data rate increases. These results match the theoretical work for JAV and FIML for multiple regression with interaction effects. In the MCAR condition, the differences between CPI and UPI under different indicator distributions are consistent with those when the indicators are completely observed.

Latent moderated structural equations

Latent moderated structural equations (LMS) belong to a class of latent variable interaction methods termed distribution analytic methods (Kelava et al., 2011). In distribution analytic methods, the measurement model for ξ₁ξ₂ is not specified. Distribution analytic methods use estimation procedures to calculate model parameters (including γ₀, γ₁, γ₂, γ₃) and make statistical inferences directly. LMS begins by decomposing the vector of ξ₁ and ξ₂ as in Equation (6) (Klein &Moosbrugger, 2000, equation 8):

$$\begin{array}{ll}\hfill \mathit{\xi }& =\mathbf{A}\mathbf{z}\hfill \\ \hfill \left(\begin{array}{c}{\xi }_1\\ {\xi }_2\end{array}\right)& =\left(\begin{array}{cc}{a}_{11}& a_0\\ a_{21}& a_{22}\end{array}\right)\left(\begin{array}{c}{z}_1\\ z_2\end{array}\right),\hfill \end{array}$$ (6)

where ξ is a column vector of ξ₁ and ξ₂; A is a lower triangular matrix produced by the Cholesky decomposition of the covariance matrix of ξ; z is a column vector of variables z₁ and z₂; z₁ and z₂ are mutually independent and are standard normally distributed. LMS also rewrites the interaction model in Equation (1) (Klein &Moosbrugger, 2000, equation 2):

$$\begin{array}{l}\eta ={\gamma }_0+\mathbf{\Gamma }\mathit{\xi }+{\mathit{\xi }}^{\mathrm{T}}\mathbf{\Omega }\mathit{\xi }+\zeta \\ \eta ={\gamma }_0+\left(\begin{array}{cc}{\gamma }_1& {\gamma }_2\end{array}\right)\left(\begin{array}{c}{\xi }_1\\ {\xi }_2\end{array}\right)+\left(\begin{array}{cc}{\xi }_1& {\xi }_2\end{array}\right)\left(\begin{array}{cc}0& {\gamma }_3\\ 0& 0\end{array}\right)\left(\begin{array}{c}{\xi }_1\\ {\xi }_2\end{array}\right)+\zeta \end{array}$$ (7)

where Γ is a row vector of regression coefficients of the lower-order effects except the intercept; Ω is a square matrix containing the interaction effect coefficient(s) in upper diagonal. Combining Equations (6) and (7), the interaction model can be decomposed into Equation (8) (Klein & Moosbrugger, 2000, equation 10):

$$\begin{array}{l}\eta ={\gamma }_0+\mathbf{\Gamma }\mathbf{A}\mathbf{z}+{\mathbf{z}}^{\mathbf{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{\Omega }\mathbf{A}\mathbf{z}+\zeta \\ \eta ={\gamma }_0+\mathbf{\Gamma }\mathbf{A}\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)+\mathbf{\Gamma }\mathbf{A}\left(\begin{array}{c}0\\ z_2\end{array}\right)+{\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)}^{\mathrm{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{\Omega }\mathbf{A}\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)+{\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)}^{\mathrm{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{\Omega }\mathbf{A}\left(\begin{array}{c}0\\ z_2\end{array}\right)+\zeta \\ \eta =\left({\gamma }_0+\mathbf{\Gamma }\mathbf{A}\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)+{\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)}^{\mathrm{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{\Omega }\mathbf{A}\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)\right)+\left(\mathbf{\Gamma }\mathbf{A}+{\left(\begin{array}{c}{z}_1\\ 0\end{array}\right)}^{\mathrm{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{\Omega }\mathbf{A}\right)\left(\begin{array}{c}0\\ z_2\end{array}\right)+\zeta .\end{array}$$ (8)

Equations (6) to (8) decompose the interactive relationship of ξ₁ and ξ₂ to η into linear and nonlinear components. The last line of Equation (8) shows that η is linearly related to z₂, but nonlinearly related to z₁. Because of the nonlinear component in Equation (8), η is nonnormally distributed even when ξ₁ and ξ₂ are multivariate normally distributed. This is why FIML for PI (as well as JAV and FIML for regression with interaction effects) incorrectly assumes that η is normally distributed.

LMS correctly specifies the nonlinear relationships between ξ₁, ξ₂, and η, as well as the nonnormal distribution of η. In turn, LMS correctly specifies the sample log-likelihood function of FIML to obtain the parameter estimates and other results. Assuming the indicators of ξ₁ and ξ₂ are multivariate normal, Klein and Moosbrugger (2000, p. 463) have shown that the conditional distribution of the indicators of all factors (ξ₁, ξ₂, and η) on z₁ are multivariate normal. Equivalently, the multivariate distribution of indicators of all factors (ξ₁, ξ₂, and η) is a mixture of multivariate normal distributions across the values of z₁ (Equation [9]; Klein &Moosbrugger, 2000, equation 15):

$$f(\mathbf{w})=\int \varphi (z_1)\varphi (\mathbf{w})d{z}_1.$$ (9)

Different from PI, w = (X₁, X₂, X₃, X₄, X₅, X₆, η) because no product indicators are involved in LMS; ϕ(z₁) is the normal density function of z₁, which equals $\frac{1}{\sqrt{2\pi }}{e}^{\frac{-z_1^2}{2}}$; ϕ(w) is the multivariate normal density function of w, which equals ${(\frac{1}{\sqrt{2\pi }})}^k(\frac{1}{\sqrt{\mid \mathbf{\sum }\mid }})e^{\frac{-{(\mathbf{w}-\mathit{\mu })}^{\mathrm{T}}{\mathbf{\sum }}^{-1}(\mathbf{w}-\mathit{\mu })}{2}}$; μ and Σ are the model-implied mean vector and covariance matrix of w; ∫(·) dz₁ is the integration function across the values of z₁ because z₁ is continuous. As discussed previously, LMS does not require any product indicators. Using Equations (3) and (9), the sample log-likelihood function of FIML for LMS is

$$\begin{array}{l}l=\sum _{i=1}^{N}ln\left(f({\mathbf{w}}_i)\right)=\sum _{i=1}^{N}ln\left(\int \varphi (z_1)\varphi ({\mathbf{w}}_i){dz}_1\right)\\ =\sum _{i=1}^{N}ln\left(\int \frac{1}{\sqrt{2\pi }}{e}^{\frac{-z_1^2}{2}}\varphi ({\mathbf{w}}_i){dz}_1\right)\\ \approx \sum _{i=1}^{N}ln\left(\sum _{j=1}^M\frac{m_j}{\sqrt{2\pi }}\varphi ({\mathbf{w}}_i)\right).\end{array}$$ (10)

To maximize the sample log-likelihood function in Equation (10), the computational algorithm is tailored to include numerical integration algorithm(e.g., rectangular integration, Hermite-Gaussian quadrature integration) to approximate the integration (Klein & Moosbrugger, 2000, pp. 464–467). The numerical integration algorithm approximates by splitting the integration to a total of M dimensions, each with a different weight m and a different estimate for ϕ(w). As discussed, FIML for LMS correctly specifies the nonlinear relationships between ξ₁, ξ₂, and η. It correctly handles the no-normal distribution of η. It assumes that all indicators of ξ₁ and ξ₂ are multivariate normal. When the distributional assumption holds, FIML for LMS shall produce unbiased γ₀, γ₁, γ₂, γ₃ estimates for MCAR and MAR indicators of ξ₁ and ξ₂. Simulation studies find that when indicators of ξ₁ and ξ₂ are completely observed and the distributional assumption holds, FIML for LMS produces unbiased γ₀, γ₁, γ₂, γ₃ estimates with lower variances compared to those by PI (Cham et al., 2012; Jackman et al., 2012; Marsh et al., 2004; Wu et al., 2013). When the distributional assumption is violated, FIML for LMS can produce biased γ₃ estimates (Cham et al., 2012).

Current study

We conducted a simulation study to investigate how FIML for CPI, GAPI, UPI, and LMS performs when the indicators of ξ₁ and/or ξ₂ have missing values. We hypothesize that when the indicators are MCAR and multivariate normal, all methods lead to unbiased estimates and valid statistical inferences. LMS results in γ₀, γ₁, γ₂, γ₃ estimates with the smallest variances. When the indicators are MAR and multivariate normal, only LMS leads to unbiased γ₀, γ₁, γ₂, γ₃ estimates and valid statistical inferences. We applied these methods to a substantive example with incompletely observed indicators of ξ₁ and ξ₂.

Simulation study: Method

Population model

We investigated the interaction model in Equation (1). To set the values of γ₀, γ₁, γ₂, γ₃ and the variance of disturbance ζ, we assumed that ξ₁, ξ₂, and η were measured directly, perfectly reliable, and analyzed via multiple regression. We set γ₁, γ₂, and disturbance variance such that the linear effects of ξ₁ and ξ₂ yield a population ρ² = 0.3. We manipulated three levels of γ₃ in terms of ρ² increment from linear model to interaction model (squared semipartial correlation, sr²) = 0 (no effect), 0.05 (small to medium effect), and 0.10 (medium effect; Cohen, 1992). We used the previous example where ξ₁ had three indictors (X₁, X₂, X₃) and ξ₂ had three indicators (X₄, X₅, X₆). To show that all methods are applicable for η as a factor, we set η having three indicators. We set the values of factor loadings and unique factor variances so that Cronbach’s α of each construct = 0.7. All unique factors were uncorrelated with each other. We set the latent intercepts of X₁ to X₆ to an arbitrary value (= 5) to investigate the performance of using FIML to mean center X₁ to X₆. Table 2 summarizes the parameters.

Table 2.

Parameters of population model.

Structural model
sr2 = 0 (no interaction effect)		sr2 = 0.05 (small to medium effect)
Parameter	Value	Parameter	Value
γ3	0.00	γ3	4.43
Variance of disturbance ζ	343.00	Variance of disturbance ζ	318.50
sr2 = 0.10 (medium effect)		For all conditions
Parameter	Value	Parameter	Value
γ3	6.26	γ0	10.00
Variance of Disturbance ζ	294.00	γ1	7.00
		γ2	7.00
Measurement model of ξ1 and ξ2		Measurement model of η
Parameter	Value	Parameter	Value
Latent intercept	5.00	Latent intercept	0.00
Factor loading	1.00	Factor loading	1.00
Unique factor Variance	1.29	Unique factor variance	630.00
Factor mean	0.00
Factor variance	1.00
Factor covariance	0.50

Sample size

To adequately represent the common situations in behavioral research, we manipulated five levels of sample size (N) = 100, 200, 500, 1,000, 5,000. N = 200 approximates the median sample size in multiple regression with interaction effects (Jaccard & Wan, 1995); N = 5,000 resembles the asymptotic situation.

Missing data rates

The indicators of ξ₁ (X₁, X₂, X₃) were incompletely observed, while those of ξ₂ (X₄, X₅, X₆) were completely observed. Our substantive example also had similar missing data patterns. Because the computational algorithms for FIML estimation handle any missing data patterns, this setting will not limit the generalizability of results; X₁, X₂, X₃ were set to three missing data rates = 0%, 15%, 25%. The 15% and 25% conditions had been studied extensively (e.g., Collins, Schafer, & Kam, 2001; Savalei, 2010).

Missing data mechanisms

To generate incompletely observed Xs in these scenarios, we first created one set of completely observed Xs. In 15% and 25% missing data rates, X₁, X₂, and X₃ were all MCAR or MAR. In MCAR condition, we generated two scenarios with different missing data patterns. In MAR condition, we generated six scenarios that had different missing data patterns and used different combinations of variables to explain the missingness of X₁, X₂, and X₃. Table 3 describes these missing data scenarios.

Table 3.

Missing data scenarios for simulation study.

(A) Missing completely at random (MCAR) – two scenarios
Scenario 1	We generated one random uniform variable. We created missing values of X1, X2, and X3 for cases in the lower quartile of the random uniform variable based on the missing data rates (15% or 25%). This missing data mechanism resulted in two missing data patterns: all X1, X2, and X3 were either observed or missing.
Scenario 2	We generated three random uniform variables (U1, U2, U3). We created missing values of X1, X2, and X3 for cases in the lower quartile of U1, U2, and U3, respectively, for each variable, based on the missing data rates (15% or 25%) (i.e., X1 with U1, X2 with U2, X3 with U3). This missing data mechanism resulted in maximum number of combinations of missing data patterns for X1, X2, and X3. (B) Missing at random (MAR) – six scenarios
Scenario 1	We computed the average scores of X4, X5, and X6, S = (X4 + X5 + X6)/3. Given the missing data rate conditions (15% or 25%), we divided the participants into quartiles according to S (i.e., 0%–24.99%, 25%–49.99%, 50%–74.99%, 75%–100%). We then used one uniform random variable to randomly delete X1, X2, and X3 in each quartile based on designated percentages. In the 15% missing data rate condition, the designated percentages from the first to the fourth quartiles were 7.5%, 12.5%, 17.5%, 22.5%. In the 25% condition, the designated percentages were 10.0%, 20.0%, 30.0%, 40.0%. These percentages result in a monotonic increasing relationship between missing data rate and S (Collins et al., 2001).
Scenario 2	The procedures were identical to those of Scenario 1 except for the designated percentages of missing data in the quartiles. In the 15% missing data rate condition, the designated percentages from the first to the fourth quartiles were 25.0%, 5.0%, 5.0%, 25.0%. In the 25% condition, the designated percentages were 10.0%, 20.0%, 30.0%, 40.0%. These percentages result in a convex relationship between missing data rate and S (Collins et al., 2001).
Scenario 3	We divided X1, X2, and X3 into quartiles according to the variables they paired with to form product indicators, respectively (i.e., X1 with X4, X2 with X5, X3 with X6). We then used three separate uniform random variable to randomly delete X1, X2, and X3 in each quartile based on designated percentages. The designated percentages were the same as those in Scenario 1.
Scenario 4	The procedures were identical to those of Scenario 3, except that we divided X1, X2, and X3 into quartiles according to the variables they did not pair with to form product indicators, respectively (i.e., X1 with X5, X2 with X6, X3 with X4).
Scenario 5	The procedures were identical to those of Scenario 3, except that we used the designated percentages that were the same as those in Scenario 2 (i.e., 15% missing data rate: designated percentages = 25.0%, 5.0%, 5.0%, 25.0%; 25% missing data rate: designated percentages = 10.0%, 20.0%, 30.0%, 40.0%).
Scenario 6	The procedures were identical to those of Scenario 4, except that we used the designated percentages that were the same as those in Scenario 2 (i.e., 15% missing data rate: designated percentages= 25.0%, 5.0%, 5.0%, 25.0%; 25% missing data rate: designated percentages = 10.0%, 20.0%, 30.0%, 40.0%).

Among these six scenarios, Scenarios 1 and 2 resulted in two missing data patterns, where all X₁, X₂, and X₃ were either observed or missing. Scenarios 3, 4, 5, and 6 resulted in maximum number of combinations of missing data patterns for X₁, X₂, and X₃.

Latent variable interaction methods

In FIML for CPI, GAPI, and UPI, we mean-centered X₁ to X₆ using the FIML estimated means and fixed their latent intercepts to zero in the models, so as to improve the chances of successful model convergence (Algina & Moulder, 2001). In FIML for LMS, we freely estimated the latent intercepts of X₁ to X₆, which is the default model specification in SEM software. We used Hermite-Gaussian quadrature integration with 16 integration points per integration dimension (Klein &Moosbrugger, 2000). All analyses were conducted using Mplus Version 7.11 (Muthén & Muthén, 1998–2015). In all methods, we overrode software defaults by increasing the maximum number of iterations and decreasing the convergence criterion. The Appendix presents the settings.

To sum up, we manipulated five factors (interaction effect size [three levels], sample size [five levels], missing data rate [three levels], missing data mechanism [two levels], latent variable interaction methods [four levels]) resulting in a total of 1,440 conditions. We randomly generated 1,200 replications for each condition in SAS/IML Version 9.3. In all conditions, the indicators X₁ to X₆ were multivariate normally distributed. We discussed the situation where X₁ to X₆ were nonnormal in the General Discussion section.

Dependent measures

To investigate the estimates of γ₀, γ₁, γ₂, and γ₃, we used these dependent measures: model convergence rate, relative bias, mean squared error, standard error ratio, coverage rate, actual Type I error rate (γ₃ only), and statistical power (γ₃ only).

Model convergence rate

A set of model results is considered to be properly converged if it satisfies three conditions: (a) no errors reported by Mplus, (b) no negative variance estimates, and (c) no out-of-bound correlation estimates. The model convergence rate in one condition is the proportion of number of properly converged replications to the total number of replications (= 1,200).

Relative bias

Relative bias of a parameter estimate is the difference between the mean parameter estimate across converged replications and the population value relative to the population value.

$$\text{Relative}\text{Bias}=\left(\overline{\widehat{\theta }}-\theta \right)/\theta ,$$ (11)

where θ refers to any parameter (γ₀, γ₁, γ₂, γ₃); θ̂ is the parameter estimate. We used the suggestion by Hoogland and Boosma (1998) that an unbiased parameter estimate should have absolute value of relative bias < 0.05.

Standard error ratio

Standard error ratio is the average ratio of estimated standard error to the standard deviation of parameter estimates across converged replications.

$$\text{Standard}\text{Error}\text{Ratio}=\left(\sum _k\left[SE\left(\widehat{\theta }\right)/SD\left(\widehat{\theta }\right)\right]\right)/k,$$ (12)

where Σ_k(·) is the summation function across converged replications; k is the number of converged replications; SE(θ̂) is the estimated standard error of θ̂; SD(θ̂) is the standard deviation of θ̂ across converged replications. Standard error ratio evaluates the bias of estimated standard error. We used the suggestion by Hoogland and Boosma (1998) that an unbiased standard error estimate should have the ratio within 0.9 to 1.1.

Mean squared error

Mean squared error (MSE) is the average squared difference between the parameter estimate and its population value across converged replications.

$$\text{MSE}=\sum _k{\left(\widehat{\theta }-\theta \right)}^2/k.$$ (13)

MSE is also the sum of squared bias and variance of parameter estimate. We prefer a parameter estimate with small MSE.

Actual Type I error rate and statistical power (γ₃ only)

Actual Type I error rate is the proportion of converged replications that incorrectly reject the null hypothesis of no interaction effect (H₀: γ₃ = 0; two-tailed test) at α (set at .05) when the interaction effect is absent (sr² = 0). Statistical power is the proportion of replications that correctly reject this null hypothesis when the interaction effect is present (sr² = 0.05 or 0.10). We used the suggestion by Savalei (2010) that actual Type I error rate should be within the interval of $\alpha \pm z_{(1-\alpha /2)}\sqrt{\alpha (1-\alpha )/k}$. This results in the suggested interval = [0.036, 0.064].

Coverage rate

Coverage rate is defined as the proportion of converged replications that the 95% Wald confidence interval of a parameter includes its population value. Coverage rate reflects both the bias of parameter estimate and the bias of estimated standard error. We used the suggestion by Collins et al. (2001) that a satisfactory coverage rate should be > 0.9.

Results

We presented the simulation study results in the following order: model convergence rate, performance of interaction effect γ₃, and performance of lower-order effects (γ₀, γ₁, γ₂). When all indicators were completely observed, the results of all dependent measures were consistent with those in the literature (Cham et al. 2012; Coenders et al., 2008; Klein & Moosbrugger, 2000; Marsh et al., 2004; Wall & Amemiya, 2001). Given the space limit, we did not present these results in the text and summarized the results in tables and figures. We focused on the results when the indicators were MCAR or MAR. The results were consistent across the two scenarios of MCAR and the six scenarios of MAR, respectively. Therefore, we aggregated the results across the various scenarios and presented the results as MCAR and MAR conditions.⁴ It is noted that the results in the complete data condition were always better than those in the MCAR or MAR conditions because completely observed data have more information. To simplify the presentation, we dropped the term FIML because all four methods (CPI, GAPI, UPI, LMS) used FIML estimation. A full report of the results is available in the online supplementary materials.

Model convergence rate

Across all conditions, LMS produced the highest average convergence rate (99.7%). UPI and CPI performed similarly but were worse than LMS (average coverage rates = 92.2% and 93.7%, respectively). GAPI had the lowest average convergence rate (71.8%, range = 39.6% to 93.3%). In particular, GAPI had low convergence rates in MCAR and MAR conditions. In subsequent analyses, we investigated the first 1,000 converged replications in each condition.

The interaction effect

Parameter estimates and relative biases

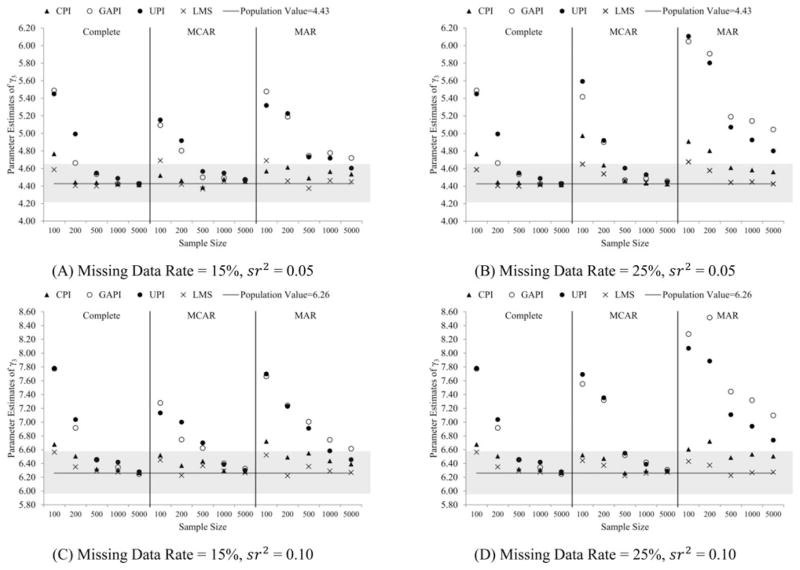
Figure 1 presents the mean estimates and relative biases of γ₃. The four panels in Figure 1 show the results of different combinations of missing data rate (15% or 25%) and interaction effect size (sr² = 0.05 or 0.1). In each panel, we presented the results according to the sample sizes (horizontal axis, from N = 100 to N = 5,000), and missingness conditions (three subpanels, left: complete data; middle: MCAR; right: MAR). The vertical axis is the mean estimates. The horizontal line indicates the population value. The gray box highlights the acceptable region of γ₃ estimates with relative bias < 0.05.

Figure 1.

Mean estimates and relative biases of interaction effect γ_3.

When X₁, X₂, X₃ were MCAR, missing data rate = 25%, and sr² = 0.05, CPI produced unbiased estimates when N ≥ 200. GAPI and UPI produced unbiased estimates when N ≥ 500 while LMS produced unbiased estimates across all sample sizes. The ranking in terms of relative bias was LMS < CPI < GAPI < UPI. When X₁, X₂, X₃ were MCAR and sr² = 0.10, CPI and LMS produced unbiased estimates across all sample sizes while GAPI and UPI produced unbiased estimates when N ≥ 1,000. The ranking was LMS < CPI < GAPI ~ UPI. When X₁, X₂, X₃ were MAR, missing data rate = 15%, and sr² = 0.05, CPI produced unbiased estimates across all sample sizes, but GAPI failed to produce unbiased estimates across all samples sizes. UPI produced unbiased estimates only when N = 5,000, and LMS produced unbiased estimates when N ≥ 200. The ranking was CPI < LMS < UPI < GAPI. When missing data rate = 25% and sr² = 0.05, CPI produced unbiased estimates when N ≥ 500. GAPI and UPI failed to produce unbiased estimates across all samples sizes. When N = 200, relative bias by GAPI and UPI = 33% and 31%, respectively. LMS produced unbiased estimates across all sample sizes, with slightly large bias at N = 100 (relative bias = 5.6%). The ranking was LMS<CPI <GAPI~UPI. When sr² = 0.10, CPI produced unbiased estimates when N ≥ 200. GAPI failed to produce unbiased estimates across all sample sizes. When N = 200 and missing data rate = 25%, relative bias by GAPI = 26%. UPI only produced unbiased estimates when missing data rate = 15%. LMS resulted in unbiased estimates across all sample sizes. The ranking was LMS < CPI < UPI < GAPI.

Mean squared error

Table 4 presents the mean squared errors (MSEs) of γ₃ estimates. MSE is the sum of squared bias and variance of γ₃ estimates. Thus, the conditions that have large relative biases also have large MSEs. In addition, the variance of γ₃ estimates decreases when sample size N increases. We prefer a latent variable interaction method with small MSEs.

Table 4.

Mean square errors (MSEs) of interaction effect γ_3.

N	Missing data rate	Complete data				Missing completely at random (MCAR)				Missing at random (MAR)
		CPI	GAPI	UPI	LMS	CPI	GAPI	UPI	LMS	CPI	GAPI	UPI	LMS
(A) sr2 = 0.05
100	15%	18.038	65.174	50.969	13.098	21.041	51.618	60.430	16.133	22.991	67.182	78.330	17.448
100	25%	18.038	65.174	50.969	13.098	25.096	65.182	84.333	16.781	26.629	117.016	94.623	17.163
200	15%	7.317	10.592	33.881	5.626	8.558	18.053	18.735	6.113	9.595	21.447	23.738	6.218
200	25%	7.317	10.592	33.881	5.626	9.505	21.121	29.555	6.050	11.185	42.852	36.609	6.439
500	15%	2.732	3.281	3.486	2.028	3.048	3.807	4.397	1.961	3.151	4.443	4.852	1.990
500	25%	2.732	3.281	3.486	2.028	3.487	4.492	5.617	2.143	3.952	7.560	7.292	2.178
1,000	15%	1.281	1.383	1.549	0.949	1.378	1.618	1.770	0.933	1.477	2.053	2.044	0.942
1,000	25%	1.281	1.383	1.549	0.949	1.459	1.749	1.914	1.013	1.757	3.270	2.954	1.035
5,000	15%	0.220	0.241	0.264	0.178	0.260	0.285	0.317	0.189	0.304	0.466	0.395	0.187
5,000	25%	0.220	0.241	0.264	0.178	0.295	0.342	0.354	0.199	0.398	1.044	0.706	0.199
(B) sr2 = 0.10
100	15%	19.621	72.081	70.521	16.171	21.713	56.324	67.656	18.166	24.396	60.920	72.557	18.612
100	25%	19.621	72.081	70.521	16.171	24.100	145.940	99.795	18.382	25.988	94.977	126.243	18.380
200	15%	8.009	13.696	15.435	5.749	8.654	14.578	21.867	6.084	9.259	22.160	26.135	6.052
200	25%	8.009	13.696	15.435	5.749	9.971	25.702	28.345	6.789	11.956	48.520	46.797	7.029
500	15%	2.682	3.628	3.834	2.035	3.359	4.606	5.657	2.226	3.611	5.878	6.651	2.204
500	25%	2.682	3.628	3.834	2.035	3.788	5.391	6.218	2.541	4.431	11.290	9.233	2.552
1,000	15%	1.304	1.615	1.701	0.908	1.435	1.817	2.063	1.048	1.640	2.540	2.505	1.063
1,000	25%	1.304	1.615	1.701	0.908	1.724	2.281	2.530	1.101	2.138	5.149	4.077	1.164
5,000	15%	0.253	0.295	0.320	0.184	0.309	0.366	0.422	0.199	0.377	0.626	0.517	0.205
5,000	25%	0.253	0.295	0.320	0.184	0.343	0.421	0.455	0.214	0.511	1.583	0.944	0.215

Note. CPI = constrained product indicators; GAPI = generalized appended product indicators; UPI – unconstrained product indicators; LMS = latent moderated

structural equations.

When X₁, X₂, X₃ were MCAR, LMS also had the lowest MSEs across all sample sizes and interaction effect sizes. CPI had larger MSEs than LMS across all conditions. When sample sizes increased, the differences of MSEs between CPI and LMS increased. GAPI and UPI had much larger MSEs than LMS when N ≤ 200 (at least two times as large). With increasing missing data rate, MSEs by GAPI and UPI further increased when N ≤ 200, suggesting large variation of γ₃ estimates in these conditions. The ranking was LMS<CPI<GAPI~UPI. When X₁, X₂, X₃ were MAR, LMS performed better than all PI methods across sample sizes, missing data rates, and interaction effect sizes. Unlike PI, MSEs of LMS were not much affected by missing data rates. CPI had larger MSEs than LMS across all conditions. At N = 5,000, the MSEs by CPI were also two times those by LMS. Given that CPI and LMS had acceptable biases of γ₃ estimates, the MSE results meant that CPI was a less efficient method than LMS that produced more variable γ₃ estimates. GAPI and UPI produced much larger MSEs compared to LMS across all conditions (at least two times as large). The ranking was LMS < CPI < GAPI ~ UPI.

Standard error ratio

Table 5 presents the standard error ratios of γ₃ estimates. When the ratio = 1, standard error (SE) is unbiasedly estimated. When the ratio < 1, SE is underestimated. When the ratio > 1, SE is overestimated. We used the suggestion that an unbiased SE estimate should have SER within 0.9 to 1.1 (Hoogland & Boosma, 1998). The results of the complete data condition were consistent with simulation studies in literature. CPI and LMS produced unbiased SEs when N ≥ 200. CPI and LMS produced slightly underestimated SEs when N = 100. The biases of LMS were smaller than those of CPI. GAPI and UPI produced unbiased SEs when N ≥ 1,000. GAPI and UPI often underestimated SEs when N ≤ 500. The ranking of the four methods was LMS < CPI < GAPI ~ UPI.

Table 5.

Standard error ratios (SERs) of interaction effects γ₃.

N	Missing data rate	Complete data				Missing completely at random (MCAR)				Missing at random (MAR)
		CPI	GAPI	UPI	LMS	CPI	GAPI	UPI	LMS	CPI	GAPI	UPI	LMS
(A) sr2 = 0.05
100	15%	0.871	0.863	0.900	0.924	0.888	1.120	1.140	0.902	0.873	1.028	1.068	0.884
100	25%	0.871	0.863	0.900	0.924	0.859	1.021	1.065	0.909	0.866	1.242	1.339	0.916
200	15%	0.913	0.890	0.778	0.939	0.906	0.826	0.846	0.938	0.891	0.826	0.864	0.938
200	25%	0.913	0.890	0.778	0.939	0.921	0.800	0.986	0.969	0.913	0.918	0.889	0.954
500	15%	0.912	0.891	0.893	0.955	0.929	0.895	0.880	1.004	0.944	0.904	0.878	1.002
500	25%	0.912	0.891	0.893	0.955	0.908	0.877	0.823	0.985	0.913	0.857	0.842	0.985
1,000	15%	0.920	0.922	0.903	0.972	0.955	0.930	0.925	1.016	0.964	0.914	0.917	1.017
1,000	25%	0.920	0.922	0.903	0.972	0.978	0.947	0.948	1.002	0.966	0.911	0.903	0.998
5,000	15%	0.985	0.967	0.950	0.997	0.973	0.964	0.943	1.002	0.972	0.925	0.922	1.011
5,000	25%	0.985	0.967	0.950	0.997	0.957	0.925	0.939	0.998	0.953	0.886	0.908	1.006
(B) sr2 = 0.10
100	15%	1.000	0.897	0.863	0.832	0.873	0.987	1.103	0.873	0.849	1.050	1.072	0.878
100	25%	1.000	0.897	0.863	0.832	0.883	0.989	1.557	0.918	0.890	1.130	1.349	0.923
200	15%	0.857	0.982	0.910	0.842	0.912	0.869	0.821	0.978	0.918	0.858	0.872	0.985
200	25%	0.857	0.982	0.910	0.842	0.919	0.790	0.863	0.969	0.898	0.866	0.906	0.958
500	15%	0.897	1.003	0.938	0.873	0.909	0.872	0.845	1.005	0.915	0.867	0.835	1.011
500	25%	0.897	1.003	0.938	0.873	0.896	0.851	0.855	0.961	0.898	0.797	0.833	0.967
1,000	15%	0.929	1.051	0.942	0.899	1.435	1.817	2.063	1.048	1.640	2.540	2.505	1.063
1,000	25%	0.929	1.051	0.942	0.899	0.920	0.871	0.876	1.012	0.914	0.823	0.844	0.993
5,000	15%	0.920	1.034	0.944	0.915	0.912	0.890	0.868	1.030	0.909	0.869	0.864	1.020
5,000	25%	0.920	1.034	0.944	0.915	0.915	0.879	0.890	1.022	0.938	0.872	0.885	1.029

Note. CPI = constrained product indicators; GAPI = generalized appended product indicators; UPI – unconstrained product indicators; LMS = latent moderated structural equations.

When X₁, X₂, X₃ were MCAR, LMS had less biased SEs than all PI methods and produced unbiased SEs when N ≥ 200. CPI and LMS produced slightly underestimated SEs when N = 100. The biases of LMS were smaller than those of CPI. When sr² = 0.05, GAPI and UPI produced unbiased SEs only when N ≥ 1,000. When sr² = 0.10, GAPI and UPI often produced biased SEs. The ranking was LMS < CPI < GAPI ~ UPI.

When X₁, X₂, X₃ were MAR, LMS also had less biased SEs than all PI methods. LMS produced unbiased SEs when N ≥ 200. CPI slightly underestimated SEs when N ≤ 500. The biases of LMS were often smaller than those of CPI. GAPI and UPI produced unbiased SEs only when N ≥ 1,000 and sr² = 0.05. The ranking was LMS< CPI < GAPI ~ UPI.

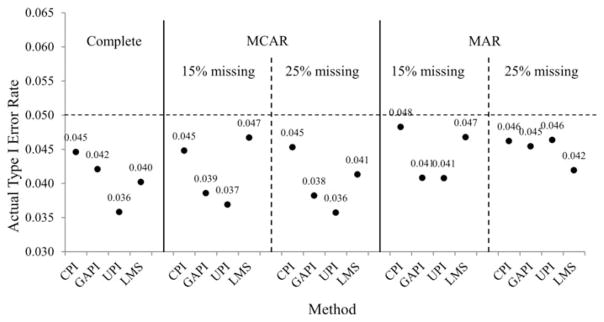
Actual Type I error rate and statistical power

Figure 2 presents the actual Type I error rates of γ₃. We averaged the results across samples sizes because the findings were consistent. We used the suggestion that actual Type I error rate should be between 0.036 and 0.064 (Savalei, 2010). All methods had acceptable Type I error rate of γ₃ when X₁, X₂, X₃ were completely observed, MCAR, or MAR. The actual Type I error rates by GAPI and UPI were on the lower bound (= 0.036) in the complete data and MCAR conditions. These results imply that GPI and UPI had lower statistical power in these conditions.

Figure 2.

Actual Type I error rate of interaction effect γ₃. The numbers are the actual Type I error rates.

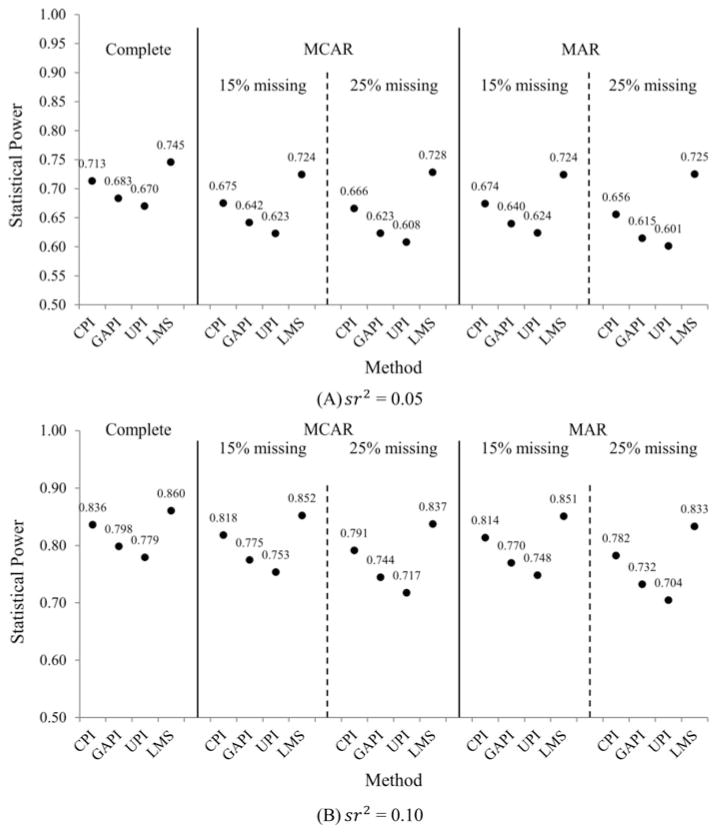
Figure 3 presents the statistical power of γ₃ when sr² = 0.05 (panel A) and 0.10 (panel B), respectively. We averaged the results across samples sizes because the findings were consistent. As expected, statistical power increased when the interaction effect size (sr²) increased. Among all methods, LMS had the highest statistical power when X₁, X₂, X₃ were completely observed, MCAR, or MAR. The ranking of the four methods in terms of statistical power was LMS > CPI > GAPI > UPI.

Figure 3.

Statistical power of interaction effect γ₃. The numbers are the statistical power.

Coverage rate

Table 6 shows the coverage rates of γ₃. Coverage rate reflects a combination of the bias of γ₃ estimate and the bias of the estimated standard error. We used the suggestion that the satisfactory coverage rate should be > 0.9 (Collins et al., 2001). When X₁, X₂, X₃ were completely observed or MCAR, all methods produced satisfactory coverage rates across sample sizes and interaction effect sizes. When X₁, X₂, X₃ were MAR, CPI and LMS produced satisfactory coverage rates across interaction effect sizes and missing data rates. When the sample size, interaction effect size, and missing data rate increased, CPI, GAPI, and UPI produced lower coverage rates than LMS. When N = 5,000, missing data rate = 25%, and sr² = 0.1, the minimum coverage rate = 91.3% for LMS, 73.8% for CPI, 42.2% for GAPI, and 64.3% for UPI.

Table 6.

Coverage rates of interaction effect γ₃ (%).

N	Missing data rate	Complete data				Missing completely at random (MCAR)				Missing at random (MAR)
		CPI	GAPI	UPI	LMS	CPI	GAPI	UPI	LMS	CPI	GAPI	UPI	LMS
(A) sr2 = 0.05
100	15%	94.0	94.4	93.5	94.3	93.0	95.1	94.2	93.8	93.5	95.1	93.8	93.6
100	25%	94.0	94.4	93.5	94.3	94.0	95.0	93.7	93.6	94.2	95.8	94.5	93.8
200	15%	91.4	92.9	92.4	92.9	93.3	93.9	93.4	94.4	93.3	94.6	93.8	94.2
200	25%	91.4	92.9	92.4	92.9	95.2	94.6	93.5	95.1	94.6	95.7	94.4	95.1
500	15%	92.3	92.9	92.5	93.5	93.4	93.1	92.5	94.7	94.1	94.1	93.3	95.1
500	25%	92.3	92.9	92.5	93.5	93.6	93.8	93.4	95.0	92.8	93.9	93.8	94.6
1,000	15%	93.4	93.4	93.4	94.5	94.1	93.3	93.4	95.4	94.1	93.3	93.9	95.4
1,000	25%	93.4	93.4	93.4	94.5	95.1	93.5	94.4	95.4	94.7	93.2	93.6	95.4
5,000	15%	94.0	94.5	93.2	95.2	93.9	94.1	94.0	94.5	93.6	89.9	92.1	94.7
5,000	25%	94.0	94.5	93.2	95.2	93.6	92.9	93.6	94.8	92.5	80.4	86.2	94.8
(B) sr2 = 0.10
100	15%	91.7	92.1	92.2	92.1	91.7	92.6	90.8	91.4	92.0	92.9	91.0	92.2
100	25%	91.7	92.1	92.2	92.1	92.5	93.2	91.4	93.1	92.9	93.6	91.9	93.1
200	15%	92.9	93.4	92.1	94.3	92.7	93.6	92.3	93.7	93.3	94.5	92.4	93.9
200	25%	92.9	93.4	92.1	94.3	93.1	93.1	92.8	94.9	93.5	94.8	93.3	94.5
500	15%	94.0	92.4	93.1	95.1	93.3	92.9	93.0	95.9	93.2	93.7	92.9	95.4
500	25%	94.0	92.4	93.1	95.1	92.3	92.1	91.9	94.7	93.3	93.2	93.5	94.2
1,000	15%	93.7	92.3	93.6	95.5	93.7	94.1	92.9	94.8	93.3	93.4	93.2	95.0
1,000	25%	93.7	92.3	93.6	95.5	93.3	92.1	92.3	95.2	92.6	89.3	91.1	95.0
5,000	15%	94.4	92.3	93.5	95.5	92.9	92.4	91.5	95.5	91.4	86.4	90.1	95.5
5,000	25%	94.4	92.3	93.5	95.5	92.6	91.5	92.2	95.2	89.4	74.2	84.3	95.5

Note. CPI = constrained product indicators; GAPI = generalized appended product indicators; UPI – unconstrained product indicators; LMS = latent moderated structural equations.

Performance of lower-order effects

In this section, we presented the results of the lower-order effects γ₀, γ₁, and γ₂. A full report of the results is available in the online supplementary materials.

Parameter estimates and relative biases

When X₁, X₂, X₃ were completely observed, CPI and LMS produced unbiased γ₀ estimates across sample sizes and interaction effect sizes. GAPI and UPI sometimes underestimated γ₀ when N = 100. All four methods produced unbiased γ₁ estimates when N ≥ 200. CPI, GAPI, and LMS produced unbiased γ₂ estimates across sample sizes and interaction effect sizes. UPI overestimated γ₂ when N = 100.

When X₁, X₂, X₃ were MCAR, the four methods also produced unbiased γ₀ estimates across sample sizes and interaction effect sizes. For all methods, the relative biases of γ₀ estimates decreased when sample size increased. When N = 100 or 200, the relative biases of γ₀ estimates by GAPI and UPI were slightly larger than those by CPI and LMS. All methods produced unbiased γ₁ estimates when N ≥ 500. When N = 200, CPI and LMS resulted in unbiased γ₁ estimates, except the condition of missing data rate = 25%, sr² = 0.05. The relative bias of γ₁ estimates by GAPI and UPI were larger than those by CPI and LMS. UPI overestimated γ₁ more often than the other methods. All methods produced unbiased γ₂ estimates when N ≥ 200. When N = 100, CPI produced unbiased γ₂ estimates, and the other methods overestimated γ₂.

All four methods generally performed worse in the MAR condition than in the complete data or MCAR conditions. CPI and LMS produced unbiased γ₀ estimates across sample sizes and interaction effect sizes. GAPI and UPI produced unbiased γ₀ estimates when N ≥ 500. All methods could overestimate γ₁ when N ≤ 200, while LMS had the least bias across conditions. When N ≥ 500, CPI and LMS produced unbiased γ₁ while GAPI and UPI overestimated γ₁. All methods could overestimate γ₂ when N ≤ 200, while CPI had the least bias across conditions. When N ≥ 500, CPI and LMS produced unbiased γ₂ while GAPI and UPI overestimated γ₂.

Mean square error

Consistent with the results for interaction effect γ₃, MSEs of the lower-order effects γ₀, γ₁, γ₂ increased when sample size increased. In addition, MSEs increased slightly when the interaction effect size increased or the missing data rates increased (MCAR or MAR). In the majority of the conditions, LMS outperformed all PI methods with the lowest MSEs. The difference between the MSEs produced by LMS and those by the PI methods decreased when N ≥ 500. GAPI and UPI produced the highest MSEs of the lower-order effects, especially under conditions with N = 100.

Standard error ratio

In general, LMS produced acceptable standard error estimates of the lower-order effects with the least bias. CPI sometimes underestimated the standard errors when N = 100 and when X₁, X₂, X₃ were MCAR or MAR. GAPI and UPI often overestimated standard errors of γ₀ when N = 100 or 200.

Coverage rate

Across all conditions, all four methods produced satisfactory and similar coverage rates of the lower-order effects γ₀, γ₁, and γ₂. LMS produced slightly better coverage rates to the reference level 95% than the PI methods. Across conditions, the variability of the coverage rates of γ₁ by GAPI and UPI were noticeable. When N = 5,000, missing data rate = 25%, sr² = 0.1, their minimum coverage rates were 15.9% and 16.3%, respectively.

Summary and discussion

The simulation results have supported our hypotheses that when the indicators are MCAR or MAR, FIML for LMS produce unbiased γ₀, γ₁, γ₂, γ₃ estimates and valid statistical inferences across sample sizes, missing data rates, and interaction effect sizes. It is because FIML for LMS makes correct distributional assumption in the sample log-likelihood function. In the simulation, the indicators of ξ₁ and ξ₂ were multivariate normally distributed, which met the assumptions of LMS. Our hypotheses concerning PI have been supported as well. In the simulation, CPI generally produced unbiased γ₀, γ₁, γ₂, γ₃ estimates and valid statistical inferences when the indicators were MCAR. Compared to LMS, CPI produced γ₃ estimates with larger biases and MSEs. GAPI and UPI could produce unbiased γ₃ estimates, especially when N ≥ 500. The results of GAPI and UPI were acceptable since they also require N ≥ 500 to produce unbiased estimates in the complete data condition (Cham et al., 2012). Therefore, the results have confirmed our hypothesis that PI produces unbiased estimates when the indicators are MCAR. When the indicators were MAR, GAPI and UPI overestimated γ₃. CPI produced less overestimated γ₃ and sometimes even unbiased estimates. These results have supported our hypothesis that PI produces biased estimates when the indicators are MAR. FIML for PI incorrectly assumes that ξ₁ξ₂ and the product indicators are normally distributed. The differences between the results by the CPI, GAPI, and UPI are due to the imposed model constraints in Table 1 that are related to the distribution of ξ₁ξ₂. CPI has the most model constraints, followed by GAPI and UPI. The results suggest that when more of these model constraints are imposed, the biases of parameter estimates reduce. However, compared to LMS, CPI produced γ₃ estimates with larger biases and MSEs. When sample size increased, MSEs of CPI became much larger than those of LMS. The results imply that CPI is much less efficient than LMS. Thus, LMS should be preferred. The convergence rates by GAPI are surprisingly low, which may imply the dependencies between the model constraints and missing values. Given the simulation study results and the complexity to specify the model constraints in PI methods in SEM software, we recommend FIML for LMS when the indicators are MCAR or MAR and when they are multivariate normally distributed.

Substantive example

We applied FIML estimation for CPI, GAPI, UPI, and LMS to a substantive example with incompletely observed indicators. Data were drawn from a study of 266 advanced cancer patients (mean age = 59.1 years, SD = 11.6) who participated in a randomized psychotherapy study (Breitbart et al., 2015). Patients were assessed at three time points: pretreatment (T1), posttreatment (T2), and two-month follow-up (T3). We adapted the results by McClain, Rosenfeld, and Breitbart (2003) to investigate the interaction effect between patients’ depression at T1 (ξ₁) and the change of their inner peace well-being between T1 and T2 (ξ₂) on their hopelessness at T3 (η). Patients’ depression at T1 was self-reported by the 21-item Beck Depression Inventory (0 to 3 points; α = .88; Beck, Ward, Mendelson, Mock, & Erbaugh, 1961). Inner peace well-being (hereafter referred to as “Peace”) was self-reported by the four-item Peace subscale of the Functional Assessment of Chronic Illness Therapy Spiritual Well-being Scale (0 = not at all to 4 = very much; Brady, Peterman, Fitchett, Mo, & Cella, 1999). Change scores of the four items (T2 minus T1) had lower Cronbach’s α (.65; Edwards, 2001). Hopelessness at T3 was self-reported by the 20-item Beck Hopelessness Scale (0 = False, 1 = True; α = .92; Beck, Weissman, Lesster, & Trexler, 1974). We used the average scores of the depression items and the sum of the hopelessness items in the latent variable interaction model. To account for unreliability of the change scores of Peace, we used a factor model for the four change scores.

Table 7 shows the missing data patterns of the variables; 129 patients (48.5%)were completely observed on all variables, 84 patients (31.6%) were missing on all four change scores of Peace and hopelessness at T3, and 44 patients (16.5%) were missing on hopelessness at T3. Little’s (1988) MCAR test showed that the variables’ means did not vary significantly between missing data patterns, χ²(29) = 15.00, p = .99. Jamshidian and Jalal’s (2010) MCAR test showed that variables’ variances and covariances were not significantly different between missing data patterns, p = .21. However, there was a small to medium relationship between treatment assignment and the three major missing data patterns, χ²(2) = 5.36, p = .07, Cohen’s ω = 0.14. Given this relationship and the treatment effect on patients’ distress (including hopelessness), we set treatment assignment as an auxiliary variable to account for missingness by letting it freely correlate with all variables in the model (Enders, 2010).

Table 7.

Missing data patterns of substantive example.

Missing data pattern	Depression (T1)	Change of inner peace well-being (T2 – T1)	Hopelessness (T3)	n (%)
1	√	√	√	129 (48.5%)
2	√	×	×	84 (31.6%)
3	√	√	×	44 (16.5%)
Other patterns				9 (3.4%)

Our simulation has suggested that FIML for CPI and LMS produce unbiased parameter estimates when N ≥ 200. Therefore, only these methods were used in this analysis. In CPI, we centered depression and all four Peace change scores at their EM estimated means. We chose the change score with the highest reliability to form the product indicator with depression. LMS permits that ξ₁ is a single variable and ξ₂ is a factor. We also centered depression (ξ₁) at its FIML estimated mean and set the mean of the change in Peace factor to zero. Table 8 shows the results by CPI and LMS. The intercept and the effect of the completely observed depression at T1 had similar estimates and standard errors between CPI and LMS (differences < 5%). The effect of the change in Peace (T2 – T1) and the interaction effect had different estimates (differences ~ 22%) and standard errors (differences ~ 8%). Several reasons can explain the differences between the two methods. First, missing data rates for the four Peace change scores were higher than the conditions in simulation study. In the simulation, when the missing data rate increased, the biases of the parameter estimates by CPI were larger than those by LMS. Second, depression at T1 (ξ₁) had skewness = 1.22 and kurtosis = 2.89. The four Peace change scores (ξ₂) had average skewness = 0.13 and kurtosis = 0.85, which exceeded the suggested values for CPI and LMS (skewness = 0, kurtosis < 1; Cham et al., 2012). When the indicators are nonnormal, CPI and LMS can produce biased parameter estimates, though CPI produces less biased estimates than LMS (Cham et al., 2012). Third, the outcome variable (hopelessness) at T3 had missing values. In this situation, LMS shall produce unbiased parameter estimates and valid inferences while CPI may produce biased parameter estimates and standard errors. We discuss the second and third reasons in more details in the General Discussion section.

Table 8.

Illustrative example results.

Regression coefficient	CPI		LMS
	Est.	SE	Est.	SE
Intercept	5.74	0.41**	5.79	0.41**
Depression (T1)	5.47	1.03**	5.74	1.04**
Change of peace well-being (T2 – T1)	−0.62	0.46	−0.82	0.50
Interaction effect	−1.14	0.65	−1.41	0.71*

Note. CPI = constrained product indicator; LMS = latent moderated structural equations; Est. = parameter estimate; SE = estimated standard error.

^*p < .05;

^**p < .01.

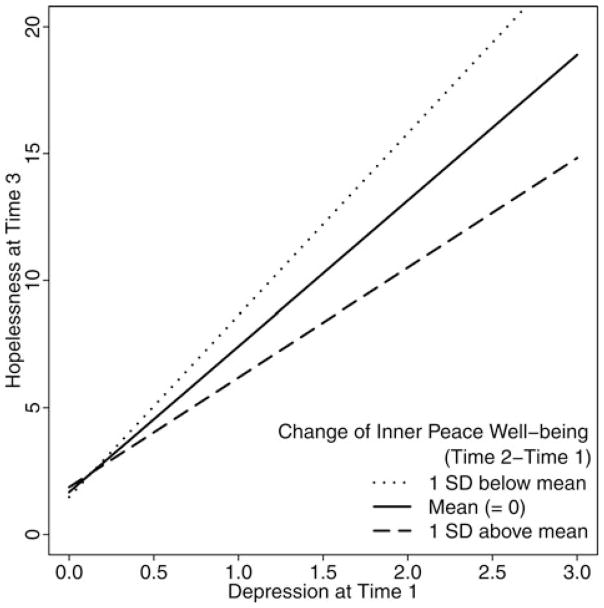
In summary, Figure 4 displays the interaction effect based on the results of LMS. Patients’ depression at T1 was positively related to their hopelessness at T3. For the patients with larger increase in their inner peace well-being from T1 to T2, this positive relationship was reduced.

Figure 4.

Interaction between depression (T1) and change of inner peace well-being (T2 – T1) on hopelessness (T3).

General discussion

In this manuscript, we investigated FIML estimation for four methods for estimation of latent variable interactions (CPI, GAPI, UPI, LMS) to handle incompletely observed indicators of ξ₁ and/or ξ₂. We conducted a simulation to investigate whether FIML for these methods produces unbiased parameter estimates and valid statistical inferences, and illustrated these methods using a substantive example. As discussed previously, we recommend FIML for LMS when the indicators are MCAR or MAR and are multivariate normally distributed. Our simulation did not consider the situation that the indicators of ξ₁ and ξ₂ are nonnormal (Cham et al., 2012; Coenders et al., 2008; Klein & Moosbrugger, 2000; Marsh et al., 2004; Wall & Amemiya, 2001). When the indicators of ξ₁ and ξ₂ are completely observed, the simulation study by Cham et al. (2012) has shown that FIML for LMS produces unbiased parameter estimates when the indicators have skewness = 0 and kurtosis < 1. FIML for GAPI and UPI produces unbiased estimates when the indicators have skewness < 2 and kurtosis < 6. When indicators are MCAR or MAR, FIML for CPI, GAPI, UPI, and LMS will not perform better than with complete data; FIML for LMS will produce biased estimates when MCAR or MAR indicators have skewness ≥ 2 and kurtosis ≥ 6.

Methods are needed to properly handle incompletely observed indicators of ξ₁ and/or ξ₂ when they are nonnormally distributed. There are several potential candidates. Kelava, Nagengast, and Brandt (2014) proposed incorporating mixture modeling with LMS to handle nonnormally distributed indicators in the complete data condition. This method also uses FIML for model estimation. Second, promising imputation procedures for interaction effects are being developed, and these procedures need to be investigated for possible use with latent variable interaction models. Doove et al. (2014) developed multiple imputation procedures using recursive partitioning, which estimates arbitrary nonlinear relationships among variables. Bartlett and Morris (2015), Bartlett et al. (2015), and Carpenter and Kenward (2013, Chapter 7) developed the multiple imputation procedures that account for the interaction effects that are being tested in the analyzed model when imputing missing values.

On the basis of our results that FIML for LMS leads to unbiased parameter estimates and valid statistics inferences for latent variable interactions, one may consider whether FIML for LMS works for multiple regression with interaction effects. As shown in the substantive example, the model is identified when ξ₁ is a single variable and ξ₂ is a factor. The specification is not identified when both ξ₁ and ξ₂ are single variables.

We did not consider all possible situations in our simulations. One interesting situation is that η or indicator of η is MCAR or MAR, which occurs in our substantive example. This situation is also not considered in the literature for multiple regression with interaction effects. In this situation, FIML for LMS still produces unbiased parameter estimates, standard error estimates, and valid statistical inferences, because it correctly handles the distribution of η. FIML for PI incorrectly assumes that η is normally distributed. It should be noted, however, that η is linearly related to ξ₁, ξ₂, and ξ₁ξ₂ in coefficients. In such case, violating the normality assumption of η in FIML has minimal effect on parameter estimates but can lead to biased standard error estimates and invalid statistical inferences (Yuan, Bentler, & Zhang, 2005). Future research is needed to examine how FIML for PI performs when η is MCAR or MAR. Another situation is when the indicators of ξ₁ and/or ξ₂ are missing not at random (MNAR). In general, FIML produces biased parameter estimates and invalid statistical inferences when variables are MNAR. Therefore, FIML for PI and LMS also produce biased parameter estimates when the indicators are MNAR. Future research is needed to investigate the applicability and performance of current MNAR methods (e.g., selection model and pattern mixture model) to latent variable interaction methods.

Appendix

Detailed settings of full information maximum likelihood (FIML) estimation for product indicator (PI) and latent moderated structural equations (LMS) methods.

Types of settings	Setting	Default
(A) PI (including CPI, GAPI, and UPI)
1. Maximum number of iterations for quasi-Newton algorithm	10,000	1,000
2. Maximum number of steepest descent iterations for quasi-Newton algorithm	100	20
3. Convergence criterion for quasi-Newton algorithm	0.000001	0.00005
(B) LMS
1. Numeric integration algorithm	Hermite-Gaussian Quadrature	Rectangular
2. Number of integration points per dimension	16	15
3. Maximum number of iterations for quasi-Newton algorithm	10,000	1,000
4. Maximum number of iterations for EM algorithm	2,000	500
5. Convergence criterion for quasi-Newton algorithm	0.000001	0.000001
6. Absolute observed-data log-likelihood change convergence criterion for EM algorithm	0.0000001	0.001
7. Relative observed-data log-likelihood change convergence criterion for EM algorithm	0.0000001	0.000001
8. Observed-data log-likelihood derivative convergence criterion for EM algorithm	0.000001	0.001

Note. CPI = constrained product indicator; GAPI = generalized appended product indicator; UPI = unconstrained product indicator.