Buffers Strongly Modulate Fibrin Self-Assembly into Fibrous Networks

Abstract

Fibrin is a plasma protein with a central role in blood clotting and wound repair. Upon vascular injury, fibrin forms resilient fibrillar networks (clots) via a multistep self-assembly process, from monomers, to double-stranded protofibrils, to a branched network of thick fibers. In vitro, fibrin self-assembly is sensitive to physicochemical conditions like the solution pH and ionic strength, which tune the strength of the noncovalent driving forces. Here we report a surprising finding that the buffer—which is necessary to control the pH and is typically considered to be inert—also significantly influences fibrin self-assembly. We show by confocal microscopy and quantitative light scattering that various common buffering agents have no effect on the initial assembly of fibrin monomers into protofibrils but strongly hamper the subsequent lateral association of protofibrils into thicker fibers. We further find that the structural changes are independent of the molecular structure of the buffering agents as well as of the activation mechanism and even occur in fibrin networks formed from platelet-poor plasma. This buffer-mediated decrease in protofibril bundling results in a marked reduction in the permeability of fibrin networks but only weakly influences the elastic modulus of fibrin networks, providing a useful tuning parameter to independently control the elastic properties and the permeability of fibrin networks. Our work raises the possibility that fibrin assembly in vivo may be regulated by variations in the acute-phase levels of bicarbonate and phosphate, which act as physiological buffering agents of blood pH. Moreover, our findings add a new example of buffer-induced effects on biomolecular self-assembly to recent findings for a range of proteins and lipids.

Introduction

Fibrin is a crucial component in human plasma based on its ability to self-assemble into elastic fibrillar networks that stem blood flow after vascular injury.¹ Fibrin also plays a major role as a scaffold for cell adhesion during wound healing.^2,3 In view of these physiological roles, fibrin is widely used as sealant during surgical procedures^4,5 and as scaffold material for regenerative tissue engineering, tumor models, and in vitro studies of cellular mechanoresponse.⁶⁻⁹ The need to understand the molecular basis of the self-assembly and mechanics of fibrin networks in the context of hemostasis, thrombosis, and cardiovascular diseases, together with the widespread use of fibrin in biomedical applications, has pushed intensive efforts over the last 70 years to explore biochemical ways to control the structure and mechanical properties of fibrin networks.^1,2

Fibrin polymerization presents a striking example of hierarchical biomolecular self-assembly. Fibrinogen, the molecular precursor of fibrin, is a hexamer comprising two identical sets of three polypeptide chains (Aα, Bβ, and γ) that are held together by disulfide bonds.¹⁰ The chains are folded into a trinodular, rod-shaped structure with a central E region and two distal D regions. Fibrinogen is enzymatically converted to fibrin by thrombin, which cleaves fibrinopeptides A and B (FpA and FpB) from the N-termini of the Aα and Bβ chains, respectively, and thus exposes so-called A and B knobs in the E region. The A knobs interact noncovalently with complementary a holes in the D regions of adjacent fibrin monomers, driving polymerization of fibrin into protofibrils consisting of two strands of fibrin molecules staggered by one-half the monomer length.^10,11 Once the protofibrils reach a critical length of about 600 nm,^12,13 they start to associate laterally, causing them to bundle into fibers that may contain 100 or more protofibrils. The fibers are branched and form a space-filling elastic network.¹⁴ The precise mechanism of protofibril bundling is unknown but has been proposed to involve B:b knob–hole interactions as well as associations of the long and flexible αC-terminal chains that protrude out from the protofibrils.^1,15,16 The network is further stabilized to become an insoluble clot via enzymatic cross-linking of the α and γ chains by Factor XIII,¹⁷ which also tightens the bundling of protofibrils.^18,19

Such a hierarchical assembly pathway, from monomers to protofibrils, to fibers, and finally to a branched network, provides multiple strategies for in vivo and in vitro regulation of fibrin self-assembly.²⁰ Indeed, it has been widely reported that the structure of the fibrin network is strongly influenced by many environmental factors, including the concentration of fibrinogen and thrombin, ions such as calcium, zinc, fluoride, and chloride, and also the solution pH and ionic strength, although the physicochemical and molecular origins remain poorly understood (Table S1).²¹⁻²⁹

One key element in the assembly conditions that has not been investigated is the presence of buffer compounds. These buffer compounds are always required to maintain constant pH during fibrin polymerization, and a variety of compounds (HEPES and Tris being the most common) and concentrations (10–100 mM being the most common) have been used for fibrin studies in the literature.²⁸⁻³⁶ While these buffer compounds have been typically considered to be inert and some, including HEPES, have actually been developed specifically to be biochemically inert (commonly termed Good’s buffers),^37,38 here we report that the structure of fibrin networks is highly sensitive to the presence of buffer compounds in the assembly solution, with all other environmental variables (i.e., pH and salt concentration, such as Cl^–1 level²⁸) kept fixed. Increasing concentrations of various Good’s buffers, including HEPES and PIPES buffer, result in fibrin networks with significantly thinner fibers. Quantitative analyses of the polymerization kinetics and the rheological response of the networks reveal that HEPES hampers the lateral association of protofibrils without altering the structural or mechanical properties of the protofibrils themselves. We show that this effect is specific neither to the activation mechanism that triggers fibrin self-assembly nor to the buffering agent and also takes place in fibrin clots formed from platelet-poor plasma (PPP). Our findings therefore suggest a universal physicochemical effect, which modulates the noncovalent driving forces of fibrin self-assembly. This finding is consistent with a range of recent studies showing a pronounced effect of buffer compounds on other self-assembling (bio)molecular systems, including lipid bilayers³⁹⁻⁴¹ and proteins.^42,43 These findings highlight the importance of resolving the challenge of understanding the complex role that water molecules play in self-assembly in aqueous environments.⁴⁴

Experimental Section

Materials

Human fibrinogen (plasminogen, von Willebrand Factor, and fibronectin depleted) and α-thrombin were obtained (in powder form in 20 mM sodium citrate-HCl, pH 7.4) from Enzyme Research Laboratories (Swansea, UK), dissolved in water, aliquoted to single-use volumes, and stored at −80 °C. Ancrod, a thrombin-like enzyme derived from the venom of the Mayalan pit viper, was obtained from the National Institute for Biological Standards and Control (Hertfordshire, UK), dissolved in water, and stored in single-use aliquots at −80 °C. Platelet-poor plasma (PPP) was obtained by two-step centrifugation of porcine blood freshly obtained from a local slaughterhouse near Eindhoven (The Netherlands) as described previously.⁴⁵ Buffer compounds HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), PIPES (piperazine-N,N′-bis(2-ethanesulfonic acid)), BHEP (1,4-bis(2-hydroxyethyl)piperazine), Tris (2-amino-2-hydroxymethylpropane-1,3-diol), and sodium bicarbonate were obtained from Sigma-Aldrich (Zwijndrecht, The Netherlands), dissolved in water, adjusted to achieve pH 7.4 by titration with 1 M NaOH (HEPES and PIPES) or 1 M HCl (BHEP, Tris, and bicarbonate), and stored at a concentration of 1 M. At pH 7.4 and 37 °C, the fractions of buffer protonation are 45% for HEPES, 15% for PIPES, 56% for BHEP, and 67% for Tris.⁴⁶

Fibrin Formation

Fibrin networks were formed by mixing fibrinogen, at final concentrations of 1, 3, or 6 mg/mL, with either thrombin or ancrod at 0.5 NIH U/mL in the indicated buffers (all at pH 7.4) containing 135 mM NaCl to provide a physiological ionic strength and 5 mM CaCl₂ to activate thrombin and FXIII at 37 °C. The final buffer concentration was varied between 20, 100, and 200 mM. The extent of fibrin polymerization (referred to as “clottability” in the hemostasis literature) was determined by pelleting the fully formed clots by centrifugation at 14 000g for 1 min and comparing the absorbance at a wavelength of 280 nm of the supernatant with that of the starting fibrinogen solution. Clotting of PPP was triggered by adding 20 mM CaCl₂ and 0.5 U/mL thrombin in the indicated buffers.

Physical Characterization of HEPES Buffers

The ionic strengths of solutions of 20, 100, and 200 mM HEPES and 150 mM NaCl, all at pH 7.4, were determined by measuring the solution conductivity using a Consort C861 multiparameter analyzer (Turnhout, Belgium) equipped with a Hanna-Instruments probe (Nieuwegein, The Netherlands). The viscosity of the solutions was measured at 37 °C by steady-shear measurements using shear rates of 50 s^–1 on a rheometer (MCR 501; Anton Paar, Graz, Austria) using a steel cone–plate geometry with 30 mm diameter and 1° cone angle.

Confocal Imaging

Confocal microscopy was used to visualize the fibrin networks in their native, hydrated state. For fluorescence imaging, Alexa Fluor 488-conjugated fibrinogen (Life Technologies, Bleiswijk, The Netherlands) was mixed with unlabeled fibrinogen in a 1:19 molar ratio. Samples containing varying final concentrations of fibrinogen and buffer molecules were prepared in sealed glass chambers made of a microscope coverslip and slide with Parafilm spacers and polymerized at 37 °C for 4 h before imaging. Imaging was performed on a Nikon Eclipse Ti inverted microscope equipped with a 100× oil-immersion lens (NA = 1.40), a 488 nm laser for illumination, and a photomultiplier tube (PMT) detector. To visualize PPP clots, confocal reflectance imaging of unlabeled samples was performed on a Zeiss LSM510 inverted microscope with a 63× oil-immersion lens (NA = 0.75). The samples were illuminated using a 488 nm laser, and the reflected light was detected using a PMT detector.

Permeability Measurement

The hydraulic permeability of fibrin networks was measured based on a standardized protocol.⁴⁷ Briefly, fibrin networks were assembled in cylindrical capillaries, after which 2 mL of buffer solution (20 mM HEPES, 150 mM NaCl, pH 7.4) was added on top of the samples and allowed to flow through. The flow rate, Q, was recorded by monitoring the drop in the height of the liquid column as a function of time, and the fibrin network permeability, κ, was calculated using Darcy’s law: κ = QLη/ΔPA, where L is the length of the sample in the capillary, η is the buffer viscosity, ΔP is the pressure drop, and A is the cross-sectional area of the sample.

Cross-Linking Analysis by SDS-PAGE

The degree of covalent cross-linking of the fibrin clots by FXIII, which copurifies with fibrinogen and is present in the fibrinogen stock solution, was analyzed using reducing SDS-PAGE. Clot formation of samples containing 1–6 mg/mL fibrinogen, 0.5 NIH U/mL thrombin, and 20–200 mM HEPES was initiated by addition of thrombin followed by incubation at 37 °C. The reaction was terminated after 4 h by addition of SDS-PAGE sample buffer (Sigma-Aldrich, Zwijndrecht, The Netherlands) and heating at 95 °C for 10 min. Samples holding the equivalent of 3 μg of fibrin per lane were run on 8% polyacrylamide gels. The gels were then stained with InstantBlue (Gentaur, Eersel, The Netherlands) and scanned for quantitative analysis.

Fibrinopeptide Release Kinetics Analysis

The kinetics of thrombin-catalyzed fibrinopeptide release was analyzed as described.¹⁹ Briefly, reaction mixtures containing 3 mg/mL fibrinogen in HEPES buffers of different concentrations were incubated with 5 mM CaCl₂ and 0.5 U/mL thrombin for different times at 37 °C, after which the reaction was quenched by placing the samples at 99 °C for 2 min. The samples were then centrifuged at 15 000g for 10 min, and the supernatant was run on an HPLC column at 40 °C. The peptide elution profile was monitored from the solution absorbance at a wavelength of 211 nm and analyzed to quantify the amount of released FpA and FpB in each time point. The data were fitted using a well-established kinetic model, assuming first-order FpA release kinetics and a consecutive reaction mechanism where FpB can be released only after FpA release.⁴⁸

Monitoring of Protofibril Formation and Lateral Association Using Turbidity

To monitor the polymerization time course upon thrombin (or ancrod) activation of fibrinogen, the extinction at 350 nm of samples containing 0.03 mg/mL fibrinogen and 0.5 U/mL thrombin in HEPES buffers of varying HEPES concentration (20, 100, or 200 mM HEPES, 150 mM NaCl, pH 7.4) was continuously monitored in quartz cuvettes (1 cm path length; Hellma Analytics, Müllheim, Germany) for 1 h at 37 °C using a Lambda 35 spectrophotometer (PerkinElmer, Groningen, The Netherlands). As there is negligible absorbance by the sample, the extinction is a direct measure of light scattering (as quantified by the turbidity, τ). The maximum turbidity (τ_max) provides information primarily about the final mass–length ratio of the fibers, whereas the slope of the τ(t)–curve provides information about the rate of protofibril lateral bundling. In addition, kinetic parameters were quantified following Hantgan and Hermans:¹³ (i) lag time, defined as the zero-intensity extrapolation of the steepest increase in τ(t), and (ii) half time, defined as the time elapsed between the end of the lag time and the time when τ(t) reaches one-half of τ_max.

Turbidimetry

Turbidimetry was used to quantify the mass–length ratio of the fibers within the fibrin network using a theoretical model for light scattering from isotropic networks of rigid rod-like particles,^18,27,49 with correction for wavelength dispersion.^19,50 Immediately after the addition of thrombin, fibrinogen solutions were transferred to quartz cuvettes (1 cm path length; Hellma Analytics, Müllheim, Germany), sealed with airtight caps to prevent evaporation, and placed in the spectrophotometer for 4 h of polymerization with sample temperature set at 37 °C. Wavelength scans were carried out in the range of 500–800 nm, except for samples formed in bicarbonate buffers, where the agreement between experimental curves and the analytical model was found in the range of 450–600 nm. These wavelength ranges were carefully selected from theoretical constraints posed by the model²⁷ and based on the sensitivity range of the spectrophometer (OD range from 0.01 to 2.8). Data analysis was done using a custom-written script in MATLAB (The MathWorks, Natick, MA).

Rheometry

The viscoelastic properties of the fibrin networks were measured using a stress-controlled Anton Paar rheometer equipped with a stainless steel cone–plate geometry (25 mm diameter, 1° cone angle). Fibrin samples were assembled in situ by transferring the fibrinogen solution immediately upon addition of thrombin onto the preheated (37 °C) bottom plate. Sample evaporation was prevented by coating the sample edges with mineral oil. Fibrin polymerization was monitored by applying an oscillatory shear strain with an amplitude of 1% and frequency of 1 Hz and recording the elastic (G′) and viscous (G″) shear modulus. After 2 h, both G′ and G″ always reached a plateau, indicating complete polymerization. To probe the mechanical response at large shear stresses, a differential prestress protocol⁵¹ was used, whereby a constant prestress σ was applied to the sample and the differential stiffness at this prestress value, K′(σ), was measured by superimposing a small oscillatory shear stress with a small amplitude of 0.1σ and a fixed frequency of 1 Hz. The prestress σ was increased from 0.1 to 10 000 Pa in 25 steps of 60 s each. All measurements were done at 37 °C.

Results

HEPES Strongly Influences Fibrin Network Structure and Permeability

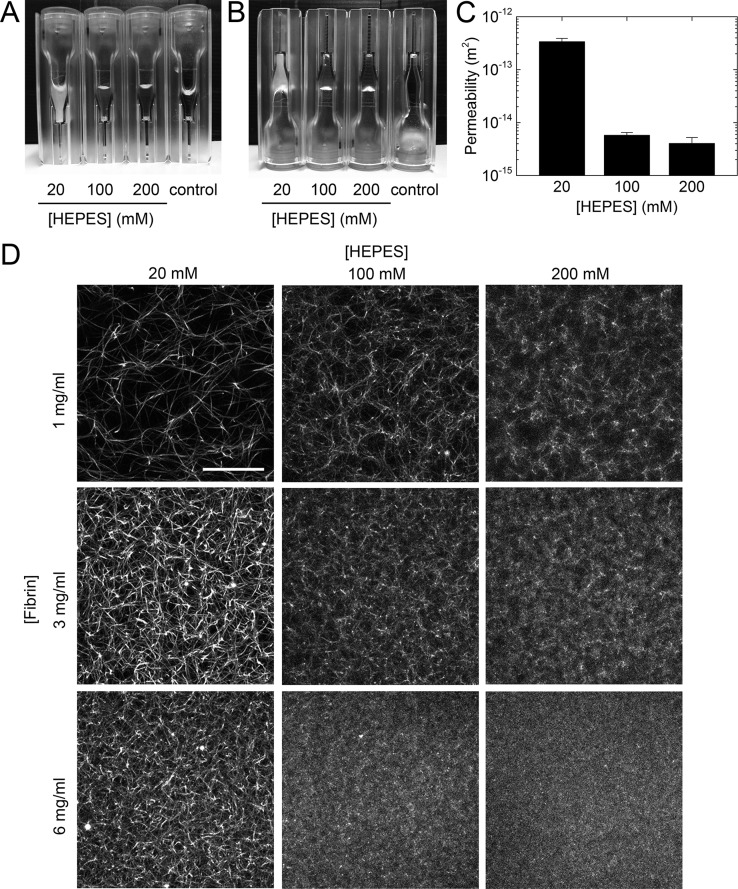
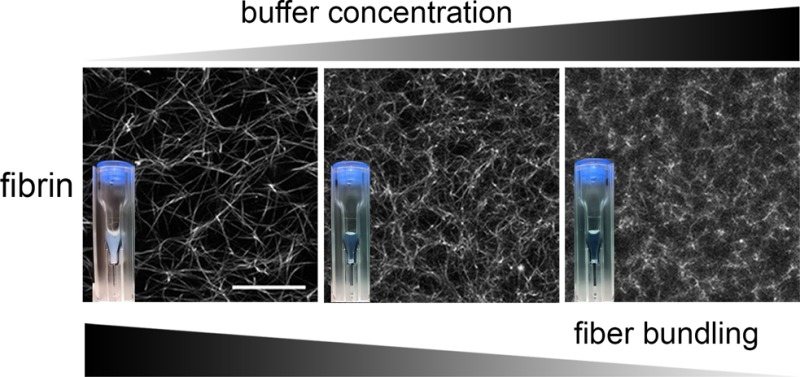
HEPES is a hydrogen ion buffer that is one of the most widely used buffers in biophysical and biochemical studies of fibrin self-assembly as well as in studies involving cells, due to its near-physiological pK_a value over a wide temperature range (7.48 at 25 °C and 7.31 at 37 °C).⁴⁶ Being one of Good’s buffers, HEPES is expected to be biochemically inert,^37,38 and a wide range of HEPES concentrations has been used in fibrin studies.^{30,31,34−36} Although HEPES has been reported to lead to complexation of copper(II) ions,^52,53 it does not sequester other metal ions such as Ca²⁺.^37,38 HEPES therefore does not affect Factor XIII binding to fibrin,⁵⁴ which influences the degree of protofibril compaction¹⁸ and fiber thickness.⁵⁵ HEPES has a relatively thermostable, concentration-independent dissociation constant and is biochemically more inert than other buffers such as Tris and phosphate.^38,56 It therefore came as a surprise to us when we discovered a strong and systematic decrease in the turbidity of fibrin networks with increasing HEPES concentration. As shown in Figure 1A, fibrin samples of 3 mg/mL polymerized by addition of 0.5 U/mL thrombin are rather turbid at low HEPES concentrations but become increasingly transparent when the HEPES concentration is raised. At 200 mM HEPES, the samples appear almost as transparent as so-called “fine” fibrin clots, in which protofibril bundling is nearly completely inhibited through a combination of high pH and high ionic strength.²³ It is important to note that in the range of HEPES concentrations tested (20–200 mM) the fibrin samples always gelled (Figure 1B), despite the change in turbidity. The measured clottability was indeed always >96%, implying that virtually all fibrin monomers were incorporated in the network. SDS-PAGE analysis furthermore revealed that all clots were cross-linked by FXIII (Figure S1) irrespective of HEPES concentration.

Figure 1.

Fibrin networks formed at different HEPES concentrations. (A) Fibrinogen at a concentration of 3 mg/mL was polymerized by addition of 0.5 U/mL thrombin at 37 °C in sealed cuvettes of 1 cm path length with 20, 100, and 200 mM HEPES. (B) After 2 h polymerization, the cuvettes were turned upside down to confirm gelation. Control sample contained 3 mg/mL fibrinogen monomers without thrombin and remained liquid throughout the experiment. (C) Permeability of 3 mg/mL fibrin networks formed with different HEPES concentrations. Data are mean ± standard deviation (n = 3). (D) Confocal fluorescence images of fibrin networks formed at different fibrinogen (1–6 mg/mL) and HEPES (20–200 mM) concentrations, showing that HEPES strongly affects the fiber thickness and network mesh size. Images are maximum intensity projections from z stacks of 20 μm with 0.5 μm z interval, starting 25 μm from the coverslip to minimize any edge effects. Scale bar 10 μm.

These observations suggest that HEPES changes the structure of the fibrin networks without compromising the formation of a space-filling fibrous network. Indeed, confocal microscopy confirmed that increasing HEPES concentration led to denser networks with smaller pore sizes (Figure 1D). This structural modulation occurred at all tested fibrin concentrations (1–6 mg/mL). At the highest fibrin (6 mg/mL) and HEPES (200 mM) concentrations, the networks were so dense that individual fibers were not resolvable with confocal microscopy. This pore size reduction should strongly influence the fluid permeability of the fibrin networks, which is an important parameter for the biological role of fibrin because it controls interstitial fluid flow, the rate of fibrin clot degradation by lytic enzymes, transport of nutrients and growth factors for cells, and the adhesion and migration of cells.⁵⁷⁻⁶¹ As shown in Figure 1C, we indeed find a strong reduction of the network permeability by 2 orders of magnitude when we keep the fibrin concentration fixed (3 mg/mL) while raising the HEPES concentration from 20 to 200 mM.

HEPES Suppresses Protofibril Bundling by Slowing down Lateral Association

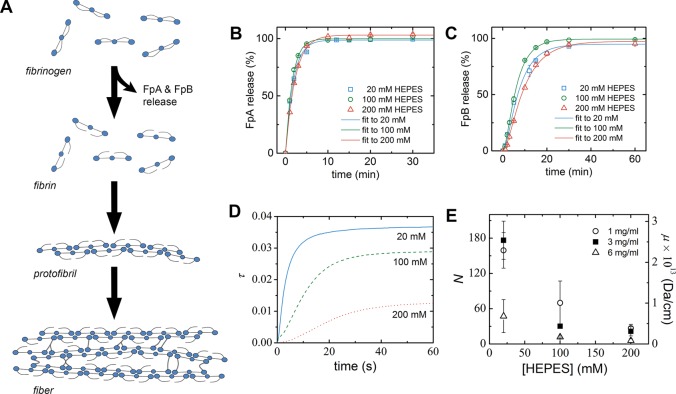
Since the structure of fibrin networks is known to be largely kinetically determined,⁶² we next investigated how HEPES influences the two main stages of fibrin network formation: the conversion of fibrinogen to activated fibrin monomers that spontaneously polymerize into protofibrils, followed by lateral association of protofibrils to form a percolating network of bundled fibers (Figure 2A).¹ We first checked whether HEPES affects the kinetics of thrombin-catalyzed fibrinogen-to-fibrin conversion by analyzing the time course of fibrinopeptide release using HPLC (Figure 2B and 2C). The obtained kinetic parameters of FpA and FpB do not show any significant or systematic dependence on HEPES concentration (Table 1), indicating that HEPES does not influence thrombin activity and the conversion of fibrinogen to fibrin monomers.

Figure 2.

Influence of HEPES on fibrin network formation. (A) Schematic of the process of fibrin network formation, starting with conversion of fibrinogen to activated fibrin monomers by release of FpA, which drives the spontaneous assembly into double-stranded fibrin protofibrils, followed by release of FpB and lateral association of protofibrils into fibers that form fibrin networks. Schematic shows the rod-like shape of fibrin monomers with a trinodular arrangement of distal D-domains and a central E-domain (blue circles) and long, flexible αC-appendages that contribute to protofibril bundling protruding from the D-domains. (B and C) Kinetic analysis of thrombin’s enzymatic activity in HEPES buffers of different concentrations (20, 100, or 200 mM). Amount of released (B) FpA and (C) FpB, normalized to the maximum amount for each condition, is plotted as a function of incubation time (symbols). Data are mean ± standard deviation (n = 2). Solid lines show fits to a kinetic model.⁴⁸ Fit parameters (k_A and k_B) are listed in Table 1. (D) Kinetics of protofibril formation and lateral association at different HEPES concentrations, as measured by the solution turbidity (τ) at a wavelength of 350 nm, for fibrin samples at 0.03 mg/mL fibrinogen concentration. (E) Average number of protofibrils per fiber cross-section, N (and the corresponding average fiber mass–length ratio, μ), after 2 h of polymerization, as measured using turbidimetry. Data are mean ± standard deviation (n ≥ 3).

Table 1. Kinetic Parameters of Fibrin Polymerization in HEPES Buffers of Different Concentrations.

	fibrinogen → fibrin conversiona		fibrin polymerizationb				steady statec
[HEPES] (mM)	kA (×104 (U/L·s)−1)	kB (×104 (U/L·s)−1)	lag time (s)	half time (s)	max rate (× 10–3 s–1)	max τ (× 10–3)	N
20	6.63 ± 0.33	1.89 ± 0.44	18 ± 5	159 ± 31	8.2 ± 1.9	36.8 ± 9.3	176 ± 32
100	7.65 ± 0.19	2.33 ± 0.22	89 ± 44	513 ± 184	1.9 ± 0.5	28.8 ± 1.7	30 ± 6
200	5.38 ± 0.13	1.43 ± 0.18	282 ± 198	732 ± 83	0.6 ± 0.2	12.6 ± 5.5	22 ± 8

^aObtained from analysis of HPLC data of thrombin-catalyzed fibrinopeptide release as described in the Experimental Section. k_A and k_B denote the best-fit kinetic constants of FpA and FpB release, respectively. Data are shown as mean ± SD (n = 2).

^bObtained from analysis of the time evolution of turbidity data of a 0.03 mg/mL fibrinogen solution polymerized with 0.5 U/mL thrombin, as described in the Experimental Section. Data are shown as mean ± SD (n = 4 for 20 mM HEPES and n = 3 for 100 and 200 mM HEPES).

^cObtained from the steady-state N value of 3 mg/mL fibrin samples, analyzed using turbidimetry, after 2 h of polymerization. Data are shown as mean ± SD (n = 3).

Next, to check whether HEPES affects the kinetics of protofibril formation and the lateral association of protofibrils, we monitored the evolution of the solution turbidity at low fibrinogen concentration (0.03 mg/mL) as a function of HEPES concentration. The two stages of fibrin formation are known to result in a characteristic time dependence of the solution turbidity, involving a lag time during which fibrinogen is activated and protofibrils are formed, a sigmoidal increase due the formation of more strongly scattering protofibril bundles, and finally a plateau where assembly has reached steady state.^12,62,63 The use of a low fibrinogen concentration ensures that the lag time is sufficiently long to be experimentally measurable. We indeed observed the expected sigmoidal shape of the curves (Figure 2D), which allowed us to quantify the assembly kinetics in terms of the lag time, half time, maximum rate of increase of scattering, and maximum scattering intensity.¹³ We found that increasing HEPES concentration caused longer lag times and half times as well as a lower maximum rate (Table 1). These three observations all signify a reduced rate of lateral association of fibrin protofibrils at higher HEPES concentration. The maximum scattering also became lower at higher HEPES concentration, indicative of thinner fibers, consistent with the confocal images.

To quantitatively test the effect of HEPES on fibril bundling at physiologically relevant fibrin concentrations, we next analyzed the wavelength dependence of the turbidity of the fibrin networks in steady state to obtain direct information about the average fiber mass–length ratio, which is proportional to the average number of protofibrils per fiber, N.^18,27 We found that N monotonically decreased with increasing HEPES concentration (Figure 2E and Table 1). For 3 mg/mL clots, N decreased 9-fold from a value of ∼180 in the presence of 20 mM HEPES to only ∼20 in the presence of 200 mM HEPES. Wavelength-dependent turbidity data recorded during network formation indicated that that the rate of increase in N over time during fibrin self-assembly dropped with increasing HEPES concentration for all tested fibrin concentrations (1, 3, and 6 mg/mL; Figure S2). Thus, the quantitative turbidimetry measurements support the qualitative observations from confocal microscopy that fibrin forms denser networks of thinner fibers and reveal that lateral association is slowed down at increasing HEPES concentrations.

HEPES Only Weakly Affects Fibrin Network Rheology

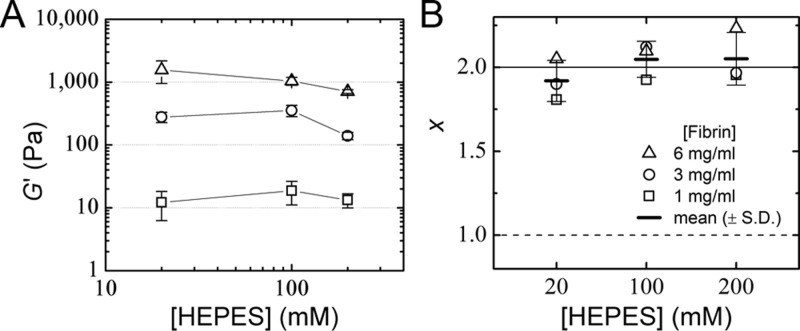
The mesoscale structure of fibrin networks and the molecular packing structure of fibrin fibers together govern the mechanical properties of clots,^{18,27,61,64−66} which in turn influence hemostasis and cell mechanosensing.⁶⁷⁻⁶⁹ Thus, we next tested whether varying HEPES concentration also influences the mechanical properties of fibrin networks. Rheological measurements showed that the elastic modulus, G′, of fibrin clots is indeed somewhat affected by HEPES concentration over a range of fibrin concentrations (Figure 3A). However, surprisingly, the dependence of G′ on HEPES concentration is weak, despite the dramatic modulation of the fiber thickness and network pore size. To explain this observation we turned to a theoretical model of bundled semiflexible polymers, which is capable of quantitatively predicting the elastic properties of fibrin in terms of the mechanical properties of the constituent fibers.^64,70 The basic idea is that the stiffness of a network composed of semiflexible fibers scales with fiber concentration, expressed as total fiber length per volume, ρ, and with the fiber bending rigidity, κ, as G′ ∝ ρ^11/5κ^7/5.⁶⁴ The fibrin fibers are modeled as bundles of N protofibrils, where N depends on HEPES concentration as measured by turbidimetry. For a fixed fibrin concentration, κ goes down with increasing HEPES concentration since N decreases but at the same time ρ goes up. These effects almost cancel, thus explaining why G′ does not significantly change with HEPES concentration. More precisely, the bending rigidity κ of the bundle goes up with bundle size according to⁷¹ κ = κ_pfN^x, where κ_pf is the bending rigidity of a protofibril and x is a parameter that measures how tightly the protofibrils are bundled together. The bounds on x are 1 for loose bundles and 2 for tight bundles. Assuming a protofibril persistence length λ_pf = κ_pf/k_BT = 75 nm,⁶⁴ where k_BT is the thermal energy, independent of HEPES concentration (see below), we can infer the variation of x with HEPES concentration from a direct comparison of the rheology data with the semiflexible bundle model. We find that x does not vary significantly when the HEPES concentration is varied (Figure 3B) and has a value close to 2, indicating tight bundling. Therefore, the rheology data indicate that although HEPES affects the extent of protofibril bundling (i.e., N), it does not alter the strength of lateral association between the protofibrils within the bundle. This is consistent with the observation from SDS-PAGE analysis that FXIII-mediated cross-linking is unaffected by HEPES.

Figure 3.

Rheology of fibrin networks formed with different HEPES concentrations. (A) Linear elastic shear modulus, G′, of 1 mg/mL (squares), 3 mg/mL (circles), and 6 mg/mL (triangles) fibrin samples is plotted against HEPES concentration. There are no significant differences across samples with different HEPES concentrations (p > 0.05). Lines connecting symbols are to guide the eye. Data are mean ± s.d. (n ≥ 3). (B) Strength of bundling between protofibrils within the fibrin fibers as a function of HEPES and fibrin concentration was quantified as the parameter x by interpreting the measured G′ in terms of a model that represents fibrin fibers as bundles of N protofibrils, with N measured by turbidimetry. In all cases, x is close to the limit of tight bundling (x = 2; solid line) and far from the limit of loose bundling (x = 1; dashed line). Mean x values (±s.d.) averaged over data at different fibrin concentrations are indicated with short horizontal lines (p > 0.05).

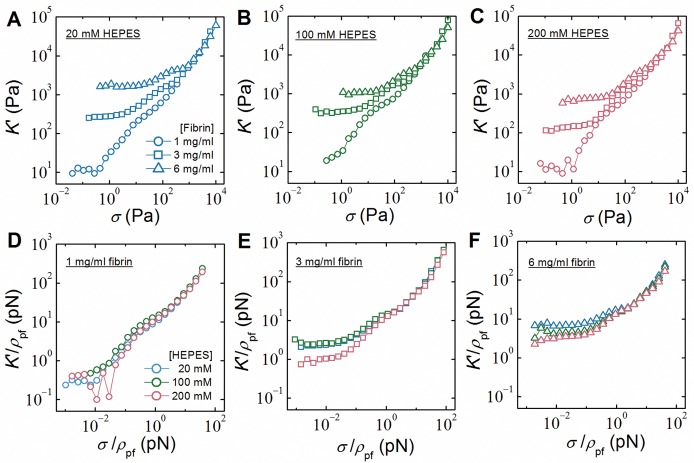
To assess whether the properties of the protofibrils themselves are directly affected by HEPES, we made use of the fact that the response of the networks to high levels of shear stress directly reveals the enthalpic stretch rigidity of the fibers and constituent protofibrils.^64,72 We measured the stiffness of the networks at increasing levels of shear stress and observed a strongly nonlinear stiffening response for all conditions studied (Figure 4A–C). To identify the nonlinear response of the individual protofibrils, we normalized both the differential elastic modulus K′ and the applied shear stress σ by the protofibril contour length density, ρ_pf, which can be directly calculated from the fibrin concentration and the known mass–length ratio of single protofibrils.⁷³ As shown in Figure 4D–F, the rescaled stiffening curves for samples with different HEPES concentrations all overlap at large forces (>10 pN), where the response is governed by stretching of individual protofibrils.⁶⁴ This demonstrates that the stretch rigidity of the protofibrils is unaffected by variations in the HEPES concentration. Thus, HEPES only affects the rheology of fibrin networks through its effect on the bundle size (N).

Figure 4.

Strain-stiffening behavior of fibrin networks formed at different fibrin and HEPES concentrations. The differential elastic modulus, K′, was measured using a prestress protocol and plotted against the applied prestress, σ, for 1 (circles), 3 (squares), and 6 mg/mL (triangles) fibrin samples formed with (A) 20 (blue), (B) 100 (green), and (C) 200 mM (red) HEPES. (D–F) To reveal the force–extension behavior of the individual protofibrils, data were rescaled by the protofibril density, ρ_pf (total protofibril length per volume). Observed collapse of the curves at forces above 10 pN independent of HEPES (and fibrin) concentration indicates that HEPES does not alter the intrinsic force–extension behavior of the protofibrils.

HEPES Effect on Fibrin Structure Is Not Mediated by Knob–Hole Interactions

To narrow in on the mechanism by which HEPES affects protofibril lateral association, we considered in more detail the role of the activation mechanism of fibrinogen and the subsequent noncovalent recognition between complementary knobs and holes that drives fibrin polymerization. Our kinetics measurements show that the effect of HEPES is mainly manifested in the late-stage fibrin formation process, where the A:a knob–hole binding that drives protofibril formation is already largely complete and B:b knob–hole interactions that contribute to protofibril lateral association are more dominant.^15,74,75 Although HEPES does not affect the kinetics of FpB release, as we have shown above, it potentially can affect the binding affinity between the B knob and the b hole. Interestingly, in Aβ peptide, it has been shown that HEPES can protonate the imidazole ring in histidine residues,⁷⁶ which is a key part of the central Gly-His-Arg sequence in the B knob.⁷⁷ Protonation of histidine in this polymerization pocket has been reported to hinder the accommodation of the positively charged complementary amino group, thus preventing fibrin polymerization.⁷⁸ Thus, HEPES-induced ionization of histidine could in principle provide a mechanism by which HEPES can influence fibril bundling.

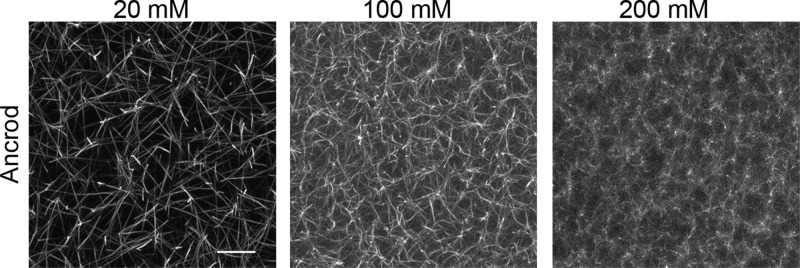
To test this hypothesis we tested the effect of HEPES on fibrin polymerized using ancrod instead of thrombin. Ancrod is a snake venom-derived enzyme that cleaves only FpA and not FpB,⁷⁹ contrary to thrombin, which cleaves both FpA and FpB. Previous studies have shown that activation by ancrod results in slower assembly of protofibril bundles with a higher degree of lateral packing order.^75,80−82 Strikingly, confocal imaging of ancrod-catalyzed fibrin networks showed that higher HEPES concentration again caused denser networks with thinner fibers (Figure 5A–C). Quantitative turbidimetry measurements confirmed that HEPES suppresses protofibril lateral association to a similar extent with thrombin and ancrod (Figure S3). Combined with the observation that HEPES does not affect the kinetics of fibrinopeptide release, this result demonstrates that the influence of HEPES is independent of the activation mechanism and the knob–hole interactions.

Figure 5.

Influence of HEPES on ancrod-induced fibrin network formation. (A–C) Confocal fluorescence images of 3 mg/mL fibrin networks formed at 20 , 100, and 200 mM HEPES concentrations. Images are maximum intensity projections from z stacks of 20 μm with 0.5 μm interval. Scale bar 10 μm.

Physicochemistry of Buffer-Mediated Effects on Fibrin Assembly

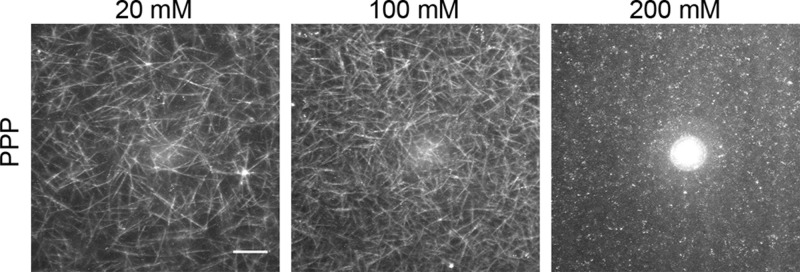
Several recent studies of buffer-mediated effects on other self-assembling biomolecular systems, including lipid membranes³⁹⁻⁴¹ and proteins,^42,43 indicated that buffers can influence biomolecular self-assembly through nonspecific, physicochemical effects. To test whether this is also the case for fibrin, we formed fibrin clots with various buffers with molecular structures that were selected to be either very similar (i.e., PIPES and BHEP) or completely different (i.e., Tris) from that of HEPES (Figure 6A). First, to check whether the effect of HEPES is mediated via its ionizing piperazine moiety, we tested PIPES and BHEP buffers, which have the piperazine moiety but contain, respectively, two or no sulfonate (SO₃^2–) moieties. We found that both buffers exerted a similar influence on fibrin bundle size as HEPES (Figures 6B and S4A,B). We then tested Tris, another widely used buffer with a completely different molecular structure that lacks a piperazine ring. Interestingly, Tris also suppresses lateral association of protofibrils in a concentration-dependent manner (Figures 6B and S4C). Notably, all buffers caused a similar reduction of bundle size as HEPES, as observed also in confocal imaging (Figure S5). Further, to test whether the effect is still observed even in more complex physiological situations, we clotted fibrin-rich platelet-poor plasma (PPP) from porcine blood in the presence of different amounts of HEPES. Visualization of the network structure of the PPP clots using label-free confocal reflectance microscopy showed that HEPES buffer also suppresses protofibril bundling in the presence of other plasma constituents (Figure 7).

Figure 6.

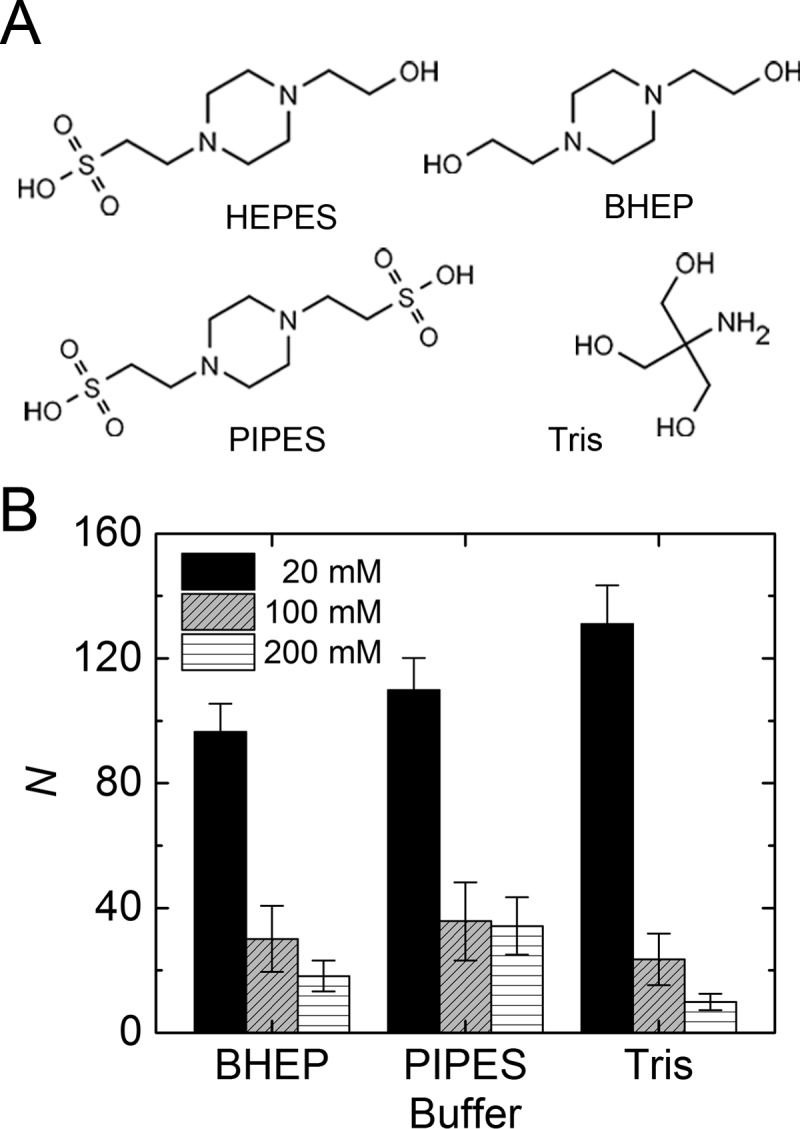
Effect of different buffering agents on fibrin self-assembly. (A) To check whether the suppression of protofibril bundling is specific to HEPES, we also formed fibrin networks in BHEP, PIPES, and Tris buffers, which differ in molecular structure as shown. (B) Average bundle size N in 3 mg/mL fibrin networks is evaluated via turbidimetry in these buffers at 20, 100, or 200 mM final concentrations.

Figure 7.

Confocal reflectance images of platelet-poor plasma (PPP) clots formed from porcine blood in the presence of different HEPES (20–200 mM) concentrations, showing that HEPES also decreases the fibrin fiber thickness in the presence of a complex mixture of plasma components. Images are maximum intensity projections from z stacks of 25 μm with 1 μm interval, starting 40 μm from the coverslip to minimize any edge effects. Scale bar 20 μm.

Altogether, our results strongly suggest a universal mechanism that these buffers share in affecting fibrin self-assembly. To check whether electrostatic effects contribute to our observations, we conducted bulk conductivity measurements of HEPES buffers at different concentrations at pH 7.4. Further, we also measured the viscosities of these buffers, as solvent viscosity may potentially play a role in the kinetics of fibrin formation by limiting monomer diffusivity. As shown in Table S2, the conductivity and viscosity of the buffers both show only a weak dependence on HEPES concentration. Zwitterionic buffer compounds are indeed expected to have little effect on the ionic strength of a solution.⁸³ The buffer viscosity increased by ∼10% (corresponding to ∼10% decrease in diffusion coefficient) when the HEPES concentration was raised from 20 to 200 mM. While the sensitivity of fibrin fiber and network formation to solution viscosity is not quantitatively known, a decrease in monomer diffusion rate is qualitatively expected to result in thicker fibers,⁶² the opposite of the thin fibers that we experimentally observed with high buffer concentration. Therefore, these physical properties of the buffer solution do not explain the dramatic effects on the fibrin structure that we observe.

Discussion

The multiscale self-assembly of fibrin clots, from fibrinogen monomers into three-dimensional networks, is driven by noncovalent interactions. The structure of the resulting fibrous networks is therefore strongly dependent on the self-assembly conditions that modulate the interactions, such as pH, salt concentration, and cosolvents. This has been widely reported and investigated (Table S1). However, to the best of our knowledge, our results establish for the first time that the structure of fibrin clots is also strongly influenced by the presence and concentration of buffer compounds, all other environmental conditions being fixed. Moreover, we uncover the physical mechanism behind this effect: higher concentrations of buffers lead to slower kinetics of protofibril association, which ultimately causes thinner bundles since the assembly process is kinetically controlled. The buffers strongly reduce the network permeability through decreased protofibril bundling but only weakly affect the elastic response of the networks to an applied shear. Quantitative analysis of the elastic response in the context of a theoretical model that treats the fibrin fibers as protofibril bundles reveals that the buffers affect clot stiffness only through their effect on protofibril bundling, while the force–extension behavior of the protofibrils themselves is unaffected.

The effect of buffering compounds on fibrin self-assembly is robustly seen with a wide range of buffering agents that differ in molecular structure. Such robustness clearly suggests a universal physicochemical origin of the influence of buffers on fibrin self-assembly. One possible mechanism is that HEPES influences protofibril lateral association by changing the strength of interactions between the αC regions that protrude from the protofibrils and help drive their lateral association.^84,85 Investigation of the influence of HEPES on the polymerization process of I-9 (or Des-αC) variant of fibrinogen, which lacks the αC regions,⁸⁶ can potentially test this hypothesis. Since the precise molecular basis of the association between αC regions is still unclear, it is difficult to pinpoint the mechanism by which HEPES might influence it. There is evidence that αC association involves beta-hairpin swapping between the N-terminal subdomains of the αC regions.⁸⁷ HEPES may influence the thermodynamics of this process by modifying the hydrogen bonding structure of water, in light of evidence that this buffer has the ability to stabilize proteins against thermal denaturation.^42,88 Indeed, recent high-resolution AFM and spectroscopic studies have shown that various buffering agents including HEPES and Tris modify the hydrogen bonding structure of water at charged interfaces⁴³ and around proteins,⁴² thereby influencing protein stability and physical properties of biomembranes.³⁹⁻⁴¹ To test whether buffer agents also influence the local hydrogen bonding network structure of the hydration layer surrounding fibrin, it will be instructive to investigate the strength and dynamics of hydrogen bonding of the buffer compounds with water and with fibrinogen, fibrin, and isolated αC regions, for instance, by femtosecond mid-infrared-spectroscopy⁸⁹ or Raman multivariate-curve-resolution hydration-shell spectroscopy.⁹⁰ In addition to the β-hairpin swapping mechanism,⁸⁷ interactions between specific residues have also been implicated in the association of αC regions.⁹¹ An ionizable histidine residue has been identified in one of the possible residue pairs involved in the interactions between αC regions,⁸⁷ although its specific role in fibrin polymerization has not been investigated. It will be interesting to measure, for example, using laser tweezers⁸⁴ or molecular dynamics simulations,⁹² the influence of buffer molecules on the binding affinity and conformation of the αC regions to disentangle the role of the β-hairpin swapping mechanism and interactions between specific residues, both of which may be affected by the presence of buffers.

In conclusion, our study shows that varying buffer concentration provides a simple and robust way to modulate fibrin fiber thickness and therefore network structure. This raises an intriguing but speculative possibility that the human body may actively regulate clot structure by controlling the acute-phase levels of bicarbonate and phosphate in blood circulation, which act as physiological buffering agents to maintain blood pH⁹³ and whose levels have been reported to vary in different hemostatic states.⁹⁴ As an illustrative test, we checked whether different concentrations of bicarbonate can modulate fibrin self-assembly. We indeed observed a similar suppression of protofibril bundling resulting in network densification for bicarbonate as for the other buffers (Figure S4D). This finding may have important biomedical implications since fiber thickness and network mesh size influence the permeability and lysis rate of fibrin clots. The permeability of fibrin blood clots controls the interstitial transport of coagulation and fibrinolytic enzymes, thus influencing the formation as well as the dissolution of blood clots.^58,60 There needs to be a precise and timely regulation of clot formation and dissolution to ensure successful hemostasis and prevent thrombosis, which is associated with severe cardiovascular diseases, including myocardial infarction, ischemic stroke, and venous thromboembolism.⁵⁷ Addition of buffer compounds may potentially also provide a way to control interactions of fibrinogen and fibrin with surfaces of materials in contact with blood, such as stents and medical implants.^95,96

Buffering agents are widely used to control the pH of aqueous solutions in biological as well as synthetic supramolecular systems. Thus, our work more generally highlights the importance to consider direct or indirect interactions of the molecule of interest with small molecules including buffer compounds.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.7b00527.

• SDS-PAGE analysis of fibrin cross-linking in HEPES buffers; time-resolved turbidity measurements of polymerizing fibrin networks with various fibrin concentrations, buffers, and activation mechanisms; confocal images of fibrin networks with different buffers; table summarizing the reported effects of additives on fibrin structure; table summarizing the effect of HEPES on the conductivity and viscosity of the buffer solution (PDF)

Author Contributions

^§ N.A.K. and T.H.S.v.K.: These authors contributed equally.

Author Contributions

N.A.K., T.H.S.v.K., and G.H.K. designed the study and wrote the paper. N.A.K., T.H.S.v.K., S.S., and T.T.R. performed SDS-PAGE, microscopy, kinetics, turbidimetry, and rheology experiments. N.A.K. and T.T.R. performed PPP experiments. B.E.V. performed conductivity and permeability measurements, experiments with bicarbonate buffers, and some control microscopy experiments. K.A.J. performed some control turbidimetry measurements. All authors reviewed the results, contributed to the interpretations, and approved the final version of the manuscript.

The authors declare no competing financial interest.