Experimental measurement of an effective temperature for jammed granular materials

Abstract

A densely packed granular system is an example of an out-of-equilibrium system in the jammed state. It has been a longstanding problem to determine whether this class of systems can be described by concepts arising from equilibrium statistical mechanics, such as an effective temperature and compactivity. The measurement of the effective temperature is realized in the laboratory by slowly shearing a closely packed ensemble of spherical beads confined by an external pressure in a Couette geometry. All of the probe particles considered in this study, independent of their characteristic features, equilibrate at the same temperature, given by the packing density of the system.

The application of the concept of effective temperature to out-of-equilibrium systems, which allows the extension of ideas from equilibrium statistical mechanics such as the fluctuation-dissipation relation (1) to nonequilibrium systems, has been extensively debated in the literature (2–6). Previous experimental measurements have been performed on structural glasses (7), colloidal suspensions (8), spin glasses (9), highly agitated granular matter (10), and a fluidized particle (11).

Until recently, the only evidence of the significance of the effective temperature in describing closely packed (jammed) granular media (3) has emerged from computer simulations of granular materials and other soft-matter systems and from analogies with glassy systems (12–21). The existence of jammed reversible states in granular materials has been also suggested by compaction experiments using tapping, oscillatory compression, or sound propagation as the external perturbation (22–26). However, macroscopic variables, such as the effective temperature for highly packed granular matter, have not been previously measured in the laboratory to our knowledge. This line of research has led to the design of the experiment that we are about to describe.

In this article we present experimental evidence suggesting the existence of a well defined effective temperature for slowly sheared granular materials very close to jamming. The particle trajectories in the sheared system yield the diffusivity and the mobility from which the temperature is deduced by using a fluctuation–dissipation relation. All of the particles considered in this study equilibrate at the same temperature, which is in turn independent of the slow shear rate, thus suggesting the condition of a physical variable to describe the jammed system.

Experiments

The experimental test involves using observational techniques to monitor the evolution of the particulate packing as it explores the available configurations. The different packing configurations are investigated by using quasistatic shear in a Couette cell geometry, depicted in Fig. 1.

Fig. 1.

Experimental setup. Transparent acrylic grains and black tracers in a refractive index and density-matched solution are confined between the inner cylinder of radius 50.8 mm and the outer cylinder of radius 66.7 mm.

The particulate system is confined between an inner and an outer cylinder. The inner cylinder of the cell is slowly rotated by a motor, whereas the outer cylinder is fixed and transparent for visualization. The walls of both cylinders are roughened by gluing a layer of particles to provide shear motion to the assembly, avoiding wall-slip. The grains are compactified by the application of an external pressure of a specific value (typically 386 Pa), introduced by a moving piston at the top of the granular matrix. We use a narrow gap Couette cell of the order of seven particle diameters wide to avoid the formation of bulk shear bands (27–31).

Since a granular assembly is optically impenetrable by its very nature, the first task consists of creating a transparent sample. This task is achieved by refractive index matching transparent particles with a suitable suspending solution. The presence of the solution reduces friction between the particles; nevertheless, the ensemble remains jammed throughout the experiment by the application of the external force via the piston. It is important to note that the liquid only partially fills the cell (see Fig. 1). In this way the pressure of the piston is transmitted only to the granular particles and not to the fluid.

Hydrodynamic effects from the partial filling of the cell are avoided by the extremely slow rotational speeds applied to our system. However, the fluid may modify the interaction between the particles, for instance, by reducing friction. Thus, the transport coefficients measured in our experiments will not be the same as those of a dry system. However, the key feature of the system is that it is closely packed, which is hereby satisfied. The random motion of the particles is caused by the “jamming” forces exerted by the enduring contacts of all of the neighboring particles, which renders the problem nontrivial.

The successful packing consists of a 1:1 mixture of two different sizes of spherical polymethyl methacrylate (acrylic) particles, of density ρ = 1.19 and index of refraction n = 1.49. We use two different packings, containing either particles of 3.17 and 3.97 mm diameter (packing 1) or particles of diameter 3.97 and 4.76 mm (packing 2). The size ratio ensures that crystallization is avoided. The mixture of particles is immersed in a solution of ≈74% weight fraction of cyclohexyl bromide and 26% decalin (32), matching not only the refractive index but more importantly the density of the acrylic particles. The density matching fluid eliminates pressure gradients associated with gravity in the vertical direction. This step avoids problems encountered in previous tests of compactivity (22) and other effects, such as convection, and size segregation, such as the Brazil nut effect inside the cell (33).

We follow the trajectories of tracer particles in the sample bulk to obtain the diffusion of the tracers and the response function (mobility) to an external force within the structure. These measurements lead to the effective temperature via a fluctuation–dissipation relation generalized to granular media. If the resulting effective temperature is a thermodynamical variable of the system, it will be independent of the properties of the tracer particles, a necessary but not sufficient condition. It is to this end that we contribute experimental results. We note that to evaluate the broader thermodynamic meaning of the temperature we would need to examine whether different measures of temperature agree as well. Such tests could be performed, for instance, by measuring the temperature for different observables in the system.

The tracer particles must experience a constant force, in response to which the mobility can be measured. Tracers of a different density to the acrylic particles are then added to the packing, as shown in Fig. 1. Two types of tracers, made of nylon (ρ = 1.12) and delrin (ρ = 1.36), are used. The role of the tracer in the system is to explore the different packing configurations, and the size of the tracers is chosen, accordingly, of similar size as the background particles. If the tracers are much larger or smaller than the background particles new physics would be brought into the problem. For instance, if a tracer is small enough to fall into the voids of the other particles then “percolation effects” (34) would prevail and the displacements would be larger than those predicted by the effective temperature. Such a tracer would no longer prove the background particle network, but would instead have different dynamics and test other interesting effects that cannot be captured by the present formalism.

Results

The first experiment uses packing 1 with 20 tracers of 3.97-mm nylon beads. The Couette cell is sheared at very slow frequencies f = 2.4 mHz defining the external shear rate 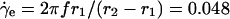1/s, where r₁ = 50.8 mm and r₂ = 66.7 mm are the radii of the inner and outer cylinders, respectively. We require a very slow shear rate so that the system is close-packed at all times. The (r(t), θ(t), z(t)) coordinates of the tracers are obtained by analyzing the images acquired by four digital cameras surrounding the shear cell [(r,θ) are obtained only at the overlaps of the cameras]. In the following we first present results for the z direction since this is the only direction where the temperature can be calculated with the present setup (the external force acts only vertically). We discuss the diffusivities in the θ and r directions at the end of this section.

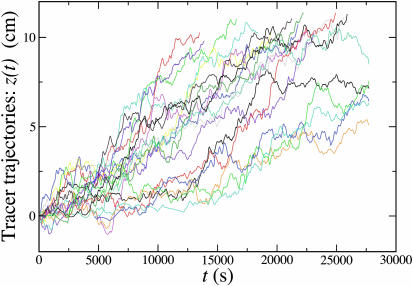
The resulting vertical trajectories of the tracers z(t) are depicted in Fig. 2, which shows that the nylon tracers not only diffuse, but also move with a constant average velocity to the top of the cell. We confine the measurements of the tracer fluctuations away from the inner rotating cylinder to avoid boundary effects and where the average tangential velocity of the tracers, v_θ(r), can be approximated linearly as v_θ(r) ≈ 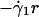with a constant local shear rate 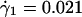1/s. The fact that 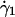is constant ensures that the diffusivity (which depends on the local shear rate) remains approximately constant in the radial direction.

Fig. 2.

Trajectories of the 3.97-mm nylon tracers in packing 1 show the diffusion and response to the gravitational force when sheared in the Couette cell. Note that the tracers diffuse distances larger than the particle diameter, indicating that we are probing fluctuations outside the cages formed by the surrounding particles.

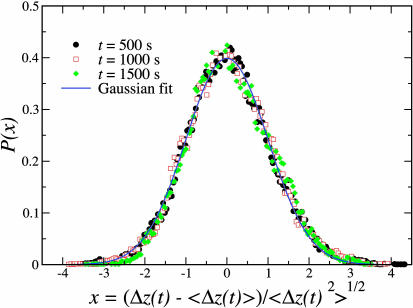
The statistical analysis of the particle displacements Δz(t) = z(t + t₀) - z(t₀) reveals a Gaussian distribution that broadens with time, as seen in Fig. 3. The rms fluctuations grow linearly for sufficiently long times (see Fig. 4a):

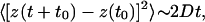[1]

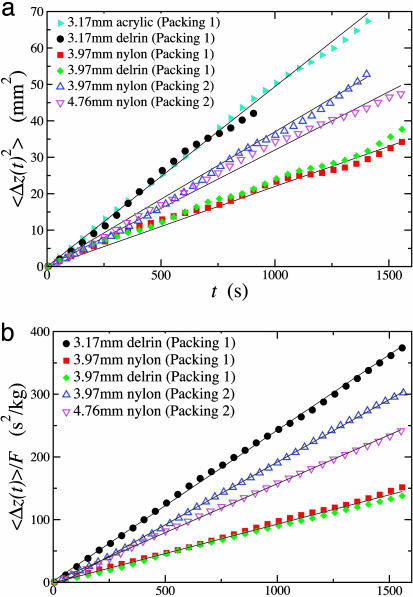
where D is the self-diffusion constant. For the 3.97-mm nylon tracer we obtain D_3.97mm = (1.1 ± 0.1) × 10^-8 m²/s.

Fig. 3.

Probability distribution of the displacements of the 3.97-mm nylon tracers in packing 1. The different distributions at different times are rescaled according to a Gaussian distribution.

Fig. 4.

Diffusion (a) and mobility (b) of tracers. We use packing 1 and packing 2 of acrylic particles and tracers of different sizes and densities. Packing 2 is run at 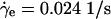. For both packings, D and χ are inversely related to the tracer sizes.

The average 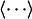denotes ensemble average over the tracers and over the initial time t₀. In practice we use the common method (see ref. 35, pages 118–122) of performing an average over the time t₀ to measure transport coefficients by splitting the trajectory of a single tracer into a series of trajectories starting at evenly spaced time intervals t₀. The diffusion constant is then obtained by averaging not only over the tracers but also over the initial time intervals. This common technique allows us to obtain an estimation of the diffusion constant by using 20 tracers for this particular system. We check that the times series are taken over intervals for which the correlations between measurements have decayed almost to zero and that our system is time-translational invariant, i.e., does not display “aging” (5). Moreover, we check that by doubling the number of tracers we obtain the same result for D for this particular type of tracer, indicating that the average diffusion constant is independent of the number of tracers used to explore the configurations.

Fig. 4b shows the mean value of the position of the tracers extracted from the peak of the Gaussian distribution as a function of time, thus yielding the mobility χ as

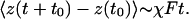[2]

Here, F = (ρ_a - ρ_t)Vg is the gravitational force applied to the tracers because of their density mismatch, and ρ_a and ρ_t are the densities of the acrylic particles and the tracers, respectively, V is the volume of the tracer particle, and g is the acceleration of gravity. The value of the mobility for the nylon 3.97-mm tracer is χ_3.97mm = (9.7 ± 0.9) × 10^-2 s/kg. We check that the mobility of the tracers is constant in the region of measurements.

We notice that the rms displacements of the tracer particles present a systematic downward curvature at long times (see Fig. 4a). This cutoff is caused by a finite size effect because the trajectories are finite. The faster the velocity of the tracers (as seen in Fig. 4b) the shorter the trajectories and the shorter the cutoff time. Thus this effect is more evident in the 3.17-mm delrin tracers in packing 1, which possesses the largest mobility, as seen in Fig. 4b, and presents the shortest cutoff time in the diffusivity, as seen in Fig. 4a. On the other hand, the 3.17-mm acrylic tracers in packing 1 present a larger cutoff since the external gravitational force is not applied to them, and they stay in the window of observation for much longer times. We would like to point out that the important issue is that the cutoff (which is inevitable in any finite time measurement) is observed for distances larger than a few particles diameters, i.e., for distances larger than the size of the “cages.” Therefore, we are testing the structural motion of the grains and not the internal motion inside the cages (see below).

An important task is to determine whether there exists a linear response regime in the system, which would imply that the mobility is independent of the external gravitational force as F → 0. The external force is varied by changing the density of the tracers of the same size. This is realized experimentally in packing 1 by the introduction of delrin tracers of 3.97-mm diameter; the density of delrin is higher than that of nylon. The analysis of the trajectories reveals that the mobility is the same for both tracers so that it is independent of the external force, as shown in Fig. 4b.

The important result that we want to emphasize is that there is a well defined linear response regime for small enough external forces where the mobility becomes independent of the force. This regime is achieved for the delrin and nylon tracers. Moreover, we find that nonlinear effects appear for tracers heavier than delrin, i.e., the mobility (which is the velocity normalized by the external force) depends on the external force for large enough forces. For instance, we find that for a 3.97-mm ceramic tracer (ρ = 3.28) the mobility is χ_ceramic = (2.2 ± 0.2) × 10^-2 s/kg and for a brass tracer (ρ = 8.4), χ_brass = (1.7 ± 0.1) × 10^-2 s/kg, smaller than the mobility of the nylon and delrin tracers of the same size. This behavior is expected since if a linear regime exists in the system, it will be valid only within certain limits. We also show that the diffusion constants of both types of tracers (delrin and nylon) are approximately the same (see Fig. 4a), confirming that the external force on the tracers does not affect the diffusion constant for the small forces used in this study.

According to a fluctuation-dissipation relation, it is the diffusivity and the mobility of the particles that enables the calculation of an effective temperature, T_eff, via an Einstein relation for sheared granular matter:

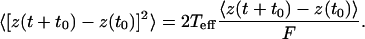[3]

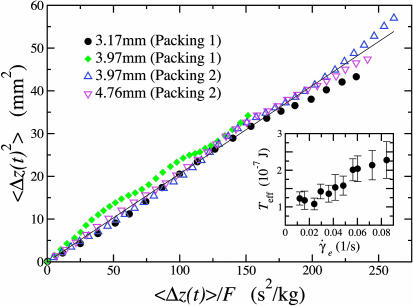
A parametric plot, with t as a parameter, of the fluctuations and responses is produced to yield the linear relationship shown in Fig. 5, the gradient of which gives 2 T_eff. We obtain for the 3.97-mm tracer T_eff = (1.1 ± 0.1) × 10^-7 J. This value is set by a typical energy scale in the system (36), for instance (ρ_a - ρ_t)Vgd, which is the gravitational potential energy to move a tracer particle a distance of the particle diameter d. The corresponding temperature that would arise from the conversion of this energy into a temperature via the Boltzmann constant, k_B,is T_eff = 2.7 × 10¹³ k_BT at room temperature. This large value is expected (36) [and agrees with computer simulation estimates (21)] since granular matter is an athermal system.

Fig. 5.

Effective temperatures for various tracers and different packings as obtained from a parametric plot of their diffusion versus mobility, as explained in the text. The slopes of the curves for different tracers consistently yield the same average value of T_eff = (1.1 ± 0.1) × 10^-7 J as given by Eq. 3. (Inset) Shown is the dependence of T_eff on the shear rate 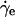for the 4.76-mm nylon tracers in packing 2.

An important evidence in examining the thermodynamical meaning of the effective temperature can be obtained from the following test: changing the tracer size should give rise to a different diffusion and mobility but they should nevertheless lead to the measurement of the same effective temperature if the system is at “equilibrium.” We next introduce tracers of 3.17-mm diameter in packing 1 and repeat the above calculations. We find that the 3.17-mm tracers produce a significantly different diffusion and mobility than their 3.97-mm counterparts as shown in Fig. 4 [D_3.17mm = (2.5 ± 0.3) × 10^-8 m²/s and χ_3.17mm = (2.4 ± 0.3) × 10^-1 s/kg]. In all cases D and χ increase with decreasing size of the tracers. However, the parametric plot of diffusivity versus mobility demonstrates that their effective temperatures are approximately the same as seen in Fig. 5 with an average value over all tracers of T_eff = (1.1 ± 0.1) × 10^-7 J.

We further check that the diffusion is not affected by the external force by calculating the diffusivity of the nontracers particles by dying acrylic tracers and analyzing their trajectories. As shown in Fig. 4a the diffusion of the acrylic tracers of size 3.17 mm (for which no external force is applied) is the same as the diffusion of the delrin tracers of the same size (for which the gravitational force is applied).

Next, we perform another measurement arising from a repeat of the experiment for a different packing of spherical particles (packing 2). The use of larger particles of approximately the same size ratio as in packing 1 still leads to the same volume fraction of particles. Because T_eff is a measure of how dense the particulate packing is (i.e., a large T_eff implies a loose configuration, e.g., random loose packing, whereas a reduced T_eff implies a more compact structure, e.g., random close packing), it holds to reason that it should be the same for both packings under investigation. Indeed, despite the change in their respective diffusivities and mobilities as shown in Fig. 4, the two packings measure approximately the same effective temperature shown in Fig. 5.

An assumption in this study is that of the system being continuously jammed despite the presence of rearrangements under shear. We show in Fig. 5 Inset that the effective temperature seems to become approximately constant, as long as the particulate motion is slow enough such that enduring contacts prevail. We find that 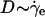and 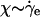, whereas T_eff = D/χ remains approximately constant for sufficiently small 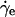. It is within this quasistatic range where the effective temperature could be identified with the exploration of the jammed states. The slow shear rate regime observed here could be analogous of the shear-rate independent regime observed in the behavior of the shear stress in slowly sheared granular materials (37, 38). This solid friction-like behavior has been studied in the past (37, 38) and occurs when frictional forces and enduring contacts dominate the dynamics. This regime has also been observed in recent computer simulations of the effective temperature of sheared granular materials (18). Our results are in accordance with these previous studies.

Given that we are dealing with an athermal system in which the notion of “bath” temperature plays no role perhaps further explanation is required in terms of the actual role of T_eff in describing granular systems. The length scale on which the particles diffuse over the long time scale of the experiment is of the order of a few particle diameters (see Figs. 2 and 4a), implying that the exploration of the available jammed configurations takes place by rearrangements of the particles outside their “cages.” The trajectory of the slow-moving system could be mapped onto the successive jammed states that the system explores. Thus, we may identify T_eff as the variable governing this exploration of the different jammed configurations.

It has been suggested that, under certain experimental conditions of reversibility, a jammed granular system could be amenable to a statistical mechanics formulation (39, 40). The main assumption of this statistical formulation is that the different jammed configurations are taken to have the same statistical weight. Thus, observables can be obtained as “flat” averages of the jammed configurations (12, 14, 17, 19, 20, 21, 41). The validity of this assumption has been extensively debated in the literature (see for instance refs. 5 and 24). Some simulations and analytical work suggest that the effective temperature obtained by applying the extension of fluctuation dissipation theorem to out-of-equilibrium systems is indeed analogous to performing a flat average over the configurational space. Numerically it has been suggested that the effective temperature can be identified with the compactivity introduced in ref. 39, arising from the entropy of the packing (12, 14, 21). Moreover, recent work (25, 41) suggests that the landscape of a granular system in the jamming limit is only flat in a majoritarian sense; i.e., it is overall flat despite a very prevalent ruggedness on the microscopic scale.

The experimental test of these ideas is very difficult since the entropy of the jammed configurations cannot be easily measured in experiments. For instance, using the present experimental setup it is not possible to obtain an estimate of the compactivity from entropic considerations. Therefore, more tests are needed to fully explore the thermodynamic meaning of the effective temperature and its relation to this statistical mechanic framework.

In contrast to the measurement of the temperature of the slow modes as exemplified by T_eff, we also measure the temperature of the fast modes as given by the instantaneous rms fluctuations of the velocity of the particles. This kinetic granular temperature is smaller than T_eff and differs for each tracer, indicating that it is not governed by the same statistics. Similar results have been obtained in experiments of vibrated granular gases (42). The significance of these results is that there are other modes of relaxation (the fast modes) that are governed by a different temperature. This result is analogous to what is found in models of glasses and computer simulations of molecular glasses (see, for instance, refs. 2–6). In these models, in the glassy phase the bath temperature is found to control the fast modes of relaxation and a different effective temperature is found for the slow modes of relaxation. Analogously, we find a granular temperature for the fast modes and an effective temperature for the slow modes of relaxation. The fact that different temperatures may govern different modes of relaxation in the system may imply that something more complicated than a Boltzmann approach may be needed to describe granular matter.

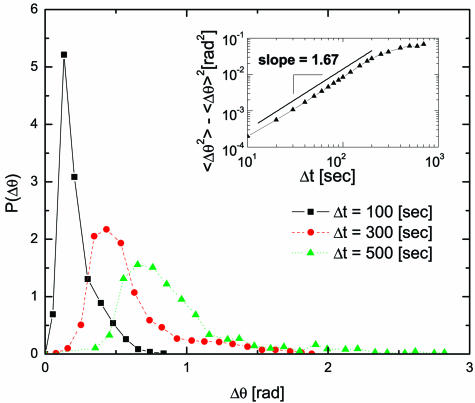
Finally, we present the analysis of the data in the θ and r directions. Fig. 6 shows the results of the probability distribution of the displacements Δθ(t) in the angular direction. The data correspond to the 3.17-mm delrin tracers in packing 1 and are taken every 200 s. We find that the probability distributions display an asymmetric tail in the direction of the flow. This extra spreading is known as the Taylor dispersion (43).

Fig. 6.

Probability distribution of the angular displacements Δθ for different time intervals. Because of Taylor dispersion effects the distribution shows an asymmetric shape. (Inset) The rms fluctuations shown reveal a faster than diffusion process.

Taylor dispersion appears when diffusion couples with the gradient of the flow, giving rise to a larger dispersion along the flow direction (see, for instance, ref. 31 for a study of Taylor dispersion in granular materials). In this case it is not possible to extract the bare diffusion constant. We clearly see the effects of Taylor dispersion as a non-Gaussian tail in the distribution, leading to a superdiffusive process as can be seen from the analysis of the fluctuations of Δθ shown in Fig. 6 Inset.

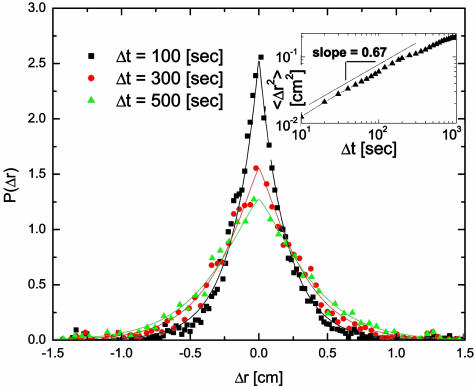
The probability distribution of the displacements in the radial direction P(Δr) is shown in Fig. 7. Interestingly, it reveals that the fluctuations are stretched exponentially with an exponent approximately equal to 1.2 (an exponent equal to 2 would correspond to a Gaussian distribution). This result does not invalidate the fact that there could be a well defined temperature in the r direction as well. To calculate such a temperature a force should be applied in the radial direction, thus its calculation goes beyond the present experimental setup. We also notice a symmetric shape for P(Δr) indicating the absence of a net flow of particles toward the inner or the outer cylinder. Therefore we conclude that shear-induced segregation is not present in the time scales of the experiment. An average motion of the tracer toward the center of the cell (a granular Magnus effect) is not observed either. The analysis of the fluctuations reveals a subdiffusion process for short times (of the order of 100 s) as shown in Fig. 7 Inset. It should be interesting to apply an external force in the radial direction to obtain the mobility and then the effective temperature to test whether the temperature is isotropic as was done in ref. 10.

Fig. 7.

Probability distribution of the displacements in the radial direction P(Δr) for different time intervals. A symmetric distribution around zero displacement indicates that there is no net flow in the radial direction. (Inset) Shown are the rms fluctuations.

Summary

We have tested the existence of the effective temperature for a given range of particle sizes and densities. It remains to be seen how robust our results would be under a more extended set of parameters, including the use of particles of different shapes, changing the interstitial liquids, etc. It would also be important to test whether the effective temperature of the packing is the same under different types of driving, for instance under tapping or shaking, and for different observables. We also note that previous numerical work on collective relaxation and self-diffusion in granular piles (44) has shown that in systems without Brownian motion the enhanced free volume in the direction of the perturbation is a more reliable indicator of diffusion than the tracers particles. It would be interesting to understand whether the analysis of the free volume gives rise to the same temperature as that measured here. Moreover, if the effective temperature is a proper state variable it should be independent of the observable. This idea has been previously suggested to be the case in computer simulations of effective temperatures of granular materials (18), and experimentally it would require the measurement of the temperature from, for instance, the volume fluctuations. More experimentation is needed to fully understand whether the present definition of effective temperature has a physical thermodynamic meaning. Our results are a step forward in this direction, but do not necessarily imply the validity of a Boltzmann type of statistics for granular materials.