What Controls the Hybridization Thermodynamics of Spherical Nucleic Acids?

Abstract

The hybridization of free oligonucleotides to densely packed, oriented arrays of DNA modifying the surfaces of spherical nucleic acid (SNA)–gold nanoparticle conjugates occurs with negative cooperativity; i.e., each binding event destabilizes subsequent binding events. DNA hybridization is thus an ever-changing function of the number of strands already hybridized to the particle. Thermodynamic quantification of this behavior reveals a 3 orders of magnitude decrease in the binding constant for the capture of a free oligonucleotide by an SNA conjugate as the fraction of pre-hybridized strands increases from 0 to ∼30%. Increasing the number of pre-hybridized strands imparts an increasing enthalpic penalty to hybridization that makes binding more difficult, while simultaneously decreasing the entropic penalty to hybridization, which makes binding more favorable. Hybridization of free DNA to an SNA is thus governed by both an electrostatic barrier as the SNA accumulates charge with additional binding events and an effect consistent with allostery, where hybridization at certain sites on an SNA modify the binding affinity at a distal site through conformational changes to the remaining single strands. Leveraging these insights allows for the design of conjugates that hybridize free strands with significantly higher efficiencies, some of which approach 100%.

Spherical nucleic acid (SNA)–gold nanoparticle (AuNP) conjugates,¹ i.e., AuNPs densely functionalized with oligonucleotides, have become an increasingly powerful tool for a variety of biomedical and materials synthesis applications including intracellular mRNA monitoring in live cells,² detection of oligonucleotide and protein markers of disease,³ gene knockdown,⁴ and programmable self-assembly of tailorable NP superlattices.⁵ Crucial to all of these functions is the ability for DNA strands anchored to the particles to hybridize to complementary oligonucleotides in a robust and efficient manner. Interestingly, whereas reports from the DNA microarray literature have found greatly decreased hybridization efficiency (i.e., the fraction of total surface-bound strands that bind) with increased surface DNA density,⁶ our group has found an enhancement to DNA hybridization with increasing surface density for strands anchored to spherical NP scaffolds.⁷ The origin of this ostensible conflict arises from a subtle but important distinction between how these experiments are conducted: complementary strands are typically added in excess for oligonucleotide-modified substrates (as in the case of microarrays),⁸ whereas complementary strands are added in precise sub-stoichiometric quantities for SNAs.^7,9 Importantly, it is significantly more relevant for the majority of applications to consider the case of relatively few strands available for capture by surface-bound oligonucleotides. For example, detection of microRNAs or intracellular mRNAs in low relative abundance,^2a,b,3a self-assembly of NP superlattices through the addition of programmable DNA linker strands,^5a,b and the intracellular manipulation of gene expression through antisense or siRNA pathways⁴ all require the hybridization of oligonucleotides in this sub-stoichiometric regime. Despite being more relevant, this regime is also considerably more complicated, as each additional binding event often results in a stepwise increase in the barrier to hybridization, an example of negative cooperativity.^9,10 To the best of our knowledge, understanding how the binding constant for DNA hybridization depends on the number of strands already bound to a surface monolayer has only recently been addressed theoretically in the planar context,¹⁰ and never for the case of a spherical NP system.

In this work, we address this question by quantifying the thermodynamics of binding as a function of the number of pre-hybridized strands, n (Scheme 1). This analysis provides important fundamental insight into the enthalpic and entropic consequences of packing charged DNA strands into a dense monolayer and reveals that SNA binding is regulated by electrostatic effects and collective conformational changes that are analogous to the phenomenon of allostery observed in many regulatory proteins. Establishing an understanding of these effects provides a crucial missing piece to the puzzle of how DNA hybridization is affected by surface confinement and establishes a more unified picture of the relative contributions of surface density, charge repulsion, and strand conformation in this important system.

Scheme 1.

Pre-hybridization of Spherical Nucleic Acid–Gold Nanoparticle Conjugates with n Strongly Bound Oligonucleotides (Blue) To Allow Independent Measurement of the Binding Constant of the n+1 Strand (Yellow)

To understand the functional form of the interaction between free oligonucleotides and SNAs, AuNPs (∼13 nm) were modified with ∼80 DNA strands and mixed with fluorescein-labeled complementary strands of varying lengths (9, 12, 15, or 18 bases) over a range of concentrations to obtain binding isotherms (Figure 1a). As strands are made longer and more complementary, the fractional occupancy of the SNA's binding sites (i.e., hybridization efficiency) is increased for a given number of equivalents added. Interestingly, only the most complementary strand (18-mer) is ever able to bind 100% of the NP-bound oligonucleotides, indicating that there exist considerable penalties to hybridization that are not steric in nature. Indeed, fluorescence melts collected from SNAs hybridized to a range of 9-mer equivalents show that as the number of duplexed strands increases, the melting transition broadens and decreases in temperature, showing that the average stability of a duplex on an SNA decreases substantially as more sites become occupied (Figure 1b). This implies that the hybridization of each strand to an SNA destabilizes the subsequent binding event; hybridization in this system is thus negatively cooperative.

Figure 1.

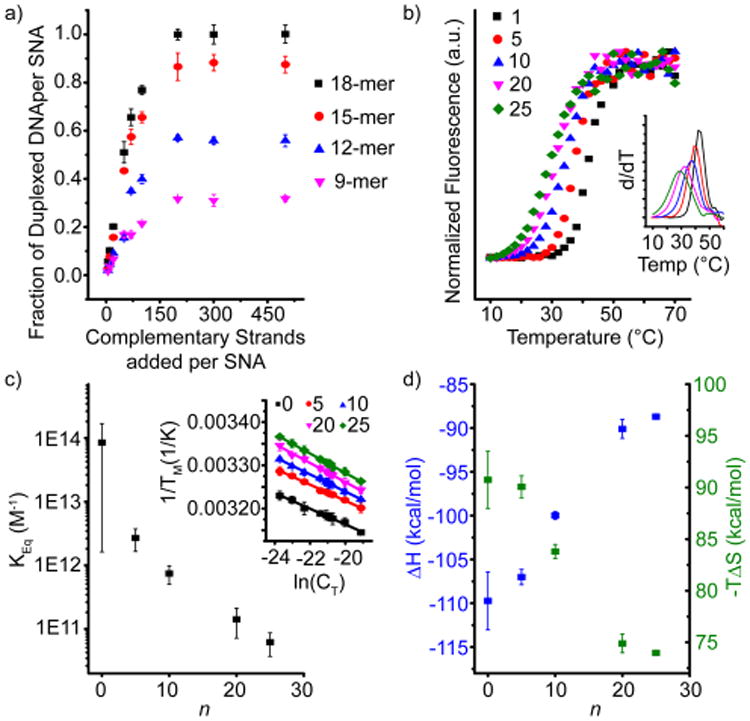
(a) Quantification of the fraction of strands that hybridize to an SNA functionalized with ∼80 complementary strands as a function of stoichiometry for oligonucleotides of several different lengths. (b) Dehybridization “melting” curves for SNAs prepared with differing numbers of hybridized 9-mer complementary strands, enumerated in the legend. Inset: the first derivative of each curve, the full width at half-maximum of which is a measure of the “sharpness” of the transition. (c) Calculated SNA binding constants as a function of the number of pre-hybridized strands. Inset: the linear van't Hoff plots from which the thermodynamic quantities have been extracted. The legend describes the values of n probed in this experiment. (d) Trends in the enthalpy (left axis, blue) and entropy (right axis, green) of SNA binding as a function of the number of pre-hybridized strands.

To better understand the thermodynamics of DNA hybridization to SNAs, we developed a method to measure the stepwise change in binding affinity as the number of already-hybridized strands increases. To do this, five different types of SNA–AuNP conjugate were prepared having 0, 5, 10, 20, or 25 strands of an 18-mer complement already hybridized to them. Next, 1 equiv per particle of a 9-mer complement was hybridized to the internal portion of the remaining thiolated single-stranded oligonucleotides in each of these types of conjugates. Because the melting transition of the 9-mer occurs at a much lower temperature and does not overlap with the melting transition of the 18-mer (Figure S1), one can determine the thermodynamic transition temperature of the 9-mer from SNAs as a function of the number of pre-hybridized 18-mer strands, n. When this analysis is repeated over a range of concentrations (maintaining the 1:1 stoichiometry of 9-mer complement: SNA) a van't Hoff plot can be generated from the following equation for non-self-complementary DNA hybridization: ^7,11

$$\frac{1}{T_{\mathrm{m}}}=\frac{R}{\mathrm{\Delta }{H}^{\circ }}ln{C}_{\mathrm{T}}+\frac{\mathrm{\Delta }{S}^{\circ }-Rln4}{\mathrm{\Delta }{H}^{\circ }}$$

where T_m is the melting temperature of the 9-mer complement from an SNA, C_T is the total concentration of SNA plus 9-mer complement, R is the gas constant, and ΔH° and ΔS° are the enthalpy and entropy of surface hybridization, respectively. Linear regression of these data allows for extraction of the enthalpy and entropy, from which the Gibbs free energy (ΔG) and binding constant can be calculated (Figure 1C, Table S1).^7,11

It is important to note that this approach considers the SNA as a single entity that binds one complementary strand and thus reveals information regarding the collective behavior of the numerous surface-bound DNA ligands rather than information on the individual surface-bound strand being hybridized. This perspective is analogous to that adopted by biochemists probing the binding properties of multivalent proteins with n receptors that are coupled through cooperative interactions;¹² in this case the SNA is analogous to the protein with each surface-bound DNA strand representing a discrete binding site. Regardless, we are most concerned with the relative changes in thermodynamic quantities with increasing n rather than their absolute values, and expect such trends to be similar, independent of how the SNA is considered. Although NP-based SNAs are unlike proteins in that they are not molecularly pure, ensemble measurements of the sort described here average over random heterogeneities and allow one to discern the contributions of deliberate changes to the system.

This analysis reveals a strong dependence of the binding constant on the number of pre-hybridized oligonucleotides. By increasing the fraction of surface hybridized strands from 0 to ∼30%, the binding constant drops over 3 orders of magnitude (Figure 1c, Table S1), demonstrating that the penalties to hybridization in this context are considerable. The origin of this hindrance to hybridization arises primarily from a decrease in the enthalpy of binding, as hybridization becomes less exothermic as more strands are hybridized (Figure 1d). We hypothesize that this enthalpic penalty is primarily a result of increased electrostatic charge repulsion between neighboring strands that is magnified as more DNA strands bind. Indeed, when hybridization is allowed to proceed in solutions of increased ionic strength (greater than the 150 mM presented in Figure 1a), the fraction of occupied strands on an SNA increases substantially, as the electrostatic repulsion is more effectively screened (Figure 2a). This is consistent with previous findings from the DNA microarray literature.^6c

Figure 2.

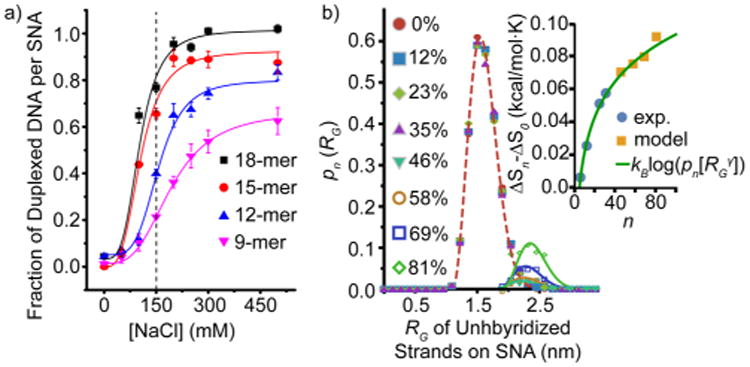
(a) Quantification of the fraction of strands that hybridize to an SNA as a function of increased bulk salt concentration. The dashed line represents the salt concentration used in prior experiments. (b) Probability distribution function (PDF) from molecular dynamics simulations indicates that the radius of gyration of unhybridized DNA on the SNA elongates as more sites on the SNA are duplexed. Inset: the change in ΔS plotted over the entire range of binding site duplexation (0–80 strands), using the PDF fits and Figure 1d. The experimental and model data are fit with a scaling exponent γ = 0.55 (green line)¹³ that predicts the behavior of both the experimental and MD simulation data.

In addition to an enthalpic impediment to hybridization, we also observe a decrease in the entropic penalty to hybridization with a greater number of pre-hybridized strands, which makes binding more favorable (Figure 1d). While it is likely that the electrostatic effects discussed above also influence the entropy, a more interesting possibility is that collective conformational changes in the SNA are responsible. This interpretation would suggest that, as more strands hybridize to SNAs and form rigid duplexes, the remaining single strands are allowed to occupy fewer configurational microstates and must adopt outstretched conformations prior to binding that are more similar to the conformations they would adopt in the duplexed state. To probe this question, we developed a coarse-grained (CG) polyelectrolyte model of the SNA that provides the relationship between the radius of gyration (R_G) of unhybridized anchored strands as a function of n (see Supporting Information for details).¹⁴ Briefly, in this bead–spring CG model, we have explicitly included NaCl salt ions and a charged DNA backbone. The inclusion of ions has two main effects on the R_G of strands—the presence of an ion profile of the SNA (Figure S7) as a function of n, and the exchange of ions between the bulk and SNA during hybridization—each of which has important effects on the ΔG of hybridization.¹⁵ The R_G of each unbound strand on the SNA provides a measure of the entropic penalty each strand must give up to bind to a complement. Molecular dynamics (MD) simulations show that as the number of duplexed strands increases, the remaining unhybridized strands elongate, as indicated by a shift in the probability distribution function (PDF, or p_n) toward higher R_G values. At higher R_G values, the PDF indicates a reduction in the number of possible microstates of the unbound anchored strands, resulting in a smaller change in the ΔS of hybridization (Figure 2b). Using a generalized Poisson fit of the MD generated p_n(R_G) (see Supporting Information), we plot the change in ΔS from Figure 1d along with the prediction from the p_n fits and find excellent agreement between the two (Figure 2b inset). Further, we find the unbound strands are well described by the scaling behavior of finite extensible chains under tension.¹⁶ The scaling exponent of the unhybridized DNA (γ = 0.55) is remarkably similar to that predicted for linear polymers (γ = 0.6, green line, Figure 2b inset). This model clearly shows the transition from the strong scaling of ΔS (0 < n < 25) to a weak scaling regime when ∼30 duplexes bind (33% sites filled) and illustrates the saturation of the entropic organization of the SNA at high-binding fractions (Figure 2b inset). This implies that DNA hybridization in the context of these NP-based systems may be thought of as analogous to the allosteric regulatory mechanisms that govern cooperative protein interactions, as binding-induced conformational changes to the structure affects the capacity for other receptors to bind.¹⁷ These insights suggest exciting future opportunities for designing artificial nanoscale protein mimics that function nonlinearly in biological systems.

These results shed an explanatory light on several phenomenological observations that have been made previously in the literature. While hybridization of target oligonucleotides to SNAs has been used to create several powerful nucleic acid detection platforms,^3b,c a mechanistic understanding for why a particular set of conditions led to high sensitivity for single binding events has been lacking. The data presented here show that although the penalties incurred by multiple hybridization events are severe, it is not until ∼10 duplexes have formed that the system is able to “feel” these effects and subsequent binding events are influenced (Figure 1c,d). Indeed, both the melting transition and the binding constant for a single 9-mer target to an SNA with no pre-hybridized strands (n = 0) are actually enhanced relative to the free-strand association of the same duplex (Figure S2).⁷ Thus, the current work is consistent with the observation that SNAs are able to capture target oligonucleotides in the extremely dilute conditions used for ultrasensitive detection methodologies.^3b,c In addition, nanoflares, SNAs with short fluorophore-labeled oligonucleotides pre-hybridized for biodetection purposes, have been observed to return the highest signal-to-noise when prepared with a 1:10 ratio of complementary strand to NP-bound strand.² The insights developed here reveal that this value likely represents saturation of the NP-based binding sites under the conditions used in the study (Figure 1a). When additional strands were added in an attempt to achieve higher hybridization efficiencies, they likely remained in solution and increased the background fluorescence signal, resulting in the observation of a lower detection sensitivity. The findings presented in this work may have important consequences for the design of future NP-based nucleic acid sensing technologies.

We next sought to take advantage of these thermodynamic insights to design better SNA conjugates that hybridize with greater efficiency and/or higher affinity. Because we expect that the enthalpic impediment to DNA hybridization arises primarily from an increase in the electrostatic surface charge density, we hypothesized that a decrease in the single-strand DNA loading on the surface of an SNA would alleviate some of these repulsive interactions and aid in hybridization. To test this, SNA conjugates were prepared with ∼40 anchored strands (using neutral diluent thiol-capped oligo ethylene glycol molecules) rather than the ∼80 strands under maximum loading (see Supporting Information). We find that the hybridization efficiency as well as the absolute number of hybridized strands per SNA increases for a given number of equivalents added (Figure 3a). Further, when these lower density conjugates are pre-hybridized with 20 complementary 18-mer strands, their binding constant for the capture of a 9-mer complement improves over 2 orders of magnitude compared to the more densely functionalized SNA conjugates prepared previously (Figure 3b). This arises from (1) a decreased enthalpic impediment to hybridization resulting from a lower density of charged, surface-bound strands and (2) an increased entropic penalty to hybridization as strands are less crowded and able to influence neighboring binding events through conformational changes (see Table S1). These results further support the proposed role of an allosteric mechanism suggested by the thermodynamic data discussed previously (Figure 1).

Figure 3.

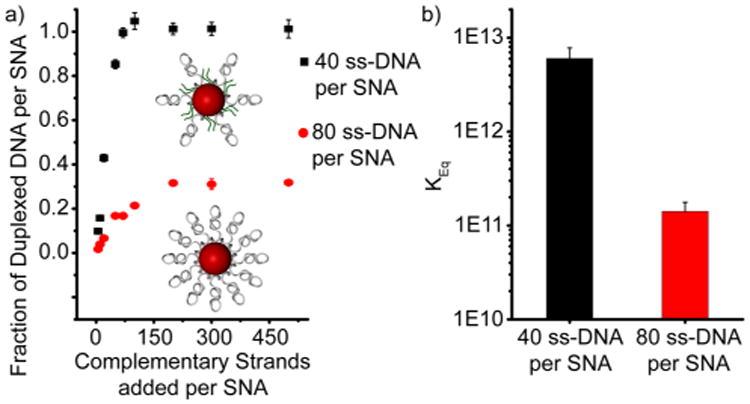
(a) Comparison of binding isotherms obtained from SNAs functionalized with either ∼40 or ∼80 DNA strands. Insets: schematic illustration of the role of oligo ethylene glycol moieties (shown in green) in diluting the surface DNA density compared to the densely functionalized particles investigated previously. (b) Comparison of the binding constants of SNAs functionalized with ∼40 or ∼80 surface-bound DNA strands and prehybridized with n = 20 duplexes.

In conclusion, we can draw several important lessons regarding the thermodynamics of oligonucleotide hybridization to SNA—AuNP conjugates. If a single oligonucleotide is anchored to a surface, the strand is configurationally restricted, causing the entropic penalty associated with hybridization to be reduced and the binding affinity to be increased. In the case of an SNA densely functionalized with many strands, two competing phenomena are observed: successive binding events cause the ΔH associated with hybridization to become less negative, resulting in a decreased binding constant, and each hybridization event affects neighboring strands in a way that causes them to further pre-organize, resulting in a less negative ΔS and an increased binding constant. These fundamental insights provide important information regarding the enthalpy and entropy of oligonucleotides packed into dense two-dimensional arrays and contribute to a deeper understanding of several empirical observations that have been made previously in the literature. With this understanding, more effective SNAs can be designed that bind a greater number of complements, and do so with greater affinity and higher efficiency. These results impact a range of fields that require robust surface hybridization including DNA micro-arrays,³ intracellular gene therapy and detection,^2,4 and materials synthesis through DNA-mediated self-assembly.^5a,b