Putting the pathway back into protein folding

The article by Liwo et al. in this issue of PNAS (1) on ab initio simulations of the folding pathway of a number of representative small proteins marks a renaissance in efforts to simulate the mechanism of protein folding without prior knowledge of the native structure. While there has been recent progress in predicting the three-dimensional native structure of a protein (2, 3), the most successful approaches incorporate many knowledge-based features (e.g., use of already solved protein structures and predicted secondary structure) that render the assembly mechanism provided by such simulations physically meaningless. On the other hand, the first principles of simulation of the folding process at complete atomic detail, including water that starts from the random state and finishes with the native structure, is computationally intractable for all but the simplest systems (4). For the near future, as in Liwo et al. (1), reduced models that describe the protein by a subset of its constituent atoms and implicitly treat solvent and that search conformational space by using Langevin or molecular dynamics (5) offer the most promising way of exploring how proteins fold.

Folding Scenarios

Remarkably, although Liwo et al. (1) examined the folding of only seven proteins, representing all secondary structural classes, their simulations demonstrate a richness that addresses key questions in protein folding. Is there native-like secondary (6) or even tertiary structure in the denatured state (7)? Does a protein collapse first and then the secondary structure (helices and β-sheets) appears, or does the secondary structure appear first, and then the native tertiary assembles (8)? Alternatively, perhaps secondary and at least loose, tertiary structures simultaneously assemble (9)? Partial evidence supporting the first and third scenarios is provided in the Liwo et al. (1) article. Furthermore, a molten globule state (10) is believed to form quite rapidly, with more or less native-like secondary structure and native topology, but with poorly defined tertiary contacts (11). What, then, drives the assembly of the global fold, if it is not specific side-chain interactions? Certainly, reduced protein models, as in Liwo et al., can provide insights, but they cannot address questions of side-chain fixation (their side chains are described by a single point) into the dense, crystalline patterns of the native structure or at what stage in folding is water squeezed out from the protein core (12). If the native topology is encoded by the interplay of local secondary structure propensities and approximate side-chain interactions (hydrophobic, hydrophilic, electrostatic, van der Waals, or other?), this finding could explain the ability of reduced protein models to assemble approximate native structures, even though their potential is not perfect [(in many approaches, the native fold is often not at the global energy minimum, (2, 3)] and many molecular details are ignored.

Native Versus Misfolded

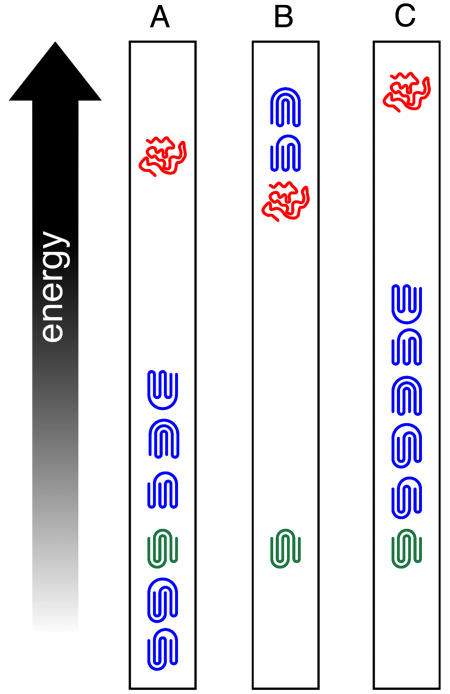
Does a protein adopt nonnative topologies and/or secondary structure on its way to the native state, or are only native-like structures explored [as in Go-like models where only native interactions are favorable (13); then, the assembly mechanism depends mainly on the native topology and reflects the most efficient way of reducing configurational entropy (14)]? Evidence for nonnative secondary structure formation along the pathway to the native state is suggested by Liwo et al. (1) for the case of 1E0G. Here, a pair of helices that form early and then unwrap are associated with the appearance of the native β-sheet, a situation that has been experimentally observed in other β proteins (15). More generally, between the native and denatured state, are there alternative, folded structures present? Certainly, as schematically depicted in Fig. 1A, structure prediction algorithms give alternative, misfolded structures (blue) that are comparable, if not lower, in energy than the native state (green) (2, 3); these misfolded structures are in the library of solved protein structures but are not adopted by the protein of interest (16). Here, the majority of the side-chain contacts and interactions are native-like, with just a few differences from native. If these permuted topologies have a much higher energy than the denatured state (red), as in Fig. 1B, then this finding implies that the “true” potential has a very strong multibody component and that all extant potentials are most likely very incomplete. On the other hand, as in Fig. 1C, suppose such misfolded structures in reality have an energy that is, say, 10 kcal higher than the native fold but much lower than the denatured state. Then, existing potentials are more or less approximately correct, but they just do not capture the interaction subtleties and reflect a physical phenomenon—namely, as in Fig. 1C, there is a “zoo” of alternative, but related, topologies near in energy to the native state; presumably, some may be visited on the pathway to the native structure. If so, by making a selected, but perhaps small, number of point mutations, an alternative fold could become populated. Moreover, the existence of energetically nearby, alternative topologies provides an attractive mechanism of fold evolution, whereby an accidental series of mutations, two related topologies might be more or less equally populated, and over the course of evolution, either or both alternatives could be selected (circumstantial evidence supporting this idea is seen in homologous proteins where the core is structurally very similar, but where there are structural variations outside the core).

Fig. 1.

Schematic representation of various scenarios of native-, nonnatured-, and denatured-state energies. (A) Energy ranking of native and nonnative topologies relative to the denatured state given by most structure prediction algorithms. (B) The situation where all nonnative topologies are higher in energy than the denatured state. (C) The situation where all nonnative topologies are higher in energy than native state but are lower in energy than the denatured state. Native topologies, nonnative topologies, and denatured structures are green, blue, and red, respectively.

Energy Landscape Sculpting

The previous discussion dealt with some issues about the nature of the energy landscape (17); however, Liwo et al.'s (1) simulations demonstrate that additional effects are operative. They argue that for all seven proteins examined, the native structure is the minimum energy one. However, for two proteins, folding is unsuccessful, and, in all cases, the lowest energy structures sampled by their molecular or Langevin dynamics simulations are at least 100 kcal higher than the minimum-energy state. Perhaps longer simulations are required to locate the global energy minimum, but Liwo et al. also argue that their potential parameterization neglects the effect of entropy, which must be included in the construction of a good folding potential. Even when the native fold is in a minimum free-energy state, how it funnels the conformational search down to the deepest energy minimum is important in dictating how a protein folds. [Here, we are assuming that the native state is both a global energy and a free-energy minimum (18).] Of course, how one goes about sculpting an energy landscape so that folding is efficient for an arbitrary, biologically relevant protein sequence is unsolved. It is not enough that there is an energy gap between the native conformation and alternative folds (required if the native conformation is thermodynamically stable and the protein has two-state thermodynamics), but there must also be a correlation between free energy or energy and the distance of a given structure from native. Some progress on this issue has been made by Scheraga et al. (19), who build their potential based on a hierarchical optimization idea that the more native the fragment, the lower its free energy. However, such an energy construction scheme could a priori bias the pathway to hierarchical assembly. Another means of introducing a correlation between energy and structure quality is discussed by Zhang et al. (3), who maximize the energy gap and the correlation of energy and backbone coordinate root mean square deviation from the native state over conformations that are nonrandomly related to the native state; such an approach should exert a smaller bias to a given mechanism of assembly, but whether it provides realistic folding pathways is not established.

The computations are tractable, and the models are sufficiently realistic to obtain insights into the folding mechanism.

The advantage of the approach used by Liwo et al. (1) is that the computations are tractable, and yet the models are sufficiently realistic that qualitative insights into the mechanism of folding can be obtained. More importantly, one can ask a series of “what if” questions. For example, one can explore the range of parameters from that where there is marginal secondary structure in the denatured state to that where all of the native secondary structure (but no tertiary structure) is present and examine how the degree of secondary structure in the denatured state affects the folding pathway. Moreover, because each simulation is fast, one can literally perform hundreds of simulations so that statistically significant results are obtained. In contrast, when only a handful of simulations can be done, one has no idea whether the results are representative or atypical. With appropriate sampling, one can examine whether there is a general trend in how a given protein folds, e.g., helix 1 forms first, followed by the hairpin between helices 1 and 2, etc. This finding would suggest that a coarse-grained picture of a folding pathway describes how the protein of interest folds or whether there is such a large multiplicity of folding events that the notion of a pathway is effectively meaningless. Because the calculations are designed to run on a PC, one might imagine using grid computing [much like the folding@home idea that was implemented for smaller systems at full atomic detail (20)] to explore a representative range of parameters and proteins to rigorously establish the predictive power of this class of models. This procedure could enable the construction of the logical equivalent of a phase diagram for the mechanism(s) of protein folding. Thus, while there have been earlier attempts at using such physics-based approaches and simplified models, the work of Liwo et al. (1) demonstrates that significant progress has been made and that the time is now ripe to put the pathway back into the protein-folding problem.