Accuracy in the Quantification of Chemical Exchange Saturation Transfer (CEST) and relayed Nuclear Overhauser Enhancement (rNOE) saturation transfer effects

Abstract

Accurate quantification of chemical exchange saturation transfer (CEST) effects, including dipole-dipole mediated relayed nuclear Overhauser enhancements (rNOE) saturation transfer, is important for applications and studies of molecular concentration and transfer rate (and thereby pH or temperature). Although several quantification methods, such as Lorentzian difference (LD) analysis, multiple-pool Lorentzian fits, and the three-point method, have been extensively used in several preclinical and clinical applications, the accuracy of these methods has not been evaluated. Here we simulated multiple-pool Z-spectra containing the pools that contribute to the main CEST and rNOE saturation transfer signals in brain, and numerically fit them using the different methods, and then compared their derived CEST metrics with the known solute concentrations and exchange rates. Our results show that the LD analysis overestimates contributions from amide proton transfer (APT) and intermediate exchanging amine protons; the three-point method significantly underestimates both APT and rNOE saturation transfer at −3.5 ppm (NOE(−3.5)). In contrast, the multiple-pool Lorentzian fit is more accurate than the other two methods, but only at lower irradiation powers (< 1 μT at 9.4 T) within the range of our simulations. At higher irradiation powers, this method is also inaccurate because of the presence of a fast exchanging CEST signal that has a non-Lorentzian lineshape. Quantitative parameters derived from in vivo images of rodent brain tumor obtained using an irradiation power of 1 μT were also compared. Our results demonstrate that all three quantification methods show similar contrasts between tumor and contralateral normal tissue for both APT and the NOE(−3.5). However, the quantified values of the three methods are significantly different. Our work provides insight into the fitting accuracy obtainable in a complex tissue model and provides guidelines for evaluating other newly developed quantification methods.

Graphical abstract

Accurate quantification of CEST and rNOE saturation transfer signals is important, but challenging. In this work, we evaluated the accuracy of several CEST quantification methods, including multiple-pool Lorentzian fit, Lorentzian difference (LD) analysis, and three-point method, and found that the three-point method (AREX_3pt) significantly underestimates APT and NOE(−3.5), the LD analysis (AREX_LD) overestimates APT and underestimates NOE(−3.5). In contrast, the multiple-pool Lorentzian fit (AREX_mfit) is more accurate than the other two methods, but only at low irradiation powers of <= 1 μT.

INTRODUCTION

Chemical exchange saturation transfer (CEST), including relayed nuclear Overhauser enhancements (rNOE) mediated by chemical exchange, can indirectly detect solute molecules in the millimolar range as well as reflect their chemical environment (e.g. pH, temperature) through measurement of water signal changes caused by a cumulative transfer effect from saturated protons ^1,2. CEST or rNOE saturation transfer thus provides amplification processes and have potential for high-sensitivity molecular and pH imaging. In CEST or rNOE saturation transfer experiments, a Z-spectrum (the water signal as a function of saturation frequency offset) is usually acquired so that the effects of exchange or dipolar interactions at a specific frequency are identified by corresponding dips. In vivo, these dips indicate saturation transfer effects from small metabolites or macromolecules that may vary with pathology and, hence, have clinical relevance. Amide proton transfer (APT), a variation of CEST at 3.5 ppm from the water peak, can detect mobile protein/peptide concentrations ³ and pH ^4–6 and has been applied to studies of tumors ^3,7–10 and ischemic stroke ^11–14. Amine-water proton transfer effects between 2 and 3 ppm have been used to detect creatine ^15–17 and glutamate ¹⁸ and have shown potential for diagnosing muscular and neurological diseases. rNOE saturation transfer centered at −3.5 ppm (NOE(−3.5)) was reported to reflect both proteins and membrane lipids ¹⁹ and has been applied in diagnosing tumors ^20–22. More recently, a new rNOE saturation transfer signal at around −1.6 ppm (NOE(−1.6)) was reported that varies between normal brain and tumor or ischemia ^23,24.

However, both CEST and rNOE saturation transfer indirectly detect solute molecules by observing water signal changes caused by chemical exchange or relayed NOEs, and thus depend on multiple non-specific tissue parameters including water longitudinal relaxation time (T_1w), direct water saturation (DS), semi-solid MT effects, and other nearby CEST or rNOE saturation transfer effects. Therefore, direct comparisons of CEST and rNOE saturation transfer signals between normal and pathological tissues may be misinterpreted due to changes in these other confounding factors. Accurate and specific quantification of CEST and rNOE saturation transfer signals is thus important for practical applications, and is also essential for measurements of molecular concentration, transfer rates, and thereby pH or temperature.

To isolate the solute contribution to a CEST or an rNOE saturation transfer signal, a reference signal is traditionally acquired that experiences similar direct DS and MT effects. However, acquisition of an accurate reference signal in a complex biological system is challenging. For example, the commonly used asymmetric analysis (MTR_asym) obtains a reference signal at the offset frequency symmetric about the water resonance ². However, while this method works well for analyzing chemical phantoms with a small number of constituents, it cannot provide an accurate reference signal in vivo because of the presence of multiple pools on both sides of the water peak, including asymmetric semi-solid macromolecular resonances ²⁵. To solve this problem, several alternative approaches, such as the Lorentzian difference (LD) analysis, multiple-pool Lorentzian fit, and three-point method, are used which avoid the use of reference signals ^{5,17,20,26–34}.

In addition to the difficulties of acquiring an accurate reference signal, recent studies have showed that conventional CEST data analyses (subtraction of label and reference signals) cannot fully remove DS and semi-solid MT effects, because CEST, DS, and semi-solid MT signals do not add linearly ³⁵. Instead, an inverse subtraction of label and reference signals may be used to cancel out confounding contributions for spin systems in a steady state. This inverse data analysis has been combined with the multiple-pool Lorentzian fit ²⁶ and the three-point method ³³ for quantification of the APT and rNOE saturation transfer in vivo. Although the specificities of these combined methods have been investigated ^33,36,37, the absolute accuracies of these three quantification methods have not yet been evaluated. For example, the LD analysis may not provide an accurate reference signal for a specific solute when there are overlapping signals from nearby pools. The multiple-pool Lorentzian fit assumes that each CEST, rNOE saturation transfer, DS, and semi-solid MT signal can be approximated as a Lorentzian lineshape ³¹. However, the exchange rate of some amine pools is much faster than the NMR time scale and are in the intermediate to fast exchange regime ². Thus these pools may coalesce with the water pool, and their CEST signals may be difficult to separate from the water signal. In particular, a previous study has reported that the fast exchanging CEST signal cannot be quantified by simple mathematical models (e.g. Lorentzian function) ³⁸. In addition, previous models typically contain a single amine pool at 2 ppm when doing a multiple-pool Lorentzian fit. However, multiple amine pools with different resonance frequency offsets and line widths have been reported ³⁹. Hence, a single Lorentzian function or a three-point method that relies on two nearby signals as a reference may not be accurate. In this paper, we evaluate the accuracies of these three quantification methods through numerical simulations, and compare their fitting results in a rodent brain tumor model.

METHODS

Lorentzian fit of reference signals

We performed Lorentzian fitting of Z-spectra using a non-linear optimization algorithm. Eq. (1) gives the model function of the Lorentzian fit method.

$$\frac{\mathrm{S}\left(\mathrm{\Delta }\omega \right)}{{\mathrm{S}}_0}=1-{\displaystyle \sum _{i=1}^N{L}_i}\left(\mathrm{\Delta }\omega \right)$$ (1)

Here, S(Δω) is the CEST signals as a function of irradiation frequency offset from water (Δω); S₀ is a control water signal with no RF irradiation; L_i(Δω)=A_i/(1+(Δω − Δ_i)²/(0.5W_i)²), which represents a Lorentzian line with central frequency offset from water (Δ_i), peak full width at half maximum (W_i), peak amplitude (A_i); N is the number of fitted pools.

We first performed a LD analysis to remove the DS and semi-solid MT effects. In this method, a two-pool (semi-solid and water) model Lorentzian fit was performed to process the Z-spectra with frequency offsets of ±4000, ±3500, ±3000, ±2500 ±200, ±150, ±100, ±50, and 0 Hz (−10 to −6.25 ppm, −0.5 to 0.5 ppm, and 6.25 to 10 ppm on 9.4 T). The fitted spectra were used as reference signals which represent the DS and semi-solid MT effects. CEST residual spectra were then created by subtracting the measured Z-spectra from the two-pool fitted spectra. To further resolve each CEST and rNOE saturation transfer peak, we also performed multiple-pool Lorentzian fits of the Z-spectra. Multiple-pool Lorentzian functions were previously used to fit Z-spectra as a combination of several components: using three pools (solute, water, and background semi-solid pool) ³¹, four pools (amide, amine, water, and NOE(−3.5)) ³⁰, and five pools (amide, amine, water, NOE(−3.5), and semi-solid MT) ²⁶. Here, we added the NOE(−1.6) pool in the multiple-pool Lorentzian fit. That is, we performed a six-pool (amide, amine, water, NOE(−1.6), NOE(−3.5), and MT) model Lorentzian fit to process the Z-spectra obtained with frequency offsets at ±4000, ±3500, ±3000, ±2500, and from −2000 to 2000 Hz with a step of 50 Hz (−10 to 10 ppm on 9.4 T), except where noted. The reference signals were obtained by setting the fitted amplitude of the target CEST or rNOE saturation transfer pools to zero according to a previous publication ²⁶.

The fitting of each spectrum was performed to achieve the lowest root mean square (RMS) of residuals between the simulated or measured data and the Lorentzian model in the selected segment. All fitting methods for in vivo experiments were performed voxel by voxel with images smoothed by a 3 × 3 median filter before fitting. Table 1 lists the starting points and boundaries of the fit for both the LD analysis and the multiple-pool Lorentzian fit. The goodness of fit was observed by the sum of squared errors.

Table 1.

Starting points and boundaries of the amplitude, width, and offset of the six-pool Lorentzian fit. The unit of peak width and offset is ppm.

	Start	Lower	Upper
Awater	0.9	0.02	1
Wwater	1.4	0.3	10
Δwater	0	−1	1
Aamide	0.025	0	0.2
Wamide	0.5	0.4	3
Δamide	3.5	3	4
Aamine	0.01	0	0.2
Wamine	1.5	0.5	5
Δamine	2	1	3
ANOE(−1.6)	0.001	0	0.2
WNOE(−1.6)	1	0	1.5
ΔNOE(−1.6)	−1.5	−2	−1
ANOE(−3.5)	0.02	0	1
WNOE(−3.5)	3	1	5
ΔNOE(−3.5)	−3.5	−4.5	2
AMT	0.1	0	1
WMT	25	10	100
ΔMT	0	−4	4

Three-point fit of reference signals

The three-point method is a simple quantification method which has been used previously to quantify APT and NOE(−3.5) ^5,33. Here, a straight line between two points at 3 and 4 ppm on a Z-spectrum was used as reference for APT quantification, and a straight line between two points at −2 and −5 ppm on a Z-spectrum was used as reference for NOE(−3.5) quantification according to a previous publication ³³.

Quantification of CEST and rNOE saturation transfer

The previous sections discussed three different approaches for determining the label and reference signals: LD analysis, multiple-pool Lorentzian fit, and the three-point method. In this section, we examine a separate question: how to use the reference and label signals to create a sensitive and specific metric. To quantify the CEST or rNOE saturation transfer signals, a direct subtraction of reference signal (S_ref(Δω)) and label signal (S_lab(Δω)) with normalization by S₀, called magnetization transfer ratio (MTR) (Eq. 2), has been previously proposed ².

$$\mathit{MTR}\left(\mathrm{\Delta }\omega \right)=\frac{S_{\mathit{ref}}(\mathrm{\Delta }\omega )-S_{\mathit{lab}}\left(\mathrm{\Delta }\omega \right)}{S_0}$$ (2)

The direct subtraction analysis has been used in the multiple-pool Lorentzian fit (named MTR_mfit here), the LD analysis (named MTR_LD here), and the three-point method (named MTR_3pt here). However, Zaiss et. al. ³⁵ showed the MTR still depends on T_1w, DS and semi-solid MT even if accurate reference signals can be obtained, and thus is not specific to the solute. Instead, an inverse subtraction analysis with correction of apparent water longitudinal relaxation rate (R_1obs), named apparent exchange-dependent relaxation (AREX), was provided ³⁶,

$$\mathit{AREX}\left(\mathrm{\Delta }\omega \right)=(\frac{S_0}{S_{\mathit{lab}}(\mathrm{\Delta }\omega )}-\frac{S_0}{S_{\mathit{ref}}(\mathrm{\Delta }\omega )})R_{\mathit{lobs}}(1+f_c)=R_{\mathit{ex}}^{\mathit{cest}}(\mathrm{\Delta }\omega )$$ (3)

where f_c is the semi-solid MT pool size ratio. The term (1+f_c), although is not shown in previous AREX imaging ⁴⁰, has been recently proved to be able to make the AREX more specific when the semi-solid MT pool is present ³⁶. Here, R^cest_ex(Δω) is independent of non-specific tissue parameters (e.g. T_1w, DS, and semi-solid MT effects), but depends only on solute concentration (f_s), solute-water exchange rate (k_sw), solute transverse relaxation (R_2s), and irradiation power (ω₁) ^35,36,40, as shown in Eq. (4).

$$R_{\mathit{ex}}^{\mathit{cest}}\left(\mathrm{\Delta }\omega \right)=\frac{f_s{k}_{sw}{\omega }_1^2}{{\omega }_1^2+\left(R_{2s}+k_{sw}\right)k_{sw}+{\left(\mathrm{\Delta }\omega -\mathrm{\Delta }\right)}^2{k}_{sw}/\left(R_{2s}+k_{sw}\right)}$$ (4)

AREX is thus a more specific data analysis method than conventional MTR. In previous works ^26,33, AREX has been combined with the three-point method (named AREX_3pt here) and the multiple-pool Lorentzian fit method ((named AREX_mfit here). Here, we also combine AREX with the Lorentzian difference analysis (named AREX_LD here).

Evaluating of the accuracy of the quantification methods

The simple analytic solution to the AREX method in Eq. (4) provides an easy way to evaluate the accuracy of the CEST or rNOE saturation transfer quantification methods through numerical simulations. Specifically, Z-spectra are first created using a multiple-pool model numerical simulation that mimics the biological tissues. AREX_mfit, AREX_fit, and AREX_3pt are then obtained from the simulated Z-spectra, and R^cest_ex(Δω) are calculated with the same tissue and sequence parameters as those used in the simulations. Comparisons between R^cest_ex and the three metrics are then performed to evaluate the accuracy of these quantification methods.

Eq. (4) was derived assuming only two pools: a solute (s) and water (w). Hence, differences between the Eq. (3) metric (derived from fitting the seven-pool simulated data) and the Eq. (4) metric (calculated directly using only data from two of the pools) are due to overlapping signal contributions, and hence indicate non-specificity in the corresponding metric.

Numerical simulations

Simulated Z-spectra were created using a seven-pool (amide at 3.5 ppm, fast exchanging amine at 3 ppm, intermediate exchanging amine at 2 ppm, NOE at −1.6 ppm, NOE at −3.5 ppm, semi-solid MT centered at −2.3 ppm ⁴¹, and water at 0 ppm) model mimicking complex biological tissues at 9.4 T. The choice of seven pools was inspired by observing in vivo Z-spectra and CEST residual spectra in Figs. 1a and 1b. Although the mechanisms of rNOEs are different from CEST and would in principle require calculation of both dipole-dipole and chemical exchange effects, the net effect is quite similar to a conventional CEST pool ⁴². Hence, we treated the rNOE saturation transfer pools as CEST pools in the simulations. In addition, we also simulated Z-spectra in which each pool was removed separately. These six-pool model simulations were used to evaluate the influence of one specific pool on the quantification of other pools.

FIG. 1.

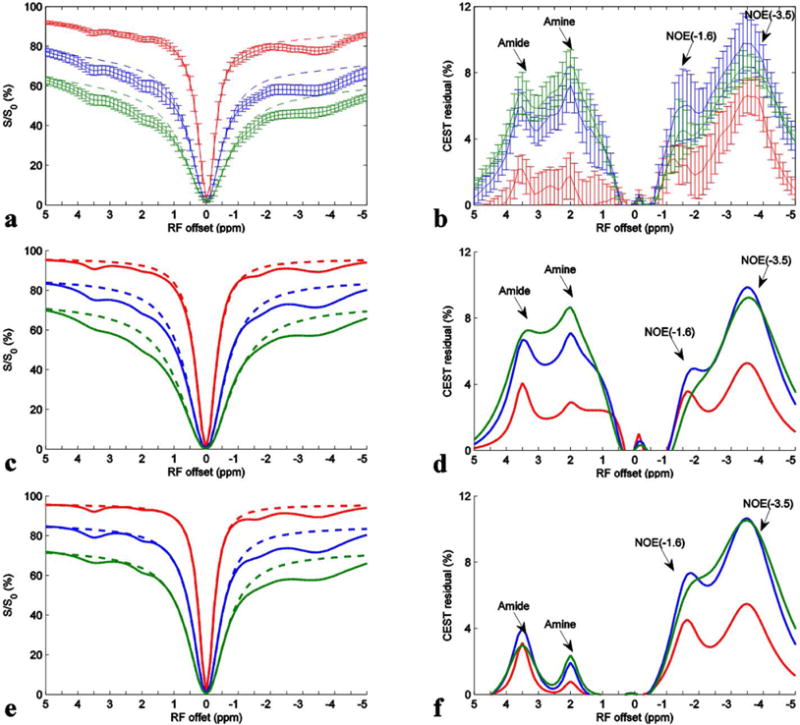
Experimental and simulated Z-spectra (a, c, and e) and CEST residual spectra (b, d, and f) with irradiation powers of 0.5 μT (solid red), 1.0 μT (solid blue), and 1.5 μT (solid green). Dashed lines in (a, c, and e) are the reference signals obtained with the Lorentzian fit of background DS and MT effects. (a and b) are from live rat brain; (c and d) are from the seven-pool model simulations; (e and f) are from a six-pool (without fast exchanging amine) model simulations.

All simulations were performed with irradiation powers of 0.5, 1, and 1.5 μT using the tissue parameters listed in Table 2. To examine the dependence on tissue parameters, we varied the water longitudinal relaxation time T_1w=1/R_1w (0.5, 1.0, 1.5, 2.0, 2.5 s), water transverse relaxation time T_2w=1/R_2w (25, 50, 75, 100, 125 ms), f_c (0, 0.05, 0.1, 0.15, 0.2), amide longitudinal relaxation time T_1s (0.5, 1.0, 1.5, 2.0, 2.5 s), amide transverse relaxation time T_2s (1, 2, 5, 10, 20 ms), and fast exchanging amine concentration f_n (0, 0.0025, 0.005, 0.0075, 0.01). Each parameter was varied individually, with all other parameters remaining at the value in bold. R_1obs was calculated according to Ref ³⁶,

$$R_{\mathrm{l}\mathit{obs}}\approx (R_{1w}+f_c{R}_{1c})/(1+f_c)$$ (5)

where R_1c is the longitudinal relaxation rate of the semi-solid MT pool.

Table 2.

Parameters for the seven-pool numerical simulation with solute concentration (f_s), solute-water exchange rate (k_sw), longitudinal relaxation time (T₁), transverse relaxation time (T₂), and solute resonance frequency offset (Δ). Water content was set to be 1.

	water	amide	intermediate amine	fast amine	NOE(−1.6)	NOE(−3.5)	MT
fs	1	0.0015	0.0003	0.005	0.003	0.007	0.1
ksw (s−1)	-	50a	500b	5000c	50	50	25
T1 (s)	1.5	1.5	1.5	1.5	1.5	1.5	1.5
T2 (ms)	50	2	10	10	1	0.5	0.015
Δ (ppm)	0	3.5	2	3	−1.6	−3.5	−2.3

^a_around 30 s⁻¹ in Ref ⁴

^b_500 to 1000 s⁻¹ in Ref ^18,55,56

^c_5000–7000 s⁻¹ in Ref ^18,55

An additional set of simulations was performed to address the narrow question of the lineshape generated by fast-exchanging amine protons. Specifically, Z-spectra were simulated using a two-pool (fast exchanging amine and water) model with solute resonance frequency offsets at 3, 6, 12, and 21 ppm. The resulting simulated Z-spectra were used as label spectra and corresponding simulated Z-spectra from a one-pool (water) model were used as reference spectra. These two spectra were used to create the simulated fast exchanging amine AREX spectra using Eq. (3). This use of a one-pool model is distinct from the approach used to calculate AREX_mfit and AREX_LD where the reference signals were obtained by fitting multi-pool simulated Z-spectra and thus may include confounding contributions from multiple exchanging pools. This simulated fast exchanging amine AREX spectra can thus accurately isolate the fast exchanging amine signal from the water signal. Through comparison with R^cest_ex spectra, we can determine whether the fast exchanging amine signal has a Lorentzian lineshape.

The seven-pool model contains nineteen coupled Bloch equations and can be written as $\frac{d\mathbf{M}}{dt}=\mathbf{A}\mathbf{M}+{\mathbf{M}}_0$, where A is a 19 × 19 matrix. The water and solute pools each has three coupled equations representing their x, y, and z components. The semi-solid MT pool has a single coupled equation representing the z component, with a Lorentzian absorption lineshape. All numerical calculations of the Z-spectra integrated the differential equations through the continuous wave (CW) sequence using the ordinary differential equation (ODE) solver in MATLAB. Z-spectra with fewer pools were simulated by setting the corresponding pool concentration to zero.

Phantom preparation

Two phantoms, 6 mM creatine and 10 mM glutamate (which are their physiological concentrations), were prepared in commercially available phosphate buffered saline (1 × PBS) buffer (10 mM PO₄³⁻, 137 mM NaCl, and 2.7 mM KCl). The pH was titrated to 7 by using NaOH/HCl and measurements were performed at 37°C.

Animal preparation

All animal experiments were approved by Animal Care and Usage Committee in Vanderbilt University. Each rat was injected with 1 × 10⁵ 9L glioblastoma cells in the right brain hemisphere, and was then imaged after 2 to 3 weeks when brain tumor was formed. Seven rats bearing 9L tumor were immobilized and anesthetized with a 2%/98% isoflurane/oxygen mixture. Respiration was monitored to be stable, and a constant rectal temperature of 37°C was maintained throughout the experiments using a warm-air feedback system (SA Instruments, Stony Brook, NY).

MRI

CEST and rNOE saturation transfer measurements were performed by applying a 5 s CW irradiation before a single-shot spin-echo Echo Planar Imaging (SE-EPI) acquisition. Z-spectra were acquired with RF offsets from −4000 Hz to −2000 Hz with step of 500 Hz, −2000 Hz to 2000 Hz with step of 50 Hz, 2000 Hz to 4000 Hz with step of 500 Hz (−10 ppm to 10 ppm on 9.4 T). Control images were acquired with RF offsets of 100000 Hz (250 ppm on 9.4 T). R_1obs and f_c were obtained using a selective inversion recovery (SIR) method ⁴³. Specifically, a 1 ms inversion hard pulse was applied to invert the free water pool with subsequent longitudinal recovery times of 4, 5, 6, 8, 10, 12, 15, 20, 50, 200, 500, 800, 1000, 2000, 4000, and 6000 ms. SE-EPI was used for the readout scheme followed by a saturation pulse train to shorten total acquisition time as described previously ^43,44. A constant delay time of 3.5 s was set between the saturation pulse train and the next inversion pulse. All measurements were performed on a Varian DirectDrive™ horizontal 9.4T magnet with a 38-mm Litz RF coil (Doty Scientific Inc. Columbia, SC). All images were acquired with matrix size 64 × 64, field of view 30 mm × 30 mm, and one acquisition.

Statistics

All statistical analyses were performed using Matlab R2013b (Mathworks, Natick, MA, USA). It was considered to be statistically significant when P < 0.05. Student’s t-test was employed to evaluate the signal difference between tumor and normal tissues.

RESULTS

Multiple CEST and rNOE saturation transfer pools in rat brain

Figs. 1a and 1b show the experimental Z-spectra from normal tissues in rat brains and the corresponding residual spectra after fitting the data between −10 ppm and −6.25 ppm, −0.5 ppm and 0.5 ppm, and 6.25 ppm and 10 ppm (not shown) to Lorentzian MT and DS effects. Signals from five rat brains were acquired with irradiation powers of 0.5 μT (red), 1.0 μT (blue), and 1.5 μT (green). It was found from Fig. 1a that the most distinct CEST and rNOE saturation transfer effects in brain in the range from −5 to 5 ppm arise from amide protons at around 3.5 ppm, amine protons at around 2 ppm, and NOE at around −1.6 and −3.5 ppm. In Fig. 1b, an additional broad peak appears to overlap with both the narrow amide CEST peak at 3.5 ppm and the narrow amine CEST peak at 2 ppm, which is consistent with the presence of multiple amine pools. Previous studies have validated two main metabolites: creatine (15–17) and glutamate (18) which have significant CEST effects from amines at 2 ppm and 3 ppm, respectively. Creatine has an exchange rate of several hundred Hertz, and thus may contribute to the narrow CEST peak at 2 ppm. Glutamate has an exchange rate of several thousands Hertz, and thus may contribute to the broad CEST peak. Here we named the amine pool with narrow peak as the intermediate exchanging amine pool and the amine pool with broad peak as the fast exchanging amine pool. The CEST effect from the fast exchanging amine pool at these irradiation powers is significant, but has not been previously noted.

To further validate the presence of the significant CEST effect from this fast exchanging amine pool at these irradiation powers, we performed multiple-pool numerical simulations with and without the fast exchanging amine pool. Figs. 1c and 1d show a seven-pool (containing all the above mentioned pools) model simulated Z-spectra and CEST residual spectra, respectively, with tissue parameters shown in Table 2. Figs. 1e and 1f show six-pool (without the fast exchanging amine pool) model simulated Z-spectra and CEST residual spectra, respectively, with tissue parameters shown in Table 2. Comparing the residual spectra in Figs. 1b, 1d, and 1f makes clear that a fast exchanging pool (as in Fig 1d) is necessary to qualitatively match the in vivo residuals (in Fig. 1b). The six pool model residuals in Fig. 1f, lacking a fast exchanging pool, are qualitatively different from the in vivo case. While the shape of the residuals using the LD analysis indicates the need for including a fast exchanging pool, the exact size and exchange rate for this pool is not clear. Furthermore, we have glossed over accuracy issues when fitting the DS and semi-solid MT effects in the LD analysis. For both these reasons, we advance to multiple-pool Lorentzian fit.

Figs. 2a and 2b show Z-spectra obtained on creatine (solid red) and glutamate (solid blue) phantoms with physiological concentrations and pH at irradiation power of 1 μT and 1.5 μT, respectively. Compared with the narrow amine peak from creatine, a broad peak from glutamate can be observed, which is consistent with the apparent broad peak in Fig. 1.

FIG. 2.

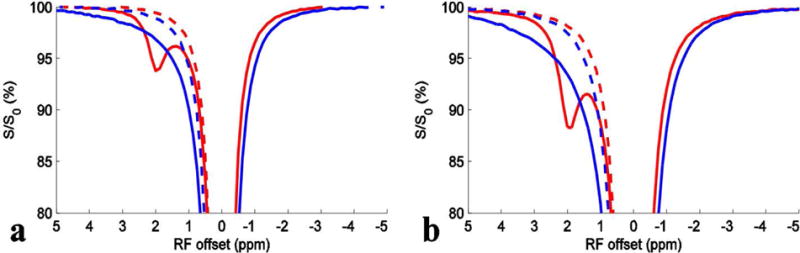
Z-spectra from creatine (solid red) and glutamate (solid blue) with irradiation power of 1 μT (a) and 1.5 μT (b), respectively. The dashed red and dashed blue curves are the mirror curves of those on the other sides of water resonance.

Quantification of CEST and rNOE saturation transfer signals

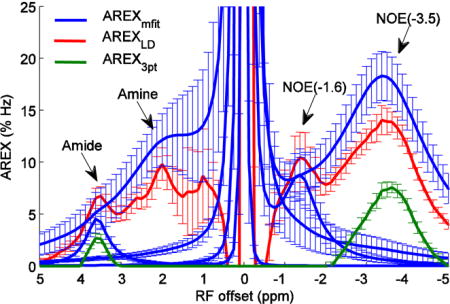
Fig. 3 shows the experimental AREX_mfit spectra, AREX_LD spectra, and AREX_3pt spectra from contralateral normal tissues of seven rat brains with irradiation powers of 1.0 μT. It was found that AREX_LD > AREX_mfit > AREX_3pt at 3.5 ppm, AREX_mfit > AREX_LD > AREX_3p at −3.5 ppm, AREX_mfit > AREX_LD at 2 ppm, and AREX_LD > AREX_mfit at −1.6 ppm. The different values obtained with these three quantification methods indicate the necessity of evaluating their accuracies.

FIG. 3.

AREX_mfit for amide, amine, NOE(−1.6), and NOE(−3.5) (blue) as well as AREX_LD (red) and AREX_3pt (green) from normal tissue of seven rat brains with irradiation powers of 1.0 μT.

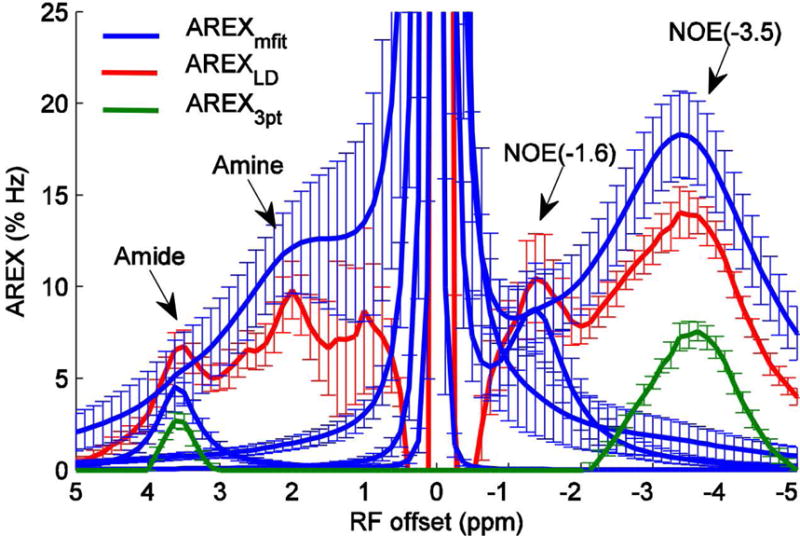
Fig. 4 shows the AREX_mfit spectra, AREX_LD spectra, and AREX_3pt spectra obtained from simulated Z-spectra, as well as the calculated R^cest_ex spectra from Eq. (4). The tissue parameters used in the simulation and calculation were the same and were from Table 2. The Z-spectra used in Fig. 4a, 4c, and 4e were from the seven-pool model numerical simulation. The R^cest_ex spectra centered at 2 ppm were calculated with the parameters of the intermediate exchanging amine pool. Table 3 lists the ratio of the peak intensities of the three AREX metrics to R^cest_ex to indicate how the AREX metrics match or deviate from the R^cest_ex.. We found that the relative magnitudes of these three metrics in Fig. 4 are in agreement with the experimental results in Fig. 3. In addition, through comparison with the R^cest_ex spectra, we found that the AREX_mfit can correctly estimates APT at irradiation powers of 0.5 and 1.0 μT, but overestimates the APT at 1.5 μT; the AREX_mfit also correctly estimates NOE(−3.5), but overestimates intermediate exchanging amine and underestimates NOE(−1.6); the AREX_LD overestimates APT and intermediate exchanging amine, but underestimates NOE(−1.6) and NOE(−3.5); the AREX_3pt significantly underestimates both APT and NOE(−3.5).

FIG. 4.

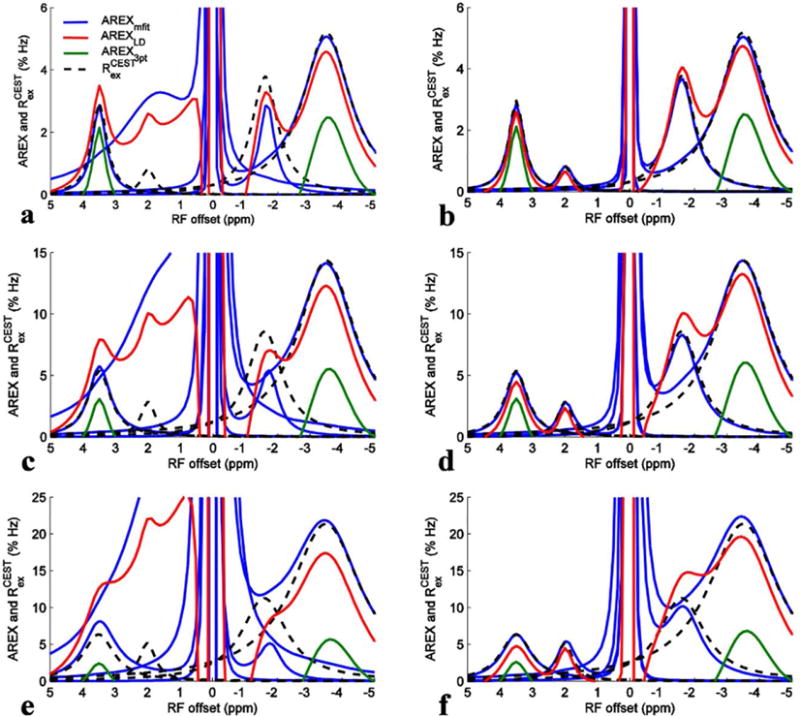
AREX_mfit for amide, amine, NOE(−1.6), and NOE(−3.5) (blue) as well as AREX_LD (red) and AREX_3pt (green) from simulated Z-spectra with irradiation powers of 0.5 μT (a and b), 1.0 μT (c and d), and 1.5 μT (e and f). Calculated R^cest_ex spectra for amide, amine, NOE(−1.6), and NOE(−3.5) (dashed black) were also plotted for comparison with these three quantification methods. (a), (c), and (e) were from the seven-pool model simulations and (b), (d), and (f) were from a six-pool model (without fast exchanging amine) simulations.

Table 3.

Ratio of the peak intensities of the three AREX metrics to R^cest_ex at three different irradiation powers. Note that when the AREX metrics match R^cest_ex well, their ratios are equal to 1.

	Amide (0.5, 1, 1.5μT)	intermediate exchanging amine (0.5, 1, 1.5μT)	NOE(−1.6) (0.5, 1, 1.5μT)	NOE(−3.5) (0.5, 1, 1.5μT)
AREX3pt/Rcestex (7 pool)	0.7, 0.6, 0.4	–	–	0.5, 0.4, 0.3
AREXLD/Rcestex (7 pool)	1.2, 1.5, 2.0	3.1, 3.5, 4.2	0.9, 0.8, 0.6	0.9, 0.9, 0.8
AREXmfit/Rcestex (7 pool)	1.0, 1.1, 1.3	3.7, 4.2, 5.5	0.8, 0.6, 0.4	1.0, 1.0, 1.0
AREX3pt/Rcestex (6 pool)	0.7, 0.6, 0.4	–	–	0.5, 0.4, 0.3
AREXLD/Rcestex (6 pool)	0.9, 0.8, 0.7	0.8, 0.8, 0.9	1.1, 1.2, 1.3	0.9, 0.9, 0.9
AREXmfit/Rcestex (6 pool)	1.0, 1.0, 1.0	1.0, 1.0, 1.0	1.0, 1.0, 0.9	1.0, 1.0, 1.0

To study the origin of the inaccuracy of these quantification methods, we also performed a six-pool model numerical simulation in which each exchanging pool was removed separately (Fig. 4 and Sup. Fig. S1-S4). We found that the fast exchanging amine pool influences the quantification of other pools greatly. Fig. 4b, 4d, and 4f show the six-pool model numerical simulations without fast exchanging amine pool. The AREX_mfit spectra for APT at 1.5 μT, intermediate exchanging amine, and NOE(−1.6) which deviate much from R^cest_ex spectra in the seven-pool model simulations, become close to R^cest_ex spectra after removal of the fast-exchanging amine pool, suggesting that it is the fast exchanging amine pool which introduces errors with this method. The AREX_LD spectra for amide and amine become more close to R^cest_ex spectra, and the AREX_LD spectra for NOE(−1.6) become higher than R^cest_ex spectra after removal of the fast exchanging amine pool, indicating that they should at the very least have contributions from the fast exchanging amine pool. The AREX_LD spectra for NOE(−3.5) still underestimates R^cest_ex spectra, which indicates that it has smaller influences from fast exchanging amines, but may be influenced by the incorrect fit of the reference due to the extent of the broad NOE(−3.5) signal on the section of Z-spectra used for reference fitting; The AREX_3pt still underestimates APT and NOE(−3.5), indicating that this three-point method has less influence from the fast exchanging amine.

To further study how the fast exchanging amine influences the quantification of other pools, we separately study this pool through numerical simulations. Fig. 5a shows the simulated fast exchanging amine AREX spectra and the R^cest_ex spectra at different resonance frequency offsets. The simulated fast exchanging amine AREX spectrum can show the lineshape of the fast exchanging amine signal by isolating it from water signal. It was found that these two spectra match well when the solute resonance frequency offsets are far from water resonance. However, these two spectra deviate significantly when they are close to water resonance. For the simulated fast exchanging amine AREX spectra at 3 ppm, it can be clearly found that (1) the simulated fast exchanging amine AREX peak is not at 3 ppm, but moves towards the water resonance; (2) the simulated fast exchanging amine AREX signal is clearly not a Lorentzian lineshape. This is caused by the coalescence of the water and amine CEST peaks at small offsets. This result indicates that Eq. (4) cannot model CEST effect in the fast exchange regime. Actually, the weird lineshape has already been previously modeled by a non-Lorentzian function, and is a complicated function of irradiation power, offset, and exchange rate ³⁸. Fig. 5b shows the simulated fast exchanging amine AREX spectra with resonance frequency offset at 3 ppm as well as AREX_mfit spectra for the fast exchanging amine and AREX_LD spectra. It was found the AREX_mfit underestimates the fast exchanging amine signal at 3.5 ppm which may contribute to the overestimation of amide by using this method. It was also found that the AREX_LD are negative upfield, which may contribute to the increased AREX_LD for NOE(−1.6) after removal of fast exchanging amine. The negative AREX_LD upfield may be caused by the incorrect fit of the reference signal due to the extent of the broad fast exchanging amine signal on the section of Z-spectra for reference fitting.

Fig. 5.

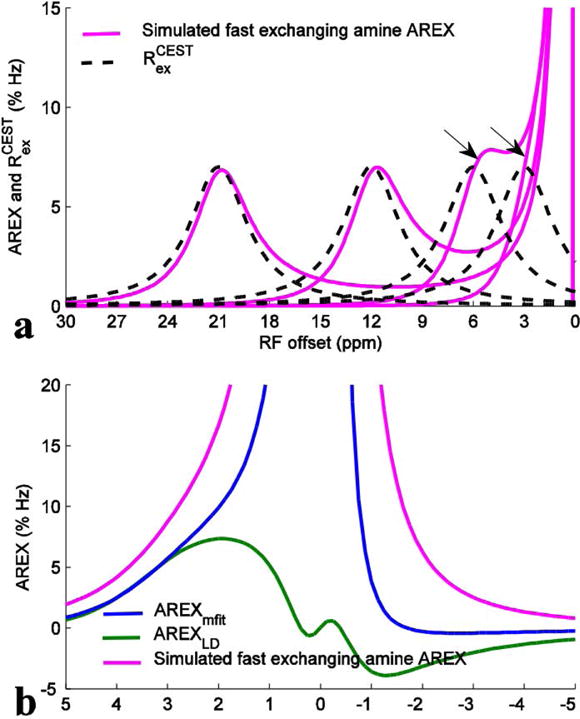
(a) Simulated fast exchanging amine AREX (magenta) and calculated R^cest_ex (dashed black) spectra with the resonance frequency offsets of the fast exchanging amine pool at 3, 6, 12, and 21 ppm (magenta). (b) Simulated fast exchanging amine AREX spectrum with resonance frequency offset of the fast exchanging amine pool at 3 ppm (magenta) as well as AREX_mfit spectra (blue) for the fast exchanging amine and AREX_LD spectra (green). The simulated fast exchanging amine AREX spectra were created by inverse subtraction of two-pool model (fast exchanging amine and water) simulated Z-spectra and one-pool model (water) simulated Z-spectra according to Eq. (3), which can accurately isolate the fast exchanging amine signal from water signal. The AREX_mfit and the AREX_LD spectrum were obtained by processing the two-pool model simulated Z-spectra. Note in (a) that although the simulated fast exchanging amine AREX spectra match the R^cest_ex spectra well when their solute resonance frequency offsets are far from water resonance, they deviate significantly from the R^cest_ex spectra when their offsets are close to water resonance (arrows), indicating that the fast exchanging amine CEST signal is not a Lorentzian lineshape. Note in (b) that both the AREX_mfit and the AREX_LD cannot successfully fit the fast exchanging amine CEST signals.

To confirm our conclusion drawn in Fig. 4 about the accuracy in the quantification of APT and NOE(−3.5) in a general case, we further performed simulations with a variety of tissue parameters. Fig. 6 shows the AREX_mfit, AREX_LD, AREX_3pt, and the calculated R^cest_ex values for amide from simulated Z-spectra with variation of T_1w (a), T_2w (b), T_1s (c), T_2s (d), f_m (e), and f_n (f) and with irradiation power of 1 μT. It was found that AREX_3pt underestimates amide and AREX_LD overestimates amide in all cases. In contrast, AREX_mfit with this irradiation power can provide better quantification of amide than the other two methods, except when fast exchanging amine concentration is high (see Fig. 6f). The AREX_3pt value is relatively closer to the R^cest_ex value with longer T_2s, suggesting that the accuracy of this method depends on CEST peak line width. It was also found that all three metrics are roughly independent on these tissue parameters, except for T_2s, supporting the view that inverse analysis has improved specificity. Fig. 7 shows the same simulations as those in Fig. 6, but with irradiation power of 1.5 μT. Similar to Fig. 6, the AREX_3pt still underestimates amide and AREX_LD still overestimates amide in all cases. However, the AREX_mfit with this relatively higher irradiation power overestimates amide in all cases which is different from that in Fig. 6. These general simulations in Fig. 6 and Fig. 7 are consistent with our conclusion drawn from Fig. 4 that the AREX_mfit correctly estimates APT at low irradiation powers, but the AREX_LD overestimates and the AREX_3pt underestimates APT. For the quantification of NOE(−3.5) in a general case, our simulations with a variety of tissue parameters (Sup. Fig. S5 and S6) also confirm the conclusion drawn from Fig. 4 that the AREX_mfit correctly estimates NOE(−3.5), but the AREX_LD and AREX_3pt underestimate NOE(−3.5).

FIG. 6.

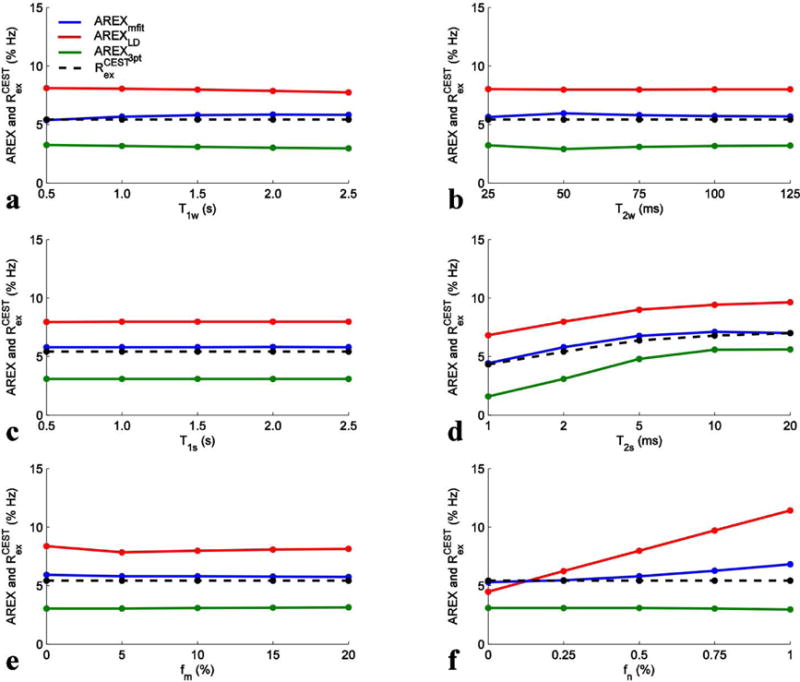
AREX_mfit (blue), AREX_LD (red), AREX_3pt (green), and calculated R^cest_ex (dashed black) for APT from simulated Z-spectra with variation of T_1w (a), T_2w (b), T_1s (c), T_2s (d), f_m (e), and f_n (f) and with irradiation powers of 1 μT.

FIG. 7.

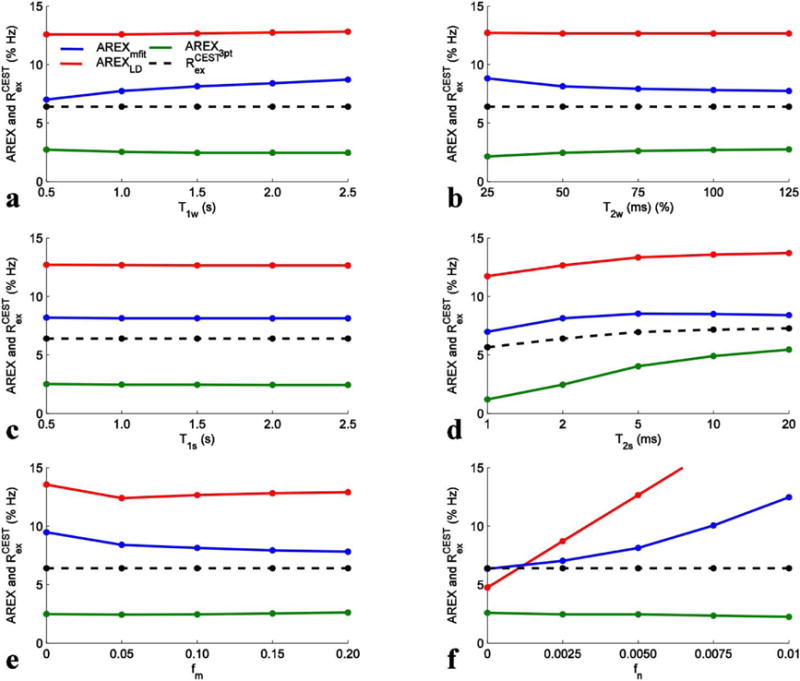
AREX_mfit (blue), AREX_LD (red), AREX_3pt (green), and calculated R^cest_ex (dashed black) for APT from simulated Z-spectra with variation of T_1w (a), T_2w (b), T_1s (c), T_2s (d), f_m (e), and f_n (f) and with irradiation powers of 1.5 μT.

APT and NOE(−3.5) contrasts in tumors

The above analysis indicates that the multiple-pool Lorentzian fit can quantify APT and NOE(−3.5) at relatively lower irradiation power (e.g. 0.5 and 1 μT at 9.4 T) that better matches R^cest_ex in comparison to other quantification methods. Here we compared the AREX_mfit acquired with irradiation power of 1 μT with the other two quantification methods on animal tumor models. Fig. 8 and Fig. 9 show the statistical differences of MTR_mfit, MTR_LD, MTR_3pt, AREX_mfit, AREX_LD, and AREX_3pt for APT and NOE(−3.5), respectively, between tumor and contralateral normal tissue from seven rat brains. Fig. 10 shows the multi-parametric images (R_1obs, R_2w, f_m, AREX_mfit for APT, AREX_LD for APT, AREX_3pt for APT, AREX_mfit for NOE(−3.5), AREX_LD for NOE(−3.5), and AREX_3pt for NOE(−3.5)) on a representative rat brain bearing 9L tumor. Note in Fig. 8 and Fig. 9 that all these quantification methods with MTR or AREX have similar contrasts between tumor and contralateral tissues: there is statistical difference for all MTR metrics for APT, but no statistical difference for all AREX metrics for APT between tumor and contralateral normal tissue. In contrast, there is no statistical difference for all MTR metrics for NOE(−3.5), but significant statistical difference for all AREX metrics for NOE(−3.5) between tumor and contralateral normal tissue. This result is in agreement with a previous publication ³³. However, although these three AREX metrics give similar contrasts between tumors and contralateral normal tissues (see Fig. 10), the quantified values (see Fig. 8 and Fig. 9) among these three methods are significantly different, suggesting the necessity to evaluate their accuracy. Based on our analysis from the simulated results, it is possible that LD and the three-point methods provide inaccurate quantification of CEST or rNOE saturation transfer effects in living tissues, but the multiple-pool Lorentzian fit at 1 μT is likely more accurate than the other two methods.

FIG. 8.

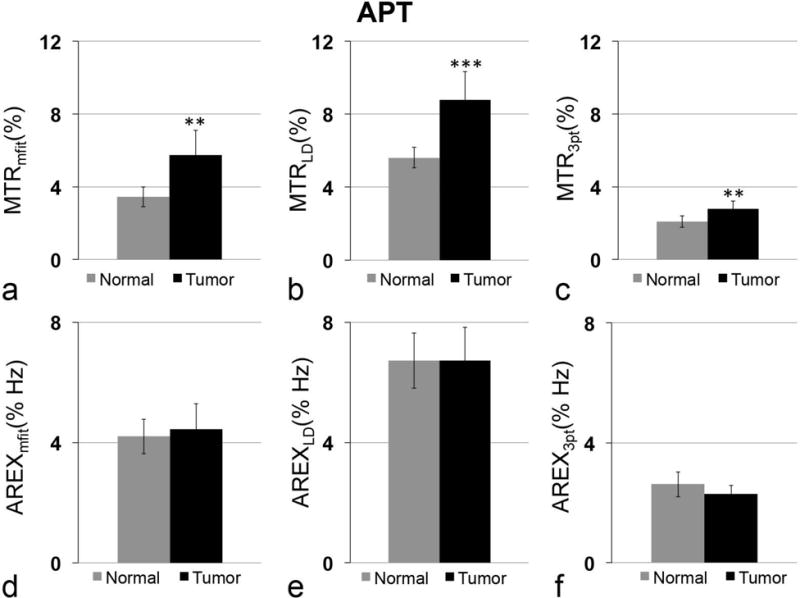
Statistical differences of MTR_mfit (a), MTR_LD (b), MTR_3pt (c), AREX_mfit (d), AREX_LD (e) and AREX_3pt (f) for APT between tumor and contralateral normal tissue in rat brain. Irradiation power is 1 μT. (n=7, **P <0.01, ***P <0.001)

FIG. 9.

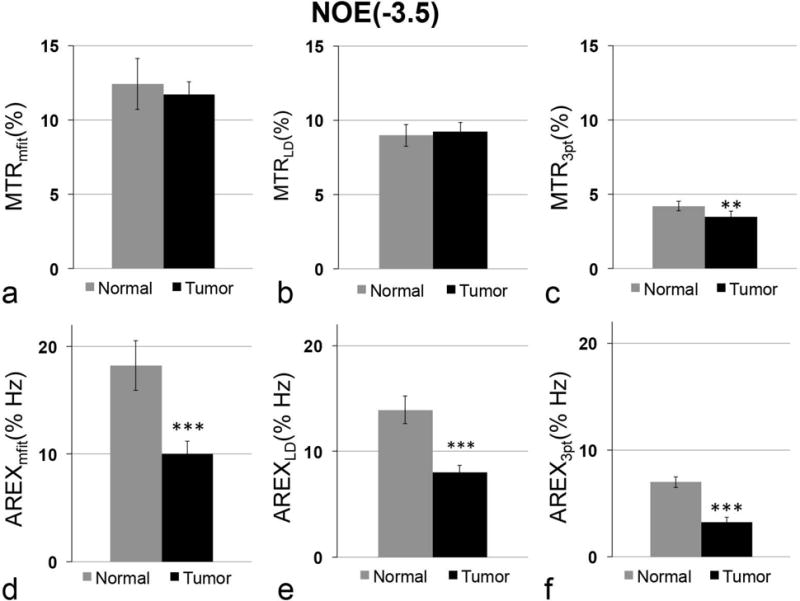
Statistical differences of MTR_mfit (a), MTR_LD (b), MTR_3pt (c), AREX_mfit (d), AREX_LD (e) and AREX_3pt (f) for NOE(−3.5) between tumor and contralateral normal tissue in rat brain. Irradiation power is 1 μT. (n=7, **P <0.01, ***P <0.001)

FIG. 10.

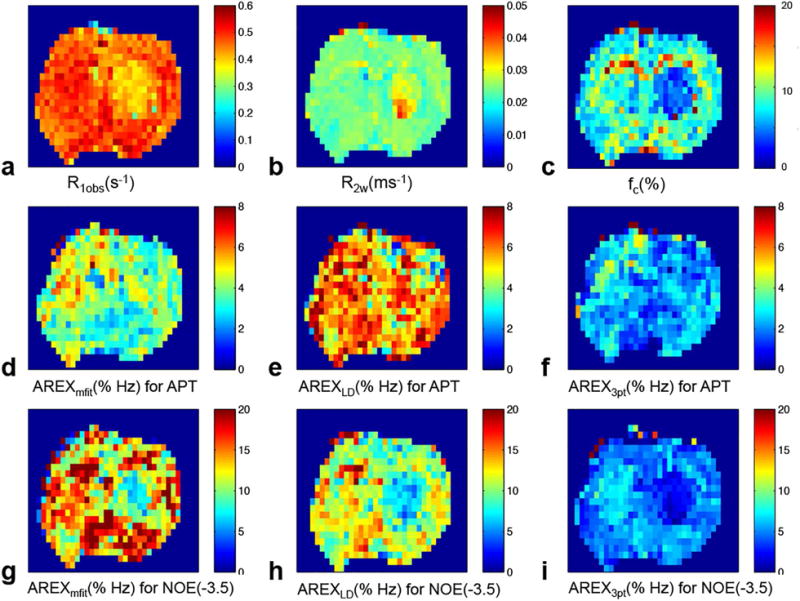
multi-parametric images of R_1obs (a), R_2W (b), f_c (c), AREX_mfit for APT (d), AREX_LD for APT (e), AREX_3pt for APT (f), AREX_mfit for NOE(−3.5) (g), AREX_LD for NOE(−3.5) (h), AREX_3pt for NOE(−3.5) (i). Irradiation power is 1 μT.

DISCUSSION

Accurate quantification of CEST or rNOE saturation transfer signals is important, but is challenging especially in complex biological system where multiple CEST and rNOE saturation transfer pools are present. Here, we evaluated the accuracy of several CEST quantification methods.

Multiple CEST and rNOE saturation transfer pools in live rat brain

At 9.4 T, several CEST and rNOE saturation transfer dips, including the amide, intermediate exchanging amine, and NOE (−3.5), can be resolved in a Z-spectrum. The fast exchanging amine pool has been noticed at very high irradiation powers (>3 μT), but has typically been ignored at lower irradiation powers possibly because that there is no clear dip from this pool on a Z-spectrum at lower irradiation power. However, our animal experiments, phantom experiments, and simulations in Fig.1 and Fig. 2 show that the fast exchanging amine CEST effect is still significant compared with that from other pools at an irradiation power of 1 μT. The fast exchanging amine, which does not maintain the condition of slow exchange relative to offset (Δ >> k_sw) ², produces signal dips that coalesce with water and thus produces signal contributions that cannot be modeled by a Lorentzian lineshape ³⁸. This signal contribution is broad and overlaps with amide and intermediate exchanging amine, and causes inaccuracy in quantification of these pools. The NOE(−1.6) is a new signal that has been overlooked. This signal is close to water resonance and thus may be buried by the DS effect. Thus, it is challenging to observe a clear NOE(−1.6) dip in a Z-spectrum (Fig. 1a). But it can be identified in the CEST residual spectra in which DS was partially removed (Fig. 1b).

Quantification of CEST and rNOE saturation transfer signals

Previously, the LD analysis has been applied to quantify amides ³². However, our study shows that this method has contamination from fast exchanging amines. This contamination is worse at higher irradiation powers where the fast exchanging amine CEST effect is more significant and at lower field where the amine and amide resonance frequencies are closer. Similarly, the NOE(−1.6) is also contaminated by the broad NOE(−3.5) peak which can be observed in Fig. 4b, 4d, and 4f. The overlapping signals indicate the necessity to perform a multiple-pool Lorentzian fit. The accuracy of the LD analysis also depends on the choice of sampling points for reference fitting. The underestimation of amide and NOE(−3.5) signals by using this method in Fig. 4b, 4d, and 4f suggest that signals from −10 to −6 ppm and 6 to 10 ppm still have contributions from NOE(−3.5) and/or fast exchanging amine pools. Farther fitting points from water resonance may avoid these contributions, but will be limited by the non-Lorentzian lineshape of the semi-solid MT ^45–47.

The multiple-pool Lorentzian fit can correctly estimate amide, but only at lower irradiation powers. The limited working range of irradiation powers with this method should be considered when performing further quantification of solute concentration and exchange rate, in which multiple irradiation powers are always required. In our study, the multiple-pool Lorentzian fit of amide works well at irradiation powers of 0.5 and 1.0 μT at 9.4 T. At lower field scanners where the amine and amide resonances are closer to each other, the working range of irradiation powers are likely more limited. It was reported that creatine is in the intermediate exchanging range (several hundreds Hertz), and thus may contribute to the narrow amine peak. Previous works have quantified the creatine by using a variation of the multiple-pool Lorentzian fit ¹⁷. However, our studies indicate that this method (which contains only a single amine pool in the model) may overestimate the creatine content, due to contamination from the fast exchanging amine pool.

The three-point method has the benefit of being simple. However, it significantly underestimates APT and NOE(−3.5) signal contributions, and is not an accurate method. This method uses a reference signal obtained by averaging two nearby signals, which may fail to capture the full extent of the CEST and rNOE saturation transfer peaks.

Several other methods such as chemical exchange rotation transfer (CERT) ^25,48, saturation with frequency alternating RF irradiation (SAFARI) ⁴⁹, and variable delay multi-pulse train (VDMP) ^50,51 et. al. have also been developed to quantify CEST or rNOE saturation transfer. However, although these methods can avoid some contaminations through repeated short-duration pulsed irradiation designed to filter out confounding effects, there is no analytic solution to the Bloch equations with pulsed-irradiations. Therefore, quantification of solute concentration and exchange rate by using these methods is very challenging. Evaluation of the accuracy of these methods is beyond the scope of this paper.

Note that our conclusions are based on multiple-pool numerical simulations, which may not mimic real tissues exactly. For example: 1) the tissue parameters in simulations may be different from those in real tissues and; 2) there may be additional CEST or rNOE saturation transfer pools in real tissues that are not included in our simulations. For the first case, our conclusions were drawn from simulations with a broad range of tissue parameters in Fig. 6 and Fig. 7 which should cover real tissue parameters. For the second case, those pools in our model appear to contribute the main CEST signals in the in vivo Z-spectra and CEST residual spectra in Figs. 1a and 1b. CEST signals from other pools may be present, but are relatively weak compared with the CEST effects from these pools in our model at such irradiation powers. In addition, the broad NOE(−3.5) peak may be composed of several small rNOE saturation transfer peaks ²⁰, but Fig. 1b shows that it can effectively be treated as a single pool with a very short T_2s in the experimental conditions examined in this work.

APT and NOE(−3.5) contrasts in tumors

The contradictory statistical results between the MTR_mfit and AREX_mfit metrics for APT and NOE(−3.5) indicate that the MTR metrics may have contributions from other tissue parameters in addition to chemical exchange or dipolar interactions from the target solutes. Previous publications indicated that variations of T_1w and/or MT in tumor may also contribute to the MTR contrast ^33,37,52. However, Lee et. al. ⁵³ recently showed that both the increased water content and enhanced T_1w in tumors influence the APT signal, and these two effects can be mostly cancelled out; therefore, there is no necessity to normalize by T_1w in order to quantify the amide content, but not the fraction of amide pool with the water pool. More recently, a new aromatic rNOE saturation transfer at 3.5 ppm, which overlaps with APT, was reported to account for the disappearance of the AREX contrast between tumor and contralateral normal tissues at 3.5 ppm ⁵⁴. While we did not include this contribution in the current work, the quantification of this new rNOE saturation transfer signal using the three methods examined in this paper will likely be subject to biases similar to those we have found. Further validation of the abilities of MTR or AREX to detect change of amides (either amide content or the fraction of amide pool with the water pool) in tumors requires accurate quantification of the underlying exchanging pools. The comparison between fitted results from multiple-model simulations with the theoretically calculated results used in this work can be also applied to evaluate the accuracy of other newly developed quantification methods.

CONCLUSION

The accuracy of CEST and rNOE saturation transfer quantification methods is important, but has not been evaluated. Our results demonstrate that the LD analysis overestimates APT and intermediate exchanging amine. The three-point method underestimates APT and NOE(−3.5) signals. In contrast, the multiple-pool Lorentzian fit is more accurate than the other two methods within the range of our simulations, but only at relatively lower irradiation powers.

Abbreviations

CEST

chemical exchange saturation transfer

NOE

nuclear Overhauser enhancement

rNOE

relayed nuclear Overhauser enhancement

APT

amide proton transfer

DS

direct water saturation

LD

Lorentzian difference

MTR

magnetization transfer ratio

MTR_LD

MTR obtained by the Lorentzian difference analysis

MTR_mfit

MTR obtained by the multiple-pool Lorentzian fit

MTR_3pt

MTR obtained by the three-point method

R_1obs

apparent water longitudinal relaxation rate

AREX

apparent exchange-dependent relaxation

k_sw

solute-water exchange rate

AREX_LD

AREX obtained by the Lorentzian difference analysis

AREX_mfit

AREX obtained by the multiple-pool Lorentzian fit

AREX_3pt

AREX obtained by the three-point method

CW

continuous wave