Quantifying veterinarians’ beliefs on disease control and exploring the effect of new evidence: A Bayesian approach

Abstract

The clinical beliefs (expectations and demands) of veterinarians regarding herd-level strategies to control mastitis, lameness and Johne’s disease were quantified in a numerical format; 94 veterinarians working in England (UK) were randomly selected and during interviews, a statistical technique called ‘probabilistic elicitation’ was used to capture their clinical expectations as probability distributions. The results revealed that markedly different clinical expectations existed for all 3 diseases, and many pairs of veterinarians had expectations with non-overlapping 95% Bayesian credible intervals; for example, for a 3 yr lameness intervention, the most pessimistic veterinarian was centred at an 11% population mean reduction in lameness prevalence (95% credible interval: 0-21%); the most enthusiastic veterinarian was centred at a 58% reduction (95% credible interval: 38-78%). This suggests that a major change in beliefs would be required to achieve clinical agreement.

The veterinarians’ clinical expectations were used as priors in Bayesian models where they were combined with synthetic data (from randomized clinical trials of different sizes) in order to explore the impact of new evidence on current clinical opinion. The mathematical models make predictions based on the assumption that veterinarians will update their beliefs logically. For example, for the lameness intervention, a 200 farm clinical trial that estimated a 30% mean reduction in lameness prevalence was predicted to be reasonably convincing to the most pessimist veterinarian; i.e. in light of this data, they were predicted to believe there would be a 0.92 probability of exceeding the median clinical demand of this sample of veterinarians, which was a 20% mean reduction in lameness. Currently controversy exists over the extent to which veterinarians update their beliefs logically, and further research on this is needed. This study has demonstrated that probabilistic elicitation and a Bayesian framework are useful for evaluating the diversity and strength of veterinarians’ clinical beliefs. The wide variations observed have implications for designing future projects. While many factors influence disease control, nonetheless the heterogeneity in beliefs also raises concern over the extent to which a broadly consistent approach is currently being achieved; it supports the argument for more randomised clinical trials, and for national programs to control the non-statutory endemic diseases.

Introduction

In the UK most major endemic diseases of cattle are not under statutory control and hence the health of the national herd is critically reliant on farmers and their advisors. The clinical beliefs held by veterinarians working in private practice are thus important because they underpin the advice provided to famers, the decisions that are made, and the way in which new research evidence is interpreted and applied. If new research is to have any impact it must be capable of changing veterinarians’ current beliefs, and ultimately the farmers, otherwise it risks being of limited value, and will not deliver a cost beneficial return on the investment necessary to conduct the work.

If the unknown parameter of interest, say θ, is defined as the effect of a specified treatment (or disease intervention), then a veterinarian’s clinical expectations regarding θ pertain to the possible values they believe θ will take, based on their current clinical experiences and knowledge (i.e. their beliefs, which includes information and influences from all possible sources). Within a Bayesian statistical framework, clinical expectations can be expressed in a numerical format as a probability distribution, using a statistical technique called ‘probabilistic elicitation’ (O'Hagan et al., 2006). Once captured as probability distributions, it is possible to quantitatively study the variation in clinical expectations, and to explore, using Bayesian statistical models, the response of veterinarians with different clinical expectations to new information (Parmar et al., 1994a). For a single continuous unknown parameter, θ, Bayes theorem can be written as

$$\pi (\theta |\mathit{\text{x}})\propto \pi (\mathit{\text{x}}|\theta )\pi (\theta ),$$ (1)

where, in the context of this paper, π(θ) is the veterinarian’s current clinical expectation for θ, expressed as a probability distribution, π(x|θ) is the likelihood function (based on new synthetic data, x), and π(θ|x) is the posterior probability distribution that encapsulates everything that is now known about θ, having updated the veterinarian’s current clinical expectation with the new information contained in the data. In Bayesian terminology, π(θ) is referred to as ‘the prior’. Equation (1) states that the extent of any logical change in belief depends on both the current clinical expectation π(θ), and the strength of the new evidence, π(x|θ); thus Bayes theorem quantifies (probabilistically) how new data should, logically, influence pre-existing expectations about an uncertain parameter.

Clinical expectations have been probabilistically elicited in human medicine and to a lesser extent in veterinary medicine (O'Hagan et al., 2006). In addition, at the same time as eliciting doctors’ clinical expectations, some studies have elicited doctors’ clinical demands, θ^min.. A new treatment almost invariably carries economic and other costs (e.g. adverse reactions, toxicity or drug resistance). As a result, doctors usually demand that a minimum clinically worthwhile effect (i.e. θ^min), must be achieved in order for them to consider the treatment worthwhile implementing when compared against alternative approaches. Eliciting a clinical demand requires a doctor to weigh all the potential advantages and disadvantages of the treatment and assign a single value (or range of values) to θ^min (Parmar et al., 1994). To the authors’ knowledge, clinical demands have not been elicited from veterinarians working in farm animal medicine.

In a Bayesian analysis (Equation 1), θ^min can be juxtaposed on the posterior distribution, π(θ|x), and the null hypothesis (no treatment effect) is rejected in favour of the alternative hypothesis (θ > θ ^min) when the posterior distribution assigns a ‘sufficiently large’ probability to θ taking values greater than θ^min (Spiegelhalter et al., 2004). This probability, denoted here by λ, is a subjective choice but ‘sufficiently large’ is often taken to be λ ≥ 0.95. The choice for λ affects when the trial is stopped and the larger λ is, the greater the probability that the minimum clinically worthwhile effect will be realised.

In a retrospective Bayesian analysis, a recent study used a range of theoretical clinical expectations (priors) aimed at representing different opinions (from ‘severely sceptic’ to ‘very enthusiastic’) in order to model the impact of a clinical mastitis trial (Green et al., 2009). The study explored how the results of the trial would be interpreted by veterinarians with theoretically constructed different initial beliefs, and predicted that important differences in opinion would exist in light of the evidence. However, to the authors’ knowledge, no studies have actually quantified veterinarians’ clinical expectations or demands concerning herd level interventions to reduce the endemic diseases of cattle. This omission is striking because, in analogy with human medicine (Spiegelhalter et al., 2004), a potentially important obstacle to the widespread implementation of veterinary interventions on farms may relate to the variability of veterinarians’ beliefs concerning the effectiveness of disease control measures. If veterinarians currently have very different clinical expectations then other approaches, such as more convincing research evidence, will be required to alter these beliefs. Although this is not to say that it is only research evidence that influences what veterinarians believe. Our hypothesis was that demonstrable variation exists for veterinarians’ clinical expectations and demands regarding mastitis, lameness and Johne’s disease.

The first objective of this study was to report a probabilistic elicitation that aimed to quantify the current variation in veterinarians’ clinical expectations and demands with respect to herd-level interventions to reduce mastitis, lameness and Johne’s disease in dairy cattle. The second objective was to explore, within a Bayesian statistical framework, the implications of the heterogeneity in beliefs. This was done by using a mathematical model to make predications regarding how new evidence will alter what veterinarians currently believe. The model makes the assumption that veterinarians will update their beliefs logically.

Materials and Methods

Recruitment of Veterinarians

It was of interest to compare the beliefs of veterinarians with, and without, postgraduate qualifications. However, without some targeted selection, it was possible that no veterinarians holding postgraduate qualifications would be included in the sample. Therefore to be eligible for selection, veterinarians must have been currently providing healthcare to dairy cattle in England during their normal working hours, and be employed by a veterinary practice that contained at least 1 veterinarian possessing a ‘postgraduate cattle qualification’ i.e. the European College of Bovine Health Management Diploma, the Royal College of Veterinary Surgeons Certificate or Diploma in Cattle Health and Production, or the University of Liverpool Diploma in Bovine Reproduction. None of the veterinarians were exclusively involved in providing emergency care, or consultancy.

A 2 stage cluster design stratified by geographic location was used. First, 20 practices were selected with probability proportional to the number of veterinarians they contained. Subsequently, if the practice had >5 eligible members, then 5 were selected using the random number generator function in the software program R version 2.15.2 (R Core Team 2012). In practices that contained ≤ 5 eligible particpants, all veterinarians were recruited. This sampling strategy meant that every veterinarian had approximately the same chance of selection, independent of the size of the practice they worked in (Kalton, 1987). The Royal College of Veterinary Surgeons online database (http://www.rcvs.org.uk/) provided a list of veterinary practices. Face-to-face, individual, interviews were conducted by HMH between the 8^th June and the 1^st September 2011. Veterinarians were provided with an inconvenience allowance of £100 per hour (pro rata). A standard script was used for consistency (see Appendix). Basic descriptive information concerning the veterinarians was gathered.

Clinical Expectations

There were 3 epistemic parameters of interest (θ_m, θ_l, θ_j), each of which related to the population mean effect of an intervention strategy aimed at reducing an endemic disease. The subscript refers to the endemic disease, such that θ_m was defined as the population mean effect of a 1 yr mastitis intervention, θ_l a 3 yr lameness intervention, and θ_j an 8 yr Johne’s disease intervention. In addition, θ_d is used to refer more generally to the population mean effect of a disease intervention (d = m, l, j). For each disease what was meant by ‘an intervention strategy’ was described to each participant in detail (see Appendix) and can be summarised as follows. For all 3 diseases, an initial assessment of any available farm data is conducted, in conjunction with a farm visit, to assess the risks and achieve a working diagnosis; for mastitis and Johne’s disease, this was additionally taken to include some strategic laboratory testing, and for lameness, some locomotion scoring. As a result, a list of farm specific recommendations are made, based on current best evidence were possible, prioritised and discussed with the farmer. During quarterly farm re-visits, the farm data and risks are re-assessed, allowing the control measures to be modified in timely manner, and encouragement and support to implement the control measures provided.

Different time periods were chosen for the interventions, and reflect the fact that the time taken to make clinically observable reductions in disease levels varies with the disease. For the task it was assumed that all dairy farms in England had been recently visited by their local veterinarian to discuss the disease in question. The population under consideration was all the farmers who, following this consultation, subsequently decided to go ahead with the disease intervention

The disease outcomes were as follows. For the mastitis intervention it was assumed that in the year before, and in the year after the intervention took place, the number of clinical cases of mastitis per 100 cows was reliably measured for each farm in the population, in order to calculate the population mean mastitis incidence before and after the intervention; subclinical mastitis was not considered. For lameness, it was assumed that for each farm in the population the entire dairy herd was reliably scored for lameness at the start of the intervention and then again at the end, in order to work out the population mean prevalence of lameness; ‘lame’ was defined as observably lame in one or more limbs, with any severity of limp. For Johne’s disease it was assumed that for each farm in the population all the adult cattle (≥ 24 months old) were blood sampled before and after the intervention and the percentage of blood test positive adults was used as an approximation for the population mean prevalence of Johne’s disease; it is acknowledged that this is an estimate because of the limited sensitivity of the test. These outcomes were chosen because veterinarians were likely to be familiar with them. The population mean outcome before and after the intervention are denoted ${\psi }_d^0$ and ${\psi }_d^1$ respectively. As before, subscript d refers to the endemic disease (d = m, l, j).

The scale used was the difference in the population mean outcome (before and after the intervention) divided by the population mean outcome before the intervention, expressed as a percentage i.e.

$${\theta }_d=\frac{{\Psi }_d^0-{\Psi }_d^1}{{\Psi }_d^0}\times 100,{\Psi }_d^0>0.$$ (2)

Hence, θ_d ∈ [−∞,+100] for d = m, l, j. On this scale, positive percentages reflect reductions in disease, and negative percentages increases in disease. Thus, for example, θ_l = 20% is a 20% reduction in lameness prevalence, averaged across all farms, with a 3 yr lameness intervention. Veterinarians’ expectations for θ_d were elicited using a method that enabled probability distributions to be fitted to their answers (see next section).

The 3 parameters (θ_d) were elicited conditional on the assumption that without an intervention delivered with the help of a veterinarian, the population mean change over the time period would be zero, for each disease. In addition, despite the fact that the population parameters related to farmers who had volunteered to participate with the intervention, nevertheless it was possible that some farmers may not actually implement any of the recommendations either at all, or to a sufficient standard, such that their intervention had no chance of having any effect at all. Therefore, veterinarians were asked to provide a single estimate for the percentage of farmers who would fall into this category of zero implementation for each disease. Veterinarians were told to exclude these farmers from the population under consideration when they made their estimates for θ_d,; however, it was also stated that even with this exclusion, there was still likely to remain a wide diversity in the scale and effectiveness of farmer implementation.

In summary, veterinarians’ beliefs were sought for the expected (future) outcome of the specified disease intervention, on average across all the farms who implemented at least some of the recommendations (θ_d). For example, for the 8 year Johne’s programme, θ_j documents veterinarians’ beliefs regarding the final outcome of this intervention, given it commenced today.

Probabilistic Elicitation Method

The fixed-interval method was used, such that for each parameter (θ_d), 5 values were elicited to allow a probability distribution to be fitted: the minimum and maximum values, median, and lower and upper quartiles. The minimum and maximum values for the parameter together constituted a plausible range, such that the veterinarian considered it ‘exceedingly unlikely’ that that the actual answer would fall outside this range. The order in which the values are elicited is important to avoid an anchoring and adjustment heuristic, thus the plausible range was elicited first so that further judgements were made relative to this range; if, for example, the median is elicited first, then there is a tendency for this to act as an anchor, and the maximum and minimum values may not be adjusted far enough away from the median (O'Hagan et al., 2006).

Current best practice for probabilistic elicitation was employed whereby a face-to-face interview between the author and each veterinarian was conducted at the veterinarian’s own place of work, and lasted between 70 to 100 minutes. The first part of the elicitation involved a 15 to 25 minute training exercise, whereby the scale upon which veterinarians needed to give their answers was explained, as well as the meaning of the 5 judgements they needed to make using a fictitious example of a veterinarian who was convinced that an unspecified disease intervention would certainly make the disease problem worse (Parmar et al., 1994). This example was used on the grounds that the majority of veterinarians would believe that the disease interventions in question would typically reduce disease, and therefore the example explained how they should give their answers but avoided biasing them towards a certain disease reduction. It is also worth noting that during their interviews the veterinarians were asked for their current clinical expectations and in particular, they were not shown any data pertaining to any of the parameters, θ_d.

The Sheffield Elicitation Framework is a freely available package of guidance documents, templates and software specifically designed for carrying out probabilistic elicitation (SHELF, O’Hagan and Oakley; http://www.tonyohagan.co.uk/shelf/). Probability distributions were fitted to the veterinarians 5 judgements using computer code provided with this package (SHELF software, version 1.01) and run in the software program R, version 2.15.2 (R Core Team, 2012). The probability distributions were fitted during the interviews and graphically presented to the veterinarian. Furthermore, some of the inferred, but not directly elicited probabilities were cited to them; this enabled veterinarians to visualise their answers and gave them the opportunity to revise their 5 judgements appropriately until they felt the fitted distributions were a fair reflection of their beliefs.

Clinical Demands

For each disease, veterinarians were asked to weigh all the benefits of implementing the intervention on many thousands of farms, against all the costs. The minimum population mean reduction they would want the intervention to deliver, in order to consider the intervention clinically worthwhile implementing on a large scale, is subsequently referred to as their ‘clinical demands’ (θ_d^min, d = m, l, j). Veterinarians were asked to either give a single value, or if they preferred, a range of values.

In addition, for each disease intervention veterinarians were asked to give a value for λ i.e. λ_d, d = m, l, j. That is, they were asked for the probability (as a % chance) that the actual mean reduction in disease would be greater than what they had stated was a minimally clinically worthwhile effect. This value for λ was placed in the context of the veterinarian needing to be ‘convinced that the disease intervention is clinically useful and worthwhile implementing on many farms’, based on the evidence produced by a clinical trial alone.

The purpose of eliciting λ was to explore any differences between veterinarians in terms of the strength of evidence needed to be convincing to them. However, it is important to note, that by doing this we are not suggesting that it is not only evidence from clinical trials that influences how convinced veterinarians are regarding the outcome of a disease intervention, in reality. Many factors (e.g. marketing campaigns, clinical experience, farmer experience, colleagues etc) can have an impact. It was beyond the scope of this project to quantify and mathematically model the influence of all possible factors. However, since it is hoped that new evidence has some influence on veterinarians confidence in the usefulness of disease interventions, it is of interest to know how veterinarians differ in terms of the strength of evidence they would like to be presented with, and by eliciting λ, this is what our study has focused on.

The study was approved by the Research and Ethics committee, School of Veterinary Medicine and Science, University of Nottingham.

Data Analysis

Due to the scale involved i.e. θ_d ∈ [−∞,+100], a suitable choice was to fit normal (Gaussian) probability density functions to the 5 elicited values for θ_m, θ_l and θ_j, for each veterinarian. The normal family of probability density functions is characterised by 2 ‘parameters’: the mean and the variance. In keeping with Bayesian terminology, these are referred to as ‘hyperparameters’ to distinguish them from the elicited (population) parameters. The R code provided in SHELF was used to find the best fitting hyperparameters by minimising the sum of the squared differences between the fitted cumulative distribution and the elicited cumulative distribution; this uses numerical optimisation based on the simplex algorithm (Nelder and Mead, 1965). In addition for each disease, the 5 raw elicited values were each arithmetically averaged (across the veterinarians), and a normal distribution fitted to these 5 averaged numbers; for each disease, this distribution will be referred to as the ‘clinical expectations for the average veterinarian’; it should be noted that this is a theoretical concept because it is unlikely to represent the actual belief of any individual person.

Visualising the diversity in clinical opinion for θ_d

To illustrate the diversity in clinical expectations amongst the sample of veterinarians, for each disease, 3 different individuals were identified: (a) the ‘most ambivalent’, (b) the ‘most pessimistic’ and (c) the ‘most enthusiastic’. Veterinarian (a) was identified based on the widest plausible range for θ_d, veterinarians (b) and (c) were identified based first on the lowest and highest median belief for θ_d, respectively, and then if tied results existed (e.g. 2 or more veterinarians had the same highest median belief) then the veterinarian was selected that had the narrowest plausible range; in other words ‘enthusiasm/pessimism’ was based on centre of location, and if more than 1 veterinarian was centred in the same enthusiastic or pessimistic place, then the most confident veterinarian was selected.

Modelling the implications of the heterogeneity in clinical beliefs

The clinical expectations of the most enthusiastic and pessimistic veterinarians were used as priors in a Bayesian analysis to predict how their current clinical expectations would be updated in the light of new data, as follows. The prior belonging to each veterinarian was combined using Bayes theorem (Equation 1) with synthetic data originating from a randomized clinical trial in order to produce a posterior distribution for each veterinarian. This posterior distribution can be considered to represent what each veterinarian would believe if they were shown the data and updated their current clinical expectations logically in accordance with Bayes theorem.

For the Bayesian analysis it was necessary to specify a likelihood function (i.e. to probabilistically specify the new information about θ_d arising from an experiment). For each disease, a clinical trial was assumed to have been conducted and designed such that farms were randomly assigned to 1 of 2 groups (control and intervention) with n farms in each group. The control farms received no intervention. For all farms enrolled in the trial, in the year before and after the intervention the clinical outcome was measured (as previously described), and from this information the sample mean change in disease was calculated for the control and intervention farms (in analogy with Equation 2) and denoted ȳ_c and ȳ_d respectively. Assuming independent random observations, then by virtue of the central limit theorem,

$${\overline{y}}_d\approx N\left({\theta }_d,\frac{{\sigma }_d^2}{n}\right)\text{and}{\overline{y}}_c\approx N\left({\theta }_c,\frac{{\sigma }_d^2}{n}\right),$$

where θ_d is the population mean change in disease for farms with an intervention in place, θ_c is the same parameter but for the control farms, and ${\sigma }_d^2$ is the population variance for the disease and is assumed to be the same for both control and intervention farms. Subscript d is used to refer generally to the diseases: d = m, l, j for mastitis, lameness and Johne’s disease.

The parameter of interest was the difference in the population mean change in disease, θ = θ_d – θ_c. A point estimate for θ from the trial data can be obtained using y = ȳ_d - ȳ_c and the normal likelihood is given by

$$y^{}\approx N^{}\left({\theta }_d-{\theta }_c,\frac{{\sigma }_d^2}{n}+\frac{{\sigma }_d^2}{n}\right);\text{that}\text{is}y\approx N\left(\theta ,\frac{{2\sigma }_d^2}{n}\right).$$ (3)

In keeping with the condition used for eliciting the veterinarians’ beliefs, θ_c is assumed to be zero for each disease and therefore θ = θ_d. Veterinarians’ clinical expectations were elicited for θ_d given θ_c = 0, and because normal distributions were fitted to their beliefs, the priors took the form

$$p\left({\theta }_{di}\right)\propto \exp \left(-\frac{1}{2}\frac{{\left({\theta }_{di}-{\varphi }_{di}\right)}^2}{{\tau }_{di}^2}\right),$$

where i denotes the veterinarian and takes values i = 1…94 (94 veterinarians were interviewed), and ϕ_di and τ_di are the fitted hyperparameters (mean and standard deviation) for each veterinarian. With the normal likelihood specified by Equation (3) i.e.

$$y|{\theta }_d\propto \exp \left(-\frac{1}{2}\frac{{\left(y-{\theta }_d\right)}^{2}n}{{2\sigma }_d^2}\right),$$

the Bayesian analysis, i.e. Equation (1), is conjugate, and it can be shown, Spiegelhalter et al. (2004), that the posterior distribution also takes the shape of a normal distribution as follows

$${\theta }_d|y~N\left(\frac{\frac{{\varphi }_{di}}{{\tau }_{di}^2}+\frac{yn}{{2\sigma }_d^2}}{\frac{1}{{\tau }_{di}^2}+\frac{n}{{2\sigma }_d^2}},\frac{1}{\frac{1}{{\tau }_{di}^2}+\frac{n}{{2\sigma }_d^2}}\right).$$ (4)

In combination with the elicited values for θ_d^min and λ_d, Equation (4) can be used to explore the implications of the heterogeneity in veterinarians’ clinical expectations because it provides the formula to calculate the posterior distribution (i.e. the ‘predicted belief’) for each veterinarian and for each disease.

In Equation (4), ϕ_di and τ_di were derived from the raw elicitation data (obtained during the interviews), the remaining variables (y, n, ${\sigma }_d^2$) require specification. The value chosen for y (i.e. the difference in the sample means between the control and intervention farms in the trial), was the median value (i.e. across the 94 participating veterinarians) of the median clinical expectation for θ_d. For each disease, the population variance ${\sigma }_d^2$ is unknown and therefore sensitivity of the results to 2 choices were explored: σ_d = 10% and 25% for d = m, l, j. As n is the number of farms in each arm of the trial, 2n is the total size of the clinical trial, and was given values of: 2n = 20, 50, 100 and 200 farms. For clinical demands, because θ_d^min was elicited from each veterinarian, the median value (across all veterinarians) was used; note that because a few veterinarians elected to give a range of values, the lower value of the range was taken to calculate the median clinical demand. As described, this Bayesian model explores how large a clinical trial would be required to ‘convince’ the most pessimistic veterinarian that the median clinical demand of this sample of veterinarians will be exceeded. It also explores, theoretically, how large a clinical trial would be required to bring the most pessimistic and most enthusiastic veterinarian into general agreement, i.e., assuming veterinarians revise their beliefs logically in keeping with Bayes theorem. As explained, the model makes some assumptions regarding the data produced by a new clinical trial.

Results

Response Rates and Description of Participants

Not all the veterinarians in one initially selected veterinary practice agreed to participate; another practice was selected from the same region and consented; from the 20 consenting practices, 94 of the 96 selected veterinarians were interviewed - 2 were unavailable during the data collection period. Of the 20 practices, 7 were located in the North, 2 in the Midlands, and 11 in the South of England

There were 36 partners and 58 assistants. Gender was split 59 males to 35 females, and ‘years qualified’ ranged from 0 to 37 years with a median of 7 years. Of the 94 veterinarians, 19 (20%) held a post-graduate cattle qualification. ‘Time spent working with dairy cows’ was as follows: 6 participants spent 0 to <25% of their time, 16 participants 25 to <50%, 27 participants 50 to <75% and 45 participants 75 to <100%.

Elicited Clinical Beliefs

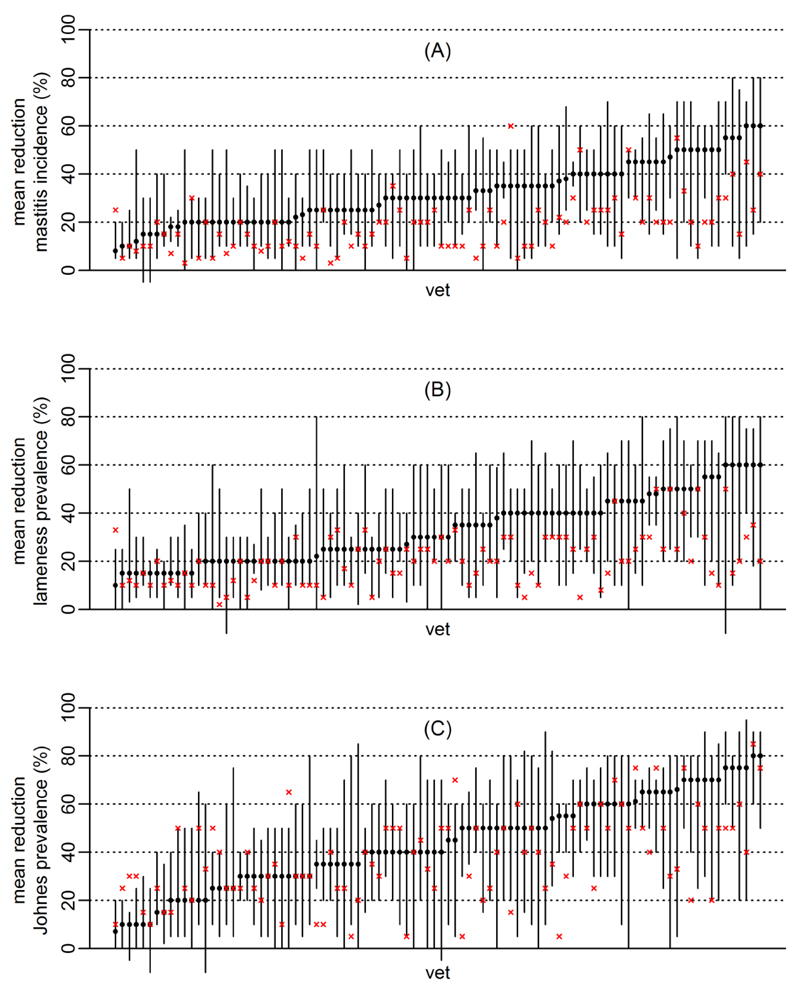
Descriptive statistics concerning the raw elicited parameters θ_d are provided in Table 1. For each disease and each veterinarian, their raw elicited plausible range and median values for θ_d are presented in Figure 1, along with θ_d^min.

Table 1.

The elicited clinical expectations of 94 veterinarians for the population mean effect of a disease intervention

Elicited value1	Population mean reduction (%)
	Mastitis incidence	Lameness prevalence	Johne’s disease prevalence
Minimum	10(5-15)	10(5-20)	10(5-30)
Lower quartile	24(17-33)	24(15-35)	33(20-50)
Median	30(20-40)	30(20-40)	40(30-60)
Upper Quartile	36(25-46)	39(25-50)	52(38-65)
Maximum	50(40-60)	50(40-65)	70(50-80)

¹Median (inter-quartile range)

Figure 1.

The clinical expectations of 94 veterinarians concerning the population mean reduction in disease achievable with (A) a 1 yr mastitis intervention (B) a 3 yr lameness intervention (C) an 8 yr Johne’s disease intervention; median beliefs (dots) and plausible range (lines). Crosses (x) denote ‘the minimum clinically worthwhile’ reduction stipulated by each veterinarian (i.e. the clinical demand). For each disease, veterinarians have been ordered horizontally by their median belief (dots).

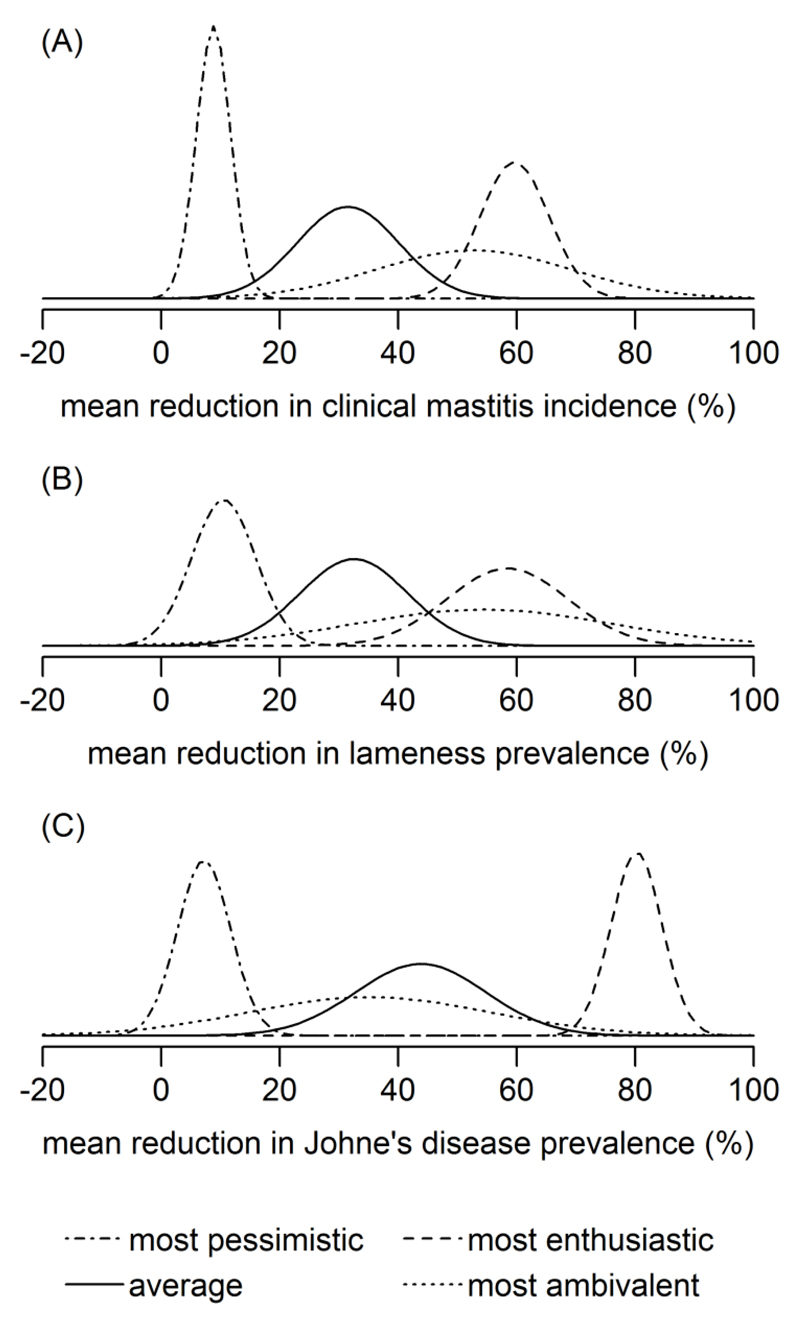
In Figure 2 the fitted normal distributions are plotted for the most ambivalent, enthusiastic, pessimistic and ‘average’ veterinarian; for example, Figure 2B shows that the most pessimistic veterinarian concerning the 3 yr lameness intervention had a normal distribution centred at an 11% population mean reduction in lameness prevalence with a 95% credible interval of 0 to 21%, whereas the most enthusiastic veterinarian was centred at a 58% reduction with a 95% credible interval of 38 to 78%; thus the enthusiastic veterinarian had a more uncertain belief (wider credible interval) compared to the most pessimistic veterinarian. Figures 1 and 2 together show the considerable heterogeneity in veterinarians’ clinical expectations, both in terms of central location and clinical confidence. The diversity in opinion was greater for the Johne’s disease intervention, compared to the other diseases, as highlighted by the marked polarisation in beliefs displayed by the most enthusiastic and pessimistic veterinarians (Figure 2C).

Figure 2.

Normal probability distributions fitted to the elicited clinical expectations (θ_d) belonging to the most ambivalent, enthusiastic, pessimistic and ‘average’ veterinarian: (A) a 1 yr mastitis intervention (B) a 3 yr lameness intervention (C) an 8 yr Johne’s disease intervention.

Across the 94 veterinarians, the median clinical demand was a 20% population mean reduction in incidence for a 1 yr mastitis intervention with an inter-quartile range of 10 to 25%, a 20% reduction in mean prevalence for a 3 yr lameness intervention (inter-quartile range 10-30%), and a 35% reduction in mean prevalence for an 8 yr Johne’s disease intervention (inter-quartile range 25-50%). Comparing these figures with Table 1, it can be seen that the median clinical demand was below the median clinical expectation for all 3 diseases.

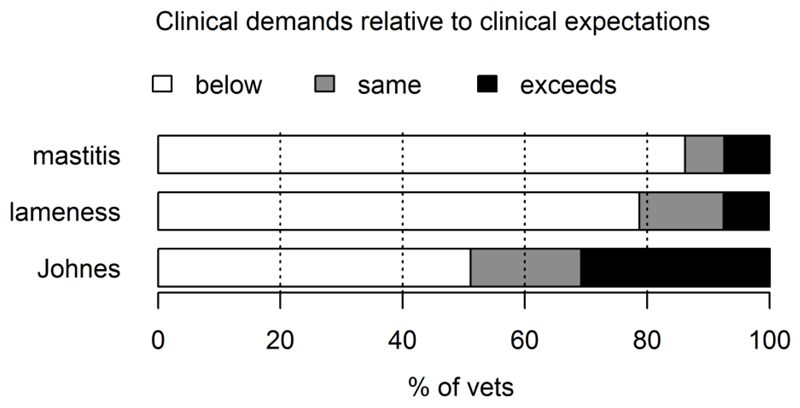
Figure 3 shows how each veterinarian’s clinical demand compared to their median (‘best guess’) clinical expectation, i.e. whether each of the crosses (Figure 1) was below, above or in the same place, as the corresponding dot. It reveals that for both the mastitis and lameness interventions the majority of veterinarians (≥ 79%) had clinical demands that were lower than their median expectation. In contrast, for Johne’s disease, only 51% of veterinarians had clinical demands that were lower than their median expectation i.e. there was more pessimism in terms of the effect that veterinarians clinically wanted, and what they expected to happen, for Johne’s disease, compared to mastitis and lameness.

Figure 3.

Each veterinarian’s clinical demand, θ_d^min, compared to their median (‘best guess’) for the expected clinical outcome, θ_d.

The summary statistics for veterinarians’ values for λ_d, i.e. the probability they would require (as a % chance) that the mean reduction would be at least their own estimate for θ_d^min, were similar for each disease intervention and are as follows. Median values: λ_m = λ_l = λ_j = 80%; lower quartile λ_m = λ_l = λ_j = 75%; upper quartile: λ_m = 88%, λ_l = λ_j = 90%.

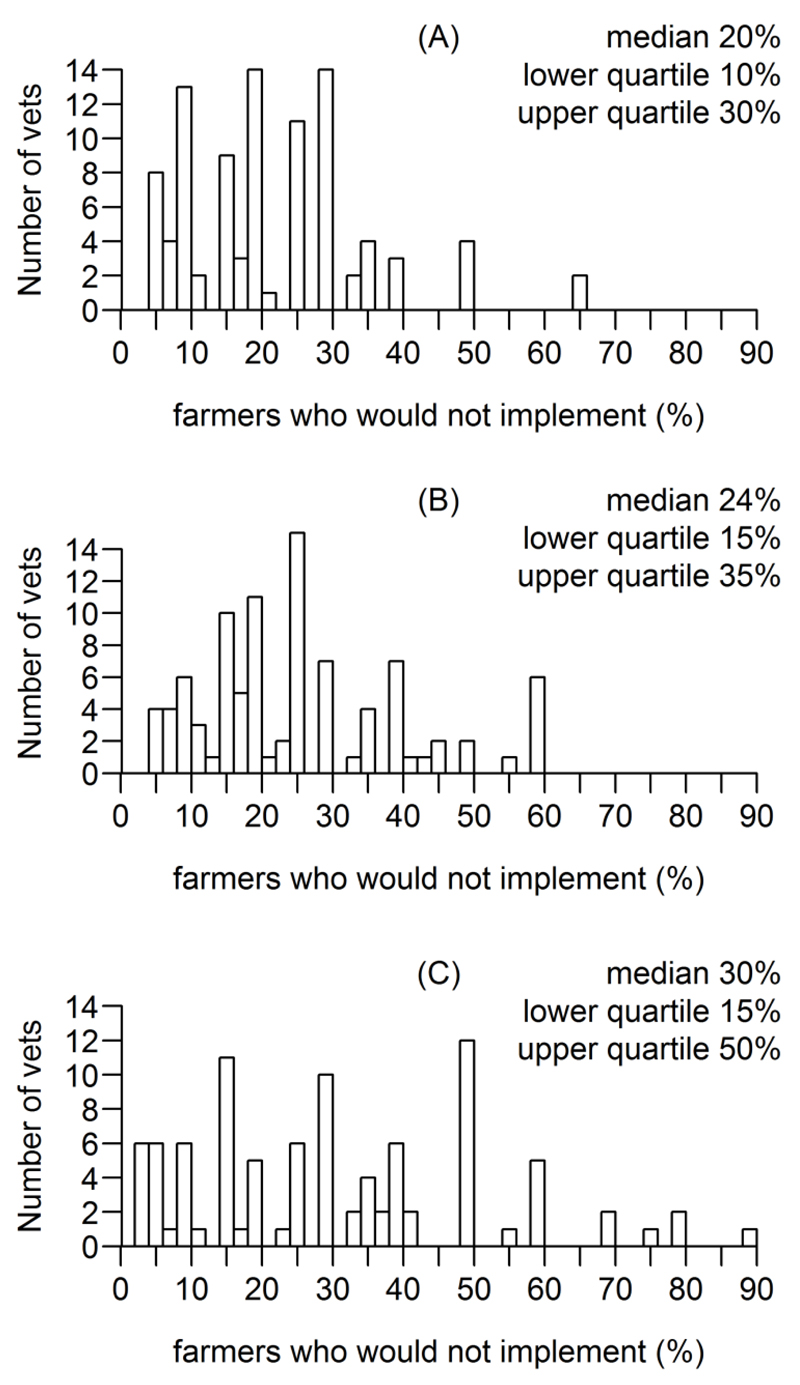
The distributions and summary statistics for veterinarians’ estimates of the percentage of farmers who they believed would implement none of the disease intervention to any effective extent, despite initially agreeing to participate, are provided in Figure 4.

Figure 4.

Veterinarians’ estimates for the percentage of dairy farmers who, having agreed to undertake a structured disease intervention and had an initial visit, subsequently fail to implement any of the required changes to any successful extent: (a) a 1 yr mastitis intervention, (b) a 3 yr lameness intervention, and (c) an 8 yr Johne’s disease interventions.

Modelling the Implications of the Heterogeneity in Beliefs

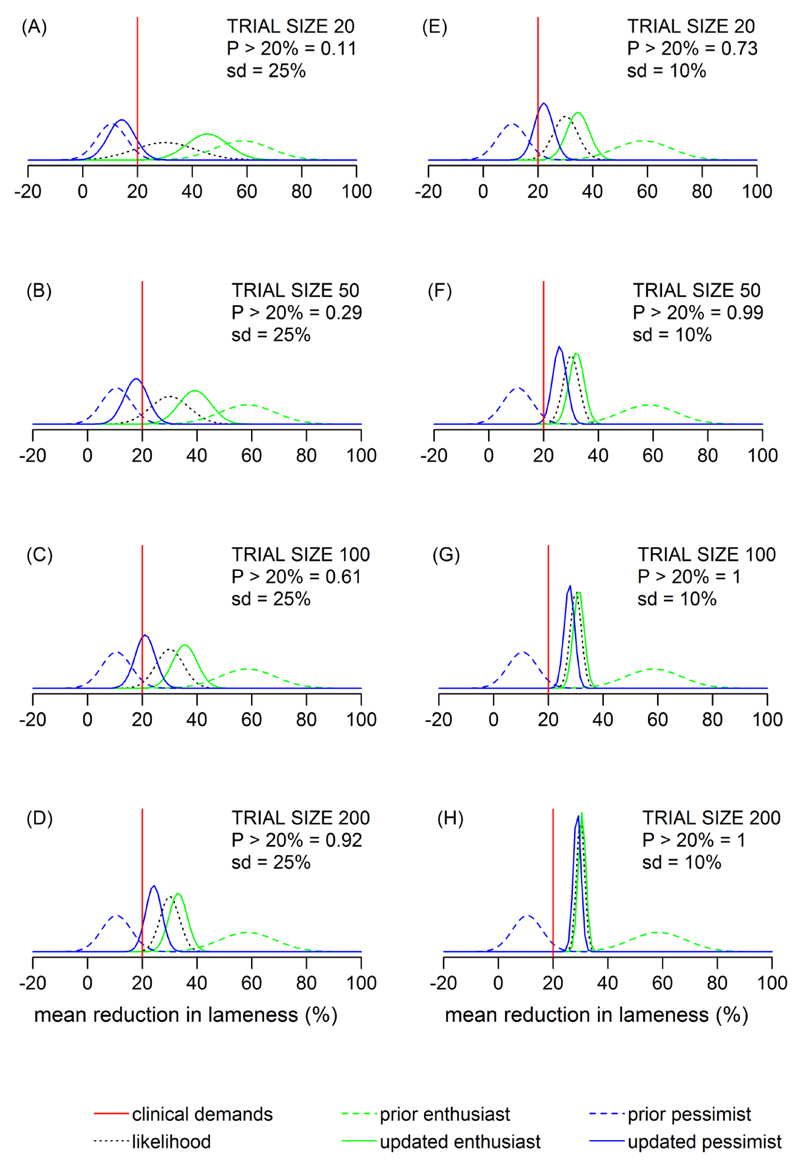
Figure 5 predicts (using Equation 4) how the veterinarian with the most pessimistic clinical expectation, and the veterinarian with the most enthusiastic clinical expectation, regarding the lameness intervention, would update their expectations in light of new (synthetic) clinical trial data of different strengths. In Figure 5, the 4 different plots (A-D) show the effects of different sized clinical trials, involving 20, 50,100 and 200 farms in total. For each clinical trial it is assumed that the data provided a point estimate, y, equal to a 30% mean reduction in lameness prevalence in favour of the intervention farms (over the control farms), and that the population variance σ_d was 25%. Hence the only difference between the clinical trials is that they are increasing in size, and since the likelihood is encapsulating the information arising from the clinical trial, it can be seen that the evidence from the trial becomes stronger (i.e. narrower and taller) from plot (5A) through to plot (5D) as the trial increases in size, but remains centred at 30%.

Figure 5.

A Bayesian analysis to predict how the most pessimistic and enthusiastic veterinarians regarding the 3 yr lameness intervention, would update their clinical opinions in light of new synthetic trial data of different sizes. For plots (A-D) the population standard deviation (sd) is assumed to be 25%; for plots (E-H), sd = 10%. In each plot, the trial data (likelihood) is assumed to provide a point estimate equal to a 30% mean reduction in lameness prevalence. ‘Updated enthusiast/pessimist’ is the posterior distribution obtained by combining the relevant prior belief with the likelihood using Bayes theorem. ‘Clinical demands’ (= 20%) is the median ‘minimum clinically worthwhile reduction’ elicited across the 94 veterinarians. The probability (P) that the ‘updated pessimist’ assigns to this value being exceeded is given (area under their curve to the right of the straight vertical line).

On each plot in Figure 5, normal distributions have been fitted to the elicited values belonging to the most pessimistic and enthusiastic veterinarians and reflect their current clinical expectations (priors), as they stated during their interviews; i.e. the ‘prior enthusiast’ and ‘prior pessimist’ curves. The plots show how the priors are updated when combined with the likelihood (i.e. the new data) using Bayes theorem. Hence the ‘updated enthusiast’ and ‘updated pessimist’ curves are the posterior distributions, and represent what the most pessimistic and enthusiastic veterinarian are predicted to believe if they had been shown the clinical trial data, and updated their opinions coherently in accordance with Bayes theorem. To emphasise, the veterinarians were not shown any data during their interviews, and the posterior distributions shown in Figure 5 are predictions arising from the Bayesian models.

Across the 94 veterinarians, the median clinical demand for the 3 yr lameness intervention was a 20% mean reduction in prevalence, shown in Figure 5 by the straight vertical line. Plot 5A shows that in light of a clinical trial involving 20 farms, the most pessimistic veterinarian is predicted to believe that there will only be an 0.11 probability (11% chance) that this clinical demand will be exceeded - area under the ‘updated pessimist’ curve to the right of the vertical 20% line, as a proportion of the total area under the curve. As the size of the clinical trial increases, the most pessimistic veterinarian is predicted to become more convinced that this goal will be realised, such that with a trial involving 200 farms, they are predicted to believe that there is a 0.92 probability that this clinical demand will be exceeded (plot 5D).

The null hypothesis is usually rejected in favour of the alternative hypothesis when the posterior distribution assigns a ‘sufficiently large’ probability to θ taking values greater than θ^min; since this probability (λ), is often taken to be ≥ 0.95, then on this basis a 200 farm clinical trial is not strong enough evidence to convince a ‘reasonable sceptic’ (i.e. the most pessimistic veterinarian in this sample) that the intervention is clinically worthwhile. However, for the lameness intervention, the majority of veterinarians interviewed provided a value for λ_l that was < 0.90 (upper quartile λ_l=90%), and therefore on this basis, a clinical trial of 200 farms may be expected to be sufficiently convincing to the majority of veterinarians who participated in this study.

Figure 5 also shows how the most enthusiastic veterinarian is predicted to have their enthusiasm damped by the trial results. The most enthusiastic veterinarian was expecting a mean reduction in prevalence centred in the region of 60% (‘prior enthusiast’ curve), and for example, plot 5C shows that this is predicted to be reduced to a more confident belief that is centred around a 35% reduction (‘updated enthusiast’ curve) with a 100 farm trial.

Figure 5C also shows that in the light of the evidence originating from a 100 farm trial, the most pessimistic and enthusiastic veterinarians are predicted to have updated beliefs that are still almost entirely in disagreement (updated curves barely overlapping).

In plots A-D (Figure 5), the population standard deviation, σ_l was assumed to be 25%. For a given size of clinical trial, taking σ_l to be 10%, results in a ‘stronger’ likelihood (because there is less variation of farms around the mean value), and therefore affects the analysis. Plots E-H (Figure 5) show an identical analysis to plots A-D (Figure 5), but with σ_l assumed to be 10%. It shows that because the evidence from the trial is stronger, a 50 farm trial is predicted to convince (with a 0.99 probability) the prior pessimist that a 20% mean reduction in lameness prevalence will be realised.

A similar analysis to that presented in Figure 5 was run for the mastitis and Johne’s disease interventions; for the mastitis intervention the median clinical demand was 20% (the same as for the lameness intervention), for Johne’s disease it was 35%. For the mastitis intervention the synthetic trial data was set to provide a point estimate of a 30% reduction in clinical mastitis incidence, and for Johne’s disease, a 40% reduction in prevalence (these figures were the median expected reduction in disease elicited across the 94 veterinarians, Table 1). The analyses were run for a population standard deviation of both 10% and 25%, and for each disease, the predicted probability of exceeding the median clinical demand in light of the clinical trial data was calculated for the most pessimistic veterinarian. The results are presented in Table 2, where the lameness results from Figure 5 have also been included to allow comparison.

Table 2.

The predicted probability of exceeding the median clinical demand (20% mastitis, 20% lameness, 35% Johne’s disease) for the most pessimistic veterinarian, when their prior clinical expectation is combined with synthetic trial data of different sizes using Bayes theorem; the trial data provided a point estimate of a 30% reduction in clinical outcome for mastitis and lameness, and 40% for the Johne’s disease intervention

Disease intervention	Population standard deviation	Size of randomised clinical trial
		20 farms	50 farms	100 farms	200 farms
Mastitis	10%	0.02	0.43	0.97	1.00
	25%	<0.001	0.001	0.01	0.12
Lameness	10%	0.73	0.99	1.00	1.00
	25%	0.11	0.29	0.61	0.92
Johne’s disease	10%	<0.001	0.037	0.41	0.94
	25%	<0.001	<0.001	<0.001	0.003

Figure 2 shows that the most pessimistic veterinarian for the mastitis intervention (plot A) was more confidently pessimistic (narrower and taller distribution), compared to the most pessimistic vet for the lameness intervention (plot B); consequently, as Table 2 reveals, this veterinarian needs stronger evidence, according to Bayes theorem, to be convinced that the clinical demand will be exceeded. Thus, the most pessimist veterinarian concerning the mastitis intervention, is predicted to be entirely unconvinced even by a trial involving 200 farms (if the population standard deviation is indeed 25%) because they are predicted to give only a 12% chance that a 20% reduction in mastitis will be achieved. This is demonstrably different to the most pessimistic veterinarian concerning the lameness intervention who would be substantially convinced by a 200 farm trial (0.92 probability), with the same population variance assumption.

Discussion

The results revealed that markedly different clinical opinions currently exist, and hence for all 3 disease interventions a major change in clinical expectations would be required to bring the most enthusiast and pessimistic veterinarians into clinical agreement. It may not be desirable for veterinarians to be completely united in their clinical beliefs, but broad agreement for the major endemic diseases is important both for the credibility of the profession and to provide a unified approach to disease control. The wide heterogeneity observed raises concerns over the extent to which a broadly consistent approach to controlling these endemic diseases is currently being achieved. This in turn supports the argument for the implementation of national disease control programmes for the non-statutory endemic diseases. This is because national disease control programmes help to provide a co-ordinated and consistent approach to disease control. As the variability between veterinarians increases, the potential gain derived from implementing a national disease control programme, also increases.

Explanation for the observed heterogeneity in clinical expectations is likely to be multi-factorial. In this regard, the paucity of literature quantifying the effects of these interventions is worth noting. To the authors’ knowledge, only 1 randomised clinical trial has estimated the effect of a clinical mastitis intervention of the type described here (Green et al., 2007); this 1 yr intervention study found a 22% reduction in the proportion of cows affected with clinical mastitis on the intervention farms compared with the control farms. There appears to be an absolute lack of randomised clinical trials estimating the effects of lameness and Johne’s disease interventions. More clinical trials to quantify the effects of intervention strategies to reduce the major endemic diseases of dairy cattle are required because there is a lack of knowledge in this area. In our dataset, we did not find any statistically significant differences in veterinarians’ beliefs by the following factors: time spent working with dairy cows, possession of postgraduate qualifications or not, job status (assistant/partner) or gender. However, this is not to say that these factors are not associated with different opinions.

Notably, clinical expectations were elicited conditional on an assumption that the population mean change in disease would be zero in the absence of a disease intervention; it is necessary to know what veterinarians were basing their clinical expectations for a disease intervention against. It is acknowledged that some may believe this to be a larger assumption to make for the Johne’s intervention, compared to mastitis and lameness. We made this assumption for the purpose of simplicity and in the absence of any data.

The results also showed considerable variation in veterinarians’ estimates for the percentage of farmers who would not effectively implement any of the intervention to any extent, despite initially agreeing to do so. The median estimates were non-trivial percentages: 20%, 24% and 30% for the mastitis, lameness and Johne’s disease interventions, respectively. This may, in part, reflect veterinarians’ practical experiences with maintaining farmer engagement with a disease intervention. Understanding ways to facilitate and support farmers to make the changes needed to implement a disease intervention is important.

‘Clinical demands’ in a herd health context could be interpreted in 4 different ways. First, the reduction the veterinarian would want in order to consider the intervention clinically worthwhile. Secondly, what the veterinarian thinks the farmer would want to hear in order to be convinced enough to implement the intervention. Thirdly, what the farmer would actually demand in order to be prepared to implement the intervention, with its associated time, financial and labour investments. Fourthly, the reduction the veterinarian needs to consider the intervention clinically worthwhile solely from the perspective of their patient i.e. the cow. In a sense, the latter is analogous to the scenarios for which clinical demands have been elicited and reported in human medicine, where the doctor is faced with deciding what is best for their patient, given the treatment will be freely available and the patient will almost certainly take it.

In this study it was stipulated that clinical demands related to the first point only. However, it may be difficult to compartmentalise these issues. Thus part of the variation in veterinarians’ clinical demands may have related to how they chose to weigh the vested interests of all stakeholders; for example, veterinarians who estimated a very small clinical demand may have given greatest weight to the interests of the cow, or the environment, whereas those who gave the highest clinical demands may have given more weight to the financial cost-effectiveness for the farmer.

It is important to note that the Bayesian analysis presented here has modelled the impact of new clinical trial data on veterinarians’ current opinions, assuming they would update their beliefs logically in accordance with Bayes theorem. This means that as the size of the trial increases, the mathematical model predicts that veterinarians will become more convinced because the evidence from larger trials is stronger. However, currently controversy remains in the literature over the extent to which people are actually able to logically value, interpret and revise their opinions when presented with new information (Tversky and Kahneman, 1974, Kynn, 2008, Westover et al., 2011). Recent findings suggests that people can update their beliefs in a Bayesian manner, but how the task is framed is important (Gigerenzer and Edwards, 2003, Gigerenzer and Hoffrage, 2007). In reality, it may be challenging for veterinarians to differentiate between evidence of varying strength and quality. Other factors, such as the perceived reputation of the scientists conducting the work, the final concluding remarks of the paper, or the point estimate alone (not in combination with the confidence or credible interval) may be more influential. More research is needed to establish how logically veterinarians’ update their beliefs about clinical parameters, using information published in veterinary journals. This is important to ascertain, because investing money in larger clinical trials in order to convince sceptical clinicians will not provide a return unless they revise their beliefs in at least a fairly logical manner. If most veterinarians do not update their beliefs logically, then money could be better spent on alternative approaches, rather than larger clinical trials. This could include communication strategies, as well as helping veterinarians to interpret new information appropriately.

It is also worth noting, that in human medicine λ has not been elicited from doctors, even though doctors’ clinical demands have been elicited. A choice for λ that is less than 0.95 may not be generally acceptable to the scientific community, because it may be not be regarded as robust enough evidence. However, it is a subjective choice and clinically useful information may go unreported if only clinical trials achieving λ ≥ 0.95 are published.

A potential limitation of this study is the repeatability of the results at a later date in the absence of any genuine change in veterinarians’ beliefs. There is no literature reporting the repeatability of the method. However, during the interviews, extra clarification was given if required. This reduced misunderstanding, which is one reason why different results may be obtained on different dates.

Interpretative Summary.

Veterinarians’ clinical beliefs concerning herd-level interventions to reduce 3 key endemic diseases of dairy cattle were captured numerically as probability distributions. Major differences in beliefs were revealed. By incorporating the beliefs into Bayesian statistical models, the strength of new data needed to change veterinary opinion was explored. The results have important implications for designing future research studies. The wide variation in beliefs also raises concern over the extent to which a broadly consistent approach to disease control is currently being achieved; it is argued that more clinical trials and national disease control programs are needed.