Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2017 Oct 3.
Published in final edited form as: Nat Mater. 2017 Apr 3;16(7):743–748. doi: 10.1038/nmat4889

An intrinsic growth instability in isotropic materials leads to quasi-two-dimensional nanoplatelets

Andreas Riedinger 1,#, Florian D Ott 1,#, Aniket Mule 1, Sergio Mazzotti 1, Philippe N Knüsel 1, Stephan J P Kress 1, Ferry Prins 1, Steven C Erwin 2,*, David J Norris 1,*
PMCID: PMC5490789  EMSID: EMS71764  PMID: 28369052

Abstract

Colloidal nanoplatelets are atomically flat, quasi-two-dimensional sheets of semiconductor that can exhibit efficient, spectrally pure fluorescence. Despite intense interest in their properties, the mechanism behind their highly anisotropic shape and precise atomic-scale thickness remains unclear, and even counterintuitive for commonly studied nanoplatelets that arise from isotropic crystal structures (such as zincblende CdSe and lead-halide perovskites). Here we show that an intrinsic instability in growth kinetics can lead to such highly anisotropic shapes. By combining experimental results on the synthesis of CdSe nanoplatelets with theory predicting enhanced growth on narrow surface facets, we develop a model that explains nanoplatelet formation as well as observed dependencies on time and temperature. Based on standard concepts of volume, surface, and edge energies, the resulting growth instability criterion can be directly applied to other crystalline materials. Thus, knowledge of this previously unknown mechanism for controlling shape at the nanoscale can lead to broader libraries of quasi-two-dimensional materials.

Nanoscale particles are now prepared with tremendous control over shape1,2. For semiconductors, liquid-phase protocols3 initially developed to create nearly spherical nanocrystals (colloidal quantum dots) have been modified to obtain rods4, tetrapods5, and arrows6,7. If the underlying crystal lattice is anisotropic, such forms arise naturally when growth is induced along specific crystallographic directions. For example, rods result when growth along the c-axis of a hexagonal lattice is enhanced by selective binding of surface ligands6 or by kinetically over-driving the reaction4. Even for isotropic lattices, ligands can control addition to distinct crystallographic facets, leading to cubes, tetrahedrons, or branched particles2,8.

However, while the formation of these shapes is understood, the mechanism behind another increasingly important nanostructure is less clear. Quasi-two-dimensional (2D) semiconductor particles known as nanoribbons9, nanoplatelets10–15, nanosheets16, and quantum belts17 have recently been reported. Among these, nanoplatelets (NPLs) have been the most studied, particularly those of CdSe10,11 and lead-halide perovskites12–15. Such samples contain thin rectangular particles remarkably uniform in thickness (e.g., all 3-monolayers thick). This precise atomic-scale thickness leads to unique behavior11,18–21, such as spectrally pure fluorescence22, large absorption cross-sections23, enhanced energy transfer20, and boosted optical gain24. These characteristics are useful in light-emitting devices25, field-effect transistors26, solar cells20, and lasers24.

Despite intense interest in these properties, the formation of NPLs remains puzzling27, especially when their highly anisotropic shape arises from an isotropic lattice. For example, CdSe NPLs grow from the zincblende cubic phase with primarily {001} facets exposed28. Consequently, their shape cannot be explained by differential growth on distinct facets. Rather, another mechanism must be responsible. One possibility, proposed to explain wurtzite (hexagonal) CdSe platelets, is growth within molecular templates29. Cd precursors such as CdCl2(RNH2)2 can produce lamellar mesophases30. When treated with chalcogens near room temperature, “magic-sized” clusters [e.g., (CdSe)13] can form within these templates and organize into rectangular arrays17. With mild annealing, these arrays can fuse, yielding wurtzite CdSe platelets31 that are dispersible via exfoliation9,17,30. Molecular templates have also been implicated in the formation of PbS nanosheets16, suggesting templated growth as the mechanism behind all NPLs29.

Here we study zincblende CdSe NPLs to understand how they form. However, in agreement with previous reports27, we find no evidence for templated growth. Rather, we show that NPLs can grow in concentrated solvent-free melts containing only Cd and Se precursors. This leads us to discover a previously unknown nanoscale shape instability that can explain NPL formation. Because the mechanism is general, it must be added to our current understanding of shape control at the nanoscale1,2.

Solvent-free growth of NPLs

In standard liquid-phase protocols for zincblende CdSe NPLs10,32, a long-chain Cd(carboxylate)2 is used as the Cd precursor and heated with Se powder in a non-coordinating solvent. Between 180 and 240 °C, a short-chain Cd(carboxylate)2 is added, and the mixture is maintained at 240 °C for 5-15 min. The addition of this short-chain carboxylate appears to be critical. The NPL thickness is regulated by the addition temperature and the NPL lateral size by the subsequent reaction time27. Without this addition, quantum dots and other shapes form instead of NPLs.

The apparent importance of the short-chain carboxylate provides a clue to the growth mechanism. To reveal this, we added short-chain carboxylic acids of various lengths to the standard NPL protocol (see Methods and Supplementary Figs. 1-2). We found that shorter carboxylic acids led to easier formation of NPLs. The reason was determined by repeating these experiments without Se. In this case, NPLs could not form, but intermediates produced in the standard protocol when a short-chain carboxylic acid is added to long-chain Cd(carboxylate)2 under reaction conditions (180 °C) could be identified (see Methods and Supplementary Figs. 3-5). These experiments showed that as the carboxylic acid became shorter, the formation of Cd(long carboxylate)2-x(short carboxylate)x coordination polymers33 via ligand exchange became more likely. The replacement of long with short chains in the Cd precursor lowers its solubility in the solvent (leading to the observation of precipitates). We therefore hypothesize that the addition of a short-chain carboxylate during the standard NPL protocol lowers the solubility of the Cd precursor in the solvent, causing it to phase separate. In this case, the solubility of the Cd(carboxylate)2 would determine if NPLs or quantum dots grow. If this Cd precursor dissolves, quantum dots would result; if the precursor is insoluble, NPLs would form.

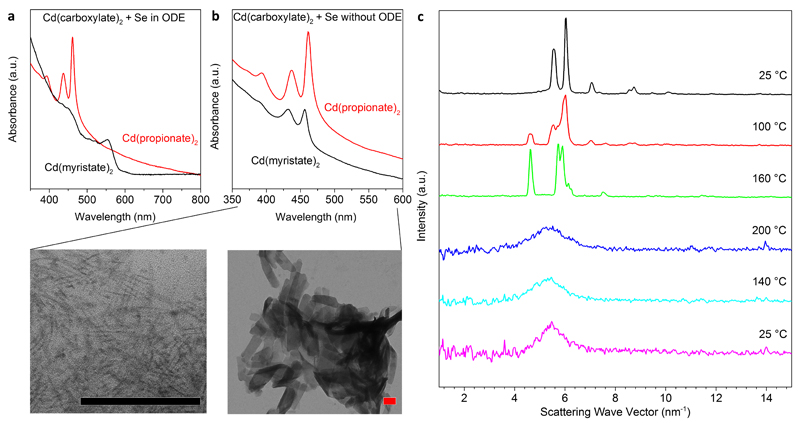
This hypothesis was supported by experiments where we heated only one type of Cd(carboxylate)2 of various length with Se in solvent to ~200 °C (Fig. 1a and Supplementary Fig. 6). With long-chain Cd(carboxylate)2, the Cd precursor dissolved and quantum dots resulted (Fig. 1a). However, with only short-chain Cd(carboxylate)2, liquid droplets phase separated above 180 °C. CdSe NPLs formed within these droplets, which solidified upon cooling (see Supplementary Figs. 7-8). The resulting NPLs were 3-monolayers thick as indicated by absorption features at 437 and 461 nm (Fig. 1a)34. (An m-layer-thick zincblende CdSe NPL contains m Se and m+1 Cd layers.) Thus, a mixture of short- and long-chain carboxylates is actually not required to obtain NPLs if the Cd precursor is already insoluble under reaction conditions. Furthermore, because NPLs grew in phase-separated droplets of short-chain Cd(carboxylate)2 rather than in solution, even the solvent is apparently unnecessary.

Figure 1. The formation of CdSe nanoplatelets in isotropic melts of Cd(carboxylate)2 and elemental Se.

Figure 1

Open in a new tab

a, The solubility of the Cd(carboxylate)2 in octadecene (ODE) determines whether quantum dots or nanoplatelets (NPLs) are formed, as shown via optical absorption. While long-chain Cd(myristate)2 dissolved in ODE and yielded quantum dots with the lowest energy peak at 554 nm (black curve), short-chain Cd(propionate)2 was insoluble above its melting point, and 3-monolayer CdSe NPLs were obtained (red curve), as indicated by the peaks at 437 and 461 nm. b, Without solvent, 3-monolayer CdSe NPLs formed in melts of either Cd precursor (over 18 h at 200 °C). Absorption peaks occurred at 432 and 457 nm for Cd(myristate)2 and 436 and 462 nm for Cd(propionate)2. Transmission electron micrographs show small NPLs obtained from Cd(myristate)2 (left) and much larger NPLs from Cd(propionate)2 (right). Both scale bars are 100 nm. c, In situ X-ray scattering experiments reveal that the initially polycrystalline Cd(propionate)2 undergoes a phase transition around 100 °C, becomes completely isotropic above the melting point, and maintains this glassy phase upon cooling.

To test this, we avoided solvent completely and simply heated blends of either long-chain Cd(carboxylate)2 or short-chain Cd(carboxylate)2 with Se powder at 200 °C for 18 h under N2. Both reactions yielded 3-monolayer zincblende CdSe NPLs28 (Fig. 1b and Supplementary Fig. 9), but with different lateral sizes. Thus, NPLs can form in melts of a single Cd(carboxylate)2, either long- or short-chained, with the length modifying lateral growth kinetics. We conclude that addition of short-chain carboxylates is only critical in standard liquid-phase protocols10,32. There, short carboxylates are required to phase separate the Cd precursor from the solvent (Supplementary Fig. 6). This implies that, even in the standard protocols, NPLs form in “solvent-free” environments. When we removed the solvent, we could grow NPLs with either long or short carboxylates.

These observations yield two clues about NPL growth. First, because NPLs can form in the presence of only a single carboxylate, models that require mixed-surfactant systems to explain NPL growth35 must be amended. Second, because we observe that NPLs can form in concentrated phase-separated droplets or melts, under these conditions their growth is not limited by diffusion of reactants. In contrast, solvent-based syntheses of nanocrystals are typically affected by diffusion (Supplementary Fig. 8 and Supplementary Section 1.a). This difference is important in the model below.

Absence of molecular mesophases

Before developing the model, we checked for molecular templates. Because NPLs form in solvent-free environments, it is unlikely that lamellar mesophases are present, especially near 200 °C36. For short-chain Cd(carboxylate)2 such phases are not even known37. Nevertheless, we looked for mesophases in reaction melts by performing in situ X-ray scattering (Fig. 1c). For a short-chain Cd(carboxylate)2 [Cd(propionate)2] we observed a polymorphic transition around 100 °C and then only a broad peak above the melting point (180 °C), indicating a disordered amorphous phase. Upon cooling to 25 °C, this broad peak remained, as the carboxylate was frozen into a glassy state. This order-to-disorder transition was further supported by differential scanning calorimetry (DSC) measurements (Supplementary Fig. 10). Attempts to observe mesophases in Cd(carboxylate)2 melts (with and without Se) via polarized optical microscopy were also negative (Supplementary Fig. 11).

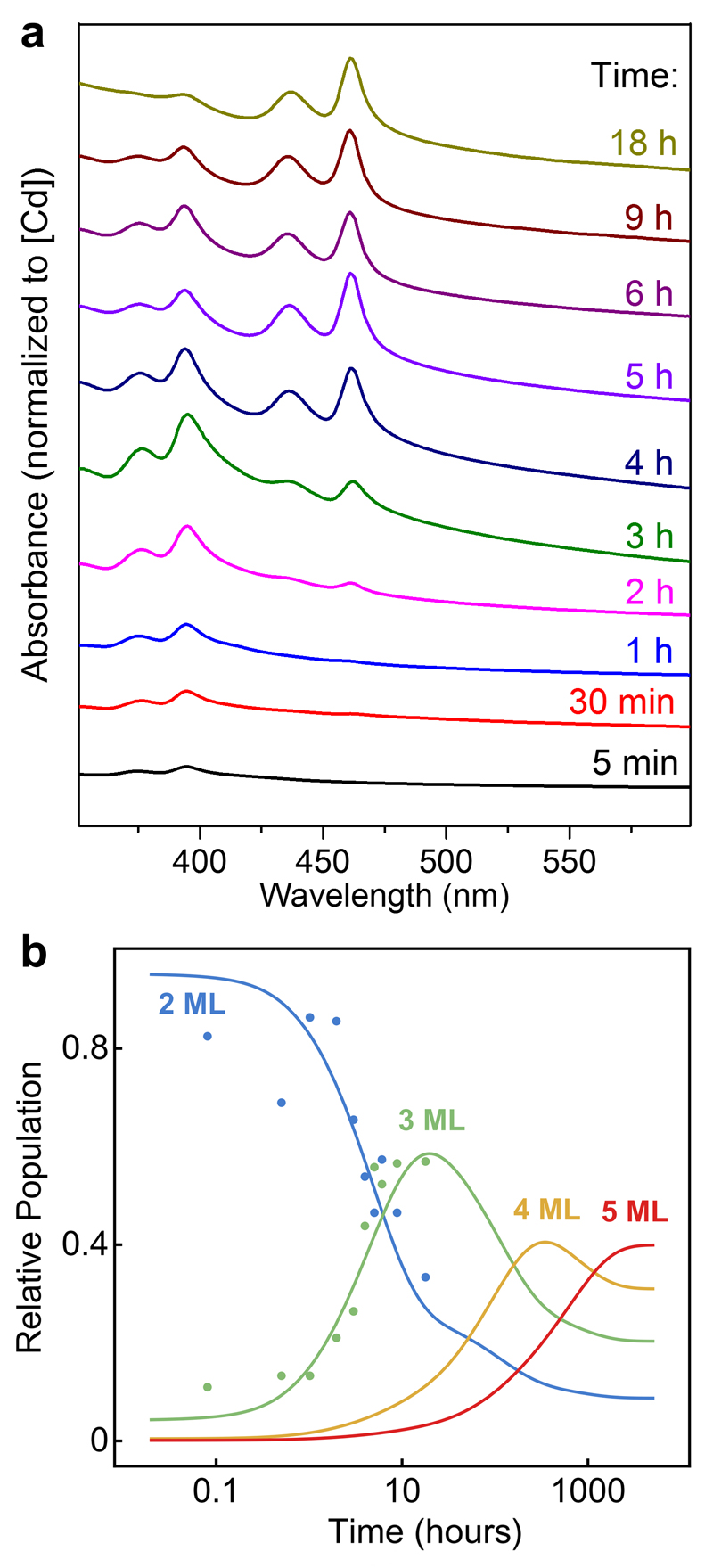
These findings indicate that zincblende CdSe NPLs can form in completely isotropic environments (see also Supplementary Fig. 12). We conclude, in agreement with previous studies27, that molecular templates are not involved in the formation of zincblende CdSe NPLs. Another model must account for their highly anisotropic shape and other key experimental observations. Namely, when such NPLs grow laterally22,36,38, their thickness remains largely fixed. Thickness can, however, increase at long times and high temperatures39,40. Figure 2a demonstrates such a transition (2 to 3 monolayers). Thus, our model must also address why the optical features of thinner NPLs disappear while those of thicker NPLs emerge.

Figure 2. Thickness transitions in CdSe nanoplatelets (NPLs).

Figure 2

Open in a new tab

a, Optical absorption spectra taken over 18 h from a blend of short-chain Cd(propionate)2 and Se powders at 200 °C. Initially 2-monolayer CdSe NPLs form, then slowly disappear with the appearance of 3-monolayer NPLs. b, Experimental data from a (solid points) for the relative populations of 2- and 3-monolayer NPLs versus growth time. Calculated relative populations for NPLs with thicknesses from 2 to 5 monolayers (MLs, solid lines), obtained from reversible first-order kinetics and Arrhenius reaction rates evaluated from the nucleation barriers in Fig. 3b, are shown for comparison.

Growth model

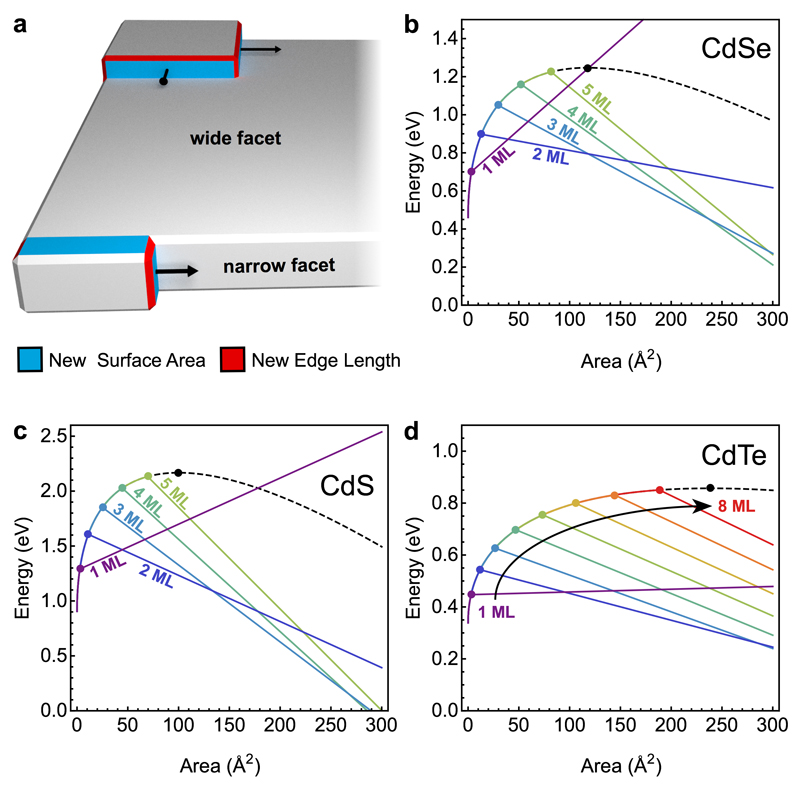
To explain these observations, we applied the general theory of 2D nucleation and growth41 to CdSe nanocrystals passivated on all exposed facets by short-chain carboxylate ligands. For a nanocrystal to grow, a new island must first nucleate on one of these facets. If this island reaches a critical size, it becomes stable and has a thermodynamic driving force to expand41,42, eventually adding a complete new layer to the facet. Because in our case the precursors are concentrated, diffusion of material to the growing island will be fast (unlike in conventional solvent-based nanocrystal growth43, as mentioned above). Thus, the overall process will be governed by island nucleation (see Supplementary Section 1.a). On large planar surfaces this nucleation process has a fixed activation barrier. Below we show that on narrow facets with dimensions below the critical island size, the nucleation barrier can be significantly reduced. This explains why an isotropic crystal structure can exhibit an anisotropic shape: faster growth can occur on thin facets compared to large planar surfaces.

Our model assumes an existing zincblende CdSe crystallite bounded by Cd-terminated {001} facets. We then investigated how the energy changes, for different facet dimensions, when an island nucleates and expands to cover the facet. For simplicity, we assumed that Cd and Se atoms are always incorporated together as “monomers.” The total energy of the system will change approximately as ΔE = ΔV EV + ΔA EA + ΔL EL. Here ΔV, ΔA, and ΔL are the difference in volume, area, and edge length of the crystallite due to growth, while EV, EA, and EL are energies per unit volume, area, and length. Solid CdSe is more stable than the melt and thus EV is negative, while EA and EL are positive. Hence, ΔE will be minimized when ΔA and ΔL are minimized.

We evaluated ΔE in two regimes: wide and narrow facets (Fig. 3a). On wide facets, the island nucleates most easily in a corner. We assumed for simplicity that it then grows as a rectangle with sides parallel to the facet edges. The energy is minimized for a square island and is given by Ewide(a) = (L1 EV) a + (4L1EA + 2EL) a1/2 + 4L1EL, where L1 is the height of one monolayer and a is the island area (Supplementary Section 1.b). For narrow facets, the island minimizes its energy by instead maintaining a single, short step edge spanning the facet. Once the island spans the facet, no additional edge energy is needed to complete the layer. Hence, in this regime the energy is given by a family of linear relationships, Emnarrow(a) = (L1 EV + 2 EA/m) a + 2mL12EA + (m + 4) L1EL, where m is the facet width (i.e., its thickness) in monolayers.

Figure 3. Theory of the intrinsic growth instability leading to nanoplatelets.

Figure 3

Open in a new tab

a, Qualitatively different growth modes on wide and narrow facets of a nanocrystal. On large facets a nucleated island grows isotropically to minimize its energy. The corresponding nucleation barrier is determined by the critical island size. On narrow facets with thickness less than this critical size, the island quickly spans the entire facet and then grows along the facet. The corresponding nucleation barrier is substantially reduced, leading to much faster growth at the experimental temperatures. Blue and red areas show new surfaces and edges formed by the islands, respectively. b-d, Calculated energy vs. island size on facets of different thicknesses based on parameters obtained from DFT calculations for CdSe (b), CdS (c), and CdTe (d). In each plot, the black dashed line represents the wide-facet limit. Colored lines represent narrow facets of different thicknesses, as labeled, in monolayers (MLs). The corresponding nucleation barriers are marked by circles.

To quantify these relationships, we used density-functional theory (DFT) to obtain EA = 5.7 meV/Å2 for acetate-passivated CdSe(001) under Se-rich conditions and EL = 37.1 meV/Å for monolayer steps on CdSe(001). Calculating EV from first principles is more challenging because the reference state is a melt. Instead, we estimated EV = −2.2 meV/Å3 from the experimental absence of 6-monolayer-thick CdSe NPLs. See Methods and Supplementary Section 1.c.

Figure 3b plots island energy versus island area in the two regimes for CdSe. Ewide(a) has the classic shape from standard heterogeneous nucleation theory (black curve) while Emnarrow(a) behaves very differently. The nucleation barriers on narrow facets (colored points) are smaller than on wide facets. For example, the barrier on 2-monolayer-thick facets is reduced from 1.25 to 0.9 eV. This implies much faster growth on narrow facets—three orders of magnitude faster at the growth temperature (200 °C). Even small changes in facet thickness dramatically affect growth rate. On average, one additional layer slows growth by a factor of ten. Consequently, as demonstrated below, even cubical nuclei can evolve into flat NPLs due to random fluctuations. This instability can lead to anisotropic NPLs even for materials with isotropic crystal structures.

Note that the model predicts that 1-monolayer-thick CdSe NPLs will have an island energy that increases indefinitely with island area (Fig. 3b). Thus, they are thermodynamically unstable. For thicker (e.g., 2-, 3-, 4- and 5-monolayer-thick) platelets, growth is suppressed with increasing thickness as the nucleation barrier approaches the wide-facet limit (assumed to be at 6 monolayers). However, for sufficiently large island areas, thicker facets eventually become more stable, as indicated by their increasingly negative slope beyond the barrier. Thus, the model predicts that 1-monolayer NPLs should not be observed, and rapid growth of 2-monolayer NPLs will eventually yield, at high temperature and long reaction times, to slower growth of thicker platelets—in agreement with experiments. Similarly, when we apply the model to other chalcogenides, it correctly predicts (Fig. 3c,d) the observed thicknesses of 2 to 5 and 2 to 8 monolayers for CdS11 and CdTe11,40,44 NPLs, respectively. Further, the nucleation barriers for CdTe NPLs of different thicknesses (Fig. 3d) are closer in energy than for CdS (Fig. 3c) and CdSe (Fig. 3b) NPLs. This explains why experiments show less selectivity for CdTe NPLs of a given thickness11.

For CdSe, we also used our model to calculate how thickness should increase with growth. We used coupled rate equations to describe how a mixture of CdSe monomers and NPLs of different thicknesses evolves in time (Supplementary Section 1.d). We estimated nucleation rates from the barriers in Fig. 3b and equilibrium constants from the reaction energies of NPLs of a given thickness. Figure 2b shows the predicted time evolution of the distribution of monomers within an ensemble of NPLs at 200 °C. At first, only 2-monolayer NPLs appear, but then 3-, 4-, and 5-monolayer NPLs appear in succession. Because the time needed for each new thickness increases by several orders of magnitude, the NPL thickness can be accurately controlled with time and temperature. Using the parameters from Fig. 3b, this simple model reproduces our experimentally observed transition from 2- to 3-monolayer platelets (Fig. 2b). Moreover, it suggests that 2-monolayer NPLs dissolve while new 3-monolayer NPLs form.

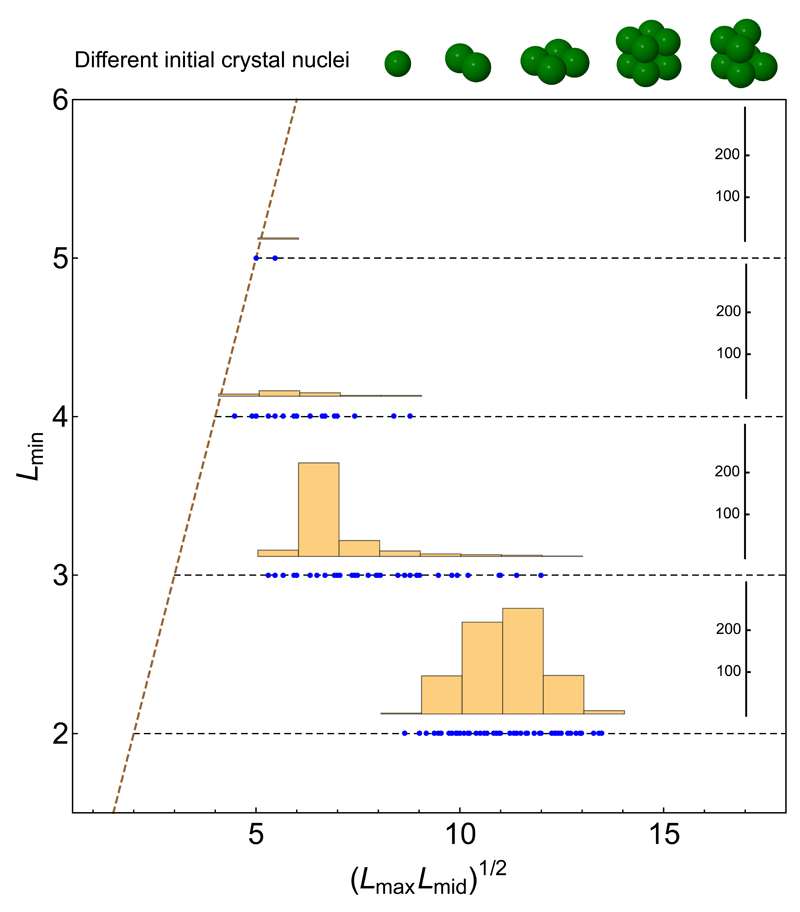
Finally, we used the kinetic Monte Carlo (kMC) method45 to demonstrate how NPLs arise from nuclei of various shapes. We simulated atomistic growth by incorporating CdSe monomers at finite temperature (650 K). For simplicity, we represented the underlying crystal lattice as simple cubic. We neglected diffusion and considered only adsorption and desorption of monomers. These steps were assumed to follow Arrhenius-type reaction rates obtained from ΔE above (see Methods and Supplementary Sections 1.e,f). Supplementary Movie 1 shows a typical growth sequence.

Figure 4 presents statistics for the simulations. The thinnest dimension (i.e., thickness) of each resulting nanocrystal (Lmin) is plotted versus the geometric mean of its other two dimensions, (Lmax Lmid)1/2. All nuclei tended to evolve into anisotropic shapes (right of the diagonal line) and were progressively more plate-like when one dimension was small. Indeed, 95% of our 1000 simulations resulted in NPLs, defined as shapes with (Lmax Lmid)1/2 > 2 Lmin. 100% and 93% of the simulated nanocrystals with 2- and 3-monolayer-thick facets, respectively, were NPLs. This effect arises directly from the reduced island nucleation barrier, and hence faster lateral growth, on thin facets. NPLs with thicknesses below 2 monolayers did not form; the low sticking probability of monomers on these thin facets caused such nanocrystals to dissolve.

Figure 4. Shape distribution of nanocrystals grown via kinetic Monte Carlo simulations.

Figure 4

Open in a new tab

Five different nuclei of various specific shapes (shown at top) were allowed to grow at 650 K. For each shape, 200 simulation runs were performed (see Supplementary Section 1.f for details). The resulting nanocrystal from each simulation was characterized by a rectangular box (in units of monomers) most closely corresponding to its shape. The plot abscissa is the geometric average of the two largest box dimensions, and the ordinate is the shortest linear box dimension. Each simulation outcome is plotted as a blue dot and the histograms show the size distributions of nanocrystals with minimum thicknesses ranging from 2 to 5 monolayers. The diagonal dashed line depicts the (hypothetical) case of isotropic shapes, i.e., cubical nanocrystals. The horizontal dashed lines indicate nanocrystals with a minimum dimension (i.e., thickness) of 2, 3, 4, and 5 monolayers. Data points far to the right on these horizontal lines are highly plate-like. Nanocrystals with 2 and 3 monolayers strongly resemble experimentally synthesized nanoplatelets. For thicker nanocrystals (4 and 5 monolayers) a trend toward forming more isotropic shapes is apparent, consistent with experimental results.

Discussion

In addition to the anisotropic shape and uniform atomic-scale thickness of NPLs, the model explains the limited range of thicknesses available for a given material. Namely, once the facet width matches the critical island size for bulk surfaces, the kinetic instability disappears and growth becomes isotropic. Further, the model clarifies why the same material, e.g., zincblende CdSe, can form quantum dots or NPLs under seemingly similar conditions. Diffusion-limited growth in solution leads to quantum dots; island-nucleation-limited growth in concentrated droplets or melts leads to NPLs (Supplementary Fig. 8).

The model also provides intuition for when NPLs will form. The interplay between EV, EA, and EL must satisfy several criteria. First, these parameters must yield a sufficiently high wide-facet nucleation barrier at the reaction temperature. Otherwise, any barrier reduction via narrow-facet growth will be irrelevant compared to the available thermal energy, leading to isotropic growth. (See Supplementary Movie 2, a kMC growth sequence at 1500 K.) Second, new edges must be energetically expensive (EL large) and new surfaces energetically inexpensive (EA small). Expensive edges (red in Fig. 3a) are continuously added as an island covers a wide facet. However, narrow facets, once spanned, do not incur additional edges during layer completion. Only inexpensive surface (blue) is added. More quantitatively, the model predicts that m-layer NPLs are stable if [ 2EA / (|EV| L1) ] < m. Thus, to obtain NPLs one should minimize EA, e.g., by using strongly binding ligands.

More generally, the quantitative evaluation of EV, EA, and EL, as done here for acetate-passivated CdS, CdSe, and CdTe, should allow a systematic search for new NPL materials. We have made preliminary efforts in this direction by exploring cubic FeS2 (pyrite), an earth-abundant semiconductor studied for photovoltaics. As in earlier DFT work46, we found that FeS2(001) is stable even without ligands. We obtained EA = 64 meV/Å2 and EL = 47 meV/Å for bare surfaces (Supplementary Section 1.g). Our model then predicts that kinetic instabilities can exist. Additionally, iron(II) carboxylates, similar to cadmium(II) carboxylates, form coordination polymers47, enabling non-diffusion-limited growth through phase separation. We confirmed these predictions by synthesizing 2-monolayer cubic FeS2 NPLs by combining Fe and S precursors at 150 °C (see Methods and Supplementary Fig. 13).

Recently, CsPbBr3 perovskite (cubic) NPLs have also been prepared12–15. Below a critical temperature, no NPLs were formed. As the reaction temperature was raised, increasingly thick NPLs (1 to 5 monolayers) were observed13. Even higher temperatures yielded cubes48. These findings can be easily rationalized by our mechanism.

The success of our model in describing the growth of zincblende CdSe NPLs does not preclude the participation of molecular templates or magic-size clusters in the growth of other quasi-2D semiconductor nanocrystals. Also, we did not consider in detail the effect of different ligands or combinations of ligands on the lateral extension of NPLs. However, we have shown that these factors are not critical for predicting NPLs.

Methods

Chemicals

Cadmium propionate (anhydrous) was purchased from MP Biomedicals (99.9%). Cadmium nitrate tetrahydrate (99.9%), cadmium acetate dihydrate (98%), selenium (99.5%), myristic acid (98%), butyric acid (99%), propionic acid (99.5%), acetic anhydride (99%), sodium hydroxide (98.5%), 1-octadecene (90%), oleic acid (90%), iron(II) acetate (95%), and deuterated chloroform (99.8 atom% deuterium) were purchased from Sigma Aldrich. Hexane and methanol were purchased from Thommen-Furler AG, and absolute ethanol from Alcosuisse AG. Acetyl sulfide (>95.0%) was purchased from Tokyo Chemical Industries. 1-Octadecene (ODE) was degassed under vacuum (0.02 mbar) for 20 h at 100 °C and stored under N2. All other chemicals were used as received.

Characterization

For nuclear magnetic resonance (NMR) experiments, samples were dissolved in deuterated chloroform and transferred to NMR tubes. All spectra were collected on a Bruker Ascend Aeon 400 MHz spectrometer. 1H-NMR spectra were recorded with predefined pulse programs. Diffusion-ordered spectroscopy (DOSY) experiments were carried out with a first gradient amplitude of 2% and a final gradient amplitude of 95% with a linear ramp (32 points).

For powder X-ray diffraction (XRD), samples were dispersed in hexane and drop-casted on zero-background Si sample holders. XRD patterns were recorded on a Bruker D8 Advance instrument (40 kV, 40 mA, λCuKα = 0.15418 nm).

X-ray scattering experiments were performed using a Rigaku MicroMax-002+ microfocused beam (40 W, 45 kV, 0.88 mA) with λCuKα = 0.15418 nm radiation to obtain direct information on the scattering patterns. The scattering intensities were collected by a Fujifilm BAS-MS 2025 imaging-plate system (15.2 cm × 15.2 cm, 50 μm resolution). An effective scattering-vector range of 1 nm-1 < q < 15 nm-1 was obtained, where q is the scattering wave vector defined as q = 4π sin θ / λCuKα with a scattering angle of 2θ. Samples were placed in a Linkam THMS600 hot-stage holder with a Linkam TMS94 temperature controller.

For polarized optical microscopy (POM), materials were studied with an optical Zeiss Axiophot microscope equipped with crossed polarizers connected to a Linkam LTS350 hot stage. Photomicrographs were taken with a Pixelink PL-A662 CMOS camera. Samples were prepared in a N2 glovebox by placing a few micrograms of thoroughly mixed Cd(propionate)2 and Se powders (molar ratio 3:1) between two standard microscope coverslips sealed with UV-curable epoxy to avoid air exposure during the experiment. The samples were removed from the glovebox, placed on the heating stage on the microscope, and studied between 25 and 200 °C with a heating rate of 10 K/min.

Differential scanning calorimetery (DSC) experiments were performed on a Mettler-Toledo DSC1 calorimeter equipped with a Huber TC100 cooling system. Samples (~10 mg) were encapsulated in 40 μL aluminum crucibles and measured under N2 with a heating/cooling rate of 10 K/min.

For absorption spectroscopy, aliquots were diluted in hexane and transferred to quartz cuvettes. Spectra were recorded on a Varian Cary 50 spectrophotometer.

For (scanning) transmission electron microscopy [(S)TEM] and energy-dispersive X-ray spectroscopy (EDS), samples were prepared on carbon-coated copper grids by drop-casting dilute dispersions (in hexane) followed by slow evaporation of the solvent. TEM micrographs were recorded on a Philips CM12 (operated at 100 kV) or on a FEI Tecnai F30 FEG (operated at 300 kV). STEM micrographs and EDS data were collected on a FEI Talos F200X microscope (operated at 200 kV).

For scanning electron microscopy (SEM), dispersions of powders (hexane) were drop-casted onto Si wafers and imaged using a Hitachi S-4800 SEM, operated at 3 kV in secondary-electron mode. EDS spectra were recorded at 10 kV with an EDAX Octane Super detector.

Synthetic methods

Cd(myristate)2 and Cd(oleate)2 were prepared by dissolving 3.54 g (15 mmol) Cd(NO3)2 · 4 H2O and 6.85 g (30 mmol) myristic acid [or 8.47 g (30 mmol) oleic acid] in 650 mL methanol under magnetic stirring. A solution of 1.81 g (45 mmol) NaOH in 50 mL methanol was added dropwise followed by vigorous stirring for 30 min. Cd(myristate)2 [or Cd(oleate)2] precipitated as a white, fluffy solid. This product was filtered, washed three times with methanol, and dried overnight in a vacuum oven at 40 °C (10 mbar).

For CdSe nanoplatelet (NPL) syntheses with short-chain carboxylic acids of various lengths (acetic anhydride, propionic, or butyric acid), the general protocol from Ref. 32 was adapted and modified. Briefly, in a 250 mL three-neck flask, 90 mL of ODE, 480 mg (1.8 mmol) Cd(acetate)2 · 2 H2O, and 1.18 g (4.2 mmol) technical grade oleic acid were degassed at 110 °C for 90 min under vacuum (0.02 mbar) and then kept under N2. A dispersion of 72 mg (0.9 mmol) Se in 2 mL degassed ODE was prepared in a N2 glovebox and injected into the reaction vessel. The temperature was set to 240 °C with a ramp of 20 °C/min. When the reaction mixture reached 180 °C, 0.5, 1, or 2 equivalents (with respect to Cd) of either acetic anhydride, propionic acid, or butyric acid were injected. Aliquots (1 mL) were taken at 175 (before injection), 190, 205, 220, and 240 °C and diluted in 5 mL hexane (see Supplementary Figs. 1-2). The temperature was maintained for 10 min at 240 °C, another aliquot was taken, and the mixture was quickly cooled to room temperature with a water bath and 10 mL oleic acid was injected. All products were precipitated from the crude reaction mixture with 5:1 excess of ethanol and centrifugation at 4000 r.p.m. (15 min). Special care was taken to ensure that the supernatants did not contain any CdSe species (quantum dots or NPLs) in order to get a representative overview of the products. The pellets were redispersed in hexane and precipitated two more times with ethanol by centrifugation (4000 r.p.m., 5 min). The washed products were redispersed and stored in 10 mL hexane.

To study ligand exchange in Cd(oleate)2 complexes, the protocol from the previous paragraph was modified, i.e. Se was removed. In a 250 mL three-neck flask, 90 mL ODE, 480 mg (1.8 mmol) Cd(acetate)2 · 2 H2O, and 1.18 g (4.2 mmol) technical grade oleic acid were degassed at 110 °C for 90 min under vacuum (0.02 mbar) and then kept under N2. At this stage, all Cd(acetate)2 was converted to Cd(oleate)2. The temperature was set to 180 °C with a ramp of 20 °C/min. When the solution reached 180 °C, 2 equivalents (with respect to Cd) of either acetic anhydride, propionic acid, or butyric acid were injected. Upon injection of acetic anhydride or propionic acid the solution became turbid, while with butyric acid no changes were observed. The reaction was continued for 30 min at 180 °C, and the mixture was cooled to room temperature. Solids were isolated by direct centrifugation of the reaction mixtures at 8000 r.p.m. (30 min), washed three times with hexane, isolated by centrifugation (8000 r.p.m., 10 min), and dried under vacuum (0.02 mbar) for 24 h. See Supplementary Figs. 3-5.

Solvent-free synthesis of CdSe NPLs involved mixing powders of anhydrous cadmium carboxylates [Cd(propionate)2 or Cd(myristate)2] with powders of Se in glass vials at a molar ratio of 3:1 [Cd(carboxylate)2 to chalcogens] and placed in a pre-heated muffle oven inside a N2 glovebox. Reactions were carried out from 5 min to 18 h at 200 °C. The initial black melt of Cd(carboxylate)2 and Se turned yellow over time. After cooling to room temperature, the samples were taken from the glovebox, and solutions of oleic acid (5 vol%) in hexane/ethanol (1:1 vol%) were added to the dry powders, followed by sonication (30 min) and centrifugation at 3000 r.p.m. (5 min). The supernatants were discarded and the pellets were resuspended in ethanol, sonicated (30 min), and then centrifuged at 4000 r.p.m. (5 min). This redispersion-precipitation-centrifugation sequence was repeated twice, and the cleaned samples were stored in hexane.

To obtain FeS2 NPLs, 104 mg (0.6 mmol) anhydrous iron(II) acetate, 0.6 mL oleic acid, and 30 mL ODE were mixed in a 100 mL three-neck flask. The mixture was degassed for 60 min at 120 °C and placed under N2. The temperature was raised to 150 °C, and 0.04 mL (0.38 mmol) acetyl sulfide was swiftly injected into the reaction mixture. The temperature was held for an hour and subsequently cooled naturally to room temperature. The FeS2 NPLs were washed with hexane and ethanol by centrifugation and redispersed in hexane. All procedures were conducted under air-free conditions.

Modelling

We used density-functional theory (DFT) total-energy calculations to determine the atomistic geometry of passivated nanocrystal surfaces, steps, and edges, as well as the binding energies of CdSe monomers and the activation barriers for desorption of Cd-acetate ligands at those surfaces. For computational efficiency, we omitted carboxylates with longer carbon chains as they can be expected to behave very similarly to acetate. Total energies and forces were calculated within the generalized-gradient approximation of Perdew, Burke, and Ernzerhof (PBE)49,50 using projector-augmented-wave potentials, as implemented in VASP51,52. The plane-wave cut-off was 300 eV. We optimized all geometries until the forces were below 50 meV/Å. See Supplementary Section 1.c for details.

We used the kinetic Monte Carlo (kMC) method45,53 to simulate nanoplatelet growth via the incorporation of CdSe monomers. To obtain the Arrhenius rates of possible monomer attachment and detachment reactions, we calculated the respective energy barriers based on the DFT parameters EA, EL, and EV and on the reaction barrier of desorbing acetate ligands from the corresponding surface site (see Supplementary Sections 1.e,f). To increase computational efficiency, we neglected attachment onto flat surfaces (which lack a step or an edge) due to the very high reaction barrier (2.1 eV).

Supplementary Material

Supplementary information is available in the online version of the paper.

Supplementary information
Supplementary video 1
Download video file (1.1MB, mp4)
Supplementary video 2
Download video file (3.2MB, mp4)

Acknowledgements

This work was supported by ETH Research Grant ETH-38 14-1, by the Swiss National Science Foundation under Grant Nrs. 200021-140617 and 200020-159228, and by the U.S. Office of Naval Research (ONR) through the Naval Research Laboratory’s Basic Research Program (SCE). F.D.O. benefitted from an ONR Global travel grant. S.J.P.K. acknowledges funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement Nr. 339905 (QuaDoPS Advanced Grant). Computations were performed at the ETH High-Performance Computing Cluster Euler and the DoD Major Shared Resource Center at AFRL. We thank A. Sánchez-Ferrer for assistance with the X-ray scattering measurements and R. Mezzenga for equipment access. We acknowledge L. Frenette, O. Hirsch, P. Kumar, D. Koziej, V. Lin, M. Mazzotti, K. McNeill, S. Meyer, M. Niederberger, F. Rabouw, A. Rossinelli, H. Schönberg, O. Waser, C. Willa, F. Rechberger, and M. Bärtsch for technical assistance and discussions. We utilized the ScopeM facility at ETH Zurich for electron microscopy.

Footnotes

Data availability.

The data that support the findings of this study are available from the corresponding authors on request.

Author contributions

A.R., F.D.O., S.C.E., and D.J.N. conceived the experiments and model. Syntheses and optical spectroscopy were performed by A.R., A.M., and P.N.K. X-ray diffraction, DSC, nuclear magnetic resonance spectroscopy, electron microscopy, and energy-dispersive X-ray spectroscopy were done by A.R and P.N.K. Polarized optical and fluorescence microscopy was performed by A.R. with help from S.J.P.K and F.P. Calculations and simulations were performed by F.D.O and S.M. The NPL growth model was developed by F.D.O and S.C.E with input from A.R. and D.J.N. Both S.C.E. and D.J.N. supervised the work. A.R., F.D.O., S.C.E., and D.J.N. wrote the manuscript. All authors contributed to the discussion of the results and to the revision of the manuscript.

Additional information

Reprints and permissions information is available online at www.nature.com/reprints.

Competing financial interests

The authors declare no competing financial interests.

References

  • 1.Yin Y, Alivisatos AP. Colloidal nanocrystal synthesis and the organic-inorganic interface. Nature. 2005;437:664–670. doi: 10.1038/nature04165. [DOI] [PubMed] [Google Scholar]
  • 2.Xia YN, Xiong YJ, Lim B, Skrabalak SE. Shape-controlled synthesis of metal nanocrystals: Simple chemistry meets complex physics? Angew Chem. 2009;48:60–103. doi: 10.1002/anie.200802248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Murray CB, Norris DJ, Bawendi MG. Synthesis and characterization of nearly monodisperse CdE (E = sulfur, selenium, tellurium) semiconductor nanocrystallites. J Am Chem Soc. 1993;115:8706–8715. [Google Scholar]
  • 4.Peng X, Manna L, Yang W, Wickham J, Scher E, Kadavanich A, Alivisatos AP. Shape control of CdSe nanocrystals. Nature. 2000;404:59–61. doi: 10.1038/35003535. [DOI] [PubMed] [Google Scholar]
  • 5.Manna L, Milliron DJ, Meisel A, Scher EC, Alivisatos AP. Controlled growth of tetrapod-branched inorganic nanocrystals. Nat Mater. 2003;2:382–385. doi: 10.1038/nmat902. [DOI] [PubMed] [Google Scholar]
  • 6.Manna L, Scher EC, Alivisatos AP. Synthesis of soluble and processable rod-, arrow-, and teardrop-, and tetrapod-shaped CdSe nanocrystals. J Am Chem Soc. 2000;122:12700–12706. [Google Scholar]
  • 7.Milliron DJ, Hughes SM, Cui Y, Manna L, Li J, Wang L-W, Alivisatos AP. Colloidal nanocrystal heterostructures with linear and branched topology. Nature. 2004;430:190–195. doi: 10.1038/nature02695. [DOI] [PubMed] [Google Scholar]
  • 8.Liu L, Zhuang Z, Xie T, Wang Y-G, Li J, Peng Q, Li Y. Shape control of CdSe nanocrystals with zinc blende structure. J Am Chem Soc. 2009;131:16423–16429. doi: 10.1021/ja903633d. [DOI] [PubMed] [Google Scholar]
  • 9.Joo J, Son JS, Kwon SG, Yu JH, Hyeon T. Low-temperature solution-phase synthesis of quantum well structured CdSe nanoribbons. J Am Chem Soc. 2006;128:5632–5633. doi: 10.1021/ja0601686. [DOI] [PubMed] [Google Scholar]
  • 10.Ithurria S, Dubertret B. Quasi 2D colloidal CdSe platelets with thicknesses controlled at the atomic level. J Am Chem Soc. 2008;130:16504–16505. doi: 10.1021/ja807724e. [DOI] [PubMed] [Google Scholar]
  • 11.Ithurria S, Tessier MD, Mahler B, Lobo R, Dubertret B, Efros A. Colloidal nanoplatelets with two-dimensional electronic structure. Nat Mater. 2011;10:936–941. doi: 10.1038/nmat3145. [DOI] [PubMed] [Google Scholar]
  • 12.Tyagi P, Arveson SM, Tisdale WA. Colloidal organohalide perovskite nanoplatelets exhibiting quantum confinement. J Phys Chem Lett. 2015;6:1911–1916. doi: 10.1021/acs.jpclett.5b00664. [DOI] [PubMed] [Google Scholar]
  • 13.Bekenstein Y, Koscher BA, Eaton SW, Yang P, Alivisatos AP. Highly luminescent colloidal nanoplates of perovskite cesium lead halide and their oriented assemblies. J Am Chem Soc. 2015;137:16008–16011. doi: 10.1021/jacs.5b11199. [DOI] [PubMed] [Google Scholar]
  • 14.Akkerman QA, Motti SG, Srimath Kandada AR, Mosconi E, D’Innocenzo V, Bertoni G, Marras S, Kamino BA, Miranda L, De Angelis F, Petrozza A, et al. Solution synthesis approach to colloidal cesium lead halide perovskite nanoplatelets with monolayer-level thickness control. J Am Chem Soc. 2016;138:1010–1016. doi: 10.1021/jacs.5b12124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Shamsi J, Dang Z, Bianchini P, Canale C, Stasio FD, Brescia R, Prato M, Manna L. Colloidal synthesis of quantum confined single crystal CsPbBr3 nanosheets with lateral size control up to the micrometer range. J Am Chem Soc. 2016;138:7240–7243. doi: 10.1021/jacs.6b03166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Schliehe C, Juarez BH, Pelletier M, Jander S, Greshnykh D, Nagel M, Meyer A, Foerster S, Kornowski A, Klinke C, Weller H. Ultrathin PbS sheets by two-dimensional oriented attachment. Science. 2010;329:550–553. doi: 10.1126/science.1188035. [DOI] [PubMed] [Google Scholar]
  • 17.Liu Y-H, Wang F, Wang Y, Gibbons PC, Buhro WE. Lamellar assembly of cadmium selenide nanoclusters into quantum belts. J Am Chem Soc. 2011;133:17005–17013. doi: 10.1021/ja206776g. [DOI] [PubMed] [Google Scholar]
  • 18.Achtstein AW, Schliwa A, Prudnikau A, Hardzei M, Artemyev MV, Thomsen C, Woggon U. Electronic structure and exciton–phonon interaction in two-dimensional colloidal CdSe nanosheets. Nano Lett. 2012;12:3151–3157. doi: 10.1021/nl301071n. [DOI] [PubMed] [Google Scholar]
  • 19.Pelton M, Ithurria S, Schaller RD, Dolzhnikov DS, Talapin DV. Carrier cooling in colloidal quantum wells. Nano Lett. 2012;12:6158–6163. doi: 10.1021/nl302986y. [DOI] [PubMed] [Google Scholar]
  • 20.Rowland CE, Fedin I, Zhang H, Gray SK, Govorov AO, Talapin DV, Schaller RD. Picosecond energy transfer and multiexciton transfer outpaces Auger recombination in binary CdSe nanoplatelet solids. Nat Mater. 2015;14:484–489. doi: 10.1038/nmat4231. [DOI] [PubMed] [Google Scholar]
  • 21.Guzelturk B, Erdem O, Olutas M, Kelestemur Y, Demir HV. Stacking in colloidal nanoplatelets: Tuning excitonic properties. ACS Nano. 2014;8:12524–12533. doi: 10.1021/nn5053734. [DOI] [PubMed] [Google Scholar]
  • 22.Olutas M, Guzelturk B, Kelestemur Y, Yeltik A, Delikanli S, Demir HV. Lateral size-dependent spontaneous and stimulated emission properties in colloidal CdSe nanoplatelets. ACS Nano. 2015;9:5041–5050. doi: 10.1021/acsnano.5b01927. [DOI] [PubMed] [Google Scholar]
  • 23.Yeltik A, Delikanli S, Olutas M, Kelestemur Y, Guzelturk B, Demir HV. Experimental determination of the absorption cross-section and molar extinction coefficient of colloidal CdSe nanoplatelets. J Phys Chem C. 2015;119:26768–26775. [Google Scholar]
  • 24.She C, Fedin I, Dolzhnikov DS, Demortière A, Schaller RD, Pelton M, Talapin DV. Low-threshold stimulated emission using colloidal quantum wells. Nano Lett. 2014;14:2772–2777. doi: 10.1021/nl500775p. [DOI] [PubMed] [Google Scholar]
  • 25.Chen Z, Nadal B, Mahler B, Aubin H, Dubertret B. Quasi-2D colloidal semiconductor nanoplatelets for narrow electroluminescence. Adv Funct Mater. 2014;24:295–302. [Google Scholar]
  • 26.Lhuillier E, Pedetti S, Ithurria S, Heuclin H, Nadal B, Robin A, Patriarche G, Lequeux N, Dubertret B. Electrolyte-gated field effect transistor to probe the surface defects and morphology in films of thick CdSe colloidal nanoplatelets. ACS Nano. 2014;8:3813–3820. doi: 10.1021/nn500538n. [DOI] [PubMed] [Google Scholar]
  • 27.Ithurria S, Bousquet G, Dubertret B. Continuous transition from 3D to 1D confinement observed during the formation of CdSe nanoplatelets. J Am Chem Soc. 2011;133:3070–3077. doi: 10.1021/ja110046d. [DOI] [PubMed] [Google Scholar]
  • 28.Hutter EM, Bladt E, Goris B, Pietra F, van der Bok JC, Boneschanscher MP, de Mello Donegá C, Bals S, Vanmaekelbergh D. Conformal and atomic characterization of ultrathin CdSe platelets with a helical shape. Nano Lett. 2014;14:6257–6262. doi: 10.1021/nl5025744. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Wang F, Wang Y, Liu Y-H, Morrison PJ, Loomis RA, Buhro WE. Two-dimensional semiconductor nanocrystals: Properties, templated formation, and magic-size nanocluster intermediates. Acc Chem Res. 2015;48:13–21. doi: 10.1021/ar500286j. [DOI] [PubMed] [Google Scholar]
  • 30.Son JS, Wen X-D, Joo J, Chae J, Baek S-i, Park K, Kim JH, An K, Yu JH, Kwon SG, Choi S-H, et al. Large-scale soft colloidal template synthesis of 1.4 nm thick CdSe nanosheets. Angew Chem Int Ed. 2009;48:6861–6864. doi: 10.1002/anie.200902791. [DOI] [PubMed] [Google Scholar]
  • 31.Wang Y, Zhang Y, Wang F, Giblin DE, Hoy J, Rohrs HW, Loomis RA, Buhro WE. The magic-size nanocluster (CdSe)34 as a low-temperature nucleant for cadmium selenide nanocrystals: Room-temperature growth of crystalline quantum platelets. Chem Mater. 2014;26:2233–2243. doi: 10.1021/cm404068e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Mahler B, Nadal B, Bouet C, Patriarche G, Dubertret B. Core/shell colloidal semiconductor nanoplatelets. J Am Chem Soc. 2012;134:18591–18598. doi: 10.1021/ja307944d. [DOI] [PubMed] [Google Scholar]
  • 33.Harrison W, Trotter J. Crystal and molecular structure of cadmium diacetate dihydrate. J Chem Soc Dalton Trans. 1972:956–960. [Google Scholar]
  • 34.Chen D, Gao Y, Chen Y, Ren Y, Peng X. Structure identification of two-dimensional colloidal semiconductor nanocrystals with atomic flat basal planes. Nano Lett. 2015;15:4477–4482. doi: 10.1021/acs.nanolett.5b00940. [DOI] [PubMed] [Google Scholar]
  • 35.Nasilowski M, Mahler B, Lhuillier E, Ithurria S, Dubertret B. Two-dimensional colloidal nanocrystals. Chem Rev. 2016;116:10934–10982. doi: 10.1021/acs.chemrev.6b00164. [DOI] [PubMed] [Google Scholar]
  • 36.Bouet C, Mahler B, Nadal B, Abecassis B, Tessier MD, Ithurria S, Xu X, Dubertret B. Two-dimensional growth of CdSe nanocrystals, from nanoplatelets to nanosheets. Chem Mater. 2013;25:639–645. [Google Scholar]
  • 37.Mirnaya TA, Volkov SV. In: Green Industrial Applications of Ionic Liquids. Rogers RD, Seddon KR, Volkov SV, editors. Springer; Netherlands, Dordrecht: 2002. pp. 439–456. [Google Scholar]
  • 38.Tessier MD, Spinicelli P, Dupont D, Patriarche G, Ithurria S, Dubertret B. Efficient exciton concentrators built from colloidal core/crown CdSe/CdS semiconductor nanoplatelets. Nano Lett. 2013;14:207–213. doi: 10.1021/nl403746p. [DOI] [PubMed] [Google Scholar]
  • 39.Li Z, Qin H, Guzun D, Benamara M, Salamo G, Peng X. Uniform thickness and colloidal-stable CdS quantum disks with tunable thickness: Synthesis and properties. Nano Res. 2012;5:337–351. [Google Scholar]
  • 40.Pedetti S, Nadal B, Lhuillier E, Mahler B, Bouet C, Abécassis B, Xu X, Dubertret B. Optimized synthesis of CdTe nanoplatelets and photoresponse of CdTe nanoplatelets films. Chem Mater. 2013;25:2455–2462. [Google Scholar]
  • 41.Lovette MA, Browning AR, Griffin DW, Sizemore JP, Snyder RC, Doherty MF. Crystal shape engineering. Ind Eng Chem Res. 2008;47:9821–9833. [Google Scholar]
  • 42.Ohara M, Reid RC. Modeling Crystal Growth Rates from Solution. Prentice-Hall; 1973. [Google Scholar]
  • 43.Thanh NTK, Maclean N, Mahiddine S. Mechanisms of nucleation and growth of nanoparticles in solution. Chem Rev. 2014;114:7610–7630. doi: 10.1021/cr400544s. [DOI] [PubMed] [Google Scholar]
  • 44.Scott R, Kickhofel S, Schoeps O, Antanovich A, Prudnikau A, Chuvilin A, Woggon U, Artemyev M, Achtstein AW. Temperature dependent radiative and non-radiative recombination dynamics in CdSe-CdTe and CdTe-CdSe type II hetero nanoplatelets. Phys Chem Chem Phys. 2016;18:3197–3203. doi: 10.1039/c5cp06623a. [DOI] [PubMed] [Google Scholar]
  • 45.Fichthorn KA, Weinberg WH. Theoretical foundations of dynamical Monte Carlo simulations. J Chem Phys. 1991;95:1090–1096. [Google Scholar]
  • 46.Hung A, Muscat J, Yarovsky I, Russo SP. Density-functional theory studies of pyrite FeS2(100) and (110) surfaces. Surf Sci. 2002;513:511–524. [Google Scholar]
  • 47.Weber B, Betz R, Bauer W, Schlamp S. Crystal structure of iron(II) acetate. Z Anorg Allg Chem. 2011;637:102–107. [Google Scholar]
  • 48.Protesescu L, Yakunin S, Bodnarchuk MI, Krieg F, Caputo R, Hendon CH, Yang RX, Walsh A, Kovalenko MV. Nanocrystals of cesium lead halide perovskites (CsPbX3, X = Cl, Br, and I): Novel optoelectronic materials showing bright emission with wide color gamut. Nano Lett. 2015;15:3692–3696. doi: 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  • 50.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1997;78:1396–1396. doi: 10.1103/PhysRevLett.77.3865. [Phys. Rev. Lett. 77, 3865 (1996)] [DOI] [PubMed] [Google Scholar]
  • 51.Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B. 1993;47:558–561. doi: 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]
  • 52.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  • 53.Ott FD, Spiegel LL, Norris DJ, Erwin SC. Microscopic theory of cation exchange in CdSe nanocrystals. Phys Rev Lett. 2014;113:156803. doi: 10.1103/PhysRevLett.113.156803. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary information
NIHMS71764-supplement-Supplementary_information.pdf (12.1MB, pdf)
Supplementary video 1
Download video file (1.1MB, mp4)
Supplementary video 2
Download video file (3.2MB, mp4)

RESOURCES