Quantifying Wheat Sensitivities to Environmental Constraints to Dissect Genotype × Environment Interactions in the Field^,

The determination of periods of sensitivity of yield and yield components to soil water potential and temperature allowed dissecting genotype × drought × heat interactions observed in wheat fields.

Abstract

Yield is subject to strong genotype-by-environment (G × E) interactions in the field, especially under abiotic constraints such as soil water deficit (drought [D]) and high temperature (heat [H]). Since environmental conditions show strong fluctuations during the whole crop cycle, geneticists usually do not consider environmental measures as quantitative variables but rather as factors in multienvironment analyses. Based on 11 experiments in a field platform with contrasting temperature and soil water deficit, we determined the periods of sensitivity to drought and heat constraints in wheat (Triticum aestivum) and determined the average sensitivities for major yield components. G × E interactions were separated into their underlying components, constitutive genotypic effect (G), G × D, G × H, and G × H × D, and were analyzed for two genotypes, highlighting contrasting responses to heat and drought constraints. We then tested the constitutive and responsive behaviors of two strong quantitative trait loci (QTLs) associated previously with yield components. This analysis confirmed the constitutive effect of the chromosome 1B QTL and explained the G × E interaction of the chromosome 3B QTL by a benefit of one allele when temperature rises. In addition to the method itself, which can be applied to other data sets and populations, this study will support the cloning of a major yield QTL on chromosome 3B that is highly dependent on environmental conditions and for which the climatic interaction is now quantified.

Grain yield is affected worldwide by abiotic constraints such as drought and heat stress (Lobell et al., 2011). In the field, these abiotic stresses are likely to occur simultaneously (Barnabás et al., 2008), at the regional scale because of the coincidence of sunny, warm, and dry weather and at the micrometeorological level due to the balance of stomatal closure in response to heat and drought (Rizhsky et al., 2002). Indeed, plants respond to drought by closing stomata, decreasing transpiration, and increasing plant temperature. On the other hand, rising air temperature increases evaporative demand between the plant and the atmosphere, resulting in increases in transpiration that, in turn, can cause tissue dehydration. This tradeoff is one cause of the strong interaction between heat and drought stresses but not the only one. More generally, the molecular and metabolic responses to several abiotic stresses are not the sum of individual effects (Rizhsky et al., 2004; Mittler, 2006). This interaction is often hypoadditive (Pradhan et al., 2012), with, for example, a greater effect of heat and drought stresses on grain filling in wheat than the sum of the effects of these individual stresses (Savin and Nicolas, 1996; Shah and Paulsen, 2003).

The interactions of drought and temperature on yield and yield components are even more complex, because they integrate many physiological processes under multigenic controls and respond dynamically to the plant microenvironment over the crop cycle. Therefore, yield and its components are highly dependent on genotype-by-environment (G × E) interactions (Tardieu, 2012; Addison et al., 2016). The associated quantitative trait loci (QTLs) also are highly dependent on temperature and water scenarios (Kuchel et al., 2007; Pinto et al., 2010; Acuna-Galindo et al., 2015; Millet et al., 2016).

The use of phenotyping platforms in controlled environments allows dissecting these G × E interactions by controlling many growth conditions and focusing on the responses of biological variables to a few targeted environmental conditions (Tardieu and Tuberosa, 2010). This strategy has been used to assess the variables related to growth and development and resulted in robust QTLs of plant dynamics such as plant growth rate (Malosetti et al., 2006; Parent et al., 2015) and plant responses to some environmental variables such as soil water potential or vapor pressure deficit (Welcker et al., 2011; Schoppach et al., 2016). However, growing conditions in controlled environments are far removed from those observed in the field (Poorter et al., 2016), resulting in trait values for biological variables such as yield or yield components that have little practical relevance. In the field, plants are grown under normal agricultural systems, but the environment is hard to define and quantify because almost all environmental variables fluctuate daily and along the crop cycle. As a result, the environment is often viewed as a qualitative factor rather than the sum of quantitative variables, with few exceptions (van Eeuwijk et al., 2010; Millet et al., 2016). Despite important progress in genetics, QTL-by-environment (QTL × E) interactions are most often analyzed in a qualitative way with significant or nonsignificant interactions across qualitative environments (El-Soda et al., 2015). This was the case in studies where wheat (Triticum aestivum) was grown under heat and/or drought conditions (Mathews et al., 2008; Pinto et al., 2010; Graziani et al., 2014; Acuna-Galindo et al., 2015; Addison et al., 2016).

Several indicators have been tested as quantitative variables to summarize the fluctuating conditions occurring in the field. The most used indicators are based on the targeted traits, such as the average yield at the considered site (Fleury et al., 2010), or indices such as the ratio of yield under stressed conditions compared with optimal conditions (Liu et al., 2015). Another strategy uses thresholds such as the number of days with temperatures above 30°C (Kuchel et al., 2007). However, none of these methods summarizes the environmental conditions sensed by plants during long periods of sensitivity. The most developed strategies considering the different environmental variables in a quantitative way are those used in crop modeling, such as growth indices, taking into account temperature, light, and nutrients, with either additional effects or the effect of limiting factors (growth indices; Fitzpatrick and Nix, 1970).

Another difficulty in quantifying the environment is that the sensitivities of integrated variables, such as yield components and environmental conditions, are not stable during the crop cycle. For example, using field-grown wheat plants and polytunnels increasing temperature around anthesis, Ferris et al. (1998) found no correlation between yield and the average temperature but found significant correlations between yield and temperature over a few days after 50% anthesis. In controlled environments, sensitivity periods can be defined when the developmental stages are defined precisely (such as the onset of meiosis or pollen tetrad breakup) and environmental conditions are controlled on individual plants (Saini and Aspinall, 1982; Westgate and Grant, 1989; Tashiro and Wardlaw, 1990). To our knowledge, no study analyzed the response of yield components in the field to both temperature and water conditions during each period of plant development, probably due to the difficulty in obtaining such phenology details for large germplasm collections or mapping populations.

This study aimed to untangle G × E and QTL × E interactions observed on yield components across 11 wheat trials using various temperatures and drought scenarios in a field platform. Two QTLs with major effects and opposite behaviors were analyzed in this study using two genetic populations, Drysdale/Gladius and RAC875/Kukri. Gladius, Drysdale, and RAC875 are modern wheat lines adapted to the Australian climate. They perform well in water-limited environments and display a similar overall response to average site yield (Fleury et al., 2010) with contrasting behaviors under stress (Rebetzke et al., 2002; Condon et al., 2006; Fleury et al., 2010). These lines provide interesting material for studying adaptive strategies to warm and dry environments. Mapping populations based on crosses between Drysdale and Gladius and between RAC875 and Kukri were studied for yield and other related traits (Bennett et al., 2012a; Maphosa et al., 2014; Parent et al., 2015). As the Gladius variety originated from RAC875 and Kukri lines (Fleury et al., 2010), the two populations showed common QTLs, such as those targeted here on chromosomes 1B and 3B. The 1B QTL found on a Gladius × Drysdale recombinant inbred line (RIL) population controlled shoot expansion rate in a glasshouse platform and tiller number in the field in a way that appears constitutive (Parent et al., 2015). This QTL overlaps with QKpsl.aww-1B for grain per spikelet and yields QTL QYld.aww-1B on the second population, RAC875/Kukri (Bennett et al., 2012a), but with lower effects than in Drysdale/Gladius. A QTL found on chromosome 3B, qYDH.3BL, in the RAC875 × Kukri double haploid population (Bennett et al., 2012b; Bonneau et al., 2013) controlled yield and thousand kernel weight and showed a strong interaction with the environment. qYDH.3BL of RAC875/Kukri (Bonneau et al., 2013) also segregates in Drysdale/Gladius (Maphosa et al., 2014), as confirmed by Bonneau et al. (2013). RAC875 and Drysdale carry the positive allele in each population, with RAC875 showing the strongest effect in the RAC875/Kukri population.

In the experiments described here, the environment was defined as independent variables averaged for different periods of the crop cycle. The periods of sensitivity of each biological trait were determined using the Gladius and Drysdale data sets, and the quantitative environment was summarized as temperature and drought conditions averaged over the relevant period of sensitivity. The response of each trait to the quantitative environment was calculated as the sum of the drought response, heat response, and response to heat and drought interaction. We then used this framework to decipher the G × E interactions observed in these two varieties. Finally, we tested the QTL × E interactions on the two QTLs that showed contrasting behaviors. This analysis allowed quantification of both the constitutive components of QTL and the responsive component to temperature and water deficit. The method itself can now be applied to larger data sets and populations, once plant development and meteorological data are recorded. More specifically, this study deciphered the strong QTL × E interaction of the QTL on chromosome 3B (qYDH.3BL), a major yield QTL but highly dependent on environmental conditions (Bennett et al., 2012a, 2012b; Bonneau et al.,2013; Maphosa et al., 2014). This should facilitate the cloning of the gene or genes underlying the 3B QTL by informing on the conditions associated with a positive impact on yield for each allele.

RESULTS

G × E Interactions on Yield Components in a Network of 11 Trials with Large Ranges of Temperature and Soil Water Status

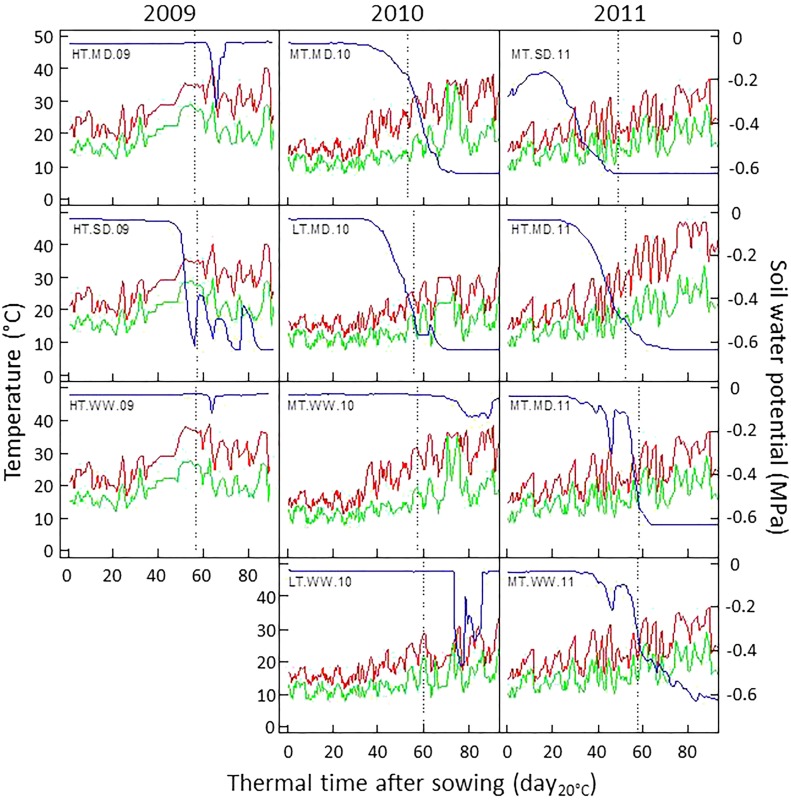
The two varieties Gladius and Drysdale were grown in 11 trials under a broad range of environmental conditions (Fig. 1; Supplemental Fig. S1) using the field platform at the University of Adelaide equipped with watering systems, polytunnels, and weather sensors (Supplemental Fig. S1; each trial is named in a similar way: temperature-drought-year, with HT, MT, and LT for high, moderate, and low temperature, respectively, and WW, MD, and SD for well watered, moderate drought, and severe drought, respectively). Drought varied in amplitude, intensity, crop stage occurrence, and duration, from well-watered conditions (in HT.WW.09 and MT.WW.10 trials) to short periods of drought after flowering (HT.MD.09 and LT.WW.10) and long periods of drought starting before flowering (HT.SD.09, LT.MD.10, and HT.MD.11). Such differences in water scenarios had large effects on yield. For example, the yield difference of Gladius was 2.3 t ha⁻¹ between the trials MT.WW.11 and MT.MD.11, differing only in the intensity of water stress after anthesis but not in the timing (Fig. 1). Temperatures increased steadily during the whole crop cycle as in the 2009 trials, or around and after flowering (e.g. HT.MD.11), or remained low (e.g. LT.WW.10). Overall, the range of temperatures was large, with maximum temperature ranging from 31°C to 46.7°C depending on the trial, and minimum temperature reaching 3.8°C in LT.WW.10 (Supplemental Fig. S1). Because no frost event occurred in these trials, the only temperature effects in the analyses are heat effects. The combination of such temperature and water scenarios resulted in a wide range of grain yield from 2.1 to 6.8 t ha⁻¹ for Gladius (Fig. 2A; Supplemental Fig. S1).

Figure 1.

Environmental conditions in 11 field trials. Time is expressed as thermal time. Red lines, Daily maximum temperature; green lines, daily average temperature; blue lines, soil water potential; dashed lines, flowering time of Gladius. More details are available in Supplemental Figure S1.

Figure 2.

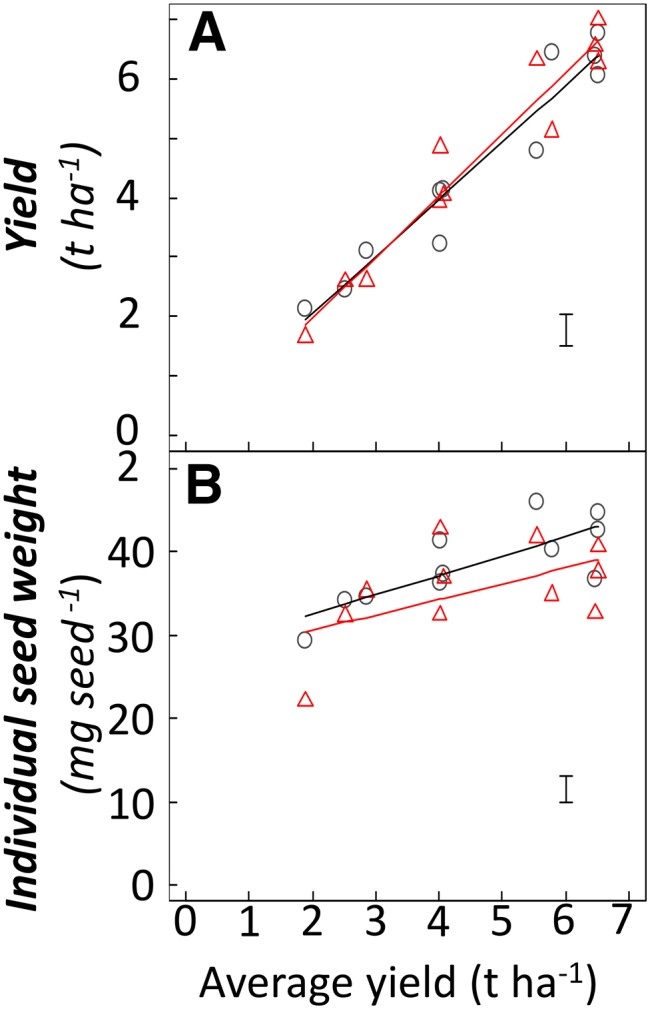
Yield and single seed weight of Gladius and Drysdale from 11 field trials. The relationship between variety values and the average yield for each trial is shown. Black circles, Gladius; red triangles, Drysdale. Straight lines are linear regressions for the considered variety. Error bars at the bottom right of each panel show mean sd for all lines-trial data.

When comparing the yield of Gladius and Drysdale with the average yield value in the treatment, the responses of the two lines were similar (Fig. 2A). However, under individual treatments, yield differences between Gladius and Drysdale could be as high as 1.6 t ha⁻¹. Individual seed weight for Gladius was, on average, higher than that for Drysdale, but with a similar relationship with the average yield of each treatment (Fig. 2B). The advantage of Gladius over Drysdale was above 5 mg seed⁻¹ in some treatments but was null in others. Similar G × E interactions were observed for other yield components and biological variables (data not shown).

This network of experiments allowed coverage of a large range of temperature and water conditions, resulting in large ranges of yield, yield components, and G × E interactions on yield and yield components.

Definitions of Independent and Quantitative Environmental Predictors

The analysis of the sensitivity of a biological variable to the environment required independent analysis for each quantitative environmental predictor. On a daily scale for the whole data set, the average temperature was highly correlated with the average vapor pressure deficit (Supplemental Fig. S2A), despite the large range of air humidity and the use of closed polytunnels increasing air humidity, which could have uncorrelated these environmental variables. Average temperature also was highly correlated with the maximum temperature and with the minimum temperature (Supplemental Fig. S2B), despite the use of the polytunnel increasing specifically day temperature. It was impossible to separate the respective effects of average temperature, average vapor pressure deficit, minimum temperature, and maximum temperature. Therefore, we decided to consider the average daily temperature as the only environmental variable related to temperature, knowing that the underlying effects could be due to any of the air variables listed above. Since any effect of the average daily temperature summarizes the effects of all air variables, and since all temperatures were above 3.8°C in all trials (Supplemental Fig. S1), the temperature variable has been called “Heat” hereafter. Conversely, average daily temperatures and soil water potentials were uncorrelated (Supplemental Fig. S2C). Soil water potential (hereafter named “Drought”) and “Heat” were considered as independent environmental predictors for analyzing the sensitivity of biological variables such as yield components.

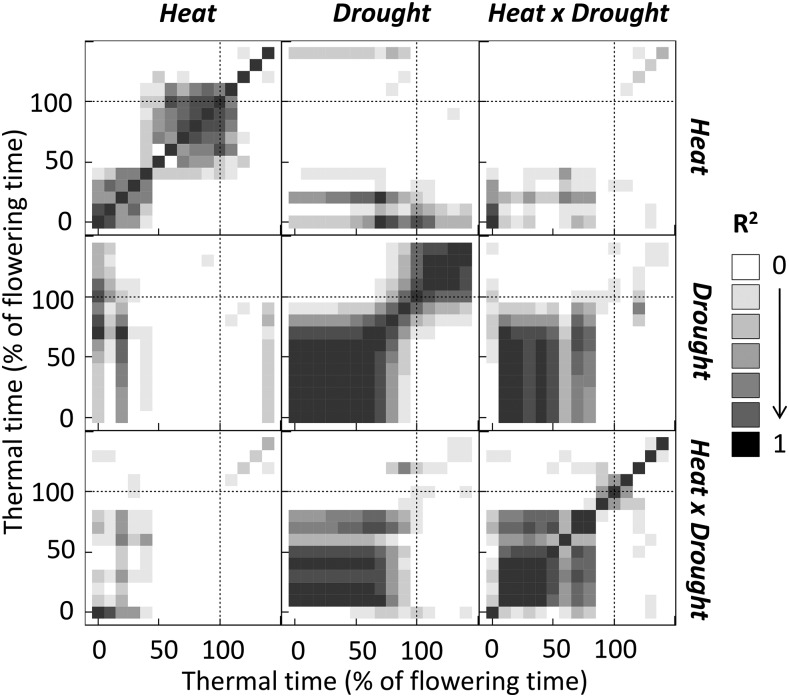
To analyze the sensitivity of biological variables to the environmental variables “Heat”, “Drought”, and their interaction, “Heat × Drought”, at several periods of the crop cycle, we first tested the independence of these environmental variables averaged at different periods of the crop cycle. Environmental variables were averaged over periods of 10% of the thermal time between sowing and flowering. The linear relationship between values in all treatments at each period and those in other periods was tested (Fig. 3) and compared with the coefficient of determination (R²) of the linear models. The “Heat” variable was poorly correlated with “Drought” or “Heat × drought” at any period, confirming the independence of “Heat” with “Drought” or “Heat × Drought” at any period of the crop cycle. A few correlations were found between the variable “Heat” at different periods (“Heat/Heat” correlations), but despite this, the “Heat” variable was able to strongly discriminate three main periods: from sowing to 50% of flowering time, from 50% to 110% of flowering time, and from 110% to 150% of flowering time. Strong correlations appeared between “Drought” variables at different periods (“Drought/“Drought” correlations), but the Drought” variable was still able to discriminate three periods: from sowing to 80% of flowering time, from 80% to 100% of flowering time, and from 100% to 150% of flowering time. During the vegetative period (from sowing to 80% of flowering time), the “Heat × Drought” variable was highly correlated to the Drought variable, but these two variables were not correlated for later periods of the crop cycle.

Figure 3.

Relationship between environmental variables (“Heat”, “Drought”, and their interaction) in 11 trials averaged in several periods of the crop cycle. Thermal time is expressed as percentage of flowering time of Gladius. Periods are 10% of flowering time long. Heat is the difference between the average temperature of each trial during the considered period and the average temperature during the same period for the coolest trial, “Drought” is the average soil water potential of the considered trial during the period, and “Heat × Drought” is the interaction. Each square displays a tested linear relationship between each environmental variable at each period and another environmental variable at another period. R² values are coefficients of determination of the linear relationship and vary from 0 (no relationship) to 1.

Overall, the combination of these three environmental variables allowed the discrimination of most periods of the crop cycle, either with only one variable or with the combination of any of the three variables “Heat”, “Drought”, and “Heat × Drought”.

Periods of Sensitivities to Drought and Heat Differ Largely among Yield Components

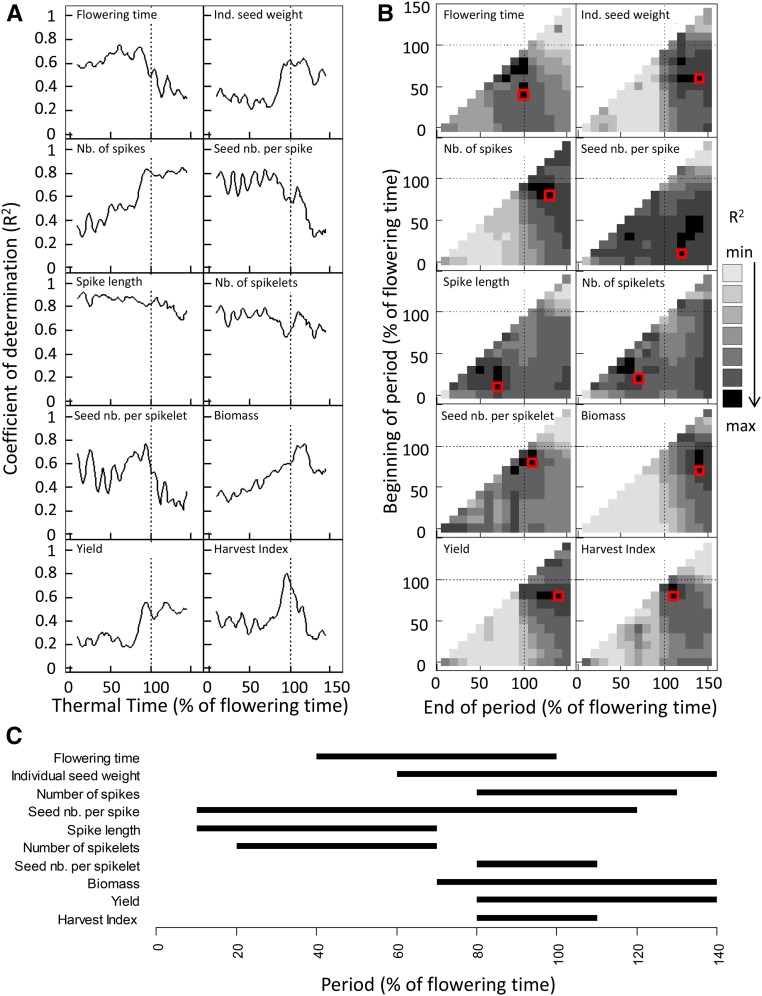
Using this framework, we identified sensitivity periods of each yield component to the averaged environmental conditions for the two lines Drysdale and Gladius measured in the 11 trials. The relationships between (1) each biological variable and (2) the environmental variables (“Heat”, “Drought”, and their interaction, “Heat × Drought”) averaged over different periods were tested with linear models and compared with the coefficient of determination of the linear model, R². In Figure 4A, environmental variables were averaged over periods of 5% of flowering time. For each biological variable (e.g. flowering time), the highest coefficient of determination at a given period indicated that the environmental variables averaged during this period were better predictors for estimating the biological variables than for other periods. For example, in Figure 4A, the flowering time expressed as thermal time was moderately correlated with environmental conditions occurring early in the crop cycle, then it was highly correlated with environmental conditions occurring up to flowering but showed only a poor correlation after flowering (as expected, environmental conditions occurring after flowering cannot affect flowering time). In Figure 4B, environmental variables were averaged over periods of any combination of start and end time with a window of 10% of flowering time. Periods were ranked from low coefficient of determination, when the averaged environmental variables in this period are poor predictors of the considered biological variable, to high coefficient of determination, when the averaged environmental variables during that period are good predictors of the considered biological variable. The best periods with the highest coefficient of determination for each biological variable are summarized in Figure 4C (or red squares in Fig. 4B). For example, the best predictors of the number of spikes were the environmental variables averaged from 80% to 130% of flowering time (Fig. 4, B and C).

Figure 4.

Relationship between 10 biological variables and environmental variables (“Heat”, “Drought”, and their interaction) averaged in several periods of the crop cycle. Time is expressed as developmental time (percentage of thermal time at flowering). Flowering time is expressed as thermal time (d_20°C). Heat is the difference between the average temperature of each trial during the considered period and the average temperature during the same period for the coolest trial, “Drought” is the average soil water tension of the considered trial during the period, and “Heat × Drought” is the interaction. The tested models are linear models linking each biological variable (e.g. flowering time and yield) and the predictors “Heat”, “Drought”, and “Heat × Drought” averaged during the considered period. R² values are coefficients of determination of the tested linear model. A, Coefficients of determination of linear relationships linking biological variables and the environmental variables averaged on several periods of 5% of flowering time across the crop cycle. B, Coefficients of determination of linear models linking plant variables and the environmental conditions averaged on periods defined by their beginning (y axis) and their end (x axis). Each square displays the R² for the considered period and the biological variable, from light gray (worst models with minimum R²) to black (best models with maximum R²). Best models are indicated by red squares and are summarized in C. C, Summary of the best models selected for each plant variable. Bars represent the development period for which the R² was maximum.

Depending on the nature of the biological variables, significant correlations with environmental conditions were found for different periods. As expected, variables related to spike development (number of spikelets per spike and spike length) were best explained by models considering environmental conditions before flowering (Fig. 4C). The number of seeds per spikelet was linked to environmental conditions around flowering. The period of sensitivity of the number of seeds per spike was large, covering periods of sensitivity of both components, number of spikelets per spike and number of seeds per spikelet. The number of spikes, biomass, yield, and single seed weight were mostly sensitive to the environment in a time window from just before flowering to after flowering.

An Increase of Temperature, Drought, or Both Constraints Affected Most Yield Components

For each of the 10 biological variables analyzed in this study, the model linking biological variables to “Heat”, “Drought”, and “Heat × Drought” environmental variables (averaged within the periods determined above) was tested together with all nested models using the Gladius and Drysdale data set over the 11 environments. The best model for each biological variable was selected with an F-test procedure (Table IA). For each model, the intercept value was the predicted value of the considered biological variable when the selected predictor “Drought”, “Heat”, or “Heat × Drought” equals zero (i.e. the maximum value in optimal conditions). For example, for yield, the intercept value of 6.1 t ha⁻¹, indicated in Table IA, can be observed graphically in Figure 5A as the model value for “Drought” = 0. For yield, the selected model considered only one predictor (“Drought”) with an effect of −9.1% (Table I, experiment A, expressed as percentage of the potential value for easier comparison of the effects; note that, for an easier comparison and being in the same order of magnitude as temperature effect, the “Drought” variable is expressed with the unit of 0.1 MPa). This value also can be observed graphically in Figure 5A as the slope of the relationship between yield and “Drought” (normalized by the intercept value).

Table I. Parameter values of the resulting linear models for the overall effects of three predictors (“Heat”, “Drought”, and their interaction, “Heat × Drought”) on 10 different biological variables, selected after the F test procedure described in “Materials and Methods”.

Empty cells indicate nonsignificant effects. The intercept value is the predicted value of the considered biological variable for drought = 0 and heat = 0. Values of predictors are the effects of “Heat”, “Drought”, or “Heat × Drought” on the tested biological variable. Significance of the intercept value is the P value of Student’s t test performed on each resulting model. Significance of the predictor is indicated by the P value of the ANOVA (***, P < 0.001; **, P < 0.01; and *, P < 0.05). For an easier comparison of values, the predictor effects in A are indicated as percentage of the intercept values. In B, C, and D, all values are percentage of average values in the considered data set. R² is the variance ratio explained by the model. A, Effects of environmental conditions on 10 variables in a data set with Gladius and Drysdale varieties in 11 treatments. B, Effects of environmental conditions on Drysdale advantage over Gladius. C, Effects of environmental conditions on the Drysdale allele at the marker wsnp_CAP11_c1902_1022590 for the 1B QTL. Differences between average values for lines carrying the Drysdale allele versus the Gladius allele are analyzed using seven different variables in 60 RILs and four trials in 2010. D, Effects of environmental conditions on the RAC875 allele at marker Xwmc236 for the 3B QTL. Differences between average values for lines carrying the RAC875 allele versus the Kukri allele were analyzed using seven different variables, 46 doubled haploid lines, and three trials in 2009.

	Variable	Unit	Intercept	Heat	Drought	Heat × Drought	R2
A	Flowering time	d20°C	57.17***		−3.7***		0.55
	Individual seed weight	mg seed−1	41.04***		−0.4**	−1.1**	0.56
	No. of spikes	plant−1	4.12***	1.8***	−8.1***		0.76
	Seed number per spike	spike−1	48.26***	−3.4***		−2.9**	0.69
	Spike length	mm	100.93***	−2.5*			0.20
	No. of spikelets	spike−1	19.88***	−2.3**			0.29
	Seed number per spikelet	spikelet−1	3.48***	−2.4***		−2.7*	0.67
	Biomass	g plant−1	14.38***		−12.1***		0.61
	Yield	t ha−1	6.31***		−9.1***		0.46
	Harvest index	%	51.78***			−0.5*	0.22
B	Flowering time	%	−3.2**				0.55
	Individual seed weight	%	−14.3**	0.4**	4.7*	−0.8**	0.56
	No. of spikes	%					0.76
	Seed number per spike	%	25.0***	−3.1**			0.69
	Spike length	%	27.0***	−2.8***			0.20
	No. of spikelets	%	11.5***				0.29
	Seed number per spikelet	%					0.67
	Biomass	%		−2.1*			0.61
	Yield	%	15.2*	−3.4**			0.46
	Harvest index	%	14.2***	−1.3**			0.22
C	Individual seed weight	%	−3.9*		−1.9*		0.05
	No. of spikes	%	4.3*				0.00
	Seed number per spike	%	−5.1*				0.00
	Spike length	%	−3.3**				0.00
	Biomass	%					0.00
	Yield	%					0.00
	Harvest index	%					0.00
D	Individual seed weight	%		15.0*	−4.3**		0.21
	No. of spikes	%					0.00
	Seed number per spike	%	−5.9**		−19.4**	37.1***	0.39
	Spike length	%	−5.5***				0.00
	Biomass	%	−17.3***	11.9**			0.15
	Yield	%	−10.9***				0.00
	Harvest index	%	−17.2***	7.5**			0.16

Figure 5.

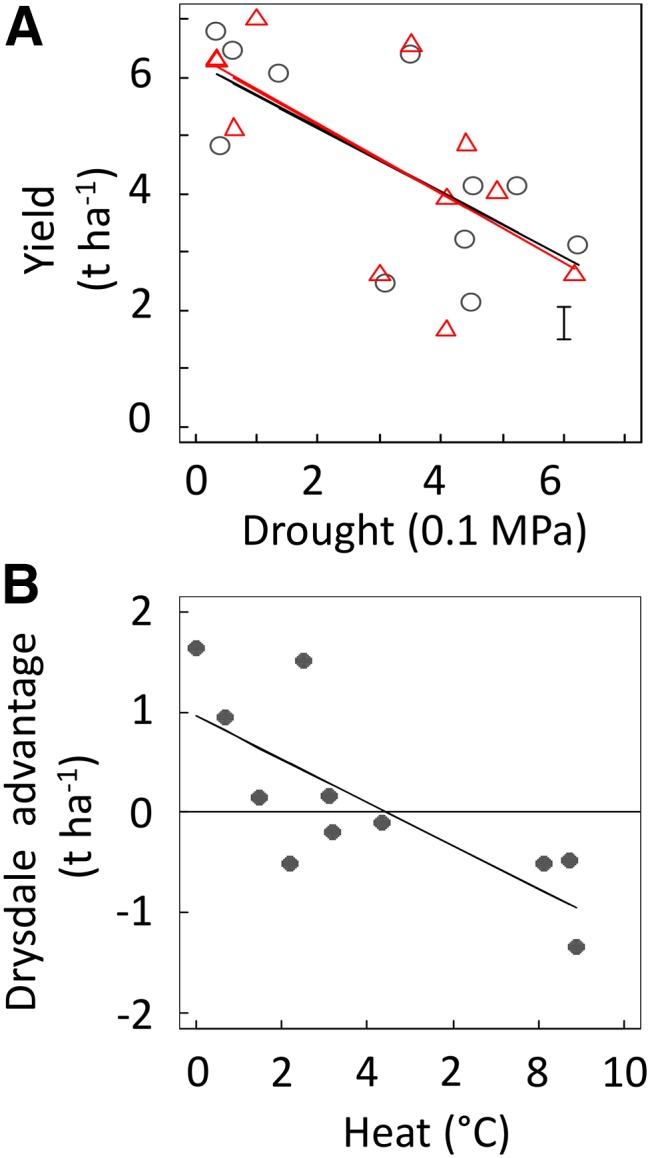
Relationship between yield and environmental variables in Gladius and Drysdale in the field trials. “Drought” and “Heat” are, respectively, the difference in soil water potential and air temperature between the value of the considered trial and the lowest values. A, Relationship between yield and the variable drought in Gladius (black circles) and Drysdale (red triangles). Straight lines are linear regressions for the considered variety. Error bars at the bottom right of each panel show mean sd for all variety-trial combinations. B, Yield advantage of Drysdale over Gladius in each trial and across the variable heat. The line is the linear regression.

Different patterns were observed for the 10 biological variables. As expected, flowering time was only significantly linked to “Drought”, indicating no “Heat” effect when time is expressed as thermal time but faster flowering under drought. Variables related to spike development were correlated significantly with heat, with slopes of −2.3% °C⁻¹ for number of spikelets per spike and −2.5% °C⁻¹ for spike length (Table IA). Variables related to seed set (seed number per spikelet and seed number per spike) were correlated significantly with “Heat” and “Heat × Drought” (−2.4% and −3.4% °C⁻¹ and −2.7 and −2.9% °C⁻¹ 0.1 MPa⁻¹, respectively). Number of spikes was correlated significantly to heat and drought, with a positive value for the “Heat” effect. Single seed weight was correlated to Drought and “Heat × Drought”. Biomass and yield were significantly related to “Drought” only, with respective effects of −12.1 and −9.1% 0.1 MPa⁻¹ (Table IA). Overall, any increase of temperature, soil water deficit, or a combination of both during the period of sensitivity was detrimental to yield components, except number of spikes per plant, which increased with temperature.

The Quantitative Description of Environment Allowed a Better Understanding of G × E Interactions

The overall response of wheat lines to environmental variables was not sufficient to understand the G × E interactions occurring in this network (Fig. 2). For instance, the yield response to “Drought” was similar in Gladius and Drysdale (Fig. 5A), but with large quantitative differences depending on the treatment. Another run of F-test model comparison was performed to find which model was best in linking differences between Gladius and Drysdale values and environmental conditions (Table IB).

The intercept was significant in seven of the 10 tested biological variables, indicating significant differences between Gladius and Drysdale when the selected predictors (“Heat”, “Drought”, or “Heat × Drought”) equal zero (Table IB). In optimal conditions, Drysdale had smaller seeds (−14%) but overall larger spikes, more seeds per spike, and larger biomass or yield (+15.2%; Table I, experiment B, which also can be observed graphically as the value for “Heat” = 0 in Fig. 5B). With rising temperature, Drysdale maintained less of its yield (−3.4% °C⁻¹) and most yield components compared with Gladius. This resulted in Gladius yield overtaking that of Drysdale with a temperature rise of about 4°C (Fig. 5B). Overall, Drysdale performed better than Gladius under cool environments, even under water deficit, while Gladius yielded more than Drysdale under high temperature, especially when both stresses occurred.

Dissecting the QTL × E Interactions Observed Previously for Two Major QTLs

The analysis described above was applied to lines of two different mapping populations cultivated in the same environments in 2009 and 2010 and for which strong QTLs were identified previously. The first data set comprised 60 Drysdale/Gladius RILs cultivated in four environments in 2010 and segregating for a spike number QTL identified previously on chromosome 1B (marker wsnp_CAP11_c1902_1022590; Parent et al., 2015). This locus collocated with a QTL for growth that was identified in a phenotyping platform and seemed to be constitutive, with the Drysdale allele being advantageous under well-watered conditions and drought in cool environments (Parent et al., 2015). In this population, significant differences between lines carrying the Gladius versus Drysdale allele were found for four yield components: single seed weight, spike number, seed number per spike, and spike length (Table IC; a positive value indicates an advantage of the Drysdale allele, while a negative value indicates an advantage of the Gladius allele). These differences were mostly constitutive: only the intercept was significant, meaning that there was no effect of the environment except for single seed weight, where drought was significant. A constitutively higher spike number in lines with the Drysdale allele was confirmed (+4.3%; Table IC). However, this effect was counterbalanced by a significantly smaller number of seeds per spike (−5.1%) and smaller seeds (−3.9%), resulting in no effect of the QTL allele on yield. Overall, this analysis confirmed the positive constitutive effect of the Drysdale allele at this QTL on number of spikes and explained the null effect on yield observed by Parent et al. (2015) due to the tradeoff between the number of spikes, the number of seeds per spike, and seed weight.

The second data set included 48 lines of the RAC875 × Kukri double haploid population cultivated in the three environments of 2009 and for which a QTL for yield and thousand kernel weight had been observed on chromosome 3B (marker Xwmc236; Bennett et al., 2012a, 2012b; Bonneau et al., 2013). This QTL was highly dependent on the environment, but no clear relationship had been observed with quantitative environmental variables. The 2009 data set showed a negative intercept for all yield components when selected predictors equaled zero (Table ID), meaning that the RAC875 allele gave a constitutive disadvantage under optimal conditions. A strong constitutive effect of this QTL was observed on yield, with an effect of −10.9% for lines with the RAC875 allele compared with lines with the Kukri allele, regardless of environmental conditions (Table ID; no environmental predictor was selected). Lines with the RAC875 allele showed significantly less individual seed weight and seed number per spike under drought in cool environments (Table ID). However, in these lines, the weight of individual seeds for lines with the RAC875 allele was significantly less sensitive to increasing air temperature, and the seed number per spike was more sensitive to a combination of high temperature and drought. Overall, this QTL displayed a strong constitutive effect, with an advantage for lines with the Kukri allele, but a strong interaction with soil and heat conditions resulting in an advantage for lines with the RAC875 allele, with increasing air temperature or a combination of high temperature and drought.

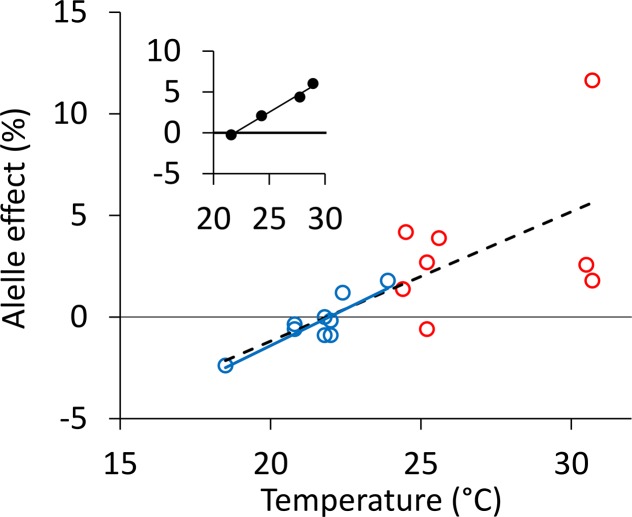
This new insight into the QTL × E interactions first observed by Bennett et al. (2012a, 2012b) and Bonneau et al. (2013) allowed a reanalysis of these previous data. This data set comprised yield records in 18 trials in Australia and Mexico with the RAC875 × Kukri doubled haploid population. Precise soil water conditions were not available, but temperature was recorded in all trials. The period of sensitivity of yield to environmental conditions determined in this study was around flowering, and we used the temperature average around flowering calculated by Bonneau et al. (2013). The lower sensitivity of yield components to temperature in lines carrying the RAC875 allele observed in this study also was observed for yield (Fig. 6). The correlation between temperature around flowering and the allele effect on yield was highly significant in Australian sites and for the whole data set. It was also highly significant when considering groups of trials obtained with a multienvironment correlation analysis performed by Bonneau et al. (2013; Fig. 6, inset).

Figure 6.

Correlation between temperature around flowering time and allele effect at simple sequence repeat marker Xwmc236 located on chromosome 3B in the RAC875 × Kukri doubled haploid population analyzed previously by Bennett et al. (2012a, 2012b) and Bonneau et al. (2013). The allele effect is expressed as percentage relative to mean yield. A positive effect indicates that the RAC875 allele increased yield. Temperatures are mean temperature values in September in Australia and February in Mexico (from Table 1 in Bonneau et al., 2013). Allele effects come from Figure 4 in Bonneau et al. (2013). Each dot represents one trial. The blue dots and lines are 10 trials carried out in Australia with a correlation of R² = 0.74 and P < 10⁻³. The red dots are eight trials carried out in Mexico with a nonsignificant correlation. The dashed line displays the correlation for the whole data set (R² = 0.52, P < 10⁻³). The three trials of 2009 in the polytunnel platform analyzed in Table I, experiment D, are not presented here. The inset shows the correlation between average temperature around flowering time (x axis) and the average allele effect (y axis) in the four groups selected based on multienvironment correlation analysis by Bonneau et al. (2013). The group comprising the three trials in the polytunnel platform and analyzed in Table I, experiment D, is not presented here. Each dot is one group, and the line is the linear correlation (R² = 0.99, P < 10⁻²).

DISCUSSION

Relevance of the Periods of Sensitivities Calculated in the Field

The analysis process used in this study determined periods of heat and drought sensitivity for several yield components. Rather than using conventional time (Tashiro and Wardlaw, 1990; Ferris et al., 1998; Shah and Paulsen, 2003), we used percentage of flowering time expressed as thermal time to allow the periods to be linked to physiological plant stages, even for genotypes with contrasting phenology (Chenu et al., 2013; Harrison et al., 2014; Millet et al., 2016). By contrast with conventional indicators used in the field, such as thresholds of temperature or drought (Kuchel et al., 2007) or average yield at a site (Fleury et al., 2010), these periods of sensitivity together with the precise monitoring of environmental conditions allowed definition of the environmental conditions as quantitative variables.

These periods of sensitivity varied depending on the yield component studied. Traits related to spike development (spike length and number of spikelets) were sensitive to environmental conditions at early developmental stages, which corresponded to the whole period of spike development (Vahamidis et al., 2014). In our study, seed number per spikelet was very sensitive during a short period around flowering, suggesting that the main processes affected by environmental conditions were related to seed abortion due to either male or female sterility during gametocyte development (Saini and Aspinall, 1982; Saini et al., 1984), pollination (Ferris et al., 1998), or carbon competition at an early stage of grain filling. Seed number per spikelet was less sensitive to early environmental conditions, which could have affected floret development (Saini and Aspinall, 1982). As expected, the sensitivity period of seed number per spike overlapped with the sensitivity periods of spikelet number per spike and seed number per spikelet. Individual seed weight was sensitive during a period from before flowering to 140% of flowering time corresponding to maturity. This result matched with Calderini et al. (1999, 2001), who demonstrated that the period when the carpels (which will become the external structures of the grain) grow determines the final individual grain weight. The number of spikes was sensitive during a late period from 80% to 130% of flowering time, suggesting that the most sensitive process was probably not tillering itself, which occurs earlier, but rather tiller abortion around flowering.

As yield is the integration of the different components cited above, it is sensitive over a long period from just before flowering to the end of grain filling. It does not mean that an early water deficit or heat stress has no impact on yield but that later periods can explain better a change in yield or biomass. This can be due to the range of environmental conditions that are less stressing during the vegetative period, even if the temperature ranges tested here cover most of what can be observed in natural conditions. This result indicates that the limiting factor for yield under drought and heat was grain weight rather than the number of grains.

The framework used in this study is novel in several ways. Most physiological or genetic studies use conventional time for measuring periods of sensitivity (Ferris et al., 1998; Shah and Paulsen, 2003). Recently, Millet et al. (2016) used thermal time centered on anthesis date for QTL detection in maize (Zea mays) for specific responses to four drought scenarios and three temperature scenarios (Chenu et al., 2013; Harrison et al., 2014). However, the environment was either still considered as a qualitative factor or analyzed in a quantitative way but only centered on anthesis. To our knowledge, our study is the first one that quantified the environment and plant responses to it during precise periods of the crop cycle.

The periods of sensitivity calculated here are dependent on the model used and reflect the environmental scenarios of the analysis. We have chosen a blind approach, with a common model for all biological variables, and the simplest model (i.e. linear). This should not be a major concern for studying drought, which has negative effects on any biological variable at some stage. On the contrary, because high and low temperatures have deleterious effects, linear models would have been a wrong choice if frost had occurred, but in our experiments, temperature did not fall below 3.8°C. This raises the question of extrapolation of these results to other environmental scenarios. For example, a scenario with a strong heat shock at an early stage may have resulted in a very early and short period of sensitivity for yield. The range of conditions tested here was realistic, and the use of a semicontrolled facility to create variations in temperature and drought covered most of the environmental scenarios found in the Australian wheat belt (Chenu et al., 2013) with only 11 trials. By comparison, the study of Millet et al. (2016), with 29 maize trials in Europe, did not cover a wider range of temperature and water deficit. Overall, the periods of sensitivity described here were consistent with results from the literature and could be extended to other environments, except perhaps in the case of frost and very unusual early heat stress.

Quantitative Responses of Yield Components to Temperature and Water Deficit in the Field

With this framework, all yield components measured in this study were affected by drought, temperature, or their interaction. The response to temperature was analyzed using the coolest condition as a baseline. The coolest environment (LT.MD.10 or LT.WW.10), defined as a control, is realistic because of the normal sowing date in 2010 and the fact that 2010 was one of coolest winters in Australian history due to La Niña weather cycle (2010-2011), which was one of the strongest on record (Australia Bureau of Meteorology). Ranges of environmental conditions during periods of sensitivity varied between traits but were realistic representations of field conditions. Traits with very early sensitive periods (spike length and number of spikelets) were not sensitive to drought in this study, probably because the water deficit was small at this stage, as is mostly the case in natural wheat field conditions in Australia (Chenu et al., 2013).

The number of spikes per plant was the only trait positively correlated with temperature or drought. Previous studies showed that high, but not extreme, temperatures (less than 35°C; Owen, 1971a) increased tiller number and spike number (Owen, 1971b). Spike length and the number of spikelets per spike were similarly affected by temperature (about −2.5% °C⁻¹). Seed number per spikelet and seed number per spike were both affected by temperature and by the interaction between temperature and drought. The calculated sensitivities were consistent: the seed number per spike was more sensitive than the seed number per spikelet because it integrates both effects on spikelet number and seed number per spikelet. In addition, the sensitivity of the number of seeds per spike to temperature (−3.4% °C⁻¹) is close to the value found in the literature (−4% °C⁻¹ during the 30 d preceding anthesis; Fischer, 1985). Surprisingly, individual seed weight was the least sensitive yield component to both drought and combined drought and heat stresses. This contrasted with some results from experiments under controlled conditions, in which heat and/or drought events had a strong effect on individual grain size (Wardlaw et al., 1989a, 1989b; Savin and Nicolas, 1996; Wardlaw, 2002; Shah and Paulsen, 2003). In this study, the range of maximum temperature was as large as 31°C to 46.7°C during grain filling, so our result cannot be due to a low range of environmental conditions. One possibility is that the two tested genotypes, Gladius and Drysdale, are at the extreme of the genetic variability for heat tolerance observed by Wardlaw et al. (1989b). Another possibility is that, under naturally fluctuating temperature, wheat plants had time to acclimate, especially photosynthesis (Yamasaki et al., 2002), which was not the case when imposing heat shocks under controlled conditions. The last possibility is that, in the driest and warmest treatments, grain number per spike was already decreased due to the environment, and this conferred an advantage on carbon mobilization per grain. This tradeoff was not observed in experiments in controlled environments where heat events happened on a stable grain set.

The sensitivity of final biomass to drought (−12.1% 0.1 MPa⁻¹) was stronger than for any other trait but was consistent with the results found recently for growth rate on the same lines in controlled conditions using an imaging platform (−10.59% 0.1 MPa⁻¹; Parent et al., 2015). Surprisingly, we found no significant effect of temperature on yield, although most yield components were affected. Yield is a highly integrated trait; therefore, yield sensitivity is the most complex response resulting from the combination of the sensitivity of all underlying components, even those that did not appear significant in this study. Overall, the detailed analysis of underlying components allowed a better understanding of yield responses to drought and heat.

Constitutive and Responsive Components of G × E and QTL × E Interactions

Gladius and Drysdale were known to have similar levels of tolerance to abiotic constraints with comparable yield (Fleury et al., 2010). Drysdale is known as a transpiration-efficient variety (Condon et al., 2006), while Gladius is known to maintain yield and, particularly, grain plumpness under drought. Here, we first confirmed that, when considering an overall response of yield with the average site yield by merging data sets from trials in cool, warm, well-watered, and dry environments, their behaviors were similar. However, when the results were examined in detail, large differences were shown, with either an advantage for Gladius or Drysdale, depending on site and year of growth. We found that, under optimal conditions (which rarely exist in Australian fields), Drysdale had a constitutive advantage for most yield components (except the individual seed weight), resulting in a large yield advantage of about 15%. This was not observed in the low-yielding environments where these two lines were bred (Fleury et al., 2010). Conversely, Gladius was more tolerant to an increase of temperature or to a combination of high temperature and drought for most traits in which we detected a genotype × heat interaction. To our knowledge, these line-specific effects in different G × E interactions have not been described previously.

Our results could be explained by a lower transpiration rate in Drysdale, bred for high transpiration efficiency. A lower transpiration rate is useful for saving ground water, which can be used at later stages of the crop cycle (Tardieu, 2012), but can be disadvantageous in situations where the crop is exposed to high temperatures. Indeed, a low transpiration rate would increase plant temperature and increase the sensitivity of yield components to heat or a combination of heat and drought. This could explain why Gladius was more tolerant to high temperature than Drysdale, as revealed by the G × E interactions. Such a tradeoff between transpiration efficiency and other important traits for yield have been reported previously, as has the tradeoff between early vigor and transpiration efficiency, indicating the necessity of coselection of these traits in breeding programs (Wilson et al., 2015). For future climatic conditions, with higher CO₂ concentrations, high transpiration efficiency could become more often a disadvantage, because of the increased transpiration efficiency with CO₂ and resulting heat stresses (Lobell et al., 2015).

Most QTLs for drought and heat tolerance in crops showed significant QTL × E interactions. Such interactions were observed in extensive studies under the Mediterranean climate using different locations in Australia, Mexico, southern Europe, and the Middle East and several years covering a range of soil moisture and temperatures (McIntyre et al., 2010; Pinto et al., 2010; Bennett et al., 2012a, 2012b; Graziani et al., 2014; Maphosa et al., 2014). Although the environmental conditions were monitored, the analytical methods did not enable the researchers to specifically measure the effects of soil moisture or temperature on QTL. The best attempt to understand G × E consisted of grouping the environments based on genetic correlation on yield (Dreccer et al., 2008) or environmental parameters (Bouffier et al., 2015) and then trying to find a pattern of QTL significance across the clustered environments (Bennett et al., 2012b; Bonneau et al., 2013). The method developed here enabled us to measure the quantitative effect of drought, for each 1-MPa decrease in soil water potential, and heat, for each 1°C increase, on two wheat QTLs.

The chromosome 1B QTL associated with growth rate in an imaging platform and tillering in the field was confirmed in this study. Only one interaction with environmental conditions was significant among the seven tested traits, for single seed weight × drought. We found significant constitutive differences between the Drysdale allele and the Gladius allele. The number of spikes was significantly higher in lines with the Drysdale allele, confirming our previous results (Parent et al., 2015). However, the number of seeds per spike and the individual seed weight were significantly lower in these lines compared with those carrying the Gladius allele, resulting in no significant difference for biomass or yield. The strong tradeoff between yield components explained why this QTL had no effect on yield in previous studies on this population (Maphosa et al., 2014; Parent et al., 2015).

The QTL × E interaction of the chromosome 3B QTL that was observed in previous studies on the RAC875/Kukri population (Bennett et al., 2012a, 2012b; Bonneau et al., 2013) was partly explained in this analysis. First, the Kukri allele conferred an advantage on seed number per spike, biomass, and yield in the absence of stress. For the two yield components displaying a significant QTL × drought interaction (individual seed weight and seed number per spike), the Kukri allele conferred an advantage with drying soil. On the other hand, for the three traits displaying a QTL × heat or QTL × heat × drought interaction, the positive allele was RAC875. The reanalysis of data from Bennett et al. (2012a, 2012b) and Bonneau et al. (2013) confirmed an advantage for lines with the Kukri allele in cool environments and a rising advantage for lines with the RAC875 allele under warmer conditions, above 25°C (Fig. 6). In other words, the Kukri allele at this locus conferred an advantage under optimal conditions and under drought in cool environments, while the RAC875 allele conferred a positive advantage under warm conditions and under a combination of drought and heat.

Overall, this study enabled us to disentangle the high QTL × E interactions observed for the 3B QTL by separating its constitutive component and its QTL × drought and QTL × heat components. Further ecophysiological studies are needed to determine the mechanisms underlying a constitutive advantage coupled with a positive effect under drought and a negative effect of temperature or temperature × drought. A strong hypothesis, compatible with the 3B QTL effect on canopy temperature observed by Bennett et al. (2012a, 2012b), would be a negative effect of the Kukri allele on transpiration. A low transpiration would confer an advantage under drought, saving water for later stages of the crop cycle, but it would increase plant temperature under high temperature, resulting in strong negative effects on yield components (Ayeneh et al., 2002).

The genetic populations studied here are not fixed for the rest of the genome, and other QTLs may have a confounding effect and dilute the effects of the 1B and 3B QTLs. Nevertheless, we could observe significant effects of each QTL in this material. Development of near isogenic lines and positional cloning of the 1B and 3B QTLs will enable us to confirm these effects and understand the physiological mechanisms underpinning them.

CONCLUSION

This framework, coupled with detailed monitoring of environmental conditions, could be used for analyzing any G × E or QTL × E interactions observed in trials under drought or temperature constraints. It is a first step in determining the mechanisms underlying such interactions. Controlled conditions could then be used for precise phenotyping of these underlying components. Such analyses also could be useful to breeders. With a changing climate and probable shift from drought to heat (Lobell et al., 2015), alleles such as the RAC875 allele at the 3B QTL conferring advantages as temperatures rise would be of high interest for breeding programs for heat-tolerant wheat selection.

MATERIALS AND METHODS

Genetic Material

Drysdale and Gladius are two modern bread wheat (Triticum aestivum) lines adapted to southern Australia conditions and subject to cyclic drought and heat events in spring in a Mediterranean type of climate. Gladius and Drysdale show 2% to 30% higher yield compared with other varieties in these environments but show different mechanisms of response to drought (Fleury et al., 2010). Their pedigrees are RAC875/Krichauff//Excalibur/Kukri/3/RAC875/Krichauff/4/RAC875//Excalibur/Kukri and Hartog × 3/Quarrion, respectively. Gladius has been selected for yield under severe drought in South Australia. Drysdale has been selected for high carbon isotope discrimination, a proxy of water use efficiency (Rebetzke et al., 2002; Condon et al., 2006).

In 2009, a subset of 46 doubled haploid lines derived from a cross between RAC875 and Kukri was grown in three environments (Supplemental Fig. S1). These lines segregated for a yield QTL on chromosome 3B found previously by Bennett et al. (2012a, 2012b) and analyzed by Bonneau et al. (2013). Among the 48 lines, 26 lines carried the RAC875 allele and 20 lines carried the Kukri allele at the Xwmc236 marker (Bonneau et al., 2013).

In 2010, a subset of 60 lines from a large Drysdale/Gladius RIL population of 5,000 lines was grown in four environments (Supplemental Fig. S1). These lines were chosen as they flowered in a narrow range of flowering time (6-d window) in a previous experiment on 250 lines. In two of these four treatments, the 250 lines were grown and analyzed by Maphosa et al. (2014) and Parent et al. (2015). The 60 Drysdale/Gladius RILs segregated for the 1B QTL, with 33 RILs carrying the Drysdale allele and 27 RILs carrying the Gladius allele at the single-nucleotide polymorphism (SNP) wsnp_CAP11_c1902_1022590 (Parent et al., 2015).

Field Trials and Growth Conditions

Eleven field trials were carried out in 2009, 2010, and 2011 under semicontrolled field conditions in the polytunnel facility of the University of Adelaide (Urrbrae, South Australia, Australia, 35° S/139° E; Supplemental Fig. S1). This facility includes bird nets and polyurethane tunnels equipped with automatic watering systems (drippers) and weather stations (MEA) recording air temperature and humidity at the plant canopy level, soil temperature, and wind. Gypsum blocks (MEA) were used to measure soil water potential at three different soil depths (15, 30, and 40 cm from soil surface; eight sensors per watering regime). All climatic data were averaged and stored every 10 min in a data logger (MEA).

A summary of growth conditions, cultivated genotypes, and protocols is available in Supplemental Figure S1 and Supplemental Table S1. Briefly, plants were grown in microplots of 16 to 32 plants at a density of 133 plants m⁻². To prevent any border effect, no gap was left between microplots and rows of Gladius were planted around plots. Three different sowing dates were used, late (2009), normal (2010), and intermediate (2011), in order to get contrasting temperature scenarios (Supplemental Table S1). Watering amount and frequency with drippers depended on the desired drought scenarios. The top 15 cm of soil was mixed before sowing, and urea (Manutec) was added to the topsoil (N rate 225 kg ha⁻¹, measured with a graduated tube for each individual microplot) in 2010 and 2011. Plants were fertilized (Aquasol; Hortico) twice in all treatments, at stem elongation stage and at flowering stage. A fungicide (Bayfidan; Bayer Australia) was applied around flowering stage. Ranges of environmental conditions are summarized in Supplemental Table S1. Time courses of temperatures and soil water potential are displayed in Figure 1.

Plant Measurements

Flowering time was scored every day from the first spike and for six spikes flowering on one third of the spike length. Flowering time was later transformed as thermal time after sowing (see below). At harvest, all tillers were harvested manually, and the number of spikes per plant was counted. The main spike of three plants per plot was harvested separately for Gladius and Drysdale varieties. After drying (10% moisture content), total grain weight and total aboveground plant weight (biomass; g) were measured and calculated per plant. A sample of 100 mL of seed was weighed, and seeds were counted with a seed counter (Pfueffer) to estimate single seed weight (g) and total seed number per spike. Grain weight per plot was converted to yield (t ha⁻¹) for an easier comparison with other studies. Harvest index was calculated as the ratio of grain weight to biomass. For the individual main spikes harvested in Gladius and Drysdale, spike length, number of spikelets, and number of seeds were scored. Seed number per spikelet was determined by dividing the number of seeds by the number of spikelets.

Thermal and Developmental Compensations of Time

Thermal time (t_20°C) was calculated as described by Parent and Tardieu (2012) from time t at temperature T. t_20°C is expressed as equivalent day at 20°C (d_20°C) and calculated with air temperature measured at the time step of 10 min. This calculation allows comparisons of durations of trials experiencing very different thermal scenarios. The unit (d_20°C) expresses each measured time by the duration if temperature was stable at 20°C. Because the high measured temperatures were far from optimal ones, a simple linear model would have predicted a very fast development rate, far from observed data (Parent and Tardieu, 2012). For an easier comparison with other data sets, flowering time expressed in d_20°C for Gladius in each trial has been transformed to growing degree day with a threshold temperature of 0°C (Supplemental Fig. S1).

Since flowering time and all developmental stages vary between lines, thermal time was transformed into developmental time, defined as the percentage of thermal time elapsed from sowing compared with thermal time at flowering of the considered line.

Quantitative Environmental Variables

Temperature and soil water potential measured at a 10-min time step were averaged for each treatment, and any considered period was defined as percentage of flowering time.

For temperature, the variable “Heat” was defined as the difference between each average temperature (T) during the considered period and the minimum average temperature T_min. An effect of “Heat” on any plant variable, therefore, is the effect of an increase of 1°C compared with the coolest condition.

“Drought” was calculated as the opposite of soil water potential and expressed in bar (0.1 MPa) in order to keep an intuitive range of water deficit measured in the treatments. An effect of “Drought” on any plant variable, therefore, is the effect of an increase of 0.1 MPa (1 bar) compared with a well-watered condition.

“Heat × Drought” was calculated as the interaction of “Heat” and “Drought”, the product of “Heat” by “Drought”. An effect of “Heat × Drought” on any plant variable, therefore, is the effect of an increase of 0.1 MPa °C⁻¹ compared with the coolest well-watered condition.

Data Analyses

All analyses used R software (R Development Core Team, 2014). All linear models were fitted with the lm() function of the R package and ANOVA with the anova() function.

Relationships between Environmental Conditions in All Periods

Crop cycle was divided into 15 periods of 10% of flowering time of Gladius (0% corresponding to sowing, 100% corresponding to flowering, and 150% corresponding to maturity). In each period and in 11 environments, the three environmental variables (heat, drought, and heat × drought) were calculated. The correlation (R²) between each of the three environmental variables at any period was tested with each of the three environmental variables and for each period (1,688 correlations in total).

Relationships between Environmental Conditions and Biological Traits

Crop cycle was divided into 145 periods of 5% of flowering time (from 0% to 145% of flowering time and 5% long). Here again, 0% corresponds to sowing, 100% corresponds to flowering, and 150% corresponds to maturity. For each period, treatment, and line (Gladius and Drysdale), the three environmental variables (heat, drought, and heat × drought) were calculated. For each period and biological trait, the relationship between the considered trait and the environmental conditions of the considered period was analyzed with a linear model (1,305 models in total).

The relationships between biological traits and environmental conditions were compared with the coefficient of determination of these models.

A similar analysis was performed with all possible periods with a definition of 10% of flowering time (any possible combination of starting and ending of the period, with a total of 113 periods). For each period, treatment, and line (Gladius and Drysdale), the three environmental variables (“Heat”, “Drought”, and “Heat × Drought”) were calculated. For each period and biological trait, the relationship between the considered trait and the environmental conditions of the considered period was analyzed with model 1 (1,013 models in total). The relationships between biological traits and environmental conditions were compared with the coefficient of determination. For each biological trait, the period of sensitivity has been defined as the period corresponding to the model with the highest coefficient of determination.

Overall Effects of Environmental Conditions on Two Genotypes

For each biological variable, treatment, and line (Gladius and Drysdale), the three environmental variables (“Heat”, “Drought”, and “Heat × Drought”) were calculated for the period of sensitivity of the considered trait. The linear model linking the biological variables to the three environmental variables (model 2) was fitted as:

With the intercept being the trait value for “Heat” = 0 and “Drought” = 0. This model was compared with all nested models with an intercept. The selected model was the model with significant components and the highest coefficient of determination.

Effects of Environmental Conditions on Drysdale over Gladius

For each biological variable and treatment, the three environmental variables (“Heat”, “Drought”, and “Heat × Drought”) were calculated for the period of sensitivity (using the average flowering time of the two lines) of the considered trait. The Drysdale advantage was calculated as the difference between Gladius and Drysdale values in each treatment. The linear model linking the Drysdale advantage for the considered trait to the three environmental variables (model 3) was fitted as:

This model was compared with all nested models with an intercept. The selected model was the model with significant components and the highest coefficient of determination.

Effects of Environmental Conditions on Allele Advantage at Specific QTLs

Similar analyses were performed in the two populations described above. In the Gladius/Drysdale population, we tested the advantage of the Drysdale allele compared with the Gladius allele at the marker wsnp_CAP11_c1902_1022590 for the chromosome 1B QTL. In the RAC875/Kukri population, we tested the advantage of the RAC875 allele compared with the Kukri allele at the simple sequence repeat (SSR) marker Xwmc236 for the chromosome 3B QTL.

For each biological variable and treatment, the three environmental variables (“Heat”, “Drought”, and “Heat × Drought”) were calculated for the period of sensitivity (using the average flowering time of the population) of the considered trait. The allele advantage was calculated as the difference between average values for each allele. The linear model linking the allele advantage for the considered trait to the three environmental variables (model 4) was fitted as:

This model was compared with all nested models with an intercept. The selected model was the model with significant components and the best coefficient of determination.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Summary of the 11 trials analyzed in this study and photograph of the facility allowing semicontrol of water deficit and high temperature in natural soil conditions.

• Supplemental Figure S2. Correlation between environmental variables in the 11 field trials.

Glossary

QTL

quantitative trait locus

RIL

recombinant inbred line