Using Machine Learning to Predict Radiation Pneumonitis in Patients with Stage I Non-Small Cell Lung Cancer Treated with Stereotactic Body Radiation Therapy

Abstract

Purpose/Objectives

To develop a patient-specific “big data” clinical decision tool to predict pneumonitis in Stage I non-small cell lung cancer (NSCLC) patients after stereotactic body radiation therapy (SBRT).

Materials/Methods

61 features were recorded for 201 consecutive patients with Stage I NSCLC treated with SBRT, in whom 8 (4.0%) developed radiation pneumonitis (RP). Pneumonitis thresholds were found for each feature individually using decision stumps. The performance of three different algorithms (Decision Trees, Random Forests, RUSBoost) was evaluated. Learning curves were developed and the training error analyzed and compared to the testing error in order to evaluate the factors needed to obtain a cross-validated error smaller than 0.1. These included the addition of new features, increasing the complexity of the algorithm and enlarging the sample size and number of events.

Results

In the univariate analysis, the most important feature selected was the diffusion capacity of the lung for carbon monoxide (DLCO adj%). On multivariate analysis, the three most important features selected were the dose to 15 cc of the heart, dose to 4 cc of the trachea or bronchus, and race. Higher accuracy could be achieved if the RUSBoost algorithm was used with regularization. To predict radiation pneumonitis within an error smaller than 10%, we estimate that a sample size of 800 patients is required.

Conclusion

Clinically relevant thresholds that put patients at risk of developing radiation pneumonitis were determined in a cohort of 201 stage I NSCLC patients treated with SBRT. The consistency of these thresholds can provide radiation oncologists with an estimate of their reliability and may inform treatment planning and patient counseling. The accuracy of the classification is limited by the number of patients in the study and not by the features gathered or the complexity of the algorithm.

1. Introduction

Thoracic malignancies are among the most common and deadly cancers worldwide and account for approximately 27% of all cancer deaths in the United States^{1, 2}. Non-small cell lung cancer (NSCLC) accounts for over 85% of all new cases diagnosed, of which approximately 15% are diagnosed with localized disease. These patients are typically treated with surgery or stereotactic body radiation therapy (SBRT), also termed stereotactic ablative radiotherapy (SABR)^1–5. Radiation induced pneumonitis (RP) remains the most important dose limiting side effect for these patients and the ability to predict RP is of paramount importance. Numerous studies have been performed attempting to identify features that correlate with RP. Dosimetric metrics that describe features of the spatial dose distribution, including V20 (the lung volume receiving a dose 20 Gy or more) ^6–11, mean lung dose ^{9, 12–15}, V30 ^{10, 13, 16} V15 ¹⁶, V40 ¹⁰ and V50 ¹⁰, as well as non-dosimetric factors, including tumor location ^{6, 17}, age ^{18, 19}, chemotherapy schedule ^{18, 20} and gender,¹⁸ have all been reported to correlate with the development of RP. These metrics have been used to estimate cutoff values with the intention of identifying patient cohorts at higher risk of developing RP. These cutoffs have failed to accurately predict RP in actual clinical practice, however, and thus new methods are needed to properly identify high risk populations.

The historical failure to predict RP is not surprising given that most cutoffs determined were those that maximized the Receiving Operating Curve (ROC) area of the data being analyzed; that is, the cutoffs that best identified RP using the data at hand. Rules that are determined based on their performance on the data being analyzed (referred to as the training set in Machine Learning) overfit the data and fail to predict new data (testing data) ²¹. For real learning to occur, metrics, algorithms and rules need to be chosen based on their performance on the testing set and not on the training set. The field of Machine Learning attempts to solve this problem. In that sense, previous studies have applied different machine learning algorithms to predict outcome, including RP, in radiation oncology^{17, 22–26}. These include the observation that multivariate analysis and the combination of dosimetric and non-dosimetric features outperform univariate analysis or mechanistic Normal Tissue Complication Probability (NTCP) models ^{17, 23–25}. The complexity of the algorithms used make them difficult to interpret, however, and studies at different institutions have demonstrated different results. Each study considered only one type of algorithm but a comparison of multiple algorithms that highlights their advantages and disadvantages of each approach is lacking. The classification accuracy of the algorithms developed to date is low, and a clear path to improve results has not been proposed. Neverthless, Machine Learning can provide a framework that can be followed to achieve the desirable accuracy and can be very useful in producing algorithms and rules that improve prediction over current methodologies.

An excellent review guiding researchers in predicting outcomes in radiation oncology using machine learning approaches was published recently by Kang et al ²⁷. Among the core principles provided, the authors emphasized: the need to consider both dosimetric and nondosimetric features (also referred to as predictors); the use of cross-validation methods that test a model using new data; and the importance of comparing multiple models. Importantly, the facts that Bayes networks cannot measure how well a model will perform on new data, and that the widely used technique of linear regression performs poorly with regard to highly collinear data (such as dose-volume histogram - DVH - data), were also highlighted.

In the present paper we predict RP using a highly curated data set characterizing RP following SBRT. Multiple machine learning algorithms are evaluated with an emphasis on interpretability, and several debugging strategies are used to identify the key factors for improving prediction accuracy and establishing a clear method to clinically useful predictions. A univariate analysis with features that satisfy both in and out-of-sample behavior is used to determine the out-of-sample rules, and complements the more accurate multivariate analysis. Finally, balanced errors that account for the imbalanced dataset are reported.

2. Material and Methods

2.1 Data collection

In an Institutional Review Board (IRB) approved retrospective analysis, the predictive value of 61 features (dosimetric and non dosimetric) was assessed in 201 consecutive stage I NSCLC patients treated with SBRT. These features were divided in 7 categories as shown below:

• -Comorbidities: Referring Provider, Reason for SBRT, Medically Inoperable vs Patient Refusal, Seen by a Thoracic Surgeon, Diabetes, Multiple lesions treated, Autoimmune/Immunosuppression, DLCO adj %, FEV1(L), FEV1/FVC and FEV1 % Predicted.
• -Drugs: Decadron/Prednisone, Metformin and COX Inhibitors.
• -Dosimetric Indices from: Lung, Heart, Chest Wall, Rib, Skin, Esophagus, Trachea and Great Vessels. All indices have been calculated with heterogeneity corrections using the Analytical Anisotropic Algorithm (AAA), Varian Inc, Palo Alto, CA.
• -Fractionation: Number of Fractions, Dose per Fraction, Total Dose.
• -Staging: TNM Stage, Histology, Stage I NSCLC, EGFR Mutation, KRAS Mutation (Y-N-Unknown), Biopsy, Tumor Size (cm), ALK Translocation (Y-N-Unknown).
• -Tumor Location: Tumor location (Right vs. Left: Upper, Medium, Lower), Mediastinal Sampling (Mediastinoscopy vs. EBUS vs. none), Lymph Node Sample.
• -Other Attributes: Marital Status, Race, COPD, Smoking Status, Pack-Years, Sex, Age, Weight, Height, BMI.

All patients were planned using a consistent set of institutional dose constraints based on Radiation Therapy Oncology Group protocols : RTOG 0618, 0813 and 0915. Specifically, the lung constraints used were: Dose 1500 cc < 7Gy, Dose 1000 cc < 7.4 Gy and V20 < 10%. Pneumonitis was graded from 0 to 5 based on CTCAE v4, as follows: Grade 0: no increase in symptoms; Grade 1: imaging changes or symptoms not requiring initiation or increase in steroids and/or oxygen; Grade 2: symptoms requiring initiation or increase in steroids; Grade 3: symptoms requiring oxygen or hospitalization; Grade 4: life threatening or symptoms requiring assisted ventilation; or Grade 5: causing death. Patients with Grade 2 and greater (Grade ≥2) were labeled as having developed RP. In total, 8 developed grade ≥2 RP.

2.2 Machine Learning Analysis

2.2.1 Univariate Analysis

Univariate pneumonitis thresholds for each of the features collected were determined using decision stumps (simple univariate thresholds) implemented in Matlab R2015a. The objective of the decision stumps was to find thresholds that would best separate patients developing RP from those who would not into different nodes, Figure 1 A). The thresholds that minimize the sum of the Gini Diversity Index over all nodes were selected. The Gini Index is a measurement of how well a threshold separates the different categories (in our case developing RP or not). This approach is equivalent to the univariate analysis performed by other investigators ^{7, 9–17}. In our case, however, each threshold was also scored according to both the probability of random occurrence, and the Generalization Score, defined as the fraction of the recall obtained using balanced cross-validation (testing) to the recall of the training set. The Generalization Score is the ratio of true positives (true RP patients identified by the algorithm as having RP) for out-of-sample and in-sample classifications and was designed to identify those thresholds that will perform best in the clinic.

Figure 1.

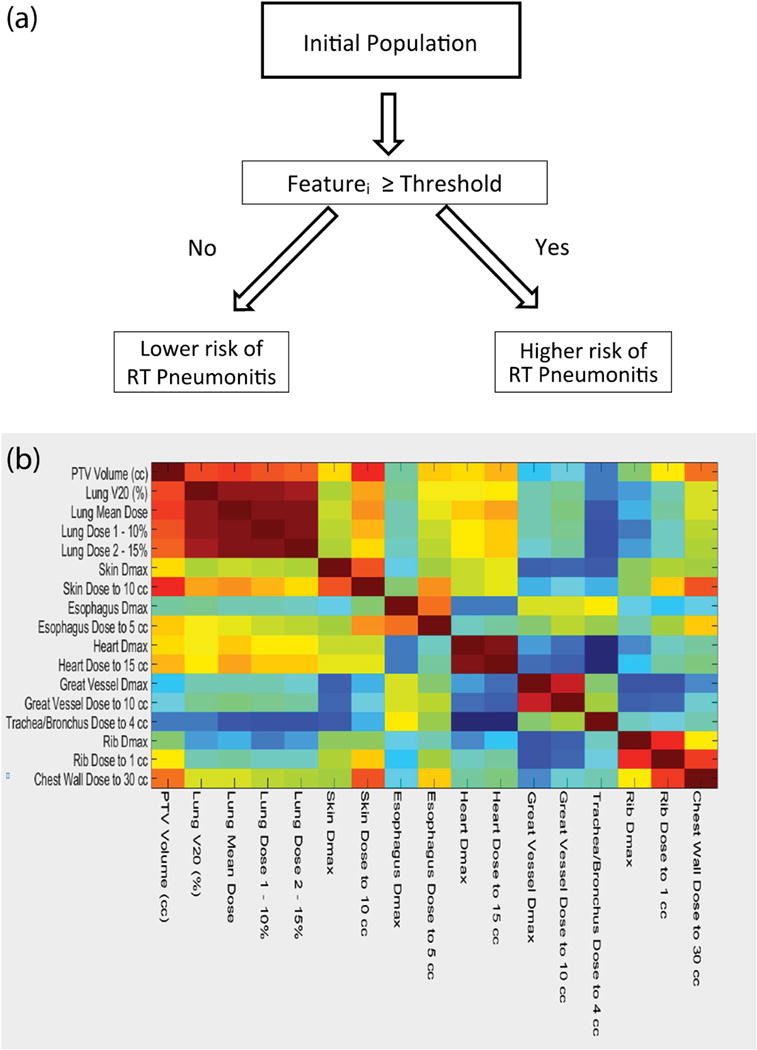
A) Schematic representation of a univariate decision stumps. The threshold that maximizes the gini’s index is found for every feature automatically. B) Correlation heat map between best dosimetric features, V20, PTV volume and prescribed dose.

2.2.1 Multivariate Analysis

In order to account for the possible interaction of features and to improve the prediction of RP, three different types of algorithms were considered using Matlab R 2015 a: Decision Trees, and two ensemble methods: boosting with RUSboost and bagging with Random Forests^28–30. Decision Trees produce interpretable models, naturally incorporate mixtures of numeric and categorical predictor variables and missing values, are invariant to scaling of predictors and are resistant to the inclusion of many irrelevant predictor variables ³¹. Decision Trees are known for overfitting the data, however, and their complexity needs to be controlled. In our case, the complexity of the decision tree was optimized through the use of feature selection, minimum number of observations per tree leaf (MinLeaf), and the prior probability of the minority sample (prior). Specifically, a forward floating sequential selection method (SFFS) with balanced cross-validation (equal representation of the minority class in all samples) using Decision Trees as the baseline algorithm was implemented ³. The Loss function used in all balanced cross-validations was the F1 score, which is commonly used on imbalanced data set³². Decision Trees suffer from high variance even when the complexity is controlled, and they do not provide, in general, accuracy comparable to other methods. Ensemble algorithms that combine the outputs of many “weak” classifiers (single trees) to produce a powerful “committee” were developed to overcome this limitation ³¹. In boosting, weak classification algorithms with high bias-low variance (shallow Decision Trees) are constructed sequentially by repeatedly modifying the weights of each observation in the data to obtain the expert “committee.” Boosting improves the accuracy of Decision Trees by reducing the bias inherent in weak learners³¹. Specifically, RUSboost was designed for and shown to outperform most algorithms in skewed data sets, such as the data used here ²⁸. The elimination of the need for artificially choosing prior probabilities makes this algorithm very attractive. Feature selection does usually improve the accuracy of the algorithm and it is required ²⁸. Regularization through shrinkage is also straight forward in RUSBoost. In contrast to boosting, Random Forests improve the accuracy of Decision Trees by combining low bias-high variance trees (deep trees) through a majority voting rule and reduces the variance of the algorithm by de-correlating them through random subsampling of the features ^{29, 30}. Compared with traditional methods including support vector machines (SVMs), neural nets, logistic regression, bayes networks, naive bayes and others, Random Forests and Gradient Boosting are the most accurate algorithms available for medium size datasets (hundred to thousands of observations) ^{29, 30}. While Random Forests require the use of prior knowledge in skewed data sets, additional feature selection is generally not necessary as it is automatically handled by the algorithm. Finally, when missing values were present, surrogate splits as implemented in Matlab R2015a were used. Surrogate splits find for each missing value on the dataset a surrogate split which uses a different feature and which most resembles the original split according to an indicator function. The feature with the maximum number of missing values was DLCO adj %, with 60% of values missing. This was generally due to patients not being assessed for or unable to physically perform this test, in comparison to their being able to complete other pulmonary function tests; no other feature had a significant percentage of missing values.

3. Results

3.1 Univariate Analysis

Univariate thresholds determined using decision stumps as described in Figure 1 A) are presented in Table 1. In contrast to earlier approaches, features that satisfy both in-sample performance (p < 0.05) and out-of-sample behavior (Generalization Score > 0.75) are shown. Only features satisfying both criteria are shown, with the exception of dosimetric indices where only the ten most important are included. Conventional dosimetric indices, such as V20, did not have both p <0.05 and generalization > 0.75. The most important threshold found to identify patients who developed RP was a non-dosimetric index, DLCO adj % < 38.5, which will result in a cohort with 0.235 probability of developing pneumonitis (4/17) vs. 0.016 (1/61) in the general population. Unfortunately, this feature also had by far the highest percent of missing values. The tumor size (cm) > 3.45 cm threshold identified a cohort of patients with a 0.25 probability of developing RP (3/12) in the in sample analysis; this feature performed slightly worse than DCLO adj % for the out of sample evaluation. Additionally, none of the genetic mutation features were identified as significant. Finally, when all 61 features are analyzed, the probability of finding one feature that splits the data with a probability of random occurrence p increases compared to when only one feature was analyzed. In fact, the probability (P) that at least one feature will have a threshold that splits the data with a probability of random occurrence smaller than p is related to the latest according to:

$$p=1-{\left(1-P\right)}^{\frac{1}{N}}=1-{\left(1-P\right)}^{\frac{1}{61}}$$ (I)

Table 1.

Relevant Features. p <= 0.05 and Generalization Score > 0.75.

Categories	Features	Thresholds	Percent of pneumonitis (N=201)
Comorbidities	1.DLCO adj %*	< 38.5	23.5% vs 1.6%
	2. Referring Provider	Pulmonology + Thoracic Surgery and Pulmonology	10.8% vs 2.4%
Dosimetric Indices	1. Chest Wall Dose to 30 cc	>2498.8 cGy	8.9% vs 0.8%
	2. Skin Dose to 10 cc	>1387 cGy	11.8% vs 1.3%
	3. Lung Dose 1 - 10%	>701.2 cGy	7.8% vs 0%
	4. Lung Mean Dose	>264.6 cGy	7.6% vs 0%
	5. Heart Dose to 15 cc	>83.2 cGy	7.5 vs 0%
	6. Heart Dmax	>114.8 cGy	3.7% vs 0%
	7. Trachea/Bronchus Dose to 4 cc	>34.85 cGy	5.7% vs 0%
	8. Rib Dmax	>5423.85 cGy	7.1% vs 1.7%
	9. Trachea/Bronchus Dose to 4 cc	>25 cGy	6.6% vs 0%
	10. Lung Dose 2–15%	>316.7	6.6% vs 0%
Fractionation	1. Number of Fractions	3 or 5 vs. 4	6.9% vs 1.8%
	2.Dose per Fraction	1000+2000 cGy	6.9% vs 1.8%
Risk Factors	1.Marial Status	Married or Divorced	6.3% vs 0%
	2. Race	White	5.9% vs 0%
	3. Weight	>153 lbs	6.6% vs 0%
Staging	1. Tumor Size (cm)	>3.45	25.0% vs 2.6%
	2. PTV Volume (cc)	>32.8	11.5% vs 0.7%
Tumor Location	Tumor location. R= right, L = left + Upper, Medium, Lower	LL+RLL+RUL	6.1% vs 0%

^*Feature with missing values. There is less than a 50% chance that the p values of the bolded features (p ≤ 0.011) happened randomly.

In that sense, in order for P to be higher than 0.5 (random occurrence), p needs to be equal or smaller than 0.011. The features with p ≤ 0.011 are shown bolded in Table 1. .All other thresholds with their respective p-values have a random probability of occurrence higher than 0.5.

Finally, the features relating to dosimetric indices were found to be highly correlated. A heat map showing the correlation of the most important dosimetric indices, as well as the PTV volume, is provided in Figure 1 B). As can be observed, all of the lung indices are highly correlated with one another and with the volume of the PTV. Therefore, the use of a threshold from one of these features will necessarily contain information regarding the others. Conversely, indices describing the dose to the heart and the maximum skin dose (to 10 cc) correlate weakly with the volumetric dose indices, and thus their thresholds are likely associated with a different mechanism. In the case of the dose to the heart, other authors have found similar indices to also be associated with pneumonitis³³. In the case of the skin dose, indices involving beam selection may be driving the correlation.

3.2 Multivariate Analysis

In order to improve the accuracy of univariate analysis, the combination of dosimetric and non-dosimetric features to predict RP using different algorithms was performed. Three algorithms were evaluated: Decision Trees for their simplicity, RUSboost for its reported accuracy handling skewed data sets and simplicity of regularization (stricter complexity control to avoid overfitting) and Random Forests for their accuracy in high variance problems. In order to control the complexity of Decision Trees and avoid overfitting in a highly correlated feature space, feature selection was performed. Because our problem is ill posed, however, the SFFS algorithm converges to different feature sets if run multiple times. Figure 2 A), shows the features that are selected by SFFS at least 10% of the maximum number of times a feature is selected when the algorithm is run 100 times. The three most important features are the dose to 15 cc of the heart, the dose to 4 cc of the trachea or bronchus, and race. Due to the high number of missing values, DLCO adj % was not selected as a feature by the algorithm. Figure 2 B) and C) show two possible Decision Trees with similar accuracy constructed using this final feature set. To construct the tree shown in Figure 2 C), the chest wall dose to 30 cc was removed to force the tree to select another feature. The existence of degenerate solutions is expected in ill posed problems with highly correlated features. Conversely, the probabilities for the high risk populations observed in Figure 2 B) and C) are an overly optimistic estimation of the real performance of these thresholds in identifying patients at high risk of RP because they represent the performance on the training data. To evaluate the performance of these trees on the testing data, a balanced cross-validation using 7/8 of the data as the training set and predicting the 1/8 left out was performed. The resulting confusion matrix is shown in Table 2. For those patients identified as high risk, the probabilities of developing RP dropped to 0.15 (4/26) and 0.23 (5/22) respectively compared to those in Figure 2. Even these probabilities obtained using cross validation are likely to be an over estimation of the true performance of the tree because, although using cross-validation, the hyperparameters and features were selected using the whole data set. In order to obtain a lower bound estimation of the error, the hyperparameters and the features selected could be obtained using only 90% of the data (80% for training 10% for hyperparameter/features selection). In a data limited problem as the one we are solving (see discussion below), however, the estimation of the error in this manner is overly pessimistic. A confusion matrix derived using this approach is shown in Table 2. The true performance of the trees derived in this paper will be between those derived using the optimistic cross validation performance and the lower bound estimation.

Figure 2.

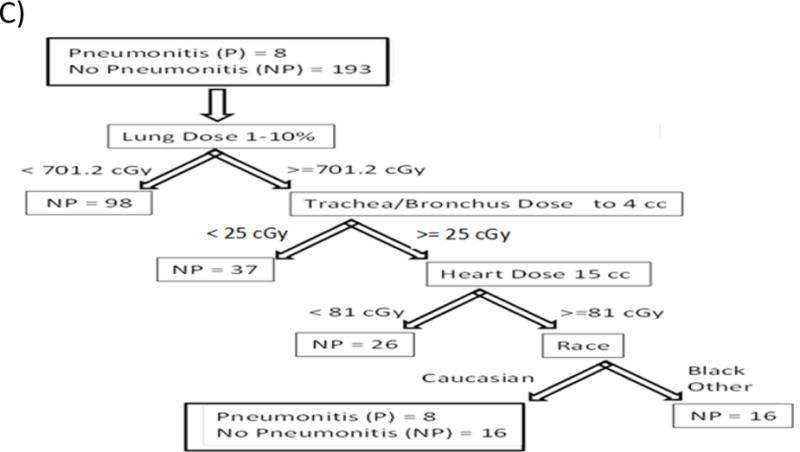
A). Features selected by the SFFS algorithm at least 10% of the time. Figure 2 B) and C) Examples of Decision tree grown using features from A).

Table 2.

Confusion Matrixes for out of sample classification of the decision trees shown in Figure 4, pessimistic tree built using only 80% of the data, Random Forests classifier and RUSBoost algorithm. For the high-risk population on the tree in Figure 4 A), 15% (4/26) of patients developed pneumonitis. On the other hand, for the high risk population of the tree on Figure a B) 22.73% (5/22) developed pneumonitis. The true performance will be in between these values and the pessimistic estimation. At this stage, the performance of the random forest is equivalent to the decision trees nevertheless, RUSBoost performs better than all the algorithms. True Positive = TP, False Negative = FN, False Positive = FP, True Negative = TN.

Figure 4 A) tree
Pneumonitis	4 TP	4 FN
No pneumonitis	22 FP	171 TN
Figure 4 B) tree
Pneumonitis	5 TP	3 FN
No pneumonitis	17 FP	176 TN
Pessimistic tree
Pneumonitis	2 TP	6 FN
No pneumonitis	45 FP	148 TN
Random Forests
Pneumonitis	5 TP	3 FN
No pneumonitis	16 FP	177 TN
RUSBoost
Pneumonitis	6 TP	2 FN
No pneumonitis	28 FP	165 TN

3.3 Different Algorithms’ Tradeoffs and Performance

Table 2 shows confusion matrixes for the Random Forests and RUSboost classifiers. The confusion matrix for the Random Forests corresponds to an algorithm grown with the original data set (not feature selection performed), deep trees, 4 features sampled at each node and a prior equal to 0.8116 which was obtained through cross-validation. The confusion matrix for RUSboost corresponds to an algorithm grown with a learning rate = 0.25 (shrinkage parameter providing regularization) and the feature set obtained on Figure 2 A). These parameters were obtained by analyzing Figure 3. The out of sample 1-F1 Score, a magnitude that describes the error on the out of sample data, is plotted against the number of trees used for RUSBoost and Random Forests for different hyperparameters. As we move from Figure 3 A) to 3 C), the number of splits on the Decision Trees used in RUSBoost and Random Forests changes from 1 split (Stump Trees) to 128 splits (Maximum Number of splits needed to separate all the points in the data set). Each panel also shows the behavior of RUSBoost for different regularization parameters (Learning Rate) and different number of features sampled at every split for Random Forests. Additionally, the errors for Deep trees (grown without control for complexity), the best Stump (univariate tree or threshold cutoff), and the complexity controlled Decision Tree (Optimum Tree) grown as explained above are shown as straight lines for comparison with the ensemble methods. In all cases, RUSBoost outperformed the other algorithms, as is the case in other skewed data sets ²⁸. It can also be appreciated in Figure 3 that all the algorithms are behaving as expected in our data set. Specifically, the expected behaviors are as follows. Deep Trees grown without control of their complexity perform poorly when trying to explain data that they have not seen. Univariate Stump trees perform better than the Deep Trees but worse than our multivariate Decision Tree were the complexity has been controlled through the hyperparameters. Random Forests improves performance as the Trees used in the ensemble grow deeper (going from Figure 3 A to 3 B). For shallow Trees (high bias), Random Forests performs better when more features are used for each split, which decreases the bias of the Trees ³¹. As the Trees get deeper (Figure 3 B and 3 C), however, smaller numbers of features are preferred by Random Forests. Conversely, RUSBoost shows the higher accuracy for 8 splits (going from Figure 3 A to 3 C) and as the number of split increases, the need for stronger regularization (smaller Learning Rate) is observed.

Figure 3.

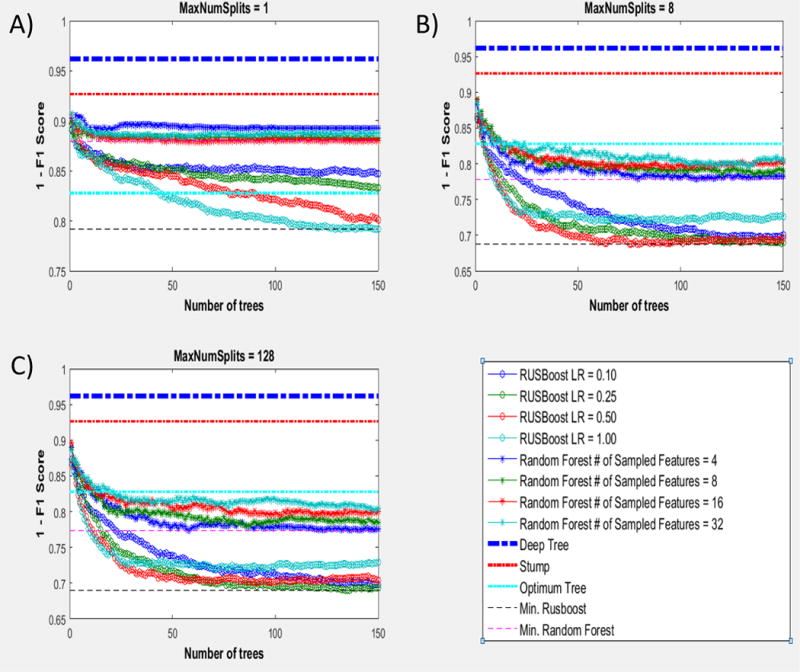
Comparison of the performance of Deep Trees, Stump trees, Optimum Trees, Random Forest and RUSBoost for different regularization factors (Learning Rate) and different number of features sampled in the case of Random Forests.

3.4 Learning Curves and Training vs Testing Error

As indicated by the results shown on Table 2, higher accuracy of the algorithms is desirable. In Machine Learning the process of evaluating different approaches to obtain higher accuracy is typically referred to as “debugging a machine learning problem”. Learning curves and the behavior of the training and the testing error offer unique insights. In sample (training) and out of sample (testing) errors plotted as a function of the number of patients used in the training sample for each algorithm are shown in Figure 4 A and B. As the number of patients in the training error is increased, the out of sample error of the classification of patients that developed RP diminishes while the training error remains constant (0) for all algorithms. The 0 classification error of the training data is an indication that Decision Trees and Random Forests are overfitting the data even when their complexity has been controlled. However, in the case of RUSBoost, stronger complexity control has been applied (regularization) through the learning rate parameter and its 0 error on the training data is not likely to indicate overfitting. In fact, for smaller number of patients the performance of the RUSBoost algorithm over Decision Trees or Random Forests in the classification of out of sample RP is at the expense of making more mistakes on the classification of patients that have not developed RP, Figure 4 B). As the number of patients is increased, however, the classification of patients that do not develop RP is similar to Decision Trees and Random Forests, while RUSBoost performs better classifying patients that develop RP. These results offer unique insights into our problem and are discussed below.

Figure 4.

Learning Curves. A) and B) the number of instances where the algorithm makes a classification mistake as a fraction of the total number of instance of each category is plotted vs the number of samples used for training. C) 1- F1 Score vs Log(Learning Rate) is plotted for RUSBoost. The Learning Rate controls the complexity of the algorithm through shrinkage. Despite RUSBoost classifying the training set on A) perfectly, is complexity has been controlled and the best complexity used.

4. Discussion

4.1 Univariate Analysis

In the present paper we aim to predict RP for stage I SBRT patients and lay out a strategy to improve the accuracy of the algorithms to desirable clinically relevant levels. In that sense, we have collected a highly curated data set of patients treating consistently at our institution as described in the material and method section. We have used a consistent dose calculation algorithm with heterogeneity corrections, one patient population (stage I) and one technique (SBRT). These factors have not been well controlled previously^{19, 23, 25} yet they are essential in order to reduce the inherited noise in the data and obtain an accurate classification. With this unique data set, univariate clinical thresholds (cutoff values) similar to those previously developed by other authors were obtained^{7–11, 13, 15, 16, 23, 25}. In this work, however, higher emphasis was placed on finding cutoff values that could best predict data that was not used in the derivation of the thresholds. This approach is fundamentally different to finding the thresholds that best predict the data at hand. This is consistent with clinical reality, in which clinicians care about predictors of RP for patients in the future, and not about finding the thresholds that best fit the data of the patients that has already been collected. The field of Machine Learning has shown extensively that these thresholds are different. In that sense, we not only identified features with thresholds that will predict RP with a probabaility of random ocurrence smaller than 0.05, but also evaluated the performance of these thresholds in out of sample data through the Generalization Score. This criteria allowed us to critically evaluate commonly used dosimetric indices like V20. While no patients with V20 <2.63% developed pneumonitis (n=81, p<0.05), the Generalization Score was low, indicating that this threshold will fluctuate depending on the data set, with poorer performance for future patients than obtained for the data analyzed. Therefore, the use of thresholds shown in Table 1 should offer better results than V20 regarding the prospective identification of RP rates. Furthermore, we note that most of these features, including those characterizing dose-volume in normal lung (ex. Lung Mean Dose and Lung Dose 1–10%) are highly correlated, as shown in Figure 1 B), and the use of one of them is equivalent to the use of other like indices. Finally, it is important to remember that when a large number of predictors is analyzed, the probability of finding at least one predictor with a significant p value increases dramatically. In fact, when 61 features are analyzed, a p ≤ 0.011 is required to guarantee that this level of significance did not happen randomly. Table 1 shows those features where p values for at least one feature could have not occurred randomly. Some of these features, such as the mean lung dose, PTV volume or PTV size have been found to be relevant in other data sets; however, DLCO adj%, heart dose, chest wall dose to 30 cc and skin dose to 10 cc have not been as widely reported. ^{7–11, 13, 15, 16, 23, 25} Specifically, DLCO adj % was found to be a very strong predictor: 4 out of 17 patients with DLCO adj %< 38.5 developed pneumonitis vs 1/63 otherwise. Nevertheless, the use of this feature as a clinical predictor is limited by the data available. While others have studied DLCO adj % and observed it to be a weak predictor of RP ²³, those analyses were always performed as multivariate analysis where the handling of missing values is quite important. Similarly, when we performed a multivariate analysis, the DLCO adj % was no longer identified as an important feature in our dataset.

4.2 Multivariate Analysis

While univariate analyses are important and help us understand the problem and drive the dose optimization during treatment planning, multivariate algorithms are inherently more accurate. Additionally, there are several important questions to address when RP is modeled using machine learning: Which algorithms should be used? Is the solution unique? How should feature selection be performed? Is the model overfitting the data? How can the accuracy be improved? The present paper is novel in answering each of these questions. First, when the algorithm is selected, a tradeoff between interpretability and accuracy is usually performed. Decision Trees, which closely mimic the human thought process, are highly interpretable but tend to overfit the data. Additionally, when used in problems with highly correlated features as in our case, the final tree depends highly on the initial data set, and the algorithm will converge to different solutions. This is demonstrated in Figure 2 A); if the SFFS algorithm is run 100 times, different features will be selected. Therefore, when Decision Trees are developed, performing feature selection and controling the complexity of the trees as we have done in this work is of paramount importance. Even when the trees are carefully constructed, however, they still can converge to different solutions and overfitt the data, specially in a correlated feature space, Figure 2 B and 2 C). This can be seen as a drawback of Decision Trees because it leaves clinicians asking which tree should be used. Despite this limitation, Decision Trees are extremely easy to interpret as can be observed in Figure 2 B and 2 C). In addition, the performance of the Decision Trees can be enhanced by previous clinical experience through selection of the Decision Trees that fits clinical intution.

Different techniques such as boosting and bagging can also be used to improve the accuracy of decision trees, but at the expense of losing interpretability. RUSBoost (boosting) and Random Forests (bagging), have consistently been shown to outperform other modern algorithms in terms of accuracy on skewed data sets^{29, 30}. As observed in Table 2, the Random Forests classifier offers similar accuracy as our Decision Trees but the results are less interpretable. Conversely, RUSBoost, especially designed to handle skewed data sets, outperforms both of them. Regularization and the simplicity of handling skewed data sets are the key factors that lead to better performance. Similar results have been reported previously for RUSBoost ²⁸. Interpretability is nevertheless lost, which is particularly important when the accuracy of the algorithms is not high. Therefore, at this stage, Decision Trees may still be preferable to more complex algorithms. As additional data are collected, however, Random Forests and especially RUSBoost should significantly outperform the Decision Trees. In that case, the prediction of the algorithms will be more reliable, and the higher accuracy and consistency of Random Forests and RUSBosst should become the key factor in the selection of the algorithm, with other techniques used to interpret their results. It is important to highlight the fact that our data set behaves as expected when analyzed with the wide set of algorithms and techniques as presented in this paper. There is no indication, therefore, that the problem of predicting RP is particularly difficult and cannot be completely solved with machine learning with sufficient data. In the following section, a discussion on how to improve accuracy is presented.

4.3 Debugging a Machine Learning Algorithim and Improving Accuracy

We can observe in Table 2 that better accuracy is needed for these algorithms to have a higher impact in the clinic. Different steps can be taken to improve the prediction accuracy in Machine Learning: gather new features from the same patient data set, use more complex algorithms, or increase the number of patients analyzed. Typically, the first two approaches are less expensive. For example, image-based features (radiomics) have been proposed to be correlated with pneumonits ³⁴ and different algorithms have been used by other investigators hoping to obtain improved results ^{23, 25, 26}. In this work, for example, radiomics-based features could have been collected or other algorithms could have been investigated. An incorrect evaluation of the state of a problem in machine learning, however, can be costly, sending an investigator down an unfruitful path. Therefore, the question of what is currently needed to improve the accuracy of an algorithm is of paramount importance. Learning curves for predicting RP were developed, and comparison of in sample (training) and out of sample (testing) errors plotted as a function of the number of patients used in training the algorithms offer unique insights, Figure 4. As can be observed from the training errors, the features and the algorithm used are complex enough that they can identify 100% of the patients developing RP if they are present in the training sample. If the complexity of the algorithms was biasing the solution (i.e., too simple to explain the data), or the features used (61 in total) were not significantly correlated to the outcome, the error obtained on the training sample would be unacceptably large. Conversely, the difference between the training and testing error as well as the slope of the testing error versus number of patients tell a different story. At the current stage, a large difference between the training and the testing error is observed for all algorithms used. Additionally, the testing error decreases as the number of patients in the training sample increases. This behavior is typical of problems where the accuracy of the algorithm is limited by the size of the data set. As Figure 4 shows, the RP testing error decreases as the number of patients in the study is increased for all algorithms. This behavior indicates that real learning is occurring, and if enough high quality data are accumulated, the algorithms will be able to predict RP with high accuracy. Additionally, by assuming exponential decay of the error, it can be estimated within a 95% confident interval that approximately 800 patients would be needed to reduce the error to less than 10%. Therefore, at the present stage, collecting additional data from new patients is the limiting factor, and gathering new features, whether radiomics-based or others, or using different algorithms, will only produce marginal improvement. Finally, while collecting additional data for one modality and one stage represents a significant challenge, it is an essential task if we are to predict RP with an even greater clinically relevant accuracy. In that sense, data sharing collaborations and distributed learning as suggested by Lambin et al may play a key role in radiation oncology³⁵. The fact that different feature sets are selected by different algorithms that are aimed at predicting the same outcome, as well as the low ROC reported, are all indications of high variance problems limited by data. ^{19, 23, 24} The need for additional data is not unique to our study, as most data sets in the literature are of similar size as ours; the low incidence of RP for stage I NSCLC patients treated with SBRT imposes further limitations in our case.

5. Conclusions

In this paper, an initial investigation in predicting radiation-induced pneumonitis using Machine Learning for stage I NSCLC patients treated with SBRT was performed. The power of learning curves and comparison of the testing and training error to guide the discovery process in the era of big data is highlighted. With the low number of RP events, we conclude that the acquisition of a data set of approximately 800 patients is needed in order to predict RP with greater accuracy, and should be the subject of future efforts. The different analyses performed on our data set indicate that predicting RP is not a particularly difficult problem, and could be solved using Machine Learning provided there is sufficient curated data.