New insights into vestibular-saccade interaction based on covert corrective saccades in patients with unilateral vestibular deficits

During active or passive head impulses while fixating stationary targets, low vestibulo-ocular gain subjects produce corrective saccades when the head is still moving. The mechanisms driving these covert saccades are poorly understood. We propose a mathematical model showing that the brain develops two separate estimates of head rotation: a lower level one, presumably in the vestibular nuclei, used to generate the slow-phase component of the response, and a higher level one, within a gaze feedback loop, used to drive corrective saccades.

Abstract

In response to passive high-acceleration head impulses, patients with low vestibulo-ocular reflex (VOR) gains often produce covert (executed while the head is still moving) corrective saccades in the direction of deficient slow phases. Here we examined 23 patients using passive, and 9 also active, head impulses with acute (< 10 days from onset) unilateral vestibular neuritis and low VOR gains. We found that when corrective saccades are larger than 10°, the slow-phase component of the VOR is inhibited, even though inhibition increases further the time to reacquire the fixation target. We also found that 1) saccades are faster and more accurate if the residual VOR gain is higher, 2) saccades also compensate for the head displacement that occurs during the saccade, and 3) the amplitude-peak velocity relationship of the larger corrective saccades deviates from that of head-fixed saccades of the same size. We propose a mathematical model to account for these findings hypothesizing that covert saccades are driven by a desired gaze position signal based on a prediction of head displacement using vestibular and extravestibular signals, covert saccades are controlled by a gaze feedback loop, and the VOR command is modulated according to predicted saccade amplitude. A central and novel feature of the model is that the brain develops two separate estimates of head rotation, one for generating saccades while the head is moving and the other for generating slow phases. Furthermore, while the model was developed for gaze-stabilizing behavior during passively induced head impulses, it also simulates both active gaze-stabilizing and active gaze-shifting eye movements.

NEW & NOTEWORTHY During active or passive head impulses while fixating stationary targets, low vestibulo-ocular gain subjects produce corrective saccades when the head is still moving. The mechanisms driving these covert saccades are poorly understood. We propose a mathematical model showing that the brain develops two separate estimates of head rotation: a lower level one, presumably in the vestibular nuclei, used to generate the slow-phase component of the response, and a higher level one, within a gaze feedback loop, used to drive corrective saccades.

the angular vestibulo-ocular reflex (VOR) stabilizes gaze on a stationary target during head rotations by rotating the eyes with the same velocity and amplitude as the head, but in the opposite direction. If the peripheral vestibular system is impaired, or head acceleration exceeds the capabilities of the vestibular system (Peng et al. 2004), the VOR does not maintain stable gaze; thus other mechanisms must be called on to minimize the time during which the image is moving on the retina and displaced from the fovea. Preprogrammed slow phases that anticipate uncompensated head motion, enhancement of the effects of neck-eye reflexes and substitution of saccades for inadequate slow phases are some of the tools used by the brain in these conditions (e.g., Kasai and Zee 1978).

Saccades are triggered in the direction of the deficient slow-phase response both when the head is still moving (covert saccades) and after head has stopped (overt saccades) (Bloomberg et al. 1991a; Kasai and Zee 1978; Schubert et al. 2010; Weber et al. 2008). Short-latency, covert saccades in particular may reduce blurred vision (oscillopsia) and improve visual performance (Ramaioli et al. 2014). The latencies of covert saccades are less than 150 ms, the typical duration of a head impulse, and can be as low as ~70 ms (Tian et al. 2000; Weber et al. 2008), which is much less than volitional saccades to a new target [~200 ms (Leigh and Zee 2015)]. Covert saccades are triggered earlier when head turns are active (Black et al. 2005; Peng et al. 2005), and when passive if head motion is predictable (Mantokoudis et al. 2016). The low latency of covert saccades suggests they are triggered by neck proprioceptive signals (Macdougall and Curthoys 2012), by residual labyrinthine function, or by other cues that the head is about to or has just begun to rotate (Schubert and Zee 2010).

Here, we investigated how patients with unilateral vestibular loss use covert saccades to compensate for inaccurate VOR slow phases in response to passive and active high-velocity head impulses (Halmagyi and Curthoys 1988). We compared the amplitude of saccades with the displacement of the head and with the residual vestibular slow-phase response, asking how well the saccades reduced gaze error. Our goals were to use patients with unilateral loss of labyrinthine function to understand better the premotor control system that generates covert corrective saccades, the contribution of residual vestibular information to programming corrective saccades, how the brain estimates head velocity when labyrinthine function is deficient, and the interaction between the vestibular and saccade commands. We also used these results in patients to better understand vestibular-saccade interactions during head movements in normal human beings.

Although our study investigates a gaze-stabilization task, we surmised that results in our labyrinthine-defective patients, who required corrective saccades to stabilize gaze, could be better interpreted using older mathematical models of saccade-vestibular interaction during active gaze shifts. These models had suggested that the brain uses feedback control of the gaze position (eye-in-space) trajectory (Galiana and Guitton 1992; Guitton and Volle 1987; Laurutis and Robinson 1986; Pelisson et al. 1988; Tomlinson 1990). Based on data collected from vestibular patients, given that their labyrinthine estimate of head velocity is inaccurate, we hypothesized that the brain uses a central recreated estimate of head movement to calculate the error in the position of gaze and then triggers the corrective saccade to compensate for the inadequate VOR slow-phase response. Moreover, our analysis of the interaction between the residual slow-phase signal and the saccade signal showed that for corrective saccades larger than 10° the VOR command appears attenuated as found during large (>20°) active gaze shifts (Pelisson et al. 1988; Tomlinson and Bahra 1986). Paradoxically, of course, any decrease in the slow-phase response during the head impulses would increase the time until gaze stability is reached and seem counterproductive.

METHODS

Subjects.

We studied 23 patients suffering from vestibular neuritis (15 left ear, 8 right ear, mean age 51±13 yr, 14 men): 16 recorded at IRCCS Mondino (Pavia, Italy) 3–10 days after the onset of symptoms, and 7 recorded at the Department of Otorhinolaryngology, Head and Neck Surgery, University Hospital, Inselspital (Bern, Switzerland), within 3 days from the onset of symptoms. Vestibular neuritis was diagnosed by either abnormal bithermal caloric or abnormal head impulse testing, an absence of neurological signs, and an MRI of the brain that showed no lesions that could account for any vestibular disturbance. All individuals gave written, informed consent to participate in the experiments. The studies were approved by the ethical committees of both institutions.

Experimental protocol.

The 16 patients recorded in Pavia underwent the functional head impulse test (Ramat et al. 2012) using the EyeSeeCam system (Colagiorgio et al. 2013; Versino et al. 2014). Briefly, the subject sat 1 m away from the screen while the experimenter, standing behind, manually imposed horizontal head impulses at varying head angular accelerations. These, in turn, elicited the brief appearance (~80 ms) of a Landolt's C optotype in one of eight possible orientations on the screen at the location where a fixation target is initially displayed. The subject reports the orientation of the optotype and based on the rate of correctly identified orientations is classified as healthy or with peripheral vestibular hypofunction related to the canal toward which the head was rotated. In the second part of the experiment the patients attempted active head impulses; nine could correctly perform this task. Later, seven patients returned for a recording of the saccade peak velocity-amplitude relationship (the “main sequence”) with the head immobilized.

The seven patients recorded in Bern underwent the traditional passive head impulse test, i.e., subjects sat 1.5 m away from the screen while the experimenter, standing behind, manually imposed horizontal head impulses. The subject was asked to maintain fixation on a constantly displayed target, while their eye movements were recorded. Each subject is then classified as healthy or with peripheral vestibular hypofunction based on the gain of the VOR computed by the EyeSeeCam software.

In both sets of experiments the number of head impulses delivered was variable and is reported in Table 1.

Table 1.

Number of head impulses performed by each patient

	Ipsilesional			Contralesional Total	Active Ipsilateral
No.	Total	LRG with CS	HRG with CS
1	34	28	0	39	23
2	30	29	0	28
3	42	39	3	43	27
4	44	0	18	44	3
5	28	1	21	32
6	25	25	0	36	31
7	27	10	10	21
8	40	0	25	40
9	25	0	12	29
10	30	21	5	33
11	33	17	11	31	20
12	37	28	3	34	32
13	29	23	0	22	13
14	23	11	3	25
15	25	19	1	34	13
16	32	7	4	35	17
17	8	0	7	10
18	16	0	12	6
19	12	4	4	11
20	20	8	3	13
21	12	0	8	12
22	20	0	17	18
23	11	4	2	8
	603	274	169	604	179

The first column reports the patient number, the following three columns refer to passive head impulses to the ipsilesional side and report their total followed by the number of analyzed impulses, i.e., those presenting a covert saccade (CS) within 150 ms from the onset of the head rotation, falling in the low residual gain (LRG) and high residual gain (HRG) groups. The following column represents the total number of head impulses performed to the healthy side and the last column reports the number of active head impulses to the ipsilesional side performed by the nine patients that were able to correctly perform them.

Eye movements recording and analysis.

In both sets of experiments, the horizontal and vertical position of the right eye was measured using the EyeSeeCam infrared video system (sampling rate 220 Hz; EyeSeeTec, Fürstenfeldbruck, Germany). The angular velocity of the head was measured using the EyeSeeCam three-axis inertial measurement unit (IMU) sensor contained in the same device as the goggle-mounted camera.

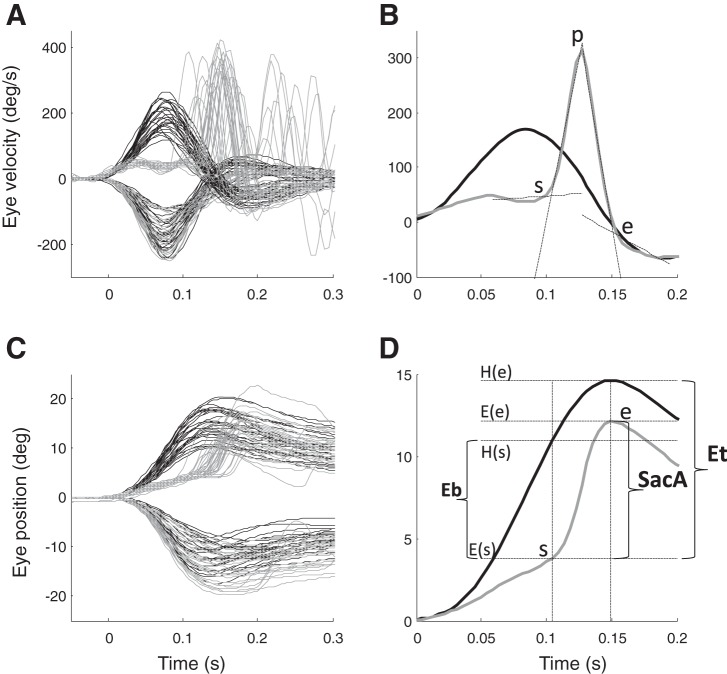
Data were analyzed offline in MATLAB (MathWorks, Natick, MA) using custom-developed software. Raw eye position was calibrated and then filtered using a second-order Butterworth low-pass filter (50-Hz cutoff frequency). Eye-velocity was calculated using a Savitzky-Golay four-point derivative filter (Ramat et al. 1999). The orientation of the IMU with respect to gravity was calculated from the accelerometer before the beginning of each head impulse; the angular components of the gyroscope are then rotated in the earth gravity frame to obtain horizontal head velocity. A threshold of 10°/s was used to detect the onset of head movement. The gain of the VOR was calculated as the mean of the ratio between horizontal eye velocity and horizontal head velocity computed over the time interval between the times of peak acceleration and peak velocity of the head. We analyzed the 400-ms period after the onset of each head impulse. To identify corrective saccades, horizontal eye velocity was high-pass filtered (10-Hz cutoff frequency) to eliminate the slow-phase component. We then searched for the peak eye velocity (p) and we identified start (s) and end (e) points of each saccade starting from p as the time when eye velocity rose above or fell below, respectively, 10°/s. The estimates of the start and end points of each saccade were then refined using the unfiltered eye velocity signal by calculating the intersection between the linear fit of the 45 ms preceding s and the linear fit from s to p, and the intersection between the linear fit of the 45 ms after e and the linear fit from p to e (Fig. 1A). We calculated the initial error (Eb), e.g., the difference between head position (H) and eye position (E) at the beginning of the saccade as Eb = H(s)−E(s). Since the head moves during the saccade we considered the total error for which the saccade must compensate as Et = H(e)−E(s), i.e., the difference between head position at the end of the saccade and eye position at the beginning. The amplitude of the saccade is therefore SacA = E(e)−E(s) (Fig. 1B). We computed the precision of saccades as SacP = SacA/Et, since the aim of corrective saccades is to return the gaze error to zero.

Fig. 1.

A: head velocity (black line), and inverted eye velocity (gray line) profiles of repetitive head turns toward the ipsilateral and contralateral side in a representative patient. B: head velocity (black line), and inverted eye velocity (gray line) in one of the impulses shown in A toward the affected side: s = start, p = peak velocity, e = end of saccade. s and e are initially computed on the high-pass filtered velocity to eliminate the slow-phase component. They are then refined based on the unfiltered signal as the intersection between the linear fit of the 45 ms before s and the linear fit between s and p and as the intersection between the linear fit of the 45 ms after e and the linear fit between p and e (black dotted lines). C: head position (black line) and inverted eye position (gray line) profiles of repetitive head turns toward the ipsilateral and contralateral side for the same patient are shown in A. D: head position (black line), and inverted eye position (gray line). Eb represents the error at the beginning of the saccade, while Et represents the total error that the saccade has to compensate to reach the 0° gaze position. SacA is the saccade amplitude.

Since the mean duration of the head impulses was 157 ± 16 ms, we analyzed saccades that began within 150 ms from the onset of the head movement. We also confirmed that the head velocity was still at least 50°/s when the saccade began to ensure the saccades that were analyzed were initiated while the head was still moving.

Statistical comparisons between two samples were performed using the Wilcoxon rank sum test, while the Kruskal-Wallis test was used for comparisons between multiple groups. These were considered significant for P values lower than 0.05.

Mathematical modeling.

We modeled the eye plant dynamics as a fourth-order transfer function with one zero, two real poles, and a complex-poles pair (Robinson 1964).

$$\text{Plant}=\frac{s{T}_z+1}{\left(s{T}_1+1\right)\left(s{T}_2+1\right)}·\frac{{\omega }^2}{s^2+2\xi \omega +{\omega }^2}$$

The final common path (Fig. 2) for this fourth order plant was modeled as the pulse-slide-step representation of saccadic innervation (Optican and Miles 1985): a neural integrator with a gain A, a direct velocity contribution (with gain B), and a low-pass filter with time constant T_z (to compensate the zero of the plant) and gain C. As proposed (Optican and Miles 1985) we set A = 1, B = T₁+T₂/T_z, C = T₁+T₂–T_z–(T₁+T₂/T_z). In this way, all the dynamics of the plant are compensated except for the high-frequency complex-poles pair, which determines the waveform of the saccade. Parameters were set to T₁ = 0.224, T₂ = 0.013, T_z = 0.08, ω = 200, ζ = 1.2 (Zee et al. 1992).

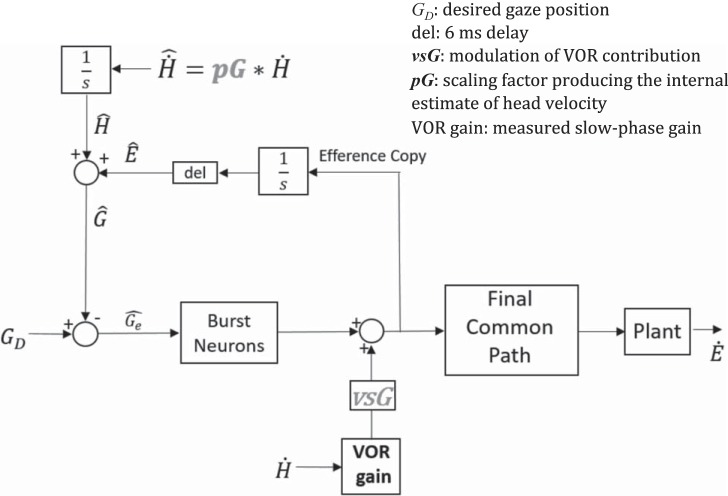
Fig. 2.

Mathematical modeling of gaze correction: the brain computes an estimate of head velocity ($\widehat{\stackrel{․}{H}}$) relying on multisensory information. We modeled $\widehat{\stackrel{․}{H}}$ with a gain (pG) that multiplies actual head velocity. An estimate of gaze position $\widehat{G}$ is thus computed by adding an estimate of eye position $\widehat{E}$ provided by the resettable integrator in the local feedback loop to the estimate of head position, $\widehat{H}$. This estimate is compared with the desired gaze ($G_D$ = 0 in a gaze-stabilization task) and their difference, gaze error (${\widehat{G}}_{\mathrm{e}}$), drives saccadic burst neurons that move the eyes until $\widehat{G}=G_D$, when the saccade stops. The VOR signal is multiplied by a coefficient (vsG), ranging between 0 and 1: if vsG = 1, the (deficient) input from the labyrinth is added to the saccadic command and sent to the final common path (linear summation hypothesis), otherwise its contribution is attenuated (0 ≤ vsG ≤ 1) or canceled (vsG = 0).

The input-output relationship of the high-gain amplifier representing the medium lead burst neurons was given by Zee and Robinson (1979):

$$B\left(G_e\right)=\{\begin{array}{c}{B}_m\left(1-e^{\frac{-\left(G_e-e_0\right)}{B_k}}\right),G_e>e_{0;}\\ 0,G_e\le e_0\end{array}$$

where G_e represents gaze error (Fig. 2) and e₀ = −1, while B_m and B_k were optimized to fit the recorded amplitude-peak velocity data for each subject considering covert saccades between 2 and 10° or, in the seven patients who performed such recording, the saccade data obtained with the head restrained. Note that the values for B_m and B_k fitted on saccades with the head restrained were not significantly different from those obtained by fitting covert saccades between 2 and 10° (P = 0.09 and P = 0.25, respectively). The mean values for all patients were B_m = 521 ± 48, B_k = 6.93 ± 1.35.

The proposed control system for generating corrective saccades (Fig. 2) during a gaze-stabilizing task is an extension of previous models for gaze-shifting saccades during combined movements of the eyes and head (Galiana and Guitton 1992; Guitton and Volle 1987; Laurutis and Robinson 1986; Pelisson et al. 1988). The VOR circuitry reacts first, but because the gain is low a gaze error accumulates and an early corrective saccade is triggered. A network to provide the error signal for triggering this corrective saccade is based on the following scheme. An internal estimate of eye position, $\widehat{E}$ (based on the resettable integrator in the local saccade feedback loop (Jürgens et al. 1981; Zee et al. 1976), is added to an internal estimate of head position, $\widehat{H}$, to create an estimate of gaze position $\widehat{G}$. $\widehat{G}$ is then compared with the desired gaze, $G_D$, which is zero during head impulses since subjects must hold gaze on a stationary target. Their difference, gaze error ($G_D-\widehat{G}$), drives saccadic burst neurons until $\widehat{G}=G_D$, when the saccade stops. The saccade command and the residual VOR signal coming from the semicircular canals are summed and sent to the final common pathway to produce the total compensatory eye movement during the saccade. The residual VOR signal — the head velocity sensed by the semicircular canals (based on the gain of the VOR) — is weighted by a coefficient (VOR summation gain: vsG) representing the modulation of the VOR contribution during saccades. Thus, if vsG equals 1, the VOR is added to the saccadic command (linear summation hypothesis); otherwise its contribution is attenuated (0 <vsG <1) or canceled (vsG = 0).

If the peripheral vestibular system is impaired the brain must rely on other sensory information to improve its estimate of head velocity to generate a more accurate compensatory movement. In our model, we assume that the central estimate of head velocity is based on a multisensory integration of visual, proprioceptive and extravestibular inputs within the vestibular nuclei (VN) (Cullen 2012) and results in a scaled version of head velocity, which we indicated as

$$\widehat{\stackrel{\mathit{․}}{\mathit{H}}}=pG*\stackrel{․}{H}$$

The value of the prediction gain (pG), ranging between 0 and 1, results in $\widehat{\stackrel{\mathit{․}}{\mathit{H}}}$ being a scaled version of actual head velocity. The estimate of head position is obtained by integration of the velocity estimate.

For simulating each head impulse, the input to the model was the recorded head velocity, the VOR gain was set to the experimentally measured value and the values of vsG and pG, which were constant for the entire duration of each head impulse, were optimized using a nonlinear least-squares solver (MATLAB, MathWorks) to fit the eye velocity data during the saccade correction. In these simulations the corrective saccade was triggered at the start point identified on the eye movement data.

A fully working version of the model together with the data acquired in Pavia and the scripts for running it are available at https://github.com/bioingpv/GazeStabilizationHeadImpulses.

RESULTS

The morphology of the ocular motor responses recorded in our patients is exemplified in Fig. 1, A and C. The patient shown was affected by vestibular neuritis on the right side, which produced low VOR gain responses to rightward head impulses, which were supplemented by covert saccades. The responses to the healthy side were of vestibular origin, with no saccadic corrections. An overall picture of the passively imposed head impulses characteristics and of the slow phase VOR gains in our patients is shown in Fig. 3. Our first aim was to know if the level of the residual VOR gain influences the precision and the dynamic properties of saccades. To this goal we arbitrarily chose a VOR gain threshold of 0.4 (mean gain of all responses was 0.36) for dividing the recorded movements of all patients into those with high residual gain (HRG) and those with low residual gain (LRG) and then compared the two groups. Table 1 shows the number of passive and active head impulses performed by each patient toward the ipsilesional and contralesional sides, together with the number of ipsilesional impulses that fell in the LRG and HRG bins.

Fig. 3.

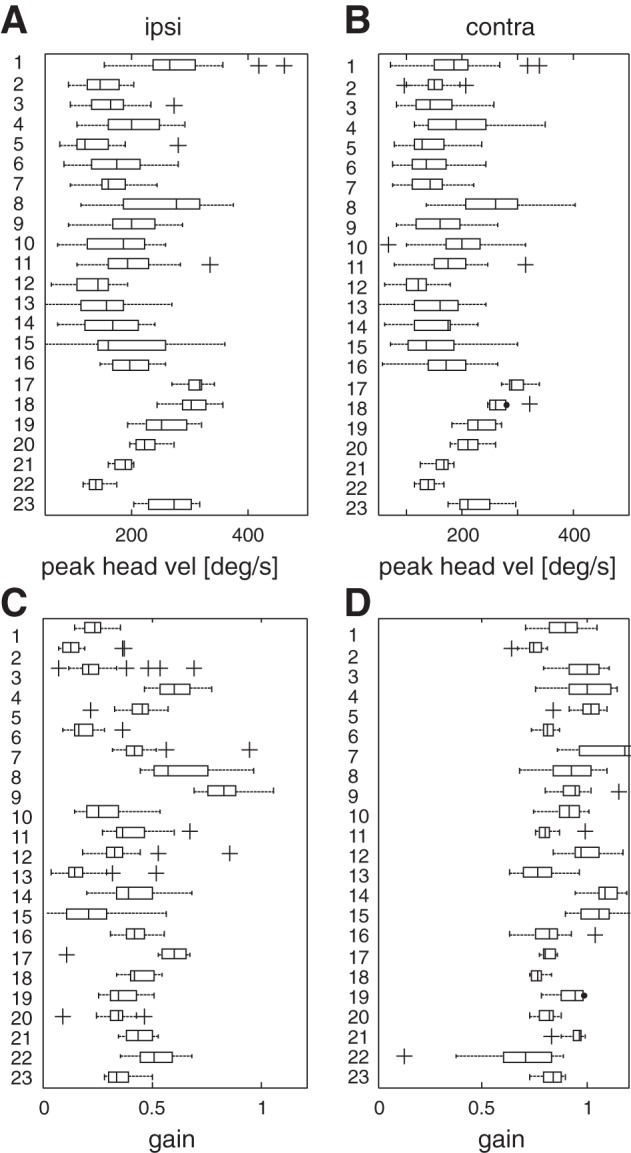
A and B: peak head velocity values for each subject for ipsilateral (ipsi) and contralateral (contra) head impulses. Peak head velocity correlates with peak head acceleration (ρ = 0.89). The range of peak head velocity is 50–400°/s while for peak head acceleration the range is 1,000–8,000°/s². C and D: VOR gains for each subject for ipsilateral and contralateral head impulses. In each box, the central mark is the median, the edges are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted individually as crosses.

Saccade precision is better if the VOR gain is only moderately deficient (HRG).

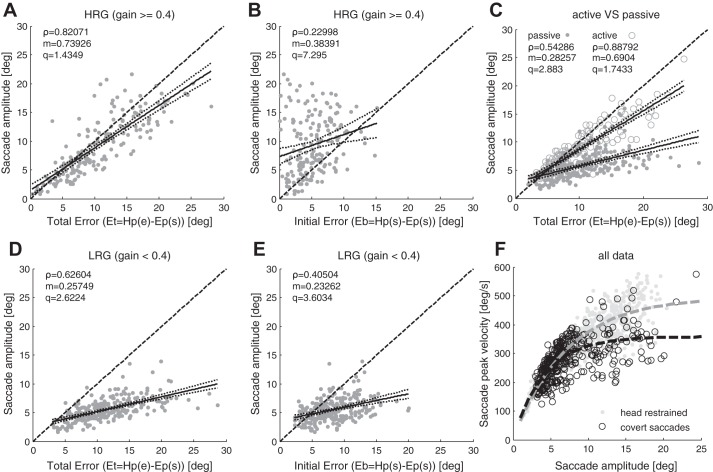
A corrective saccade must compensate for any error that has accumulated up to the time the saccade begins and for additional error during the subsequent displacement of the head that occurs while the saccade is executed (Fig. 1B). We found a mean SacP (saccade precision, SacA/Et) of 0.85 ± 0.33 for HRG movements and 0.51 ± 0.17 (mean ± standard deviation) for LRG movements. Therefore, compensation was better when the residual VOR gain was higher (P < 0.001). In Fig. 4, A and D, saccade amplitudes are plotted against Et: for HRG movements (Fig. 4A) the amplitude of the saccades is highly correlated with Et (sample correlation coefficient ρ = 0.82, P < 0.001) and the slope of the linear regression (m) is 0.74; for LRG movements (Fig. 4D) both the correlation (ρ = 0.62, P < 0.001) and the slope of the linear regression are significantly lower (m = 0.26, P < 0.001). In HRG movements the mean saccade amplitude was 9.3 ± 5.5° while in LRG movements it was 5.0 ± 1.9°. Thus during movements with higher residual gain the brain triggers larger saccades (P < 0.001).

Fig. 4.

A–E: sample correlation coefficient ρ; dark solid lines represent the linear fit y = mx+q with dotted lines representing the bounds of the coefficient’s confidence interval; dark dashed line represents the bisector. Significance level of the parameters *P < 0.05, **P < 0.01, ***P < 0.001). A: saccade amplitude against Et for HRG (ρ***, m***, q**). B: saccade amplitude against Eb for HRG (ρ**, m**, q***). C: saccade amplitude against Et for passive (gray dots, ρ***, m***, q***) and active head rotations (gray circles, ρ***, m***, q***). If the head movement is active, saccades are more accurate. D: saccade amplitude against Et for LRG (ρ***, m***, q***). E) Saccade amplitude against Eb for LRG [(ρ***, m***, q***). Saccades are triggered to compensate Et; high residual VOR gain improves the precision of saccades. Main sequence exponential fit y = A*[1−e^(−x/C)]. In head restrained condition A = 496, C = 7, gray dashed line; for covert saccades during head impulses A = 358, C = 4, black dashed line.

If the residual VOR gain is higher, the first corrective saccade is more accurate and on average 82% of gaze error during head movements is compensated, while with a lower residual gain, on average, only 62% of gaze error is compensated (Fig. 4, A and D). As previously reported (Tian et al. 2000; Weber et al. 2008) we also found that VOR gain was inversely related to head acceleration. The latencies of covert saccades averaged 114 ± 22 ms and were not correlated to VOR gain.

Saccades also compensate for the displacement of the head that occurs during the saccade.

Figure 4, A and B shows saccade amplitude plotted against the final error Et and the initial error Eb, respectively, for HRG movements. The amplitude of the saccades is better correlated with Et (ρ = 0.82, P < 0.001) than with Eb (ρ = 0.23, P < 0.01). Moreover, in HRG movements saccades are frequently overcompensatory with respect to Eb (data in Fig. 4B above the bisector line). Also for LRG movements the correlation with Et is higher than with Eb (ρ respectively 0.62 and 0.40, P < 0.001, Fig. 4, D and E). Unlike in HRG movements, in LRG movements saccades are less accurate and are overcompensatory with respect to Eb only when the errors are very small (<3°, Fig. 4E). Therefore, since corrective saccades can be over compensatory with respect to Eb and are better correlated with Et, the control system producing them must anticipate and take into account the displacement of the head that will occur as the saccade is being executed. This behavior suggests that information on head movement must be available during saccade execution and it contributes to determining when the saccade stops, and consequently the amplitude of the saccade.

Active head movements enhance both VOR gain and saccade accuracy.

In the nine patients who could perform the active head impulse task we investigated how the availability of an efference copy of the motor command influences the gain of the VOR and the precision of corrective saccades. The mean VOR gain computed on the subset of patients that performed active head impulses increased significantly from 0.29 ± 0.13 during passive head movements to 0.63 ± 0.18 during active head movements (P < 0.001), which agrees with previous reports that VOR gain is higher in active than in passive head rotations (Black et al. 2005; Della Santina et al. 2002; Halmagyi et al. 2003). In addition, overall saccade precision (SacP) also significantly improved from 0.59 ± 0.21 during passive head movements to 0.92 ± 0.21 during active head movements (P < 0.001). On the other hand, on an individual basis, there was no improvement in saccade precision with the increasing number of head impulses performed, except in one of the 23 patients. Figure 4C shows how during passive head movements saccade amplitudes are correlated with Et (ρ = 0.54, P < 0.001), but when the same patients made active head movements the correlation between saccade amplitudes and Et significantly increased (ρ = 0.89, P < 0.001), as did the slope of the linear regression, from 0.28 to 0.69. In these patients saccade latencies were significantly lower (P < 0.001) in active head movements (99 ± 28 ms) than in passive ones (114 ± 22 ms).

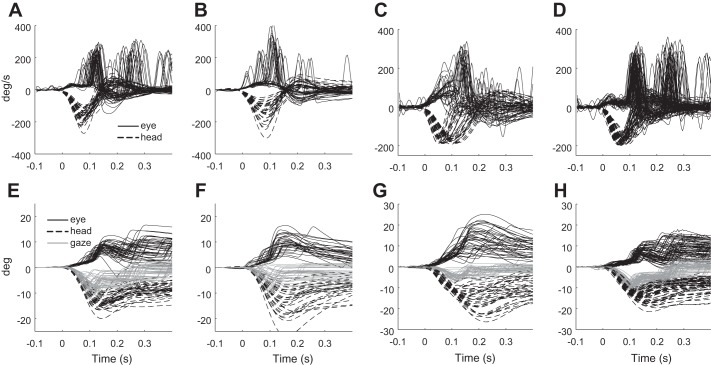
Figure 5 shows the raw passive and active head movements and ocular motor responses in one representative subject (Fig. 5, A, B, E, and F) together with the HRG and LRG responses recorded in all patients to head impulses with peak head velocities within 150 to 200°/s (Fig. 5, C, D, G, and H).

Fig. 5.

Raw data. Top row: head velocity (black dashed lines) and eye velocity (black solid lines) traces. Bottom row: corresponding head position (black dashed lines), eye position (black solid lines), and gaze (gray lines) traces. A and E: responses to passive head impulses in a representative patient. B and F: responses to active head impulses in the same patient. Mean gain increases from 0.24 in passive impulses to 0.61 in active impulses (P < 0.001); saccade precision increases from 0.59 to 1 (P < 0.001). Saccades are triggered with lower latency and are more accurate, so that gaze error is mostly compensated with a single movement, while in passive head impulses the patient needs a second correction. C and G: passive head impulses in all patients in HRG movements with peak head velocities ranging between 150 and 200°/s. D and H: passive head impulses in all patients in LRG movements with peak head velocities ranging between 150 and 200°/s. Mean gain is 0.18 in LRG and 0.55 in HRG impulses. Saccade precision is 0.51 in LRG and 0.81 in HRG impulses. In HRG movements gaze error is mostly corrected with a single covert saccade, while in LRG at least two corrections are required.

Effects on the main sequence.

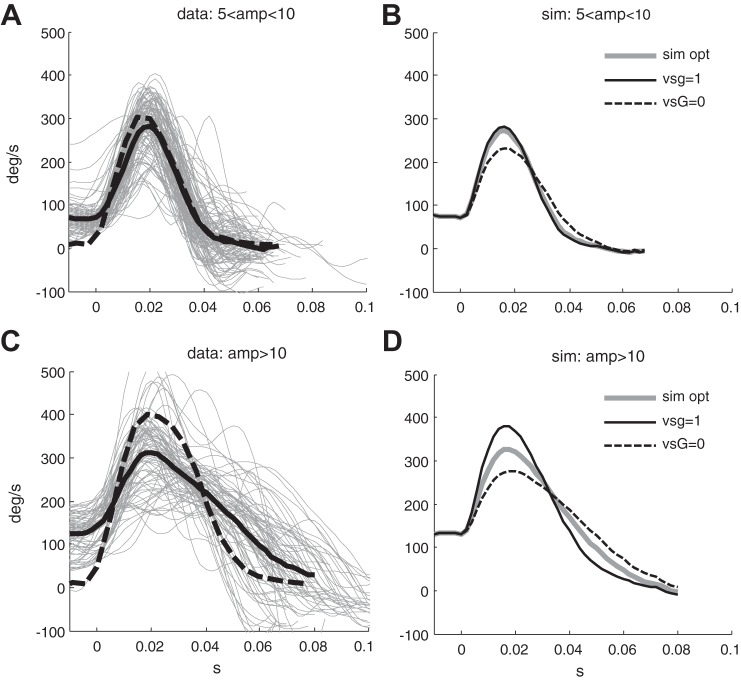
Figure 4F shows the peak velocity-amplitude relationship of the saccade (the main sequence) in the head-restrained condition and during head impulses. The main sequence of corrective saccades is similar to the main sequence of head-restrained horizontal saccades for small amplitudes (less than 10°), but at larger amplitudes saccades with head impulses are slower than saccades of the same amplitude made with head restrained (see also the velocity profiles in Fig. 9, A and C). This result agrees with prior reports (Peng et al. 2005; Tian et al. 2000).

Fig. 9.

A and C: eye velocity of individual covert saccades between 5 and 10° (A) and greater than 10° (C) (gray lines) and their means (black bold line), respectively. Black dashed lines represent the mean velocity of saccades of the same range of amplitudes made in the head-restrained condition. B and D: Mean of all simulations of covert saccades having an initial eye velocity greater than 50°/s, between 5 and 10° and greater than 10° amplitude, respectively. Gray lines represent the simulation with pG and vsG estimated through optimization, while solid black lines represent the simulation forcing vsG = 1 (linear summation hypothesis) and dashed black line forcing vsG = 0 (VOR command disengaged during the saccade).

In our experiments the mean peak velocity of saccades between 5 and 10° was 320 ± 46°/s (mean amplitude 7.5 ± 1.1°) in the head-restrained condition and 254 ± 48°/s for covert saccades begun while the head was moving (mean amplitude 6.3 ± 1.2°). Amplitude of saccades between 5 and 10° were on average 1.2° smaller for covert saccades (P < 0.001), and peak velocity was on average 70°/s lower (P < 0.001) for covert saccades.

The mean peak velocity of saccades larger than 10° was 419 ± 64°/s (mean amplitude 13.2 ± 2.4°) in the head-restrained condition and 334 ± 77°/s for covert saccades (mean amplitude 13.3 ± 2.1°). The amplitudes of saccades larger than 10° were not statistically different in the two groups (P = 0.7), while peak eye velocities were on average 90°/s lower for covert saccades (P < 0.001).

Gaze feedback control model of corrective saccades.

Our data suggest that corrective saccades are triggered to compensate for gaze position errors. The amplitude of corrective saccades is greater than the initial gaze error; thus these saccades must also account for the displacement of the head that will occur while the saccade is being made (Fig. 4, A and B). This behavior supports the idea that the brain uses a feedback control system based on gaze. Several key questions follow from this formulation: What is the error representing the input to the saccadic system and why does a higher residual VOR gain improve the accuracy of saccades?

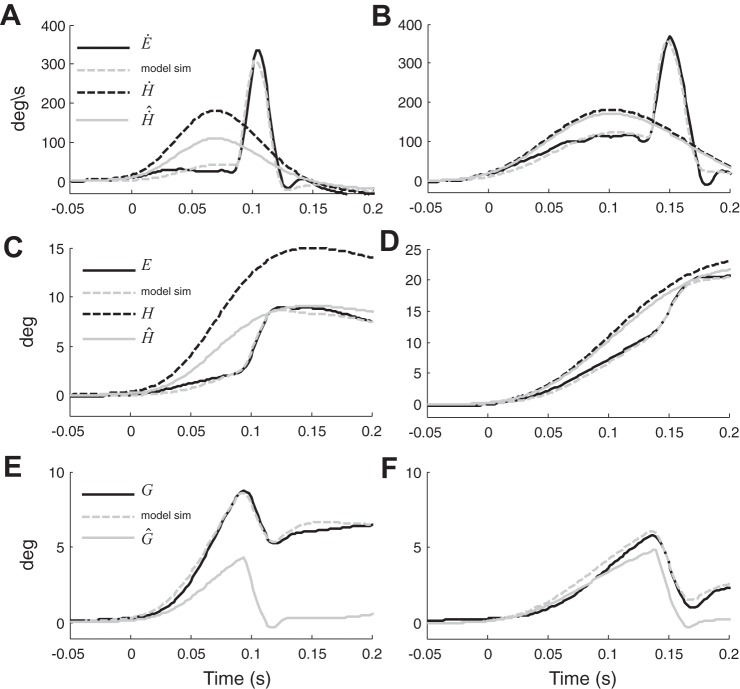
To explore these questions we used a mathematical model (Fig. 2) derived from the model of eye-head gaze shifts proposed by Laurutis and Robinson (1986). The low gain of the VOR in our patients leads to a gaze position error that drives a corrective saccade to bring the eyes back to the initial position in space. Gaze position ($\widehat{G}$) is estimated by adding an internal estimate of eye position ($\widehat{E}$) to an internal estimate of head position ($\widehat{H}$) which in our model is a scaled version of H through the gain pG and does not simply originate from semicircular canals information as was hypothesized in previous models. $\widehat{H}$ is a better estimate of head position than can be directly computed from the inadequate afferent information from the labyrinth, yet vestibular signals do contribute to $\widehat{H}$. When the residual VOR gain is low, $\widehat{H}$ is highly inaccurate (Fig. 6, A, C, and E, pG = 0.64). In these conditions, as shown in Fig. 6C, the triggered saccade moves the eyes toward $\widehat{H}$ and the predicted, but imperfect gaze estimate ($\widehat{H}+\widehat{E}$) reaches 0°, shutting off the saccadic mechanism. Since the resulting gaze position is not fully compensatory, a gaze position error (~5° in Fig. 6E) persists, reflecting the difference between the estimated and the real position of gaze. When the residual gain is high, however, $\widehat{H}$ is more accurate (Fig. 6, B, D, and F, pG = 0.94), so that the estimate of gaze position is nearly correct with the resulting gaze being almost perfectly compensatory [gaze error < 1.0° (Fig. 4F)].

Fig. 6.

Simulation (sim) of the model on two movements, one with residual VOR gain of 0.24 (A, C, E) and one with residual VOR gain of 0.7 (B, D, F). Black dashed lines represent head movement, black solid lines represent eye movement, gray solid lines represent the estimate of head movement predicted by the model (pG*head movement) and gray dotted lines represent eye movement simulations. Eye movement is inverted for the comparison with head movement. In A, the estimate of head movement is inaccurate (pG = 0.6), thus the triggered saccade is not adequate (C) and when the predicted gaze reaches 0°, stopping the saccade, the actual gaze correction is too small, leaving a final gaze error of 5° (E). In B, the estimate of head movement is accurate (pG = 0.94), hence the size of the corrective saccade is correct (D) and the final gaze position nearly reaches 0° (F).

As explained under methods, the model was fit with the head and eye movement response of each head impulse. The optimization procedure minimized the difference between the recorded and the predicted eye velocity during the saccade, with pG and vsG as free parameters, while the inputs to the model were the recorded head velocity and the computed VOR gain.

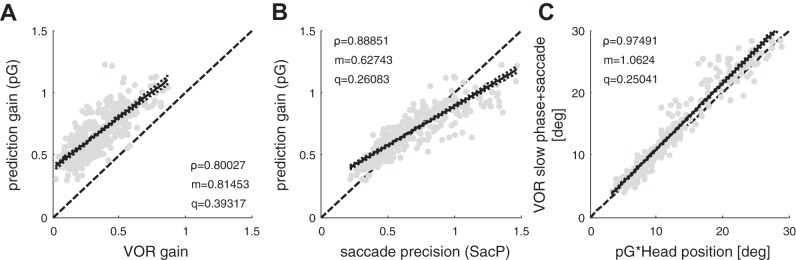
The resulting pG values for all passive movements are shown in Fig. 7, A–C, based on their correlations with the VOR gain, saccade precision, and the position of the eyes in the orbit at the end of the saccade correction. Our results on pG show that

Fig. 7.

Analysis of the correlations between the values of pG obtained by fitting the model to values of the variables associated with each head impulse. Dark solid lines represent the linear fit y = mx+q and the dotted lines represent the coefficients’ confidence interval bounds; dashed black lines represent the bisector. Significance level of the parameters *P < 0.05, **P < 0.01, ***P < 0.001. A: pG against residual VOR gain (ρ***, m***, q***). B: pG against saccade precision SacP (ρ***, m***, q***). C: cumulative VOR slow phase and saccade amplitude against predicted head position (ρ***, m***).

• pG correlates with residual VOR gain (Fig. 7A, pG = 0.81*VORgain+0.39, ρ = 0.8, P < 0.001), thus a higher residual VOR gain improves the estimate of head velocity and the precision of corrective saccades;

• pG is correlated with saccade precision SacP (Fig. 7B, pG = 0.62*SacP+0.26, ρ = 0.89, P < 0.001), thus the more precise the estimate, the more precise the saccades;

• the position of the eyes in the orbit at the end of the corrective saccade, i.e., the sum of the VOR slow phase + saccade amplitude, is highly correlated with the estimate of head position at the end of the corrective saccade [Fig. 7C, $\widehat{H}$ = pG*H = 1.06*(VOR slow phase + saccade amplitude), ρ = 0.97, P < 0.001]. Thus the corrective eye movement (slow phase + saccade) compensates for the estimate of head movement predicted by the model.

During active head movements pG values were significantly larger than during passive ones (P < 0.001), they were less correlated with VOR gain (ρ = 0.68), and the best regression line was pG = 0.54*VORgain+0.58 (P < 0.001).

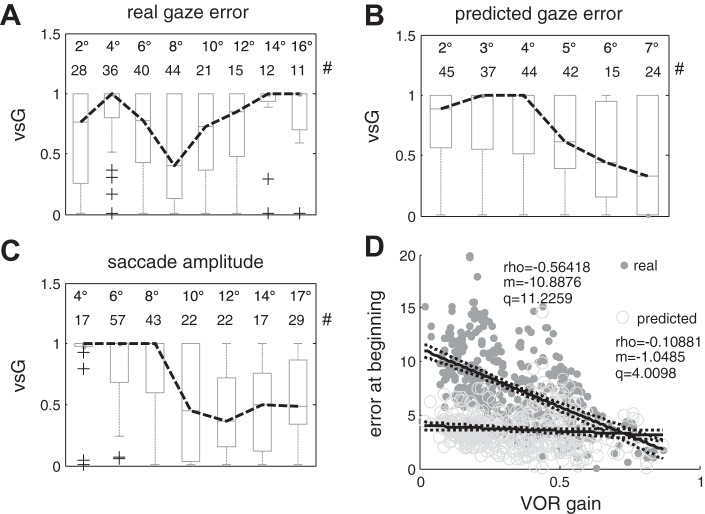
The vsG (VOR summation gain) values obtained from the model optimization procedure, which indicate the contribution of the VOR to the eye movement during the corrective saccade, are shown in Fig. 8, A–C. A and B show the vsG values with respect to gaze error and to the estimate of gaze error at the onset of the saccade, respectively, and in C with respect to saccade amplitude. Box plots summarize the distribution of vsG values for saccade amplitudes or gaze errors falling in each bin. The data suggest a reduction of the contribution of the VOR to the overall eye movement for saccades larger than ~8–10° and for estimates of gaze error larger than 5–6°, while no such relationship can be seen for actual gaze error. These results suggest that the brain relies on an estimate of gaze position, albeit erroneous. In statistical terms the relationship to saccade amplitude (Fig. 8C) is stronger, with the vsG values in the first three bins, i.e., those corresponding to smaller saccades, being significantly different from those of the last four bins (P < 0.01). Considering the estimates of gaze errors (${\widehat{G}}_{\mathrm{e}}$) computed at the beginning of the saccade (Fig. 8B) vsG values for errors in the 6 and 7° bins are significantly smaller (P < 0.05) than those for the 3 and 4° bins.

Fig. 8.

A–C: relationships between the vsG parameter, i.e., the parameter regulating the contribution of the VOR to the eye movement response during covert saccades, to the real gaze error, to the internal estimate of gaze error and to the recorded saccade amplitude. For vsG = 1 the VOR is added to the saccade command, for vsG = 0 the VOR contribution is entirely suppressed. For all plots the top two rows show the amplitude and the number of saccades for each bin, respectively. In each box, the central mark is the median, the edges are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted individually as crosses. The black dashed line connects the median of each bin. A: vsG against gaze error measured at the beginning of the saccade and binned in groups 1–3, 3–5, 5–7, 7–9, 9–11, 11–13, 13–15, 15–17°; B: vsG against predicted gaze error estimated at the beginning of the saccade and binned in groups 0–2, 2–3,3–4,4–5,5–6,6–8°; C: vsG against saccade amplitudes binned in groups 2–5, 5–7, 7–9, 9–11, 11–13, 13–15, 15–19°. D: real gaze error [dark gray dots, (ρ***, m***, q***)] and predicted gaze error (gray circles, ρ*, m*, q***) at the beginning of saccades against residual VOR gain.

Interaction of the VOR and saccade commands.

Figure 9, A and C shows eye velocity during covert saccades. We divided saccades in two groups based on their amplitude: between 5 and 10° and greater than 10°. As previously reported (Peng et al. 2005; Tian et al. 2000), covert saccades larger than 10° (Fig. 9C, solid line) have a reduced peak velocity and increased duration with respect to saccades of the same amplitude made with the head restrained (Fig. 9C, dotted line). We modeled this behavior by modulating the summation of the VOR command to the saccadic command during the correction as have others (Guitton and Volle 1987; Pelisson et al. 1988; Ramat et al. 2003; Tomlinson 1990). Although previous studies have shown that the contribution of the VOR varies during the saccade (Pelisson et al. 1988), we chose to use a constant value for the vsG parameter during the execution of a saccade both because the saccades in our patients are smaller and hence have a shorter duration compared with the Pelisson et al. study due to the different experimental protocols, and because in our experiments head velocities were continuously changing, making an estimate of a time varying VOR contribution difficult.

The mean traces of simulated saccades were superimposed on an initial eye velocity greater than 50°/s to clearly see the effect of the slow phase of the VOR on the saccade command (Fig. 9, B and D). Figure 8C shows the optimized vsG values for increasing saccade amplitudes. The values of vsG decrease to a median of 0.5 for saccades with amplitudes greater than 8–10° (groups 1–3 are significantly different from groups 4–7, P < 0.001). Simulations of saccades between 5 and 10° show that the VOR command is added to the saccadic command (linear summation hypothesis), otherwise peak velocity would be smaller (Fig. 9B, dashed black line). On the other hand, for saccades greater than 10° the VOR command is attenuated, since adding the entire command would increase peak eye velocity to ~400°/s as in the head restrained condition (Fig. 9D solid black line), which is not the case in our experimental data (thick gray line). A similar relationship is found between optimized vsG values and the estimate of gaze error at the beginning of each saccade (Fig. 8B). In this case the attenuation of the VOR contribution becomes manifest with errors between 5 and 6° (bins 5 and 6 in Fig. 8B). The 3 to 4° offset between the two relationships, i.e., between saccade amplitude or estimated gaze error and vsG, further shows that corrective saccades also compensate for the head rotation during the saccade and are therefore presumably controlled through a gaze feedback loop. These results indicate that the VOR command is added to the saccade command for small saccades, but is gradually suppressed for saccades larger than 8–10°. This behavior would account for the lower saturation of peak eye velocity in the main sequence for covert saccades (Fig. 4F).

Which error triggers covert saccades?

The gaze error accumulated at the beginning of corrective saccades decreases with increasing VOR gain (Fig. 8D, ρ = −0.56 and the slope m = −10.8) making it unlikely it is the signal used for triggering corrective saccades. The predicted gaze error $\widehat{G}$ at the onset of corrective saccades, instead, was always ~4°, across all experimental VOR gains (Fig. 8E, ρ = −0.1 and the slope m = −1.04), suggesting that with passive head impulses a threshold mechanism for triggering saccades is independent of VOR gain and uses the prediction error $G_D-\widehat{G}$ rather than real gaze error. The same is not evident for active head movements, during which the predicted and the real gaze error at the beginning of the corrective saccade are similar since the slow-phase gain is higher and saccades are triggered over a larger range of predicted gaze errors that, for VOR gains greater than 0.8, are lower than 4°.

DISCUSSION

First we recapitulate the key findings to put them in the context of a new model of generation of saccades when vestibular slow phases are deficient. We focused on the characteristics of the corrective “covert” saccades that occurred during head impulses while patients attempted to fix on a stationary target in front of them. The precision of these corrections depended on the residual gain of the VOR, with their amplitude being larger than the gaze error at the beginning of the correction. Furthermore, those corrections larger than ~10° had lower peak velocities than saccades of corresponding amplitudes made with the head fixed. During active head movements both the gain of the slow-phase response and the precision of the corrective saccades were higher. We simulated these behaviors building on previous mathematical models for gaze shifts in normal subjects in which a gaze feedback loop was central to producing accurate combined movements of the head and eyes. Here, based on our results in patients, we added several novel features: 1) an internally generated, multisensory estimate of head velocity contributing to the estimate of instantaneous gaze position and 2) modulation of the VOR contribution to eye movements during the corrective saccade with the amount depending on the value of the estimate of gaze error. This analysis emphasizes that during passive head impulses the residual vestibular information primarily determines the estimate of the head rotation, which in turn is used for predicting gaze position, and that the contribution of the VOR to eye movements during saccades is reduced beginning when saccades are larger than ~10°, which corresponds to an estimated gaze error of ~5°. When the parameter (vsG, Fig. 2) regulating the estimate of head position and the parameter (pG, Fig. 2) regulating the multisensory estimate of head movement were optimized to simulate eye velocity during the saccade, the model faithfully reproduced the entire repertoire of ocular motor responses of our patients as well as responses in normal subjects when the VOR gain is 1.0 (not shown). A key aspect underlying the success of the model is the use of two separate estimates of head velocity, one driving slow-phase eye movements and the other driving corrective saccades. This critical dichotomy is discussed further at the end of the next section.

Estimates of motion of the head.

Patients with unilateral vestibular neuritis compensate for a deficient VOR both by boosting the slow-phase response at the level of the VN and by using corrective compensatory saccades during gaze-stabilization tasks. The first saccade (covert saccade, triggered within 150 ms from the start of the head movement) was more accurate when the residual VOR gain was higher; the precision of the corrective saccade was 0.51 ± 0.17 for LRG and 0.85 ± 0.33 for HRG movements. Based on this result we hypothesize that corrective saccades are generated using an internally generated estimate of head velocity that is more faithful than the inaccurate head velocity signal transduced by the affected semicircular canals. The VN, however, receive information from many sources including somatosensory and visual sensory inputs, efference copies of motor commands, and signals from higher order structures such as the cerebral cortex and the cerebellum (see Anatomical substrate for head motion estimate below). By combining information from these inputs the VN could develop a better estimate of head motion and further modify the response based on a knowledge of the context and goals in which movement occurs. Such a process must be constantly monitored and adaptively modified based on the reliability of the different contributing signals.

Here we have shown that during active head movements both the gain of the vestibular slow phases and saccade precision are significantly larger than when head movements are passive, yet in both conditions the accuracy of the slow and the fast components of the ocular motor response differ, i.e., the slow-phase gain is significantly lower than saccade precision (SacP). Furthermore, our model simulations predict that during active impulses the estimate of the head movement (pG) relies less on the gain of the slow phase (VOR gain) than during passive stimuli, and that the correlation of pG and VOR gain is also lower in the active vs. the passive condition. Note that in our model the VOR gain parameter accounts for the gain of the actual slow-phase response, i.e., it represents the gain of the ocular motor command at the output of the VN and thus includes all the processing and signal integrations that may occur at that site. During active head impulses, then, the VOR gain parameter also uses the contribution of efference copy to the slow-phase response. Taken together these findings suggest that 1) in patients with peripheral vestibular disorders an efference copy of the head command improves both the VOR response and the higher order estimate of head motion based on internal feedback, and, as discussed earlier, 2) the estimate of head movement that is generated in the VN (which produces the slow phase) and the estimate based on the internal gaze feedback loop (which produces the saccade) are different.

Anatomical substrate for head motion estimate.

During self-motion the brain integrates information from many sources in an attempt to get a best estimate of where the head and body are in the environment. If the movements are active, efference copies of motor commands are also available for the computation, through internal models, of the best estimate of head movement and so the brain plans corrective responses accordingly (Cullen et al. 2011; Cullen and Brooks 2015). Extravestibular signals encoding head velocity are available in the cerebral cortex (Fukushima 1997) as well as at the earliest stages of vestibular processing in the VN to construct a central estimate of self-motion (Cullen 2012). There are three populations of neurons in the VN that receive afferent vestibular information: the position-vestibular-pause neurons (PVP), the floccular target neurons (FTN), and the vestibular-only neurons (VO). The first two groups are part of the direct three neuron arc implementing the VOR, while the VO neurons do not drive eye movements directly but project to the cerebellum, thalamus, and cerebral cortex (reviewed in Cullen 2012). Such neurons provide vestibular information to higher order structures responsible for spatial orientation, motor adaptation, and learning, including the cerebellum and the rostral fastigial nuclei. The last, being reciprocally connected to the VN, appears to be one structure responsible for the integration of proprioceptive and vestibular information and has been related to the development of internal models and sensory prediction errors for control of active and passive movements (Cullen and Brooks 2015).

The synergy of slow and fast eye movements.

By adaptively decreasing the VOR gain Bloomberg and colleagues (Bloomberg et al. 1991a, 1991b) found that it was the combined saccade and slow-phase response that reflected the attenuated response. A similar synergy between slow and fast phases was shown in the translational VOR (tVOR) in which the compensatory responses always relies on the cooperation of a slow eye movement and a saccade providing contributions that scale proportionally with different viewing distances (Ramat and Zee 2003). Those data showed that the control of gaze has access to an estimate of head movement that is more accurate than the one driving the pure tVOR response. Further studies investigating the influence of cognitive factors on the tVOR showed that expectation about the movement of the target and of the direction of self-motion can modify both the gain of the slow-phase response and the amount of the saccadic contribution (Ramat et al. 2005).

Here we investigated patients with a vestibular deficiency and found that corrective saccades were more accurate when the residual VOR gain was higher, indicating that better labyrinthine information gives a better estimate of head movement. The residual VOR is then crucial for a correct prediction of the head movement, and the results of the model optimization on the passive responses suggest that the vestibular contribution may account for ~80% of the estimate of head movement used in the prediction of gaze position. Moreover, the nine patients that performed active head impulses exhibited both a higher residual VOR gain and more precise corrective saccades (Fig. 4C) than during passive, unpredictable head impulses. Therefore, with active impulses, both the central estimate of head movement and the gain of the slow-phase response are improved by the availability of an efference copy of the motor command and possibly by the awareness of movement direction. Taken together these findings suggest that although the signals driving the slow phase differ from those representing the goal of covert saccades, the synergy of slow and fast eye movements, which is tailored to optimize gaze, holds for both passive and active head impulses.

Gaze feedback loop.

Another key finding was that covert saccades, which are triggered while the head is still moving, were often larger than the error accumulated before they began (Fig. 4B). This implies that the programming of corrective saccades not only uses the error cumulated before they begin but also a signal predicting the displacement of the head during the saccade. Indeed, several studies based on head movement perturbations suggest that the brain does use feedback control of gaze trajectory to change the line of sight during head-free gaze shifts (Boulanger et al. 2012; Daye et al. 2014; Goossens and Van Opstal 1997; Guitton and Volle 1987; Laurutis and Robinson 1986; Pelisson et al. 1988; Segal and Katsarkas 1988; Sylvestre and Cullen 2006; Tomlinson 1990). This feedback allows relatively accurate control of gaze even when the VOR is not functioning. Sylvestre and Cullen (2006) showed that saccadic premotor neurons change their response during head-free saccades when the head is perturbed, providing evidence that burst neurons are inside an eye-head feedback loop. More recently, Daye et al. (2015) analyzed gaze trajectories with and without whole body rotation imposed during the execution of a saccade. They found that even when no head movement is planned the brain uses feedback control of gaze and not of the eye alone.

The recent model of eye-head gaze shifts by Haji-Abolhassani et al. (2016) shares several features in common with our gaze-stabilization model. In particular they hypothesize the existence of a higher level estimate of head motion relying on vestibular and extravestibular, e.g., neck spindle afferents, as we do, which is then used to compute a gaze error signal along a gaze feedback loop driving the saccadic mechanism. Nonetheless, the two models have differences in their purpose, neurophysiological hypotheses, and emphasis as ours includes applications not only to normal humans, but to both active and passive gaze stabilization in patients with unilateral vestibular deficits. The Haji-Abolhassani model focuses on being able to reproduce the different eye-head gaze shift patterns experimentally recorded in both primates and in the cat using the same model topology. It achieves this by exploiting a nonlinear gain field sharing the gaze-shifting load between the head and eye platforms and different parameter sets for reproducing remarkable patterns presented in the literature. Our model instead focuses on the gaze-stabilizing eye movement produced in response to given active and passive head impulses. Our model reproduces the responses of both healthy subjects and patients based on the recorded VOR gain and the optimization of two parameters, vsG and pG, regulating the gain of the vestibular pathway during gaze corrective saccades and the faithfulness of the higher level estimate of head motion, respectively.

From a neurophysiological standpoint, instead, while the Haji-Abolhassani et al. model considers that the output of the “Distributed Head Velocity Estimation” block is an accurate estimate of head velocity, our data on unilateral vestibular patients shows that such an estimate, which is used to compute gaze error and drive corrective saccades in our model, strongly depends on vestibular gain (see the correlation of pG with VOR gain) and may therefore be inaccurate when VOR gain is low. This differs from the presentation of the Haji-Abolhassani et al. model.

Furthermore, the Haji-Abolhassani model hypothesizes a more complex processing of the gaze error signal, which is based on an accurate estimate of head velocity and is then low-pass filtered and nonlinearly processed in the superior colliculus projecting to tectoreticular neurons and fed to the burst neurons in the paramedian pontine reticular formation (PPRF) that they hypothesize receives projections carrying PVP and VO signals (their Fig. 3). In our model, instead, the higher level estimate of head displacement, combined with the efference copy of eye position from the NPH, is used to compute the gaze error directly driving the saccadic mechanism within a feedback loop. This is sufficient to reproduce our experimental data, without hypothesizing direct projections from PVP and VO neurons to the burst neurons in the PPRF, which have not yet been demonstrated. Nevertheless, deciding which model is best or even accords with all the neurophysiological data will require further experimentation, but, as with all models, both point to specific experiments that address these questions.

What might be the physiological correlate of the online control of saccade (gaze) amplitude during head movements? We hypothesize that 1) the head motion signal used in the computation of gaze is an estimate derived from the integration of extravestibular signals through an internal model computing head displacement and 2) such an estimate is not available to the direct VOR circuitry including PVP and FTN neurons but is provided by extravestibular structures, possibly in the cerebellum. This gaze-feedback circuit could rely on VO neurons projecting to the rostral FN through which it might enter the gaze feedback loop regulating the amplitude of saccades.

During active head rotations the gain of the slow-phase response is increased with respect to the passive condition. One previously hypothesized mechanism (Halmagyi et al. 2003) was that active head rotations increase the sensitivity of second order neurons. We hypothesize that the enhancement of the VOR response during active head rotations may occur at the level of type I PVP neurons, which have already been shown to be responsible for scaling VOR responses with viewing distance (McCrea et al. 1999). In fact the convergence of multisensory and cerebellar inputs together with premotor head movement commands to the VN makes PVP neurons the most likely candidate for modulating VOR responses as a function of context, i.e., the goal of the response, gaze changing or gaze stabilizing (Roy and Cullen 2002). Consistent with this hypothesis the responses of these neurons were significantly attenuated during voluntary eye-head gaze shifts while they faithfully encoded head motion when stabilizing gaze whether head motion was active or passive (Roy and Cullen 2002). Our data comparing active vs. passive movements also suggests that an efference copy of the head command improves both the VOR response and the higher order estimate of head motion available to the presumed gaze feedback loop. Thus these anatomical considerations taken together with our experimental findings and modeling results lead us to hypothesize, first, that our vestibular-deficient patients implemented adaptive processes in the VN to boost the impact of the efference copy of the head movement command on the slow-phase response, possibly through PVP neurons in the direct VOR pathway. Second, we propose that the brain uses a higher level estimate of gaze error, possibly through a gaze-feedback loop and internal models in the cerebellum, which integrates head movement related information from both PVP and VO neurons together with extravestibular signals.

VOR modulation during covert saccades.

The peak velocity of corrective saccades increased proportionally with saccade amplitude up to 10° as in the head-restrained condition; however, with larger saccades peak velocities were less than those of the same-size saccades made with the head fixed (Fig. 4F). A similar finding has been reported by others using high-acceleration, transient head rotations; corrective movements larger than 10° were slower than head-fixed saccades of corresponding amplitudes (Peng et al. 2005; Tian et al. 2000). Analogously, during active combined eye (saccade)-head movements that redirect gaze, and especially for larger movements, the brain may suppress the VOR slow-phase response and the degree of suppression is correlated with the amplitude of the desired change in gaze (Guitton and Volle 1987; Laurutis and Robinson 1986; Pelisson et al. 1988; Tomlinson 1990; Tomlinson and Bahra 1986).

At large gaze-shift amplitudes, head rotations are typically fast so that the VOR component is large and is counterproductive with respect to the gaze-shifting goal as it opposes saccade velocity and thereby increases the time to complete the gaze shift. On the other hand, at smaller amplitudes relatively slow head velocities contribute little to the change in gaze (Daye et al. 2014). Indeed, Tomlinson and Bahra (1986) perturbed head movement unpredictably during combined eye-head gaze shifts of varying amplitude in monkeys and found that 1) perturbations delivered during smaller gaze shifts were entirely compensated by the VOR, 2) there was a range of gaze-shift amplitudes during which the VOR functioned with a smaller than normal gain, and 3) for even larger gaze shifts the VOR was completely turned off. These authors suggested that small gaze shifts, <20°, are commonly accomplished without a head movement or without any significant contribution from the movement of the head and hence do not inhibit the VOR, while larger gaze shifts (>40°), which are typically achieved with an active combined eye-head movement, cause the suppression of the VOR. Similar results in humans were obtained by other groups (Guitton and Volle 1987; Laurutis and Robinson 1986; Lefèvre et al. 1992; Pelisson et al. 1988) and neural correlates for this behavior were later found in monkeys in the activity of PVP neurons being modulated by saccadic burst neurons in the PPRF (Roy and Cullen 1998, 2002). One can speculate this behavior reflects the natural circumstances that smaller and usually slower head movements are associated with passive perturbations, in which case the VOR needs to be engaged to hold gaze stationary, and larger and usually faster head movements are associated with active perturbations in which case the VOR needs to be turned off to facilitate a change in gaze. Note that although a few studies found that the suppression of the VOR varies during the saccade, being more effective at its beginning and decreasing toward its end (Cullen et al. 2004; Lefèvre et al. 1992; Pelisson et al. 1988; Tomlinson and Bahra 1986), our conceptual model uses a constant vsG value throughout the saccade for two reasons. The saccades recorded in our patients were generally small and brief (mean duration 38 ms), which is comparable to the gain restoration period found by Lefèvre and colleagues (Lefèvre et al. 1992), and because the gain of our patients’ VOR was generally low (see Fig. 2) so that its partial restoration toward saccade end would have little influence on the overall eye movement.

In our case the VOR appears to be progressively disengaged beginning with small saccadic amplitudes (above ~10°), possibly because high accelerations, as with head impulse testing, could cause relatively large gaze errors even for small head rotations. On the other hand, unlike active, gaze-shifting eye-head movements during which VOR inhibition helps gaze reach the new target more quickly, during the compensatory task performed by our patients, VOR inhibition is counterproductive as it increases the time to reacquire the fixation target. In fact, in our experimental conditions, with the subject having to maintain fixation of a stationary target, the VOR acts in the same direction of the covert saccade and would therefore help reduce the time during which gaze is off target. This apparently counterproductive behavior may be related to the artificiality of the head impulse test paradigm as high velocities and high accelerations of the head are rarely experienced during natural tasks that require stabilization of gaze. Though the question of what signal is used to modulate the gain of the VOR during the execution of larger saccades cannot be answered from our behavioral results alone, we found that both the estimate of gaze error and the amplitudes of corrective saccades were inversely related to the VOR slow-phase contribution to eye movements during saccades. On the other hand, the finding that patients with a reduced VOR gain significantly underestimate head rotations suggests that such a VOR contribution is not modulated based on the actual gaze error as was suggested by studies investigating gaze shifts in healthy subjects (Daye et al. 2014; Guitton and Volle 1987; Laurutis and Robinson 1986; Panouillères et al. 2012). Rather our patients are using an estimate, or the percept, of such an error, albeit erroneous in our case, possibly similar to what has been suggested by Bloomberg and colleagues in their adaptation studies in normal subjects (Bloomberg et al. 1991a).

Finally, we note that gaze error at the beginning of the saccade decreases with increasing VOR gain because the higher the gain, the smaller the accumulated error. In contrast, the predicted gaze error at the time when saccades are triggered remains roughly constant across VOR gain values. This finding supports the idea that during passive head impulses saccades are triggered based on a threshold on the internal estimate of gaze error, in our case when ${\widehat{G}}_{\mathrm{e}}$ becomes larger than ~4°. On the other hand, the values of the latencies of covert saccades were not correlated with the gain of the VOR, possibly because the gain of the VOR decreases with increasing head acceleration so that during more abrupt impulses, when the error accumulates faster, the accuracy of the estimate of the movement of the head decreases.

A few caveats need to be emphasized. While our conceptual model nicely accounts for our data it does not directly address the role of the long-term adaptation that has taken place in response to the initial insult. Only by following the behavior of such patients over time might we be able to determine how these parameters are adaptively adjusted. On the other hand, we found no evidence for adaptation taking place during the course of collection of the experimental data. Second, our stimulus, the high-acceleration, passively imposed head impulse is an unnatural one so any previous exposure to it is unlikely and therefore any adaptation to it is likely minimal. Nevertheless, by its nature it may reveal important features of the circuits that help stabilize gaze in natural circumstances.

In conclusion, our data and simulations support the hypothesis that the amplitude of corrective saccades in labyrinthine defect patients is controlled by a gaze feedback loop, similarly to what has been proposed for combined eye-head gaze shifts in normal subjects. Our data on patients, however, shows that this process must rely on a more complex multisensory estimate of head movement. Such an estimate would be more reliable than that based on the defective labyrinthine signals alone and could reach the gaze control loop through the VO neurons in the VN, possibly via projections to the rostral fastigial nuclei. The latter could then be a key structure in making these estimates since it has neurons that precisely encode sensory prediction errors and are therefore active during externally imposed head movements. The peak velocity of corrective saccades of more than 10° amplitude was lower than those made in the head restrained condition. This finding may be an unwanted byproduct of the circuit that normally modulates VOR gain during active gaze shifts, although in our gaze-stabilization task the contribution of the VOR would help reduce the time needed to reacquire the target. We implemented these ideas in a conceptual mathematical model based on a gaze feedback loop in which the multisensory estimate of head velocity is a scaled version of actual head velocity and the VOR contribution to the eye movement during saccades is modulated by a gain factor depending on the same internal estimate of gaze error used in the gaze feedback loop. Furthermore, such an estimate of gaze error could also be the signal used to trigger corrective saccades when it reaches a relatively small value. A different mechanism in the VN modulates the response of the direct VOR pathway using the available information defining the context in which the head movement occurs, including the efference copy of the motor command during active head impulses. Finally, the model can be applied to both gaze-changing and gaze-stabilizing behaviors whenever a saccade is associated with a specific head movement.

GRANTS

This research was supported by Ministero dell'Istruzione, dell'Università e della Ricerca (Ministry of Education, Research and Universities): Stefano Ramat 2010R277FT_004; Ministero della Salute (Ministry of Health, Italy): Maurizio Versino RF-2011-02352379.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

P.C., M.V., S.C., S.Q., M.M., E.Z., and G.M. performed experiments; P.C. analyzed data; P.C., M.V., S.C., D.S.Z., and S.R. interpreted results of experiments; P.C. prepared figures; P.C. and S.R. drafted manuscript; M.V. and S.R. conceived and designed research; D.S.Z. and S.R. edited and revised manuscript; D.S.Z. and S.R. approved final version of manuscript.