Modeling the diversity of spontaneous and agonist-induced electrical activity in anterior pituitary corticotrophs

We and others recently demonstrated that the electrical activity and calcium dynamics of corticotrophs are strikingly diverse, both spontaneously and in response to the agonists CRH and AVP. Here we demonstrate this diversity with electrophysiological measurements and use mathematical modeling to investigate its possible sources. We compare the known mechanisms of agonist-induced activity in the model, showing how the context of ionic conductances dictates the effects of agonists even when their target is fixed.

Abstract

Pituitary corticotrophs fire action potentials spontaneously and in response to stimulation with corticotropin-releasing hormone (CRH) and arginine vasopressin (AVP), and such electrical activity is critical for calcium signaling and calcium-dependent adrenocorticotropic hormone secretion. These cells typically fire tall, sharp action potentials when spontaneously active, but a variety of other spontaneous patterns have also been reported, including various modes of bursting. There is variability in reports of the fraction of corticotrophs that are electrically active, as well as their patterns of activity, and the sources of this variation are not well understood. The ionic mechanisms responsible for CRH- and AVP-triggered electrical activity in corticotrophs are also poorly characterized. We use electrophysiological measurements and mathematical modeling to investigate possible sources of variability in patterns of spontaneous and agonist-induced corticotroph electrical activity. In the model, variation in as few as two parameters can give rise to many of the types of patterns observed in electrophysiological recordings of corticotrophs. We compare the known mechanisms for CRH, AVP, and glucocorticoid actions and find that different ionic mechanisms can contribute in different but complementary ways to generate the complex time courses of CRH and AVP responses. In summary, our modeling suggests that corticotrophs have several mechanisms at their disposal to achieve their primary function of pacemaking depolarization and increased electrical activity in response to CRH and AVP.

NEW & NOTEWORTHY We and others recently demonstrated that the electrical activity and calcium dynamics of corticotrophs are strikingly diverse, both spontaneously and in response to the agonists CRH and AVP. Here we demonstrate this diversity with electrophysiological measurements and use mathematical modeling to investigate its possible sources. We compare the known mechanisms of agonist-induced activity in the model, showing how the context of ionic conductances dictates the effects of agonists even when their target is fixed.

corticotrophs are a subpopulation of secretory anterior pituitary cells that produce adrenocorticotropic hormone (ACTH) under the control of two hypothalamic neurohormones, corticotropin-releasing hormone (CRH) and arginine vasopressin (AVP). ACTH is secreted into the systemic circulation to stimulate the production and secretion of glucocorticoids (CORT; cortisol in humans or corticosterone in rodents) from the adrenal glands. CORT in turn provides negative feedback to the hypothalamus and pituitary to control ACTH release. The secretory function of corticotrophs is critically dependent on the patterns of electrical activity and the associated fluctuations of intracellular calcium concentration ([Ca²⁺]_i) (Tse et al. 2012).

There have been a variety of reported levels and patterns of spontaneous corticotroph electrical activity, ranging from quiescence in all recorded male rat (Lee and Tse 1997) and mouse (Lee et al. 2011) cells to activity in nearly all female (Liang et al. 2011) and male (Duncan et al. 2015, 2016) mouse corticotrophs. We and others have reported ~60% active cells in mixed-sex mouse (Zemkova et al. 2016) and male rat (Kuryshev et al. 1995) corticotrophs, with quiescent cells significantly more hyperpolarized than active cells (Zemkova et al. 2016). Reported spontaneous electrical activity consists typically of low-frequency, high-amplitude single action potentials but may also include plateau-like bursting with tall spikes and pseudoplateau-like bursting with small-amplitude spikes superimposed on a plateau (Liang et al. 2011; Zemkova et al. 2016). The sources of this variation are not understood but may include intrinsic heterogeneity of corticotroph ion channel expression or differences in cell preparations and recording techniques.

CRH facilitates electrical activity and Ca²⁺ influx by activating the CRH receptor type 1-dependent PKA signaling pathway (Aguilera et al. 2004). CRH action in quiescent corticotrophs is characterized by a pacemaking depolarization, leading to electrical activity that includes spiking and bursting (Kuryshev et al. 1995; Lee and Tse 1997; Zemkova et al. 2016). Depolarization due to CRH has not always been reported for initially silent cells, such as AtT-20 cells and ACTH-secreting pituitary adenoma cells (Guérineau et al. 1991). Electrically active corticotrophs display a smaller depolarization along with increased firing frequency of spikes and bursts and may transition between spiking and bursting (Kuryshev et al. 1995, 1997; Liang et al. 2011; Zemkova et al. 2016). Several potential mechanisms for CRH action have been postulated based on activation of inward cationic currents and/or inhibition of outward K⁺ currents. The inability of CRH to depolarize corticotrophs bathed in Na⁺-deficient medium suggested the contribution of a background Na⁺ current (I_Nab) in pacemaking depolarization (Liang et al. 2011). However, we recently reported that CRH could trigger depolarization and activity in either Na⁺- or Ca²⁺-deficient medium (Zemkova et al. 2016), suggesting involvement of a conductance such that these two cations could substitute for one another. Such a conductance has been shown in other rodent pituitary cell types (Tomić et al. 2011) and human pituitary adenoma cells (Takano et al. 1996). A major, but not exclusive, component of the CRH response was found to be mediated by the inwardly rectifying K⁺ current (I_Kir) in rat (Kuryshev et al. 1997) but not mouse (Liang et al. 2011) corticotrophs. A CRH-dependent reduction in current due to the TWIK-related K⁺ (TREK)-1 channel, which provides a background K⁺ leak current (I_K,leak), has also been shown (Lee et al. 2011, 2015). The increase in a high-voltage-gated Ca²⁺ current (I_Ca) was observed in AtT-20 immortalized corticotrophs (Luini et al. 1985) and used as the primary mechanism of CRH action in several mathematical modeling studies (Duncan et al. 2015, 2016; LeBeau et al. 1997, 1998; Shorten et al. 2000). Another line of experiments showed that CRH inhibits large-conductance Ca²⁺- and voltage-activated K⁺ currents (I_BK) in a PKA-dependent manner, an effect blocked by CORT in AtT-20 cells (Shipston et al. 1996). Furthermore, CRH-induced bursting activity, but not spike frequency increase, was reduced by blocking BK channels and in BK channel-knockout mice (Duncan et al. 2015, 2016). Whether, and to what degree, all these mechanisms overlap during the CRH response remains to be determined.

AVP stimulates corticotrophs through G_q/11-coupled AVP receptor type 1b, leading to an early inositol 1,4,5-trisphosphate-dependent Ca²⁺ release from the endoplasmic reticulum (ER) and sustained electrical activity-driven Ca²⁺ influx. These changes in [Ca²⁺]_i are accompanied by a transient hyperpolarization of the membrane potential followed by an increase in spiking and bursting activity. Lee et al. (2015) showed that the transient hyperpolarization could be abolished by the small-conductance Ca²⁺-activated K⁺ channel blocker apamin. This unmasked a concomitant membrane depolarization, which was argued to be due to PKC-dependent inhibition of TREK-1 channels. In other tissues, AVP has been shown to stimulate cationic currents, such as TRPC6 (Mani et al. 2009). Duncan et al. (2015) reported that AVP increased frequency of single-spiking activity but did not trigger bursting, which they modeled by increasing a nonspecific cationic current. We recently showed that AVP could also trigger bursting in addition to increasing spike frequency (Zemkova et al. 2016). In both CRH and AVP responses, it is unclear whether the ionic mechanisms responsible for depolarization and event frequency changes are the same as or distinct from those responsible for transitions between spiking and bursting activity patterns.

Here we present electrophysiological recordings and a mathematical model of corticotroph electrical activity and Ca²⁺ dynamics with the aim of capturing the reported variability in spontaneous and agonist-induced activity patterns. We demonstrate how variation in the background currents I_Nab, I_Kir, and I_K,leak contributes to whether cells are active or silent. Because I_BK has been reported to contribute to the patterns of spontaneous activity in corticotrophs (Duncan et al. 2015, 2016) and other pituitary cells (Van Goor et al. 2001a), we also examine the effect of variation of I_BK in spontaneous and agonist-induced electrical activity patterns. Using the model, we test the hypothesis that while direct CRH-induced modulation of BK channels can cause transitions from spiking to bursting activity, this is not necessary; other CRH mechanisms can trigger bursting as well, depending on the amount of BK present. We compare the extent to which each of the proposed mechanisms of CRH, AVP, and CORT action can lead to observed agonist-induced changes in activity patterns and show that the different ionic mechanisms can contribute in different but complementary ways to generate the different phases of CRH- and AVP-induced responses. The dependence of CRH and AVP responses on the context of intrinsic corticotroph parameters is similar to state-dependent neuromodulation, which has been studied in neurons and neuronal networks (Goldman et al. 2001; Marder et al. 2014). We take advantage of the parallel computation capabilities of modern graphics processors to show how model parameters of interest affect electrical activity across full two-parameter planes in addition to time courses at single representative points in parameter space. Our parameter sampling technique, which aims to provide a more global perspective of model behavior, shares similarities with model database approaches (Günay 2015), in which multiple parameter combinations have been shown to give rise to similar neuronal activity (Goldman et al. 2001; Prinz et al. 2004; Taylor et al. 2009).

MATERIALS AND METHODS

Animals.

Experiments were performed on transgenic mice expressing the tdimer2 (12) engineered form of DsRed protein under the control of proopiomelanocortin regulatory elements (Hentges et al. 2009). Breeding pairs of congenic C57BL/6J homozygous mice were used to generate mice for pituitary harvest. Euthanasia was performed by decapitation after CO₂ sedation. All animal procedures were approved by the National Institute of Child Health and Human Development Animal Care and Use Committee.

Cell cultures.

Pituitary glands from three to five mice of both sexes were collected in ice-cold Dulbecco’s phosphate-buffered saline. After removal of the neurointermediate lobe, anterior pituitary tissue was washed in Dulbecco’s phosphate-buffered saline containing 0.3% BSA, 2 mM glutamine, and MEM Vitamin Solution (Invitrogen, Carlsbad, CA) and treated with 0.4% trypsin for 15 min at 37°C. The cells were mechanically dispersed, filtered through a 40-µm nylon mesh, centrifuged at 300 g for 10 min, and resuspended in medium 199 containing Earle’s salts, sodium bicarbonate, 10% heat-inactivated horse serum, penicillin (100 U/ml), and streptomycin (100 µg/ml). For experiments, 0.1–0.2 million cells were plated onto 25-mm glass coverslips coated with 1% poly-l-lysine and cultured in a humidified 5% CO₂ atmosphere at 37°C.

Electrophysiology.

Electrophysiological measurements were performed during the first 24 h after cell dispersion. Membrane potentials and CRH- or AVP- stimulated responses were measured in identified corticotrophs with the nystatin-perforated patch-clamp technique (Zemkova et al. 2016). Cells were continuously perfused with an extracellular solution containing (in mM) 150 NaCl, 3 KCl, 2 CaCl₂, 1 MgCl₂, 10 HEPES, and 10 glucose; pH was adjusted to 7.3 with NaOH. The pipette solution contained (in mM) 70 K-aspartate, 70 KCl, 3 MgCl₂, and 10 HEPES; pH was adjusted to 7.2 with KOH. Before measurement, Pluronic F-127, a dispersing agent, and then nystatin were added to the intracellular solution from stock solutions (nystatin, 50 mg/ml in dimethyl sulfoxide, always freshly prepared) to obtain a final concentration of 500 µg/ml Pluronic F-127 and 250 µg/ml nystatin. Recordings were performed with an Axopatch 200B amplifier (Axon Instruments, Union City, CA). Data were captured and stored with the pCLAMP 10 software package in conjunction with a Digidata 1322A A/D converter (Axon Instruments). The recordings were not corrected for the liquid junction potential, which was +9.6 mV. Solutions containing CRH or AVP (from Bachem, Torrance, CA) were delivered to the recording chamber by a gravity-driven microperfusion system (RSC-200 Rapid Solution Changer, BioLogic). Electrophysiological experiments were performed at room temperature (21–23°C).

Mathematical model and numerical simulations.

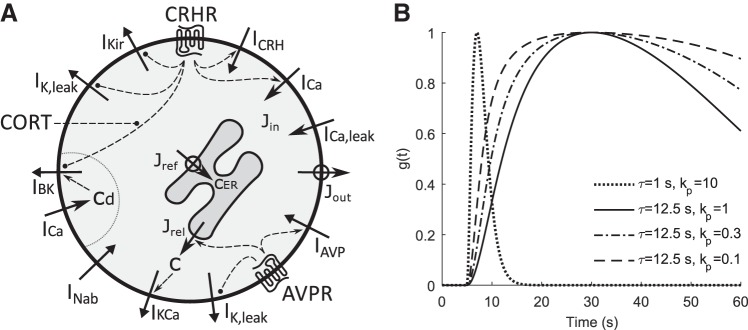
We use a biophysical model (Fig. 1A) based on in vitro data, similar in structure to a previously published model (Duncan et al. 2015, 2016). The model includes the several subthreshold currents that set the rest potential in silent cells. I_Nab has been shown in corticotrophs (Liang et al. 2011; Zemkova et al. 2016), similar to that reported in other pituitary cell types (Tomić et al. 2011). We include I_Kir (Kuryshev et al. 1997) and I_K,leak (Lee et al. 2011, 2015; Lee and Tse 1997) as potential targets of agonist-induced signaling. We also include a Ca²⁺ leak (I_Ca,leak) current to maintain store calcium levels in silent cells. Voltage- and Ca²⁺-dependent currents are also included for their contributions to patterns of electrical activity in corticotroph cells. These include voltage-dependent Na⁺ current (I_NaV), I_Ca, delayed-rectifier K⁺ current (I_K), A-type transient K⁺ current (I_A), Ca²⁺-activated K⁺ current (I_KCa), and I_BK. As putative targets of agonist action, CRH- and AVP-activated nonspecific cationic currents are also included as I_CRH and I_AVP, respectively. The membrane potential V is governed by the current balance equation

$$C_{\text{m}}\frac{\mathrm{d}V}{\mathrm{d}t}=-\left(I_{\text{NaV}}+I_{\text{Nab}}+I_{\text{Ca}}+I_{\text{Ca,leak}}+I_{\text{K}}+I_{\text{Kir}}+I_{\text{A}}+I_{\text{KCa}}+I_{\text{BK}}+I_{\text{K,leak}}+I_{\text{CRH}}+I_{\text{AVP}}\right)$$

where C_m is the membrane capacitance. The ionic currents are defined as follows:

Fig. 1.

Mathematical model of pituitary corticotrophs. A: diagram showing agonist-modulated ion currents and Ca²⁺ fluxes. Variability in electrical activity patterns is modeled by variation in large-conductance Ca²⁺ activated K⁺ (I_BK) and background Na⁺ (I_Nab) currents. Bulk cytosolic and ER Ca²⁺ concentrations are denoted c and c_ER, respectively. The Ca²⁺ concentration in a microdomain near the mouth of open voltage-gated Ca²⁺ channels is denoted c_d. CRH modulates five ionic currents: I_CRH, inward cationic; I_K,leak, K⁺ leak; I_Kir, inwardly rectifying K⁺; I_Ca, high voltage gated Ca²⁺; I_BK (activated by c_d). CORT is assumed to inhibit CRH action on BK channels (Shipston et al. 1996). The Ca²⁺ influx J_in depends on I_Ca and I_Ca,leak, a Ca²⁺ leak current. The Ca²⁺ fluxes into and out of the ER and out of the cell are J_ref, J_rel, and J_out, respectively. AVP increases J_rel, releasing Ca²⁺ from the ER and activating a Ca²⁺ activated K⁺ current, I_KCa. In parallel, AVP activates an inward leak current, I_AVP, or inhibits I_K,leak. ER Ca²⁺ dynamics are only included for simulations involving AVP. Activation and inhibition are denoted by dashed lines terminating in arrows or circles. CRHR, CRH receptor; AVPR, AVP receptor. B: time courses of pulses used to simulate CRH and AVP application. CRH application targeting g_CRH, V_m, and k_CaBK and AVP’s effect on g_AVP were modeled with a pulse with τ = 12.5 s and k_p = 1 (solid line). CRH effects on g_Kir and g_K,leak were simulated with τ = 12.5 s and k_p = 0.3 and 0.1, respectively (dash-dotted and dashed lines). AVP action on Ca²⁺ release from the ER was simulated with a pulse with τ = 1 s and k_p = 10 (dotted line).

$$I_{\text{NaV}}=g_{\mathrm{N}\mathrm{a}\mathrm{V}}{m}_{\text{Na},\infty }^3{h}_{\text{Na}}\left(V-E_{\text{Na}}\right)$$

$$I_{\text{Nab}}=g_{\text{Nab}}\left(V-E_{\text{NS}}\right)$$

$$I_{\text{Ca}}=g_{\text{Ca}}{m}_{\text{Ca,}\infty }\left(V-E_{\text{Ca}}\right)$$

$$I_{\text{Ca,leak}}=g_{\text{Ca,leak}}\left(V-E_{\text{Ca}}\right)$$

$$I_{\text{K}}=g_{\text{K}}n\left(V-E_{\text{K}}\right)$$

$$I_{\text{Kir}}=g_{\text{Kir}}{n}_{\text{Kir},\infty }\left(V-E_{\text{K}}\right)$$

$$I_{\text{A}}=g_{\text{A}}{n}_{\text{A},\infty }{h}_{\text{A}}\left(V-E_{\text{K}}\right)$$

$$I_{\text{KCa}}=g_{\text{KCa}}{n}_{\text{KCa,}\infty }\left(V-E_{\text{K}}\right)$$

$$I_{\text{BK}}=g_{\text{BK}}{n}_{\text{BK}}\left(V-E_{\text{K}}\right)$$

$$I_{\text{K,leak}}=g_{\text{K,leak}}\left(V-E_{\text{K}}\right)$$

$$I_{\text{CRH}}=g_{\text{CRH}}\left(V-E_{\text{NS}}\right)$$

$$I_{\text{AVP}}=g_{\text{AVP}}\left(V-E_{\text{NS}}\right)$$

Gating variables are governed by equations of the form

$${\tau }_x\frac{\text{d}x}{\text{d}t}=x_{\infty }-x$$

where x ∈ {h_Na, n, h_A, n_BK}. The steady-state activation and inactivation functions are of the form

$$x_{\infty }=1/\left(1+e^{\left(V_x-V\right)/s_x}\right)$$

for x ∈ {m_Na, h_Na, m_Ca, n, n_Kir, n_A, h_A, n_BK}. We model a subset of BK similar to the stress-related exon splice variant (Shipston et al. 1999; Xie and McCobb 1998), as in prior theoretical work (Duncan et al. 2015, 2016). I_BK is assumed to depend on the [Ca²⁺] in a microdomain near open calcium channels, c_d. This is approximated by including Ca²⁺ domain dependence in the steady-state activation function for BK as follows:

$$V_{\text{nBK}}=0.1-18\log \left({\mathrm{c}}_{\text{d}}/k_{\text{CaBK}}\right)$$

where c_d = −AI_Ca and A converts ionic current to microdomain [Ca²⁺] (Tsaneva-Atanasova et al. 2007). With the default parameters, BK activation is a steep function of membrane potential with half-maximal activation at approximately −15.1 mV. When k_CaBK is increased, the activation curve shifts to the right and becomes less steep preferentially at voltages above the half-maximal activation value. The activation of I_KCa depends on the [Ca²⁺] in the cytosol, c, according to the activation function

$$n_{\text{KCa,}\infty }=\frac{{\mathrm{c}}^2}{{\mathrm{c}}^2+k_{\text{KCa}}^2}$$

Dynamics for c and [Ca²⁺] in the ER, c_ER, are governed by the equations

$$\frac{\mathrm{d}\mathrm{c}}{\mathrm{d}t}=f_{\text{cyt}}\left(J_{\text{in}}-J_{\text{out}}+J_{\text{rel}}-J_{\text{ref}}\right)$$

$$\frac{\mathrm{d}{\mathrm{c}}_{\text{ER}}}{\mathrm{d}t}=f_{\text{ER}}{\sigma }_{\text{ER}}\left(J_{\text{ref}}-J_{\text{rel}}\right)$$

where σ_ER is the ratio of cytosolic to ER volume and f_cyt and f_ER are the fractions of free Ca²⁺ in the cytosol and ER, respectively. The calcium fluxes into the cell (J_in), out of the cell (J_out), into the ER (J_ref), and out of the ER (J_rel) are given by

$$J_{\text{in}}=-\alpha \left(I_{\text{Ca}}+I_{\text{Ca,leak}}\right)$$

$$J_{\text{out}}={\nu }_{\text{c}}\frac{{\mathrm{c}}^2}{{\mathrm{c}}^2+k_{\text{c}}^2}$$

$$J_{\text{ref}}=k_{\text{ref}}\mathrm{c}$$

$$J_{\text{rel}}=p_{\text{rel}}\left({\mathrm{c}}_{\text{ER}}-\mathrm{c}\right)$$

Here, α converts ionic current to [Ca²⁺]_i, ν_c is the maximal calcium efflux rate across the plasma membrane, k_c is the [Ca²⁺]_i at which the plasma membrane pump is half-maximally active, p_rel is the rate of Ca²⁺ release from the ER, and k_ref is the rate of ER Ca²⁺ refilling. The terms involving ER Ca²⁺ are only included in simulations of AVP application, otherwise p_rel = k_ref = 0 and the c_ER equation is not included. Default parameter values are given in Table 1.

Table 1.

Default model parameter values

Parameter	Value	Parameter	Value
gNaV	10 nS	Vn	0 mV
gNab	0.205 nS	sn	5 mV
gCa	1.4 nS	τn	20 ms
gCa,leak	0.025 nS	VnA	−20 mV
gK	2.2 nS	snA	10 mV
gKir	1.3 nS	VhA	−60 mV
gA	0.5 nS	shA	−10 mV
gKCa	2 nS	τhA	20 ms
gBK	0.5 nS	kKCa	0.4 µM
gK,leak	0.1 nS	A	0.11 µM·ms·fC−1
gCRH	0 nS	sBK	5 mV
gAVP	0 nS	kCaBK	1.5 µM
ENa	75 mV	τBK	5 ms
ECa	60 mV	VKir	−55 mV
EK	−75 mV	sKir	−10 mV
ENS	0 mV	fcyt	0.01
cm	6 pF	fER	0.01
VmNa	−15 mV	α	0.0015 µM/fC
smNa	5 mV	νc	0.03 µM/ms
VhNa	−60 mV	kc	0.1 µM
shNa	−10 mV	prel	0.0001 ms−1
τhNa	2 ms	kref	0.1 ms−1
VmCa	−12 mV	σ	31
smCa	10 mV

To capture variability in activity patterns, we study model behavior across two-parameter planes in addition to single representative points in parameter space. The steady-state behavior at each point in 64 × 64 grids across two parameters of interest is simulated, and the number of peaks in a depolarization event is recorded. A depolarization event is an oscillatory simulation trajectory beginning at and returning to a small neighborhood of the point in state-space defined at the trajectory’s global minimum in membrane potential. The behavior of the model throughout the grid is summarized as a heat map indicating the number of peaks per event, where quiescent, spiking, and bursting patterns of activity are represented by zero, one, or greater than one peak per event, respectively.

We examine five different ways in which CRH can affect electrical activity (Fig. 1A): increasing g_CRH, decreasing g_Kir, decreasing g_K,leak, enhancing I_Ca by decreasing V_mCa, and inhibiting I_BK by increasing k_CaBK. AVP response is modeled by increasing p_rel and in parallel increasing g_AVP or decreasing g_K,leak. The effects of CRH or AVP are explored in two ways. First, the steady-state behavior is studied with the parameter plane approach described above, where the parameter on the x-axis is the CRH- or AVP-modulated parameter of interest and the parameter on the y-axis represents a parameter for which intrinsic variability is being investigated. Second, the time courses of selected points in parameter space are displayed.

The second approach involves simulating a dynamic increase or decrease of a parameter according to a pulse profile (Fig. 1B) to approximate the application of agonists and intracellular signaling. This generates time courses for comparison to experimentally observed traces. The pulse function g(t) is designed to begin at 0 and peak at a value of 1. The quantityΔ_pg(t) is then added to the agonist-modulated parameter value to simulate agonist application, where Δ_p is the maximum change in the parameter value. To construct the pulse we start with the function

$$f\left(t\right)={\left(t-t_0\right)}^2\exp \hspace{0.17em}\left[-\left(t-t_0\right)/\tau \right]/\left[4{\tau }^2\exp \left(-2\right)\right]$$

where t₀ is the time of initiation of the pulse and the maximum value f(t) = 1 occurs at time t₀ + 2τ. For some simulations it was necessary to better control the rate of increase and shape of the pulse, conveniently achieved by passing f(t) through a saturating Michaelis-Menten nonlinearity. The pulse equation is

$$g\left(t\right)=\left(1+k_{\mathrm{p}}\right)f\left(t\right)/\left[f\left(t\right)+k_{\text{p}}\right]$$

where the positive parameter k_p is the value of f(t) that yields g(t) = 0.5 and the factor (1 + k_p) renormalizes the pulse so that g(t) = 1 when f(t) = 1. The new pulse function g(t) also peaks at t₀ + 2τ. When k_p is small, the pulse will rise to saturation rapidly and have a long duration, while as k_p becomes large g(t)→f(t), with slower rise rate and a shorter duration.

Simulations were performed with the fourth-order Runge-Kutta method with a time step of 0.5 ms and custom software written in OpenCL (Fletcher et al. 2016). This software computes the simulations required for the two-parameter grids in parallel on a modern programmable graphics processing unit in a fraction of a second, allowing for a rapid exploration of the model’s parameter space. The model equations are defined in freely available files (http://lbm.niddk.nih.gov/sherman) that can also be directly simulated with XPPAUT software (Ermentrout 2002), which is freely available at http://www.math.pitt.edu/~bard/xpp/xpp.html.

RESULTS

Spontaneous and agonist-induced electrical activity of mouse corticotrophs in vitro.

Reports of spontaneous corticotroph activity patterns vary from silent (Lee et al. 2011, 2015; Lee and Tse 1997) to active (Duncan et al. 2015; Liang et al. 2011) to a mix of active and silent (Kuryshev et al. 1997; Zemkova et al. 2016), with a variety of activity patterns observed (Liang et al. 2011; Zemkova et al. 2016). In our perforated-patch recordings, essentially three patterns were observed in spontaneously active cells, plateau-like bursting, large-amplitude single-spiking activity, and pseudoplateau-like bursting, examples of which are shown in Fig. 2A. In agreement with previous reports (Liang et al. 2011), the majority of spontaneously active cells were spiking and a minority displayed bursting patterns (Zemkova et al. 2016).

Fig. 2.

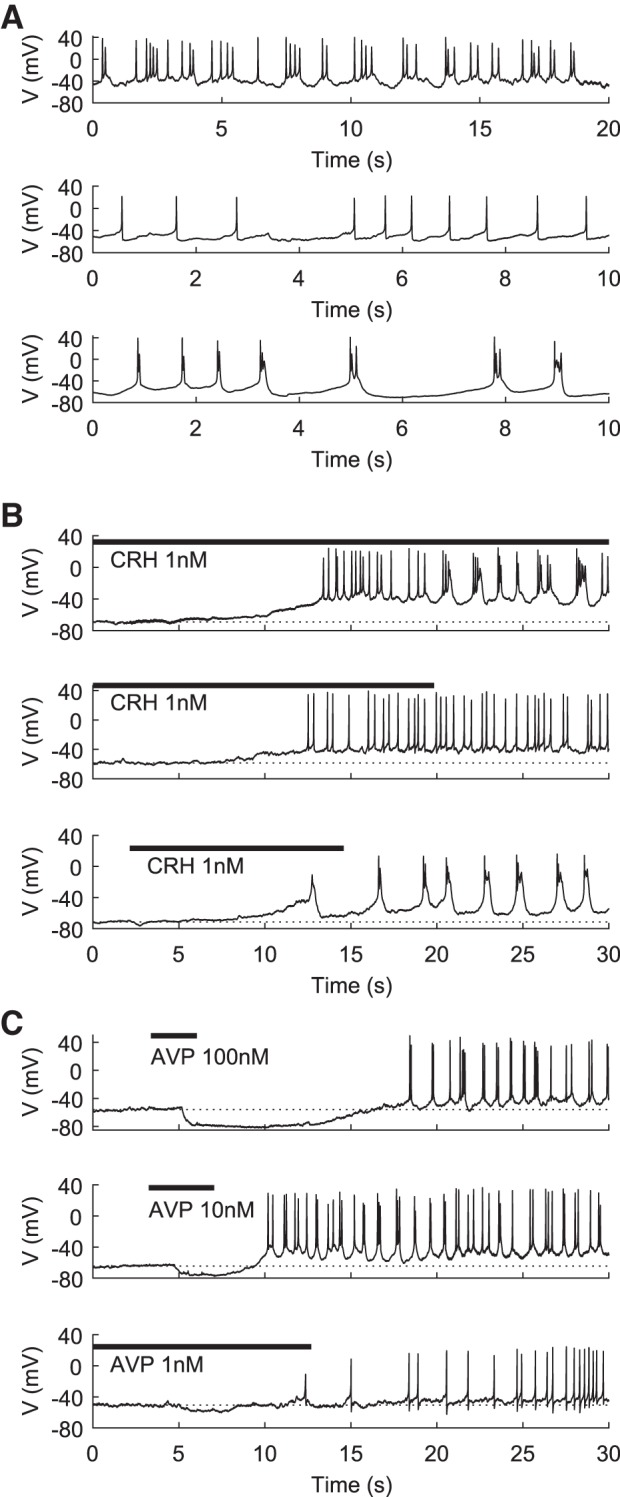
Representative patterns of spontaneous and agonist-induced electrical activity in mouse corticotrophs in vitro. A: examples of spontaneous plateau-like bursting (top), low-frequency spiking (middle), and pseudoplateau-like bursting (bottom). B: 3 cells that become gradually depolarized and then active in response to 1 nM CRH. Top: cell undergoes transitions from quiescence to spiking to plateau-like bursting. Middle: cell transitions from quiescence to spiking only. Bottom: cell transitions directly from quiescence to pseudoplateau-like bursting. C: 3 cells in which AVP causes a transient hyperpolarization and then a depolarization and transition to activity. Top: cell transitions directly to plateau-like bursting after a prolonged hyperpolarization in response to a 100 nM pulse of AVP. Middle: cell displays a brief hyperpolarization before a transition to irregular spikes and then plateau-like bursting in response to a 10 nM pulse of AVP. Bottom: cell shows a small hyperpolarization before transitioning to spiking only, in response to a 1 nM pulse of AVP. Horizontal bars in B and C indicate duration of CRH or AVP application.

CRH stimulation characteristically causes depolarization and increased electrical activity. Initially silent cells responded to CRH with a larger depolarization of ~10–30 mV (Kuryshev et al. 1995; Lee et al. 2011; Zemkova et al. 2016), while initially active cells were more modestly depolarized by 5–10 mV (Duncan et al. 2015; Kuryshev et al. 1995; Zemkova et al. 2016). It was previously reported that CRH only triggers pseudoplateau-like bursting in spiking cells (Duncan et al. 2015), but we found a greater diversity of transitions including transitions from silent or spiking to plateau or pseudoplateau-like bursting and silent to spiking (Zemkova et al. 2016). Figure 2B shows the responses of three cells to 1 nM CRH, demonstrating transitions from silent to spiking to plateau-like bursting, silent to spiking, and silent to pseudoplateau-like bursting, respectively.

Electrical responses to AVP in corticotrophs are characterized by an early transient hyperpolarization in response to release of Ca²⁺ from the ER and followed by depolarization and increased firing rate (Duncan et al. 2015; Lee et al. 2015; Zemkova et al. 2016). During the second phase, Duncan et al. (2015) observed only spiking with increased frequency, while we (Zemkova et al. 2016) observed spiking and/or plateau-like bursting. Figure 2C shows initially silent cells with three different AVP responses, which include varying degrees of first-phase hyperpolarization and subsequent transition to plateau bursts with tall spikes or spiking only.

Modeling spontaneous corticotroph electrical activity.

We study spontaneous activity by focusing on currents that can affect silent/active electrical status and currents that control the pattern of electrical activity. Kuryshev et al. (1997) suggested that I_Kir helps maintain the negative resting membrane potential (V_rest), and the TREK-1 has also been reported (Lee et al. 2011). I_Nab has been shown to provide a depolarization (Liang et al. 2011; Zemkova et al. 2016) that counterbalances outward subthreshold currents, and we reported variability in the degree of expression of I_Nab based on variability of hyperpolarization responses to Na⁺-deficient medium (Zemkova et al. 2016). Although not experimentally reported to our knowledge in corticotrophs, we find that a background Ca²⁺ conductance needs to be present in the model to maintain ER Ca²⁺ stores. Spontaneous activity occurs when there is a small net inward pacemaker current at hyperpolarized potentials, causing a depolarization and eventual crossing of the spike threshold. Variation in pacemaker or background conductances could therefore account for the presence or absence of spontaneous activity. For default values of model parameters, spontaneous activity emerges for approximately g_Nab > 0.2 nS (Fig. 3A), g_Kir < 1.3 nS (Fig. 4C), and g_K,leak < 0.1 (Fig. 4E). Activity patterns near this transition have low frequencies of 1–3 Hz or less, compatible with previous reported observations (Liang et al. 2011; Zemkova et al. 2016).

Fig. 3.

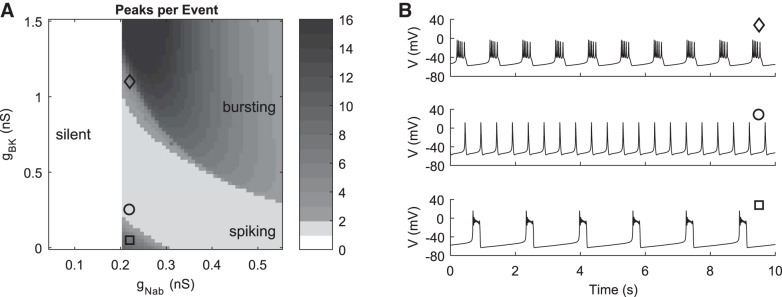
Spontaneous activity in the model as BK and background Na⁺ conductances are varied. A: heat map in this and subsequent figures shows the number of peaks per depolarization event as a function of 2 parameters, here g_BK and g_Nab. Silent, spiking, and bursting time courses have 0 (white), 1 (light gray), or >1 (shades of dark gray) peak per event, respectively. There is a BK-independent transition from silent to active at g_Nab  = 0.2 nS. The number of peaks per event was measured for each parameter combination of a 64 × 64 grid. B: 3 selected parameter combinations indicated by markers in A (each with g_Nab = 0.22 nS) that reproduce plateau-like bursting (◇; g_BK = 1.1 nS), spiking (○; g_BK = 0.25 nS), and pseudoplateau activity (□; g_BK = 0.05 nS), similar to the time courses presented in Fig. 2.

Fig. 4.

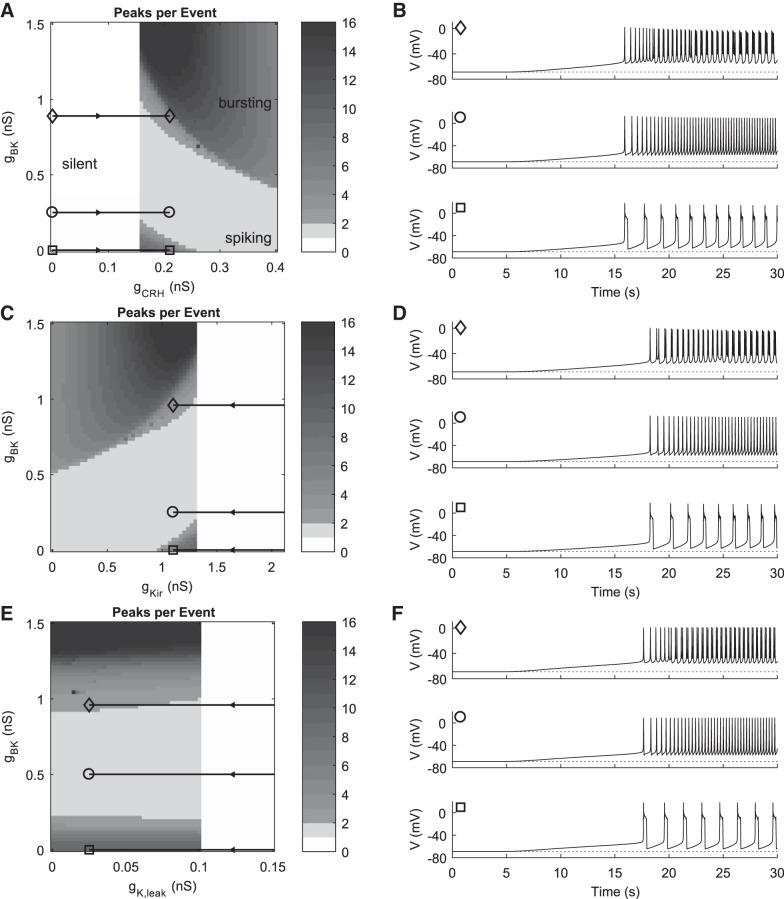
Simulation of CRH response by modulation of pacemaker currents. A, C, and E: peaks per event as a function of BK and CRH-induced inward, K_ir, and K⁺ leak conductances, respectively. Horizontal black trajectories with markers indicate the g_BK values and range of pacemaker conductances used in pulse simulations. B: time courses showing response to increasing g_CRH from 0 nS to 0.22 nS at values of g_BK indicated in A (g_BK = 0.89 nS, g_BK = 0.25 nS, and g_BK = 0 nS). Default parameter values were used, except g_Nab = 0.05 nS, and pulse parameter k_p = 1. D: time courses showing response to decreasing g_Kir from 3.5 nS to 1.1 nS at values of g_BK indicated in C (g_BK = 0.96 nS, g_BK = 0.25 nS, and g_BK = 0 nS). All other parameters had default values, and pulse parameter k_p = 0.3. F: time courses showing response to decreasing g_K,leak from 1.9 nS to 0.025 nS at values of g_BK indicated in E (g_BK = 0.96 nS, g_BK = 0.5 nS, and g_BK = 0 nS). All other parameters had default values, and pulse parameter k_p = 0.1. In B, D, and F, the pulse of simulated CRH begins at 5 s and peaks at 30 s. Dotted lines indicate the initial V_rest of −69 mV, and top, middle, and bottom time courses show a depolarization of ~15 mV, 13 mV, and 5 mV, respectively.

In addition to background currents, the pattern of spontaneous activity depends on the combination of voltage- and Ca²⁺-dependent conductances. Because BK channels have been implicated in contributing to the patterns of bursting activity in corticotrophs (Duncan et al. 2015, 2016) and other pituitary cells (Van Goor et al. 2001a), we examined the effect of variation in g_BK on spontaneous and agonist-induced activity. The dependence of activity patterns on g_Nab and g_BK is summarized in a two-parameter heat map (Fig. 3A). Silent cells have zero peaks (white in the heat map), spiking cells have one peak (light gray), and bursting cells have more than one peak per event (shades of dark gray). The transition from silent to active at g_Nab = 0.2 nS is vertical, that is, BK independent. This is because the BK open probability at resting membrane potentials in silent models (less than −50 mV) is very near zero, which means that increasing g_BK has no effect on whether the cell is active or silent. Within the active region (g_Nab > 0.2 nS) the levels of both g_BK and g_Nab control whether the model spikes or bursts; the boundaries between spiking and bursting are sloped curves. There are two bursting regions. The first, smaller region comprises pseudoplateau-like bursting when both g_BK and g_Nab are low, while for higher g_BK there is a larger region with both plateau-like and pseudoplateau-like bursting. In both regions, bursting patterns tend to have taller spikes near the boundary with the spiking region. Including I_A in the model helped to widen this boundary of plateau bursts consisting of few (2 or 3) tall spikes in the upper burst region. Representative time courses for which the model activity mimics the patterns observed in the data were generated at parameter combinations indicated by the circle, diamond, and square markers (Fig. 3B). Time courses with higher g_BK have lower amplitude because fast-activating K⁺ currents such as I_BK act to limit spike amplitude and thus compete with depolarizing currents such as I_NaV and I_Ca.

CRH-facilitated electrical activity.

Next we compare mechanisms of CRH-induced electrical activity in the model. All the proposed mechanisms except modulation of BK current involve increasing the net inward current at hyperpolarized potentials and are therefore hypothesized to be capable of causing a silent-to-active transition. It follows that at least one mechanism other than BK must be present to explain CRH’s effects on silent cells (Duncan et al. 2015). The first mechanism considered is the activation of a putative cationic current, modeled here as I_CRH. To simulate the CRH effect on an initially silent cell, we set g_Nab = 0.05 nS so that the model is hyperpolarized with V_rest = −69 mV. The effect of increasing g_CRH across a range of g_BK values is then examined, summarized across a two-parameter grid in terms of the number of peaks per event (Fig. 4A). As in Fig. 3A, there is a BK-independent transition from silent to active, while in the active region both g_BK and g_CRH control the activity pattern. Choosing appropriate values of g_BK and imposing a dynamic pulse increase [see the pulse equation g(t) in materials and methods] in g_CRH from 0 to 0.22 nS (horizontal trajectories in Fig. 4A) reproduces time courses with the experimentally observed patterns (compare Fig. 4B to Fig. 2B). The degree of depolarization achieved depends on the degree of initial hyperpolarization and on the nature of the activity pattern (specifically its baseline potential) obtained by CRH stimulation. In this case, all three time courses have the same V_rest of −69 mV, and they achieve depolarization of ~15 mV, 13 mV, and 5 mV for high (diamond), medium (circle), and low (square) g_BK, respectively. At the silent-spiking transition, increasing levels of g_BK lead to increasingly depolarized baselines in the activity patterns, because activation of BK preempts activation of the delayed rectifier I_K (Van Goor et al. 2001a). At silent-to-bursting transitions, the baseline potential is expected to be lower because during a burst there is more time during the burst active phase to activate I_K and I_KCa, leading to stronger repolarization.

CRH stimulation by reduction of I_Kir, modeled by reducing g_Kir, is also consistent with reported experimental data. The value of g_Nab was set to 0.205 nS, which makes the silent to active transition occur at the default value of g_Kir = 1.3 nS. With these parameters, it was necessary to set g_Kir = 3.5 nS to have V_rest = −69 mV. The boundary at g_Kir  = 1.3 nS between silent and active is again vertical and g_BK independent (Fig. 4C). Depending on the level of g_BK, decreases in g_Kir from 3.5 to 1.1 nS yield transitions from silent to spiking to bursting, silent to spiking only, or silent to pseudoplateau-like bursting as experimentally observed (Fig. 4D). The same degree of depolarization as was seen using the g_CRH mechanism is obtained here, for the same reasons. However, while the top 30% of the change in g_CRH lies in the active region of the plane (Fig. 4A), only ~8% of the total change in g_Kir is in the active region. To cross the silent-active threshold at a comparable latency to the g_CRH simulations therefore required a more rapidly rising pulse profile that saturates before peaking in the active region (obtained by decreasing k_p from 1 to 0.3).

Inhibition of an outward leak is evaluated next. With g_Nab = 0.205 nS, the transition from silent to active occurs at the default value of g_K,leak = 0.1 nS (Fig. 4E). To obtain V_rest = −69 mV without changing any other parameters, g_K,leak had to be increased dramatically to 1.9 nS. Decreasing g_K,leak can also cause activation of silent cells in a BK-independent manner. However, in this case there is a much narrower range of g_BK values for which changes in g_K,leak are able to cause the double transition of silent to spiking to bursting. In Fig. 4E, the bursting regions have relatively horizontal boundaries; changes in g_K,leak are only weakly able to cause transitions between spiking and bursting. The same degree of depolarization is again possible with this mechanism (Fig. 4F). However, only the last 4% of the change in g_K,leak lies in the active region, necessitating an even broader and more rapidly saturating pulse (k_p = 0.1).

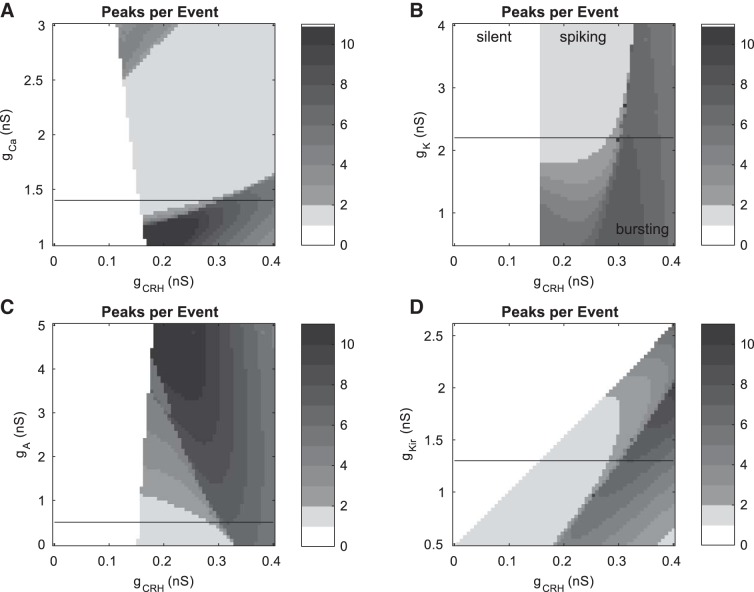
While variations in g_BK support a wide range of experimentally observed spontaneous and agonist-induced electrical activity patterns, these can also be achieved by variation in other intrinsic model parameters. With g_BK fixed at 0.6 nS, we demonstrate this with two-parameter grids featuring g_CRH and each of g_Ca, g_K, g_A, and g_Kir (Fig. 5, A–D, respectively). The horizontal lines in Fig. 5 indicate the default value of the parameter on the y-axis. In each case, there is a range of g_Ca, g_K, g_A, or g_Kir values for which trajectories beginning in the silent region and moving rightward will undergo experimentally observed transitions patterns: silent to spiking, silent to bursting, and silent to spiking to bursting. In the case of g_Ca (Fig. 5A), there exist two burst regions; in this case the upper region has pseudoplateau-like bursting. The lower burst region in Fig. 5A shares commonalities with the burst region seen in the remaining panels. Namely, there is a region of plateau-like bursts with few tall spikes for lower g_CRH values bordering the spiking region. For higher g_CRH values, there is a transition to bursting with a higher number of peaks per event, which becomes progressively more pseudoplateau-like. The nature of the burst mechanisms involved in these two-parameter grids will be the subject of future investigation. The BK current is important for producing this bursting region (it is the same region as the upper burst region in Figs. 3 and 4). It has the correct shape relative to the silent and spiking regions to support the silent-to-spiking-to-bursting transition in response to CRH simulation using only one mechanism at a time. We note that it is also possible to achieve this compound transition when g_BK = 0, but two or more CRH mechanisms must be invoked in tandem (not shown).

Fig. 5.

Variation in intrinsic model conductances with fixed g_BK can give rise to variation in CRH-stimulated activity patterns. With g_BK set to 0.6 nS, varying g_Ca (A), g_K (B), g_A (C), or g_Kir (D) allows the model to support the experimentally observed transitions from silent to spiking, silent to bursting, and silent to spiking to bursting as g_CRH is increased. Horizontal black lines indicate the default parameter values for the 4 parameters.

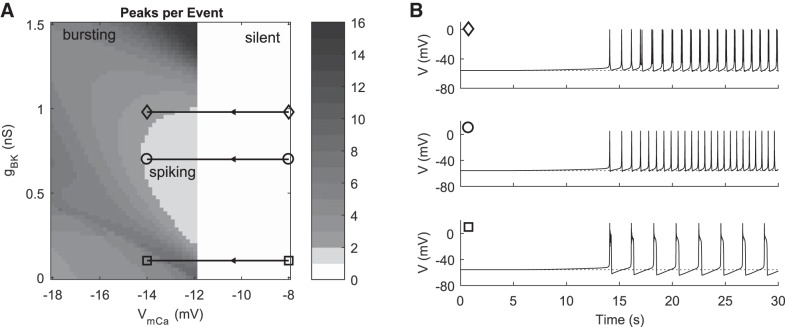
The model can also reproduce corticotroph-like pattern transitions in response to increases in I_Ca as was seen in earlier models (Duncan et al. 2015, 2016; LeBeau et al. 1997, 1998; Shorten et al. 2000). We increase I_Ca by left shifting the steady-state activation curve by decreasing V_mCa. With g_Nab = 0.205 nS, a transition between silent and active occurs near the default value of V_mCa = −12 mV (Fig. 6A). A hyperpolarized silent starting point was obtained by setting V_mCa = −8 mV. This current is poorly activated at hyperpolarized potentials, so V_rest was relatively depolarized at −56 mV, with further increases in V_mCa unable to appreciably hyperpolarize V_rest. This limits the potential for depolarization by this mechanism, consistent with previous models (LeBeau et al. 1997, 1998; Shorten et al. 2000). Decreasing V_mCa from −8 mV to −14 mV (horizontal trajectories in Fig. 6A) at three representative values of g_BK produces transitions from silent to active and between spiking and bursting activity patterns (Fig. 6B).

Fig. 6.

Simulation of CRH response by left shifting the steady-state activation curve of I_Ca. A: peaks per event as a function of BK conductance and V_mCa. Horizontal black trajectories with markers indicate g_BK values and range of V_mCa used in pulse simulations. B: time courses showing response to decreasing V_mCa from −8 mV to −14 mV at values of g_BK indicated in A (g_BK = 0.98 nS, g_BK = 0.7 nS, and g_BK = 0.1 nS). The pulse of simulated CRH begins at 5 s and peaks at 30 s with pulse parameter k_p = 1. Dotted lines indicate the initial V_rest of −56 mV.

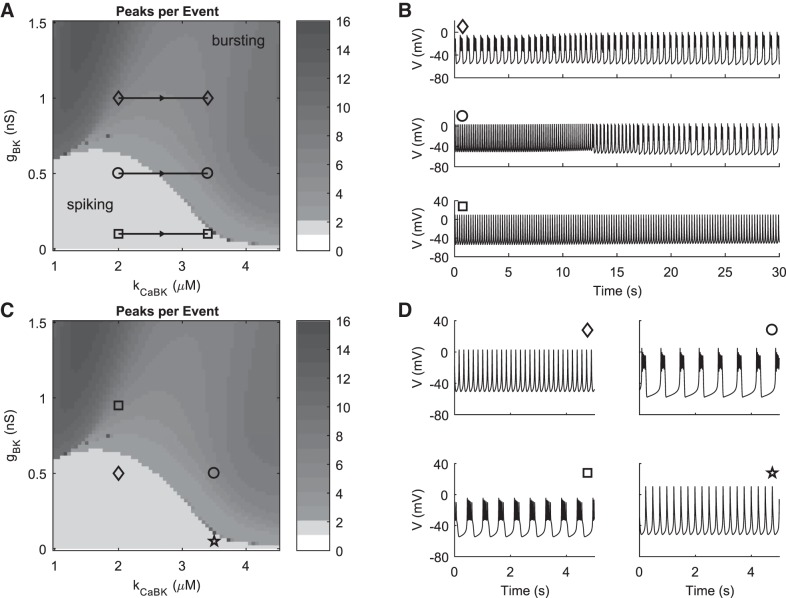
CRH-dependent suppression of BK current has been reported to be due to a right shift in its activation function and a reduction in its time constant (Duncan et al. 2015, 2016). We model the CRH effect by increasing the parameter k_CaBK but maintain a fixed small time constant (τ_nBK = 5 ms) for BK activation. Because BK channels are inactive at hyperpolarized potentials, further BK inhibition cannot account for depolarization from a hyperpolarized V_rest and is only expected to be able to cause transitions between already active electrical patterns. Activity is ensured by setting g_Nab = 0.205 nS and g_CRH = 0.105 nS. g_CRH is not changed dynamically so that we can focus on the effect of BK modulation. The effect of increasing k_CaBK is to right-shift the BK activation curve. Above k_CaBK = 2 μM, there is also a significant reduction in the slope of the activation curve, preferentially for voltages above the half-maximal activation so that the activation curve saturates more gradually as voltage increases. The g_BK-k_CaBK parameter plane (Fig. 7A) shows that the model indeed predicts a transition from spiking to bursting for g_BK values less than ~0.6 nS and for sufficient increase in k_CaBK. The model also predicts such a transition if k_CaBK is reduced, but only for a small range of g_BK values. Time courses of responses to a dynamic increase of k_CaBK for three representative values of g_BK are shown in Fig. 7B, corresponding to the horizontal trajectories shown in Fig. 7A. Increasing k_CaBK from 2 to 3.4 increases the half-maximal BK activation from −14.7 mV to −13.7 mV. The shift in BK activation does not appreciably increase the frequency of depolarization events, further supporting the hypothesis that one of the other mechanisms for CRH action should be present in addition to changes in BK activation.

Fig. 7.

Simulations of changes in BK conductance and CORT-sensitive CRH-induced bursting. A: peaks per event as a function of BK conductance and k_CaBK, with g_Nab = 0.205 nS. A steady-state CRH-induced increase in frequency is also included by setting g_CRH = 0.105 nS. Horizontal black trajectories with markers indicate g_BK values and range of k_CaBK used in pulse simulations. B: time courses showing the response to increasing k_CaBK from 2 μM to 3.4 μM (corresponding to increasing the half-maximal BK activation from −14.7 mV to −13.7 mV) at values of g_BK indicated in A (g_BK = 1 nS, g_BK = 0.5 nS, and g_BK = 0.1 nS). The pulse of simulated CRH begins at 5 s and peaks at 30 s with pulse parameter k_p = 1. C: peaks per event as in A but showing the parameter combinations used to simulate BK conductance changes and CORT effects on CRH-induced bursting. D: steady-state time courses for the points of interest in C. CRH action on k_CaBK induces rightward motion in the plane, causing a spiking-to-bursting transition (◇ to ○). Subsequent block of BK conductance (or subtraction, as in a dynamic-clamp experiment) induces downward motion in the plane, causing a transition back to spiking (○ to ☆). CORT prevents CRH-induced rightward shift in BK activation, so CORT+CRH is modeled as remaining at the ◇ marker. Subsequently increasing BK conductance (for instance by dynamic clamp) causes upward motion in the plane (◇ to □), leading to a recovery of bursting behavior. (k_CaBK, g_BK) parameter combinations: ◇, (2, 0.5); ○, (3.5, 0.5); ☆, (3.5, 0.05); □, (2, 0.95).

The CRH-induced transition from spiking to bursting was shown to be reversed by subtraction of BK current with dynamic clamp (Duncan et al. 2016). In the same study, CORT-pretreated corticotrophs no longer burst in response to CRH, but bursting could be restored by addition of BK via dynamic clamp. These results can be reproduced in our model as follows. CRH induces rightward motion in the g_BK-k_CaBK plane and thus a transition from spiking to bursting (diamond to circle in Fig. 7C). Spiking is recovered by decreasing g_BK (circle to star in Fig. 7C). CORT pretreatment is hypothesized to prevent the PKA-dependent change in BK channel activation via activation of a phosphatase (Tian et al. 1998), although it also has BK-independent effects (Duncan et al. 2016). We consider only the prevention of BK modulation by CORT, such that the CRH+CORT condition is simulated by simply remaining at the initial parameter point (diamond in Fig. 7C). Bursting is restored in this case by upward motion in the g_BK-k_CaBK plane (diamond to square in Fig. 7C). The time courses for each of the indicated parameter combinations are shown with matching markers in Fig. 7D.

AVP-facilitated electrical activity.

To model AVP responses, we include an ER Ca²⁺ compartment, as described in materials and methods. The ohmic Ca²⁺ current I_Ca,leak is set to 0.05 nS to maintain ER Ca²⁺ store levels, and I_Kir is increased to 1.5 nS to compensate the extra background conductance. Variation in g_BK and g_Nab leads to a similar pattern of silent, spiking, and bursting regions as before (compare Fig. 8A to Fig. 3A). We highlight three parameter combinations in the g_BK-g_Nab plane for which the main features of the experimental time courses are reproduced when an AVP-like stimulus is applied (compare Fig. 8B to Fig. 2C). Note that g_Nab is not varied in the AVP stimulus, so only points and not trajectories are shown in Fig. 8A. AVP-induced hyperpolarization is reproduced with a dynamic increase in the ER Ca²⁺ release rate p_rel, following a rapid pulse profile. Increasing p_rel causes release of Ca²⁺ from the ER and a transient spike in cytosolic Ca²⁺, activating I_KCa and thereby causing hyperpolarization. To reproduce the sustained depolarization with spiking- or bursting-driven Ca²⁺ influx, we tested two alternative mechanisms: the activation of an inward ohmic current, I_AVP (Fig. 8), and the inhibition of I_K,leak (not shown). These modulations in ionic currents were triggered at the same moment (time = 5 s) but followed a slower pulse profile identical to the above CRH manipulations. For the same reasons as in Fig. 4, the activation of I_AVP or inhibition of I_K,leak can both cause transitions from silent to active as well as transitions between spiking and bursting activity depending on the level of g_BK. The three doses of AVP are modeled with different maximal changes in p_rel and g_AVP, as indicated in Fig. 8. The duration of hyperpolarization and the sequence of transitions between activity patterns are all captured by the model. For strong ER Ca²⁺ release, the resulting high [Ca²⁺]_i saturates the membrane calcium pumps, leading to a longer Ca²⁺ spike phase and hyperpolarization. The Ca²⁺ dynamics in the model also naturally provide a small depolarization as a consequence of store depletion, even without changes in I_AVP or I_K,leak. The release of store Ca²⁺ leaves the ER depleted and [Ca²⁺]_i eventually drops below pre-AVP levels, in turn causing depolarization due to reduction of I_KCa (Li et al. 1997). This effect is small, however, and can only trigger silent-to-active transitions if the pre-AVP model parameters are set close enough to the transition boundary. Depolarization is less dramatic in these cases compared with CRH responses mainly because the initial V_rest is more depolarized, similar to the traces shown in Fig. 2C.

Fig. 8.

Simulation of AVP responses in a model including ER Ca²⁺ dynamics. A: peaks per event as a function of variation in the 2 parameters g_BK and g_Nab. Three representative parameter combinations are indicated by markers for which AVP stimulation reproduces the experimental time courses. ER Ca²⁺ dynamics are included, and the calcium leak and inward rectifier conductances were increased to g_Ca,leak = 0.05 nS and g_Kir = 1.5 nS, respectively. Parameter combinations (g_Nab, g_BK): ◇, (0.14, 1); ○, (0.18, 0.85); □, (0.17, 0.35). All other parameter values had default values. B: time courses for AVP responses of the model at the 3 parameter combinations indicated by corresponding markers in A. AVP application is simulated beginning at time = 5 s by increasing the ER leak rate from default value p_rel = 0.0001 s⁻¹ transiently following a fast pulse profile (τ = 1 s, k_p = 10), and by simultaneously activating an inward ohmic conductance g_AVP following a slower pulse profile (τ = 12.5 s, parameter k_p = 1). To model the different doses of AVP in Fig. 2C, maximum increase in p_rel during the pulse was 0.01 s⁻¹, 0.0025 s⁻¹, and 0.001 s⁻¹, and peak g_AVP was 0.07 nS (top), 0.055 nS (middle), and 0.04 nS (bottom).

DISCUSSION

We have presented a mathematical model that captures many aspects of the diversity in spontaneous and agonist-stimulated electrical activity and Ca²⁺ dynamics of pituitary corticotrophs in vitro. Although it is likely that there is variation in several ionic conductances underlying this diversity, we show that variation in as few as two parameters is sufficient to capture this diversity: g_Nab to control activity status and g_BK to determine activity pattern. We found at least two distinct bursting mechanisms giving plateau and pseudoplateau burst patterns in close proximity in the g_BK-g_Nab parameter plane, along with silent and spiking states. We compared five potential mechanisms of action for CRH action and two for AVP action. Our comparative analysis of these mechanisms within a single mathematical model employed analysis of two-parameter planes to observe the totality of behaviors associated with each mechanism. We found that the different CRH mechanisms can each explain different subsets of the phases of the CRH response, including pacemaking depolarization and transitions between activity patterns. Specifically, the mechanisms involving I_CRH, I_Kir, and I_K,leak could account for all features of the CRH response, I_CRH most efficiently. The I_Ca mechanism could account for transitions from silent to active and between activity patterns but not depolarization, while the BK mechanism could only account for transitions between spiking and bursting. The BK current is important for generating a bursting region in parameter space such that the silent-to-spiking-to-bursting transition could be obtained with a single one of these CRH mechanisms. By including ER Ca²⁺ dynamics and I_AVP, we were also able to reproduce the phases of AVP responses. Taken together, these results suggest that several redundant mechanisms for agonist-induced electrical activity may coexist in corticotroph cells and that intrinsic variability or experimental perturbations may bias the cell toward a subset of these mechanisms.

To study the diversity in corticotroph electrical activity patterns in the model, we focused on the role of the ionic currents controlling whether the cell is active and currents that could generate diversity in the activity pattern. The background currents (I_Nab, I_Kir, I_K,leak, and I_Ca,leak) are the dominant factors controlling whether the cell is silent or active. Variations in these currents, either intrinsic or due to experimental perturbations during cell culture or electrophysiological recording, could influence V_rest and the percentage of cells observed to be spontaneously active. For instance, in whole cell recordings the concentrations of intracellular polyamine and other cations mediating the inward rectification of I_Kir are expected to run down, effectively converting I_Kir to I_K,leak. In the model, such an increase in I_K,leak would strongly suppress spontaneous activity but would not prevent depolarization due to the subsequent activation of I_CRH or inhibition of I_Kir and/or I_K,leak.

We found that variation of two parameters, g_BK and g_Nab, was sufficient to observe spiking, plateau-like bursting, and pseudoplateau-like bursting, but questions remain as to the sources of diversity in corticotrophs. A diversity of activity patterns could also be achieved in the model with fixed nonzero g_BK and variation in other parameters including one of g_Ca, g_K, g_A, or g_Kir. Fast-activating K⁺ conductances such as g_BK limit action potential overshoot, because they directly compete with voltage-gated inward currents such as I_NaV. It remains to be seen whether tall-spiking corticotrophs indeed have lower BK currents or other fast-activating K⁺ currents and higher I_NaV. We did not include some other ionic currents reported in corticotrophs, such as the transient Ca²⁺ (Guérineau et al. 1991; Marchetti et al. 1987), hyperpolarization-activated cyclic nucleotide-gated (Tian and Shipston 2000), or other K⁺ channels. These other currents may be necessary for reproducing the full complement of diversity in activity patterns observed in corticotrophs (Liang et al. 2011; Zemkova et al. 2016). Further modeling could provide additional insight by incorporating recent reports of responses of corticotrophs to Na⁺- and Ca²⁺-deficient medium, inhibition of I_NaV by tetrodotoxin, and modulation of L-type Ca²⁺ channels by nifedipine and BAY K 8644 (Zemkova et al. 2016). Finally, we chose not to include noise in our simulated time courses, but this would help to reproduce experimentally observed features such as stochastic transitions between patterns (expected in our model for parameter sets near transition curves) and very low-frequency firing (expected for parameter sets in the silent region near silent-to-active transition).

Our comparative analysis shows that the different CRH mechanisms have different but complementary effects in generating the CRH response. Our results are largely consistent with previous theoretical results but extend them in several ways. Previous modeling studies found that reduction of I_K,leak (LeBeau et al. 1997) or I_Kir (Shorten et al. 2000) alone could not trigger activity in silent cells. An increase in I_Ca was required, although a combination with one of the other two mechanisms was more efficient than a change in I_Ca alone. The CRH response by the I_Ca mechanism is comparable in our model to previous studies, showing activation of silent cells without depolarization. However, we show using two-parameter plane analysis that reduction of either of the K⁺ currents alone can trigger many features of the CRH response. This suggests that the context of model parameters may favor one or another mechanism; our model favored the mechanism of I_CRH activation for reproducing all CRH response features, while still being permissive for the K_ir and K⁺ leak mechanisms. Combinations of CRH mechanisms are also more efficient than individual CRH mechanisms alone in our model (not shown). The BK mechanism for converting spiking to bursting was coupled to an increase in I_Ca in a previous study to explain the CRH response (Duncan et al. 2015). We have clarified that using any of the other four mechanisms will allow silent cells to become activated, while any of the three pacemaker currents would be required to explain a gradual depolarization from rest to threshold. Once active, the cell’s activity pattern could be converted from spiking to bursting by CRH-induced changes in BK channel activation (or one of the other mechanisms in the case of lack of BK channel modulation).

The steady-state effects of AVP on corticotroph electrical and Ca²⁺ dynamics have been modeled previously (Duncan et al. 2015). We have extended this by including the full transient response to AVP. This required only simple Ca²⁺ dynamics in the cytosol and ER, as well as a parallel mechanism to directly affect ion channels similarly to CRH action. Our model could be further used to study how CRH and AVP synergize in their corticotroph-stimulating effects. The ability of AVP to trigger hyperpolarization in already silent cells required in the model a basal level of Ca²⁺ influx for filling the ER Ca²⁺ store while the membrane is at rest, accomplished here with an ohmic leak conductance. These components were sufficient to reproduce all phases of the AVP response. If present, a store-operated Ca²⁺ current would also promote both store refilling and AVP-induced depolarization and increased activity.

To compare model simulations of CRH and AVP to experimental time courses, we increased or decreased relevant parameters according to a time-dependent pulse profile. This was necessary to control transient features of the responses including latency to first spike and rate of depolarization. The latency to first spike reflects the distance from the initial parameter value of the silent-to-active transition point and the speed at which this distance is traversed. The first likely reflects variability in expression of pacemaker currents. The second depends on the properties of the intracellular signaling pathways linking receptors to ion channels. We did not model the biophysical details of these pathways, instead employing a phenomenological pulse function that approximated the latency in the CRH and AVP responses. In the cases of I_Kir and I_K,leak mechanisms for CRH action, a large fraction of the initial conductance had to be blocked rapidly in order to reproduce the correct latency and depolarization rates, as reflected in the pulse properties used for those simulations. Whether differences exist in the kinetics controlling each of the different CRH- and AVP-modulated currents remains to be clarified experimentally.

The diversity of electrical activity patterns observed in corticotrophs includes patterns seen in other pituitary cell types, and they appear to be more diverse than other pituitary cell types. For example, corticotrophs often fire single action potentials with large overshoot and express I_NaV, much like gonadotrophs (Marchetti et al. 1987; Van Goor et al. 2001b). On the other hand, there is evidence that in at least some corticotrophs BK channels are involved in promotion of bursting patterns such as pseudoplateau-like bursting, which is characteristic of somatotroph and lactotroph activity (Tsaneva-Atanasova et al. 2007; Van Goor et al. 2001b). Tall-spiked bursting not typically seen in the other pituitary cell types is also observed (Liang et al. 2011; Zemkova et al. 2016). During embryonic development, corticotrophs are the earliest cell type to mature (Stojilkovic et al. 2010). It is tempting to speculate that the corticotroph is closest in its electrical signaling system to a common ancestor from which all pituitary cell types specialize. If this is the case, the anterior pituitary progenitor cell could have electrical activity, a property that has not yet been studied to our knowledge. From this perspective, one could imagine that expression of the components of the electrical signaling system of this common ancestor would be activated or repressed to give rise to the specific patterns of activity of the adult anterior pituitary cell types.

The dependence of hormone responses on the context of the cell’s intrinsic parameter values and initial activity status is similar to state-dependent neuromodulation, a ubiquitous phenomenon that has been well studied in neurons and neuronal networks (Goldman et al. 2001; Marder et al. 2014). We showed with two-parameter plane analysis that the pattern of activity triggered by a modulator depends on the initial context of intrinsic cell parameters. It remains unclear which subset of the intrinsic parameters of corticotroph cells, such as the maximal conductances, display variability in vivo or in vitro and which parameters are affected by physiological modulators or experimental procedures such as those required for the presently reported in vitro electrophysiological recording.

The organization of corticotrophs and other pituitary cell types into functional networks in the intact pituitary gland is likely to influence spontaneous and agonist-induced electrical activity in vivo. Recent studies have used three-dimensional imaging to reveal complex organization of several pituitary cell types (Le Tissier et al. 2012). In particular, proopiomelanocortin-positive cells in the anterior pituitary form homotypic strands of cells, which are in close proximity to homotypic networks of LH-positive cells and pituitary microvasculature (Budry et al. 2011). These reports suggest that a combination of intrinsic cell properties, network organization (including the effects of paracrine modulators and cell-cell coupling), and hormonal inputs from outside the gland will likely be needed to fully understand corticotroph function in vivo.

Advances in computing power have allowed large-scale explorations of the parameter space of models of neurons and neuronal networks, sometimes called the model database approach (Günay 2015; Prinz et al. 2003). Studies of this type have revealed the possibility that multiple parameter combinations can give rise to similar neuronal activity (Goldman et al. 2001; Prinz et al. 2004; Taylor et al. 2009). Conversely, the same modulation can have different effects depending on the starting point of the system in parameter space. Our use of parameter sampling on two-parameter grids demonstrates that in the corticotroph model several ionic mechanisms of agonist action give rise to similar responses.

GRANTS

This work was supported by the Grant Agency of the Czech Republic [Grant 16-12695S (H. Zemkova)] and by funding from the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases (P. A. Fletcher and A. Sherman) and the National Institute of Child Health and Human Development (S. S. Stojilkovic).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at the institutional website of one of the authors, which at the time of publication they indicate is: http://lbm.niddk.nih.gov/sherman. These materials are not a part of this manuscript, and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

P.A.F., S.S.S., and A.S. conceived and designed research; P.A.F., H.Z., S.S.S., and A.S. interpreted results of experiments; P.A.F. prepared figures; P.A.F. drafted manuscript; P.A.F., H.Z., S.S.S., and A.S. edited and revised manuscript; P.A.F., H.Z., S.S.S., and A.S. approved final version of manuscript; H.Z. performed experiments; H.Z. analyzed data.