Frequency and function in the basal ganglia: the origins of beta and gamma band activity

Abstract

Key points

• Neuronal oscillations in the basal ganglia have been observed to correlate with behaviours, although the causal mechanisms and functional significance of these oscillations remain unknown.

• We present a novel computational model of the healthy basal ganglia, constrained by single unit recordings from non‐human primates.

• When the model is run using inputs that might be expected during performance of a motor task, the network shows emergent phenomena: it functions as a selection mechanism and shows spectral properties that match those seen in vivo.

• Beta frequency oscillations are shown to require pallido‐striatal feedback, and occur with behaviourally relevant cortical input. Gamma oscillations arise in the subthalamic–globus pallidus feedback loop, and occur during movement.

• The model provides a coherent framework for the study of spectral, temporal and functional analyses of the basal ganglia and lays the foundation for an integrated approach to study basal ganglia pathologies such as Parkinson's disease in silico.

Abstract

Neural oscillations in the basal ganglia (BG) are well studied yet remain poorly understood. Behavioural correlates of spectral activity are well described, yet a quantitative hypothesis linking time domain dynamics and spectral properties to BG function has been lacking. We show, for the first time, that a unified description is possible by interpreting previously ignored structure in data describing globus pallidus interna responses to cortical stimulation. These data were used to expose a pair of distinctive neuronal responses to the stimulation. This observation formed the basis for a new mathematical model of the BG, quantitatively fitted to the data, which describes the dynamics in the data, and is validated against other stimulus protocol experiments. A key new result is that when the model is run using inputs hypothesised to occur during the performance of a motor task, beta and gamma frequency oscillations emerge naturally during static‐force and movement, respectively, consistent with experimental local field potentials. This new model predicts that the pallido‐striatum connection has a key role in the generation of beta band activity, and that the gamma band activity associated with motor task performance has its origins in the pallido‐subthalamic feedback loop. The network's functionality as a selection mechanism also occurs as an emergent property, and closer fits to the data gave better selection properties. The model provides a coherent framework for the study of spectral, temporal and functional analyses of the BG and therefore lays the foundation for an integrated approach to study BG pathologies such as Parkinson's disease in silico.

Key points

• Neuronal oscillations in the basal ganglia have been observed to correlate with behaviours, although the causal mechanisms and functional significance of these oscillations remain unknown.

• We present a novel computational model of the healthy basal ganglia, constrained by single unit recordings from non‐human primates.

• When the model is run using inputs that might be expected during performance of a motor task, the network shows emergent phenomena: it functions as a selection mechanism and shows spectral properties that match those seen in vivo.

• Beta frequency oscillations are shown to require pallido‐striatal feedback, and occur with behaviourally relevant cortical input. Gamma oscillations arise in the subthalamic–globus pallidus feedback loop, and occur during movement.

• The model provides a coherent framework for the study of spectral, temporal and functional analyses of the basal ganglia and lays the foundation for an integrated approach to study basal ganglia pathologies such as Parkinson's disease in silico.

Abbreviations

BG

basal ganglia

DDE

delay differential equation

GPe

globus pallidus external

GPi

globus pallidus internal

LDLE

long duration late excitation

LFP

local field potential

MAP

maximum a posteriori

MSN

medium spiny neuron

PSTH

peristimulus time histogram

SMC‐ABD

sequential Monte‐Carlo approximate Bayesian computation

STN

subthalamic nucleus

VAF

variance accounted for

Introduction

While much has been learned about the basal ganglia (BG) over recent years (Graybiel, 2005; Redgrave & Gurney, 2006; Brittain & Brown, 2014; Nelson & Kreitzer, 2014), there are still many gaps in our understanding. Local field potentials (LFPs) have been measured from the subthalamic nucleus (STN) of human Parkinson's patients undergoing neurosurgery to implant deep brain stimulation electrodes. These data have shown that synchronous neural activity in the beta frequency range is increased in Parkinson's disease and correlates well with rigidity, one of the cardinal motor symptoms of the disease (Chen et al. 2010; Little et al. 2012). In healthy subjects synchronised neural oscillations of different frequency ranges correlate well with various aspects of behaviour (Engel & Fries, 2010; Jenkinson et al. 2013; Brittain & Brown, 2014). While there are models that attempt to explain pathological activity (Gillies et al. 2002; Terman et al. 2002; Leblois et al. 2006; Nevado Holgado et al. 2010; Moran et al. 2011; Marreiros et al. 2013; Corbit et al. 2016), the reliability of these results is questionable given the lack of understanding of how similar oscillations arise in the healthy BG. Furthermore, they are divorced from any hypothesis of BG function. Thus, they cannot be used to examine the purpose of the network or the purpose of the oscillations that they describe.

Numerous studies have recorded the phasic responses of various BG nuclei following stimulation of an afferent population (Nambu et al. 2000; Kita et al. 2004, 2006; Tachibana et al. 2008). Although a qualitative explanation for the generation of these phasic responses has been published (Jaeger & Kita, 2011), there is currently no quantitative model that can fully capture these phenomena. Thus, we currently have little insight into how these phasic responses relate to the different frequencies at which the BG is observed to oscillate.

Functional descriptions of the BG have successfully demonstrated that the network can, in principle, act as a selection mechanism, inhibiting or disinhibiting access to downstream neural processing (Frank et al. 2001; Gurney et al. 2001a; Humphries et al. 2006; Leblois et al. 2006; Liénard & Girard, 2013). However, these models fail to capture much of the diversity of experimental data concerning phasic responses and oscillatory properties of healthy BG. As such, their usefulness in terms of explaining experimental observations or making quantitative predictions is somewhat limited.

What emerges from existing work is a heterogeneous set of explanations for different features of the same network. There is no account of the BG that can simultaneously explain time domain dynamics, BG functionality and spectral properties. To progress understanding of the BG and its related pathologies we require a framework within which temporal, spectral and functional descriptions are unified.

We address this issue here by creating a novel firing rate model of the BG, constrained by existing single unit recordings in monkey internal globus pallidus (GPi) (Tachibana et al. 2008), STN and external globus pallidus (GPe) (Nambu et al. 2000). The average GPi neuronal response to cortical stimulation has been repeatedly observed to be triphasic (Tachibana et al. 2008; Nishibayashi et al. 2011). However, the authors of these studies also note the occurrence of neurons that have qualitatively different responses. Most modelling studies make the strong but often unstated assumption that these different responses originate through noise and therefore play no part in the generation of the system's mean field behaviour. Here, we take a novel approach by examining the possibility that these different responses could arise as a consequence of the structured interaction between neurons encoding competing inputs with different magnitudes. In this case the response types would be mutually dependent, and rely on each other for the generation of their characteristic profiles.

We show that a rate‐coded model, constrained by these time‐domain impulse responses and driven by inputs that might be expected during the performance of a motor task, naturally gives rise to behaviourally relevant beta and gamma frequency oscillatory activity. Furthermore, specific mechanisms are identified which can explain the origin of these oscillations. In addition, we show that action selection functionality is also an emergent property of the network and that the selection ability improves with model fit to the time‐domain data. Thus, for the first time, we present a quantitative hypothesis of the healthy BG that links its frequency characteristics to its impulse response and its function as a selection mechanism.

Results

Clustering of GPi responses reveals two response types

Some of the data used in this modelling study are drawn from a data set previously published in a different form (Tachibana et al. 2008), in which stimulation was applied to M1 cortex and unit activity in the GPi was recorded, with responses of GPe and STN to cortical impulse stimulation taken from Nambu et al. (2000). In those studies, recordings from many different neurons were averaged. Here we use these data in a novel way, before any averaging has taken place, and use the resulting analysis to constrain the mathematical model. Four Japanese monkeys and one rhesus monkey were surgically implanted with bipolar stimulating electrodes in the forelimb region of M1 cortex. The unit responses of 42 GPi neurons were recorded following a 0.3 ms stimulation of M1. Each GPi neuron was recorded 100 times. One PSTH (bin width 1 ms) was created for each neuron. The reader is referred to the original paper for a full description (Tachibana et al. 2008).

Tachibana et al. (2008) reported the mean response of 42 GPi neurons (average PSTH) consisting of an early excitation, then an early inhibition, followed by a long duration late excitation (LDLE), known as a triphasic response. However, our visual inspection of the original single unit data showed a subset of the neurons lacking a late excitation; instead they had a biphasic response consisting of an early excitation followed by a long duration inhibition. To separate these biphasic and triphasic responses quantitatively, each time series was normalised relative to its tonic firing rate by first subtracting the mean of the pre‐stimulation firing rate. Each response was then divided by the maximum of the modulus of the response. This yields a set of 42 time series with amplitude in the range [−1 1], where zero corresponds to the tonic firing rate of each neuron. The mean firing rate over the time period during which the late excitation would ordinarily occur (10–20 ms after the first inhibition) was calculated. Confirming the visual inspection, a histogram of these values shows the separation of the time series into two clusters (Fig. 1 A). The time series averages of these two clusters (Fig. 1 B and C) confirm that the data can effectively be divided into triphasic and biphasic populations.

Figure 1. Clustering of experimentally recorded GPi single unit activity.

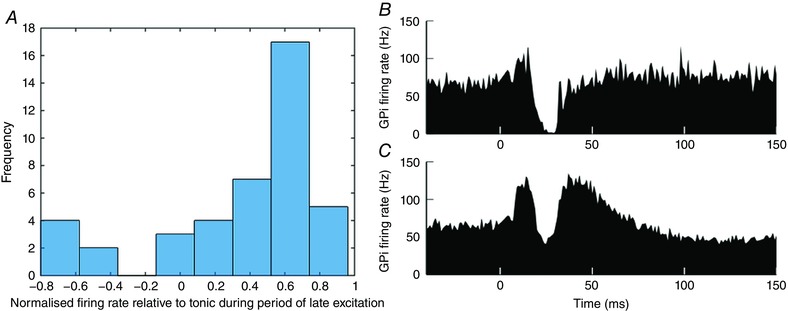
A, bar chart of mean normalised firing rate of each neuron over the time period 10–20 ms after the first inhibition (n = 42; zero corresponds here to tonic firing rate). B and C, means of PSTH data across the two identified clusters. B, mean of GPi neurons whose response to cortical impulse stimulation is biphasic (n = 6). C, mean of GPi neurons whose response to the same stimulus is triphasic (n = 36). Data from Tachibana et al. (2008). [Color figure can be viewed at wileyonlinelibrary.com]

We propose a circuit‐based explanation of BG dynamics and the bimodality of GPi responses based on the idea that the BG is arranged in functionally segregated channels (Alexander & Crutcher, 1990; Hoover & Strick, 1993; Romanelli et al. 2005). The action selection hypothesis posits that each channel encodes a particular action, and the interaction between these channels allows the BG to disinhibit one action and completely inhibit competing actions (Redgrave et al. 1999). A channel is conceived as a flow of neural signals from cortical activity encoding the salience of an action request, through the nuclei of the BG, ultimately disinhibiting the precise cortical neurons that encode the action to be performed (Gurney et al. 2001a,b). We create a model whose parameters are constrained by the BG's impulse response, then investigate the emergent spectral properties of the network under various cortical inputs.

Spatial variation in cortical stimulus input modelled as two channels

In the stimulation studies whose data are used to constrain the model, a bipolar stimulating electrode is placed in the forelimb region of motor cortex (Nambu et al. 2000; Tachibana et al. 2008). This cortical region has been observed to encode stereotyped movements of the limb to various locations. The size of a motor territory in M1 that mediates movements of a limb has been observed to be approximately 0.5 mm (Donoghue et al. 1992). Given that cortical stimulation in Tachibana et al. (2008) and Nambu et al. (2000) is performed using a bipolar stimulating electrode with an inter‐tip distance of 2 mm, it is likely that stimulation excites multiple cortical regions that encode different movement commands. Furthermore, it has been observed that the BG is arranged into segregated channels (Alexander & Crutcher, 1990; Hoover & Strick, 1993; Romanelli et al. 2005). It is assumed that each of the ∼0.5 mm cortical regions provides inputs to one of these BG channels. It is assumed that many channels are stimulated. We make the assumption that one channel is more greatly stimulated than the others. This is shown in Fig. 2 B. Cortical regions are shown as contiguous areas for clarity but our analysis is not dependent on this.

Figure 2. Model inputs and model schematic.

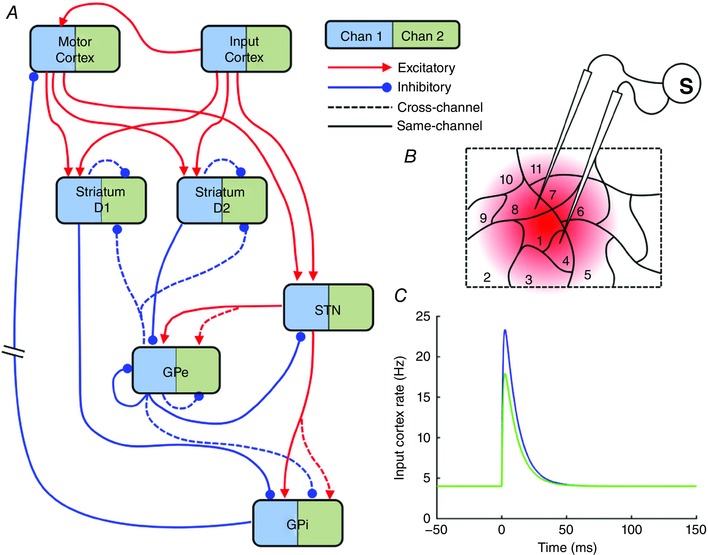
A, schematic diagram of model BG connectivity. The model has two channels: Channel 1 (blue) and Channel 2 (green). For clarity only Channel 1's connections are shown. Thus the model has 16 populations, two of each of the nuclei shown. The two input cortical populations are modelled as hard coded time series of firing rates (see C). B, computational modelling proceeds under the assumption that a small number of cortical cells receive a higher stimulation (region 1) than the majority of cells that are activated by the bipolar stimulating electrode (other regions). C, bi‐exponential cortical input to model, representing the response of pyramidal cells to a 0.3 ms stimulation.

In the interests of creating the simplest possible model that can capture the emergent dynamics, we model only two of the many BG channels: one representing the channel whose cortical stimulation is the highest, and another representing the activity of the other neighbouring channels which are activated to a lesser extent. The inputs to each of the two channels of the model are shown in Fig. 2 C, and represent the average dynamics of the firing rates of pyramidal neurons in either region 1 (the primary‐channel input, IN _P) or the mean activity of regions 2–11 (the secondary‐channel input, IN _S), in response to the 0.3 ms stimulation current injection. Form and duration is estimated from Plenz & Aertsen (1996). The inputs are defined as

$$\mathit{IN}=B_{ctx}+g\left(\frac{ab}{a-b}\right)(e^{-bt}-e^{-at})$$ (1)

where B _ctx is the average background firing rate of the cortical neurons and g is the gain of the signal. The parameters a and b are chosen such that the maximum cortical firing rate is ∼20 Hz (Riehle et al. 1997; Maynard et al. 1999) and the duration of the cortical response to the stimulus is physiologically realistic (Plenz & Aertsen, 1996) (see Table 1 for values).

Table 1.

Table of model parameters

Parameter	Meaning (reference)	Value
Tctx‐str	Axonal transmission delay (Jaeger & Kita, 2011 )	2.5 ms
Tctx‐STN	Axonal transmission delay (Jaeger & Kita, 2011 )	2.5 ms
TSTN–GPe	Axonal transmission delay (Jaeger & Kita, 2011 )	2.5 ms
TSTN‐GPi	Axonal transmission delay (Jaeger & Kita, 2011 )	2.5 ms
TGPe‐STN	Axonal transmission delay (Jaeger & Kita, 2011 )	1 ms
Tstr‐GPe	Axonal transmission delay (Jaeger & Kita, 2011 )	7 ms
Tstr‐GPi	Axonal transmission delay (Jaeger & Kita, 2011 )	12 ms
TGPe‐GPe	Axonal transmission delay (Jaeger & Kita, 2011 )	1 ms
TGPe–GPi	Axonal transmission delay (Jaeger & Kita, 2011 )	1 ms
TGPi‐mctx	TGPi‐Thal [=1.8 ms (Uno et al. 1978 )] + TThal‐ctx [=1.2 ms (Gil & Amitai, 1996 )]	3 ms
τ	Time constant (all nuclei). Ionotropic synaptic time constant (Nambu & Llinas, 1994 )	2 ms
Mstr	Maximum firing rate of striatum (Gittis et al. 2010 )	90 Hz
Bstr	Baseline firing rate of striatum (Adler et al. 2013 )	0.1 Hz
MSTN	Maximum firing rate of STN (Nambu et al. 2000 )	250 Hz
BSTN	Baseline firing rate of STN	50 Hz
MGP	Maximum firing rate of GPe (Kita et al. 2006 ) and GPi (Tachibana et al. 2008 )	300 Hz
BGP	Baseline firing rate of GPe (Kita et al. 2006 ) and GPi (Tachibana et al. 2008 )	150 Hz
Mctx	Maximum firing rate of cortex (Maynard et al. 1999 )	22 Hz
Bctx	Baseline firing rate of cortex (Maynard et al. 1999 )	4 Hz
da	Dopaminergic input (normalised)	0.3
[a,b]	Biexponential parameters – Input stimulation	[100,1000]
gp	The primary‐channel input gain. Tuned to give maximum of ∼22 Hz (Maynard et al. 1999 )	0.25
gs	The secondary‐channel input gain.	0.17
Wmc‐stn	Motor cortex–STN connection strength *	20
Wge‐stn	GPe–STN connection strength *	3
Ws2‐ge	D2 striatum–GPe connection strength *	40
Wstn‐ge	STN–GPe connection strength *	0.72
Wge‐ge	Strength of GPe cross‐channel connections *	1.37
Wge‐gi	GPe–GPi connection strength *	0.8
Ws1‐gi	D1 striatum–GPi connection strength *	4
Wstn‐gi	STN–GPi connection strength *	0.2
Ws‐s	Strength of striatal MSN cross‐channel connections *	0.3
Wgi‐mc	GPi to motor cortex connection strength *	0.25
Wsc‐s	Input cortex to striatum connection strength *	4
Wsc‐stn	Input cortex to STN connection strength *	20
Wmc‐s	Motor cortex to striatum connection strength *	0.65
Wsc‐mc	Input cortex to motor cortex connection strength	1
Wge‐s	GPe to striatum connection strength *	0.1
WgeR	Strength of recurrent inhibition in GPe *	0.3

^*MAP values from SMC–ABC to minimise deviation from experimental data.

Experimental observations have shown qualitatively different pallidal responses depending on the location of the recorded neuron in the pallidal zone of influence of the stimulation site: neurons close to the centre of the zone of influence show markedly different responses to those at the periphery (Tremblay et al. 1989). Thus, a spatially inhomogeneous stimulation may act on action channels within the BG to create the pair of pallidal responses described above. We now explore the plausibility of this hypothesis using a computational model. A schematic diagram of the model's connectivity is shown in Fig. 2 A.

Model architecture

One channel (hereafter primary‐channel, shown in blue in all figures) of the model GPi was fitted to the biphasic response, and the other channel (hereafter secondary‐channel, shown in green in all figures) to the triphasic response. In clustering the data, we found many more triphasic neurons (the secondary‐channel) than biphasic neurons (the primary‐channel). The population average activity recorded experimentally from the GPe and STN was therefore assumed to be represented by the secondary‐channel of the model (Fig. 3 B and C).

Figure 3. Constraint of model connection strength parameters using time series data.

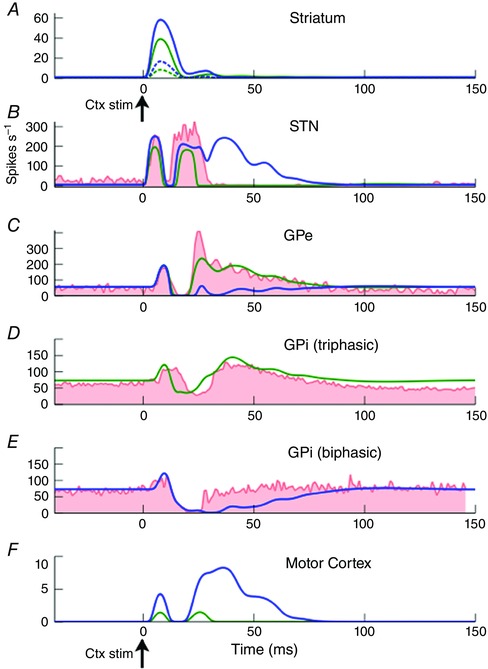
Experimental data shown in red [STN and GPe (Nambu et al. 2000), GPi (Tachibana et al. 2008)]. The two channel responses obtained from our cluster analysis in GPi are show in separate panels (GPi triphasic and GPi biphasic). Primary channel model output shown in blue, and secondary channel model outputs shown in green. Secondary channel fitted to STN, GPe and GPi‐triphasic populations. Primary channel fitted to GPi‐biphasic population. In striatum, D1 MSNs shown as continuous lines, D2 MSNs as dotted lines.

We initially attempted to fit the BG's impulse response using a firing rate model in which the dynamics of each population's average firing rate is given by a first order delay differential equation (DDE). However, this first‐order model yielded results that differ significantly from the data. While it was able to capture the main features of the impulse response, the model reacts too quickly to the impulse. The variance accounted for (VAF) between the first‐order model and the PSTH data is 0.188. The fit to the data can be much improved (VAF = 0.584) by modelling each population using second‐order DDEs rather than first‐order DDEs. The average firing rate dynamics of each neural population is defined as

$${\ddot{y}}_n{\tau }_n^2+2{\dot{y}}_n{\tau }_n+y_n=\sum _m{W}_{mn}f\left(y_m^{(t-T_{mn})}\right)$$ (2)

in which y_n is the activation of the nth nucleus, and the dot and double dot accents represent the first and second time derivatives respectively. τ_n is the time constant of the nth nucleus. W_mn is the connection strength between the mth afferent nucleus and the current nucleus, n. f is a sigmoidal transfer function that converts the activation y into the firing rate of the nucleus (see eqn 3). Thus, f(y_m ^{( t‐Tmn )}) is the firing rate of the mth afferent nucleus at T_mn seconds in the past, where T_mn is the axonal transmission delay between nuclei m and n. Delay is shown in superscript for clarity. This second‐order formulation has the advantage of being physiologically more realistic without increasing the dimensionality of the parameter space of the model. The model is therefore composed of a set of DDEs, with each equation describing the firing rate dynamics of each of the nuclei of the BG; D1 and D2 striatum; STN; GPe; GPi and motor cortex. Since the model has two channels, there are 12 DDEs in total. The action of dopamine in the model is captured by including a multiplicative factor on the cortico‐striatal connection strength parameters. Medium spiny neurons (MSNs) of the striatum have been shown to express either D1 receptors, which increase the propensity of the neuron to fire when dopamine is present, or D2 receptors, which decrease firing rates in the presence of dopamine (Surmeier et al. 2007). The action of dopamine is defined by multiplying the cortex–D1 striatum connection strength by 1+da, and the cortex–D2 striatum connection strength by 1‐da, where da is a parameter in the range [0,1] describing the proportion of dopamine receptors that are currently occupied (Gurney et al. b). Thus, the parameter da is a normalised measure of the quantity of extracellular dopamine in the striatum. The cortico‐striatal connection strengths are the same for both D1 and D2 MSNs, so the differences in their firing rates are due to the way they are respectively modulated by dopamine. See Methods for a full description of the model.

Model explains time domain features of BG dynamics

The model is able to fit the data well (Fig. 3). The model quantifies the origins of the time domain features that are present in a range of experimental BG stimulation studies and provides a quantitative explanation for the generation of the BG's impulse response. The generation of the impulse response is described qualitatively in Fig. 4.

Figure 4. Graphical description of the causative mechanisms of the main features of the response of BG nuclei to a cortical impulse stimulation.

 

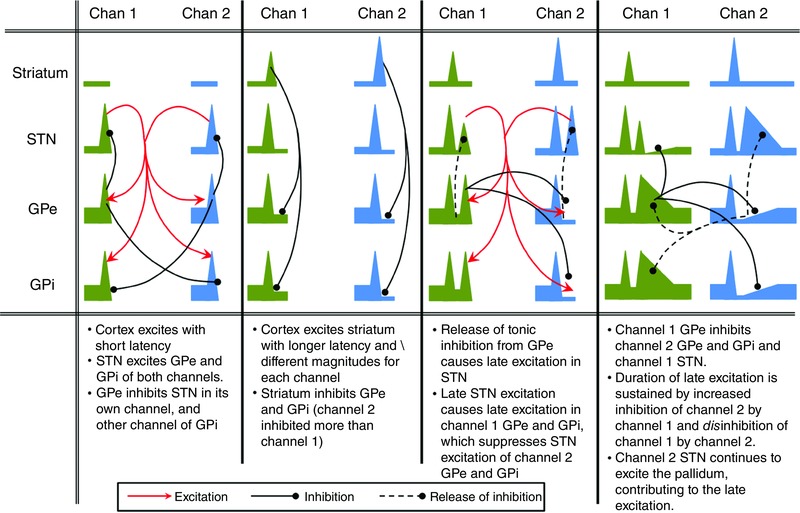
We go on to validate the model by a replication of the results of stimulation experiments in which the free parameters of the model were not fitted. In a study by Kita et al. (2006) the striatum of Japanese macaque monkeys was stimulated and single unit recordings were taken from multiple GPe and GPi neurons. Stimulations were either a single current pulse (lasting 0.3 ms) or a 200 ms burst of pulses at varying frequencies. The stimulation protocols were simulated by adding an additional excitatory input to the striatal populations. This was in addition to the cortical background input of 4 Hz (see Table 2 A–H). Stimuli were modelled as square pulses of input to the stimulated nucleus, with magnitudes that were sufficient to bring the firing rate of the maximally stimulated nucleus to close to its maximum firing rate. The direct input to the STN was the cortical background firing rate only. Burst stimulations were a train of the above single stimulations delivered at 50 Hz for 200 ms.

Table 2.

Parameters used to generate validation plots in Fig. 5

Sub‐figure	Original experimental protocol	Recorded nucleus	Model manipulation	Input magnitude [gP,gS] [INP, INS] Hz
A	Impulse striatum [1]	GPe	–	[1000, 400] [87, 54] Hz
B		GPi	–
C	50 Hz stimulation striatum [1]	GPe	–	[1000, 400] [87, 54] Hz
D		GPi	–
E	Impulse striatum – Local gabazine [1]	GPe	Wstr2‐GPe = 0.1 W	[1000, 400] [87, 54] Hz
F		GPi	Wstr1‐GPi = 0.1 W
G	50 Hz stimulation striatum – Local gabazine [1]	GPe	Wstr2‐GPe = 0.1 W	[1000, 400] [87, 54] Hz
H		GPi	W str1‐GPi = 0.1 W W GPe–GPi = 0.1 W
I	GPe impulse [2]	GPi	–	[5000, 2000] [300, 278] Hz
J	Cortex impulse – muscimol in GPe [2]	GPi	W GPe–GPi = 0 W W GPe‐STN = 0 W W GPe‐GPe = 0 W W GPeRec = 0 W W GPe‐str = 0 W	[0.25, 0.17] [22, 17] Hz
K	Cortex impulse – muscimol in STN [2]	GPi	W STN–GPe = 0 W W STN‐GPi = 0 W	[0.25, 0.17] [22, 17] Hz
L	Cortex impulse – D2 – GPe pathway lesioned [3]	GPe	Wstr2‐GPe = 0 W	[0.25, 0.17] [22, 17] Hz

The experiments modelled are either in Kita et al. (2006) or Tachibana et al. (2008) or Sano et al. (2013), designated [1], [2] and [3], respectively, in column 2, which describes the original expermental protocol. In the case of cortical inputs, the input parameters g _P (g _S) are the gains of the biexponential input function on the primary channel (secondary channel). In the case of striatal or GPe inputs, they are the maximum values of the square wave current input. The pairs [INp, INs] are the corresponding peak firing rates in the stimulated nucleus on the primary channel (secondary channel). The model manipulation comprises a weight change expressed in the form W _mn = xW, where W is the original value of W _mn and x is a multiplying factor.

Results of the validation experiments are shown in Fig. 5. The model outputs closely resemble the experimental PSTHs. Either a single stimulation (Fig. 5 A and B) or multiple stimulations (Fig. 5 C and D) of the striatum evoke an inhibition followed by LDLE in the secondary channel of both GPe (Fig. 5 A and C) and GPi (Fig. 5 B and D). Experimental results have shown an excitation of the pallidum in response to striatal stimulation, after local administration of GABA antagonists. This counterintuitive result has been observed, but not directly investigated experimentally. It has been assumed that the excitation is due to the unintended stimulation of thalamic‐STN fibres of passage. However, the current model suggests a possible alternative or coexistent mechanism. If it is assumed that the GABA antagonists do not block inhibitory afferents completely, then a small number of GPe neurons see their activity reduced. This reduces the level of tonic inhibition seen by the GPe to which they are connected, thus causing an apparent excitation in both GPe and GPi (see Fig. 5 E–H). Experimental data shown in the insets to Fig. 5 I–K (from Tachibana et al. 2008) may best be compared to the primary‐channel model results (blue dotted), since the authors state that they selected cortical stimulation sites that gave rise to the largest response for each GPi neuron. This would mean that the stimulation site and recorded neuron belong to the same channel.

Figure 5. Model validation.

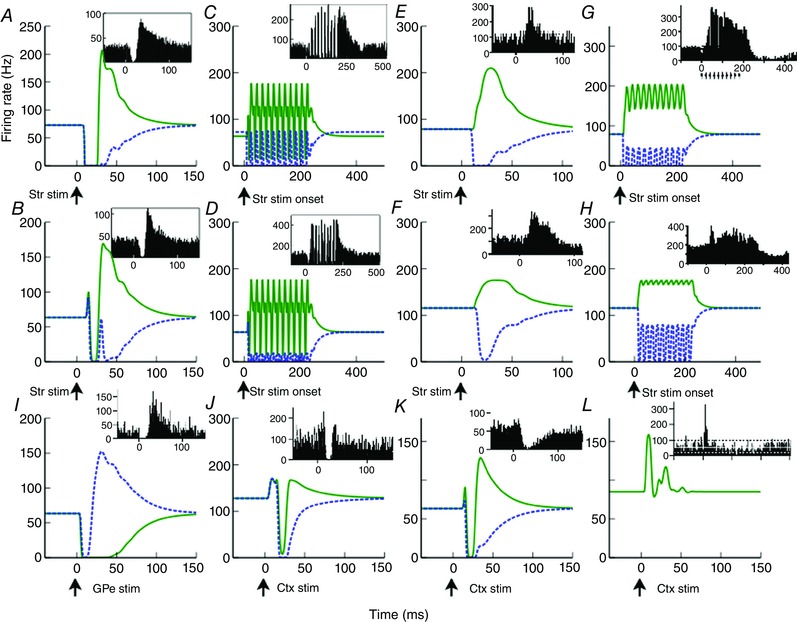
Performance of the model in 12 experimental manipulations on which the free parameters of the model were not fitted. Model primary channel/secondary channel responses are shown as blue dotted/green continuous lines, respectively. Experimental data [A–H: Kita et al. (2006), I–K: Tachibana et al. (2008), L: Sano et al. (2013)] are shown in insets. A (B), GPe (GPi) response to striatal impulse stimulation. C (D), GPe (GPi) response to striatal 50 Hz stimulation. E (F), GPe (GPi) response to striatal impulse stimulation following local application of muscimol. G (H), GPe (GPi) response to striatal 50 Hz stimulation following local application of muscimol. I, GPi response to impulse stimulation of GPe. J, GPi response to cortical M1 impulse stimulation following administration of muscimol into the GPe. K, GPi response to M1 cortical impulse stimulation following administration of muscimol into the STN. A–H insets are PSTHs averaged across all recorded neurons, and should thus be compared to the secondary channel model (green continuous lines) since we assume that the majority of neurons are in this channel. I–K insets are averages of GPi neurons whose cortical stimulation sites were chosen to yield largest responses. Thus, these figures should be compared to the model's primary channel output (blue dotted lines). L, D2 striatum to GPe connections lesioned. See Table 1 for model manipulations used to represent these experimental conditions.

Fig. 5 L differs from the other validation data in that they were recorded from behaving mice rather than non‐human primates. The similarity between the model and the data in this case demonstrates that the inhibition of the GPe is essential for the generation of the LDLE in the GPe. Since excitation from the STN is still present in this manipulation, it cannot be solely responsible for the LDLE. Only one channel is visible because lesioning the D2 striatum to GPe pathway causes both channels to behave identically.

The fact that the model solutions are similar to observed firing rate dynamics in a diverse range of experimental manipulations is taken as good evidence that the model accurately reflects the average network activity of the BG in vivo.

Model has spectral properties that match experimental observations

Spectral properties of the BG and related networks are an extremely well‐studied area, and include LFP recordings from human BG nuclei taken during procedures to implant deep brain stimulation electrodes for the treatment of various neurological disorders. Coherent beta (13–30 Hz) and gamma (30–90 Hz) oscillations are present throughout cortical–thalamic–BG networks in healthy animals: beta oscillations have been observed in spontaneous LFPs recorded from motor regions of the GPs of healthy non‐human primates (Connolly et al. 2015) and rats (Tort et al. 2008; Leventhal et al. 2012). Many studies have found that beta activity is relatively high during static force maintenance (Sanes & Donoghue, 1993; Klostermann et al. 2007) or following a cue that is later used to initiate movement (Leventhal et al. 2012; Oswal et al. 2012; Tan et al. 2015). Beta power has thus been conceptualised as encoding anti‐movement, or ‘maintenance of the status quo’ (Cassidy, 2002; Kühn et al. 2004; Gilbertson et al. 2005; Engel & Fries, 2010). Beta power as observed in the LFP of the STN is often observed to decrease shortly before movement onset, replaced by higher activity in the gamma frequency range (Alegre et al. 2005; Jenkinson et al. 2013). Spectral power in the LFP of the STN is largely confined to below ∼35 Hz or from 50 to 90 Hz (Boraud et al. 2005). We now examine each of these phenomena in turn.

Model supports beta frequencies when cortical inputs are similar in magnitude

We examined the emergent oscillatory properties of the model over a wide range of input cortex firing rates (Fig. 6). The model was simulated using every combination of input cortical firing rates between 4 and 22 spikes s⁻¹ in steps of 0.2 spikes s⁻¹. Initial firing rates and activations were set to zero. Input firing rates were constant over the duration of each simulation (0.3 s). Input firing rates are now considered to represent some measure of salience or urgency of performing a particular action (Gurney et al. 2001a). Thus, the cortical inputs are conceived as originating from relevant activity across possibly spatially separated regions of cortex. We calculate the spectral properties of the model by simulating for 0.3 s and calculating the frequency at which the spectral power is maximal over the last 0.2 s.

Figure 6. Oscillatory and selection properties of the model depend on cortical inputs and dopamine level.

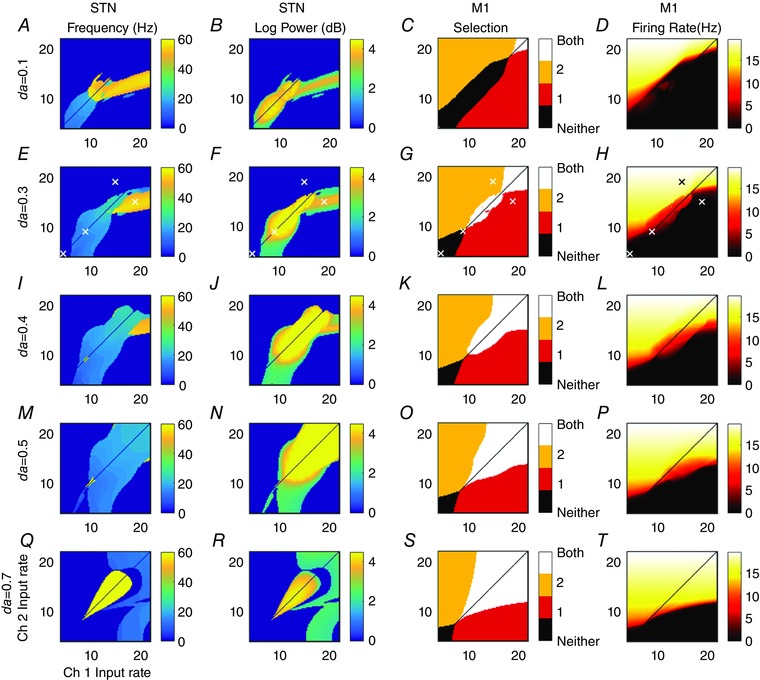
Each panel shows a feature of channel 2's activity over the last 0.2 s of the 0.3 s simulation, and for a range of cortical input pairs with different firing rates. Column 1: Frequency of maximum power of channel 2 STN's weighted sum of inputs (simulated LFP). Column 2: the corresponding maximum log power of the frequency shown in column 1. Column 3: displays which of the action channels has a motor cortical firing rate above the 4 Hz cortical background level. Column 4: firing rate of channel 2 motor cortex. Channel 1 results for columns 1, 2 and 4 (not shown) are identical plots reflected in the line ch1 = ch2. A–D: da = 0.1. E–H: da = 0.3. I–L: da = 0.4. M–P: da = 0.5. Q–T: da = 0.7. Identical inputs (diagonals) not calculated to avoid unphysiological symmetries. White crosses in row da = 0.3 indicate parameter values used in Fig. 7 and selection analysis.

While the relationship between cellular processes and the LFP is not fully understood, an often used approximation is that it best corresponds to synchronous post‐synaptic potentials (Eccles, 1951; Kühn et al. 2005). The firing rate model by definition represents synchronised neural activity since it has been constrained by average population activity. The LFP was therefore modelled as the weighted sum of inputs to the STN. Peak frequencies below 3 Hz or with an amplitude less than 2 spikes s⁻¹ are set to zero. This was done so that the power of low frequency (highly damped) transients did not obscure the oscillatory data. Fig. 6 is therefore a conservative approximation of the presence of oscillatory activity, since any transients that have reduced to negligible power within 100 ms are not detected by this analysis. In a noisy neural system, however, transients may be a significant driver of spectral power (Blenkinsop et al. 2012).

The first column of Fig. 6 shows the frequency for which spectral power is maximum in the weighted sum of all inputs to channel 2 STN (a similar plot for channel 1 would be identical, but reflected in the line y = x). The second column displays the log of the power of that frequency. Oscillatory activity in the model is confined to two frequency bands; beta and gamma. The model does not exhibit stable oscillations outside of these ranges. Beta frequency oscillations arise naturally in the model when the inputs to both channels are roughly equal. This beta frequency oscillation causes above‐threshold mean activity in both action‐channels in motor cortex (Fig. 6 column 3). The corresponding firing rates of channel 2's motor cortex are shown in column 4. Similarly to other plots, channel 1's motor cortical firing rate plots would be identical but for a reflection in the line y = x.

The behavioural interpretation of the model requires us to define what is represented by each channel of the mathematical model. Observations of the areas of motor cortex that project to the BG show that cortical territories are divided into regions that give rise to stereotyped movements when stimulated (Georgopoulos et al. 1986). It is therefore assumed that a BG channel encodes one of these movement commands. Following the hypothesis that the BG selects between competing inputs (Redgrave et al. 1999) we make the assumption that cross channel projections in the BG will be present between channels encoding actions that are by definition incompatible, for example move arm left and move arm right. That such a relationship may exist is indicated by the results of Georgopoulos et al. (1986) in which elevated motor cortical activity in cells encoding a movement in one direction is accompanied by a decrease in activity in cells encoding the opposite direction. Co‐activation of a pair of such channels may therefore be the mechanism responsible for the generation of muscle tone.

Given the interpretation that the pair of action channels encode a pair of antagonistic movement commands, this could offer an explanation as to why beta frequencies are raised between a warning cue and movement itself (Leventhal et al. 2012). Thus, dual activation of antagonistic movement commands could increase muscle tone in readiness for the movement to come. Decreasing the dopamine level causes the level of activation required to produce high power beta frequency oscillations to decrease. This is in agreement with spectral STN LFP data recorded from 1‐methyl‐4‐phenyl‐1,2,3,6‐tetrahydropyridine (MPTP)‐treated primates, which show an increase in beta power at rest in the pathological condition (Bergman et al. 1994). Furthermore, if the Levodopa dose is sufficiently high, gamma oscillation power replaces beta frequencies when inputs are equal and above baseline (Brown et al. 2001) (Fig. 6 Q and R).

To observe, in the time domain, how the BG–cortical‐loop model behaves in response to changing inputs, the model was simulated using the input cortex input shown in the top left panel of Fig. 7. The model was run for 1 simulated second. Every 0.25 s the input cortical firing rates of each action channel were changed. This divides the 1 s simulation into four epochs. The location in parameter space of the inputs in each epoch are shown as white crosses in Fig. 6. To avoid physiologically implausible numerical artefacts caused by symmetries in the inputs, similar inputs are never set to exactly equal values (they differ by 0.1 Hz). Inputs were chosen to reflect a range of conditions: Rest: 4 Hz background (during 0 < t < 0.25); Preparedness: a higher but still undifferentiated pair of inputs for the initiation of increased muscle tone (0.25 < t < 0.5); Movement: channel‐1 activity greater than channel‐2 by an amount sufficient for the BG model to cleanly select channel‐1 over channel‐2 (0.5 < t < 0.75); and action‐channel‐2 activity greater than channel‐1 by an amount sufficient for the BG model to cleanly select channel‐2 over channel‐1 ( 0.75 < t < 1).

Figure 7. Spectral and selection properties of the cortico‐BG model as a function of time.

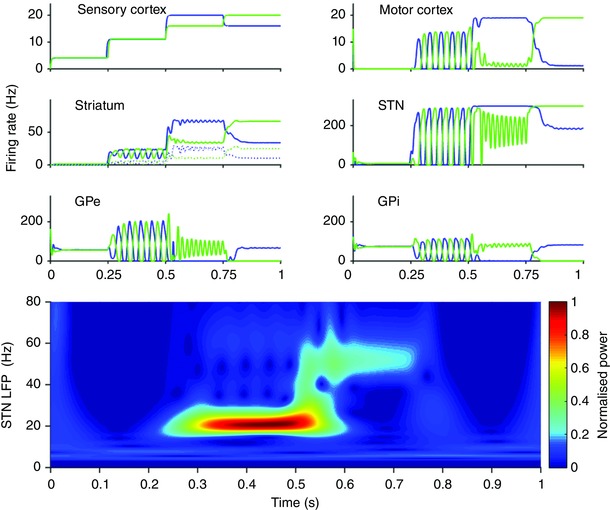
Cortical input: firing rate of input cortex for channel 1 (blue) and channel 2 (green). Striatum: firing rate of D1 striatum (continuous lines) and D2 striatum (dotted lines). Motor cortex, STN, GPe and GPi: firing rates of respective nuclei. Bottom: pseudo‐frequency of weighted sum of inputs to both STN channels calculated using a Mortlet wavelet.

With 4 Hz cortical background input, the BG fully inhibits activity in motor cortex (Fig. 7 top right). Increasing the overall magnitude of BG inputs, but keeping the two inputs roughly equal, gives rise to ∼20 Hz oscillations in all nuclei of both channels. These oscillations are in anti‐phase and arise chiefly as a consequence of the interaction between the competitive cross‐inhibition within the GPe and the loop through cortex. They propagate throughout all nuclei in the BG and motor cortex. An analysis of the relative phase relationship between the beta oscillations in motor cortex and STN shows that the cortex leads the STN by 130 deg or ∼30 ms. This is consistent with experimental observations of beta frequencies that show that the cortex leads the STN in healthy rats (Sharott et al. 2005), in levodopa‐treated Parkinson's patients (Williams, 2002; Litvak et al. 2011) and the 6‐hydroxydopamine (6‐OHDA) rat model of Parkinson's disease (Mallet et al. 2008). Our analysis suggests that, although the cortex leads the BG at beta frequencies, the oscillations may arise as a consequence of network interactions within the BG–cortical circuit as a whole. Once the inputs have a sufficiently large difference between them (t > 0.5), the symmetry between the two channels of the model is broken, causing one action channel to be disinhibited and the other more greatly inhibited. The gamma frequency (∼50–60 Hz) oscillations between the STN and GPe of each channel occur following the change in inputs. These results are consistent with experimental results (Tort et al. 2008; Tan et al. 2015).

Gamma power is associated with channel selection and is generated in the GPe–STN loop

Gamma band (30–90 Hz) oscillations occur in the model in two regimes. At low dopamine levels they occur when both channels’ inputs are relatively high, but are sufficiently different for one to be selected over the other (Fig. 6 da< = 0.4). If the inputs are too similar then beta oscillations in both channels dominate. Gamma oscillations, in the regime in which dopamine levels are less than 0.4, occur when a decision has been resolved. Importantly, gamma oscillations occur most readily in the channel that is not selected. That is to say that the neurons encoding the action that is expressed in behaviour are not the neurons that are generating the gamma power. This is a result that requires further experimental work to investigate.

Increasing the level of striatal dopamine increases the propensity of the model to oscillate at gamma frequencies. At high dopamine levels, dual channel selection is common and is accompanied by gamma in the STN (Fig. 6 da = 0.7). However, the reduced D2 MSN firing rate leads to an elevated average GPe activity. This causes the firing of the GPi to be completely silenced. As such, gamma oscillatory activity is not passed forward to the motor cortex. Activity in the motor cortex of both channels is cleanly disinhibited. However, at moderate dopamine levels (∼0.3) cortical input combinations exist whereby both channels pass gamma frequencies to motor cortex (e.g. ch1 = 12 Hz, ch2 = 17 Hz).

A lesion study of the model shows the effect of lesioning the GPe to STN pathway (Fig. 8 H–K). The absence of gamma band activity in this condition indicates that the gamma frequency activity seen in the STN LFP of the model arises in the STN–GPe feedback loop. The only requirement for the transmission of gamma oscillations to motor cortex, given the presence of gamma oscillations in the STN–GPe loop, is that the GPi's and motor cortex's firing rates remain in their dynamic range. For this condition to be met, the weighted sum of inputs to the GPi must neither be so high that the GPi saturates at its maximum rate, nor so low its rate is pushed to zero. The transfer of gamma power to cortical targets has been observed (Williams, 2002), but it should be noted that this study used LFP from the STN and electroencephalogram from cortex in patients with advanced Parkinson's disease. It remains as future work to study the changes observed in the Parkinsonian brain using this model.

Figure 8. Effect of lesioning GPe–striatum and GPe–STN pathways.

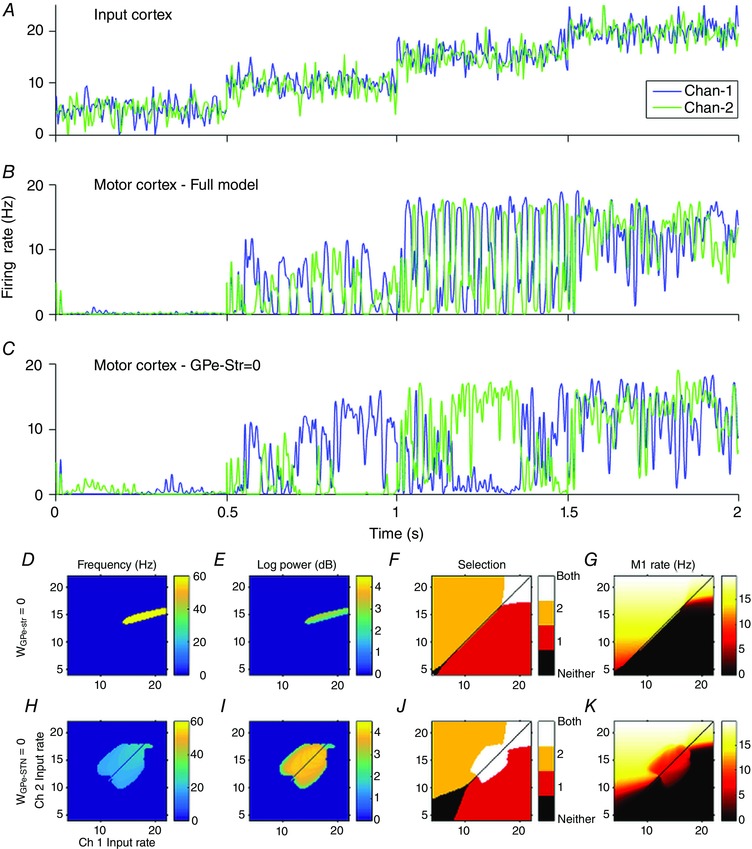
A, action channel 1 (blue), and action channel 2 (green) have identical mean firing rates within each 0.5 s interval. Each channel has 100 Hz, 2 spikes s⁻¹ amplitude Gaussian noise added. B, motor cortex output with connections intact. C, motor cortex output with GPe–striatum connection set to zero. D–G, similar plots to Fig. 6 with GPe–striatum connection strength set to zero (no noise applied to inputs). H–K, similar plots to Fig. 6 with GPe–STN connection strength set to zero (no noise applied to inputs). GPe–striatum connection strength is set to its healthy value.

GPe–striatum pathway critical for beta generation and simultaneous selection of motor commands

The GPe–striatum pathway is often omitted from models of the BG. We explored the network effects of lesioning this connection and compared the results with the unlesioned model. The model was run for 2 simulated seconds. Every 0.5 s the mean firing rate was increased (5, 10, 15, 20 spikes s⁻¹). Mean firing rates on both channels were equal within each 0.5 s interval, but each channel had a 100 Hz (2 spikes s⁻¹ amplitude) Gaussian noise applied independently. The criteria (also used above) to define whether a channel is selected was that the average firing rate of a channel was above the cortical baseline rate of 4 Hz.

In the intact model equal inputs give rise to antiphase beta oscillations in BG output. Since the average firing rate of both channels during the anti‐phase beta oscillations are above this threshold, both channels are selected. The average firing rate of both channels’ outputs are approximately equal (Fig. 8 B).

Motor cortical output is significantly altered when the GPe–striatum connection is lesioned (Fig. 8 C). Despite the mean input firing rate of both channels being identical, the model with the GPe–striatum connection lesion often selects one channel over the other in response to the noise, and persists with that selection long after the event that caused the selection has ceased.

In the model with connections intact, the GPe–striatum connection is essential in the generation of the beta frequency anti‐phase oscillations discussed above. Cross‐channel inhibition in the GPe causes one channel to be active and the other to be silenced. The silent channel ceases to inhibit the striatum of the other channel, allowing it to become active. In this way oscillations are maintained so long as the inputs to both channels are similar in magnitude. The strength of the GPe to striatum connection defines how dissimilar the inputs need to be to permit one channel to be selected over the other (Fig. 8 D–G).

Models with a close fit to the data function as selection mechanisms

The hypothesis that the BG acts as a selection mechanism, mediating competition between action representations vying for control of motor resources, has gathered much support (Chevalier & Deniau, 1990; Mink & Thach, 1993; Prescott et al. 1999; Redgrave et al. 1999; Hikosaka et al. 2000). That the BG can, in principle, act as a selector has been demonstrated in numerous computational models (Beiser & Houk, 1998; Gurney et al. b; Frank, 2005; Humphries et al. 2006). In this view, the akinesia, and bradykinesia associated with Parkinson's disease are viewed as malfunctions of selection. In this paper we seek independent theoretical corroboration that the healthy BG network is tuned to perform action selection. To test the ability of the model to select between competing inputs, each of the two channels (channel‐1 and channel‐2) was driven by time‐varying cortical inputs (see Fig. 7, top left) to simulate a time‐varying pattern of competing actions. A channel was classed as selected if the motor cortex firing rate in the relevant epoch is above the 4 Hz cortical background firing rate.

The model selects between the test inputs and responds in a physiologically plausible way to dopaminergic modulation (see Fig. 6, third column). Increasing the simulated dopamine level increases the range of input cortex firing rates that give rise to both channels being selected, indicating that selection becomes more promiscuous (Swanson et al. 1998; Humphries & Gurney, 2002). Decreasing the dopamine level decreases the range of inputs that yield dual channel selection and increases the range of inputs that fail to disinhibit any action. This effect can be seen at its most extreme in the top row of Fig. 6 in which dopamine level is 0.1. In this case dual activation of antagonistic actions is not possible no matter how high the inputs from input cortex are. It seems likely that this regime is physiologically undesirable. It remains as future work to test the hypothesis that the network changes that are observed in Parkinson's disease serve to mitigate the effects of this transition.

If the BG is a selection mechanism, there should be an anticorrelation between the model's deviation from the data of Nambu et al. (2000) and Tachibana et al. (2008) and the model's ability to select between inputs. The relationship between deviation‐from‐data and selection was done by perturbing the connection strength parameters from those found to allow a good model fit to the data, as described above. Each perturbed parameter set (of which there were 750) was constructed by applying Gaussian noise to the MAP estimates of the values. The motor cortical firing rate of each model was tested for selection (increasing above the 4 Hz background rate) in each of the four epochs in both a high and a low dopamine condition. Selection properties were adapted from Gurney et al. (2004). An additional test ensures that the tonic firing rate of the GPi is within a biologically plausible range. This yields a suite of nine selection tests. The degree of selection ability was determined by the number of these tests a model passed, N, and the deviation from data expressed as root mean square error.

Selection tests

• (1) Tonic firing rate of GPi should be between 20 and 150 Hz.

Low dopamine (DA = 0.3)

• (2) In epoch 1 channel 1 and channel 2 should not be selected.
• (3) In epoch 2 channel 1 and channel 2 should be selected.
• (4) In epoch 3 channel 2 should be selected and channel 1 should not be selected.
• (5) In epoch 4 channel 1 should be selected and channel 2 should not be selected.

High dopamine (DA = 0.6)

• (6) In epoch 1 channel 1 and channel 2 should not be selected.
• (7) In epoch 2 channel 1 and channel 2 should be selected.
• (8) In epoch 3 channel 1 and channel 2 should be selected.
• (9) In epoch 4 channel 1 and channel 2 should be selected.

Fig. 9 shows N plotted against root mean square error. The significant anti‐correlation between the two variables (correlation of means: R = −0.93, P = 0.003) indicates that the closer the model network gets to the experimental data, the better the network functions as a selection mechanism. We take this as evidence that the BG network is tuned to perform as a selection mechanism.

Figure 9. Correlation between selection ability (number of selection test passed) and deviation from experimental data (root mean squared error, RMSE).

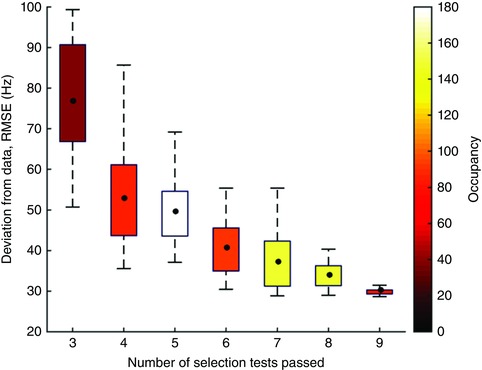
The model was simulated using 750 randomly generated parameter sets derived from Gaussian kernels whose means are the MAP parameter values. Number of parameter sets within each box and whisker is shown on the colour bar. Black dots show the locations of means. Boxes show interquartile ranges, and whiskers show data outside 1.5 times the interquartile range. Correlation of means: R = −0.93, P = 0.003. There were no parameter sets that passed fewer than three tests. See text for a list of the nine selection tests.

Methods

Model architecture

The model architecture is similar to our previous work (Gurney et al. 2001a,b) but includes several additional features (see Fig. 2 A). Firstly, both main populations of striatal projection neurons – defined by preferentially expressing D1 or D2 dopamine receptors – have cross‐channel inhibitory connections (Grillner & Graybiel, 2006). Lateral connections may exist between D1 and D2 MSNs of the same channel. However, these connections would have a similar effect to the action of dopamine in the model. To avoid causing degenerate solutions during parameter optimisation, these have been omitted. Recent observations have shown that the GPe consists of two separate populations: those that have mainly striatal efferents (arkypallidal cells), and those that project chiefly to the GPi and STN (prototypical cells) (Mallet et al. 2008, 2012). However, there is currently an absence of any data regarding differences between their respective afferents. Furthermore their activity is uncorrelated in the healthy BG. They are therefore modelled as a single population. Since the axons of the pallido‐striatal neurons have been observed to arborise across large regions of the striatum we assume that the GPe to striatum connection is cross‐channel. It should be noted that this connection is GPe to MSN rather than the GPe to striatal interneuron connection (Mallet et al. 2012; Corbit et al. 2016). The GPe contains cross‐channel inhibitory connections (Kita & Kita, 1994). While it would be possible to include within‐channel GPe–GPi and GPe–striatum connections, these additional connections would not yield additional information about how channel‐wise structure in the BG contributes to the observed dynamics. They would also greatly increase the dimensionality of the parameter space, leading to over‐fitting. They have therefore been omitted.

There is much precedence for the modelling of the BG in cortical loops (Humphries & Gurney, 2002; Leblois et al. 2006; van Albada & Robinson, 2009; Moran et al. 2011; Marreiros et al. 2013). As well as afferents from motor areas, BG inputs include those from a broadly sensory origin, which project excitation to a cortical motor area to initiate an action, as well as to the striatum and STN. The cortical motor area also projects to the BG and receives tonic inhibition from the BG output nuclei via the ventrolateral thalamus. Many experimental studies have examined cortical motor control in the context of reach movements. In this context a candidate for the input cortical region could be the ventral premotor cortex, in which potential reach targets are known to be encoded, possibly in an effector‐ (i.e. hand) centred coordinate system (Graziano & Gross, 1998). A candidate for the motor region could be primary motor cortex. The ventral premotor cortex makes glutamatergic connections with primary motor cortex (M1) in order to effect a movement to the target location (Davare et al. 2009). Both ventral premotor cortex and M1 make reciprocal connections with the BG (Alexander et al. 1986; Hoover & Strick, 1993). However, our analysis is not reliant on any precise anatomical interpretation.

With the aim of making the simplest possible model, the above connectivity is modelled with the following approximations. Firstly, that both input cortical area and motor area provide input to the BG, but only the motor area receives tonic inhibition from the BG. This is similar to other modelling studies which focus on a single BG–cortex loop (Humphries & Gurney, 2002). Secondly, it is assumed that the thalamus acts only as a relay between the BG and cortex. The ventrolateral thalamus is therefore not modelled explicitly and its effect is approximated by an additional delay. The input cortex to motor cortex connection strength was set to 1. Each population reacts to its inputs with the time constant of ionotropic post‐synaptic potentials (∼2 ms) (Nambu & Llinas, 1994).

The connection strength parameters in the model govern the magnitude of the input that a nucleus receives from its afferent. In the brain, this may be mediated by a large variety of factors, such as number of synapses between the two nuclei, location of the synapses relative to the soma, number of receptors within each synapse, number of neurons in the two populations and many other factors. These variables are often difficult to quantify with any accuracy. A strength of firing rate models in general is that all the uncertainty associated with the precise nature of the connections can be encapsulated by a single parameter that simply multiplies the output of the upstream nucleus. The value of this parameter can then be inferred from the mean firing rate of both nuclei.

Model formalism

The model BG has two channels. Each channel is composed of an STN, a D1 striatum, a D2 striatum, a GPe population, a GPi and a motor cortex. The dynamics of each of these nuclei is governed by eqn (4). Second‐order dynamics are a common choice in neural mass models, which have explicit expressions governing the membrane potential of each post‐synaptic receptor‐type (for BG examples see Moran et al. 2011; Marreiros et al. 2013). We here use second‐order dynamics to capture firing rates in a phenomenological way.

The dynamic variable, y, is named the activation of the nucleus, and is analogous to an average membrane potential. This activation is converted to the firing rate of the nucleus by a non‐linear transfer function, f. A usual choice for this function is a sigmoid, since its output approaches constant values at the extremes of high and low input magnitudes. However, the shape of a standard sigmoid means that it is impossible to set a sub‐1 Hz baseline firing rate without steepening the gradient of the function, and thus sacrificing the dynamic input range of the nucleus. This is a particular problem when modelling MSNs, since they are generally virtually silent until activated. To remedy this issue we use a Gompertz function, which shares the desirable saturation properties of the standard sigmoid, but falls far more rapidly to its lower asymptote, meaning that a modest amount of self‐inhibition can reduce the firing rate of the nucleus to effectively zero, as required by the physiology. The proportion of the curve that is approximately linear is also larger than for the standard sigmoid, again giving a better representation of the physiology of neurons, MSNs in particular (Humphries et al. 2009). The firing rate, f, is related to the activation, y, by

$$f(y)=M{\left(\frac{B}{M}\right)}^{\exp (-ey/M)}$$ (3)

in which M is the upper asymptote of the function and represents the maximum firing rate of the nucleus, B is the intercept with the f‐axis, and represents the firing rate of the nucleus in the absence of all inputs (baseline firing rate) and e is the base of the natural logarithm. This function is constructed such that it is parameterised by values that can be found from experimental literature and that the maximum gradient is set to 1. There are six DDEs per channel, and therefore 12 DDEs in the complete model. The complete model is given by set of the set of eqns (4).

$$\begin{array}{c}\hfill \mathit{Channel}-\mathbf{1}:\\ \hfill {\ddot{y}}_{Ps1}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s-s}f(y_{Ss1})+W_{sc-s}(1+da)\mathit{IN}{}_P+W_{mc-s}(1+da)f(y_{Pmc})-W_{ge-s}f(y_{Sge})\right\}-\frac{2}{\tau }{\dot{y}}_{Ps1}-\frac{1}{{\tau }^2}{y}_{Ps1}}\hfill \\ \hfill {\ddot{y}}_{Ps2}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s-s}f(y_{Ss2})+W_{sc-s}(1-da)\mathit{IN}{}_P+W_{mc-s}(1-da)f(y_{Pmc})-W_{ge-s}f(y_{Sge})\right\}-\frac{2}{\tau }{\dot{y}}_{Ps2}-\frac{1}{{\tau }^2}{y}_{Ps2}}\hfill \\ \hfill {\ddot{y}}_{Pstn}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{ge-stn}f(y_{Pge})+W_{mc-stn}f(y_{Pmc})+W_{sc-stn}\mathit{IN}{}_P\right\}-\frac{2}{\tau }{\dot{y}}_{Pstn}-\frac{1}{{\tau }^2}{y}_{Pstn}}\hfill \\ \hfill {\ddot{y}}_{Pge}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s2-ge}f(y_{Ps2})+W_{stn-ge}f(y_{Pstn})+W_{stn-ge}f(y_{Sstn})-W_{ge-ge}f(y_{Sge})-W_{geR}f(y_{Pge})\right\}-\frac{2}{\tau }{\dot{y}}_{Pge}-\frac{1}{{\tau }^2}{y}_{Pge}}\hfill \\ \hfill {\ddot{y}}_{Pgi}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s1-gi}f(y_{Ps1})+W_{stn-gi}f(y_{Pstn})+W_{stn-gi}f(y_{Sstn})-W_{ge-gi}f(y_{Sge})\right\}-\frac{2}{\tau }{\dot{y}}_{Pgi}-\frac{1}{{\tau }^2}{y}_{Pgi}}\hfill \\ \hfill {\ddot{y}}_{Pmc}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{gi-mc}f(y_{Pgi})+W_{sc-mc}\mathit{IN}{}_P\right\}-\frac{2}{\tau }{\dot{y}}_{Pmc}-\frac{1}{{\tau }^2}{y}_{Pmc}}\hfill \\ \hfill \mathit{Channel}-\mathbf{2}:\\ \hfill {\ddot{y}}_{Ss1}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s-s}f(y_{Ps1})+W_{sc-s}(1+da)\mathit{IN}{}_S+W_{mc-s}(1+da)f(y_{Smc})-W_{ge-s}f(y_{Pge})\right\}-\frac{2}{\tau }{\dot{y}}_{Ss1}-\frac{1}{{\tau }^2}{y}_{Ss1}}\hfill \\ \hfill {\ddot{y}}_{Ss2}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s-s}f(y_{Ps2})+W_{sc-s}(1-da)\mathit{IN}{}_S+W_{mc-s}(1-da)f(y_{Smc})-W_{ge-s}f(y_{Pge})\right\}-\frac{2}{\tau }{\dot{y}}_{Ss2}-\frac{1}{{\tau }^2}{y}_{Ss2}}\hfill \\ \hfill {\ddot{y}}_{Sstn}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{ge-stn}f(y_{Sge})+W_{mc-stn}f(y_{Smc})+W_{sc-stn}\mathit{IN}{}_S\right\}-\frac{2}{\tau }{\dot{y}}_{Sstn}-\frac{1}{{\tau }^2}{y}_{Sstn}}\hfill \\ \hfill {\ddot{y}}_{Sge}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s2-ge}f(y_{Ss2})+W_{stn-ge}f(y_{Pstn})+W_{stn-ge}f(y_{Sstn})-W_{ge-ge}f(y_{Pge})-W_{geR}f(y_{Sge})\right\}-\frac{2}{\tau }{\dot{y}}_{Sge}-\frac{1}{{\tau }^2}{y}_{Sge}}\hfill \\ \hfill {\ddot{y}}_{Sgi}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{s1-gi}f(y_{Ss1})+W_{stn-gi}f(y_{Pstn})+W_{stn-gi}f(y_{Sstn})-W_{ge-gi}f(y_{Pge})\right\}-\frac{2}{\tau }{\dot{y}}_{Sgi}-\frac{1}{{\tau }^2}{y}_{Sgi}}\hfill \\ \hfill {\ddot{y}}_{Smc}& =& {\displaystyle \frac{1}{{\tau }^2}\left\{-W_{gi-mc}f(y_{Sgi})+W_{sc-mc}\mathit{IN}{}_S\right\}-\frac{2}{\tau }{\dot{y}}_{Smc}-\frac{1}{{\tau }^2}{y}_{Smc}}\hfill \end{array}$$ (4)

in which y_n is the activation of the nth nucleus. Subscripts denoting Primary‐Channel and Secondary‐Channel nuclei begin with P and S, respectively. Axonal transmission delays are modelled as the delays in the DDEs. For ease of readability the suffix terms denoting the delays have been omitted. Thus, expressions such as W_mnf(y_m(t−T_mn)) have been shortened to w_mnf(y_m), where T_m‐n is the delay between nuclei m and n. f is the transfer function that converts an activation into a firing rate, and is given by eqn (3). Cortical inputs to primary and secondary channels are IN _P and IN _S, respectively. The level of dopaminergic innervation of the striatum is governed by the normalised parameter, da. The above system of equations was solved using Matlab's (Mathworks, Natick, MA, USA) DDE solver, DDE23.

Model parameters

Model parameters were obtained from experimental studies (Table 1) with the exception of inter‐nuclei connection‐strength parameters, which are inferred by fitting the model to data obtained from stimulation studies using sequential Monte‐Carlo approximate Bayesian computation (SMC‐ABC) (Toni et al. 2009; Beaumont, 2010), with hand‐tuned prior distributions. Specifically, we used the two GPi time series clusters, identified in this paper (see Results) from data published in Tachibana et al. (2008), and peristimulus time histograms (PSTHs) of STN and GPe responses from Nambu et al. (2000). The error function used in the SMC‐ABC algorithm is created by comparing data from these studies with model output. The parameter fitting was done using data in the temporal range beginning 40 ms before the cortical stimulation and ending 150 ms after the stimulation. Thus, the SMC‐ABC algorithm is compelled to fit the equilibrium firing rates observed before the stimulus as well as the dynamical behaviour after stimulus. Each time series was interpolated to create a vector of firing rates at 600 evenly spaced sampling times. The simulation was run using the parameter values generated by SMC‐ABC. The resulting vector of firing rates was truncated to the temporal range of the experimental data and then interpolated to the same 600 sampling times. To generate the value of the error statistic from this vector we apply a simple root‐mean‐squared function. The value of this error statistic for the maximum a posteriori (MAP) estimate of the parameter values is 28.9. Priors of connection weight parameters were Gaussian distributions. Initial approximations of the means were defined as the ratio between the maximum firing rates of the sending and receiving populations. The means of the priors were further refined to improve the fit to the data. Standard deviations of the priors were set equal to the mean. Posterior distributions of the free connection strength parameter values are shown in Fig. 10.

Figure 10. Inter‐nucleus connection strength parameter value posterior distributions.

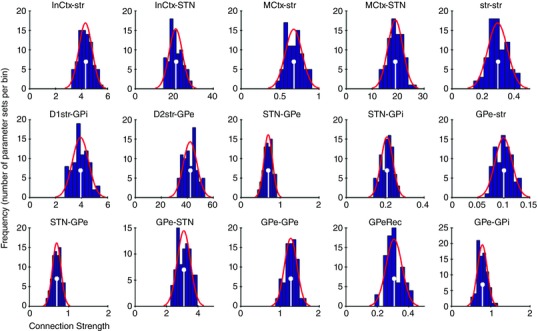
Histograms shown in dark blue. Gaussian fit to histograms shown in red. Maximum a posteriori (MAP) estimate of each parameter value marked with white stems.

Discussion

We have created a model of the BG that includes separate channels and their interaction. The model was constrained and validated using a variety of experimental data, some of which were subject to a novel re‐analysis. The overarching conclusion of this work is that while multiple interacting channels are necessary to allow selection, they could also be the key factor that generates the often observed oscillatory activity and the temporal dynamics of BG. By invoking the heterogeneity of pallidal responses to cortical stimulation (rather than averaging across all neurons), we have shown that the commonly observed beta and gamma band activity emerge naturally, and in a behaviourally relevant context.

A novel explanation for time domain phenomena

In general, a system's time domain properties (impulse response) are intimately linked to those in the spectral (frequency) domain (Billings, 2013). As such, uncovering the mechanisms that give rise to the BG's impulse response, as observed in stimulation experiments, is of vital importance since only then can we fully understand the origins of the commonly observed neural oscillations.

The LDLE seen in the mean pallidal response to phasic stimulation is an obvious feature of the BG impulse response. An obvious candidate for the generation of this phenomenon is the activation of NMDA receptors. However, the LDLE is attenuated only slightly by administration of the NMDA receptor antagonist 3‐(2‐Carboxypiperazin‐4‐yl)propyl‐1‐phosphonic acid (CPP) (Tachibana et al. 2008). Alternatively one might suggest that rebound excitation of GPe neurons following a phasic inhibition could generate the LDLE (Nambu & Llinas, 1994). However, impulse stimulation of the STN yields a long duration excitation in the GPe, with no prior inhibition (Kita et al. 2005). A network‐level explanation is suggested by data showing that the LDLE is present only if STN–GPe connections are intact (Ammari et al. 2010). Furthermore, EPSPs are present in GPe cells during the LDLE (Ammari et al. 2010). However, single unit recordings, taken from non‐human primates following a cortical impulse stimulation, show that the mean STN activity during a pallidal LDLE is virtually zero (Nambu et al. 2000). Thus we have an excitation apparently being elicited by a nucleus that is almost completely quiescent.

Our model suggests a resolution to this apparent contradiction. In our model the LDLE is caused by a combination of asymmetric cross‐channel inhibition and excitation of GPe neurons by the small number of highly active STN neurons that encode the channel with the highest cortical input (the primary channel in this model). Since the majority of neurons belong to other channels, the mean field activity of the STN during the pallidal LDLE looks extremely low. However, the small number of primary channel STN cells project diffusely to all pallidal channels, and therefore contribute to generating the excitation. The model therefore suggests that the LDLE requires both cross‐channel inhibition within the GPe as well as the diffuse excitatory feedback from the STN. This mechanism may also be the explanation for the observation that STN stimulation induces both excitation and inhibition in pallidal neurons (Kita et al. 2005). Our work suggests that the pallidal impulse response profile, and therefore the BG's spectral properties, arise as a consequence of structured channel‐wise interactions. Our model predicts that there should be differing responses to impulse stimulation depending on the location of the recorded neuron in the projective field of the stimulated neuron. This has been observed experimentally (Tremblay et al. 1989), although it is not a subject that has received much subsequent attention. Our work suggests that experimental analysis of the relationship between different responses may yield important insights into how information is encoded in the BG.

Spectral phenomena as an emergent property

The main result of the current work is an identification of possible mechanisms that are responsible for generating beta and gamma band activity. Some of the cardinal motor symptoms of Parkinson's disease are correlated with the pathological increase in beta power within the BG. As a consequence there has been much theoretical work attempting to identify possible mechanisms for the generation of beta activity in the BG. Studies have shown how beta activity can emerge from networks of interconnected neurons (Terman et al. 2002; McCarthy et al. 2011; Corbit et al. 2016). McCarthy et al. (2011) propose a striatal origin involving M‐current activation, while Terman et al. (2002) investigate how frequency of oscillations changes with pallidal and subthalamic coupling strengths. Holgado et al. (2010) examine the conditions whereby the STN–GPe loop alone could support beta frequency activity (Nevado Holgado et al. 2010). Similar to our work, Corbit et al. (2016) identify the pallido‐striatal pathway as being important in the generation of beta rhythmic activity in the BG (Corbit et al. 2016). Their work focuses on the role of the GPe's projection to striatal interneurons rather than MSNs. That our current work yields similar results using channel‐specific GPe–MSN connections indicates that the pallido‐striatal pathway could be important in beta generation by multiple mechanisms, and highlights that the nature and purpose of the pathway requires further research.

Many analyses explore the generation of beta power only in a ‘parkinsonian’ condition of reduced dopaminergic input (Leblois et al. 2006; Nevado Holgado et al. 2010). Using these studies to make inferences about beta generation in the healthy condition may be unsafe, since experimental work has identified two distinct GPe neuronal populations that oscillate at beta frequencies in a parkinsonian condition but whose activity remains uncorrelated in the control group (Mallet et al. 2008). They also do not address the purpose that these oscillations may serve.

Repeated observations have shown that beta spectral power in motor cortex is correlated with maintenance of posture or application of isometric force (Baker et al. 2001; Gilbertson et al. 2005; Chakarov et al. 2009). Furthermore, strong coherence in the beta range has been observed between motor cortical LFPs and EMGs recorded from muscles controlling the effector limb (Baker et al. 1997; Kilner et al. 1999; Chakarov et al. 2009). If the two channels are conceptualised as representing an antagonistic pair of movement commands, the beta oscillations represent the activation of one movement command quickly followed by its opposite. If this putative oscillatory force is low‐pass filtered at the level of biomechanics (or in downstream neural processing), our model predicts an increase in muscle tone due to the beta oscillation. This is testable by examining the relative LFP and EMG activity of pairs of antagonistic muscles under a cued movement paradigm. Our hypothesis gives a possible explanation as to why the overexpression of beta in Parkinson's disease is correlated with rigidity (Narabayashi & Oshima, 2014).

Power in the gamma frequency range has been observed in recordings from the GPi and the STN of healthy rats (Brown et al. 2002; Leventhal et al. 2012) and has been observed in multiple nuclei in humans undergoing neurosurgery (Cassidy, 2002; Alegre et al. 2005; Androulidakis et al. 2007). Our model shows increased gamma with increased cortical input, which is consistent with observations that gamma oscillation's power increases during voluntary movement, and is decreased during periods of low cortical activation (Brown et al. 2001; Androulidakis et al. 2007; Kempf et al. 2009). Gamma frequencies in the model most often arise in channels that encode the channel(s) that are not selected. This is an important issue since correlations are often sought between spectral features of experimental data and behaviour (Brücke et al. 2012; Jenkinson et al. 2013). These relationships may be spurious if the oscillations are related to action representations that are not expressed in behaviour.

A complete understanding of how beta and gamma band activity arise in healthy BG is necessary if we are to fully understand how pathological oscillatory activity in Parkinson's gives rise to the motor symptoms of the disease. The current model can therefore serve as a foundation from which to study the development of Parkinsonian motor symptoms, modelling the gradual development of the condition.

Action selection as an emergent phenomenon

That action selection emerges naturally from the model is taken as further indication that this is likely to be a primary function of the BG. The current model is able to link the spectral properties of the network to its function as a selection mechanism.

Our methodology to test the validity of the action selection hypothesis was to tune the network to minimise deviation from experimental data and then, post hoc, to test the model for its ability to select between inputs. This methodology allows more confidence in the conclusion: rather than demonstrating that a network can perform selection given the right choice of parameters, the network has parameter values that predispose it to be an effective selection mechanism.

Our model also suggests a functional purpose for the significant GPe–striatum pathway. The strength of the GPe–striatum connection mediates the decisiveness of the BG model's selection mechanism. GPe neurons express D2 receptors (Hoover & Marshall, 2004; Kita, 2007) (not included in this model), and as such their firing rates are reduced in the presence of dopamine. Dopaminergic modulation of the GPe neurons that project to the striatum may therefore be an additional mechanism that mediates the trade‐off between exploitation and exploration.

In 6‐OHDA rat models of Parkinson's disease, two distinct populations of GPe neurons have been identified: the arkypallidal and prototypical populations oscillate in anti‐phase with each other (Mallet et al. 2008, 2012). However, this distinction is not apparent in healthy rats so has not been included in this model. This suggests that acute dopamine denervation of the BG may cause a breakdown or unlearning of functional cross‐channel inhibition in the GPe, leading to the inhibition between the arkypallidal and the prototypical populations to dominate. This issue will be explored in models of the Parkinsonian BG.

Relationship to other models

Other models of the BG have enjoyed success in using functional (Frank et al. 2001; Gurney et al. b; Humphries et al. 2006), equilibrium (Gillies et al. 2002; van Albada & Robinson, 2009; Nevado Holgado et al. 2010) or spectral (Moran et al. 2011; Marreiros et al. 2013) information to constrain their unknown parameters. However, none have been able to unify such a wide raft of experimental data with a functional description using an anatomically constrained model of BG such as that presented here. The current work could be extended by creating a neural mass model of the system in which the synaptic dynamics of each receptor type are modelled individually (as is the case in Moran et al. 2011 and Marreiros et al. 2013). This would allow analysis of the relative contributions of AMPA, NMDA, GABA_A and GABA_B receptors.

Other models have focused solely on the STN–GPe feedback loop (Gillies et al. 2002; Terman et al. 2002; Nevado Holgado et al. 2010). Our model additionally includes the striatal populations and the GPi in order to test the hypothesis that the BG performs action selection. Importantly, adequate data have been obtained to constrain the connection strengths between the GPi and its afferents, guarding against the risk of over‐fitting. A conductance‐based spiking neuron version of the current model (similar to Terman et al. 2002) would be of great benefit to investigate the relative contributions of other possible mechanisms for BG dynamics, such as rebound excitation in the GPe. However, finding sufficient data with which to accurately parameterise such a model may be problematic.

Perhaps the model most similar to our own is that of Leblois et al. (2006). Their study generated the triphasic pallidal response, some limited spectral features, and basic selection functionality using the network level interaction between the hyper‐direct and direct pathways in BG–thalamo‐cortical loops. It differs from our work in that their model does not contain a GPe. In our model, the inclusion of the GPe and its associated pathways was essential to capture the temporal and spectral features that are observed in healthy BG, which were not accounted for in the study by Leblois.

Predictions

In the model, we showed gamma power in the STN LFP is at its highest when a selection has been made between two opposing channels with relatively high inputs. Thus the model predicts that gamma power will be relatively low when uncued movements are made to a well‐defined target, and higher when movements are preceded by a cue and the required movement direction is unknown until the target is presented.

While data are only currently available for GPi, the model predicts a stimulus‐driven LDLE in a small minority of STN responses (in the model the primary channel) and a biphasic one (excitation – long duration inhibition) in GPe.

The model shows beta power in the STN LFP when opposing channels are activated by similar amounts, peaking when both cortical inputs are close to the middle of their dynamic range. It is therefore a prediction of the model that the generation of a moderate amount of muscle tone, by co‐activation of two opposing motor commands, yields high beta power in the STN LFP. Increasing the level of static force close to the subject's maximum effort is predicted to show a reduction in beta power.

Based on the considerations above, our model appears to provide a plausible framework for the study of spectral, temporal and functional analyses of the BG. As such, it lays the foundation for investigation of BG function, both in healthy and in pathological states and, as well as supplying plausible explanations for existing experimental data, also makes several testable predictions.

Additional information

Competing interests

We have no competing interests.

Authors’ contributions

AB carried out the modelling and parameter estimation, drafted the manuscript and participated in the design of the study; SA participated in parameter estimation, participated in the design of the study, and participated in coordination of the study; KG conceived and coordinated the study and participated in drafting the manuscript. All authors gave final approval for publication.

Funding

All authors were funded by EU grant FP7‐ICT‐2013‐10 NoTremor and EU Horizon 2020 Dreams4cars (grant number: 731593).