Mechanical tuning and amplification within the apex of the guinea pig cochlea

Abstract

Key points

• A popular conception of mammalian cochlear physiology is that tuned mechanical vibration of the basilar membrane defines the frequency response of the innervating auditory nerve fibres

• However, the data supporting these concepts come from vibratory measurements at cochlear locations tuned to high frequencies (>7 kHz).

• Here, we measured the travelling wave in regions of the guinea pig cochlea that respond to low frequencies (<2 kHz) and found that mechanical tuning was broad and did not match auditory nerve tuning characteristics.

• Non‐linear amplification of the travelling wave functioned over a broad frequency range and did not substantially sharpen frequency tuning.

• Thus, the neural encoding of low‐frequency sounds, which includes most of the information conveyed by human speech, is not principally determined by basilar membrane mechanics.

Abstract

The popular notion of mammalian cochlear function is that auditory nerves are tuned to respond best to different sound frequencies because basilar membrane vibration is mechanically tuned to different frequencies along its length. However, this concept has only been demonstrated in regions of the cochlea tuned to frequencies >7 kHz, not in regions sensitive to lower frequencies where human speech is encoded. Here, we overcame historical technical limitations and non‐invasively measured sound‐induced vibrations at four locations distributed over the apical two turns of the guinea pig cochlea. In turn 3, the responses demonstrated low‐pass filter characteristics. In turn 2, the responses were low‐pass‐like, in that they occasionally did have a slight peak near the corner frequency. The corner frequencies of the responses were tonotopically tuned and ranged from 384 to 668 Hz. Non‐linear gain, or amplification of the vibrations in response to low‐intensity stimuli, was found both below and above the corner frequencies. Post mortem, cochlear gain disappeared. The non‐linear gain was typically 10–30 dB and was broad‐band rather than sharply tuned. However, the gain did reach nearly 50 dB in turn 2 for higher stimulus frequencies, nearly the amount of gain found in basal cochlear regions. Thus, our data prove that mechanical responses do not match neural responses and that cochlear amplification does not appreciably sharpen frequency tuning for cochlear regions that respond to frequencies <2 kHz. These data indicate that the non‐linear processing of sound performed by the guinea pig cochlea varies substantially between the cochlear apex and base.

Key points

• A popular conception of mammalian cochlear physiology is that tuned mechanical vibration of the basilar membrane defines the frequency response of the innervating auditory nerve fibres

• However, the data supporting these concepts come from vibratory measurements at cochlear locations tuned to high frequencies (>7 kHz).

• Here, we measured the travelling wave in regions of the guinea pig cochlea that respond to low frequencies (<2 kHz) and found that mechanical tuning was broad and did not match auditory nerve tuning characteristics.

• Non‐linear amplification of the travelling wave functioned over a broad frequency range and did not substantially sharpen frequency tuning.

• Thus, the neural encoding of low‐frequency sounds, which includes most of the information conveyed by human speech, is not principally determined by basilar membrane mechanics.

Abbreviations

ANOW

auditory nerve overlapped waveform

BM

basilar membrane

CAP

compound action potential

FFT

fast Fourier transform

Hel

helicotrema

ME

middle ear

Mod

modiolus

OoC

organ of Corti

RM

Reissner's membrane

ST

scala tympani

SV

scala vestibuli

SPL

sound pressure level

VOCTV

volumetric optical coherence tomography and vibrometry

Introduction

Sound pressure waves enter the mammalian cochlea and vibrate the basilar membrane. The vibratory response is tuned so that the peak magnitude is at the basal end of the cochlea for high‐frequency sounds and at the apical end for low‐frequency sounds (von Békésy, 1960). Outer hair cells are selectively stimulated near the peak (Lee et al. 2016) and generate forces that amplify the basilar membrane vibrations. This amplification creates sharply tuned mechanical responses. Inner hair cells at the same cochlear location then transduce the vibration and convey the afferent signal to the auditory nerve fibres connected to them. Thus, the popular concept of sound encoding within the mammalian cochlea is that each auditory nerve fibre has a characteristic frequency that corresponds to its tonotopic location along the length of the cochlea and a tuning curve sharpness that reflects the mechanical response of the basilar membrane. This concept derives from many studies replicated across multiple mammalian species demonstrating that basilar membrane vibration and single‐unit auditory neuron responses have nearly identical frequency responses (Rhode, 1971; Liberman, 1982; Nuttall et al. 1991; Cooper & Rhode, 1992a; Tsuji & Liberman, 1997; Narayan et al. 1998; Ren & Nuttall, 2001; Taberner & Liberman, 2005; Russell et al. 2007; Lee et al. 2015). However, while auditory nerve fibres with characteristic frequencies ranging from nearly 0.1 to 100 kHz in these different species have been studied, mechanical recordings of basilar membrane vibration have mostly been limited to cochlear locations tuned to frequencies >7 kHz because of technical limitations in accessing the cochlear apex in low‐frequency‐hearing animals.

Importantly, it may not be accurate to extrapolate this concept to lower frequency regions of the cochlea. For example, auditory nerve fibre recordings suggest important differences in response phases and tuning curve shapes above and below 5 kHz (Temchin et al. 2008, 2012). Only a few mechanical measurements have been made in low‐frequency cochlear regions, primarily the apex of the guinea pig cochlea (Cooper & Rhode, 1995, 1997; Khanna & Hao, 1999; Zinn et al. 2000; Dong & Cooper, 2006; Ramamoorthy et al. 2016). Frankly, however, the data are difficult to interpret given the technical difficulties in performing the experiments and/or the artefacts that result from opening the otic capsule bone to visualize the organ of Corti. A recent publication details the results of in vivo experiments performed in the apex of unopened guinea pig cochleae (Warren et al. 2016), but because only responses to 90 dB sound pressure level (SPL) stimuli were reported, it is impossible to draw any conclusions regarding non‐linear properties of the apex of the cochlea such as level‐dependent amplification and compression.

Recently, we described an approach we developed to make mechanical recordings within the apex of the mouse cochlea, termed volumetric optical coherence tomography and vibrometry (VOCTV) (Gao et al. 2014; Lee et al. 2015). However, hearing in the mouse drops off significantly below 4 kHz (Zheng et al. 1999; Heffner et al. 2001). Thus, it is an inappropriate animal model to use when studying cochlear mechanisms of sound encoding for lower frequencies. Low‐frequency hearing is important because most of the information of human speech is carried by frequencies <2 kHz. Herein, we used VOCTV to overcome historical limitations and non‐invasively study the apical two turns of the guinea pig cochlea, where the innervating auditory neurons are tuned to these low frequencies. We compared the vibratory responses we measured to previously measured single‐unit auditory nerve tuning curves to determine the role of cochlear amplification in mammalian low‐frequency hearing.

Methods

Ethical approval

All procedures were approved by the Stanford University Institutional Animal Care and Use Committee. The laboratory animal care programme at Stanford is accredited by the Association for Assessment and Accreditation of Laboratory Animal Care.

Guinea pig preparation

Adult albino guinea pigs between 350 and 450 g of either sex were used Charles River Laboratories (Wilmington, MA, USA). Each guinea pig was anaesthetized with ketamine (40 mg kg⁻¹) and xylazine (5 mg kg⁻¹) administered subcutaneously. Every 15 min, a paw pinch test was performed and supplemental doses of anaesthetic were administered at one‐quarter the induction dose to maintain areflexia. The head was fixed in a head holder. We then resected the posterior half of the body of the mandible, all the mandibular ramus, and most of the muscles of mastication within the infratemporal fossa. This allowed us to open the left middle ear bulla and image the cochlear apex with an optical axis that was transverse to the basilar membrane. Thus, rather than visualizing the cochlea from the side or the base, we could look directly down onto the apical turn of the cochlea. We did not open the otic capsule bone to perform imaging or vibrometry.

A speaker completely enclosed within an aluminium housing except for a 10 mm long by 4 mm diameter brass tube centred over the cone was used to bring sound stimuli to the left ear of the guinea pig. The speaker was positioned so that the brass tube passed through the cartilaginous ear canal to reach the bony ear canal. The tensor tympani tendon was sectioned. After performing all the desired experiments in the living guinea pig, the animal was killed by anaesthesia overdose so as not to move the head. Further measurements were made post mortem. In some animals, we opened the otic capsule bone and repeated the measurements to assess the impact of this manipulation. Finally, vibration measurements were made from the middle ear ossicular chain to define the magnitude and phase of the sound entering the cochlea. The guinea pig was then decapitated in accordance with our animal protocol.

Volumetric optical coherence tomography and vibrometry

Vibrations of the organ of Corti were measured using VOCTV. Our VOCTV system was custom‐built and has been described previously (Lee et al. 2015). Briefly, it was composed of a broadband swept‐source with a centre wavelength of 1300 nm and 200 kHz sweep rate (MEMS‐VCSEL, Thorlabs, Newton, NJ, USA), a dual‐balanced photodetector (WL‐BPD600MA, Wieserlabs, Munich, Germany), and a digitizer (NI‐5761, National Instruments, Austin, TX, USA). An adaptor attached to the bottom of a dissecting microscope (Stemi‐2000, Zeiss, Jena, Germany) scanned the beam in both the x and y directions. For all experiments, the power on the sample was 16 mW. Each individual pixel imaged by our system has a lateral resolution of 9.8 μm and axial resolution of 11.4 μm (Lee et al. 2015) in water. The vibratory accuracy and linearity or our system was verified using a commercial laser Doppler vibrometer (OFV‐5000, Polytech, Irvine, CA, USA).

Sound stimuli were synthesized in software and calibrated using a microphone as previously described (Oghalai, 2004; Xia et al. 2010, 2013). The duration of the sound stimulus was 200 ms. We presented pure tones from 100 to 2000 Hz in frequency steps of 100 Hz at intensities from 10 to 76 dB SPL. During the calibration process, we verified that harmonic distortions were at least 60 dB below the fundamental for all frequency–intensity combinations.

During the sound stimulus, we recorded the vibratory response from the point of interest. We selected points for study that had strong signal intensity on the image, because these provided the lowest noise floor for the vibratory measurements and minimized the risk of phase corruption (Lin et al. 2017). No averaging of adjacent points was performed. However, we did repeat the measurements up to five times and average the time domain vibratory responses to achieve a lower noise floor. We analysed the data by performing a fast Fourier transform (FFT) on the vibratory response and determining the peak vibratory magnitude at the stimulus frequency. Next, we determined the mean and standard deviation (SD) of the noise floor by averaging the vibratory magnitude over the FFT bins contained within a 100 Hz band adjacent to the stimulus frequency. If the peak vibratory magnitude at the stimulus frequency was less than the noise floor threshold defined by the mean + 3 SD of the vibratory noise floor, we threw out that measurement. Because of this criterion, all the vibratory responses to 10 dB SPL stimuli were too small to be used.

Compound action potential measurements

Compound action potentials (CAPs) were measured as previously published (Oghalai, 2004). Briefly, we varied the frequency of the sound stimulus from 600 Hz to 40 kHz and at each frequency studied, we applied sound stimuli of alternating polarity from 10 to 80 dB SPL. We amplified the electrical signal measured by a silver wire that touched the round window membrane 1000×, and filtered the signal between 300 and 3000 Hz. Offline, we calculated the CAP threshold to be the stimulus intensity required to evoke a response at least 5 SD above the root mean square of the noise floor.

Data adjustment and statistical analysis

To average data collected from different guinea pigs, vibratory magnitudes and phases were averaged separately, and the mean and standard error of the mean (SEM) for all data points were calculated. Phase unwrapping was performed so that all phases that were averaged together at each frequency were within π radians of the mean. Data from an animal were not included in statistical analyses if the vibratory response at that frequency–intensity combination was below the noise floor threshold. Similarly, for all figures, we did not plot data at those frequency–intensity combinations where the vibratory responses from two or more of the 11 guinea pigs studied were below the noise floor threshold. Student's non‐paired, two‐tailed t test was used two compare cochlear gain between the measurements in turn 3 and turn 2. A P‐value <0.05 was considered significant. All values given in the text are the mean ± SEM.

Results

Auditory sensitivity

We first measured the compound action potential (CAP), a field potential generated by the synchronous activation of auditory nerve fibres at the onset of a sound stimulus, to verify that the surgical preparation did not affect cochlear sensitivity. To do this, we delivered 24 sine wave tone pips of alternating polarity, ranging from 10 to 80 dB SPL and 0.6 to 40 kHz, and averaged the field potential measured by a ball‐ended silver wire placed on the round window membrane (Fig. 1). CAP thresholds were within the normal range (Heffner et al. 1971), indicative of normal cochlear function. At lower frequencies, the field potential not only contained the CAP response but also a superimposed alternating response that did not average out with the use of alternating‐polarity sound stimuli. This additional response is normal and reflects asymmetrical distortion of the cochlear microphonic waveform (Sirjani et al. 2004) and the auditory nerve overlapped waveform (ANOW) (Lichtenhan et al. 2014) due to auditory nerve phase locking to low‐frequency stimuli (Rose et al. 1967).

Figure 1. Compound action potential recordings.

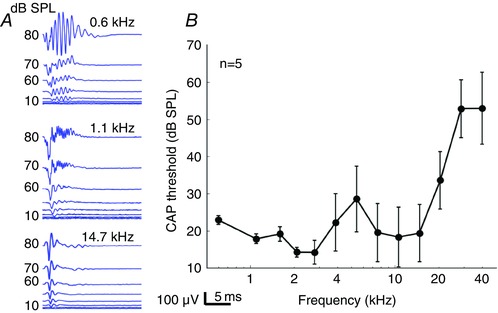
A, representative raw data collected at 0.6, 1.1 and 14.7 kHz in one guinea pig. Note that the compound action potential (CAP) waveform was clearly visible at 14.7 kHz, but that a superimposed AC response contaminates the CAP response at lower frequencies. This AC response represents a combination of asymmetrical distortion in the cochlear microphonic and the auditory nerve overlapped response (ANOW). B, CAP thresholds over the frequency spectrum recorded in five guinea pigs. Error bars are the SEM. Below 3 kHz, the error bars for the thresholds are smaller than those above 3 kHz because the cochlear microphonic and ANOW waveforms dominate the response.

Anatomic imaging

Next, we used our VOCTV system to image the cochlea in cross‐section (Fig. 2 A–D). The optical axis of the imaging beam paralleled the central axis of the cochlear spiral and permitted visualization of the apical two cochlear turns. The most obvious structures visible in the images were the surrounding otic capsule bone, Reissner's membrane (RM), the basilar membrane (BM), the modiolus (Mod), and the organ of Corti (OoC). The imaging resolution of our system did not permit differentiation between subcomponents of the organ of Corti, such as the tectorial membrane, hair cells or supporting cells.

Figure 2. In vivo imaging and vibratory responses from one representative guinea pig demonstrate low‐pass‐like filter responses.

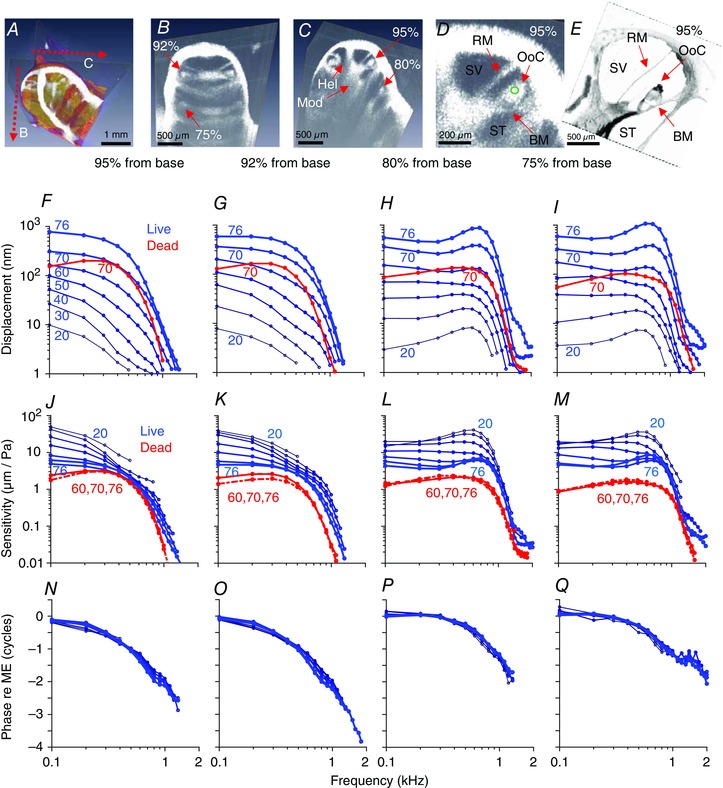
A, 3D volumetric image of the guinea pig cochlea. Two perpendicular cross‐sections are highlighted. These two cross‐sections were selected in every guinea pig we studied to consistently measure vibrations from the same four locations. B and C, the helicotrema (Hel) was identified to determine the apical end of the guinea pig cochlea, and defined the first cross‐section. The second cross‐section was then obtained by rotating the scan angle 90 deg. The auditory neurons sit within the modiolus (Mod). Recording sites are labelled as the percentage distance from the base (95%, turn 3.5; 92%, turn 3.25; 80%, turn 2.5; 75%, turn 2.25). D, enlarged view of the 95% location. The site where vibratory measurements were made is shown (green circle). BM, basilar membrane; RM, Reissner's membrane; OoC, organ of Corti; ST, scala tympani; SV, scala vestibuli. E, plastic‐embedded cross‐section of the 95% location. Osmium stained the Hensen cells particularly dark. F–I, vibratory magnitudes at the four different measurement locations. Data at all stimulus intensities from the living guinea pig are blue and at 70 dB SPL from the dead guinea pig are red. J–M, the sensitivity was calculated by normalizing the vibratory magnitude to the stimulus intensity. Non‐linear gain was found in living (blue), but not dead (red), guinea pigs. N–Q, vibratory phases for the living guinea pig are shown. Post mortem responses were identical and thus not plotted. The phase responses were normalized by subtracting the phase of the ossicular chain. Negative phase indicates a phase delay.

Vibratory responses have low‐pass‐like filter characteristics

After identifying the helicotrema, where the perilymph of scala vestibuli (SV) and scala tympani (ST) connect at the apical end of the cochlea, we could rotate the scan angle of our cross‐sectional imaging to track the cochlear spiral down towards the base. Using this approach, we measured the vibratory responses to sound stimuli at four specific locations in every guinea pig, 3.5, 3.25, 2.5 and 2.25 turns up from the cochlear base. We converted these measurement locations to the distance from the base along the basilar membrane using published data about the 3D anatomy of the guinea pig cochlea (Hofman et al. 2009). Thus, the four measurement locations were 95%, 92%, 80% and 75% from the base, respectively. At each location, we measured vibrations at a point within the centre of the organ of Corti (green circle in Fig. 2 D) because this region reliably had the highest signal intensity and thus provided the lowest vibratory noise floor. Based upon analysis of histological sections at the same cochlear location (Fig. 2 E), this measurement point appears to be near the reticular lamina at the lateral edge of the outer hair cell region or medial edge of the Hensen cells. The points were not within the lateral compartment region of the organ of Corti, which is adjacent to the spiral ligament and has a different vibratory phase response (Gao et al. 2014).

Data from one representative guinea pig are shown in Fig. 2. The vibratory magnitudes were quite large, with peak magnitude displacements >1 μm in some animals to 76 dB SPL stimuli. We found low‐pass‐like filter characteristics at all four cochlear locations we studied (Fig. 2 F–I). The vibrations measured in the third turn (95% and 92% locations) had nearly pure low‐pass filter characteristics, whereas those measured in the second turn (80% and 75% locations) sometimes had slight, but distinct, peaks near the corner frequency. This peaking was only found in 2/11 guinea pigs at the 80% location and 3/11 guinea pigs at the 75% location. The rest of the measurements had simple low‐pass filter roll‐off characteristics. In either case, these responses differ from the much sharper band‐pass filter responses found in either the base of the guinea pig cochlea (Sellick et al. 1982; Nuttall & Dolan, 1996) or the apex of the mouse cochlea (Gao et al. 2014; Lee et al. 2015). However, it should be noted that the studies cited above measured basilar membrane locations tuned to frequencies in the 9–20 kHz range, which are much higher than the responses we measured in the apex of the guinea pig cochlea. Interestingly, these types of low‐pass filter responses were similar to what has been reported in the apex of the chicken basilar papilla, which also is most responsive to frequencies <1 kHz (Xia et al. 2016).

Evidence for non‐linear cochlear gain

Next, we calculated the sensitivity by dividing the vibratory magnitude by the stimulus intensity. Data are shown for the one representative guinea pig (Fig. 2 J–M) and for the cohort average (Fig. 3). Using the data measured in 11 live guinea pigs, we calculated the corner frequency, or F _3dB, at each location by determining the frequency where the vibratory magnitude dropped by 3 dB from the average response at 100–400 Hz when using 70 dB SPL stimuli. We found that the F _3dB increased as the recording location moved toward the base (95%: 384 ± 13 Hz; 92%: 416 ± 11 Hz; 80%: 551 ± 61 Hz; 75%: 668 ± 83 Hz). The characteristic frequency of these tonotopic locations predicted by single‐unit auditory nerve recordings shifted similarly (95%: 176 Hz; 92%: 219 Hz; 80%: 433 Hz; 75%: 596 Hz) (Tsuji & Liberman, 1997).

Figure 3. Non‐linear gain is present both below and above the F _3dB corner frequency.

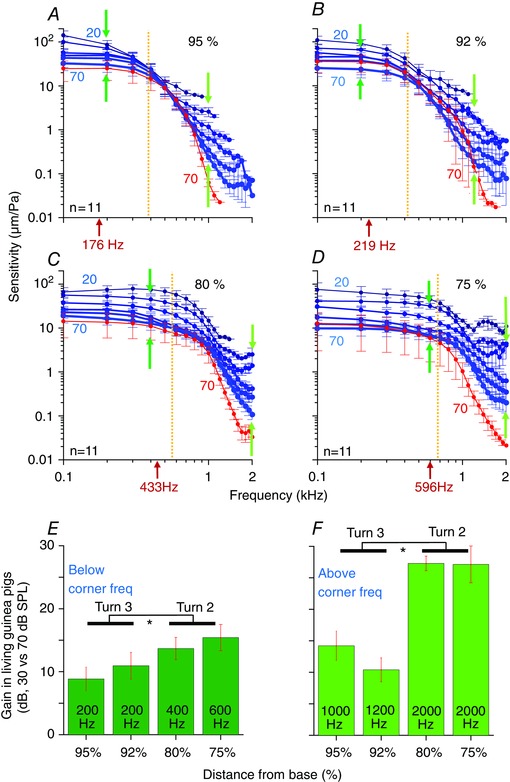
A–D, the average sensitivity is shown for the four different measurement locations (live: blue curves; dead: red curves). The stimulus intensity is shown next to the curves, ranging from 20 to 70 dB SPL in live. We only plotted the response to 70 dB SPL stimuli in the dead guinea pigs because the curves all overlapped. The characteristic frequency of the auditory nerve fibres innervating each location is given (red arrows under the x‐axis). The F _3dB corner frequency is shown by the orange dotted line. The average gain was calculated below and above the corner frequency at the highlighted frequencies (dark green and light green arrows). E and F, the average gain, calculated as the ratio of the sensitivities measured between 30 and 70 dB SPL stimuli in live guinea pigs, below and above the corner frequency. The frequency where the gain was calculated is given. All error bars are the SEM. Statistical analyses compare the average gain between the two measurements in turn 3 and the two measurements in turn 2.

Like in the raw magnitude responses, low‐pass characteristics are evident in the sensitivity functions. In addition, non‐linear responses were detected at most frequencies. Non‐linear effects were more prominent above the F _3dB frequency, but because the absolute level of vibration dropped substantially as the stimulus frequency was increased, the responses quickly fell into the noise floor and became undetectable.

The post mortem responses are also given (Figs 2, and 3, red curves). Since the post mortem responses were linear, all the sensitivity curves overlapped. The general shapes of the curves continued to demonstrate low‐pass‐like filter characteristics. Post mortem responses had similar or slightly reduced vibratory amplitudes over most frequencies, with the largest reductions found for frequencies >1 kHz. Thus, there was evidence for gain even for 70 dB SPL stimuli, which was particularly noticeable above the corner frequency.

Cochlear gain was calculated over the frequency spectrum by dividing the sensitivity to 20 dB in the live condition by the sensitivity to 70 dB in the dead condition (Fig. 4). These data demonstrate the broad‐band behaviour of gain in the guinea pig cochlear apex, with significant amplification both above and below the corner frequency. The maximal gain we identified between live and dead guinea pigs reached ∼50 dB for frequencies between 1 and 2 kHz at the 75% position, which approaches that found in the cochlear base. At the other positions, and for lower frequency stimuli at the 75% position, however, the level of gain ranged between 10 and 30 dB.

Figure 4. Cochlear gain in live guinea pigs using 20 dB SPL stimuli.

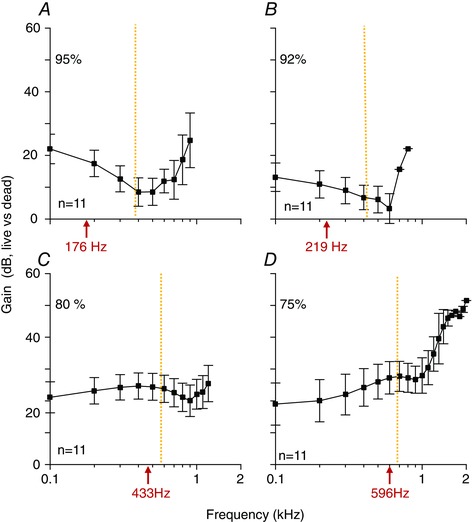
The sensitivity in response to 20 dB SPL stimuli in live guinea pigs was divided by the sensitivity to 70 dB SPL stimuli in dead guinea pigs. The characteristic frequency of the auditory nerve fibres innervating each location are given (red arrows under the x‐axis). The F _3dB corner frequency is shown by the orange dotted line.

To quantify and compare the non‐linear aspects of the gain in living guinea pigs below and above the F _3dB frequency, we calculated the difference in sensitivity between the responses at 30 dB and 70 dB SPL stimuli (Fig. 3 E and F, respectively). In general, there was more non‐linear gain in turn 2 than in turn 3. We averaged the gains at specific frequencies (dark and light green arrows in Fig. 3 A–D) from the two locations in turn 3 and compared them to the gains from the two locations in turn 2. Below the F _3dB frequency, the gain was 9.8 ± 1.4 dB in turn 3 and 14.5 ± 1.3 dB in turn 2 (P = 0.02, n = 10 and 10 measurements, respectively, from 11 guinea pigs). Above the F _3dB frequency, the gain was 12.3 ± 1.6 dB in turn 3 and 27.2 ± 3.2 dB in turn 2 (P = 0.007, n = 4 and 6 measurements, respectively, from 11 guinea pigs).

Phase responses

The vibratory phase of the organ of Corti, referenced to the middle ear response, demonstrated progressive lags as the stimulus frequency was increased (Fig. 2 N–Q). This is consistent with the concept of travelling wave propagation. The increase in the slope of the phase versus frequency plots indicates that waves of higher frequency propagate more slowly than those of lower frequency (i.e. the group delay increases with frequency) (Robles & Ruggero, 2001). At the F _3dB frequency, the average phase lag was calculated for all 11 guinea pigs: 95%: 0.90 ± 0.03; 92%: 0.85 ± 0.06; 80%: 0.48 ± 0.03; 75%: 0.61 ± 0.05 cycles. At the F _6dB frequency, the average phase was: 95%: 1.1 ± 0.04; 92%: 1.07 ± 0.06; 80%: 0.72 ± 0.05; 75%: 0.79 ± 0.04. For comparison, the phase has been measured to be ∼1–2 cycles at the characteristic frequency (∼16 kHz) at the base of the guinea pig cochlea but 0.5 cycles or less at the peak of the passive response (∼11 kHz) (Robles & Ruggero, 2001). In the apex of the mouse cochlea, the phase responses are similar to that in the guinea pig base (i.e. ∼0.5 cycles at the passive response peak at 5 kHz but 2 cycles at the characteristic frequency of 10 kHz) (Gao et al. 2014; Lee et al. 2016). The chicken apical basilar papilla only has a passive response and the phase is ∼0.5 cycles at the F _3dB frequency (Xia et al. 2016). Thus, the F _3dB frequency in the guinea pig cochlear apex has a phase lag between what is found at the peak of the passive and the peak of the active response in higher frequency regions of mammalian cochleae with sharp mechanical tuning, and its phase lag is greater than that found at the F _3dB frequency in chickens.

Comparison of mechanical tuning within the cochlear apex to tuning of low‐frequency auditory neurons

We then calculated iso‐response curves by interpolating the magnitude data to identify the stimulus level necessary to evoke a vibration amplitude of 5 nm at each frequency. The individual iso‐response curves for 11 guinea pigs at each cochlear location were similar; as an example, the data from turn 80% are shown (Fig. 5 A). We then averaged these data for each location (Fig. 5 B). Thresholds were low at low frequencies and the threshold plateau extended to higher frequencies at more basal locations. Thresholds increased as the frequency increased for all positions.

Figure 5. Vibratory thresholds do not match neural thresholds below the characteristic frequency.

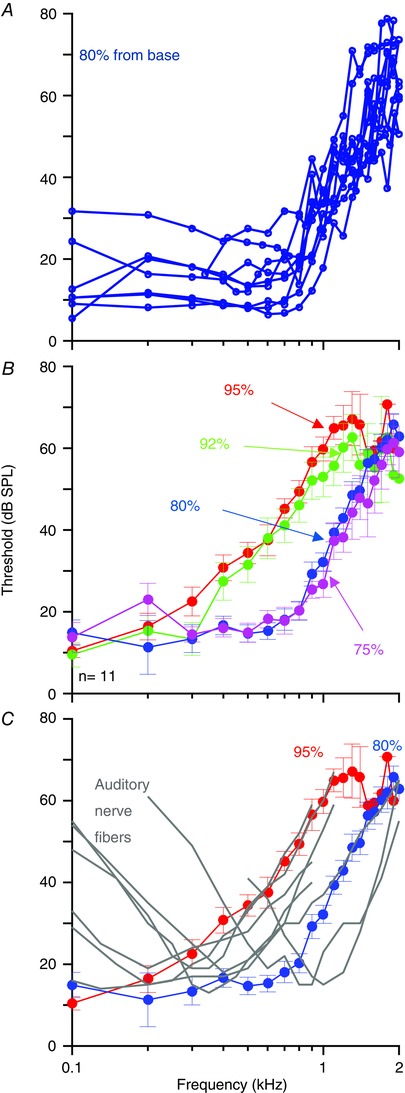
A, the individual vibratory thresholds from 11 guinea pigs at the 80% location calculated as the minimum sound intensity required to elicit a 5 nm response. B, average vibratory thresholds from all four cochlear locations. C, the average vibratory thresholds for the 95% and 80% locations are shown; superimposed are a series of neural tuning curves collected in guinea pigs (Cooper & Rhode, 1995). Note that while the high‐frequency side of the neural tuning curve matches the mechanical response, the low‐frequency side does not. All error bars are the SEM.

Next, we compared the mechanical data to previously published single unit tuning curves measured in low‐frequency auditory neurons in guinea pigs (Cooper & Rhode, 1995). For simplicity, we only plotted the iso‐response curves for the 95% and 80% locations, and we superimposed data from seven auditory nerve fibres over a range of characteristic frequencies (Fig. 5 C). To facilitate the comparison, the neural data were shifted along the vertical axis to match the average mechanical threshold near the fibre's characteristic frequency. These data demonstrate that while both responses match in slope and character on the high‐frequency side of the curves, there were obvious differences on the low‐frequency side. While the neural tuning curve data demonstrated thresholds that were higher below the characteristic frequency, the mechanical responses did not. This difference is substantially different from higher frequency measurements in the guinea pig base and in other mammals, where the iso‐response curves, based on either constant displacement or velocity, nearly overlap with neural tuning curves around the characteristic frequency (Sellick et al. 1982; Narayan et al. 1998).

Comparison of mechanical tuning in the intact and opened cochlea

In four guinea pigs, we also measured vibratory responses after opening the cochlea as a control experiment to compare our measurements to previously published reports using laser Doppler vibrometry that required this approach. Importantly, we did not open the bone directly overlying the measurement location to minimize trauma. We simply opened the bone over the helicotrema, and then made vibratory measurements at one or two positions as previously described.

The gain and phase of vibration from two representative dead guinea pigs at the 95% and 80% locations are presented (Fig. 6). The magnitude responses of the intact and open preparations had similar high‐frequency roll‐off characteristics. However, there was a more significant low‐frequency roll‐off in the open cochlea compared to the intact cochlea, making the responses in the open cochlea appear to have band‐pass filter characteristics. Phase responses were similar in the intact and open preparations.

Figure 6. Opening the cochlea reduces the vibratory response to low‐frequency sound stimuli.

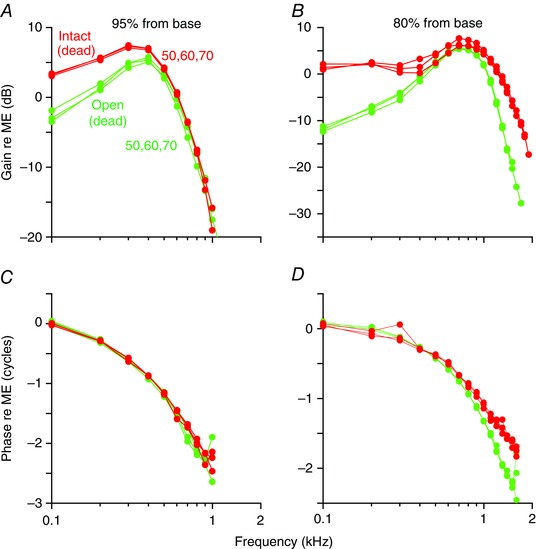
Data from two different representative guinea pigs are shown in response to 50, 60 and 70 dB SPL stimuli. The gain and phase are normalized to the middle ear (ME) response at the 95% location (A and C) and the 80% location (B and D). In the dead intact cochlea (red), the gain response is low‐pass‐like. After opening the bone over the helicotrema and repeating the measurements, the opened cochleae demonstrated vibratory responses that were more band‐pass. However, there were no substantive changes to the phase response.

These data support and are consistent with previously published findings (Dong & Cooper, 2006). Importantly, our data confirm and extend their experimental data whereby the apical guinea pig cochlea was sealed with a glass coverslip after opening it to record either from Hensen cells or from a bead dropped on the tectorial membrane. Low‐pass‐like responses were found in the sealed preparation and band‐pass‐like responses were found in the open preparation. Thus, opening the cochlea introduces artefactual high‐pass filtering. Because of technical limitations, the experiments of Dong & Cooper (2006) were limited to distal apical regions, to 80 dB SPL stimuli, and to non‐sensitive cochlear preparations. Taken together with our new measurements in the intact sensitive cochlea, we show that the normal response in the apical two turns of the living, hearing guinea pig is low‐pass‐like for all stimulus intensities and that cochlear amplification does not sharpen frequency tuning like it does in higher frequency cochlear locations.

Discussion

The key evolutionary factor permitting high‐frequency hearing in mammals was the development of cochlear amplification (Davis, 1983), whereby outer hair cells produce force to amplify sound‐induced vibrations of the basilar membrane and sharpen frequency tuning. In tandem, the inner hair cells and auditory nerves function to transmit the mechanical response to the brainstem. Herein, we show that this popular description of mammalian cochlear physiology does not hold true for very low‐frequency hearing. Our data demonstrate that the mechanical response within the cochlea to sound stimuli <2 kHz cannot account for the sharpness of tuning in the guinea pig auditory nerve.

Our data differ from most previous measurements of sound‐induced vibrations in the apex of the guinea pig (Cooper & Rhode, 1992b; Hao & Khanna, 1996; Zinn et al. 2000) and the chinchilla (Rhode & Cooper, 1996; Cooper & Rhode, 1997) in two key ways. First, we show that the vibratory response does not significantly roll off at extremely low frequencies. Thus, the native passive mechanical response of the apical guinea pig cochlea acts as a low‐pass rather than a band‐pass filter. As far as we are aware, no published cochlear models support a low‐pass function in the cochlear apex. We attribute our ability to detect this difference to the fact that we did not need to open the cochlea, which has been shown to alter the pressure difference across the organ of Corti and reduce the low‐frequency response (Cooper & Rhode, 1996; Dong & Cooper, 2006; Olson, 2013). Second, the vibratory sensitivity in our preparation ranged from 10 to 1000× higher than all previous measurements and the vibratory magnitudes were quite large. In some cases, the displacement was >1 μm. This is likely to be because we did not need to open the cochlea nor disturb Reissner's membrane. However, a caveat is that the magnitude of vibration we measured reflects only that vector component directed along the optical axis of the VOCTV setup. Nevertheless, these robust responses support our argument that these experimental preparations were healthy and reliable.

Furthermore, we found evidence of vibratory gain over a wide bandwidth, both below and above the F _3dB corner frequency of the response. Below the corner frequency, the gain we measured is similar to what has recently been measured in the mouse reticular lamina and tectorial membrane below the characteristic frequency (Lee et al. 2016; Ren et al. 2016). Above the corner frequency, the level of gain we measured was, in some cases, as high as gains measured in the cochlear base at the characteristic frequency (Robles & Ruggero, 2001). Together, these data indicate that outer hair cell force generation plays a significant role in low‐frequency mammalian hearing. However, this statement must be tempered by the fact that cochlear amplification does not sharpen tuning for low‐frequency regions of the cochlea. Furthermore, because the raw magnitude responses dropped off quickly above the corner frequency, the non‐linear gain found in this frequency range (1–2 kHz) would seem to have little physiological relevance to low‐frequency hearing. Nevertheless, while the frequency response in the third turn was clearly low‐pass, there were small tuning peaks in the vibratory characteristics of the second turn. Given the exquisitely sharp mechanical tuning found in the basal regions of the cochlea, these data suggest that the ability of cochlear amplification to sharpen tuning changes along the cochlear tonotopic map. Stated another way, the frequency sharpening effects of cochlear amplification are distinct from the gain of cochlear amplification, as has been previously suggested (Gao et al. 2014).

Therefore, our data argue that another process besides cochlear amplification must be required to establish tuning in low‐frequency regions of the mammalian cochlea. In non‐mammals, basilar membrane mechanical responses are either not tuned or broadly tuned whereas their auditory nerve responses are sharply tuned (Peake & Ling, 1980; O'Neill & Bearden, 1995; Xia et al. 2016), and thus tuning derives from electrical resonance within hair cells (Crawford & Fettiplace, 1981; Lewis & Hudspeth, 1983; Fuchs et al. 1988). It is conceivable that hair cells from low‐frequency regions of the mammalian cochlea also have electrical resonance that has not yet been established, since patch clamp studies of guinea pig hair cells have typically been done in isolated cells that may have their physiology altered to some degree because of the trauma associated with the dissection procedures. Nevertheless, these studies have demonstrated that apical guinea pig outer hair cells do not have electrical resonance (Ashmore & Meech, 1986) and that isolated guinea pig inner hair cells only have a strongly damped transient response with a low‐quality factor (Kros & Crawford, 1990). Furthermore, studies of inner hair cells from mice and vestibular hair cells from mice, guinea pigs and humans clearly demonstrate a lack of electrical resonance in both isolated cells and cells patch clamped in situ (Rennie & Ashmore, 1991; Rusch & Eatock, 1996; Oghalai et al. 1998). Thus, it is highly unlikely that the primary mechanism underlying the sharpness of low‐frequency guinea pig auditory nerve fibres is electrical resonance.

However, in vivo intracellular recordings from both outer and inner hair cells indicate that their receptor potentials are as sharply tuned as single‐unit auditory nerve responses in both the apex and the base of the guinea pig (Russell & Sellick, 1978; Dallos et al. 1982; Dallos, 1986). While there is little doubt that basilar membrane mechanics underlies sharp tuning in the cochlear base (Narayan et al. 1998), what underlies sharp tuning in the apex? One possibility is the superposition of two different filtering mechanisms, one high pass and one low pass. For example, the high‐frequency side of the hair cell receptor potential tuning curve could derive from the low‐pass filter roll‐off found in the basilar membrane mechanical response, which we show has a similar slope to auditory nerve single unit threshold curves. In contrast, the low‐frequency side of the tuning curve must stem from something that lies between the mechanical vibratory response and the hair cell receptor potential. This concept has previously been suggested based upon non‐linear features found in the phase response in low‐frequency auditory nerve studies in the chinchilla (Temchin & Ruggero, 2010).

One possibility is that the displacement of the inner hair cell stereociliary bundle has a different frequency response from the displacement of the point within the organ of Corti we measured. Since the bundle is not attached to the tectorial membrane, the fluid mechanics that stimulate the bundle may provide a high‐pass filtering mechanism. Another possibility is that fast adaptation of the stereociliary bundle plays a role. Adaptation of the bundle has been shown to act as a high‐pass filter (Kennedy et al. 2003) with the adaption time constant setting the corner frequency in the acoustic frequency range (Ricci et al. 2005). Since the magnitude of adaptation in mammalian hair cells can approach 100% (Peng et al. 2013), another consequence would be to make the hair cell and auditory nerve responses appear to be sensitive to velocity rather than displacement, as has been reported (Zwislocki & Sokolich, 1973; Russell & Sellick, 1983). Consistent with this premise, in vivo extracellular recordings of AC potentials generated by inner hair cells are consistent with tuning of the transduction currents (Cheatham & Dallos, 2000). While this has previously thought to be due to the mechanical properties of the basilar membrane, our data argue that it stems from bundle stimulation or transduction channel mechanics. We therefore suggest that a role of hair cell stereociliary bundle adaptation and/or fluid viscosity in the subtectorial space may be to provide high‐pass filtering, sharpening the frequency response of the inner hair cell receptor potential to aid the discrimination of low‐frequency sounds. However, we do acknowledge that these effects may not explain all our observations.

Additional information

Competing interests

The authors declare no competing interests.

Author contributions

A.R.S. and J.S.O. performed all aspects of this research, including designing the experiments, performing the experiments, analysing the data, and writing the manuscript.

Funding

This project was funded by NIH‐NIDCD DC014450, DC013774, DC010363, and DC00419.

Data

Data spreadsheets used to create the plots for this article are available for download at https://github.com/jso111/guineapigcochlearapex. This material has not been peer reviewed.