Distinguishing Lead and Molecule States in Graphene-Based Single-Electron Transistors

Abstract

Graphene provides a two-dimensional platform for contacting individual molecules, which enables transport spectroscopy of molecular orbital, spin, and vibrational states. Here we report single-electron tunneling through a molecule that has been anchored to two graphene leads. Quantum interference within the graphene leads gives rise to an energy-dependent transmission and fluctuations in the sequential tunnel-rates. The lead states are electrostatically tuned by a global back-gate, resulting in a distinct pattern of varying intensity in the measured conductance maps. This pattern could potentially obscure transport features that are intrinsic to the molecule under investigation. Using ensemble averaged magneto-conductance measurements, lead and molecule states are disentangled, enabling spectroscopic investigation of the single molecule.

Graphene electrodes are advantageous for use in single-molecule devices,¹⁻⁵ because unlike metal electrodes, they do not suffer from high atomic mobility and screening.^1,3 Large area single-layer graphene can be grown and patterned into devices with electrodes separated by nanogaps,^6,7 and molecules bridging the gap can be anchored to the electrodes via covalent bonding⁴ or π–π-stacking.^1−3,8,9 However, the nontrivial density of states and transmission in graphene nanostructures, combined with the fact that graphene can be electrostatically gated, can lead to the observation of transport features in graphene-based single-molecule devices that are not intrinsic to the molecule under investigation, but are rather a property of the leads. Experimental and theoretical studies have shown that quantum interference in graphene ribbons¹⁰⁻¹³ and nanoconstrictions¹⁴ lead to conductance fluctuations at cryogenic temperatures. Quantum confinement in the source and drain electrodes of semiconductor single-electron transistors results in the observation of density of states oscillations in the sequential electron tunneling transport through these devices.^15,16 It is therefore to be expected that quantum interference effects in graphene electrodes will also influence the charge transport in single-molecule devices.

Here we present a transport spectroscopy investigation of a graphene-based single-electron transistor where we attribute the sequential electron tunneling to the presence of a single molecule bridging the graphene nanogap. While the charge island is most likely formed by an individual zinc-porphyrin dimer, the observed transport features are completely independent of the type of molecule used, and in fact can also be observed in graphene quantum dots in a similar device geometry (see Supporting Information, where we present experimental data of zinc-porphyrin monomers and graphene quantum dots). Our experiments show how the graphene leads couple electrostatically to a global back-gate, and that hybridization between the lead and molecule states results in distinct fluctuation patterns as a function of gate and bias voltage. This behavior is captured by a simple tight-binding model, which we solve both analytically and numericially. Finally, we present a strategy to recover transport features that are intrinsic to the molecule, and might be obscured by the density of states fluctuations in the leads, by disentangling lead and molecular states.

Results and discussion

We measured charge transport in single-molecule transistors at 4.2 K (sample A) and 20 mK (sample B) as a function of bias voltage V_b and gate voltage V_g. Individual molecules were contacted using chemical vapor deposition (CVD) grown graphene nanogaps on a silicon substrate with a 300 nm thermally grown oxide layer that was prepatterned with metal (Cr/Au) contacts. The single-layer nature of the graphene was confirmed by Raman spectroscopy.¹⁴ The graphene nanogaps were fabricated using feedback-controlled electroburning.⁷ Single zinc-porphyrin dimer molecules were deposited from a chloroform solution, and were identified by comparing current maps as a function of V_b and V_g before and after deposition (see Supporting Information).

We have measured a total of 171 successfully electroburnt devices (meaning they were successfully burnt, did not break during the wire-bonding and cool-down procedure, and resulted in a measurable tunnel current at 77 K.) From these 171 devices, 109 were measured again at 77 K after the molecular deposition after which 26 devices appeared empty before the deposition (i.e., no Coulomb diamonds) and showed sequential tunneling after molecular deposition. We observed conductance fluctuation in 4 devices.

The conductance through the single zinc-porphyrin dimers was investigated via single-electron tunneling from a metallic source reservoir via the left graphene lead, through the molecule, to the metallic drain reservoir via the right graphene lead (Figure 1a). The silicon substrate was used as a backgate to apply V_g. In contrast with metal-based single-molecule transistors, where the metal electrodes screen the gate electric field, in our devices the electrostatic gating influences both the molecular orbital states and the states in the graphene leads (Figure 1b). Previous experiments using partially electroburnt graphene nanoconstrictions have shown that the transmission of our graphene leads fluctuates as a function of V_b and V_g, which we attribute to either universal conductance fluctuations (UCFs) resulting from random disorder or the presence of multimode Fabry-Pérot interferences.¹⁴ These fluctuations in the graphene leads influence the transmission through the molecule as orbital states are tuned in and out of resonance with the lead states.

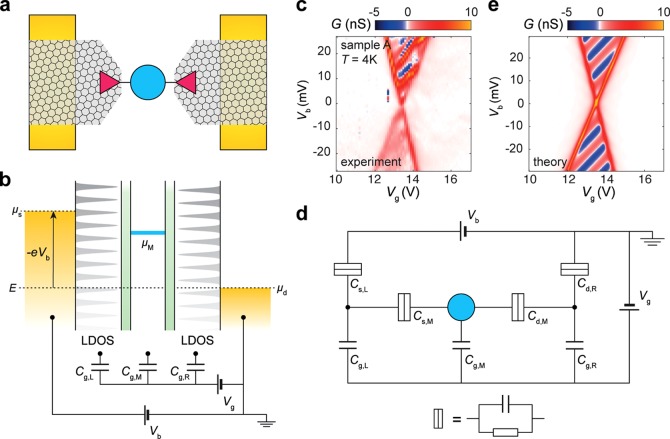
Figure 1.

Measurement and theory of a graphene-based single-electron transistor. (a) Schematic depiction of the device. Graphene lead electrodes are connected to gold reservoirs left and right; a single molecule bridges the gap between the graphene electrodes. Details on the fabrication and the setup are provided in Figure S1. (b) Schematic energy diagram of the graphene–molecule–graphene junction. (c) Measured differential conductance G = dI/dV_b as a function of bias and gate voltage (sample A). (d) Equivalent circuit diagram of (a) and (b); the Ohmic approximation for a tunnel barrier is valid in the low bias regime of (c) and (e). (e) Calculated differential conductance as a function of bias and gate voltage.

Figure 1c shows the differential conductance measured as a function of the applied bias and gate voltage for sample A. The data reveal a dense set of positive and negative conduction resonances visible as red and blue lines of positive slope that we attribute to fluctuations in the graphene leads. A striking feature of the data is that the red and blue lines do not run parallel to the lines at the edges of white regions of suppressed conductance. In what follows, we will discuss the origin of the conduction resonances and analyze the electrostatic gating of the molecule and the lead states.

For charge to flow through a molecule, electrons need to be added and removed from it. The energy required to add one electron to the molecule, i.e., its electron affinity, is given by the electrochemical potential μ_M(N) = U(N) – U(N – 1), where U(N) is the total energy of the N-electron redox state.¹⁷ This electrochemical potential consists of the discrete orbital energy plus the electrostatic contribution to the energy, which depends linearly on the source (drain) V_s(d) and gate V_g voltage as μ_M = −|e|(C_s,MV_s + C_d,MV_d + C_g,MV_g)/(C_s,M + C_d,M + C_g,M), where the capacitance C_s(d,g),M describes the electrostatic interaction between the source (drain, gate) electrode and the molecule.¹⁸ Electrons can tunnel through the molecule when its electrochemical potential is within the bias window defined by the electrochemical potentials μ_s = −|e|V_s and μ_d = −|e|V_d in the source and drain reservoirs, respectively. When μ_d is outside this bias window, electrons do not have the necessary energy to occupy/empty an orbital, resulting in diamond-shape regions of Coulomb blockade in the conductance versus bias and gate voltage map. The slopes of these Coulomb diamonds are given by the conditions μ_M = μ_d and μ_M = μ_s. When the device is biased asymmetrically and the gate voltage is set relative to one of the electrodes, in our case the drain, i.e., V_s = V_b and V_d = 0, these conditions yield the slopes C_g,M/(C_d,M + C_g,M) and −C_g,M/C_s,M.

Similar to the molecular orbital states, the states in the graphene leads shift linearly as a function of the applied bias and gate voltage. The energy shift of the states in the left lead, which is coupled to the source reservoir, is given by Δϵ_L = −|e|(C_s,LV_s+C_g,LV_g/(C_s,L+C_g,L), and for the right lead coupled to the drain reservoir Δϵ_R = −|e|(C_d,RV_d+C_g,RV_g/(C_d,R+C_g,R). In the case of asymmetric biasing, lines in the conductance map for which a molecular orbital aligns with a state in the left lead have a slope given by μ_M = Δϵ_L, which yields

1

and for states in the right lead μ_M = Δϵ_R yields

2

When the lead states are clamped to the electrochemical potential of the reservoirs, i.e., if the capacitive coupling between the leads and the gate is zero, the slope of the lines for which the molecular orbitals align with the lead states run parallel to the edges of the Coulomb diamonds. Parallel lines in conductance maps resulting from disorder and confinement in the leads of single-electron transistors have been studied extensively, for example in STM-fabricated devices in silicon.¹⁵ However, when there is capacitive coupling between the leads and the gate, these lines no longer run parallel to the edges of the Coulomb diamonds, and resonances between molecular and lead states shift in and out of the bias window.

From the slopes of the edges of the Coulomb diamonds in Figure 1c we infer that the ratio C_g,M/C_s,M = (33 ± 1) × 10^–3, and C_g,M/C_d,M = (20 ± 1) × 10^–3. The relatively strong coupling to the source and drain electrodes compared to the gate electrode is due to the fact that the backgate is separated from the device by a 300 nm layer of SiO₂. Next, we estimate the electrostatic coupling of the lead states to the backgate. We only observe conduction resonances with positive slopes, which implies that we predominantly probe the left lead. From the positive slope of the conduction resonances we find C_g,L/C_s,L = (7 ± 1) × 10^–3, indicating that the gate coupling to the molecule is approximately 3–5 times stronger than to the lead states. We attribute the difference in gate coupling between the molecule and the lead states to the higher carrier concentration in the graphene leads, which results in a more effective screening of the gate electric field. The average spacing between the conduction resonances is approximately 5 meV, which is consistent with the conductance fluctuations we have previously observed in partially electroburnt graphene nanoconstrictions.¹⁴

We will now discuss the hybridization between the lead states and the molecular orbitals as they are tuned in and out of resonance. The current through a molecular orbital is given by the Landauer formula¹⁹

3

where f_L,R denotes the Fermi distribution of the reservoirs, which in the case of asymmetric biasing depends on the bias voltage V_b and temperature T as f_L = [exp((E–eV_b)/k_BT) + 1]⁻¹ and f_R = [exp(E/k_BT) + 1]⁻¹.

To investigate the role of scattering in the leads on the transmission through the molecular orbital we employ a simple Hückel (tight-binding) model as shown in Figure 2a. The molecule is represented by a single site at n = 0 with an on-site energy μ_M and a hopping integral γ_L,R to the left and right lead, respectively. The left and right leads are represented by semi-infinite chains with on-site energies ϵ_L,R and nearest-neighbor hopping integrals α_L,R. We introduce scattering into the left and right compound electrodes at n = −N_L and n = N_R by adjusting the hopping integrals β_L,R.

Figure 2.

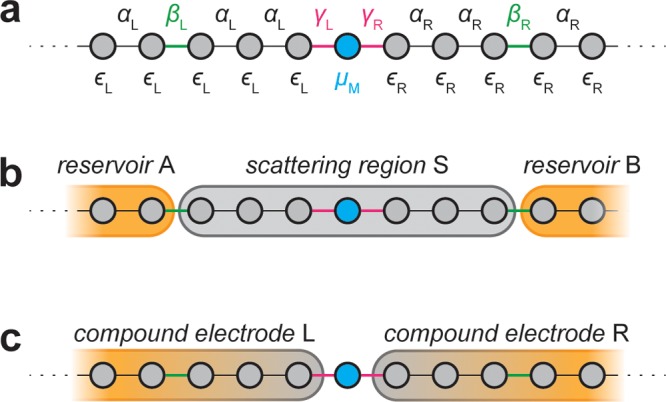
Partitioning the molecule-lead system. (a) Schematic depiction of the Hückel model. (b) Partitioning of the system into simple electrodes A and B with a complex scattering region S, and (c) into “compound electrodes” L and R and a simple scatting site M.

Traditionally one would regard this structure as a complicated scatterer (S) consisting of the region between −N_L ≤ n ≤ N_R (shaded gray in Figure 2b) and two simple crystalline leads (shaded orange in Figure 2b) along which electrons propagate ballistically into and from the reservoirs. For such a system,

4

where Γ_A and Γ_B describe the level broadening due to contact with the crystalline semi-infinite leads, A and B. In this expression, the scatterering region is a complex combination of the molecule and graphene and G_SS is the Green’s function of the scattering region in the presence of the simple crystalline leads. Our aim is to separate the contributions to scattering from the molecule and graphene and therefore we adopt an alternative formulation²⁰ in which the left graphene, and left semi-infinite lead, i.e., the region n < 0, are regarded as a compound electrode (L) and the right graphene and right semi-infinite lead (n > 0) form the right compound electrode (R). This viewpoint is encapsulated in the following alternative expression for the transmission coefficient, which is mathematically equivalent to eq 4

5

In this equation, the level broadening due to contact between the molecule and the left and right compound electrodes are described by

6

7

where g_LL(RR) is the Green’s function of the isolated left(right)-hand compound electrode, and H_L(R)M denotes the coupling between the left(right) compound electrode and the molecule. The Green’s function of the molecule in the presence of the compound electrodes is given by

8

where the self-energies of the left and right compound electrode are

9

10

Using eqs 5 and 6–10, we obtain the Breit–Wigner formula

11

In the case of the simple Hückel model, this implies that the tunnel-rate Γ_L is proportional to the local density of states at site n = −1 and Γ_R is proportional to the local density of states at site n = +1. Both the tunnel-rates and the energy shifts depend on the electrode density of states, which in turn is determined by the random locations of scattering centers within the graphene electrodes. The self-energies of the compound electrodes in the Hückel model can be found numerically by decimation (for details see Supporting Information), or analytically by solving Dyson’s equation (see Supporting Information). The latter yields

12

where x_L = β_L²/α_L – 1 and k_L = cos^–1 (ϵ_L – E)/2α. Similarly Γ_R is obtained by replacing L by R in the above expression. Here we have derived the transmission for a simple one-dimensional Hückel model, however eqs 4 and 5 are completely general, and the transmission function will depend on the details of the system Hamiltonian (see Supporting Information for a more sophisticated system Hamiltonian). Experimentally, we find that the position of the molecular energy level with respect to the Fermi energy of the leads and the strength of the coupling between the molecule and the graphene leads varies significantly from device to device.

Figure 3a,b shows the real and imaginary part of the self-energies for strong and weak reflections in the leads. For strong reflection (β_L,R² = 0.1α_L,R) we find sharp peaks in the imaginary part of the self-energies, i.e., the density of states at the surface sites (n = ± 1), arising from quasi-bound states between the molecule and the reflection sites (n = −N_L, N_R). By contrast, for weak reflections (β_L,R² = 0.9α_L,R) we find a small sinusoidal modulation of both the tunnel-rates Γ_L,R and the energy shift σ_L,R. The tunnel-rate is maximum on resonance with the quasi-bound lead states while the hybridization energy changes sign upon crossing the resonance condition. The transmission as a function of energy and electrochemical potential of the molecule μ_M (Figure 3c) shows both the effect of the modulation of the tunnel-rate and the hybridization energy. The transmission is maximum upon resonance, reflecting the increase in tunnel-rate, and a avoided crossing appear around the resonance condition due to level repulsion resulting from the hybridization between the molecular orbital and the lead states.

Figure 3.

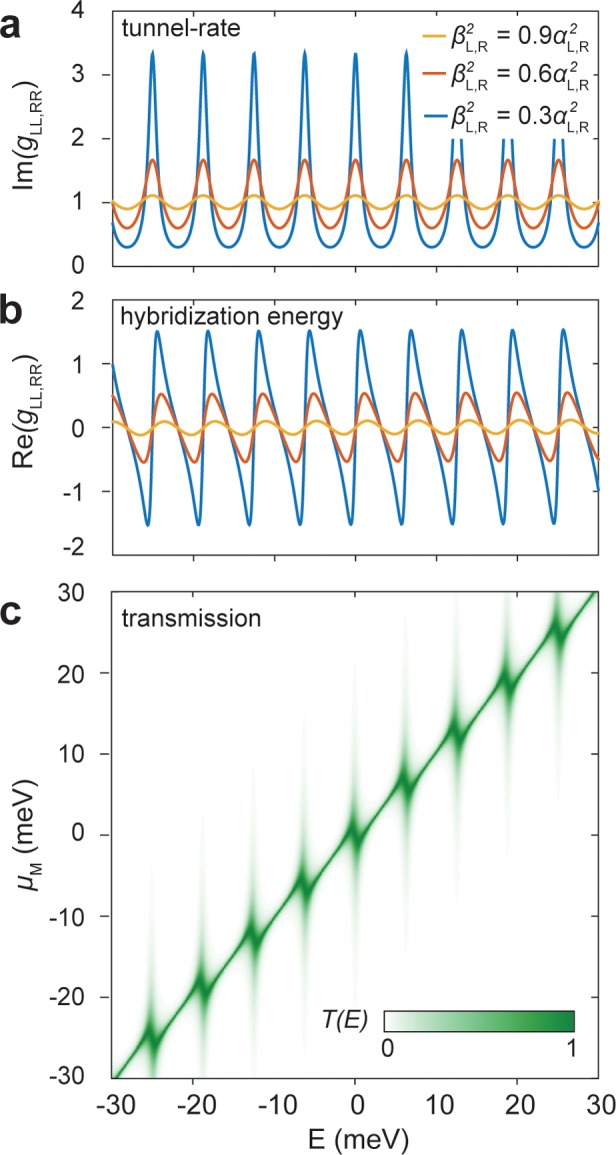
Tunnel-rate and hybridization energy. (a,b) Real and imaginary part of the surface Green’s function calculated for α_L,R = 3 eV, ϵ_L,R = 0 eV and l = 1000. (c) Transmission as a function of energy E and on-site potential μ_M for γ_L,R = 20 meV.

To calculate the current and differential conductance as a function of bias and gate voltage as shown in Figure 1e, we introduce the experimentally extracted capacitive coupling parameters to the on-site energies as discussed in the previous section. By choosing α_L,R = 1 eV and N_L = N_R = 1000 we obtain an energy-level spacing between the quasi-bound lead states of 2 meV, close to the observed energy spacing in our experiment. We find that choosing the hopping integrals γ_L = 4 μeV and γ_R = 20 meV results in a good qualitative agreement between the experimental and theoretical differential conductance maps. Due to strong asymmetry in coupling strength between the left and right lead, i.e. ,Γ_L ≪ Γ_R, the amplitude of the Breit–Wigner resonance ∼ Γ_L and is only sensitive to states in the left lead.

The conductance fluctuations observed in the sequential tunnelling regime arise from interference effects in the leads, which can either be the result of scattering of random impurities leading to universal conductance fluctuations (UCFs, see Figure 4a), or Fabry-Pérot (FP, see Figure 4b) interferences resulting from reflections at potential barriers. UCFs can be observed if electron waves scatter along closed trajectories and the phase coherence length l_ϕ is larger than the mean free path. This scattering leads to random, energy dependent interferences within segments of l_ϕ² inside the conductor which appear as aperiodic conductance fluctuations as a function of gate voltage. When a magnetic field is applied perpendicular to the graphene leads, electron waves acquire an additional phase due to the vector potential, resulting in an Aharonov–Bohm phase ΔB_AB = Φ₀/S, where Φ₀ = h/e, for a trajectory enclosing an area S. When the conductance is measured for different magnetic fields within the correlation field scale ΔB_c ≈ Φ₀/(L_x + L_y), where L_x and L_y correspond to the smallest relevant dimension in x and y direction, similar features corresponding to a specific impurity configuration are observed in each conductance curve.^21,22 However, when the increments in external magnetic field are larger than ΔB_c, a different impurity configuration is probed for each conductance curve. As a result, UCFs can be suppressed by ensemble averaging measurements recorded at B > ΔB_c, denoted by ⟨...⟩_B. This technique was successfully used to distinguish between UCF and weak-localization effects in nanowires²³ and carbon nanotubes.²⁴ Theoretically, the UCFs can be reduced by a factor of √N where N is the size of the ensemble.²⁴Figure 4f shows bias traces as a function of magnetic field recorded at V_g = 29.75 V of sample B measured at 20 mK (indicated by the dotted line in Figure 4c). We recorded 40 traces in B_⊥ = B_z (Figure 4d) and 40 traces in B_∥ = B_x,y (Figure 4e). For a phase coherence length l_ϕ ≈ 400 nm¹⁴ found in our graphene samples ΔB_c ≈ 25 mT, and therefore ΔB_⊥, ΔB_∥ > ΔB_c. While the out-of-plane magnetic field changes the conductance fluctuations (Figure 4e), the in-plane field up to 6 T does not affect the oscillations (see Figure 4d). The fact that only the out-of-plane magnetic field influences the conductance fluctuations further strengthens our assumption that they are intrinsic to two-dimensional graphene leads rather than the molecule. By comparing the conductance at B = 0 with the data averaged over B we find a reduction of UCFs of var(G(B = 0))/var(⟨G(B)⟩_B) ≈ 6 very close to the theoretical value of .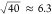

Figure 4.

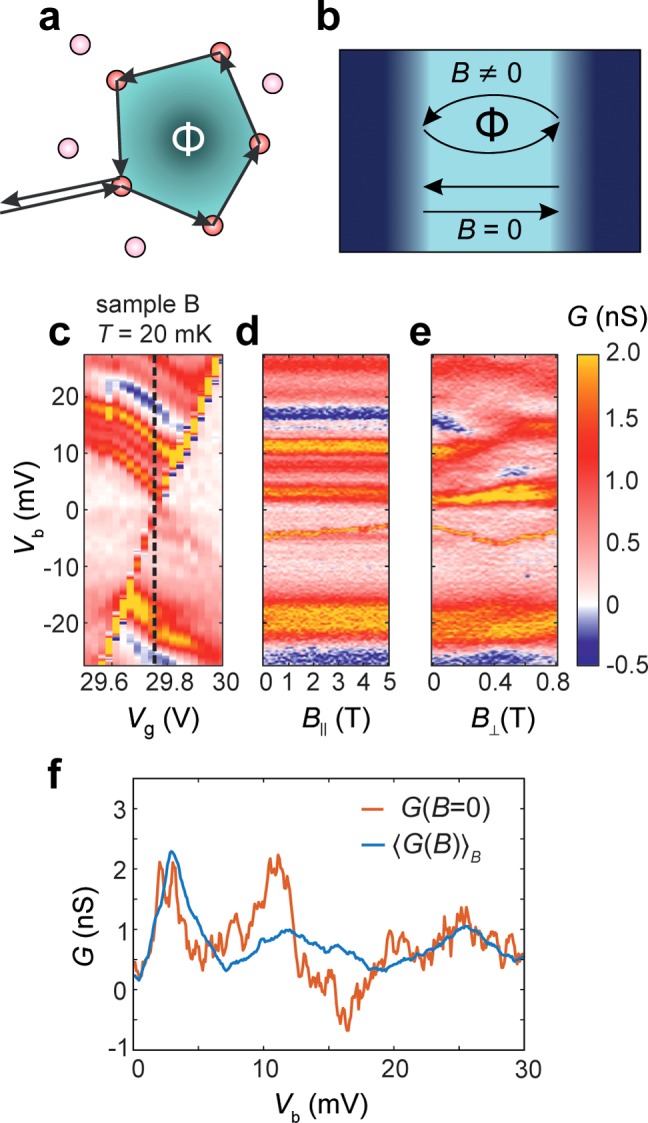
Magnetic field dependence of conductance fluctuations. (a,b) Schematic depiction of Universal Conductance Fluctuations and Fabry-Pérot interference. (c) Differential conductance map measured at B = 0 T (sample B). (d,e) Differential conductance measured as a function of bias voltage and magnetic field in (∥) and out (⊥) of the device plane. (f) Differential conductance measured at B = 0 T compared with the ensemble averaged differential conductance.

Single- and multimode FP interference effects have previously been observed in graphene ribbons and nanoconstrictions.¹⁴ The Lorentz force acting on the electrons in a FP cavity will curve their trajectories when an external magnetic field is applied, which leads to the semiclassical (kinetic) phase difference ϕ_WKB between two neighboring trajectories.²⁵ In addition, bent trajectories enclosing an area S will accumulate an Aharonov–Bohm phase ϕ_AB = eB_⊥S/ℏ = Φ/Φ₀. Finally, back-reflected electrons in graphene acquire a Berry phase ϕ_Berry, which is π for single-layer graphene and can take values between 0 and 2π in bilayer graphene depending on its carrier density and asymmetry parameter, which is defined as the difference in on-site energies of the two graphene layers.²⁶ Since the Berry phase is not affected by the external magnetic field, and therefore does not play a role in magnetic-field averaging, it can be ignored in this discussion. The resonance condition for Fabry-Pérot interferences is met when ϕ_WKB + ϕ_AB + ϕ_Berry = 2πj, where 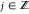. Variations of the external magnetic field will change this condition and thus shift the conductance maxima due to the combined influence on ϕ_WKB and ϕ_AB (see Supporting Information). Ensemble averaging of the magneto-conductance traces will therefore result in the suppression of density of states fluctuations. This behavior can be illustrated by a tight-binding model shown in Figure 5a, in which the leads contain circular regions through which a magnetic flux can pass. Again the transmission coefficient can be obtained analytically as a function of the flux Φ passing through each of the loops. This is imposed via a Peierls substitution by adding a phase factor θ = 2πΦ/Φ₀ to nearest neighbor hopping integrals. In the absence of a magnetic field, Figure 5b,c shows an example of the transmission and differential conductance, which reflects the density of states fluctuations in such a model. The ensemble averaged curves show a strong reduction of the fluctuations, in correspondence with the experimental results.

Figure 5.

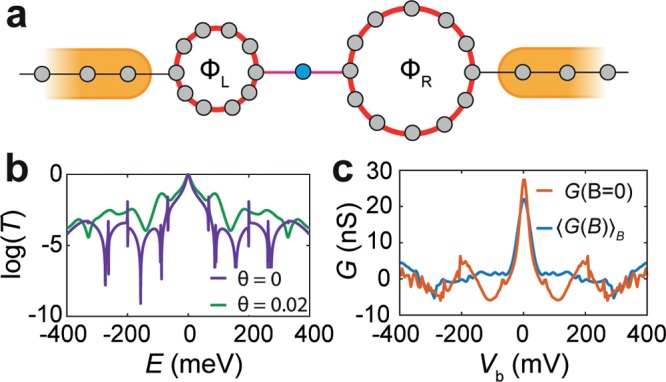
Electrodes with ring-paths. (a) Tight binding model describing a molecular orbital connected to semi-infinite one-dimensional leads via ring paths. (b) Calculated transmission for two different values of θ = 2πΦ/Φ₀. (c) Differential conductance at B = 0 compared to the ensemble averaged values, calculated for α_ring,L = α_ring,R = 0.7α_L,R and γ_L = γ_R = 0.075α_L,R.

Conclusions

In this work we have investigated the role of density of states fluctuations in single-molecule devices contacted to single-layer graphene nanoelectrodes. By analyzing local measurements of the quasi-bound lead states, we find that the electrostatic coupling to the global back-gate is weaker than the gate coupling to the molecule. This enables electrostatic control over the hybridization between lead and molecule states. While the effect of quantum interference is in most cases detrimental to the investigation of molecular properties, because intensity variations in the conductance maps are hard to distinguish from the molecular features, it may provide a pathway toward interference-based molecular transistors. If the energy-spacing between the quasi-bound lead states can be increased by further quantum confinement, they may act as an energy filter for the transport through the molecular orbitals.^27,28

Our approach of ensemble averaging magnetoconductance traces provides an effective way of distinguishing between features that are intrinsic to the molecule and those that are the result of quantum interference in the leads. This provides a useful tool for the spectroscopic investigation of single molecules, for example for the identification of vibrational states.²⁹ However, orbital excited states are likely to shift as a function of the magnetic field due to their orbital angular momentum, and will therefore not be amenable to the ensemble averaging technique described in this work. The same holds for single-molecule magnets, which exhibit a large magnetic anisotropy. Nevertheless, the fact that the conductance lines resulting from the lead states do not run parallel to the edges of the Coulomb diamond may still be used to distinguish between lead and molecular states. In the case where magnetic ensemble averaging is not possible, e.g., when studying magnetic molecules, a coplanar gate³⁰ could potentially reduce the effects of density of states fluctuations in the leads as it will only gate the molecule states locally.

To conclude, our results highlight the importance of the electronic properties of the lead electrodes in single-molecule electronics. While graphene may be a material system that is very well suited to host these devices, further understanding of the hybridization between graphene and molecules will be needed to develop these devices into a technology. Atomically precise control of the structure and edge termination of the graphene leads,³¹ together with stacked two-dimensional material approaches³² could enable functional graphene-molecule hybrid systems.

Methods

Devices are fabricated using feedback-controlled electroburning of CVD grown graphene ribbons that were wet-transferred onto a pre-patterned Si/SiO₂ chip containing Au/Cr contact pads. We deposit molecules from a 10 μM chloroform solution. Devices were measured in an Oxford Instruments Triton 200 dilution refrigerator and a custom-built liquid helium dipper. Measurements were performed using low-noise, battery powered electronics. We measure the transport characteristics of the device before and after molecular deposition and select those device that only show Coulomb blockade after deposition.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b00570.

• Synthesis; synthetic scheme; device fabrication; electrostatic characterization; theoretical model; additional ZnP monomer, dimer, and graphene quantum dot data; and magnetic field dependence information (PDF)

The authors declare no competing financial interest.