Broadband Cooling Spectra of Hot Electrons and Holes in PbSe Quantum Dots

Abstract

Understanding cooling of hot charge carriers in semiconductor quantum dots (QDs) is of fundamental interest and useful to enhance the performance of QDs in photovoltaics. We study electron and hole cooling dynamics in PbSe QDs up to high energies where carrier multiplication occurs. We characterize distinct cooling steps of hot electrons and holes and build up a broadband cooling spectrum for both charge carriers. Cooling of electrons is slower than of holes. At energies near the band gap we find cooling times between successive electronic energy levels in the order of 0.5 ps. We argue that here the large spacing between successive electronic energy levels requires cooling to occur by energy transfer to vibrational modes of ligand molecules or phonon modes associated with the QD surface. At high excess energy the energy loss rate of electrons is 1–5 eV/ps and exceeds 8 eV/ps for holes. Here charge carrier cooling can be understood in terms of emission of LO phonons with a higher density-of-states in the valence band than the conduction band. The complete mapping of the broadband cooling spectrum for both charge carriers in PbSe QDs is a big step toward understanding and controlling the cooling of hot charge carriers in colloidal QDs.

Colloidal semiconductor quantum dots (QDs) are of interest because of the possibility of tuning their optical and electronic properties by variation of composition and size. In combination with their solution-processability this offers promising prospects for application in devices such as field-effect transistors, light-emitting diodes, photodetectors, and solar cells.¹ PbSe QDs receive much attention due to their exceptionally strong quantum confinement properties, and in particular because of the occurrence of carrier multiplication (CM).²⁻⁶ CM is a process in which one sufficiently energetic photon excites two or more electrons across the band gap. In this way the power conversion efficiency of a solar cell can be enhanced above the Shockley–Queisser limit. CM occurs in competition with cooling of initially energetic electrons or holes via LO phonon emission or other relaxation channels.⁷⁻⁹

Until now, studies on charge carrier cooling in PbSe QDs involved low photoexcitation energies close to the band gap.¹⁰⁻¹³ Here, the distance between adjacent electronic energy levels is typically several LO phonon energies, requiring simultaneous emission of multiple phonons for a charge carrier to cool from one level to the one below. This is referred to as the “phonon bottleneck” and was originally suggested to increase the CM efficiency of nanocrystals over bulk.^14,15 However, clear evidence of the phonon bottleneck has not been found in PbSe QDs.^12,16 Near the band edge other cooling channels can become dominant, such as trapping at defects, energy transfer to vibrational modes of ligand molecules, or surface related phonon modes.^13,17−21 In agreement with this, it was found that electron cooling near the band edge in CdSe QDs is slowed down several orders of magnitude by decoupling the electron from the surface, so that it could relax only through emission of LO phonons.^22,23

The competition between CM and other relaxation channels takes place at higher energies where an electron or a hole has an excess energy that is at least equal to the band gap. At such high excess energy the electronic structure of PbSe QDs approaches that of bulk PbSe and LO phonon emission will not be restricted by the availability of electronic energy levels at a spacing equal to the phonon energy. Currently, little is known of cooling at high charge carrier excess energy, except that it is very fast.²⁴⁻²⁸ In addition, hot carrier cooling in QDs is usually described as a single cooling time.^12,29−31 We stress however that each transition of a charge carrier from an energy level to a level of lower energy is a discrete quantum mechanical transition with its own characteristic time constant. Hence carrier cooling times are a function of energy and should ideally be described by a cooling spectrum, separate for electrons and holes.

In this work, we determine cooling times of charge carriers in PbSe QDs between discrete electronic states near the band edge, and at higher excess energy where the electronic states form a quasi-continuum with a character close to that of bulk PbSe. We build up a broadband cooling spectrum for both charge carriers and find that holes cool faster than electrons, in agreement with our earlier work.³² Strikingly, we can resolve five discrete cooling steps (three for electrons and two for holes) near the band edge before the onset of the quasi-continuum. We argue that at lower energies charge carrier cooling involves energy transfer to vibrational modes associated with the surface of the QD. At high carrier excess energy cooling can be explained in terms of emission of LO phonons, which we verify by k·p calculations. We show that we expect an asymmetric density-of-states (DOS) with a denser valence band than conduction band to account for the differences in cooling times of electrons and holes.

Results and Discussion

Measurements and Modeling of Electron and Hole Cooling Dynamics

PbSe QDs with a diameter of 3.9 nm and band gap of 0.93 eV were synthesized via the method by Steckel et al.,³³ washed twice, and dispersed in toluene (see Methods). The QD dispersion was investigated using transient absorption (TA) spectroscopy with a time resolution of ∼0.15 ps and a probe spectral range of 375–1600 nm (see Methods). In all measurements discussed below the pump laser fluence was sufficiently low that on average much less than one photon per QD was absorbed (⟨N_abs⟩ < 0.15). We show in Figure 1a the hyperspectral TA image that results from photoexcitation by a pump laser pulse with photon energy of 3.35 eV (370 nm), which is high above the band gap. At this photoexcitation energy CM takes place and Auger recombination of multiexcitons can be observed in the first tens of picoseconds. After that only single cold excitons are left and no further decay is observed in the considered time window of 2.5 ns, since the single exciton lifetime in PbSe QDs is several hundreds of nanoseconds.^13,34 The main aim of this work is to study charge carrier cooling, which can be observed in the first few picoseconds after photoexcitation. To highlight the spectral features of charge carrier cooling, we show spectral slices at short (averaged 0.5–1.0 ps) and long (averaged 0.5–2.5 ns) pump–probe delay in Figure 1b, together with the ground-state absorption spectrum. Vertical dashed lines are added to indicate the position of several optical transitions as identified in the past (labeled S for the 1S_e–1S_h transition, P for 1P_h–1P_e, D for 1D_h–1D_e, and Σ for quantum confined transitions around the Σ-point in the bulk Brillouin Zone).³⁵

Figure 1.

(a) Hyperspectral TA image for 3.9 nm PbSe QDs photoexcited by a pump laser pulse with photon energy of 3.35 eV (370 nm). The TA image is corrected for dispersion of the probe light (see Methods). (b) Spectral slices taken at short (averaged 0.5–1.0 ps) and long (averaged 0.5–2.5 ns) pump–probe delay, together with the ground-state absorption spectrum and vertical dashed lines to indicate several optical transitions.

The spectral features at long pump–probe delay in Figure 1b are due to single cold 1S_h–1S_e excitons, as discussed in our previous work.³² The negative TA signal near 1330 nm is due to ground state bleaching and stimulated emission resulting from 1S_h–1S_e excitons. The negative TA signal at 400–500 nm results from blocking of transitions to the second conduction or valence band by the presence of either a hole in the valence band (1S_h) or an electron in the conduction band (1S_e).³² Between these bleach features, the transient absorption spectrum is caused by a red-shift of the ground-state absorption spectrum due to biexciton interactions and possible intraband absorption.³⁶

The negative TA signals are very different at short pump–probe delay when hot excitons are cooling down to the band edge. The band edge bleach is already present, but accompanied by a photoinduced absorption (PA) signal below the band gap. Moreover, a PA contribution shifts the TA signal at 400–500 nm toward positive values. These PA signals result from biexciton interactions caused by hot excitons and largely disappear when cooling has completed.^37,38

In literature, charge carrier cooling is often studied by considering single wavelength TA signals at the 1S_h–1S_e and 1P_h–1P_e transitions.^{12,13,22,26,39} This however does not take into account the PA signal caused by biexciton interactions near these transitions.^29,40,41 As cooling takes place, the PA signal decreases and the band edge bleach increases, since fewer hot excitons are present and more excitons have arrived at the band edge. To quantitatively describe the band edge bleach while correcting for biexciton interactions, one can either fit or integrate.^29,40 We choose here to fit because it alleviates problems with a coherent artifact and boundaries, but we show in Figure S1 of the Supporting Information that identical results can be obtained. We first fit a Gaussian function to the 1S_h–1S_e transition peak in the ground-state absorption spectrum A as a function of photon energy. We then assume that the bleach of the transition is directly proportional to the number of 1S_h–1S_e excitons present. The corresponding absorption peak of the excited state absorption spectrum A* at time t after the pump laser pulse is then given by

1

where the parameters C, E₀, and σ are obtained from the Gaussian fit to the ground-state absorption spectrum. The function f(t) is the sum of the fraction of QDs containing a hole in the 1S_h valence band state and the fraction of QDs containing an electron in the 1S_e conduction band state and is therefore a measure of the bleach at the band edge. The parameter δE(t) is the time-dependent shift in energy of the 1S_h–1S_e transition of a photoexcited QD. As was discussed in literature this shift in energy and the function f(t) can be determined independently.^29,36 The shift δE(t) is largest for hot excitons that are present on short time scales and decreases to a constant when all excitons have cooled down to the band edge. The factor ³/₄ brings into account the 8-fold degeneracy of the 1S_h and 1S_e states and the fact that the bleach results from both reduced absorption and stimulated emission.^13,29,40,42Equation 1 can be rearranged to obtain the TA signal around the band edge bleach, which is given by

2

Fitting eq 2 to the TA spectrum at each pump–probe delay yields the time-dependent function f(t). Note that when CM occurs the presence of two or more excitons in some QDs is included in the value of f(t).

Fits of eq 2 to the TA spectrum of Figure 1 around the 1S_h–1S_e transition for short and long pump–probe delay are shown in Figure 2a. The fits reproduce the bleach of the 1S_h–1S_e transition and are truncated at the high-energy side to avoid effects of higher energy transitions that are not included in eq 2. The red curve in Figure 2b shows the time-dependent function f(t) obtained from the fit, as well as exponential fits to describe f(t) as discussed below. The uncertainty in the fit of eq 2 at a particular pump–probe delay gives rise to noise in the function f(t) of approximately 10%.

Figure 2.

(a) TA spectrum around the band edge bleach for 3.9 nm QDs excited by a pump laser pulse with photon energy of 3.35 eV (370 nm) for short and long pump–probe delay, together with fits of eq 2. (b) The function f(t) obtained from fitting eq 2 to the experimental data, as well as exponential fits to describe f(t) as discussed in the text.

In previous studies a single exponential function (of the form 1 – e^–kt, which is characteristic for a first order decay process) has been used to describe cooling of hot charge carriers to the band edge states.^12,29−31 As can be seen in Figure 2b, a fit of such a single exponential function does not reproduce f(t). This is not surprising, because we previously found that holes cool much faster than electrons and therefore a sum of at least two exponential functions would be needed.³² However, we show in Figure 2b that a double exponential function does not reproduce f(t) either. Rather, the “S-like” shape of f(t) indicates that cooling of electrons and holes to the band edge states takes place in several sequential steps. Thus, a model to describe f(t) must include successive cooling steps of charge carriers from higher energy levels to the band edge states.³⁹ In the next paragraph we discuss the analysis of our experimental data on the basis of such a kinetic model for electron and hole cooling in PbSe QDs.

Determination of Electron and Hole Cooling Times between Successive Energy Levels

We can describe charge carrier cooling as a sequence of steps between successive electronic energy levels as schematically shown in Figure 3a. The time-dependent population of the different electronic states can be described by kinetic equations for relaxation of the electron and the hole, given by

3a

3b

with N_i,e the population of electrons in level e_i and N_i,h the population of holes in level h_i. The function f(t) as shown in Figure 2b can then be described as

3c

with A_e (A_h) the relative contribution of electrons (holes) to f(t) and therefore to the bleach at the band edge.

Figure 3.

(a) Schematic model of the PbSe QD electronic structure with cooling time constants for transitions between successive energy levels. (b–e) Fits of eq 3 to measured data for f(t) for photoexcitation energies and transitions as indicated, which are just above the threshold at which a new level and cooling time had to be included in eq 3.

We obtain the time constants (τ_i,e, τ_i,h) for the different cooling steps by fitting eq 3 to experimental data for f(t), such as those shown in Figure 2 and Figure 3, while increasing the photoexcitation energy in small steps. For multiple photoexcitation energies we find that the time constants for specific transitions remain unchanged. Whenever the set of coupled rate equations requires the time constants to change in order to describe f(t) accurately, we fix the time constants obtained thus far and add a next hole and electron level. We stop adding more discrete energy levels in the case where the time constant remains within the experimental time resolution of ∼0.15 ps or increases continuously with photoexcitation energy. From that energy we consider the electronic structure of the PbSe QDs to resemble a quasi-continuum. In Figure 3 panels b–e we show f(t) with fits for photoexcitation energies just above successive thresholds at which a new energy level had to be included in eq 3. These photoexcitation energies coincide with the transitions in the ground-state absorption spectrum in Figure 1.

When photoexciting at 1.15 eV (resonant with the 1P_h–1P_e transition) we can reproduce the measured f(t) by including one cooling step for the electron (from level e₁ to e₀) and one for the hole (from level h₁ to h₀) in eq 3, see Figure 3b. This results in a double exponential function of which one exponential describes the first electron cooling step (with cooling time τ_1,e from e₁ to e₀) and the other the analogous first hole cooling step. We distinguish between electron and hole, as described in the next paragraph. The measured f(t) in Figure 3c for photoexcitation at 1.55 eV can only be reproduced by adding a second cooling step for the electron and hole, while the first cooling times τ_1,e and τ_1,h are kept fixed to the value obtained for lower photoexcitation energies. We continue with this procedure until we no longer find discrete cooling steps between energy levels. For electrons we find that τ_4,e increases continuously with photoexcitation energy. Instead of defining a new energy level for each photoexcitation energy, we consider the electronic structure above the fourth electronic energy level (e₄) to approach a quasi-continuum. For holes we find that τ_3,h and higher are much smaller than our time resolution, and we therefore consider the electronic structure for holes to approach a quasi-continuum above the third electronic energy level (h₃). The cooling times determined from the procedure described above are given between the corresponding energy levels in Figure 3a. We note that in our data, we have a rise time of f(t) due to the pulse width of our laser. In Figure S2 of the Supporting Information we show f(t) for band edge excitation where cooling is absent and determine an experimental time resolution of 0.15 ps from the rise time. The cooling time constants we list in Figure 3 are convolved with this time resolution.

We attributed cooling times to electrons or holes by making use of the high energy L_4–6 and L_5–7 transitions studied in our previous work that are visible as bleach features at 400–500 nm in Figure 1.³² These are transitions from the second valence band to the first conduction band (L_4–6, 2.7 eV) and from the first valence band to the second conduction band (L_5–7, 2.5 eV). These transitions are selectively sensitive either to the 1S_e electron (L_4–6) or the 1S_h hole (L_5–7) at the band edge, when photoexciting with energy lower than these transition energies. In Figure 4a we show f(t) for 1.77 eV (700 nm) photoexcitation together with the fit of eq 3 to f(t). For the same photoexcitation energy we show a separate electron and hole bleach transient as determined from the L_4–6 and L_5–7 transitions in Figure 4b. The black curves in Figure 4b are the separate contributions of eq 3c due to electrons (A_eN_0,e(t)) or holes (A_hN_0,h(t)) as obtained from the fit of eq 3 to f(t) in Figure 4a. As can be observed, the L_4–6 bleach due to 1S_e electrons is very well described by one set of cooling times. Likewise the L_5–7 bleach due to 1S_h holes is properly described by the other set of cooling times. Therefore, we can safely ascribe each set of cooling times to the corresponding charge carrier. We observe that electrons cool slower than holes in agreement with our previous work.³²

Figure 4.

(a) Fit of eq 3 to f(t) for 1.77 eV photoexcitation of 3.9 nm PbSe QDs. (b) Separate electron and hole bleach as determined from the high energy L_4–6 (2.7 eV) and L_5–7 (2.5 eV) transitions described by the electron (L_4–6) and hole (L_5–7) contributions in eq 3c.

Equation 3c also yields the relative contribution A_e/A_h to f(t) of electrons and holes. We show A_e/A_h as a function of photoexcitation energy in Figure S3 of the Supporting Information. We find that A_e/A_h is approximately 1.2 for all photoexcitation energies up to 2.1 eV, comparable to the relative contribution of electrons and holes to the band edge bleach as determined in our previous work using an electron scavenging molecule.³² For photoexcitation energies exceeding 2.1 eV however, A_e/A_h increases to values up to 3. We believe that our model shown in Figure 3a is no longer valid at higher photoexcitation energy due to additional relaxation pathways for electrons and holes such as CM and the simultaneous excitation of various electron and hole states at different points in the band structure (e.g., with Σ or W character). We therefore no longer assign electrons and holes to the two contributions, but rather realize that we have a slow and a fast cooling component that consists of both electrons and holes. We point out that this happens above 2.1 eV photoexcitation energy where our results suggest that the electronic structures of both electrons and holes approach a quasi-continuum. The constant cooling times found between energy levels near the band edge remain valid.

The procedure described above yields the time constants for electron and hole cooling steps between successive discrete energy levels, as well as the cooling times from energies in the quasi-continuum to the highest discrete energy level that is distinguished. Taken together this constitutes a broadband cooling spectrum as shown in the upper panel of Figure 5. We also indicate the position of the optical transitions, as determined from the absorption spectrum in the lower panel of Figure 5 and include electron and hole cooling times as obtained from the L_4–6 and L_5–7 transitions, which agree with the data resulting from fitting eq 3 to f(t).

Figure 5.

Broadband cooling spectrum for 3.9 nm PbSe QDs for electrons (filled symbols) and holes (open symbols). The optical absorption spectrum with its second derivative is included to obtain the position of the optical transitions, as indicated by the vertical dashed lines. Data from the L_4–6 and L_5–7 transitions allow us to attribute cooling times to electrons or holes.

Figure 5 shows that the 1P–1S cooling times for electrons and holes are discrete and fully account for cooling up to hν ≈ 1.4 eV. At that point discrete 1D–1P cooling channels become available, followed by Σ–1D channels at hν ≈ 1.9 eV. From that point on the cooling times increase continuously as the density-of-states (DOS) forms a quasi-continuum. Figure 5 further shows that each individual hole cooling step is faster than the corresponding step for an electron. This agrees with our earlier finding that the total cooling time from high energy down to the band edge is shorter for a hole than for an electron.³² A second finding is the decrease of both the electron and hole cooling time constants on going from the lowest energy transition to higher transitions. The electron cooling time constants for transitions between discrete levels decrease slightly with energy but remain in the same order of magnitude of ∼0.5 ps. The hole cooling time constant for the first transition is slightly smaller than that for the electron. Interestingly, the hole cooling time constants for the next transitions are significantly shorter than the corresponding electron cooling time constants and have values within the ∼0.15 ps time resolution of our experiment.

Factors Governing Electron and Hole Cooling Times

According to calculations in the literature, emission of LO phonons mediates charge carrier cooling in PbSe QDs at high excess energy.^11,16,43 The energy of LO phonons in PbSe is ∼17 meV and the typical time of one LO phonon emission event in bulk PbSe is ∼25 fs.⁴³ For large charge carrier excess energy, the quasi-continuum of electronic states will contain levels with spacing (nearly) equal to an LO phonon energy and charge cooling via LO phonon emission can be efficient. However, for the lowest cooling steps near the band gap the energy difference between the discrete electronic states (>100 meV) is much larger than the LO phonon energy. To overcome these large electronic energy differences, each cooling step would require simultaneous emission of multiple LO phonons. Theoretical calculations show that this is very unlikely and would lead to cooling times in the order of nanoseconds, which is orders of magnitude longer than our findings.⁴⁴

In addition to LO phonon emission, charge carrier cooling can be facilitated by energy transfer to vibrational modes of the oleate ligands. In agreement with the latter it was found for CdSe QDs that ligands have a large influence on charge carrier cooling.^22,23 In Figure S4 of the Supporting Information we show an FTIR spectrum of our PbSe QDs with oleate ligands, revealing oleate vibrational modes in the energy range of 100–200 meV and near 350 meV (corresponding to the carbonyl stretch vibration and CH stretch vibrations in the aliphatic chain, respectively). We also show electronic transition energies as obtained from the optical absorption spectrum that overlap with the ligand vibration energies. Hence, energy transfer to ligand vibrational modes can facilitate charge carrier cooling near the band edge. Beside ligand vibrational modes, the surface of QDs also enables other strong phonon interactions that could assist charge carrier cooling.¹⁹

The above considerations do not explain why holes cool much faster than electrons. To gain more insight into carrier relaxation by LO phonon emission we calculate the PbSe bulk band structure and QD electronic structure using a k·p Hamiltonian with states around both the L-point and the Σ-point in the first Brillouin Zone of the rock-salt lattice.⁴⁵⁻⁴⁸ We parametrize this Hamiltonian using ab initio DFT to solve the Kohn–Sham equation for bulk PbSe in the CASTEP plane waves based parallel DFT code.^49,50 We use the TB-mBJ exchange potential with treatment of spin–orbit interactions at the scalar (or vector, see Supporting Information) relativistic level (see Methods).⁵¹ We show the calculated bulk band structure including a schematic QD electronic structure to incorporate our experimental cooling time constants in Figure 6. In Figure S5 of the Supporting Information we include a comparison of the calculated QD electronic structure with treatment of spin–orbit interactions both at the scalar and vector relativistic level showing the same qualitative behavior.

Figure 6.

PbSe bulk band structure (left) and schematic PbSe QD electronic structure (right) including our experimental cooling time constants.

From Figure 6 and Figure S5 of the Supporting Information we observe that the first electronic energy levels in the QDs in the conduction band arise predominantly from the bulk L-point, followed by energy levels that also have Σ-point character. This gives rise to a quasi-continuum. In the valence band the Σ-point is mixed into the QD electronic structure at much lower energy, resulting in a much lower onset of the quasi-continuum. As first suggested by Zunger et al.,⁵² this is caused by the smaller energy difference between the L and Σ extrema in the valence band than in the conduction band, which is also evident in Figure 6. The result is a higher DOS in the valence band than in the conduction band, in line with previous results from Zunger⁵² and Liljeroth,⁵³ resulting in faster hole cooling rates. These observations agree very well with the experimental cooling time constants and corresponding optical transitions in Figure 5.

To describe charge carrier cooling in the quasi-continuum, the energy loss rate γ of electrons and holes at high excess energy above the first Σ-point level can be obtained from the experiments using

4

where τ is the cooling time and hν is the photoexcitation energy. If it is assumed that the photon energy in excess of the band gap is equally distributed over the electron and the hole (admittedly a strong simplification considering the discussion above), the data in Figure 5 yield an energy loss rate for the electron of 1 eV/ps at low energy, increasing to 5 eV/ps at high energy. This seems reasonable considering previous calculations.^11,16,43 The hole cooling time is faster than the ∼0.15 ps experimental time resolution, leading to an energy loss rate of at least 8 eV/ps even near the bottom of the quasi-continuum. This very high energy loss rate for holes could be due to additional relaxation pathways such as CM not considered in eq 3. In addition, an asymmetric division of the energy between electron and hole due to the difference in DOS puts most energy in the electron, enhancing the apparent difference in energy loss rates. When photoexcitation occurs via the L_4–6 or the L_5–7 transition,³² all excess energy is transferred either to the hole or the electron and a very asymmetric division of energy is achieved. These effects occur above the Σ-point transition in the quasi-continuum and do not affect the cooling time constants we find between discrete energy levels near the band edge.

If charge carrier cooling in the quasi-continuum occurs solely due to emission of LO phonons with an energy of ∼17 meV,^11,16,43 the energy loss rate for electrons of 1–5 eV/ps leads to a net LO phonon emission time of 3.4–17 fs. Likewise the energy loss rate for holes of at least 8 eV/ps leads to a net LO phonon emission time <2.1 fs. Using the calculated electronic states from Figure S5, we can describe carrier relaxation in PbSe QDs through emission of LO phonons with the Wigner–Weisskopf description in the strong coupling regime (see Methods).⁵⁴ We assume LO phonon decay through the Ridley LO → TO + TA channel due to the large anharmonicity of LO phonons in the rock-salt structure (see Methods).⁵⁵⁻⁵⁷ We find the shortest LO phonon emission time for resonance of the transition energy with the LO phonon energy of 17 meV. This emission time is 3.6 fs and agrees well with our experimental energy loss rates mentioned above.

Conclusions

We identify five discrete cooling steps (three for electrons and two for holes) before the onset of a continuously increasing cooling time in PbSe QDs. The cooling time constants for both electrons and holes between discrete electronic states close to the band edge are of the order of 0.5 ps and require energy transfer to surface ligand vibrational modes or surface phonon modes. At high excess energy electrons and holes cool via emission of LO phonons due to the convergence of the electronic structure to a quasi-continuum. There the experimental energy loss rate is 1–5 eV/ps for electrons and at least 8 eV/ps for holes. These results agree well with theoretical carrier relaxation results. We find the start of the quasi-continuum for holes much closer to the band edge than for electrons and therefore confirm an asymmetric density-of-states for PbSe QDs. The results constitute the first broadband cooling spectrum for electrons and holes in colloidal nanocrystals.

Methods

Synthesis of PbSe QDs

PbSe QDs with a diameter of 3.9 nm were synthesized using the method described by Steckel et al.³³ In brief, 4.77 g of lead acetate trihydrate (99.999%, Aldrich), 3.42 g of oleic acid (90%, Aldrich) and 13.14 g of 1-octadecene (90%, Aldrich) were placed into a flask and dried and reacted under vacuum for at least 2 h at 120 °C. A second mixture containing 1.12 g of selenium (99.999%, Alfa Aesar), 0.13 mL of diphenylphospine (98%, Aldrich), and 14.87 mL of trioctylphosphine (90%, Fluka) was prepared. Subsequently, the lead mixture was heated to 180 °C under nitrogen and the selenium mixture was injected. The reaction was allowed to proceed for 10 s at 150 °C after which the reaction was quenched using 15 mL of butanol (99.8 anhydrous, Aldrich). The crude synthesis mixtures were washed twice by precipitating with methanol, centrifugation, and redispersion of the sediment in toluene. This resulted in particles with a diameter of 3.9 ± 0.3 nm as determined by TEM.

Hyperspectral TA Spectroscopy

We studied charge carrier cooling in PbSe QDs using broadband optical pump–probe spectroscopy. The QD samples were dispersed in toluene in a 2 mm stirred quartz cuvette at a typical optical density of 0.05 at the band gap. The QD dispersion was stirred during TA experiments to prevent photocharging.

Femtosecond laser pulses were generated in a Yb:KGW oscillator (Light Conversion, Pharos SP) at 1028 nm and amplified. A small fraction of the 1028 nm fundamental beam was split off to generate the broadband probe spectrum in a sapphire (500–1600 nm) or CaF₂ (375–600 nm) crystal. The probe pulse was delayed up to 2.5 ns using an automated delay stage. The majority of the 1028 nm fundamental beam was used as a pump pulse after nonlinear frequency mixing in an OPA and second harmonics module (Light Conversion, Orpheus) to achieve wavelengths of 310–1330 nm. The pump and probe pulses overlap on the sample position under an angle of ∼8 degrees, after which the pump pulse is dumped and the probe light is led to a detector suitable for the probe spectrum selected (Ultrafast Systems, Helios). We calculate the pump-induced change in absorption according to

5

with I₀ the intensity of the probe beam incident on the sample and I_on and I_off the intensity of the probe beam transmitted through the sample with the pump beam either on or off. All shown data is corrected for dispersion by fitting a polynomial function to the solvent response. The time resolution of the TA measurements is determined by the rise time of the TA signal at band edge excitation as shown in Figure S2 of the Supporting Information and is 0.15 ps.

In all experiments the laser pump fluence was taken sufficiently low to prevent multiple photons being absorbed in a single QD. Assuming Poissonian statistics for photoexcitation, the probability P_N for a QD to absorb N photons is given by

6

with the average number of photons absorbed per QD equal to ⟨N_abs⟩ = Jσ where J is the laser pump fluence and σ is the photon absorption cross section. During the measurements we take J low enough, so that P_N≥2 is negligible, that is, ⟨N_abs⟩ < 0.15, and P_N≥2 = 1 – P₀ – P₁ = 0.01.

Electronic Structure Calculations

We calculate the electronic structure of PbSe QDs using a k·p Hamiltonian with states around the L-point in the first Brillouin zone of the rock-salt lattice,⁴⁵⁻⁴⁸ augmented with states around the Σ-point. This Hamiltonian is parametrized using ab initio DFT (without fitting the band structure) to solve the Kohn–Sham equation in the CASTEP plane waves based parallel DFT code.^49,50 Many electron effects are approximated using the Tran-Blaha (TB-mBJ) exchange correlation functional as implemented in CASTEP.^47,51 Spin–orbit effects are taken into account at the scalar (vector) relativistic level. For parametrization of the k·p Hamiltonian we use the room temperature value of the effective masses at the L-point, while at the Σ-point we use those obtained from DFT.⁵⁸ This leads to good agreement between the experimental (∼110 meV if assumed equal for electron and hole) and theoretical (147 meV) 1P_e–1S_e transition. We find that the energetic difference between the top of the valence band at the Σ-point and the top of the valence band at the L-point is much smaller than the energetic difference between the corresponding band extrema in the conduction band. This results in a higher density-of-states in the valence band. Energy gaps and effective masses are given in the Supporting Information.

Electron–Phonon Scattering Calculations

To describe charge carrier cooling by the emission of LO phonons, we follow the Wigner–Weisskopf description in the strong coupling regime. This allows us to couple electrons to the LO phonon when the energy between electronic energy levels is not resonant with the LO phonon energy. We can then calculate the phonon emission rate by⁵⁴

7

Here Δ_if = E_i – E_f ± ℏω_LO is the detuning of the LO phonon energy ℏω_LO from the difference in energy between the initial and final electronic energy levels E_i and E_f, W_ph is the phenomenological rate of LO phonon decay into two less energetic phonons due to anharmonicity and g_if is the coupling strength of an electron to the LO phonon. Assuming the Fröhlich interaction for coupling between electrons and LO phonons g_if is given by

8

where n_LO is the phonon occupation number, F_if(q) = ⟨i|e^iqr|f⟩ is the electron–phonon coupling matrix element, and q is the phonon momentum vector. We take care of momentum conservation throug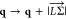h with 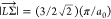∼ 0.544 Å^–1 while calculating τ_if^ph according to eqs 7 and 8. We assume that the Ridley LO → TO + TA channel is the most dominant LO phonon decay channel, significantly faster than any other channel such as Klemens or Vallee-Bogani,⁵⁵⁻⁵⁷ due to the large Grüneisen parameter of the TO mode in PbSe, γ(TO) = 15.⁵⁹ For this channel we estimate W_ph ∼ 277 ps^–1 at room temperature.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b02506.

• Detailed comparison between integration of TA spectra and the fitting method of eq 2 that we apply to show the identical time evolution of the band edge bleach found from these methods; determination of the rise time of f(t) for band edge excitation; information on the relative contribution of the electron and hole components in our fit model as a function of excitation energy; FTIR spectrum showing the energy of vibrational modes in the QD ligands that overlap with transitions between discrete electronic energy levels of the QD; calculations of the PbSe QD electronic structure taking spin–orbit interactions into account at the scalar and vector relativistic levels (PDF)

Author Contributions

The experiments and fits were performed by F.C.M.S. Calculations were done by S.T. A.J.H. and L.D.A.S. managed the project.

The authors declare no competing financial interest.