Abstract
Objectives
Static radiostereometric analysis (RSA) using implanted markers is considered the most accurate system for the evaluation of prosthesis migration. By using CT bone models instead of markers, combined with a dynamic RSA system, a non-invasive measurement of joint movement is enabled. This method is more accurate than current 3D skin marker-based tracking systems. The purpose of this study was to evaluate the accuracy of the CT model method for measuring knee joint kinematics in static and dynamic RSA using the marker method as the benchmark.
Methods
Bone models were created from CT scans, and tantalum beads were implanted into the tibia and femur of eight human cadaver knees. Each specimen was secured in a fixture, static and dynamic stereoradiographs were recorded, and the bone models and marker models were fitted to the stereoradiographs.
Results
Results showed a mean difference between the two methods in all six degrees of freedom for static RSA to be within -0.10 mm/° and 0.08 mm/° with a 95% limit of agreement (LoA) ranging from ± 0.49 to 1.26. Dynamic RSA had a slightly larger range in mean difference of -0.23 mm/° to 0.16 mm/° with LoA ranging from ± 0.75 to 1.50.
Conclusions
In a laboratory-controlled setting, the CT model method combined with dynamic RSA may be an alternative to previous marker-based methods for kinematic analyses.
Cite this article: K. Stentz-Olesen, E. T. Nielsen, S. De Raedt, P. B. Jørgensen, O. G. Sørensen, B. L. Kaptein, M. S. Andersen, M. Stilling. Validation of static and dynamic radiostereometric analysis of the knee joint using bone models from CT data. Bone Joint Res 2017;6:376–384. DOI: 10.1302/2046-3758.66.BJR-2016-0113.R3.
Keywords: Radiostereometric analysis, Dynamic, CT bone model
Article focus
Validation of the accuracy of a method using CT bone models for measuring knee joint kinematics in static and dynamic radiostereometric analysis using the marker method as the benchmark.
Key messages
Our results show that the accuracy of the CT model method combined with static and dynamic radiostereometry is sufficient when examining large joints. However, for the method to be truly effective, an automated analysis method should be developed.
The CT model method could be the preferred method in future kinematic studies of large joints, since no implanted markers are needed.
Limitations
Eight donor legs were used for this study, and potentially the small sample size may have lead to an overestimation of the accuracy.
The following processes were automated, and the reproducibility of the processes was therefore not investigated: CT segmentation of the bone model; placing the anatomical coordinate system; detection and creation of the marker model.
The comparison of the model method and the marker method was not blinded.
Introduction
To perform kinematic analysis of joints, an accurate and reliable method of tracking bone movement is needed.1 In radiostereometric analysis (RSA), tantalum markers are inserted into the bone during surgery to track the bones with stereoradiographs. This is currently widely used to monitor implant fixation and wear over time.2-4 RSA measurements have been shown to be very precise at the submillimetre level.2,5,6
Dual-plane fluoroscopy using CT bone models has been used to record and calculate knee joint kinematics without markers.7-9 In 2003, a model-based RSA method was introduced, allowing prosthesis tracking without the use of markers at the expense of a slight loss of accuracy.10,11
The accuracy of dynamic RSA using CT bone models is expected to be similar to that of dynamic RSA using models of prostheses, which would be acceptable in studies examining movements of large joints. The CT-bone-model-RSA method would be superior to skin marker-based joint kinematic measurements that are exposed to soft-tissue artefacts.1,12,13 Furthermore, the model method enables kinematics and stability comparisons between pre-operative and post-operative, and injured and healthy joints without the need to insert bone markers.
The purpose of this study was to evaluate the accuracy of the CT model method for measuring knee joint kinematics with static and dynamic RSA, using the marker method as the benchmark.
Materials and Methods
Specimens and dissection
Eight paired fresh-frozen human (four female, four male) cadaver legs, including foot, knee and hemipelvis, were used for this study. Two of the donor knees had degenerative changes. The mean age of the specimens was 77 years (58 to 94).
Preparations for the RSA analysis
A bead insertion instrument (Kulkanon; Wennbergs Finmek AB, Gunnilse, Sweden) was used to place eight to 12 1 mm tantalum beads, broadly distributed, in the cortical bone of femur and tibia, approximately 5 cm from the joint line, through a 4 mm drill hole on the lateral side of the proximal tibia and the medial side of the distal femur.
CT bone model
The intact frozen leg specimens were scanned in a Phillips Brilliance 40 CT scanner, (Phillips, Amsterdam, The Netherlands) using axial slices (120 kVp, 150 mAs, slice thickness = 0.9 mm, slice increment = 0.45 mm, pixel size = 0.39 mm × 0.39 mm). The bone models were constructed using an automatic graph-cut segmentation method.14,15 The method uses eigen analysis of the Hessian matrix to identify the sheet-like structure of the bone surface and formulate a sheetness measure, which is subsequently used in a graph-cut optimisation.16
The reconstructed bone models (Fig. 1) included approximately 15 cm of both the distal femur and proximal tibia. For each bone model, a local coordinate system was created using a modified version of the automatic method introduced by Miranda et al,17 where the diaphysis was fitted using a cylinder instead of the principal component analysis used by Miranda et al.17
Fig. 1.
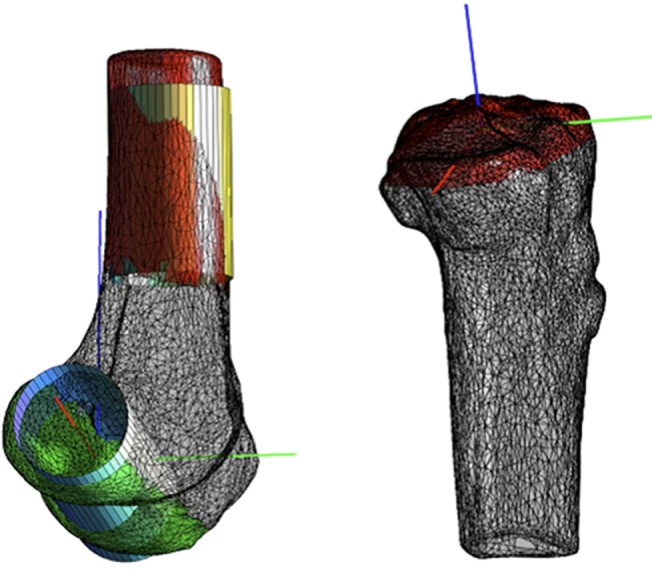
CT bone model of the femur to the left, and the tibia to the right, with their local coordinate systems (red = laterally, green = anteriorly and blue = proximally). Colored areas and cylinders were used for placing the coordinate systems. The colored bone areas were used to fit the cylinders and the medial-lateral axis (red axis) and the proximal-distal axis (blue axis) was determined from the cylinders.
Experimental set-up and equipment
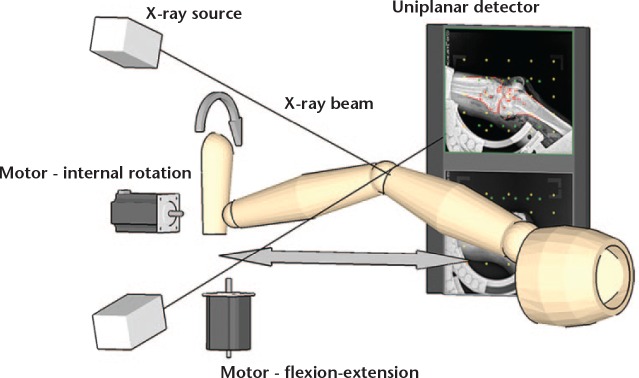
A custom-built motorised fixture was constructed to support the thigh and lower leg while the area of the knee was kept completely free of materials to avoid image artefacts. The hemipelvis was fixed to the base of the apparatus using three regular screws in the sacrum, iliac crest and pubic bone. The foot and ankle joint were fixed in a standard Pro+ Fixed Walker (VQ OrthoCare, Irvine, California). A stepper motor (NEMA 23, 3 Nm; National Instruments, Austin, Texas) was installed, along with pulley wheels, a timing belt and two linear slides to perform the controlled dynamic knee flexion movement from 0° to 60° of flexion and back at 0.1 m/s. Due to limitations in the size of the system’s region of interests (window of recording), the recorded knee flexion angles were limited to be from 0° to 60°. Another NEMA 23 motor was mounted to the foot rest, making the internal rotation of the foot automatic at a speed of 0.001 m/s. The slow speed enabled a manual stop of the motor when the desired torque was reached. The torque was measured using a torque sensor (TQ 201-500; OMEGA, Norwalk, Connecticut) (accuracy = ± 0.15%, repeatability = ± 0.03%) and an adjacent meter (DP25B-S-230; OMEGA). Both motors were controlled using a driver (DM542A; Longs Motor, Changzhou, China) and a breakout board (DB25; Shanghai Sunwin International Trading Co. Ltd, Shanghai, China). Figure 2 shows a schematic of the set-up.
Fig. 2.
Schematic drawing of the set-up, showing how the tubes are positioned in front of the knee, while the detectors are located behind the knee. The two motors are visualising how the knees are moved during the dynamic recording.
Radiographic set-up
The stereoradiographs were recorded using a dynamic RSA system (Adora RSAd; Nordisk Røntgen Teknik A/S, Hesselager, Denmark). A sampling frequency of ten frames per second, a vertically placed calibration box with uniplanar detectors (Box 14; Medis Specials B.V., Leiden, The Netherlands) and a vertical tube set-up (± 16° tube angle to horizontal) were used to maximise the visualisation of the knee joint line during movement. The full detector size of 37 cm (horizontal) x 42 cm was used for each detector to record the knee movement from 0° to 60° of knee flexion. The source image distance was 2.94 m and the focus skin distance was 2.4 m, and were chosen to increase the region of interest. The exposure settings for static radiographs were 70 kV and 10 mAs. For the dynamic radiographs, they were 90 kV, 500 mA, 2.5 ms Roentgen pulse width and a synchronisation delay between tubes of approximately 0.002 ms (maximum allowed by the system = 0.1 ms). The resolution of the static radiographs was 2208 × 2688 pixels (0.16 mm/pixel) and for the dynamic radiographs it was 1104 × 1344 pixels (0.32 mm/pixel). The difference in resolution is due to limitations of the RSA system.
Test protocol
Step 1: Static stereoradiographs were recorded with the donor legs positioned in 0°, 30° and 60° of knee flexion measured with a goniometer. Internal rotation torque of 4 Nm was applied to the foot to simulate a loaded knee before recording. Step 2: dynamic RSA series (ten frames per second) were recorded in two successive runs of motorised driven knee movement (0.08 m/s) from 0° to 60° of knee flexion. Internal rotation torque of 4 Nm was applied to the foot before recording, and the internal rotation angle achieved was maintained throughout the sequence, meaning that the applied internal torque varied during the recording. Step 3: the leg was repositioned, and steps 1 and 2 were repeated. The specimens were simultaneously used in another study that assessed ligament stability in five situations, where the anterior cruciate ligament (ACL) and the anterolateral ligament (ALL) were successively cut, reconstructed and compared with the intact knee. A total of eight (legs) × three (flexion angles) × two (double examinations) × five (ligament situations), or, 240 static radiographs were recorded.
From the dynamic series, radiographs were selected to match the static radiographs with knee flexion angles of 0°, 30° and 60°, as determined by the model positions of the tibia and femur during radiographic image analysis in model-based RSA (MBRSA). Two ligament situations were used, resulting in a total of 96 dynamic radiographs (eight legs × three angles × two ligament situations × two examinations).
Analysis of the radiographs
Of the 240 planned static radiographs and 96 dynamic stereoradiographs, 228 static and 89 dynamic radiographs were used. Six static and three dynamic trials were not recorded due to error, and in six static images and four dynamic trials, the fixture was positioned incorrectly. Of the 228 static radiographs, 139 (60% of the 240, minus exclusions) were used to obtain a good alignment between the local coordinate systems of the model method and the marker method. The remaining 89 (40%, minus exclusions) static and dynamic radiographs were used to calculate the difference between the model method and the marker method.
The static and dynamic radiographs were analysed using the commercially available software, model-based RSA version 4.02 (RSAcore, Leiden, The Netherlands). Model-based RSA automatically detects the bone contours and an operator needs to select the contours to be included in the pose estimation algorithm. The selected contours (Fig. 3) for the femur were the shaft, condyles and the articular surface, while for the tibia the shaft, eminences and the medial and lateral plateau were selected. The process of fitting the bone models to the radiographs was done by two observers (KS-O, ETN), who, in a previous pilot study, fitted 25 femur and tibia bone models, and together developed a consistent workflow to ensure that the same contours were used as much as possible.
Fig. 3.
Left: static radiographic image. Right: dynamic radiographic image. The magnified images show the resolution in the static image being twice that of the dynamic image. The yellow and green circles indicate the fiducial and control markers in the calibration box. The dynamic radiograph is inverted compared with the static radiograph and is a standard setting of the radiostereometric analysis system, which was not changed prior to the recordings, however, this difference poses no issues in analysis of the radiographs.
The three algorithms of the MBRSA software18 were applied and used to estimate the pose of each CT model by minimising the matching error between the virtual projection of the bone model and the detected projection (contours) in the radiograph.
The mean error of rigid body fitting is used to assess the mean error of marker detection between frames within a rigid body, and is recommended to be below 0.35 mm.19 The mean condition number is used to ensure an acceptable scatter of the injected markers, and is recommended to be below 120 in studies of the knee.19,20 The average mean error and the condition number for femur and tibia were calculated in 89 static and 89 dynamic radiographs.
Inter- and intra-observer reliability measurements of the manual contour selection
Inter- and intra-reliability measurements were performed of the manual contour selection and were completed by three observers (KS-O, PBJ, ETN). The observers (‘Obs.’) were categorised as: experienced (Obs. 1 with more than 500 RSA analyses); less experienced (Obs. 2 with more than 300 RSA analyses); and inexperienced (Obs. 3 with more than 50 RSA analyses). For both static and dynamic radiographs, three of the previously analysed radiographs (0°, 30° and 60°) from each of the eight knees (n = 24) were used. Each of the selected 24 static and 24 dynamic radiographs was re-analysed twice (series 1 and series 2), one week apart, by all observers. The original image calibration and marker model were kept intact in the radiographs, while the manual contour selection was redone and, therefore, the only possible difference in accuracy would be due to differences in the bone model translation and rotation. After both analyses, the bone model kinematic translation and rotation were extracted in all six degrees of freedom (6DOF).
Statistical analysis
The raw kinematic data from the MBRSA were extracted and processed in custom-developed software (MATLAB R2015b; MathWorks, Natick, Massachusetts).
For the following two statistical comparisons of the marker method and the model method, a mixed model was used, taking into account the repeated measurements on cadaver, pair, knee flexion angle, ligament combination and repetitions. Model validation was performed by visually inspecting the residuals and fitted values. Wald tests were used to analyse the systematic difference using a 0.05 level of significance.
To compare the bones individually, we calculated the error in translation and rotation between the marker method and the model method using the Pythagorean theorem:
, with x, y and z being the error for either translations or rotations. Normally, the Pythagorean theorem cannot be used for rotations, but since the error in rotations is small, it is a good approximation.2 The measured knee movement between the marker method and the model method was illustrated using Bland-Altman plots.21
The mean error of rigid body fitting in the femur and tibia was compared between static and dynamic radiographs using a Student’s t-test.
For the intra-observer reliability measurements, the two image series from each observer were compared using the intraclass correlation coefficient (ICC) and 95% confidence intervals (CIs). For the inter-observer reliability measurements, the three observers were compared using the ICC and 95% CIs.
Results
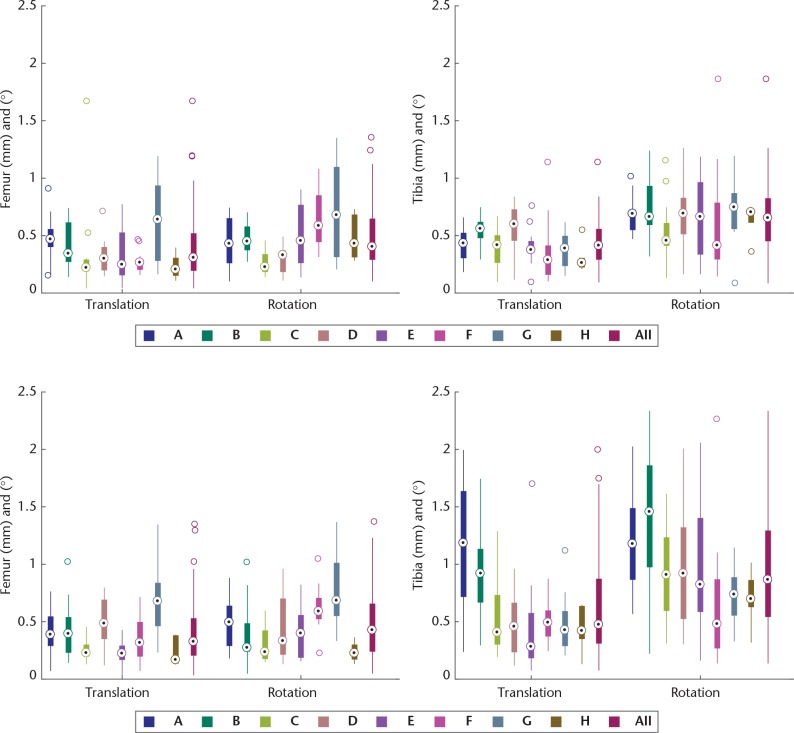
Figure 4 illustrates, for each leg, the error in translation and rotation between the model method and the marker method in both static and dynamic radiographs. The box to the far right marked “all” combines the errors of all legs, and Table I shows the statistical outcome of these combinations. The maximum mean error in translation was 0.62 mm and 0.96° for rotations. The femur had a significantly lower error rate compared with the tibia in all examined groups except for translation in static radiographs. Comparing static and dynamic radiographs, the errors in the dynamic radiographs were significant for the tibia, while errors of the femur were not significant.
Fig. 4.
The upper boxplots show the combined three-axis translation error and three-axis rotation error between the model method and the marker method in the static radiographs, while the lower boxplots illustrate the dynamic radiographs. Each box displays the median, the 25th and 75th percentiles, while the whiskers extend to the most extreme points not considered outliers. Circles are outliers > ± 2.7 standard deviations. Each bar (A-H) is a donor leg and the bar marked “all” is data from all the cadavers combined. A-B, C-D, E-F and G-H are paired legs from the same subject.
Table I.
Mean error of the boxes marked “all” from Figure 4. The p-value indicates the comparison of static and dynamic radiographs in the upper part of the table, while the total error of femur and tibia are compared in the lower part of the table. The statistics were calculated using the mixed model. All values presented as mean (confidence interval)
| Mean error | p-value | ||
|---|---|---|---|
| (n = 89) | Static | Dynamic | |
| Femur – translation (mm) | 0.384 (0.284 to 0.484) | 0.391 (0.296 to 0.487) | 0.833 |
| Femur – rotation | 0.477° (0.349° to 0.605°) | 0.479° (0.389° to 0.610°) | 0.948 |
| Tibia – translation (mm) | 0.425 (0.344 to 0.506) | 0.619 (0.506 to 0.733) | 0.000 |
| Tibia – rotation | 0.659° (0.571° to 0.746°) | 0.960° (0.840° to 1.081°) | 0.000 |
| Femur | Tibia | ||
| Static – translation (mm) | 0.387 (0.317 to 0.457) | 0.429 (0.375 to 0.482) | 0.190 |
| Static – rotation | 0.483° (0.358° to 0.608°) | 0.665° (0.531° to 0.799°) | 0.000 |
| Dynamic – translation (mm) | 0.391 (0.291 to 0.490) | 0.620 (0.496 to 0.743) | 0.000 |
| Dynamic – rotation | 0.469° (0.381° to 0.557°) | 0.955° (0.823° to 1.087°) | 0.000 |
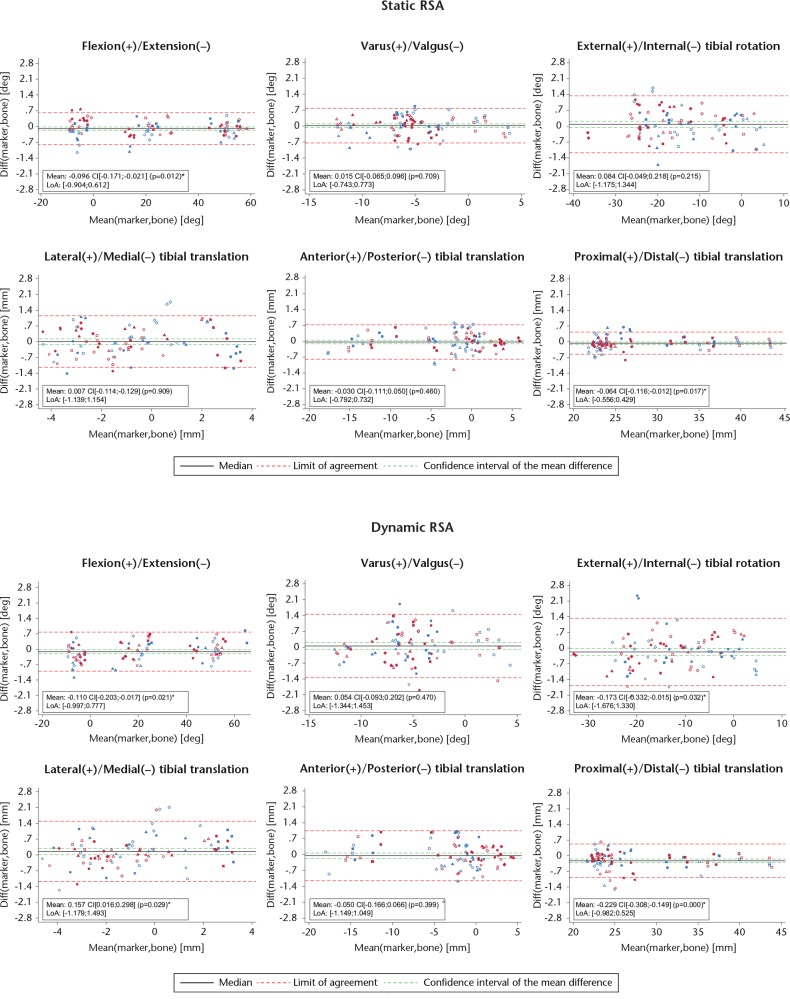
The mean differences between the model method and marker method of the 6DOF measured knee movement in the static and dynamic radiographs are shown in the Bland-Altman (BA) plots in Figure 5. The BA plot for the static radiographs demonstrated a mean difference for all three rotations within -0.10° to 0.08° and a limit of agreement (LoA) in the range of ± 0.76° to 1.26°, while for the three translations, the mean was within -0.06 mm to 0.007 mm, LoA ± 0.49 mm to 1.15 mm. The dynamic radiographs showed a mean difference for the three rotations within -0.17° to 0.05°, LoA ± 0.89° to 1.50° and for the three translations, the mean difference was within -0.23 mm to 0.16 mm, LoA ± 0.75 mm to 1.34 mm. The individual means and LoAs are presented in each subplot in Figure 5. The differences in the means between the static and dynamic radiographs were small, while there was a tendency towards the dynamic radiographs having a larger LoA in all 6DOF. Visual inspections of the BA plots for all 6DOF confirmed no concentration of observations and therefore no effect of either DOF or difference between the intact and the ligament deficient knee.
Fig. 5.
The upper Bland-Altman (BA) plots show the CT bone model compared with the marker method of the static radiographs in all six degrees of freedom, while the lower BA plots show data from the dynamic radiographs. Circles, 0°, Crosses, 30°, Squares, 60°. Blue observations, intact knee. Pink observations, with both the anterior cruciate ligaments and anterolateral ligaments cut. The p-value indicates if the mean is significantly different from zero (CI, confidence interval; LoA, limit of agreement).
The Roentgen system’s post-processing software optimised continuously the image contrast of each radiograph during the dynamic sequences. Depending on the amount of the metal fixture visible in the radiograph, the image contrast changed, making the bone model less visible. The highest amount of metal was included in 60° of knee flexion. With reduced clarity of the bone model, the edge detection during analysis was harder due to some “washed out” bone edges. The contrast also changed in the static radiographs, but due to their high quality we did not experience difficulties with edge detection.
The mean error in rigid body fitting of the femur in static and dynamic radiographs was 0.046 mm and 0.060 mm (p = 0.003), respectively, and for the tibia in static it was 0.071 mm and dynamic, 0.080 mm (p = 0.116, Student’s t-test).
The mean condition number and standard deviation for the femur were 29.5 ± 19.1 and for the tibia 29.8 ± 19.9, indicating a good scatter of the markers.
The intraclass correlation coefficient (ICC) for intra-observer reliability in the static radiographs was 0.98 (95% CI 0.96 to 0.99), or better, for all observers in all 6DOF. The ICC for inter-rater reliability for static radiographs was 0.99 (95% CI 0.98 to 1.00), or better, when comparing the kinematic results between all three observers in the 6DOF.
For the dynamic radiographs, the ICC for intra-observer reliability was 0.86 (95% CI 0.68 to 0.94), or better, for all observers. The ICC for inter-rater reliability among all observers was 0.95 (95% CI 0.90 to 0.98), or better, in the dynamic radiographs.
It should be noted, that the less experienced observer made a mistake during the manual bone contour detection in one dynamic radiograph, which resulted in a translation error of -5.43 mm between the tibia bone model and marker model.
The mean difference between the model method and marker method of the 6DOF measured knee movement in the static and dynamic radiographs was compared between all observers. In six of the 18 comparisons of static radiographs, a significant difference in the mean was found. No significant difference in the mean was found in the 18 comparisons in dynamic radiographs between observers.
Discussion
This study evaluated the accuracy of the CT model method for measuring knee joint kinematics in static and dynamic RSA, using the marker method as the benchmark. As expected, the results generated with the model method differed from those with the marker method.
The mean difference between the model method and the marker method (systematic error) of all 6DOF in the kinematic analysis of the knee joint was found to be 0.23 mm/°, or better, for both dynamic and static radiographs. The random error in terms of 95% LoA was largest in both static RSA ±1.3° and dynamic RSA ±1.5° in internal/external tibial rotation. This is to be expected since the model method is generally less accurate for rotation about the long axis due to the cylindrical shape of long bones. The second and third largest LoA in dynamic RSA was found in medial-lateral translation and varus-valgus rotation, respectively. These directions were out-of-plane, which previously have been reported to have inferior accuracy to in-plane movement.10 For the static RSA, the out-of-plane medial-lateral translation had the second largest LoA, as expected, while the in-plane anteroposterior tibial translation had a slightly larger LoA compared with the out-of-plane varus-valgus rotation.
The LoA of the three in-plane DOF in static radiographs was ±0.8 mm or better, while for the dynamic radiographs it was ±1.1 mm or better. The LoA was larger in all 6DOF when comparing the error of the dynamic with the static radiographs, which is similar to the results reported by Anderst et al7 when using biplane fluoroscopy and bone models. Compared with that study,7 the present study found better or similar results for accuracy with dynamic RSA and bone models, while for static RSA and bone models our results were generally better for rotations, and generally worse for translations.
A comparison of the marker method versus model method in dynamic and static radiographs (Table I) for the two bones showed that the femur generally had a significantly lower mean total error compared with the tibia. This difference might be explained by the large size of the femoral condyles, compared with the tibial plateau containing the eminences, which are smaller bone parts and harder to locate on the radiographs. The result of the mean total difference between the femur marker method and model method did not differ when comparing dynamic and static radiographs as it did for the tibia. A difference between static and dynamic radiographs was expected for both bones due to motion artefacts and the difference in resolution between the two types of radiograph.
For both the static and dynamic radiographs, the mean rigid body errors were within the limit of 0.35 mm that are normally used in RSA. The mean error of the markers was significantly higher for the femur in the dynamic radiographs compared with that in the static radiographs, while it was not for the tibia. This difference may be due to two things: first, the lower resolution of the dynamic radiographs results in less accurate marker projection detection; and second, the motion artefacts of the bone moving in the dynamic radiographs results in less accurate marker projection detection. We suspect the lower resolution has the greater influence as the leg moved very slowly compared with the 2.5 ms pulse width, and the Roentgen tubes were synchronised within 0.002 ms with a maximum possible allowed time delay of 0.1 ms.
A probable cause for the observed difference in error for the tibia between static and dynamic radiographs could be the anatomical shape of the tibia bone. The pose estimation of the tibia might have been less accurate, due to poorer software recognition of the tibial plateau and eminences when detecting edge contours. Furthermore, the model method was sensitive to image contrast changes which inevitably occurred when the metal fixture moved into the image during knee flexion. This automatic contrast adjustment of the Roentgen system may also have had a negative effect on the visibility of thin bone parts of the tibial plateau as compared with the thicker cortical bone of the femoral condyles.
The Bland-Altman plots confirmed no concentration of observations, which was possible, since the clarity of the bone model was reduced with the metal fixture gradually moving into the image. Thus, the difference between the model method and the marker method could have been greatest at 60°. Additionally, no concentration was found between the intact knees and the knees with ACL and ALL ligament removed, confirming the model method to be reliable in measurements of the knee joint with different ligament situations.
Both the intra- and inter-observer reliability measurements for the manual contour detection in static and dynamic radiographs were very good. These results are similar to the results found in a study using model-based RSA to detect hip arthroplasty wear, where the correlation in both intra- and inter-observer reliability measurements was 0.997, or better, in all cases.22
However, in the present study, the ICC calculated by observer 2 for medial-lateral tibial translation in the dynamic radiographs was notably lower than the rest of the calculated ICCs, and was 0.86 (95% CI 0.68 to 0.94). The lower ICC score was due to a mistake during analysis of one radiograph, which resulted in a translation error of -5.43 mm between the tibia bone model and marker model. We did not re-analyse the radiograph, but it was detected as an outlier during the kinematic calculations, and could normally have been re-analysed. By removing this single erroneous radiograph from the ICC calculation, the ICC increased from 0.86 (95% CI 0.68 to 0.94) to 0.98 (95% CI 0.95 to 0.99).
High correlations were expected in the present study, as the bone contours are detected automatically by the software and only have to be selected by the observer. As the contours are clickable, the “correct” contours are easy to select, and we would expect lower correlations if the observers were to draw the bone contours themselves instead of selecting them.
The mean kinematic difference between the marker method and the model method was calculated for the first series of analysis by each observer. These differences were calculated in order to investigate whether one observer was significantly more accurate than the others. Ultimately, no observer was found to be better than the others, regardless of their different experience level with model-based RSA.
It is not easy to compare our results with previously reported results. Most studies have either used biplane fluoroscopy and bone models,7,23,24 RSA combined with metal prosthesis models,10,25 or bone models alone,26 while, to our knowledge, no accuracy studies have been reported using dynamic RSA and bone models. Metal prosthesis models have clear edges for contrast detection while bones differ due to bone quality, and comparisons between these methods are therefore not valid. The accuracy results of the study by Seehaus et al26 are inferior to the results presented in the current study, which is most likely caused by cutting away the proximal tibia and distal femur for the placement of a knee prosthesis.
Knowledge of the accuracy and limitations of both the marker method and the model method will help us in choosing the most appropriate method in future studies. The marker method is still the benchmark (markers = submillimetre precision), but the advantage of the model method is that measurements are also possible pre-operatively without implanted markers. In addition, the bone model offers a good non-invasive alternative method for measurements of in vivo knee kinematics, and no other similarly precise methods or tools are available. However, even though no implanted markers are needed, it is important to consider the additional required CT radiation dose before applying this method to patients. Furthermore, researchers should be encouraged to perform relatively short dynamic experiments using live tissue.
In future, we believe the bone model method could be used for in vivo studies of knee joint kinematics performed at a slow pace, and could potentially be developed further for clinical use as a diagnostic tool for assessment of ligament laxity. However, for the method to be truly effective, an automated image analysis system with minimal human interaction is required, since the time spent on manual analysis is prohibitive.
In summary, this study found the mean error of CT bone models combined with static RSA to be -0.001°, with a maximum LoA in rotations of ± 1.26° or better, while for translations it was -0.03 mm and LoA ± 1.15 mm or better. For the dynamic radiographs, the mean error for rotations was -0.11° ± 1.50° or better, and -0.04 mm LoA ± 1.34 mm or better for translations. These results may encourage the use of bone models and dynamic RSA for non-invasive kinematic knee joint analysis in the future. In conclusion, the CT model method combined with dynamic RSA may be an alternative to prior marker-based methods for kinematic analyses in a laboratory-controlled setting.
Footnotes
Author Contribution: K. Stentz-Olesen: Substantial contribution to the research design, Acquisition of data, Analysis and interpretation of data, Writing the first draft of the paper.
E. T. Nielsen: Substantial contribution to the research design, Acquisition, analysis and interpretation of data, Revising the paper critically.
S. De Raedt: Substantial contributions to research design, Analysis of data, Interpretation of data, Revising the paper critically.
P. B. Jørgensen: Substantial contribution to the research design, Acquisition of data, Revising the paper critically.
O. G. Sørensen: Substantial contribution to the research design, Acquisition of data, Revising the paper critically.
B. L. Kaptein: Substantial contributions to analysis and interpretation of data, Revising the paper critically.
M. S. Andersen: Substantial contributions to analysis and interpretation of data, Revising the paper critically.
M. Stilling: Substantial contribution to the research design acquisition of data, Interpretation of data, Revising the paper critically.
ICMJE Conflicts of Interest: None declared
Funding Statement
This work was supported by six funds: Innovation Fund Grant 69-2013-1 “Transforming radiological technology for assessment of implant fixation: from research tool to clinical application”; Civilingeniør Frode V. Nyegaard og Hustrus fond; Ortopædkirurgisk forskningsfond i Aarhus; A.P Møller Fonden – Fonden til Lægevidenskabens fremme; Grosserer L. F. Foghts Fond; Helga og Peter Kornings Fond. These six funds had no influence on the study design or the results.
References
- 1. Benoit DL, Ramsey DK, Lamontagne M, et al. Effect of skin movement artifact on knee kinematics during gait and cutting motions measured in vivo. Gait Posture 2006;24:152–164. [DOI] [PubMed] [Google Scholar]
- 2. Selvik G. Roentgen stereophotogrammetry. A method for the study of the kinematics of the skeletal system. Acta Orthop Scand Suppl 1989;232:1–51. [PubMed] [Google Scholar]
- 3. van Embden D, Stollenwerck GA, Koster LA, et al. The stability of fixation of proximal femoral fractures: a radiostereometric analysis. Bone Joint J 2015;97-B:391–397. [DOI] [PubMed] [Google Scholar]
- 4. Molt M, Toksvig-Larsen S. 2-year follow-up report on micromotion of a short tibia stem. Acta Orthop 2015;86:594–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kärrholm J. Roentgen stereophotogrammetry. Review of orthopedic applications. Acta Orthop Scand 1989;60:491–503. [DOI] [PubMed] [Google Scholar]
- 6. Bojan AJ, Bragdon C, Jönsson A, Ekholm C, Kärrholm J. Three-dimensional bone-implant movements in trochanteric hip fractures: precision and accuracy of radiostereometric analysis in a phantom model. J Orthop Res 2015;33:705–711. [DOI] [PubMed] [Google Scholar]
- 7. Anderst W, Zauel R, Bishop J, Demps E, Tashman S. Validation of three-dimensional model-based tibio-femoral tracking during running. Med Eng Phys 2009;31:10–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Tashman S, Anderst W. In-vivo measurement of dynamic joint motion using high speed biplane radiography and CT: application to canine ACL deficiency. J Biomech Eng 2003;125:238–245. [DOI] [PubMed] [Google Scholar]
- 9. Anderst WJ, Baillargeon E, Donaldson WF, Lee JY, Kang JD. Validation of a noninvasive technique to precisely measure in vivo three-dimensional cervical spine movement. Spine (Phila Pa 1976) 2011;36:E393–E400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kaptein BL, Valstar ER, Stoel BC, Rozing PM, Reiber JHC. A new model-based RSA method validated using CAD models and models from reversed engineering. J Biomech 2003;36:873–882. [DOI] [PubMed] [Google Scholar]
- 11. Valstar ER, De Jong FW, Vrooman HA, Rozing PM, Reiber JHC. Model-based Roentgen stereophotogrammetry of orthopaedic implants. J Biomech 2001;34:715–722. [DOI] [PubMed] [Google Scholar]
- 12. Stagni R, Fantozzi S, Cappello A, Leardini A. Quantification of soft tissue artefact in motion analysis by combining 3D fluoroscopy and stereophotogrammetry: a study on two subjects. Clin Biomech 2005;20:320–329. [DOI] [PubMed] [Google Scholar]
- 13. Garling EH, Kaptein BL, Mertens B, et al. Soft-tissue artefact assessment during step-up using fluoroscopy and skin-mounted markers. J Biomech 2007;40(Suppl 1):S18-S24. [DOI] [PubMed] [Google Scholar]
- 14. Krcˇah M, Székely G, Blanc R. Fully automatic and fast segmentation of the femur bone from 3D-CT images with no shape prior. https://www.vision.ee.ethz.ch/en/publications/papers/proceedings/eth_biwi_00818.pdf (date last accessed 15 May 2017).
- 15. De Raedt S, Mechlenburg I, Stilling M, et al. Automated measurement of diagnostic angles for hip dysplasia. SPIE Proceedings 2013;8670. [Google Scholar]
- 16. Boykov Y, Funka-Lea G. Graph cuts and efficient N-D image segmentation. Int J Comput Vis 2006;70:109–131. [Google Scholar]
- 17. Miranda DL, Rainbow MJ, Leventhal EL, Crisco JJ, Fleming BC. Automatic determination of anatomical coordinate systems for three-dimensional bone models of the isolated human knee. J Biomech 2010;43:1623-1626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Kaptein BL, Valstar ER, Stoel BC, Rozing PM, Reiber JHC. Evaluation of three pose estimation algorithms for model-based roentgen stereophotogrammetric analysis. Proc Inst Mech Eng H 2004;218:231–238. [DOI] [PubMed] [Google Scholar]
- 19. Valstar ER, Gill R, Ryd L, et al. Guidelines for standardization of radiostereometry (RSA) of implants. Acta Orthop 2005;76:563–572. [DOI] [PubMed] [Google Scholar]
- 20. No authors listed. Implants for surgery — Roentgen stereophotogrammetric analysis for the assessment of migration of orthopaedic implants. https://www.iso.org/obp/ui/#iso:std:iso:16087:ed-1:v1:en (Date last accessed 15 May 2017).
- 21. Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res 1999;8:135–160. [DOI] [PubMed] [Google Scholar]
- 22. Pineau V, Lebel B, Gouzy S, Dutheil JJ, Vielpeau C. Dual mobility hip arthroplasty wear measurement: experimental accuracy assessment using radiostereometric analysis (RSA). Orthop Traumatol Surg Res 2010;96:609–615. [DOI] [PubMed] [Google Scholar]
- 23. Li G, Van de Velde SK, Bingham JT. Validation of a non-invasive fluoroscopic imaging technique for the measurement of dynamic knee joint motion. J Biomech 2008;41:1616–1622. [DOI] [PubMed] [Google Scholar]
- 24. Tashman S, Bey MJ, Anderst W, Demps E, Zauel R. Model-based tracking of knee kinematics from biplane radiographs: in-vivo validation [abstract]. Orthopaedic Research Society, 52nd Annual Meeting, Chicago, Illinois, 2006. [Google Scholar]
- 25. Hurschler C, Seehaus F, Emmerich J, Kaptein BL, Windhagen H. Comparison of the model-based and marker-based roentgen stereophotogrammetry methods in a typical clinical setting. J Arthroplasty 2009;24:594–606. [DOI] [PubMed] [Google Scholar]
- 26. Seehaus F, Olender GD, Kaptein BL, Ostermeier S, Hurschler C. Markerless Roentgen Stereophotogrammetric Analysis for in vivo implant migration measurement using three dimensional surface models to represent bone. J Biomech 2012;45:1540–1545. [DOI] [PubMed] [Google Scholar]