Detecting Allosteric Networks Using Molecular Dynamics Simulation

Abstract

Allosteric networks allow enzymes to transmit information and regulate their catalytic activities over vast distances. In principle, molecular dynamics (MD) simulations can be used to reveal the mechanisms that underlie this phenomenon; in practice, it can be difficult to discern allosteric signals from MD trajectories. Here, we describe how MD simulations can be analyzed to reveal correlated motions and allosteric networks, and provide an example of their use on the coagulation enzyme thrombin. Methods are discussed for calculating residue-pair correlations from atomic fluctuations and mutual information, which can be combined with contact information to identify allosteric networks and to dynamically cluster a system into highly correlated communities. In the case of thrombin, these methods show that binding of the antagonist hirugen significantly alters the enzyme’s correlation landscape through a series of pathways between Exosite I and the catalytic core. Results suggest that hirugen binding curtails dynamic diversity and enforces stricter venues of influence, thus reducing the accessibility of thrombin to other molecules.

1. INTRODUCTION

Many enzymes have evolved complex control mechanisms that involve the binding of an effector molecular at one location regulating substrate recognition or catalysis at a distant functional site. This phenomenon of allostery is central to the function of several critical protein families, including kinases, proteases, G-protein coupled receptors, and transcription factors (Beckett, 2009; Conn, Christopoulos, & Lindsley, 2009; Kornev & Taylor, 2015; Merdanovic, Monig, Ehrmann, & Kaiser, 2013). Indeed, the modification of allosteric mechanisms by naturally occurring mutations or targeted drug binding has been shown to alter cellular networks and is a prominent mechanism for both the cause and treatment of disease (Nussinov & Tsai, 2013; Nussinov, Tsai, & Ma, 2013). Therefore, understanding the physical basis for allostery has been a central goal of enzymology research over the past 50 years (Huang et al., 2014), resulting in several general models that describe allosteric effects. For brevity, an overview of these models is presented here, however the reader is directed to some of the many excellent reviews on the topic for further details (Cui & Karplus, 2008; Hilser, Wrabl, & Motlagh, 2012; Motlagh, Wrabl, Li, & Hilser, 2014; Ribeiro & Ortiz, in press).

The classical view of allostery involves structural transitions of the target protein through either induced fits or conformational selection models. When an enzyme is allosterically enhanced via the induced fit mechanism, agonist binding forces the enzyme to undergo a conformational change into a new state that is more beneficial to substrate binding and/or catalysis (Koshland, Nemethy, & Filmer, 1966; Sullivan & Holyoak, 2008). In the conformational selection approach, the favorable state is already accessible to the enzyme, but agonist binding drastically increases the population of the improved substrate binding conformation (Changeux, 2013; Monod, Wyman, & Changeux, 1965). Both of these models can be considered specific cases of a more general ensemble-based allostery model that treats conformational transitions with a statistical, instead of a deterministic, approach (Hilser et al., 2012).

More recently, the idea of allosteric influences without large-scale conformational transitions has been proposed (Allain et al., 2014; Cooper & Dryden, 1984; McLeish, Cann, & Rodgers, 2015; McLeish, Rodgers, & Wilson, 2013). In these cases, networks created by the cumulative perturbation of residue-pair correlations propagate dynamic changes between substrate and allosteric sites (del Sol, Fujihashi, Amoros, & Nussinov, 2006; Tsai, del Sol, & Nussinov, 2008; Tzeng & Kalodimos, 2011; Van Wart, Durrant, Votapka, & Amaro, 2014). This understanding compliments conformational techniques by providing insight to systems with little structural change (Motlagh et al., 2014) or even those without well-defined structures (Hilser & Thompson, 2007). In many cases, one or several residues within a protein act as allosteric “hotspots” and play a prominent role in its dynamic network structure (Amitai et al., 2004; Bhattacharya & Vaidehi, 2014; Bowerman & Wereszczynski, 2016; Scarabelli & Grant, 2014). Mutations along these allosteric networks are often linked to clinically relevant mutations, as was recently shown in the case of the kinesin-5 motor domain (Scarabelli & Grant, 2014).

Although general models for allosteric mechanisms have been extensively developed, the molecular mechanisms that underlie these effects are highly specific to the system of interest. In theory, the detailed information necessary for describing these processes is contained in a well-converged molecular dynamics (MD) trajectory. In practice, it can be difficult to filter these signals from the high-dimensional and noisy dynamics that are inherent to MD. Here, we describe several methods for detecting and analyzing allosteric effects from MD trajectories. In particular, methods for calculating correlations and contacts are compared, and the processes for mapping dynamic networks and creating coarse-grain representations of these interactions are presented. These methods are illustrated on the serine protease thrombin, and it is shown that binding of the antagonist hirugen enhances the allosteric connection between Exosite I and the catalytic core.

2. THEORY

2.1 Calculating Residue–Residue Correlations

The calculation of correlated motions between residues can be performed at multiple mathematical levels. Historically, the most straightforward and widely used approach is the dynamic cross-correlation of atomic fluctuations (Hünenberger, Mark, & van Gunsteren, 1995), which is a Pearson correlation calculated from covariance matrix elements:

$$C_{i,j}=\frac{\langle \left(r_i-\langle r_i\rangle \right)\cdot \left(r_j-\langle r_j\rangle \right)\rangle }{\sqrt{\left(\langle r_i^2\rangle -{\langle r_i\rangle }^2\right)\left(\langle r_j^2\rangle -{\langle r_j\rangle }^2\right)}}$$ (1)

where bracket-enclosed quantities represent time-averaged values, and r_i and r_j are the positional vectors of atoms i and j, respectively. Cross-correlation values span the range of −1 (perfectly anticorrelated) to +1 (perfectly correlated). Although ubiquitous, this metric has two significant limitations. First, the dot product of vectors in the numerator results in orthogonal motions always yielding a correlation of zero. Therefore, by this metric, even perfectly correlated motions may be unobserved if they are perpendicular to one another. Second, the averaging assumes that the correlations are linear in time. For example, two perfectly correlated oscillators that have a phase separation of π/2 are considered noncorrelated in the cross-correlation method (〈sin(t)sin(t + π/2〉 = 0). These limitations may cause the cross-correlation undervalue slowly propagating, long-range connections that are important to allosteric signaling.

To overcome these shortcomings, methods have been developed to make use of the mutual information metric of information theory. While extensive explanations of the underlying theory can be found elsewhere (Kraskov, Stogbauer, & Grassberger, 2004; Lange & Grubmuller, 2006), the main concepts are summarized here. In general, the mutual information (I_i,j) between two atoms can be determined via the equation:

$$I_{i,j}={\displaystyle \iint p\left(x_i,x_j\right)\text{log}\left(\frac{p\left(x_i,x_j\right)}{p\left(x_i\right)p\left(x_j\right)}\right)d{x}_{i}d{x}_j}$$ (2)

where p(x_i) and p(x_j) are the marginal distributions of x_i and x_j and p(x_i,x_j) is the observed joint distribution. While mathematically more complex than the standard cross-correlation, this method does not rely on the resulting geometries of the correlated motions. Rather, Eq. (2) answers the question: “How does knowledge of atom x_i improve knowledge of x_j (and vice versa)?” For linearly independent data, p(x_i,x_j) = p(x_i)(x_j) and I_{i, j} = 0. As p(x_i) and p(x_j) become increasingly correlated, the value of I_{i, j} diverges toward infinity. A Pearson-like correlation can be computed from mutual information using the following relationship:

$$C_{i,j}=\sqrt{1-e^{-\left(2/d\right)I_{i,j}}}$$ (3)

where d is the dimensionality of the data (d = 3 for Cartesian trajectories).

Mutual information based correlations are typically conducted at two levels of theory: linear, which only accounts for correlations that are temporally in-phase, and generalized correlation, which includes out of phase contributions. The linear mutual information is solved analytically by the equation:

$$I_{i,j}=\frac{1}{2}\left[\text{log}{C}_i+\text{log}{C}_j-\text{log}{C}_{i,j}\right]$$ (4)

where C_i and C_j are marginal–covariance matrices and C_i,j is the pair-covariance matrix, respectively. While this linear approximation yields only the lower limit of the mutual information between two atoms, the computation time is comparable to that of the cross-correlation. The generalized correlation calculation is significantly more taxing and must be solved numerically. However, in many cases the added cost is justified as the generalized correlation can identify physically relevant allosteric connections that escape the other two methods (see Section 4.1).

2.2 Identifying Allosteric Pathways

In biomolecular systems, the motions of adjacent residues are often highly correlated with one another. This can produce a “domino effect” wherein perturbations to one residue create long-range allosteric influences by propagating through networks of highly correlated neighbors (McLeish et al., 2015; Van Wart et al., 2014). One class of methods for identifying and studying these allosteric propagations is with a graph theory approach, where each protein residue forms a “node” in the graph and “edges” connect nodes representing residues that are considered to be in contact with one another. These edges are weighted according to residue-pair correlations (Van Wart, Eargle, Luthey-Schulten, & Amaro, 2012):

$$d_{i,j}=-\text{log}\left|C_{i,j}\right|$$ (5)

where d_i,j is the “distance” between contacting nodes i and j and C_i,j is the pairwise correlation between them. Eq. (5) produces a graph in which strongly correlated residues are separated by short distances, whereas residues with a weak correlation have longer distances between them. In this graph theory approach, the likely allosteric pathway between residues s and t is described by the shortest path between their respective nodes. The shortest path between nodes can be found quickly via search heuristics, such as Dijkstra’s algorithm (Dijkstra, 1959), whereas longer pathways, termed the “suboptimal pathways,” can be identified by other search methods, eg, Yen’s algorithm (Yen, 1971).

The importance of an individual residue to all of the optimal dynamic networks in a system can be expressed through its centrality (Brandes, 2001):

$$c_i=\frac{1}{N}{\displaystyle \sum _{i\ne s\ne t}{\sigma }_i\left(s,t\right)}$$ (6)

where N is the total number of pathways, σ_i(s,t) equals one if residue i is in the shortest pathway between residues s and t and zero otherwise, and the summation is carried out for all paths not starting or ending at residue i. Similarly, the collective importance of a residue across all of the suboptimal pathways connecting two nodes can be expressed by its prominence, calculated using Eq. (6) for a fixed s and t.

2.3 Constructing Dynamic Communities

The data resulting from interresidue correlation or allosteric network analyses can often be difficult to interpret. Therefore, in many cases, a coarse-grain representation of the network graph can provide unique insights into the dynamic regulation of a system (Sethi, Eargle, Black, & Luthey-Schulten, 2009). In this method, called “community structure analysis” a large number of residue nodes are clustered into “communities,” which are then connected to one another through edges that are weighted to reflect the strength of their interactions. This reduction can be done using the iterative algorithm of Girvan and Newman (2002):

1. Represent the system as a graph (as described in Section 2.2).

2. Calculate the edge “betweenness” by counting the number of shortest paths traversing each edge.

3. Remove the edge with the largest betweenness from the graph.

4. Cluster nodes based on edge distances.

5. Calculate the “modularity” of the graph using Eq. (7).

6. Repeat Steps 2–5 until all communities are connected by only a single edge.

The modularity (Q) of the graph is calculated by:

$$Q={\displaystyle \sum \left(e_i-a_i^2\right)}$$ (7)

where e_i is the percent of total edges in community i and $a_i^2$ is the expected percentage if the edges were randomly associated. Graphs with high modularity possess a higher organization above random noise (Newman, 2006).

For an initial graph with N edges and M nodes, the earlier algorithm will produce (N − M) unique graphs in which there are no isolated communities. The model with the largest modularity, or the most structure above random noise, is typically chosen as the one that best fits the data. The result of this algorithm is a new graph in which nodes represent communities of highly intercorrelated residues, and the strength of the linkage between two communities is dictated by the number of shortest paths that traverse their connecting edges.

3. METHODS

3.1 System Construction and Simulation Details

The analyses of a series of MD simulations of the enzyme thrombin are presented as a case study. This well-studied protein possesses two distinct allosteric binding sites, Exosites I and II (Fuglestad et al., 2012; Stubbs & Bode, 1993). Here, two systems were constructed: isolated thrombin (PDB: 1PPB) (Bode, Turk, & Karshikov, 1992) and thrombin complexed with hirugen (PDB: 1HAH) (Vijayalakshmi, Padmanabhan, Mann, & Tulinsky, 1994). In both systems, the PPACK molecule was removed from the catalytic pocket, and each system was neutralized by either Na⁺ or Cl⁻ ions and solvated in a box of TIP3P water that extended at least 10 Å from the solute (Jorgensen, Chandrasekhar, Madura, Impey, & Klein, 1983). Atoms were modeled by the Amber ff14SB force field, with altered monovalent ion parameters (Hornak et al., 2006; Joung & Cheatham, 2009; Maier et al., 2015). Hirugen was parameterized using GAFF (Wang, Wang, Kollman, & Case, 2006; Wang, Wolf, Caldwell, Kollman, & Case, 2004). Simulations were conducted with the GPU accelerated pmemd.cuda program in the AMBER suite (v14) (Salomon-Ferrer, Gotz, Poole, Le Grand, & Walker, 2013).

Each system was geometrically minimized for 10,000 steps (5000 with protein heavy atoms restrained and 5000 without restraints), then gradually heated three separate times from 10 to 300 K in the NVT ensemble while restraining protein heavy atoms. Following heating, the restraints in each simulation were slowly released over 150 ps, and the simulations were extended in the NPT ensemble for an additional 200 ns. Each trajectory was observed to equilibrate in 30 ns based upon RMSD calculations. This resulted in three separate 170 ns coordinate sets (510 ns total) for use in the analysis of each system.

3.2 Correlation Calculations

Residue–residue correlations were calculated at three levels of theory: the cross-correlation, the linear mutual information, and the (nonlinear) generalized correlation. Each calculation was done using GROMACS tools (g_covar for cross-correlations and g_correlation otherwise) (Lange & Grubmuller, 2006; Lindahl, Hess, & van der Spoel, 2001). Mutual information calculations were converted to their analogous correlation values using Eq. (3). Cα coordinates from every 100 ps of the simulation were used to improve calculation efficiency. Each set of coordinates was least squares fit to the average structure prior to correlation calculations. The generalized correlation matrix was converted to a “correlation distance” matrix using Eq. (5).

3.3 Graph Construction and Calculations

There is no single, rigorous definition for a contact in MD simulations. Therefore, we tested an exhaustive range of distance cutoffs using both Cα–Cα and heavy atom separations. Separation distances ranged from 8 to 12 Å for Cα–Cα and 3 to 6 Å for heavy atoms. Contacts were only defined between two residues that satisfied these distances in at least 75% of frames. The Cα–Cα metric routinely identified nonphysical contacts (see Section 4.2); therefore, graphs were created using only heavy atom contact matrices. Each graph was formed by an element-wise multiplication of the corresponding contact matrix and the edge matrix calculated from the generalized correlations. Any zero-value elements (self- and noncontacts) were removed, and the matrix was converted into a graph format for analysis in the NetworkX Python module (Hagberg, Schult, & Swart, 2008).

The community structure of each graph was constructed using the Girvan–Newman algorithm. The contact definition of 5.5 Å, which produced the smallest number of communities in both thrombin and thrombin–hirugen, was selected for further analysis. Shortest pathways between all residue-pairs were calculated using Dijkstra’s algorithm in NetworkX, and allosteric hotspots in each system were identified using Eq. (6). Furthermore, the 150 suboptimal paths between Exosite I residue T74 and the catalytic core H57 residue were calculated using the Weighted Implementation of Suboptimal Pathways method (Van Wart et al., 2014).

4. RESULTS AND DISCUSSION

4.1 Comparison of Correlation Methods

Comparison of the cross-correlation, linear, and nonlinear mutual information approaches shows that the level of interresidue correlation is consistently weakest in the cross-correlation and strongest when using the nonlinear generalized method (Fig. 1). All three methods correctly identify strong correlations in the catalytic core (residues 79 and 135) and across the disulfide bond connecting the light and heavy chains (residues 9 and 155). In addition, all three methods show the expected strong correlation between neighboring β-sheet residues (ie, L40–F34 (residues 62 and 55) and F34–L64 (residues 55 and 95)).

Fig. 1.

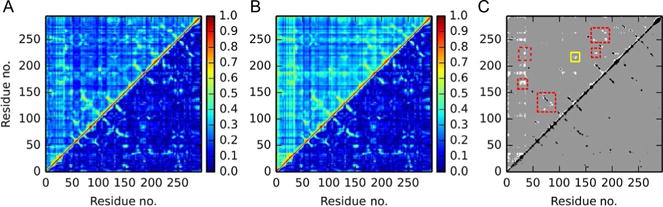
Comparison of the standard cross-correlation (lower triangle) with the upper triangle populated by the (A) linear mutual information metric and (B) nonlinear generalized correlation. (C) A filtered comparison between the cross-correlation (lower triangle) and the generalized correlation (upper triangle), where only correlations >0.5 are shown. Black regions denote strong correlations that were identified by both methods, while white regions show sections of strong correlation that are identified by the general correlation but not the cross-correlation. In particular, the allosteric connection between Exosite II and the catalytic core is highlighted (solid yellow (white in the print version) box), along with several expected interactions between contacting residues and three-body interactions (dotted red (gray in the print version) boxes).

However, cross-correlation and linear mutual information fail to capture a number of correlations that are both physically intuitive and biologically relevant. In contrast, these couplings are readily identified by the generalized correlation method to have strong correlations (c>0.5). For example, only the generalized correlation displays a significant signal between the catalytic core (residue 135) and Exosite II (residue 214), which is the binding site for the allosteric inhibitor heparin (Yang, Sun, Gailani & Rezaie, 2009). Furthermore, generalized correlation calculations highlight several three-body correlations, such as the F34-mediated interaction between L40 and L64 and the K107-mediated interaction between R50 (residue 72) and K87 (residue 119).

Comparison of isolated thrombin with the thrombin–hirugen complex reveals several notable differences (Fig. 2). First, the average strength of correlations in thrombin is reduced upon the addition of hirugen. Second, the light chain, which has been shown to have an allosteric role in normal thrombin function (Carter, Vanden Hoek, Pryzdial, & Macgillivray, 2010; Gasper, Fuglestad, Komives, Markwick, & McCammon, 2012), has more prominent correlations in isolated thrombin. A similar decrease in light chain correlations has been observed upon binding of a truncated thrombomodulin molecule, which also binds to Exosite I (Gasper et al., 2012). This common trend highlights the importance of the site in allosteric signaling. Furthermore, the binding of hirugen produces a system-wide increase in correlation with the 148_CT loop and with Exosite I, most notably residue T74. Interestingly, residues in and neighboring the catalytic triad experience significant increases in correlations with T74, showing that the binding of hirugen to Exosite I acts as an allosteric signal to regulate catalytic activity.

Fig. 2.

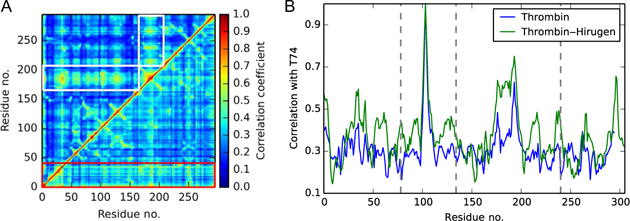
(A) Comparison of generalized correlations in isolated thrombin (lower triangle) and thrombin–hirugen (upper triangle). The prominent role of the light chain in isolated thrombin is outlined by the red (dark gray in the print version) box, and the global increase of correlation with the 148_CT Loop in thrombin–hirugen is highlighted by white boxes. (B) The pairwise correlations between thrombin residues and Exosite I residue T74. The binding of hirugen raises correlations with T74 system wide, but the catalytic residues (vertical dotted lines) experience a significant increase in correlation strength.

4.2 Contact Definition Analysis

Graph-based allosteric methods require a consistent definition of two residues that are in contact with one another. Typically, residues are considered to be in contact if either their Cα–Cα distance or their minimum heavy atom separation is closer than a specified cutoff value for more than a certain percentage of the simulation.

Although commonly used, we note that the choice of Cα–Cα distance may be prone to produce false contacts. For example, the Cα-based metric may identify interactions of nonneighboring β-strands as direct contacts, even if a third β-strand is located between them (Fig. 3A). These errant contacts can produce “short-circuits” in a network graph, and thus significantly alter the resulting allosteric pathway or community structure. While these false positives can be avoided by reducing the contact distance, decreasing the distance will conversely increase the number of false negatives, since residue contacts formed by the interaction of long side chains will be missed if one measures only the Cα–Cα distance. For an example in isolated thrombin, a Cα distance of 9.0 Å is stringent enough to avoid the false contact shown in Fig. 3A, but it also fails to identify the electrostatic contact between K202 and E14C (Fig. 3B). Therefore, we used the heavy atom contact definition, which is able to correctly identify contacts similar to those shown in Fig. 3 and avoid both false positives and negatives.

Fig. 3.

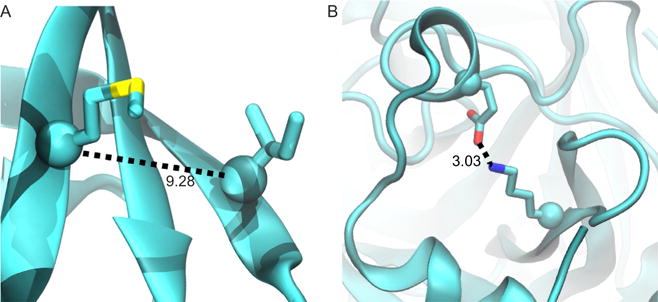
Examples of a false contact (A) and a false noncontact (B) identified by the Cα–Cα distance definition. If a heavy atom definition is used instead, then the false positive in (A) is removed and the contact in (B) is properly identified.

The choice of a cutoff distance is also not well defined, thus a series of values from 3.0 to 6.0 Å were tested. A distance of 5.5 Å was chosen as it minimizes the number of communities in both thrombin systems (Table 1). Finally, we tested different values for the contact frequency criterion, but this parameter had minimal impact on the final results and a value of 75% was chosen.

Table 1.

The Number of Communities Identified in Isolated Thrombin and Thrombin–Hirugen Using the Specified Heavy Atom Contact Distance

Cut-Off Distance (Å)	Thrombin	Thrombin–Hirugen
3.0	19	16
3.5	18	17
4.0	14	10
4.5	15	10
5.0	14	11
5.5	12	10
6.0	13	11

4.3 Allosteric Pathways in Thrombin

The optimal and suboptimal pathways between T74 and catalytic H57 show that hirugen binding strengthens the correlation between Exosite I and the catalytic core. Although the shortest path between T74 and the catalytic site traverses the same nodes in both systems, the length is shorter in thrombin–hirugen, suggesting stronger correlations between these sites in the bound state. Furthermore, there is a reduction in pathway diversity in the suboptimal pathways connecting these regions (Fig. 4). In isolated thrombin, pathways traverse directly to the catalytic core and through the surface exposed 60s and 70s loops, resulting in a total of 42 residues accessed. In the thrombin–hirugen complex, the hirugen molecule replaces the 70s loop and pathways never access the 60s loop, resulting in the 150 pathways accessing only 29 residues in a direct path to the catalytic core. This strong intercorrelation between the 29 nodes in thrombin–hirugen streamlines the transfer of dynamics from Exosite I to the catalytic core, thus strengthening the net correlation between the regions and overpowering other allosteric influences. This allows the dynamics of Exosite I to be the prominent allosteric signal to catalytic dynamics.

Fig. 4.

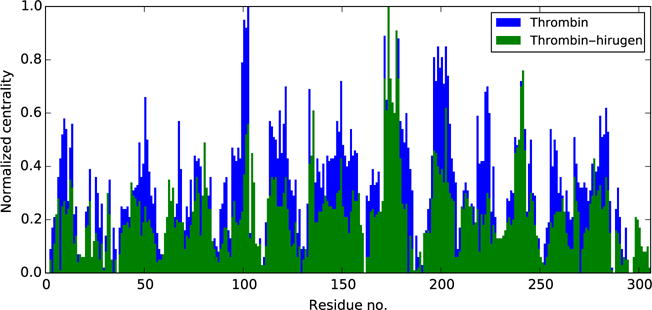
Normalized centrality values in isolated thrombin (blue (black in the print version)) and thrombin–hirugen (green (dark gray in the print version)). While the trend in peak values is the same, the average centrality score in thrombin–hirugen is less than that of isolated thrombin, which is indicative of a reduction in diversity in global pathways.

The locations of allosteric hotspots further suggest that hirugen binding may serve to focus the diverse dynamic networks of isolated thrombin into shorter pathways between Exosite I and the catalytic core. While the 70s loop is the most central region in isolated thrombin, hirugen replaces its role in local networks and reduces its centrality to the average peak height (Fig. 5). Furthermore, hirugen binding reduces the centrality scores of the light chain and Exosite II, signifying their decreased importance in allosteric signaling. Ultimately, the general trend of centrality values is similar within each system, but the average score is higher in isolated thrombin. This narrowed route of communication in thrombin–hirugen may serve to combat the effects from binding other allosteric molecules or substrates.

Fig. 5.

The suboptimal pathways in (A) isolated thrombin and (B) thrombin–hirugen. T74 is identified by the black sphere, and H57 is shown as a blue (dark gray in the print version) sphere. (C) Path length histograms for the two systems. (D) The prominence of residues in the pathways of each system. The pathways of isolated thrombin “detour” through the 70s and 60s loops, thus increasing their path lengths and decreasing their strength of interaction.

4.4 Community Analysis

Comparison of the community structures of isolated thrombin and thrombin–hirugen reveals several noteworthy changes (Fig. 6). While the catalytic triad is unified in isolated thrombin, H57 and D102 are in a separate, but strongly linked, community from S195 in thrombin–hirugen. Both systems show a connection between the catalytic triad communities and Exosite I. In the thrombin–hirugen complex, the connection is especially strong between Exosite I and the S195 community, in agreement with our correlation observations, but the strength of direct interaction between Exosite I and the H57/60s loop community appears to be quite weak. This agrees with the pathway analysis (Section 4.3) which showed the allosteric signal between Exosite I and H57 in thrombin–hirugen propagating through the S195 community and minimally accessing regions around the 60s loop. These results support the claim that hirugen binding creates a strong allosteric signal between Exosite I and the catalytic core to inhibit thrombin function. Lastly, the thrombin–hirugen complex consistently forms fewer communities than isolated thrombin, regardless of the choice of contact distance (Table 1). The decreased number of communities suggests that the thrombin–hirugen system may be harder to dynamically perturb, as the structural regions move as highly correlated domains and reduce the ability of further binding factors altering the activity of the molecule.

Fig. 6.

Community structure of (A) isolated thrombin and (B) thrombin–hirugen with the 3D structures colored according to community membership. Catalytic residues are also shown as purple sticks. Relevant regions of the community graphs are labeled accordingly. While the catalytic residues in thrombin–hirugen are split between two communities, the interaction strength between their respective groups and Exosite I is increased.

5. CONCLUSION

In this chapter, multiple techniques for identifying allosteric effects in enzymes are presented and applied to the sample case of hirugen binding to thrombin. We have focused on methods grounded in interresidue correlations and contacts; however, we note that complementary techniques may provide additional insights (Allain et al., 2014; LeVine & Weinstein, 2014; McClendon, Hua, Barreiro, & Jacobson, 2012). The generalized correlation calculation provides a better understanding of the correlation landscape than the standard cross-correlation, justifying its increased computational cost. Furthermore, the importance of using heavy atom separation as a contact definition rather than the colloquially used Cα separation is highlighted. In thrombin, these methods show that binding of hirugen significantly changes the residue-pair correlations, increasing the importance of the 148_CT loop and strengthening the correlation between Exosite I and the catalytic core. Mapping communication pathways between this exosite and the catalytic core show that hirugen streamlines the propagation of dynamics, creating shorter pathways, and stronger correlations. Furthermore, binding of hirugen reduces the total number of communities in thrombin and causes Exosite I to act as a single dynamic community, increasing the strength of interaction between Exosite I and catalytic communities. The combination of methods presented here show that hirugen binding reduces the dynamic diversity in thrombin and restricts the possible venues of influence by interaction with substrates or other allosteric molecules.