High-Resolution ¹H-MRSI of the Brain Using Short-TE SPICE

Abstract

Purpose

To improve signal-to-noise ratio (SNR) for high-resolution spectroscopic imaging using a subspace-based technique known as SPICE (SPectroscopic Imaging by exploiting spatiospectral CorrElation).

Methods

The proposed method is based on a union-of-subspaces model of MRSI signals, which exploits the partial separability properties of water, lipid, baseline and metabolite signals. Enabled by this model, a special scheme is used for accelerated data acquisition, which includes a double-echo CSI component used to collect a “training” dataset (for determination of the basis functions) and a short-TE EPSI component used to collect a sparse “imaging” dataset (for determination of the overal spatiospectral distributions). A set of signal processing algorithms are developed to remove the water and lipid signals and jointly reconstruct the metabolite and baseline signals.

Results

In vivo ¹H-MRSI results show that the proposed method can effectively remove the remaining water and lipid signals from sparse MRSI data acquired at 20 ms TE. Spatiospectral distributions of metabolite signals at 2 mm in-plane resolution with good SNR were obtained in a 15.5 min scan.

Conclusions

The proposed method can effectively remove nuisance signals and reconstruct high-resolution spatiospectral functions from sparse data to make short-TE SPICE possible. The method should prove useful for high-resolution ¹H-MRSI of the brain with improved SNR.

INTRODUCTION

SPectroscopic Imaging by exploiting spatiospectral CorrElation (SPICE) is a promising tool to achieve high-resolution MR spectroscopic imaging (MRSI) of the brain (1, 2). As voxel size gets smaller, further improvement of signal-to-noise ratio (SNR) becomes essential. Compared to conventional long echo-time acquisitions (e.g., TE ≥ 130 ms), acquisitions that use a shorter TE (e.g., TE ≤ 30 ms) can improve SNR considerably by minimizing the signal loss caused by T₂ relaxation (3–5) and better detect metabolites with coupled spin systems (6–8), such as myo inositol (mI), glutamate (Glu) and glutamine (Gln).

One practical issue with short-TE SPICE is due to the presence of overwhelming nuisance signals (e.g., water and lipid signals), even with suppression pulses during data acquisition [e.g., those in (9–13)]. The lipid signals, especially, in short-TE acquisitions can be much larger than those in long-TE acquisitions due to their short T₂ values (13). However, the conventional methods for nuisance signal removal, such as the Hankel singular value decomposition (HSVD) method for water removal (14) and the extrapolation (15, 16) and dual-density methods (17–19) for lipid removal, cannot be applied for the sparsely sampled (k, t)-space data in SPICE.

Another practical issue is the presence of baseline signals, primarily originating from macromolecules that overlap with the metabolite signals of interest in the frequency domain. Removal of the baseline signals from short-TE MRSI data results in more accurate metabolite quantification (20, 21). The baseline signals can be saturated by inversion pulses at the cost of the SNR of metabolite signals (22). Alternatively, they can be modeled as smooth functions, e.g., as a sum of spline (23, 24), wavelet (25) or polynomial functions (20); and then reconstructed jointly along with the metabolite signals (26). However, such a nonparametric model can require a large number of unknowns to represent the underlying baseline signals.

In this work, we propose a novel extension of the SPICE data acquisition and processing method to enable the use of short TEs. In this method, the measured short-TE MRSI data consisting of nuisance signals, baseline signals, and metabolite signals is modeled by a sum of partially separable (PS) functions, or subspaces (27, 28). Enabled by this model, a special scheme is developed for accelerated data acquisition, which includes: 1) a double-echo CSI (29) component used to collect a “training” dataset (for determination of spectral basis for each signal component), and 2) an EPSI (30) component used to collect an “imaging” for image reconstruction. A set of subspace-based algorithms are also developed for signal processing to remove the nuisance signals and to jointly reconstruct the metabolite and baseline signals. In vivo experiments performed at 3T demonstrate that the proposed method can recover spatiospectral distributions of metabolite signals acquired with a 20 ms TE at 2 mm in-plane resolution with good SNR in a 15.5 min scan. A preliminary account of this work was presented in (31).

THEORY

Union-of-subspaces modeling

We represent the spatiotemporal signal ρ(x, t) as

$$\begin{array}{l}\rho (\mathbf{x},t)={\rho }_{\mathrm{W}}(\mathbf{x},t)+{\rho }_{\mathrm{L}}(\mathbf{x},t)+{\rho }_{\mathrm{B}}(\mathbf{x},t)+{\rho }_{\mathrm{M}}(\mathbf{x},t)\\ ={\sum }_{p=1}^{P_{\mathrm{W}}}{u}_{\mathrm{W},p}(\mathbf{x})v_{\mathrm{W},p}(t)+{\sum }_{p=1}^{P_{\mathrm{L}}}{u}_{\mathrm{L},p}(\mathbf{x})v_{\mathrm{L},p}(t){\sum }_{p=1}^{P_{\mathrm{B}}}{u}_{\mathrm{B},p}(\mathbf{x})v_{\mathrm{B},p}(t)+{\sum }_{p=1}^{P_{\mathrm{M}}}{u}_{\mathrm{M},p}(\mathbf{x})v_{\mathrm{M},p}(t),\end{array}$$ [1]

where ρ_W(x, t) represents the water signal, ρ_L(x, t) the lipid signal, ρ_B(x, t) the baseline signal, and ρ_M(x, t) the desired “metabolite” signal. This model exploits the PS properties of each signal component, which is described by sets of temporal basis functions and spatial coefficients for each component (e.g., ${\{v_{\mathrm{W},p}(t)\}}_{p=1}^{P_{\mathrm{W}}}$ and ${\{u_{\mathrm{W},p}(\mathbf{x})\}}_{p=1}^{P_{\mathrm{W}}}$ for the water signal). This model is also called a union-of-subspaces model, noting that every signal component resides in a union of subspaces such that

$$\mathcal{V}=\text{span}\left\{{\{v_{\mathrm{W},p}(t)\}}_{p=1}^{P_{\mathrm{W}}}\right\}\cup \text{span}\left\{{\{v_{\mathrm{L},p}(t)\}}_{p=1}^{P_{\mathrm{L}}}\right\}\cup \text{span}\left\{{\{v_{\mathrm{B},p}(t)\}}_{p=1}^{P_{\mathrm{B}}}\right\}\cup \text{span}\left\{{\{v_{\mathrm{M},p}(t)\}}_{p=1}^{P_{\mathrm{M}}}\right\}.$$ [2]

This model significantly reduces the degrees-of-freedom of the underlying signals and enables special data acquisition and processing schemes to remove the nuisance signals and jointly reconstruct the metabolite and baseline signals, which are described in the following sections.

Data acquisition: Sparse sampling and short-TE acquisition

As in SPICE (1), the proposed method uses a hybrid data acquisition scheme to sparsely sample (k, t)-space. In this scheme, two complementary datasets are acquired: a “training” dataset that has high spectral bandwidth (for estimating temporal/spectral bases) and a sparse (k, t)-space “imaging” dataset that has extended k-space coverage (for determining spatial coefficients). To accelerate data acquisition, the training dataset has limited k-space coverage and the imaging dataset has limited spectral encodings. The proposed method uses a dual-echo CSI sequence to acquire the training data at both short and long TE and an EPSI sequence to acquire the sparse imaging data at short TE.

To achieve a short TE, a pair of slice selective 90°–180° RF pulses are used in the CSI and EPSI sequence to form an echo. Compared to the conventional point-resolved spectroscopy (PRESS) method (32), which uses three RF pulses, this scheme can effectively reduce the minimum TE. We reduced the minimum TE from 30 ms for PRESS to 20 ms using the proposed scheme and the traditional paired excitation/refocusing RF pulses.

In addition, the CSI sequence employs a double-echo acquisition in the same repetition time (TR): the first one collects a free induction decay (FID) signal at short TE; and the second one collects an echo signal at long TE. These two signals at different TEs capture different spectral components due to thier relaxation. More specifically, the short-TE signal contains short-T₂ metabolite components (e.g., mI, Glu, and Gln), long-T₂ metabolite components [e.g., N-acetylaspartate (NAA), creatine (Cr), and choline (Cho)], and baseline signals, while the long-TE signal only contains long-T₂ metabolite components. As described next, this unique feature of the double-echo CSI data is exploited for better separating the metabolite signals and the baseline signals.

Data processing: A subspace-based approach

For notation convenience, denote the short-TE and long-TE training data collected by the double-echo CSI sequence as 𝒟_1S and 𝒟_1L, respectively, and the sparse data collected by the EPSI sequence as 𝒟₂. We use a three-step procedure to reconstruct the spatiospectral distributions of metabolite signals from the measured data: 1) removal of the nuisance signals from 𝒟_1S, 𝒟_1L, and 𝒟₂; 2) determination of the temporal bases of the metabolite and baseline signals from 𝒟_1S and 𝒟_1L after nuisance signal removed; and 3) joint estimation of the spatial coefficients of the metabolite and baseline signals from 𝒟₂ after nuisance signal removed.

Nuisance signal removal

We adopt the recently proposed union-of-subspaces method in (33) to remove the nuisance signals from 𝒟_1S, 𝒟_1L, and 𝒟₂. Since the water and lipid signals dominate short-TE acquisitions, even with nominal water and lipid suppression, only a rough estimation of the metabolite and baseline signals is sufficient for nuisance signal removal. Therefore, we temporarily ignore the baseline signals and assume the metabolite signals only contain major resonance peaks of NAA, Cr, and Cho.

To estimate the temporal bases of the water, lipid, and metabolite signals from 𝒟_1S and 𝒟_1L, we 1) use the method in (34) to correct the magnetic field inhomogeneity effects, which extends the conventional conjugate phase method (35, 36) by incorporating prior edge information from anatomical images; 2) extract the water signals using the HSVD method; 3) separate the metabolite and lipid signals from the leakage-contaminated (due to limited k-space coverage) 𝒟_1S data by taking advantage of the known spatial support derived from anatomical images and resonance frequencies of the metabolite and lipid signals (see (33) for more detail); and 4) estimated the temporal bases from the extracted water, lipid, and metabolite signals using singular value decomposition (SVD).

After the temporal bases of the water, lipid, and metabolite signals are determined, high-resolution water and lipid signals can be estimated from 𝒟₂ and subsequently removed. More specifically, denoting the tem-poral bases of the water, lipid, and metabolite signal estimated from D_1S as ${\{{\widehat{v}}_{\mathrm{W},p}(t)\}}_{p=1}^{P_{\mathrm{W}}},{\{{\widehat{v}}_{\mathrm{L},p}(t)\}}_{p=1}^{P_{\mathrm{L}}}$ and ${\{{\widehat{v}}_{\mathrm{M},p}^{\prime }(t)\}}_{p=1}^{P_{\mathrm{W}}}$, the spatial coefficients of the lipid and water signals are estimated by fitting 𝒟₂:

$$\widehat{\mathbf{U}}=arg\underset{\mathbf{U}}{min}{\Vert {\mathbf{d}}_2-\mathbf{\Omega }{\mathbf{F}}_{\mathrm{B}}\{\mathbf{WU}\widehat{\mathbf{V}}\}\Vert }_2^2+\lambda {\Vert \mathbf{U}\Vert }_F^2,$$ [3]

where the first term describes data consistency, the second term penalizes noisy reconstructions with a regularization parameter λ, d₂ is a vector containing data in 𝒟₂, Ω is the corresponding sampling operator, F_B is a Fourier encoding operator including the magnetic field inhomogeneity induced phase term, W = diag{W_W, W_L, W_M} is a weighting matrix for incorporating the spatial support of each signal component, $\mathbf{U}=[{\mathbf{U}}_{\mathrm{W}},{\mathbf{U}}_{\mathrm{L}},{\mathbf{U}}_{\mathrm{M}}^{\prime }]$ contains the spatial coefficients to be determined, and $\widehat{\mathbf{V}}={[{\widehat{\mathbf{V}}}_{\mathrm{W}},{\widehat{\mathbf{V}}}_{\mathrm{L}},{\widehat{\mathbf{V}}}_{\mathrm{M}}^{\prime }]}^{\mathrm{H}}$ contains the estimated temporal bases.

The estimated high-resolution lipid signals are then used to remove the leaked lipid signals from D_1S. We model the discrepancies between D_1S and 𝒟₂ as general series (GS) functions (37, 38):

$${\rho }_{\mathrm{L}}^{\prime }(\mathbf{x},t)=\mid {\widehat{\rho }}_{\mathrm{L}}(\mathbf{x},t)\mid \sum _{p=1}^{P_{\text{GS}}}{e}^{-i2\pi {\mathbf{k}}_p·\mathbf{x}}{v}_{\text{GS},p}(t),$$ [4]

where ${\rho }_{\mathrm{L}}^{\prime }(\mathbf{x},t)$ represent the underlying lipid signals in D_1S, ρ̂_L(x, t) the high-resolution lipid signals estimated from 𝒟₂, ${\{v_{\text{GS},p}(t)\}}_{p=1}^{P_{\text{GS}}}$ the GS model coefficients to be determined, and P_GS the number of encodings of D_1S. We determine the GS model coefficients in [4] by fitting D_1S:

$$\begin{array}{c}[{\widehat{\mathbf{V}}}_{\text{GS}},{\widehat{\mathbf{U}}}_{\mathrm{M}}^{\prime }]=arg\underset{{\mathbf{V}}_{\text{GS}},{\mathbf{U}}_{\mathrm{M}}^{\prime }}{min}{\Vert {\mathbf{d}}_{1S}-\mathbf{\Omega }{\mathbf{F}}_{\mathrm{B}}\{{\mathbf{W}}_{\mathrm{M}}{\mathbf{U}}_{\mathrm{M}}^{\prime }{\widehat{\mathbf{V}}}_{\mathrm{M}}^{\prime }+\mid {\widehat{\mathit{\rho }}}_{\mathrm{L}}\mid \circ ({\widehat{\mathbf{U}}}_{\text{GS}}{\mathbf{V}}_{\text{GS}})\}\Vert }_2^2\\ +\mu {\Vert {\mathbf{V}}_{\text{GS}}\Vert }_F^2+\lambda {\Vert {\mathbf{U}}_{\mathrm{M}}^{\prime }\Vert }_F^2,\end{array}$$ [5]

where d_1S represents the water-removed D_1S data, ‘○’ the entry-wise matrix product, Û_GS a matrix discretizing e^{−i2πk_p·x} over a given grid, and V_GS the GS coefficients to be determined.

The underlying lipid signals in D_1L can be estimated and subsequently removed in a similar fashion. Note that the lipid signals of the left-hand and right-hand side of the echo signal in D_1L should be modeled and removed separately, as the signal decay rates of the two sides are different.

Determination of the temporal bases of the metabolite and baseline signals

We denote the nuisance signal removed D_1S and D_1L as $D_{1S}^{\prime }$ and $D_{1L}^{\prime }$. To determine the temporal bases of the metabolite and baseline signals, we need to separate the metabolite and baseline signals from $D_{1S}^{\prime }$. The temporal bases are then determined from the separated signals using SVD. However, the challenge is that these two signals overlap with each other in the frequency domain. We address this issue by modeling the baseline signals as linear combinations of spline functions in the frequency domain and estimating the model coefficients by fitting $D_{1S}^{\prime }$ and $D_{1L}^{\prime }$ voxel-by-voxel. Including the long-TE signal $D_{1L}^{\prime }$ in the data fitting results in more accurate estimation of the long-T₂ metabolite signals. These signals are dominant in the nuisance signal removed data, and thus, improves the estimation of the baseline signals.

Ignoring the spatial dependence of the signal for simplicity, the data in $D_{1S}^{\prime }$ at each pixel can be written as

$$\begin{array}{l}{\stackrel{\sim }{\rho }}_{1S}(m_S\mathrm{\Delta }t)=e^{-m_S\mathrm{\Delta }t/T_2^{\prime }}{\sum }_{n=1}^{N_S}{c}_{S,n}{e}^{-(m_S\mathrm{\Delta }t+T_E^S)/T_{2,n}^S}{e}^{-i2\pi f_{S,n}{m}_S\mathrm{\Delta }t}\\ +e^{-m_S\mathrm{\Delta }t/T_2^{\prime }}{\sum }_{n=1}^{N_L}{c}_{L,n}{e}^{-(m_S\mathrm{\Delta }t+T_E^S)/T_{2,n}^L}{e}^{-i2\pi f_{L,n}{m}_S\mathrm{\Delta }t}\\ +{\sum }_{n=1}^{N_B}{b}_n{B}_n(m_S\mathrm{\Delta }t,{\mathit{\beta }}_{\mathit{n}})+\xi (m_S\mathrm{\Delta }t),\end{array}$$ [6]

where m_S = 0, 1, ···, M_S − 1 (M_S is the total number of samples of the FID signal); c_S,n, $T_{2,n}^S$, and f_S,n represent the concentration, T₂ relaxation time constant, and resonance frequency of the nth short-T₂ metabolite, respectively; c_L,n, $T_{2,n}^L$, and f_L,n are the parameters of the nth long-T₂ metabolite; $T_2^{\prime }$ is introduced to model the signal decay caused by magnetic field inhomogeneities; $T_E^S$ is the echo time; b_n and B_n(m_SΔt, β_n) are the coefficient and basis function of the baseline signals; and ξ(m_SΔt) is measurement noise. Note that since the baseline signals are modeled by spline functions in the frequency domain, B_n(m_SΔt, β_n) is the inverse Fourier transform of the corresponding spline function (with parameter β_n). In [6], the metabolite signals are modeled as linear combinations of Lorentzian resonance peaks, although more advanced models that incorporate prior knowledge of metabolite spectra can also be used.

We assume that the data in $D_{1L}^{\prime }$ only contains the long-T₂ metabolite signals and can be written as

$${\stackrel{\sim }{\rho }}_{1L}(m_L\mathrm{\Delta }t)=e^{-\mid m_L\mathrm{\Delta }t\mid /T_2^{\prime }}\sum _{n=1}^{N_L}{c}_{L,n}{e}^{-(m_L\mathrm{\Delta }t+T_E^L)/T_{2,n}^L}{e}^{-i2\pi f_{L,n}{m}_L\mathrm{\Delta }t}+\xi (m_L\mathrm{\Delta }t),$$ [7]

where m_L = −M_L,L, −M_L,L − 1, ···, M_L,R − 1, M_L,L is the total number of samples before the echo time, and M_L,R is the total number of samples after the echo time.

The baseline signals can be then estimated by solving the following nonlinear least-squares problem:

$$\begin{array}{c}\underset{{\mathit{\alpha }}_S,{\mathbf{c}}_S,{\mathit{\alpha }}_L,{\mathbf{c}}_L,\mathit{\beta },\mathbf{b},T_2^{\prime }}{argmin}{\Vert {\stackrel{\sim }{\mathit{\rho }}}_{1S}-{\mathbf{\Phi }}_{1S,S}({\mathit{\alpha }}_S,T_2^{\prime }){\mathbf{c}}_S-{\mathbf{\Phi }}_{1S,L}({\mathit{\alpha }}_L,T_2^{\prime }){\mathbf{c}}_L-{\mathbf{\Phi }}_{1S,B}(\mathit{\beta })\mathbf{b}\Vert }_2^2\\ +{\Vert {\stackrel{\sim }{\mathit{\rho }}}_{1L}-{\mathbf{\Phi }}_{1L,L}({\mathit{\alpha }}_L,T_2^{\text{'}}){\mathbf{c}}_L\Vert }_2^2+\lambda R({\mathbf{\Phi }}_{1S,B}(\mathit{\beta })\mathbf{b}),\end{array}$$ [8]

where Φ_1S,S(·),Φ_1S,L(·) and Φ_1S,B(·) are matrices containing the basis functions of the short-T₂ metabolite, long-T₂ metabolite and baseline signals in Eq. [6]; Φ_1L,L(·) is a matrix containing the basis functions of the long-T₂ metabolite signal in Eq. [7]; ρ̃_1S and ρ̃_1L are vectors containing ρ̃_1S(m_SΔt) and ρ̃_1L(m_LΔt); c_S and c_L are vectors containing the linear parameters (concentrations) of the short-T₂ and long-T₂ metabolite signals; α_S and α_L are vectors containing the nonlinear parameters (T₂ relaxation time constants and resonance frequencies) of the short-T₂ and long-T₂ metabolite signals; b and β are vectors containing the linear and nonlinear parameters of the baseline signals; λ is a regularization parameter; and R(Φ_1S,B(β)b) penalizes the smoothness of the baseline signals in the frequency domain (40).

However, estimating baseline signals by directly solving the nonlinear least-squares problem in Eq. [8] is challenging because of the large number of nonlinear parameters. We propose to address this issue by exploiting the temporal separability of the short-TE signals in $D_{1S}^{\prime }$. More specifically, note that the baseline signals become negligible a few milliseconds after TE and short-T₂ metabolite signals decay quickly. In other words, given a short-TE signal ρ̃_1S(m_SΔt) we can construct ${\stackrel{\sim }{\rho }}_{1S}^{(1)}(m_S\mathrm{\Delta }t)$ and ${\stackrel{\sim }{\rho }}_{1S}^{(2)}(m_S\mathrm{\Delta }t)$ by truncating ρ̃_1S(m_SΔt) differently such that the baseline signal can be ignored in ${\stackrel{\sim }{\rho }}_{1S}^{(1)}(m_S\mathrm{\Delta }t)$ and that both the baseline and short-T₂ metabolite signals can be ignored in ${\stackrel{\sim }{\rho }}_{1S}^{(2)}(m_S\mathrm{\Delta }t)$ (as shown in Fig. 1). This segmentation enables us to reformulate the optimization problem in [8] as three subproblems, each of which can be solved with a significantly reduced number of nonlinear parameters:

Figure 1.

Temporal separability of a double-echo CSI dataset. The short-TE signal ρ̃_1S(t) can be segmented such that ${\stackrel{\sim }{\rho }}_{1S}^{(1)}(t)$ only contains short-T₂ and long-T₂ metabolite signals while ${\stackrel{\sim }{\rho }}_{1S}^{(2)}(t)$ only contains long-T₂ metabolite signals. In comparison, the long-TE signal ρ̃_1L(t) only contains long-T₂ metabolite signals.

1. The long-T₂ metabolite signals are estimated by fitting ${\stackrel{\sim }{\rho }}_{1S}^{(2)}(m_S\mathrm{\Delta }t)$ and ρ̃_1L(m_LΔt):

   $$\{{\mathit{\alpha }}_L^{\ast },{\mathbf{c}}_L^{\ast },T_2^{\prime \ast }\}arg\underset{{\mathit{\alpha }}_L,{\mathbf{c}}_L,T_2^{\prime }}{min}{\Vert {\stackrel{\sim }{\mathit{\rho }}}_{1S}^{(2)}-{\mathbf{\Phi }}_{1S,L}^{(2)}({\mathit{\alpha }}_L,T_2^{\prime }){\mathbf{c}}_L\Vert }_2^2+{\Vert {\stackrel{\sim }{\mathit{\rho }}}_{1L}-{\mathbf{\Phi }}_{1L,L}({\mathit{\alpha }}_L,T_2^{\text{'}}){\mathbf{c}}_L\Vert }_2^2,$$ [9]

   where ${\stackrel{\sim }{\mathit{\rho }}}_{1S}^{(2)}$ is a vector containing ${\stackrel{\sim }{\rho }}_{1S}^{(2)}(m_S\mathrm{\Delta }t)$ and ${\mathbf{\Phi }}_{1S,L}^{(2)}(·)$ is a matrix containing the truncated basis functions for the long-T₂ metabolite signals in ${\stackrel{\sim }{\rho }}_{1S}^{(2)}(m_S\mathrm{\Delta }t)$.

2. The short-T₂ metabolite signals are estimated by fitting ${\stackrel{\sim }{\rho }}_{1S}^{(1)}(m_S\mathrm{\Delta }t)$:

   $$\{{\mathit{\alpha }}_S^{\ast },{\mathbf{c}}_S^{\ast }\}=arg\underset{{\mathit{\alpha }}_S,{\mathbf{c}}_S}{min}{\Vert {\stackrel{\sim }{\mathit{\rho }}}_{1S}^{(1)}-{\mathbf{\Phi }}_{1S,L}^{(1)}({\mathit{\alpha }}_L^{\ast },T_2^{\prime \ast }){\mathbf{c}}_L^{\ast }-{\mathbf{\Phi }}_{1S,S}^{(1)}({\mathit{\alpha }}_S,T_2^{\prime \ast }){\mathbf{c}}_S\Vert }_2^2,$$ [10]

   where ${\stackrel{\sim }{\mathit{\rho }}}_{1S}^{(2)}$ is a vector containing ${\stackrel{\sim }{\rho }}_{1S}^{(1)}(m_S\mathrm{\Delta }t)$ and ${\mathbf{\Phi }}_{1S,L}^{(1)}$ and ${\mathbf{\Phi }}_{1S,S}^{(1)}$ are matrices containing the truncated basis functions for the long-T₂ and short-T₂ metabolite signals in ${\stackrel{\sim }{\rho }}_{1S}^{(1)}(m_S\mathrm{\Delta }t)$, respectively.

3. The baseline signals are determined by solving the following optimization problem:

   $$\{{\mathit{\beta }}^{\ast },{\mathbf{b}}^{\ast }\}=arg\underset{\mathit{\beta },\mathbf{b}}{min}{\Vert {\stackrel{\sim }{\mathit{\rho }}}_{1S}-{\mathbf{\Phi }}_{1S,S}({\mathit{\alpha }}_S^{\ast },T_2^{\prime \ast }){\mathbf{c}}_S^{\ast }-{\mathbf{\Phi }}_{1S,L}({\mathit{\alpha }}_L^{\ast },T_2^{\prime \ast }){\mathbf{c}}_L^{\ast }-{\mathbf{\Phi }}_{1S,B}(\mathit{\beta })\mathbf{b}\Vert }_2^2+\lambda R({\mathbf{\Phi }}_B(\mathit{\beta })\mathbf{b}).$$ [11]

The nonlinear least-squares problems in Eqs. [9] and [10] are solved using the variable projection algorithm (VARPRO) (39). The optimization problem in [11] is solved using the algorithm in (40) [implemented by the MATLAB function csaps (MathWorks, Inc., Natick, MA)].

Joint reconstruction of the metabolite and baseline signals

After the temporal bases of the metabolite and baseline signals are determined, denoted as ${\{{\widehat{v}}_{\mathrm{M},p}(t)\}}_{p=1}^{P_{\mathrm{M}}}$ and ${\{{\widehat{v}}_{\mathrm{B},p}(t)\}}_{p=1}^{P_{\mathrm{B}}}$, the spatial coefficients of the metabolite and baseline signals are determined jointly by solving the following optimization problem:

$$[{\widehat{\mathbf{U}}}_{\mathrm{M}},{\widehat{\mathbf{U}}}_B]=arg\underset{{\mathbf{U}}_{\mathrm{M}},{\mathbf{U}}_{\mathrm{B}}}{min}{\Vert {\mathbf{d}}_2^{\prime }-\mathbf{\Omega }{\mathbf{F}}_{\mathrm{B}}\{{\mathbf{U}}_M{\widehat{\mathbf{V}}}_{\mathrm{M}}+{\mathbf{U}}_B{\widehat{\mathbf{V}}}_{\mathrm{B}}\}\Vert }_2^2+\lambda R_M({\mathbf{U}}_M)+\mu R_B({\mathbf{U}}_B),$$ [12]

where ${\mathbf{d}}_2^{\prime }$ represents the nuisance signal removed 𝒟₂ data, the first term describes data consistency, and the last two terms are regularization penalties for the metabolite and baseline signals, respectively. This joint reconstruction formulation allows incorporating different prior knowledge of the metabolite and baseline signals. We choose $R_M({\mathbf{U}}_M)={\Vert \mathbf{\Psi }{\mathbf{D}}_x{\mathbf{U}}_M\mathbf{\Lambda }{\widehat{\mathbf{V}}}_M\Vert }_F^2$ to penalize the spatial smoothness of the metabolite signals, wherein Ψ contains edge weights derived from a high-resolution anatomical reference image (41), D_x is a finite difference operator in the image domain, and Λ is an additional diagonal weighting matrix to penalize noisy basis and is determined from the singular value distribution of the Casorati matrix (1); and $R_B({\mathbf{U}}_B)={\Vert {\mathbf{U}}_B{\widehat{\mathbf{V}}}_B{\mathbf{F}}_t{\mathbf{D}}_f\Vert }_F^2$ to penalize the spectral smoothness of the baseline signals, wherein F_t is a Fourier operator in the time domain and D_f is a finite difference operator in the frequency domain. The resultant optimization problem is a weighted-ℓ₂ regularized least-squares problem that can be solved efficiently.

METHODS

Simulation study

We carried out simulation studies to show the “theoretical” benefits of short-TE acquisitions in the terms of Cramér-Rao lower bound and to compare the baseline estimation results obtained by the “subtract” method (20) and by the proposed method.

Simulation study I: Cramér-Rao lower bound analysis

Cramér-Rao lower bound (CRLB) is a lower bound on the variance of the estimated parameters for an unbiased estimator (42). We calculated the CRLB on the variance of the metabolite amplitude estimate as a function of TE to study the theoretical benefits of short-TE acquisitions.

More specifically, we assume the measured signal can be modeled as

$$\rho [m]=\sum _{n=1}^N{a}_{n,TE}{\varphi }_{n,TE}[m]e^{-m\mathrm{\Delta }t/T_{2,n}^{\ast }}+\sum _{n=1}^{N_B}{b}_n{B}_n[m]+\xi [m],$$ [13]

where a_n,TE = c_ne^−TE/T₂,n is the amplitude of the nth metabolite, wherein c_n and T_2,n are the concentration and T₂ relaxation time constant of the nth metabolite; ϕ_n,TE[m] is the basis function of the nth metabolite; $T_{2,n}^{\ast }=1/(1/T_{2,n}+1/T_2^{\prime })$, wherein $T_2^{\prime }$ models the signal decay caused by magnetic field inhomogeneities; b_n and B_n[m] represent the coefficient and basis of a baseline signal; and ξ[m] is Gaussian noise. The parameters to be estimated from the measured data are ${\{a_{n,TE},T_{2,n}^{\ast }\}}_{n=1}^N$ and ${\{b_n\}}_{n=1}^{N_B}$.

We calculated the so called coefficient of variation bound (CVB) of the estimated metabolite amplitude as a function of TE, which is related to CRLB and is given by

$${\mathit{CVB}}_{a_{n,TE}}=\frac{\sqrt{\mathit{CRL}{B}_{a_{n,TE}}}}{a_{n,TE}}=\frac{\sqrt{J_{a_{n,TE}}^{-1}}}{a_{n,TE}},$$ [14]

where $J_{a_{n,TE}}^{-1}$ is the diagonal entry of the inverse of the Fisher information matrix that is corresponding to the variance in the estimated a_n,TE (see Ref. (21) for more detail on how to calculate the Fisher information matrix for an unbiased estimator that estimates ${\{a_{n,TE},T_{2,n}^{\ast }\}}_{n=1}^N$ and ${\{b_n\}}_{n=1}^{N_B}$ from the signal in Eq. [13]).

In this simulation study, the signal model in Eq. [13] consisted of six metabolites, commonly detected in a short-TE MRSI experiment: three long-T₂ metabolites (NAA, Cr and Cho) and three short-T₂ metabolites (mI, Glu and Gln). Their basis functions were obtained using GAVA quantum mechanical simulations (43); their concentrations and T₂ values were based on the literature values (3, 44). The baseline signals and $T_2^{\prime }$ were estimated from in vivo experimental data.

Simulation study II: Baseline estimation

An FID signal at 20 ms TE (ρ̃_1S(m_SΔt)) was synthesized, consisting of two short-T₂ Lorentzian peaks, three long-T₂ Lorentzian peaks, and a baseline signal that contains two Lorentzian peaks with short T₂ values. An echo signal at 300 ms TE (ρ̃_1L(m_SΔt)) was also synthesized, only consisting of three long-T₂ Lorentzian peaks. Gaussian noise were added to the synthesized signal to simulate realistic SNR. The sampling bandwidth was 2000 Hz. The length of ρ̃_1S(m_SΔt) was 250; the length of ρ̃_1L(m_SΔt) was 682, wherein the number of samples before echo time was 170. These parameters were set based on the acquisition parameters of a double-echo CSI sequence implemented on our 3.0 T scanner.

The baseline signal was estimated from the short-TE FID and long-TE echo signals using the proposed baseline estimation method, i.e., solving the optimization problem in Eqs. [9] to [11] sequentially. ρ̃_1S(m_SΔt) was truncated by removing the first 30 and 50 points to form ${\stackrel{\sim }{\rho }}_{1S}^{(1)}(m_S\mathrm{\Delta }t)$ and ${\stackrel{\sim }{\rho }}_{1S}^{(2)}(m_S\mathrm{\Delta }t)$, respectively. For comparison, the baseline signal was also estimated from the short-TE FID signal using the “subtract” method. In the “subtract” method, the first 30 points of ρ̃_1S(m_SΔt) were subtracted to obtain a “baseline-free signal” for metabolite signal estimation. Both the short-T₂ and long-T₂ metabolite signals were then estimated by fitting the “baseline-free” signal to Lorentzian peaks. The resultant optimization problem was solved by VARPRO.

Phantom experiment

Experimental studies on a structured phantom were carried out on a 3T Siemens Trio scanner (Siemens Health-care) equipped with a 12-channel headcoil to demonstrate the performance of the proposed method. The phantom was built using a cylindrical jar filled with NaCl doped water and 10 vials in three rows with different diameters. The vials were filled with solutions of NAA, Cr, Cho, and mI with physiological relevant concentrations [see Ref. (2) for more detail].

For the proposed method, a low-resolution short-TE CSI dataset and a high-resolution EPSI dataset were acquired. As there was no need to remove baseline signals for phantom experimental data, the CSI dataset contained only one echo data. The imaging parameters of the CSI scan were: 220×220 mm² FOV, 10 mm slice thickness, 16×16 spatial encodings, TR/TE = 1600/20 ms, and 2000 Hz readout bandwidth. The imaging parameters of the EPSI scan were: TR/TE = 1600/20 ms, 110×110 spatial encodings (2 mm nominal in-plane resolution), 100 kHz readout bandwidth, bipolar acquisition, 55 echo pairs, 2.66 ms echo spacing (spacing between echoes collected in two neighboring positive gradient lobes) and 6 signal averages. Water suppression enhanced through T₁ effects (WET) pulses were used in both CSI and EPSI acquisitions for water suppression (10). For comparison, the same acquisitions were repeated with TE = 300 ms. Note that the T₂ values of the metabolites of the phantom were larger than the literature reported values for in vivo experiments at 3T. Therefore, a relatively long TE was chosen to demonstrate the benefits of the proposed method over the conventional long TE acquisitions. An equivalent-acquisition time short-TE EPSI dataset was also acquired with the same imaging parameters expect with 8 signal averages to compare the proposed method with the conventional EPSI method. A GRE dataset was acquired to measure the magnetic field inhomogeneity and to provide a structural reference image. In data processing, the residual water signals were removed from the CSI data using the HSVD method. The residual water signals in the EPSI data were removed using the proposed method by setting the lipid and baseline signals to be zero. The echo shift and phase mismatch in the bipolar EPSI acquisition, which were caused by eddy currents, were corrected as described in Ref. (33).

In vivo experiment

In vivo experiment I: Feasibility of short-TE SPICE

In vivo data were acquired from two healthy volunteers approved by our local Institutional Review Board. The first experiment was carried out to show the feasibility of the proposed short-TE SPICE method. In the beginning of the experiment, a 3D MPRAGE (magnetization prepared rapid gradient echo) dataset was acquired for localization at 0.9×0.9×1 mm³ resolution in a 5 min scan. A double-echo CSI dataset was acquired in a 15.4 min scan with WET pulses for water suppression and eight OVS bands surrounding the brain for lipid suppression. The imaging parameters of the CSI scan were: 220×220 mm² FOV, 10 mm slice thickness, 24×24 spatial encodings (9.2 mm nominal in-plane resolution), TR/TE1/TE2 = 1600/20/300 ms, and 2000 Hz readout bandwidth. An EPSI dataset was acquired in a 11.7 min scan with the same FOV, slice thickness, and saturation pulses as the CSI scan. The imaging parameters of the EPSI scan were: TR/TE = 1600/20 ms, 110×110 spatial encodings (2 mm nominal in-plane resolution), 100 kHz readout bandwidth, bipolar acquisition, 49 echo pairs, 2.66 ms echo spacing and 4 signal averages. A GRE dataset was acquired in a 3 min scan to measure the magnetic field inhomogeneity and derive the supports of the lipids.

The MPRAGE data were used as a reference image to derive edge weights for magnetic field inhomogeneity correction and SPICE reconstruction. The center 12×12 spatial encodings of the CSI dataset were used as the training dataset (𝒟_1S and 𝒟_1L) of SPICE. The equivalent acquisition time of SPICE was 15.5 min (3.8 min for a CSI scan with 12×12 spatial encodings plus 11.7 min for an EPSI scan with 110×110 spatial encodings and 4 signal averages). The nuisance signals in the EPSI and CSI datasets were then removed as described as in the Theory section, and a SPICE reconstruction was obtained from the nuisance signal removed data by solving Eq. [12].

In vivo experiment II: Comparison of short-TE and long-TE SPICE

The second experiment was carried out to show the SNR improvement of short-TE SPICE acquisitions over long-TE SPICE acquisitions. A short-TE SPICE dataset was acquired, consisting of a double-echo CSI dataset with 16×16 spatial encodings and an EPSI dataset with 110×110 spatial encodings and 8 signal averages. The other imaging parameters of the short-TE SPICE dataset were the same as those in Experiment I. Another long-TE SPICE dataset was acquired with 130 ms TE. Since no baseline removal was needed for long-TE SPICE, the second echo of the CSI scan was not used. Additional MPRAGE and GRE datasets were also acquired as in Experiment I. For a fair comparison, a SPICE reconstruction of the short-TE data was obtained by solving Eq. [12] with the weighting matrix Λ being an identity matrix; a SPICE reconstruction of the long-TE data was obtained by solving Eq. [12] with the same Λ, model order for the metabolite signal and regularization parameters, except that the baseline signals were ignored.

Results

Simulation study

Simulation study I: Cramér-Rao lower bound analysis

Figure 2 shows the CRB analysis results for the signal model described in the Method section. As can bee seen, short-TE acquisitions improve the CVB’s of both the short-T₂ metabolite components (mI, Glu, and Gln) and the long-T₂ metabolite components (NAA, Cr, and Cho). Furthermore, properly removing baseline signals in advance improves estimation accuracy as well. These observations, consistent with what were reported in Ref.(21), illustrate the potential benefits of using short-TE acquisitions over the conventional long-TE acquisitions.

Figure 2.

Cramér-Rao lower bound analysis. (a) to (f) CVB as a function of TE for NAA, Cr, Cho, mI, Glu and Gln, respectively. (black line: 6 metabolite + baseline model; blue line: 6 metabolite model; red line: 3 metabolite model)

Simulation study II: Baseline estimation

Baseline estimation results are shown in Fig. 3. The baseline signal obtained by the proposed method was more close to the true one than that obtained by the “subtract” method, as shown in Fig. 2d and Fig. 2e. This is because the proposed method utilizes an additional long-TE signal for better estimation of the long-T₂ metabolites (as show in Fig. 2b and 2c), which are often dominate in in vivo metabolite signals.

Figure 3.

Simulation results of baseline estimation. (a) Simulated short-TE signal, where peak (1) to (4) are due to long-T₂ components and peak (5) and (6) are due to short-T₂ components. (b) and (c) Metabolite signals estimated by the “subtract” method and by the proposed method, respectively (blue line: estimated metabolite signal; red line: ground truth of the metabolite signal). (d) and (e) Baseline signals estimated by the “subtract” method and by the proposed method (blue line: estimated baseline signal; black line: residual signal obtained by subtracting the estimated metabolite signal from (a); red line: ground truth of the baseline signal).

Phantom experiment

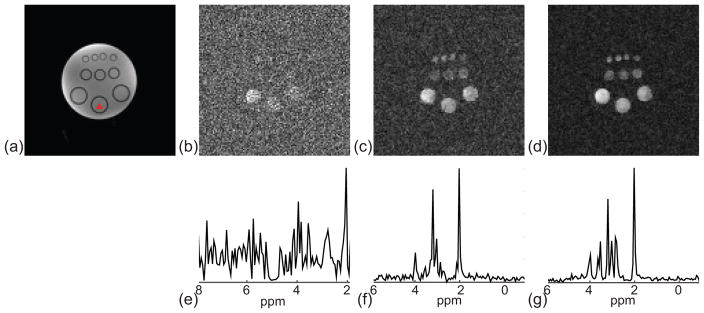
Phantom results are shown in Fig. 4. Compared to the conventional EPSI method (Figs. 4b and 4e), SPICE reconstructions (Figs. 4c, 4d, 4f, and 4g) showed significantly improved SNR, which is consistent with the results reported in Refs. (1,2). Compared with the SPICE results obtained from a long-TE acquisition, the short-TE acquisition further improved the SNR of SPICE, as can be clearly seen by comparing both the reconstructed metabolite maps (Figs. 4c and 4f) and representative spectra (Figs. 4d and 4g).

Figure 4.

Phantom experiment results. (a) Reference structural image. (b) to (d) Concentration maps of NAA obtained by the conventional EPSI method, long-TE SPICE, and short-TE SPICE, respectively. (e) to (f) Representative spectra corresponding to each method. Note that the spectra obtained by the conventional EPSI method span about 6 ppm determined by the echo spacing. The spectra obtained by the SPICE method, however, span about 16 ppm because the spectral basis functions are estimated from a CSI acquisition with high spectral bandwidth.

In vivo experiment

In vivo experiment I: Feasibility of short-TE SPICE

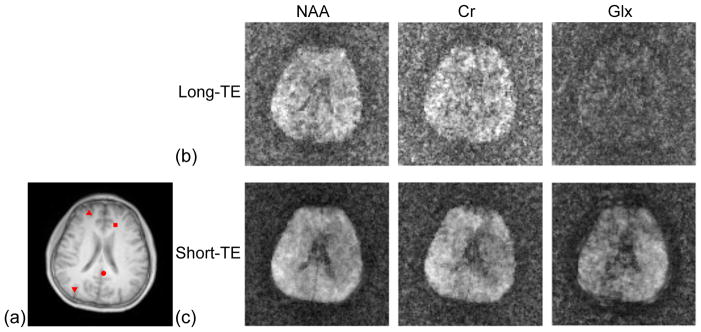
Figure 5 shows nuisance signal removal results of a short-TE SPICE dataset. Significant residual water and lipid signals can be seen in the integrals of the magnitudes of the spectra of the EPSI dataset (Fig. 5a). The integrals of the remaining signals after nuisance signal removal (Fig. 5b) are noise-like (due to the very low SNR of the EPSI dataset) with negligible residual water and lipid signals. After water signal removal using the HSVD method for the training dataset of SPICE (the center 12×12 spatial encodings of the CSI dataset), an NAA concentration map (Fig. 5c) was obtained by taking the integral of the magnitude of spectra in a range of 2.01±0.1 ppm, showing significant leakages of lipid signals. After lipid signal removal by the proposed method, the resultant NAA concentration map of the training dataset had negligible lipid leakages as shown in Fig. 5d. A representative spectrum of the training dataset before and after nuisance signal removal are shown in Fig. 5e and 5f, respectively, further demonstrating that the proposed method was able to effectively remove the dominate water and lipid signals from the low-resolution training dataset of SPICE.

Figure 5.

Nuisance signal removal for a short-TE SPICE dataset. (a) and (b) Spectral integrals of the EPSI data before and after nuisance signal removal. (c) and (d) NAA maps obtained from the short-TE FID signals of the CSI data before and after lipid signal removal (after water removal using HSVD). (e) and (f) Spectra from the marked voxel in (d) before and after nuisance signal removal (Glx: Gln+Glu).

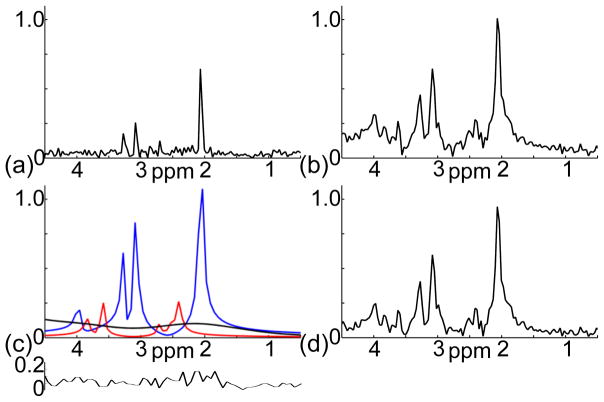
Figure 6 shows a set of results on separating the metabolite and baseline signals from the nuisance signal removed training dataset. The proposed method used both the long-TE (Fig. 6a) and short-TE (Fig. 6b) data to estimate the metabolite signals (the blue and red lines in Fig. 6c) and fitted the baseline signal by smooth spline functions (the black in Fig. 6c). The residual signal obtained by subtracting the estimated metabolite and baseline signals in Fig. 6c from the short-TE signal in Fig. 6b is noise-like (the insert plot at the bottom of Fig. 6c), indicating effective modeling. The baseline removed short-TE spectrum is shown in Fig. 6d.

Figure 6.

Separation of the metabolite and baseline signals from a short-TE double-echo CSI dataset (after nuisance signal removal). (a) Spectrum of the echo signal acquired at 300 ms TE. (b) Spectrum of the FID signal acquired at 20 ms TE. (c) Spectra of the long-T₂ metabolite signal (blue line), short-T₂ metabolite signal (red line), and baseline signal (black line) estimated by the proposed method; the insert plot below is the residual signal. (d) Spectrum of the baseline removed short-TE signal.

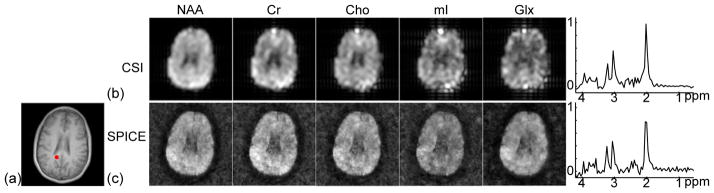
Figure 7 shows metabolite concentration maps and representative spectra obtained by the conventional CSI method and SPICE (with almost equivalent acquisition time). The metabolite concentration maps were obtained by taking the integral of the magnitude of spectra in different ranges: 2.01±0.1 ppm for NAA, 2.40±0.1 ppm for Gln+Glu (Glx), 3.03±0.1 ppm for Cr, 3.20±0.1 ppm for Cho, and 3.60±0.1 ppm for mI. The metabolite concentration maps of the CSI dataset were zero-padded to the same matrix size of the SPICE reconstruction for comparison. As can been seen, the metabolite concentration maps obtained by the conventional CSI method (Fig. 7b) have significant blurring artifacts, while SPICE achieved both high spatial resolution and good SNR (Fig. 7c).

Figure 7.

SPICE reconstruction from a nuisance signal removed short-TE SPICE dataset. (a) Reference anatomical image. (b) Metabolite concentration maps and a representative spectrum obtained from a CSI dataset (20 ms TE, 24×24 spatial encodings, 9.2 mm nominal in-plane resolution, 15.4 min scan). (c) Metabolite concentration maps and a representative spectrum (real part) obtained by SPICE (20 ms TE, 110×110 spatial encodings, 2 mm nominal in-plane resolution, 15.5 min scan).

In vivo experiment II: Comparison of short-TE and long-TE SPICE

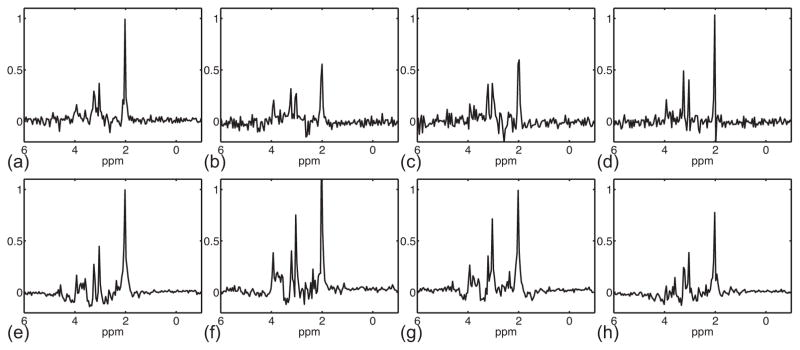
Figures 8 to 10 show comparisons of short-TE and long-TE SPICE results. The intrinsic higher SNR of a short-TE acquisition over a long-TE acquisition can bee seen in the representative spectra of the training datasets as shown in Fig. 8. This SNR advantage resulted in significantly improved SPICE reconstructions as shown in Figs. 9 and 10. While the representative spectra from a short-TE SPICE acquisition clearly have higher SNR than that from a long-TE SPICE acquisition, the improvement is most noticeable in the metabolite concentration maps. This is because the spatial coefficients of the PS model were estimated from sparse EPSI data acquired with high readout bandwidth and thus low SNR.

Figure 8.

NAA concentration maps and representative spectra (real part) reconstructed from a 130 ms TE CSI acquisition and a 20 ms TE CSI acquisition, respectively. Note that the baseline signal was removed in advance for the short-TE spectrum.

Figure 10.

Representative spectra (real part) of short-TE and long-TE SPICE reconstructions. (a) to (d) Spectra obtained by the long-TE SPICE reconstruction, whose location is indicated by the circle, down-pointing triangle, up-pointing triangle, and square in Fig. 9a. (e) to (g) Spectra obtained by the short-TE SPICE reconstruction.

Figure 9.

Comparison of short-TE and long-TE SPICE reconstructions. (a) Reference anatomical image. (b) and (c) Metabolite concentration maps from 130 ms TE and 20 ms TE SPICE acquisitions, respectively.

DISCUSSION

Motivated by the theoretical benefits of short-TE acquisition on quantitation accuracy in the terms of CRLB (Fig. 2), we have developed a new data acquisition and processing method to enable short-TE SPICE. The benefits of short-TE acquisition on SPICE reconstruction itself can be characterized by analyzing the noise properties of the estimated temporal basis and spatial coefficients, respectively. Assuming there is no modeling error, the reconstruction error of SPICE is purely caused by noise. The temporal basis is estimated from the training dataset by SVD. Therefore, its noise is determined by the noise in training dataset, which is often acquired with good SNR. After the temporal basis is determined, the spatial coefficients are determined by solving the weighted-ℓ₂ regularized least-squares problem in Eq. [12]. The affects of noise on the estimated spatial coefficients can be characterized by the well-known matrix perturbation theory (45). For a well-conditioned weighted least-squares problem (i.e., with properly chosen regularization parameters), the noise in the estimated spatial coefficients are determined by the noise in the dataset 𝒟₂. The dataset 𝒟₂ is often acquired in a rapid scan with significantly higher readout bandwidth than the acquisition for the training dataset, resulting in a much larger variance of noise. Therefore, the noise in the estimated spatial coefficients has dominate effects on the resultant SPICE reconstructions. While improving the intrinsic SNR of the acquired signals, short-TE acquisitions will effectively reduce the spatial variations of SPICE reconstructions over long-TE acquisitions (as shown in Fig. 8).

Short-TE acquisitions lead to increased nuisance signals and non-negligible baseline signals. We address these issues in a union-of-subspaces framework, wherein the PS properties of the nuisance, baseline, metabolite signals are exploited. In vivo experimental results in Fig. 4 show that the proposed method can effectively remove the nuisance signals (residuals after nominal suppression) from the sparsely sampled SPICE data with negligible residuals. In the proposed method, the baseline signals are jointly reconstructed along with the metabolite signals from the nuisance signal removed SPICE data, which allows incorporating different prior knowledge of the baseline and metabolite signals into the SPICE reconstruction. In our current implementation, we impose an edge constraint on the reconstructed metabolite signals and a spectral smoothness constraint on the reconstructed baseline signals. Alternative constraints include the spatial and spectral sparsity constraints on the metabolite signals. Joint estimation of the baseline and metabolite signals could also result in more accurate quantitation as indicated by the CRLB analysis shown in Fig. 2.

We proposed a new method to separate baseline and metabolite signals using a double-echo acquisition, which may also prove useful for conventional MRSI experiments. Besides exploiting the temporal separability of a short-TE signal as in the “subtract” method, the proposed method uses an additional long-TE echo signal for better estimation of long-T₂ metabolite signals (the dominate components in a short-TE spectrum) and thus improves the estimation of the baseline signals. In the proposed double-echo acquisition, there is an inherent tradeoff between the spectral resolution (or the length) of the short-TE FID signal and the SNR (or the echo-time) of the long-TE echo signal. According to our experience, this tradeoff does not impose significant limitations on MRSI experiments at high field (≥ 3 T), especially when quantitation methods (e.g., LCModel (23)) that take advantage of prior knowledge of metabolite spectrum are used in the subsequent analysis. The acquisition time of 𝒟₂ per TR is the same as the short-TE FID signal of the training dataset. The tradeoff does not impose significant limitations on SPICE reconstructions neither, because the condition number of the least-squares problems in Eq. [12] quickly stabilizes as the acquisition time per TR increases according to our experience. In our current implementation, only the short-TE signals of the EPSI acquisition are used for SPICE reconstruction. It is also possible to extend SPICE to utilize both the short-TE and long-TE signals of a double-echo EPSI acquisition for better reconstruction of long-T₂ metabolites.

CONCLUSIONS

Short-TE acquisitions can effectively improve the SNR of SPICE reconstructions over long-TE acquisitions. The proposed union-of-subspaces based method can effectively remove the nuisance and baseline signals and reconstruct high-resolution spatiospectral distributions of the metabolite signals from sparsely sampled (k, t)-space data. The proposed method enables short-TE SPICE, which should prove useful for high-resolution ¹H-MRSI studies of the brain.