Addressing current challenges in cancer immunotherapy with mathematical and computational modelling

Abstract

The goal of cancer immunotherapy is to boost a patient's immune response to a tumour. Yet, the design of an effective immunotherapy is complicated by various factors, including a potentially immunosuppressive tumour microenvironment, immune-modulating effects of conventional treatments and therapy-related toxicities. These complexities can be incorporated into mathematical and computational models of cancer immunotherapy that can then be used to aid in rational therapy design. In this review, we survey modelling approaches under the umbrella of the major challenges facing immunotherapy development, which encompass tumour classification, optimal treatment scheduling and combination therapy design. Although overlapping, each challenge has presented unique opportunities for modellers to make contributions using analytical and numerical analysis of model outcomes, as well as optimization algorithms. We discuss several examples of models that have grown in complexity as more biological information has become available, showcasing how model development is a dynamic process interlinked with the rapid advances in tumour–immune biology. We conclude the review with recommendations for modellers both with respect to methodology and biological direction that might help keep modellers at the forefront of cancer immunotherapy development.

1. Introduction

The involvement of the immune system in all stages of the tumour life cycle, including prevention, maintenance and response to therapy is now recognized as central to understanding cancer development from a systemic point of view. Therefore, it is not surprising that one of the most rapidly developing and exciting fields in cancer treatment is that of cancer immunotherapy, i.e. therapy that boosts the function of the patient's own immune system in targeting the cancer. The development of a knowledge-base of tumour–immune interactions and basic and clinical work on cancer immunotherapy has been paralleled by the development of mathematical and computational models that use this knowledge-base to design in silico model systems upon which immune-based and other treatments can be modelled. In the best case scenario, these models can serve to guide clinicians and developers of clinical trials towards optimizing mono- and combination therapies and basic scientists in understanding the underlying mechanisms of the effectiveness (or, ineffectiveness) of therapy combinations. Therefore, in a field as rapidly developing and clinically important as cancer immunotherapy, mathematical and computational modelling can play a central role in helping to guide the direction the field takes.

In this review, we survey the mathematical modelling work in cancer immunotherapy organized by the ‘major challenges’ that the immunotherapy community is currently grappling with. We will also outline strategies that modellers, ideally in collaboration with experimentalists, can use to further enhance their contribution to addressing these challenges.

This review is organized as follows. In §2, we give a brief overview of tumour immunology and cancer immunotherapy. We also outline ‘major challenges’ that have been posed in the immunotherapy community. In §§3–5, we survey how each challenge has been addressed by the modelling community; in §6, we provide recommendations as to what techniques the community can employ to further progress on each challenge and to address other rising challenges, and in §7 we summarize our findings.

2. The major challenges for cancer immunotherapy

A tumour can, in principle, be recognized and controlled by the patient's immune system via a coordinated process that has recently been summarized as the ‘cancer-immunity’ cycle [1]. Dying tumour cells present and release proteins that contain unique tumour-associated antigens that are either mutated or differentially modified post-translationally relative to normal cells [2]. Tumour cells also release inflammatory signals in the form of cytokines and other factors (such as heat-shock proteins) that lead to a local innate inflammatory response. Dendritic cells (DCs), which form a part of this response, can uptake these antigens and, if properly activated by other factors in the tumour microenvironment, differentiate to present these antigens to lymphoid cells via their MHC class I and II molecules. Activation of cytotoxic CD8⁺ T cells results in their proliferation and trafficking to the tumour site in order to kill the tumour cells, leading to the release of more tumour-associated antigens and thus repeating the cycle. This process by which the immune system keeps a tumour in check is defined as cancer immunosurveillance. Via a counter-process termed immunoediting, tumour cells can evolve and strengthen various mechanisms to escape immunosurveillance [3–5].

The goal of cancer immunotherapy is to boost the response of the immune system to the tumour by intervening at one or several points of the cancer-immunity cycle. The antigen-based activation of DCs can be achieved by administration of a therapeutic vaccine harbouring one or multiple tumour-associated antigens, with or without additional factors that prime DCs for activation. Another approach has been to extract peripheral blood monocytes and stimulate them using cytokines and/or other mechanisms [6] to become DCs ex vivo before reintroducing them into the patient. An FDA-approved example of the latter is the drug Provenge (sipuleucel-T; Valeant Pharmaceuticals), which improves median survival time in advanced prostate cancer by approximately 4% [7]. Therapies that directly boost anti-tumour T-cell activity include adoptive T-cell therapy and inhibition of T-cell checkpoint molecules. In adoptive cell therapy (ACT), T cells are collected from a patient, expanded ex vivo and reintroduced into the patient. This method has been highly successful in melanoma and is being explored for other cancers [8]. The success of ACT can be further boosted by genetic modification of the T cells with chimaeric antigen receptors (CARs), which are fusion proteins of a TCR signalling domain and an antigen-binding moiety specific for tumour-associated antigens [9]. There are currently over 100 clinical trials in progress on CAR T-cell therapy [10]. Checkpoint therapy involves antagonizing T-cell inhibitory receptors (such as CTLA-4 or PD-1). Reciprocally, there are a number of activating costimulatory receptors on T cells (such as OX40, 4-1BB, GITR and CD27) that can be engaged to boost T-cell clonal expansion and acquisition of tumouricidal effector functions [11]. Major successes using this method include the FDA-approved Yervoy (ipilimumab; Bristo-Myers Squibb), a monoclonal antibody (mAb) to CTLA-4 that is used for patients with melanoma [12,13]. In 2016, the FDA approved Tecentriq (atezolizumab; Genentech), an inhibitor of the ligand for PD-1 (PD-L1) that is expressed on tumour cells and that would otherwise engage PD-1 on tumour-infiltrating T cells, for treatment of locally advanced or metastatic bladder cancer [14]. For a more extensive discussion of cancer immunotherapies and drugs in clinical development, see [1,11,15].

There are particular challenges that present themselves in almost all applications of cancer immunotherapy and have been addressed by the mathematical community. These major challenges include

• (i) tumour classification for treatment and prediction of response;

• (ii) optimal scheduling and dosage of treatment; and

• (iii) design and identification of combination treatment regimens.

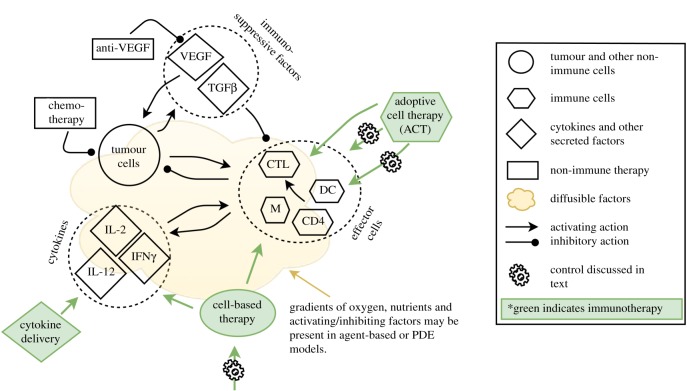
In this review, we use these ‘major challenges’ as a means by which to present how mathematical modelling can help to address each challenge and thereby help to progress the field of immunotherapy research and application. A summary of the tumour–immune and immunotherapy interactions consistently addressed by the models across these challenges is depicted in figure 1.

Figure 1.

Summary of modelling efforts in immunotherapy. Generally, models (both mathematical and computational) are at the cell-population level and consist of tumour and immune cells (immune cells may be represented cumulatively as effector cells or more specifically by cell types), cytokines and other immune-activating or inhibiting factors such as VEGF or TGFβ, with therapies (in green) targeting any of these factors. Models can assume spatial homogeneity (ordinary differential equation, ODE models) or be spatially heterogeneous (agent-based and partial differential equation (PDE) models). For addressing tumour classification for treatment (Challenge 1, §3), analytical, numerical and/or parameter sensitivity analysis is performed on the models to determine which system parameters contribute most strongly to prediction of treatment response. Control theory and evolutionary algorithms (depicted by cogwheels) are applied to modelled treatments to optimize scheduling and dosage (Challenge 2, §4), and all these methods can be applied to multiple treatments, including non-immune therapy such as chemo- and molecular therapy, to model combination treatment regimens (Challenge 3, §5). CTL, cytotoxic T cells; DC, dendritic cells; CD4, CD4⁺ T cells, M, macrophages.

3. Challenge: tumour classification for treatment and prediction of response

Tumour classification, usually based on histopathological grading, does not serve as a strong predictive tool for post-treatment outcome. More sophisticated methods of tumour classification, such as immune profiling [16], inclusion of markers of the tumour microenvironment [17] and incorporation of high-throughput data [18], can improve the predictive strength of the classifications. Nevertheless, due to both the increasing availability of patient data and the treatment options, it can become difficult to predict how a patient with a specific set of tumour characteristics will respond to a given treatment. Modelling efforts in this regard have been used to identify which patient parameters may be most important to predicting therapy outcomes. As mathematical models, unlike statistical models, are typically mechanistic, they can be used to predict the effect of therapy or therapy combinations that have not yet been tried in the clinic (i.e. for which patient data are as yet unavailable).

We begin with the Panetta–Kirschner (PK) model [19], one of the first to layer immunotherapy into a tumour–immune model. The PK model consists of system of three ordinary differential equations (ODEs) that model the dynamics of effector (E) and tumour (T) cells, and the cytokine IL-2 (I_L). For the sake of expediency and since one of the parameters is especially important in the analysis of model behaviour, we only show the equation for E,

3.1

The antigenecity of the tumour is modelled by the parameter c, μ₂ represents the death rate of E, and the proliferative effect of I_L on E is in Michaelis–Menten form to model saturation of response. Therapies are considered by terms s₁ and s₂ added to the right-hand side of dE/dt and dI_L/dt, respectively. Michaelis–Menten terms are also used to model the negative effect of E-induced tumour destruction on T, and the positive effect of tumour-resident E on I_L production. Tumour growth is modelled using the logistic growth function. The authors show that with no therapy, if c is below a critical c₀, the only stable steady state is a large tumour. As c increases, the tumour size oscillates between large and small, with the time it spends in its ‘large’ state (and the magnitude of the ‘large’ state) decreasing with increasing c. Adding therapy s₁ creates a tumour-free equilibrium that is stable if s₁ > s¹_crit, where s¹_crit depends on several parameters of the model. A bifurcation diagram of s¹_crit versus c shows that there exist regions where the tumour will either die or survive depending on c, hence providing a mathematical basis for tumour classification for treatment. The authors show similar results for s₂ > 0 and both s₁ and s₂ > 0.

Models with a relatively small number of equations can be analysed in this way and have consistently shown that knowledge of system parameters can help lead to tumour classification for treatment via bifurcation and stability analysis (e.g. [20–23]). Identification of parameters where thresholds exist with respect to system response to therapy can aid in the identification of effective therapies. For example, for the system modelled in [19], a therapy that increases the antigenecity, c, of the tumour can push the tumour past the critical point necessary for response to other therapies and/or towards a reduction in size to a small, stable steady state. An excellent review of simpler tumour–immune models and their associated analyses, which may or may not incorporate immunotherapy, can be found in [24]. A meta-modelling approach was taken by d'Onofrio et al. [25] to synthesize the analytical results of such models. These models can serve as baseline models that can be extended to incorporate immunotherapy.

Numerical analysis of models has also focused on the concept of thresholds for predicting patient response. For example, Kronik et al. [26] set out to answer the question whether ‘mathematical modelling would help to define the prerequisites of an effective immunotherapy approach’. They extended a previously published model of T-cell transfer immunotherapy for glioblastoma [27] to a model of ex vivo expanded tumour-specific T-cell transfer for melanoma and used clinical data to retroactively validate it. The model consists of a system of ODEs with five equations representing tumour and immune cells, and critical signalling molecules produced by the two cell populations (TGFβ, IFNγ and MHC class I molecules). The authors varied initial tumour size and growth rate to imitate a virtual population of patients with heterogeneous tumour profiles. Four different T-cell therapy regimens were then simulated over this population that corresponded to four different clinical trials. For one such trial, the model was able to offer an explanation for the lack of a dose–response relationship with therapy: the model showed that for patients with large enough tumours, the therapy would have no effect, whereas in smaller tumours a dose–response relationship could be identified, again pointing to a threshold for therapy effectiveness, this time via simulation in lieu of a bifurcation analysis. Indeed, the authors suggested that volumetric tumour analysis is a better predictor for clinical effectiveness of T-cell therapy than the traditional staging method. The authors also called for large doses of T-cell therapy due to the presence of thresholds for efficacy of T-cell killing with respect to T-cell concentrations, although this recommendation should be considered in light of potential toxicities. More broadly, parameter sensitivity analysis has played a critical role in the numerical analysis of models of immunotherapy (e.g. [28–31]) by helping to elucidate which tumour characteristics are most predictive of therapy success.

To investigate how spatial organization of different cell types can impact tumour–immune evolution and response to therapy, Wells et al. [32] developed a hybrid discrete-continuous (HDC) agent-based model (ABM). These models treat cells as agents that sit on a lattice and can interact with and respond to other cells in a stochastic manner through growth factors and cytokines that can diffuse throughout the lattice. The cell types in this model were naive, M1 (tumour-suppressive), and M2 (tumour-promoting) macrophages, and live and dead tumour cells. In addition to secreted factors, oxygen diffusion was also implemented in the model, thereby creating oxygen-rich and hypoxic regions in the tumour and its microenvironment. The authors used a multiparametric sensitivity analysis to observe that the ratio of M2 to other cell types (termed the Macrophage Polarization Index, MPI) early in the simulation is predictive of tumour survival. Another key predictive outcome of the model was that increased tumour heterogeneity is associated with tumour survival. Tumour heterogeneity was associated with locally elevated stimulated macrophages, leading to local peaks of M2 differentiation which increased overall MPI. It followed that a decrease in secretion of differentiation factors for M2 cells abrogated the association between tumour heterogeneity and survival in the simulation. Therefore, the model provided a novel hypothesis for tumour-induced immunosuppression via increases in tumour-heterogeneity, but also a potential new prognostic tool for tumours where biopsies and cell-specific stains are available. This observation was further used by the authors to hypothesize and test in silico that introduction of genetically engineered macrophages that could block the M2 transition would be effective in killing the tumour by blocking the feedback loop that generates localized sites of highly concentrated immunosuppressive M2 cells, thereby constructing a novel treatment using their observations of the most critical contributors to tumour growth.

Lattice- and/or ABMs can provide additional information regarding spatially explicit parameters influencing tumour–immune interactions and response to immunotherapies. In addition to [32], this approach has been used by Papalardo and colleagues [33,34] to develop an agent-based simulator of the Triplex vaccine, SimTriplex, which is effective in preventing mammary carcinoma in HER-2/neu transgenic mice, and Dréau et al. [35] to examine the interactions between a vascularized tumour and the immune response. While partial differential equation (PDE) models have been much more sparsely employed to model immunotherapy, they can be especially useful when modelling a large number of interacting cells in a tissue, in which case building a corresponding ABM would be too computationally costly. For example, Eikenberry et al. [36] developed a PDE of melanoma with immune infiltrate, and showed that surgical removal of primary tumours with high levels of immune infiltrate could promote growth of satellite metastases, as was observed clinically, thereby providing a model-based hypothesis for tumour classification with respect to responsiveness to therapy (in this case, surgery).

4. Challenge: optimal scheduling and dosage of treatment

For any given treatment, an exhaustive experimental search for optimal dosage and/or scheduling is unrealistic. There are several techniques which developers of mathematical models for immunotherapy have used to identify optimal treatment schedules in silico, including optimal control and genetic algorithms.

4.1. Optimal control theory

Optimal control theory has played a prominent role for using mathematical models of cancer immunotherapy for design of optimal therapy regimens. We can consider a system of ordinary differential equations,

4.1

where 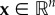and 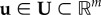is a control parameter (e.g. x(t) can represent concentrations of tumour cells, immune cells and cytokines and u(t) can represent an immunotherapy treatment), and an initial condition x⁰. The optimal u, u*, is chosen from a space U of admissible controls based on constraints on x and u via calculation of an extremal of an objective functional

4.2

where r is termed the running payoff and g the terminal payoff [37]. This formulation is termed the Bolza form. The optimal u* found using this method then represents the best possible therapy given conditions on the control parameters (such as minimization of tumour cells, minimization of therapy dosage, maximization of immune response, etc.).

Optimal control theory has been applied extensively to the PK model [19], described in §3. Burden et al. [38] made ACI therapy in the PK model into a control parameter, u, and built an objective functional

4.3

where x(t) are activated effector cells, y(t) are the tumour cells, z(t) the local concentration of IL-2, and B the strength of patient tolerance to treatment (i.e. B is inversely correlated to side effects of treatment). For t ∈ [0,T], the class of admissible controls was set to

and u* was found such that 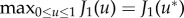, which minimized tumour mass and therapy administration, and maximized effector cell and IL-2 concentration. A down-side to the model was that at the end of treatment, tumour mass tended to start regrowth. Ghafferi & Naserifar [39] improved upon the model of Burden et al. [38] by including a linear penalty, −ωy(t_f), where ω is constant, y is the quantity of cancer cells and t_f is the final time-point of observation, such that their objective functional is J₂(u) = −ωy(t_f) + J₁(u) (note that −ωy(t_f) is the terminal payoff for J₂(u), as defined above). The updated objective functional allowed for identification of a treatment that stops tumour regrowth and also acts faster than the treatment identified with J₁(u).

Similarly, Castiglione & Piccoli [40] used optimal control for a model they developed to investigate dendritic cell vaccine (DCV) therapy for solid avascular tumours. For N total number of vaccinations and η total time for one vaccination, the space of admissible controls, U, was taken to be

where S = {t_i : i = 0, …, N − 1, 0 ≤ t₀ ≤ T − η} is in the space of DCV injections schedules U_S, and for every S ∈ U_S, the control u was taken to be

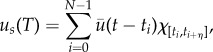4.4

where 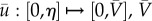, maximum vaccine amount and χ the indicator function. For every u_s, the therapy consisted of vaccine injections, modelled by 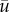, at time-intervals [t_i − η, t_i] for all t_i in S. The objective functional (here termed the cost functional since it was minimized) was taken to be the final value of the tumour mass M, and the optimal control problem was stated as follows: for initial condition x⁰, what is the schedule S ∈ U_S such that M attains a minimum? The problem stated as such is known as the Mayer form, which can be used when the running payoff, r, is zero in equation (4.2). The authors took T = 6 months, N = 10 DCV injections and η = 0. An initial schedule S₀ was chosen randomly and 2000 optimization steps were taken to find the optimal 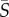, which resulted in almost complete clearance of a tumour. Nevertheless, resurgence of tumour cells occurred between vaccinations and the final value of the tumour mass was highly dependent on the timing of the last vaccination.

In order to correct for this effect, Piccoli & Castiglione [41] expanded the cost functional in [40] to also minimize the time during which the tumour is above a maximum mass, M^max, necessitating a switch back to the Bolza form for their objective functional. The authors emphasized that the optimal injection schedule u* obtained is highly dependent on the parameter values and initial conditions of the system, indicating that the parametrization of the system from patient characteristics or other relevant knowledge should be performed carefully. Castiglione & Piccoli [42] further expanded the cost functional in [41] to include, in addition to the previous constraints, drug holidays and minimization of vaccine injected to lower toxicity. The authors also considered different types of cost functions: continuous, impulsive (similar to equation (4.4), but with η = 0), or hybrid (equation (4.4), η ≠ 0), to take into account the different scales between duration of drug injection and tumour growth. The hybrid method was found to be most effective for their system and the optimal treatment schedule that was identified consisted of a high initial dose and repeated smaller follow-up doses.

One can find further examples of optimal control theory applied to immunotherapy in [43,44]. Notably, both studies layer an optimal control approach upon previously developed cancer immunotherapy models. Similarly, the examples discussed above of optimal control theory applied to cancer immunotherapy show that the controls are developed slowly, with complex control functions often built upon more simple and established ones.

4.2. Genetic algorithms

For computational agent-based models, function optimizers such as genetic algorithms (GAs) are more suitable. GAs are part of a class of evolutionary algorithms that work as follows: a set of n initial binary strings, {S⁽¹⁾_i}ⁿ_i=1, sometimes termed ‘chromosomes’, representing possible solutions to the problem of interest are processed via an evaluation function, E_i = E_i(S_i), which gives a measure of the string's performance, and a fitness function, F_i = F_i({E_i}), that compares the performance of all the strings to each other. In the intermediate selection phase, strings S⁽¹⁾_i are kept and duplicated with probability proportional to their respective fitness functions, F_i. The strings of this intermediate population, {S^(1*)_i} are then recombined with each other by cross-over and mutated at a low rate to obtain a new generation of strings, {S⁽²⁾_i} (note that the i do not represent the same string between the generations (1), (1*) and (2)). This process is repeated until an ‘optimal’ string is found, either via running the algorithm for a fixed number of generations, or until a string is found that surpasses a threshold set by the fitness function. This optimal string, like u* in optimal control theory, represents an optimal therapy solution given constraints imposed by the evaluation and/or fitness functions. Importantly, an agent-based or other computational model can be run with any possible therapy (string), and the results can be used to determine the output of the evaluation function, thus the optimal string will give the optimal therapy vis-a-vis the computational model. We have described the ‘canonical genetic algorithm’ [45] originally developed in [46], and there exist many modifications that will not be presented here [45,47].

Lollini et al. [48] set out to use a GA to develop an optimal vaccine schedule for the agent-based SimTriplex model [33] described in §3. The Triplex vaccine is a cell-based vaccine that stimulates an immune response via engineered HER-2/neu-positive cells that express allogenic MHC class I molecules (for increased recognition by CD8⁺ T cells) and IL-12, which boosts both humoral and adaptive immunity [49]. The GA was initialized with 80 binary 1200-bit strings, where each bit represents a time-step where a vaccine injection is/is not (1/0) given. For each string, the SimTriplex simulator was used to determine mouse survival time (s) and maximum number of cancer cells in the transient (N¹_cc) and steady (N²_cc) tumour growth phases. The evaluation function was then taken to be

4.5

where n is the number of injections specified by the test string, and β = β(N¹_cc, N²_cc) is proportional to the maximum number of cancer cells. Note that in this implementation, the aim was to minimize the fitness function. Via tournament selection (the fitness functions of two or more strings are compared and the probability of selecting a string is proportional to the fitness ranking of the string), followed by mutation and elitism (the best strings are not mutated), an optimal string (i.e. vaccination schedule) was selected. Also, in this case, equation (4.5) was referred to as the ‘fitness’ function, which is not to be confused with our definition above.

An extension of this fitness function was applied in the algorithm in [48] which incorporated several instances of in silico mice with varying immune backgrounds to choose the optimal vaccination schedule, S*. This schedule was applied to two sets of 100 virtual HER-2/neu-positive mice and resulted in 90% survival rate (this is in comparison to a chronic protocol, which requires four vaccinations in a 2-week ‘on’ and 2-week ‘off’ protocol, over the course of at least 1 year, and has 100% success rate, but is not realistic for clinical development). A previous ‘trial-and-error’ schedule was found to reduce the number of injections by approximately 27% over the chronic schedule, whereas the one identified by the GA reduced it by approximately 42%, yielded excellent survival, and generated similar immune dynamics to the current protocol. In a follow-up study, Palladini et al. [34] showed excellent agreement between the in silico predictions and in vivo experiments, and made additional observations, such as the importance of vaccination density in the early phase of the immune response and dependence of vaccine success on age of the mouse. GAs and evolutionary algorithms have also been used to identify potential epitopes for vaccine development [50], to develop an initial guess for a discrete optimal control problem based on the model in [42,51], and to solve a multi-objective optimization problem for a model of combination chemo- and immunotherapy [52].

By example of optimal control theory and genetic algorithms, we have shown how mathematical methods in optimization used in conjunction with appropriate models yield treatment schedules derived in a systematic, rather than experimental or computational ‘trial-and-error’ method, that can be used not only to create optimal treatment schedules, but to also better understand immune response to treatment, such as the observations obtained from both methods above to the relative importance of early versus late immunization protocols.

5. Challenge: design and identification of combination treatment regimens

Just as combination therapy using non-immunotherapeutic approaches is a mainstay in cancer treatment, combination immunotherapy either with just immunotherapeutic agents or with immune- and non-immunotherapeutic agents can and should be designed rationally to maximize treatment response [11,17]. Modelling can contribute to this process as it can aid in the development of a mechanistic understanding for effectiveness of combination versus monotherapies and make the search for an optimal combination therapy more efficient. For example, de Pillis et al. developed a system of six ODEs for combination chemo- and immunotherapy that included tumour, NK, CD8⁺ and white blood cells, as well as bloodstream concentrations of chemotherapy (doxorubicin) and immunotherapy drugs, the latter of which include tumour-infiltrating-lymphocyte (TIL) therapy and IL-2 stimulation [53]. The model extended an earlier model by de Pillis et al. [54] to include more recent biological findings. The effect of chemotherapy, M, was modelled using a saturation term, 1 − e^−δM, where δ represents the efficacy of M, and the boost to CD8⁺ activity by addition of IL-2 was modelled using a Michaelis–Menten interaction term, similar to what we see in equation (3.1) from [19]. Cell–cell interaction terms were modelled using previously fit equations, often of Michaelis–Menten type. For example, the CD8⁺ T-cell stimulation by the tumour was taken to be

5.1

where T and L represent the tumour and CD8⁺ populations, respectively, and j and k are parameters. Following [54], several parameters of the model, which collectively determine CD8⁺ T-cell efficacy at tumour cell killing, were fitted to patient-specific data. The authors found that the success of combination versus monotherapy differed based on initial patient characteristics. For example, patients with higher CD8⁺ T-cell efficacy would benefit more strongly from immuno- or combination therapy than patients with low efficacy, since an injection of IL-2 for the latter group would result in more CD8⁺ T cells, but not enough to increase overall anti-tumour response. Notably, had the authors modelled an immunotherapy that altered these variables directly (such as injection of CD8⁺ T-cell costimulator agonists that boost CD8⁺ effector activity), they would have obtained different success rates for the therapy combinations. Nevertheless, the model can serve as a forerunner to models parametrized with patient-specific parameters that can then be used to identify optimal therapy combinations.

Targeted therapies, such as antibodies against the breast cancer cell receptors HER2 and EGFR, elicit a strong, adaptive immune response, raising the implication that combination immunotherapy with targeted therapy can achieve a synergistic anti-tumour immune response [55,56]. The humanized antibody to VEGF, Avastin (bevacizumab), is FDA-approved for a number of different cancers, and in addition to blocking the pro-angiogenic activity of tumour-produced VEGF, also blocks the immunosuppressive activity of VEGF, which includes suppression of DC maturation [57]. Soto-Ortiz et al. [58] hypothesized that a combination therapy of an anti-VEGF antibody followed by administration of DC cells would result in a strong anti-tumour response by the immune system. The authors built upon a model that focuses on tumour–immune interactions [59] to develop a system of 18 ODEs that include tumour, immune and vascular endothelial cells, and a number of cytokines and growth factors including IL-2, TGFβ and VEGF (both TGFβ and VEGF are considered to be immunosuppressive). The authors simulated treatment with injection of anti-VEGF antibody and/or unstimulated DC cells and analysed the results numerically. The simulations showed that for tumours with low immunosuppression and high antigenecity, which is represented by a parameter that models the strength of maturation of DCs after encounter with a tumour antigen, the immune system can keep the tumour at a small size and administration of either therapy can kill the entire tumour. When tumour antigenecity was lowered and immunosuppression increased, the simulated tumour grew and vascularized without therapy. The authors observed that for tumours with high immunosuppression, DC therapy alone was not sufficient to kill the tumour without additional modification of the immunosuppressive microenvironment, which is an example of a prediction for effectiveness of a mono- versus combination therapy when given initial system parameters. The authors made a number of other observations regarding the interdependencies of tumour growth, antigenecity and immunosuppression that would not have been possible in a simpler model. A prediction arising from this analysis was that there exists a therapeutic window for optimal effectiveness of different immunotherapies that is dependent on the tumour size and growth rate, and thus knowledge of these tumour characteristics can be used to design the optimal mono- or combination therapy for a given tumour/patient. Moreover, synergy in combination therapy was predicted to occur when immunotherapy followed anti-VEGF treatment, thus the model was able to address questions of efficacy prediction and optimal time and selection of treatment, and hence effectively address all the major challenges we have discussed.

Models for various combinations of traditional and immunotherapies have been developed [60–63], which generally build on earlier tumour–immune, monotherapy or even combination therapy models. For example, Chareyron & Alamir [64] extended earlier models developed by de Pillis et al. [28,65] to include chemo- and immunotherapy and used control theory to determine optimal therapy protocols, again addressing multiple major challenges discussed herein. Such models can give insights as to mechanism and efficacy of combination therapies in order to guide clinical development.

6. Recommendations

6.1. Intracellular and multi-scale modelling

Most current immunotherapy models are developed at the resolution level of cell populations. However, modelling intracellular signalling cascades and metabolic responses in specific cell types can give insight into how therapies can act at the intracellular level, and what the relative contribution of different therapies is to cell response: intracellular versus cell–cell. As in the case of population-level models of immunotherapy, where the therapy component is often added to an existing, validated model of tumour–immune interactions, the intracellular models of therapy can build on known signalling pathways that interact with proposed therapies in tumours and T cells. Intracellular signalling models have been developed for cancer signalling pathways for a variety of tumour types [66,67], and can be modified to include subpathways of interest, such as induction of PD-L1 or secreted immunosuppressive factors. Saez-Rodriguez et al. [68] built a Boolean network model of a signalling network activated upon T-cell receptor and coreceptor activation and validated it using both the literature and experimental wild-type and knock-out data that matched in silico predictions. This network could be made more specific for different T cells (CD4⁺, CD8⁺, Treg), receptors of therapeutic interest (e.g. CTLA-4, PD-1) and their downstream signalling targets, which can be added to the model in order to examine how therapy would affect T-cell activation status. Other intracellular-level models that can be incorporated into a multi-scale setting include models at TCR-level resolution, which are particularly important for therapies that target the TCR, such as CAR T-cell therapies. For example, James et al. [69] derived a logistic-type growth equation for chimaeric CAR to show that in a high-antibody environment, T-cell death and exhaustion or CAR downmodulation acted as limiting factors to CAR activity. Also, optimal CAR densities/cell were derived for maximal efficacy. Modification of networks and other intracellular models identified in the literature may require additional experimental input, depending on the current availability of data. Such models would allow a more granular systems-level analysis of mechanisms of pharmaceutical action and subsequent therapy optimization and combination. Furthermore, since immunotherapy drugs can act on multiple cell targets, for example, CTLA-4 is expressed not only on CD8⁺ T cells but also Tregs, development of multi-scale models that incorporate both the interactions of different immune and tumour cell types and their respective intracellular dynamics would have the power to elucidate the multi-scale mechanisms of therapy action. Indeed, multi-scale modelling has already been identified as an important method for generating systems-level predictions of cancer progression and therapy effectiveness [70,71].

6.2. Addressing toxicity

Immune-mediated toxicities, including retinal dysfunction, liver toxicity and pancreatitis can occur upon administration of immunotherapy. Toxicity, which is generally caused by targeting of self-antigens by the treatment-strengthened immune response, is often associated with clinical response [72]. Incorporation of immunotherapy-related toxicity into models can result in estimates of therapy dose that take into account toxicity-related effects, as was already done in [38]. Development of more mechanistic models can help to optimize therapies to maximize effectiveness and minimize toxicity if mechanisms for each are not entirely overlapping. This may be especially important in models of combination immunotherapy, where toxicity-related events tend to be more common than with monotherapies [73]. One route of interest towards this goal can be a joint experimental-modelling focus on Fc–FcR interactions. Immunomodulatory mAbs such as ipilimumab, a mAb to CTLA-4, are most often of IgG isotope: in addition to containing two antigen-binding (Fab) domains, they contain a fragment crystallizable (Fc) ‘tail’ that can bind Fc receptors (FcRs) found on effector cells such as macrophages and DCs. Fc–FcR interactions have been shown to contribute to cytokine-related adverse events during mAb treatment, and hence modulation of these interactions during mAb design could help to decouple therapeutic from toxic responses. A better mechanistic understanding of Fc–FcR engagement and response during treatment could help lead to rational design of mAbs that reduce adverse events related to Fc–FcR interactions (reviewed in [74]). By developing models of Fc–FcR action in concert with experimentalists, modellers can hasten this process and use their models to guide development of optimized therapy options.

6.3. Experimental and clinical validation of immunotherapy models

We have shown how the models have been retrospectively (e.g. [26,54]) or prospectively (e.g. [34]) experimentally validated for a portion of their predictions, but do generally provide more predictions than are validated. An example of a cancer immunotherapy model that has been prospectively validated can be found in Elishmereni et al. [75], who extended a previously published system of ODEs describing the interaction of the cytokine IL-21 with immune and tumour cells to include pharmacokinetic (PK) and pharmacodynamic (PD) data on the IL-21 effect in tumour-bearing mice from an earlier preclinical study. The authors used a ‘multiple-modelling’ approach to determine the most robust model that fit the available data. The model was retrospectively validated using additional data from the same preclinical study. The model was then used to search for a treatment regimen that would be more effective than the one identified in the preclinical study. Model simulations showed that fractionating a daily dose of 50 μg IL-21 into two daily doses of 25 μg per day decreased overall tumour volume, which was verified in tumour-bearing mice to whom the treatment regimen was applied. The model also showed that a daily dose of just 12 μg d⁻¹ would give similar results to 50 μg d⁻¹, which was also prospectively validated in mice. It is possible that a control algorithm such as described in §4 would have produced an even more effective regimen that could be prospectively validated in a similar manner. Similarly, Gorelik et al. [76] used, as a starting point, a previously published model of vascular tumour growth, and used patient-specific data along with mouse xenograft data of the patient's tumour to develop a combination chemotherapy regimen. Model parameters were partially fit using an evolutionary optimization algorithm (the cross-entropy, CE, method) [77]. Xenograft data were scaled back to the patient using gene expression ratios between the patient and xenograft tumours. This regimen was then applied to the patient, which stabilized the metastatic progression. While the therapy regimen did not include immunotherapy, the method of translation from model to clinical application can be applied to combination therapies involving an immunotherapy component.

In the modelling/experimental cycle, models are developed and parametrized using a portion of existing data, and often partially validated using data that are already available, but have not been used in model development. Nevertheless, a model will often provide novel predictions of system behaviour whose results are not available for testing given current data. Testing these predictions is most often done through new or existing collaborations between modellers and experimentalists or clinicians. In some cases, publicly available data may also be used. While there is an increasing number of such collaborations, as well as research groups that integrate both areas of expertise, this requirement could be considered the main bottleneck for wider validation and use of mathematical and computational models for the purpose of developing novel immune therapies for cancer patients. Both communities would benefit from outreach efforts for this purpose. Further recommendations on extending existing models for experimental and clinical applications can be found in [78,79].

7. Conclusion

Immunotherapy is one of the most exciting recent developments in cancer treatment, with new drugs coming on the market at an increasing rate, for an ever-larger number of cancers. But, as this review highlights, many unanswered questions remain, and the field faces several challenges. Mathematical modellers have addressed these challenges as early as the 1980s (e.g. [80]). The models we have reviewed here and their use in understanding various aspects of immunotherapy crucial for effective treatment, show that mathematical and computational models can play the role of a key enabling technology to improve the application of this type of treatment. However, as this review also discusses, there is much work to be done. Almost all immunotherapy-specific modelling efforts we could identify focus on the population level, even though it is clear that a multi-scale approach is needed that also incorporates the molecular scale. To aid this process and to stay at the forefront of immunotherapy technology development, high-throughput data derived from technologies such as microarrays and RNA-Seq for cell-level transcriptional information and mass cytometry (CyTOF) for population-level marker distribution can be incorporated into model development [81].

Collaborations between modellers, basic scientists and clinicians are crucial for the realization of the translational potential of mathematical modelling in the service of a precision medicine approach to this revolutionary new cancer treatment. As many of the models show, parameter values matter greatly in predicting treatment outcomes and devising optimal treatment approaches. Personalized models that can be calibrated with parameters characteristic of an individual patient will turn mathematical models into powerful tools that can play an essential role at the bedside, not just in the laboratory.

Data accessibility

This article has no additional data.

Authors' contributions

The idea for the subject and structure of the manuscript was conceived by R.C.L. and A.K. A.K., A.T.V. and A.J.A. co-drafted §2, the introductory paragraphs for §§3–5 and §6b. A.K. and R.C.L. co-drafted the remainder of the sections. All co-authors provided commentary on all sections, and reviewed the manuscript before publication.

Competing interests

We declare we have no competing interests.

Funding

This work was partially supported by the National Cancer Institute of the National Institutes of Health postdoctoral fellowship F32CA214030 awarded to A.K., and the National Cancer Institute of the National Institutes of Health grant 1R1R01CA188025-01 supporting R.C.L.