How do prosthetic stiffness, height and running speed affect the biomechanics of athletes with bilateral transtibial amputations?

Abstract

Limited available information describes how running-specific prostheses and running speed affect the biomechanics of athletes with bilateral transtibial amputations. Accordingly, we quantified the effects of prosthetic stiffness, height and speed on the biomechanics of five athletes with bilateral transtibial amputations during treadmill running. Each athlete performed a set of running trials with 15 different prosthetic model, stiffness and height combinations. Each set of trials began with the athlete running on a force-measuring treadmill at 3 m s⁻¹, subsequent trials incremented by 1 m s⁻¹ until they achieved their fastest attainable speed. We collected ground reaction forces (GRFs) during each trial. Prosthetic stiffness, height and running speed each affected biomechanics. Specifically, with stiffer prostheses, athletes exhibited greater peak and stance average vertical GRFs (β = 0.03; p < 0.001), increased overall leg stiffness (β = 0.21; p < 0.001), decreased ground contact time (β = −0.07; p < 0.001) and increased step frequency (β = 0.042; p < 0.001). Prosthetic height inversely associated with step frequency (β = −0.021; p < 0.001). Running speed inversely associated with leg stiffness (β = −0.58; p < 0.001). Moreover, at faster running speeds, the effect of prosthetic stiffness and height on biomechanics was mitigated and unchanged, respectively. Thus, prosthetic stiffness, but not height, likely influences distance running performance more than sprinting performance for athletes with bilateral transtibial amputations.

1. Background

During running, the vertical position of an athlete's centre of mass (CoM) reaches its lowest position at mid-stance and its highest position at the middle of the aerial phase. This fundamental cyclic movement is due to the spring-like behaviour of the stance leg and is well described by a spring–mass model [1–6]. The model simplifies the leg's musculoskeletal system during running to a massless linear leg spring supporting a point mass that represents the athlete's CoM [1–6] (figure 1). During the first half of ground contact, elastic potential energy is stored in the compressed leg spring. Subsequently, the stored mechanical energy is released during the second half of ground contact as the leg spring recoils, thereby accelerating the CoM forward and upward into the aerial phase [7]. The magnitude of the stored and returned mechanical energy is inversely related to leg stiffness, and is thought to influence running performance by altering the generation of muscular mechanical work [7–9], and contraction velocities [10].

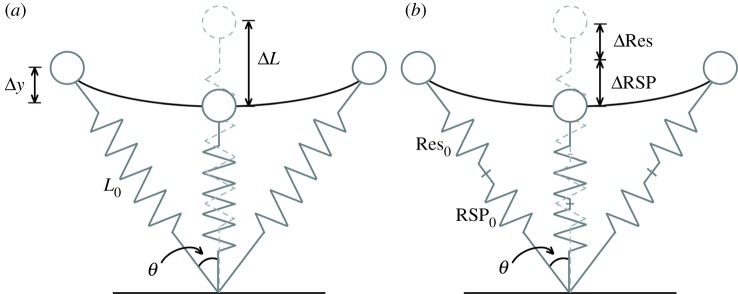
Figure 1.

Illustration of a (a) spring–mass model and (b) spring–mass model with two in-series leg springs. Body mass is represented as a point mass (circle) and the touch-down angle is indicated by θ. (a) The stance leg is represented by a massless linear spring for non-amputees, and (b) two in-series massless linear springs for athletes with bilateral amputations. The initial leg length (L₀) shortens (ΔL), and vertical height (Δy) decreases during the stance phase of running. Modelled residual limb length (Res₀) and prosthetic height (RSP₀) compress and extend (ΔRes and ΔRSP) during the stance phase of running.

Fundamentally, the spring–mass model characterizes running biomechanics for athletes with [6,11–13] and without lower-limb amputations [1–6]; however, the product of step length and step frequency ultimately dictates running speed. Step length can be determined from the product of the horizontal distance travelled by the CoM during ground contact (contact length) and the stance average vertical ground reaction force (GRF) magnitude normalized to body weight [14,15]. Step frequency can be calculated from the reciprocal of the sum of ground contact time and the subsequent aerial time [14,15]. Thus, the spring–mass model describes running biomechanics, while kinematic and kinetic parameters dictate running speed.

There is limited available information regarding how athletes with bilateral transtibial amputations, who run with passive-elastic running-specific prostheses (RSPs), adapt their biomechanics to achieve different running speeds. That is because to date merely three studies have reported biomechanics from a total of two athletes with bilateral transtibial amputations across running speeds [6,16,17], and because the running biomechanics of athletes with unilateral transtibial amputations (affected and unaffected leg) and non-amputees differ from those of athletes with bilateral transtibial amputations [6,16–18]. Collectively, as constant running speed is increased from 2.5 to 8.0 m s⁻¹, athletes with bilateral transtibial amputations decrease leg stiffness, increase contact length [6], increase stance average vertical GRF [16], decrease contact time and maintain a nearly constant aerial time [16]. Beyond 8 m s⁻¹, the same biomechanical trends persist except that stance average vertical GRFs plateau and aerial times decrease [16]. Therefore, athletes with bilateral transtibial amputations increase both step length and step frequency to achieve running speeds from 2.5 to 8.0 m s⁻¹, while they primarily increase step frequency to achieve speeds faster than 8.0 m s⁻¹. However, these trends are based on data from two athletes, thus a greater sample size is needed to confirm or refute these results.

Further, it is uncertain if the biomechanical changes with altered running speeds are inherent to athletes with bilateral transtibial amputations or if they are due to the characteristics of their RSPs. For example, many researchers and governing institutions speculate that prosthetic stiffness and height have a strong influence on the biomechanics and running performance of athletes with bilateral transtibial amputations [6,11,19,20]. In our previous study [11], we found that the use of stiffer RSPs by athletes with bilateral transtibial amputations was correlated with increased overall leg stiffness, increased residual limb stiffness, faster step frequencies and increased metabolic cost at relatively slow running speeds (2.5 and 3.0 m s⁻¹). Yet, it remains uncertain whether running speed alters the influence of prosthetic stiffness on biomechanics. Because prosthetic stiffness slightly increases with greater applied force [21], and residual limb stiffness is positively associated with prosthetic stiffness [11], the leg stiffness and step frequency of athletes with bilateral transtibial amputations should theoretically increase with running speed. Yet, the leg stiffness of such athletes has been reported to decrease with faster running speeds [6], indicating that the influence of prosthetic stiffness may be mitigated at faster running speeds.

Athletes with bilateral transtibial amputations participate in events that span a broad range of running speeds; therefore, it is important to understand how prosthetic stiffness, height and speed affect biomechanics. Accordingly, the purpose of this study was to quantify how changes in prosthetic stiffness, height and running speed affect the biomechanics of athletes with bilateral transtibial amputations. Based on our previous study [11], we hypothesized that across running speeds, (i) the use of stiffer RSPs would increase leg stiffness and step frequency and (ii) the use of taller RSPs would be independent of the biomechanical variables that govern leg stiffness and running speed. We also hypothesized that (iii) faster running speeds would lessen the influence of prosthetic stiffness on biomechanical parameters.

2. Participants and methods

2.1. Participants

Five male athletes with bilateral transtibial amputations participated (table 1). Four athletes primarily compete in sprinting (less than or equal to 400 m) and/or jumping track and field events and one athlete primarily competes in distance running events (greater than or equal to 5000 m) (table 1). Each athlete had over 1 year of experience running with passive-elastic RSPs, and gave informed written consent according to the protocol that was approved by the Colorado Multiple Institutional Review Board and the USAMRMC Office of Research Protection, Human Research Protection Office.

Table 1.

Participant characteristics: age, mass, cause of amputations and primary event(s). The maximum standing height and corresponding leg lengths allowed in track and field races sanctioned by the International Paralympic Committee (IPC) [19]. The resulting Catapult, Cheetah Xtend and 1E90 Sprinter prosthesis leg lengths represent the closest attainable maximum IPC-regulated leg lengths from each participant and prosthetic model combination [19]. Leg lengths were measured from the greater trochanters to the most distal locations of the unloaded prostheses.

participants	age (years)	mass (kg)	cause of amputations	primary event(s)	max IPC height (m)	max IPC leg length (m)	Catapult leg length (m)	Cheetah Xtend leg length (m)	1E90 Sprinter leg length (m)
1	25	69.3	congenital	100 m/200 m	1.80	0.97	1.12	0.97	0.97
2	23	76.3	congenital	long jump	1.88	1.07	1.07	1.07	1.04
3	18	75.0	congenital	100 m/200 m	1.87	1.05	1.05	1.05	1.05
4	31	70.4	trauma	400 m	1.90	1.10	1.10	1.10	1.10
5	27	70.5	infection	5000 m	1.87	1.06	1.06	1.06	1.06
average	24.8	72.3			1.86	1.05	1.08	1.05	1.04
s.d.	4.8	3.1			0.04	0.05	0.03	0.05	0.04

2.2. Protocol

Initially, each participant completed a fitting and accommodation session. During this session, we collected anthropometric measurements to determine the tallest prosthetic height that each participant could use to compete in track and field races according to the International Paralympic Committee (IPC) guidelines [19]. Next, a certified prosthetist aligned each participant with three commonly used prosthetic models (Freedom Innovations Catapult FX6, Irvine, CA, USA; Össur Cheetah Xtend, Reykjavik, Iceland; Ottobock 1E90 Sprinter, Duderstadt, Germany) at the manufacturer's recommended and ±1 stiffness categories at the prosthetic height that produced the IPC maximum competition height and ±2 cm. We chose these stiffness and height configurations because they have been reported to elicit biomechanical changes during running in athletes with transtibial amputations [11,22,23] and they enabled us to recruit athletes spanning a wide range of body masses and heights.

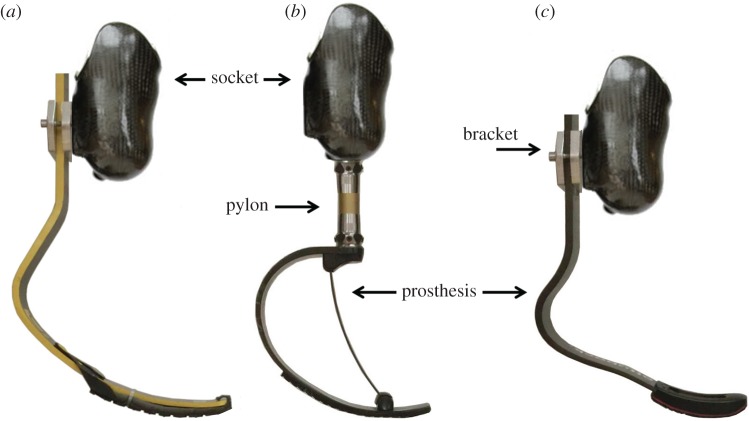
Each RSP functions as a spring through the storage and return of mechanical energy during stance. The Catapult prostheses are ‘C’ shaped and attach distally to sockets via connecting aluminium pylons. Each carbon-fibre or fibreglass socket (check socket) surrounds a residual limb and is secured with suction or a locking mechanism (figure 2). The Cheetah Xtend and 1E90 Sprinter prostheses are ‘J’-shaped and mount to the posterior wall of the socket. After establishing the heights of the J-shaped RSPs, the prostheses are typically bolted directly to the sockets. To preserve the J-shaped RSPs, secure them to the sockets, and alter prosthetic height between trials, we constructed custom aluminium brackets that were bolted to the sockets (figure 2).

Figure 2.

From left to right, (a) the Össur Cheetah Xtend prosthesis (J-shaped) at a representative recommended height, (b) the Freedom Catapult FX6 prosthesis (C-shaped) at a representative height of +2 cm and (c) the Ottobock 1E90 Sprinter prosthesis (J-shaped) at a representative height of −2 cm. The C-shaped prostheses are connected to sockets via aluminium pylons, and the J-shaped prostheses are connected to sockets via custom aluminium brackets. (Online version in colour.)

Owing to participant residual limb lengths and available prosthetic components, we were unable to match the maximum IPC competition height for some participants with certain prosthetic models. For these cases, we set prosthetic height as close as possible to the maximum IPC competition height. If the closest attainable height was taller than the maximum IPC competition height, we set that height as the baseline height for the respective participant and RSP combination and ensuing prosthetic height alterations were +2 and +4 cm. If the closest achievable height was shorter than the maximum IPC competition height, we set that height as the baseline height for the respective participant and RSP combination and subsequent prosthetic height alterations were −2 and −4 cm (table 1).

After participants were aligned to a prosthetic configuration, they ran on a motorized treadmill (Treadmetrix, Park City, UT, USA) at self-selected speeds until both the prosthetist and participant were satisfied with the comfort and function of the respective RSPs. Generally, athletes accommodated to each prosthetic model at the recommended stiffness category and height. When using C-shaped RSPs, athletes also ran at additional heights (i.e. ±2 cm) to determine proper alignment with the taller/shorter pylons. When using J-shaped RSPs, the components and alignment were the same at each height per model, hence athletes did not typically accommodate to the additional heights. Four athletes used their personal competition sockets for the trials with the J-shaped RSPs, and they used their everyday/walking sockets when equipped with the C-shaped RSPs. For the other athlete, a prosthetist fabricated custom sockets that replicated the participant's competition sockets (suspension, internal dimensions, etc.) for use with the C- and J-shaped RSPs.

On subsequent days, participants performed a session of one to three sets of treadmill running trials [6]. Each set of treadmill running trials started with the participant running at 3 m s⁻¹ and following successful trials, treadmill speed was incremented 1 m s⁻¹ for the next trial. A successful trial was determined if the participant was able to maintain forward position on the treadmill while taking 20 consecutive steps [6,14,16,24]. If the participant was unable to maintain forward position on the treadmill for 20 consecutive steps, the trial was deemed unsuccessful. Ad libitum rest followed each trial. Following unsuccessful trials and rest periods, participants were given the option to retry the preceding trial's speed, or deem the last successful trial as their top speed with the given prosthetic configuration.

Participants were given two options to commence each treadmill running trial. The first option began with the participant straddling the treadmill belt while it sped up to the desired speed. Once the treadmill was up to speed, the participant lowered himself onto the moving treadmill belt using the handrails. The participant then took a few steps on the belt and, when comfortable, began to run without handrail assistance, initiating the step count. The second option allowed each participant to begin by standing on the static treadmill belt. The participant then accelerated with the treadmill belt until the target speed was achieved. Once the treadmill achieved the desired speed, we began to count steps as the participant continued to run on the treadmill. For each trial, participants were allowed to choose either starting technique.

Each participant ran using 15 different combinations of prosthetic model, stiffness category and height. At first, participants ran using each model at three different stiffness categories (recommended and ±1) at the IPC maximum competition height. The stiffness category for each prosthetic model that elicited the fastest top speed was considered optimal. Subsequently, participants ran using the optimal stiffness category of each prosthetic model at two additional heights (±2 cm). We randomized the trial order beginning with the nine prosthetic model and stiffness category combinations at the maximum IPC competition height. Once a participant completed trials at all three stiffness categories with a certain prosthetic model, we randomly inserted the altered height trials for a respective model at the optimal stiffness category into the trial order.

2.3. Prosthetic stiffness

Prosthetic stiffness categories are recommended to athletes by the respective manufacturers based on user body mass, with larger athletes being recommended numerically greater stiffness categories [25–27]; numerically greater stiffness categories indicate mechanically stiffer (kN m⁻¹) prostheses [21]. As recommended stiffness (kN m⁻¹) differs between prosthetic models [21], we calculated prosthetic stiffness using the peak vertical GRFs measured from each leg during each trial (present study) and the force–displacement equations from Beck et al. [21]. Next, we divided the measured peak GRF magnitude by the estimated prosthetic displacement to yield stiffness. Prosthetic stiffness values were previously only recorded from participants with transtibial amputations running at 3 and 6 m s⁻¹ [21]. Thus, we calculated prosthetic stiffness for trials at 3 and 6 m s⁻¹ and then derived prosthetic stiffness at 4, 5 and 7 m s⁻¹ assuming a linear relationship between prosthetic stiffness and running speed. We did not estimate prosthetic stiffness beyond 7 m s⁻¹.

2.4. Data collection and stride count

We measured GRFs throughout the duration of each running trial. We collected GRFs at 1000 Hz, filtered them using a fourth-order low-pass Butterworth filter with a 30 Hz cut-off [11,22,28,29], and then used the filtered data to calculate the mean GRF parameters, stride kinematics and leg stiffness values with a custom Matlab script (Mathworks Inc., Natick, MA, USA). We set the vertical GRF threshold at 20 N to detect periods of ground contact. For each trial, participants ran with a reflective marker on the distal end of one of their RSPs, and we tracked its position at 200 Hz (Vicon Nexus, Oxford, UK). We filtered the position data using a fourth-order low-pass Butterworth filter with a 7 Hz cut-off [30,31] to determine the running speed during ground contact of the respective RSP using a custom Matlab script.

2.5. Data analysis

We calculated overall leg stiffness (k_leg) as the quotient of peak vertical GRF (F_peak) and peak leg spring compression (ΔL) during ground contact (figure 1):

2.1

Peak leg spring compression (ΔL) was calculated using initial leg length (L₀), the distance from the greater trochanter to the distal end of the unloaded RSP [6,11,24], theta (θ), the angle of the leg spring at initial ground contact relative to vertical (figure 1), running speed (v) and ground contact time (t_c):

2.2

Next, peak leg spring compression (ΔL) was determined using peak vertical displacement of the CoM during ground contact (Δy), calculated by twice integrating the vertical acceleration of the CoM with respect to time [32]:

2.3

Moreover, because biological legs and RSPs have relatively linear force–displacement profiles [2,21], we modelled participant leg stiffness (k_leg) as two in-series linear springs (figure 1). We incorporated established measurements of prosthetic stiffness (k_RSP) [21], and current measurements of leg stiffness to determine residual limb stiffness (k_res) using the following equation:

2.4

As aforementioned, running speed (v) is the product of step length (L_step) and step frequency (F_step):

2.5

Steps lengthen by increasing the horizontal distance travelled by the runner's CoM during stance (contact length) (L_c), and by producing greater stance average vertical GRFs (F_avg) relative to bodyweight (BW) [14,15]. Therefore, step length can be calculated using the following equation:

2.6

We used the above equation because it enables us to further investigate the biomechanical variables that govern step length (i.e. L_c and F_avg/BW) and therefore running speed. Step frequency is calculated from the reciprocal of the sum of ground contact time (t_c) and subsequent aerial time (t_a) [14,15]:

2.7

Thus, by combining equations (2.5), (2.6) and (2.7), running speed (v) is calculated using the following equation:

2.8

For the complete derivation of the above equation, refer to [14,15].

2.6. Statistical analyses

We used a linear mixed model to evaluate the influence of prosthetic stiffness (kN m⁻¹), height and running speed (3–9 m s⁻¹) on the biomechanical variables that comprise the spring–mass model and running speed (variables from equations (2.1) through (2.8)). We report the fixed effect (β) from each statistically significant association (dependent variable = β independent variable + constant). We tested for all potential stiffness/speed and height/speed interactions. Additionally, prosthetic stiffness depends on the magnitude and orientation of the applied force [21], thus we performed a one-way ANOVA to determine whether running speed statistically influenced prosthetic stiffness. We set the level of significance at p = 0.05 and performed statistical analyses using R-studio (Boston, MA, USA).

3. Results

Owing to the difficulties of determining running speed during the acceleration phase, some trials contained fewer than 20 steps at the desired speed. Consequently, we used the motion capture data to determine instantaneous running speed and only analysed steps that were taken at the desired speed. We excluded data from the last two steps of each trial to remove any potential biomechanical alterations that occurred while participants prepared to dismount the treadmill. We also excluded data from trials that had fewer than four consecutive steps at the desired speed. Additionally, due to saturation in the force signal, we removed 16 trials from the analysis. Nonetheless, we analysed 73 trials at speeds of 3, 5 and 6 m s⁻¹, 74 trials at 4 m s⁻¹, 72 trials at 7 m s⁻¹, 65 trials at 8 m s⁻¹ and 37 trials at 9 m s⁻¹.

3.1. Prosthetic stiffness

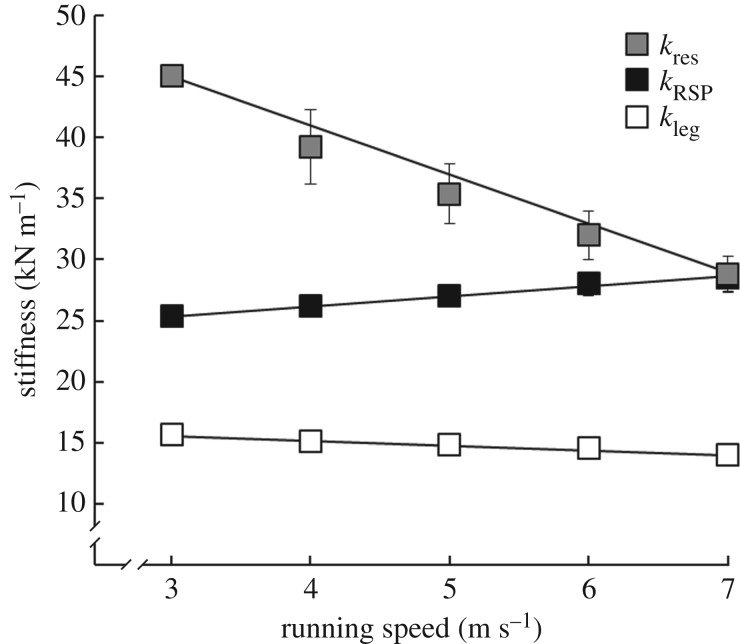
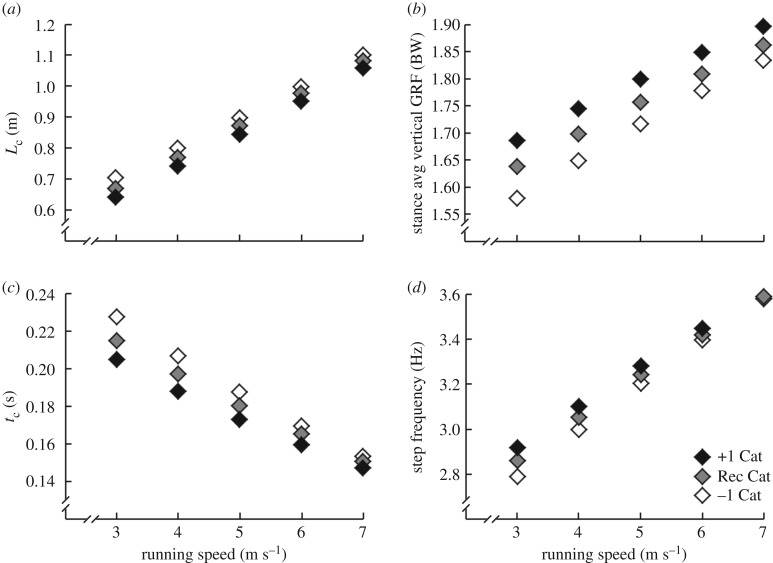
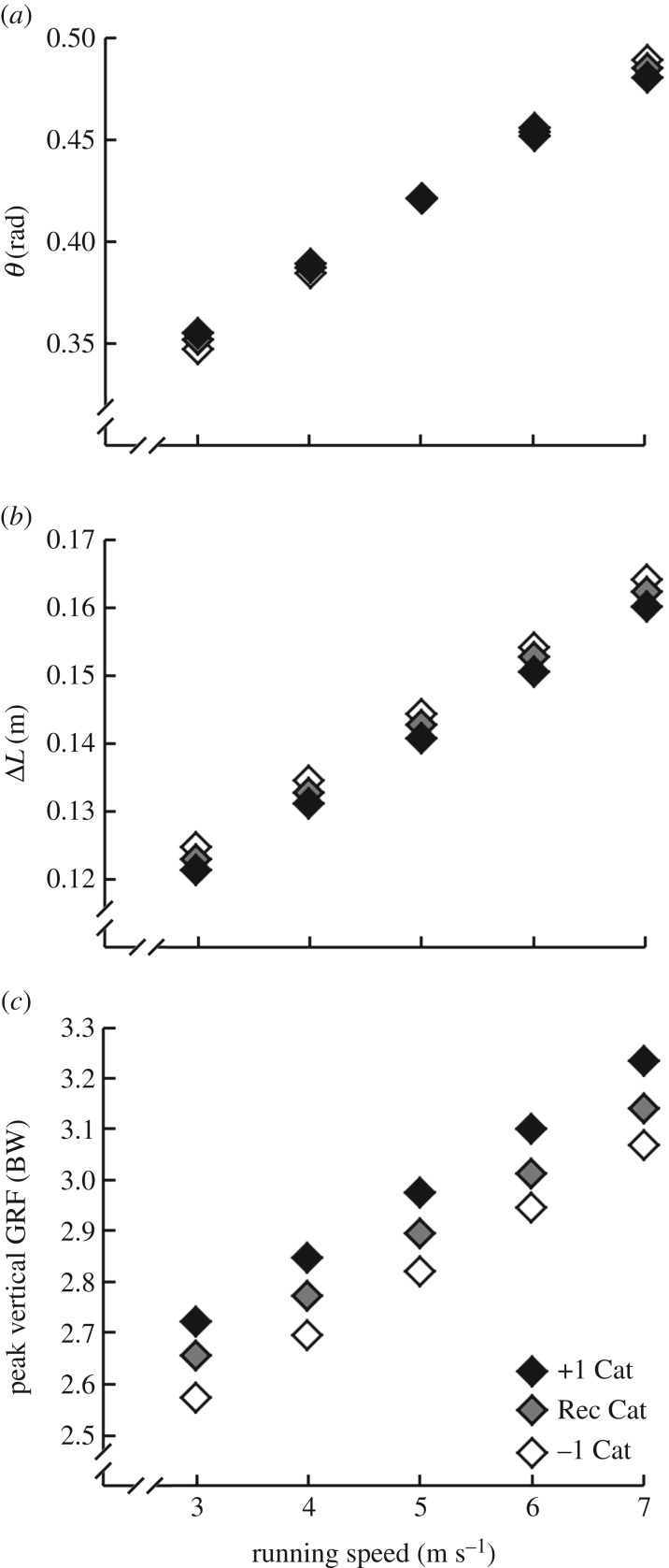
Prosthetic stiffness increased with faster running speeds (p < 0.001) (table 2). From 3 to 7 m s⁻¹, overall prosthetic stiffness averaged (±s.d.) 25.4 ± 3.0, 26.1 ± 3.4, 27.1 ± 4.0, 28.0 ± 4.8 and 28.6 ± 5.6 kN m⁻¹ at each successive speed (figure 3). Unless otherwise specified, all results were interpreted while controlling for covariates (e.g. interpreting the effect of prosthetic stiffness on biomechanics while controlling for prosthetic height, running speed and interactions between prosthetic height and running speed). For every 1 kN m⁻¹ increase in prosthetic stiffness, overall leg stiffness increased 0.21 kN m⁻¹ (p < 0.001), residual limb stiffness decreased 2.09 kN m⁻¹ (p < 0.001) (figure 3), contact length decreased 1.7 cm (p < 0.001) and step frequency increased 0.042 Hz (p < 0.001) (figure 4). Regarding the other spring–mass model variables, for every 1 kN m⁻¹ increase in prosthetic stiffness, θ increased 0.004 rad (p = 0.012), Δy decreased 0.19 cm (p < 0.001) (figure 5), peak vertical GRF increased 0.03 times BW (p < 0.001) and ΔL decreased 0.07 cm (p < 0.001). Concerning the rest of the biomechanics that govern running speed, for every 1 kN m⁻¹ increase in prosthetic stiffness, stance average vertical GRF increased 0.03 times BW (p < 0.001) and contact time decreased 0.007 s (p < 0.001) (figure 5).

Table 2.

Average (±s.d.) recommended (Rec) prosthetic stiffness values (kN m⁻¹) for a 70 kg athlete across running speeds and prosthetic stiffness values (kN m⁻¹) from ±1 stiffness categories across speeds. We averaged prosthetic stiffness values at each category for each model, and then averaged stiffness values across models for the respective recommended category (i.e. Rec, or ±1). Prosthetic stiffness was related to running speed (p < 0.001).

stiffness category	running speed (m s−1)
	3	4	5	6	7
−1	22.6 ± 1.7	23.4 ± 2.2	24.3 ± 3.1	25.2 ± 4.2	26.0 ± 5.3
Rec	25.3 ± 1.6	26.0 ± 2.1	26.8 ± 3.0	27.4 ± 3.8	28.4 ± 5.0
+1	27.5 ± 2.1	28.4 ± 2.5	29.4 ± 3.2	30.3 ± 4.1	31.5 ± 5.4

Figure 3.

The average (±s.e.) stiffness of the overall leg (k_leg), the prosthesis (RSP; k_RSP) and the residual limb (k_res) across 3 through 7 m s⁻¹ and across all prosthetic configurations. Across all conditions, simple linear regression equations follow as: k_leg = −0.30 Speed + 16.4, R² = 0.05, p < 0.001; k_res = −4.0 Speed + 56.0, R² = 0.16, p < 0.001; k_RSP (kN m⁻¹) = 0.82 Speed + 22.9, R² = 0.07, p < 0.001. Error bars indicate inter-subject variability and may be hidden behind the symbols.

Figure 4.

(a) Contact length (L_c), (b) stance average vertical GRF, (c) contact time (t_c) and (d) step frequency, while using RSPs averaged from three different models at one stiffness category below recommended (−1 Cat), at recommended (Rec Cat) and at one stiffness category greater than recommended (+1 Cat) across running speeds. Prosthetic stiffness categories correspond to a 70 kg athlete. See table 2 for prosthetic stiffness values (k_RSP in kN m⁻¹) used at each speed (v) and stiffness category recommendation. Biomechanical data are derived from statistical linear mixed models. The linear mixed model regression equations follow as: (a) L_c = 0.08 v − 0.02 k_RSP + 0.001 v · k_RSP + 0.76; (b) avg vertical GRF = 0.11 v + 0.03 k_RSP − 0.003 v · k_RSP + 0.75; (c) t_c = −0.038 v − 0.007 k_RSP + 0.001 v · k_RSP + 0.446; (d) step frequency = 0.315 v + 0.042 k_RSP − 0.005 v · k_RSP + 1.258.

Figure 5.

(a) Touch-down angle (θ), (b) leg spring compression (ΔL) and (c) peak vertical GRF averaged from three different running-specific prosthetic models at one stiffness category below recommended (−1 Cat), at recommended (Rec Cat) and at one stiffness category greater than recommended (+1 Cat) across running speeds. Prosthetic stiffness categories correspond to a 70 kg athlete. See table 2 for prosthetic stiffness values (k_RSP in kN m⁻¹) used at each speed (v) and stiffness category recommendation. Biomechanical data are derived from statistical linear mixed models. The regression equations follow as: (a) θ = 0.055 v + 0.004 k_RSP − 0.001 Speed · k_RSP + 0.145; (b) ΔL = 0.010 v − 0.001 k_RSP + 0.109; (c) peak vertical GRF = 0.10 v + 0.03 k_RSP + 1.59.

3.2. Prosthetic height

Increasing prosthetic height by 2 cm resulted in no significant changes in overall leg stiffness (p = 0.756) or residual limb stiffness (p = 0.668), but did correlate with a 2.3 cm increased contact length (p < 0.001) and 0.021 Hz decreased step frequency (p = 0.009). For every 2 cm increase in prosthetic height, θ decreased 0.012 rad (p < 0.001), Δy increased 0.16 cm (p < 0.001) and peak vertical GRF decreased by 0.02 times BW (p = 0.047). Furthermore, for every 2 cm increase in prosthetic height, stance average vertical GRF decreased 0.25 times BW (p < 0.001) and contact time increased 0.003 s (p < 0.001). Prosthetic height did not influence ΔL (p = 0.130).

3.3. Running speed

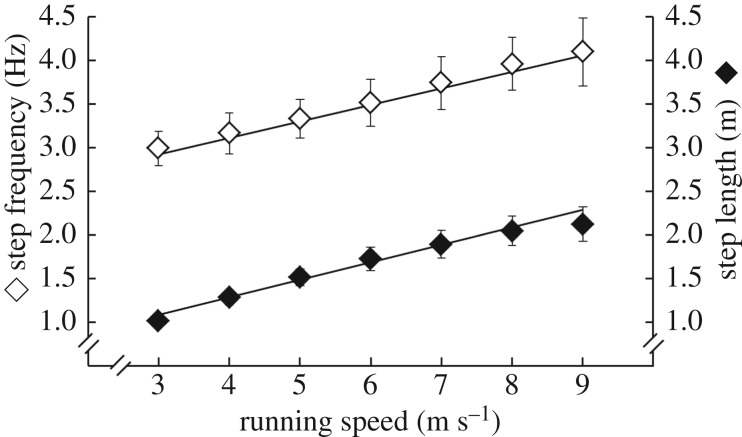
Each participant was able to achieve a running speed of 9 m s⁻¹ with at least one prosthetic configuration. For every 1 m s⁻¹ increase in running speed, overall leg stiffness decreased 0.58 kN m⁻¹ (p < 0.001), residual limb stiffness decreased 9.42 kN m⁻¹ (p < 0.001) (figure 3), contact length increased 7.8 cm (p < 0.001) and step frequency increased 0.32 Hz (p < 0.001) (figures 4 and 7). For every 1 m s⁻¹ increase in running speed, θ increased 0.055 rad (p < 0.001), Δy decreased 1.15 cm (p < 0.001), peak vertical GRF increased 0.01 times BW (p < 0.001) and ΔL increased 1.00 cm (p < 0.001) (figure 5). Moreover, for every 1 m s⁻¹ increase in running speed, stance average vertical GRF increased 0.12 times BW (p < 0.001), and contact time decreased 0.038 s (p < 0.001) (figure 4). Independently, running speed did not change peak vertical GRF magnitude (p = 0.743).

Figure 7.

The average (±s.e.) elicited step frequency (StF) and step length (StL) at each running speed (v) across all prosthetic configurations. Linear regression equations follow as: StF = 0.20 v + 2.35, R² = 0.67, p < 0.001; StL = 0.20 v + 0.49, R² = 0.88, p < 0.001.

3.4. Prosthetic stiffness/height and speed interaction effects

At faster running speeds, the influence of prosthetic stiffness on residual limb stiffness (β = 0.23; p = 0.020), contact length (β = 0.13; p = 0.019) and step frequency (β = −0.005; p = 0.004) (figure 5) was all diminished. Furthermore, for every 1 m s⁻¹ increase in running speed, the effect of increasing prosthetic stiffness 1 kN m⁻¹ was associated with a 0.001 rad decreased θ (p = 0.001) (figure 4), and 0.03 cm increased Δy (p < 0.001). For every 1 m s⁻¹ increase in running speed, every 1 kN m⁻¹ increase in prosthetic stiffness was related with a 0.003 times body weight decreased stance average vertical GRF (p < 0.001), and a 0.001 s increase in contact time (p < 0.001) (figure 5). No other prosthetic stiffness/height and speed interactions achieved statistical significance (p > 0.05).

4. Discussion

The purpose of this study was to quantify how altered prosthetic stiffness, height and running speed affect the biomechanics of athletes with bilateral transtibial amputations. We accepted our initial hypothesis that the use of stiffer RSPs would result in increased overall leg stiffness and step frequency (figures 3 and 4). This extends the previous research, which concluded that at a single, slow running speed, athletes with bilateral transtibial amputations increase overall leg stiffness and step frequency with the use of stiffer RSPs [11]. However, the previous study's athletes demonstrated an extremely weak positive correlation between prosthetic stiffness and residual limb stiffness [11], contrasting this study's finding of an inverse relationship between prosthetic stiffness and residual limb stiffness (figure 3). This study's finding corresponds with the established observation that non-amputees inversely alter overall leg stiffness with changed in-series surface stiffness to maintain nearly constant leg stiffness during running [33–35]. Furthermore, we report an inverse relationship between leg stiffness and running speed, despite a positive association between prosthetic stiffness and running speed (figure 3). This occurs because leg stiffness only increases 0.21 kN m⁻¹ with each integer increase in prosthetic stiffness, whereas it decreases 0.58 kN m⁻¹ with every 1 m s⁻¹ increase in running speed. For example, the 3.2 kN m⁻¹ average increase in prosthetic stiffness from 3 to 7 m s⁻¹, coupled with the influence of faster running speed yields a 1.65 kN m⁻¹ reduction in leg stiffness (figure 3).

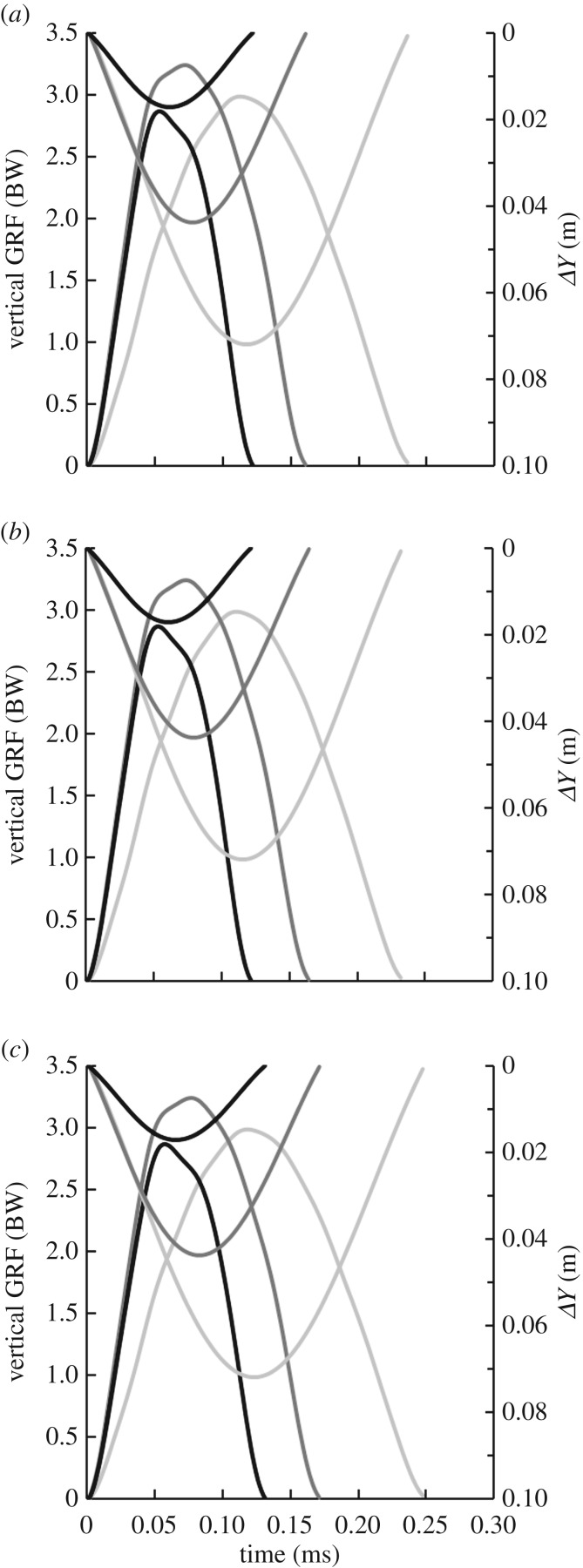
The leg joint mechanics that govern overall leg spring behaviour may differ between athletes with and without transtibial amputations. A previous study indicated that the affected leg knee joints of athletes with unilateral transtibial amputations do not act like sagittal plane torsional springs during running [12], which is dissimilar to that of non-amputees [36,37] whose knee joint mechanics greatly influence leg stiffness [38]. We confirmed that at each speed, the overall leg mechanics of athletes with bilateral transtibial amputations follow the main assumptions of the spring–mass model [1–6], where the vertical GRFs and displacement of the runner's CoM gradually increase then decrease with both maximums occurring at approximately 50% of the stance phase (figure 6). Future analyses of residual limb joint mechanics (hip, knee, residual limb/socket interface, etc.) are necessary to determine if leg joints and the limb–socket interface of athletes with bilateral transtibial amputations perform like springs (linear and torsional springs) during running and how they contribute to the spring-like behaviour of the overall leg.

Figure 6.

Representative vertical GRF traces (left axis), and CoM vertical displacements (ΔY; right axis) as a function of time for a participant using Össur Cheetah Xtend prostheses at (a) −1 prosthetic stiffness category, (b) recommended prosthetic stiffness category and (c) + 1 prosthetic stiffness category. Light grey lines represent running at 3 m s⁻¹, medium grey lines represent running at 6 m s⁻¹ and black lines represent running at 9 m s⁻¹. On average, peak and stance average vertical GRFs increased with speed (v) (p < 0.001). Linear regressions for all participant and prosthetic combinations that achieved speeds 3 through 9 m s⁻¹ were peak vertical GRF = 0.115 v + 2.439, R² = 0.48, p < 0.001; stance average GRF = 0.047 v + 1.513, R² = 0.38, p < 0.001. However, some participant and prosthetic combinations (e.g. this figure) increased running speed despite decreasing vertical GRFs from 6 to 9 m s⁻¹.

We rejected our second hypothesis that prosthetic height would be independent of the biomechanical variables that comprise the spring–mass model and govern running speed. Notably, increased prosthetic height was associated with longer contact lengths, ground contact times and step lengths. Intuitively, athletes with longer legs take longer steps during running, yet non-amputees exhibit a very weak association between leg length and step length during running [39]. Thus, leg length may have a stronger influence on step length in athletes with bilateral transtibial amputations compared with non-amputees.

Regarding distance running performance, the metabolic cost of running for athletes with bilateral transtibial amputations is independent of prosthetic height, but is reduced with lower leg stiffness, step frequency and peak braking horizontal GRFs [11]. In this study, increased prosthetic height was independent of leg stiffness, but it did reduce step frequency. Perhaps taller RSPs increase lower-limb mass and/or inertia, counteracting the potentially beneficial effects of running with slower step frequencies [40,41]. Moreover, many surmise that increased prosthetic height augments sprinting performance for athletes with bilateral transtibial amputations [19,20]. Overall sprinting performance is beyond the scope of this study. Nonetheless, increased prosthetic height resulted in diminished stance average vertical GRFs and prolonged ground contact durations, both of which suggest slower running speeds [14,15]. Assuming that leg segment geometry is unchanged, perhaps the vertical GRF impairment with taller RSPs is related to worse hip and knee joint effective mechanical advantages [15,42]. Alternatively, achieving the same running speed with lower stance average vertical GRFs may be beneficial for sprinting performance. Thus, future research is warranted to better understand leg segment geometry and the effective mechanical advantage of the leg joints with changes in prosthetic height.

The influence of prosthetic stiffness on biomechanics was mitigated at faster running speeds (figures 4 and 5), leading us to accept our third hypothesis. The stiffness of a system encompassing two in-series springs is primarily influenced by the softer spring (equation (2.4)). Because the residual limb stiffness of athletes with bilateral transtibial amputations is roughly twice that of the RSP at 3 m s⁻¹, and approximately equal to that of the RSP at 7 m s⁻¹, prosthetic stiffness has a greater influence on running biomechanics at slower speeds than at faster speeds (figure 3).

It has yet to be established whether athletes with and without bilateral transtibial amputations take similar step lengths at matched running speeds. In this study, from 3 to 5 m s⁻¹, participants exhibited greater overall leg stiffness [5], decreased contact lengths and durations, and lower stance average vertical GRFs, leading to 7–11% shorter steps compared with non-amputees [39,43]. From 5 to 8 m s⁻¹, the leg stiffness values of athletes with and without transtibial amputations converge as running speed increases [2,4,44] (figure 3), leading to similar leg stiffness, contact length/duration and step length values between groups. At speeds faster than 8 m s⁻¹, step length comparisons made in previous studies between one athlete with bilateral transtibial amputations and non-amputees are conflicting. Initially, Brüggemann et al. [18] reported no difference in step length between an athlete with bilateral transtibial amputations and performance matched non-amputees at approximately 9 m s⁻¹ during over ground running (2.26 m for the athlete with bilateral transtibial amputations). Alternatively, Weyand et al. [16] reported that the same athlete (during a subsequent test) took shorter steps at 10 m s⁻¹ versus a different non-amputee control group during treadmill running (2.03 versus 2.37 m, respectively). The athletes in this study took step lengths that averaged 2.24 m at 9 m s⁻¹, consistent with Brüggemann et al.'s report [18] (figure 7). Yet, different athletes and testing procedures may confound inter-study comparisons [16,18].

Regardless, because prosthetic stiffness and height affect step length for athletes with bilateral transtibial amputations, there is likely a prosthetic configuration that yields similar step lengths for athletes with and without amputations at each speed. Furthermore, during some sets of running trials, participants increased running speed beyond 7 m s⁻¹ by using shorter and more rapid steps. This adaptation may explain the shorter step lengths measured by Weyand et al. [16] at 10 m s⁻¹ versus that of Brüggemann et al. [18] at 9 m s⁻¹. Altogether, athletes with bilateral transtibial amputations generally increase both step length and step frequency to achieve faster running speeds (figure 7), but they can also increase running speed by decreasing step length and rapidly increasing step frequency.

We excluded the analysis of prosthetic model on running biomechanics because models, like running shoe models, are continually changing. Still, many differences exist between prosthetic models (figure 2), including but not limited to geometry (figure 2), stiffness [21], socket attachment (figure 2), hysteresis [21], mass [11,22] and moment of inertia [45]. Thus, a detailed analysis and simulation of RSP design on the running biomechanics of athletes with bilateral transtibial amputations may be insightful to further optimize RSPs.

A limitation of this study includes the use of different prosthetic sockets with C- versus J-shaped RSPs. This may have led to altered residual limb movement within the socket, potentially leading to altered running biomechanics. Participant fatigue may have limited our protocol. To mitigate fatigue, we limited the performed sets of running trials for each respective session to 0 (rest), 1, 2 or 3 sets, depending on athlete feedback. Owing to our efforts in minimizing fatigue plus the randomization of prosthetic configuration, we believe that participant fatigue had a negligible influence on the RSP configuration results. Yet, potential fatigue may have influenced the running speed results because of the systematic trial order. Furthermore, our relatively small sample size may have led us to falsely accept null hypotheses.

5. Conclusion

Athletes with bilateral transtibial amputations change their running biomechanics when using RSPs that differ in stiffness, height and while running at different speeds. Namely, the use of stiffer RSPs increased leg stiffness, step frequency, peak and stance average vertical GRF production, and decreased ground contact time. The use of taller RSPs increased step length. Running speed was inversely associated with leg stiffness. Moreover, faster running speeds mitigate the effect of prosthetic stiffness, but not height, on running biomechanics. Therefore, prosthetic stiffness, but not height, likely has a greater influence on distance running performance than on sprinting performance for athletes with bilateral transtibial amputations.

Data accessibility

Running mechanics data: https://figshare.com/s/5ab1b28c7eb9b5476f9a [46].

Authors' contributions

A.M.G. contributed to the concept and design of the study, analysis and interpretation of data, drafting and revising of the manuscript, and approved the version of the manuscript to be published. P.T. and O.N.B. contributed to the acquisition of data, analysis and interpretation of data, drafting and revising of the manuscript, and approved the version of the manuscript to be published. All authors agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of the work are appropriately investigated and resolved.

Competing interests

We declare we have no competing interests.

Funding

This project was supported by the BADER Consortium, a Department of Defense Congressionally Directed Medical Research Programs cooperative agreement (W81XWH-11-2-0222).