The morphological heterogeneity of cricket flow-sensing hairs conveys the complex flow signature of predator attacks

Abstract

Arthropod flow-sensing hair length ranges over more than an order of magnitude, from 0.1 to 5 mm. Previous studies repeatedly identified the longest hairs as the most sensitive, but recent studies identified the shortest hairs as the most responsive. We resolved this apparent conflict by proposing a new model, taking into account both the initial and long-term aspects of the flow pattern produced by a lunging predator. After the estimation of the mechanical parameters of hairs, we measured the flow produced by predator mimics and compared the predicted and observed values of hair displacements in this flow. Short and long hairs respond over different time scales during the course of an attack. By harbouring a canopy of hairs of different lengths, forming a continuum, the insect can fractionize these moments. Short hairs are more agile, but are less able to harvest energy from the air. This may result in longer hairs firing their neurons earlier, despite their slower deflection. The complex interplay between hair agility and sensitivity is also modulated by the predator distance and the attack speed, characteristics defining flow properties. We conclude that the morphological heterogeneity of the hair canopy mirrors the flow complexity of an entire attack, from launch to grasp.

1. Introduction

The ability of animals to sense biotic and abiotic changes in their environment depends greatly on the performance of their sensors. The peripheral sensory structures and their associated sensory neural circuits have evolved to deal with complex sensory information, by matching their properties to the characteristics of the most crucial sensory stimulus they need to detect [1,2]. Arthropods can detect the movement of the surrounding fluid, usually through the deflection of long filiform hairs from their resting position [3]. The survival of wood crickets, living on forest litter, is at least partly dependent on their ability to detect their predators with hundreds of these filiform hairs, each of which is lodged into a socket and connected to a single neuron [4]. When a hair moves to a given angle from its resting position, it transfers enough energy to the attached neuron to trigger an action potential. The disturbances of air flow upstream of running spiders have been assessed by particle image velocimetry and computational fluid dynamics with the finite-element method [5,6]. It appears that the perturbation of the surrounding air flow in front of running arthropods is similar to the perturbation produced by the predators of fish prey in water [7]. The relationship between attack speed and the maximal distance at which the cricket can perceive the danger is parabolic. This implies an immediate perception of the danger, from the onset of predator attack, at the distances and speeds observed in nature [6]. The cricket cercal system is known to be one of the most sensitive sensory systems in existence, and it is widely assumed that increasing hair length is associated with greater individual hair sensitivity [8,9]. However, longer hairs are heavier and more inert, and would therefore be expected to be less responsive. These conflicting views may result from the use of different criteria for optimality, but they may also be due to differences in the nature of the stimuli used in experimental studies. In most studies, the filiform hairs were considered to respond to highly controlled oscillating flows [8–10] or to generic impulse flows [11]. Historically, the cricket mechanosensor has been described as an inverted pendulum, a second-order mechanical system, and studied through engineering approaches, through the determination of its harmonic response. However, studies of biologically relevant stimuli focusing on the flow generated by running spiders have shown that the flow is neither a simple sinusoidal nor an impulse flow, instead a hybrid between the two [5,6].

Elucidating the response of sensors to this complex stimulus will provide us with information about their specific functionality. We know, for instance, that short hairs are sensitive to high-frequency flows, but does it translate to an increase in their sensitivity to a specific predator attack strategy? Hair responses to biologically relevant stimuli have been studied by Kant & Humphrey [12] and, more recently, by Cummins & Gedeon [11]. In earlier models, preceding that of Kant and Humphrey, the hair was considered as a harmonic oscillator, oscillating in a harmonic flow, without taking into account its initial motion. Kant and Humphrey showed that early movements were of key importance and could not be neglected. They predicted the deflection of hairs of various lengths subjected to a flow generated by an accelerating sphere. They modelled the flow as an accelerating pulsation that decreased in magnitude over time and with increase in the distance from the source. This temporal decay was approximated by a Gaussian function, itself the function of a binary rectangular switch that produces the pulsation resulting in the impulse characteristics. The authors were interested in both the increase and decay of the flow perturbation. The use of this approximation enabled them to model the flow boundary layer and, thus, the drag forces promoting hair deflection. Based on the results they obtained with this novel approach, they claimed that shorter hairs could respond more sharply and with a greater amplitude than longer hairs. Cummins & Gedeon [11] calculated the impulse response function (IRF) of the hairs and their response to a rapid change, as a Dirac pulse. They did not convolve this IRF with different air velocities to predict the hair response to relevant signals but restricted their analysis to the IRF of different arrangements of hairs. Their prediction of an earlier and stronger reaction of shorter hairs is consistent with the findings of Kant and Humphrey, but completely opposed to previous thinking, ascribing low sensitivity to short hairs. Unfortunately, the temporal changes in flow velocity and acceleration generated by an approaching predator and the deflection of the stimulated hairs were not quantified in any of these studies, leaving these more realistic situations untested. In this study, we consider the entire temporal history of the flow field generated by a predator, rather than focusing exclusively on a sudden flow generated by an accelerated cylinder, as in the study by Kant and Humphrey. We aimed to find an explanation for the presence of a continuum of hair lengths in real hair canopies, as observed in crickets. The resolution of the discrepancy between short-hair responsiveness and long-hair sensitivity required the deconstruction of a long-held analogy in which the cricket cercus is compared with the hardware implementation of a spectrum analyser. This deconstruction is described in our general theory of hair moving in impulsive transient flow. This model was validated on experimental data on large deflections and extrapolated to smaller deflections, to resolve the conflict and demonstrate that both short and long hairs are optimal, but in response to different inputs. The resolution of this conflict is possible only with the use of new and comprehensive optimality criteria based upon both sensitivity and responsiveness.

2. A general theory of hair moving in impulsive transient flows

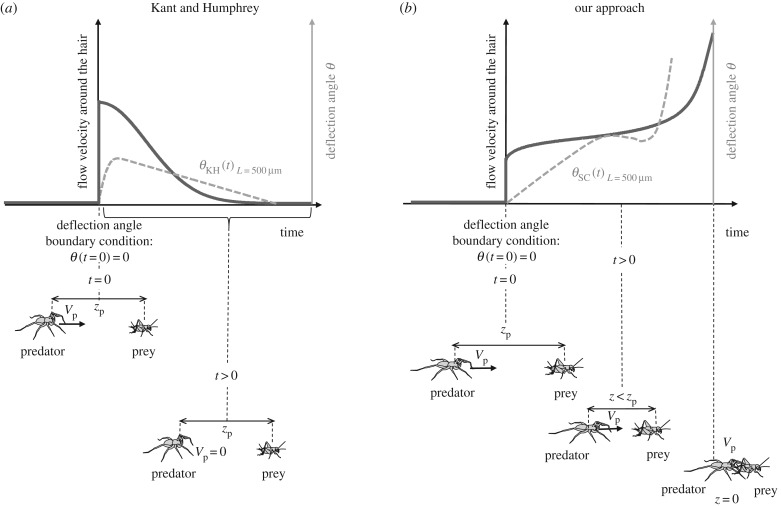
Both this study and that of Kant & Humphrey [12] involve the development of a physical–mathematical model simulating the response of a filiform hair to an airflow pulsation V_f(t) generated by the sudden attack of a predator running at a velocity V_p. Our model of hair deflection is based on that of Kant and Humphrey. The main difference between the two approaches concerns the choice of temporal history of predator approach, and, thus, flow conditions. In the Kant and Humphrey model, the predator stops immediately after making a very rapid movement, producing an instantaneous flow impulse that attenuates in a Gaussian fashion (figure 1a). By contrast, we chose to model the entire time history of the flow produced by the predator, from its start until eventual prey capture (figure 1b). The knowledge of the temporal evolution of hair deflection during the approach of a predator will inform us of the specific capability to detect more accurately an attack at a particular velocity.

Figure 1.

Differences between Kant and Humphrey's model (a) and our approach (b). (a) The flow velocity produced by a predator around a hair jumps from 0 to its initial and maximal value at t = 0, decreasing thereafter. The distance between predator and prey z_p is constant. (b) The flow velocity around a hair also jumps from 0 to its initial value at t = 0, but it is initially minimal and subsequently increases. The distance between predator and prey z_p decreases with time.

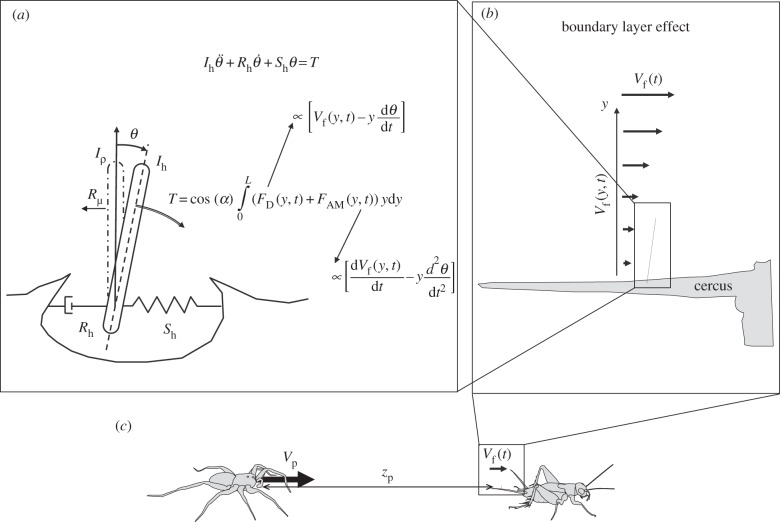
We provide below a detailed description of the differences between the two approaches. We first explain the equation for the motion of a hair, linking the hair deflection angle θ to the total torque T due to the drag force, added mass force and pressure gradient force (figure 2a, §§2.1 and 2.2). The total torque T acting on a hair depends on the deflection of the hair itself, as the forces applied to the hair depend on its motion relative to the surrounding fluid V_f: (figure 2a). We separated all components relating to hair deflection from those relating to flow velocity in the expression of torque. This made it possible to express the forcing function Q_SC, related only to fluid velocity V_f and independent of hair deflection angle θ. We describe (i) the analytical expression of pulse fluid velocity V^KH_f used in the Kant and Humphrey model and its corresponding Fourier series V^mKH₀ and (ii) the numerical temporal flow generated by a simulated predator attack V^SC_f and its corresponding Fourier series V^mSC₀, the input of our model. In §2.3, we focus on our choices for the boundary layer effect, describing the modification of flow velocity V_f by the hair substrate (figure 2b). Section 2.4 provides a resolution of the equation of motion and the development of a general analytical solution. After defining the boundary conditions for hair deflection, we obtained a general solution superimposing (i) the homogeneous solution of the equation of motion, i.e. the natural response of the system, and (ii) the particular solution of the equation of motion, i.e the forced response of the system. Finally, §2.5 describes the relationship between hair sensitivity and agility.

Figure 2.

Main components of models of the response of the hair to a flow pulsation produced by a running predator. The spider runs at a velocity V_p towards the cricket initially placed at a distance z_p from the spider. The movement of the predator in the incompressible fluid produces a flow displacement up to several centimetres in front of its body. (a) Summary of the mathematical formalism used to model the dynamics of the filiform hairs. The total torque acting on hair T is a function of (i) the drag force F_D, proportional to the relative flow velocity V_r and (ii) the added mass force F_AM, proportional to the time derivative of V_f. (b) At distance z_p, the flow velocity V_f(t) produced by predator displacement is modified in the vicinity of the cricket cercus supporting the filiform hairs. Flow velocity in this boundary layer is V_f(y, t), with the boundary conditions V_f(∞, t) = V_f(t) and V_f(0, t) = 0. (c) Diagramatic representation of predator/prey interaction.

2.1. Modelling the intrinsic response of a hair

A hair is represented as a straight cylinder of length L and diameter d, standing vertically on a flat plate and rotating around its base (figure 2a). The conservation of angular momentum for the motion of a filiform hair, approximated as a forced, damped harmonic oscillator, is given by

2.1

where θ (rad), (rad s⁻¹) and (rad s⁻²) are the angular displacement, velocity and acceleration of the hair about its pivot point, respectively. I_h (N m s² rad⁻¹) is the moment of inertia of the hair; S_h (N m rad⁻¹) and R_h (N m s rad⁻¹) are the hair torsional restoring constant and damping constant, respectively; and T (N m) is the total torque acting on the hair. This model was introduced by Humphrey et al. [9].

The joint linking the hair to the cuticle is modelled as a linear viscoelastic element that resists hair deflection θ with a torque −S_hθ and also experiences a frictional torque , reflecting the rotational energy dissipated by the hair at the joint. In the Kant and Humphrey approach, the total torque acting on the hair is determined from the hair and flow geometry and is given by

2.2

where (i) F_D (N m⁻¹), (ii) F_AM (N m⁻¹), and (iii) F_PG (N m⁻¹) are forces per unit length acting on the hair, due to (i) the viscous drag, (ii) the added mass of air around the hair, and (iii) a pressure gradient force, respectively. The Reynolds number is low, Re = V_rd/ν < 0.1, with d the filiform hair diameter (ranging from 5 to 10 μm) and ν = 1.56 × 10⁻⁵ m² s⁻¹ the kinematic viscosity of air. The viscous forces thus dominate, and the drag force is given by the classical Oseen [13] equation. F_D simplifies to

2.3

with μ = 1.81 × 10⁻⁵ kg (ms)⁻¹ being the dynamic viscosity of air. The added mass force F_AM is due to the added mass of air accelerated with the hair it surrounds and is given by

2.4

The pressure gradient force F_PG is the force required to accelerate the air that would occupy the volume of the length of the hair if it were absent and is equal to

2.5

where V_r = V_f − V_h (m s⁻¹) is the relative velocity of the air (V_f) with respect to that of the hair (V_h). The velocity of the hair depends on its distance y (m) from the substrate and is given by 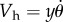. Replacing this value in the integral of total torque T_KH gives

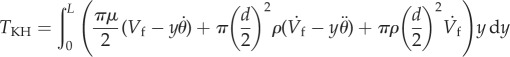2.6

and

2.7

Substituting equation (2.7) in the equation of motion (2.1) gives

2.8

with

2.9

and

2.10

being additional inertia and damping contributions due to the air medium, respectively. The quantity Q_KH is the forcing function used by Kant and Humphrey:

2.11

In our approach, previously described for harmonic flows in the study by Bathellier et al. [14] and generalized here to impulse flows, the total torque acting on the hair is defined as

2.12

with

2.13

and

2.14

and cos(α) reflecting the effect of the preferential directionality of the hair and α (rad) being the angle between the direction of flow and the preferential orientation of the hair.

Replacing equations (2.13) and (2.14) in equation (2.12) gives

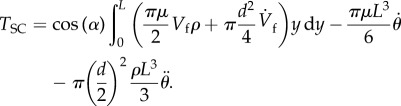2.15

Substituting equation (2.15) in equation of motion (2.1) gives

2.16

The quantity Q_SC is our forcing function:

2.17

Thus, in our model, equation (2.16) is equivalent to eqn (8) in the Kant and Humphrey model. In summary, a first difference between the two models is the smaller contribution of the time derivative of flow velocity to the forcing function of equation (2.17) in our model. We do not explicitly include the pressure gradient force F_PG in the balance of forces acting on an element of hair length dy, as it is already contained in F_AM. We chose to neglect this pressure gradient force, as we estimated that its analytical expression introduced by Kant and Humphrey was redundant with the added mass force. Moreover, as explained in electronic supplementary material, appendix A, the added mass force and the pressure gradient force are negligible compared with the drag force.

2.2. Modelling forcing flows away from the hair

In the forcing function of Kant and Humphrey, Q_KH, the velocity of the flow V_f is the analytical solution of a flow field parallel to the longitudinal axis of an infinitely long cylinder representing the cercus. The authors assume that the velocity distribution due to a flow produced by a predator lunging towards its prey will consist of linearly superposed harmonic sinusoids with arbitrary frequencies, ω_m = 2πmΔf, with Δf being the frequency step of the discrete Fourier transform of V_f. The summation of these harmonic sinusoids results in the following expression of the velocity flow:

2.18

where V_{0 KH}^m is the amplitude of the sinusoidal wave associated with frequency ω_m. In the Kant and Humphrey model, the flow results from the sudden movement of a predator in the vicinity of its prey, represented by a pulsation velocity function with a rich frequency content. They chose to use a temporal Gaussian pulsation that was a function of a binary rectangular switch, as they were interested in both the development of this perturbation and its decay. Thus they modelled the movement of a hair due to a infinitely quick acceleration of an incoming predator at a distance z_p from its prey, moving at a velocity V_p and stopping immediately after the start of the movement. The distance from the prey thus remains de facto unaltered in their model. In their model, the frequency content of the stimulus flow is not a function of the velocity of the attack, but is instead determined by the characteristic duration of the pulsation σ = (2β)^−1/2. This duration varies between 7 and 220 ms. The impulse flow can thus be described as follows:

2.19

This equation of impulse flow can be expressed in terms of a Fourier series, in the same spirit as equation (2.18); V_f^KH can also be expressed as

2.20

with the amplitude of the sinusoidal waves associated with the frequency ω_m:

2.21

We chose to use the discrete Fourier series of more biologically relevant flows directly, rather than using a forcing function to represent the Gaussian decay of the flow. These flows correspond to the entire temporal flow produced by a piston mimicking the predator, measured as described in electronic supplementary material, appendix B.

2.3. Modelling forcing flows in the vicinity of the hair and cercus

The flow velocity V_f(t) is modified in the vicinity of the hair substrate (figure 2b). We describe here the Kant and Humphrey expression for the boundary layer, and the boundary layer effect in their model. At this scale, V_f is not merely a function of time t, but also depends on the distance to the substrate y. The velocity of flow in this boundary layer is expressed as V_f(y, t), with the boundary conditions V_f(∞, t) = V_f(t) and V_f(0, t) = 0.

Kant and Humphrey solved their equation of motion (2.8) by determining an explicit analytical form of the velocity V_f^KH that was a function of the boundary layer effect dependent on the distance y from the surface of the cercus. They used the Fourier decomposition of V_f^KH(t) and estimated the boundary layer affecting each harmonic component of the Fourier series. The equation for a boundary layer in a harmonic oscillatory flow past a longitudinal cylinder (i.e. the cercus) was given by Humphrey et al. [9]. The shape of this boundary layer depends mainly on flow frequency and cercus diameter. Assuming that V_f^KH(t) is the sum of sinusoidal flows of amplitude V_{0 KH}^m and frequency ω_m, Kant and Humphrey expressed the velocity profile along component y as

2.22

where λ_m = (D/2)(iω_m/ν)^1/2, the flow oscillation ω_m = m(2πf), R = 1 + y/(D/2), D is the cercus diameter, V_{0 KH}^m is the amplitude of the sinusoidal wave associated with the frequency ω_m, ν is the kinematic viscosity of the air and K₀() is the modified Bessel function operator of the second kind. Equation (2.22) reflects the fact that non-harmonic flow in the boundary layer over a substrate is the sum of the boundary layers of each of its frequency-dependent components [15]. Taking equations (2.11), (2.18) and (2.22), and using V_f^KH(y, t) and its time derivative, Kant and Humphrey defined the forcing function Q_KH as

2.23

The parameter K_KH in equation (2.23) encompasses the boundary layer effect and was explicitly calculated by Kant and Humphrey as

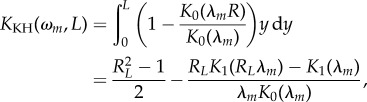2.24

with R_L = 1 + L/(D/2).

In our model, we chose to use another expression of the velocity V_f (according to [16]):

2.25

so that our forcing function becomes

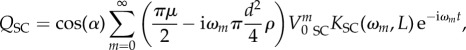2.26

with the boundary layer effect factor being

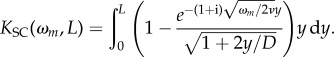2.27

While the formulations are different between Kant and Humphrey and ours, the underlying physics is identical, as confirmed by the very similar numerical outputs of equations (2.24) and (2.27).

2.4. Synthesis: hairs moving under impulsive transient flows

The final steps for solving the equation of a hair movement consist in solving the second-order inhomogeneous differential equation (2.16). Here, we do not describe the resolution of the Kant and Humphrey hair deflection equation, but rather focus on the resolution of our model. We, however, followed the method of Kant and Humphrey. Some of the following steps are well known and kept here only for comprehensiveness. The general solution (θ(t)) of equation (2.16) consists of the homogeneous (θ_h(t)) and particular (θ_p(t)) solutions [17]. The classical steps of solving such an equation (see electronic supplementary material, appendix C) lead to

2.28

where

and

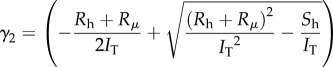and where, I_T = (I_h + I_ρ) is the total moment of inertia. This expression is similar to the solution of Kant and Humphrey, except that the quotient in the sum factor of our equation (2.28), which we will name the mechanical transfer function F_mec,

2.29

is different from the one appearing in Kant and Humphrey equations (2.29), (2.31), (2.32) and (2.33):

2.30

2.31

We give a new equation for the mechanical transfer function F^SC_mec because the use of the Kant and Humphrey equation of F^KH_mec leads to inconsistent results. We assume there might be a mistake in their paper because we were unable to retrace their results.

The disparity of formalism between the hair deflection equations of Kant & Humphrey [12] and Bathellier et al. [14] blurs the fact that the formalism used by Bathellier et al. [14] is actually just a particular part of the general Kant and Humphrey solution. Electronic supplementary material, appendix A, highlights the analogies between the model of Kant and Humphrey and our model.

In order to get an intuitive feeling of the internal working of equation (2.28), we work through an example to determine the deflection of a 500 μm hair, using a single mono-frequency input. To achieve this, we first set the discrete frequency step (frequency sampling interval) to Δf = 20 Hz and V^m₀ = 0 for all values of m, except for m = 1 where V¹₀ = 1 m s⁻¹. This results in the equation

2.32

becoming

2.33

This temporal expression of velocity corresponds to a sinusoidal wave flow of amplitude 1 m s⁻¹ and frequency 20 Hz. At time t = 0, the velocity is set to V_f(t = 0⁺) = 1 m s⁻¹. Using equation (2.28), we can derive the expression of the change in hair deflection over time:

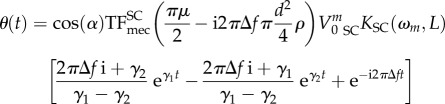2.34

equivalent to θ(t) = Γ₁ e^γ₁t + Γ₂ e^γ₂t + Γ₃ e^−i2πΔft, with the boundary conditions θ(0) = 0 and 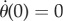. For short times t ≪ 1/2πf, the homogeneous part (Γ₁e^γ₁t + Γ₂e^γ₂t) is much larger than the particular part Γ₃ e^−i2πΔft. The movement of the hair is constrained by the boundary conditions at t = 0 and is determined principally by the homogeneous coefficients. This means that the natural response of the hair drives its behaviour at early time points, as shown in figure 3, in which the general solution follows its homogeneous component for times below 1 ms. For times exceeding 2.5 ms, the general solution much more closely resembles the particular solution, indicating that the movement of the hair is then dependent principally on its forced response.

Figure 3.

Comparison of the natural and forced response components of the total response (red) of a 500 μm long hair to a 20 Hz single-frequency air flow impulse. The natural response of the hair is described by the homogeneous solution of the equation of motion (2.34), whereas the forced response is described by the particular solution of equation (2.34). The total response of a hair is determined as the sum of its natural and forced responses.

2.5. Hair agility and threshold angle of firing

The aim of this part is to describe the complex interplay between hair sensitivity that will determine the maximal angle of deflection of the sensory hair, and hair agility, which will determine the angle at which the nerve cell connected to the hair fires, the threshold angle for perception. By definition, the threshold angle for firing is smaller than the maximal angle of deflection. The two key factors conditioning the ability of a hair to reach its minimal threshold angle are its impulse response time τ₉₅ and the energy available in the fluid medium (i.e. the flow velocity) between t = 0 and t = τ₉₅. The impulse response time of the hair, τ₉₅, provides an estimate of the agility of the hair. It should be noted that the impulse response time (τ₉₅) is not necessarily equal to the reaction time. τ₉₅ is only the time required for the hair to reach 95% of its maximal achievable angle when subjected to a velocity step function. The maximal achievable angle is dependent on the mechanical parameters of the hair, but it is also a function of velocity step function amplitude. If this maximal achievable angle is smaller than the threshold angle, the hair sensory neuron will never trigger an action potential. By contrast, if the maximal achievable angle is larger than the threshold angle, the deflection of the hair will eventually reach the threshold angle.

The impulse response time is equal to

2.35

where .

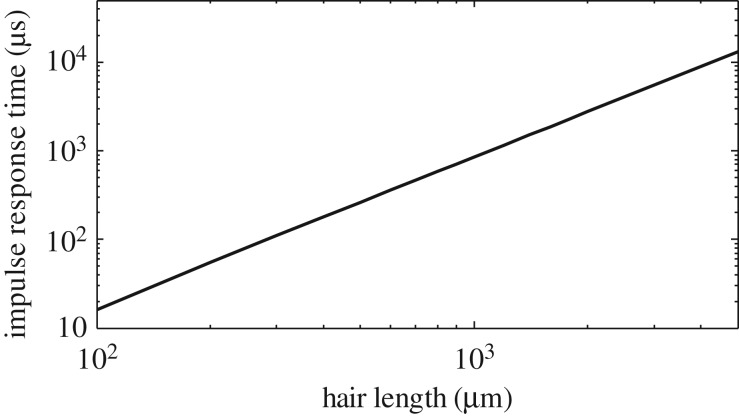
The computation of τ₉₅ for different hair lengths shows that short hairs of 100 μm have very small response times, of the order of 100 μs, whereas the response times of long hairs last up to 2 or 5 ms (figure 4).

Figure 4.

Impulse response time τ₉₅ for hair lengths ranging from 100 μm to 5000 μm.

Our model of hair deflection in impulsive transient flows can be used to predict the time elapsed between the start of predator movement and the instant at which the hair reaches its minimal threshold angle. Knowledge of the threshold angle for deflection makes it possible to evaluate hair reaction times for different velocities. This reaction time is the time elapsed between the instant the impulsion starts (i.e. the start of the predator attack), and the instant at which the hair reaches its threshold angle. This is the threshold angle that must be reached to compress the tubular body sufficiently for the sensory neuron at the base of the hair to deliver an action potential [4].

The deflection angle of the mechanosensor triggering an action potential was estimated by Shimozawa et al. [18] to be from 0.001° to 0.1°. Moreover, Barth & Höller [19] showed that, physiologically and regardless of their length, the trichobothria of spiders are all broadly tuned to a frequency range between about 50 and 100 Hz, with threshold deflection angles of about 0.1°, but as small as 0.01° in some cases [19]. This triggering angle represents the minimal angle at which the movement of a hair may be considered not to be due to Brownian thermal noise anymore, but to result from a biotic or abiotic change in the surrounding air flow. Rather than choosing an arbitrary fixed threshold angle, we choose to define the threshold angle for deflection as proposed by Droogendijk et al. [20]. These authors defined a Brownian noise equivalent angle θ_n by integrating the mechanical–thermal noise due to the Brownian motion of molecules in air over the full frequency spectrum. The noise due to Brownian motion is estimated as the product of the spectral density of white noise 4k_BT₀R and the mechanical transfer function |F(ω, r, ω_s, ω_i)|:

2.36

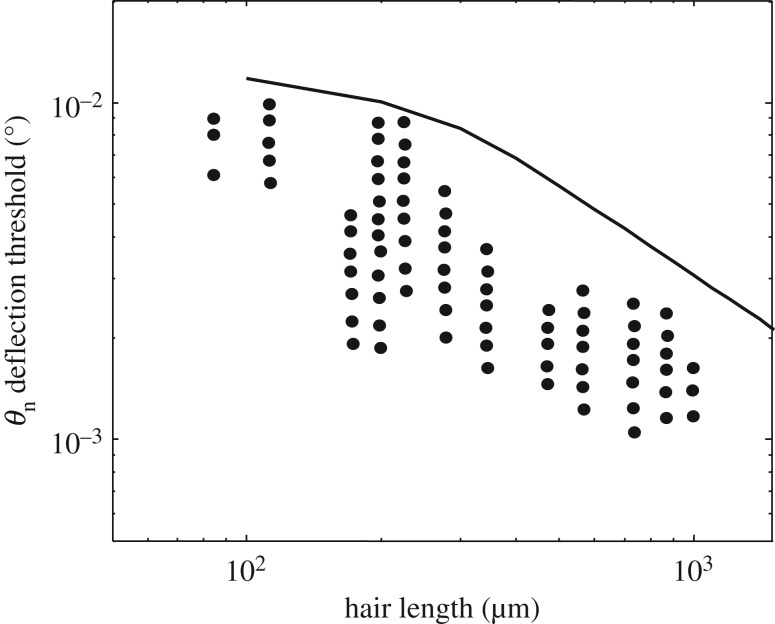
Figure 5 represents the deflection threshold angle estimated by equation (2.36) and shows that equation (2.36) leads to an overestimation of the sensory threshold compared with the measurements of Shimozawa et al. [18]. For long hairs, the qualitative trend of decline of the deflection sensory threshold is, however, appropriate.

Figure 5.

Deflection angle threshold against hair length. (black line) Numerical estimation of the deflection threshold due to Brownian noise from equation (2.36) [20]. (dots) Measurements of the detection threshold of filiform hairs of Grillus bimaculatus for sinusoidal flows of various frequencies, ranging from 5 Hz to 100 Hz. Taken from Shimozawa et al. [18].

3. Experimental validation of the new model

We validated our model by comparing the model output θ_SC(t) (equation (2.28)) with measurements of hair deflection under the flow produced by an approaching piston. As explained in §2.4, the deflection of the hair is dependent principally on its mechanical parameters I_T, R_h, R_μ, S_h, γ₂ and γ₁ and on the flow produced by the piston V_{0 SC}^m. The methodology used to estimate the mechanical parameters is described in detail in electronic supplementary material, appendix D. Electronic supplementary material, appendix B, introduces the techniques used to determine the flow produced by the piston and explains the influence of the piston movement velocity on the spectral distribution of flow velocity in the vicinity of the hair.

3.1. Methods

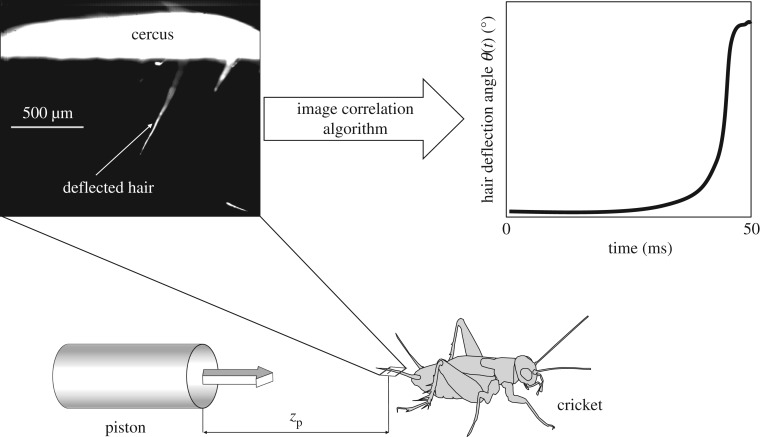
Adult male and female crickets (Acheta domesticus) were anaesthetized by chilling, and the legs, wings and female ovipositor were removed to prevent unwanted flow perturbation. The crickets were fixed on a micromanipulator placed in a sealed glass box. The moving piston, also placed in the box, was positioned to move along the anterioposterior axis of the body of the cricket (figure 6). Hair deflection was monitored with a high-speed video camera, at 1000 frames per second with a shutter speed of 500 μs (Vision Research Phantom V9.1), through a binocular lens. We had to work at high magnification (10× ) to obtain an accurate estimate of hair deflection. The time origin (t = 0) was estimated as the time at which the piston started moving.

Figure 6.

Experimental set-up used to measure hair by the piston flow. In a sealed glass box, the 8 mm diameter moving piston was placed at a distance of z_p = 5 cm in front of the test specimen. The piston was moved along the anterioposterior axis of the cricket body. A 1000 fps high-speed camera mounted on a 10× binocular lens was used to monitor hair deflection.

The velocity of hair deflection was extracted from 1000 Hz video recordings, by comparing subpixel displacement in successive images, using a correlation algorithm on an area of 32 pixels² (Dantec Dynamic Studio 2.30 2009). With this subpixel interpolation correlation algorithm, a 2-megapixel camera for imaging and a field of view of 2 × 2 mm², we expected to obtain a theoretical displacement resolution of 0.1 μm. This represents a theoretical minimal deflection angle of 0.01° for a hair with a length of 500 μm. The deflection measurements were restricted to larger attack velocities (30 cm s⁻¹ and 58 cm s⁻¹), due to background noise from unwanted residual low-amplitude air displacements and piston vibrations transmitted through the cricket cerci. For the two attack velocities (30 cm s⁻¹ and 58 cm s⁻¹), we fixed the initial distance between the piston and the cricket sensory hair to z_p = 5 cm. This distance has been chosen as it is the maximal spider pursuit distance estimated in behavioural studies [21,22]. We measured the deflection of six isolated hairs (L = 382, 386, 632, 795, 870 and 1063 μm) during the approach of the piston at these velocities. All measurements were made on independent videos with the six hairs in different frames. We tried to identify hairs having representative lengths spanning the entire spectrum of length. They also had to move in the plane of the video recording. The hair diameter can be precisely estimated from the hair length, as there is a strong allometric relationship between these two variables [8,10,23,24]. The base diameter varies with hair length according to

3.1

One key element taken into account when fitting our model (equation (2.28)) was the preferential plane of deflection of the hair. This factor greatly affects the resistance of the hair to rotation [24,25]. Unlike its length, the directionality α of the hair was not known and had to be estimated by regression. We first fitted equation (2.28), using the V_{0 SC}^m estimated for the piston approaching at 58 cm s⁻¹, with directionality α as the sole fit parameter, from measurements on hairs of six lengths, for a velocity of 58 cm s⁻¹. This made it possible to estimate the directionality of the hair. We then cross-validated our model by estimating the deflection of the hair subjected to air flow from the piston approaching at 30 cm s⁻¹, using α as a fixed parameter in equation (2.28), with V_{0 SC}^m estimated at that speed. At 30 cm s⁻¹, we were able to record deflection for only four hairs. The deflections of the 386 and 870 μm hairs under the flow produced by the piston moving at 30 cm s⁻¹ were too small to be detected.

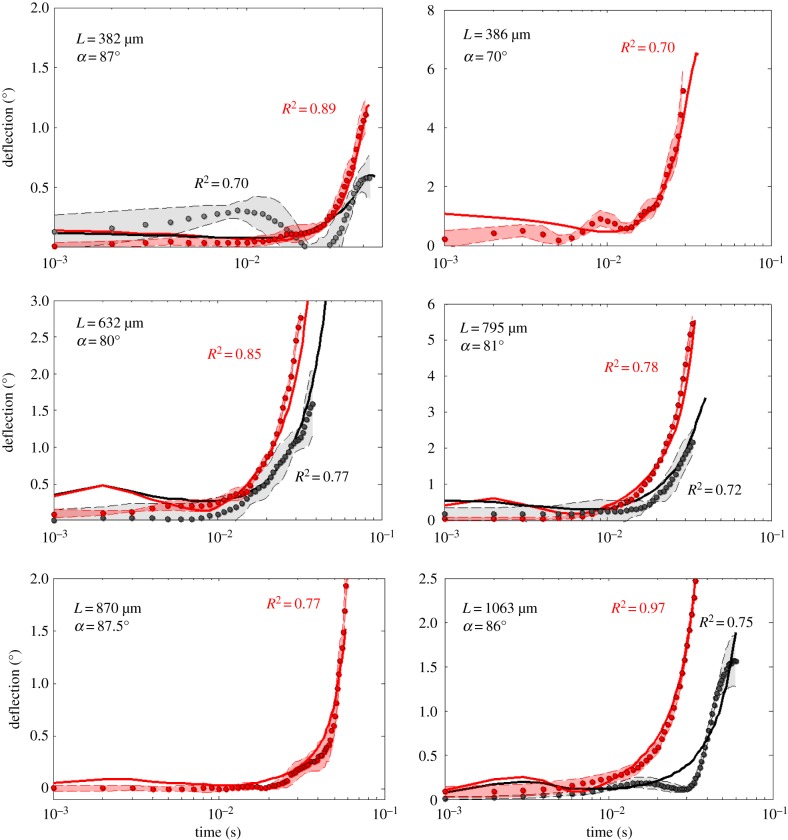
3.2. Results

The results are summarized in figure 7. In each of the six panels of the figure, the grey and red solid curves represent the deflection as modelled with equation (2.28). In this equation, parameters I_T, R_h, R_μ, S_h, γ₂ and γ₁ are predetermined as they are constrained by hair length, as shown in electronic supplementary material, appendix D. V_{0 SC}^m is a complex parameter determined by flow and estimated in electronic supplementary material, appendix B. The model predictions are reasonably good, at least for the three longest hairs. For the smallest hair (382 μm), we recorded a large mean deflection at intermediate times that the model was unable to predict.

Figure 7.

Comparing hair deflection measurement and model prediction. The points represent the measurements of deflection for six isolated hairs (L = 382, 386, 632, 795, 870 and 1063 μm), and the thick red and black lines represent the model prediction of hair deflection. The grey points represent the average deflection time for a hair of the given length in response to the flow produced by the piston approaching at 30 cm s⁻¹. The thin black lines and the grey area represent the standard deviation. The red points represent the mean deflection for the same hair subjected to the flow produced by a piston approaching at 58 cm s⁻¹. The thin red lines and the red area represent the standard deviation.

4. Discussion

While our model represents a generalization of previous ones, it contains three major assumptions which we discuss, first starting with aspects related to the flow and its modelling. Assumptions regarding the mechanical properties of single hairs and viscous coupling among multiple hairs are dealt with under their respective headings.

4.1. Assumptions regarding boundary flows

Our model describes only the deflection of sensory hairs placed on a straight cylinder in a longitudinal flow. However, Humphrey et al. [9] observed that flow velocity profiles are quite different in transverse and in longitudinal flows, transverse flows producing local velocities up to 1.6 times stronger than the far-field values. Steinmann et al. [16] also observed that velocities would be stronger in transverse flow than in longitudinal flow, as long as the angle is between 60° and 120°. By contrast, the maximal amplification of the far-field value is only 1.1 for longitudinal flows. The strong spatial heterogeneity of flow velocities around appendages in transverse flow could be a rich source of information for flow-sensing hairs. The relative importance of these transverse and longitudinal air flow components will be a function of circumferential location of the hair on the cercus and of the hair length. Steinmann et al. [16] estimated that short hairs were more sensitive than long hairs to the transverse component of flow from almost any direction, as the largest differences between longitudinal and transverse flows are in the boundary layer, in which the small hairs are totally immersed. Thus, the implications for our model is that it underestimates the deflections, of short hairs in particular, in a flow different from a longitudinal one.

Furthermore, Fourier series decomposition is classically used to model the impulsive transient boundary layer V^SC_f(y, t) in descriptions of the theoretical evolution of turbulent boundary layers [15]. The implicit superimposition should, however, be validated by means of further particle image velocimetry experiments on the changes in the boundary layer over a cricket cercus during the increase in impulsive flow generated by the approach of a piston. Alternatively, computational fluid dynamics can be used for the numerical validation of this approach.

4.2. Assumptions regarding preferential plane of deflection and functioning of the socket of single hairs

The fact that a hair has a preferential plane of deflection greatly affects its resistance to rotation. The preferential plane of motion of each sensory hair is an excitatory direction along each hair and its existence can be explained by the anisotropy of the mechanical properties of the socket [24–26]. The crucial morphological features conditioning this directionality are the bilaterally symmetrical form of the hair base and the way in which the hair shaft is seated in the socket floor [4]. This translates into the existence of a plane of smallest oscillations, perpendicular to the preferred plane, that passes through the more rigid part of the socket floor. Each sensory hair is thus constrained to move back and forth in a preferential plane by this cuticular hinge at the base of the hair [24]. We implemented this preferential plane of deflection through the use of the factor cos(α) in the expression of our forcing function (equation (2.26)).

Most of the studies of sensory hairs and the results presented here are based on the representation of the suspension of the hair by a spring and dashpot viscoelastic model, with two parameters, a spring and a resistance. This choice of model, which may seem arbitrary at first sight, has been used many times [9,14,27]. However, studies concerning the morphology of the hair itself and of the suspension located in the socket indicate that these two primary elements are secreted by two types of epithelial cells with different mechanical and elastic characteristics [27,28]. In addition, Barth & Höller [19] assumed that the particular viscoelastic properties of the dendrites themselves could explain the phasic response patterns of the sensory cells. These sensory cells react preferentially to movements but not at all to static deformations or compressions. Shimozawa et al. [28] even assumed a divergence between viscoelastic models of long and small hairs. In a recent study, Joshi & Miller [26] recall that the structure of the socket was only rudimentarily characterized from a mechanical point of view. Their finite-element model indicates that this structure acts indeed as a spring. However, these authors also evoke the existence of two spring stiffness, both of which are numerically obtained by the simulation of the movement of deflection of the hair, the first spring stiffness being determined before the contact of the base of the hair with the socket iris. The second one has been inferred after the contact and has been numerically estimated as being four times as high as the first.

It turns out that the mechanical properties of the hair suspension in the socket have never been directly measured. The numerical values of these mechanical constants are generally inferred via the harmonic response of the sensory hairs in oscillatory flows. Methods of experimentally estimating the mechanical properties of sensory hairs have already been proposed by Barth et al. [29]. The method used by these authors consisted in estimating the forces involved in the return of tactile hairs to their original positions by stimulating them by means of glass capillaries which deformed under the resistances of sensory hairs. Schaber & Barth [30] have also used this technique to measure the spring stiffness of the tactile hairs of the tibia–metatarsus junction in spiders Cupiennius salei. The atomic force microscopy (AFM) method is even more precise than the one based on deformation of glass capillaries. AFM has been used to study mechanosensing structures, from the mechanical properties of vibration receptors in the cuticule of spiders [31–33] to the nanomechanical properties of the cupula of the superficial neuromasts in fish [34]. McConney et al. [35] used AFM in contact mode to study the mechanical properties of suspensions of C. salei spider sensory hairs. These authors used AFM probes to deflect these sensory hairs, allowing to determine simultaneously their deflection and the force applied to them. They describe the suspension by means of a new viscoelastic model comprising three elements. The application of AFM to the study of cricket sensory hairs could also be useful to the understanding of the specific roles of small and long hairs.

4.3. Assumptions regarding viscous coupling among multiple hairs

Our model assumes that hairs are independent, and does not, therefore, take into account the viscous medium coupling effect between hairs. Humphrey et al. [9] were the first to consider viscous coupling, especially the phase shift between hairs in a cluster, and how it could affect the combined action potentials of sensory neurons. Despite its absence from the model and previous demonstrations of its importance [36–38], we can predict the quantitative impact of viscous coupling on the response of hairs to impulsive flows. In Casas et al. [38], the study of the viscous coupling between tandem hairs shows that the reduction in the flow velocity inside a hair canopy will depend on the combination of (i) the frequency of the flow and (ii) the hair spacing. The statistical analysis of hair spacing shows that most long hairs (longer than 500 μm) are regularly distributed over the cercus at distances up to 60 μm, corresponding to a normalized distance of six (hair spacing/hair diameter) [39]. The perturbation can be equal to 50% for an inter-hair distance of six diameters in a 40 Hz flow [38]. The power spectrum analysis of the flow produced by the piston moving at 30 cm s⁻¹ shows that 90% of the energy contained in the flow is bounded between 5 Hz and 40 Hz (electronic supplementary material, appendix B). So, given the inter-hair spacing and the frequency content of the flow, we can expect that long hairs will experience strong viscous coupling in a flow produced by the approach of a piston at 30 cm s⁻¹, reducing their sensitivity by a factor of 2. The power spectrum analysis of the flow produced by the piston moving at 58 cm s⁻¹ shows that 90% of its energy is contained between 5 Hz and 80 Hz, the low frequency components decreasing with increase in the velocity of attack. The perturbation would thus drop to 30% for an inter-hair distance of six diameters (in an 80 Hz flow). So we can expect that long hairs will experience a reduced viscous coupling during the approach of a piston at 58 cm s⁻¹. Short hairs are inserted randomly over the surface of the cercus with spacing ranging from 20 to 60 μm and diameter ranging from 3 to 7 μm, corresponding to a normalized distance ranging from 3 to 20 [39]. Heys et al. [25] quantified the spatial distribution of hairs for various sizes of circular search windows. They determined that, for a small search area less than 750 μm, the pattern of hairs corresponded to what would be expected for a random Poisson process of positioning. So, given the large span of inter-hair spacing and their spatial random distribution, the conclusion on the effect of a small viscous coupling on short hairs is not straightforward. We can expect that the closest hairs will experience a strong viscous coupling, up to 80% in a flow produced by the approach of a piston at 30 cm s⁻¹. By contrast, the most widely spaced hairs will experience a very low coupling of 5% in a flow produced by the approach of a piston at 58 cm s⁻¹. Bathellier et al. [36] extended their viscous coupling theory to hairs of dissimilar lengths. Short hairs surrounded by a cluster of longer hairs should experience strong coupling up to 30% in a 40 Hz flow. Thus, the general implication for our model is that viscous coupling might lead to a diminution of a hair response, which is nonlinear in flow frequency and hair length. Any further development requires one to become very specific about the stimulus nature and the canopy structure, as illustrated above.

The impact of viscous coupling between hairs is not only mechanical, but is also felt at the neuronal ensemble reaction of an entire cricket cercus. This has been measured by Mulder-Rosi et al. [40]. They successively stimulate the sensory hairs positioned at different locations on the cercus, from its base to its tip, with the help of a multi-nozzle air-current stimulus device. They discovered that the ensemble response of sensory hairs was maximized when the stimulus was directed from the point at the base of the cercus. They suggested that the cercal system of the cricket functioned as a delay line, the hairs closer to the stimulus sources reacting before the furthest hairs. Dupuy et al. [41] have also measured the ensemble reaction of an entire cricket cercus. They have shown that the cumulative number of spikes, recorded through the abdominal connectives from the terminal abdominal ganglion, is a function of the velocity of the flow perceived at the rear of the cricket, multiplied by a factor that increases linearly with the attack velocity. Our model can predict the ensemble reaction of a group of hairs of various lengths. We can predict the ensemble reaction of an entire cercus, i.e. the different moments at which hairs of different lengths will reach their threshold angle of reaction one after the other. For instance, in the flow produced by a predator launching its attack at a distance of 1 cm and a velocity of 40 cm s⁻¹, the sensory neuron of a 200 μm hair will fire 40 μs after the start of the attack, whereas the sensory neuron of a 2000 μm hair will fire 1000 μs after the start of the attack (figure 8b). This temporal pattern of action potentials could be the first step of the transduction of the characteristic of an attack, like its velocity. To be realistic, such an ensemble modelling does, however, require much more information than available, including viscous coupling, a map of the hairs and their preferential planes of movement.

Figure 8.

Comparison of the deflections of hairs of different lengths, ranging from 500 μm to 3000 μm, subjected to two different flows produced during an attack. (a) Slow increasing flow velocity, lasting 125 ms, produced by a predator launching its attack at a distance of 2.5 cm and a velocity of 10 cm s⁻¹. (b) Rapidly increasing flow velocity, lasting 12.5 ms, produced by a predator launching its attack at a distance of 1 cm and a velocity of 40 cm s⁻¹.

4.4. Resolution of conflict: short and long hairs are both optimal, but to different inputs

The assumptions and limitations of the model having been covered, we can now proceed to the resolution of the conflict between the two views regarding the performance of long and short hairs.

The major result arising from the Kant and Humphrey model is that short hairs are more responsive than long hairs to their particular flow pulsation, due to a lower total inertia, torsional restoring constant and total damping constant. This is at odds with previous results, which identified long hairs as the most sensitive ones. This discrepancy results from the use of different definitions of hair reactions, and the focus exclusively on steady sinusoidal flows in previous studies [9,27,28]. Our model resolves this discrepancy by providing the general solution, a superposition of natural and forced responses.

We provide now an intuitive illustration of the various parts of the solution of our model, by working through an example of a solution to a simpler ‘harmonic impulsion’: single-frequency sinusoidal flow. There is a great variability and heterogeneity in the signals produced during an attack. However, due to the difficulty to explain and visualize the superposition of responses of hairs to complex sums of harmonic flows, we rather focus our illustration to two simplified extreme cases of idealized mono-harmonic flows. Real flows are, of course, multi-frequential and our model also deals with this more complicated case. Let us first consider four different hairs, 500, 1000, 2000 and 3000 μm in length, all subjected to attacks at a speed of 10 cm s⁻¹ and at a distance of 2.5 cm, corresponding to a frequency of 4 Hz (half-period 125 ms). We extended the range of hair lengths beyond the observed range of lengths in order to highlight the lack of response improvement of even longer hairs at high frequencies. The natural responses of the hairs drive their behaviour at early time points (i.e. before 40 ms), at which the general solution follows the homogeneous solution (figure 8a). After 40 ms, the general solution closely follows the particular solution, indicating that the movement of the hairs is dependent mostly on their forced responses. Short hairs react quickly, but they cannot harvest much energy from the fluid, and may, therefore, not reach their threshold angle. Long hairs pick up the flow velocity later, but they deflect to a much greater extent, due to the combination of a larger surface area and a projection into a region further away from the body. Long hairs are optimal for picking up such ‘slow’ flows. Let us now consider a faster attack at 40 cm s⁻¹ and at a distance of 1 cm, corresponding to a signal of 40 Hz (half-period 12.5 ms). Short hairs again react quickly, resulting in large hair deflections as the input provides sufficient energy (figure 8b). The neurons attached to these hairs are, therefore, likely to fire first. Long hairs cannot follow the first phase of the signal due to their inertia, and they attain their threshold angles much later. Thus, the neurons connected to long hairs cannot fire sufficiently quickly for the detection of fast flows, a task for which short hairs are much better suited.

In these calculations, the threshold angle for detection is the key to determine which hair neuron fires first. Thus, the sensitivity of a given hair relative to another hair depends not only on its ability to reach a given triggering angle rapidly, but also its capacity to extract energy from the fluid medium and translate it into mechanical energy dissipated at the basal joint. The trade-off between mechanical agility, which declines with increase in hair length, and sensitivity, which increases with increase in hair length as explained in §2.5, defines the time required to reach the firing threshold. Furthermore, this trade-off keeps hair lengths and firing times in a bounded region. We, therefore, conclude that prey animals make full use of an array of hairs of all lengths to cope with interactions as complex and crucial as the launch of a predator attack, pursuit and final assault. The morphological heterogeneity of the hair canopy thus mirrors the flow complexity of an entire attack, from launch to grasp, and provides another example of a dynamic matched filter [1,2].

Data accessibility

The Matlab code of our model is accessible online as the electronic supplementary material.

Authors' contributions

J.C. and T.S.: conceived and designed the experiments; T.S.: performed the experiments and the model derivation; J.C. and T.S.: analysed the data; J.C. and T.S.: wrote the paper. This work is part of the PhD thesis of T.S. under the supervision of J.C.

Competing interests

We declare we have no competing interests.

Funding

We had no particular funding for this study.