Energy-based analysis of biomolecular pathways

Abstract

Decomposition of biomolecular reaction networks into pathways is a powerful approach to the analysis of metabolic and signalling networks. Current approaches based on analysis of the stoichiometric matrix reveal information about steady-state mass flows (reaction rates) through the network. In this work, we show how pathway analysis of biomolecular networks can be extended using an energy-based approach to provide information about energy flows through the network. This energy-based approach is developed using the engineering-inspired bond graph methodology to represent biomolecular reaction networks. The approach is introduced using glycolysis as an exemplar; and is then applied to analyse the efficiency of free energy transduction in a biomolecular cycle model of a transporter protein [sodium-glucose transport protein 1 (SGLT1)]. The overall aim of our work is to present a framework for modelling and analysis of biomolecular reactions and processes which considers energy flows and losses as well as mass transport.

1. Introduction

The term ‘pathway analysis’ is used very broadly in systems biology to describe several quite distinct approaches to the analysis of biomolecular networks [1–3] and often the definition of a ‘pathway’ is somewhat nebulous. In this work, we are concerned with those pathways defined in terms of the stoichiometric analysis of biomolecular reaction networks [4–8]; in particular, the null space¹ of an appropriate stoichiometric matrix¹ is used to identify the pathways of a biomolecular network. Two alternative concepts of pathways: elementary modes and extreme pathways are compared and contrasted by Papin et al. [3]. Computational issues are considered by Schuster & Hilgetag [9], Pfeiffer et al. [10], Schilling et al. [11] and Schuster et al. [12]. A brief introduction to the relevant concepts appears in appendix B.

These approaches have proven to be very useful in determining network properties and emergent behaviour of biomolecular reaction networks in terms of the pathway ‘building blocks’ of these networks. However, these approaches are solely focused on mass flows of biomolecular reaction networks. However, to date, little attention has been given to the identification and analysis of pathways in the context of energy flows in biomolecular reaction networks. This paper extends the pathway concept to include such energy flows using an engineering-inspired method: the bond graph.

Like engineering systems, living systems are subject to the laws of physics in general and the laws of thermodynamics in particular [13–17]. This fact gives the opportunity of applying engineering science to the modelling, analysis and understanding of living systems. The bond graph method of Paynter [18] is one such energy-based engineering approach [19–24] which has been extended to include chemical systems [20,25], biological systems [26] and biomolecular systems [27–32]. A brief introduction to the bond graph approach appears in appendix A.

Applying the bond graph method to modelling biomolecular pathways moves the focus from mass flow to energy flow. Hence this paper brings together stoichiometric pathway analysis with energy-based bond graph analysis to identify the pathways of steady-state free energy transduction in biomolecular networks. Although the bond graph approach is well established in the field of engineering, and the stoichiometric pathway analysis approach well established in the field of biochemical analysis, they have not hitherto been brought together. As illustrated in the sodium-glucose transport protein example of §6, this interdisciplinary synthesis gives new insight into the energetic behaviour of living systems.

Section 2 introduces the bond graph approach to pathway analysis using glycolysis as an exemplar. As a preliminary to the energy-based approach, §3 discusses the stoichiometric approach to pathway analysis. Section 4 combines the energy-based reaction analysis of §2 with the stoichiometric pathway analysis of §3 to give an energy-based pathway analysis of biomolecular systems. Section 5 looks at the generic biomolecular cycle transporter model of Hill [14] focusing on the energy transduction aspects; in particular, a two-pathway decomposition provides insight into free-energy dissipation and efficiency. Section 6 uses this two-pathway decomposition to look at a particular transporter—the sodium-glucose transport protein 1 (SGLT1)—using parameters drawn from the experimental results of Eskandari et al. [33]. Section 7 draws some conclusions and indicates future research directions. Appendix A provides a short introduction to those features of the bond graph approach necessary to understand this paper and appendix B similarly introduces systems biology. The complete equations describing the examples are given in the electronic supplementary material.

2. Energy-based reaction analysis

As reviewed in the Introduction, and as discussed by Gawthrop & Crampin [29,31] and appendix A, chemical equations can be written in the form of bond graphs to enable energy-based analysis. As an introductory and illustrative example, the glycolysis example from the seminal book of Heinrich & Schuster [5], fig. 3.4 has the following chemical equations:

$$\begin{array}{rl}& \mathrm{ATP}\stackrel{r1}{\rightleftharpoons }\mathrm{ADP}\mathrm{ATP}+\mathrm{F}6\mathrm{P}\stackrel{r2}{\rightleftharpoons }\mathrm{ADP}+\mathrm{F}2\mathrm{P}\mathrm{F}2\mathrm{P}\stackrel{r3}{\rightleftharpoons }\mathrm{F}6\mathrm{P}\\ & \mathrm{GLC}+\mathrm{ATP}\stackrel{r4}{\rightleftharpoons }\mathrm{ADP}+\mathrm{G}6\mathrm{P}\mathrm{G}6\mathrm{P}\stackrel{r5}{\rightleftharpoons }\mathrm{F}6\mathrm{P}\mathrm{ATP}+\mathrm{F}6\mathrm{P}\stackrel{r6}{\rightleftharpoons }\mathrm{ADP}+2\mathrm{TP}\\ & 2\mathrm{ADP}+\mathrm{TP}\stackrel{r7}{\rightleftharpoons }\mathrm{Pyr}+2\mathrm{ATP}\mathrm{ATP}+\mathrm{AMP}\stackrel{r8}{\rightleftharpoons }2\mathrm{ADP}\mathrm{G}6\mathrm{P}\stackrel{r9}{\rightleftharpoons }\mathrm{G}1\mathrm{P}\end{array}$$

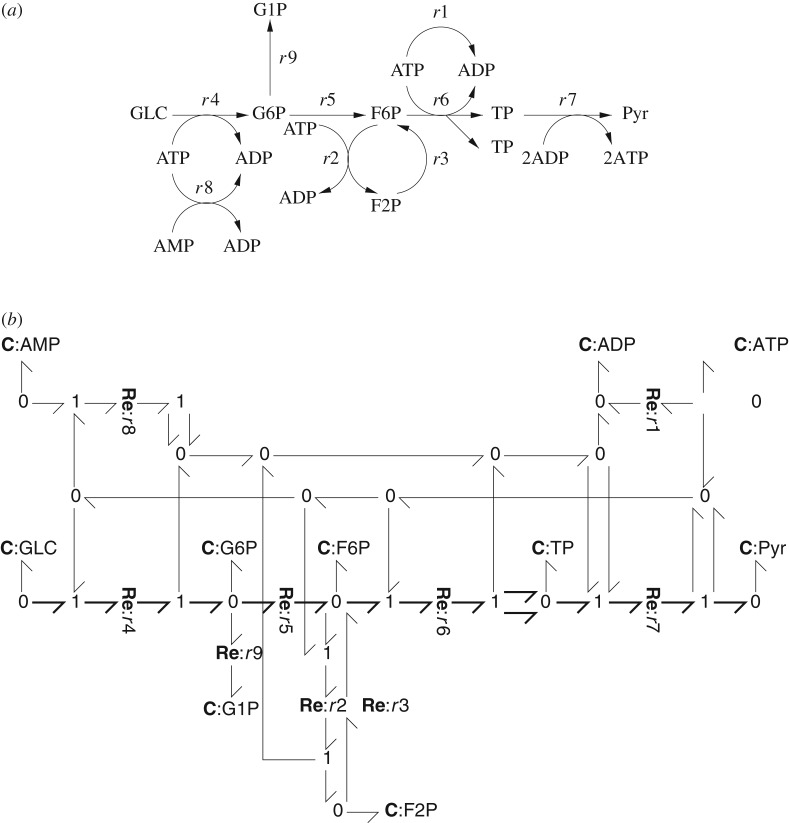
These equations can be represented by the biomolecular reaction diagram of figure 1a or the equivalent bond graph of figure 1b. Briefly, each reaction is represented by an Re component and each species by a C component. The (Gibbs) energy flows are represented by bonds $\rightharpoondown$ which carry both chemical potential and molar flow. Bonds are connected by 0 junctions which imply a common chemical potential on each bond and 1 junctions which imply a common molar flow on each bond. C components store, Re components dissipate and bonds and junctions transmit Gibbs energy. Further details are given in appendix A and references [29–32].

Figure 1.

Glycolysis example from Heinrich & Schuster [5]. (a) Biomolecular reaction diagram of the glycolysis pathway. (b) Bond graph representation of the biomolecular pathway.

Closed biomolecular systems are described in stoichiometric form as:

$$\dot{X}=NV,$$ 2.1

where X is the n_X×1 system state, V the n_V×1 vector of reaction flows and N is the n_X×n_V stoichiometric matrix which can be derived from the bond graph representation [29,32]. In the case of the example of figure 1:

$$X=\left(\begin{array}{c}{x}_{\mathrm{GLC}}\\ x_{\mathrm{Pyr}}\\ x_{\mathrm{ATP}}\\ x_{\mathrm{ADP}}\\ x_{\mathrm{G}1\mathrm{P}}\\ x_{\mathrm{G}6\mathrm{P}}\\ x_{\mathrm{F}6\mathrm{P}}\\ x_{\mathrm{TP}}\\ x_{\mathrm{F}2\mathrm{P}}\\ x_{\mathrm{AMP}}\end{array}\right),N=\left(\begin{array}{ccccccccc}0& 0& 0& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0\\ -1& -1& 0& -1& 0& -1& 2& -1& 0\\ 1& 1& 0& 1& 0& 1& -2& 2& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& -1& 0& 0& 0& -1\\ 0& -1& 1& 0& 1& -1& 0& 0& 0\\ 0& 0& 0& 0& 0& 2& -1& 0& 0\\ 0& 1& -1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& -1& 0\end{array}\right)\mathrm{and}V=\left(\begin{array}{c}{v}_{r1}\\ v_{r2}\\ v_{r3}\\ v_{r4}\\ v_{r5}\\ v_{r6}\\ v_{r7}\\ v_{r8}\\ v_{r9}\end{array}\right)$$ 2.2

In the case of mass-action kinetics [8], the reaction flows are generated by the formula:

$$V=\kappa (\exp \frac{A^{\mathrm{f}}}{RT}-\exp \frac{A^{\mathrm{r}}}{RT}),$$ 2.3

where A^f and A^r are the forward and reverse² reaction affinities. As discussed by Gawthrop & Crampin [29,31], these affinities are given by:

$$A^{\mathrm{f}}=N^{\mathrm{f}}{\hspace{0.17em}}^{\mathrm{T}}\mu \mathrm{and}{A}^{\mathrm{r}}=N^{\mathrm{r}}{\hspace{0.17em}}^{\mathrm{T}}\mu$$ 2.4

where superscript ‘T’ indicates matrix transpose and μ is the (vector of) chemical potentials where the ith element is a logarithmic function of the ith element x_i of X:

$${\mu }_i=RT\mathrm{ ln }{K}_i{x}_i$$ 2.5

where K_i is a species-specific positive constant. N^f and N^r are the forward and reverse stoichiometric matrices, respectively, and conservation of energy requires that:

$$-N^{\mathrm{f}}+N^{\mathrm{r}}=N.$$ 2.6

By definition, all stoichiometric parameters, that is the elements N^f_ij of N^f and the elements N^r_ij of N^r have the following properties:

$$N_{ij}^{\mathrm{f}}\text{ is integer}{N}_{ij}^{\mathrm{f}}\ge 0N_{ij}^{\mathrm{r}}\text{ is integer}{N}_{ij}^{\mathrm{r}}\ge 0$$ 2.7

As discussed by Gawthrop & Crampin [31], open biomolecular systems can be described and analysed using the notion of chemostats [34,31]. Chemostats have two biomolecular interpretations:

• (i) one or more species are fixed to give a constant concentration (for example, under a specific experimental protocol); this implies that an appropriate external flow is applied to balance the internal flow of the species,

• (ii) as a C component with a fixed state imposed on a model in order to analyse its properties [30].

Additionally, in the context of a control systems analysis, the chemostat can be used as an ideal feedback controller, applied to species to be fixed with setpoint as the fixed concentration and control signal an external flow.

When chemostats are present, the reaction flows are determined by the dynamic part of the stoichiometric matrix. In this case, the stoichiometric matrix N can be decomposed as the sum of two matrices [31]: the chemostatic stoichiometric matrix N^cs and the chemodynamic stoichiometric matrix N^cd, where N=N^cs+N^cd and:

$$N^{\mathrm{cs}}=I^{\mathrm{cs}}N{N}^{\mathrm{cd}}=I^{\mathrm{cd}}N{I}_{ii}^{\mathrm{cs}}=\{\begin{array}{ll}1& \text{if }i\in {\mathcal{I}}^{\mathrm{cs}}\\ 0& \text{if }i\notin {\mathcal{I}}^{\mathrm{cs}}\end{array}{I}_{ii}^{\mathrm{cd}}=\{\begin{array}{ll}0& \text{if }i\in {\mathcal{I}}^{\mathrm{cs}}\\ 1& \text{if }i\notin {\mathcal{I}}^{\mathrm{cs}}.\end{array}$$ 2.8

Note that N^cd is the same as N except that the rows corresponding to the chemostat variables are set to zero. In this case, N^cd is given by N of equation (2.2) with rows 1–4 set to zero.

With these definitions, an open system can be expressed as

$$\dot{X}=N^{\mathrm{cd}}V.$$ 2.9

The stoichiometric properties of N^cd, rather than N, determine system properties when chemostats are present. Using equation (2.8), $\dot{X}$ in equation (2.9) can also be written as

$$\dot{X}=NV-N^{\mathrm{cs}}V=NV+V^s,\text{where }{V}^s=-N^{\mathrm{cs}}V$$ 2.10

V ^s can be interpreted as the external flows required to hold the chemostat states constant. The reaction flows are given by the same formulae (2.3) and (2.4) as closed systems.

3. Stoichiometric pathway analysis

As discussed in the textbooks [4–8] and appendix B, the (non-unique) n_V×n_P null-space matrix K_p of the open system stoichiometric matrix N^cd has the property that

$$N^{\mathrm{cd}}{K}_p=0,\text{where }{n}_P=n_V-r$$ 3.1

and r is the rank of N. Furthermore, if the reaction flows V are constrained in terms of the n_P pathway flows V _p as

$$V=K_p{V}_p,$$ 3.2

then substituting equation (3.2) into equation (2.1) and using equation (3.1) implies that $\dot{X}=0$. This is significant because the biomolecular system of equation (2.1) may be in a steady state for any choice of V _p.

As mentioned above, K_p is not unique: there are many possible approaches to choosing K_p such that equation (3.1) holds. As discussed by, for example, Pfeiffer et al. [10], K_p can be computed in such a way as to give useful features such as integer entities and maximal number of zero elements; moreover, if all reactions are irreversible, the columns of K_p must correspond to a convex space.³ As discussed in §4, the analysis of this paper requires that all elements K_pij of K_p must satisfy the same conditions as those on N^f_ij and N^r_ij (2.7), namely:

$$K_{p_{ij}}\text{ is integer}{K}_{p_{ij}}\ge 0.$$ 3.3

For this reason, K_p is referred to as the positive-pathway matrix (PPM) in the sequel. This does not imply that reactions are assumed to be irreversible; however, one approach to generating such a K_p is using software such as metatool [10] as if all reactions were irreversible.

In the case of the glycolysis system of figure 1, Heinrich & Schuster [5] choose the chemostats to be: GLC, Pyr, ATP and ADP. Using the algorithm of Pfeiffer et al. [10],⁴ K_p for the glycolysis system of figure 1 was computed as

$$K_p=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 1\\ 0& 0& 1\\ 0& 0& 2\\ 0& 0& 0\\ 0& 0& 0\end{array}\right).$$ 3.4

The pathways corresponding to the three columns of K_p, (referring to figure 1a), are: {r1}, {r2 r3} and {r4 r5 r6 2r7}. The latter pathway is marked on the bond graph of 1b using bold bonds. As pointed out by Heinrich & Schuster [5], these three pathways are independent insofar as they have no reactions in common; as will be seen in the rest of this section and in the examples of §§5 and 6, this is not always the case.

The number of pathways, and their independence, not only depend on the network structure, but also on the choice of chemostats. To illustrate this point, consider the same glycolysis system of figure 1, but choose an additional chemostat to be G1P. In this case, K_p is given by

$$K_p=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 1\\ 0& 0& 1& 0\\ 0& 0& 1& 0\\ 0& 2& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right)$$ 3.5

The first three columns of equation (3.5) are identical to the three columns of equation (3.4). The fourth column corresponds to the additional pathway {r4 r9}, which shares reaction r4 with the pathway {r4 r5 r6 2r7} corresponding to the third column of equations (3.5) and (3.4).

4. Energy-based pathway analysis

This section combines the energy-based reaction analysis of §2 with the stoichiometric pathway analysis of §3 to give an energy-based pathway analysis of biomolecular systems.

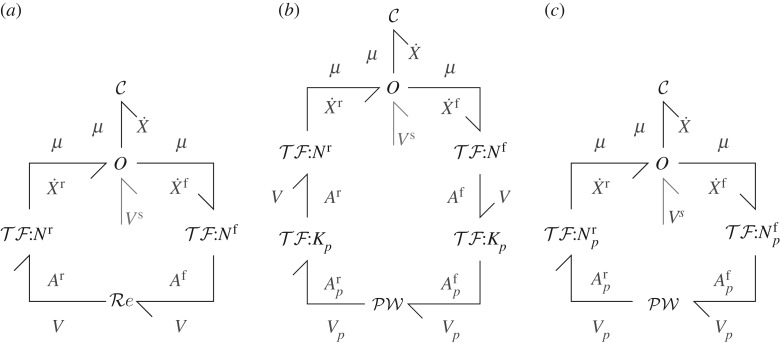
As discussed by Gawthrop & Crampin [29,31], equations (2.1), (2.4) and (2.6) can be summarized by the diagram of figure 2a. The key point here is that the energy flow from the reaction components represented by the vectors of covariables A^r and V is transformed without energy loss by $\mathcal{T}\mathcal{F}:N^{\mathrm{r}}$ into the energy flow to the $\mathcal{C}$ components represented by the vectors of covariables μ and ${\dot{X}}^{\mathrm{r}}$ and the energy flow from the $\mathcal{C}$ components represented by the vectors of covariables μ and ${\dot{X}}^{\mathrm{f}}$ is transformed without energy loss by $\mathcal{T}\mathcal{F}:N^{\mathrm{f}}$ into the energy flow to reaction components represented by the vectors of covariables A^f and V. Dissipation of energy occurs at the reaction components $\mathcal{R}e$. The challenge for an energy-based pathway analysis is to determine the energy flow associated with each pathway.

Figure 2.

Energy-based analysis. (a) Reaction-based system [31]. The bond symbols $\rightharpoondown$ correspond to vectors of bonds; $\mathcal{C}$, $\mathcal{R}e$ and $\mathcal{O}$ correspond to arrays of C, Re and 0 components; the two $\mathcal{T}\mathcal{F}$ components represent the intervening junction structure comprising bonds, 0 and 1 junctions and TF components. N^f and N^r are the forward and reverse stoichiometric matrices, respectively. V ^s represents the chemostatic flows. (b) The positive-pathway matrix K_p maps the n_P positive-pathway flows V _p onto the n_V reaction flows V and also maps the n_V reaction affinities onto the n_P positive-pathway affinities. $\mathcal{P}\mathcal{W}$ conceptually represents the non-linear function generating the steady-state positive-pathway flows in terms of the positive-pathway affinities; unlike $\mathcal{R}e$, it does not have a diagonal structure. (c) $\mathcal{T}\mathcal{F}$ components have been merged using $N_p^{\mathrm{f}}=N^{\mathrm{f}}{K}_p$ and $N_p^{\mathrm{r}}=N^{\mathrm{r}}{K}_p$.

The key result of the stoichiometric pathway analysis summarized in §3 is equation (3.2) relating the pathway flow vector V _p to the reaction flow vector V by V =K_pV _p. To bring this result into the energy domain, we define the forward and reverse pathway affinities $A_p^{\mathrm{f}}$ and $A_p^{\mathrm{r}}$, respectively, and the pathway affinity A_p, as

$$A_p^{\mathrm{f}}={K_p}^{\mathrm{T}}{A}^{\mathrm{f}}{A}_p^{\mathrm{r}}={K_p}^{\mathrm{T}}{A}^{\mathrm{r}}{A}_p=A_p^{\mathrm{f}}-A_p^{\mathrm{r}}={K_p}^{\mathrm{T}}(A^{\mathrm{f}}-A^{\mathrm{r}})={K_p}^{\mathrm{T}}A.$$ 4.1

With these definitions, we can define powers (energy flows) associated with pathways:

$$\begin{array}{rl}{P}_p^{\mathrm{f}}& =A_p^{\mathrm{f}}{\hspace{0.17em}}^{\mathrm{T}}{V}_p=(K_p{\hspace{0.17em}}^{\mathrm{T}}{A}^{\mathrm{f}}){\hspace{0.17em}}^{\mathrm{T}}{V}_p=A^{\mathrm{f}}{\hspace{0.17em}}^{\mathrm{T}}{K}_p{V}_p=A^{\mathrm{f}}{\hspace{0.17em}}^{\mathrm{T}}V=P^{\mathrm{f}}\end{array}$$ 4.2

$$\begin{array}{rl}\text{similarly }{P}_p^{\mathrm{f}}& =A_p^{\mathrm{r}}{\hspace{0.17em}}^{\mathrm{T}}{V}_p=(K_p{\hspace{0.17em}}^{\mathrm{T}}{A}^{\mathrm{r}}){\hspace{0.17em}}^{\mathrm{T}}{V}_p=A^{\mathrm{r}}{\hspace{0.17em}}^{\mathrm{T}}{K}_p{V}_p=A^{\mathrm{r}}{\hspace{0.17em}}^{\mathrm{T}}V=P^{\mathrm{r}}.\end{array}$$ 4.3

Thus, the net forward pathway energy flow $P_p^{\mathrm{f}}$ equals the net forward reaction energy flow P^f and the net reverse pathway energy flow $P_p^{\mathrm{f}}$ equals the net reverse reaction energy flow P^r. Hence K_p can be considered as an energy transmitting transformer for both forward and backward pathway energies and is represented in figure 2b by the symbol $\mathcal{T}\mathcal{F}:K_p$.

Figure 2c can be obtained from figure 2b by combining equations (2.1) and (2.6) with equation (3.2), and equations (4.1) with equations (2.4) to give:

$$\begin{array}{rlrlrlrl}\dot{X}& =N_p{V}_p& & A_p^{\mathrm{f}}& =N_p^{\mathrm{f}}{\hspace{0.17em}}^{\mathrm{T}}\mu & & A_p^{\mathrm{r}}& =N_p^{\mathrm{r}}{\hspace{0.17em}}^{\mathrm{T}}\mu ,\end{array}$$ 4.4

$$\begin{array}{r}\\ \text{where }{N}_p& =N{K}_p& & N_p^{\mathrm{f}}& =N^{\mathrm{f}}{K}_p& & N_p^{\mathrm{r}}& =N^{\mathrm{r}}{K}_p.\end{array}$$ 4.5

Equation (4.5) defines the forward $N_p^{\mathrm{f}}$ and reverse $N_p^{\mathrm{r}}$ pathway stoichiometric matrices; using conditions (2.7) and (3.3), it follows that $N_p^{\mathrm{f}}$ and $N_p^{\mathrm{r}}$ have positive integer elements:

$$N_{p_{ij}}^{\mathrm{f}}\text{ is integer}{N}_{p_{ij}}^{\mathrm{f}}\ge 0N_{p_{ij}}^{\mathrm{r}}\text{ is integer}{N}_{p_{ij}}^{\mathrm{r}}\ge 0.$$ 4.6

A property of N_p follows from combining equations (4.5), (2.8) and (3.1); in particular, N_p may be rewritten as

$$N_p=(N^{\mathrm{cs}}+N^{\mathrm{cd}})K_p=N^{\mathrm{cd}}{K}_p=I^{\mathrm{cs}}N{K}_p$$ 4.7

Hence N_p has the property that the only non-zero rows correspond to the chemostats.

In the case of the example of figure 1:

$$N_p=\left(\begin{array}{ccc}0& 0& -1\\ 0& 0& 2\\ -1& -1& 2\\ 1& 1& -2\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),N_p^{\mathrm{f}}=\left(\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ 1& 1& 2\\ 0& 0& 4\\ 0& 0& 0\\ 0& 0& 1\\ 0& 1& 1\\ 0& 0& 2\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)\mathrm{and}{N}_p^{\mathrm{r}}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 2\\ 0& 0& 4\\ 1& 1& 2\\ 0& 0& 0\\ 0& 0& 1\\ 0& 1& 1\\ 0& 0& 2\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)$$ 4.8

Using equation (4.4) and N_p from equation (4.8), the affinity associated with each of the three pathways is, as expected:

$${A_p}_1={A_p}_2={\mu }_{\mathrm{ATP}}-{\mu }_{\mathrm{ADP}}{A_p}_3=({\mu }_{\mathrm{GLC}}+2{\mu }_{\mathrm{ADP}})-(2{\mu }_{\mathrm{Pyr}}+2{\mu }_{\mathrm{ATP}})$$ 4.9

Because conditions (4.6) agree with conditions (2.7), $N_p^{\mathrm{f}}$ and $N_p^{\mathrm{r}}$ could correspond to the forward and reverse stoichiometric matrices of the following three reactions:

$$\begin{array}{rl}& \mathrm{ATP}\hspace{0.17em}\underset{PP}{\overset{p1}{\rightleftharpoons }}\hspace{0.17em}\mathrm{ADP}\\ & \mathrm{ATP}+\mathrm{CS}2\hspace{0.17em}\underset{PP}{\overset{p2}{\rightleftharpoons }}\hspace{0.17em}\mathrm{ADP}+\mathrm{CS}2\\ & \mathrm{GLC}+2\mathrm{ADP}+\mathrm{CS}3\hspace{0.17em}\underset{PP}{\overset{p3}{\rightleftharpoons }}\hspace{0.17em}2\mathrm{Pyr}+2\mathrm{ATP}+\mathrm{CS}3,\end{array}$$

where CS2=F6P+F2P and CS3=2ATP+2ADP+G6P+F6P+2TP. However, some care must be taken in this interpretation. Firstly, the kinetics are not mass-action even if the original equations correspond to mass-action kinetics. Secondly, and unlike conventional reactions, these three reactions are not independent; the consequences of this fact are discussed in §5. Nevertheless, such a pathway decomposition provides insight into the energy flows in a reaction network. This is illustrated using a generic example of Hill [14] in §5 and using a specific example, the sodium-glucose transport protein of Eskandari et al. [33], in §6.

5. Example: free energy transduction and biomolecular cycles

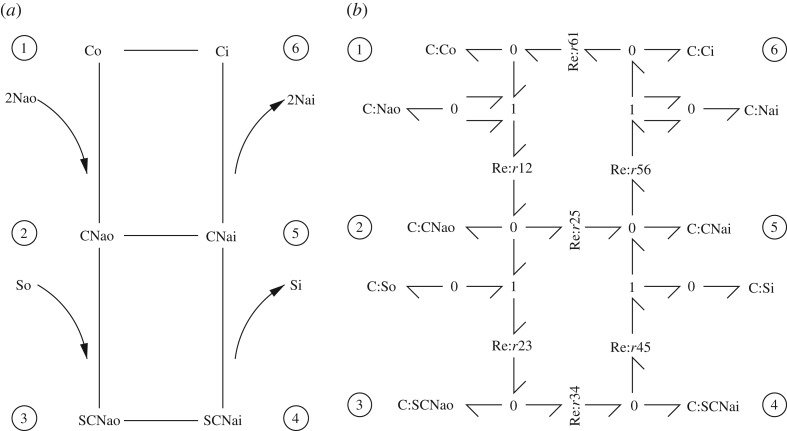
In his classic monograph, ‘Free energy transduction and biomolecular cycle kinetics’ Hill [14] discusses how the difference between the concentration of a species M_o outside a membrane and the concentration of the same species M_i inside the membrane can be used to transport another species L_i inside the membrane to outside the membrane L_o via a large protein molecule with two conformations E and E^★ the former allowing successive binding to M_i and L_i and the latter to M_o and L_o. This biomolecular cycle is represented by the diagram of figure 3a which corresponds to that of Hill [14], fig. 1.2(a). There are seven reactions

$$\begin{array}{rl}& {\mathrm{M}}_i+\mathrm{E}\stackrel{em}{\rightleftharpoons }\mathrm{EM}{\mathrm{L}}_i+\mathrm{EM}\stackrel{lem}{\rightleftharpoons }\mathrm{LEM}\mathrm{LEM}\stackrel{lesm}{\rightleftharpoons }\mathrm{L}{\mathrm{E}}^{\star }\mathrm{M}\mathrm{L}{\mathrm{E}}^{\star }\mathrm{M}\stackrel{esm}{\rightleftharpoons }{\mathrm{L}}_o+{\mathrm{E}}^{\star }\mathrm{M}\\ & {\mathrm{E}}^{\star }\mathrm{M}\stackrel{es}{\rightleftharpoons }{\mathrm{M}}_o+{\mathrm{E}}^{\star }{\mathrm{E}}^{\star }\stackrel{e}{\rightleftharpoons }\mathrm{E}\mathrm{EM}\stackrel{slip}{\rightleftharpoons }{\mathrm{E}}^{\star }\mathrm{M}\end{array}$$

Figure 3.

Free energy transduction and biomolecular cycles: model. (a) As discussed in the text, this is a generic model of a transmembrane transporter due to Hill [14] and based on the conformations of the protein E which uses the chemical gradient of M to pump L across the membrane against an adverse gradient. An ideal cycle would have no ‘slippage’: the link from EM to E^★M would not exist. As discussed in the text, two pathways: loop and slip have been marked. (b) The bond graph is geometrically the same as (a) but gives a precise description. (Es is used in place of E^★ for syntactical reasons).

where the last reaction is the so-called slippage⁵ term in which the enzyme changes conformation without transporting species L. The original Hill diagram does not name the seven reactions, they are named here to provide a link to the bond graph which explicitly names reactions.

The corresponding bond graph appears in figure 3b where E^★ is replaced by Es for syntactical reasons. The bond graph clearly shows the cyclic structure of the chemical reactions and is geometrically similar to the diagram of figure 3a. As discussed by Hill [14], the four species M_o, M_i, L_o and L_i, are assumed to have constant concentration: therefore, they are modelled by four chemostats.

The states X, stoichiometric matrix N and reaction flows V of this system are

$$X=\left(\begin{array}{c}{x}_{L_i}\\ x_{L_o}\\ x_{M_i}\\ x_{M_o}\\ x_E\\ x_{EM}\\ x_{LEM}\\ x_{E^{\star }}\\ x_{E^{\star }M}\\ x_{L{E}^{\star }M}\end{array}\right),N=\left(\begin{array}{ccccccc}0& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ -1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ -1& 0& 0& 0& 0& 1& 0\\ 1& -1& 0& 0& 0& 0& -1\\ 0& 1& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& -1& 0\\ 0& 0& 0& 1& -1& 0& 1\\ 0& 0& 1& -1& 0& 0& 0\end{array}\right)\mathrm{and}V=\left(\begin{array}{c}{v}_{em}\\ v_{lem}\\ v_{lesm}\\ v_{esm}\\ v_{es}\\ v_e\\ v_{\mathrm{slip}}\end{array}\right).$$ 5.1

The matrix N^cd is the same as N but with the first four rows (corresponding to the four chemostats) deleted. The rank of N^cd is r=5 corresponding to the four chemostats and the conserved moiety of the remaining states; thus the null space has dimension n_V−r=2.

As discussed in §4, two positive pathways were identified both by bond graph pathway analysis and using metatool.⁶ The corresponding PPM K_p is

$$K_p^{\mathrm{T}}=\left(\begin{array}{ccccccc}1& 1& 1& 1& 1& 1& 0\\ 1& 0& 0& 0& 1& 1& 1\end{array}\right).$$ 5.2

Apart from the ordering of the two columns, the PPM for this system is unique. These two columns correspond to the path involving the six reactions: {e em lem es esm lesm} and the upper loop involving the four reactions: {e em es slip}. These are the only positive pathways for this system. For convenience, the first (outer) pathway will be named loop and the second pathway (involving the ‘slip’ reaction) will be named slip; this nomenclature is indicated in figure 3a.

For the purposes of illustration, the thermodynamic constants of the 10 species are taken to be unity, the total amount of E, EM, LEM, E^★, E^★M and LE^★M is taken as E_tot=10, the amount of M_o and L_i is taken as unity, the amount of L_o as two and M_i is variable. The rate constant of the slippage reaction is varied in the sequel, and that of the other reactions is 10.

The system was simulated with a slow change of the amount of M_i from 2 to 100 such that the system was effectively in a steady state for each value of the amount of M_i; these values were then refined using a steady-state finder. The conserved moiety was automatically accounted for using the method of Gawthrop & Crampin [29], §3(c). The results were checked using explicit expressions for the steady-state values using the software of Qi et al. [37], which is based on the method of King & Altman. The system equations are given in the electronic supplementary material.

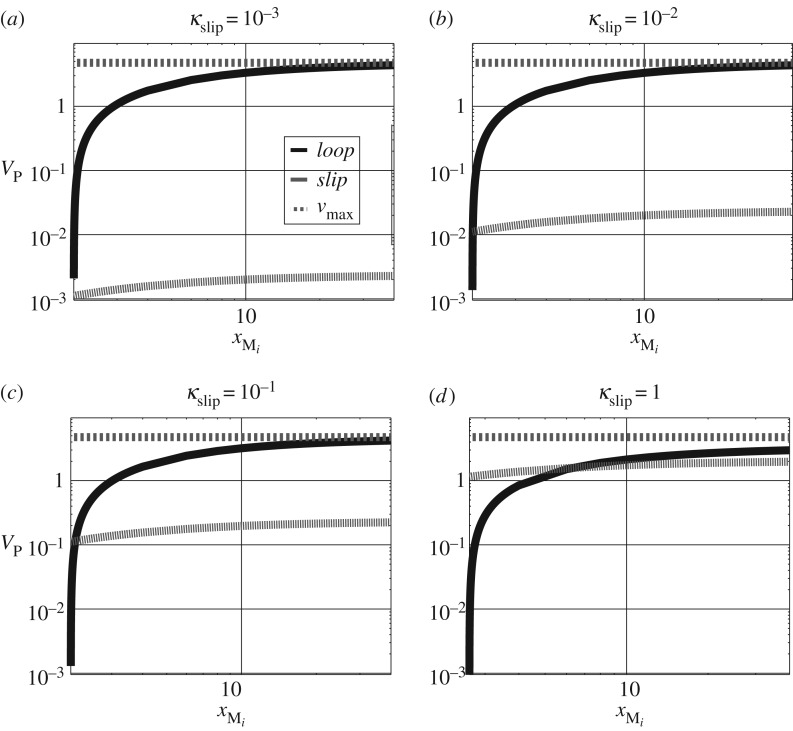
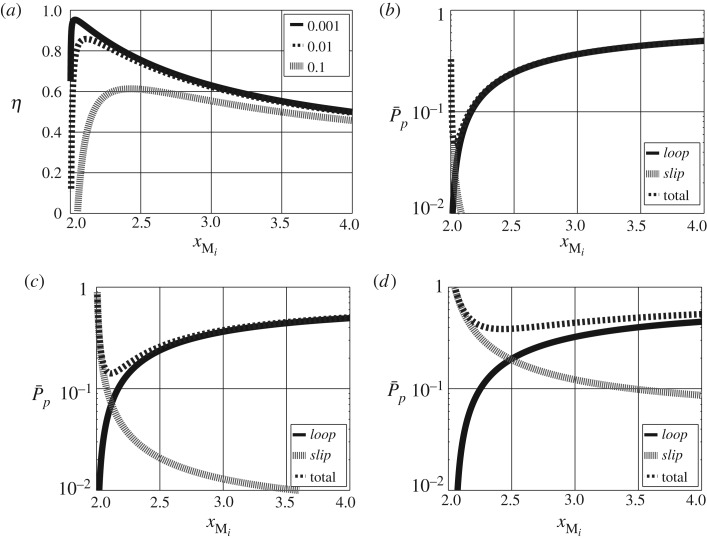
Figure 4 shows the two pathway flows $v_1^P$ and $v_2^P$ against the amount x_Mi of M_i for four values of κ_slip. As derived in the electronic supplementary material, the maximum flow when the κ_slip=0 is given by $v_{max}=100/21=4.76$ and this value is also plotted on each graph.

Figure 4.

Free energy transduction and biomolecular cycles: positive flow regime. (a) The flow in the two pathways labelled loop and slip in figure 3a are shown together with the maximum flow $v_{max}$ for slippage coefficient κ_slip=10⁻³. (b)–(d) The same information for three further values of the slippage coefficient κ_slip.

The purpose of this cycle is to use the excess of M to pump L against the concentration gradient. In addition to viewing the cycle as a mass transport system, it may also be viewed as a system for transducing free energy from M to L. From this point of view, it is interesting to investigate the (steady-state) efficiency η of the energy transduction [14], §1.4, which we define as

$$\eta =\frac{P_L}{P_M}\text{where }{P}_L=({\mu }_{Lo}-{\mu }_{Li})v_L\text{and}{P}_M=({\mu }_{Mi}-{\mu }_{Mo})v_M$$ 5.3

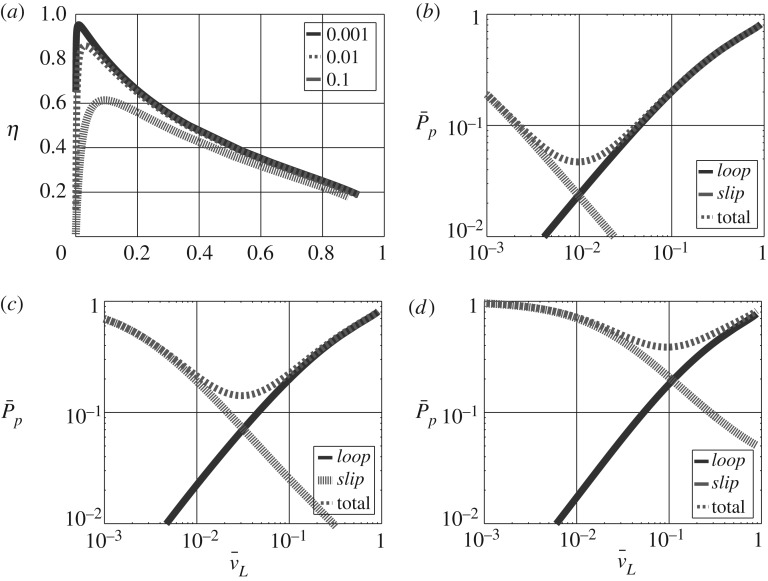
The simulated η is plotted against normalized flow ${\overline{v}}_L=v_{Lo}/v_{max}$ in figure 5a for the four values of κ_slip and reveals three features:

• (i) with negligible slip, the maximum efficiency occurs at low flow rates.

• (ii) the efficiency decreases as κ_slip increases

• (iii) the flow rate corresponding to maximum efficiency increases with κ_slip.

Figure 5.

Free energy transduction and biomolecular cycles: energy-based analysis. (a) The free energy transduction efficiency η is plotted against normalized flow ${\overline{v}}_L$ of L for the three values of the slippage coefficient κ_slip used in (b–d). (b–d) The normalized pathway free energy dissipation ${\overline{P}}_p$ is plotted against normalized flow ${\overline{V}}_L$ of L for the two pathways loop and slip marked on figure 3a together with the total normalized free energy dissipation. (a) Efficiency η for different κ_slip; normalized dissipation (b) ${\overline{P}}_p$: κ_slip=10⁻³, (c) ${\overline{P}}_p$: κ_slip=10⁻² and (d) ${\overline{P}}_p$: κ_slip=10⁻¹.

To further investigate the source of the inefficiency, the pathway dissipation P_p was computed and normalized to give ${\overline{P}}_p=P_p/P_M$. This is plotted for each pathway, together with the total normalized dissipation, against the normalized flow ${\overline{v}}_L$ of L in figure 5b,d for three values of κ_slip. As can be seen, the main loop pathway dissipation increases with flow of L with all of the free energy associated with M dissipated at the maximum flow rate. By contrast, the slippage pathway dissipation decreases with flow of L with all of the free energy associated with M dissipated at zero flow rate. The combined normalized dissipation thus has a minimum (i.e. energy transduction is most efficient) at an intermediate flow rate dependant on κ_slip.

Figure 6 is similar to figure 5 except that the efficiency η and normalized energy flows ${\overline{P}}_p$ are plotted against M_i in the positive flow regime. The minima occur at values of M_i towards the lower end of the positive flow regime. This reflects the fact that, as shown in figure 4, large changes in flow v_P correspond to small changes in concentration x_Mi towards the lower end of the positive flow regime; for larger values of x_Mi, the effect of changes in x_Mi on v_P is smaller.

Figure 6.

Free energy transduction and biomolecular cycles: energy-based analysis. Figure 5 is replotted with x_Mi replacing ${\overline{V}}_L$. (a) Efficiency η for different κ_slip; normalized dissipation (b) ${\overline{P}}_p$: κ_slip=10⁻³, (c) ${\overline{P}}_p$: κ_slip=10⁻² and (d) ${\overline{P}}_p$: κ_slip=10⁻¹.

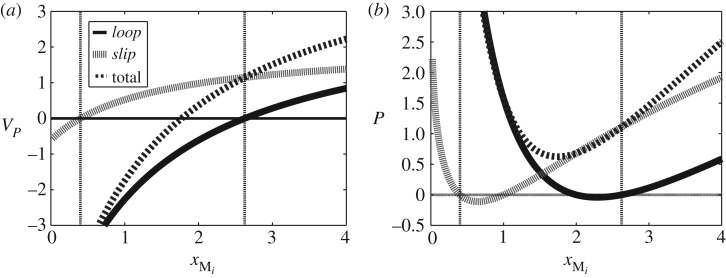
As mentioned in §4, the reactions corresponding to the two pathways of this example are not independent. To examine the consequences of this interaction, figure 7 focuses on the system behaviour in the crossover region where the two pathway flows have opposite directions. Figure 7a shows the two mass flows which have opposite sign in the crossover region 0.42<M_i<2.62 delineated by the two vertical lines. Within this region, figure 7b shows that the individual pathway energy dissipations may be negative; of course, as indicated in figure 7b, the total dissipation remains positive. This behaviour is a consequence of the intersection of the two pathways leading to a non-diagonal $\mathcal{P}\mathcal{W}$ (figure 2). Furthermore, the sum of the two pathway flows, corresponding to the flow of M_i and M_o, also changes sign thus causing the associated energy flow P_M (5.3) to also change sign. Thus normalizing the pathway energy transduction in the crossover region using equation (5.3) is not helpful. However, the normal operating region of such a biomolecular cycle is outside the crossover region and hence this situation does not normally arise.

Figure 7.

Mass and energy flows in the crossover region. For sufficiently small M_i, the cycle no longer acts as a transporter as the flows in the two pathways labelled loop and slip in figure 3a become negative. This figure examines the crossover regime (delineated by the two vertical lines) where one pathway flow is positive and the other negative—with a large value (κ_slip=1) of slippage to exaggerate the effect. Note the negative pathway dissipations when the sign of the pathway flows is different—this is due to the intersection of the two pathways leading to a non-diagonal $\mathcal{P}\mathcal{W}$. (a) Mass flows and (b) energy flows.

6. Example: the sodium-glucose transport protein 1

The SGLT1 (also known as the Na⁺/glucose transporter) was studied experimentally by Parent et al. [38] and explained by a biophysical model [39]; further experiments and modelling were conducted by Chen et al. [40]. Eskandari et al. [33] examined the kinetics of the reverse mode using similar experiments and analysis to Parent et al. [38,39] but with reverse transport and currents. This example looks at a bond graph-based model of SGLT1 based on the model of Eskandari et al. [33]. For simplicity, it is assumed that the membrane potential is zero and thus there are no electrogenic effects.

The model of Eskandari et al. [33], fig. 6B, given in diagrammatic form in figure 8a is based on the six-state biomolecular cycle of fig. 2 of Parent et al. [39]. When operating normally, sugar is transported from the outside to the inside of the membrane driven against a possibly adverse gradient by the concentration gradient of Na⁺. The diagram of figure 8a is similar to the Hill model of figure 3a. Apart from the renaming of components, and the reversal of inside and outside, the major difference is that the single driving molecule M_i and M_o replaced by two driving molecules 2Na⁺_o and 2Na⁺_i. This change is reflected in the bond graph of 8b by the double bonds. This also means that the stoichiometric matrix N is the same as that of equation (5.1) except that the rows corresponding to Na⁺_o and Na⁺_i are multiplied by 2. However, as Na⁺_o and Na⁺_i are chemostats, this change does not affect the PPM K_p which is still given by (5.2). The actual matrices are given in the electronic supplementary material.

Figure 8.

The SGLT1. (a) Diagram with the six states marked. (b) The corresponding bond graph.

The seven sets of reaction kinetic parameters are given in Eskandari et al. [33], fig. 6B and listed in the first two columns of table S1 of the electronic supplementary material and the third column gives the corresponding equilibrium constants. The vector of seven equilibrium constants K^eq is converted into the vector of 10 thermodynamic constants K of table S2 of the electronic supplementary material using the formula of Gawthrop et al. [30]:

$$K^{\mathrm{eq}}=\mathbf{\text{Exp}}\hspace{0.17em}({-N}^{\mathrm{T}}\mathbf{\text{Ln}}\hspace{0.17em}K),$$ 6.1

where N is the 10×7 stoichiometric matrix. The corresponding rate constants κ are then computed as discussed by Gawthrop et al. [30] and listed in the final column of table S1 of the electronic supplementary material. The system was simulated as described in §5 and the system equations are given in the electronic supplementary material.

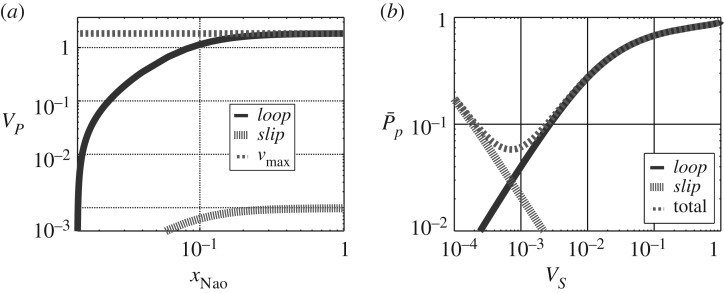
As in figure 4, figure 9a shows the two pathway flows and, as in figure 5, figure 9b shows the corresponding pathway dissipation. As in §5, but using parameters corresponding to experimental data, the combined normalized dissipation has a minimum (i.e. energy transduction is most efficient) at an intermediate flow rate.

Figure 9.

The SGLT1. (a) Simulated flows (normalized) in the two pathways labelled loop and slip in figure 3a. (b) The normalized pathway dissipations as a function of normalized flows.

7. Conclusion

It has been shown that standard methods of mass-flow pathway analysis can be extended to energy-flow pathway analysis making use of the bond graph method arising from engineering science. The method has been applied to a glycolysis example of Heinrich & Schuster [5], fig. 3.4 and the biomolecular cycle of Hill [14], fig. 1.2(a) to enable comparison with standard approaches.

The analysis of the biomolecular transporter cycle was shown to apply to a model of the SGLT1 based on the experimentally determined parameters of Eskandari et al. [33], fig. 6B. Intriguingly, it was found that the rate of energy dissipation has a minimum value at a particular normalized flow rate which in turn corresponds to a particular driving concentration. This minimum is due to the interaction of a number of factors including the system parameters, the presence of two interacting pathways and the concentration of Na⁺ (or M in the case of §5) needed to generate the transporter flow. It would be interesting to compare this theoretical flow rate to that found in nature.

The bond graph approach can be used to decompose complex systems into computational modules [30,31]. Combining such modularity with the energy-based pathway analysis approach of this paper would provide an approach to analysing and understanding energy flows in complex biomolecular systems, for example, those within the Physiome Project [41], which is the subject of current research.

Although this paper is restricted to flows of chemical energy, the bond graph approach enables models to be built across multiple energy domains including chemoelectrical transduction [42,43]. Hence the pathway approach can be equally well applied to systems with electrogenic features such as excitable membranes [44] and the mitochondrial electron transport chain [45].

The effective use of energy is an important determinant of evolution [13,17,46,47]. Therefore, the energy-based pathway analysis of this paper is potentially relevant to investigating why living systems have evolved as they have. For example, do real SGLT1 transporters operate near the point of minimal energy dissipation?

The supply of energy is essential to life and disruption of energy supply has been implicated in many diseases such as cardiac failure [48,49], Parkinson’s disease [50–54] and cancer [55–57]. Therefore, it seems natural to apply the energy-based methods of this paper to investigate such systems. In particular, mitochondria are important for energy transduction in living systems and mitochondrial dysfunction is hypothesized to be the source of ageing [58], ch. 14, cancer [59,60] and other diseases [61]. Mathematical models of mitochondria exist already [62–65], and it is hoped that the energy-based pathway analysis of this paper will shed further light on the function and dysfunction of mitochondria, and this is the subject of current research.

Appendix A. A short introduction to bond graph modelling

The purpose of this section is to provide the bond graph background necessary to understand the paper itself. More information is to be found in references [29–32].

Bond graphs unify the modelling of energy within and across multiple physical domains using the concepts of effort and flow variables whose product is power. Thus, in the electrical domain the effort variable voltage V with units of V and flow variable current i with units of A have the product P=V i with units of J s⁻¹. In the biomolecular domain, the effort variable is chemical potential μ with units of J mol⁻¹ and the flow variable is reaction flow rate v with units of mol s⁻¹; μv also has units of J s⁻¹.

The bond graph C component is a generic energy storage component corresponding to a capacitor in the electrical domain and the amount of a chemical species in the biomolecular domain. If q is the time integral of the flow variable, the electrical capacitor generates voltage V according to the linear relationship: V =q/C, where C is the capacitance in Farads and q is the charge in Coulombs. By contrast, the chemical species generates chemical potential μJ mol⁻¹ according to the nonlinear relationship: $\mu =RT\mathrm{ ln }Kx$, where R is the universal gas constant with units of J mol⁻¹ K⁻¹, T is the absolute temperature with units of K, x=q/q₀, where q₀ is the reference quantity and K is a species-dependent constant which is dimensionless and depends on the reference quantity.

The bond graph R component is a generic energy dissipation component corresponding to a resistor in the electrical domain. In the linear case, it generates current i according to the linear relationship: i=κΔV , where κ is the conductance and ΔV is the net voltage across the resistor. The R component corresponds to a chemical reaction in the biomolecular domain. Assuming mass-action kinetics it generates molar flow v according to the nonlinear relationship: $v=\kappa (\exp A^{\mathrm{f}}/RT-\exp A^{\mathrm{r}}/RT)$, where A^f (the forward affinity) and A^r (the reverse affinity) are the net chemical potentials (with units of J mol⁻¹) of the reactants and products of the reaction, respectively; κ is the reaction rate constant with units of mol s⁻¹. Because this relationship treats the forward and reverse affinities differently, this reaction version of the R component is given a special symbol: Re.

Bond graphs represent the flow of energy between components by the bond symbol $\rightharpoondown$ where the direction of the harpoon corresponds to the direction of positive energy flow; this is a sign convention. The bonds connect components via junctions which transmit, but do not store or dissipate energy. There are two junctions: the 0 junction where all impinging bonds have the same effort and the 1 junction where all impinging bonds have the same flow. The expression for the flows associated with the 0 junction, and the efforts associated with the 1 junction, are determined by the energy conservation requirement.

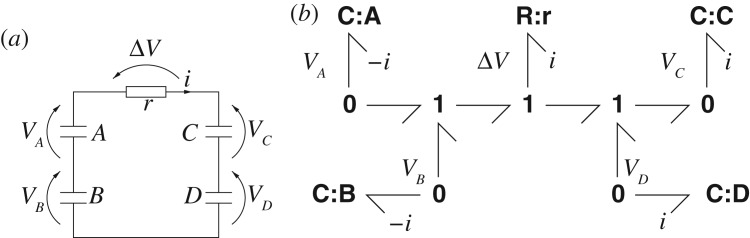
Figure 10 illustrates bond graph modelling in the electrical domain. The four capacitors and one resistor are connected as in the schematic diagram of figure 10a. In bond graph colon notation, the symbol before the colon indicates the component type and the symbol after the colon indicates the component name. Thus, the bond graph of figure 10b has four C components named A–D to represent the four capacitors and a single R component named r to represent the resistor. The two 0 junctions on the left reverse the sign of the flow associated with C:A and C:B. The two 0 junctions on the right are not necessary, but are convenient for connecting to others via bonds components to form a larger system. The left 1 junction corresponds to V ^f=V _A+V _B and the right 1 junction corresponds to V ^r=V _C+V _D; the centre 1 junction corresponds to ΔV =V ^f−V ^r=(V _A+V _B)−(V _C+V _D). Given the constitutive relations for the C and R component, the dynamical equations describing the system can be automatically generated from the bond graph of figure 10b.

Figure 10.

Modelling electrical systems. (a) Electrical schematic diagram. (b) Bond graph: ΔV =(V _A+V _B)−(V _C+V _D).

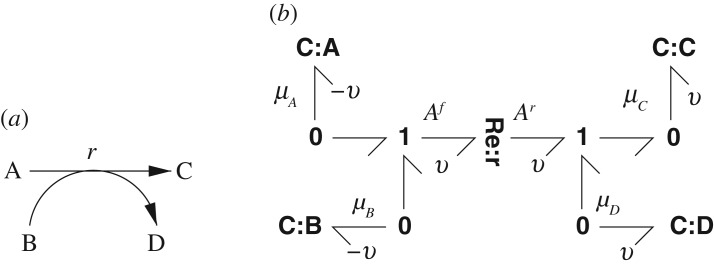
Figure 11 illustrates bond graph modelling in the chemical domain; the corresponding reaction is A+B r $\stackrel{r}{\rightleftharpoons }$ C+D. In a similar manner to the electrical system of figure 10, the bond graph of figure 11b has four C components named A–D to represent the four species and a single Re component named r to represent the reaction. The major difference is the use of the Re component to replace the 1 and R combination within the dotted box of figure 10b; as mentioned previously this is because the forward and reverse affinities are treated differently. In particular, with reference to the example of figure 11, A^f=μ_A+μ_B, A^r=μ_C+μ_D which, with reference to equation (2.4) corresponds to

$$N^{\mathrm{f}}={(1100n)}^{\mathrm{T}}{N}^{\mathrm{r}}={(0011)}^{\mathrm{T}}.$$

Using equations (2.3) and (2.5), it follows that:

$$\begin{array}{rl}{A}^{\mathrm{f}}& =RT(\mathrm{ ln }{K}_A{x}_A+\mathrm{ ln }{K}_B{x}_B)=RT\mathrm{ ln }{K}_A{x}_A{K}_B{x}_B,\\ A^{\mathrm{r}}& =RT(\mathrm{ ln }{K}_C{x}_C+\mathrm{ ln }{K}_D{x}_D)=RT\mathrm{ ln }{K}_C{x}_C{K}_D{x}_D{x}_D\\ \text{and}V& ={\kappa }_{\mathrm{r}}({\text{e}}^{A^{\mathrm{f}}/RT}-{\text{e}}^{A^{\mathrm{r}}/RT})={\kappa }_{\mathrm{r}}(K_A{x}_A{K}_B{x}_B-K_C{x}_C{K}_D{x}_D).\end{array}$$

This is a form of the mass-action kinetics equation discussed in the textbooks [8]. In particular, the equation can be rewritten as follows:

$$V=k_{\mathrm{f}}{x}_A{x}_B-k_{\mathrm{r}}{x}_C{x}_D,$$

where

$$k_{\mathrm{f}}=\kappa K_A{K}_B\text{and}{k}_{\mathrm{r}}=\kappa K_D{K}_C.$$

As mentioned above, the K constants are dimensionless and thus k_f and k_r are dimensionless. The dimensionless equilibrium constant K_eq is defined as

$$K_{\mathrm{eq}}=\frac{k_{\mathrm{f}}}{k_{\mathrm{r}}}.$$

As discussed by Gawthrop et al. [30], K_eq and K_A, K_B, K_C and K_D are related by the general formula (6.1).

Figure 11.

Modelling biomolecular systems: A+B r $\stackrel{r}{\rightleftharpoons }$ C+D. (a) Biomolecular schematic diagram. (b) Bond graph: A^f=μ_A+μ_B, A^r=μ_C+μ_D.

In both the electrical and biomolecular systems, there is only one flow: the current i in the electrical case and the molar flow v in the biomolecular case. This flow f is out of C:A and C:B and into C:C and C:D. Hence, in the biomolecular case, $-{\dot{x}}_A=-{\dot{x}}_B={\dot{x}}_C={\dot{x}}_D=v$. This implies that x_A+x_C=x_AC, x_A+x_D=x_AD and x_B+x_C=x_BC where x_AC, x_AD and x_BC are constant. Each of these three equations represents a conserved moiety: the total amount of the charge or species involved remains constant. The choice of conserved moieties in a given situation is generally not unique; this is discussed further in appendix B.

Replacing A,B,C and D by GLC, G6P, ATP and ADP, respectively, and r by r4 in figure 11 corresponds to the reaction to the left of the diagram in figure 1. The apparently redundant 0 junctions in figure 11 are used to provide connections between this particular reaction and the overall reaction network of figure 1. The reaction diagram of figure 1a has the entities ATP and ADP represented more than once. Although this enhances clarity by removing the need for intersecting lines on the diagram, it reduces clarity by having each entity appear in multiple locations. By contrast, the bond graph of figure 1b represents ATP and ADP each by a single C component (ATP and ADP, respectively) with appropriate connections to each of the reactions represented by Re:r1–Re:r9.

This idea of representing biomolecular reaction networks by C components (representing species) and Re components (representing reactions) connected by bonds ($\rightharpoondown$) and 0 and 1 junctions is summarized and formalized in figure 2a. This representation is summarized in the caption to figure 2 and is discussed in detail by Gawthrop & Crampin [29,31].

Bond graphs provide one foundation for this paper, the other is the systems biology concept of pathways outlined in the next section.

Appendix B. A short introduction to systems biology

The purpose of this section is to provide the systems biology background necessary to understand the paper itself.

As discussed in the basic textbooks (for example, that of [8]), the stoichiometric matrix N is a fundamental construct in describing and understanding biomolecular systems. In particular, given n_X chemical species with molar amounts contained in the column vector X and n_V reactions with molar flow rates contained in the column vector V ; the n_X×n_V stoichiometric matrix N relates the rate of change $\dot{X}$ of X to V by equation (2.1) repeated here:

$$\begin{array}{cc}& \dot{X}=NV.\end{array}$$ 2.1

The elements of N are integers that determine the amount of each species participating in the reaction. For example, the reaction A+B r $\stackrel{r}{\rightleftharpoons }$ C+D of figure 11 can be represented by equation (2.1) where:

$$X={(x_A{x}_B{x}_C{x}_D)}^{\mathrm{T}}N={(-1-111)}^{\mathrm{T}}V=v_{\mathrm{r}},$$

where x_A is the molar amount of substance A, etc., and v_r is the reaction flow.

As discussed in the basic textbooks (for example, that of [8]), the mathematical concept of a null space of N gives useful information about the fundamental properties of the biomolecular system described by N. These are two null spaces: the left null space described by the matrix G where GN=0 and the right null space described by the matrix K_p where NK_p=0. In the case of the open systems discussed in §2, N is replaced by N^cd.

The significance of G is that pre-multiplying both sides of equation (2.1) by G gives

$$G\dot{X}=GNV=0.$$

Hence the linear combinations of X implied by the rows of G are constant; in systems biology nomenclature such combinations are known as conserved moieties. In the case of the example system, one possible matrix G is

$$G=\left(\begin{array}{cccc}1& 0& 1& 0\\ 1& 0& 0& 1\\ 0& 1& 1& 0\end{array}\right).$$

It can be verified that GN=0 and the corresponding three conserved moieties are

$$x_A+x_C{x}_A+x_D{x}_B+x_C.$$

The significance of K_p is that if the elements of V are not independent but rather defined by V =K_pv then equation (2.1) gives

$$\dot{X}=N{K}_{p}v=0.$$

Hence the columns of K_p determine pathways: combinations of non-zero flows which lead to constant species amounts. In this example, there is no K_p such that NK_p=0. However, in the special case that the four species A–D are chemostats (their values are held constant by some external flows) then N now has four zero entries and K_p=1 and thus the four species have constant amounts for any v and thus the single reaction r trivially becomes a pathway. As discussed in the paper, the more complex systems of figures 1, 3 and 8 have non-trivial pathways.

Neither G nor K_p are unique. The seminal contribution discussed by Heinrich & Schuster [5] was to examine the case where the entries of K_p are both integer and non-negative thus defining pathways where all reaction flows have the same sign and are integer multiples of some base flows. This idea forms the basis of analysing large-scale biomolecular systems by flux-balance analysis (FBA) [8]. Together with the bond graph concepts outlined in appendix A, this idea provides the foundation for this paper.

Data accessibility

A virtual reference environment [66] is available for this paper at http://dx.doi.org/10.5281/zenodo.165180. The simulation parameters are listed in the electronic supplementary material.

Authors' contributions

All authors contributed to drafting and revising the paper, and they affirm that they have approved the final version of the manuscript.

Competing interests

We declare we have no competing interests.

statement

This research was in part conducted and funded by the Australian Research Council Centre of Excellence in Convergent Bio-Nano Science and Technology (project no. CE140100036).