Protein Structure Refinement via Molecular-Dynamics Simulations: What works and what does not?

Abstract

Protein structure refinement during CASP11 by the Feig group is described. Molecular dynamics simulations were used in combination with an improved selection and averaging protocol. On average, modest refinement was achieved with some targets improved significantly. Analysis of the CASP submission from our group focused on refinement success vs. amount of sampling, refinement of different secondary structure elements and whether refinement varied as a function of which group provided initial models. The refinement of local stereochemical features was examined via the MolProbity score and an updated protocol was developed that can generate high-quality structures with very low MolProbity scores for most starting structures with modest computational effort.

INTRODUCTION

Computational protein structure prediction has long aspired to overcome experimental limitations and provide structures at the same rate as new sequences are discovered. Today, this has been achieved at least in part¹. Useful models can be built for most sequences by taking advantage of available structures in the PDB either as a whole or in the form of fragments that are assembled during the prediction process. However, structural accuracy that is high enough to make experimental validation nonobligatory has not become routine yet. While the question of when predicted structures can be trusted in lieu of experiment is a complex issue that depends on the questions that are being asked², an ambitious conservative goal that we wish to put forward are Cα RMSD values below 1 Å or GDT-HA scores above 80 when compared to experimental structures. Sometimes, models with such accuracy can be generated but typical predictions with modern template-based methods fall short of this goal by producing models with 2–10 Å RMSD values and GDT-HA scores between 40 and 70 based on examples from CASP¹. Recent rounds of CASP suggest that template-based modeling and derivative fragment assembly protocols have reached a plateau where significant further improvements in accuracy have become unlikely³. Some room for improving alignment accuracy and model generation and selection remains, and the use of contact predictions based on evolutionary conservation⁴ may provide additional gains but overall we have probably come close to the limits of knowledge-based structure prediction.

Physics-based methods offer an alternative strategy for structure prediction based on first principles. While such methods involve substantial computational costs and require finely tuned complex force fields, there is increasing evidence that such methods can match and surpass the accuracy in structure prediction that is achievable via template-based methods. This is evidenced by successful protein folding simulations from a number of groups. Most notable is the landmark study by the Shaw group where eight out of twelve small proteins were folded to within 2 Å RMSD from their respective native structures by simply using molecular dynamics (MD) simulations with a recent force field⁵. MD-based structure prediction will remain far too expensive for most structure prediction applications especially when protein sizes reach hundreds of residues, but one practical approach is the incorporation of limited knowledge from bioinformatics or experimental data to reduce the conformational search space⁶.

Another strategy is the application of physics-based sampling in the refinement of approximate template-based models. The idea of refinement of template-based models via MD simulations is not new and anecdotal success stories have appeared in the literature for a while^7–25. However, consistent success with MD-based structure refinement for a large set of targets was only recently demonstrated²⁶. At CASP10, our group managed to refine all but two out of 27 targets via MD simulations¹³. As described in detail previously, this success was attributed to a number of factors: extensive sampling with 30 × 20 ns = 600 ns per target under restraints to prevent large deviations from the initial models, a recently refined version of the CHARMM force field, generation of ensemble averages rather than selection of a single structure, and the use of quality assessment filters to remove decoy sets where scoring was likely not going to discriminate native-like from non-native structures. The averaging was especially important since it reproduces the ensemble averaging in experiment but also amplifies recurring native-like features in a large set of structures over non-native elements as discussed in detail recently²⁷. Achieving consistency in refining template-based models was a significant milestone, but the extent of refinement remained rather modest with an average of 2.6 GDT-HA units and a maximum improvement by 6.5 GDT-HA units for model 1 submissions.

In this paper we are describing further progress with MD-based structure refinement during CASP11. As a result of methodological improvements we were able to improve structures by on average 3.8 GDT-HA units while four targets refined by more than 10 GDT-HA units. In the following, our CASP11 structure refinement protocol is described in detail before results are presented und discussed. Finally, we will look forward and outline where we see the major challenges towards routinely reaching experimental accuracy via refinement of template-based models.

METHODS

CASP11 refinement protocol

We employed molecular dynamics (MD) based sampling followed by structure filtering and averaging to obtain refined structures from initial models provided by the assessors during CASP11 as refinement targets (see Figure 1). The MD stage consisted of 40 × 30 ns simulations in explicit solvent, each started from the same initial model but using different initial velocity distributions. Therefore, a total of 1.2 μs was simulated for each target at an approximate average cost of 100,000 core hours per target. The use of multiple shorter trajectories instead of a single long trajectory facilitates the broader exploration of conformational space with limited amount of resources but is also more convenient from a computational perspective. In each simulation, the recent c36 version of the CHARMM force field was used²⁸. Water was modeled using the CHARMM version of the TIP3P model²⁹. Na⁺ or Cl⁻ counterions were added as needed to neutralize each system. Periodic systems were constructed with enough water to maintain at least 10 Å from any protein atom to the edge of the box. Electrostatics were evaluated using particle-mesh Ewald³⁰ with a 1 Å grid spacing. A 10 Å cutoff (switched beginning at 8.5 Å) was applied to the direct space part of the Ewald sum and to Lennard-Jones interactions. A 2 fs time step was used in combination with holonomic constraints to keep waters rigid and maintain other bonds involving hydrogens at their equilibrium values. All simulations were initially equilibrated by minimization and step-wise heating to 298K. In the production phase, a Langevin thermostat and barostat were used to maintain an NPT ensemble at 298 K and 1 bar. Since unrestrained simulations have a greater tendency to move away from the native state rather than move towards it, we applied weak harmonic positional restraints on all Cα atoms using a force constant of 0.05 kcal/mol/Ų. The uniform use of weak restraints for all targets differs from the use of partial restraints with stronger force constants for some targets during CASP10 for those regions where we believed that the initial models were already very accurate. Post-analysis of CASP10 suggested that the indiscriminate use of weak restraints is the better strategy. All simulations were carried out using NAMD³¹, version 2.9, on high-performance clusters.

Figure 1.

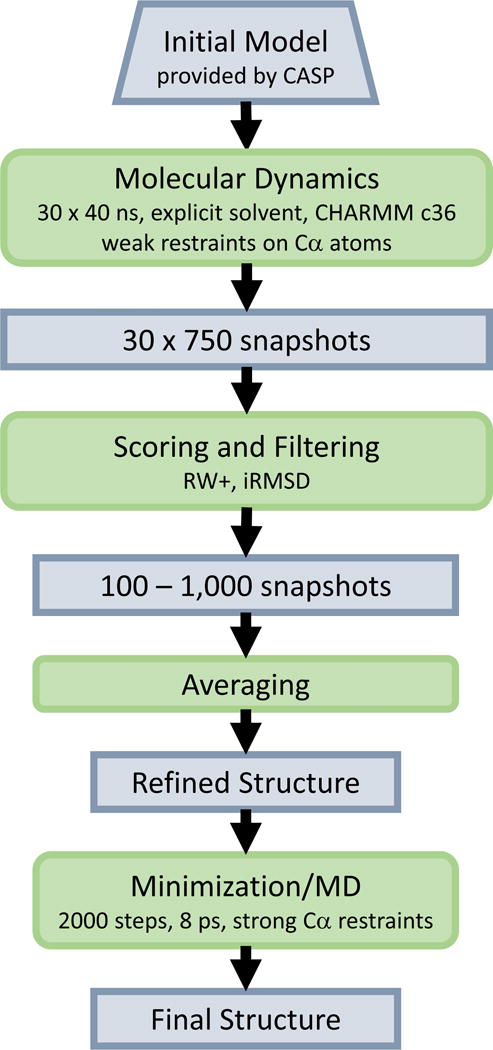
Refinement protocol of FEIG group during CASP11.

Once the simulations were completed, 750 snapshots were extracted at 40 ps intervals from each 30 ns trajectory resulting in a total of 30,000 snapshots for each target. Each snapshot was then scored using RW+³². While we used DFIRE³³ in CASP10, we found slightly better performance using RW+ in preliminary tests. As in CASP10¹³, we also calculated the RMSD of each snapshot from the respective initial models for each target (“initial RMSD”, iRMSD). Again, as in CASP10, we used a combined filter based on the knowledge-based score and iRMSD with the rationale that proximity to the initial model and low RW+ scores are orthogonal predictors of structures being close to the native structure. As in CASP10, we selected structures with scores in a radial segment relative to the center of the distribution. The exact selection criterion used in CASP11 was slightly modified from CASP10, again as a result of CASP10 post-analysis: If s and r denote the RW+ and iRMSD scores, we first calculated normalized scores according to:

$$\widehat{s}=\frac{s-\overline{s}}{{\sigma }_s}$$

and

$$\widehat{r}=\frac{r-\overline{r}}{{\sigma }_r}$$

where $\overline{s}$ and $\overline{r}$ are the mean and σ_s and σ_r the standard deviations of the two scores.

Then, we required that

$${\widehat{s}}^2+{\widehat{r}}^2\ge {\rho }^2$$

and

$$\text{arccos}\left(\frac{\widehat{s}\text{cos}\theta +\widehat{r}\mathit{sin}\theta }{\sqrt{{\widehat{s}}^2+{\widehat{r}}^2}}\right)<\gamma$$

with ρ=1, θ=240, and γ=35. The first criteria selects scores at a radial distance from the origin, the second further limits scores to an angular segment between 240 +/− 35 degrees.

Using this criterion, we selected between 2,000 and 6,600 structures for each target. The structures in the resulting subset were then averaged based on the Cartesian coordinates. The averaging step mimics the ensemble averaging that is inherent in experiments, but it also greatly reduces sensitivity to noise in the scoring function. Because the averaging step results in locally distorted geometries, a final short refinement step consisting of 2000 steps of minimization followed by 8 ps of MD simulation was used to improve the model quality. In the final step, Ca atoms were restrained with a force constant of 100 kcal/mol/Ų to maintain improvements in the backbone geometry while allowing the refinement of bonds, angles, and side chains.

The final structure from the protocol described above was submitted as model 1. Using the refined model, additional, shorter, simulations were carried out to explore whether a second round of refinement can lead to further refinement. In the second round, regions that moved most during the initial refinement step were allowed to move further while keeping the remainder of the structure highly restrained. In some cases, the additional simulations led to further refinements but we did not see consistent improvements. On average, the first round refined models were the best predictions. Thus, the following discussion will focus only on the model 1 submissions from our group.

Optimization of MolProbity scores

A more extensive protocol for optimizing MolProbity³⁴ scores was applied during the post-analysis of CASP11. The protocol is outlined in Figure 6. It involves a series of restrained minimization steps that alternate with targeted backbone and side chain rebuilding steps to correct cis-backbones in non-proline residues, bonds crossing ring residue side chains (tyrosine, phenylalanine, histidine, tryptophan), and side chains with poor rotamers. After the final minimization step, a series of short MD simulations (over 10 ps) at different temperatures and with different restraint force constants were carried out to generate an ensemble of snapshots. Since MolProbity scoring does not require knowledge of the native structure, MolProbity scores were calculated for each ensemble snapshot and the snapshot with the lowest score was chosen as the final model.

Figure 6.

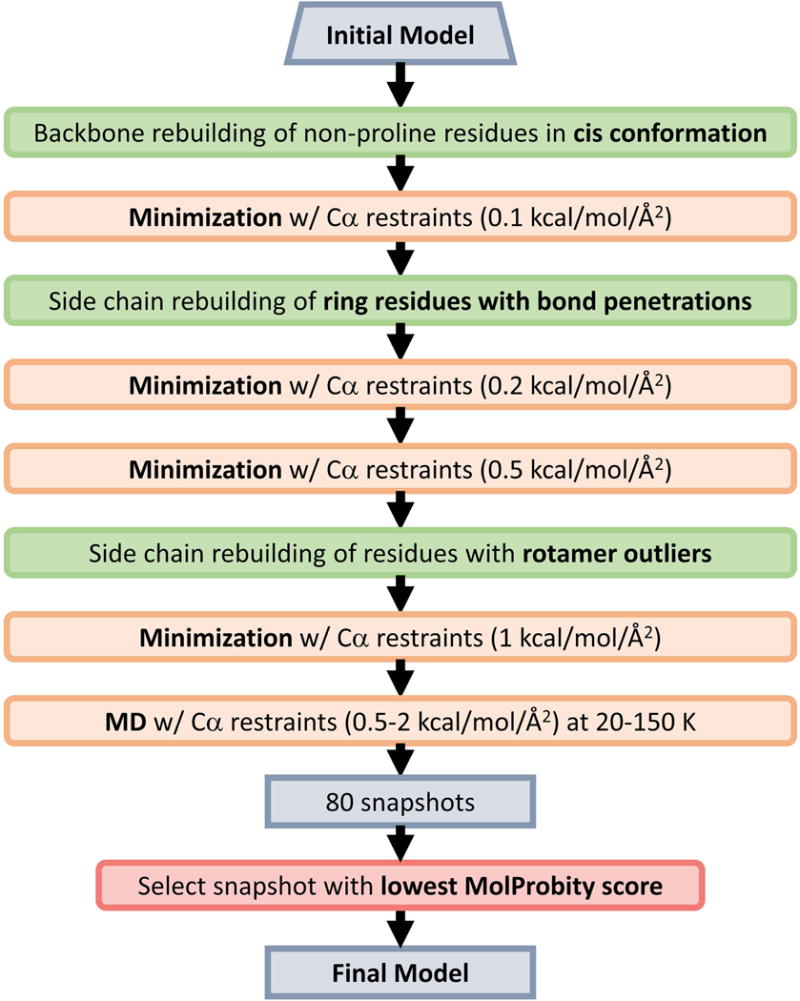
Protocol for optimization of MolProbity applied in CASP11 post-analysis.

All of the minimization and MD steps used a distance-dependent dielectric (∈=4) implicit solvent model for speed. Two variants of the CHARMM c36 force field were used²⁸. In the first, force constants for backbone bonds and angles were increased to bring the respective bonds and angles closer to the minima of the harmonic functions. In the second variant, in addition to the modified bonds and angles, a modified CMAP potential was used where sampling outside the most populated areas of the Ramachandran map according to crystallography was penalized further over the original CMAP of the c36 force field.

CHARMM was used for the minimization and MD steps and the MMTSB Tool Set^35,36 was used for backbone and side chain rebuilding.

RESULTS AND DISCUSSION

Overall CASP11 performance

Table I provides a detailed account of model 1 predictions resulting from our MD-based refinement protocol during CASP11. The results shown here were obtained by our own analysis and since we did not have experimental structures available for two targets (TR795 and TR828) the corresponding results are not shown and those two targets were excluded from further analysis. The results show that, as in CASP10, refinement was possible in most cases. On average, GDT-HA scores were improved by 3.8 GDT-HA units. Four targets were improved by more than 10 GDT-HA units, one (TR765) by almost 20 units. However, for five targets the GDT-HA scores became significantly worse (by more than 0.5 units). Table I also lists the improvement in GDT-HA for the best individual snapshots generated during the MD sampling. If those structures could have been selected, an average GDT-HA improvement of 8.7 units would have been achieved. For eleven targets, the best structures are better by 10 GDT-HA units indicating that the MD sampling is able to routinely generate significantly improved models. An interesting observation is for two targets (TR217 and TR817) the best individual snapshot is actually worse than the refined model obtained via ensemble averaging in our protocol.

Table I.

Overview of CASP11 refinement targets. ‘Initial’ models were provided by CASP, ‘Model 1’ refers to the first refined model submitted by the FEIG group, and ‘Best’ refers to the best snapshot with respect to either RMSD or GDT-HA generated during the MD simulations. RMSD and GDT-HA values were calculated with respect to given experimental structures. No native structures were available for TR795 and TR828.

Target	Residues	Residues in Exp. Structure	Initial RMSD [Å]	Initial GDT-HA	Model 1 Δ RMSD [Å]	Model 1 ΔGDT-HA	Best ΔRMSD [Å]	Best ΔGDT-HA
TR217	224	210	1.86	64.40	−0.18	0.00	−0.02	−2.26
TR228	84	84	3.92	54.76	−0.37	2.09	−0.90	9.23
TR274	194	183	6.80	28.96	−0.10	−0.54	−0.44	3.69
TR280	96	96	4.03	59.38	−0.21	5.46	−0.86	12.50
TR283	168	156	3.93	41.19	−0.05	0.32	−0.36	4.32
TR759	62	62	4.23	43.95	−0.53	12.50	−1.15	21.62
TR760	201	201	3.14	57.34	−0.14	1.37	−0.44	4.48
TR762	257	257	3.07	70.43	−0.05	−3.89	−0.36	−1.85
TR765	76	76	2.58	57.89	−0.18	19.74	−0.73	23.36
TR768	143	143	2.61	63.81	0.60	6.12	−0.31	7.34
TR769	97	97	1.76	59.79	−0.03	−0.25	−0.41	10.83
TR772	198	198	4.78	52.40	−0.16	1.01	−0.51	3.66
TR774	155	150	5.00	37.67	0.02	3.16	−0.28	5.50
TR776	219	219	2.82	62.79	−0.03	6.50	−0.44	8.79
TR780	95	95	2.73	53.95	−0.23	4.21	−0.58	14.47
TR782	110	110	1.93	64.77	−0.15	8.64	−0.28	12.50
TR783	243	243	3.26	57.30	0.00	5.05	−0.22	8.34
TR786	217	217	3.62	47.81	−0.45	4.61	−0.98	7.60
TR792	80	80	1.99	58.13	−0.54	13.12	−0.87	20.31
TR795	136	N/A	N/A	N/A	N/A	N/A	N/A	N/A
TR803	134	134	5.97	33.21	0.08	4.48	−0.42	8.95
TR810	243	225	12.45	53.89	−0.19	1.89	−0.74	6.00
TR811	251	251	1.45	73.21	0.07	−4.58	0.00	−3.09
TR816	68	68	2.53	52.21	−0.29	3.67	−0.72	15.07
TR817	265	265	1.81	65.38	−0.05	−0.76	−0.12	−1.23
TR821	255	255	2.45	48.33	−0.32	12.26	−0.74	16.87
TR822	117	114	4.21	30.26	−0.04	6.58	−0.46	15.57
TR823	288	288	4.36	40.54	−0.12	5.99	−0.43	8.68
TR827	193	193	3.75	33.94	−0.24	1.81	−0.70	9.07
TR828	84	N/A	N/A	N/A	N/A	N/A	N/A	N/A
TR829	67	67	6.16	50.37	−0.01	0.38	−0.96	9.70
TR833	108	108	4.72	61.34	−0.12	2.32	−0.78	5.10
TR837	121	121	2.95	43.39	0.10	−2.27	−0.33	3.51
TR848	138	138	3.78	58.15	0.06	1.45	−0.33	7.43
TR854	70	70	2.27	58.57	−0.19	6.07	−0.48	14.29
TR856	159	159	2.68	61.48	−0.06	−0.16	−0.26	4.71
TR857	96	96	4.00	33.07	−0.28	4.17	−0.61	8.60
Average					−0.13	3.79	−0.52	8.68

Figure 2 shows refinement in terms of GDT-HA as a function of the GDT-HA scores of the initial models. It seems that one could divide the targets into three categories: If initial scores are below about 45, refinement is not always possible with our protocol (two targets were not refined) and while refinement was possible in other cases, the overall best snapshots did not surpass GDT-HA scores of 50. On the other hand, for initial GDT-HA scores between 45 and 65, essentially all targets were refined and the GDT-HA scores of the best snapshots approached or surpassed 70 for most targets. Finally, for the best initial models, refinement was again challenging. None of the three best initial models (with initial GDT-HA scores between 65 and 75) could be refined and even the best snapshots generated via MD were worse than the initial models. This interesting observations suggests that our current MD-based refinement protocol is not effective for the very best template-based models and that the goal of routinely reaching GDT-HA scores of 80 with MD-based refinement remains very challenging. It could be that further improvements in the force fields are necessary, but it is also likely that we are starting to see the effects of crystal packing, possible oligomerization, omitted parts of the structure that were present in the experiment but not the initial models provided by CASP, and/or other experimental conditions (salt, co-solvents, temperature) that are not fully reproduced in the refinement simulations.

Figure 2.

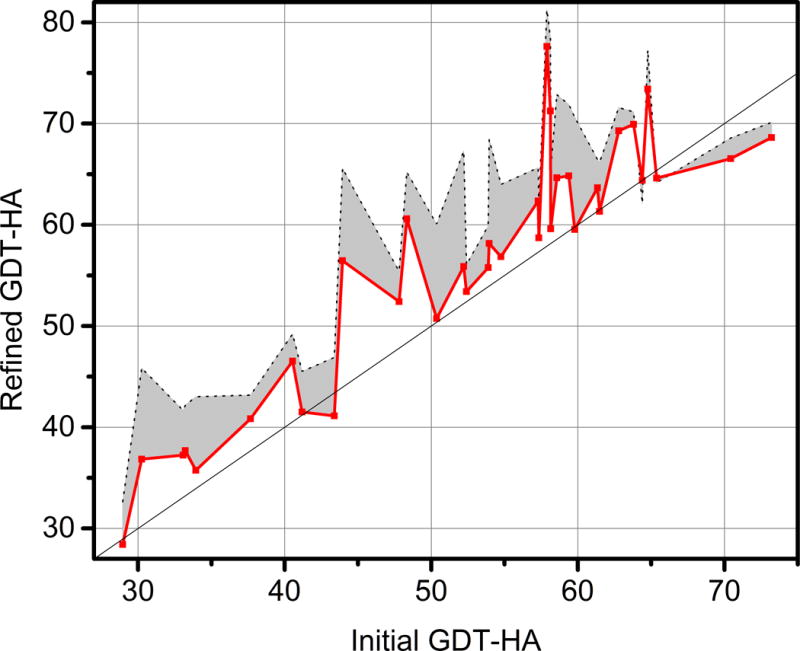
GDT-HA scores of model 1 submissions from the FEIG group (red) and best snapshots generated during sampling for each target (grey) vs. GDT-HA scores of initial models provided by CASP.

Refinement in terms of RMSD is less obvious with an average decrease of −0.13 Å for Ca atoms and with the largest reductions in RMSD only slightly better than 0.5 Å for our submitted models. And even if the best snapshots are considered, there is only one target (TR759) where the best structure is improved by more than 1 Å. Since the calculated RMSD may depend on how structures are superimposed, we also tried to superimpose only those Cα atoms that are involved in regular secondary structures (α-helices or β-sheets), but we did not find a significant difference in the resulting RMSD values. Figure 3 shows the improvement in RMSD vs. the RMSD of the initial model. Generally, RMSD improvements are greater when initial models are closer than 5 Å from the experimental structure. The limited improvement in the global RMSD score is easily understood as a direct consequence of our sampling protocol that employs weak overall restraints with respect to the initial model. On the other hand, given the more significant improvements in GDT scores, which focus only on the most accurate parts of a given model, it appears that our protocol may trade improvements in parts of a structure in exchange for making other parts worse. This will be discussed in the following section.

Figure 3.

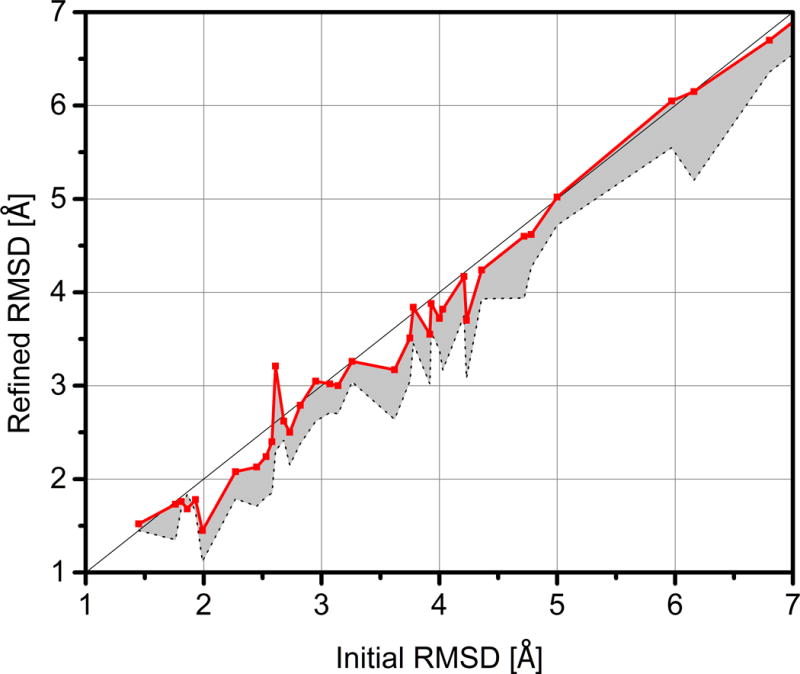
Cα RMSD values of model 1 submissions from the FEIG group (red) and best snapshots generated during sampling for each target (grey) vs. Cα RMSD values of initial models provided by CASP.

Which parts of a structure can be refined?

An important question is which parts of a given model were improved with our protocol. Figure 4 shows both successful and unsuccessful refinement in different parts of target TR759. Refinement was successful for residues 75 to 94 where the two helices were brought closer to the experimental structures by shifting/rotating the two helices. However, for residues 53 to 60, a long loop connecting to β sheet strands the initially very different structure could not be improved significantly towards the experimental structure. The use of restraints in our protocol prevented the large conformational change to reach the correct native structure while the more subtle rearrangements of the helices were possible within the restraint envelope. Therefore, it is clear that larger steps in refinement will require at least in part unrestrained sampling and that challenges with unrestrained sampling tending to at least initially move away from the native state will have to be overcome. One could argue that the refinement of the helices near the core of this structure is more relevant than the failure to improve the presumably more flexible loop. However, this question is difficult to address without having more detailed structural data from experiment, ideally from both NMR and crystallography, along with biochemical data that confirms which structural aspects are most important for function.

Figure 4.

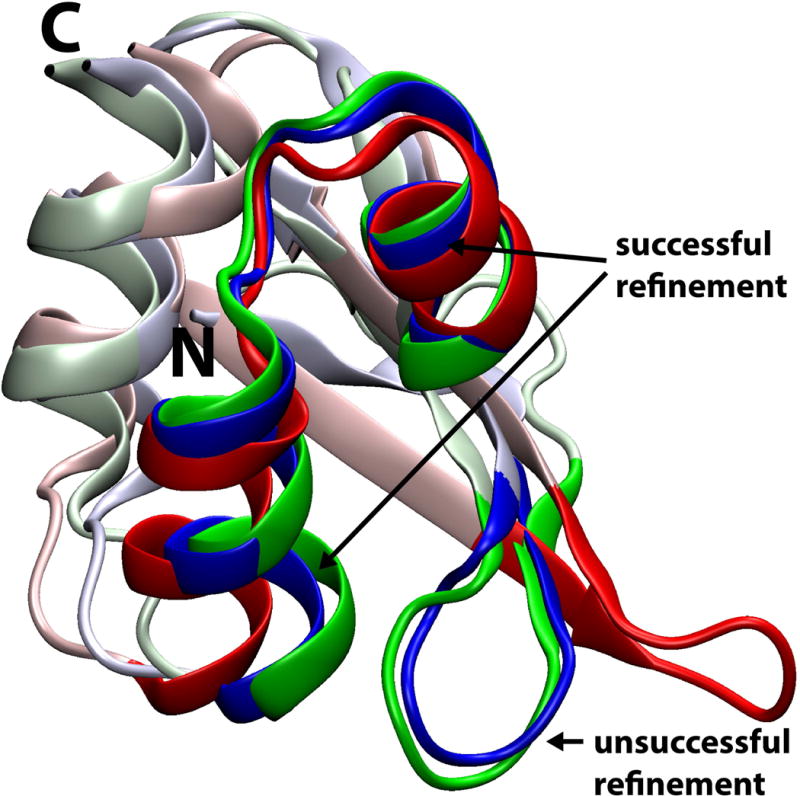
Successful and unsuccessful refinement in target TR759. The experimental reference is shown in red, the initial model provided by CASP in green, and the refined model submitted by us in blue. Residues 75–94 (successful refinement) and residues 53–60 (unsuccessful refinement) are highlighted with saturated colors.

Leaving the issue aside of whether refinement success differs for more and less important parts of a structure, we analyzed simply how refinement varies as a function of secondary structure and initial deviation according to residue-by-residue RMSD deviations. The results in Table II, averaged over all CASP11 targets, suggest that refinement of helical regions may indeed have been more successful than extended or coil regions, although the difference in the overall average is not dramatically different (−0.15 Å vs. −0.1 Å change in RMSD). It may be understandable that coil regions are more difficult to improve because of the large sampling space. On the other hand, elements of β sheets could be difficult to move if many hydrogen bonds would have to be broken and reconnected.

Table II.

Average RMSD change in Cα positions relative to the experimental reference in Å as a function of secondary structure and initial distance from the native. The secondary structure was determined using DSSP on the experimental reference structure. Initial and refined models were superimposed onto the experimental reference structures using only Cα atoms and per-residue RMSD values rmsd_i,initial and rmsd_i,refined were calculated for the Cα atom of each residue i. The differences Δrmsd_i = rmsd_i,refined – rmsd_i,initial were then averaged over all targets according to the secondary structure of residue i and according to the value of rmsd_i,initial.

	Helical	Extended	Coil
0–1 Å	0.113	0.079	0.350
1–2 Å	−0.156	−0.171	−0.073
2–3 Å	−0.269	−0.268	−0.177
3–4 Å	−0.260	−0.181	−0.348
4–5 Å	−0.200	−0.144	−0.395
>5 Å	−0.399	−0.091	−0.255
All	−0.148	−0.087	−0.101

The picture becomes more complicated when the analysis is broken down as a function of the initial model accuracy. Especially striking is that residues that are already within 1 Å are more likely to move away from the experimental structure than towards it while the opposite is true for residues further away than 1 Å. This appears to be especially true for residues in coil regions which are less restricted and therefore are likely to sample a larger conformational space within the refinement MD simulations. Structural deviations in parts of a model that are already very close to the experimental structure during MD simulations are not unexpected. Individual snapshots of a dynamic structure at finite temperature will always deviate from the ensemble average that is captured in the experiment. Force field inaccuracies and differences between the simulated system and the experimental crystals as mentioned above further aggravate the issue. This justifies the use of restraints during the MD simulations without which this effect would become dominant over refinement successes and motivates the averaging step employed in our refinement protocol.

We also analyzed refinement success as a function of amino acid type (see Table III). Overall, we noticed that only the Cα atoms of the sulfur-containing amino acids cysteine and methionine became worse on average pointing at possible force field issues. On the other hand, the largest improvements were seen for histidine, phenylalanine, proline, serine, and asparagine, but at the same time, essentially correct proline and histidine residues (with initial RMSD values of less than 1 Å) were also made worse to the largest extent by refinement. One explanation would be that more attention needs to be paid to cis-trans isomerization in proline and Nδ vs. Nε protonation in histidine.

Table III.

Average RMSD change in Cα positions relative to the experimental reference in Å as a function of amino acid type and initial distance from the native calculated in a similar way as Table II. The range 4–5 Å is not given separately because of insufficient statistics.

	Ala	Ile	Leu	Val	Gly	Pro	Cys	Met	Phe	Tyr	Trp	His	Ser	Thr	Asn	Gln	Asp	Glu	Arg	Lys
0–1 Å	0.16	0.10	0.13	0.10	0.23	0.52	0.14	0.10	0.09	0.21	0.28	0.49	0.28	0.13	0.15	0.31	0.29	0.13	0.10	0.20
1–2 Å	−0.18	−0.12	−0.20	−0.08	−0.05	−0.18	−0.04	−0.06	−0.20	−0.04	−0.05	−0.29	−0.21	−0.12	−0.06	−0.21	−0.03	−0.15	−0.18	−0.11
2–3 Å	−0.19	−0.38	−0.36	−0.28	−0.05	−0.23	−0.51	−0.09	−0.26	−0.28	−0.22	−0.26	−0.07	−0.27	−0.17	−0.17	−0.21	−0.21	−0.40	−0.20
3–4 Å	−0.32	−0.22	−0.21	−0.14	−0.39	−0.15	−0.61	−0.26	−0.26	−0.57	−0.16	−0.17	0.01	−0.45	−0.32	−0.39	−0.19	−0.37	−0.36	−0.40
>4 Å	−0.11	−0.36	−0.16	−0.31	−0.09	−0.43	0.21	0.12	−0.48	−0.31	−0.29	−0.52	−0.41	−0.11	−0.41	−0.30	−0.35	−0.29	−0.08	−0.33
All	−0.07	−0.36	−0.16	−0.31	−0.09	−0.43	0.21	0.12	−0.48	−0.31	−0.29	−0.52	−0.41	−0.11	−0.41	−0.30	−0.35	−0.29	−0.08	−0.33

This analysis may suggest that structural regions that are highly accurate in the initial model should be restrained more strongly than other regions. However, we tried such a protocol in CASP10 and found that weaker restraints applied to all residues actually result in better refinement. One reason for that may be that it is difficult to accurately guess without knowing the experimental structure which parts are likely already within 1 Å and that overconstraining residues further away that could be refined otherwise is overall less effective. Another reason may be that in order to refine incorrect parts while maintaining structural integrity may require minor adjustments of correct parts, at least on the time scale of the short refinement simulations, so that fixing presumably correct parts may prevent refinement elsewhere.

Does it matter where the models come from?

The initial models provided by CASP were chosen from top predictions in the regular prediction category. This resulted in models that were generated with a variety of methods (see Table IV). While it is not always clear what exactly was done, we attempted to roughly classify different methods into the following groups: ‘Modeller’, ‘Raptor’, ‘Zhang’ group, ‘Rosetta’, ‘Lee’ group, and ‘Other’. Using this classification we then examined whether the method used to generate the initial models affected the refinement results. The results are given in Table V. It can be seen that the average improvement in GDT-HA does indeed seem to depend on how the models were generated, with Modeller and Raptor models being improved only modestly while models from Lee and Other methods were improved most. However, the initial GDT-HA also varies greatly as different methods are optimal for different types of targets. Therefore, the most meaningful comparison is between methods with similar initial average GDT-HA scores. There are two such pairs. In comparing Modeller vs. Raptor models, Modeller models were more difficult to improve and in Zhang vs. Rosetta models, Zhang models were more difficult to improve. Although the differences are relatively small it may reflect different degrees of refinement that is already included in the respective prediction pipelines.

Table IV.

Predictor groups from which initial models for refinement targets were taken and likely method(s) that were used to generate the respective models.

Target	Group	Group Name	Method
TR217	156	Atome2_CBS	Modeller
TR228	73	SAM-T08-Server	Other
TR274	184	ROSETTA Server	Rosetta
TR280	184	ROSETTA Server	Rosetta
TR283	38	Nns	Lee
TR759	38	Nns	Lee
TR760	41	MULTICOM-NOVEL	Rosetta?
TR762	50	RaptorX	Raptor
TR765	499	QUARK	Zhang
TR768	50	RaptorX	Raptor
TR769	277	Zhang-Server	Zhang
TR772	50	RaptorX	Raptor
TR774	381	FALCON_MANUAL	Other
TR776	184	ROSETTA Server	Rosetta
TR780	499	QUARK	Zhang
TR782	184	ROSETTA Server	Rosetta
TR783	300	PhyreX	Modeller
TR786	184	ROSETTA Server	Rosetta
TR792	216	myprotein-me	Other (Rosetta/Zhang)
TR795	41	MULTICOM-NOVEL	Rosetta?
TR803	216	myprotein-me	Other (Rosetta/Zhang)
TR810	184	ROSETTA Server	Rosetta
TR811	216	myprotein-me	Other (Rosetta/Zhang)
TR816	277	Zhang-Server	Zhang
TR817	156	Atome2_CBS	Modeller
TR821	216	myprotein-me	Other (Rosetta/Zhang)
TR822	251	TASSER-VMT	Other
TR823	184	ROSETTA Server	Rosetta
TR827	38	Nns	Lee
TR828	277	Zhang-Server	Zhang
TR829	499	QUARK	Zhang
TR833	420	MULTICOM-CLUSTER	Rosetta?
TR837	499	QUARK	Zhang
TR848	184	ROSETTA Server	Rosetta
TR854	184	ROSETTA Server	Rosetta
TR856	277	Zhang-Server	Zhang
TR857	454	eThread	Other

Table V.

Average refinement success in terms of GDT-HA and Molprobity scores as a function of the method that was used to generate the initial models.

	Avg. Initial GDT-HA	Avg. ΔGDT-HA	Avg. Initial Molprobity	Avg. Refined Molprobity
Modeller	62.4	1.38	3.29	0.91
Raptor	62.2	1.67	1.63	0.84
Zhang	54.2	3.33	2.98	0.70
Rosetta	54.0	3.72	1.94	0.70
Lee	39.7	4.92	2.84	0.62
Other	46.1	5.12	2.79	0.87

Another point for comparison are MolProbity scores that measure local structural accuracy. There is a surprisingly wide range of initial scores with Modeller models for example having MolProbity scores that are twice those of Raptor despite similar initial GDT-HA values. However, after refinement and further optimization of MolProbity scores (see below) we did not find a strong trend in the final MolProbity scores as a function of how the initial models were generated.

Amount of sampling vs. refinement success

In CASP11 we used twice as much sampling per target (40 × 30 ns = 1.2 μs) compared to CASP 10 (30 × 20 ns = 600 ns). A key question is whether the increased sampling correlated with improved refinement. A direct comparison between CASP10 and CASP11 is problematic because of possible variations in the difficulty of the targets. Instead, we re-generated predictions for the CASP11 targets using varying subsets of the full trajectories. Figure 5 shows that the average GDT-HA improves with increasing sampling and the maximum improvement in the GDT-HA score is indeed observed for the maximum amount of sampling (1.2 μs). However, after a rapid initial increase, there is only slight improvement in GDT-HA from 200 ns to 1200 ns total sampling time. Increasing trajectory length leads to better refinement but the benefit levels off beyond 20 ns. On the other hand, using multiple trajectories vs. a single trajectory improves GDT-HA scores when five or ten trajectories are used, but there is little additional benefit of using more than ten trajectories. In general, it appears that given an amount of total sampling time that can be afforded, fewer longer trajectories are better than larger numbers of shorter simulations.

Figure 5.

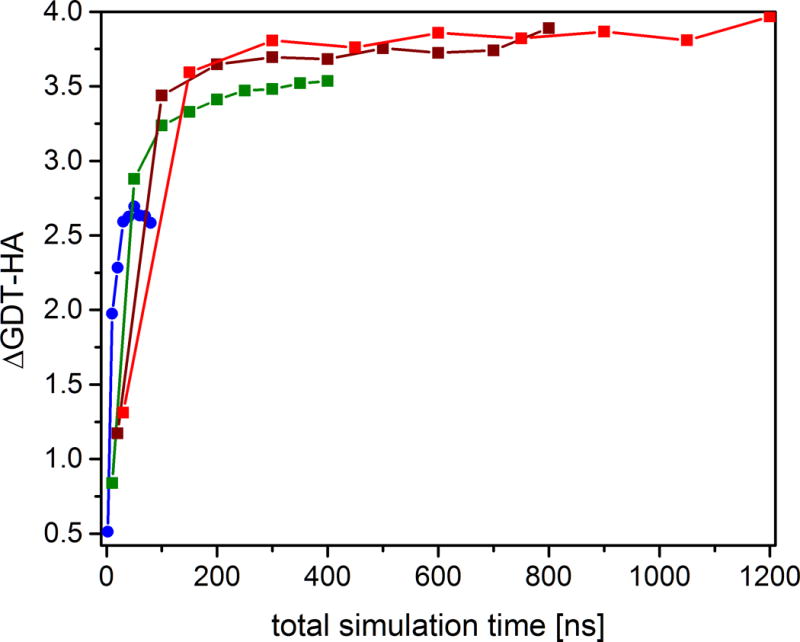
Average improvement of GDT-HA score for 35 CASP11 refinement targets as a function of total simulation time using snapshots from 1–40 trajectories over 2 ns (blue), 10 ns (green), 20 ns (brown), or 30 ns (red).

Based on the data in Figure 5, an optimal balance between computational cost and improvement in GDT scores is the use of 5 × 30 ns or 10 × 20 ns, less than the amount of sampling used in CASP10 (30 × 20 ns). Therefore, we have to conclude that using more and longer simulations in CASP11 vs. CASP10 offered just a small benefit at significant additional computational costs.

One possibility for why additional sampling seems to offer little additional benefit is that significant kinetic barriers prevent broader exploration of conformational space. The use of enhanced sampling methods could address such an issue. However, it is more likely that hundreds of nanoseconds may actually be sufficient to explore the majority of the restricted conformational space under the weak positional restraints that were applied here. In the latter case, weakening the restraints further may be necessary to reach more refined structures but this strategy is limited by an increased likelihood of sampling diverting to non-native states as restraints are reduced to near zero.

Finishing touches: generating models with low MolProbity scores

A key step in our refinement protocol is the averaging of an ensemble subset. The resulting structures are consistently closer to the native structure when measured base on backbone Cα positions, but the averaging compromises local bonding geometries, especially for parts that exhibit significant dynamics. As a result, the averaged models have very poor MolProbity scores. A short restrained MD simulation before submitting the refined structures greatly improved MolProbity scores with a minimal effect on GDT scores but the resulting average MolProbity scores of 1.88 indicate that there were still significant issues with the quality of the local structure. Specifically, we identified a number of problems that are not easily fixed with simple MD simulations: occasional cis-pepitde bonds for non-proline residues, ring penetrations where bonds cross tyrosine, phenylalanine, or tryptophan side chains, clashes involving poorly packed side chains that cannot move out of the way because of restraints on the backbone, and a large number of statistically unlikely bonds, angles, and backbone and sidechain torsion angles when compared to crystallographic data.

In order to address the above issues we devised a more extensive protocol that consisted of multiple minimization and MD steps in addition to targeted backbone and side chain rebuilding (see Figure 6 and Methods section). Furthermore, we used a modified force field to reduce the sampling of bonds, angles, and torsion angles away from typical values seen in crystallographic structures. This strategy results in models that are mostly below 1.0 with an average of 0.76 while still maintaining almost the same improvement in GDT-HA scores as without the aggressive refinement of MolProbity scores (see Table VI). Not using the modified force field still provided structures of significantly higher quality than the submitted models with an average score of 0.85. The computational cost of the protocol proposed here is on the order of tens of minutes using a single core and therefore it seems that probably most reasonable models could be readily transformed into stereochemically acceptable models.

Table VI.

Molprobity scores for initial models, for submitted model 1 structures, and after further optimization.

Target	Initial MolProbity	Model 1 MolProbity	Extra Min./MD w/c36	Extra Min./MD w/mod. c36	GDT-HA after final optimization
TR217	3.374	2.325	0.952	0.979	64.17
TR228	3.088	1.861	0.500	0.591	56.85
TR274	1.976	1.831	1.182	1.081	27.87
TR280	2.507	1.359	0.920	0.530	65.10
TR283	3.225	1.928	0.871	0.792	41.51
TR759	2.751	1.236	0.500	0.500	56.85
TR760	3.357	1.618	0.952	0.779	56.34
TR762	1.443	1.838	0.875	0.576	67.02
TR765	3.278	1.905	0.813	0.813	76.97
TR768	1.352	2.372	1.084	0.979	70.45
TR769	4.293	1.810	0.727	0.763	59.02
TR772	2.101	2.298	1.146	0.973	54.17
TR774	3.562	2.204	1.160	1.122	40.83
TR776	1.227	1.717	0.986	0.855	68.95
TR780	2.754	1.932	0.535	0.500	57.63
TR782	1.251	1.769	0.644	0.500	73.86
TR783	3.099	1.796	0.982	0.892	62.24
TR786	1.375	2.380	0.789	0.808	52.53
TR792	2.206	2.293	0.716	0.612	71.88
TR803	2.701	1.826	0.865	0.865	37.87
TR810	2.195	1.858	0.787	0.661	55.56
TR811	1.260	1.713	0.835	0.648	68.13
TR816	2.713	1.148	0.500	0.500	55.51
TR817	3.402	2.488	0.988	0.867	64.81
TR821	2.074	1.348	0.770	0.693	60.10
TR822	4.063	3.005	1.611	1.610	36.40
TR823	1.447	1.960	0.901	0.848	45.66
TR827	2.557	1.686	0.522	0.561	35.49
TR829	2.090	2.331	0.821	0.683	51.49
TR833	2.506	1.392	0.755	0.651	63.89
TR837	2.791	1.401	0.500	0.500	40.29
TR848	2.234	1.288	0.666	0.500	59.42
TR854	1.231	1.446	0.666	0.500	65.36
TR856	2.948	2.270	1.247	1.149	61.48
TR857	3.386	2.316	0.920	0.795	37.50
Average	2.509	1.884	0.848	0.762	56.09 Δ =3.69

Targeting lower MolProbity significantly increases the overall quality of predicted structures. However, not all structures fit exactly in the statistically prescribed norms what high-quality structures are expected to look like. Furthermore, there may be concerns that the structure quality norms are at least in part influenced by pre-conceived bond distances and angles and torsion angle distributions that are imposed by crystallography software during the structure determination process. As all-atom force fields continue to improve it will be interesting to see how exactly crystallographic structures compare with MD-generated ensemble averages and inform to what extent MD-generated structures may be preferable over structures with perfect MolProbity scores.

CONCLUSIONS

The prediction of protein structures at a level of accuracy that is truly comparable to experiment remains a formidable challenge. Results from our group in CASP11 described here suggest that the refinement of template-based models via physics-based molecular dynamics simulations maybe a route for reaching that goal. Our MD-based protocol allowed for consistent improvements of most targets to at least some degree while some targets were refined significantly by more than 10 GDT units. Most successful was the refinement of targets where initial structures had GDT-HA scores between 45 and 65. At the lower end, refinement was mixed, while all of the targets with GDT-HA scores above 65 were made worse. Refinement appeared to be somewhat more successful for residues in helical regions vs. extended or coil regions and we found small variations in refinement success as a function of how the initial models were generated. However, it is not entirely clear how to use such information to devise a more successful refinement protocol.

The performance of our method in CASP11 exceeded our CASP10 performance but overall the amount of refinement is still relatively modest. Increased sampling in CASP11 played only a limited role with additional contributions coming from protocol optimizations. Going forward this suggests that new algorithms are likely necessary to make more substantial progress.

While refinement success is primarily measured in terms of GDT or RMSD improvements, increasing attention has been paid to local structural accuracy as for example measured by the MolProbity score. While we did not pay special attention to this aspect during CASP11, we applied a more extensive protocol for improving MolProbity scores to our CASP11 predictions that resulted in average MolProbity scores well below one at relatively little computational expense. This suggests that refining models in terms of their local stereochemistry is not a key challenge.

The use of physics-based methods in protein structure refinement is highly encouraging because it is highly complementary to knowledge-based methods and should at least in principle allow the eventual routine refinement of protein structures to experimental accuracies. It will be exciting to see further success in moving in this direction in future rounds of CASP.